Abstract
Positional information describes pre-patterns of morphogenetic substances that alter spatio-temporal gene expression to instruct development of growth and form. A wealth of recent data indicate bioelectrical properties, such as the transmembrane potential (), are involved as instructive signals in the spatiotemporal regulation of morphogenesis. However, the mechanistic relationships between and molecular positional information are only beginning to be understood. Recent advances in computational modeling are assisting in the development of comprehensive frameworks for mechanistically understanding how endogenous bioelectricity can guide anatomy in a broad range of systems. represents an extraordinarily strong electric field (~1.0 × 106 V/m) active over the thin expanse of the plasma membrane, with the capacity to influence a variety of downstream molecular signaling cascades. Moreover, in multicellular networks, intercellular coupling facilitated by gap junction channels may induce directed, electrodiffusive transport of charged molecules between cells of the network to generate new positional information patterning possibilities and characteristics. Given the demonstrated role of in morphogenesis, here we review current understanding of how can integrate with molecular regulatory networks to control single cell state, and the unique properties bioelectricity adds to transport phenomena in gap junction-coupled cell networks to facilitate self-assembly of morphogen gradients and other patterns. Understanding how integrates with biochemical regulatory networks at the level of a single cell, and mechanisms through which shapes molecular positional information in multicellular networks, are essential for a deep understanding of body plan control in development, regeneration and disease.
1. Introduction
A deep understanding of morphogenesis is essential for the identification and application of strategies that will mitigate birth defects and restore damaged and diseased tissues, organs, and anatomy in humans. Since its inception by early embryologists (Wolpert, 1969, 2011), morphogenesis has been routinely approached in terms of positional information: the hypothesis that a pattern of a morphogenetic substance (i.e. regulator of gene expression) or property (i.e. mechanical stress) serves to differentially alter gene expression in a field of cells, ultimately acting as an instructive signal to induce properly proportioned tissues and anatomical forms. Allen Turing theoretically demonstrated that chemical positional information patterns can be generated by regulatory relationships between diffusing chemical morphogens (Turing, 1952), thereby introducing the reaction-diffusion mechanism of positional information control (Kuttler, 2011; Green and Sharpe, 2015; Meinhardt, 2008; Meinhardt and Gierer, 2000). A striking example of reaction-diffusion control of positional information in morphogenesis is the emergent periodic pattern of Sox9 expression, which has been found to underly the specification of digit versus interdigit cell fates in the developing limb bud, and to be controlled by a Turing network comprised of interacting BMP, Sox9 and Wnt (Raspopovic et al., 2014). The roles of both temporally stable spatial morphogen gradients (Jaeger et al., 2012; Jansen et al., 2007; Lander and Petersen, 2016; McCusker and Gardiner, 2013; Nachtrab et al., 2013; Phan et al., 2015; Matsuo and Kimura-Yoshida, 2014; Raspopovic et al., 2014; Anderson et al., 2012; Harris et al., 2005), as well as dynamic mechanisms involving genetic oscillators (Bajard et al., 2014; Cooke and Zeeman, 1976; Cotterell et al., 2015; Sheeba et al., 2014; Zhu et al., 2010; Ferjentsik et al., 2009; Portes et al., 2015; Shimojo et al., 2016; Tsiairis and Aulehla, 2016; Uriu and Morelli, 2014; Uriu, 2016), are becoming well-established mechanisms underpinning spatiotemporal control of genetic expression in morphogenesis.
A wealth of recent data indicate endogenous bioelectrical signals also play important functional roles in the spatiotemporal regulation of positional information in development, regeneration, and disease (Levin, 2014; Levin and Stevenson, 2012; McCaig et al., 2005; Nuccitelli, 2003; Borgens, 1982; Robinson and Messerli, 2003) (Fig. 1). Every living cell maintains an electrical potential energy difference across its plasma membrane, which represents an extraordinarily strong electric field (~1.0 × 106 V/m) active over the thin membrane (Wright, 2004) (Fig. 2). This transmembrane voltage difference () is ultimately generated and maintained by ATP-powered ion pumps such as the ubiquitous Na+,K+-ATPase enzyme, which use the chemical energy of ATP to move ions against transmembrane voltage and concentration gradients to generate both net charge density inside the cell (the origin of ) and electrochemical gradients of ions (Sachs, 1977; Noske et al., 2010; Brodie et al., 1987) (Fig. 2A and B). The electrochemical gradients generated by the Na+,K+-ATPase favor passive K+ movement out of cells (which increases the electro-negativity of , a change referred to as hyperpolarization) and passive movement of Na+ into cells, which decreases the electronegativity of and is called depolarization (Wright, 2004). The passive transmembrane fluxes of ions are controlled by proteinaceous transmembrane ion channels, which are typically selective to a specific ion type and therefore modulate in different ways (Fig. 2C and D). Feedbacks between and ion flux are generated as can alter the shape of transmembrane protein channels, thereby conferring voltage-sensitivity to their ion permeability (Pospischil et al., 2008). Ion channels can also be regulated chemically, which creates feedbacks between charged substances and a cell's state (Pietak and Levin, 2017). Importantly, while past experimentation with bioelectrical signaling required work with electrodes and applied fields, the more recent development of fluorescent, -sensitive reporter dyes (Adams and Levin, 2012a; Baker et al., 2005; Loew, 2010; Oviedo et al., 2008; Adams and Levin, 2012b), and the ability to genetically introduce/manipulate expression of ion pumps and channels – including the emerging technology of optogenetics (light-activated channels and pumps) (Adams et al., 2014; Jewhurst et al., 2014) — has greatly accelerated progress in understanding the many ways bioelectricity acts as an instructive signal in development and regeneration.
Fig. 1.
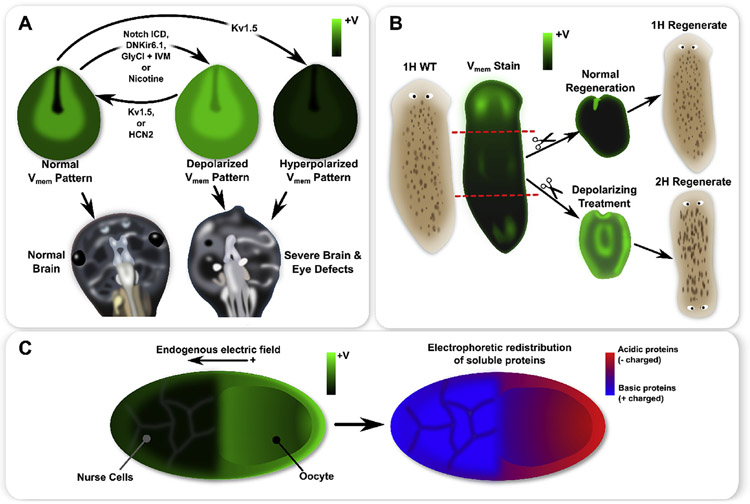
A schematic of functional patterns observed in frog and insect development, as well as planaria regeneration. Xenopus laevis neurula exhibit a characteristic pattern with strong hyperpolarization in cells of the closing neural tube and depolarization in the surrounding neural folds (A). Genetic mis-expression of specific ion channels or pharmacological treatments can flatten the endogenous pattern by creating a more uniform depolarization or hyperpolarization, where both induced severe brain and eye defects (A). Moreover, for depolarization treatments (e.g. Notch ICD or nicotine), expression of Kv1.5 or HCN2 restored the normal pattern and produced normal brain and eye development (A). In whole planaria flatworms (B), an anterior-posterior gradient of exists with significantly stronger depolarization at the anterior (B). During normal regeneration, a strong anterior depolarization appears, which is believed to be instructive for anterior-posterior axis polarity (B). Depolarizing a fragment during regeneration induces 2H outcomes in regenerates (B). In insect ovarian follicles, an endogenous gradient features an oocyte which is more depolarized than the nurse cells (C). Patterns of soluble acidic (negatively charged) and basic (positively charged) proteins may be correlated with the pattern in the ovarian follicle, with more acidic proteins found in the oocyte and more basic proteins found in the nurse cells, thereby supporting the hypothesis that small charged molecules travel by electrodiffusion across intercellular connections such as gap junctions (C).
Fig. 2.
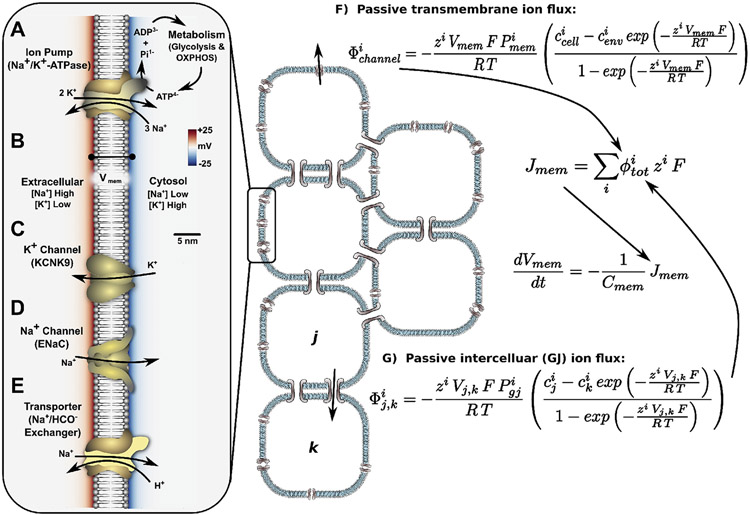
A summary of basic concepts underlying generation, modulation, and dynamics in a gap junction-coupled somatic cell network. Ion pumps such as the ubiquitous Na+,K+-ATPase (A) use chemical energy released in ATP hydrolysis to maintain concentration gradients of Na+ (low inside the cell) and K+ (high inside the cell) across the plasma membrane, and generate an electronegative (B). Ion channels (C, D) provide ion-specific pores in the membrane to allow ions to passively move down their electrochemical gradients, altering in the process by changing the net charge distribution across the membrane. The open/closed state of ion channels can be modulated by (voltage-sensitive channels) or chemicals (ligand-gated channels), which in combination with the altering effects of ion channels, introduces the possibility for positive and negative feedbacks to the bioelectrochemical system. Transporters, such as the Na+/HCO3− exchanger (E), utilize the potential energy of electrochemical gradients generated by ion pumps to perform a host of functions including maintenance of balanced pH, levels of glucose and metabolites; regulation of neurotransmitter signaling (e.g. monoamine reuptake transporters); and a host of other functions. Passive transmembrane ion flux for any channel can be described in terms of chemical and electrical gradients across the membrane (F), with a similar description for ion flux between two gap junction-coupled cells (G).
Bioelectricity acts, not only at the level of a single cell, but via intercellular interactions facilitated by gap junction channels, which enable exchange of electrical and chemical signals (Schilling et al., 2008; Rook et al., 1992; Revel et al., 1971; Giepmans, 2004; Cooper et al., 1989; Weber et al., 2004). Gap junctional communication has been identified as a key aspect in certain development and regeneration processes (Levin, 2007; Chernet et al., 2015; Chanson et al., 2005; Oviedo and Levin, 2007; Mathews and Levin, 2016; Levin and Mercola, 1998; 1999a; 1999b). When coupled together by gap junctions, the voltage differences in the cytosol of each cell (which is equivalent to the difference between the coupled cell membranes) creates a strong electric field (~1.0-50.0 × 104 V/m) across the gap junction channels (Fig. 2). This intercellular electrochemical coupling has been identified as a unique transport mechanism in gap junction-coupled cell networks (Cooper et al., 1989; Woodruff and Cole, 1997; Cole and Woodruff, 2000; Levin and Mercola, 1998; 1999a, 1999b; Pietak and Levin, 2017), which as we will examine in detail here, may augment reaction-diffusion patterning mechanisms by introducing bioelectrically modulated transport and feedbacks.
Analogous to chemical positional information, bioelectrical patterns comprised of differential values throughout cells of a tissue (Pai et al., 2015a, 2012a; Beane et al., 2011; Krüger and Bohrmann, 2015; Vandenberg et al., 2011), and patterns of endogenous current flow (and corresponding electric fields) in tissues and organisms (Altizer et al., 2001; Hotary and Robinson, 1994, 1992; Robinson, 1979,1983; Hotary and Robinson, 1991; Nuccitelli, 2003; Jaffe, 1981), have been experimentally observed during development and regeneration. Moreover, as targeted manipulations of these patterns can generate severe birth defects, this supports the concept that bioelectricity serves functional roles in morphogenic regulation (Hotary and Robinson, 1994; Altizer et al., 2001; Pai et al., 2015a, 2018) (Fig. 1). Pioneering work in this field has characterized the electrophysiological properties of Xenopus and chick embryos, including electrical potentials and endogenous currents associated with the blastopore and neural tube, demonstrating that manipulation of endogenous currents using microelectrodes was associated with severe developmental defects (Hotary and Robinson, 1991; 1994, 1992, 1990). Endogenous current flows in developing mouse and chick have also been implicated in normal limb development (Altizer et al., 2001).
The bioelectrical characteristics of Xenopus embryos were further studied using molecular techniques employing fluorescent reporter dyes to visualize gradients, alongside genetic mis-expression of ion channels, to visualize and alter bioelectric cell states in a targeted manner (Pai et al., 2015a, b; 2012a, b; Vandenberg et al., 2011). In Xenopus neurula, beginning at approximately stage 12, a characteristic hyperpolarization forms in cells lining the neural tube prior to closure (Pai et al., 2015a) (Fig. 1A). This characteristic pattern in the neurula has been found to be essential for proper brain and eye development (Pai et al., 2015a, 2012a). Genetic mis-expression of specific ion channels allowed for precise manipulation of cell to emphasize the instructive nature of the characteristic pattern. For example, the introduction of dominant-negative Kir6.1 channels (DNKir6.1), or the introduction of glycine gated chloride channels (GlyR, with ivermectin treatment to open the channels), were used as two very different manipulations to flatten (i.e. minimize the contrast of) the characteristic pattern by depolarization (Pai et al., 2015a) (Fig. 1A). Furthermore, the introduction of over-expressed Kv1.5 channels was used to flatten the contrast of the characteristic pattern by hyperpolarization (Pai et al., 2015a) (Fig. 1A). Both depolarization- and hyperpolarization-flattening of the characteristic pattern was found to induce severe brain and eye defects (Pai et al., 2015a) (Fig. 1A). Furthermore, induction of Notch overexpression (Notch ICE) was found to induce a depolarization-flattening of the pattern, along with brain and eye defects. Importantly, rescuing the characteristic pattern was achievable by introducing overexpression of Kv1.5 channels to a depolarization-flattened scenario (including by the genetic Notch ICE manipulation). Remarkably, restoring the bioelectric pattern significantly reduced the number and severity of brain and eye defects (Pai et al., 2015a). In later work, depolarization-disruption of the characteristic bioelectric pattern in the neurula was achieved by nicotine treatment, which acts via both activation of acetylcholine receptors and by directly blocking K+ channels to generate depolarization-flattening of the characteristic pattern of the neurula (Pai et al., 2018). Consistently, nicotine-treatment induced severe neural defects (Pai et al., 2018). The native pattern was rescued by homogeneous expression of HCN2 channels, and HCN2 expression also mitigated neural defects, further emphasizing that the pattern of the neurual is required for proper development. These results also provide insight into how teratogens such as nicotine may induce birth defects by altering bioelectric patterning (Pai et al., 2018).
Later Xenopus development is also associated with electrophysiological states (Hotary and Robinson, 1994), where patterns of hyperpolarization have been observed in association with the developing face, including hyperpolarization preceding the formation of mouth and eyes (Vandenberg et al., 2011). Craniofacial hyperpolarization patterns were found to be mediated by the V-ATPase H+ pump, which when inhibited, resulted in craniofacial defects (Vandenberg et al., 2011). In a variety of species, craniofacial defects are also induced by Kir2.1 channel inhibition (Adams et al., 2016) (a chanelopathy known as Anderson-Tawil syndrome in humans), in a mechanism that may involve regulation of BMP-related signaling (Dahal et al., 2017, 2012). In Xenopus eye developmental stage 22, spots of hyperpolarization develop, which were found to precede eye induction and the expression of genes controlling the eye placode (e.g. Pax6) (Pai et al., 2012a). Manipulation of the characteristic patterns via channel mis-expression was found to generate ectopic eyes, including in regions such as the lateral mesoderm, which lays outside of the nervous system, and in which genetic manipulations such as Pax6 are unable to induce ectopic eyes (Pai et al., 2012a).
In planarian flatworms (Dugesia japonica), a characteristic pattern exists with depolarization at the anterior, and in the form an anteior-posterior gradient of (Beane et al., 2011; Durant et al., 2017) (Fig. 1B). Manipulation of this characteristic gradient using pharmacological treatments targeting ion channels and pumps during regeneration was found to alter regeneration outcomes, with depolarization being associated with two-headed (2H) regenerates (Fig. 1B), and hyperpolarization inducing loss of head regeneration (0H) (Beane et al., 2011). Moreover, depolarization of planaria fragments during regeneration appears to persist in regenerates, and is associated with persistent 2H regeneration long after the depolarizing pharmaceutical has been washed out of the tissue (Durant et al., 2017). Furthermore, manipulation of bioelectrical patterns by targeting the H+,K+-ATPase ion pump (which has been found to be depolarizing in planaria) were found to alter regenerated head shape (Beane et al., 2013; Emmons-Bell et al., 2015). Additionally, brief exposures to gap junction blockers such as octanol and heptanol during regeneration are able to induce a variety of multi-headed regeneration outcomes (Oviedo et al., 2010; Oviedo and Levin, 2007), as well as to alter regenerated head shape (Emmons-Bell et al., 2015).
Bioelectrical positional information patterns may also play an instructive role in the early development of insects. In ovarian follicles of fruitfly (Drosophila melanogaster), cecropia moth (Hyalophora cecropia), and luna moth (Actias luna), a characteristic pattern has been observed where the oocyte is depolarized with respect to the nurse cells (Jaffe and Woodruff, 1979; Woodruff and Cole, 1997; Cole and Woodruff, 2000; Krüger and Bohrmann, 2015) (Fig. 1C). Paralleling patterns appearing in the development of other model organisms (described above), the pattern of the ovarian follicle may be mediated by heterogeneous expression of H+ pumps (V-ATPase), which are concentrated in the nurse cell population (Bohrmann and Braun, 1999; Krüger and Bohrmann, 2015) . Evidence suggests that the endogenous pattern of the ovarian follicle generates a strong electric field across intercellular connections between cells, leading to electrophoretic movement of charged molecules, and the appearance of emergent concentration gradients (Telfer et al., 1981; Woodruff and Cole, 1997; Woodruff and Telfer, 1980; Cole and Woodruff, 2000). For example, soluble acidic (negatively charged) and basic (positively charged) proteins show correlation with the pattern in the ovarian follicle, with more acidic proteins found in the oocyte and more basic proteins found in the nurse cells (Telfer et al., 1981; Woodruff and Cole, 1997; Woodruff and Telfer, 1980; Cole and Woodruff, 2000) (Fig. 1C).
Given the demonstrated roles of in morphogenesis, it is apparent that a deep understanding of biological pattern formation in development, regeneration, and disease requires a solid comprehension of how bioelectrical signals such as integrate with molecular signaling networks to control single cell state, and what unique properties bioelectricity adds to transport phenomena in gap junction-coupled cell networks to provide coordination and order at the organ level.
2. Bioelectricity from a molecular perspective
and ion concentrations exist in inexorably interdependent relationships as is generated by the concentration of ions inside and out of the cell, while ionic transmembrane mass fluxes are in turn both influenced by , and alter state as they change concentrations. This interdependent relationship is important as it represents a primary functional link between and molecular signaling. In order to facilitate study of bioelectrical signaling in development and regeneration, while preserving the interdependent relationships between and molecular signaling, the BioElectrical Tissue Simulation Engine (BETSE) software platform has been developed (Pietak and Levin, 2016; 2017). In contrast and complement to more commonly used equivalent circuit descriptions of bioelectricity (Cervera et al., 2014, 2015; 2016a, 2016b; Pospischil et al., 2008; Chay and Keizer, 1983; Maciunas et al., 2016), BETSE utilizes a molecular perspective of bioelectric phenomena, which maintains the important relationship between cell and ion concentrations (Pietak and Levin, 2017; 2016). Maintaining this relationship between and concentrations is important for the longer time scales over which somatic bioelectricity operates in development and regeneration (minutes to days), where , ion pumps and transporters have the opportunity to generate significant changes in the electrochemical potentials of ions (as implicated by the example simulation of Fig. 3). BETSE software is open source and freely available from: https://gitlab.com/betse/betse
Fig. 3.
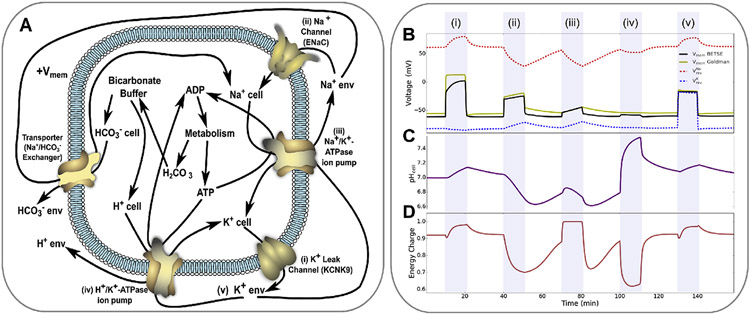
Bioelectricity encompasses several interrelated phenomena, including ; ion channel, pump and transporter dynamics; and instructive correlations between downstream signaling regimes including pH and metabolism. This bioelectrical example simulation of Na+,K+-ATPase pumps, H+,K+-ATPase pumps, K+ and Na+ leak channels, and a Na/HCO3− transporter, with bicarbonate buffer and metabolic production equations, is detailed in (A), and was simulated in BETSE. The simulation explored a series of 10 min interventions, each separated by 20 min, including: blocking K+ leak channels (i), opening Na+ leak channels (ii), blocking Na+,K+-ATPase pumps (iii), activating H+,K+-ATPase pumps (iv), and increasing extracellular K+ levels (v). , intracellular pH, and energy charge of the cell are shown in B, C and D, respectively. Blocking K+ leak channels depolarizes , and leads to an increase in both cytosolic pH and the energy charge of the cell (i). Opening Na+ leak channels also depolarizes , but leads to significant drops in cell pH and energy charge (ii). Blocking the Na+,K+-ATPase pump leads to slight depolarization and significant increases in cell pH and energy charge (iii). Activating an H+,K+-ATPase has minimal effect on , but significantly increases cell pH and decreases energy charge (iv). Increasing extracellular K+ depolarizes (v). Note that the molecular perspective of bioelectricity provides an accurate estimation of ( BETSE and Goldman series of B), while managing interventions that alter ion reversal potentials (B).
ultimately arises from net surface charge density of ions across the plasma membrane, which behaves like a capacitor (Fig. 2), where mathematical details are outlined in the Appendix. Ion concentrations and net charge density inside the cell change as ion pumps/transporters, ion channels, and gap junctions contribute components of transmembrane mass flux of an ion. Active fluxes of ion pumps and transporters can be described using chemical thermodynamics principles, where the activity of the pump or transporter is considered to be a reaction occurring across the membrane (as described in Pietak and Levin (2017)). Passive outward transmembrane ion flux through ion channels depends on the electrochemical gradient of the ion across the membrane and the permeability of the channel to the ion and can be described using the GHK-flux equation (Pietak and Levin, 2017; 2016). Dynamic voltage or chemical gating of ion channels can be simulated by modulating the channel's permeability to ions using Hill equations to describe concentration-dependent regulation by a gating ligand (as described further in Pietak and Levin (2017) and the Appendix), or full Hodgkin-Huxley differential equation formalism fit to experimentally-derived data curves (see Ranjan et al. (2011)).
In addition to transmembrane mass fluxes, some ionic molecules participate in chemical reactions (e.g. HCO3−, H+, and ATP4−), leading to changing cell concentrations. Moreover, molecular substances can regulate gene expression and other processes, which can be described using activator and inhibitor expressions based on Hill equations (Karlebach and Shamir, 2008; Pietak and Levin, 2017). Chemical reactions representing a mass conversion of network substances into other network substances can be incorporated in BETSE by using rate equations based on fundamental chemical concepts, as described in detail in Pietak and Levin (2017). Furthermore, production/decay relationships involving various regulatory relationships can also be defined in BETSE, thereby facilitating the construction of bioelectricity-integrated gene and reaction networks (Pietak and Levin, 2017).
The change in concentration of a substance in time can be described as the net movement of the substance's flux across the membrane, where total flux takes into account all sources of ion flux in the system (see Appendix for details). Thus, a description of can be approached from a perspective that maintains focus on the molecular origins of and endogenous currents, in contrast to the more commonly used equivalent circuit model of bioelectricity (Cervera et al., 2016a, b; 2015; 2014; Pospischil et al., 2008).
It is worthwhile to emphasize the similarities and differences between the molecular and equivalent circuit perspectives of bioelectricity. The equivalent circuit model of bioelectricity treats the cell membrane as a capacitor and resistor in parallel, and updates dynamically in terms of transmembrane currents, which in contrast to the molecular perspective defined above, are assumed to be driven by voltage sources specific to each ion (reversal potentials) in proportion to membrane ion conductances for an ion in a linearized description based on Ohm's law (Cervera et al., 2015, 2016b, 2016a, 2014). The equivalent circuit model of bioelectricity assumes ion concentrations inside and outside of the cell, and therefore the reversal potentials, to remain constant (see Appendix for details).
While the equivalent circuit formulation is an accurate and computationally lightweight method to determine dynamics, especially for excitable cell systems that change over the course of milliseconds, allowing for dynamic updates to ion concentrations presents several advantages. A primary advantage of the molecular perspective is that it does not rely on fixed reversal potentials for ions. By evaluating dynamic changes in intra- and extra-cellular ion concentrations, which occur as a consequence of ion pump, transporter, channel, and gap junction channel activity, the molecular perspective used in BETSE can predict the potentially significant effects that these dynamic concentration changes will have on (Fig. 3). As a simple example, it is well established that increasing extracellular K+ concentrations leads to depolarization (Avendano et al., 1990; Boatright et al., 1989); the dynamics of this phenomenon (which, from the equivalent circuit perspective occurs because of a change in the reversal potential of K+ ions) are naturally accounted for by the molecular bioelectricity model (Fig. 3 B, v). Moreover, by keeping track of concentrations, the more complex activity of ion pumps and transporters — many of which have been found to be important in development and regeneration pattering control (Adams et al., 2006; Adams, 2006; Aw et al., 2008; Beane et al., 2011; Bohrmann and Braun, 1999; Levin et al., 2002; Vandenberg et al., 2011) — can be accounted for in terms of both changes and interrelated pH and other molecular changes arising from pump/transporter flux (Fig. 3 B, C, D). Finally, the expected dynamics with channel activity are still accurately and robustly calculated by the molecular perspective of bioelectricity, which in steady-state shows close correspondence with predictions of the Goldman Equation (Fig. 3) (Pietak and Levin, 2016) .
In summary, by estimating spatiotemporal changes to ion concentrations in relation to , and by describing in terms of the resulting mass fluxes of ion concentration, the molecular perspective of bioelectricity closely integrates bioelectrical states with cell biochemistry. This is especially important for bioelectrical activity in development and regeneration patterning processes, which may involve long time scales (minutes to hours) over which and ion concentrations (and therefore reversal potentials for ions) are subject to change.
3. Bioelectricity: a key control system of the cell
3.1. Interdependent relationships between Vmem and molecular signaling cascades
Bioelectric phenomena encompass a complex set of interrelated phenomena, including the electrical potential energy gradient represented by ; ion channel, pump and transporter dynamics; and instructive correlations between downstream signaling regimes including pH, metabolism, calcium and neurotransmitter signaling. A deep understanding of the dynamics of bioelectrical control systems and their relationships with molecular signaling cascades at the level of a single cell is a necessary first step to begin comprehending pattern formation in multicellular tissues (Pietak and Levin, 2017).
To demonstrate the interrelations between and other downstream factors, an example of a (relatively simple) bioelectrical system with links to pH and metabolism is detailed in Fig. 3. This example bioelectrical system was simulated in BETSE, and examined the effect of a series of ion channel and pump manipulations on , intracellular pH, and the metabolic state of the cell as represented by the energy charge, (Atkinson and Walton, 1967) (Fig. 3, i, through iv). The example simulation includes an active Na+,K+-ATPase pump, an inactive H+,K+-ATPase pump, an open K+ leak channel such as KCNK9 (Talley and Bayliss, 2002; Talley et al., 2003)), a closed Na+ leak channel such as ENaC (Chifflet and Hernandez, 2016; Bhalla and Hallows, 2008)), and the ions Na+, K+, Cl−, H+, HCO3−, as well as the substances ATP and ADP (assumed for this example to be uncharged), and dissolved CO2 as H2CO3. A chemical reaction describing the reversible bicarbonate buffer was also included, where:
| (1) |
The bicarbonate buffer was handled in the simulation using the chemical reaction formalism detailed elsewhere (Pietak and Levin, 2017) .
Additionally, an extremely simple reaction describing metabolism was included, which was assumed to be an irreversible reaction with:
| (2) |
The energy charge of the cell (, representative of the cell's metabolic status) was calculated according to (Atkinson and Walton, 1967):
| (3) |
Where AMP concentrations were estimated assuming activity of the adenylate cyclase enzyme, where (Özer and Scheit, 1978):
| (4) |
The simulation examined the effects of blocking K+ leak channels (Fig. 3 i), opening Na+ leak channels (Fig. 3 ii), blocking Na+,K+-ATPase pumps (Fig. 3 iii), activating H+,K+-ATPase pumps (Fig. 3 iv), and increasing extracellular K+ levels (Fig. 3 v), each as 10 min interventions, separated by 20 min. The effects on , pH and are shown in Fig. 3 B through D. Each intervention alters, not only (Fig. 3 B), but through the inexorable links between and ion concentrations, multiple factors are altered including the reversal potentials for K+ and Na+ (Fig. 3 B), pH in the cell (Fig. 3 C), and the energy charge (metabolic status) of the cell (Fig. 3 D). Note that all interventions show expected behavior (as can be deduced by inspection of the relationships in Fig. 3 A): blocking K+ leak channels (which is known to occur under hypoxic conditions as these channels are oxygen-sensitive (Talley et al., 2003; Patel and Honore, 2001; Tang et al., 2004)) depolarizes , and is also indicated to increase both cytosolic pH and the energy charge of the cell — both favourable changes for a cell responding to hypoxia. These downstream effects on pH and would alleviate metabolic stress induced by hypoxia, and occur as the Na+,K+-ATPase pump does not work as hard due to lack of K+ efflux from the cell, and consequentially consumes less ATP, leading to lower metabolic load. In contrast, opening Na+ leak channels (such as ENaC) also depolarizes , but leads to significant drops in cell pH and energy charge, as increased cytosolic Na+ is stimulating to the H+,K+-ATPase pump, and leads to increased ATP consumption and increased metabolic rate (Pellerin and Magistretti, 1996). Consistently, blocking the Na+,K+-ATPase pump leads to slight depolarization and significant increases in cell pH and energy charge as the pump is not consuming ATP (Fig. 3 iii). Activating an H+,K+-ATPase pump has a minimal effect on due to the electroneutral nature of the pump, but significantly increases cell pH via proton efflux, while decreasing energy charge due to increased ATP hydrolysis to run the pump (Fig. 3 iv). Finally, increasing extracellular K+ minimizes the electrochemical gradient supporting passive K+ efflux from K+ leak channels, leading to depolarization of ; this is a well known mechanism to depolarize cells (Avendano et al., 1990; Boatright et al., 1989) and has similar effects to blocking K+ leak channels ((Avendano et al., 1990; Boatright et al., 1989) v). This relatively simple bioelectrical system simulation illustrates the interrelations between bioelectric phenomena and other molecular systems of the cell, including pH and metabolism, where Ca2+ and neurotransmitter signaling are other important downstream targets of bioelectrical signaling (Pietak and Levin, 2017).
3.2. Vmem as a functionally-integrated transducer in a multitude of molecular signaling systems
; the bioelectric toolkit of transmembrane channels, pumps, transporters; and downstream secondary messenger cascades confer an exceptional degree of control over individual cell states. Two key benefits of bioelectrical signaling are rapid changes ( can change on the order of 1.0 ms), and the robustness of bioelectric signaling, as dynamics are associated with steady and cyclic attractors which maintain reproducibility and stability in bioelectrical signaling (Pietak and Levin, 2016). The stability of makes it well-suited as a control parameter or “master regulator” for downstream cell signaling and states (Pietak and Levin, 2016). Basic factors such as ion pump type and rate, membrane permeability profiles, and extracellular concentration profiles ultimately establish a stable attractor state of (the “resting” ), to which the system robustly returns after perturbation (Pietak and Levin, 2016; Taylor, 2010) (for the example simulation in Fig. 3, the resting is −60 mV, to which consistently returns after each perturbation). For this reason, is a suitable control parameter, not only for excitable cells of the brain, heart, skeletal muscle, and smooth muscle like the intestinal system, but also for emerging roles in development and regeneration.
At the level of a single cell, bioelectricity represents a robust complex dynamic system where can be seen as both a sensor of various signals and as an actuator of downstream changes to molecular signaling cascades and gene expression. is able to interface with molecular signaling through a variety of mechanisms. At the simplest level, controls transmembrane flux of ions via ion channels, but also via voltage sensitive transporters such as the divalent metal transporter DMT1 (Mackenzie et al., 2006; Skjørringe et al., 2015), the organic cation transporter OCT3 (Kekuda et al., 1998), and the dopamine transporter DAT (Torres et al., 2003; Lin et al., 2011). By altering steady-state concentration of substances inside cells, the state of signaling regulatory networks can be set in relation to the state of a cell (Pietak and Levin, 2017).
As a sensor, allows a cell to rapidly sense and respond to external and internal stimuli such as metabolic state (e.g. via depolarizing ATP-sensitive K+ channels used to sense metabolic state in the pancreas and induce insulin secretion (Bertram et al., 2010; Fridlyand et al., 2010)), oxygenation (via oxygen-sensitive K+ leak channels that depolarize with hypoxia (Patel and Honore, 2001; Tang et al., 2004)), extracellular pH (e.g. via H+ sensitive K+ leak channels that depolarize under acidic conditions (Ma et al., 2012)), osmotic and mechanical pressure (e.g. via transient receptor potential ion channels that depolarize with pressure/cell stretching (Liedtke et al., 2000; Martinac, 2004; Rosenbaum and Simon, 2007; Sachs, 2010)), light (via light-sensitive ion channels such as rhodopsin, which depolarize with light intensity), temperature (via transient receptor ion channels that depolarize with hot or cold temperature), and injury (e.g. via ATP release and extracellular-ATP gated ion channels such as P2X, which depolarize with elevated extracellular ATP released from wounded cells (Block and Klarlund, 2008; Vliet and Bove, 2011)).
As an actuator, can directly regulate the level of cytosolic Ca2+ (e.g. via an extensive variety of -sensitive Ca2+ channels), extracellular levels of neurotransmitters (e.g. via Vmem-sensitive reuptake transporters such as OCT3, SERT, and DAT, which alter or even reverse the direction of tranmembrane flux of neurotransmitters), regulate levels of reversible epigenetic markings (e.g. by altering the transmembrane flux of endogenous histone deacetylase (HDAC) inhibitor molecules, such as pyruvate and butyrate, via -sensitive sodium monocarboxylate transporter SMCT1 (Thangaraju et al., 2009a, 2009b; Miyauchi et al., 2004, 2006) ), and bioelectrical signals can be transduced to mechanical ones (e.g. via proteins such as Prestin which convert voltage changes into mechanical force at the membrane (Zhang et al., 2007)). By coupling channel state to other signaling proteins in the membrane, can also activate sophisticated downstream pathways such as cell proliferation (Sundelacruz et al., 2008, 2009).
Thus, as a robust parameter and signal transducer with a multitude of means to influence and interrelate with molecular signaling pathways and networks, has a clear place as a node in molecular signaling networks, and evidence indicates integration of is required for a deep understanding of molecular signaling cascades. For this reason, the Bioelectricity-Integrated Gene and Reaction (BIGR) network concept has been introduced and developed, and can be studied using BETSE software (Pietak and Levin, 2017).
Feedback relationships between molecular signaling and states confer additional functionality to ’s role in a regulatory network, allowing for properties such as bistability (state switching), homeostasis (goal seeking), and oscillation (timing; cell clocks) (Pietak and Levin, 2017; Cervera et al., 2014, 2016a; Law and Levin, 2015). Importantly, as is tightly integrated with molecular signaling, this means -mediated cell state switches, homeostats, and oscillators may be functionally-integrated with gene expression (Pietak and Levin, 2017).
Understanding aspects of the bioelectrical control system at the level of a single cell is important, but in order to develop a deeper understanding of bioelectrical control of positional information the next step is to understand how might and its functionally-integrated relationships can be implemented in multicellular collectives to drive long-range order.
4. Electrodiffusion-based patterning mechanisms in gap junction-coupled somatic cell networks
In a network comprised of gap junction-coupled somatic cells with different values, gap junctions may play instrumental roles in patterning by both modulating values of the cell collective, and by enabling directed transport of charged substances.
By producing currents between cells, the state of gap junction-coupled cells can be highly modulated in proportion to gap junction state. Using a feedback loop between and gene expression, simulations have shown that the gap junction modulation of can alter cell fate in multicellular domains in proportion to gap junction conductivity (Cervera et al., 2016b).
Gap junctions may also facilitate directed electrodiffusive transport between coupled cells with different states. Electric fields exert mechanical forces on charged matter, and are defined in relation to a voltage gradient; therefore, a difference between two gap junction-coupled cell membranes represents an electric force field between the cytoplasm of both cells with the ability to draw charged substances across the gap junction channel in relation to the transjunctional field (see Appendix for details).
Charged and gap junction permeable (<1 kDa in size) substances that are important in cell signaling cascades include spermine3+ (and other polyamines) (Desforges et al., 2013; Hamon et al., 2016; Watanabe et al., 2012), Ca2+(Schumacher et al., 2012; Jørgensen et al., 1997; Haughey and Mattson, 2003), ATP4−(Kanaporis et al., 2011), IP33−(Leybaert and Sanderson, 2012; Balaji et al., 2017), and serotonin+(Esser et al., 2006), among others (Weber et al., 2004; Veenstra et al., 1995; Beblo and Veenstra, 1997; Beblo et al., 1995; Veenstra, 1996), including short RNAin− (Valiunas et al., 2005).
4.1. Gating-electrodiffusion: a bioelectrically-mediated patterning mechanism
A variety of charged, gap junction permeable, molecular substances may travel by electrodiffusion in gradients between cells, while also regulating ion channel state, thereby establishing spatial feedbacks, which if self-reinforcing, produce correlated spatial patterns of and gating ion concentration (Pietak and Levin, 2017). Charged and gap junction permeable substances that also regulate ion channel state include polyamines such as spermine3+, which block K+ channels and voltage-gated Na+ and Ca2+ channels (Cino and Formenti, 2008; Fleidervish et al., 2008; Haghighi and Cooper, 1998; Huang and Moczydlowski, 2001; Kurata et al., 2006; Makary et al., 2005; Yan et al., 2005); intracellular Ca2+, which gates calcium-sensitive K+ and Cl− channels (Hallworth et al., 2003; Perez-Cornejo and Arreola, 2004; Boton et al., 1989; Gomez-Hernandez et al., 1997; Isoldi et al., 2004); cAMP1− which regulates K+ and Cl− channels (Anderson and Welsh, 1991; Berrera et al., 2006; Blumenthal and Kaczmarek, 1992; Bolton et al., 2006; Do et al., 2004); and ATP4−, which regulates the state of K+ channels (Ashcroft, 2005; Aw et al., 2010; Dzeja and Terzic, 1998; Sim et al., 2002). The electrodiffusive movement of molecules between cells in gradients creates organism-wide correlations between and potentially important signaling molecules, with self-reinforcing feedbacks demonstrating capacity to produce a range of pattern types, some of which are reminiscent of the spots and stripes of Turing patterns (Pietak and Levin, 2017) (Fig. 4). The potential for self-reinforcing spatial feedbacks in a system of gap junction-coupled cells represents a new bioelectrically-controlled, “gating-electrodiffusion” patterning mechanism, which may serve as an alternative patterning strategy to standard reaction-diffusion systems.
Fig. 4.
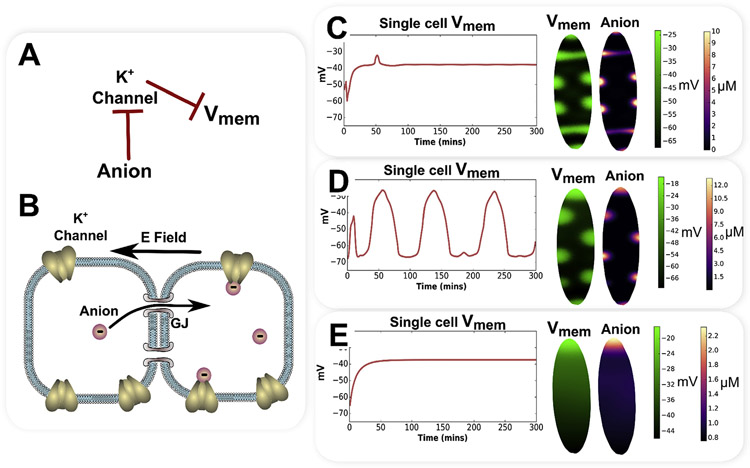
Bioelectrically-mediated gating-electrodiffusion mechanisms can generate a variety of categorically different patterns. A simple gating-electrodiffusion mechanism involving a gap junction permeable anion that inhibits a K+ leak channel, leading to self-reinforcing spatial feedback, is shown as a regulatory network in (A) and schematically in (B). By varying parameters for channel gating and anion charge, categorically different patterns of and correlated anion concentration patterns are indicated (C through E). With anion charge of and channel Hill gating constants of and , a stable patterns of stripes and spots are generated (C). With anion charge of and channel Hill gating constants of and , with a fixed small gradient of along the long axis of the elliptical model, a spatiotemporal pattern of traveling depolarization spots and correlated anion concentration are indicated (D). With anion charge of and channel Hill gating constants of and , emergent, smooth, stable gradients form (E).
An example of the categorically different patterns that can be generated by a simple gating-electrodiffusion mechanism is presented in Fig. 4. A single gap junction permeable anion inhibits a K+ leak channel, leading to a self-reinforcing spatial feedback through the gap junction-coupled cell network as the anion is drawn into cells with the most depolarization, and results in more depolarization as it inhibits K+ leak channels (Fig. 4 A). The appendix supplies mathematical details of this simple gating-electrodiffusion model involving a single K+ leak channel inhibited by an anionic, gap junction permeable gating ligand.
A variety of different multicellular patterns, and correlated anion concentrations, are predicted results from simulations with differences in channel gating properties and anion charge (Fig. 4C-E), and reflect similar results to those previously exhibited (Pietak and Levin, 2017). A low anion charge of , with K+ leak channel Hill gating constants of and (see Appendix for details) produces smooth, stable and anion concentration gradients (Fig. 4E). In contrast, increasing anion charge to , with steeper Hill gating constants for the K+ leak channel of and produces a stable stripe and spot pattern, reminiscent of Turing patterns from reaction-diffusion mechanisms (Fig. 4C). An anion charge of and channel Hill gating constants of and , with a fixed small gradient of along the long axis of the elliptical model, produces a spatiotemporal pattern consisting of depolarization spots and correlated anion concentration that persistently travel along the long axis of the elliptical model (Fig. 4D).
4.2. Gating-electrodiffusion and scale-free morphogen gradients
The planarian flatworm is routinely used as a model organism to study regeneration, on account of its remarkable ability to regenerate (Lobo et al., 2012; Sanchez Alvarado and Newmark, 1998; Sanchez Alvarado, 2007; Sater, 2011; Gentile et al., 2011; Durant et al., 2016). Following cutting, each fragment regenerates with the anatomical polarity of the original worm, including the reformation of a brain and eye-spots (Fig. 5A).
Fig. 5.
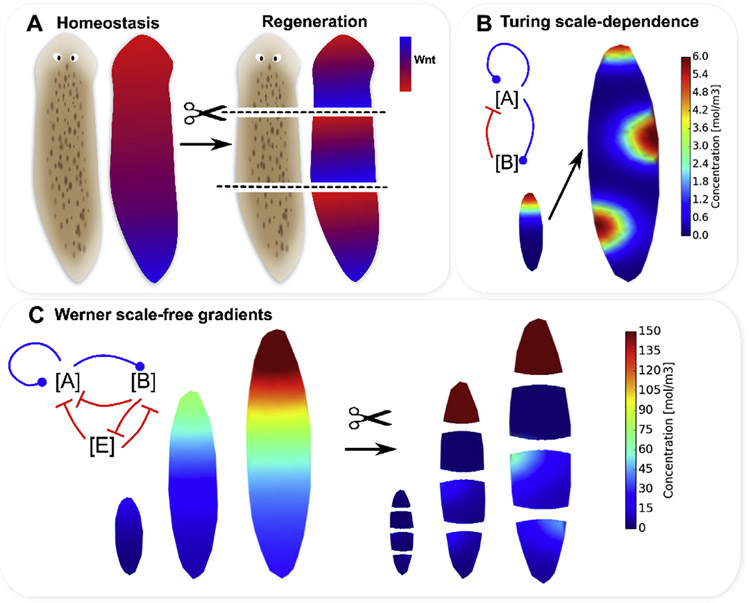
The experimentally-observed, emergent, scale-free morphogen gradients of Notum, Wnt and ERK observed in planaria homeostasis and regeneration, are difficult to describe using standard reaction-diffusion mechanism due to their dependence on system size. In homeostasis, planaria show gradients with high Wnt1 at the posterior (A), and high Notum at the anterior. Cutting across the anterior-posterior axis leads to reformation of gradients of Wnt1, Notum and ERK which have the original anterior-posterior polarity in each cut fragment (A). Reaction-diffusion mechanisms can describe emergent gradients, but are limited by their dependence on system size, which leads to fundamentally different patterns as the size of the tissue is increased (B). An elegant reaction-diffusion scheme introduced by Werner et al. (2015) produces stable, emergent gradients for various system sizes, but with the limitations of strong dependence of absolute concentration magnitude on system size and imperfect gradients in 2D for shapes that are imperfect long ellipses, which arise naturally with cutting (C).
Positional information is known to play a role in body plan control in planaria regeneration, where gene product gradients are well known to exist in both homeostasis and regenerating fragments (Adell et al., 2010; Almuedo-Castillo et al., 2012) (Fig. 5A). Both whole planaria in homeostasis, and a planarian fragment ~15 h after amputation, exhibit stronger Wnt1, Wnt11, and -Catenin expression at the posterior (Owlarn and Bartscherer, 2016), and conversely, enhanced Notum (Owlarn and Bartscherer, 2016; Petersen and Reddien, 2011) and ERK (Agata et al., 2014) signaling at the anterior. Furthermore, Wnt1 was found to be primarily expressed at the posterior edges of wounds (and Notum at the anterior edges) (Petersen and Reddien, 2011) (Fig. 5A). Gradients in ERK signaling are known to be formed as canonical Wnt/-Catenin signaling inhibits ERK (Agata et al., 2014), and therefore head induction.
While canonical Wnt/-Catenin positional information gradients are strongly implied in inhibiting regeneration of head at anterior-facing wounds (Gurley et al., 2008; Owlarn and Bartscherer, 2016), it is difficult to account for the development of two profoundly different concentration levels on either side of a single bisection using traditional reaction-diffusion mechanisms (Fig. 5). This is primarily because the patterning outcomes of reaction-diffusion mechanisms are strongly dependent on system size, such that a model with a particular form and parameters will exhibit profoundly different patterns depending on the system size (Werner et al., 2015). For instance, using an adaption of a well-known Turing mechanism involving the concentration of two substances, and , where is an activator of expression which is active over a short spatial range, and is a long-range acting inhibitor of expression (see Appendix for mathematical details), a gradient may develop on a small model, but the pattern changes to spots when the tissue size is increased by a factor of three (Fig. 5B and (Werner et al., 2015)). Therefore, while several reaction-diffusion models have been developed to account for the formation of morphogen gradients in planaria (Lobo and Levin, 2015; Stückemann et al., 2017; Meinhardt, 2009; Scimone et al., 2016), these models should be tested for their dependence on size scale, and their ability to regenerate polar gradients in a range of variable sizes.
To address the scale-dependence of classical reaction-diffusion models, Werner et al. have developed an elegant scale-free reaction-diffusion model capable of emergent gradient formation and reformation in a one-dimensional system (Fig. 5C and (Werner et al., 2015)). The model of Werner et al. (2015) involves the dynamics of three morphogens: a short-range activator , a long-range inhibitor , and an “extender” substance which enhances degradation of both [A] and [B] to create a self-scaling gradient system (see Appendix for details and the original material reported by Werner et al. (2015)). Using the Werner model we have found that while the model works well in 1D, in 2D the scale-free reaction-diffusion model produces non-realistic gradients in cut fragments (Fig. 5C). Additionally, while the model does produce emergent gradients in long ellipses of all size scales we investigated, the absolute magnitudes of concentrations in the gradients are highly dependent on the size of the model, which presents difficulties for downstream biological signaling where consistent concentration magnitudes are required (Fig. 5C).
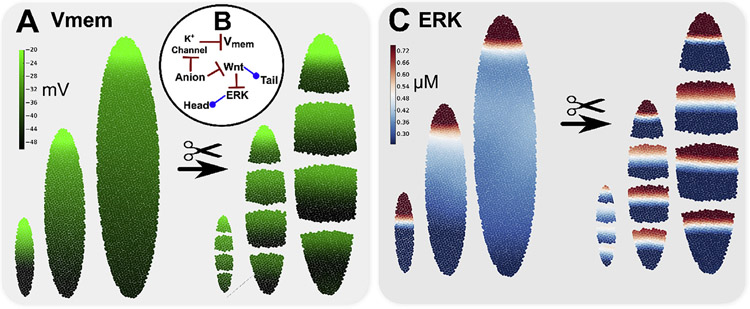
In contrast, gradients produced by a gating-electrodiffusion mechanism are stable, virtually independent of size scale, and reach similar steady-state values that are ideal for gene regulation (Fig. 6) (Pietak and Levin, 2017). Using the same gating-electrodiffusion mechanism described in Section 4.1 and the Appendix (a single gap junction permeable anion that engages in self-reinforcing spatial feedback by inhibiting K+ leak channels), a smooth, stable gradient of and anion concentration was generated with a fixed small gradient of (~10 mV) along the long axis of the elliptical mode, anion charge of and with K+ leak channel Hill gating constants of and (see Appendix for mathematical details). Emergent gradients produced on three different model sizes spontaneously arise with gradient polarity and absolute magnitudes that are virtually independent of model size (Fig. 6A). In this example toy model of planaria regeneration, the electrodiffusing anion also inhibited canonical Wnt signaling, which may occur through such mechanisms as ATP4− inhibition of canonical Wnt signaling via the chromatin remodeling and transcription factor CHD8 (Nishiyama et al., 2012; Thompson et al., 2008). Consistent with known RNAi experiments, in the model, canonical Wnt/-Catenin inhibited ERK signaling (Agata et al., 2014) to define opposing Wnt and ERK signaling gradients consistent with head and tail anatomical domains in both whole worms of diverse size and multiple cut fragments of diverse size, with the simulated ERK gradient shown in Fig. 6 C. Note that the concept of a large, negatively charged substance that electrodiffuses in the extracellular region was first proposed by Lange and Steel (Lange and Steele, 1978; Steele and Lange, 1977).
Fig. 6.
Gradients produced by a gating-electrodiffusion mechanism are stable, essentially independent of size scale, and reach similar steady-state values which are ideal for gene regulation. Emergent gradients produced on three different model sizes (A) spontaneously arise for a regulatory system involving a gap junction permeable anion, which inhibits a K+ leak channel to generate a self-reinforcing spatial feedback (B). The electrodiffusing anion also inhibited canonical Wnt signaling (e.g. via ATP4− inhibition of Wnt signaling through CHD8 (Thompson et al., 2008; Nishiyama et al., 2012)). Canonical Wnt/-Cat signaling then inhibited ERK signaling to define both Wnt and ERK signaling gradients (C) consistent with head and tail anatomical domains in both whole worms of diverse size and multiple cut fragments.
4.3. Evidence for electrodiffusive gap junction transport
Electrophoretic transfer of small molecules between gap junction-connected cells with variable between the cells has been hypothesized to underly establishment of left-right asymmetry in Xenopus, where a difference between blastomeres (established by heterogeneously localized V-ATPase pumps) has been proposed to lead to electrophoretic movement of serotonin+ (5HT+) in the intercellular gradient (Levin and Mercola, 1998; 1999a, 1999b; Levin, 2003; Levin et al., 2006). Similarly, in insect ovarian follicles (fruitfly, cecropia moth and luna moth), electrophoretic movement of charged ions and molecules has been identified as a significant patterning mechanism for a network of cells coupled by intercellular channels, where patterns of soluble acidic (negatively charged) and basic (positively charged) proteins are correlated with the pattern in the ovarian follicle (Telfer et al., 1981; Woodruff and Cole, 1997; Woodruff and Telfer, 1980; Jaffe and Woodruff, 1979; Cole and Woodruff, 2000) (Fig. 1C). Using the patch clamp technique to maintain a difference between two gap junction-connected cells, electrophoretic transfer of charged fluorescent dyes such as Lucifer Yellow (z = 2−) has been demonstrated (Kanaporis et al., 2011). Additionally, the application of external electric fields has been shown to induce an electric field in the cytoplasm of gap junction-coupled cells, which was found to reorganize charged, gap junction permeable molecules consistent with the internal electric field polarity (Cooper et al., 1989). However, while there is solid evidence that gap junctions enable diffusive transport of molecules between coupled cells (Guthrie et al., 1988; Olesen et al., 2012; Hanani, 2012; Burke et al., 2014; Bahima et al., 2006; Levin and Mercola, 1999a, b), and that gap junctions are able to propagate electrical signals (via depolarization activation of NaV channels) and calcium waves (via intercellular diffusion of IP3) (Balaji et al., 2017; Boitano et al., 1992), evidence that charged molecules move electrodiffusively in intercellular gradients, to spontaneously form concentration gradients in relation to , requires further assessment (Bohrmann and Gutzeit, 1987; Landesman et al., 2000). A simple experiment involving microinjection of gap junction permeable (but plasma membrane impermeable) dyes (such as Lucifer Yellow) into one-cell Xenopus embryos, with visualization of both the charged gap junction tracer dye and a reporter dye (Adams and Levin, 2012b) at the 8 and 16 cell stages, would help support the plausibility of significant electrodiffusive transport in gap junction-connected cells. A non gap-junction permeable dye would also be injected at the one-cell stage as a control. A supportive result from the test experiment would show anionic dyes concentrating in the most depolarized cell of the embryo (and depleted from the most hyperpolarized), and cationic cells concentrating in the most hyperpolarized cell (and depleted from the most depolarized).
5. Conclusions
The interplay between electrical and chemical signaling represents a versatile and powerful system for coordinating cell activity toward long-range order. Unsurprisingly, evolution discovered how to exploit these dynamics for morphogenesis from the single cell (Jaffe et al., 1974) to whole organism (Sullivan et al., 2016) levels. Recent conceptual and computational advances indicate a variety of ways that bioelectrical properties such as can act as instructive signals in positional information control during morphogenesis and regeneration. Indeed, such biophysical systems are an ideal way to amplify individual cell processes, such as symmetry breaking, toward the remarkable large-scale pattern homeostasis observed in regulative development and regeneration (Levin, 2006). Additionally, while electrophoretic transport through gap junctions may be a key mediator of bioelectrical signaling, recent works have shown that morphogen gradients are shaped by other forms of unique morphogen transport, such as specialized cell protrusions called cytonemes (Kornberg and Roy, 2014; Kornberg, 2017; Fairchild and Barna, 2014; Sanders et al., 2013). Further work will investigate how bioelectrical forces and electrophysiological properties may influence these unique forms of intercellular communication. The next steps in the exciting emerging field of developmental bioelectricity involve developing quantitative, biorealistic, fully-spatialized models of morphogenesis and pattern regulation that combine genetic, bioelectrics, and physical forces. The recent development of theoretical models incorporating bioelectricity (Cervera et al., 2016a, 2015; Pietak and Levin, 2017; 2016) facilitate the application of these ideas towards the understanding of the origins of multicellularity, the evolution of body-plans, human channelopathies that manifest as birth defects (Levin, 2014, 2012a; 2012b), and increased control over growth and form for synthetic morphology (Doursat and Sánchez, 2014).
Acknowledgements
The authors express gratitude to Joshua Finkelstein of the Allen Discover Center at Tufts University, and other members of the Levin Lab for their very helpful advice and commentary during the construction of this manuscript. Sincere thanks to Cecil Curry for his extensive assistance with BETSE software development.
Funding
This work was supported by an Allen Discovery Center award from The Paul G. Allen Frontiers Group (12171). The authors gratefully acknowledge support from the National Institutes of Health (AR055993, AR061988), the G. Harold and Leila Y. Mathers Charitable Foundation (TFU141), National Science Foundation award # CBET-0939511, the W. M. KECK Foundation (5903), and the Templeton World Charity Foundation (TWCF0089/AB55).
Appendix
Mathematical details of bioelectricity from a molecular perspective
can be described as a capacitor that holds a surface charge, (Fig. 2):
| (5) |
Where is the surface charge (in units C/m2), and is the patch capacitance of the membrane (~ 0.01 F/m2 (Liang et al., 2017) ).
In turn, can be expressed as the sum of ion concentrations inside the cell multiplied by their charge , Faraday's constant (F = 96,845 F/mol), and the ratio of cell volume to cell surface area :
| (6) |
Note that net charge in the cell exists in condensed layers at the membrane interior and exterior due to electrical charge screening considerations in the conductive electrolyte, which leave the bulk electrolyte with zero net charge (Bazant et al., 2004; Philpott and Glosli, 1995).
Ion concentrations and net charge density inside the cell change as ion pumps/transporters , ion channels , and gap junctions contribute components of transmembrane mass flux of an ion :
| (7) |
Active fluxes of ion pumps and transporters can be described using chemical thermodynamics principles, where the activity of the pump or transporter is considered to be a reaction occurring across the membrane (as described in Pietak and Levin (2017)).
Passive outward transmembrane ion flux of an ion via an ion channel depend on the electrochemical gradient of the ion across the membrane and the permeability of the channel to the ion and can be described using the GHK-flux equation (Pietak and Levin, 2017; 2016):
| (8) |
Dynamic voltage or chemical gating of ion channels can be simulated by modulating using Hill equations to describe concentration-dependent regulation by a gating ligand (as described further in Pietak and Levin (2017)), or full Hodgkin-Huxley differential equation formalism fit to experimentally-derived data curves (see Ranjan et al. (2011)).
Note that in the limit of zero or zero charge , the GHK-flux equation reduces to that of Fick's First Law, as expected:
| (9) |
The total ionic current density across the membrane can be described in terms of the sum of total transmembrane mass flux for all ions:
| (10) |
And provides an alternative method to update :
| (11) |
The change in concentration of a substance in time can be described as the divergence of the total flux , where total flux takes into account all sources of ion flux in the system, and and represent possible production and decay constants from chemical reactions and regulatory relationships with other substances (Pietak and Levin, 2017):
| (12) |
Mathematical basics of the equivalent circuit perspective of bioelectricity
The equivalent circuit model of bioelectricity treats the cell membrane as a capacitor in parallel with a resistance with zero net current across the membrane, and updates dynamically in terms of transmembrane currents, which in contrast to the molecular perspective defined above, are assumed to be driven by voltage sources specific to each ion (reversal potentials, ) in proportion to membrane ion conductances for an ion in a linearized description based on Ohm's law (Cervera et al., 2015, 2016b, 2016a, 2014). For an isolated cell:
| (13) |
Reversal potentials for each ion are calculated using the Nernst Equation:
| (14) |
Mathematical details of electrodiffusion-based patterning mechanisms in gap junction-coupled somatic cell networks
A difference between two gap junction-coupled cell membranes represents an electric force field between the cytoplasm of both cells with the ability to draw charged substances across the gap junction channel in relation to the transjunctional field , which has an approximate magnitude:
| (15) |
Here and are the transmembrane potentials of cells and , and is the length of the gap junction channel, which is approximately 15 nm (Weber et al., 2004). Thus, a difference of merely 1 mV between two gap junction-connected membranes produces a strong electric field magnitude of .
The GHK-flux equation can be used to estimate trans-junctional mass flux of ion across gap junctions coupling membranes of cells and in a cell network, with positive flux moving from cell to cell (Fig. 2G):
| (16) |
Where and represent the concentration of ion in cells and of the cell network, and the transjunctional potential, is defined in terms of the difference between the two gap junction-coupled cells:
| (17) |
Mathematical details of gating electrodiffusion
The flux through a K+ leak channel can be described by:
| (18) |
Where the anion concentration modulates the permeability of the K+ leak channel according to the Hill function:
| (19) |
The flux of the anion through gap junctions connecting cells and is defined as:
| (20) |
Here represents the effective permeability of the anion through gap junctions, and is the anion's charge. Note the concentration of the anion is on the order of , which is too low to significantly affect as it moves through the gap junction-coupled network. The anion was also subject to electroneutral production and decay with and . The initial concentration of the anion was zero in all cells.
Mathematical details of reaction-diffusion morphogen gradient models
A well-known Turing mechanism involves the concentration of two interacting substances, and , which change in time according to (Werner et al., 2015):
| (21) |
With , , , , , , and , a gradient may develop on a small model using Eqn (21), but the pattern changes to spots when the tissue size is increased by a factor of three (Fig. 5B).
To address the scale-dependence of classical reaction-diffusion models, Werner et al. have developed an elegant scale-free reaction-diffusion model capable of emergent gradient formation and reformation in a one-dimensional system (Werner et al., 2015) (Fig. 5C), and which involves the dynamics of three morphogens, , , and :
| (22) |
for which a viable parameter set is: , , , , , , , , , and .
Footnotes
Appendix A. Supplementary data
Supplementary data related to this article can be found at https://doi.org/10.1016/j.pbiomolbio.2018.03.008.
References
- Adams DS, 2006. Early, H+-V-ATPase-Dependent proton flux is necessary for consistent left-right patterning of non-mammalian vertebrates. Development. V 133 (9), 1657–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams DS, Levin M, 2012a. General principles for measuring resting membrane potential and ion concentration using fluorescent bioelectricity reporters. Cold Spring Harbor Protocols. IV 2012, 4 pdb.top067710–pdb.top067710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams DS, Levin M, 2012b. Measuring resting membrane potential using the fluorescent voltage reporters DiBAC4(3) and CC2-DMPE. Cold Spring Harbor protocols 2012 (4), 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams DS, Masi A, Levin M, 2006. Xenopus tadpole tail regeneration requires the activity of the proton pump V-ATPase, and proton pumping is sufficient to partially rescue the loss-of-function phenotype. Dev. Biol 295 a76. 355–356. [Google Scholar]
- Adams DS, Lemire JM, Kramer RH, Levin M, 2014. Optogenetics in developmental biology: using light to control ion flux-dependent signals in Xenopus embryos. Int. J. Dev. Biol 58, 851–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams DS, Uzel SG, Akagi J, Wlodkowic D, Andreeva V, Yelick PC, Devitt-Lee A, Pare JF, Levin M, 2016. Bioelectric signalling via potassium channels: a mechanism for craniofacial dysmorphogenesis in KCNJ2-associated andersentawil syndrome. J Physiol 594 (12), 3245–3270 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adell T, Cebria F, Salo E, 2010. Gradients in planarian regeneration and homeostasis. Cold Spring Harbor Perspectives in Biology. I 2 (1) a000505–a000505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agata Kiyokazu, Tasaki Junichi, Nakajima Elizabeth, Umesono Yoshihiko, 2014. Recent identification of an ERK signal gradient governing planarian regeneration. Zoology. VI 117 (3), 161–162. [DOI] [PubMed] [Google Scholar]
- Almuedo-Castillo Maria, Sureda-Gómez Miquel, Adell Teresa, 2012. Wnt signaling in planarians: new answers to old questions. Int. J. Dev. Biol 56, 1–2-3. 53–65. [DOI] [PubMed] [Google Scholar]
- Altizer Alicia M., Moriarty Loren J., Bell Sheila M., Schreiner Claire M., Scott William J., Borgens Richard B., 2001. Endogenous electric current is associated with normal development of the vertebrate limb. Dev. Dynam 221 (4), 391–401. [DOI] [PubMed] [Google Scholar]
- Anderson MP, Welsh MJ, 1991. Calcium and cAMP activate different chloride channels in the apical membrane of normal and cystic fibrosis epithelia. Proc. Natl. Acad. Sci. U.S.A VII 88 (14), 6003–6007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson Eve, Peluso Silvia, Lettice Laura A., Hill Robert E., 2012. Human limb abnormalities caused by disruption of hedgehog signaling. Trends in Genetics. VIII 28 (8), 364–373. [DOI] [PubMed] [Google Scholar]
- Ashcroft FM, 2005. ATP-sensitive potassium channelopathies: focus on insulin secretion. Journal of Clinical Investigation. VIII 115 (8), 2047–2058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson Daniel E., Walton Gordon M., 1967. Adenosine triphosphate conservation in metabolic regulation rat liver citrate cleavage enzyme. J. Biol. Chem X 242 (13), 3239–3241. [PubMed] [Google Scholar]
- Avendano Gary, Butler Bonnie Johnson, Michael Iuvone P., 1990. K+-Evoked depolarization induces serotonin N-Acetyltransferase activity in photoreceptor-enriched retinal cell cultures. Involvement of calcium influx through l-type channels. Neurochem. Int I 17 (1), 117–126. [DOI] [PubMed] [Google Scholar]
- Aw S, Adams DS, Qiu D, Levin M, 2008. H,K-ATPase protein localization and Kir4.1 function reveal concordance of three axes during early determination of left-right asymmetry. Mech. Dev 125, 353–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aw Sherry, Koster Joseph C., Pearson Wade, Nichols Colin G., Shi Nian-Qing, Carneiro Katia, Levin Michael, 2010. The ATP-sensitive K+-Channel (KATP) controls early left–right patterning in Xenopus and chick embryos. Dev. Biol X 346 (1), 39–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajard Lola, Morelli Luis G., Ares Saúl, Pécréaux Jacques, Jülicher Frank, Oates Andrew C., 2014. Wnt-regulated dynamics of positional information in zebrafish somitogenesis. Development. III 141 (6), 1381–1391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker Bradley J., Kosmidis Efstratios K., Vucinic Dejan, Falk Chun X., Cohen Lawrence B., Djurisic Maja, Zecevic Dejan, 2005. Imaging brain activity with voltage- and calcium-sensitive dyes. Cellular and Molecular Neurobiology. IV 25 (2), 245–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balaji Ramya, Bielmeier Christina, Harz Hartmann, Bates Jack, Stadler Cornelia, Hildebrand Alexander, Classen Anne-Kathrin, 2017. Calcium spikes, waves and oscillations in a large, patterned epithelial tissue. Sci Rep. II 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahima Laia, Aleu Jordi, Elias Marc, Martín-Satué Mireia, Muhaisen Ashraf, Blasi Joan, Marsal Jordi, Solsona Carles, 2006. Endogenous hemichannels play a role in the release of ATP from Xenopus oocytes. J. Cell. Physiol I 206 (1), 95–102. [DOI] [PubMed] [Google Scholar]
- Bazant Martin Z., Thornton Katsuyo, Ajdari Armand, 2004. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E VIII 70 (2), 021506. [DOI] [PubMed] [Google Scholar]
- Beane Wendy Scott, Morokuma Junji, Adams Dany Spencer, Levin Michael, 2011. A chemical genetics approach reveals H,K-ATPase-Mediated membrane voltage is required for planarian head regeneration. Chem Biol. I 18 (1), 77–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beane WS, Morokuma J, Lemire JM, Levin M, 2013. Bioelectric signaling regulates head and organ size during planarian regeneration. Development. I 140 (2), 313–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beblo Dolores A., Veenstra Richard D., 1997. Monovalent cation permeation through the Connexin40 gap junction channel. J Gen Physiol. IV 109 (4), 509–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beblo Dolores A., Wang Hong-Zhan, Beyer Eric C., Westphale Eileen M., Veenstra Richard D., 1995. Unique conductance, gating, and selective permeability properties of gap junction channels formed by Connexin40. Circ. Res X 77 (4), 813–822. [DOI] [PubMed] [Google Scholar]
- Berrera Marco, Pantano Sergio, Carloni Paolo, 2006. cAMP modulation of the cytoplasmic domain in the HCN2 channel investigated by molecular simulations. Biophys. J V 90 (10), 3428–3433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram Richard, Sherman Arthur, Satin Leslie S., 2010. Electrical bursting, calcium oscillations, and synchronization of pancreatic islets. Adv. Exp. Med. Biol 654, 261–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhalla Vivek, Hallows Kenneth R., 2008. Mechanisms of ENaC regulation and clinical implications. JASN (J. Am. Soc. Nephrol.) I 19 (10), 1845–1854. [DOI] [PubMed] [Google Scholar]
- Block Ethan R., Klarlund Jes K., 2008. Wounding sheets of epithelial cells activates the epidermal growth factor receptor through distinct short- and long-range mechanisms. Mol Biol Cell. XI 19 (11), 4909–4917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blumenthal EM, Kaczmarek LK, 1992. Modulation by cAMP of a slowly activating potassium channel expressed in Xenopus oocytes.J. Neurosci I 12 (1), 290–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boatright Jeffrey H., Hoel Martha J., Michael Iuvone P., 1989. Stimulation of endogenous dopamine release and metabolism in Amphibian retina by light- and K+-Evoked depolarization. Brain Research. III 482 (1), 164–168. [DOI] [PubMed] [Google Scholar]
- Bohrmann Johannes, Braun Barbara, 1999. Na, K-ATPase and V-ATPase in ovarian follicles of Drosophila Melanogaster. Biology of the Cell. III 91 (2), 85–98. [DOI] [PubMed] [Google Scholar]
- Bohrmann J, Gutzeit H, 1987. Evidence against electrophoresis as the principal mode of protein transport in vitellogenic ovarian follicles of Drosophila. Development. X 101 (2), 279–288. [DOI] [PubMed] [Google Scholar]
- Boitano Scott, Dirksen Ellen R., Sanderson Michael J., 1992. Intercellular Propagation of Calcium Waves Mediated by Inositol Trisphosphate. X. [DOI] [PubMed] [Google Scholar]
- Bolton Sally, Greenwood Kirsty, Hamilton Nicola, Butt Arthur M., 2006. Regulation of the astrocyte resting membrane potential by cyclic AMP and protein kinase a. Glia. IX 54 (4), 316–328. [DOI] [PubMed] [Google Scholar]
- Borgens RB, 1982. What is the role of naturally produced electric current in vertebrate regeneration and healing. Int. Rev. Cytol 76, 245–298. [DOI] [PubMed] [Google Scholar]
- Boton R, Dascal N, Gillo B, Lass Y, 1989. Two calcium-activated chloride conductances in Xenopus Laevis oocytes permeabilized with the ionophore A23187. The Journal of physiology 408, 511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodie C, Bak A, Shainberg A, Sampson SR, 1987. Role of Na-K ATPase in regulation of resting membrane potential of cultured rat skeletal myotubes. J. Cell. Physiol II 130 (2), 191–198. [DOI] [PubMed] [Google Scholar]
- Burke Shoshana, Nagajyothi Fnu, Thi Mia M., Hanani Menachem, Scherer Philipp E., Tanowitz Herbert B., Spray David C., 2014. Adipocytes in both Brown and white adipose tissue of adult mice are functionally connected via gap junctions: implications for chagas disease. Microbes Infect. XI 16 (11), 893–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cervera Javier, Alcaraz Antonio, Mafe Salvador, 2014. Membrane potential bistability in nonexcitable cells as described by inward and outward voltage-gated ion channels. J. Phys. Chem. B X 118 (43), 12444–12450. [DOI] [PubMed] [Google Scholar]
- Cervera Javier, Manzanares Jose Antonio, Mafe Salvador, 2015. Electrical coupling in ensembles of nonexcitable cells: modeling the spatial map of single cell potentials. The Journal of Physical Chemistry B. II 119 (7), 2968–2978. [DOI] [PubMed] [Google Scholar]
- Cervera Javier, Alcaraz Antonio, Mafe Salvador, 2016a. Bioelectrical signals and ion channels in the modeling of multicellular patterns and cancer biophysics. Scientific Reports. II 6, 20403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cervera Javier, Meseguer Salvador, Mafe Salvador, 2016b. The interplay between genetic and bioelectrical signaling permits a spatial regionalisation of membrane potentials in model multicellular ensembles. Sci. Rep X 6, 35201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chanson Marc, Derouette Jean-Paul, Roth Isabelle, Foglia Bernard, Scerri Isabelle, Dudez Tecla, Kwak Brenda R., 2005. Gap junctional communication in tissue inflammation and repair. Biochimica et Biophysica Acta (BBA) - Biomembranes. The Connexins Part II VI 1711 (2), 197–207. [DOI] [PubMed] [Google Scholar]
- Chay TR, Keizer J, 1983. Minimal model for membrane oscillations in the pancreatic beta-cell. Biophys. J V 42 (2), 181–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernet BT, Fields C, Levin M, 2015. Long-range gapjunctional signaling controls oncogene-mediated tumorigenesis in Xenopus Laevis embryos. Front. Physiol 5, 519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cino Ilaria, Formenti Alessandro, 2008. Spermine biphasically affects N-Type calcium channel currents in adult dorsal root ganglion neurons of the rat. Biochim. Biophys. Acta Biomembr. X 1778 (10), 2437–2443. [DOI] [PubMed] [Google Scholar]
- Chifflet Silvia, Hernandez Julio A., 2016. The epithelial sodium channel and the processes of wound healing. BioMed Research International. VII 2016 e5675047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole, null, Woodruff, null, 2000. Vitellogenic ovarian follicles of Drosophila exhibit a charge-dependent distribution of endogenous soluble proteins. J. Insect Physiol IX 46 (9), 1239–1248. [DOI] [PubMed] [Google Scholar]
- Cooke J, Zeeman ECA, 1976. Clock and wavefront model for control of the number of repeated structures during animal morphogenesis. J. Theor. Biol I 58 (2), 455–476. [DOI] [PubMed] [Google Scholar]
- Cooper Mark S., Miller John P., Fraser Scott E., 1989. Electrophoretic repatterning of charged cytoplasmic molecules within tissues coupled by gap junctions by externally applied electric fields. Developmental Biology. III 132 (1), 179–188. [DOI] [PubMed] [Google Scholar]
- Cotterell James, Robert-Moreno Alexandre, Sharpe James, 2015. A local, self-organizing reaction-diffusion model can explain somite patterning in embryos. Cell Systems. X 1 (4), 257–269. [DOI] [PubMed] [Google Scholar]
- Dahal Giri Raj, Pradhan Sarala Joshi, Bates Emily Anne, 2017. Inwardly rectifying potassium channels influence Drosophila wing morphogenesis by regulating dpp release. Development. VIII 144 (15), 2771–2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahal Giri Raj, Rawson Joel, Gassaway Brandon, Kwok Benjamin, Tong Ying, Ptácek Louis J., Bates Emily, 2012. An inwardly rectifying K+ channel is required for patterning. Development. X 139 (19), 3653–3664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desforges Bénédicte, Curmi Patrick A., Bounedjah Ouissame, Nakib Samir, Hamon Loic, Bandt Jean-Pascal De, Pastré David, 2013. An intercellular polyamine transfer via gap junctions regulates proliferation and response to stress in epithelial cells. Mol. Biol. Cell V 24 (10), 1529–1543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do Chi-Wai, Peterson-Yantorno Kim, Mitchell Claire H., Civan Mortimer M., 2004. Camp-activated Maxi-Cl− channels in native bovine pigmented ciliary epithelial cells. Am. J. Physiol. Cell Physiol X 287 (4), C1003–C1011. [DOI] [PubMed] [Google Scholar]
- Doursat René, Sánchez Carlos, 2014. Growing fine-grained multicellular robots. Soft Robotics. VI 1 (2), 110–121. [Google Scholar]
- Durant Fallon, Lobo Daniel, Hammelman Jennifer, Levin Michael, 2016. Physiological controls of large-scale patterning in planarian regeneration: a molecular and computational perspective on growth and form: physiological controls of anatomy. Regeneration. IV 3 (2), 78–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durant Fallon, Morokuma Junji, Fields Christopher, Williams Katherine, Adams Dany Spencer, Levin Michael, 2017. Long-term, stochastic editing of regenerative anatomy via targeting endogenous bioelectric gradients. Biophys. J V 112 (10), 2231–2243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dzeja Petras P., Terzic Andre, 1998. Phosphotransfer reactions in the regulation of ATP-sensitive K+ channels. FASEB J. I 12 (7), 523–529. [DOI] [PubMed] [Google Scholar]
- Emmons-Bell M, Durant F, Hammelman J, Bessonov N, Volpert V, Morokuma J, Pinet K, Adams DS, Pietak A, Lobo D, Levin M, 2015. Gap junctional blockade stochastically induces different species-specific head anatomies in genetically wild-type girardia dorotocephala flatworms. Int. J. Mol. Sci 16 (11), 27865–27896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esser Axel T., Smith Kyle C., Weaver James C., Levin Michael, 2006. Mathematical model of morphogen electrophoresis through gap junctions. Dev. Dyn VIII 235 (8), 2144–2159. [DOI] [PubMed] [Google Scholar]
- Fairchild Corinne L., Barna Maria, 2014. Specialized filopodia: at the tip of morphogen transport and vertebrate tissue patterning. Curr. Opin. Genet. Dev 27, 67–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferjentsik Zoltan, Hayashi Shinichi, Dale J. Kim, Bessho Yasumasa, Herreman An, Strooper Bart De, Monte Gonzalo del, Pompa Jose Luis de la, Maroto Miguel, 2009. Notch is a critical component of the mouse somitogenesis oscillator and is essential for the formation of the somites. PLOS Genetics. IX 5 (9) e1000662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleidervish Ilya A., Libman Lior, Katz Efrat, Gutnick Michael J., 2008. Endogenous polyamines regulate cortical neuronal excitability by blocking voltage-gated Na+ channels. PNAS. II 105 (48), 18994–18999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fridlyand LE, Tamarina N, Philipson LH, 2010. Bursting and calcium oscillations in pancreatic -cells: specific pacemakers for specific mechanisms. Aust. J. Pharm.: Endocrinology and Metabolism X 299 (4), E517–E532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentile Luca, Cebrià Francesc, Bartscherer Kerstin, 2011. The planarian flatworm: an in vivo model for stem cell biology and nervous system regeneration. Disease Models and Mechanisms. I 4 (1), 12–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giepmans Ben N.G., 2004. Gap junctions and connexin-interacting proteins. Cardiovasc. Res V 62 (2), 233–245. [DOI] [PubMed] [Google Scholar]
- Gomez-Hernandez Juan-Manuel, Stühmer Walter, Parekh Anant B., 1997. Calcium dependence and distribution of calcium-activated chloride channels in Xenopus oocytes. J. Physiol 502 (3), 569–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green Jeremy B.A., Sharpe James, 2015. Positional information and reaction-diffusion: two big ideas in developmental biology combine. Development. IV 142 (7), 1203–1211. [DOI] [PubMed] [Google Scholar]
- Gurley KA, Rink JC, Alvarado AS, 2008. -Catenin defines head versus tail identity during planarian regeneration and homeostasis. Science. I 319 (5861), 323–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guthrie S, Turin L, Warner A, 1988. Patterns of junctional communication during development of the early Amphibian embryo. Development. VIII 103 (4), 769–783. [DOI] [PubMed] [Google Scholar]
- Haghighi Ali Pejmun, Cooper Ellis, 1998. Neuronal nicotinic acetylcholine receptors are blocked by intracellular spermine in a voltage-dependent manner. J. Neurosci 18 (11), 4050–4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallworth Nicholas E., Wilson Charles J., Bevan Mark D., 2003. Apamin-sensitive small conductance calcium-activated potassium channels, through their selective coupling to voltage-gated calcium channels, are critical determinants of the precision, pace, and pattern of action potential generation in rat subthalamic nucleus neurons in vitro. J. Neurosci VIII 23 (20), 7525–7542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamon Loic, Savarin Philippe, Pastré David, 2016. Polyamine signal through gap junctions: a key regulator of proliferation and gap-junction organization in mammalian tissues? Bioessays. VI 38 (6), 498–507. [DOI] [PubMed] [Google Scholar]
- Hanani Menachem, 2012. Lucifer Yellow – an angel rather than the devil. J. Cell Mol. Med I 16 (1), 22–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris Matthew P., Williamson Scott, Fallon John F., Meinhardt Hans, Prum Richard O., 2005. Molecular evidence for an activator–inhibitor mechanism in development of embryonic feather branching. Proc. Natl. Acad. Sci. U. S. A 102 (33), 11734–11739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haughey Norman J., Mattson Mark P., 2003. Alzheimer's amyloid beta-peptide enhances ATP/gap junction-mediated calcium-wave propagation in astrocytes. Neuromol Med. VI 3 (3), 173–180. [DOI] [PubMed] [Google Scholar]
- Hotary Kevin B., Robinson Kenneth R., 1990. Endogenous electrical currents and the resultant voltage gradients in the chick embryo. Dev. Biol 140 (1), 149–160. [DOI] [PubMed] [Google Scholar]
- Hotary Kevin B., Robinson Kenneth R., 1991. The neural tube of the Xenopus embryo maintains a potential difference across itself. Dev. Brain Res 59 (1), 65–73. [DOI] [PubMed] [Google Scholar]
- Hotary Kevin B., Robinson Kenneth R., 1992. Evidence of a role for endogenous electrical fields in chick embryo development. Development 114 (4), 985–996. [DOI] [PubMed] [Google Scholar]
- Hotary Kevin B., Robinson Kenneth R., 1994. Endogenous electrical currents and voltage gradients in Xenopus embryos and the consequences of their disruption. Dev. Biol 166 (2), 789–800. [DOI] [PubMed] [Google Scholar]
- Huang CJ, Moczydlowski E, 2001. Cytoplasmic polyamines as permeant blockers and modulators of the voltage-gated sodium channel. Biophys. J III 80 (3), 1262–1279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isoldi MC, Pereira EA, Visconti MA, Castrucci AML, 2004. The role of calcium, calcium-activated K+ channels, and tyrosine/kinase in psoralen-evoked responses in human melanoma cells. Brazilian Journal of Medical and Biological Research. IV 37 (4), 559–568. [DOI] [PubMed] [Google Scholar]
- Jaeger Johannes, Manu Reinitz, John, 2012. Drosophila blastoderm patterning. Current Opinion in Genetics & Development. Genetics of system biology XII 22 (6), 533–541. [DOI] [PubMed] [Google Scholar]
- Jaffe LF, 1981. The role of ionic currents in establishing developmental pattern. Phil. Trans. Biol. Sci 295 (1078), 553–566. [DOI] [PubMed] [Google Scholar]
- Jaffe Linoel F., Woodruff Richard I., 1979. Large electrical currents traverse developing ceropia follicles. Proc. Natl. Acad. Sci. Unit. States Am 76 (3), 1328–1332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffe LF, Robinson KR, Nuccitelli R, 1974. Local cation entry and self-electrophoresis as an intracellular localization mechanism. Ann. N. Y. Acad. Sci 238, 372–389. [DOI] [PubMed] [Google Scholar]
- Jansen Hans J., Wacker Stephan A., Bardine Nabila, Durston Antony J., 2007. The role of the spemann organizer in anterior–posterior patterning of the trunk. Mechanisms of Development. IX 124 (9–10), 668–681. [DOI] [PubMed] [Google Scholar]
- Jewhurst K, Levin M, McLaughlin KA, 2014. Optogenetic control of apoptosis in targeted tissues of Xenopus Laevis embryos. J. Cell Death 7, 25–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jørgensen Niklas R., Geist Steven T., Civitelli Roberto, Steinberg Thomas H., 1997. ATP-and gap junction–dependent intercellular calcium signaling in osteoblastic cells. The Journal of cell biology 139 (2), 497–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanaporis G, Brink PR, Valiunas V, 2011. Gap junction permeability: selectivity for anionic and cationic probes. Am J Physiol Cell Physiol. III 300 (3), C600–C609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlebach Guy, Shamir Ron, 2008. Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol X 9 (10), 770–780. [DOI] [PubMed] [Google Scholar]
- Kekuda Ramesh, Prasad Puttur D., Wu Xiang, Wang Haiping, Fei You-Jun, Leibach Frederick H., Ganapathy Vadivel, 1998. Cloning and functional characterization of a potential-sensitive, polyspecific organic cation transporter (OCT3) most abundantly expressed in placenta. J. Biol. Chem VI 273 (26), 15971–15979. [DOI] [PubMed] [Google Scholar]
- Kornberg Thomas B., 2017. Distributing signaling proteins in space and time: the province of cytonemes. Curr. Opin. Genet. Dev 45, 22–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kornberg Thomas B., Roy Sougata, 2014. Cytonemes as specialized signaling filopodia. Development 141 (4), 729–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krüger Julia, Bohrmann Johannes, 2015. Bioelectric patterning during oogenesis: stage-specific distribution of membrane potentials, intracellular pH and ion-transport mechanisms in Drosophila ovarian follicles. BMC Dev. Biol 15 (1), 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurata Harley T., Marton Laurence J., Nichols Colin G., 2006. The polyamine binding site in inward rectifier K+ channels.J. Gen. Physiol V 127 (5), 467–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuttler Christina, 2011. Reaction-diffusion Equations with Applications. Lecture script. Technische Universit ät München. [Google Scholar]
- Lander Rachel, Petersen Christian P., 2016. Wnt, Ptk7, and FGFRL expression gradients control trunk positional identity in planarian regeneration. eLife. IV 5 e12850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landesman Yosef, Goodenough Daniel A., Paul David L., 2000. Gap junctional communication in the early Xenopus embryo. J Cell Biol. VIII 150 (4), 929–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange CS, Steele VE, 1978. The mechanism of anterior-posterior polarity control in planarians. Differentiation 11 (1), 1–12. [DOI] [PubMed] [Google Scholar]
- Law Robert, Levin Michael, 2015. Bioelectric memory: modeling resting potential bistability in Amphibian embryos and mammalian cells. Theoretical Biology and Medical Modelling. XII 12, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin M, 2003. Electric embryos: endogenous ion fluxes and voltage gradients in left-right asymmetry. Dev. Biol 259, 482. [Google Scholar]
- Levin Michael, 2006. Is the early left-right Axis like a plant, a kidney, or a Neuron? The integration of physiological signals in embryonic asymmetry. Birth Defects Research Part C: Embryo Today: Reviews. IX 78 (3), 191–223. [DOI] [PubMed] [Google Scholar]
- Levin M, 2007. Gap junctional communication in morphogenesis. Prog. Biophys. Mol. Biol 94 (1–2), 186–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin Michael, 2012a. Molecular bioelectricity in developmental biology: new tools and recent discoveries: control of cell behavior and pattern formation by transmembrane potential gradients. BioEssays. III 34 (3), 205–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin Michael, 2012b. Morphogenetic fields in embryogenesis, regeneration, and cancer: non-local control of complex patterning. Biosystems. IX 109 (3), 243–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin M, 2014. Molecular bioelectricity: how endogenous voltage potentials control cell behavior and instruct pattern regulation in vivo. Molecular Biology of the Cell. XII 25 (24), 3835–3850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin M, Mercola M, 1998. Gap junctions are involved in the early generation of left-right asymmetry. Dev. Biol 203 (1), 90–105. [DOI] [PubMed] [Google Scholar]
- Levin M, Mercola M, 1999a. Gap junction-mediated transfer of left-right patterning signals. Mol. Biol. Cell 10, 39. [DOI] [PubMed] [Google Scholar]
- Levin M, Mercola M, 1999b. Gap junction-mediated transfer of left-right patterning signals in the early chick blastoderm is upstream of shh asymmetry in the node. Development 126, 4703–4714. [DOI] [PubMed] [Google Scholar]
- Levin Michael, Stevenson Claire G., 2012. Regulation of cell behavior and tissue patterning by bioelectrical signals: challenges and opportunities for biomedical engineering. Annual Review of Biomedical Engineering. VIII 14 (1), 295–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin Michael, Thorlin Thorleif, Robinson Kenneth R., Nogi Taisaku, Mercola Mark, 2002. Asymmetries in H+/K+-ATPase and cell membrane potentials comprise a very early step in left-right patterning. Cell X 111 (1), 77–89. [DOI] [PubMed] [Google Scholar]
- Levin M, Buznikov GA, Lauder JM, 2006. Of minds and embryos: left-right asymmetry and the serotonergic controls of pre-neural morphogenesis. Dev. Neurosci 28 (3), 171–185. [DOI] [PubMed] [Google Scholar]
- Leybaert Luc, Sanderson Michael J., 2012. Intercellular Ca(2+) waves: mechanisms and function. Physiol. Rev VII 92 (3), 1359–1392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang Wenfeng, Zhao Yuliang, Liu Lianqing, Wang Yuechao, Li Wen Jung, Lee Gwo-Bin, 2017. Determination of cell membrane capacitance and conductance via optically induced electrokinetics. Biophys. J 113 (7), 1531–1539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liedtke Wolfgang, Choe Yong, Martí-Renom Marc A., Bell Andrea M., Denis Charlotte S., Andrej Šali, Hudspeth AJ, Friedman Jeffrey M., Heller Stefan, 2000. Vanilloid receptor–related osmotically activated channel (VR-OAC), a candidate vertebrate osmoreceptor. Cell X 103 (3), 525–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Zhicheng, Canales Juan J., Björgvinsson Thröstur, Thomsen Morgane M., Qu Hong, Liu Qing-Rong, Torres Gonzalo E., Caine S. Barak, 2011. Monoamine transporters: vulnerable and vital doorkeepers. Prog Mol Biol Transl Sci. 98, 1–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lobo Daniel, Levin Michael, 2015. Inferring regulatory networks from experimental morphological phenotypes: a computational method reverse-engineers planarian regeneration. PLoS Comput. Biol 11 (6) e1004295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lobo Daniel, Beane Wendy S., Levin Michael, 2012. Modeling planarian regeneration: a primer for reverse-engineering the worm. PLOS Comput Biol. IV 8 (4) e1002481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loew Leslie M., 2010. Design and Use of Organic Voltage Sensitive Dyes//Membrane Potential Imaging in the Nervous System. Springer New York, New York, NY, pp. 13–23. [Google Scholar]
- Ma Liqun, Zhang Xuexin, Zhou Min, Chen Haijun, 2012. Acid-sensitive TWIK and TASK two-pore domain potassium channels change ion selectivity and become permeable to sodium in extracellular acidification. J. Biol. Chem X 287 (44), 37145–37153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maciunas Kestutis, Snipas Mindaugas, Paulauskas Nerijus, Bukauskas Feliksas F., 2016. Reverberation of excitation in neuronal networks interconnected through voltage-gated gap junction channels. The Journal of General Physiology. III 147 (3), 273–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackenzie Bryan, Ujwal ML, Chang Min-Hwang, Romero Michael F., Hediger Matthias A., 2006. Divalent metal-ion transporter DMT1 mediates both H+ -coupled Fe2+ transport and uncoupled fluxes. Pflügers Archiv - European Journal of Physiology. I 451 (4), 544–558. [DOI] [PubMed] [Google Scholar]
- Makary Samy MY., Claydon Tom W., Enkvetchakul Decha, Nichols Colin G., Boyett Mark R., 2005. A difference in inward rectification and polyamine block and permeation between the Kir2.1 and kir3.1/kir3.4 K+ channels. J Physiol. XI 568 (Pt 3), 749–766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinac B, 2004. Mechanosensitive ion channels: molecules of mechanotransduction. J. Cell Sci V 117 (12), 2449–2460. [DOI] [PubMed] [Google Scholar]
- Mathews Juanita, Levin Michael, 2016. Gap junctional signaling in pattern regulation: physiological network connectivity instructs growth and form. Devel Neurobio. VI 77 (5), 643–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuo Isao, Kimura-Yoshida Chiharu, 2014. Extracellular distribution of diffusible growth factors controlled by heparan sulfate proteoglycans during mammalian embryogenesis. Philosophical Transactions of the Royal Society B: Biological Sciences. XII 369, 1657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCaig Colin D., Rajnicek Ann M., Song Bing, Zhao Min, 2005. Controlling cell behavior electrically: current views and future potential. Physiological Reviews. VII 85 (3), 943–978. [DOI] [PubMed] [Google Scholar]
- McCusker Catherine D., Gardiner David M., 2013. Positional information is reprogrammed in blastema cells of the regenerating limb of the axolotl (Ambystoma Mexicanum). PLoS One. IX 8 (9) e77064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinhardt H, 2008. Models of biological pattern formation: from elementary steps to the organization of embryonic axes. Curr. Top. Dev. Biol 81, 1–63. [DOI] [PubMed] [Google Scholar]
- Meinhardt Hans, 2009. Beta-catenin and Axis formation in planarians. Bioessays I 31 (1), 5–9. [DOI] [PubMed] [Google Scholar]
- Meinhardt Hans, Gierer Alfred, 2000. pattern formation by local self-activation and lateral inhibition. Bioessays 22 (8), 753–760. [DOI] [PubMed] [Google Scholar]
- Miyauchi Seiji, Gopal Elangovan, Fei You-Jun, Ganapathy Vadivel, 2004. Functional identification of SLC5A8, a tumor suppressor down-regulated in colon cancer, as a Na+-Coupled transporter for short-chain fatty acids. J. Biol. Chem 279 (14), 13293–13296. [DOI] [PubMed] [Google Scholar]
- Nachtrab Gregory, Kikuchi Kazu, Tornini Valerie A., Poss Kenneth D., 2013. Transcriptional components of anteroposterior positional information during zebrafish fin regeneration. Development. IX 140 (18), 3754–3764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiyama Masaaki, Skoultchi Arthur I., Nakayama Keiichi I., 2012. Histone H1 recruitment by CHD8 is essential for suppression of the wnt–beta-catenin signaling pathway. Mol. Cell Biol I 32 (2), 501–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuccitelli R, 2003. Endogenous electric fields in embryos during development, regeneration and wound healing. Radiat Prot Dosimetry 106 (4), 375–383. [DOI] [PubMed] [Google Scholar]
- Olesen Niels Erik, Hofgaard Johannes P., Holstein-Rathlou Niels-Henrik, Nielsen Morten Schak, Jacobsen Jens Christian Brings, 2012. Estimation of the effective intercellular diffusion coefficient in cell monolayers coupled by gap junctions. European Journal of Pharmaceutical Sciences. Modelling for Pharmaceutical Sciences VII 46 (4), 222–232. [DOI] [PubMed] [Google Scholar]
- Oviedo NJ, Levin M, 2007. Smedinx-11 is a planarian stem cell gap junction gene required for regeneration and homeostasis. Development. VIII 134 (17), 3121–3131. [DOI] [PubMed] [Google Scholar]
- Oviedo NJ, Nicolas CL, Adams DS, Levin M, 2008. Live imaging of planarian membrane potential using DiBAC4(3). Cold Spring Harbor Protocols. X 2008, 11 pdb.prot5055–pdb.prot5055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oviedo Néstor J., Morokuma Junji, Walentek Peter, Kema Ido P., Gu Man Bock, Ahn Joo-Myung, Hwang Jung Shan, Gojobori Takashi, Levin Michael, 2010. Long-range neural and gap junction protein-mediated cues control polarity during planarian regeneration. Developmental Biology. III 339 (1), 188–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owlarn Suthira, Bartscherer Kerstin, 2016. Go ahead, grow a head! A Planarian's guide to anterior regeneration: planarian anterior regeneration. Regeneration. VI 3 (3), 139–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Özer Inci, Scheit Karl Heinz, 1978. Steady-state kinetic studies on adenylate cyclase from brevibacterium liquefaciens. European Journal of Biochemistry. IV 85 (1), 173–180. [DOI] [PubMed] [Google Scholar]
- Pai VP, Aw S, Shomrat T, Lemire JM, Levin M, 2012a. Transmembrane voltage potential controls embryonic eye patterning in Xenopus Laevis. Development. I 139 (2), 313–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pai VP, Vandenberg LN, Blackiston D, Levin M, 2012b. Neurally derived tissues in Xenopus Laevis embryos exhibit a consistent bioelectrical left-right asymmetry. Stem Cell. Int 2012, 353491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pai VP, Lemire JM, Pare JF, Lin G, Chen Y, Levin M, 2015a. Endogenous gradients of resting potential instructively pattern embryonic neural tissue via Notch signaling and regulation of proliferation. J. Neurosci 35 (10), 4366–4385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pai Vaibhav P., Lemire Joan M., Chen Ying, Lin Gufa, Levin Michael, 2015b. Local and long-range endogenous resting potential gradients antagonistically regulate apoptosis and proliferation in the embryonic CNS. Int. J. Dev. Biol 59, 7–8-9. 327–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pai Vaibhav P., Pietak Alexis, Willocq Valerie, Ye Bin, Shi Nian-Qing, Levin Michael, 2018. HCN2 Rescues brain defects by enforcing endogenous voltage pre-patterns. Nat. Commun 9 (1), 998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel AJ, Honore E, 2001. Molecular physiology of oxygen-sensitive potassium channels. Eur. Respir. J 18 (1), 221–227. [DOI] [PubMed] [Google Scholar]
- Pellerin L, Magistretti PJ, 1996. Excitatory amino acids stimulate aerobic glycolysis in astrocytes via an activation of the Na+/K+ ATPase. Dev. Neurosci 18 (5–6), 336–342. [DOI] [PubMed] [Google Scholar]
- Perez-Cornejo Patricia, Arreola Jorge, 2004. Regulation of Ca(2+)-Activated chloride channels by cAMP and CFTR in parotid acinar cells. Biochem. Biophys. Res. Commun IV 316 (3), 612–617. [DOI] [PubMed] [Google Scholar]
- Petersen Christian P., Reddien Peter W., 2011. Polarized Notum activation at wounds inhibits Wnt function to promote planarian head regeneration. Science. V 332 (6031), 852–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phan Anne Q., Lee Jangwoo, Oei Michelle, Flath Craig, Hwe Caitlyn, Mariano Rachele, Vu Tiffany, Shu Cynthia, Dinh Andrew, Simkin Jennifer, Muneoka Ken, Bryant Susan V., Gardiner David M., 2015. Positional information in axolotl and mouse limb extracellular matrix is mediated via heparan sulfate and fibroblast growth factor during limb regeneration in the axolotl (Ambystoma Mexicanum). Regeneration. VIII 2 (4), 182–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philpott Michael R., Glosli James N., 1995. Screening of charged electrodes in aqueous electrolytes. J. Electrochem. Soc I 142 (2), L25–L28. [Google Scholar]
- Pietak Alexis, Levin Michael, 2016. Exploring instructive physiological signaling with the bioelectric tissue simulation engine. Front. Bioeng. Biotechnol 55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pietak Alexis, Levin Michael, 2017. Bioelectric gene and reaction networks: computational modelling of genetic, biochemical and bioelectrical dynamics in pattern regulation. J R Soc Interface IX 14, 134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portes Maria Teresa, Damineli Daniel Santa Cruz, Moreno Nuno, Colaço Renato, Costa Sílvia, Feijó José A., 2015. The pollen tube oscillator: integrating biophysics and biochemistry into cellular growth and morphogenesis. Rhythms in Plants 121–156. [Google Scholar]
- Pospischil Martin, Toledo-Rodriguez Maria, Monier Cyril, Piwkowska Zuzanna, Bal Thierry, Frégnac Yves, Markram Henry, Destexhe Alain, 2008. Minimal hodgkin–huxley type models for different classes of cortical and thalamic neurons. Biological Cybernetics. XI 99 (4–5), 427–441. [DOI] [PubMed] [Google Scholar]
- Noske Raimund, Cornelius Flemming, Clarke Ronald J., 2010. Investigation of the enzymatic activity of the Na+,K+-ATPase via isothermal titration microcalorimetry. Biochimica et Biophysica Acta (BBA) - Bioenergetics. VIII 1797 (8), 1540–1545. [DOI] [PubMed] [Google Scholar]
- Ranjan Rajnish, Khazen Georges, Gambazzi Luca, Ramaswamy Srikanth, Hill Sean L., Schürmann Felix, Markram Henry, 2011. Channelpedia: an integrative and interactive database for ion channels. Front Neuroinform. XII 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raspopovic J, Marcon L, Russo L, Sharpe J, 2014. Digit patterning is controlled by a bmp-sox9-wnt turing network modulated by morphogen gradients. Science. VIII 345 (6196), 566–570. [DOI] [PubMed] [Google Scholar]
- Revel JP, Yee AG, Hudspeth AJ, 1971. Gap junctions between electrotonically coupled cells in tissue culture and in Brown fat. Proc. Natl. Acad. Sci. Unit. States Am 68 (12), 2924–2927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson KR, 1979. Electrical currents through full-grown and maturing Xenopus oocytes. Proc Natl Acad Sci U S A. II 76 (2), 837–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson Kenneth R., 1983. Endogenous electrical current leaves the limb and prelimb region of the Xenopus embryo. Dev. Biol V 97 (1), 203–211. [DOI] [PubMed] [Google Scholar]
- Robinson Kenneth R., Messerli Mark A., 2003. Left/right, up/down: the role of endogenous electrical fields as directional signals in development, repair and invasion. BioEssays. VIII 25 (8), 759–766. [DOI] [PubMed] [Google Scholar]
- Rook MB, Ginneken A. C. van, Jonge B. de, Aoumari A. el, Gros D, Jongsma HJ, 1992. Differences in gap junction channels between cardiac myocytes, fibroblasts, and heterologous pairs. American Journal of Physiology - Cell Physiology. XI 263 (5), C959–C977. [DOI] [PubMed] [Google Scholar]
- Rosenbaum Tamara, Simon Sidney A., 2007. TRPV1 Receptors and Signal Transduction. TRP Ion Channel Function in Sensory Transduction and Cellular Signaling Cascades. CRC Press/Taylor & Francis, Boca Raton (FL) (Frontiers in Neuroscience). [Google Scholar]
- Sachs JR, 1977. Kinetic evaluation of the Na-K pump reaction mechanism. The Journal of physiology 273 (2), 489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachs F, 2010. Stretch-activated ion channels: what are they? Physiology. II 25 (1), 50–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez Alvarado A, 2007. Stem cells and the planarian schmidtea mediterranea. C R Biol. 330 (6–7), 498–503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez Alvarado A, Newmark PA, 1998. The use of planarians to dissect the molecular basis of metazoan regeneration. Wound Repair Regen. 6 (4), 413–420. [DOI] [PubMed] [Google Scholar]
- Sanders Timothy A., Llagostera Esther, Barna Maria, 2013. Specialized filopodia direct long-range transport of SHH during vertebrate tissue patterning. Nature 497 (7451), 628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sater Amy K., 2011. A jump-start for planarian head regeneration. Chemistry & Biology. I 18 (1), 4–5. [DOI] [PubMed] [Google Scholar]
- Schilling AF, Filke S, Lange T, Gebauer M, Brink S, Baranowsky A, Zustin J, Amling M, 2008. Gap junctional communication in human osteoclasts in vitro and in vivo. J. Cell Mol. Med 12 (6A), 2497–2504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schumacher Jennifer A., Hsieh Yi-Wen, Chen Shiuhwei, Pirri Jennifer K., Alkema Mark J., Li Wen-Hong, Chang Chieh, Chuang Chiou-Fen, 2012. Intercellular calcium signaling in a gap junction-coupled cell network establishes asymmetric neuronal fates in C. Elegans. Development. XI 139 (22), 4191–4201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scimone M. Lucila, Cote Lauren E., Rogers Travis, Reddien Peter W., 2016. Two FGFRL-wnt circuits organize the planarian anteroposterior Axis. eLife 5 e12845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheeba Caroline J., Andrade Raquel P., Palmeirim Isabel, 2014. Limb patterning: from signaling gradients to molecular oscillations. Journal of Molecular Biology. II 426 (4), 780–784. [DOI] [PubMed] [Google Scholar]
- Shimojo Hiromi, Isomura Akihiro, Ohtsuka Toshiyuki, Kori Hiroshi, Miyachi Hitoshi, Kageyama Ryoichiro, 2016. Oscillatory control of delta-like1 in cell interactions regulates dynamic gene expression and tissue morphogenesis. Genes Dev. I 30 (1), 102–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sim Jae Hoon, Yang Dong Ki, Kim Young Chul, Park Sung Jin, Kang Tong Mook, So Insuk, Kim Ki Whan, 2002. ATP-sensitive K+ channels composed of Kir6.1 and SUR2B subunits in Guinea pig gastric myocytes. Am. J. Physiol. Gastrointest. Liver Physiol I 282 (1), G137–G144. [DOI] [PubMed] [Google Scholar]
- Skjørringe Tina, Burkhart Annette, Johnsen Kasper Bendix, Moos Torben, 2015. Divalent metal transporter 1 (DMT1) in the brain: implications for a role in iron transport at the blood-brain barrier, and neuronal and glial pathology. Front Mol Neurosci. VI 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele Vernon E., Lange Christopher S., 1977. Characterization of an organ-specific differentiator substance in the planarian dugesia etrusca. Development 37 (1), 159–172. [PubMed] [Google Scholar]
- Stückemann Tom, Cleland James Patrick, Werner Steffen, Vu Thi-Kim, Hanh Bayersdorf, Robert Liu, Shang-Yun Friedrich, Benjamin Jülicher, Frank Rink, Christian Jochen, 2017. Antagonistic self-organizing patterning systems control maintenance and regeneration of the anteroposterior Axis in planarians. Dev. Cell II 40 (3), 248–263 e4. [DOI] [PubMed] [Google Scholar]
- Sullivan KG, Emmons-Bell M, Levin M, 2016. Physiological inputs regulate species-specific anatomy during embryogenesis and regeneration. Commun. Integr. Biol 9 (4) e1192733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sundelacruz Sarah, Levin Michael, Kaplan David L., 2008. Membrane potential controls adipogenic and osteogenic differentiation of mesenchymal stem cells. PLoS One. XI 3 (11) e3737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sundelacruz Sarah, Levin Michael, Kaplan David L., 2009. Role of membrane potential in the regulation of cell proliferation and differentiation. Stem Cell Reviews and Reports. IX 5 (3), 231–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talley Edmund M., Bayliss Douglas A., 2002. Modulation of TASK-1 (Kcnk3) and TASK-3 (Kcnk9) potassium channels volatile anesthetics and neurotransmitters share a molecular site of action. J. Biol. Chem V 277 (20), 17733–17742. [DOI] [PubMed] [Google Scholar]
- Talley Edmund M., Sirois Jay E., Lei Qiubo, Bayliss Douglas A., 2003. Two-pore-domain (kcnk) potassium channels: dynamic roles in neuronal function. Neuroscientist. I 9 (1), 46–56. [DOI] [PubMed] [Google Scholar]
- Tang Xiang Dong, Santarelli Lindsey Ciali, Heinemann Stefan H, Hoshi Toshinori, 2004. Metabolic regulation of potassium channels. Annual Review of Physiology. III 66 (1), 131–159. [DOI] [PubMed] [Google Scholar]
- Taylor Robert LV., 2010. Attractors: Nonstrange to Chaotic. Society for Industrial and Applied Mathematics, pp. 72–80. Undergraduate Research Online. [Google Scholar]
- Telfer WH, Woodruff RI, Huebner E, 1981. Electrical polarity and cellular differentiation in meroistic ovaries. Am. Zool 21 (3) , 675–686. [Google Scholar]
- Thangaraju Muthusamy, Gopal Elangovan, Martin Pamela M., Ananth Sudha, Smith Sylvia B., Prasad Puttur D., Sterneck Esta, Ganapathy Vadivel, 2006. SLC5A8 triggers tumor cell apoptosis through pyruvate-dependent inhibition of histone deacetylases. Cancer Res. XII 66 (24), 11560–11564. [DOI] [PubMed] [Google Scholar]
- Thangaraju Muthusamy, Carswell Kristina N., Prasad Puttur D., Ganapathy Vadivel, 2009a. Colon cancer cells maintain low levels of pyruvate to avoid cell death caused by inhibition of HDAC1/HDAC3. Biochem. J 1417 (1), 379–389. [DOI] [PubMed] [Google Scholar]
- Thangaraju Muthusamy, Karunakaran Senthil K., Itagaki Shiro, Gopal Elangovan, Elangovan Selvakumar, Prasad Puttur D., Ganapathy Vadivel, 2009b. Transport by SLC5A8 with subsequent inhibition of histone deacetylase 1 (HDAC1) and HDAC3 underlies the antitumor activity of 3-bromopyruvate. Cancer. X 115 (20), 4655–4666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson Brandi A., Tremblay Véronique, Lin Grace, Bochar Daniel A., 2008. CHD8 is an ATP-dependent chromatin remodeling factor that regulates beta-catenin target genes. Mol. Cell. Biol VI 28 (12), 3894–3904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torres Gonzalo E., Gainetdinov Raul R., Caron Marc G., 2003. Plasma membrane monoamine transporters: structure, regulation and function. Nat. Rev. Neurosci I 4 (1), 13–25. [DOI] [PubMed] [Google Scholar]
- Tsiairis Charisios D., Aulehla Alexander, 2016. Self-organization of embryonic genetic oscillators into spatiotemporal wave patterns. Cell. II 164 (4), 656–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turing Alan Mathison, 1952. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci 237 (641), 37–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uriu Koichiro, 2016. Genetic oscillators in development. Develop. Growth Differ I 58 (1), 16–30. [DOI] [PubMed] [Google Scholar]
- Uriu Koichiro, Morelli Luis G., 2014. Collective cell movement promotes synchronization of coupled genetic oscillators. Biophysical Journal. VII 107 (2), 514–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valiunas V, Polosina YY, Miller H, Potapova IA, Valiuniene L, Doronin S, Mathias RT, Robinson RB, Rosen MR, Cohen IS, Brink PR, 2005. Connexin-specific cell-to-cell transfer of short interfering RNA by gap junctions. J Physiol 568 (Pt 2), 459–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg Laura N., Morrie Ryan D., Adams Dany Spencer, 2011. V-ATPase-Dependent ectodermal voltage and ph regionalization are required for craniofacial morphogenesis. Developmental Dynamics. VIII 240 (8), 1889–1904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veenstra RD, Wang HZ, Beblo DA, Chilton MG, Harris AL, Beyer EC, Brink PR, 1995. Selectivity of connexin-specific gap junctions does not correlate with channel conductance. Circ. Res. 77, 1156–1165. [DOI] [PubMed] [Google Scholar]
- Veenstra Richard D., 1996. Size and selectivity of gap junction channels formed from different connexins. J. Bioenerg. Biomembr 28 (4), 327–337. [DOI] [PubMed] [Google Scholar]
- Vliet Albert van der, Bove Peter F., 2011. Purinergic signaling in wound healing and airway remodeling. Purinergic Regulation of Respiratory Diseases 139–157 (Subcellular Biochemistry). [DOI] [PubMed] [Google Scholar]
- Watanabe Masakatsu, Watanabe Daisuke, Kondo Shigeru, 2012. Polyamine sensitivity of gap junctions is required for skin pattern formation in zebrafish. Sci. Rep 2, 473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber Paul A., Chang Hou-Chien, Spaeth Kris E., Nitsche Johannes M., Nicholson Bruce J., 2004. The permeability of gap junction channels to probes of different size is dependent on connexin composition and permeant-pore affinities. Biophys J. VIII 87 (2), 958–973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner Steffen, Stückemann Tom, Amigo Beirán, Manuel Rink, Jochen C, Jülicher Frank, Friedrich Benjamin M., 2015. Scaling and regeneration of self-organized patterns. Physical Review Letters. IV 114, 13. [DOI] [PubMed] [Google Scholar]
- Wolpert Lewis, 1969. Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol 25 (1), 1–47. [DOI] [PubMed] [Google Scholar]
- Wolpert Lewis, 2011. Positional information and patterning revisited. J. Theor. Biol I 269 (1), 359–365. [DOI] [PubMed] [Google Scholar]
- Woodruff RI, Cole RW, 1997. Charge dependent distribution of endogenous proteins within vitellogenic ovarian follicles of Actias Luna. J. Insect Physiol III 43 (3), 275–287. [DOI] [PubMed] [Google Scholar]
- Woodruff RI, Telfer WH, 1980. Electrophoresis of proteins in intercellular bridges. Nature. VII 286 (5768), 84–86. [DOI] [PubMed] [Google Scholar]
- Wright SH, 2004. Generation of resting membrane potential. Aust. J. Pharm.: Advances in Physiology Education XII 28 (4), 139–142. [DOI] [PubMed] [Google Scholar]
- Yan Ding-Hong, Nishimura Kazuhiro, Yoshida Kaori, Nakahira Kei, Ehara Tsuguhisa, Igarashi Kazuei, Ishihara Keiko, 2005. Different intracellular polyamine concentrations underlie the difference in the inward rectifier K+ currents in atria and ventricles of the Guinea-Pig heart. J Physiol. III 563 (Pt 3), 713–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Rui, Qian Feng, Rajagopalan Lavanya, Pereira Fred A., Brownell William E., Anvari Bahman, 2007. Prestin modulates mechanics and electromechanical force of the plasma membrane. Biophys J. VII 93 (1), L07–L09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Jianfeng, Zhang Yong-Tao, Alber Mark S., Newman Stuart A., 2010. Bare bones pattern formation: a core regulatory network in varying geometries reproduces major features of vertebrate limb development and evolution. PLoS One V 5, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]