Abstract
Transcatheter aortic valves (TAV) are symmetrically designed, but they are often not deployed inside cylindrical conduits with circular cross-sectional areas. Many TAV patients have heavily calcified aortic valves, which often result in deformed prosthesis geometries after deployment. We investigated the effects of deformed valve annulus configurations on a surgical bioprosthetic valve as a model for TAV. We studied valve leaflet motions, stresses and strains, and analog hydrodynamic measures (using geometric methods), via finite element (FE) modeling. Two categories of annular deformations were created to approximate clinical observations: (1) noncircular annulus with valve area conserved, and (2) under-expansion (reduced area) compared to circular annulus. We found that under-expansion had more impact on increasing stenosis (with geometric orifice area metrics) than noncircularity, and that noncircularity had more impact on increasing regurgitation (with regurgitation orifice area metrics) than under-expansion. We found durability predictors (stress/strain) to be the highest in the commissure regions of noncircular configurations such as EllipMajor (noncircular and under-expansion areas). Other clinically relevant performance aspects such as leaflet kinematics and coaptation were also investigated with the noncircular configurations. This study provides a framework for choosing the most challenging TAV deformations for acute and long-term valve performance in the design and testing phase of device development.
Keywords: transcatheter aortic valve, noncircular, durability, finite element modeling, hydrodynamics, geometric orifice area, regurgitant orifice area, coaptation surface area
Introduction
Transcatheter aortic valve (TAV) replacement is a relatively new treatment option for patients with a diseased aortic valve [1]. For patients with aortic stenosis, heavy calcium deposits on the native valve leaflets and in the aortic root can cause cross-sectional noncircular distortions in the TAV annular geometry when deployed [2–5], which may affect the acute and long-term hydrodynamic functions of the prosthesis. Schultz et al. evaluated the Medtronic CoreValve TAV in 30 patients with multislice computed tomography and found that a majority of the devices did not achieve nominal cross-sectional circular configurations [2]. Similarly, Delgado et al. showed that 14% of Edwards Lifesciences Sapien TAV were deployed noncircularly [4]. Gooley et al. assessed the Boston-Scientific Lotus TAV in 40 patients and found that 25% of prostheses were noncircular postimplantation due to native annular eccentricity [5]. These TAV stent frames could be elliptical, triangular, or D-Shaped based on the interaction between the TAV and the native calcified aortic valve. Kuetting et al. showed that more pronounced ovality impaired prosthesis function and increased regurgitation [6]. TAV under-expansion in valve-in-valve procedures [7–12] has been shown to distort the coaptation of the leaflets [3] and can affect transvalvular pressure gradients and the valve opening area [9].
Sun et al. [13] showed that for a pericardial bioprosthetic TAV with an elliptical eccentricity of 0.68 (leaflet thickness ~0.24mm), the peak leaflet stress increased by 143% compared with the nominal circular TAV and valve leakage also increased. These results were further confirmed by Gunning et al. [14], in which elliptically deployed TAVs were shown to have increased leaflet bending and strains particularly in the commissural regions. Duraiswamy et al. [15] investigated five noncircular configurations and showed the maximum in-plane principal stresses and strains were obtained in an elliptical configuration with an aspect ratio of 1.25 and the commissure aligned along the minor axis. The principal stresses increased by 218% and principal strains increased by 80% compared with the circular configuration. The presence of “sagging” and “stretched” leaflets in the same noncircular valve configuration was highlighted. These leaflet patterns were also evident in other studies [13,14]. The model [15] was “quasi-static,” simulating the valve geometry only at the end of diastole. Moreover, isotropic material properties were considered which could cause discrepancies with the anisotropic behavior of bovine pericardial tissues. Similarly, Abbasi and Azadani [16] found the average principal stress of the commissures in diastole was increased and, in contrast, the maximum principal stress in the belly region decreased as the postinflation diameter of the TAV increased. However, these studies did not provide a comprehensive framework that looked into clinically relevant valve performance metrics that correlate with long-term leaflet durability in a variety of noncircular configurations. These metrics may be related to the valve hydrodynamics, leaflet stresses and strains, and leaflet kinematics. ISO 5840–3 international standards for transcatheter heart valve substitutes recommends the use of noncircular valve configurations for bench testing; however, with many possible geometries that may occur after postdeployment depending on the transcatheter valve design, choosing the most challenging valve configurations can be difficult. This study uses dynamic finite element (FE) analysis to investigate the effects of area-preserved and area-reduced noncircular configurations on valve hydrodynamics, kinematics, and stresses, and additionally analyzes clinically relevant performance metrics. The contribution of such measures may provide additional insight into the expected acute or long-term performance of a symmetric TAV that experiences noncircular postdeployment configurations and may likely be helpful for manufacturers in determining challenging valve configurations during their device design development and verification testing.
Materials and Methods
Model Development.
A 25-mm-diameter surgical bovine pericardial bioprosthetic aortic valve was imaged using a MicroCT scanner system (Scanco Medical, scan parameters: 90kV, 88μA, voxel size 24.6μm) followed by segmentation and reconstruction in Mimics (Materialise, Inc., Plymouth, MI) with an output STL file format (similar to Ref. [17]). The measured annulus diameter was 22.5mm, and the average thickness of the leaflet was ~0.6mm. A custom-designed MATLAB (The MathWorks, Inc., Natick, MA) program was created to rescan the contours of the irregular geometries for each leaflet, and the ventricular and aortic surfaces of each leaflet were approximated to create a volume spanning the distance between these surfaces using ANSYS (ANSYS, Canonsburg, PA). Figures 1(a) and 1(b) show the stereolithography (STL) geometry of the valve and the valve geometry after meshing. Geometric data from ANSYS was imported into fe software LS-Dyna 971 (LSTC, Livermore, CA). Friction between the leaflets was not considered. The simulation time was accelerated by shortening the time over which the physiological pressure differential between the aorta and the left ventricle was applied by ten times, as previous analyses with real-time and scaled time yielded results within 2% due to small inertial loads thus showing that the acceleration in loading was insignificant [18]. A central difference explicit method was used as the time-wise solver with an automatic time-step update to achieve numerical stability of the solution; the ratio of internal energy to strain energy in the simulations was >95%, indicating a stable converged solution.
Fig. 1.
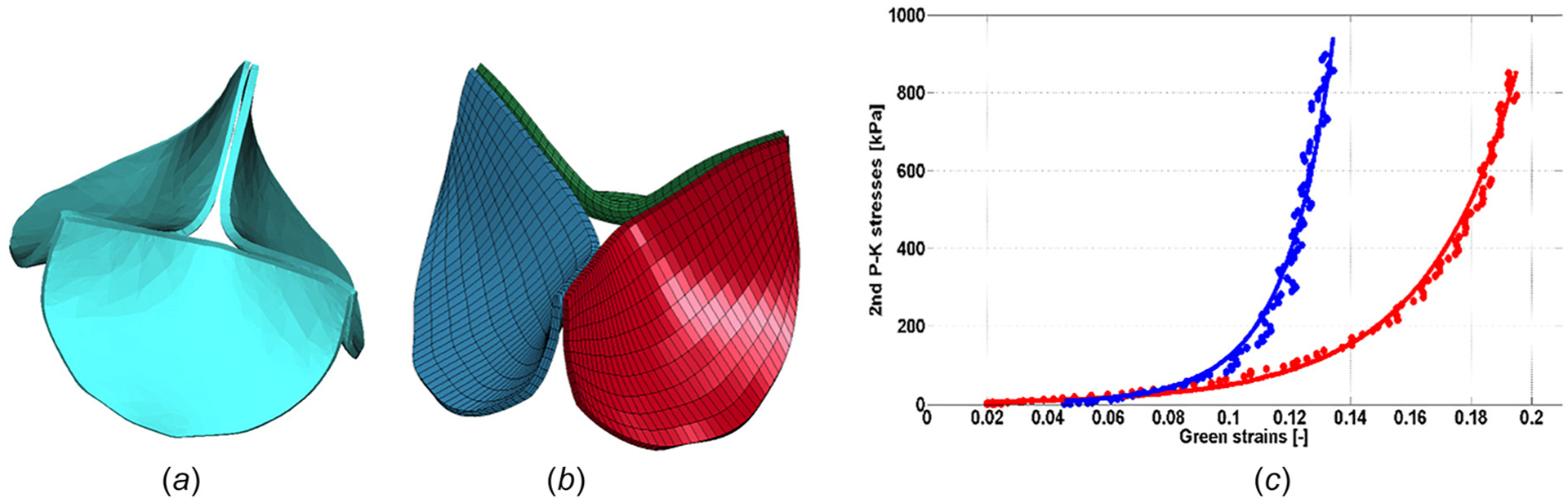
The geometry of the prosthetic aortic valve (a) imaged using a MicroCT scanner system and reconstructed using Mimics, (b) after meshing in ANSYS (the leaflets were evenly meshed resulting in 3,600 eight-noded brick elements for the whole valve), and (c) experimental data of a glutaraldehyde-fixed bovine pericardium from Ref. [21] (solid circles) fitted to Guccione’s model (solid lines); blue and red colors represent the data pertaining to fiber and cross-fiber directions, respectively
Material Properties.
The material properties of the glutaraldehyde-fixed bovine pericardium leaflets were obtained from planar biaxial experiments and published in Ref. [19–21]. For this study, experimental data from Kim et al. [21] were used to fit to Guccione’s material model (Table 1, Fig. 1(c), previously used in Ref. [18]). The stress and strain data used do not extend beyond ~13% strain for fiber and ~19% strain for cross fiber directions (Fig. 1(c)). The principal directions of the anisotropic model for the leaflets were defined by the edges of the hexahedral elements, with the stiffer (fiber) direction running mostly circumferentially (Fig. 1(b)), and the softer directions being radial and through the thickness.
Table 1.
Material constants for Guccione’s model, derived from an equibiaxial protocol [20]
| c1 (kPa) | C 2 | C 3 | C 4 | R2-FD | R2-XD |
|---|---|---|---|---|---|
| 1.50 (0.10) | 28.69 (0.80) | 45.98 (0.69) | 0.00 (1.82) | 0.99 | 1.00 |
The strain energy function W was expressed in LS-Dyna as , where c1 – c4 are the material constants, Exy are the deformations (green strain components modified to only include the effects of volumetric work), and xy refers to the subscripts θ, z, and r corresponding to the circumferential, through-thickness, and radial directions, respectively. P is a Lagrange multiplier numerically enforcing the material nearincompressibility whereby J, the determinant of the deformation gradient tensor, is almost equal to 1. The values in parentheses report half the span of the 95% confidence interval. R2-FD and R2-XD represent Pearson’s product–moment correlation coefficients in fiber and cross-fiber directions, respectively.
Deformed Valve Configurations and Boundary Conditions.
Two sets of annular deformations were considered to study several potential noncircular configurations:
-
(1)
The area-preserved deformation where the circular area of the valve was preserved (consistent with Ref. [15]).
-
(2)
The area-reduced deformation where the valve area was reduced with a constraint of the maximum diagonal length of the deformed valve to be equal to the control valve diameter, except for the area-reduced circular configuration where the diameter of the valve was reduced.
Besides the control (circular) configuration, twelve area-preserved and area-reduced noncircular configurations, and four area-reduced circular configurations were considered [2–4,15]. The deformed configurations were simulated previously in Ref. [15] using shape factors as defined below.
-
(1)
Elliptical-major (EllipMajor): with a commissure aligned along the major axis.
-
(2)
Elliptical-minor (EllipMinor): with a commissure aligned along the minor axis.
Deformation in EllipMajor and EllipMinor configurations was determined by the eccentricity of an ellipse, de, defined as , where b and a are the length of the minor and major axes of the ellipse, respectively.
-
(3 and 4)
D-Shape: a combination of partly elliptical and partly circular configurations. The D-Shape deformation, dd, was defined as the ratio of the radius of the semicircle to the semi-minor axis length of the semi-ellipse. D-Shape 1 and D-Shape 2 have commissures aligned along the minor and major axis, respectively.
-
(5)
Tri-vertex: triangular shape with commissures located at the vertices. The Tri-vertex deformation, dv, was defined as the ratio of the distance from the middle of the attachment (or suturing) line to the commissural chord, before and after deformation.
-
(6)
Tri-sides: triangular shape with commissures located at the middle of the triangle sides. The Tri-Sides deformation, ds, was calculated as the ratio of the distance from a commissure to the line connecting the midpoints of the adjacent attachment (or suturing) lines, before and after deformation.
-
(7)
Area-reduced Circular: C-ratio was defined as the control valve diameter to the diameter of a circularly deformed valve.
The control valve was deformed to obtain the desired noncircular and unpressurized shape with residual stresses, and the pressure was ramped from 0 to 80mmHg to represent physiologically relevant conditions before the cardiac cycle started in early systole. To simulate one cardiac cycle, a time-varying pressure difference between the aorta and the left-ventricle of the heart was applied to the ventricular side of the valve [18] (with systolic to diastolic pressure of 120–80 mmHg). The duration of diastole was shortened to 0.1 s (from 0.6 s) to save computational time.
Postprocessing.
The maximum values of von Mises mechanical stress (VMS) in the leaflets were determined, along with their location and timing, since VMS is often construed as a durability indicator. Clinically, a measure of aortic valve area (AVA) reflects the degree of valve stenosis and regurgitation reflects the efficiency of valve function. Clinical recommendations for grading stenotic and regurgitant valves are based on effective orifice area (EOA: calculated using the aortic positive pressure gradient and flow rate in the left ventricular outflow tract) and effective regurgitant orifice (ERO: calculated as ratio of regurgitant volume over regurgitant jet time-velocity integral), respectively, they are taken from echocardiographic measurements [22–25]. To estimate AVA and regurgitation from the simulations, the maximum geometric area orifice (GOA, the projected area left open by the leaflets during systole), regurgitant orifice area (ROA, the area left open by the leaflets at the end of diastole), and leaflet coaptation surface area (CSA, the sum of the areas of three coapting leaflets at the end of diastole with contact pressure of 0.1mmHg [26]) of the valve were measured in midsystole and end of diastole. With regard to stenosis and regurgitation, the GOA and ROA are the primary planimetric measurements from the simulations that were considered similar to EOA and ERO, respectively [27,28].
To substantiate the accuracy of the computational analysis for validation, the simulated valves were compared with prior in vitro hydrodynamic tests of the same bioprosthetic valves [15]. The geometries of the experimented and simulated area-preserved valves after prescribed deformation (i.e., unpressurized) and during valve opening (i.e., at midsystole) were similar, as depicted in Figs. 2 and 3, respectively. Comparison of the experimented and simulated area-preserved valve shape factors was similar (0.64 for elliptical configurations, 1.38 for D-Shapes, 1.2 for Tri-Vertex, and 1.35 for Tri-Sides configurations). The GOA of the simulated valves in the unpressurized condition after the deformation was slightly higher than that of the experimental valves; the impact of this was not substantial when the valve was pressurized during the cardiac cycle. The comparison of qualitative and quantitative aspects of deformation from experimented and simulated valves was acceptable.
Fig. 2.
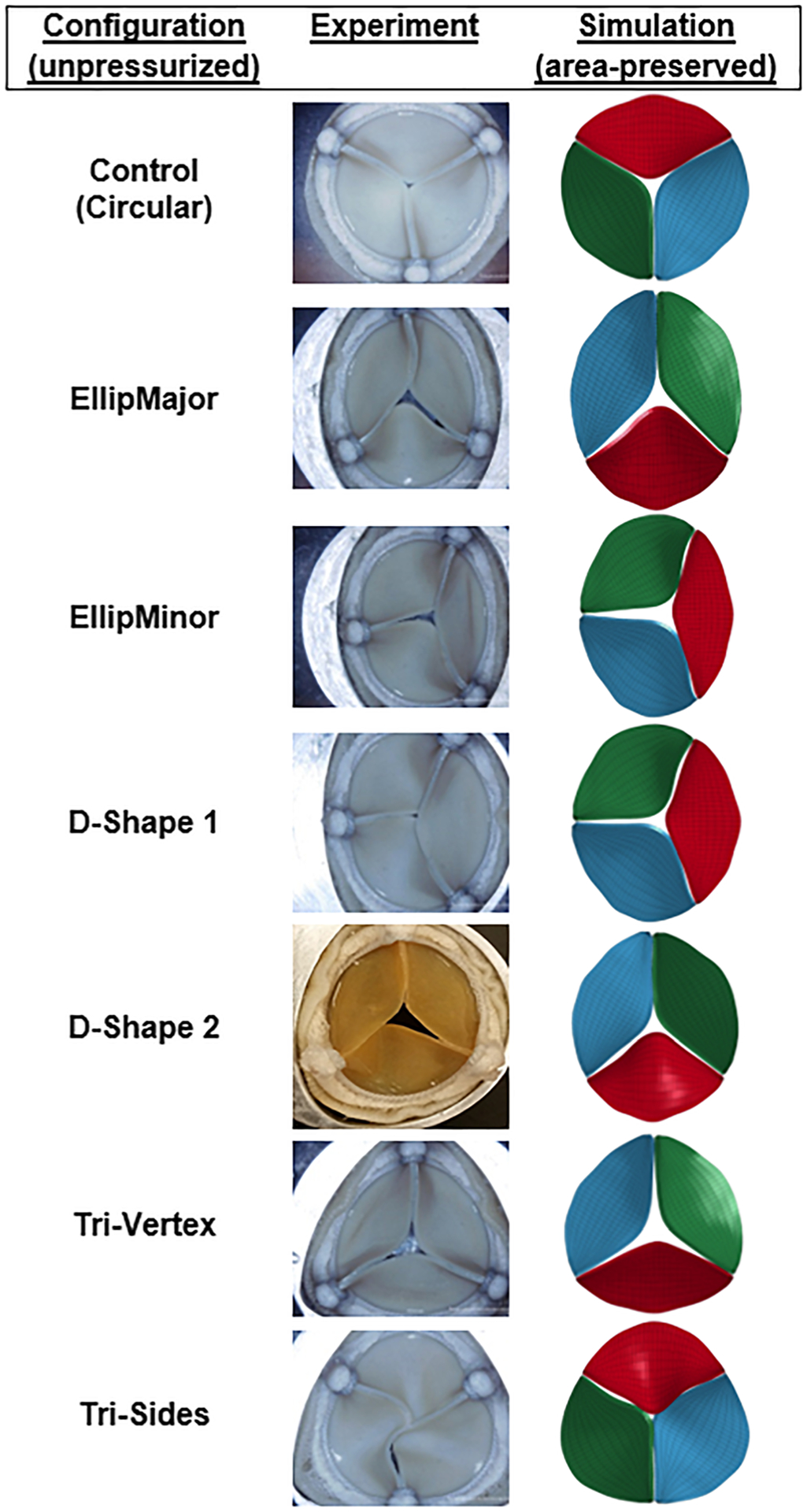
Top view of the experimented (reprinted by permission from Springer: Biomedical Engineering Society (BMES): Cardiovascular Engineering and Technology (CVET) [15], Copyright 2016; all pictures except D-shape 2) and simulated valves (area-preserved) in the unpressurized state in different configurations
Fig. 3.
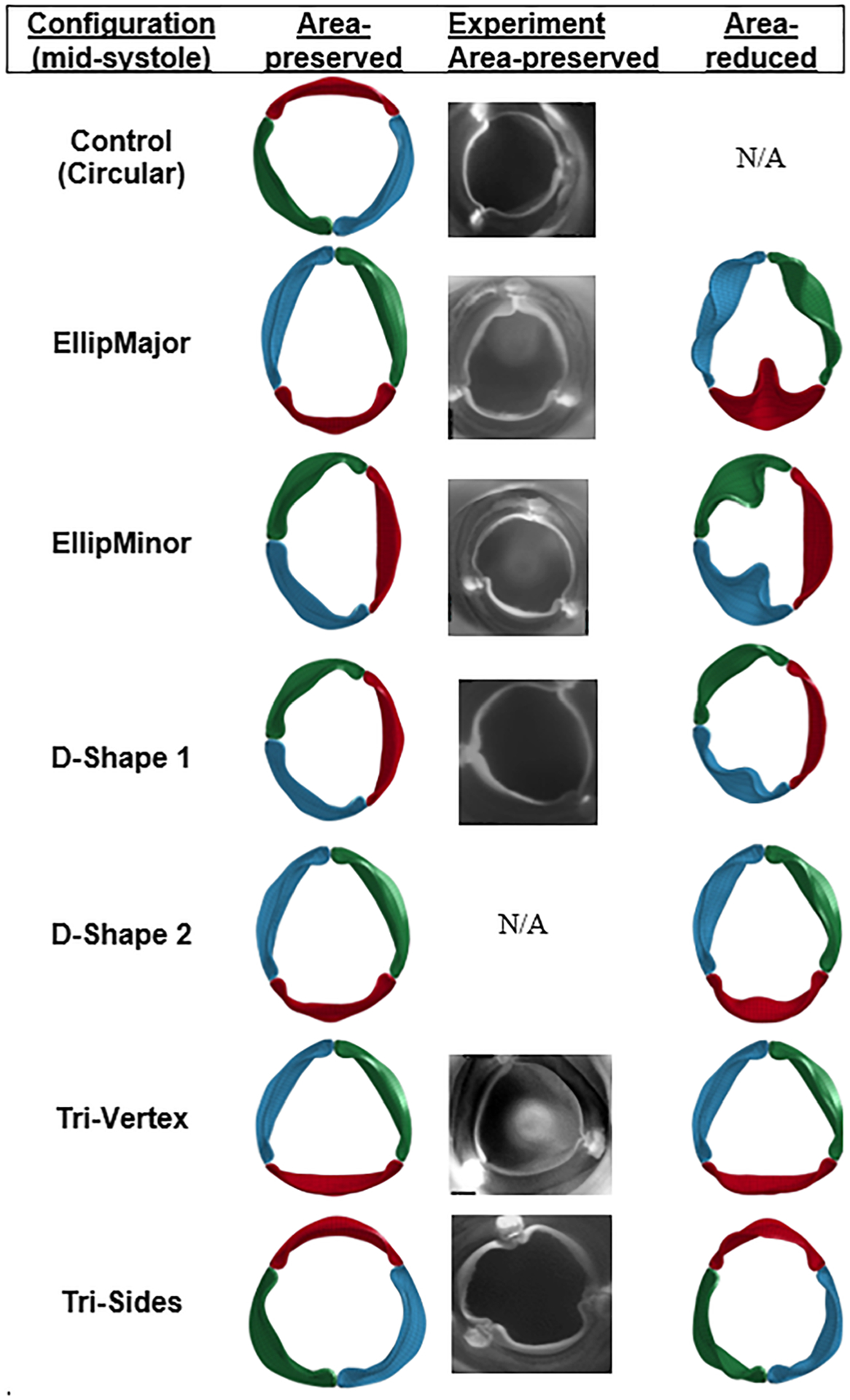
Top view of the simulated valves (area-preserved and area-reduced) and experimented valves (area-preserved) at midsystole in different configurations. Hydrodynamic experiments with D-Shape 2 were not performed. N/A indicates not applicable.
A mesh sensitivity study showed that the maximum stress in diastole increased by 19%, and the maximum stress in systole and the coaptation surface area decreased by 15% and 22%, respectively, when using the finer mesh. However, GOA, ROA, and valve closing and opening velocities (CV, OV) did not change substantially between the two meshes in the control circular valve (Table 2). A single simulation with a coarse mesh took ~4h to complete on a workstation with two Intel Xeon E5640 2.67GHz 4-core processors and 6 GB of random access memory (RAM). The run time depended on the complexity of the interference between the neighboring leaflets. The difference in maximum stress was ~20% between the coarse and fine mesh; however, the coarser mesh was chosen for solution convergence to save computational time and further to quantify relative differences between simulated configurations.
Table 2.
The parameters of the circular control valve dynamics using two different meshes
| Mesh type | GOA (cm2) | OV (cm2/s) | CVs (cm2/s) | CVr (cm2/s) | VMSsys (MPa) | ROA (mm2) | CSA (mm2) | VMS1 (MPa) | VMS2 (MPa) | vms3 (MPa) | VMSdia (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Normal | 2.6 | 42 | 2 | 42 | 0.41 | 0.5 | 111 | 0.836 | 0.505 | 0.663 | 0.836 |
| Fine | 2.6 (0) | 42 | 6 | 53 | 0.35 (−15) | 0.4 | 87 (−22) | 0.999 (19) | 0.621 (23) | 0.803 (21) | 0.999 (19) |
The percentage difference relative to the normal mesh is given in parentheses. Normal (fine) mesh consisted of 40 (50) brick elements along the leaflet free edge length and the proximal attachment line, 10 (20) elements along the commissures and the leaflet height, and 3 (3) elements across the leaflet thickness.
Results
Effect of Varying Noncircular Configurations on Leaflet Kinematics and Valve Performance.
The geometric valve configurations open fully in midsystole except in area-reduced elliptical (Fig. 3) and circular configurations with C-ratio ≥1.15 (Fig. 4). Area-reduced valves showed lower GOA compared to area-preserved ones for each configuration, with substantial decrease in GOA with elliptical configurations (comparing Figs. 5(a) and 5(b)). The maximum GOA for each configuration is shown in Fig. 5(c) and also given in Tables 3 and 4 for area-preserved and area-reduced valves, respectively. Unlike the area-reduced configurations, area-preserved valves showed comparable maximum GOA and opening and closing velocities with respect to the control valve (Table 3). The area-preserved configurations qualitatively showed varying degrees of leaflet bending and curvature along the free edge of the leaflet at midsystole among leaflets in the same valve configuration (such as EllipMajor and EllipMinor) and also among valves (such as Tri-Vertex and Tri-Sides) (see Fig. 3). The area-reduced valves, however, exhibited incomplete opening of leaflets and increased bending of leaflets at the free edge at midsystole, particularly with the elliptical configurations. Like GOA, the ROA was higher in the area-preserved valves compared to the area-reduced ones (Fig. 5(d)); the largest ROA occurred in the elliptical configurations (Tables 3 and 4). Unlike GOA, the CSA was lower in area-preserved valves compared to area-reduced ones.
Fig. 4.
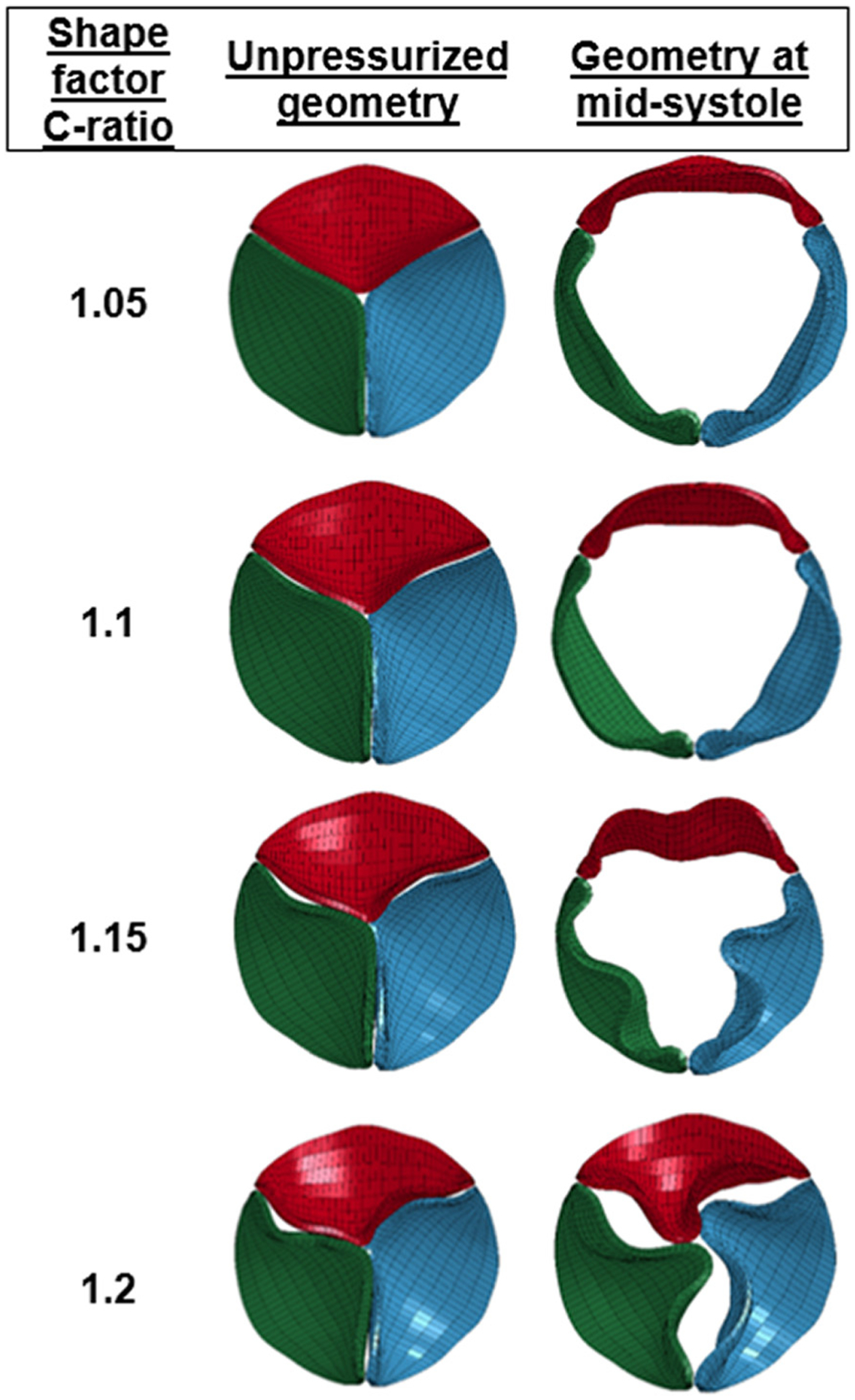
Top view of the area-reduced circular valves with different C-ratios at the beginning of the cardiac cycle and at midsystole. Hydrodynamic experiments with these area-reduced circular configurations were not performed.
Fig. 5.
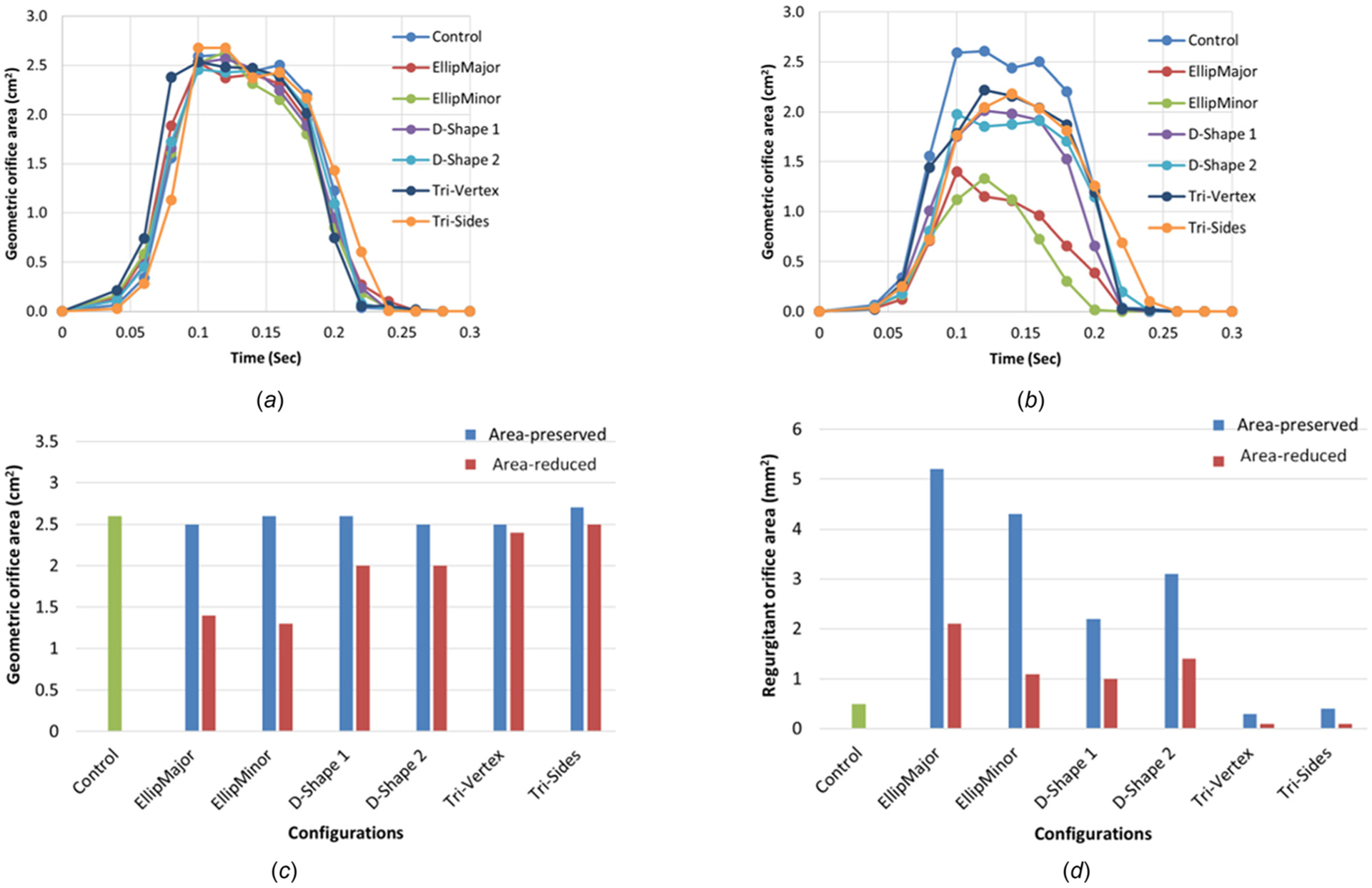
The variation of the geometric orifice area with time for (a) the area-preserved valves, (b) the area-reduced valves, (c) maximum GOA, and (d) ROA for the control, area-preserved, and area-reduced valves
Table 3.
Maximum GOA, opening and closing velocities (OV, CV), ROA, CSA, and maximum leaflet VMS for different area-preserved configurations
| Configuration | Shape factor | GOA (cm2) | OV (cm2/s) | CVS (cm2/s) | CVr (cm2/s) | VMSSyS (MPa) | ROA (mm2) | CSA (mm2) | VMS1 (MPa) | VMS2 (MPa) | vms3 (MPa) | VMSdia (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Control | _ | 2.6 | 42 | 2 | 42 | 0.41 | 0.5 | 111 | 0.836 | 0.505 | 0.663 | 0.836 |
| EllipMajor | 0.64 | 2.5 | 40 | 4 | 29 | 0.39 (−4) | 5.2 | 108 | 1.425 | 0.599 | 0.841 | 1.425 (70) |
| EllipMinor | 0.64 | 2.6 | 39 | 6 | 27 | 0.41 (2) | 4.3 | 104 | 0.941 | 0.796 | 0.793 | 0.941 (13) |
| D-Shape 1 | 1.38 | 2.6 | 40 | 5 | 28 | 0.44 (8) | 2.2 | 112 | 0.946 | 0.698 | 0.661 | 0.946 (13) |
| D-Shape 2 | 1.38 | 2.5 | 39 | 1 | 30 | 0.34 (−16) | 3.1 | 116 | 1.084 | 0.561 | 0.782 | 1.084 (30) |
| Tri-Vertex | 1.2 | 2.5 | 39 | 2 | 40 | 0.47 (15) | 0.3 | 115 | 0.732 | 0.427 | 0.52 | 0.732 (−12) |
| Tri-Sides | 1.35 | 2.7 | 44 | 4 | 30 | 0.36 (−11) | 0.4 | 115 | 1.187 | 0.747 | 0.97 | 1.187 (42) |
The percentage difference relative to the control case is given in parentheses. Subscripts 1, 2, and 3 refer to the red, blue, and green leaflets, respectively (shown in Fig. 3).
Table 4.
Maximum GOA, opening and closing velocities (OV, CV), CSA, and maximum leaflet VMS for different area-reduced configurations
| Configuration | Shape factor | GOA (cm2) | OV (cm2/s) | CVS (cm2/s) | CVR (cm2/s) | ROA (mm2) | CSA (mm2) | VMS1 (MPa) | VMS2 (MPa) | vms3 (MPa) | VMSdia (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Control | _ | 2.6 | 42 | 2 | 42 | 0.5 | 111 | 0.836 | 0.505 | 0.663 | 0.836 |
| EllipMajor | 0.64 | 1.4 | 23 | 9 | 16 | 2.1 | 156 | 1.116 | 0.515 | 0.82 | 1.116 (33) |
| EllipMinor | 0.64 | 1.3 | 18 | 10 | 8 | 1.1 | 151 | 0.649 | 0.667 | 0.68 | 0.680 (−19) |
| D-Shape 1 | 1.38 | 2.0 | 28 | 3 | 38 | 1.0 | 129 | 0.748 | 0.623 | 0.657 | 0.748 (−11) |
| D-Shape 2 | 1.38 | 2.0 | 32 | 3 | 43 | 1.4 | 144 | 1.059 | 0.549 | 0.796 | 1.059 (27) |
| Tri-Vertex | 1.2 | 2.4 | 29 | 1 | 47 | 0.1 | 129 | 0.753 | 0.432 | 0.61 | 0.753 (−10) |
| Tri-Sides | 1.35 | 2.5 | 29 | 1 | 39 | 0.1 | 130 | 1.034 | 0.591 | 0.822 | 1.034 (24) |
| Circular | 1.05 | 2.2 | 34 | 1 | 33 | 0.1 | 136 | 0.880 | 0.527 | 0.711 | 0.880 (5) |
| Circular | 1.10 | 1.8 | 27 | 1 | 28 | 0.0 | 147 | 0.888 | 0.489 | 0.666 | 0.888 (6) |
| Circular | 1.15 | 1.4 | 17 | 2 | 16 | 0.0 | 150 | 0.655 | 0.468 | 0.525 | 0.655 (−22) |
| Circular | 1.20 | 0.8 | 19 | 2 | 12 | 0.0 | 164 | 0.680 | 0.485 | 0.525 | 0.680 (−19) |
The percentage difference relative to the control case is given in parentheses. Subscripts 1, 2, and 3 refer to the red, blue, and green leaflets, respectively (shown in Fig. 3).
Leaflet Stress and Strain Distributions in the Noncircular Configurations.
The VMS and green strain distributions in the leaflets at the end of diastole for the area-preserved and the area-reduced valves are depicted in Figs. 6 and 7. In all configurations, the maximum stress and strain occurred in late diastole and in the regions near commissures (commonly found in stress analysis of bioprosthetic heart valves). Peak strains near the commissures were ~90%. The maximum VMS values of each leaflet at the end of diastole are given in Tables 3 and 4 for area-preserved and area-reduced valves, respectively. Subscripts 1, 2, and 3 refer to the red, blue, and green leaflets, respectively (Fig. 3). The maximum stress in the three leaflets was the highest in the area-preserved EllipMajor configuration, being 70% higher than the control circular configuration. To better resolve the stress distribution, each leaflet was divided into five regions: attachment, free edge, coaptation, commissure, and belly (Fig. 8 top left). In all the area-preserved configurations, the average VMS was the highest at the commissures and the lowest at the free edge region (Fig. 8(a)). In the D-Shape, Tri-Vertex, and Tri-Sides configurations, the average VMS was the lowest in the free edge region similar to the control (Fig. 8(a): d and e). In the elliptical configurations, the average VMS at the free edge region increased to be similar to the attachment, coaptation, and belly regions (Fig. 8(a): b and c); however, these average VMSs was lower than at the commissures. In all area-reduced configurations, the average VMS was the highest at the commissures and the lowest in the free edge region similar to the control (Fig. 8(b)). In the elliptical, D-Shape, and triangular configurations, the average VMS in the attachment region was higher than the stress in the free edge region and in the belly region (Fig. 8(b): a–c). In area-reduced circular configurations with C-ratios ≥1.15, the average stress in the attachment region was comparable to that in the commissures (Fig. 8(b): d–f).
Fig. 6.
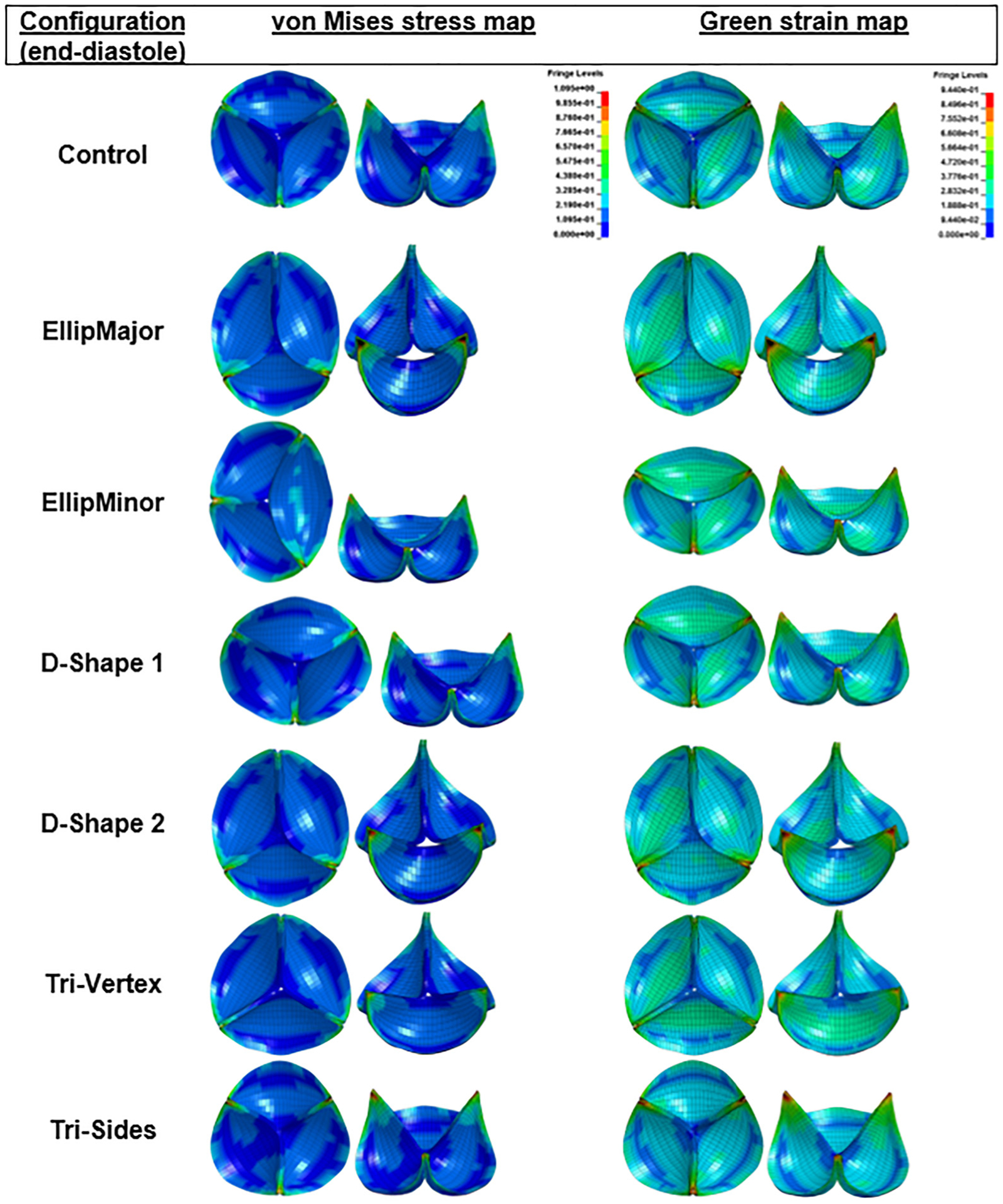
von Mises stress and green strain distributions of the area-preserved valves at the end of diastole in different deformation configurations (top and 45 deg tilted views). To help visualize regions of highest stresses and strains, both top and 45 deg tilted views are illustrated. To facilitate comparisons, the fringe levels were set to the same range for all the stress and strain distributions. All regions having stress values above the maximum value of the fringe are shown in black. Sagging and stretching of leaflets are also observed in the elliptical and D-Shape configurations.
Fig. 7.
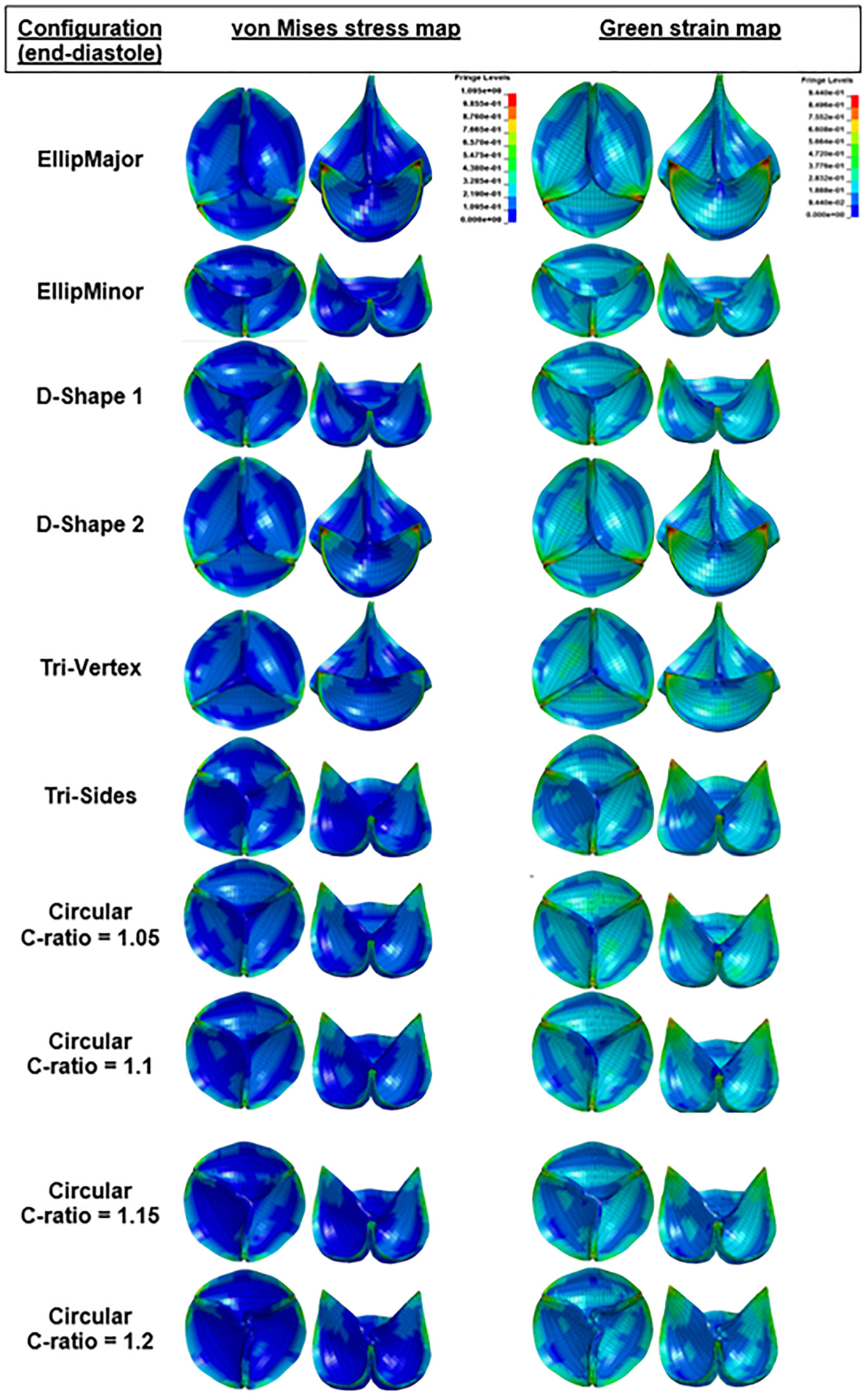
Stress and green strain distributions of the area-reduced valves at the end of diastole in different deformation configurations (top and 45 deg tilted views). The minimum and maximum of the fringe levels were set the same for all the stress or strain distributions for the sake of comparison. Sagging and stretching of leaflets are also observed in the elliptical and D-Shape configurations. Pin-wheeling observed in circular configuration with C-ratio = 1.2.
Fig. 8.
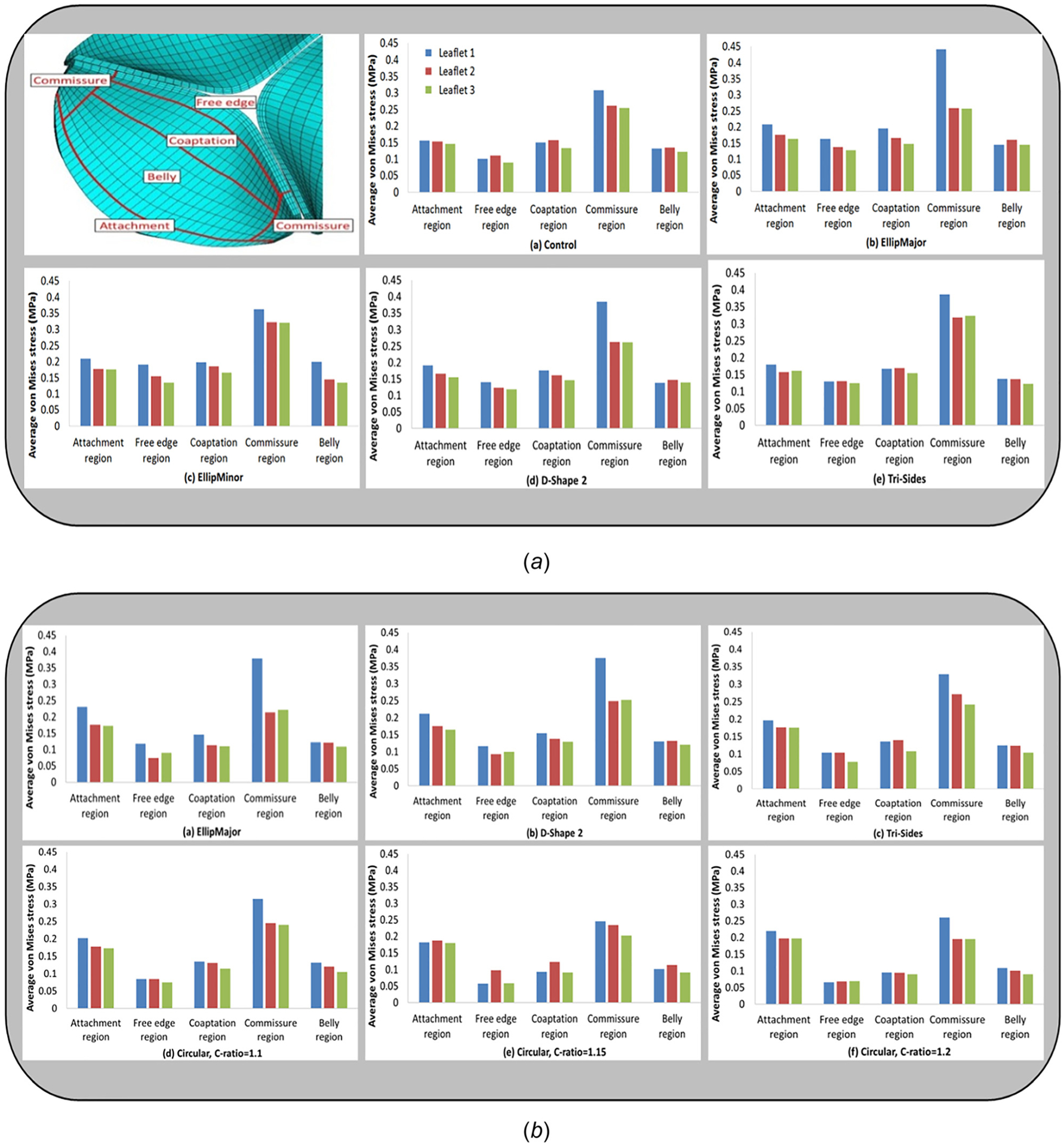
Illustration of five different sections of a leaflet: attachment, free edge, coaptation, commissure, and belly regions (top left). Average von Mises stress in five sections of interest (attachment, free edge, coaptation, commissure, and belly regions) on each of the leaflets for some area-preserved configurations ((a): a–e) and area-reduced configurations ((b): a–f).
Discussion
Review of 45 clinical studies on 12,926 Transcatheter aortic valve replacement (TAVR) patients reported valve undersizing (susceptible to orifice area reduction) to be prevalent [29,30]. Several studies show the valve-in-valve technique caused the second valve implanted to be undersized in order to help prevent coronary obstruction [31,32]. Each TAV manufactured has an intended (nominal) orifice area; however, differences from nominal deployment are reported. Zegdi et al. reported that underdeployment (≥3 mm difference between the aortic annulus and the stent external diameter) was present in all bicuspid valves they studied. The shape of the stent was mostly noncircular for both tricuspid and bicuspid valves with ellipticity prevalent in bicuspid valves [3]. Willson et al. evaluated computed tomography (CT) and transesophageal echocardiography (TEE) pre- and postimplantation data from 120 patients undergoing balloon-expandable TAVR procedures [33]. CT versus TEE measurements resulted in 20% versus 33.3% of patients receiving area-reduced valves, respectively. Due to the prevalence of undersizing and reduction of orifice area after valve implantation, our computational study focused on area-preserved and area-reduced configurations and their effect on valve leaflet stresses and strains, and other clinically relevant metrics such as maximum GOA, ROA, and CSA.
Effect of Noncircular Configurations on the Rate of Leaflet Motion During the Cardiac Cycle.
Handke et al. [34] calculated the EOA after examining 19 normal aortic valves using three-dimensional TEE. The maximum EOA determined by three-dimensional TEE was 2.70 ± 0.63 cm2, similar to the maximum GOA of the simulated control valve (2.6 cm2). Normal valve movement was observed to proceed in three phases: rapid OV, slow closing (CVS), and rapid closing (CVR); these velocities were measured to be 42 ± 23, 8.0 ± 5.2, 50 ± 23 cm2/s, respectively. The valve opening and rapid closing velocities for each simulated configuration were in the normal range (Tables 3 and 4) except for the area-reduced elliptical and circular configurations with C-ratio ≥1.15. Large variation in the velocities was reported from echocardiographic measurements of normal aortic valve patients (as mentioned previously); however, the relevant parameters from our simulations were within the range of those clinically measured.
Effect of Noncircular Configurations on Hydrodynamics, Specifically Aortic Valve Area and Regurgitation.
A valve with a threshold EOA < 1.5 cm2 or <1.0 cm2 is considered clinically to be moderately stenotic or severely stenotic, respectively [22,23]. Garcia et al. showed that for leaflets that are not severely calcified, the EOA may be approximated to GOA [27]. The stenosis indicator GOA does not have a 1:1 correlation with clinically measured EOA; however, GOA is used as a gross measure of stenosis here; if GOA is larger for a given geometry than another similar geometry, then the given geometry will tend to have a larger EOA. From Fig. 5(c) and Tables 3 and 4, all area-preserved configurations had GOA ranging from 2.5 to 2.7 cm2; however, area-reduced elliptical with shape factor of 0.64 and circular configurations with shape factor ≥1.15 were characterized as geometries having GOA < 1.5 cm2. The area-reduced circular configuration with shape factor 1.2 was the configuration with the lowest GOA of 0.8 cm2 and the only case which might result in a patient-prosthesis mismatch leading to reduced ventricular function over time. Area-reduced valves beyond a critical deformation shape factor of 1.14 for the circular configuration, 0.62 for the elliptical configurations, 1.6 for the D-Shape configurations, 1.55 for the Tri-Vertex, and 1.7 for the Tri-Sides configuration (Table 5) may result in lower AVAs, leading to variable flow mechanics and eventually a relatively higher risk of stenosis.
Table 5.
Shape factor threshold for each area-reduced configuration resulting in a maximum GOA of 1.5 cm2
| Configuration | Shape factor | CSA (mm2) | VMS1 (MPa) | VMS2 (MPa) | VMS3 (MPa) | VMSdia (MPa) |
|---|---|---|---|---|---|---|
| EllipMajor | 0.62 | 155 | 1.114 | 0.523 | 0.82 | 1.114 (33) |
| EllipMinor | 0.62 | 148 | 0.654 | 0.654 | 0.642 | 0.654 (−22) |
| D-Shape 1 | 1.59 | 146 | 0.709 | 0.67 | 0.669 | 0.709 (−15) |
| D-Shape 2 | 1.63 | 155 | 1.093 | 0.521 | 0.786 | 1.093 (31) |
| Tri-Vertex | 1.55 | 160 | 0.565 | 0.5 | 0.438 | 0.565 (−32) |
| Tri-Sides | 1.7 | 143 | 0.942 | 0.742 | 0.755 | 0.942 (13) |
| Circular | 1.14 | 148 | 0.687 | 0.478 | 0.559 | 0.687 (−18) |
A valve with a threshold ERO of 10 mm2, 10–29 mm2, or ≥30 mm2 is considered clinically to be mildly regurgitant, moderately regurgitant, or severely regurgitant, respectively [23,24]. Mizushige et al. showed from a study of 22 patients with chronic aortic regurgitation that ERO correlated well with ROA [25]. The regurgitation indicator ROA does not have a 1:1 correlation with clinically measured ERO, which may be para- and intravalvular leakage combined in TAVs with the former being more dominant in total regurgitation leakage. However, ROA is used as a gross measure of intravalvular leakage here. ROA was larger in the area-preserved elliptical configurations (4.3–5.2 mm2) compared to the control (0.5 mm2, Fig. 5(d) and Table 3); however, all the valves had an ROA much lower than the threshold for characterizing regurgitation. Therefore, regurgitation was not an issue in any of the area-preserved or area-reduced valves. This indicated intravalvular leakage is not substantially affected by these noncircular configurations as paravalvular leakage appears to play a more dominant role in total regurgitation leakage for TAVs and associated mortality [1]. The leaflet CSA did not change substantially in area-preserved configurations (Table 3), but increased in area-reduced valves compared to the control (Table 4) as the leaflets get closer together, which increased the CSA and further decreased the ROA [17].
All simulated configurations were ranked according to GOA, ROA, CSA, and VMS metrics (Table 6) to help assess most challenging configurations for bench testing from a combination of factors. The impact of each metric and therefore the ranking of configurations were different. In area-preserved configurations, GOA was maintained in spite of slight differences in ROA (Table 3). Decreases in ROA resulted in increases in GOA (Table 4) with the exception of area-reduced circular configurations, while increases in CSA resulted in decreases in GOA with area-reduced circular configurations. Due to the differences with how noncircularity may affect the interrelationships between GOA, ROA, and CSA, these metrics may be used carefully when inferring valve performance based on simulations. Although ROA and CSA may be evaluated using a static computational analysis, GOA can be evaluated only using a dynamic computational analysis.
Table 6.
Ranking order of all simulated configurations for GOA, ROA, CSA, and VMS
| Configuration | Shape factor | GOA (cm2) | ROA (mm2) | CSA (mm2) | VMSdia (MPa) |
|---|---|---|---|---|---|
| Control | _ | 2 | 9 | 10 | 8 |
| Area-preserved EllipMajor | 0.64 | 3 | 1 | 11 | 1 |
| Area-preserved EllipMinor | 0.64 | 2 | 2 | 12 | 7 |
| Area-preserved D-Shape 1 | 1.38 | 2 | 4 | 9 | 7 |
| Area-preserved D-Shape 2 | 1.38 | 3 | 3 | 7 | 4 |
| Area-preserved Tri-Vertex | 1.2 | 3 | 11 | 8 | 11 |
| Area-preserved Tri-Sides | 1.35 | 1 | 10 | 8 | 2 |
| Area-reduced EllipMajor | 0.64 | 7 | 5 | 1 | 3 |
| Area-reduced EllipMinor | 0.64 | 8 | 7 | 2 | 12 |
| Area-reduced D-Shape 1 | 1.38 | 6 | 8 | 6 | 10 |
| Area-reduced D-Shape 2 | 1.38 | 6 | 6 | 4 | 5 |
| Area-reduced Tri-Vertex | 1.2 | 5 | 12 | 6 | 9 |
| Area-reduced Tri-Sides | 1.35 | 4 | 12 | 5 | 6 |
| Area-reduced Circular | 1.15 | 8 | 13 | 3 | 13 |
Based on the specific metric of interest, the configurations that ranked among the top three were highlighted in bold and gray.
Effect of Noncircular Configurations on Valve Leaflet Coaptation and Kinematics.
The degree of coaptation between the leaflets varied between the area-preserved and area-reduced configurations (Figs. 6 and 7). The existence of sagging and stretched leaflets in the same valve has been shown previously (e.g., EllipMajor and EllipMinor configurations in Fig. 6) based on the degree of coaptation between the leaflets [13–15]. In such valve configurations, stretched leaflets lie on top of sagging leaflets, and the length between any two commissures varies with each noncircular deformation. Therefore, the coaptation length, i.e., the length of the leaflet tissue along the free edge between commissures, could vary. Longer coaptation leaflet lengths between commissures may redistribute and lower the stresses, but also result in more abundant leaflet tissue causing pin-wheeling as seen in the circular configuration with a shape factor of 1.2 (Fig. 7). The differences in leaflet coaptation (in a closed valve) between area-preserved and area-reduced configurations could be evaluated using a simpler static analysis instead of the more complex dynamic analysis employed in this work. However, with the anisotropic dynamic analysis, the area-preserved configurations showed differences in leaflet kinematics (leaflet bending, curvature along the free edge of the leaflet) at midsystole among leaflets in the same valve configuration (e.g., EllipMajor and EllipMinor in Fig. 3) and also among valve configurations (e.g., Tri-Vertex and Tri-Sides). The area-reduced valves also showed differences in leaflet kinematics at midsystole, such as incomplete opening of leaflets and increased curvature in leaflets at the free edge likely due to increased leaflet coaptation length, particularly with the elliptical configurations (sagging leaflet colored red in EllipMajor configuration, and sagging leaflets colored green and blue in the EllipMinor configuration in Fig. 3). The above-mentioned specific differences in leaflet kinematics observed during the systolic and diastolic phases of the cardiac cycle in the noncircular configurations may be evaluated with the complex dynamic analysis compared to the simpler static analysis. Due to increased curvature, these sagging leaflets may have higher tensile stresses at the free edges of the leaflet from the inflow side. There is evidence that higher curvatures during bending can increase flexural compressive stresses, causing structural deterioration over time [35,36]. In addition, these leaflet patterns can only be observed with the dynamic analysis. Due to the lack of clinical bioprosthetic valve failure rates relating to structural deterioration, it is unclear to what extent these distinct leaflet coaptation and kinematic patterns (that exist in these noncircular configurations) may affect long-term leaflet wear and durability clinically.
Effect of Noncircular Configurations on Valve Leaflet Stresses.
In most area-preserved and area-reduced configurations (Fig. 8), the average VMS was the highest at the commissures and the lowest at the free edge. The attachment region had the second highest stress (Figs. 8(a) and 8(b)) particularly in the area-reduced configurations, while the stress in the coaptation and belly regions was comparable; in contrast, the stress in these regions were comparable in the area-preserved configurations. The commissure and the free edge stresses in the area-reduced configurations were lower and their attachment region stresses appeared to be slightly higher than those in the area-preserved configurations. Table 6 shows that the area-preserved EllipMajor, Tri-Sides, and area-reduced EllipMajor configurations have the top three maximum VMS, followed by the area-preserved and area-reduced D-Shape 2 configuration. Duraiswamy et al. [15] showed EllipMinor was one of the configurations with the maximum principal stress; however, it was located near the center of the free edge of stretched leaflets. In Ref.[15], the most challenging configurations with high leaflet stresses were EllipMinor followed by EllipMajor and D-Shape configurations. Simulations were performed in Ref. [15] using isotropic material properties and shell elements for the leaflets and regions near the commissures showed high leaflet stresses. On the contrary, our current simulations used anisotropic material properties and solid elements for the leaflets. If area-preserved configurations were alone ranked in order to compare with the results of Ref. [15], the most challenging configurations with high leaflet stresses were EllipMajor, Tri-Sides, and D-Shape 2 (Table 3). Current simulations also show that commissures are the regions of the highest stress in all configurations (Figs. 6–8) and therefore indicate that the commissures could potentially be the regions where first signs of structural deterioration may occur. With both the isotropic quasi-static simulations as in Ref. [15] and the current anisotropic dynamic simulations, the ranking order for most challenging area-preserved configurations (as seen previously) was not the same; however, EllipMajor was a common area-preserved configuration predicted by both analysis that was deemed to have high leaflet commissure stresses. The highest commissural stress occurred in one of the stretched leaflets in both the area-preserved and area-reduced EllipMajor configurations (colored blue in Figs. 2 and 8). Figure 8 showed that the average free edge stresses were slightly higher in the area-preserved noncircular configurations (except for Tri-Vertex configuration which was similar to circular configuration) than the circular control, indicating that the degree of coaptation between leaflets also affects the free edge stresses. The greater the coaptation area between the leaflets, the lower the leaflet stress [16,17]. The free edge VMS are the lowest, suggesting that the free edge is the least likely location for failure. However, some recent evidence from bench testing indicated that in addition to commissure tears, the more sagging in a leaflet, the greater the likelihood of free edge tears in the leaflet and therefore reduced durability [37,38]. More reliable fatigue damage models are needed to understand the primary modes of leaflet failure (particularly sagging leaflets) and long-term performance of the TAV undergoing varying leaflet kinematics in vivo.
There are several limitations to this study. A surgical bioprosthetic valve was used to approximate the behavior of a bioprosthetic TAV because of similarities in purpose and basic leaflet configurations. The geometrical modeling captured the details of only one bioprosthetic valve to a high resolution (24.6μm voxels in MicroCT scans), including minor manufacturing variations. However, the thickness of the leaflets was larger than that in generic TAVs [13]; the attachment of the leaflets to the valve components was also different from generic TAVs. Sensitivity analyses of a variety of constitutive models on the resulting strain field in the leaflet can be challenging to assess in a dynamic analysis with nonlinear hyperelastic pericardial soft tissues but may be evaluated in the future. Bioprosthetic pericardial leaflets are anisotropic in nature; sensitivity studies using isotropic and anisotropic material properties with both shell and solid elements in the future may further elucidate the importance of choosing anisotropic versus isotropic material properties for the leaflets when investigating clinically relevant aspects of noncircular valve configurations. The valve stent frame was rigid, which would tend to overestimate the stresses by constraining the leaflet material (with short coaptation length) more than they would be in a flexible frame. The fluid frictional forces on the leaflets and viscous damping due to blood were ignored, although valve dynamics were achieved using a timewise varying pressure distribution as valvular loads [39]. Although there were differences in results between the coarse and fine mesh, the computational model with the coarse mesh was validated in a limited qualitative and quantitative sense. Fluid–structure interactions and other validation methods for estimating accurate physiological leaflet loading may be considered in the future. The conclusions from this study are meaningful in a comparative sense.
In conclusion, the effects of circular and six noncircular postdeployment TAV configurations on valve function using clinically relevant performance metrics such as leaflet stresses, maximum GOA, ROA, and CSA were investigated through dynamic finite element modeling of a marketed surgical bioprosthetic heart valve. Among all configurations, the EllipMajor configuration (both area-preserved and area-reduced) experienced the maximum leaflet stress at the commissures of one of the stretched leaflets and had the maximum ROA; increasing noncircularity in area-preserved configurations such as with elliptical and D-Shape increased regurgitation. In addition, the area-reduced elliptical and circular configurations with shape factor ≥1.15 had the lowest GOAs, and the free edges of the sagging leaflets in these area-reduced configurations showed increased bending during systole and pin-wheeling during diastole, suggesting likely increased stenosis due to under-expansion. The dynamic computational analysis was important to evaluate the clinically relevant leaflet characteristics such as leaflet kinematics and GOA in noncircular valve configurations; however, static computational analysis may be sufficient for evaluating leaflet commissural stresses, coaptation patterns, and ROA in noncircular valve configurations. The framework described herein along with the findings could assist in the selection of proper valve geometric configurations for a specific TAV design using the clinically relevant performance metrics with the dynamic computational analysis for further hydrodynamic and durability bench testing.
Acknowledgment
We are thankful for support from the FDA’s Office of Women’s Health grants and the ORISE Research Participation Program at the FDA/CDRH, administered by the Oak Ridge Institute for Science and Education through an interagency agreement between the U.S. Department of Energy and FDA/CDRH. We thank Srinidhi Nagaraja, Jason Galginaitis, and Laura Bracaglia, for helping us with MicroCT reconstruction of the valve. Thanks to Benjamin Desvaux and Gabriel Sportes for their matlab programs to reconstruct the valve geometry from STL data. We appreciate the assistance of Edwards Lifesciences in the purchase of valves and constructive discussions on some results of this study.
The mention of commercial products, their sources or their use in connection with materials reported herein is not to be construed as either an actual or implied endorsement of such products by the Department of Health and Human Services.
Nomenclature
- AVA
aortic valve area
- C-ratio
deformation ratio for area-reduced circular configuration
- CSA
coaptation surface area
- CVR
rapid closing velocity
- CVS
slow closing velocity
- d d
D-Shape deformation ratio
- d e
ellipse eccentricity
- d s
Tri-Sides deformation ratio
- d v
Tri-Vertex deformation ratio
- EOA
effective orifice area (dynamic measure of AVA)
- ERO
effective regurgitant orifice
- GOA
geometric orifice area (planimetric measure of AVA)
- OV
valve opening velocity
- P dia
diastolic pressure
- P sys
systolic pressure
- R2-FD
Pearson product–moment correlation coefficients in fiber direction
- R2-XD
Pearson product–moment correlation coefficients in cross-fiber direction
- ROA
regurgitant orifice area (planimetric measure of ERO)
- VMS
maximum leaflet von Mises stress
- VMSdia
maximum von Mises stress in diastole
- VMSsys
maximum von Mises stress in systole
- VMS1
maximum von Mises stress of leaflet 1 (red) in diastole
- VMS2
maximum von Mises stress of leaflet 2 (blue) in diastole
- VMS3
maximum von Mises stress of leaflet 3 (green) in diastole
Footnotes
This work is in part a work of the U.S. Government. ASME disclaims all interest in the U.S. Government’s contributions.
Contributor Information
Reza Jafar, Cardiovascular Mechanics Laboratory, Department of Mechanical Engineering, University of Ottawa, Ottawa, ON K1N 6N5, Canada.
Michel R. Labrosse, Cardiovascular Mechanics Laboratory, Department of Mechanical Engineering, University of Ottawa, Ottawa, ON K1N 6N5, Canada
Jason D. Weaver, Division of Applied Mechanics (DAM), Office of Science and Engineering Laboratories (OSEL), Center for Devices and Radiological Health (CDRH), Food and Drug Administration (FDA), Silver Spring, MD 20993
Stephen M. Retta, Office of Product Evaluation and Quality (OPEQ), Center for Devices and Radiological Health (CDRH), Food and Drug Administration (FDA), Silver Spring, MD 20993
Changfu Wu, Office of Product Evaluation and Quality (OPEQ), Center for Devices and Radiological Health (CDRH), Food and Drug Administration (FDA), Silver Spring, MD 20993.
Nandini Duraiswamy, Division of Applied Mechanics (DAM), Office of Science and Engineering Laboratories (OSEL), Center for Devices and Radiological Health (CDRH), Food and Drug Administration (FDA), 10903 New Hampshire Avenue, WO62, #2206, Silver Spring, MD 20993.
References
- [1].Dasi LP, Hatoum H, Kheradvar A, Zareian R, Alavi H, Sun W, Martin C, Pham T, Wang Q, Midha PA, Raghav V, and Yoganathan AP, 2017, “On the Mechanics of Transcatheter Aortic Valve Replacement,” Ann. Biomed. Eng, 45(2), pp. 310–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Schultz CJ, Weustink A, Piazza N, Otten A, Mollet N, Krestin G, van Geuns RJ, de Feyter P, Serruys PW, and de Jaegere P, 2009, “Geometry and Degree of Apposition of the CoreValve ReValving System With Multislice Computed Tomography After Implantation in Patients With Aortic Stenosis,” J. Am. Coll. Cardiol, 54(10), pp. 911–918. [DOI] [PubMed] [Google Scholar]
- [3].Zegdi R, Ciobotaru V, Noghin M, Sleilaty G, Lafont A, Latremouille C, Deloche A, and Fabiani JN, 2008, “Is It Reasonable to Treat All Calcified Stenotic Aortic Valves With a Valved Stent? Results From a Human Anatomic Study in Adults,” J. Am. Coll. Cardiol, 51(5), pp. 579–584. [DOI] [PubMed] [Google Scholar]
- [4].Delgado V, Ng ACT, van de Veire NR, van der Kley F, Schuijf JD, Tops LF, de Weger A, Tavilla G, de Roos A, Kroft LJ, Schalij MJ, and Bax JJ, 2010, “Transcatheter Aortic Valve Implantation: Role of Multi-Detector Row Computer Tomography to Evaluate Prosthesis Positioning and Deployment in Relation to Valve Function,” Eur. Heart J, 31(9), pp. 1114–1123. [DOI] [PubMed] [Google Scholar]
- [5].Gooley RP, Cameron JD, and Meredith IT, 2015, “Assessment of Geometric Interaction Between the Lotus Transcatheter Aortic Valve Prosthesis and the Native Ventricular Aortic Interface by 320-Multidetector Computed Tomography,” JACC Cardiovasc. Interv, 8(5), pp. 740–749. [DOI] [PubMed] [Google Scholar]
- [6].Kuetting M, Sedaghat A, Utzenrath M, Sinning JM, Schmitz C, Roggenkamp J, Werner N, Schmitz-Rode T, and Steinseifer U, 2014, “In Vitro Assessment of the Influence of Aortic Annulus Ovality on the Hydrodynamic Performance of Self-Expanding Transcatheter Heart Valve Prostheses,” J. Biomech, 47(5), pp. 957–965. [DOI] [PubMed] [Google Scholar]
- [7].Milburn K, Bapat V, and Thomas M, 2014, “Valve-in-Valve Implantations: Is This the New Standard for Degenerated Bioprostheses? Review of the Literature,” Clin. Res. Cardiol, 103(6), pp. 417–413. [DOI] [PubMed] [Google Scholar]
- [8].Chen HL, and Liu K, 2016, “Clinical Outcomes for Transcatheter Valve-in-Valve in Treating Surgical Bioprosthetic Dysfunction: A Meta-Analysis,” Int. J. Cardiol, 212, pp. 138–141. [DOI] [PubMed] [Google Scholar]
- [9].Chevalier F, Leipsic J, and Genereux P, 2014, “Valve-in-Valve Implantation With a 23-mm Balloon-Expandable Transcatheter Heart Valve for the Treatment of a 19-mm Stentless Bioprosthesis Severe Aortic Regurgitation Using a Strategy of ‘Extreme’ Underfilling,” Catheter Cardiovasc. Interv, 84(3), pp. 503–508. [DOI] [PubMed] [Google Scholar]
- [10].Gurvitch R, Cheung A, Ye J, Wood DA, Willson AB, Toggweiler S, Binder R, and Webb JG, 2011, “Transcatheter Valve-in-Valve Implantation for Failed Surgical Bioprosthetic Valves,” J. Am. Coll. Cardiol, 58(21), pp. 2196–2209. [DOI] [PubMed] [Google Scholar]
- [11].Cribier A, Eltchaninoff H, Bash A, Borenstein N, Tron C, Bauer F, Derumeaux G, Anselme F, Laborde F, and Leon MB, 2002, “Percutaneous Transcatheter Implantation of an Aortic Valve Prosthesis for Calcific Aortic Stenosis: First Human Case Description,” Circulation, 106(24), pp. 3006–3008. [DOI] [PubMed] [Google Scholar]
- [12].Willson AB, Webb JG, Gurvitch R, Wood DA, Toggweiler S, Binder R, Freeman M, Madden M, Hague C, and Leipsic J, 2012, “Structural Integrity of Balloon-Expandable Stents After Transcatheter Aortic Valve Replacement: Assessment by Multidetector Computed Tomography,” JACC Cardiovasc. Interv, 5(5), pp. 525–532. [DOI] [PubMed] [Google Scholar]
- [13].Sun W, Li K, and Sirois E, 2010, “Simulated Elliptical Bioprosthetic Valve Deformation: Implications for Asymmetric Transcatheter Valve Deployment,” J Biomech, 43(16), pp. 3085–3090. [DOI] [PubMed] [Google Scholar]
- [14].Gunning PS, Saikrishnan N, Yoganathan AP, and McNamara LM, 2015, “Total Ellipse of the Heart Valve: The Impact of Eccentric Stent Distortion on the Regional Dynamic Deformation of Pericardial Tissue Leaflets of a Transcatheter Aortic Valve Replacement,” J. R. Soc. Interface, 12(113), p. 20150737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Duraiswamy N, Ekrami Y, Weaver JD, Retta SM, and Wu C, 2016, “A Parametric Computational Study of the Impact of Non-Circular Configurations on Heart Valve Leaflet Deformations and Stresses,” Cardiovasc. Eng. Technol, 7(2), pp. 126–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Abbasi M, and Azadani AN, 2015, “Leaflet Stress and Strain Distributions Following Incomplete Transcatheter Aortic Valve Expansion,” J. Biomech, 48(13), pp. 3663–3671. [DOI] [PubMed] [Google Scholar]
- [17].Claiborne TE, Xenos M, Sheriff J, Chiu W-C, Soares J, Alemu Y, Gupta S, Judex S, Slepian MJ, and Bluestein D, 2013, “Toward Optimization of a Novel Trileaflet Polymeric Prosthetic Heart Valve Via Device Thrombogenicity Emulation,” Asaio J, 59(3), pp. 275–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Labrosse MR, Lobo K, and Beller CJ, 2010, “Structural Analysis of the Natural Aortic Valve in Dynamics: From Unpressurized to Physiologically Loaded,” J. Biomech, 43(10), pp. 1916–1922. [DOI] [PubMed] [Google Scholar]
- [19].Sun W, Abad A, and Sacks MS, 2005, “Simulated Bioprosthetic Heart Valve Deformation Under Quasi-Static Loading,” ASME J. Biomech. Eng, 127(6), pp. 905–914. [DOI] [PubMed] [Google Scholar]
- [20].Sun W, and Sacks MS, 2005, “Finite Element Implementation of a Generalized Fung-Elastic Constitutive Model for Planar Soft Tissues,” Biomech. Model Mechanobiol, 4(2–3), pp. 190–199. [DOI] [PubMed] [Google Scholar]
- [21].Kim H, Chandran KB, Sacks MS, and Lu J, 2006, “An Experimentally Derived Stress Resultant Shell Model for Heart Valve Dynamic Simulations,” Ann. Biomed. Eng, 35(1), pp. 30–44. [DOI] [PubMed] [Google Scholar]
- [22].Baumgartner H, Hung J, Bermejo J, Chambers JB, Evangelista A, Griffin BP, Iung B, Otto CM, Pellikka PA, and Quiñones M, 2009, “Echocardiographic Assessment of Valve Stenosis: EAE/ASE Recommendations for Clinical Practice,” J. Am. Soc. Echocardiogr, 22(1), pp. 1–23. [DOI] [PubMed] [Google Scholar]
- [23].Nishimura RA, Otto CM, Bonow RO, Carabello BA, Erwin JP III, Fleisher LA, Jneid H, Mack MJ, McLeod CJ, O’Gara PT, Rigolin VH, Sundt TM III, and Thompson A, 2014, “2014 AHA/ACC Guidelines for the Management of Patients With Valvular Heart Disease: Executive Summary,” J. Am. Coll. Cardiol, 63(22), pp. 2438–2488. [DOI] [PubMed] [Google Scholar]
- [24].Zoghbi WA, Enriquez-Sarano M, Foster E, Grayburn PA, Kraft CD, Levine RA, Nihoyannopoulos P, Otto CM, Quinones MA, Rakowski H, Stewart WJ, Waggoner A, and Weissman NJ, 2003, “Recommendations for Evaluation of the Severity of Native Valvular Regurgitation With Two-Dimensional and Doppler Echocardiography,” J. Am. Soc. Echocardiogr, 16(7), pp. 777–802. [DOI] [PubMed] [Google Scholar]
- [25].Mizushige K, Nozaki S, Ohmori K, and Matsuo H, 2000, “Evaluation of Effective Aortic Regurgitant Orifice Area and Its Effect on Aortic Regurgitant Volume With Doppler Echocardiography,” Angiology, 51(3), pp. 241–246. [DOI] [PubMed] [Google Scholar]
- [26].Sohmer B, Hudson C, Atherstone J, Lambert AS, Labrosse MR, and Boodhwani M, 2013, “Measuring Aortic Valve Coaptation Surface Area Using Three-Dimensional Transesophageal Echocardiography,” Can. J. Anaesth, 60(1), pp. 24–31. [DOI] [PubMed] [Google Scholar]
- [27].Garcia D, and Kadem L, 2006, “What Do You Mean by Aortic Valve Area: Geometric Orifice Area, Effective Orifice Area, or Gorlin Area?,” J. Heart Valve Dis, 15(5), pp. 601–608. [PubMed] [Google Scholar]
- [28].Tribouilloy CM, Enriquez-Sarano M, Bailey KR, Seward JB, and Tajik J, 2000, “Assessment of Severity of Aortic Regurgitation Using the Width of the Vena Contracta: A Clinical Color Doppler Imaging Study,” Circulation, 102(5), pp. 558–564. [DOI] [PubMed] [Google Scholar]
- [29].Stäahli BE, Nguyen-Kim TD, Gebhard C, Erhart L, Frauenfelder T, Tanner FC, Falk V, Landmesser U, Nietlispach F, Luscher TF, Maier W, and Binder RK, 2015, “Prosthesis-Specific Predictors of Paravalvular Regurgitation After Transcatheter Aortic Valve Replacement: Impact of Calcification and Sizing on Balloon-Expandable Versus Self-Expandable Transcatheter Heart Valves,” J. Heart Valve Dis, 24(1), pp. 10–21. [PubMed] [Google Scholar]
- [30].Athappan G, Patvardhan E, Tuzcu EM, Svensson LG, Lemos PA, Fraccaro C, Tarantini G, Sinning JM, Nickenig G, Capodanno D, Tamburino C, Latib A, Colombo A, and Kapadia SR, 2013, “Incidence, Predictors, and Outcomes of Aortic Regurgitation After Transcatheter Aortic Valve Replacement: Meta-Analysis and Systematic Review of Literature,” J. Am. Coll. Cardiol, 61(15), pp. 1585–1595. [DOI] [PubMed] [Google Scholar]
- [31].Giri J, Bortnick AE, Wallen T, Walsh E, Bannan A, Desai N, Szeto WY, Bavaria J, and Herrmann HC, 2012, “Procedural and Clinical Outcomes of the Valve-in-Valve Technique for Severe Aortic Insufficiency After Balloon-Expandable Transcatheter Aortic Valve Replacement,” Catheter Cardiovasc. Interv, 80(1), pp. 139–147. [DOI] [PubMed] [Google Scholar]
- [32].Stock S, Scharfschwerdt M, Meyer-Saraei R, Richardt D, Charitos EI, Sievers HH, and Hanke T, 2016, “Does Undersizing of Transcatheter Aortic Valve Bioprostheses During Valve-in-Valve Implantation Avoid Coronary Obstruction? An In Vivo Study,” Thorac. Cardiovasc. Surg, 65(3), pp. 218–224. [DOI] [PubMed] [Google Scholar]
- [33].Willson AB, Webb JG, Freeman M, Wood DA, Gurvitch R, Thompson CR, Moss RR, Toggweiler S, Binder RK, Munt B, Cheung A, Hague C, Ye J, and Leipsic JA, 2012, “Computed Tomography-Based Sizing Recommendations for Transcatheter Aortic Valve Replacement With Balloon-Expandable Valves: Comparison With Transesophageal Echocardiography and Rationale for Implementation in a Prospective Trial,” J. Cardiovasc. Comput. Tomogr, 6(6), pp. 6–14. [DOI] [PubMed] [Google Scholar]
- [34].Handke M, Heinrichs G, Beyersdorf F, Olschewski M, Bode C, and Geibel A, 2003, “In Vivo Analysis of Aortic Valve Dynamics by Transesophageal Three-Dimensional Echocardiography With High Temporal Resolution,” J. Thorac. Cardiovasc. Surg, 125(6), pp. 1412–1419. [DOI] [PubMed] [Google Scholar]
- [35].Vesely I, Boughner D, and Song T, 1988, “Tissue Buckling as a Mechanism of Bioprosthetic Valve Failure,” Ann. Thorac. Surg, 46(3), pp. 302–308. [DOI] [PubMed] [Google Scholar]
- [36].Sacks MS, and Schoen FJ, 2002, “Collagen Fiber Disruption Occurs Independent of Calcification in Clinically Explanted Bioprosthetic Heart Valves,” J. Biomed. Mater. Res, 62(3), pp. 359–371. [DOI] [PubMed] [Google Scholar]
- [37].Duraiswamy N, Fathi P, Retta SM, and Weaver JD, 2016, “Effects of Sagging Versus Stretched Leaflets on Bioprosthetic Heart Valve Durability,” SB3C Conference, National Harbor, DC, June 29th–July 2nd. [Google Scholar]
- [38].Sritharan D, Fathi P, Weaver JD, Retta SM, Wu C, and Duraiswamy N, 2018, “Impact of Clinically Relevant Elliptical Deformations on the Damage Patterns of Sagging and Stretched Leaflets in a Bioprosthetic Heart Valve,” Cardiovasc. Eng. Technol, 9(3), pp. 351–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Conti CA, Votta E, Della Corte A, Del Viscovo L, Bancone C, Cotrufo M, and Redaelli A, 2010, “Dynamic Finite Element Analysis of the Aortic Root From MRI-Derived Parameters,” Med. Eng. Phys, 32(2), pp. 212–221. [DOI] [PubMed] [Google Scholar]


