Abstract
In deterministic models of epidemics, there is a host abundance threshold above which the introduction of a few infected individuals leads to a severe epidemic. Studies of weather-driven animal pathogens often assume that abundance thresholds will be overwhelmed by weather-driven stochasticity, but tests of this assumption are lacking. We collected observational and experimental data for a fungal pathogen, Entomophaga maimaiga, that infects the gypsy moth, Lymantria dispar. We used an advanced statistical-computing algorithm to fit mechanistic models to our data, such that different models made different assumptions about the effects of host density and weather on E. maimaiga epizootics (epidemics in animals). We then used Akaike information criterion analysis to choose the best model. In the best model, epizootics are driven by a combination of weather and host density, and the model does an excellent job of explaining the data, whereas models that allow only for weather effects or only for density-dependent effects do a poor job of explaining the data. Density-dependent transmission in our best model produces a host density threshold, but this threshold is strongly blurred by the stochastic effects of weather. Our work shows that host-abundance thresholds may be important even if weather strongly affects transmission, suggesting that epidemiological models that allow for weather have an important role to play in understanding animal pathogens. The success of our model means that it could be useful for managing the gypsy moth, an important pest of hardwood forests in North America.
Keywords: host population threshold, environmental stochasticity, SEIR model, fungal pathogen, biological control, stochastic disease model
Introduction
Understanding how weather and density combine to drive the dynamics of animal pathogens is a long-standing challenge in disease ecology. Classical epidemiological models assume that host-pathogen dynamics are driven entirely by density-dependent transmission (Keeling and Rohani 2008), and this assumption has been supported by field data on a range of animal pathogens (Dwyer and Elkinton 1993; McCallum 2016). Field studies of other pathogens have instead documented strong effects of weather and climate (Harvell et al. 2002), but these latter studies have usually relied on linear or generalized linear statistical models (Cooch et al. 2012; Tjaden et al. 2018). Such models effectively assume that the effects of weather overwhelm the effects of host density, but it seems likely that this assumption is often incorrect.
Given these parallel results, it further seems likely that the dynamics of animal pathogens are often driven by both density-dependent transmission and weather, but direct tests of this hypothesis are sorely lacking. Part of the problem is that disentangling the effects of density and weather requires a combination of extensive data sets and advanced model-fitting algorithms (King et al. 2008), but such a combination is rare in studies of animal pathogens. We therefore collected a data set on the effects of weather and density on a fungal pathogen of the gypsy moth, Lymantria dispar, and we used an advanced computational algorithm to fit mechanistic models to our data. This allowed us to choose between mechanistic models that allow for effects of weather, effects of density-dependent transmission, or both.
In addition to understanding the interaction between weather and density-dependent transmission, one of our goals is to understand how environmental stochasticity affects disease dynamics. In theoretical ecology, the term “environmental stochasticity” refers to any type of random variation in a model’s parameter values (Keeling and Rohani 2008), as distinct from demographic stochasticity, which results from the chance events that befall individuals (Hilborn and Mangel 1997). Although it seems likely that environmental stochasticity could be induced by the effects of random dispersal and spatial structure (Bolker and Pacala 1999), in practice environmental stochasticity is almost invariably assumed to be due to the capricious effects of weather (Wang and Kotamarthi 2015). In studying the effects of weather on disease spread, we are thus attempting to understand how disease spread is affected by environmental stochasticity.
The distinction between environmental stochasticity and demographic stochasticity is important partly because theories of the effects of stochasticity on pathogens have largely focused on demographic stochasticity (Daley and Gani 1999). In many deterministic disease models, there is a host population threshold above which an epidemic can result from the introduction of just a few infected individuals and below which the epidemic fails altogether (Kermack and McKendrick 1927). This is important because, for many animal diseases, host population sizes or densities often vary strongly over time and space (Lloyd-Smith et al. 2005). This in turn means that, in applications, it is often important to ask, Is the host density high enough for an epizootic to occur? (An epizootic is an epidemic in an animal population.) Because the better-known net reproductive ratio R0 assumes that host densities are constant, the host population threshold is often a more useful summary statistic than R0.
Understanding the effects of stochasticity on host density thresholds is therefore an important goal in disease ecology. In particular, including demographic stochasticity can lead to at least mild epizootics below the threshold or no epizootic at all above the threshold (Daley and Gani 1999). Demographic stochasticity can thus turn the vanishingly narrow threshold density of deterministic models into a range of densities over which an epizootic may occur. This variation in the threshold has been proposed as an explanation for why efforts to quantify thresholds in the field have often been unsuccessful (Lloyd-Smith et al. 2005).
The effects of demographic stochasticity, however, are quite weak unless the host density threshold and the initial number of infected hosts are both low (fig. 1). This requirement may be met in some host-pathogen systems (Lloyd-Smith et al. 2005), but in others epizootics occur only when the initial number of hosts is high (Moreau and Lucarotti 2007). In such cases, demographic stochasticity likely plays a limited role. This is important because if weather has strong enough effects, environmental stochasticity may eliminate host density thresholds altogether.
Figure 1:
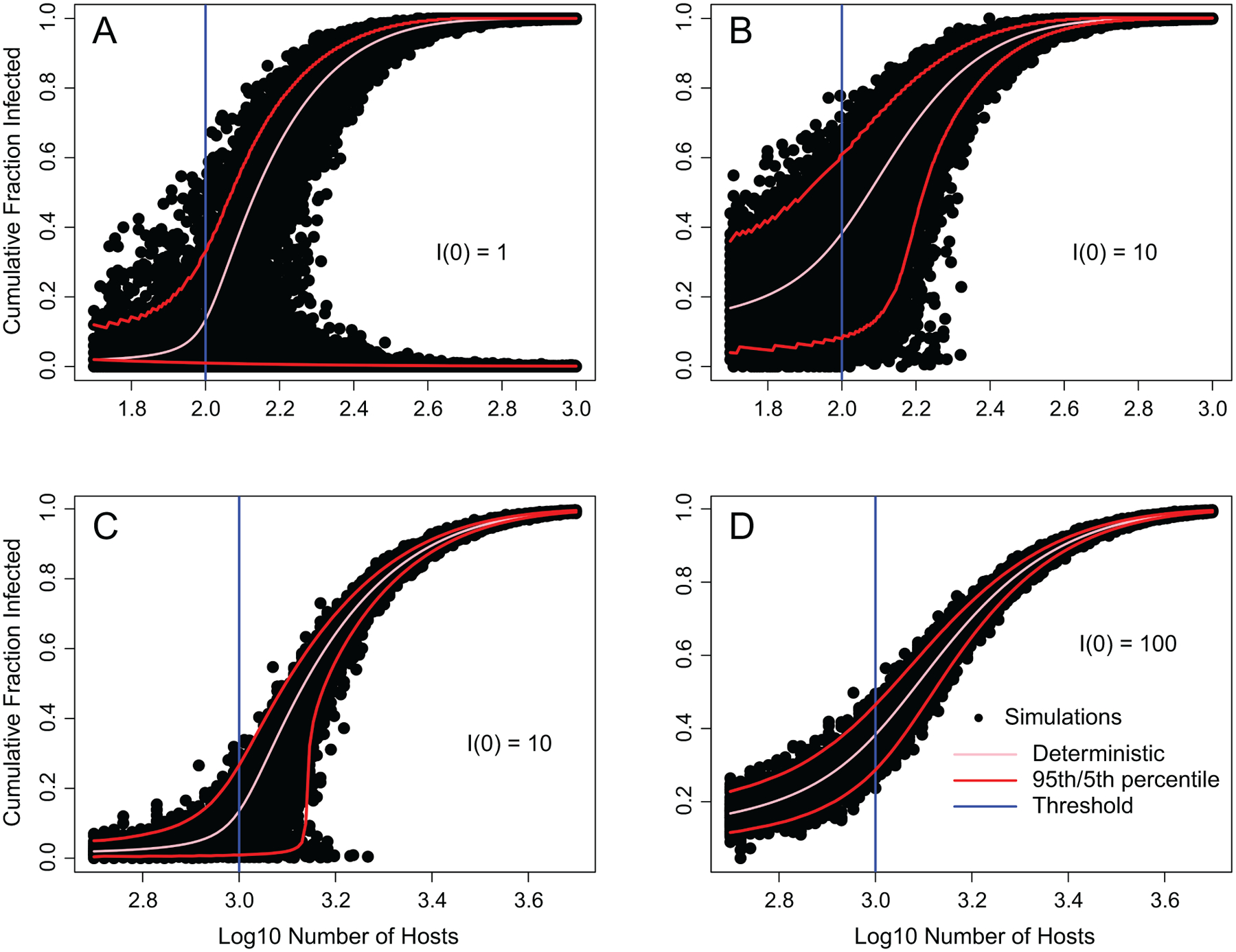
Cumulative infection rates versus number of hosts for the deterministic susceptible-infected-recovered (SIR) model (pink line; vertical blue line is the threshold) and the SIR model with demographic stochasticity (black points are simulations, 100 at each population size; red lines are upper 95th and lower 5th percentiles; appendix). Above the threshold in A (initial number infected I(0) = 1), there is a significant probability of either no epidemic or a severe epidemic, but unless the susceptible population is small, there is only a small probability of a moderate epidemic. When susceptible and infected populations are large, as in D, the stochastic SIR predictions approach the deterministic SIR prediction. Here we use a simple SIR model, but see Dallas et al. (2018) for a similar but more detailed model of fungal epizootics in Daphnia dentifera in the laboratory.
Environmental stochasticity may thus have much stronger effects on disease dynamics than demographic stochasticity. Models of environmental stochasticity, however, have only rarely been fit to data from nature. The effects of environmental stochasticity on disease density thresholds are therefore poorly understood.
To better understand the interaction between weather and density-dependent transmission, we collected data on epizootics of Entomophaga maimaiga, a fungal pathogen of the gypsy moth. We used our data to choose between models that make different assumptions about the effects of weather and density-dependent transmission, and we used the models to understand the extent to which weather obscures the host density threshold for this disease. For fungal insect pathogens like E. maimaiga, variability in host density is often paired with strong effects of weather (Hesketh et al. 2010), so fungal insect pathogens provide useful systems for testing models that include effects of both weather and host abundance.
Choosing between models required that we calculate the maximum likelihood of each model. To do this, we fit mechanistic epidemiological models to our data (Kennedy et al. 2015). Mechanistic model fitting has similarly been used in work showing that some human pathogens are affected by both weather and host abundance (King et al. 2008; Laneri et al. 2010; He et al. 2011). Weather presumably has even stronger effects on animal pathogens, but data sets on animal pathogens are often insufficient to allow for mechanistic model fitting, especially for the vertebrate pathogens that are the focus of many studies in disease ecology (McCallum 2016).
Moreover, previous applications of model-fitting algorithms, whether to human or animal pathogens, have used only observational data, which can make it harder to choose between mechanistic ecological models (Cobey and Baskerville 2016). For some animal pathogens, however, and especially for pathogens of invertebrates (Civitello et al. 2013; Dallas et al. 2018; Shocket et al. 2018), experiments are feasible (Rachowicz et al. 2006; Adelman et al. 2015). For insect pathogens like E. maimaiga in particular, the small size of the host makes experiments straightforward (Elderd 2013). We therefore fit our models to a combination of observational and experimental data on E. maimaiga.
Our results show that the best model includes effects of both host density and weather, such that infection rates increase with increasing host density, increasing rainfall and relative humidity, and decreasing temperature. Previous work has similarly shown that cool, moist weather has positive effects on E. maimaiga (Weseloh and Andreadis 1992; Hajek 1999; Reilly et al. 2014) and has provided mixed but reasonably convincing evidence for positive effects of host density (Weseloh and Andreadis 1992; Liebhold et al. 2013; Hajek et al. 2015; Hajek and van Nouhuys 2016). We then show that weather-driven stochasticity adds substantial variation to the host density threshold without obliterating it. The effect is that there is a range of host densities over which epizootic severity varies widely depending on weather conditions. This range is far broader than in models with demographic stochasticity, illustrating the strong effects that weather and environmental stochasticity can have on animal pathogens. As we discuss, the gypsy moth is an introduced pest of hardwood forests in North America (Elkinton and Liebhold 1990), so our work has implications for gypsy moth control as well as for our understanding of the many diseases that are affected by variation in weather (Harvell et al. 2002; Altizer et al. 2013).
Methods
Modeling the Gypsy Moth–Entomophaga maimaiga Interaction
Entomophaga maimaiga Natural History and General Model Structure. Like many outbreaking insects (Hunter 1991), the gypsy moth has only one generation per year, and E. maimaiga only infects larvae. The models that we used therefore describe only single epizootics and do not include host reproduction. To allow for a realistic delay between infection and infectiousness, we began with a susceptible-exposed-infectious-recovered (SEIR) model from human epidemiology. SEIR models allow for a delay by including equations for multiple exposed-but-not-yet-infectious stages (Keeling and Rohani 2008).
We modified this model to allow for the two infectious stages of E. maimaiga. The first infectious stage consists of resting spores (Hajek 1997), which overwinter in the soil before germinating in the spring (Hajek 1999). Resting spore germination ends partway through the larval season, but larvae infected by resting spores die and release aerial infectious spores known as conidia, the second infectious stage. Conidia drive transmission during most of the larval period, leading to multiple rounds of transmission that can decimate the host population. Near the end of the larval period, infectious larvae instead produce resting spores, which overwinter instead of germinating. In our study area in the lower peninsula of Michigan, larvae hatch in early May and pupate in early to mid-July, so the model describes the period between early May and early to mid-July.
Including both resting spores and conidia is important partly because previous work has shown that resting spore transmission rates are largely unaffected by host density (Hajek 1999; Hajek and Eastburn 2001), whereas conidia-driven transmission is strongly affected by host density (Weseloh and Andreadis 1992). We thus assume that transmission from conidia is density dependent, but we also assume that resting spore transmission is density dependent. We make this latter assumption because the reason why resting spore transmission is unaffected by host density is probably that resting spore transmission leads only to the production of conidia rather than to additional resting spores. A lack of evidence for effects of host density on resting spore transmission therefore does not mean that resting spore transmission is not density dependent.
In outbreaking gypsy moth populations, host densities are generally at least one larva per square meter of foliage (Dwyer and Elkinton 1993), while outbreaks typically encompass areas of at least square kilometers. The total number of host larvae in outbreaking populations is thus at least in the hundreds of thousands of individuals. It is therefore likely that demographic stochasticity has no more than weak effects on E. maimaiga epizootics, so our models include environmental stochasticity but not demographic stochasticity. One consequence of this assumption is that the state variables in our models are expressed as real numbers. In models of demographic stochasticity, in contrast, the state variables are instead expressed as integers, as they are in figure 1.
Because gypsy moth densities vary greatly between populations (Elkinton and Liebhold 1990), in our models we allow for density-dependent transmission instead of frequency-dependent transmission. More broadly, insect pathogens are well known to show density-dependent transmission (Elderd 2013), so our main goal was to understand the interacting effects of density-dependent transmission and weather rather than to test whether transmission is density dependent instead of frequency dependent. As we will show, infection rates clearly increase with increasing host density, supporting this assumption.
In allowing for stochasticity, we assumed that stochastic perturbations occur on a daily timescale. The disease ecology literature in contrast often assumes that stochastic perturbations occur over infinitesimal timescales (Ionides et al. 2006; King et al. 2008), yielding what are known as stochastic differential equations (Oksendal 2013). Models like ours, in which the stochastic perturbations occur over a discrete timescale, have been referred to as random ordinary differential equations (Han and Kloeden 2017). An advantage of our approach is that, conditional on the values of the stochastic terms, random ordinary differential equations can be numerically integrated using methods from deterministic calculus (Han and Kloeden 2017), whereas numerical integration of stochastic differential equations requires more complex algorithms (Oksendal 2013). We were therefore able to use an integration routine for ordinary differential equations, specifically a Runge-Kutta-Fehlberg predictor-corrector routine from the GNU Scientific Library (Gough 2009). Daily stochastic perturbations also provide an intuitive description of the effects of stochasticity in our system, in the sense that weather fronts in our study area passed over on timescales of 1–4 days, while the host insect has a 24-h activity cycle (Lance et al. 1987).
For each day τ in our model, where τ is an integer, we use the Runge-Kutta-Fehlberg routine to integrate from t = 0 days to t = 1 day, where t is a real number. The general structure of our within-day models is then
| (1) |
| (2) |
| (3) |
| (4) |
Here, Sτ(t) is the density of uninfected or “susceptible” larvae during day τ, and Rτ(0) is the density of resting spores during that day. Resting spores only cause infections during the resting spore germination period, 0 ≤ τ ≤ T. Because we have little information about resting spore dynamics during the germination period, we assumed for simplicity that resting spore density is constant during germination. To allow for variation in resting spore density across populations, we assumed that each population has its own resting spore density, which we estimated from the data.
In our weather-dependent models, the weather on day τ determines the conidial decay rate μC,τ and the transmission rates νR,τ for resting spores R and νC,τ for conidia C. As part of the transmission functions νC,τ and νR,τ, we include a function D(τ) to allow for larval growth. We included this function so that the model could account for the sharp increases in infection rates that are apparent in epizootics late in the larval season. These increases are likely due to larval growth during the epizootic because bigger larvae make bigger targets for conidia (Weseloh and Andreadis 1992). Because larvae grow faster when temperatures are higher (Elkinton and Liebhold 1990), D(τ) is a simple degree-day function, in which larval size increases linearly as temperatures increase above 10°C, the lowest temperature at which larvae can grow (Weseloh and Andreadis 1992). Thus, D(τ) serves as a proxy for larval growth.
Infected larvae in the models transition through m exposed classes Eτ,j at rate λ. Because the time in each exposed class is thus exponentially distributed, the total time between infection and death follows a gamma distribution, with mean 1/λ and variance 1/(mλ2) (Keeling and Rohani 2008). In practice, we observed that variation in the time to death is sufficiently low that we set m = 50, thereby ensuring low variation in the speed of kill. Larvae that have progressed through all 50 stages die, producing conidia Cτ that infect additional larvae.
From one day to the next, the initial conditions for (equations 1)–(4) are updated according to:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
For each population, the initial density of hosts S0(0) is given in our data set, and the resting spore density Rτ ≤ T(0) is a fit parameter.
Given this model specification, our numerical integration algorithm works as follows (see the appendix, available online, for a pseudo-code version of this algorithm). In each day, the algorithm draws a set of stochasticity terms, and it uses the stochasticity terms and that day’s weather to calculate the decay rate and the transmission rates, where the weather data are given as part of the data set. Next, the algorithm initializes the state variables, such that the initial conditions for the day are equal to the ending values from the preceding day. The algorithm then uses a Runge-Kutta-Fehlberg routine to numerically integrate equations (1)–(4) for the day.
When we fit models to our infection rate data, our weather data set provides covariates in the form of rainfall, relative humidity, and temperature. The weather on each day is therefore fixed in the fitting routine rather than acting as a source of environmental stochasticity. It might also have been interesting to instead vary the weather data during the fitting process, perhaps by making random draws from the weather data before fitting the models or by using simulated data. Fitting our models to the data, however, required weeks of wall-clock time, so varying the weather data in a systematic way was beyond what we could accomplish.
In our models, we also include environmental stochasticity that is not due to weather variation. Because we do not attempt to identify the sources of this stochasticity, in what follows we refer to it as “inherent environmental stochasticity.” When we quantified the effects of environmental stochasticity on the host density threshold, however, we also allowed the weather to vary stochastically. In that latter case, we thus included both inherent environmental stochasticity and weather-driven environmental stochasticity.
Allowing for Stochasticity without Weather Effects on the Pathogen.
In the density-dependence-only model, we include inherent environmental stochasticity, but we do not include weather effects on E. maimaiga. In this model, the transmission functions are
| (10) |
| (11) |
Here, the effects of stochasticity are represented by the random variates ϵR,τ and ϵC,τ, while the parameters ψ1 and ψ2 determine the rate at which transmission increases with degree-days D(τ). New values of ϵR,τ and ϵC,τ are drawn independently each day τ, from normal distributions with mean 0 and with respective standard deviations σR and σC. The effect is that transmission of each type of infectious particle varies randomly each day. Because we exponentiate ϵR,τ, and ϵC,τ, both νR,τ and νC,τ follow lognormal distributions, with medians ψ1D(τ) and ψ2D(τ), respectively. Including more than two types of stochasticity would likely have led to the nonidentifiability of the standard deviation parameters, so we do not include stochasticity in conidia decay.
The assumption that νR,τ and νC,τ are lognormal has the advantage of guaranteeing that the two transmission rates are always positive. In a lognormal distribution, however, the mean and the variance depend on both the mean and the variance of the corresponding normal distribution (see the appendix). This means that changing the standard deviations σR and σC of the normally distributed random variates ϵR,τ and ϵC,τ changes both the mean and the standard deviation of the transmission rates νR,τ and νC,τ (see the appendix).
Because D(τ) depends on temperature, strictly speaking this model includes an effect of weather. Because the effect is manifest only through the host population, however, and because the literature on E. maimaiga has emphasized that weather mainly affects the pathogen, we refer to this model as the “density-dependence-only” model. As we will show, weather stochasticity has only weak effects on this model, supporting our use of this label.
Modeling Weather Effects.
To allow for weather effects, we define functions that translate our observed weather data into effects on transmission and conidia decay. First, previous work showed that transmission increases strongly with rainfall but that it saturates at high rainfall (Hajek and Eastburn 2001; Reilly et al. 2014). We therefore assumed that transmission is a logistic function of rainfall, according to
| (12) |
Here, the function p(τ) consists of our measurements of rainfall, while the parameters ψ3–ψ5 describe how rainfall is translated into effects on transmission. To avoid having nonzero transmission when there was no rainfall, we constructed P(τ) so that when p(τ) = 0, P(τ) = 0. Because Weseloh et al. (1993) showed that cumulative rainfall is a better predictor of infection rates than daily rainfall, p(τ) is the sum of the daily rainfall over the preceding 10 days. Preliminary tests showed that summing over moderately shorter or moderately longer intervals gave worse fits to the data.
We also allowed for effects of relative humidity and temperature because conidia production is known to increase with increasing relative humidity and because conidia survival decreases with increasing temperature (Hajek et al. 1990). Because there is no reason to believe that these changes saturate with increasing humidity or temperature, we used exponential functions in each case, according to
| (13) |
| (14) |
The functions m(τ) (m for moisture) and h(τ) (h for heat) consist of our observations, on day τ, of relative humidity and temperature, respectively. Parameters ψ6 and ψ7 then describe how humidity affects transmission, while ψ8 and ψ9 describe how temperature affects transmission or conidia breakdown, depending on the model. To improve our ability to detect the effects of weather on transmission, we used the minimum relative humidity and the maximum temperature on each day. Doing so ensured that there would be high variability in each covariate, which in turn made it easier for us to distinguish between the effects of the different weather covariates.
Allowing for Weather but Not Density-Dependent Transmission.
In the weather-only models, we eliminated density dependence in transmission by assuming that per capita infection risk depends only on weather conditions, not on resting spore or conidia densities. In these models, there is thus no distinction between resting spores and conidia. We therefore symbolize transmission as νF,t, where F stands for “fungus,” and we do not include a separate equation for conidia density:
| (15) |
| (16) |
| (17) |
Here, transmission is dependent on daily changes in weather, so that the transmission function νF,τ changes with day τ, where again τ is an integer. Between days, the state variables Sτ and Ej,τ are updated as in the difference equations (5)–(9).
In the weather-only models, transmission νF,τ is then allowed to be the product of all possible combinations of the weather functions P(τ), M(τ), and H(τ) and the degree-day function D(τ):
| (18) |
Here, stochasticity is represented by the random variate ϵF,τ, which is again normally distributed with mean 0, here with standard deviation σF. As in the density-dependence-only model, this means that transmission νF,τ follows a lognormal distribution, with median D(τ)P(τ)M(τ)H(τ). Also, changes in the standard deviation σF of the normally distributed random variate ϵF,τ again change both the mean and the standard deviation of transmission νF,τ.
The functions P(τ), M(τ), and H(τ) then depend on our observed values of rainfall, relative humidity, and temperature, as described in equations (12)–(14). Because the weather functions are multiplied together, the parameters ψ3, ψ6, and ψ8 can only be estimated as the product ψF = ψ3 × ψ6 × ψ8. Here we show a model that depends on all three weather variables, but in practice we used the data to choose between models that included different combinations of P(τ), M(τ), and H(τ).
Allowing for Density Dependence, Weather, and Stochasticity.
Our combined density-dependence-plus-weather models allow for effects of density-dependent transmission, weather, and environmental stochasticity. These models resemble the weather-only models in assuming that resting spore transmission increases logistically with increasing rainfall, that conidia transmission increases exponentially with increasing rainfall, and that conidia survival decreases exponentially with increasing temperature. At the same time, they resemble the density-dependence-only model in distinguishing between conidia and resting spores.
For the combined models, the transmission parameters νR,τ and νC,τ and the decay parameter μC,τ are then
| (19) |
| (20) |
| (21) |
Here, again D(τ) is the effect of accumulated degree-days, P(τ) is the rainfall function, M(τ) is the relative humidity function, and H(τ) is the temperature function, with the latter three functions specified by equations (12)–(14). In this model, however, we assume that H(τ) is an exponentially increasing function of temperature, so that the conidia decay rate increases with temperature instead of transmission decreasing with temperature, as in equations (14) and (18). Because here each weather function affects a different process, we include all three of the weather dependence parameters ψ3, ψ6, and ψ8.
As in the two previous models, the stochastic terms ϵR,τ and ϵC,τ are normally distributed random variates, each with mean 0 and respective standard deviations σR and σC. Also as in the previous models, the transmission rates νR,τ and νC,τ follow lognormal distributions, with respective medians D(τ)P(τ) and D(τ)M(τ). Changes in the standard deviations σR and σC of the normally distributed random variates ϵR,τ and ϵC,τ again change both the mean and the standard deviation of νR,τ and νC,τ.
Model Behavior.
Figure 2A and figure 2B show that for the density-dependence-only model, epizootic intensity increases with increases in host density, as we would expect for that model. Figure 2C and figure 2D in contrast show that for the weather-only model, epizootic intensity increases with cool temperatures, high rainfall, and high relative humidity, as we would expect for that model (fig. 2C and fig. 2D are based on simulated data, but in fitting models to data we used our observed weather data). Figure 3 then shows that for the combined density-dependence-plus-weather model, epizootic intensity increases with either increased host density or more favorable weather. As we will show, the combined model provides the best explanation for our data, but if the effects of weather had been strong enough, a weather-only model might have been the best model.
Figure 2:
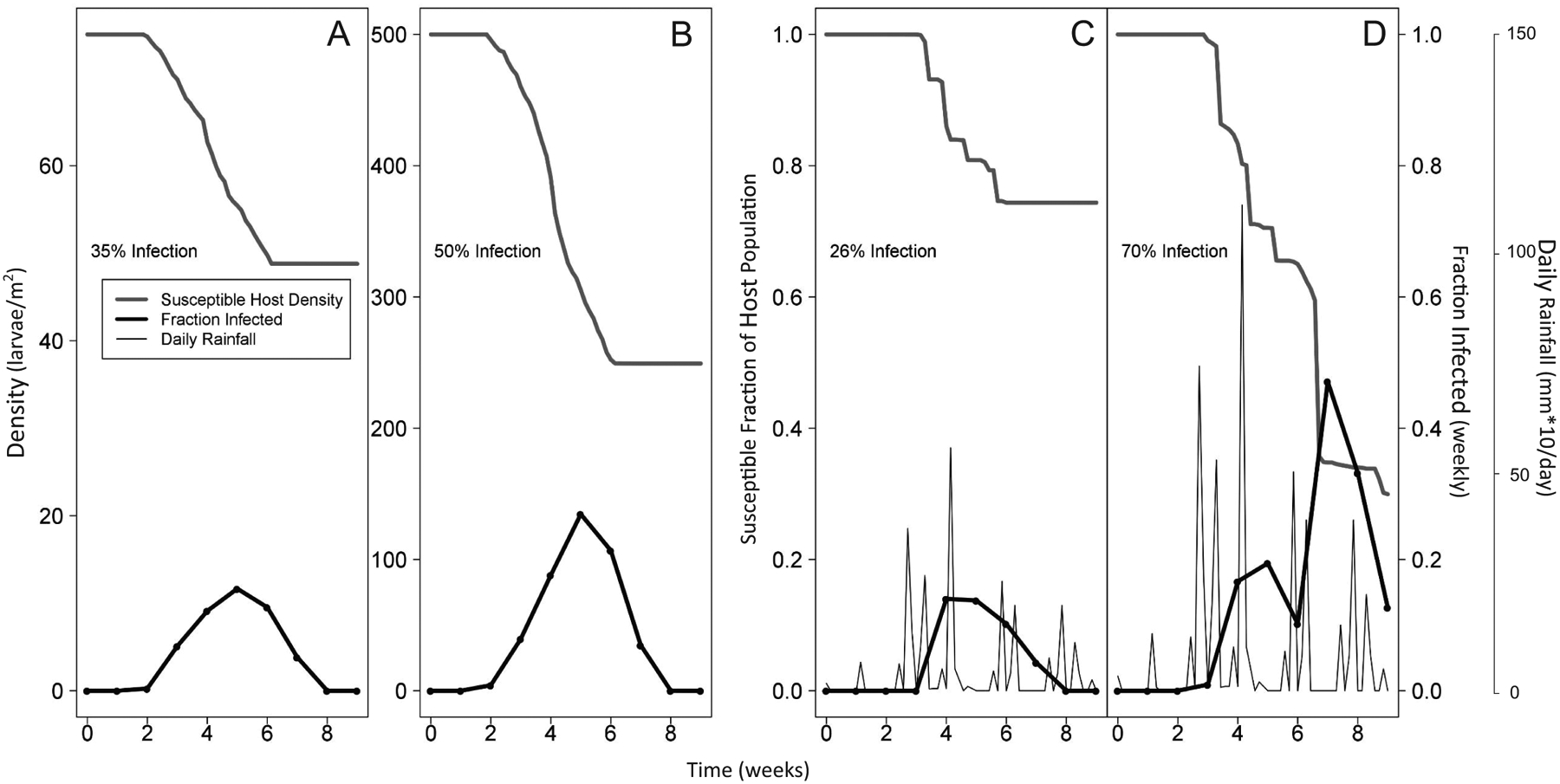
Single realizations of the density-dependence-only model (A, B) and the weather-only model (C, D). In A the initial host density is 75 larvae per square meter, while in B the initial host density is 500 larvae per square meter. C and D have the same temporal distribution of rainfall events, but in D the volume of rain is twice as high as in C. Percent infection values indicate cumulative infection over the entire epizootic.
Figure 3:
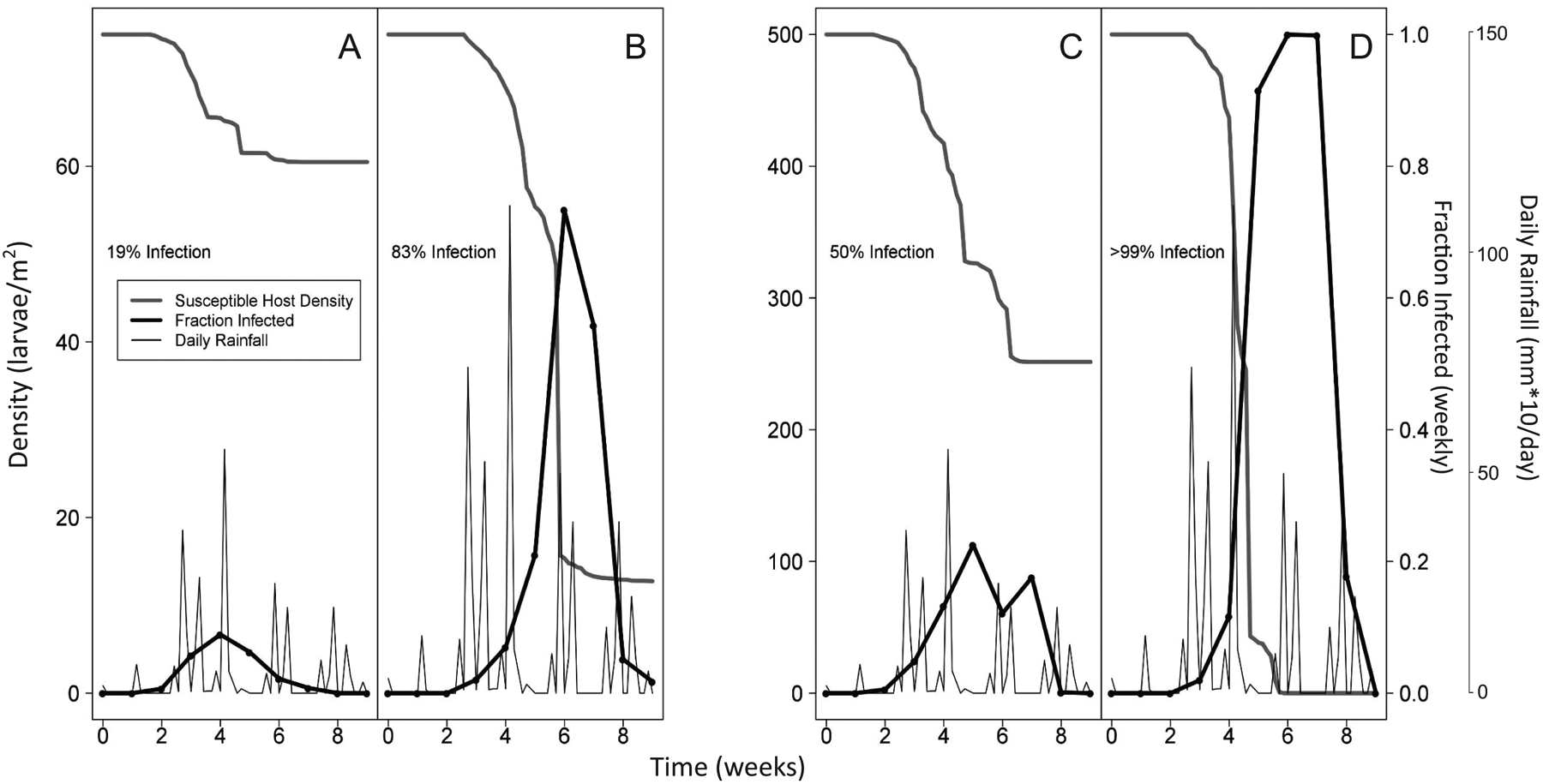
Single realizations of the combined density-dependence-plus-weather model. The four panels demonstrate how the model responds to different combinations of low (A, C) and high (B, D) rainfall and low (A, B) and high (C, D) initial host densities. A and B have an initial host density of 75 larvae per square meter, while C and D have an initial host density of 500 larvae per square meter. In B and D, the total amount of rain is twice that in A and C, but the timing of rainfall events is the same in all panels.
Data Collection
To improve our chances of detecting both density and weather effects, we collected data in three consecutive years, along a north-south transect that spanned more than three degrees of latitude (fig. 4). In each year, we attempted to find a southern plot, a central plot, and a northern plot along the transect. Because some populations collapsed, each year we searched within each general area to maintain the transect. These searches were successful except in the southern area in 2012 (table 1). Also, at the south 2011 and north 2012 sites, we were able to locate egg masses before hatch occurred, but the egg mass density was so low that we were unable to locate larvae after hatch. In those two populations, we only collected data from experiments, which only required laboratory-reared larvae.
Figure 4:
Plot locations.
Table 1:
Latitudes and longitudes of our study plots, together with the distance (km) from each plot to the nearest plot to the south (“Distance from S/C”) and the total south-to-north distance in each year (“Total S/N distance”)
| Year, location | Latitude | Longitude | Distance from S/C | Total S/N distance |
|---|---|---|---|---|
| 2010: | ||||
| South | 42.36 | −85.35 | … | … |
| Central | 44.46 | −84.60 | 240.96 | … |
| North | 45.48 | −84.68 | 113.57 | 354.53 |
| 2011: | ||||
| South | 42.61 | −85.45 | … | … |
| Central | 44.47 | −84.60 | 217.04 | … |
| North | 45.19 | −84.23 | 85.44 | 302.48 |
| 2012: | ||||
| South | NA | NA | … | … |
| Central | 44.47 | −84.60 | … | … |
| North | 45.48 | −84.68 | 85.44 | 85.44 |
Note: NA = not available.
In each population, we quantified host densities at the beginning of each larval season, using standard methods of surveying gypsy moth densities (Elkinton and Liebhold 1990; appendix). We also recorded temperature, rainfall, and relative humidity in each population. To estimate E. maimaiga infection rates, we collected live larvae, and we reared them individually in the laboratory to see if they were infected.
To collect larvae, we searched branches and trunks that were within easy reach. Late-stage larvae sometimes climb down to the base of a tree when they are infected (Hajek 1999), but that behavior occurs only at the very end of the larval season. Our collections were therefore unlikely to have been biased by differences in behavior between infected and uninfected larvae.
We collected 100 larvae from each plot in each week. This sample size proved to be large enough to detect the rise and fall in infection rates that is predicted by density-dependent transmission models (Keeling and Rohani 2008) and that has sometimes been observed in E. maimaiga epizootics (Weseloh and Andreadis 1992; Weseloh 1999; Hajek and van Nouhuys 2016). This in turn made it easier for us to detect density dependence in transmission. In previous studies, in contrast, sample sizes were often small enough that researchers were forced to rely on cumulative infection rates (Liebhold et al. 2013; Hajek et al. 2015), which by definition cannot reveal fluctuations in infection rates during epizootics.
Even though theory predicts that infection rates should decline near the end of epizootics, in some cases it was difficult to detect this decline because most larvae were dead by then. This is important because when infection rates first rise in an epizootic, the increase is effectively exponential (Champredon and Earn 2016; Chowell et al. 2016). If our data had consisted simply of observations of exponential increases in the fraction infected, it would have been difficult to separately estimate transmission rates and host removal rates (in our case, removal is equivalent to conidia decay). This is especially true given that epizootics last for less than 10 weeks. This problem in turn might have made it hard to accurately identify the effects of weather, which is important because conidia transmission and conidia decay depend on weather in different ways.
We therefore augmented our data by carrying out experiments in which we quantified the force of infection, the rate at which susceptible larvae become infected (Keeling and Rohani 2008). To do this, we followed an established experimental protocol (Weseloh and Andreadis 1992) in which uninfected laboratory-reared larvae are placed in cages in the environment, in our case for 24 h, before being reared in the laboratory to determine whether they have become infected. Twenty-four hours is long enough that some of the larvae became infected, but it is short enough that none of the infected larvae died and that conidia decay was probably modest. The only process operating among the caged larvae was thus transmission, so the experiments allowed us to estimate transmission separately from host and conidia death rates. Because these larvae were confined in cages, however, they might have had an infection risk different from that of feral larvae. We therefore included parameters in our models that allowed for differences in infection risk between wild-caught and experimental larvae while nevertheless allowing transmission rates to fluctuate in the same way as in the naturally occurring population (appendix).
To prevent transmission in the laboratory, both wild-collected larvae and experimental larvae were reared individually in plastic cups with tightly fitting lids that contained artificial diet. Larvae were then held in the laboratory at 21°C until death or pupation. Larvae that die and produce conidia can usually be identified easily, but we also examined smears from dead larvae at 400× under a light microscope to look for conidia and resting spores (Hajek 1999).
Model-Fitting Algorithm
Likelihood Calculation.
The ultimate goal of our modeling efforts was to choose between competing models of E. maimaiga dynamics, such that one model included only density-dependent transmission, a set of models included different combinations of weather variables, and a set of models included both weather variables and density-dependent transmission. In the first step in our model selection procedure, we fit our models to our data. To do this, we used Bayesian statistical techniques to calculate the posterior probability of the parameters for each model. We then used the mode of each posterior as the maximum likelihood for the associated model, and we used the (lowest) Akaike information criterion (AIC) score to identify the best model, where the AIC takes into account both goodness of fit and model complexity (Burnham and Anderson 2002).
We assumed that the initial resting spore densities were specific to individual populations because it is likely that these densities vary across space and time. Because there is no reason to believe that other processes varied between populations, we assumed that the remaining parameters were the same in every population. Also, as we explained above, we used our weather data as covariates in the models. In practice, this meant that we assumed that the dynamics in each population were determined by the host density in that population, by the weather in that population, and by inherent environmental stochasticity. In calculating likelihood scores, we averaged over the stochasticity, as we will describe.
Because our data consisted of mortality rates, in principle a binomial distribution could have provided a useful likelihood function (Pawitan 2001). In practice, however, it seemed likely that small-scale variation in the infection rate within the forest could have caused the variance in the data to be larger than binomial, an effect known as “overdispersion” (McCullagh and Nelder 1989). To allow for this possibility, we used a beta-binomial likelihood (appendix). Compared with a binomial, a beta-binomial includes an extra parameter, which makes it possible to allow for the increase in the variance that is due to the sampling error.
Given a likelihood function, we calculated likelihoods by averaging across realizations of the model. The underlying idea is that the stochasticity terms are effectively nuisance parameters, so we integrated out their effects to produce an integrated likelihood (Berger et al. 1999), as follows:
| (22) |
Here, the average likelihood is an average across realizations L(ϵ1, ϵ2, …, ϵD), where each realization in turn depends on the sequence of daily stochasticity terms ϵi. The function f(ϵ1, ϵ2, …, ϵD) is then the joint density of the ϵis. As we indicated in describing the models, the ϵis are independent and normally distributed, with identical means and standard deviations.
Our models are sufficiently complex that evaluating the integral in equation (22) using a numerical quadrature rule was impractical (Press et al. 1992). We therefore instead used Monte Carlo integration (Ross 2002). To implement this approach, we used the MISER algorithm (Gough 2009), which uses recursive, stratified sampling to reduce the uncertainty in estimates of the average likelihood (Press et al. 1992).
Line-Search Markov chain Monte Carlo (MCMC).
To sample efficiently from the posterior distribution of the parameters, we used an algorithm known as line-search MCMC (Kennedy et al. 2015). Line-search MCMC makes use of modern, massively parallel computing environments via a preprocessing step that coarsely maps the likelihood or posterior surface using line search (see the appendix for a pseudo-code version of this algorithm).
In line search, parameters are varied one at a time over a predefined region of parameter space, over many iterations through the parameter list. The algorithm loops over each parameter in order, comparing the likelihood or posterior value at each iteration to the highest value found up to that point. The highest value is then updated, so that the algorithm climbs toward improved values of the likelihood or the posterior.
Line search, on its own, could in principle locate the parameters that give the maximum likelihood or maximum posterior. In practice, however, correlations between parameters are often strong enough that ordinary line search will tend to get stuck on ridges of the objective surface. It is therefore unlikely that the line search algorithm will find the best parameter set, especially if it is begun at only a single set of initial parameter values. We therefore instead used hundreds of realizations of line search, each begun at a parameter set chosen randomly from a region of likely parameter values.
Once we have output from a large number of line searches, the next step is to construct proposal distributions. To do this, line-search MCMC applies principal component analysis (PCA) to the highest 5%–10% of the likelihood or posterior values found by the line searches. The fraction of line searches used can be adjusted to create the best representation of the surface, as determined visually by inspection of the PCA results. Note that when PCA is used in statistical analyses, typically only a fraction of the components are retained, but here the full set of components is needed to re-create the entire surface.
In the final step in line-search MCMC, the PCA results are used to construct multivariate normal proposal distributions for use in Metropolis-Hastings MCMC. Parameters are proposed in PCA space and then back-transformed onto the original scale for use in calculating the posterior density value. Proposing in PCA space greatly reduces the correlations between parameters, improving the mixing of the MCMC chains and speeding the convergence to the posterior. Inspection of trace plots and calculation of Gelman-Rubin statistics (Gelman et al. 2014) confirmed that our routines converged (for the worse-fitting weather-only models, the AIC scores may be slightly less reliable than for the other models; see the appendix).
The advantage of line-search MCMC over standard Metropolis-Hastings MCMC has to do with the structure of modern, high-performance computing environments, which consist of hundreds to thousands of computing nodes (Fuller and Millett 2011). Because line-search MCMC first implements line searches at hundreds or thousands of random starting points in parameter space and then uses these line searches to speed convergence of MCMC, line-search MCMC makes effective use of large numbers of computing nodes in a single preprocessing step (Kennedy et al. 2015).
Simulating Weather
To understand the general behavior of our models—for example, in figures 2 and 3—we produced model realizations using artificial weather, where the artificial weather was generated using a Richardson weather generator (Richardson 1981). In this generator, we set the daily probability of rainfall to 40%, the rainfall frequency in our weather data. For each rainfall event, the generator draws the amount of rain from a lognormal distribution. The generator then uses linear regressions of temperature and relative humidity versus rainfall, which we fit to our data, to generate the maximum temperature and the relative humidity for that day (appendix). In some cases, we altered the mean and variance of the rainfall distribution to generate a wider range of conditions than we observed in nature.
Results
The Data
Our data show clear effects of weather on Entomophaga maimaiga infection rates (fig. 5; data are available in the Dryad Digital Repository [https://doi.org/10.5061/dryad.3nv3ss2; Kyle et al. 2020]). Infection rates were generally higher after rainstorms and when conditions were cool and moist. These effects are apparent from visual inspection of the data, but detecting the effects of density from visual inspection is more difficult. Visual comparison of the observational and experimental data nevertheless makes it possible to infer some of the simpler effects of density.
Figure 5:
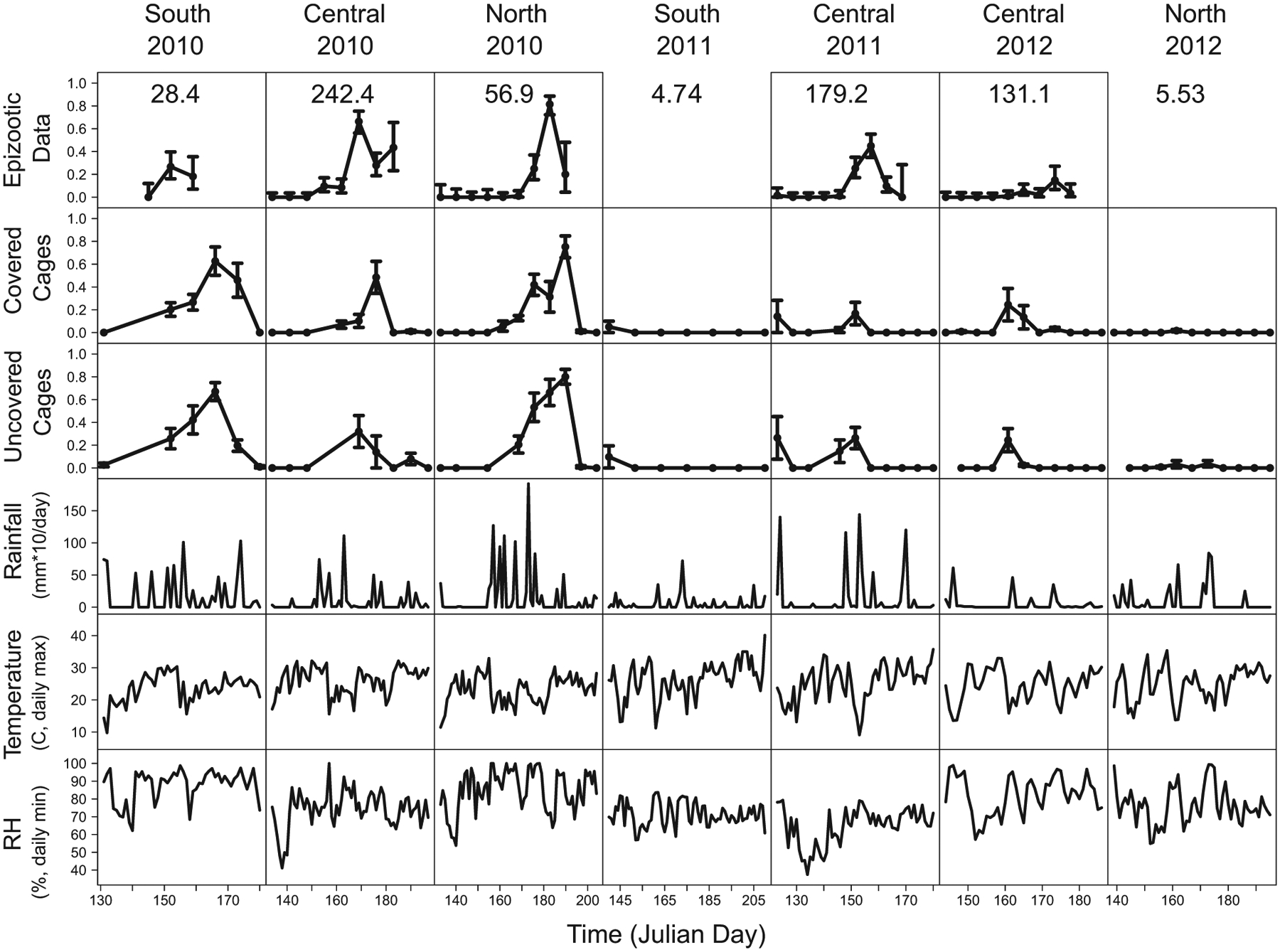
Observational and experimental data on Entomophaga maimaiga infection rates, together with weather data in each population, for each year of our study. Error bars represent 1 SEM. The values in the top row show the initial host density S(0) for each site in units of larvae per square meter. “Covered Cages” refers to an experimental treatment in which plastic boxes were placed over cages to limit exposure to conidia, while “Uncovered Cages” refers to an experimental treatment that had no boxes. Box effects were modest, and therefore we do not consider them further (see the appendix). The data in this figure have been deposited in the Dryad Digital Repository (https://doi.org/10.5061/dryad.3nv3ss2; Kyle et al. 2020).
These comparisons rely on the observation that the rise and fall of the fraction infected in the experimental data tracks the rise and fall of the fraction infected in the observational data. Given this observation, the experimental data from the south 2011 and north 2012 sites, in which we could not find larvae after hatch, then provide useful comparisons to the sites in which we could find larvae after hatch.
At the south 2011 and north 2012 sites, a few infections occurred among the experimental larvae, confirming that resting spores were present and germinating, but the infection rate was near zero throughout the larval period in both plots (fig. 5). This low infection rate presumably reflects the lack of conidia in those plots. In contrast, infection rates in the other populations were often very high, suggesting that epizootics are driven largely by conidia. Additional support for this conclusion comes from the observation that weather conditions at the south 2011 and north 2012 sites were similar to what they were at the central 2010 site, where the gypsy moth density was high and a severe epizootic occurred.
The effects of weather were nevertheless strong enough that more quantitative effects of density are not obvious from inspection of the data. Infection rates at the central 2010 site, for example, were comparable to infection rates at the north 2010 site, even though the initial host density was more than four times higher at the central 2010 site than at the north 2010 site. Disentangling the effects of weather and host density thus required that we fit mechanistic models to our data.
Models versus Data
The best-fit density-dependence-only model qualitatively reproduces the data, especially the rise and fall in infection rates that is typical of density-dependent transmission (fig. 6, “D-D Only”). That model nevertheless misses the sharp increases in infection rates that result from rainstorms, with their attendant increases in humidity and reductions in temperature.
Figure 6:
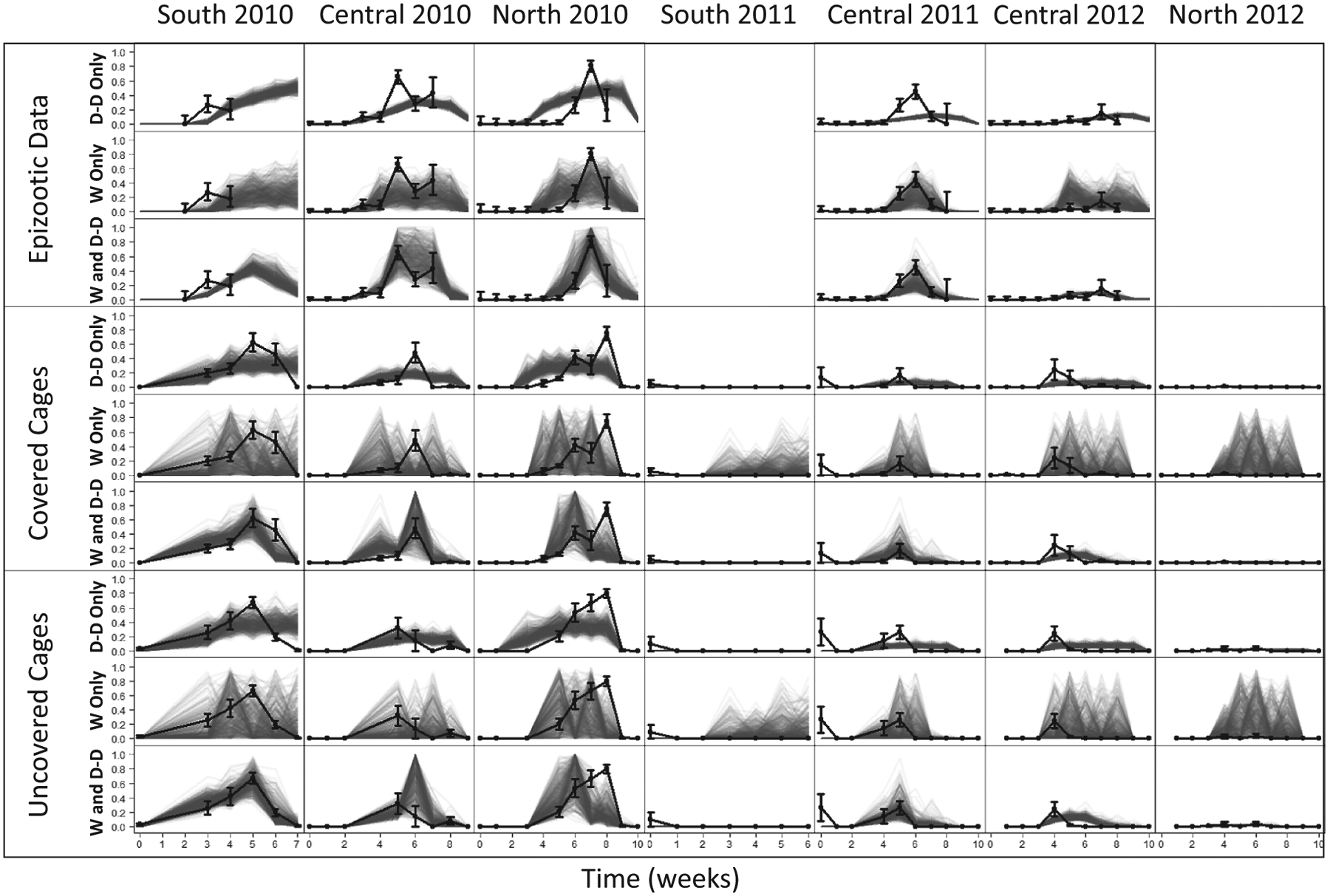
Comparison of multiple realizations of the models to the data. “D-D Only” refers to the density-dependence-only model, “W Only” refers to the best weather-only model, and “W and D-D” refers to the best combined weather and density dependence model. Black solid lines are the data (±1 SE), and the gray transparent lines are 25 realizations of the models using the best-fit parameter sets.
The best weather-only model, in contrast, easily reproduces weather-driven increases in infection rates, but it often predicts that infection rates should be high when infection rates were low (fig. 6, “W Only”). This overestimation is most obvious early in the season at the central 2010, north 2010, and central 2012 sites. The overestimation likely occurs because, in nature, transmission early in the season is constrained by a lack of conidia, whereas in the weather-only models, transmission is unconstrained by a lack of conidia. In the south 2011 and north 2012 plots, in which no larvae could be found after hatch, this lack of conidia caused the best weather-only model to badly overestimate the force of infection throughout the season.
Meanwhile, the best combined model correctly predicts the infection rate and the force of infection in most weeks in most plots. Because that model includes both density-dependent transmission and weather, it allows transmission to be high only when densities are high and conditions are cool and moist.
These visual comparisons are confirmed by AIC analysis, which shows that the data are indeed best explained by a model that includes effects of density-dependent transmission and weather (table 2). The AIC score of the best model is almost 80 points better than the score of the density-dependence-only model, almost 40 points better than the AIC score of the best weather-only model, and more than 20 points better than all but one of the other density-dependence-plus-weather models. An AIC difference of more than 10 indicates that there is essentially zero support for the hypothesis that a given model is better than the best model (Burnham and Anderson 2002). Our best model thus provides a vastly better fit to the data than almost any other model.
Table 2:
Akaike information criterion (AIC) analysis
| Model | Likelihood | No. parameters | AIC | DAIC |
|---|---|---|---|---|
| Density dependence only | −640.5 | 23 | 1,326.9 | 79.2 |
| Weather only: | ||||
| Rain | −689.0 | 11 | 1,400.0 | 152.3 |
| Relative humidity | −660.5 | 10 | 1,341.0 | 93.2 |
| Temperature | −644.0 | 10 | 1,307.9 | 60.2 |
| Rain + relative humidity | −641.4 | 12 | 1,306.9 | 59.1 |
| Rain + temperature | −631.1 | 12 | 1,286.2 | 38.4 |
| Relative humidity + temperature | −658.1 | 11 | 1,338.3 | 90.5 |
| Rain + relative humidity + temperature | −634.6 | 13 | 1,295.3 | 47.5 |
| Density dependence + weather: | ||||
| Rain | −640.2 | 25 | 1,330.3 | 82.5 |
| Relative humidity | −601.2 | 24 | 1,250.3 | 2.54 |
| Temperature | −640.5 | 24 | 1,328.9 | 81.2 |
| Rain + relative humidity | −610.7 | 26 | 1,273.3 | 25.5 |
| Rain + temperature | −643.4 | 26 | 1,338.8 | 91.1 |
| Relative humidity + temperature | −610.1 | 25 | 1,270.3 | 22.5 |
| Rain + relative humidity + temperature | −596.9 | 27 | 1,247.8 | 0 |
Note: The overall best model is shown in boldface, while the best weather-only model is shown in italicized boldface. Sample sizes were large enough that the small sample size–corrected AIC criterion gave essentially identical values to the uncorrected AIC, so for simplicity we show only the uncorrected AIC.
The one exception is a model that includes effects of density-dependent transmission and weather and that assumes that the only weather variable that matters is relative humidity. This second-best model has an AIC score that is only 2.54 points higher than the score for the best model, which includes effects of not just relative humidity but also rainfall and temperature. An AIC difference of 2.54 is small enough to indicate that there is at least weak support for the second-best model. We thus cannot rule out the possibility that if we were to collect more of the same kind of data, the second-best model would become the best model (Burnham and Anderson 2002). Visual comparison of the fit of the second-best model to the data, however, shows that the second-best model clearly provides a worse fit to the data than the best model (appendix). Moreover, other types of data have provided strong support for the hypothesis that both rainfall and temperature affect E. maimaga epizootics (Hajek et al. 1990). It therefore seems likely that, in a larger sense, the model that our data have identified as the best model is indeed the best model of E. maimaiga epizootics. In what follows, we therefore focus on the best model.
It is nevertheless important to remember that although our weather functions were based on the known biology of E. maimaiga, our choices of the functions that relate weather to conidia breakdown and transmission were somewhat arbitrary. Other functions might have given better fits to the data and at least slightly different conclusions about which weather variables are most important. This point emphasizes that the not-great but not-terrible performance of the second-best model means that there is some uncertainty as to which is the best model.
Environmental Stochasticity and the Host Density Threshold
Although we were able to detect effects of host density on E. maimaiga epizootics, that does not mean that these effects are biologically meaningful. To better understand the interaction of weather and host density, we quantified the effects of weather on E. maimaiga’s host density threshold. To do this, we simulated epizootics across a range of densities and a range of weather conditions, and we calculated the cumulative fraction infected in each epizootic.
As we mentioned earlier, in this case we are including not just inherent environmental stochasticity, as in our fitting routines, but also environmental stochasticity that is due to stochastic variation in weather. To do this, we included inherent environmental stochasticity exactly as we did in our fitting routines, but we also used our Richardson weather generator to produce artificial weather. Because the artificial weather is stochastic, it serves as an additional source of environmental stochasticity. In this case, we are thus including two sources of environmental stochasticity, and we are not distinguishing between the two.
In figure 7 we show the results of these simulations for the best combined model and for the density-dependence-only model, in terms of the cumulative fraction infected versus host density (the second-best model gives very similar results; see the appendix). As the figure shows, the infection rate in the best combined model increases sharply with host density, displaying the characteristic feature of a host density threshold. This threshold, however, is strongly blurred by stochasticity, so that there is a broad range of densities over which high or low infection rates may occur, depending on weather stochasticity and inherent stochasticity. The effects of host density are nevertheless clearly apparent. We therefore conclude that an understanding of the host density threshold provides significant insight into the dynamics of this pathogen.
Figure 7:
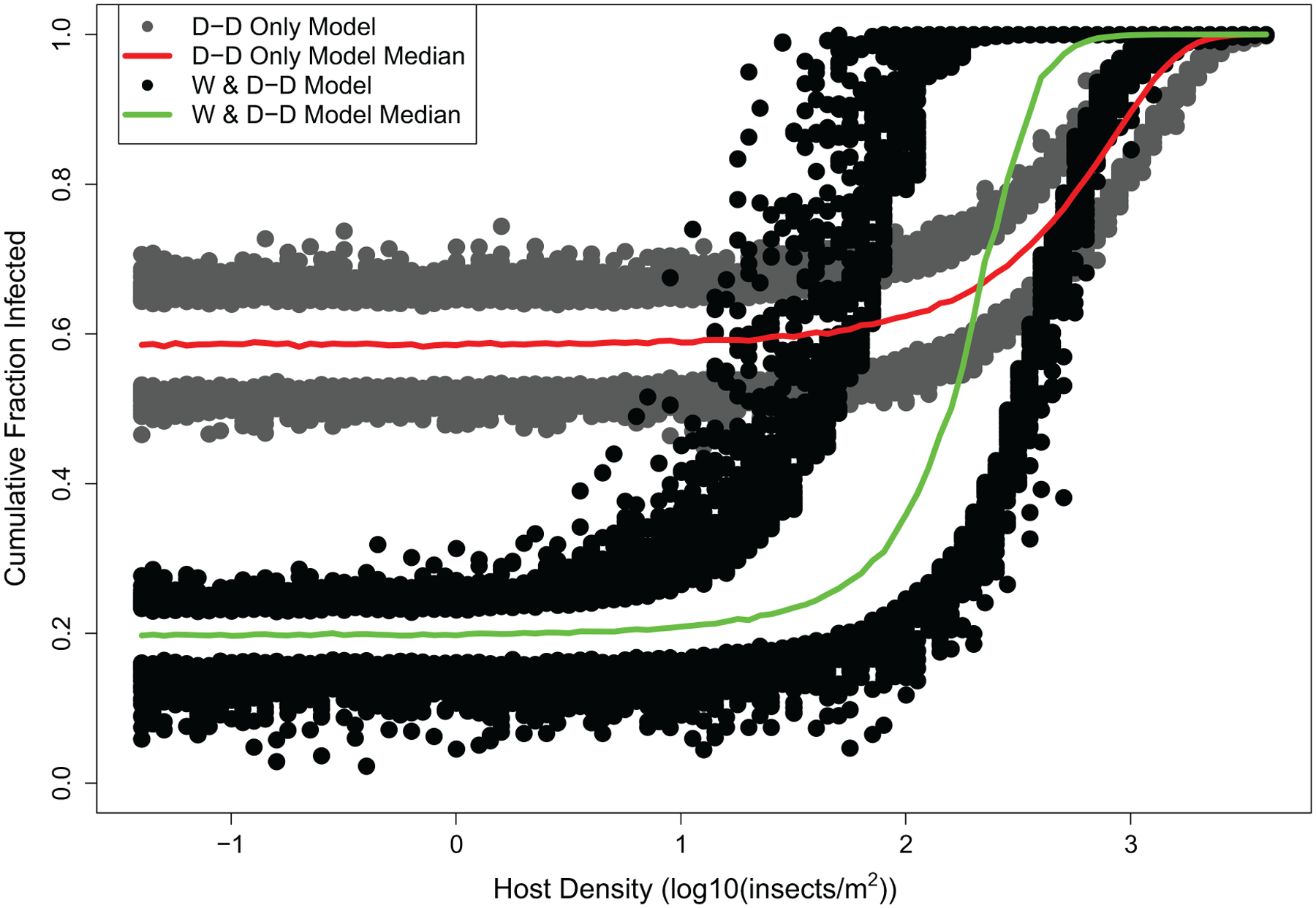
Predictions of the best density-dependence-only model and the best combined model, across a range of densities. For each model, the points depict the upper 95% and lower 5% of 1,000 realizations at each density, while the solid lines show the median at each density. For each simulation of the combined model, we generated weather using a Richardson weather generator (Richardson 1981), which we fit using weather data from our study plots. The initial resting spore density for each model was taken from the respective model’s best-fit value for the central 2010 population. This density was lower for the density-dependence-only model than for the best combined model (appendix), but the density-dependence-only model nevertheless has a high infection rate at low densities due to its high resting spore transmission rate.
The effects of environmental stochasticity in our models are much stronger than the analogous effects in models with demographic stochasticity. In the SIR model with demographic stochasticity (fig. 1), variation in epizootic severity is slight unless the population is small, and most of the variation occurs at densities near the threshold. In our model, in contrast, variation in epizootic severity is high unless the host density is very high.
Counterintuitively, the effects of density in the best-fit density-dependence-only model are much weaker than in the best combined model (fig. 7). This effect likely occurs because the density-dependence-only model can only explain weather-driven epizootics by invoking high resting spore transmission. For example, in the south 2010 and north 2010 populations, host densities were intermediate, but favorable weather conditions nevertheless led to intense epizootics. To fit the data from those populations, the density-dependence-only model was therefore forced to use a high resting spore transmission rate (appendix). Because of this high resting spore transmission rate, conidia transmission in the density-dependence-only model plays a much less important role than in the best combined model. In the density-dependence-only model, the infection rate therefore varies only modestly across host densities. Also, because the density-dependence-only model allows for inherent environmental stochasticity but only very simple effects of weather-driven environmental stochasticity, its predictions are substantially less variable than the predictions of the combined model.
Discussion
Our main result is that the strong effects of weather-driven stochasticity on Entomophaga maimaiga do not eliminate the pathogen’s host density threshold. Moreover, in our best model, variation in the threshold is much stronger than it is in models of demographic stochasticity. We therefore argue that models that include environmental stochasticity may sometimes provide a better explanation for variation in host density thresholds than models that include only demographic stochasticity. More broadly, our results provide a clear example of how weather and density-dependent transmission can together drive the dynamics of an animal pathogen.
In arguing that stochasticity can make it difficult to estimate host population thresholds, Lloyd-Smith et al. (2005) used models of demographic stochasticity. Given that the host threshold in our models is more strongly blurred than in models of demographic stochasticity, our results could be viewed as providing support for Lloyd-Smith et al.’s argument that the threshold concept is of limited practical value. Indeed, the uncertainty in the host density threshold in our best model spans an order of magnitude (fig. 7). In the gypsy moth, however, the amplitude of the fluctuations in the insect population is three to five orders of magnitude (Elkinton and Liebhold 1990), as is often the case in outbreaking insects (Anderson and May 1981). The uncertainty in our estimate of the threshold is thus dwarfed by variation in the density of the insect. The high uncertainty in our threshold estimate therefore does not mean that the estimate would not be useful in management. We therefore argue that the threshold concept can be useful for understanding disease dynamics in nature, even if weather effects are strong.
Our work also shows that constructing weather-driven host-pathogen models can be extremely challenging, which is likely why theoreticians often focus on demographic stochasticity (Daley and Gani 1999). Previous efforts to estimate host density thresholds have nevertheless invoked weather variation to explain variation in the disease density threshold, for example, in sylvatic plague in great gerbils (Davis et al. 2007) and in sea lice in salmon (Frazer et al. 2012). Models that allow for weather-driven stochasticity may thus be useful for understanding many different host-pathogen systems, even as the model details vary between systems. Moreover, previous efforts to quantify thresholds have often relied on deterministic models, so our work provides a useful example of how general theory can be extended to allow for environmental stochasticity.
Although tests of general theory necessarily require a consideration of biological specifics, by keeping our models as general as possible we have been able to consider broader conceptual issues. Previous modeling work on E. maimaiga has in contrast used models whose structure has strongly differed from the structure of classical, general theory (Weseloh et al. 1993). Previous work was presumably motivated by a desire to increase model realism, but our more general model is realistic enough to provide accurate predictions of E. maimaiga epizootics. In fact, given that E. maimaiga–driven population collapses obviate the need for the use of artificial insecticides (Woods et al. 1991), our model predictions could be practically useful.
Previous studies of the effects of weather or climate on animal pathogens have often estimated model parameters using laboratory data alone (Voyles et al. 2012; Molnár et al. 2013). These studies have provided important insights into disease dynamics, but there is at least some risk that the behavior of such models reflects the artificial environment of the laboratory. Because we instead estimated model parameters from field data, the predictions of our models may better reflect conditions in nature. Meanwhile, some previous modeling studies of animal pathogens have allowed for environmental stochasticity, but only while using a one-step-ahead fitting algorithm (Webb et al. 2006; Smith et al. 2009). One-step-ahead algorithms do not distinguish between measurement error and environmental stochasticity and therefore do not allow for direct tests of the relative importance of environmental stochasticity and host abundance. By incorporating weather covariates and by separately estimating stochasticity and measurement error, we were able to carry out just such a test.
A related point is that by combining experimental and observational data, we were able to estimate essentially all of our model’s parameters while using data from only a handful of epizootics. Experimental data may thus permit estimation of thresholds in cases for which observational data alone are insufficient. Our work thus demonstrates the usefulness of experimental data in disease ecology.
The gypsy moth is an introduced pest of hardwood forests in eastern North America, and its outbreaks have often caused extensive tree mortality (Elkinton and Liebhold 1990). It is therefore worth considering the implications of our work for gypsy moth outbreak cycles. Before E. maimaiga first occurred at high levels in 1989 (Elkinton et al. 1991)—the circumstances of the original introduction are somewhat mysterious (see Hajek et al. 1995)—gypsy moth outbreaks in North America were driven by a combination of a species-specific baculovirus and generalist predators (Dwyer et al. 2004), and severe defoliation occurred frequently (Johnson et al. 2006). Since the introduction of E. maimaiga, however, the baculovirus has almost disappeared, and defoliation levels have been much lower throughout the gypsy moth’s range in North America (Asaro and Chamberlin 2015). In New England in particular, gypsy moth outbreaks effectively ceased after 1996 (Allstadt et al. 2013), and defoliation has been very low since the early 1990s. Allstadt et al. (2013) argued that this change could be explained by stochastic variation in generalist-predator attack rates. The near coincidence of the first E. maimaiga epizootics and the decline in gypsy moth defoliation suggests that E. maimaiga may provide an alternative explanation. If this hypothesis is correct, then the explanation for the lack of outbreaks since the early 1990s may be that E. maimaiga has maintained gypsy moth populations at low, stable equilibria.
Models of insect outbreaks also support the hypothesis that the introduction of E. maimaiga has turned the gypsy moth’s population cycles into a low, stable equilibrium. In these models, low pathogen survival in the environment, as in the gypsy moth baculovirus (Fuller et al. 2012), leads to long-period, large-amplitude cycles (Dwyer et al. 2000, 2004). The model cycles match data on gypsy moth outbreak cycles before the introduction of E. maimaiga (Johnson et al. 2006), when the baculovirus was the dominant mortality source in outbreaks, suggesting that the models provide a reasonable description of gypsy moth dynamics before the introduction of E. maimaiga. In contrast to the short survival time of the baculovirus in the environment, the survival of E. maimaiga resting spores in the environment is very high (Weseloh and Andreadis 1997). In insect outbreak models, high long-term pathogen survival turns population cycles into a stable point equilibrium (Dwyer et al. 2000). The advent of E. maimaiga may therefore have led to a drastic change in the dynamics of the gypsy moth in North America.
Gypsy moth outbreaks have nevertheless occurred at least sporadically in states outside New England since the advent of E. maimaiga, and an outbreak occurred in New England itself in 2015–2018 (Pasquarella et al. 2018). Moreover, compared with baculovirus infection rates (Fuller et al. 2012), E. maimaiga infection rates rise much more rapidly with density (fig. 7). This difference likely occurs because there is little to no variation in the gypsy moth’s resistance to E. maimaiga, whereas a trade-off between resistance and fecundity maintains extensive variation in the gypsy moth’s resistance to the baculovirus (Páez et al. 2015, 2017). A lack of variation in resistance to a pathogen is destabilizing in outbreak models (Dwyer et al. 2000) and could therefore counterbalance the stabilizing effects of the high survival of resting spores. Understanding these effects requires that we extend our E. maimaiga models to allow for long-term dynamics, and such an extension is therefore a priority in future research.
Fungal diseases affect a range of animal species, including chytridiomycosis of amphibians (Pounds et al. 2006) and white nose syndrome in bats (Langwig et al. 2012). Although the quantitative effects of weather on fungal pathogens are often poorly understood (Fisher et al. 2012), most fungal pathogens require high humidity (Hesketh et al. 2010). Given that climate change models predict that humidity will change in a region-specific fashion (Wang and Kotamarthi 2015), the long-term effects of climate change on fungal pathogens cannot be easily predicted without disease models that take regional weather into account. In our study area in the lower peninsula of Michigan, for example, rainfall and temperatures are both predicted to increase (Wang and Kotamarthi 2014). Given that increased rainfall and increased temperature have opposite effects on E. maimaiga infection rates, intuiting the net effects of these changes is difficult. This is important because if infection rates decline and if E. maimaiga has been keeping the gypsy moth in check, climate change could lead to the insect’s resurgence. Extending our models to allow for climate change is therefore another priority for future work.
Supplementary Material
Acknowledgments
Our work was funded by National Institutes of Health grant R01GM96655, awarded to G.D., V.D., and B. Rehill, and by a National Science Foundation Graduate Research Fellowship awarded to C.H.K. Research was conducted under US Department of Agriculture Animal and Plant Health Inspection Service permit P526P-12–01466 (to G.D). D. Murnane provided invaluable assistance in the field. J.L. was supported by the Chinese Scholarship Council. S. Allesina, T. Wootton, R. Kotamarthi, S. Cobey, and especially J. Mihaljevic made helpful comments on the text.
Literature Cited
- Adelman JS, Moyers SC, Farine DR, and Hawley DM. 2015. Feeder use predicts both acquisition and transmission of a contagious pathogen in a North American songbird. Proceedings of the Royal Society B 282:20151429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allstadt AJ, Haynes KJ, Liebhold AM, and Johnson DM. 2013. Long-term shifts in the cyclicity of outbreaks of a forest-defoliating insect. Oecologia 172:141–151. [DOI] [PubMed] [Google Scholar]
- Altizer S, Ostfeld RS, Johnson PT, Kutz S, and Harvell CD. 2013. Climate change and infectious diseases: from evidence to a predictive framework. Science 341:514–519. [DOI] [PubMed] [Google Scholar]
- Anderson RM, and May RM. 1981. The population dynamics of microparasites and their invertebrate hosts. Philosophical Transactions of the Royal Society B 291:451–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asaro C, and Chamberlin LA. 2015. Outbreak history (1953–2014) of spring defoliators impacting oak-dominated forests in Virginia, with emphasis on gypsy moth (Lymantria dispar L.) and fall cankerworm (Alsophila pometaria Harris). American Entomologist 61:174–185. [Google Scholar]
- Berger JO, Liseo B, and Wolpert RL. 1999. Integrated likelihood methods for eliminating nuisance parameters. Statistical Science 14:1–28. [Google Scholar]
- Bolker BM, and Pacala SW. 1999. Spatial moment equations for plant competition: understanding spatial strategies and the advantages of short dispersal. American Naturalist 153:575–602. [DOI] [PubMed] [Google Scholar]
- Burnham KP, and Anderson DR. 2002. Model selection and multimodel inference: a practical information-theoretic approach. 2nd ed. Springer, New York. [Google Scholar]
- Champredon D, and Earn DJ. 2016. Understanding apparently non-exponential outbreaks: comment on “Mathematical Models to Characterize Early Epidemic Growth: A Review” by Gerardo Chowell et al. Physics of Life Reviews 18:105–108. [DOI] [PubMed] [Google Scholar]
- Chowell G, Sattenspiel L, Bansal S, and Viboud C. 2016. Mathematical models to characterize early epidemic growth: a review. Physics of Life Reviews 18:66–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Civitello DJ, Pearsall S, Duffy MA, and Hall SR. 2013. Parasite consumption and host interference can inhibit disease spread in dense populations. Ecology Letters 16:626–634. [DOI] [PubMed] [Google Scholar]
- Cobey S, and Baskerville EB. 2016. Limits to causal inference with state-space reconstruction for infectious disease. PLoS ONE 11:e0169050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooch EG, Conn PB, Ellner SP, Dobson AP, and Pollock KH. 2012. Disease dynamics in wild populations: modeling and estimation: a review. Journal of Ornithology 152:485–509. [Google Scholar]
- Daley DJ, and Gani J. 1999. Epidemic modelling: an introduction. Cambridge University Press, Cambridge. [Google Scholar]
- Dallas TA, Krkošek M, and Drake JM. 2018. Experimental evidence of a pathogen invasion threshold. Royal Society Open Science 5:171975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis S, Leirs H, Viljugrein H, Stenseth NC, De Bruyn L, Klassovskiy N, Ageyev V, and Begon M. 2007. Empirical assessment of a threshold model for sylvatic plague. Journal of the Royal Society Interface 4:649–657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwyer G, Dushoff J, Elkinton JS, and Levin SA. 2000. Pathogen-driven outbreaks in forest defoliators revisited: building models from experimental data. American Naturalist 156:105–120. [DOI] [PubMed] [Google Scholar]
- Dwyer G, Dushoff J, and Yee SH. 2004. The combined effects of pathogens and predators on insect outbreaks. Nature 430:341–345. [DOI] [PubMed] [Google Scholar]
- Dwyer G, and Elkinton JS. 1993. Using simple models to predict virus epizootics in gypsy moth populations. Journal of Animal Ecology 62:1–11. [Google Scholar]
- Elderd BD 2013. Developing models of disease transmission: insights from ecological studies of insects and their baculoviruses. PLoS Pathogens 9:e1003372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elkinton JS, Hajek AE, Boettner GH, and Simons EE. 1991. Distribution and apparent spread of Entomophaga maimaiga (Zygomycetes: Entomophthorales) in gypsy moth (Lepidoptera: Lymantriidae) populations in North America. Environmental Entomology 20:1601–1605. [Google Scholar]
- Elkinton JS, and Liebhold AM. 1990. Population dynamics of gypsy moth in North America. Annual Review of Entomology 35:571–596. [Google Scholar]
- Fisher MC, Henk DA, Briggs CJ, Brownstein JS, Madoff LC, McCraw SL, and Gurr SJ. 2012. Emerging fungal threats to animal, plant and ecosystem health. Nature 484:186–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frazer LN, Morton A, and Krkošek M. 2012. Critical thresholds in sea lice epidemics: evidence, sensitivity and subcritical estimation. Proceedings of the Royal Society B 1735:1950–1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuller E, Elderd BD, and Dwyer G. 2012. Pathogen persistence in the environment and insect-baculovirus interactions: disease-density thresholds, epidemic burnout and insect outbreaks. American Naturalist 179:E70–E96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuller SH, and Millett LI. 2011. The future of computing performance: game over or next level? National Academy Press, Washington, DC. [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, and Rubin DB. 2014. Bayesian data analysis, third edition. Chapman & Hall/CRC, New York. [Google Scholar]
- Gough B 2009. GNU scientific library reference manual. Network Theory, Boston. [Google Scholar]
- Hajek AE 1997. Entomophaga maimaiga reproductive output is determined by the spore type initiating an infection. Mycological Research 8:971–974. [Google Scholar]
- —1999. Pathology and epizootiology of Entomophaga maimaiga infections in forest Lepidoptera. Microbiology and Molecular Biology Reviews 63:814–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajek AE, Carruthers RI, and Soper RS. 1990. Temperature and moisture relations of sporulation and germination by Entomophaga maimaiga (Zygomycetes, Entomophthoraceae), a fungal pathogen of Lymantria dispar (Lepidoptera, Lymantriidae). Environmental Entomology 19:85–90. [Google Scholar]
- Hajek AE, and Eastburn CC. 2001. Effect of host insects on activation of Entomophaga maimaiga resting spores. Journal of Invertebrate Pathology 77:290–291. [DOI] [PubMed] [Google Scholar]
- Hajek AE, Humber RA, and Elkinton JS. 1995. Mysterious origin of Entomphaga maimaiga in North America. American Entomologist 41:31–43. [Google Scholar]
- Hajek AE, Tobin PC, and Haynes KJ. 2015. Replacement of a dominant viral pathogen by a fungal pathogen does not alter the collapse of a regional forest insect outbreak. Oecologia 177:785–797. [DOI] [PubMed] [Google Scholar]
- Hajek AE, and van Nouhuys S. 2016. Fatal diseases and parasitoids: from competition to facilitation in a shared host. Proceedings of the Royal Society B 283:20160154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han X, and Kloeden PE. 2017. Random ordinary differential equations and their numerical solution. Springer, New York. [Google Scholar]
- Harvell CD, Mitchell CE, Ward JR, Altizer S, Dobson AP, Ostfeld RS, and Samuel MD. 2002. Climate warming and disease risks for terrestrial and marine biota. Science 296:2158–2162. [DOI] [PubMed] [Google Scholar]
- He D, Dushoff J, Day T, Ma J, and Earn DJ. 2011. Mechanistic modelling of the three waves of the 1918 influenza pandemic. Theoretical Ecology 4:283–288. [Google Scholar]
- Hesketh H, Roy HE, Eilenberg J, Pell JK, and Hails RS. 2010. Challenges in modelling complexity of fungal entomopathogens in semi-natural populations of insects. BioControl 55:55–73. [Google Scholar]
- Hilborn R, and Mangel M. 1997. The ecological detective: confronting models with data. Princeton University Press, Princeton, NJ [Google Scholar]
- Hunter A 1991. Traits that distinguish outbreaking and nonoutbreaking Macrolepidoptera feeding on northern hardwood trees. Oikos 60:275–282. [Google Scholar]
- Ionides E, Bretó C, and King A. 2006. Inference for nonlinear dynamical systems. Proceedings of the National Academy of Sciences of the USA 103:18438–18443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DM, Liebhold AM, Tobin PC, and Bjørnstad ON. 2006. Allee effects and pulsed invasion by the gypsy moth. Nature 444:361–363. [DOI] [PubMed] [Google Scholar]
- Keeling MJ, and Rohani P. 2008. Modeling infectious diseases in humans and animals. Princeton University Press, Princeton, NJ. [Google Scholar]
- Kennedy DA, Dukic V, and Dwyer G. 2015. Combining principal component analysis with parameter line-searches to improve the efficacy of Metropolis-Hastings MCMC. Environmental and Ecological Statistics 22:247–274. [Google Scholar]
- Kermack WO, and McKendrick AG. 1927. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society A 115:700–721. [Google Scholar]
- King AA, Ionides EL, Pascual M, and Bouma MJ. 2008. In-apparent infections and cholera dynamics. Nature 454:877–880. [DOI] [PubMed] [Google Scholar]
- Kyle CH, Liu J, Gallagher ME, Dukic V, and Dwyer G. 2020. Data from: Stochasticity and infectious disease dynamics: density and weather effects on a fungal insect pathogen. American Naturalist, Dryad Digital Repository, 10.5061/dryad.3nv3ss2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lance D, Elkinton J, and Schwalbe C. 1987. Behaviour of late-instar gypsy moth larvae in high and low density populations. Ecological Entomology 12:267–273. [Google Scholar]
- Laneri K, Bhadra A, Ionides EL, Bouma M, Dhiman RC, Yadav RS, and Pascual M. 2010. Forcing versus feedback: epidemic malaria and monsoon rains in northwest India. PLoS Computational Biology 6:e1000898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langwig KE, Frick WF, Bried JT, Hicks AC, Kunz TH, and Marm Kilpatrick A. 2012. Sociality, density-dependence and microclimates determine the persistence of populations suffering from a novel fungal disease, white-nose syndrome. Ecology Letters 15:1050–1057. [DOI] [PubMed] [Google Scholar]
- Liebhold AM, Plymale R, Elkinton JS, and Hajek AE. 2013. Emergent fungal entomopathogen does not alter density dependence in a viral competitor. Ecology 94:1217–1222. [DOI] [PubMed] [Google Scholar]
- Lloyd-Smith JO, Cross PC, Briggs CJ, Daugherty M, Getz WM, Latto J, Sanchez MS, Smith AB, and Swei A. 2005. Should we expect population thresholds for wildlife disease? Trends in Ecology and Evolution 20:511–519. [DOI] [PubMed] [Google Scholar]
- McCallum H 2016. Models for managing wildlife disease. Parasitology 143:805–820. [DOI] [PubMed] [Google Scholar]
- McCullagh P, and Nelder JA. 1989. Generalized linear models. Chapman & Hall, London. [Google Scholar]
- Molnár PK, Kutz SJ, Hoar BM, and Dobson AP. 2013. Metabolic approaches to understanding climate change impacts on seasonal host-macroparasite dynamics. Ecology Letters 16:9–21. [DOI] [PubMed] [Google Scholar]
- Moreau G, and Lucarotti CJ. 2007. A brief review of the past use of baculoviruses for the management of eruptive forest defoliators and recent developments on a sawfly virus in Canada. Forestry Chronicle 83:105–112. [Google Scholar]
- Oksendal B 2013. Stochastic differential equations: an introduction with applications. Springer, New York. [Google Scholar]
- Páez DJ, Dukic V, Dushoff J, Fleming-Davies A, and Dwyer G. 2017. Eco-evolutionary theory and insect outbreaks. American Naturalist 189:616–629. [DOI] [PubMed] [Google Scholar]
- Páez DJ, Fleming-Davies A, and Dwyer G. 2015. Effects of pathogen exposure on life history variation in the gypsy moth (Lymantria dispar). Journal of Evolutionary Biology 28:1828–1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasquarella VJ, Elkinton JS, and Bradley BA. 2018. Extensive gypsy moth defoliation in southern New England characterized using Landsat satellite observations. Biological Invasions 20:3047–3053. [Google Scholar]
- Pawitan Y 2001. In all likelihood: statistical modeling and inference using likelihood. Oxford University Press, New York. [Google Scholar]
- Pounds J, Bustamante M, Coloma L, Consuegra J, Fogden M, Foster P, La Marca E, et al. 2006. Widespread amphibian extinctions from epidemic disease driven by global warming. Nature 439:161–167. [DOI] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, and Flannery BP. 1992. Numerical recipes in C. Cambridge University Press, Cambridge. [Google Scholar]
- Rachowicz LJ, Knapp RA, Morgan JA, Stice MJ, Vredenburg VT, Parker JM, and Briggs CJ. 2006. Emerging infectious disease as a proximate cause of amphibian mass mortality. Ecology 87:1671–1683. [DOI] [PubMed] [Google Scholar]
- Reilly JR, Hajek AE, Liebhold AM, and Plymale R. 2014. Impact of Entomophaga maimaiga (Entomophthorales: Entomophthoraceae) on outbreak gypsy moth populations (Lepidoptera: Erebidae): the role of weather. Environmental Entomology 43:632–641. [DOI] [PubMed] [Google Scholar]
- Richardson RW 1981. Stochastic simulation of daily precipitation, temperature, and solar radiation. Water Resources Research 17:182–190. [Google Scholar]
- Ross S 2002. Simulation. 3rd ed. Academic Press, New York. [Google Scholar]
- Shocket MS, Strauss AT, Hite JL, Šljivar M, Civitello DJ, Duffy MA, Cáceres CE, and Hall SR. 2018. Temperature drives epidemics in a zooplankton-fungus disease system: a trait-driven approach points to transmission via host foraging. American Naturalist 191:435–451. [DOI] [PubMed] [Google Scholar]
- Smith MJ, Telfer S, Kallio ER, Burthe S, Cook AR, Lambin X, and Begon M. 2009. Host-pathogen time series data in wildlife support a transmission function between density and frequency dependence. Proceedings of the National Academy of Sciences of the USA 106:7905–7909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjaden NB, Caminade C, Beierkuhnlein C, and Thomas SM. 2018. Mosquito-borne diseases: advances in modelling climate-change impacts. Trends in Parasitology 34:227–245. [DOI] [PubMed] [Google Scholar]
- Voyles J, Johnson LR, Briggs CJ, Cashins SD, Alford RA, Berger L, Skerratt LF, Speare R, and Rosenblum EB. 2012. Temperature alters reproductive life history patterns in Batrachochytrium dendrobatidis, a lethal pathogen associated with the global loss of amphibians. Ecology and Evolution 2:2241–2249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, and Kotamarthi VR. 2014. Downscaling with a nested regional climate model in near-surface fields over the contiguous United States. Journal of Geophysical Research: Atmospheres 119:8778–8797. [Google Scholar]
- —2015. High-resolution dynamically downscaled projections of precipitation in the mid and late 21st century over North America. Earth’s Future 3:268–288. [Google Scholar]
- Webb CT, Brooks CP, Gage KL, and Antolin MF. 2006. Classic flea-borne transmission does not drive plague epizootics in prairie dogs. Proceedings of the National Academy of Sciences of the USA 103:6236–6241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weseloh RM 1999. Entomophaga maimaiga (Zygomycete: Entomophthorales) resting spores and biological control of the gypsy moth (Lepidoptera: Lymantriidae). Environmental Entomology 28:1162–1171. [Google Scholar]
- Weseloh RM, and Andreadis TG. 1992. Epizootiology of the fungus Entomophaga maimaiga, and its impact on gypsy moth populations. Journal of Invertebrate Pathology 59:133–141. [DOI] [PubMed] [Google Scholar]
- —1997. Persistence of resting spores of Entomophaga maimaiga, a fungal pathogen of the gypsy moth, Lymantria dispar. Journal of Invertebrate Pathology 69:195–196. [DOI] [PubMed] [Google Scholar]
- Weseloh RM, Andreadis TG, and Onstad DW. 1993. Modeling the influence of rainfall and temperature on the phenology of infection of gypsy moth, Lymantria dispar, larvae by the fungus Entomophaga maimaiga. Biological Control 3:311–318. [Google Scholar]
- Woods SA, Elkinton JS, Murray KD, Liebhold AM, Gould JR, and Podgwaite JD. 1991. Transmission dynamics of a nuclear polyhedrosis virus and predicting mortality in gypsy moth (Lepidoptera: Lymantriidae) populations. Journal of Economic Entomology 84:423–430. [DOI] [PubMed] [Google Scholar]
References Cited Only in the Online Enhancements
- Barbosa P, and Greenblatt J. 1979. Suitability, digestibility and assimilation of various host plants of the gypsy moth Lymantria dispar. Oecologia 43:111–119. [DOI] [PubMed] [Google Scholar]
- Bell RA, Owens CD, Shapiro M, and Tardif JR. 1981. Pages 599–655 in Mass rearing and virus production. The gypsy moth: integrated pest management. USDA Technical Bulletin, Washington, DC. [Google Scholar]
- Cox DR, and Snell EJ. 1989. Analysis of binary data. Vol. 32. Chapman & Hall/CRC, New York. [Google Scholar]
- Dwyer G, and Elkinton JS. 1995. Host dispersal and the spatial spread of insect pathogens. Ecology 76:1262–1275. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


