Abstract
Hybridization of short nucleic acid segments (<4 nt) to single-strand templates occurs as a critical intermediate in processes such as nonenzymatic nucleic acid replication and toehold-mediated strand displacement. These templates often contain adjacent duplex segments that stabilize base pairing with single-strand gaps or overhangs, but the thermodynamics and kinetics of hybridization in such contexts are poorly understood because of the experimental challenges of probing weak binding and rapid structural dynamics. Here we develop an approach to directly measure the thermodynamics and kinetics of DNA and RNA dinucleotide dehybridization using steady-state and temperature-jump infrared spectroscopy. Our results suggest that dinucleotide binding is stabilized through coaxial stacking interactions with the adjacent duplex segments as well as from potential noncanonical base-pairing configurations and structural dynamics of gap and overhang templates revealed using molecular dynamics simulations. We measure timescales for dissociation ranging from 0.2–40 μs depending on the template and temperature. Dinucleotide hybridization and dehybridization involve a significant free energy barrier with characteristics resembling that of canonical oligonucleotides. Together, our work provides an initial step for predicting the stability and kinetics of hybridization between short nucleic acid segments and various templates.
Significance
Processes in biology and nanotechnology rely on hybridization of nucleic acid segments as short as mononucleotides. In this context, the binding stability and timescale of dehybridization ultimately inhibit or enable biochemical reactions or structural rearrangements to occur after binding. Understanding the energetics and time dependence of short nucleic acid hybridization, particularly to larger templates, is critical for understanding processes such as nonenzymatic RNA replication and toehold-mediated strand displacement. We demonstrate an approach for extracting temperature-dependent energetics and kinetics of dinucleotide hybridization to gap and overhang templates using steady-state and time-resolved infrared spectroscopy. Our findings indicate that binding between a dinucleotide and template is stabilized beyond standard hybridization, and the methods established here can be applied broadly to various sequences and templates.
Introduction
DNA and RNA duplex hybridization has been investigated for more than 60 years with the aim of developing predictive models for how thermodynamic and kinetic properties will vary with molecular factors such as strand length, sequence, and chemical modifications (1,2,3). The development of numerous models, such as the quantitatively accurate nearest-neighbor (NN) models (4,5) for thermodynamics or the kinetic zipper model (6,7), shape the modern understanding of nucleic acid properties as well as the development of nucleic acid technology (8,9). However, most of these models were developed for oligonucleotides, and the hybridization properties of nucleic acid segments shorter than 6 nt in length have largely been neglected. Hybridization of such short segments is often perceived as irrelevant because of their poor binding stability in aqueous solution, but there are biological processes where segments as short as mononucleotides must hybridize. Many of these processes, such as the binding of 2′-deoxynucleotide triphosphates to single-strand DNA (ssDNA) during strand replication or binding between 3-nt anticodons of tRNA and their complement mRNA, utilize additional protein-nucleic acid interactions to promote binding (10,11). However, processes such as nonenzymatic replication of nucleic acids and toehold-mediated strand displacement require hybridization of 1- to 4-bp patches without the help of proteins (8,12,13,14).
A conserved feature among the examples of short oligonucleotide hybridization is that a short segment binds to a single-strand overhang adjacent to a duplex region or in a gap between two duplex segments. The adjacent duplexes offer coaxial stacking interactions that stabilize hybridization of the short oligonucleotide. The thermodynamic benefit of coaxial stacking has been measured for DNA and RNA oligonucleotides and is often found to be similar to stacking in B-DNA or A-RNA, respectively (15,16,17,18,19,20). The structural constraints of the sugar-phosphate backbone at a nick site are relaxed relative to a covalently linked base-pair step and may enable more stabilizing stacking configurations (21,22). Additionally, the single-strand segments in overhang and gap templates may have physical properties different from free single strands, such as reduced configurational flexibility, increased stacking, and different hydration, that influence the stability and dynamics of binding with short oligonucleotides. A few studies have shown evidence of increased rigidity of gap and overhang single-stranded regions relative to free single strands as well as bending of duplexes containing 1- or 2-nt gaps (23,24,25,26,27,28,29), and these properties are likely highly sensitive to nucleobase sequence and cation concentrations (30,31,32).
The binding stability of mononucleotides with overhang and gap templates has been studied recently. NMR-monitored titrations of mononucleotides with overhangs revealed dissociation constant () values ranging from ∼10 mM for G:C base-pairing to ∼200 mM for A:T base-pairing (33,34). Isothermal titration calorimetry (ITC) and fluorescence resonance energy transfer-monitored titrations have shown that the for binding to a gap decreases nearly 3 orders of magnitude to values of 0.2–0.6 mM (35,36), which corresponds to a ∼12 kJ mol−1 increase in the dissociation free energy () and is consistent with forming an additional NN step (4,37). These studies give a sense for the stability of short oligonucleotide hybridization to overhangs and gaps and indicate that it depends on sequence and whether DNA or RNA is used, but, with the exception of ITC, the thermodynamic information is limited to dissociation constants ( or ) at the measurement temperature. A detailed understanding of hybridization onto overhangs and gaps requires knowledge of enthalpic and entropic contributions to stability and the role of relevant environmental variables such as temperature and counterion concentration (38,39,40). More importantly, no studies have directly monitored the time dependence of hybridization and dehybridization for short oligonucleotides onto templates, and these timescales determine whether reactions such as nonenzymatic extension or toehold-mediated strand displacement are possible.
Here we report the temperature-dependent thermodynamics and kinetics of short oligonucleotide dehybridization from overhangs and gaps using steady-state and temperature-jump infrared (T-jump IR) spectroscopy. IR spectroscopy is sensitive to base-pairing and stacking interactions and distinctly resolves changes in A:T and G:C base-pairing without the need for synthetic labels (41,42). Characterization of temperature-dependent binding stability enables accurate determination of enthalpic and entropic contributions and is particularly relevant in nonenzymatic replication, where temperature variations may play a key role (38,39). We focus on the binding of DNA and RNA dinucleotides and demonstrate our approach with a model system of adenine-adenine (AA) dinucleotide binding next to pure G:C duplex regions. This model system was chosen to maximize spectral contrast between binding of the dinucleotide and the structural changes and dynamics within the template itself, but our approach is applicable to any nucleobase sequence. We find quantitative agreement between thermodynamic results obtained from IR spectroscopy and those from complementary temperature-dependent 1H-NMR and ITC measurements of binding. From T-jump IR measurements, we extract a time constant ranging from 200 ns to 40 μs for dissociation of AA from the template that depends on the temperature and template, while the time constant for association is a few microseconds and shows a minor dependence on temperature. We also study the binding of 3-mer (AAA) and 4-mer (AAAA) adenine DNA oligonucleotides to assess the length dependence of association in this short oligonucleotide regimen. Our experimental results as well as all-atom molecular dynamics (MD) simulations suggest that differences in the structure and dynamics of the bound complex and template compared with free oligonucleotides lead to significantly different binding thermodynamics and kinetics for overhangs and gaps.
Materials and methods
Synthesis and purification of RNA oligonucleotides
RNA oligonucleotides were synthesized in house on a K&A (Schaafheim, Germany) H-6 solid-phase synthesizer. Phosphoramidites and reagents for the K&A synthesizer were purchased from Glen Research (Sterling, VA) and Chemgenes (Wilmington, MA). 1.5 mL of a 1:1 mixture of 28% aqueous ammonium hydroxide and 40% aqueous methylamine was used to cleave the RNA from the solid support for 15 min at room temperature, followed by deprotection in the same solution for 15 min at 65°C. After cooling, the solutions were evaporated for 1 h in a SpeedVac vacuum concentrator and lyophilized to dryness. The dried 2′-O-tertbutyldimethylsilyl-protected RNA was dissolved in 115 μL DMSO, 60 μL triethylamine, and 75 μL triethylamine trihydrofluoride and deprotected for 2.5 h at 65°C. After cooling, the RNA was purified by two different methods depending on its length.
Short (≤6 nt) oligonucleotides were purified by a modified Glen-Pak protocol (Glen Research). After the RNA was quenched, bound to the resin, and washed to remove failed sequences, it was eluted with 50% acetonitrile/water (v/v). Following evaporation to dryness, the RNA was dissolved in 500 μL 2% trifluoroacetic acid to deprotect the 5′-O-dimethoxytitryl for 5 min at room temperature. The deprotection reaction was quenched with 500 μL 1 M triethylammonium bicarbonate (pH 9) and desalted using Sep-Pak C18 cartridges (Waters).
Longer (>7 nt) oligonucleotides were precipitated with 25 μL 5 M ammonium acetate and 1 mL 2-propanol at −78°C for 20 min; washed with 1 mL 80% ethanol in water (v/v); air dried; dissolved in 5 mM EDTA, 99% formamide in water (v/v); and purified by preparative 20% polyacrylamide gel electrophoresis (19:1 with 7 M urea). After crushing and soaking the desired gel band in 5 mM sodium acetate, 2 mM EDTA for 16 h at room temperature, the extracted RNA was desalted using Sep-Pak C18 cartridges (Waters, Milford, MA).
Purified RNA was characterized by high-resolution mass spectrometry on an Agilent (Santa Clara, CA) 6540 Q-TOF mass spectrometer.
Preparation of DNA oligonucleotides
DNA oligonucleotides were purchased from Integrated DNA Technologies (Coralville, IA) at desalt-grade purity. Short (≤6 nt) oligonucleotides were further desalted using Sep-Pak C18 cartridges (Waters), evaporated for 1 h in a SpeedVac vacuum concentrator, and lyophilized to dryness. Longer (>7 nt) oligonucleotides were dialyzed in ∼1.5 L ultrapure water for 24 h using Slide-A-Lyzer cassettes (2-kDa cutoff, Thermo Scientific, Waltham, MA), where the water was replaced every ∼6 h, and then lyophilized to dryness. For all measurements, oligonucleotides were prepared in deuterated 400 mM sodium phosphate buffer (SPB; [Na+] = 600 mM; pH 6.8). Oligonucleotide concentration was verified with UV absorbance using a NanoDrop UV-visible spectrometer (Thermo Scientific).
FTIR spectroscopy
Fourier transform IR (FTIR) spectra were measured with a Bruker (Billerica, MA) Tensor 27 FTIR spectrometer at 2-cm−1 resolution. 30 μL of sample was placed between two 1-mm-thick CaF2 windows with a path length defined by a 50-μm Teflon spacer. The windows were enclosed in a brass jacket that was temperature-controlled using a recirculating chiller (Ministat 125, Huber, Offenburg, Germany). The temperature at the sample was measured with a thermocouple in thermal contact with one CaF2 window for chiller set points from −3°C to 105°C, which was used to calibrate the temperatures reported in this work.
Prior to titration experiments performed at 1°C, the gap or overhang template solution was incubated at 85°C for 2 min and cooled to room temperature under ambient conditions. Samples were prepared with an AA-to-template molar ratio ranging from 0–4 with a constant template concentration of 1 mM. Samples were incubated at 1°C for 10 min prior to each measurement. For FTIR temperature series, all oligonucleotides were prepared at a 1 mM concentration and annealed prior to measurements as for titration measurements. Temperature series were performed in ∼2.6°C steps, and the sample was equilibrated for 3 min at each temperature prior to acquiring spectra. A discrete wavelet transform using the Mallat algorithm and symlet family was applied to the 1490- 1750-cm−1 region of the FTIR spectra to separate and subtract the D2O background absorption from each spectrum (43).
Two-dimensional IR spectroscopy
Two-dimensional IR (2D IR) measurements were performed using a previously described setup with a pump-probe beam geometry (44). Spectra were collected using parallel pulse polarization (ZZZZ) at a fixed waiting time () of 150 fs. The pump pulse pair delay () was scanned from −160 to 1900 fs in 16-fs steps. Samples were prepared identically as for FTIR measurements. Sample temperature was controlled using a recirculating chiller (Ministat 125, Huber). Temperature-dependent drift of the sample out of the pump and probe focus and overlap region was minimized by programmatically maximizing the pump-probe signal at each temperature using a motorized translation stage prior to measuring the 2D IR data.
Temperature-jump IR spectroscopy
The T-jump IR spectrometer used in this work has been described previously (45,46). Optical heating increases the sample temperature within 7 ns, and the ensuing changes in base-pairing and stacking of DNA and RNA are monitored with heterodyned dispersed vibrational echo spectroscopy (HDVE) (47) from nanosecond to millisecond time delays. The HDVE spectrum is collected with parallel pulse polarization (ZZZZ) and at a fixed waiting time of 150 fs and reports on the nucleobase ring and carbonyl vibrational bands similarly as an IR pump-probe spectrum. The T-jump laser power was attenuated with a polarizer to set a T-jump magnitude () of ∼13°C for all measurements. The initial temperatures () were set using a recirculating chiller connected to a brass sample jacket, and ΔT was determined from the change in mid-IR transmission following the T-jump pulse.
Given the complex form of the T-jump relaxation kinetics spanning multiple timescales, we chose a model-free analysis method to extract experimental relaxation rates. The time-domain HDVE response at different IR frequencies was converted into a rate spectrum using an inverse Laplace transform that employs a maximum entropy regularization method, which is described elsewhere (48,49). We calculate the observed relaxation rate, , for a given process by calculating the amplitude-weighted mean value of the rate for a corresponding peak in the rate spectrum.
Isothermal titration calorimetry
ITC measurements were performed using a MicroCal iTC200 (Malvern Panalytical, Malvern, United Kingdom). Template oligonucleotides were placed in the cell with a concentration that varied from 60 μM to 3 mM depending on the sequence, and the complement short oligonucleotide was placed in the syringe with a concentration of 100–300 μM. Sample conditions for each measurement are listed in Table S2. All samples were prepared in deuterated 400 mM SPB (pH 6.8) and degassed under a vacuum for more than 20 min at the experimental temperature prior to each measurement. ITC measurements started with an initial 0.4-μL injection, followed by 19 injections of 2-μL aliquots of the titrant oligonucleotide solution into the cell. The syringe needle constantly stirred the cell solution with a spin rate of 1000 rpm, and the injection duration and time interval between injections were adjusted to avoid signal saturation in high-concentration samples. The injection settings for each sample are listed in Table S2.
NMR spectroscopy
NMR spectra were acquired on a Bruker AVANCE III 500-MHz spectrometer equipped with a Bruker TXI probe. Temperature series were performed in 2.5°C steps, and the sample was equilibrated for 5 min and auto gradient and lock shimmed with TopShim at each temperature. prior to acquiring spectra. Samples were prepared in fully deuterated 400 mM SPB for all measurements and contained ∼1 mM 3-(trimethylsilyl)propionic-2,2,3,3-d4 acid (Sigma-Aldrich, St. Louis, MO) as a frequency reference.
Total correlation spectroscopy measurements were measured with decoupling in the presence of scalar interactions (DIPSI II) isotropic mixing and a mixing time of 60 ms. 2048 and 256 complex points were acquired in and , respectively, over sweep widths of 24 ppm.
Diffusion-ordered spectroscopy was performed on a Bruker AVANCE IIIHD 600-MHz spectrometer. Measurements were performed using a 2D stimulated echo pulse sequence with bipolar gradients and WATERGATE solvent suppression (Bruker TopSpin, stebpgp1s19). Spectra were acquired from 0%–95% of the maximum gradient field strength at 5% intervals where the maximum field strength was 5.35 T/cm. The magnetic field gradient was calibrated with a 3D-printed phantom with known spacing between the water samples.
MD simulations
DNA and RNA duplex topologies were constructed using AMBERTools22 (50) in canonical B and A forms, respectively. AA-gap complexes were generated from the canonical topologies by removing phosphate atoms after the sixth-position (5′-GA-3′) and eighth-position (5′-AG-3′) nucleotides and adding terminal 5′ and 3′ hydrogens using the GROMACS molecular modeling suite (51). Gap templates were generated by entirely removing the A nucleotides from the canonical topologies. MD simulations were performed with the force fields that are currently most accurate for modeling canonical DNA and RNA duplex structure: the parmbsc1 force field (bsc1-AMBER) (52) with the TIP3P (53) water model for DNA systems and the AMBER RNA force field developed by Shaw and co-workers (DES-AMBER) (54) with the TIP4P water model (55) for RNA systems. To enable more direct comparisons between DNA and RNA simulation results, we performed additional simulations of DNA using the DES-AMBER force field for DNA (56) with the TIP4P water model and simulations of RNA using the bsc1-AMBER force field with the TIP3P water model (Section S5). Cubic simulation boxes with periodic boundaries were constructed to ensure a minimum of 1 nm of spacing between any nucleic acid atoms and the boundaries. For 14-mer DNA, this corresponded to a box with 7.16-nm side lengths with 11,770 water molecules and for 14-mer RNA a box with 6.77-nm side lengths with 9845 water molecules. NaCl ion pairs were added to the simulation box to maintain an ionic concentration of 600 mM, and additional Na+ ions were added to balance the negatively charged phosphate backbone.
Energy minimization was performed on each topology using the steepest descent algorithm until the maximum force was below 1000 kJ mol−1 nm−1. Equilibration was performed for 100 ps in the NVT ensemble and then 100 ps in the NPT ensemble. Production runs were performed for up to 4 μs in the NVT ensemble. Simulations were propagated with a 2-fs time step using a leapfrog integrator, and frames were saved every 200 ps. Simulation temperature was set to 310 K and maintained by a velocity-rescaling thermostat (57). In the NPT equilibration runs, pressure was set to 1 bar and maintained using a Parinello-Rahmen barostat. Particle mesh Ewald (58) was used to calculate long-range electrostatic interactions, employing a 1.0-nm real-space cutoff and a 0.16 Fourier grid spacing that was optimized during runtime, and constraints were placed on hydrogen bonds using the linear constraint solver (LINCS) algorithm (59).
Cambridge conventional helical parameters (60) and backbone torsions were calculated from MD trajectories using a Biobb BioExcel Building Blocks workflow (61,62), which leverages the Curves+ program and its associated Canal tool (63,64). Intra-molecular residue distances and solvent distributions were calculated using the MDTraj Python library. Additional statistical analyses and visualizations were generated using the PyEMMA and Seaborn Python libraries (65,66).
Results and discussion
Low-temperature hybridization of dinucleotides to overhangs and gaps
Fig. 1a illustrates the model sequences we designed to study the hybridization of a 2′-deoxyadenosine dinucleotide onto G:C-rich DNA templates incorporating a single-stranded thymine overhang or thymine gap. Overhang templates (TTo) are composed of a 6-mer primer strand bound to the 3′ end of a 14-mer template strand. Gap templates also have a 6-mer helper strand bound to the 5′-end of the template. Additionally, we studied the binding of an adenosine dinucleotide onto a single-stranded uracil RNA gap template (UUg). The abbreviation AA will be used to refer to the 2′-deoxyadenosine dinucleotide for DNA and adenosine dinucleotide for RNA samples throughout. The primer and helper segments consist of six guanine:cytosine (G:C) base pairs to maximize their binding stability while keeping their size relatively small to minimize IR absorption from the template itself. The hybridized product between the template and AA is termed the AA-overhang (TTo:AA) or AA-gap complex (TTg:AA, UUg:AA). Although formation of a fully formed gap or overhang complex can potentially involve numerous binding equilibria, the choice of an AA bound weakly to a far more stable GC-rich template means that the dissociation of the complex is well described through two equilibrium constants: for the dissociation of AA from the template and ,Temp for dissociation of the template.
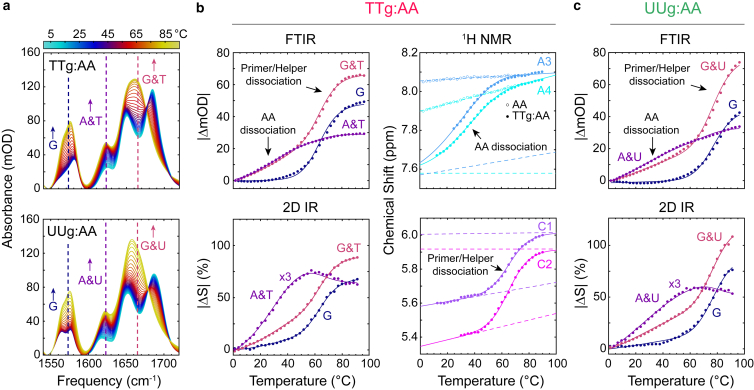
Figure 1.
Hybridization of the AA dinucleotide to gap and overhang at low temperature. (a) Model sequences studied in this work. Gap templates are comprised of a 14-mer template strand bound to 6-mer primer and 6-mer helper strands, whereas the overhang templates are only bound to the primer strand. (b–d) FTIR spectra at 1°C of 1 mM gap and overhang templates in 400 mM sodium phosphate buffer (SPB) at pH 6.8 without AA (black lines) and after adding 1 mM AA (colored lines). Difference spectra upon addition of AA are shown as insets. Labels indicate the nucleobases contributing to each frequency region of the FTIR spectra. (e) Titrations of AA against 1 mM TTg, TTo, and UUg templates at 1°C monitored with FTIR. The fraction of template bound to AA is determined from fitting the second singular value decomposition component of FTIR data between 1650 and 1720 cm−1 to a two-state binding model (solid lines, Eq. S2). The fraction of AA bound to template at a 1:1 M AA:template ratio () and the dissociation constant () are listed for each complex. Additional spectra and fitting details are provided in supporting material, Section S1.1. To see this figure in color, go online.
We first test for evidence that AA binds to gaps and overhangs at low temperature (1°C) using FTIR spectroscopy. Fig. 1 compares the FTIR spectra in the 1540- 1720-cm−1 region of isolated TTg, TTo, and UUg templates with samples containing an equimolar mixture of template and AA. This spectral region contains in-plane carbonyl and ring stretching vibrations of the nucleobases that are sensitive to base-pairing and stacking interactions and have been studied previously in detail (41,42,67,68). The templates are fully intact at 1°C so that spectral changes from adding AA report on binding of AA to the template. Each mixed sample exhibits an increase in absorbance near 1575 and 1625 cm−1, resulting from the A ring vibrations of AA. The 1650- 1700-cm−1 region primarily contains carbonyl vibrations. The shifting of intensity from 1665 to 1685 cm−1 indicates increased stacking and base-pairing of guanines adjacent to the gap, and the overlapping gain in intensity of the thymine carbonyl band near 1695 cm−1 indicates the formation of A:T base-pairing (41). The intensity of the 1625-cm−1 band directly reports on the stacking and base-pairing interactions experienced by AA, and its suppression in TTg:AA and UUg:AA relative to TTo:AA indicates greater binding of AA in the gap at 1°C. Further, FTIR-monitored titrations of AA with each template indicate an increase in the fraction of TTg bound to AA at equimolar conditions (), progressing from TTo:AA to UUg:AA to TTg:AA (Figs. 1 e and S1). decreases by over an order of magnitude in switching the template from an overhang to a gap, as observed previously for binding of guanosine monophosphate to RNA (35).
AA binding equilibrium monitored with temperature-dependent IR and NMR spectroscopy
To accurately measure temperature-dependent AA binding stability, IR and NMR spectroscopy probes are employed to monitor changes in base-pairing as a function of temperature that are then modeled to extract melting curves for AA dissociation. FTIR temperature series were performed to track AA binding stability from 1°C–96°C (Fig. 2 a and b). Both AA-gap complexes show two melting transitions that correspond to dissociation of AA from the template, followed by dissociation of the primer and helper from the template strand. The AA dissociation transition in TTg:AA and UUg:AA is observed between 1°C and 60°C as an increase in intensity of the adenine ring mode at 1625 cm−1 and the change of carbonyl bands at 1685–1695 and 1665 cm−1. The sharper dissociation transition of the primer and helper, characterized exclusively by changes in guanine ring and carbonyl bands, occurs at higher temperature as a single-step melting transition because the binding stabilities of the primer and helper to the template strand are nearly identical. The midpoint for primer and helper dissociation is shifted 13°C higher in UUg:AA because of the more stabilizing nature of GC base-pair steps in A-RNA relative to B-DNA (4,5). AA unbinding in TTo:AA is already halfway complete at 1°C, as indicated in Fig. 1 e, and is completed by ∼40°C (Fig. S2).
Figure 2.
Temperature-induced dissociation of AA. (a) FTIR spectra of TTg:AA and UUg:AA from 1°C–96°C in ∼2.6°C steps. Solutions contain 1 mM each of AA, primer, helper, and template strands. (b) Thermal AA and template dissociation of the TTg:AA complex monitored with FTIR, 2D IR, and 1H-NMR. FTIR traces are plotted as the absolute value change in absorption relative to 1°C for select frequencies marked in (a) that primarily report on intensity changes in G (1573 cm−1, blue), A & T (1623 cm−1, purple), and G & T (1665 cm−1, pink). 2D IR traces at select frequencies similar to the FTIR data are plotted as the absolute value percent change in signal relative to 1°C (|ΔS|). From 1H-NMR, the AA dissociation transition is monitored using the chemical shift of two aromatic protons from adenine (A3 and A4) and H5 aromatic protons of cytosine (C1 and C2). The temperature-dependent chemical shifts of A3 and A4 in free AA are shown as open circles. The corresponding 1H-NMR spectra are shown in Fig. S9. (c) Thermal AA and template dissociation transitions of the UUg:AA complex monitored with (top) FTIR and (bottom) 2D IR. Solid lines for each dataset correspond to fits to a three-state sequential model. FTIR and 2D IR data are globally fit together. The four 1H-NMR peaks are globally fit to the same three-state model and include upper and lower baselines (dashed lines). Temperature-dependent FTIR and 2D IR data for TTo:AA and TTg, TTo, and UUg are shown in supporting material, Sections S1.2 and S1.3. To see this figure in color, go online.
The sigmoidal character of the AA thermal dissociation transition is superimposed on other slowly varying temperature-dependent changes, primarily a result of solvation. We account for additional independent spectral changes by measuring FTIR temperature series of TTg, TTo, and UUg and fully complementary duplexes (TTgd, UUgd) for reference, as described in supporting material, Section S1.2. In contrast, we find that these linear background changes are only minor contributions in temperature series monitored by 2D IR spectroscopy (supporting material, Section S1.3). The 2D IR temperature series show profiles for AA dissociation and primer and helper dissociation transitions that correlate closely with the transitions observed in FTIR data but with reduced linear baseline contribution to the sigmoidal transitions. We also obtain similar AA dissociation and primer and helper dissociation transitions from 1H-NMR of TTg:AA (Fig. 2 b; supporting material, Section S1.4), lending confidence to the profiles of the IR-monitored dissociation transitions.
T-jump IR spectroscopy of AA dissociation kinetics
To directly monitor the time dependence of AA dehybridization from gaps and overhangs, we employed T-jump IR spectroscopy (45,46) using T-jumps of ΔT 13°C across the center of the AA melting transition (Figs. 3 and S11). The absorption change at 1605 cm−1 by the adenine ring mode and at 1545 cm−1 by the guanine ring mode provide selective reporters for changes in A:T and G:C base-pairing, whereas the 1672 cm−1 band tracks A:T and G:C base-pair disruption through the thymine and guanine carbonyl vibrations (49,69). For all complexes, time traces at these three frequencies exhibit what appears to be a single kinetic component from 500 ns to 10 μs prior to decay of the signal because of thermal re-equilibration of the sample from 1–10 ms (Fig. 3 b). The large amplitude of the A:T response at 1605 cm−1 and its microsecond timescale support assignment of the process to AA unbinding.
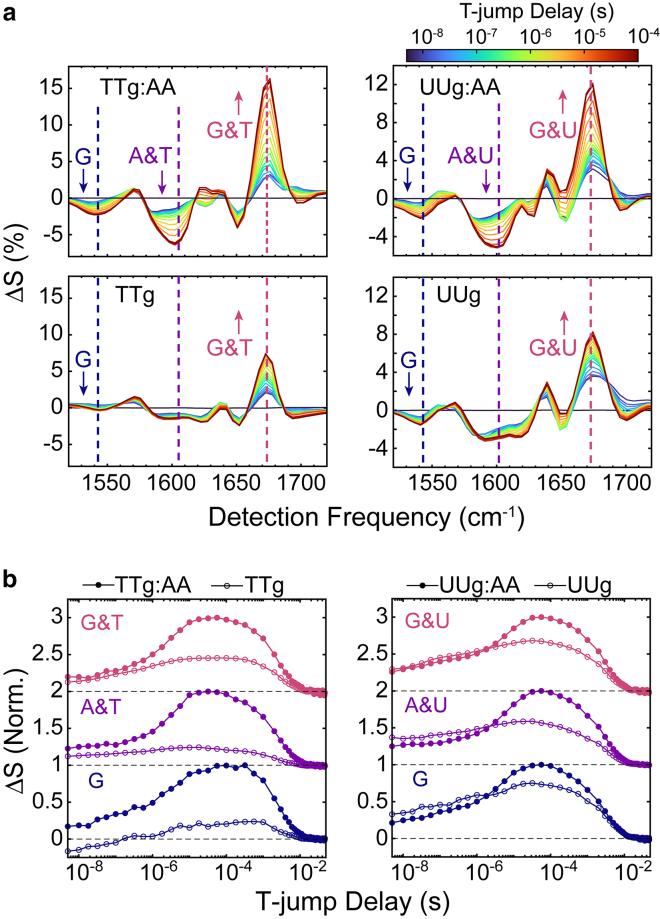
Figure 3.
Time dependence of AA dissociation from DNA and RNA gaps directly observed with T-jump IR spectroscopy. (a) Transient heterodyned dispersed vibrational echo difference spectra (t-HDVE) at T-jump delays ranging from 5 ns to 180 μs for TTg:AA, TTg, UUg:AA, and UUg following a T-jump from 19°C to 33°C. Spectra are plotted as the change relative to the maximum signal value of the initial temperature spectrum (). (b) Normalized time traces at 1545 cm−1 (blue, guanine ring mode), 1605 cm−1 (purple, adenine ring mode), and 1672 cm−1 (red, guanine and thymine carbonyl modes) for TTg:AA and UUg:AA (filled circles) as well as TTg and UUg (open circles). The probe frequencies are marked as vertical dashed lines in the t-HDVE spectra. Traces at different frequencies are shifted vertically with respect to one another, and dashed lines indicate respective baselines. AA dissociation is observed as a single kinetic component from 1–10 μs, and additional base-pairing dynamics from the template itself occur on an overlapping timescale. To see this figure in color, go online.
Without AA, the gap and overhang templates also exhibit a response over a similar time window but with lower amplitude, particularly at the adenine ring mode, relative to the AA-template complexes. The dominant G:C character of the response suggests that it may arise from base-pair disruption adjacent to the gap or at the primer and helper termini; however, the same response is also observed in the fully formed duplexes (Figs. S12 and S13), which indicates that it arises from fraying of the primer and helper G:C termini. This observation is consistent with previous NMR studies that found G:C base pairs adjacent to a gap to be more stable than those at the duplex termini (28) and T-jump experiments indicating G:C fraying in DNA oligonucleotides on microsecond timescales (70). G:C fraying occurs faster than AA dissociation but with enough temporal overlap that only a single kinetic component is resolved at each frequency. AA dissociation dominates the observed kinetic component at most frequencies, but the signal change at 1672 cm−1 contains enough amplitude from G:C fraying that the extracted observed rate is faster than at 1605 cm−1 for TTg:AA at low temperature (Figs. S14 and S15).
Thermodynamic analysis of AA dissociation
The results demonstrate steady-state and time-resolved thermal dissociation of AA, which we self-consistently model to extract quantitative thermodynamic and kinetic information. In general, complete dissociation of the AA-template complex may proceed through multiple pathways differentiated by the order in which AA, primer, or helper segments dissociate. Exact treatment of these coupled equilibria leads to a fourth or higher-order dependence of each binding fraction on the concentration of a given species, which, we find, does not have a stable solution over the full temperature range of each transition. However, the much greater binding stability of the primer and helper allows us to neglect species with AA bound to the template strand without the primer and helper. We also model primer and helper dissociation from the template strand as an unimolecular equilibrium between the template and “dissociated” template that is equivalent to treating binding of the primer and helper as folding of hairpins (16). This results in a three-state sequential model described by equilibrium constants for AA dissociation () and dissociation of the primer and helper (). Using TTg:AA as an example:
| (1a) |
| (1b) |
where dTTg is the “dissociated” template. The assumption in Eq. 1b sharpens the primer and helper melting profile relative to its true bimolecular form, as illustrated in Fig. S23, but this is not a serious concern because this only affects our analysis in the temperature range where the transitions overlap.
To extract melting curves for AA dissociation, FTIR and 2D IR temperature series for a given sequence are globally fit to Eqs. 1a and 1b using the spectral decomposition described in supporting material, Section S3 and constraints from the titration at 1°C. The resulting melting curves are shown in Fig. 4, thermodynamic parameters are shown in Fig. 4 and Table 1, and the corresponding spectral components are shown in Figs. S20 and S21. Overall, the global fit describes both datasets well (Fig. 2). The first spectral component corresponds to AA dissociation and contains signatures of A:T base-pair breaking, whereas the second component contains only G:C base-pair-breaking features. The AA dissociation curves resemble the raw temperature-dependent change in absorbance and start from a bound fraction less than 1 at 1°C. We also find quantitative agreement between the TTg:AA dissociation curves determined from FTIR and 2D IR and from global fitting of temperature-dependent 1H-NMR chemical shifts (Fig. S9), lending support to the accuracy of the IR dissociation curves.
Figure 4.
Thermodynamics of AA dissociation from gap and overhang templates extracted with three-state global fitting of FTIR and 2D IR temperature series. (a) AA (solid) and primer and helper (dashed) dissociation curves for TTg:AA, TTo:AA, and UUg:AA, extracted from global fitting of FTIR and 2D IR temperature series to a three-state sequential model (Eqs. 1a and 1b; supporting material, Section S3). Dark gray lines correspond to dissociation components of TTg:AA obtained from 1H-NMR temperature series (Fig. S9). (b–e) AA dissociation (b) enthalpy (), (c) entropy (), (d) free energy at 37°C (), and (e) melting temperature () determined for each sequence. Dark gray bars indicate values from 1H-NMR. Error bars are propagated from 95% confidence intervals in fit parameters and . To see this figure in color, go online.
Table 1.
Thermodynamics for dissociation of AA from templates determined with global fitting to a three-state sequential model
| Sequence | Method | (°C)a | (kJ mol−1) | (J mol−1 K−1) | (kJ mol−1)b |
|---|---|---|---|---|---|
| TTg:AA | IRc | 26 ± 2 | 91 ± 2 | 245 ± 6 | 21.7 ± 1.1 |
| NMR | 28 ± 3 | 79 ± 5 | 203 ± 20 | 21.5 ± 4.5 | |
| ITCd | – | 83 ± 5 | – | 23.1 ± 1.3 | |
| UUg:AA | IRc | 24 ± 1 | 56 ± 1 | 131 ± 3 | 19.2 ± 0.6 |
| ITCd | – | 51 ± 1 | – | 23.5 ± 0.4 | |
| TTo:AA | IRc | 5 ± 1 | 67 ± 1 | 182 ± 4 | 16.1 ± 0.8 |
Errors are derived from 95% confidence intervals in fit parameters and . and the dissociation free energy at 8°C () from ITC measurements are also listed, where errors correspond to 95% confidence intervals from two-state fits (supporting material, Section 4.2).
is defined as the temperature where half of the total AA concentration is bound to the template.
Free energy change for AA dissociation at 8°C.
IR refers to global fits of FTIR and 2D IR temperature series.
ITC was performed at 8°C.
The shape of AA dissociation curves varies between DNA and RNA as well as the type of template. TTg:AA and UUg:AA exhibit similar transition midpoints (), defined as the temperature where half of the total AA concentration is bound to the template, but UUg:AA shows a broader transition with a dissociation curve slope at of 0.013 K−1 relative to 0.021 K−1 in TTg:AA. The broader transition width in UUg:AA arises from a 35 kJ mol−1 lower dissociation enthalpy () and 115 J mol−1 K−1 lower dissociation entropy () relative to TTg:AA. This difference in is also directly observed through ITC measurements (Table 1; supporting material, Section S4.2). Although TTg:AA and UUg:AA exhibit a similar dissociation free energy at 37°C (), the larger and values lead to greater binding stability for TTg:AA at lower temperatures and UUg:AA at higher temperatures, but we note that ITC gives similar for each sequence at 8°C. Thymine contributes greater π-π stacking interactions than uracil (71,72), which is why AA is the only dinucleotide step with NN and parameters that are larger for DNA (33 kJ mol−1; 93 J mol−1 K−1) than RNA (28 kJ mol−1; 79 J mol−1 K−1) (4,5). This effect contributes to the larger values of and in TTg:AA relative to UUg:AA but cannot solely account for the observed magnitude of this difference. The free energy of AA dissociation at 37°C is roughly 4 kJ mol−1 higher in TTg:AA than TTo:AA because of the added stacking stabilization from the 3′-G, and this value is similar to previous measurements of coaxial stacking in 5′-AG-3′ steps of DNA oligonucleotides (15,17,18).
Kinetic analysis of AA dissociation
The observed relaxation rates for AA dissociation kinetics, , are extracted from T-jump measurements with varying initial temperature across the AA melting transition of each sequence (Figs. 5 and S11–S13). Only AA dissociation and G:C fraying are observed below final temperatures of 42°C for DNA and 52°C for RNA. At higher temperatures, primer and helper dissociation is observed on 100-μs timescales and is more than 100-fold slower than AA dissociation (Fig. S13). The timescale separation between AA dissociation and primer and helper dissociation is sufficient to treat with two-state kinetics (73). Using TTg:AA as an example,
| (2) |
where and are the rate constants for AA association and dissociation. Because , these rate constants are extracted using the concentrations of template, [TTg], and AA, [AA], determined from the AA dissociation curves in Fig. 4. Because of the broad observable temperature range of AA-gap dissociation transitions, T-jump measurements can be performed at multiple Tf values below where is dominated by . Over this temperature range, the dissociation rate follows Arrhenius behavior and increases from 3 × 103 to 2 × 106 s−1, while shows just a minor two- to fivefold increase. Such contrasting temperature dependence of and has been observed consistently in studies of short DNA and RNA oligonucleotides (5–20 bp) (6,7,49,74,75) and has been used to characterize the transition state between hybridized and dissociated states. We fit the temperature trends of and to a Kramers-like model for diffusive barrier crossing where the rate is inversely proportional to the solvent viscosity, . Written for the dissociation rate:
| (3) |
and the same expression applies for association. Here the free energy barrier () is written in terms of the enthalpic () and entropic () barriers. The temperature-dependent viscosity of D2O is taken relative to its value at 37°C () (76). Also, c° is the standard state concentration of 1 M, and m is the reaction molecularity (m = 1 for and m = 2 for ). We use a simple form of the Eyring pre-factor (). This approximation is known to overestimate the frequency of diffusive motion at the barrier for biomolecular folding and binding (77,78). While this approximation impacts the absolute magnitudes of and , we assume that the true pre-factor is the same across our sequences so that relative values of and are meaningful. Fitting of our data indicates that the free energy barrier for AA dissociation arises from an enthalpic penalty ( > 50 kJ mol−1) that is partially compensated by a positive , whereas the free energy barrier for AA association () is dominated by an entropic barrier ( < 0).
Figure 5.
Kinetics of AA association and dissociation from gaps and overhangs. (a) Illustration of a series of T-jumps performed from various initial to final temperatures (Ti →Tf) with ΔT∼13°C across the AA dissociation transition of TTg:AA. (b) t-HDVE time traces of TTg:AA probed at the adenine ring mode (1605 cm−1) for each temperature condition shown in (a). (c) Observed relaxation rate () for AA unbinding as a function of Tf for all sequences. Rates correspond to the amplitude-weighted mean across the adenine ring mode response (1585–1610 cm−1) in the rate-domain spectra determined from an inverse Laplace transform that employs a maximum entropy regularization method (48,49). Vertical error bars indicate standard deviation over the rate spectra, and horizontal error bars correspond to the measured standard deviation in T-jump magnitude. (d) Rate constants for AA association () in M−1 s−1 and dissociation () in s−1 as a function of Tf determined from a two-state analysis of (Eq. 2). Data for all sequences are shown in Fig. S27. (e) Enthalpic (, ), entropic (, ), and free energy (37°C, , ) barriers determined from fitting and temperature trends to a Kramers-like model (Eq. 3). Error bars indicate 95% confidence intervals propagated from the fits. To see this figure in color, go online.
The kinetics of AA association and dissociation vary substantially depending on the template. is ∼4.5 kJ mol−1 smaller for TTo:AA than TTg:AA at 37°C, which matches the difference in , suggesting that the fivefold faster unbinding of AA from an overhang compared with a gap primarily comes from reduced binding stability. The rate of association or is essentially the same for TTo:AA and TTg:AA but with small differences in its temperature dependence, as quantified by . There are also significant differences between the kinetics of AA dissociation in UUg:AA and TTg:AA. increases more sharply with temperature in TTg:AA, as quantified by an ∼25 kJ mol−1 larger relative to UUg:AA, which likely comes from enhanced stacking interactions in the hybridized state of TTg:AA and is consistent with the thermodynamic results presented above. On the other hand, is similar for each sequence across the measured temperature range.
Structural properties of AA-gap complexes from MD simulations
The energetics of AA hybridization onto overhangs and gaps differs from free strand hybridization because of a combination of differences in the template and AA-gap complex structural configurations relative to canonical duplexes and single strands. We characterized the differences in conformation between these species using all-atom MD simulations, finding that most configurational differences are localized near the central AA binding site. Gap templates adopt bent configurations in high population as observed previously, leading to a reduction in hydration of the gap relative to free single strands (Figs. S29 and S30) (27,28,79). AA-gap complexes exhibit greater configurational freedom than canonical duplexes (Figs. 6 and S31–S33), with the largest differences found in backbone and base-stacking structure rather than base pair geometry. TTg:AA exhibits broadened distributions in shift, slide, and twist parameters at the 5′-GA-3′ and 5′-AG-3′ nicks, whereas the stacking geometry between adenine bases is nearly identical to B-DNA (ΔDx, ΔDy < 0.4 Å and ΔΩ < 4°). A broader spread of stacking orientations at the nick sites is unsurprising given the greater flexibility in the backbone, particularly for glycosidic bond angles (χ) of the A and G bases on the 3′ side of each nick (22). The nick sites enable greater local flexibility in the backbone and in particular for the glycosidic bond angles (χ) of the A and G bases on the 3′ side of each nick. The greater freedom of the backbone near the nick sites also reduces the effective population of BII backbone configurations across the 5′-CGAAGG-3′ motif (Fig. S34). The fluctuations along slide, twist, shift, and χ coordinates are partially correlated in a given nick site (Fig. 6 b). In contrast, the structural fluctuations in the 5′-GA-3′ and 5′-AG-3′ nicks appear to be largely independent of one another (Fig. 6 c).
Figure 6.
Structural properties of AA-gap complexes from all-atom MD simulations. (a) Comparison of structural variation between the AA-gap complex and canonical duplex. Violin plots show structural distributions for base-pair twist (Ω) and shift (Dx) and glycosidic bond dihedral angle (χ) for the three central base pair steps of TTgd (red, light), TTg:AA (red, dark), UUgd (green, light), and UUg:AA (green, dark). Black horizontal bars indicate the distribution’s median value obtained from a Gaussian kernel estimation using Scott’s rule (80). Distributions were generated from 1.5 μs of simulation for each sequence using the bsc1-AMBER force field for DNA and DES-AMBER force field for RNA. Only Watson-Crick-Franklin (WCF) base-pair configurations are included in the distributions. Other structural parameters using both force fields are shown in Figs. S31–S33. (b) Contour plots showing the correlation of 5′-AG-3′ twist versus shift. Nine contours with uniform 10% spacing are plotted for each sequence. Diagonally elongated distributions indicate that fluctuations along different base-pair coordinates within the same nick site are partially correlated with Pearson correlation coefficients of −0.61 for DNA and −0.56 for RNA. (c) Contour plots showing the correlation of 5′-GA-3′ shift versus 5′-AG-3′ shift. Symmetrical distributions indicate that fluctuations at each nick site are uncorrelated with Pearson correlation coefficients of −0.04 for DNA and 0.05 for RNA. (d) 4-μs trajectory of TTg:AA, showing the A:T base pairs switching from WCF to an anti-Hoogsteen (aHG) geometry. Trajectories are plotted in terms of the mean WCF (purple) and aHG (pink) distances across each A:T base pair. The WCF distance is defined as the mean of adenine-N6 to thymine-O4 and adenine-N1 to thymine-N3 distances, and the aHG distance is the average of adenine-N7 to thymine-N3 and adenine-N6 to thymine-O2 distances. Visualizations of each base-pair geometry at time points marked with filled circles indicate WCF distances as purple dashed lines and aHG distances as pink dashed lines. To see this figure in color, go online.
The structural differences between UUg:AA and an A-RNA duplex are also minor but distinct from DNA in a few regards. Overall, UUg:AA exhibits larger changes in stacking orientation (twist, shift) and less change in the backbone torsional angles (χ, δ, γ) relative to DNA. Further, the base-pairing and stacking geometry of the AA differs with broader distributions of shear, stretch, and buckle values, an increase in mean rise from 3.0 to 3.3 Å, and subpopulations with larger shift and twist values. In contrast to DNA, distinct states are observed along twist and shift coordinates for 5′-GA-3′ and 5′-AG-3′, and the mean values differ from A-RNA by as much as 20° and 1.5 Å, respectively.
During one of two 4-μs trajectories for TTg:AA, we observed AA switch from canonical Watson-Crick-Franklin (WCF) to anti-Hoogsteen (aHG) base-pairing geometry. As shown in Fig. 6 d, the 5′-A flips at 700 ns, followed by the 3′-A 200 ns afterward; however, both adenines remain poorly aligned with the gap until reaching the final aHG geometry at 1.3 μs. Our 8 μs of total simulation time for this sequence is insufficient to determine the relative stability of WCF and HG configurations; therefore we applied the on-the-fly probability enhanced sampling method to calculate the free energy differences for AA dissociation from a WCF or aHG geometry (; supporting material, Section S5.3). WCF and aHG geometries have nearly the same population and stability at 37°C with 0 kJ mol−1. Although not tested previously for dinucleotide-gap complexes or aHG base-pairing, simulations with the bsc1-AMBER force field typically capture accurate relative stabilities between WCF and syn-Hoogsteen base-pairing geometries (81,82). Simulations with the DES-AMBER force field instead suggest that the WCF geometry is more stable ( ∼ −8 kJ mol−1). For UUg:AA, WCF and aHG geometries have similar stabilities regardless of the employed force field (Fig. S35). The high stability of an aHG geometry may appear unusual, but this has been reported as the dominant base-pairing geometry between AA and TT DNA dinucleotides mediated through self-assembling tripyridyl-triazinine-capped hydrophobic cages in aqueous solution, so far the only structural characterization of dinucleotide duplexes in aqueous solution (83).
Length scaling of An dissociation from templates
To assess the scaling of dissociation thermodynamics and kinetics for 2- to 4-nt sequences, we experimentally examined the dehybridization of AAA (A3) and AAAA (A4) from DNA gaps and overhangs using the extended templates shown in Fig. 7 a. As expected, longer An oligonucleotides bind with greater stability and show a decrease in and (Figs. 7 b–d and S27). Gaps and overhangs exhibit an average increase in of 2.7–3.0 kJ mol−1 bp−1, but and increase more sharply with length for overhangs and become equivalent to the gap for A4 dissociation. The overhang values for , , and are still well below the 33 kJ mol−1 bp−1, 94 J mol−1 K−1 bp−1, and 6.7 kJ mol−1 bp−1 values predicted for appending AA dinucleotide steps by Santa Lucia’s DNA NN model (Fig. 7 e) (4).
Figure 7.
Comparing length-dependent dissociation thermodynamics in gaps, overhangs, and free strands. (a) Extended templates for 3- and 4-nt gap (TTTg:A3, TTTTg:A4) and overhang (TTTo:A3, TTTTo:A4) sequences bound to A3 and A4 oligonucleotides. Dissociation of An (n = 2, 3, 4) segments from gaps and overhangs is compared with dissociation of GAnG single strands with their complement strands. (b and c) An melting curves for gaps and overhangs extracted from global fitting of FTIR and 2D IR temperature series to a three-state sequential model ((1a), (1b)). GAnG melting curves are shown in (b) and were extracted from a two-state model fit to FTIR temperature series (supporting material, Section S4.1). GAnG melting curves were measured at 10 mM oligonucleotide concentration and corrected to 2 mM. (d) , , and dissociation free energy at 8°C () for all sequences. Red-orange bars correspond to DNA An-gap complexes, blue-purple bars correspond to DNA An-overhang complexes, light blue-green bars are for GAnG strands, and black-gray indicate GAnG dissociation parameters calculated from Santa Lucia’s nearest-neighbor (NN) model and corrected to [Na+] = 600 mM (4,84). Values for gap and GAnG systems are an average over those determined from IR spectroscopy and ITC (Section S4.2), while overhang values are only from FTIR and 2D IR global fits. Error bars indicate 95% confidence intervals from fits to thermodynamic models. (e) Slopes from linear fits of each thermodynamic parameter across An length (solid lines in d). Data are presented as the change per appended A:T base pair in the dissociation enthalpy (), entropy (), and free energy at 8°C (). Although AA-gap complex binding is more stable than GA2G, , , and are each more than twofold greater in GAnG strands than for An dissociation from gaps. To see this figure in color, go online.
To test for the origin of different length-scaling dissociation thermodynamics between overhangs, gaps, and the NN model, we compare to dissociation of oligonucleotides 5′-GAAG-3′ (GA2G), 5′-GAAAG-3′ (GA3G), and 5′-GAAAAG-3′ (GA4G) duplexed with their respective complement strands (Figs. 7 and S24–S26). and are greater for GA2G than AA-gap dissociation, while is ∼4 kJ mol−1 lower for GA2G. As a result, the GA2G dissociation transition is much sharper than for AA-gap dissociation but with Tm shifted ∼15°C lower in temperature. Values of , , and for GAnG are more than twofold greater than for gap sequences and are much closer the NN model values (Fig. 7 e). This leads to nearly equivalent for TTTTg:A4 and GA4G, and binding between free single-strands may progressively become more stable than binding of longer oligonucleotides onto gaps and overhangs. Additionally, we find that length scaling of the dissociation free energy barrier () is ∼2.5-fold greater than for gaps (Fig. S28), which is a much larger difference than reported previously for dehybridization of free single strands (74,85). This sharp dependence of (and ) on length is important for predicting dissociation kinetics in template systems and also indicates a length dependence in the free energies of the association transition state and/or the unbound state (86,87).
Based on previous studies of gap and overhang structure (23,24,25,26,27,28), it is possible that the single-stranded binding region in gaps and overhangs becomes less ordered as the length increases from 2 to 4 nt. However, our all-atom MD simulations indicate essentially no difference in the structural distribution of the canonical unbent Tn configurations in gaps, but instead highly bent configurations and alternative stacking geometries are observed for certain gap lengths (Fig. S29). AMBER force fields, including bsc1-AMBER, tend to overestimate base-stacking stability in ssDNA because they are parameterized for duplex DNA (56,88), and therefore these results should be interpreted with caution.
Conclusions
We demonstrate an approach for measuring temperature-dependent binding thermodynamics and kinetics of nucleic acids as short as dinucleotides onto gaps and overhangs using IR spectroscopy. By determining accurate melting curves, our method extracts enthalpic and entropic contributions to binding that are typically missing in previous titration studies. Further, to our knowledge, we provide the first measurements of dinucleotide association and dissociation timescales (0.5–20 μs) through application of T-jump IR spectroscopy. Although our study is limited to pure An segments, we identify striking energetic differences between cases of association onto gaps or overhangs with free-strand association that have not been observed previously.
Most notable is that association of AA onto a gap with G:C base pairs on each side is energetically more favorable than association between 5′-GAAG-3′ and 5′-CTTC-3′ ( = 4 kJ mol−1; Fig. 7 d). This distinction may arise from energetic differences in either the bound or dissociated states or a combination of both through factors such as single-strand stacking, optimized coaxial stacking, or non-canonical base-pairing. Most association measurements, including the approach in this work, directly probe energetic differences between the bound and dissociated states but not energetic differences between the respective bound or dissociated states of different samples. As a result, we cannot directly dissect the enhanced stability of AA-template complexes but rather infer how the energy of the associated and dissociated states may change between gap, overhang, and free single-strand scenarios.
A clear distinction between gap and free single-strand binding scenarios is present in the enthalpic and entropic contributions to association. and are lower for the gap, and therefore the extra stability of TTg:AA relative to GA2G arises from an entropic benefit. Enhanced binding stability of dinucleotides onto gaps and overhangs may arise from greater base-pair ordering and constraints in water dynamics in the single-strand binding region and/or increased configurational flexibility in the AA-template complexes relative to canonical B-DNA, which we observe in MD simulations near the nick sites (Figs. 6 a, S30, and S31). The former effect decreases the entropy of the dissociated state, while the latter increases that of the hybridized state, each of which will decrease relative to free-stand hybridization. The same effect that may increase rigidity and stacking interactions in the gap single strand will also reduce the enthalpy of the dissociated state. Another reduction in enthalpy may arise from bending about the single-stranded segment in gap templates, as observed in our MD simulations (Fig. S29) and reported in previous studies (26,28,29,89,90). Last, our simulations of TTg:AA suggest that AA can bind in WCF or aHG geometries with significant population, although the relative stability depends on the choice of force field (Fig. S35). aHG configurations are likely only relevant for binding of pure A:T or A:U dinucleotides or G:G mismatch pairing, where the aHG configuration is a stable option. To date, the only crystallography studies of dinucleotide binding to a gap or overhang template are for G:C base-pairing of modified GG RNA dinucleotides (91,92,93), a scenario where aHG configurations are highly improbable. Unfortunately, we cannot indicate or disprove the presence of A:T aHG base-pairing using the IR and NMR measurements presented in this work, and further structural characterization is necessary to clarify the role of aHG base-pairing.
The energetics of dinucleotide association onto gaps and overhangs differs from free-strand hybridization, and these effects stem from underlying dynamics of association and dissociation. Our T-jump IR measurements of DNA and RNA AA association and dissociation kinetics provide a first step toward understanding the structural dynamics. We determine a value of ∼5 × 107 M−1 s−1 that corresponds to a time constant of 20 μs at 1 mM oligonucleotide concentration. This value is nearly 100-fold slower than an estimated diffusion-limited rate constant () of 5 × 109 M−1 s−1, calculated using the translational diffusion coefficients of AA and TTg determined from diffusion-ordered spectroscopy NMR measurements and estimated radii of gyration from experimental length scaling of ssDNA and a worm-like chain model of duplex DNA (Section S6) (94,95). Although faster than association between oligonucleotides 5–20 nt in length, the 100-fold difference between AA association and diffusion-limited rates suggest that numerous unsuccessful collisions and/or significant structural rearrangement occur prior to successful binding. Association rate constants for longer oligonucleotides are also reported consistently to be 100- 1000-fold smaller than (74), suggesting that each system’s hybridization transition state and encounter complex may share certain characteristics. Even for longer oligonucleotides, these properties are still poorly understood but are thought to involve some degree of single-strand ordering, a small number of base-pair contacts, and potential rearrangement of water molecules and counterions. In the case of dinucleotide association with gaps and overhangs, water and counterion rearrangement is still necessary, and the ordering of the binding region of the gap or overhang contains a large penalty. The time ordering of these events is unclear for each system and must be investigated further to develop a molecular picture of the dynamics of short oligonucleotide hybridization.
We primarily focused on short DNA oligonucleotide association, and it is important to assess whether similar characteristics are found for short RNA oligonucleotides, which are more relevant in the context of nonenzymatic replication (96). Our results show large differences in energetics and kinetics of AA dissociation from DNA and RNA gaps. and values for UUg:AA are approximately half of those predicted by NN models and obtained for TTg:AA (Fig. S26). and are likely higher in DNA for multiple reasons. The AA dinucleotide in particular contains enhanced stacking arising from the C5-methyl groups of thymine (71,72,97). Another contribution may come from the wider breadth of stacking configurations observed in UUg:AA relative to UUgd. However, RNA duplexes are generally more thermodynamically stable than an equivalent-sequence DNA duplex because of multiple effects from the C2′-OH groups. Differences in base stacking, hydrogen bonding between C2′-OH groups and water molecules, and greater uptake and ordering of cations and water molecules are effects that contribute to larger , , and in A-RNA than B-DNA (98,99). Therefore, we predict that binding of other RNA dinucleotide sequences will generally be more stable than the equivalent DNA sequence.
Gaps and overhangs are expected to have a qualitatively similar thermodynamic and kinetic impact on DNA and RNA hybridization, but the relative magnitude may generally differ. For instance, single- and double-stranded RNA are shown to have a longer persistence length than DNA, and the change in strand rigidity upon introducing an overhang or gap may differ, as well as the propensity for bending of gapped RNA (30,100). MD simulations of UUg:AA and UUgd indicate that the distribution of stacking geometries at nick sites between primer and helper segments and AA differ from A-RNA while the backbone geometry is relatively unchanged, but the opposite is found for DNA (Fig. 6 a). Such differences in geometry may influence the enthalpy of the AA-gap complex while the enhanced configurational flexibility increases its entropy. Together, the combination of differences between DNA and RNA templates and dinucleotide-template complexes may promote significant contrast in their association energetics and kinetics across variations in dinucleotide sequence and template construction.
Our experimental and computational results indicate multiple structural, energetic, and kinetic factors that differentiate hybridization between short nucleic acids and templates with hybridization between free single strands, and these differences may play an important role in processes such as nonenzymatic replication. In addition to various structural and chemical factors, the efficiency of this process depends on the binding probability, dissociation rate of the bound complex, and structural dynamics of the complex (93,101). The structural dynamics of the gap template and bound complex suggested by our experimental and computational results are likely to influence the efficiency of nonenzymatic extension. Further, we measure an AA dissociation rate from UUg:AA that is orders of magnitude higher than the catalytic rate ( of non-enzymatic primer extension for a 2-aminoimidaloze (2AI)-bridged dinucleotide in an equivalent sequence context (101), indicating that, on average, the 2AI dinucleotide binds and dissociates from the gap numerous times before extension occurs. Although measured under different solution conditions, the dissociation constant of UUg:AA at 25°C ( = 1.05 mM) is similar to the Michaelis-Menten constant of the 2AI system ( = 0.64 mM) extracted from a Michaelis-Menten analysis of the extension rate (101). These observations support use of a Michaelis-Menten kinetic model for nonenzymatic extension of this sequence and template, and our study demonstrates a method for direct measurement of energetics and kinetics for dinucleotide binding that is applicable to a wide range of oligonucleotide sequences and template designs.
Author contributions
B.A., M.S.J., J.W.S., A.L.F., and A.T. designed the research. B.A., A.R., Y.L., and J.R.S. performed experiments. M.S.J. and S.K. performed simulations. B.A. and M.S.J. analyzed the data. B.A. and A.T. wrote the manuscript. All authors provided feedback on the manuscript.
Acknowledgments
This work was supported by the National Institute of General Medical Sciences of the National Institutes of Health (award R01-GM118774), the National Science Foundation under grants CHE-2152521 and CHE-2155027, and the Simons Foundation (grant 290363). J.W.S. is an Investigator of the Howard Hughes Medical Institute. B.A. acknowledges support from the NSF Graduate Research Fellowship Program. We thank Marco Todisco and Jakob Schauss for helpful discussions and feedback on the manuscript. This work was completed in part with resources provided by the University of Chicago Research Computing Center. We gratefully acknowledge computing time on the University of Chicago high-performance GPU-based cyberinfrastructure supported by the National Science Foundation under grant DMR-1828629.
Declaration of interests
A.L.F. is a co-founder and consultant of Evozyne, Inc. and a co-author of US Patent Applications 16/887,710 and 17/642,582; US Provisional Patent Applications 62/853,919, 62/900,420, 63/314,898, and 63/479,378; and International Patent Applications PCT/US2020/035206 and PCT/US2020/050466.
Editor: Susan J. Schroeder.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2023.07.009.
Supporting references
References (102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127) appear in the supporting material.
Supporting material
Data availability
Experimental and simulation data is uploaded to Zenodo and available at https://zenodo.org/record/7662738#.ZMQWvnbMKUk.
References
- 1.Yin Y., Zhao X.S. Kinetics and dynamics of DNA hybridization. Acc. Chem. Res. 2011;44:1172–1181. doi: 10.1021/ar200068j. [DOI] [PubMed] [Google Scholar]
- 2.Wetmur J.G. Hybridization and renaturation kinetics of nucleic acids. Annu. Rev. Biophys. 1976;5:337–361. doi: 10.1146/annurev.bb.05.060176.002005. [DOI] [PubMed] [Google Scholar]
- 3.Wartell R.M., Benight A.S. Thermal denaturation of DNA molecules: A comparison of theory with experiment. Phys. Rep. 1985;126:67–107. [Google Scholar]
- 4.SantaLucia J., Jr. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Xia T., SantaLucia J., Jr., Turner D.H., et al. Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson− Crick base pairs. Biochem. 1998;37:14719–14735. doi: 10.1021/bi9809425. [DOI] [PubMed] [Google Scholar]
- 6.Craig M.E., Crothers D.M., Doty P. Relaxation kinetics of dimer formation by self complementary oligonucleotides. J. Mol. Biol. 1971;62:383–401. doi: 10.1016/0022-2836(71)90434-7. [DOI] [PubMed] [Google Scholar]
- 7.Pörschke D., Eigen M. Co-operative non-enzymatic base recognition III. Kinetics of the helix—coil transition of the oligoribouridylic· oligoriboadenylic acid system and of oligoriboadenylic acid alone at acidic pH. J. Mol. Biol. 1971;62:361–381. doi: 10.1016/0022-2836(71)90433-5. [DOI] [PubMed] [Google Scholar]
- 8.Simmel F.C., Yurke B., Singh H.R. Principles and applications of nucleic acid strand displacement reactions. Chem. Rev. 2019;119:6326–6369. doi: 10.1021/acs.chemrev.8b00580. [DOI] [PubMed] [Google Scholar]
- 9.Wei X., Nangreave J., Liu Y. Uncovering the self-assembly of DNA nanostructures by thermodynamics and kinetics. Acc. Chem. Res. 2014;47:1861–1870. doi: 10.1021/ar5000665. [DOI] [PubMed] [Google Scholar]
- 10.Kiefer J.R., Mao C., et al. Beese L.S. Visualizing DNA replication in a catalytically active Bacillus DNA polymerase crystal. Nature. 1998;391:304–307. doi: 10.1038/34693. [DOI] [PubMed] [Google Scholar]
- 11.Steitz T.A. A structural understanding of the dynamic ribosome machine. Nat. Rev. Mol. Cell Biol. 2008;9:242–253. doi: 10.1038/nrm2352. [DOI] [PubMed] [Google Scholar]
- 12.Zhou L., Ding D., Szostak J.W. The virtual circular genome model for primordial RNA replication. RNA. 2021;27:1–11. doi: 10.1261/rna.077693.120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Duzdevich D., Carr C.E., et al. Szostak J.W. Competition between bridged dinucleotides and activated mononucleotides determines the error frequency of nonenzymatic RNA primer extension. Nucleic Acids Res. 2021;49:3681–3691. doi: 10.1093/nar/gkab173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Leveau G., Pfeffer D., et al. Richert C. Enzyme-free copying of 12 bases of RNA with dinucleotides. Angew. Chem. Int. Ed. 2022;61 doi: 10.1002/anie.202203067. e202203067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pyshnyi D.V., Goldberg E.L., Ivanova E.M. Efficiency of coaxial stacking depends on the DNA duplex structure. J. Biomol. Struct. Dyn. 2003;21:459–468. doi: 10.1080/07391102.2003.10506940. [DOI] [PubMed] [Google Scholar]
- 16.Lane M.J., Paner T., et al. Benight A.S. The thermodynamic advantage of DNA oligonucleotide ‘stacking hybridization’reactions: Energetics of a DNA nick. Nucleic Acids Res. 1997;25:611–617. doi: 10.1093/nar/25.3.611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Vasiliskov V.A., Prokopenko D.V., Mirzabekov A.D. Parallel multiplex thermodynamic analysis of coaxial base stacking in DNA duplexes by oligodeoxyribonucleotide microchips. Nucleic Acids Res. 2001;29:2303–2313. doi: 10.1093/nar/29.11.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yakovchuk P., Protozanova E., Frank-Kamenetskii M.D. Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Res. 2006;34:564–574. doi: 10.1093/nar/gkj454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Walter A.E., Turner D.H., et al. Zuker M. Coaxial stacking of helixes enhances binding of oligoribonucleotides and improves predictions of RNA folding. Proc. Natl. Acad. Sci. USA. 1994;91:9218–9222. doi: 10.1073/pnas.91.20.9218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Walter A.E., Turner D.H. Sequence dependence of stability for coaxial stacking of RNA helixes with Watson-Crick base paired interfaces. Biochemist. 1994;33:12715–12719. doi: 10.1021/bi00208a024. [DOI] [PubMed] [Google Scholar]
- 21.Parker T.M., Hohenstein E.G., et al. Sherrill C.D. Quantum-mechanical analysis of the energetic contributions to π stacking in nucleic acids versus rise, twist, and slide. J. Am. Chem. Soc. 2013;135:1306–1316. doi: 10.1021/ja3063309. [DOI] [PubMed] [Google Scholar]
- 22.Häse F., Zacharias M. Free energy analysis and mechanism of base pair stacking in nicked DNA. Nucleic Acids Res. 2016;44:7100–7108. doi: 10.1093/nar/gkw607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Israels B., Albrecht C.S., et al. Marcus A.H. Submillisecond conformational transitions of short single-stranded DNA lattices by photon correlation single-molecule Förster resonance energy transfer. J. Phys. Chem. B. 2021;125:9426–9440. doi: 10.1021/acs.jpcb.1c04119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Qu P., Yang X., et al. Zhao X.S. Direct measurement of the rates and barriers on forward and reverse diffusions of intramolecular collision in overhang oligonucleotides. J. Phys. Chem. B. 2010;114:8235–8243. doi: 10.1021/jp101173y. [DOI] [PubMed] [Google Scholar]
- 25.Rivetti C., Walker C., Bustamante C. Polymer chain statistics and conformational analysis of DNA molecules with bends or sections of different flexibility. J. Mol. Biol. 1998;280:41–59. doi: 10.1006/jmbi.1998.1830. [DOI] [PubMed] [Google Scholar]
- 26.Lin S., Horning D.P., et al. Chaput J.C. Conformational analysis of DNA repair intermediates by time-resolved fluorescence spectroscopy. J. Phys. Chem. A. 2009;113:9585–9587. doi: 10.1021/jp906746w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kashida H., Kurihara A., et al. Asanuma H. Orientation-dependent FRET system reveals differences in structures and flexibilities of nicked and gapped DNA duplexes. Nucleic Acids Res. 2017;45:e105. doi: 10.1093/nar/gkx200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Roll C., Ketterlé C., Boulard Y., et al. Conformations of nicked and gapped DNA structures by NMR and molecular dynamic simulations in water. Biochem. 1998;37:4059–4070. doi: 10.1021/bi972377w. [DOI] [PubMed] [Google Scholar]
- 29.Craggs T.D., Sustarsic M., et al. Kapanidis A.N. Substrate conformational dynamics facilitate structure-specific recognition of gapped DNA by DNA polymerase. Nucleic Acids Res. 2019;47:10788–10800. doi: 10.1093/nar/gkz797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen H., Meisburger S.P., et al. Pollack L. Ionic strength-dependent persistence lengths of single-stranded RNA and DNA. Proc. Natl. Acad. Sci. USA. 2012;109:799–804. doi: 10.1073/pnas.1119057109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dans P.D., Balaceanu A., et al. Orozco M. The static and dynamic structural heterogeneities of B-DNA: Extending Calladine–Dickerson rules. Nucleic Acids Res. 2019;47:11090–11102. doi: 10.1093/nar/gkz905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Harris P.D., Hamdan S.M., Habuchi S. Relative contributions of base stacking and electrostatic repulsion on DNA nicks and gaps. J. Phys. Chem. B. 2020;124:10663–10672. doi: 10.1021/acs.jpcb.0c06941. [DOI] [PubMed] [Google Scholar]
- 33.Kervio E., Claasen B., et al. Richert C. The strength of the template effect attracting nucleotides to naked DNA. Nucleic Acids Res. 2014;42:7409–7420. doi: 10.1093/nar/gku314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Izgu E.C., Fahrenbach A.C., et al. Szostak J.W. Uncovering the thermodynamics of monomer binding for RNA replication. J. Am. Chem. Soc. 2015;137:6373–6382. doi: 10.1021/jacs.5b02707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tam C.P., Fahrenbach A.C., et al. Szostak J.W. Downstream oligonucleotides strongly enhance the affinity of GMP to RNA primer–template complexes. J. Am. Chem. Soc. 2017;139:571–574. doi: 10.1021/jacs.6b09760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kashida H., Kokubo Y., et al. Asanuma H. Selective binding of nucleosides to gapped DNA duplex revealed by orientation and distance dependence of FRET. Org. Biomol. Chem. 2019;17:6786–6789. doi: 10.1039/c9ob00946a. [DOI] [PubMed] [Google Scholar]
- 37.Spasic A., Berger K.D., et al. Mathews D.H. Improving RNA nearest neighbor parameters for helices by going beyond the two-state model. Nucleic Acids Res. 2018;46:4883–4892. doi: 10.1093/nar/gky270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Salditt A., Keil L.M.R., et al. Braun D. Thermal habitat for RNA amplification and accumulation. Phys. Rev. Lett. 2020;125 doi: 10.1103/PhysRevLett.125.048104. [DOI] [PubMed] [Google Scholar]
- 39.Mast C.B., Schink S., et al. Braun D. Escalation of polymerization in a thermal gradient. Proc. Natl. Acad. Sci. USA. 2013;110:8030–8035. doi: 10.1073/pnas.1303222110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ianeselli A., Mast C.B., Braun D. Periodic melting of oligonucleotides by oscillating salt concentrations triggered by microscale water cycles inside heated rock pores. Angew. Chem. Int. Ed. 2019;58:13155–13160. doi: 10.1002/anie.201907909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sanstead P.J., Stevenson P., Tokmakoff A. Sequence-dependent mechanism of DNA oligonucleotide dehybridization resolved through infrared spectroscopy. J. Am. Chem. Soc. 2016;138:11792–11801. doi: 10.1021/jacs.6b05854. [DOI] [PubMed] [Google Scholar]
- 42.Banyay M., Sarkar M., Gräslund A. A library of IR bands of nucleic acids in solution. Biophys. Chem. 2003;104:477–488. doi: 10.1016/s0301-4622(03)00035-8. [DOI] [PubMed] [Google Scholar]
- 43.Mallat S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989;11:674–693. [Google Scholar]
- 44.Ashwood B., Lewis N.H.C., et al. Tokmakoff A. Temperature-jump 2D IR spectroscopy with intensity-modulated CW optical heating. J. Phys. Chem. B. 2020;124:8665–8677. doi: 10.1021/acs.jpcb.0c07177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chung H.S., Khalil M., et al. Tokmakoff A. Transient two-dimensional IR spectrometer for probing nanosecond temperature-jump kinetics. Rev. Sci. Instrum. 2007;78 doi: 10.1063/1.2743168. [DOI] [PubMed] [Google Scholar]
- 46.Jones K.C., Ganim Z., et al. Tokmakoff A. Transient two-dimensional spectroscopy with linear absorption corrections applied to temperature-jump two-dimensional infrared. J. Opt. Soc. Am. B. 2012;29:118–129. [Google Scholar]
- 47.Jones K.C., Ganim Z., Tokmakoff A. Heterodyne-detected dispersed vibrational echo spectroscopy. J. Phys. Chem. A. 2009;113:14060–14066. doi: 10.1021/jp906256s. [DOI] [PubMed] [Google Scholar]
- 48.Kumar A.T.N., Zhu L., et al. Champion P.M. On the rate distribution analysis of kinetic data using the maximum entropy method: Applications to myoglobin relaxation on the nanosecond and femtosecond timescales. J. Phys. Chem. B. 2001;105:7847–7856. [Google Scholar]
- 49.Sanstead P.J., Tokmakoff A. Direct observation of activated kinetics and downhill dynamics in DNA dehybridization. J. Phys. Chem. B. 2018;122:3088–3100. doi: 10.1021/acs.jpcb.8b01445. [DOI] [PubMed] [Google Scholar]
- 50.Case D.A., Aktulga H.M., et al. Kollman P.A. University of California; 2022. AMBER 2022. [Google Scholar]
- 51.Abraham M.J., Murtola T., et al. Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1–2:19–25. [Google Scholar]
- 52.Ivani I., Dans P.D., et al. Orozco M. Parmbsc1: A refined force field for DNA simulations. Nat. Methods. 2016;13:55–58. doi: 10.1038/nmeth.3658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mark P., Nilsson L. Structure and dynamics of the TIP3P, SPC, and SPC/E water models at 298 K. J. Phys. Chem. A. 2001;105:9954–9960. [Google Scholar]
- 54.Tan D., Piana S., et al. Shaw D.E. RNA force field with accuracy comparable to state-of-the-art protein force fields. Proc. Natl. Acad. Sci. USA. 2018;115:E1346–E1355. doi: 10.1073/pnas.1713027115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Jorgensen W.L., Chandrasekhar J., et al. Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 56.Tucker M.R., Piana S., et al. Shaw D.E. Development of force field parameters for the simulation of single-and double-stranded DNA molecules and DNA–protein complexes. J. Phys. Chem. B. 2022;126:4442–4457. doi: 10.1021/acs.jpcb.1c10971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Bussi G., Donadio D., Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126 doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 58.Darden T., York D., Pedersen L. Particle mesh Ewald: An N · log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 59.Hess B., Bekker H., et al. Fraaije J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. [Google Scholar]
- 60.Diekmann S. Definitions and nomenclature of nucleic acid structure parameters. J. Mol. Biol. 1989;205:787–791. doi: 10.1016/0022-2836(89)90324-0. [DOI] [PubMed] [Google Scholar]
- 61.Bayarri G., Andrio P., et al. Gelpí J.L. BioExcel Building Blocks Workflows (BioBB-Wfs), an integrated web-based platform for biomolecular simulations. Nucleic Acids Res. 2022;50:W99–W107. doi: 10.1093/nar/gkac380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Andrio P., Hospital A., et al. Gelpi J.L. BioExcel Building Blocks, a software library for interoperable biomolecular simulation workflows. Sci. Data. 2019;6:169–178. doi: 10.1038/s41597-019-0177-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Lavery R., Moakher M., et al. Zakrzewska K. Conformational analysis of nucleic acids revisited: Curves+ Nucleic Acids Res. 2009;37:5917–5929. doi: 10.1093/nar/gkp608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Blanchet C., Pasi M., et al. Lavery R. CURVES+ web server for analyzing and visualizing the helical, backbone and groove parameters of nucleic acid structures. Nucleic Acids Res. 2011;39:W68–W73. doi: 10.1093/nar/gkr316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Scherer M.K., Trendelkamp-Schroer B., et al. Noé F. PyEMMA 2: A software package for estimation, validation, and analysis of Markov models. J. Chem. Theor. Comput. 2015;11:5525–5542. doi: 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- 66.Waskom M. Seaborn: Statistical data visualization. J. Open Source Softw. 2021;6:3021. [Google Scholar]
- 67.Peng C.S., Jones K.C., Tokmakoff A. Anharmonic vibrational modes of nucleic acid bases revealed by 2D IR spectroscopy. J. Am. Chem. Soc. 2011;133:15650–15660. doi: 10.1021/ja205636h. [DOI] [PubMed] [Google Scholar]
- 68.Lee C., Cho M. Vibrational dynamics of DNA. II. Deuterium exchange effects and simulated IR absorption spectra. J. Chem. Phys. 2006;125 doi: 10.1063/1.2213258. [DOI] [PubMed] [Google Scholar]
- 69.Ashwood B., Jones M.S., Tokmakoff A., et al. Disruption of energetic and dynamic base pairing cooperativity in DNA duplexes by an Abasic Site. Proc. Natl. Acad. Sci. USA. 2023;120 doi: 10.1073/pnas.2219124120. e2219124120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Jones M.S., Ashwood B., et al. Ferguson A.L. Determining sequence-dependent DNA oligonucleotide hybridization and dehybridization mechanisms using coarse-grained molecular simulation, Markov State models, and infrared spectroscopy. J. Am. Chem. Soc. 2021;143:17395–17411. doi: 10.1021/jacs.1c05219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Wang S., Kool E.T. Origins of the large differences in stability of DNA and RNA helixes: C-5 methyl and 2’-hydroxyl effects. Biochem. 1995;34:4125–4132. doi: 10.1021/bi00012a031. [DOI] [PubMed] [Google Scholar]
- 72.Huang Y., Weng X., Russu I.M. Enhanced base-pair opening in the adenine tract of a RNA double helix. Biochemist. 2011;50:1857–1863. doi: 10.1021/bi1014997. [DOI] [PubMed] [Google Scholar]
- 73.Bernasconi C. Academic Press; 1976. Relaxation Kinetics. [Google Scholar]
- 74.Dupuis N.F., Holmstrom E.D., Nesbitt D.J. Single-molecule kinetics reveal cation-promoted DNA duplex formation through ordering of single-stranded helices. Biophys. J. 2013;105:756–766. doi: 10.1016/j.bpj.2013.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Chen C., Wang W., et al. Zhao X.S. Influence of secondary structure on kinetics and reaction mechanism of DNA hybridization. Nucleic Acids Res. 2007;35:2875–2884. doi: 10.1093/nar/gkm177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Cho C.H., Urquidi J., et al. Robinson G.W. Thermal offset viscosities of liquid H2O, D2O, and T2O. J. Phys. Chem. B. 1999;103:1991–1994. [Google Scholar]
- 77.Hori N., Denesyuk N.A., Thirumalai D. Frictional effects on RNA folding: Speed limit and Kramers turnover. J. Phys. Chem. B. 2018;122:11279–11288. doi: 10.1021/acs.jpcb.8b07129. [DOI] [PubMed] [Google Scholar]
- 78.Neupane K., Hoffer N.Q., Woodside M.T. Measuring the local velocity along transition paths during the folding of single biological molecules. Phys. Rev. Lett. 2018;121 doi: 10.1103/PhysRevLett.121.018102. [DOI] [PubMed] [Google Scholar]
- 79.Fontana F., Bellini T., Todisco M. Liquid crystal ordering in DNA double helices with backbone discontinuities. Macromolecules. 2022;55:5946–5953. [Google Scholar]
- 80.Scott D.W. On optimal and data-based histograms. Biometrika. 1979;66:605–610. [Google Scholar]
- 81.Stone S.E., Ray D., Andricioaei I. Force field dependent DNA breathing dynamics: A case study of Hoogsteen base pairing in A6-DNA. J. Chem. Inf. Model. 2022;62:6749–6761. doi: 10.1021/acs.jcim.2c00519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Pérez de Alba Ortíz A., Vreede J., Ensing B. Sequence dependence of transient Hoogsteen base pairing in DNA. PLoS Comput. Biol. 2022;18 doi: 10.1371/journal.pcbi.1010113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Sawada T., Yoshizawa M., et al. Fujita M. Minimal nucleotide duplex formation in water through enclathration in self-assembled hosts. Nat. Chem. 2009;1:53–56. doi: 10.1038/nchem.100. [DOI] [PubMed] [Google Scholar]
- 84.Owczarzy R., Moreira B.G., Walder J.A., et al. Predicting stability of DNA duplexes in solutions containing magnesium and monovalent cations. Biochem. 2008;47:5336–5353. doi: 10.1021/bi702363u. [DOI] [PubMed] [Google Scholar]
- 85.Rejali N.A., Ye F.D., et al. Wittwer C.T. Nearest-neighbour transition-state analysis for nucleic acid kinetics. Nucleic Acids Res. 2021;49:4574–4585. doi: 10.1093/nar/gkab205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Szabo A. Kinetics of hemoglobin and transition state theory. Proc. Natl. Acad. Sci. USA. 1978;75:2108–2111. doi: 10.1073/pnas.75.5.2108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Eaton W.A., Henry E.R., Hofrichter J. Application of linear free energy relations to protein conformational changes: the quaternary structural change of hemoglobin. Proc. Natl. Acad. Sci. USA. 1991;88:4472–4475. doi: 10.1073/pnas.88.10.4472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Oweida T.J., Kim H.S., et al. Yingling Y.G. Assessment of AMBER force fields for simulations of ssDNA. J. Chem. Theor. Comput. 2021;17:1208–1217. doi: 10.1021/acs.jctc.0c00931. [DOI] [PubMed] [Google Scholar]
- 89.Roll C., Ketterlé C., et al. Boulard Y. Solution structures of a duplex containing an adenine opposite a gap (absence of one nucleotide) An NMR study and molecular dynamic simulations with explicit water molecules. Eur. J. Biochem. 1999;264:120–131. doi: 10.1046/j.1432-1327.1999.00585.x. [DOI] [PubMed] [Google Scholar]
- 90.Guo H., Tullius T.D. Gapped DNA is anisotropically bent. Proc. Natl. Acad. Sci. USA. 2003;100:3743–3747. doi: 10.1073/pnas.0737062100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Zhang W., Tam C.P., et al. Szostak J.W. Insight into the mechanism of nonenzymatic RNA primer extension from the structure of an RNA-GpppG complex. Proc. Natl. Acad. Sci. USA. 2017;114:7659–7664. doi: 10.1073/pnas.1704006114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Zhang W., Tam C.P., et al. Szostak J.W. Structural rationale for the enhanced catalysis of nonenzymatic RNA primer extension by a downstream oligonucleotide. J. Am. Chem. Soc. 2018;140:2829–2840. doi: 10.1021/jacs.7b11750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Zhang W., Walton T., et al. Szostak J.W. Crystallographic observation of nonenzymatic RNA primer extension. Elife. 2018;7 doi: 10.7554/eLife.36422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Sim A.Y.L., Lipfert J., et al. Doniach S. Salt dependence of the radius of gyration and flexibility of single-stranded DNA in solution probed by small-angle x-ray scattering. Phys. Rev. E. 2012;86 doi: 10.1103/PhysRevE.86.021901. [DOI] [PubMed] [Google Scholar]
- 95.Chen Z.Y., Noolandi J. Renormalization-group scaling theory for flexible and wormlike polymer chains. J. Chem. Phys. 1992;96:1540–1548. [Google Scholar]
- 96.Giurgiu C., Fang Z., et al. Szostak J.W. Structure–activity relationships in nonenzymatic template-directed RNA synthesis. Angew. Chem. Int. Ed. 2021;60:22925–22932. doi: 10.1002/anie.202109714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Conte M.R., Conn G.L., et al. Lane A.N. Conformational properties and thermodynamics of the RNA duplex r (CGCAAAUUUGCG) 2: Comparison with the DNA analogue d (CGCAAATTTGCG) 2. Nucleic Acids Res. 1997;25:2627–2634. doi: 10.1093/nar/25.13.2627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Cruz-León S., Schwierz N. RNA captures more cations than DNA: Insights from molecular dynamics simulations. J. Phys. Chem. B. 2022;126:8646–8654. doi: 10.1021/acs.jpcb.2c04488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Auffinger P., Westhof E. Water and ion binding around r (UpA) 12and d (TpA) 12Oligomers-comparison with RNA and DNA (CpG) 12 duplexes. J. Mol. Biol. 2001;305:1057–1072. doi: 10.1006/jmbi.2000.4360. [DOI] [PubMed] [Google Scholar]
- 100.Abels J.A., Moreno-Herrero F., et al. Dekker N.H. Single-molecule measurements of the persistence length of double-stranded RNA. Biophys. J. 2005;88:2737–2744. doi: 10.1529/biophysj.104.052811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Ding D., Zhou L., et al. Szostak J.W. Kinetic explanations for the sequence biases observed in the nonenzymatic copying of RNA templates. Nucleic Acids Res. 2022;50:35–45. doi: 10.1093/nar/gkab1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Stootman F.H., Fisher D.M., et al. Aldrich-Wright J.R. Improved curve fitting procedures to determine equilibrium binding constants. Analyst. 2006;131:1145–1151. doi: 10.1039/b604686j. [DOI] [PubMed] [Google Scholar]
- 103.Movileanu L., Benevides J.M., Thomas G.J., Jr. Temperature dependence of the raman spectrum of DNA. Part I—Raman signatures of premelting and melting transitions of poly (dA–dT)· poly (dA–dT) J. Raman Spectrosc. 1999;30:637–649. doi: 10.1002/bip.10022. [DOI] [PubMed] [Google Scholar]
- 104.Owczarzy R. Melting temperatures of nucleic acids: Discrepancies in analysis. Biophys. Chem. 2005;117:207–215. doi: 10.1016/j.bpc.2005.05.006. [DOI] [PubMed] [Google Scholar]
- 105.Mergny J.-L., Lacroix L. Analysis of thermal melting curves. Oligonucleotides. 2003;13:515–537. doi: 10.1089/154545703322860825. [DOI] [PubMed] [Google Scholar]
- 106.Krummel A.T., Zanni M.T. DNA vibrational coupling revealed with two-dimensional infrared spectroscopy: Insight into why vibrational spectroscopy is sensitive to DNA structure. J. Phys. Chem. B. 2006;110:13991–14000. doi: 10.1021/jp062597w. [DOI] [PubMed] [Google Scholar]
- 107.Lee C., Park K.-H., et al. Cho M. Vibrational dynamics of DNA. III. Molecular dynamics simulations of DNA in water and theoretical calculations of the two-dimensional vibrational spectra. J. Chem. Phys. 2006;125 doi: 10.1063/1.2213259. [DOI] [PubMed] [Google Scholar]
- 108.Braunlin W.H., Bloomfield V.A. Proton NMR study of the base-pairing reactions of d (GGAATTCC): Salt effects on the equilibria and kinetics of strand association. Biochem. 1991;30:754–758. doi: 10.1021/bi00217a026. [DOI] [PubMed] [Google Scholar]
- 109.Mikulecky P.J., Feig A.L. Heat capacity changes associated with DNA duplex formation: salt-and sequence-dependent effects. Biochemist. 2006;45:604–616. doi: 10.1021/bi0517178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Marky L.A., Breslauer K.J. Calculating thermodynamic data for transitions of any molecularity from equilibrium melting curves. Biopolymers. 1987;26:1601–1620. doi: 10.1002/bip.360260911. [DOI] [PubMed] [Google Scholar]
- 111.Böttcher A., Kowerko D., Sigel R.K.O. Explicit analytic equations for multimolecular thermal melting curves. Biophys. Chem. 2015;202:32–39. doi: 10.1016/j.bpc.2015.04.001. [DOI] [PubMed] [Google Scholar]
- 112.van Stokkum I.H.M., Larsen D.S., Van Grondelle R. Global and target analysis of time-resolved spectra. Biochim. Biophys. Acta. 2004;1657:82–104. doi: 10.1016/j.bbabio.2004.04.011. [DOI] [PubMed] [Google Scholar]
- 113.Mullen K.M., Vengris M., van Stokkum I.H.M. Algorithms for separable nonlinear least squares with application to modelling time-resolved spectra. J. Global Optim. 2007;38:201–213. [Google Scholar]
- 114.Lee Y., Gorka M., et al. Anna J.M. Ultrafast energy transfer involving the red chlorophylls of cyanobacterial photosystem I probed through two-dimensional electronic spectroscopy. J. Am. Chem. Soc. 2018;140:11631–11638. doi: 10.1021/jacs.8b04593. [DOI] [PubMed] [Google Scholar]
- 115.Freire E., Schön A., Velazquez-Campoy A. Isothermal titration calorimetry: General formalism using binding polynomials. Methods Enzymol. 2009;455:127–155. doi: 10.1016/S0076-6879(08)04205-5. [DOI] [PubMed] [Google Scholar]
- 116.Todisco M., Szostak J.W. Hybridization kinetics of out-of-equilibrium mixtures of short RNA oligonucleotides. Nucleic Acids Res. 2022;50:9647–9662. doi: 10.1093/nar/gkac784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Chen Z., Znosko B.M. Effect of sodium ions on RNA duplex stability. Biochem. 2013;52:7477–7485. doi: 10.1021/bi4008275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Invernizzi M. OPES: On-the-fly probability enhanced sampling method. arXiv. 2021 https://arxiv.org/abs/2101.06991 Preprint at. [Google Scholar]
- 119.Invernizzi M., Parrinello M. Rethinking metadynamics: from bias potentials to probability distributions. J. Phys. Chem. Lett. 2020;11:2731–2736. doi: 10.1021/acs.jpclett.0c00497. [DOI] [PubMed] [Google Scholar]
- 120.Laio A., Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA. 2002;99:12562–12566. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Ensing B., De Vivo M., et al. Klein M.L. Metadynamics as a tool for exploring free energy landscapes of chemical reactions. Acc. Chem. Res. 2006;39:73–81. doi: 10.1021/ar040198i. [DOI] [PubMed] [Google Scholar]
- 122.Best R.B., Hummer G., Eaton W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA. 2013;110:17874–17879. doi: 10.1073/pnas.1311599110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Bottaro S., Di Palma F., Bussi G. The role of nucleobase interactions in RNA structure and dynamics. Nucleic Acids Res. 2014;42:13306–13314. doi: 10.1093/nar/gku972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Tribello G.A., Bonomi M., et al. Bussi G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014;185:604–613. [Google Scholar]
- 125.PLUMED consortium Promoting transparency and reproducibility in enhanced molecular simulations. Nat. Methods. 2019;16:670–673. doi: 10.1038/s41592-019-0506-8. [DOI] [PubMed] [Google Scholar]
- 126.Berg O.G., von Hippel P.H. Diffusion-controlled macromolecular interactions. Annu. Rev. Biophys. 1985;14:131–160. doi: 10.1146/annurev.bb.14.060185.001023. [DOI] [PubMed] [Google Scholar]
- 127.Stejskal E.O., Tanner J.E. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 1965;42:288–292. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Experimental and simulation data is uploaded to Zenodo and available at https://zenodo.org/record/7662738#.ZMQWvnbMKUk.