Abstract
Sulfide-based solid-state lithium-ion batteries (SSLIB) have attracted a lot of interest globally in the past few years for their high safety and high energy density over the traditional lithium-ion batteries. However, sulfide electrolytes (SEs) are moisture-sensitive which pose significant challenges in the material preparation and cell manufacturing. To the best of our knowledge, there is no tool available to probe the types and the strength of the basic sites in sulfide electrolytes, which is crucial for understanding the moisture stability of sulfide electrolytes. Herein, we propose a new spectral probe with the Lewis base indicator BBr3 to probe the strength of Lewis basic sites on various sulfide electrolytes by 11B solid-state NMR spectroscopy (11B-NMR). The active sulfur sites and the corresponding strength of the sulfide electrolytes are successfully evaluated by the proposed Lewis base probe. The probed strength of the active sulfur sites of a sulfide electrolyte is consistent with the results of DFT (density functional theory) calculation and correlated with the H2S generation rate when the electrolyte was exposed in moisture atmosphere. This work paves a new way to investigate the basicity and moisture stability of the sulfide electrolytes.
Keywords: sulfide electrolyte, B-NMR, Lewis acid probe, moisture stability
1. Introduction
All-solid-state lithium metal batteries (ASSLMBs) with high volumetric energy density and excellent safety have become one of the most promising candidates in energy storage systems in recent years.1 Especially, sulfide-based electrolytes such as glass–ceramic Li7P3S11 (LPS), argyrodite cubic Li6PS5Cl (LPSC), and tetragonal Li10GeP2S12 (LGPS) receive lot of attention due to their liquid-electrolyte-like ion conductivity at room temperature, high flexibility, and easy processing.2−5 However, the primary challenge in utilizing sulfide electrolytes for commercial processing in the future is their high sensitivity to moisture, which can result in the generation of toxic H2S gas in ambient environments.6 Consequently, sulfide electrolytes need to be operated in a dry room or an inert gas environment during the material synthesis and cell manufacture, which poses great challenges for their practical applications. Understanding the origin of their moisture-caused instability is essential to resolve this issue effectively. Although a few approaches such as hard and soft acid and base (HSAB) theory-guided doping,7 metal oxide absorption, and core–shell nanomaterial coating8 have been reported to improve the moisture stability of sulfide electrolytes, very limited reports have provided deep insights into this topic due to the lack of an effective tool. Therefore, developing a method to explore the origin of moisture instability for sulfide electrolytes is of great interest and crucial.
NMR is a great tool to understand the status of the molecule adsorption state by the electron shielding effect. Chu et al. and Lewis et al. have used Lewis acid site probes, trimethyl phosphine (TMP) and trimethyl phosphine oxide (TMPO), which adsorb on Lewis acid materials to measure the strength of acid sites by 31P solid-state NMR chemical shift.9,10 Therefore, this Lewis acid site probe is a unique and practical technique for characterizing the strength of Lewis acid. From the Lewis acid–base theory, it is observed that sulfide electrolytes are Lewis-based materials that provide electron pairs on active sulfur sites. According to the HSAB theory, active sulfur sites could be bonded or attacked by an acid-type material. We took advantage of this feature and chose one of Lewis acids with appropriate strength as a probe for NMR measurements for the first time. Meanwhile, the selected Lewis acid will not provide protons to sulfide and causes sulfur loss. Although many works have used a base-type indicator to probe the acid site in NMR,9−13 an acid-type indicator is rarely reported. Herein, we proposed a new type of spectral probe, BBr3 acid, as a base indicator by 11B solid-state NMR (11B-NMR) to study the Lewis base strength of the sulfide electrolyte, including Li7P3S11, Li6PS5Cl, Li10GeP2S12, and the precursor Li2S. The electron-deficient Lewis acid BBr3 would adsorb on the active sulfur sites of sulfide electrolytes. The 11B chemical shift from the electron shielding effect on the active sulfur sites can be applied to indicate the correlation with the Lewis base strength. We could estimate the molecular state changes before/after adsorption by their chemical shift. Furthermore, we combine the DFT adsorption energy calculation and H2S generation measurement with the 11B-NMR results to describe the relationship of Lewis basic strength, adsorption energy, and rate of H2S generation in each sulfide electrolyte material. We hope that the new spectral probe method can give a fair comparison and shed light on improving the moisture stability of sulfide base solid-state electrolytes.
2. Results and Discussion
2.1. Feasibility of Probing Sulfur Site Basicity of Sulfide Electrolytes by Lewis Acid BBr3
The sulfide-based solid-state electrolyte LPSC was well mixed with BBr3 for 11B-NMR measurements. Since LPSC exhibits a large number of sulfur sites providing electron lone pairs in the PS43– moiety, the electron-deficient BBr3 will adsorb on the Lewis base sulfide sites. Figure 1a shows the boron chemical shift (δ 11B) in 11B solid-state NMR spectra for the BBr3-treated LPSC sample; there are two peaks in the range of δ 11B = 10–20 ppm and δ 11B = 0–5 ppm corresponding to the tricoordinated boron structure and tetracoordinated boron structure, respectively.14 Since boron is a nuclear quadrupole element, the asymmetric tricoordinated peaks are broader at the lower magnetic field. It indicates that the BBr3-treated LPSC at least exhibits two types of basic sulfur sites. On the other hand, to determine whether the sulfide exhibits acidic sites, the basic type indicator TMPO that is well known in the catalysis study was mixed with LPSC thoroughly for 31P-NMR measurement, as shown in Figure S1. The 31P-NMR results show the PS43– structure at 84.4 ppm and the additional two new peaks at 54.7 ppm and 43.4, which are attributed to TMPO physisorption and TMPO crystal, respectively.11 It suggests that no active acidic site on LPSC is allowed to react with TMPO; only active basic sites exist. To further understand the interactions between BBr3 and the sulfide electrolyte, 31P NMR and 2D multiple quantum magic angle spinning (MQMAS)-11B NMR were measured, as shown in Figures S2 and 1b. The 31P NMR spectra of the two samples show the same peak at 84.4 ppm representing the PS43– moiety structure in LPSC.3 It implies that BBr3 is a nonaggressive acid to the sulfide electrolyte and does not damage its PS43– structure in BBr3-treated LPSC samples. Furthermore, due to the boron quadrupolar nuclei which have trouble in the large line width of the NMR signal, 2D MQMAS 11B NMR allows for the differentiation of overlapping signals and the extraction of fine details in the spectra, enabling a more accurate analysis of quadrupolar nuclei to split the contribution of each material.15 Thus, the 2D MQMAS 11B NMR result has been applied to eliminate the quadrupolar interaction and to elucidate the asymmetric signal split in 1D 11B NMR. The results in Figure 1b show that there is no plural boron chemical environment on the asymmetric splitting peak, which is the tricoordinated boron in δ 11B = 10–20 ppm, and the tetracoordinated boron δ 11B = 0–5 ppm shows one boron chemical environment, respectively.14 It clearly indicates that the BBr3-treated LPSC has the presence of two boron sites that differ in their chemical environments. According to the results of the above 31P-NMR and 11B-NMR, the LPSC structure remains stable after the BBr3 adsorption and generates two different boron chemical environments. It is suggested that these two types of boron chemical environments are the BBr3 physisorption and chemisorption on the active sulfur sites in LPSC. This phenomenon is similar to that observed in the case of Lewis base TMPO adsorbed on Lewis acidic sites.16
Figure 1.

BBr3-treated LPSC surface with (a) 1D 11B solid-state NMR spectra; (b) 2D MQMAS 11B solid-state NMR spectra and the scheme of the tricoordinate and tetracoordinate structures in 11B solid-state NMR; molecule remarks (1) B: dark green, (2) S: light yellow, (3) P: purple, (4) Br: brown.
To further verify the existence of B–S interaction, FTIR spectrometry and XPS measurements were carried out to provide clear evidence for the treatment of BBr3 on the active sulfur sites. Four new peaks at 732, 813, 854, and 1270 cm–1 appear after the treatment of BBr3 on LPSC, as shown in Figure 2a. The peak at 732 cm–1 corresponds to the out-of-plane bending (2σ2) of a trigonal planar unit BBr3 and sulfur bond, and 813 and 854 cm–1 peaks are from the B–Br stretching vibration.17 The presence of the FT-IR signal indicates that the BBr3 bond is with the active sulfur site and it is not decomposed after BBr3 interacts with LPSC. In addition, the peak at 1270 cm–1 provides a similar peak with that of B2S3 which might be a boron–sulfur bonding, but it needs to be further confirmed.18 Furthermore, comparing the S2p XPS spectra in Figure 2b,e before/after BBr3 treatment, respectively, it is found that after BBr3 treatment, the peak signal at 161.3 eV corresponds to the PS43– peak shift to 161.7 eV, and the peak at 163.3 eV which is due to the boron–sulfur bonding appears.19 The results indicate that the boron of BBr3 mainly absorbs on the active sulfur site of the PS43– moiety. Meanwhile, the XPS results of P2p and Li1s spectra were also measured, as shown in Figure 2c,d,f,g. Interestingly, the P 2p peak at 133.0 eV (PS43–) and Li1s peak at 55.4 eV (Li+) remained unchanged after LPSC was treated with BBr3, indicating that BBr3 is a nondestructive probe. It only interacts with the active sulfur on LPSC, consistent with the previous discussion on 31P and 11B NMR.
Figure 2.
FT-IR and XPS analyses of LPSC before/after BBr3 treatment: (a) FT-IR; (b) S2p (c) P2p and (d) Li1S. BBr3-treated LPSC of (e) XPS S2p, (f) XPS P2p, and (g) XPS Li1S. The blue dashed lines in the FT-IR result are the out-of-plane bending (2 σ2) of a trigonal planar unit BBr3 and sulfur bond, B–Br stretching vibration, and B–S bonding vibration. The green region in S2p XPS is due to B–S bonding which can be identified at 163.3 eV.
2.2. Sulfur Site Basicity of Various Sulfide Electrolytes Probed by BBr3
To confirm whether BBr3 has enough credibility to measure the basicity of sulfide electrolytes, both pKa and pKb of dimethyl sulfide (DMS) and pyridine are well-known measurements, which are obtained to verify the BBr3 probing ability.20,21 The 11B-NMR results of DMS- and pyridine-treated BBr3 have been studied experimentally and computationally in Figure S3 and Table S2. According to the experimental and computational results, DMS-treated BBr3 and pyridine-treated BBr3 show the same trends in B chemical shift for basicity ordering. It indicates that BBr3 has the ability to detect the degree of basicity. Following the above concept, BBr3 was also employed as an indicator of probing the basic sites and the basicity of Li2S and the other common sulfide electrolytes Li7P3S11 (LPS) and Li10GeP2S12 (LGPS). In addition, FT-IR, 31P-NMR, and XPS of these sulfides are shown in Figures S4–S6. In Figure S3, 31P-NMR indicates that the structure was maintained after the adsorption of BBr3, which ensures that BBr3 is a nondestructive probe for sulfide basicity.3,22,23 The peaks of LPSC and LGPS did not exhibit any changes after being mixed with BBr3, as seen on the 31P-NMR graph in Figure S4;24 however, an unidentified peak appeared at 68.3 ppm in LPS 31P-NMR, which warrants further investigation. The same feature of B–S interaction like that in LPSC was observed in the range of 1268–1270 cm–1 of the FT-IR spectrum and 164.1–164.5 eV of the XPS spectrum, as shown in Figures S5 and S6, respectively. Meanwhile, out-of-plane bending (715–718 cm–1) and B–Br stretching vibration (812–813 cm–1) were also observed. In addition, the structure of the sulfide materials was investigated by in-house XRD before/after BBr3 treatment, as shown in Figure S7. The results also showed that the structure of the sulfide materials remained unchanged after BBr3 treatment with all of the sulfide materials. It is concluded again that BBr3 is a nondestructive probe to sulfide materials and can be used as a powerful indicator to probing the basicity of sulfide materials.
The 11B-NMR spectra of various sulfide electrolytes after BBr3 adsorption are shown in Figure 3a. After BBr3 treatment in various sulfide materials, similar 11B chemical shifts corresponding to the tricoordinate and tetracoordinate compounds were observed in the range of δ 11B = 10–20 ppm and δ 11B = −5–5 ppm, respectively. The tricoordinate B with a high quadrupolar constant (CQ) around 2.5–2.9 MHz results in a broad peak. On the contrary, the tetracoordinate B with low CQ around 0.4–0.6 MHz shows a narrow peak.14 The relationship of the quadrupolar constant and the corresponding B–S compound is presented in Figure 3b. Therefore, δ 11B of the tetracoordinate compound is more distinguishable compared to that of the tricoordinate B and can be a good descriptor for the basicity of sulfur sites, which is ascribed to BBr3 chemisorption on active sulfur sites. To further investigate the basicity of the sulfur sites in the LPS, Li2S, LPSC, and LGPS sulfide materials, we compared their δ 11B in the tetracoordinate region. The peak position of BBr3 chemisorption in LPS, Li2S, LPSC, and LGPS was presented at 2.28, 0.62, 0.47, and 0.22 ppm, respectively. Since δ 11B of the standard BBr3 is at 38 ppm, the difference of the boron chemical shift (△δ 11B) of LPS, Li2S, LPSC, and LGPS was 35.55, 37.41, 37.53, and 37.71 ppm, respectively. From the electron shielding effect, △δ 11B indicates the amounts of electrons donated from active sulfur to BBr3. It means that the greater the chemical shift, the more electrons are donated to boron from active sulfur. A sulfur site donating more electrons would have stronger Lewis basicity. According to the results of △δ 11B of the sulfide materials, it was suggested that the basicity of active sulfur sites would be in the order: LGPS > LPSC > Li2S > LPS. The higher the basicity of the Lewis base, the better is the stability of the active sulfur site to moisture. On the contrary, the weaker the basicity of the Lewis base, the worse is the stability of the active sulfur site to moisture. According to the B-NMRs result, LPS is the weakest Lewis base, and LGPS is the strongest Lewis base, indicating that LPS will be the most vulnerable with moisture and LGPS will be the most stable one among these four sulfide materials. Furthermore, we tried to integrate the areas of physisorption and chemisorption peaks and then we calculated the molar ratio of chemisorption and physical adsorption (4C.N/3C.N.) with the results of 11B-NMR in Figure 3c. LPS has a larger 4C.N./3C.N. ratio because there are two different structures P2S74– and PS43–, and LPS has a triclinic structure with a larger open volume in the lattice structure, resulting in more reaction area potentially.25,26 On the other hand, the 4C.N./3C.N ratio of cubic Li2S, LPSC, and tetragonal LGPS structures was 0.13, 0.1, and 0.1, respectively. The molar ratio of 4C.N./3C.N. indicated the amount of chemisorption, which means more active sulfur sites can be attacked. The results are summarized in Table 1, and it was briefly concluded that the moisture stability was of the order LGPS > LPSC > Li2S > LPS. To prove the relationship between the Lewis base strength of the active sulfur site and the moisture stability of the sulfide materials, the adsorption energy of BBr3 on the active sulfur sites of sulfide materials was calculated by the DFT computation, and moisture stability was measured for the investigated sulfide materials.
Figure 3.
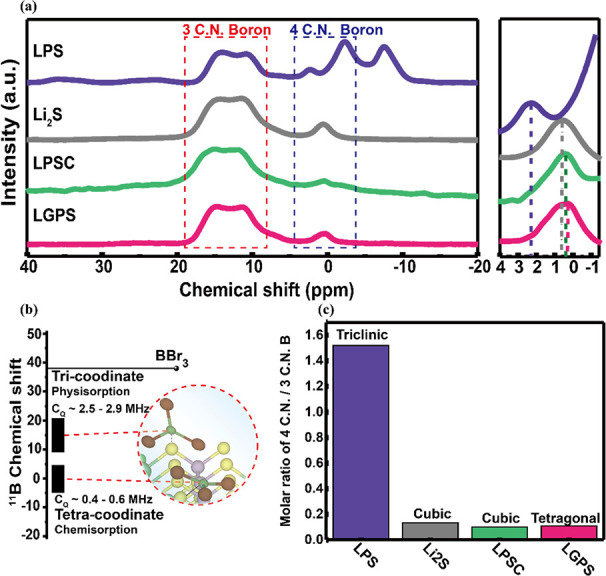
(a) 11B solid-state NMR results with different commercial sulfide materials including Li2S, LPS, LPSC, and LGPS. (b) Quadrupolar constants with tricoordinates and tetracoordinates in 11B NMR. (c) Molar ratio of tetracoordinate number to tricoordinate number boron compound.
Table 1. Tetracoordinate 11B Chemical Shift and the Molar Ratio of Tetracoordinate/Tricoordinate Boron Compound.
| Li7P3S11 (LPS) | Li2S | Li6PS5Cl (LPSC) | Li10GeP2S12 (LGPS) | |
|---|---|---|---|---|
| δ-ppm | 2.45 | 0.59 | 0.47 | 0.29 |
| Δδ-ppm | 35.55 | 37.41 | 37.53 | 37.71 |
| molar ratio of 4 C.N/3 C.N | 1.52 | 0.13 | 0.1 | 0.1 |
2.3. DFT Calculation of Adsorption Energy
In order to further prove 11B-NMR results, BBr3 was selected and made to adsorb on the sulfide surface of selected facets for each species to investigate their degree of sensitivity to moisture. Since BBr3 is a well-known Lewis acid, it was expected that a Lewis acid–base interaction could be formed between the BBr3 adsorbate and the sulfide facet surface. Based on this concept, the corresponding adsorption energy (Ead) was calculated for each molecule of the sulfide materials using DFT. The DFT calculations were performed using the Vienna ab initio simulation package (VASP) software with the pseudopotentials of the projector augmented wave (PAW).27,28 Generalized gradient approximation (GGA) was applied using the revised Perdew–Burke–Ernzerhof (PBE) functional to describe the electron’s exchange–correlation energy.29 We examined slabs with facets of (100), (010), and (001) for every sample to determine the adsorption energy. Additional facets were also considered, based on the Miller indices of the samples’ XRD patterns. Following structural optimization, we selected the most stable facet for each sample: (311) for LPSC, (203) for LGPS, (211) for LPS, and (111) for Li2S surfaces, as indicated in Table S3. The adsorption energy Ead with each sulfide was −3.65, −3.03, −7.54, and −3.97 eV, respectively. According to the adsorption energy definition, more negative adsorption energy means a stronger interaction between adsorbates and the substrate. BBr3 is adsorbed on the sulfide surface in its molecular form, with the B atom closest to the surface and the Br atoms furthest from the surface, as shown in Figure 4a. If the calculated adsorption energies between the sulfide surfaces and the BBr3 molecule were high, this means the interaction between BBr3 and the sulfides was likely strong. As summarized in Figure 4, the (2 1 1)-faceted LPS had the most negative Ead, which formed strong interaction with the BBr3 molecule, indicating its high degree of sensitivity to moisture. Conversely, the adsorption of BBr3 molecule on the (2 0 3)-faceted LGPS surface provides the lowest Ead, which shows LGPS was less sensitive to moisture as compared to the other sulfides. We made a regression curve with the previous 11B-NMR results and the adsorption energy in Figure 4e. R2 of the regression curve was 0.9924, which indicates a great correlation with the difference of δ 11B. It suggests that the calculated Ead of BBr3 absorbed on the Lewis base active sulfur site and the experiment data displayed an excellent linear relationship. Accordingly, the sulfide order of sensitivity toward moisture, from strong to weak, derived computationally was: LPS > Li2S > LPSC > LGPS, consistent with the experimental 11B-NMR chemical shift.
Figure 4.

Schematic illustration of the sulfide material adsorption structure of BBr3 on each optimized sulfide surface and DFT-calculated adsorption energy (Ead) on the optimized surface of (a) LPS (2 1 1), (b) Li2S (1 1 1), (c) LPSC (3 1 1), and (d) LGPS (2 0 3). (e) Linear regression plot using △δ11B and the DFT-calculated adsorption energy on the different plane which dominates from XRD. Remarks: (1) Li: light green, (2) B: dark green, (3) P: purple, (4) S: light yellow, and (5) Br: brown.
In addition to the adsorption energy, dipole effect was investigated at different possible adsorption sites for each sulfide molecule. As can be seen in Table S4, the dipole in the molecule arises insignificantly due to the redistribution of electron density on the adsorbate caused by the presence of the polar adsorbent surface. The polar adsorbent surface, with its partial positive and negative charges, can attract the electron cloud of the nonpolar adsorbate, causing it to become polarized, and can contribute to an increase in the adsorption energy. Despite being a nonpolar molecule, BBr3 becomes slightly polarized when it is adsorbed on the adsorbent surfaces. Nevertheless, the polarization of BBr3 is insignificant, which can show the formation of only weak attractive interactions between the adsorbate and the polar adsorbent surface. In general, the polarizability of BBr3 is more pronounced in LPS, followed by Li2S, showing a stronger interaction with the adsorbate than in the case of LPSC and LGPS. This induced dipole in the nonpolar BB3 can result in stronger attractive interactions with the LPS and Li2S slap surfaces and can contribute to an increase in the adsorption energy which is in good agreement with the Ead values.
2.4. H2S Generation of Various Sulfide Materials
To correlate the moisture stability to the basicity of the sulfide materials, the H2S generation experiment was carried out. The H2S generation measurement device setup is shown in Figures 5a and S8. The humidity was controlled by the 43.4 wt % H2SO4 solution in the 6.8 L desiccator, which provided 50% relative humidity at room temperature, as shown in Figure 5b.30 After measuring the humidity of the desiccator, the sample, H2S sensor, humidity sensor, and fan were put into a 0.9 L container.30,31 The sample container was placed in an Ar-filled glovebox. The H2S generation started to be monitored once 100 mL of humid air from the desiccator was injected into the sample container. The relative humidity and the H2S generation in the sample container were recorded for each sulfide material, as shown in Figures S9 and 5c, respectively. It was found that the generation of H2S from the highest to the lowest was 8.03 H2S ppm/g (LPS), 5.62 H2S ppm/g (Li2S), 4.09 H2S ppm/g (LPSC), and 0.74 H2S ppm/g (LGPS). The amount of H2S generation for LPS is the highest, but it is the lowest for LGPS. The active sulfur site of LPS has a relatively low Lewis basicity; the active sulfur is more likely to break the bond with phosphorus and generate H2S during the moisture exposure. On the contrary, the relatively strong Lewis basicity LGPS sulfur site reacts with moisture to form the SH group; it will not immediately break the bond with phosphorus to generate H2S. It is in good agreement with the 11B-NMR and DFT computation results. It indicated that the proposed probe, the acid indicator BBr3, is an effective probe for analyzing the basicity of the Lewis base of the active sulfur sites on the sulfide electrolyte by 11B-NMR measurement. The chemical shift of 11B-NMR is strongly correlated to the absorption energy of BBr3 at the sulfur site and the H2S generation rate of the sulfide electrolyte.
Figure 5.

(a) Schematic of the H2S generation measurement device. (b) Calibration of relative humidity amount in 10 min. (c) H2S generation measurement with each sulfide material in 10 min; the H2S amount (ppm) was divided by the sulfide weight (g).
Exploring the moisture-sensitive site will give new possibilities for future investigations concerning the improvement of the moisture instability of sulfide solid electrolytes. For instance, this research has paved the way to prevent the reaction of moisture-sensitive sites by safeguarding the sulfide solid electrolytes using electron acceptor additives. Moreover, the molecular probe concept developed can be extended to study other air-sensitive materials, such as halide-type solid electrolytes or electrode materials. This facilitates the rapid advancement of battery materials (e.g., sulfides, halides, etc.) and the development of next-generation batteries.
3. Conclusions
A new type of Lewis base indicator, BBr3, is proposed to investigate the basicity of sulfur sites in sulfide electrolytes via the 11B solid-state NMR. The electron-deficient BBr3 molecules are chemically adsorbed on the active sulfur sites of sulfide electrolytes based on the HSAB theory. The basicity of the sulfide materials, including Li2S, LPS, LPSC, and LGPS, has been examined successfully by the proposed probe. From the results of 1D and 2D δ 11B, the signals of δ 11B = 10–20 ppm and δ 11B = 0–5 ppm for BBr3 physisorption and chemisorption were observed, respectively. The existence of boron–sulfur bonding has also been successfully confirmed by FT-IR and S2p XPS. In addition, BBr3 has been confirmed to be a nondestructive probe for the determination of basic sites and the basicity of sulfide materials. The tetracoordinated chemisorption result△δ 11B suggested that the moisture stability of sulfides follows the order: LGPS > LPSC > Li2S > LPS, which agrees well with the DFT calculation result. The H2S generation measurement also verified the evidence of the order of moisture stability. It strongly indicated that the moisture stability of sulfide could be described by the basicity of the Lewis base at the active sulfur site probed by 11B-NMR. This work paves a new way to investigate the basicity of Lewis base sites of sulfide materials and provide an in-depth understanding of the moisture stability mechanism of sulfide-based electrolytes, which is essential to develop moisture-resistant sulfide-based materials.
4. Experimental Section
4.1. Preparation of Sulfide-Based Material
The glass ceramic Li7P3S11 was synthesized by the procedure reported by Yamane et al.25 0.651 g Li2S (Alfa Asear, 99.9%, 200 mesh) and 1.349 g P2S5 (Sigma-Aldrich, 98%) were mixed by hand-milling for 10 min, and then the mixture was loaded into a 125 mL Al2O3 jar filled with zirconium beads (diameter = 10 mm) for mechanical milling for 20 h under a rotating speed of 500 rpm. A desktop planetary ball-mill apparatus (Retsch, PM100) was used.
The ground powder of 0.05 g was pressed 3 tons to a pellet (diameter = 10 mm) by a hydraulic pressing machine. The pellet was put into an Al2O3 crucible and was sintered at 573 K for 2 h in a cubic furnace that was placed in an Ar-filled glovebox. All the above processes were performed in the Ar-filled glovebox, with H2O and O2 levels below 0.55 ppm and O2 1 ppm, respectively. Other sulfide materials such as Li2S, Li6PS5Cl, and Li10GeP2S12 were purchased from Alfa-Asear (99.9%, 200 mesh), NEI Corporation, and MTI Corporation, respectively. All of the sulfide materials were also kept in the Ar-filled glovebox.
4.2. 11Boron Solid-State and 31Phosphorus Solid-State NMR Measurements
The sulfide materials (1 mg) were dispersed in the BBr3 solution (1 μL) under a rotating speed of 150 rpm for 1 h. The extra BBr3 was removed under vacuum at room temperature for 1 h. The TMPO solution was prepared by dissolving 50 mg TMPO powder into 15 mL of xylene, and then the sulfide materials (1 mg) were dispersed in the TMPO solution (40 μL) under a rotating speed of 150 rpm for 1 h. The extra xylene was removed by vacuum at room temperature for 1 h. Solid-state boron-11 and solid-state phosphorus-31 cross-polarization/magic-angle spinning nuclear magnetic resonance (11B CP-MAS ssNMR and 31P CP-MAS ssNMR) spectra were acquired on a 14.1 T wide-bore Bruker Avance III spectrometer equipped with a 3.5 mm double-resonance MAS probe head in National Taiwan University. The Larmor frequencies for 11B CP-MAS ssNMR and 31P CP-MAS ssNMR were calculated to be 192.5 and 242.9 MHz, respectively. The rotating speed was 16,000 Hz. All the data were analyzed by Topspin 4.0.9 to pick up the peak position and area.
4.3. FT-IR and XPS Measurements
The sulfide material and KBr powder were mixed and added into a NICOLET iS50 FT-IR cell holder in an Ar-filled glovebox. The weight percentage of the sulfide material and KBr was 30:70 in the mixture powder of 0.2 g. The gas channels of the cell holder were sealed by Parafilm. Then, the sample in the sealed holder was measured by FT-IR analysis at room temperature. The analytic software is OMNIC.
XPS spectra were measured at the beamline TLS 24A1 in the National Synchrotron Radiation Research Center (NSRRC) in Hsinchu, Taiwan. All energies of the spectra were calibrated with a polluting carbon peak at 284.5 eV. The grating energy is 400 eV. S 2p XPS fitting was conducted following the spin–orbit splitting effect, with the energy difference of 1.16 eV between S 2p3/2 and S 2p1/2 and a peak area ratio of 2:1 (S2p3/2: S 2p1/2). P2p XPS fitting was conducted following the spin–orbit splitting effect, with the energy difference of 0.87 eV between P 2p3/2 and P 2p1/2 and a peak area ratio of 2:1 (P2p3/2: P 2p1/2). Both S 2p and P 2p XPS fitting were done after subtracting a linear background and deconvoluting by a Gaussian line shape.
4.4. H2S Generation Measurement
A 50 mg pellet of sulfide material was employed in the H2S generation measurement. The pellet was obtained by pressing the powders under 375 MPa. The measurement device is shown in Figures 5a and S8. An H2S sensor, a fan, an H2O sensor, and the pellet sample were put into a 0.9 L sample container. The container was sealed by Parafilm to ensure no leakage occurs from the container. A 43.4% H2SO4 solution was used to prepare the air with 50 RH% in a desiccator of 6.8 L according to the method reported by Wilson.30 Then, the air with 50 RH% humidity of 100 mL was injected into the container. All of the sample preparation processes were operated in an Ar-filled glovebox except the preparation of the humidity air. Each sample was measured for 10 min. The amount of H2S generation was divided by the pellet weight.
4.5. DFT Calculation of Adsorption Energy and Prediction Chemical Shift of 11B-NMR
DFT calculations presented in this work were conducted using the Vienna ab-initio simulation package (VASP) software27,32 with the pseudopotentials of the projector-augmented wave (PAW).28 GGA was applied using the revised PBE functional to describe the electron’s exchange–correlation energy.29,33 The adsorption energy was estimated using DFT-D3, where the energy calculation was performed with D3-correction on the minimum energy structure obtained from an optimization that did not include the correction. For the adsorption energy calculation, one facet was chosen for each sulfide system as our model. The sulfide surfaces were modeled with five-layer slabs, where the two topmost layers and the BBr3 adsorbate were fully relaxed and the rest of the layers were constrained in the optimized lattice. A vacuum of 20 Å was adopted to separate the adjacent slabs. 500 eV plane-wave cutoff energy and a (3 × 3) mesh were used for geometry optimization. The conjugate gradient algorithm was utilized with a convergence threshold of 10–5 eV. The adsorbate and the two uppermost surface layers were allowed to move freely, and the bottom three layers were fixed. Moreover, the adsorption energy Ead is defined as Ead = Eads/slab – Eads – EslabE, where Eads, Eslab, and Eads/slab represent the total energy of the isolated adsorbate, the relaxed clean slab, and the slab covered with adsorbates, respectively.34,35 Moreover, the dipole moment (μ) of BBr3 on each slab was studied at different possible adsorption sites to understand the dipole effect and calculated using the following formula:
where V is the slab volume, ρel is the negative charge density of electrons, qi is the charge of the ith atom, and ri is the position vector of the ith atom.
For the chemical shift of 11B-NMR calculation, the DFT calculations in this research were performed by the Amsterdam Density Functional (ADF) software.36 The geometries of molecular structures were optimized using GGA with the PBE functional.33 The corrections for dispersion forces were considered by Grimme’s D3 model with Becke–Johnson (BJ) damping.37 The triple-zeta polarization (TZP) function was used as the basis set.38 For the calculation of 11B-NMR, the basis sets were chosen from triple-zeta with two polarization functions (TZ2P).38 Besides, the spin–orbit relativistic effect was taken into account for using the zero-order regular approximation (ZORA) throughout the calculations.39,40 The isotropic magnetic shielding constants (σ) of 11B-NMR were derived and translated into chemical shifts (δ) based on the magnetic shielding constants of the reference compounds considered by boron trifluoride-diethyl etherate (BF3-OEt2).41,42
Acknowledgments
Financial support from the National Science and Technology Council of Taiwan (NSTC 111-2639-E-011-001-ASP, 111-2923-E-011-001; 111-2923-E-011-002; MOST 111-3116-F-011-004, 111-3116-F-011-006), the Ministry of Education of Taiwan (MOE U2RSC program 1080059 and “Sustainable Electrochemical Energy Development Center (SEED)” project), Academia Sinica (AS-KPQ-106-DDPP), as well as the supporting facilities from National Taiwan University of Science and Technology (NTUST), National Center for High Performance Computing (NCHC), and National Synchrotron Radiation Research Centre (NSRRC) are all gratefully acknowledged.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.3c00242.
Precursor preparation; computational model and results; 31P-, 11B-NMR, FT-IR, and XPS results; and estimated dipole moment of the adsorbate on various sulfide electrolytes (PDF)
Author Contributions
S.-K.J. and B.J.H. conceived the main idea of the project. S.-K.J. and S.-C.Y. performed the characterization, including XPS, FT-IR analysis, and H2S generation test. S.-C.Y. and Y.N. performed the DFT calculation of adsorption energy. S.-K.J. and S.-J.H. performed the 13B-NMR. K.-Y.L., Y.-H.K., and J.-C.J. did the theoretical calculation of 13B-NMR. B.Y.T., J.-N.L., and S.D.L. assisted to perform FT-IR analysis. S.-K.J. and B.J.H. prepared the manuscript. W.-N.S., S.-H.W., and B.J.H. reviewed and edited the manuscript. All authors participated in experimental data/result analysis and discussion.
The authors declare no competing financial interest.
Supplementary Material
References
- Lee Y.-G.; Fujiki S.; Jung C.; Suzuki N.; Yashiro N.; Omoda R.; Ko D.-S.; Shiratsuchi T.; Sugimoto T.; Ryu S.; et al. High-energy long-cycling all-solid-state lithium metal batteries enabled by silver–carbon composite anodes. Nat. Energy 2020, 5, 299–308. 10.1038/s41560-020-0575-z. [DOI] [Google Scholar]
- Zhang N.; Ding F.; Yu S.; Zhu K.; Li H.; Zhang W.; Liu X.; Xu Q. Novel Research Approach Combined with Dielectric Spectrum Testing for Dual-Doped Li7P3S11 Glass-Ceramic Electrolytes. ACS Appl. Mater. Interfaces 2019, 11, 27897–27905. 10.1021/acsami.9b08218. [DOI] [PubMed] [Google Scholar]
- Tan D. H. S.; Wu E. A.; Nguyen H.; Chen Z.; Marple M. A. T.; Doux J.-M.; Wang X.; Yang H.; Banerjee A.; Meng Y. S. Elucidating Reversible Electrochemical Redox of Li6PS5Cl Solid Electrolyte. ACS Energy Lett. 2019, 4, 2418–2427. 10.1021/acsenergylett.9b01693. [DOI] [Google Scholar]
- Kato Y.; Hori S.; Kanno R. Li10GeP2S12-Type Superionic Conductors: Synthesis, Structure, and Ionic Transportation. Adv. Energy Mater. 2020, 10, 2002153 10.1002/aenm.202002153. [DOI] [Google Scholar]
- Kato Y.; Hori S.; Saito T.; Suzuki K.; Hirayama M.; Mitsui A.; Yonemura M.; Iba H.; Kanno R. High-power all-solid-state batteries using sulfide superionic conductors. Nat. Energy 2016, 1, 16030. 10.1038/nenergy.2016.30. [DOI] [Google Scholar]
- Zhu Y.; Mo Y. Materials Design Principles for Air-Stable Lithium/Sodium Solid Electrolytes. Angew. Chem., Int. Ed. Engl. 2020, 59, 17472–17476. 10.1002/anie.202007621. [DOI] [PubMed] [Google Scholar]
- Kwak H.; Park K. H.; Han D.; Nam K.-W.; Kim H.; Jung Y. S. Li+ conduction in air-stable Sb-Substituted Li4SnS4 for all-solid-state Li-Ion batteries. J. Power Sources 2020, 446, 227338 10.1016/j.jpowsour.2019.227338. [DOI] [Google Scholar]
- Jung W. D.; Jeon M.; Shin S. S.; Kim J. S.; Jung H. G.; Kim B. K.; Lee J. H.; Chung Y. C.; Kim H. Functionalized Sulfide Solid Electrolyte with Air-Stable and Chemical-Resistant Oxysulfide Nanolayer for All-Solid-State Batteries. ACS Omega 2020, 5, 26015–26022. 10.1021/acsomega.0c03453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu Y.; Yu Z.; Zheng A.; Fang H.; Zhang H.; Huang S.-J.; Liu S.-B.; Deng F. Acidic Strengths of Brønsted and Lewis Acid Sites in Solid Acids Scaled by 31P NMR Chemical Shifts of Adsorbed Trimethylphosphine. J. Phys. Chem. C 2011, 115, 7660–7667. 10.1021/jp200811b. [DOI] [Google Scholar]
- Lewis J. D.; Ha M.; Luo H.; Faucher A.; Michaelis V. K.; Román-Leshkov Y. Distinguishing Active Site Identity in Sn-Beta Zeolites Using 31P MAS NMR of Adsorbed Trimethylphosphine Oxide. ACS Catal. 2018, 8, 3076–3086. 10.1021/acscatal.7b03533. [DOI] [Google Scholar]
- Zheng A.; Huang S. J.; Liu S. B.; Deng F. Acid properties of solid acid catalysts characterized by solid-state 31P NMR of adsorbed phosphorous probe molecules. Phys. Chem. Chem. Phys. 2011, 13, 14889–14901. 10.1039/c1cp20417c. [DOI] [PubMed] [Google Scholar]
- Gao P.; Wang Q.; Xu J.; Qi G.; Wang C.; Zhou X.; Zhao X.; Feng N.; Liu X.; Deng F. Brønsted/Lewis Acid Synergy in Methanol-to-Aromatics Conversion on Ga-Modified ZSM-5 Zeolites, As Studied by Solid-State NMR Spectroscopy. ACS Catal. 2018, 8, 69–74. 10.1021/acscatal.7b03211. [DOI] [Google Scholar]
- Koito Y.; Nakajima K.; Hasegawa R.; Kobayashi H.; Kitano M.; Hara M. Lewis acid properties of some metal salts for lactic acid formation in water: 31 P NMR spectroscopy with trimethylphosphine oxide as a molecular probe. Catal. Today 2014, 226, 198–203. 10.1016/j.cattod.2013.10.071. [DOI] [Google Scholar]
- Tricot G.; Alpysbay L.; Doumert B. Solid State NMR: A Powerful Tool for the Characterization of Borophosphate Glasses. Molecules 2020, 25, 428. 10.3390/molecules25020428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Love A. M.; Thomas B.; Specht S. E.; Hanrahan M. P.; Venegas J. M.; Burt S. P.; Grant J. T.; Cendejas M. C.; McDermott W. P.; Rossini A. J.; et al. Probing the Transformation of Boron Nitride Catalysts under Oxidative Dehydrogenation Conditions. J. Am. Chem. Soc. 2019, 141, 182–190. 10.1021/jacs.8b08165. [DOI] [PubMed] [Google Scholar]
- Chen W.-H.; Ko H.-H.; Sakthivel A.; Huang S.-J.; Liu S.-H.; Lo A.-Y.; Tsai T.-C.; Liu S.-B. A solid-state NMR, FT-IR and TPD study on acid properties of sulfated and metal-promoted zirconia: Influence of promoter and sulfation treatment. Catal. Today 2006, 116, 111–120. 10.1016/j.cattod.2006.01.025. [DOI] [Google Scholar]
- Wentink T.; Tiensuu V. H. Vibrational Spectra of BBr3and BI3. J. Chem. Phys. 1958, 28, 826–838. 10.1063/1.1744279. [DOI] [Google Scholar]
- Cho J.Preparation and characterization of B2S3-based chalcogenide glasses. 1995, 194, 10890, 10.31274/rtd-180813-11338. [DOI]
- Gonbeau D.; Bouih H.; Pfister-Guillouzo G.; Menetrier M.; Levasseur A. X-ray photoelectron spectrum of glassy B2S3. Experimental and theoretical study. J. Chem. Soc., Faraday Trans. 1995, 91, 93–97. 10.1039/FT9959100093. [DOI] [Google Scholar]
- Tam J. P.; Heath W. F.; Merrifield R. B. An SN2 deprotection of synthetic peptides with a low concentration of hydrofluoric acid in dimethyl sulfide: evidence and application in peptide synthesis. J. Am. Chem. Soc. 1983, 105, 6442–6455. 10.1021/ja00359a014. [DOI] [Google Scholar]
- Bauer L.; Anderson H. J. Comments on the Treatment of Aromaticity and Acid-Base Character of Pyridine and Pyrrole in Contemporary Organic Chemistry Textbooks. J. Chem. Educ. 1999, 76, 1151. 10.1021/ed076p1151. [DOI] [Google Scholar]
- Kuhn A.; Gerbig O.; Zhu C.; Falkenberg F.; Maier J.; Lotsch B. V. A new ultrafast superionic Li-conductor: ion dynamics in Li11Si2PS12 and comparison with other tetragonal LGPS-type electrolytes. Phys. Chem. Chem. Phys. 2014, 16, 14669–14674. 10.1039/c4cp02046d. [DOI] [PubMed] [Google Scholar]
- Seino Y.; Nakagawa M.; Senga M.; Higuchi H.; Takada K.; Sasaki T. Analysis of the structure and degree of crystallisation of 70Li2S–30P2S5 glass ceramic. J. Mater. Chem. A 2015, 3, 2756–2761. 10.1039/c4ta04332d. [DOI] [Google Scholar]
- Kuhn A.; Duppel V.; Lotsch B. V. Tetragonal Li10GeP2S12 and Li7GePS8 – exploring the Li ion dynamics in LGPS Li electrolytes. Energy Environ. Sci. 2013, 6, 3548. 10.1039/c3ee41728j. [DOI] [Google Scholar]
- Yamane H.; Shibata M.; Shimane Y.; Junke T.; Seino Y.; Adams S.; Minami K.; Hayashi A.; Tatsumisago M. Crystal structure of a superionic conductor, Li7P3S11. Solid State Ionics 2007, 178, 1163–1167. 10.1016/j.ssi.2007.05.020. [DOI] [Google Scholar]
- Zhang Q.; Cao D.; Ma Y.; Natan A.; Aurora P.; Zhu H. Sulfide-Based Solid-State Electrolytes: Synthesis, Stability, and Potential for All-Solid-State Batteries. Adv. Mater. 2019, 31, e1901131 10.1002/adma.201901131. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter 1993, 47, 558–561. 10.1103/physrevb.47.558. [DOI] [PubMed] [Google Scholar]
- Blochl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter 1994, 50, 17953–17979. 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
- Wilson R. E. Humidity Control by Means of Sulfuric Acid Solutions, with Critical Compilation of Vapor Pressure Data. J. Ind. Eng. Chem. 1921, 13, 326–331. 10.1021/ie50136a022. [DOI] [Google Scholar]
- Tan D. H. S.; Banerjee A.; Deng Z.; Wu E. A.; Nguyen H.; Doux J.-M.; Wang X.; Cheng J.-H.; Ong S. P.; Meng Y. S.; Chen Z. Enabling Thin and Flexible Solid-State Composite Electrolytes by the Scalable Solution Process. ACS Appl. Energy Mater. 2019, 2, 6542–6550. 10.1021/acsaem.9b01111. [DOI] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Wei X.; Dong C.; Chen Z.; Xiao K.; Li X. A DFT study of the adsorption of O2 and H2O on Al(111) surfaces. RSC Adv. 2016, 6, 56303–56312. 10.1039/c6ra08958e. [DOI] [Google Scholar]
- Gao W.; Chen Y.; Li B.; Liu S. P.; Liu X.; Jiang Q. Determining the adsorption energies of small molecules with the intrinsic properties of adsorbates and substrates. Nat. Commun. 2020, 11, 1196. 10.1038/s41467-020-14969-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Van Lenthe E.; Baerends E. J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
- Autschbach J. Two-component relativistic hybrid density functional computations of nuclear spin-spin coupling tensors using Slater-type basis sets and density-fitting techniques. J. Chem. Phys. 2008, 129, 094105 10.1063/1.2969100. [DOI] [PubMed] [Google Scholar]
- Autschbach J. Erratum: Two-component relativistic hybrid density functional computations of nuclear spin-spin coupling tensors using Slater-type basis sets and density-fitting techniques [J. Chem. Phys. 129, 094105 (2008)]. J. Chem. Phys. 2009, 130, 209901. 10.1063/1.3131724. [DOI] [PubMed] [Google Scholar]
- Autschbach J.; Patchkovskii S.; Pritchard B. Calculation of Hyperfine Tensors and Paramagnetic NMR Shifts Using the Relativistic Zeroth-Order Regular Approximation and Density Functional Theory. J. Chem. Theory Comput. 2011, 7, 2175–2188. 10.1021/ct200143w. [DOI] [PubMed] [Google Scholar]
- Huang C.-J.; Lin K.-Y.; Hsieh Y.-C.; Su W.-N.; Wang C.-H.; Brunklaus G.; Winter M.; Jiang J.-C.; Hwang B. J. New Insights into the N–S Bond Formation of a Sulfurized-Polyacrylonitrile Cathode Material for Lithium–Sulfur Batteries. ACS Appl. Mater. Interfaces 2021, 13, 14230–14238. 10.1021/acsami.0c22811. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




