The box-circle illusion

Abstract

A novel geometrical optical illusion is reported in this article: the horizontal distances of the contextual structures distort the perceived vertical positions of observed objects. Specifically, the illusion manifests in the form of connected boxes of varying widths but equal heights, each containing a circle at the center. Despite identical vertical positioning of the circles, they appear misaligned. The illusion diminishes when the boxes are removed. Potential underlying mechanisms are discussed.

Many geometrical optical illusions have been documented on length (Müller–Lyer illusion, vertical–horizontal illusion, and Ponzo illusion), orientation (café wall illusion, Zöllner illusion, and corner effect), size (Delboeuf illusion and Ebbinghaus illusion), position (Poggendorff illusion), and parallelism (Hering illusion). In these illusions, a particular aspect of a line image distorts the perception of another aspect. For instance, the Poggendorff illusion, illustrated in Figure 1A, features an obscuring structure at the front, which perturbs the perceived position of the continuation of the traversing line (Ponzo, 1910), possibly due to constancy misapplication (Green & Hoyle, 1963) or acute angle expansion (Morgan, 1999). In the Hering illusion, illustrated in Figure 1B, a radiating pattern in the background distorts the perceived straightness and parallelism of the two lines in the foreground, potentially due to angle overestimation or background optic flows (Hering, 1861; Vaughn & Eagleman, 2013). Lateral inhibition within the visual cortex and probability distribution statistics of real-world visual sources have been proposed as underlying mechanisms to explain these illusions (Howe & Purves, 2005).

Figure 1.

(A) An example of the Poggendorff illusion and (B) an example of the Hering illusion.

Here we report a novel illusion that, unlike previous geometrical illusions, does not necessarily involve angles formed by converging lines or lines and boundaries. The illusion, hereafter termed the box-circle illusion, is composed of horizontally connected boxes of differing widths but equal heights, each containing a circle of the same size. Despite the circles being positioned at the same vertical level, they appear to be at different heights to the observer. An example of this illusion is shown in Figure 2A. The illusion seems to reduce when the boxes are removed, illustrated in Figure 2B.

Figure 2.

The box-circle illusion. (A) The vertical positions of the circles in the boxes appear to be different while they are actually the same. (B) The illusion is reduced without the boxes. (C) Aligned circles with equal distances as control.

Twenty one participants (16 females, ranging from 15 to 25 years of age, mean age = 20.05 years) were recruited for an experiment to examine the illusion. Stimuli were presented using PsychoPy (Peirce et al., 2019) on a Sony Trinitron Multiscan CPD-200 ES monitor with a refresh rate of 120 Hz and an iOS 12.1 operating system. Participants sat ∼ 50 cm away from the screen.

To disguise the illusion condition, a total of 24 different visual patterns were included. Specifically, 12 of the patterns comprised circles only, while the other 12 contained both the circles and boxes. Each set of 12 patterns was further segregated into two groups of 6, with one group having equal spacing between the circles and the other featuring unequal spacing. Further, each set of 6 patterns was then subdivided into 3 horizontal and 3 vertical patterns. Each group of 3 patterns had three degrees of misalignment, namely level 0, level 3, and level 10. Each of the 24 patterns was presented to subjects 10 times, leading to a total of 240 trials. The presentation order of the patterns was fully randomized. Participants viewed visual patterns for 1 s and rated them on a scale from 0 to 10, denoting different degrees of perceived misalignment within the patterns. Participants were given instructions to rate the degree of misalignment using an illustration depicting the aforementioned three levels at the onset of the experiment (Figure 3).

Figure 3.

Participant instruction for misalignment ratings at the onset of the experiment. The illustrated three levels of misalignment (levels 0, 3, and 10) were artificially generated. (A) Example pattern for a misalignment rating of 0. (B) Example pattern for a misalignment rating of 3, and (C) Example pattern for a misalignment rating of 10.

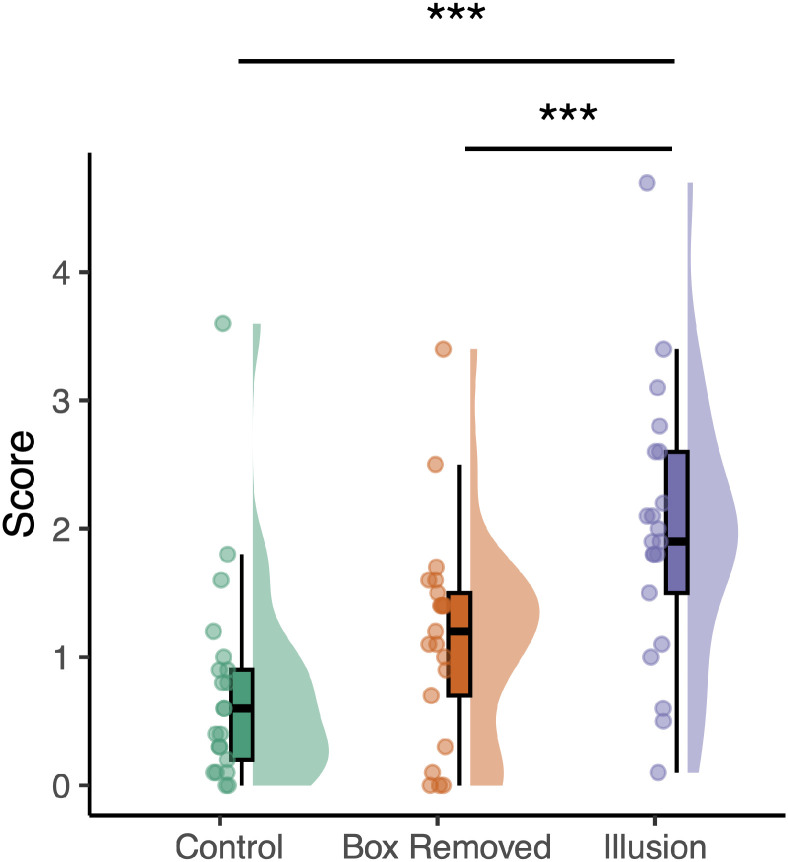
Paired one-tailed t-tests were conducted to compare the original illusory pattern (Figure 2A) with the control pattern (Figure 2C), as well as with its version where the boxes were removed (Figure 2B). For each test, a Bonferroni-adjusted alpha level of 0.025 (0.05/2) was applied. The misalignment ratings for the original illusory pattern (M = 1.98, SEM = 0.22) were significantly higher than those for the control pattern (M = 0.75, SEM = 0.18) (t[20] = 5.10, p < .001, Cohen's d_z= 1.14) and were significantly higher than those for the version with the boxes removed (M = 1.16, SEM = 0.18) (t[20] = 3.92, p < .001, Cohen's d_z= 0.86) (Figure 4).

Figure 4.

Distribution of mean misalignment ratings for the control pattern (left) (Figure 2C), the original illusory pattern (right) (Figure 2A), and the version of the illusory pattern with the boxes removed (middle) (Figure 2B). One-tailed paired t-test showed that the misalignment ratings for the original illusory pattern were significantly higher than those for the control pattern (p < .001) or those for the version with the boxes removed (p < .001).

A four-way repeated measures ANOVA was performed to analyze the effects of boxes (present or absent), pattern orientations (horizontal or vertical), distances between circles (equal or unequal), and levels of misalignment (levels 0, 3, and 10). Results showed main effects of only boxes (F[1, 20] = 17.70, p < .001) and levels of misalignment (F[1, 20] = 304.50, p < .001), with the presence of boxes and higher levels of misalignment found to contribute to increased misalignment ratings. No significant interaction was found. The subject-level mean ratings for all conditions examined, as well as the 24 patterns used in the experiment, can be found in this public repository: https://osf.io/375df/.

In the box-circle illusion, the horizontal distances of the visual contexts (the boxes) distort the vertical positions of the perceived objects (the circles), with no physical contact between the two. In this regard, the illusion differs from previous ones regarding orientation and position, such as the café-wall illusion or Poggendorff illusion, which usually involve contacts between the contextual structures and the illusion-generating structures. The observation that the removal of boxes reduces the illusory effect implies the necessity of the contextual structures in generating the illusion, potentially by facilitating perceptual unit segmentation. Contrary to our expectations, we did not find any main effect of the distances between circles. It is possible that this effect was masked by other factors, such as the different levels of misalignment (levels 0, 3, and 10). In fact, a post-hoc paired t-test revealed that when the circles are aligned (at level 0), horizontal patterns with boxes and unequal distances between circles (Figure 2A) (M = 1.98, SEM = 0.23) showed significantly higher misalignment ratings compared to those with boxes but equal distances between circles (M = 1.19, SEM = 0.14) (t[20] = 5.38, p < 0.001, Cohen's d_z= 1.17). Future studies should investigate the effects of the distances between circles specifically when the circles are aligned or only mildly misaligned.

The human visual system tends to perceive objects with smaller retinal sizes as farther away, while objects with larger retinal sizes as closer. Depending on the observer's viewpoint, the visual system also appears to hold priors associating perceived distance and the location in the visual field, as demonstrated in Figure 5. More specifically, Figure 5B and E shows the accidental views where the observer's viewpoint must be exactly in front of the boxes to perceive them as aligned. In contrast, Figure 5A, C, D, and F shows the generic views that occur much more frequently. In these views, boxes that are farther away appear shifted in the visual field. The visual system holds a bias towards perceiving generic views, based on real-life viewing experiences, as they occur more often than accidental views. Such 3D rules are usually inverted to interpret 2D images (Ooi et al., 2001; Wolfe et al., 2006). One possible explanation for the illusion is that if each box, together with the circle inside it, is perceived as a 2D unit projected from a 3D object in the environment, narrower box-widths would typically imply further distances. Consequently, the perceptual system utilizes its associations between object distance judgment and location in the visual field to generate priors regarding the circle's location in 2D images. Specifically, narrower widths generate priors of visual sources located farther away, which in turn generate priors, based on the aforementioned bias towards generic views, of a potential location shift (direction not determined) in the visual field. Future studies could compare patterns in 3D box settings with different viewing perspectives to test this hypothesis.

Figure 5.

An illustration with cubes of the associations between object distance and location in the visual field. (A) A visual perspective to the front and to the left shows that the further box is shifted to the left in the visual field. (B) A visual perspective to the front shows that the two boxes are aligned in the visual field. (C) A visual perspective to the front and to the right shows that the further box is shifted to the right in the visual field. (D) A visual perspective looking down towards the front shows that the further box is shifted upwards in the visual field. (E) A visual perspective to the front shows that the two boxes are aligned in the visual field. (F) A visual perspective looking up towards the front shows that the further box is shifted downwards in the visual field.

Another hypothesis is that, in the illusion, the vertical lines between boxes may impede perceptual fluency as one's eyes move horizontally or vertically to view the image, potentially leading to eye movements that generate the illusory effect observed. This hypothesis could be examined by presenting the illusions for a shorter duration than necessary for the initiation of saccades to explore the necessity of eye movements. Further research is needed to better understand the underlying mechanisms and how one may explain the illusion based on statistics from real-life viewing experiences.