Dynamic prediction of competing risk events using landmark sub-distribution hazard model with multiple longitudinal biomarkers

Abstract

The cause-specific cumulative incidence function (CIF) quantifies the subject-specific disease risk with competing risk outcome. With longitudinally collected biomarker data, it is of interest to dynamically update the predicted CIF by incorporating the most recent biomarker as well as the cumulating longitudinal history. Motivated by a longitudinal cohort study of chronic kidney disease, we propose a framework for dynamic prediction of end stage renal disease using multivariate longitudinal biomarkers, accounting for the competing risk of death. The proposed framework extends the local estimation based landmark survival modeling to competing risks data, and implies that a distinct sub-distribution hazard regression model is defined at each biomarker measurement time. The model parameters, prediction horizon, longitudinal history and at-risk population are allowed to vary over the landmark time. When the measurement times of biomarkers are irregularly spaced, the predictor variable may not be observed at the time of prediction. Local polynomial is used to estimate the model parameters without explicitly imputing the predictor or modeling its longitudinal trajectory. The proposed model leads to simple interpretation of the regression coefficients and closed-form calculation of the predicted CIF. The estimation and prediction can be implemented through standard statistical software with tractable computation. We conducted simulations to evaluate the performance of the estimation procedure and predictive accuracy. The methodology is illustrated with data from the African American Study of Kidney Disease and Hypertension.

1. Introduction

Patients with chronic kidney disease (CKD) are at increased risk of end stage renal disease (ESRD). Accurate prediction of the timing is of great importance in clinical research and practice to facilitate preparation for renal replacement therapy and individualize clinical decisions.¹ The typical ESRD risk equations are “static” prediction models in the sense that they are developed from survival regression models that relate the predictors at an earlier time point, such as baseline, to the time of ESRD.^2,3 Longitudinal data of those biomarkers between baseline and the terminal event are often available and potentially informative to the disease progression, but they are not used in prediction model development.

In statistical literature, the prediction of the risk of clinical events using longitudinal data is often referred to as dynamic prediction in the sense that the prediction can be updated with accumulating longitiudinal data. Important fundamental work has been published in the last decade.^4–9 There are a number of challenges when this methodology is applied to the prediction of ESRD among CKD population. First, CKD patients have increased chance of mortality before reaching ESRD. Proper adjustment for competing risk is often needed in CKD studies.¹⁰. Second, previous literature has identified a large number of risk factors, including multiple biomarkers that are known to be causally associated with ESRD.¹ Put in the longitudinal context, it requires that the dynamic prediction model should accommodate multiple biomarkers with tractable computation. Some biomarkers, such as the estimated GFR, have diverse nonlinear progression trajectories.^11,12 This feature could add to the complexity of the statistical analysis if modeling subject-specific longitudinal trajectories is needed. Third, it may take many years before a CKD patient reaches ESRD or death. The strength of association between biomarkers and the disease outcome may vary over time, leading to time-varying effects. Fourth, it is common that patients do not always follow a pre-specified clinical visits schedule. Even if the visit times are non-informative in the sense that they are not related to the health condition of the patients, the irregularly spaced and unsynchronized biomarker measurement times pose a challenge to the development of dynamic prediction model, as elucidated below.

On the topic of dynamic prediction with competing risks data, Bayesian Markov chain Monte Carlo methods have been developed to model the joint distribution of longitudinal data and competing risks with shared random effects.^13,14 However, when a large number of random effects are needed to accommodate multiple and possibly nonlinear longitudinal trajectories per subject, fitting the joint model is computationally infeasible.¹⁵ An alternative, computationally simpler dynamic prediction approach called landmark modeling⁴ has been applied to competing risk problems.^16–20 These methods adapted to the dynamic prediction setup some existing competing risk regression models, such as cause-specific hazard model¹⁷, pseudo-observations¹⁸, multi-state model¹⁶, and the Fine-Gray subdistribution hazard model^19,20. The Fine-Gray model²¹ imposes a parsimonious relationship between predictors and the cumulative incidence function (CIF) of ESRD without a separate model for death, which is difficult to establish due to the heterogeneity in the causes of death. Based on this consideration, we extended our previous work²² to a landmark sub-distribution hazard model with the following flexibilities: the baseline sub-distribution hazard function is a bivariate function of both the landmark time and the survival time without pre-specified functional structure; all the model parameters are estimated nonparametrically in a coherent local polynomial estimation framework. In a related recent work, Liu et al^19,20 extended the idea of “Super Cox model”⁴ to a landmark sub-distribution hazard model for competing risk data. Motivated by the specific needs of CKD research, our proposed methodology in this paper is also different from the aforementioned literature in how the landmark times are selected and how the irregularly spaced longitudinal data are handled. The typical landmark approach involves pre-specifying a number of landmark time points distributed over the follow-up period, creating a landmark dataset at each landmark time point that consists of at-risk subjects and their predictor variables and time-to-event, and fitting the model to the stacked landmark datasets.^4,17,19,20. The predictor variable is not always measured at the landmark times due to irregularly spaced and unsynchronized measurement times. Imputing the unknown value by the last or closest measurement is difficult to apply because that measurement could be years apart and because the progression of CKD includes both chronic periods, when biomarkers change slowly, and acute episodes, when biomarkers change more quickly. Our proposed method does not require pre-specification of the landmark times, which is important given that there is currently no guideline in the literature on how to set the number and locations of the landmark times. It can also accommodate the irregularly spaced observational times without explicit imputation.

This paper is organized as follows. In section 2, we introduce the dynamic prediction model for competing risk data. In section 3, we provide model estimation procedures for the quantities of interest. In section 4 we propose estimators of predictive accuracy measures within the dynamic competing risk context. In section 5, we conduct numerical studies to evaluate the performance of the proposed methodology. The application to the AASK data is presented in section 6. Discussion and future work are presented in section 7.

2. The landmark dynamic prediction model for competing risks data

2.1. The notation and data structure

Let $T_i$ and $C_i$ be the time to event and censoring for subject $i$, and ${ϵ}_i\in \{1,\dots ,K\}$ be the $K$ causes of the event. We observe the follow-up time ${\tilde{T}}_i=\text{min}\left(T_i,C_i\right)$, the censoring indicator ${\Delta }_i=1\left(T_i\le C_i\right)$, and the observed event type ${\Delta }_i{ϵ}_i\in \{0,\dots ,K\}$. Without loss of generality, we assume $K=2$ throughout this paper. In the context of the data application, event 1 denotes ESRD, the clinical event of interest, and event 2 denotes death, the competing event. Let the $n_i\times q$ matrix ${\mathit{Y}}_i=\left[{\mathit{Y}}_{i1},{\mathit{Y}}_{i2},\dots ,{\mathit{Y}}_{iq}\right]$ denote the repeated measured covariates for subject $i$, i.e. $q$ covariates with each measured $n_i$ times. The matrix notation ${\mathit{Y}}_i$ covers both time-dependent (longitudinal) and time-independent (baseline) covariates. Each column of this matrix includes the $n_i$ repeated measurements of that variable at time points ${\mathit{t}}_i={\left(t_{i1},t_{i2},\dots t_{i{n}_i}\right)}^T$, where all $t_{ij}<{\tilde{T}}_i$. We use the scalar variable $Y_{imj}$ to denote the $j$-th repeated measure $\left(j=\mathrm{1,2},\dots ,n_i\right)$ of the $m$-th covariate $(m=\mathrm{1,2},\dots ,q)$ from the $i$-th subject $(i=\mathrm{1,2},\dots ,n)$. Hence ${\mathit{Y}}_{im}={\left(Y_{im1},Y_{im2},\dots ,Y_{im{n}_i}\right)}^T$. For ease of presentation, we will also express $Y_{imj}=Y_{im}\left(t_{ij}\right)$, i.e., subject $i$’s $m$-th covariate measured at time $t_{ij}$ is the value of the trajectory function $Y_{im}(.)$ at that time.We assume that the distribution of ${\mathit{t}}_i$ is non-informative in the sense that it is independent of ${\mathit{Y}}_i$ and $T_i$. We assume independent censoring in the sense that $C$ is conditionally independent of $T$ and $ϵ$ given the baseline covariates. We observe independent and identically distributed training data ${𝒟}_n=\left\{{\tilde{T}}_i,{\Delta }_i{ϵ}_i,{\mathit{Y}}_i,{\mathit{t}}_i,i=1,\dots ,n\right\}$, from which the dynamic prediction model is to be developed. Our interest is to estimate the probability of event 1 (e.g., ESRD) in the next ${\tau }_1$ years (called prediction horizon) for a generic individual, indexed by subscript ${}_o$, given the covariates and survival up to time $s:P\left(T_o\in \left(s,s+{\tau }_1\right],{ϵ}_o=1\mid {\tilde{T}}_o>s,\overline{{\mathit{Y}}_o\left(s\right)}\right)$, where $\overline{{\mathit{Y}}_o\left(s\right)}=\left\{t_{oj},Y_{o1j},Y_{o2j},\dots ,Y_{oqj}\mid 1⩽j⩽\right.$ $n_o$ and $\left.t_{oj}⩽s\right\}$ denotes the covariate history prior to $s$ for subject ${}_o$.

In the following, we describe the construction of landmark dataset. We use notation $T\left(s\right)=T-s$ to denote the residual lifetime when a generic subject is at risk at time $s$, and $\overline{\mathit{Y}\left(s\right)}$ to denote covariate history up to $s$, as defined above. For subject $i$ in the development dataset, we define $T_{ij}=T_i-t_{ij}$ and $C_{ij}=C_i-t_{ij}$ as the subject-specific residual times to event and censoring, starting from $t_{ij}$. For prediction up to the horizon ${\tau }_1$, we can artificially censor the residual times at ${\tau }_1$, i.e., we observe ${\tilde{T}}_{ij}=\text{min}\left(T_{ij},C_{ij},{\tau }_1\right)$ and the event indicator ${\tilde{\delta }}_{ij}=1\left(T_{ij}\le \text{min}\left(C_{ij},{\tau }_1\right)\right)\times {ϵ}_i$, where 1(⋅) is the indicator function. The artificial censoring helps to reduce the chance of misspecifying certain model assumptions⁴. Throughout this paper, we focus on modeling the relationship between $T\left(s\right)$ and $\overline{\mathit{Y}\left(s\right)}$ at any landmark time $s$. In the model development dataset, $T\left(s\right)$ and $\overline{\mathit{Y}\left(s\right)}$ are observed at the longitudinal measurement times $t_{ij}\left(i=\mathrm{1,2},\dots ,n,j=\mathrm{1,2},\dots ,n_i\right)$, leading to the observed outcome and predictor pairs $\left\{{\tilde{T}}_{ij},{\tilde{\delta }}_{ij},{\tilde{\mathit{Y}}}_i\left(t_{ij}\right)\right\}$. Here the notation ${\tilde{\mathit{Y}}}_i\left(t_{ij}\right)$ denotes the vector of predictors at time $t_{ij}$ for the corresponding residual lifetime; this vector includes features of the longitudinal history $\overline{\mathit{Y}\left(s\right)}$ that are selected as predictors. These features can be viewed as functions of $\overline{\mathit{Y}\left(s\right)}$. Therefore, we also call $t_{ij}$ as the landmark time as they are the starting time of the residual lifetime outcome. When making a prediction, the new prediction is often made when new measurements become available, i.e., at a new $t_{ij}$ of that subject. From this perspective, the prediction time is also called a landmark time.

2.2. Sub-distribution hazard model with baseline covariates

We first briefly review the sub-distribution hazard (SDH) model for competing risks²¹ with baseline covariates $\mathit{X}$. For prediction, the quantity of interest is the cumulative incidence function (CIF) at time $t^{*}$ given $\mathit{X}:{\pi }_1\left(t^{*};\mathit{X}\right)=P\left(T\le t^{*},ϵ=1\mid \mathit{X}\right)$. Under Fine and Gray’s formulation, this CIF is formulated as

$$P\left(T\le t^{*},ϵ=1\mid \mathit{X}\right)=1-exp\left(-{\int }_0^{t^{*}}{\lambda }_1\left(t\mid \mathit{X}\right)dt\right)$$ (1)

with ${\lambda }_1(t\mid \mathit{X})={\lambda }_{10}\left(t\right)\text{exp}\left({\mathit{\alpha }}^T\mathit{X}\right)$, where ${\lambda }_{10}\left(t\right)$ can be any non-negative function of time $t>0$ and $\mathit{\alpha }$ is a real vector. Fine and Gray further developed an interpretation for the ${\lambda }_1(t\mid \mathit{X})$ function. They showed that it can be interpreted as a sub-distribution hazard, in the sense that ${\lambda }_1(t;\mathit{X})={\text{lim}}_{\Delta t\to 0} \frac{1}{\Delta t}P(t\le T\le t+\Delta t,ϵ=1\mid \{T\ge t\}\cup \{T\le t\cap ϵ\ne 1\},\mathit{X})=-\frac{d\text{log}\left(1-{\pi }_1(t;\mathit{X})\right)}{dt}$. Such a definition can be viewed as the hazard function for an improper random variable $1(ϵ=1)\times T+1(ϵ\ne 1)\times \mathrm{\infty }$. This interpretation also helps the development of an estimation procedure that is analogous to that of the Cox model.

As far as prediction is of concern, characterizing the bilateral relationship between time to event $T$ $(ϵ=1)$ and the covariate vector $\mathit{X}$ is all that is needed. The sub-distribution hazard value at a time $t$ $(t>0)$ is not of direct relevance to this prediction. The sub-distribution hazard function ${\lambda }_1(t\mid \mathit{X})$ serves as the internal machinery that helps the estimation of model (1). This is a key observation that motivates the working model in the next subsection.

2.3. Landmark proportional sub-distribution hazard model

By extending model (1) to the context of dynamic prediction, we propose the following landmark proportional SDH model at landmark time $s$:

$$P\left(T\left(s\right)\le t^{*},ϵ=1\mid \overline{\mathit{Y}\left(s\right)},T>s\right)=1-exp\left(-{\int }_0^{t^{*}}{\lambda }_1\left(t\mid \tilde{\mathit{Y}}\left(s\right),s\right)dt\right).$$ (2)

As the notation on the left hand side of (2) suggests, at any given landmark time $s$, this model is specified for those subjects still at risk $(T>s)$ at that time. If we treat the given $s$ as a new baseline, then this model is equivalent to a model (1) specified for the residual life time $T\left(s\right)$ among the at-risk subjects at time $s$, given the history $\overline{\mathit{Y}\left(s\right)}$. Since there are in theory infinitely many landmark time $s$, model (2) is formulated under the working assumption that these models hold simultaneously. For a specific landmark dataset $\left\{{\tilde{T}}_{ij},{\tilde{\delta }}_{ij},{\tilde{\mathit{Y}}}_i\left(t_{ij}\right),t_{ij};i=1,\dots ,n,j=1,\dots ,n_i\right\}$, this model implies that the bilateral relationship between each residual time to event $\left({\tilde{T}}_{ij},{\tilde{\delta }}_{ij}\right)$ and the corresponding “baseline” predictor variables ${\tilde{\mathit{Y}}}_i\left(t_{ij}\right)$ satisfies model (2) at the corresponding landmark time $s=t_{ij}$. To fit this model, we define a working SDH function as:

$${\lambda }_1\left(t^{*}\mid {\tilde{\mathit{Y}}}_i\left(t_{ij}\right),t_{ij}\right)={\lambda }_{10}\left(t^{*},t_{ij}\right)\text{exp}\left({\mathit{\beta }}^T\left(t_{ij}\right){\tilde{\mathit{Y}}}_i\left(t_{ij}\right)\right),t^{*}\in \left(0,{\tau }_1\right],$$ (3)

where ${\lambda }_{10}\left(t^{*},t_{ij}\right)$ is a bivariate smooth baseline SDH function, defined on the scale of the residual lifetime $t^{*}\in \left(0,{\tau }_1\right]$ and landmark time $t_{ij}$. The time-varying coefficients $\mathit{\beta }(.)$ are assumed to besmooth functions to allow the association to vary with the landmark time. For the bilateral relationship between $\left({\tilde{T}}_{ij},{\tilde{\delta }}_{ij}\right)$ and ${\tilde{\mathit{Y}}}_i\left(t_{ij}\right)$, the corresponding value of the coefficient function is $\mathit{\beta }\left(t_{ij}\right)$.

Our landmark dataset construction resembles that in the partly conditional model⁷, which resets the follow-up time scale at each measurement time. From this perspective, the basic idea of the proposed methodology is more closely related to that model than the “super Cox model” type approaches^5,19,20. However, besides the accommodation of competing risk outcome, another difference between our approach and Zheng and Heagerty’s⁷ is that the time-varying coefficients are functions of the landmark time $t_{ij}$ instead of the derived follow-up time $t^{*}$. Therefore it differs from the usual time-varying coefficient model in survival analysis that is commonly used to deal with non-proportional hazards²³. With the artificial censoring at ${\tau }_1$, the covariate effect is more likely to be constant over $t^{*}\in \left(0,{\tau }_1\right)$ (but still vary with $t_{ij}$) and the proportional sub-distribution assumption is more likely to hold.²⁴.

Model (3) is called a “working” sub-distribution hazard function because it is used to facilitate the model fitting using the estimating equations developed by Fine and Gray²¹. While it implies that a subject’s residual sub-distribution hazard at landmark time $s$ is ${\lambda }_1\left(t^{*}=0\mid \overline{\mathit{Y}\left(s\right)},s\right)$, it does not imply that this subject’s sub-distribution hazard at time $s+t^{*}\left(t^{*}>0\right)$ given the history $\overline{\mathit{Y}\left(s\right)}$, is still given by (3). The hazard at time $s+t^{*}$ depends on $\overline{\mathit{Y}\left(s+t^{*}\right)}$. In general, the hazard at time $s+t^{*}$ conditional on $\overline{\mathit{Y}\left(s\right)}$ depends on both the hazard at time $s+t^{*}$ conditional on $\overline{\mathit{Y}\left(s+t^{*}\right)}$ and the conditional distribution of the paths of longitudinal predictors $\tilde{\mathit{Y}}\left(u\right)\left(u\in \left(s,s+t^{*}\right)\right)$ given $\overline{\mathit{Y}\left(s\right)}$. This is elucidated by the concept of consistency²⁵. Like other landmark (or partly conditional) models, the proposed model has not been proven as a consistent prediction model. However, this working model can still be a useful prediction tool as long as (2) provides a good approximation to the bilateral relationship between $\left({\tilde{T}}_{ij},{\tilde{\delta }}_{ij}\right)$ and ${\tilde{\mathit{Y}}}_i\left(t_{ij}\right)$.

3. Model estimation and dynamic prediction of the CIF

For estimation, we extend the kernel approach in Li et al²² to the competing risk context and formalize the idea of borrowing information from lagging covariates^26,27. Assume that $\mathit{\beta }\left(.\right)$ has a continuous second derivative in a neighborhood of $s$, by local linear approximation, $\mathit{\beta }\left(t_{ij}\right)\approx \mathit{\beta }\left(s\right)+{\mathit{\beta }}^{\prime }\left(s\right)\left(t_{ij}-s\right)$ for subject-specific time points $t_{ij}$ around $s$. The landmark dataset ${ℒ}_m$ are clustered multivariate time-to-event data with competing events, where the $n_i$ records from the same subject are correlated. For clustered competing risk data²⁸, we define the counting process for event 1 as $N_{ij}\left(t^{*}\right)=1\left(t_{ij}\le T_i\le \right.\left.t_{ij}+t^{*},{\tilde{\delta }}_{ij}=1\right)$ and the at-risk process $R_{ij}\left(t^{*}\right)=1-N_{ij}\left(t^{*}-\right)=1\left(T_i>t_{ij}+t^{*}\right)+1\left(t_{ij}\le T_i\le \right.\left.t_{ij}+t^{*},{\tilde{\delta }}_{ij}\ne 1\right)$. Based on a local “working independence” partial likelihood function^28, for any given landmark point $s$, we can estimate the parameters $\mathit{\beta }\left(s\right)$ using a kernel-weighted estimation equation, by borrowing biomarker measurements from the neighboring time points, $\left\{t_{ij}\in (s-h,s+h)\right\}$:

$$\sum _{i=1}^n\sum _{j=1}^{n_i}{K}_h\left(t_{ij}-s\right){\int }_0^{t^{*}}{w}_{ij}\left(t\right)\cdot \left\{{\tilde{\mathit{Z}}}_{ij}\left(1,t_{ij}-s\right)-\overline{\mathit{Z}}\left(\mathit{\beta }\left(s\right),t\right)\right\}\cdot \text{d}{N}_{ij}\left(t\right).$$ (4)

In the above expression, $K(\cdot )$ is a kernel function with bounded support on $[-\mathrm{1,1}];K_h\left(x\right)=h^{-1}K(x/h)$ and $h$ is the bandwidth; ${\tilde{\mathit{Z}}}_{ij}\left(1,t_{ij}-s\right)={\tilde{\mathit{Y}}}_i\left(t_{ij}\right)\otimes \left(1,t_{ij}-s\right)$ with $\otimes$ denoting the Kronecker product. In addition, we have the notations $\overline{\mathit{Z}}\left(\mathit{\beta }\right(s),t)=\frac{{\stackrel{\mathit{ˆ}}{\mathit{S}}}^{\left(1\right)}\left(\mathit{\beta }\right(s),t)}{{\stackrel{\mathit{ˆ}}{\mathit{S}}}^{\left(0\right)}\left(\mathit{\beta }\right(s),t)}$, and

$$\begin{gathered} {\widehat{\mathit{S}}}^{\left(r\right)}\left(\mathit{\beta }\left(s\right),t\right)=n^{-1}\sum _{i=1}^n\sum _{m=1}^{n_i}{K}_h\left(t_{im}-s\right)w_{im}\left(t\right)R_{im}\left(t\right)\times {\tilde{\mathit{Z}}}_{im}{\left(1,t_{im}-s\right)}^{\otimes r} \\ \times \text{exp}\left({\mathit{b}}^T\left(s\right){\tilde{\mathit{Z}}}_{im}\left(1,t_{im}-s\right)\right), \end{gathered}$$

where $\mathit{b}\left(s\right)={\left({\mathit{b}}_0(s{)}^T,{\mathit{b}}_1(s{)}^T\right)}^T$ is used to estimate $\mathit{\beta }\left(s\right)$ and ${\mathit{\beta }}^{\prime }\left(s\right)$ respectively. ${\tilde{\mathit{Z}}}^{\otimes 0}=1$ and ${\tilde{\mathit{Z}}}^{\otimes 1}=\tilde{\mathit{Z}}$. The $w_{ij}\left(t\right)$ in (4) denotes the inverse probability censoring weight for competing events²¹:

$$w_{ij}\left(t\right)=1\left(C_{ij}\ge T_{ij}\wedge t\right)\frac{G\left(t\mid s\right)}{G\left(T_{ij}\wedge t\mid s\right)},$$

where $\wedge$ denotes the minimum of the two values and $G(\cdot \mid s)$ denotes the distribution of the residual censoring time at landmark $s$. This distribution is estimated by a kernel-weighted Kaplan-Meier estimator:

$$\widehat{G}\left(t\mid s\right)=\prod _{\zeta \in \Omega ,\zeta \le t}\left\{1-\frac{{\sum }_{im}{K}_h\left(t_{im}-s\right)\cdot 1\left({\tilde{C}}_{im}=\zeta ,{\tilde{\delta }}_{im}=0\right)}{{\sum }_{im}{K}_h\left(t_{im}-s\right)\cdot 1\left({\tilde{C}}_{im}\ge \zeta \right)}\right\},$$

where $\Omega$ is the set of distinct observed censoring times $\left\{{\tilde{C}}_{im}\right\}$. The coefficient $\mathit{\beta }\left(s\right)$ is estimated at each landmark $s$ by $\stackrel{\mathit{ˆ}}{\mathit{\beta }}\left(s\right)={\stackrel{\mathit{ˆ}}{\mathit{b}}}_0\left(s\right)$. The variance of $\stackrel{\mathit{ˆ}}{\mathit{\beta }}\left(s\right)$ can be estimated by bootstrap, which involves randomly sampling $n$ subjects from the original dataset with replacement, estimating the point estimator from each randomly sampled bootstrap dataset, and calculating the sample variance of the point estimators from all bootstrap datasets²⁹. Once we obtain the estimates of $\mathit{\beta }\left(s\right)$, the baseline cumulative SDH function at time $s$ can be estimated by plugging in $\stackrel{\mathit{ˆ}}{\mathit{\beta }}\left(s\right)$:

$${\tilde{\Lambda }}_{10}\left(t^{*},s\right)=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^{n_i}{K}_h\left(t_{ij}-s\right){\int }_0^{t^{*}}\frac{1}{{\widehat{\mathit{S}}}^{\left(0\right)}\left(\widehat{\mathit{\beta }}\left(s\right),t\right)}{\widehat{w}}_{ij}\left(t\right)\text{d}{N}_{ij}\left(t\right).$$

The conditional CIF for any future subject ${}_o$ can be estimated as

$${\widehat{\pi }}_1\left(t^{*}\mid s,\overline{{\mathit{Y}}_o\left(s\right)}\right)=\widehat{P}\left(s<T_o\le s+t^{*},{ϵ}_o=1\mid {\widehat{T}}_o>s,\overline{{\mathit{Y}}_o\left(s\right)}\right)=1-\text{exp}\left(-{\tilde{\Lambda }}_{10}\left(t^{*},s\right)\times \text{exp}\left({\widehat{\mathit{\beta }}}^T\left(s\right){\widehat{\mathit{Y}}}_o\left(s\right)\right)\right).$$

4. Quantifying the dynamic predictive accuracy

In this section, we study two predictive accuracy measures, the time-dependent receiver operating characteristic (ROC) curve, in particular the area under the ROC curve (AUC); and the Brier score (BS). In the dynamic prediction framework, the time-dependent predictive accuracy measures are functions of two time scales, the landmark time $s$ and the prediction horizon ${\tau }_1$. The following procedure for estimating sensitivity, specificity, and BS were modified from the non-parametric kernel-weighted approach of Wu and Li³⁰ for competing risk data.

4.1. The dynamic time-dependent ROC curve and AUC

At any landmark time $s$, we want to evaluate how well the risk score, i.e., the estimated CIF, discriminates between subjects with the event of interest in the window $\left(s,s+{\tau }_1\right]$ versus those without. For any at-risk subject at time $s$ who experiences the main event within the time interval $\left(s,s+{\tau }_1\right]$, that occurrence is defined as a case: $D^{+}\left(s,{\tau }_1\right)=\left\{i:s<T_i\le s+{\tau }_1,{ϵ}_i=1\right\}$. When a subject is event-free at $s+{\tau }_1$, that occurrence is defined as a control: $D^{-}\left(s,{\tau }_1\right)=\left\{i:T_i>s+{\tau }_1\right\}$. An alternative definition for a control is to use the complementary set ${\bar{D}}^{+}\left(s,{\tau }_1\right)=\left\{i:\left(s<T_i\le s+{\tau }_1,{ϵ}_i\ne 1\right)\cup \left(T_i>s+{\tau }_1\right)\right\}$, including subjects who experience a competing event within the time interval $\left(s,s+{\tau }_1\right]$ or remain event-free at $s+{\tau }_1$. To illustrate the ideas, we present the estimators for the former in this subsection. A similar extension can be made for the latter. For simplicity, we use the notation $U\left({\tau }_1\mid s\right)$ to denote the individual predicted CIF (i.e., the risk score). Given a threshold value $c\in \left(\mathrm{0,1}\right)$, the time-dependent sensitivity and specificity functions are defined as $Se\left(c,s,{\tau }_1\right)=P\left(U\left({\tau }_1\mid s\right)>c\mid D^{+}\left(s,{\tau }_1\right)\right)$ and $Sp\left(c,s,{\tau }_1\right)=P\left(U\left({\tau }_1\mid s\right)\le c\mid D^{-}\left(s,{\tau }_1\right)\right)$. The estimators of sensitivity and specificity are

$$\begin{array}{l}\widehat{Se}\left(c,s,{\tau }_1\right)=\frac{{\sum }_{i\in {\Re }_s}{\widehat{W}}_{1i}^{dyn}\cdot 1\left(U_i\left({\tau }_1\mid s\right)>c\right)}{{\sum }_{i\in {\Re }_s}{\widehat{W}}_{1i}^{dyn}}\\ \widehat{Sp}\left(c,s,{\tau }_1\right)=\frac{{\sum }_{i\in {\Re }_s}\left(1-{\sum }_{k=1}^K{\widehat{W}}_{ki}^{dyn}\right)\cdot 1\left(U_i\left({\tau }_1\mid s\right)\le c\right)}{{\sum }_{i\in {\Re }_s}\left(1-{\sum }_{k=1}^K{\widehat{W}}_{ki}^{dyn}\right)},\end{array}$$

where $W_{1i}^{dyn}=P\left(T_i\left(s\right)\in \left(0,{\tau }_1\right],{ϵ}_i=1\mid {\tilde{T}}_i\left(s\right),{\delta }_i,U_i\right)=1\left({\tilde{\delta }}_{ij}=0\right)\cdot \frac{F_1\left({\tau }_1\mid U_i,s\right)-F_1\left({\tilde{T}}_i\left(s\right)\mid U_i,s\right)}{S\left({\tilde{T}}_i\left(s\right)\mid U_i,s\right)}+1\left({\tilde{\delta }}_{ij}=1\right),T_i\left(s\right)=T_i-s,{\tilde{T}}_i\left(s\right)={\tilde{T}}_i-s$ and $U_i$ is short for $U_i\left({\tau }_1\mid s\right)$. ${\mathfrak{R}}_s$ is risk set within the neighborhood of $s$ which includes the most recent record at $t_{ij}$ for each subject $i\left\{i:{\tilde{T}}_i\ge s,\left|t_{ij}-s\right|\le \right.\left.\left|t_{i{j}^{\prime }}-s\right|,\forall j^{\prime }=\mathrm{1,2},\dots ,n_i,t_{ij}\in (s-h,s+h)\right\}.F_1\left(x\mid U_i,s\right)=P\left(T_i\left(s\right)\le x,{ϵ}_i=1\mid U_i,s\right)$ and $S\left(x\mid U_i,s\right)=P\left(T_i\left(s\right)\ge x\mid U_i,s\right)$.

For estimating the conditional probability weight $W_{1i}^{dyn}$, we treat the at-risk data set at landmark $s$ as the new baseline data set. The time-dependent ROC curve is a plot of sensitivity $Se\left(c,s,{\tau }_1\right)$ over 1-specificity $1-Sp\left(c,s,{\tau }_1\right)$, i.e., for $x\in \left[\mathrm{0,1}\right],R\widehat{OC}\left(x,s,{\tau }_1\right)=\widehat{Se}\left({\widehat{Sp}}^{-1}\left(1-x,s,{\tau }_1\right),s,{\tau }_1\right)$. The AUC is estimated as $\widehat{AUC}\left(s,{\tau }_1\right)={\int }_0^1 \widehat{ROC}\left(x,s,{\tau }_1\right)\text{d}x$.

4.2. The dynamic time-dependent Brier score

The time-dependent BS under the dynamic competing risk framework is defined as $BS\left({\tau }_1,s\right)=E{\left(1\left(s<T\le s+{\tau }_1,ϵ=1\right)-U\left({\tau }_1\mid s\right)\mid T>s\right)}^2$, where $1(\cdot )$ is the indicator function. Applying the weight $W_{1i}^{dyn}$, the BS can be estimated as

$$\widehat{BS}\left({\tau }_1,s\right)=\frac{1}{n_s}\sum _{i=1}^{n_s}\left({\widehat{W}}_{1i}^{dyn}\times {\left(1-U_i\left({\tau }_1\mid s\right)\right)}^2+\left(1-{\widehat{W}}_{1i}^{dyn}\right)\times {\left(0-U_i\left({\tau }_1\mid s\right)\right)}^2\right),$$

where $n_s$ is the number of subjects at risk at landmark time $s$.

The AUC and BS assess different aspects of the predictive model. AUC evaluates the discrimination between a case and a control, and BS quantifies the deviance of the predicted probability from the observed data. A model with perfect discrimination will have $AUC=1$, while AUC close to 0.5 indicates poor discrimination that resembles a random guess. BS is a prediction error metric, with smaller values indicating better prediction.

5. Simulation

The simulation in this section mainly evaluates the prediction accuracy of the proposed model. A separate simulation, which evaluates the estimation of model parameters and bandwidth selection under the assumptions of the working model, is presented in Section B of the online supplementary materials. Similar to other studies evaluating the prediction accuracy of landmark models³¹, we simulated longitudinal and competing risks data from a joint frailty model with shared random effects³². Details of the data generation process are described in Section A of the online supplementary materials. The data generating model included a baseline covariate and three longitudinal biomarkers. We considered two scenarios: (S1) the longitudinal biomarkers are non-informative for survival in the sense that their effects on both time-to-event outcome are zero, and (S2) the longitudinal biomarkers are informative in the sense that they have non-zero regression coefficients on both time-to-event outcomes. The incremental contribution of the longitudinal biomarkers to the prediction accuracy is expected to be zero under S1 and non-zero under S2.

Table 1 presents the predictive accuracy of the proposed model under both S1 and S2. The full model (M1) includes both the longitudinal biomarkers and the baseline covariate; the null model (M0) only includes the baseline covariate. Since the data were simulated from a joint frailty model³², the proposed landmark SDH model worked under misspecification. However, regardless of whether the data generating model matches the fitting model, the predictive performance can always be evaluated. We considered both discrimination and calibration measures in Table 1. For discrimination, we reported the true positive (TP) fraction and false positive (FP) fraction at a given threshold value, and the AUC as a global discrimination summary. For calibration, we used the Brier score. The predictive accuracy measures were evaluated at three landmark times $s=\mathrm{3,5},7$ with prediction horizon ${\tau }_1=\mathrm{1,3}$. For each simulation, the proposed model was fit to a simulated training data set and the predictive accuracy measures were calculated from another simulated validation dataset from the same distribution. When all the longitudinal biomarkers are non-informative, the predictive accuracy measures of the full model and the null model are very similar. When the three longitudinal biomarkers are informative, including the longitudinal biomarkers in the prediction model substantially improves both discrimination and calibration.

Table 1.

The means (EST) and empirical standard deviations (ESD) of estimated predictive accuracy metrics comparing the full model with longitudinal biomarkers $\left(M_1\right)$ and the null model with only the baseline covariate but without longitudinal biomarkers $\left(M_0\right)$ in the simulation. Prediction horizon ${\tau }_1=3$. S1: non-informative longitudinal biomarkers. S2: informative longitudinal biomarkers. AUC: area under the ROC curve comparing the group experiencing the event of interest with those who experienced competing events or event-free. $TP\left(c\right)$: true positive fraction at threshold $c.FP\left(c\right)$: false positive fraction at threshold $c$. BS: Brier score. Sample size $n=500$.

			AUC		TP (0.25)		FP (0.25)		BS
			$M_1$	$M_0$	$M_1$	$M_0$	$M_1$	$M_0$	$M_1$	$M_0$
S1	$s=1$	EST	0.703	0.707	0.514	0.512	0.272	0.290	0.161	0.165
		ESD	0.031	0.030	0.088	0.209	0.064	0.173	0.011	0.012
	$s=3$	EST	0.691	0.698	0.726	0.675	0.529	0.499	0.199	0.203
		ESD	0.034	0.032	0.092	0.223	0.099	0.237	0.011	0.015
	$s=5$	EST	0.660	0.676	0.751	0.705	0.614	0.594	0.211	0.223
		ESD	0.050	0.049	0.125	0.285	0.133	0.309	0.014	0.027
S2	$s=1$	EST	0.894	0.611	0.595	0.176	0.091	0.126	0.082	0.126
		ESD	0.031	0.061	0.117	0.217	0.027	0.175	0.034	0.077
	$s=3$	EST	0.882	0.578	0.738	0.477	0.240	0.452	0.142	0.205
		ESD	0.030	0.059	0.132	0.345	0.122	0.342	0.064	0.070
	$s=5$	EST	0.884	0.531	0.831	0.553	0.350	0.552	0.162	0.242
		ESD	0.030	0.058	0.082	0.400	0.113	0.392	0.035	0.052

Under S1, the estimated regression parameters of the proposed sub-distributional hazard model are close to zero for the longitudinal biomarkers (first row of supplemental Figure 1). In contrast, the estimated regression parameters under S2 demonstrate that the effects of the three longitudinal biomarkers are notably different from zero and in the right direction (second row of supplemental Figure 1).

We conducted additional simulation to compare the predicted and true conditional risks at individual level. The true conditional risk of an individual (indexed by subscript $o$, at landmark time $s$, conditional on biomarker history $\overline{\mathit{Y}\left(s\right)}$, and with prediction horizon ${\tau }_1$) is defined as $P\left(T_o\in \left(s,s+{\tau }_1\right],{ϵ}_o=1\mid {\tilde{T}}_o>\right.\left.s,\overline{{\mathit{Y}}_o\left(s\right)}\right)$ Since the true conditional risk varies by subject, landmark time and history, and does not have a tractable analytical expression, we calculated it empirically at 9 representative landmark time by history combinations (supplementary Table 1) as follows. We simulated data using the procedure in Section A of online supplementary materials but with one informative longitudinal biomarker $Y_2$ (the effect of $Y_1,Y_3$, and $X$ on the time-to-event outcome were all set to zero). The true CIF for the event of interest in the next ${\tau }_1=3$ years were obtained empirically as the proportion of subjects with that event within $\left(s,s+{\tau }_1\right.$] give survival up to time $s$, among those with nearly identical $Y_2$. For illustration, we chose three target $Y_2$ values: $m=\mathrm{0,2}$ and 4 in supplementary Table 1. Subjects with marker values within ±0.05 of the target value were counted in the denominator of the proportion calculation. To ensure that there were enough subjects in the denominator, we simulated a very large dataset $(n=\mathrm{1,000,000})$. We restricted to the case of a single informative biomarker $\left(Y_2\right)$ because it is less feasible to match subjects on multiple biomarkers. The conditional CIFs for hypothetical subjects with marker value 0, 2, 4 at landmark times 1,3,5 were estimated from 500 Monte Carlo repetitions. The average estimated CIF (EST), empirical standard deviation (ESD), percent bias (% Bias) and mean squared error (MSE) are presented in supplementary Table 1. Being a working model, the proposed semi-parametric landmark SDH model worked under mis-specification in this simulation. However, the result suggests that the estimated CIF has little bias and the MSE is low. It may indicate that the proposed model was flexible enough to provide approximate the data well at multiple landmark times, despite that the simulated data do not exactly satisfy the working assumptions. Unlike the simulation results in Table 1, the results in supplementary Table 1 pertain to the quality of predictions at individual level.

The proposed landmark SDH model is a working model and it is not yet clear whether there exists a joint distribution of longitudinal and competing risk data such that the model holds at all landmark times. This is a well known difficulty with landmark dynamic prediction models in general^4,22 and it is not specific to our landmark model, though limited progress has been made in problems without competing risks^7,33,34. Due to this difficulty, researchers often evaluate the numerical performance of the landmark models using data simulated from the joint model with shared random effects^31,35. This is also the simulation strategy that we chose. When the data generation model and the analysis model do not match, the estimated model parameters are difficult to evaluate and interpret, but prediction accuracy can still be assessed. We have designed scenarios S1 and S2 to demonstrate that incorporating informative longitudinal biomarkers improves predictive accuracy. This qualitative conclusion is unlikely to be invalidated by the magnitude of model misspecification. We designed three longitudinal biomarkers with complicated trajectories to demonstrate that the proposed model works in situations where joint modeling approaches may be difficult to apply.

6. Application to the AASK data

The AASK study (African American Study of Kidney Disease and Hypertension) is an NIH funded longitudinal cohort study.^36–38 It started as a multicenter clinical trial where participants were randomly assigned in a 3 × 2 factorial design to three antihypertensive drugs (ramipril, amlodipine, metoprolol) and two levels of blood pressure control (mean arterial pressure $⩽92$ or 102 – 107Hg). ³⁶ The trial included 1,094 African Americans of age 18 to 70 years who were diagnosed with hypertensive renal disease and had baseline eGFRs between $20-65mL/min/1.73m^2.$³⁷ After the trial phase ended, the study continued to follow the trial participants in a cohort phase to monitor their long-term progression.³⁸ Altogether the follow-up period was up to 12 years, with follow-up visits every 6 months. By the end of the study, 318 (29%) individuals developed ESRD, the event of research interest, and 176 (16%) died before ESRD. The median time to ESRD was 4.3 years and the median time to death was 5.2 years. We chose clinically relevant prediction horizons of ${\tau }_1=1$ or 3 years and illustrated the dynamic prediction at years 3, 5, and 7. The key longitudinal biomarker is eGFR (estimated Glomerular Filteration Rate). Our previous publication demonstrated that this biomarker have diverse and possibly nonlinear individual progression patterns¹¹. In addition, some CKD patients experienced acute kidney injury (AKI) during the follow-up, which may cause substantial short term variation in the eGFR (e.g., see Figure 2 of Li et al²²). The number of repeated measurements for eGFR ranged from 3 to 30, with over 50% of individuals providing 17 or more measurements. In addition to the current value of eGFR at a clinical visit, we derived the rate of change in eGFR (linear eGFR slope) during the history window of ${\tau }_2=3$ years, because the eGFR slope is often used by clinicians to characterize the speed of progression in CKD³⁹. The estimation of eGFR slope followed the approach in our recent paper²². Additional biomarkers included longitudinal measurements of serum albumin (Alb), urine protein to creatinine ratio (UP/Cr), serum phosphorus (Phos) and urine potassium (Upot). These biomarkers were considered because they have known biological association with disease progression and have been used in other CKD risk equations¹. Also included in the prediction model were age at the time of prediction and an indicator of any hospitalization during the previous year.

Figure 2.

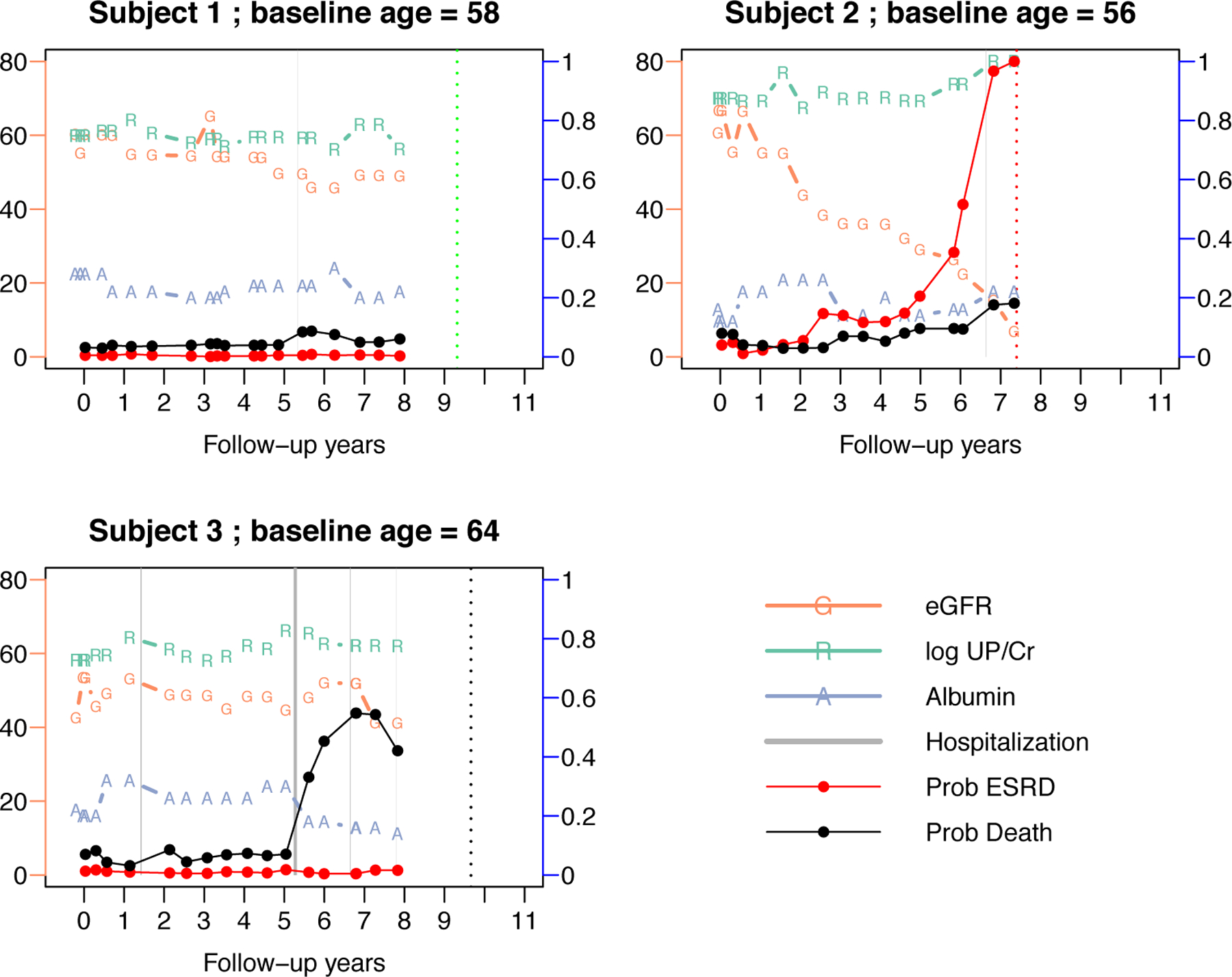
Individual risk predictions for three selected subjects: subject 1 was censored (dotted vertical green line), subject 2 had ESRD (dotted vertical red line) and subject 3 died (dotted vertical black line). Three biomarkers are plotted over time: “G” is eGFR $\left(\mathit{\text{ml}}/\mathit{\text{min}}/1.73m^2\right)$, “R” is log-urine protein-to-creatinine ratio $(g/g)$, and “A” is albumin $(g/dL)$. The connected red dots are predicted probabilities of ESRD within a horizon of ${\tau }_1=3$ years. The gray vertical bars represent episodes of hospitalization, with the two vertical borders being admission and discharge dates. The connected black dots are the predicted probability of death within ${\tau }_1=3$ years. The y-axis to the left is the scale of eGFR, and the y-axis to the right is the scale of predicted probabilities (0 to 1). The other two biomarkers, log-UP/CR and albumin, are re-scaled to be displayed in the same plot with eGFR but their respective scales are not shown. The dynamic predicted probabilities of ESRD are calculated using the dynamic SDH model with four predictors: eGFR, eGFR slope in the past three years, log-UP/CR and phosphorus. The dynamic predicted probabilities of death are calculated using the dynamic SDH model with four predictors: current age, serum albumin, any hospitalization within the past year, and log urine potassium.

For the competing events of ESRD and death, we fit landmark SDH models separately using the same set of candidate predictors (supplementary Figure 2). The eGFR, its rate of change, and log UP/Cr were significantly associated with time to ESRD but not with time to death. In contrast, age, Alb and hospitalization are risk factors related to death. This indicates that the progression to ESRD and death may be related to different pathological processes, which justifies the proposal of modeling the competing events separately rather than as a composite outcome. After removal of the non-significant covariates, the final model for ESRD included eGFR, eGFR.slope, log UP/Cr and Phos, and the final model for death included age, Alb, log-Upot and hospitalization (online Figure 3). We conducted bandwidth selection using 5-fold cross-validation. Predictive accuracy metrics were evaluated in the cross-validation dataset, and they were robust to different bandwidths (up to 3 digits after the decimal point). Therefore, we used the bandwidth of $h=1.5$ in the final model, which provided a relatively smooth curve for the log-SDH ratio curve. The surface plots of the CIF for ESRD and death are illustrated in Figure 1.

Figure 3.

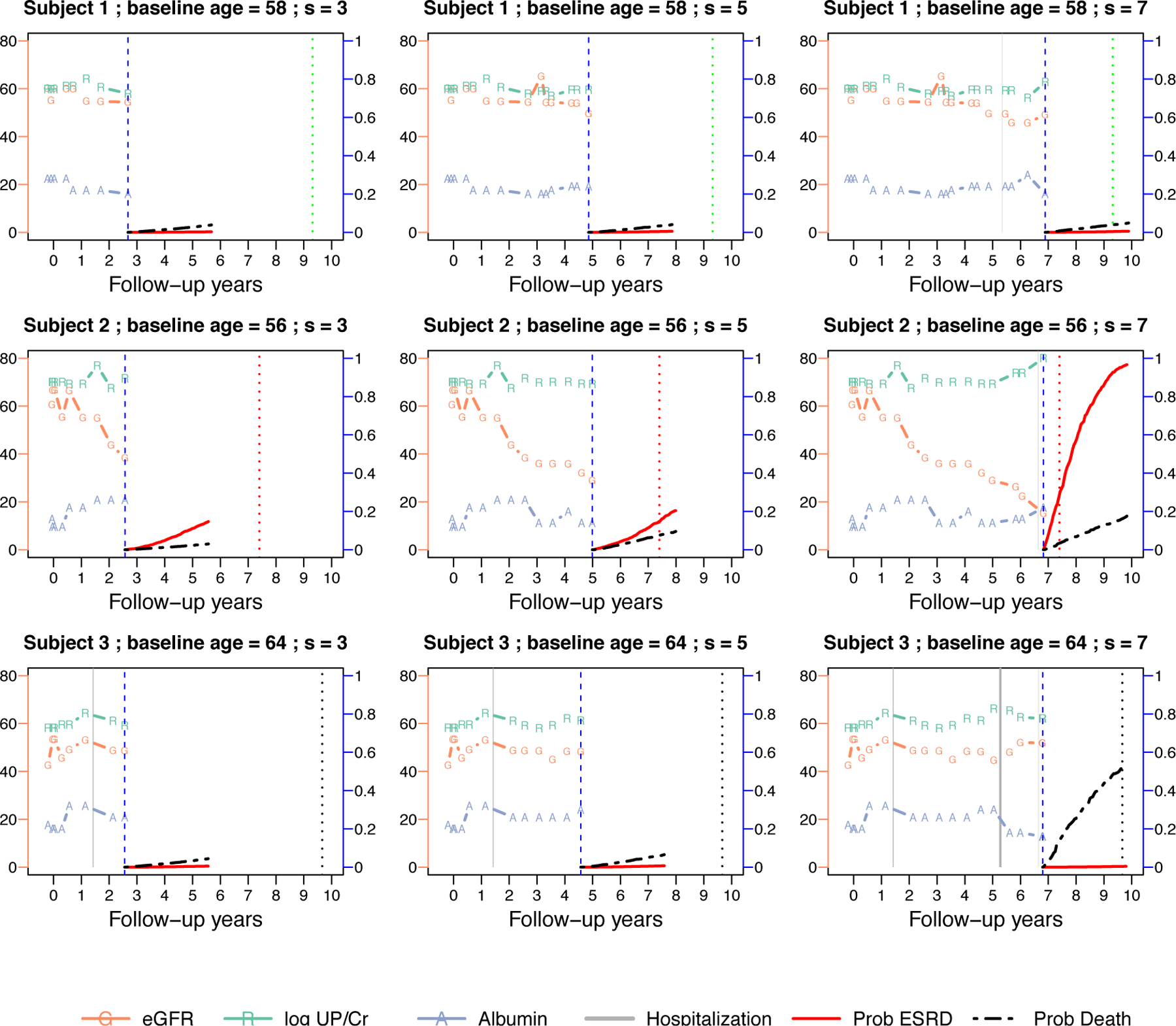
Individual dynamic predicted CIF for the three selected subjects in Figure 2. Each row in the panel represents one subject, the three columns are the predictions made at landmark years $s=\mathrm{3,5},7$. The prediction is made at the vertical blue dashed lines. The predicted CIFs up to ${\tau }_1=3$ years are plotted for the event of ESRD (red curve) and death (black curve). Symbols in the figure are similar to Figure 2.

Figure 1.

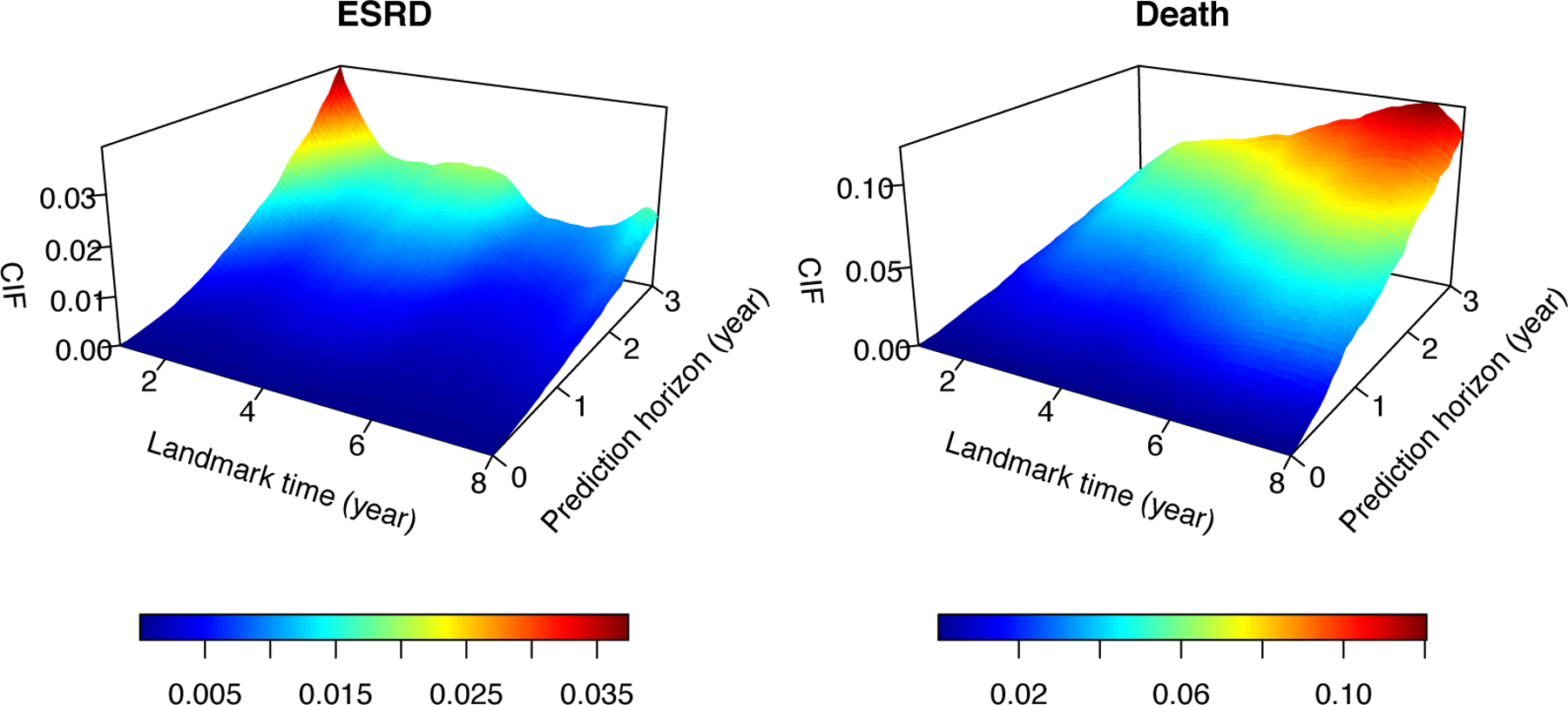
Estimated surface of the cumulative incidence function over the landmark time and prediction horizon. This shows an examplary population with age = 55, $\text{eGFR}=45ml/min/1.73m^2$, eGFR. $\text{slope}=0$, $\text{UP}/\text{Cr}=0.3g/g$, $\text{albumin}=4g/\mathit{\text{dL}}$, and hospitalization within the past year.

Figure 2 presents the longitudinal profiles and individual dynamic predictions from three AASK subjects: subject 1 was event-free by the end of the study, subject 2 experienced ESRD after 7.5 years, and subject 3 died after 9.7 years. We demonstrated the biomarker values with real-time predicted 3-year probabilities of ESRD and death. The risk prediction was dynamically updated at each new clinical visit. Subject 1 demonstrated stable disease. Subject 2 demonstrated persistent decline in eGFR and notable increase in proteinuria (log-UP/Cr), which led to drastic increase in the risk of ESRD after year 5. In contrast, the risk of death for subject 2 increased moderately, which may be explained by the Alb level and hospitalization around year 7. For subject 3, the relatively stable eGFR and log-Up/Cr also stablized the subject’s susceptibility to ESRD, but the frequent hospitalization and decreasing Alb level were associated with increased risk of death, possibly due to other co-morbidity. We did not estimate the model after year 8 because the number of observed clinical events was relatively small near the end of the follow-up.

Figure 3 presents the profiles of the same three patients but with their dynamic CIFs (up to ${\tau }_1=3$ years) at landmark times $s=\mathrm{3,5},7$ years. For subject 1, the predicted CIFs for both ESRD and death were flat. In contrast, the predicted CIF of ESRD for subject 2 started to increase after year 5 and the increase became very prominent by year 7. This was likely caused by a combination of deteriorated renal function (eGFR) and proteinuria (log-UP/Cr). This patient reached ESRD shortly after year 7. The predicted CIF of ESRD for subject 3 stayed flat, but the CIF of death increased at year 7, after frequent hospitalization. This subject eventually died at year 9.6 without ESRD.

In Table 2, we summarized the predictive accuracy of the landmark SDH models for prediction horizons ${\tau }_1=\mathrm{1,3}$ at three landmark years $s=\mathrm{3,5},7$. The model for ESRD achieved good discrimination with AUCs between 0.93–0.96. When we used the cutoff value of 0.05, the sensitivity (TP) and specificity (1-FP) could be controlled within 0.80–0.90 range under all scenarios. The prediction accuracy metrics were similar with different prediction horizons. In contrast, the model for death discriminated no better than a random guess, resulting in AUCs around 0.5; the prediction errors were also at least twice as large as those from predicting ESRD. More importantly, the AUCs from the proposed model improved in comparison with previous studies where AUCs were around 0.8 and always less than 0.9^22,31. One possible explanation is that these previous studies treat “time to ESRD or death” as a composite outcome. This introduces noise and diminishes the predictive accuracy because all-cause death is difficult to predict with the selected biomarkers, which are prognostically specific to renal disease. The ROC curves for predicting ESRD were plotted in supplementary Figure 4.

Table 2.

Measures of predictive accuracy from the landmark SDH model for ESRD and death in the analysis of AASK data. The estimates were obtained at three landmark years, $s=\mathrm{3,5},7$, with prediction horizon ${\tau }_1=\mathrm{1,3}$ years. AUC: area under the ROC curve. $TP\left(c\right)$: true positive rate at threshold $c;FP\left(c\right)$: false positive rate at threshold $c$; thresholds $c$ are selected to be 0.05 for ESRD and 0.01 for death. BS: Brier score.

		AUC		TP(c)		FP(c)		BS
		ESRD	Death	ESRD	Death	ESRD	Death	ESRD	Death
${\tau }_1=1$	$s=3$	0.957	0.545	0.925	0.568	0.075	0.539	0.024	0.191
	$s=5$	0.925	0.547	0.885	0.585	0.100	0.596	0.026	0.043
	$s=7$	0.965	0.584	0.832	0.692	0.099	0.675	0.021	0.035
${\tau }_1=3$	$s=3$	0.944	0.558	0.876	0.468	0.119	0.378	0.054	0.119
	$s=5$	0.943	0.520	0.852	0.498	0.140	0.549	0.052	0.093
	$s=7$	0.957	0.492	0.863	0.343	0.131	0.405	0.048	0.110

7. Discussion

For CKD patients, estimating the time to ESRD is crucial for the timely treatment management. Dynamic prediction is an attractive tool for this purpose, because it is adaptive to the changing health condition and prognostic history of the patient. It enables real-time monitoring of patient risk. In this paper, we develop novel methodology for dynamic prediction of ESRD among the CKD patients, and we overcome a number of analytical hurdles, including competing events of death, irregularly spaced clinical visit times, multiple biomarkers with complicated longitudinal trajectories, time-varying at-risk population, and time-varying covariate-outcome association. Our proposed methodology is flexible, because the model parameters are estimated semi-parametrically. Hence, it can effectively mitigate the risk of model misspecification. This feature is very important for dynamic prediction models, because, as explained in Section 5, the landmark dynamic prediction model is a working model and needs to provide adequate approximation to the data at all landmark times. Another advantage of the proposed methodology is that it is computationally simple, and it can be implemented through standard statistical software for competing risks analysis, regardless of how many longitudinal biomarkers are included as predictors. In this paper, the estimation process was accomplished with the available R function coxph() after translating the competing events into a counting process⁴⁰. We believe that the simplicity in computation makes the proposed methodology attractive for various practical situations, including applications with large datasets, a large number of biomarkers with complicated longitudinal trajectories, and other longitudinal prognostic information that cannot be easily modeled at an individual-level (e.g., hospitalization episodes and medication history).

Our kernel-based estimation approach relies on the assumption that the clinical visit times are noninformative. Future work is needed to study dynamic prediction when the frequency of clinical visits is related to the health condition of the patients. The predictors in our proposed model framework include pre-specified features extracted from the data history. Automatic extraction of predictive features from the longitudinal history is another topic that we will pursue in future research.

In this paper, we consider death as a competing risk to ESRD. Although death can also be observed after ESRD, a semi-competing risk analysis is not justified in this context and hence is not pursued. Our study population is CKD. Once a CKD patient reaches ESRD, that patient either becomes a kidney graft recipient or a dialysis patient, and the health condition, care, etiology and prognosis are fundamentally different. GFR, an important biomarker and predictor used in this paper for CKD, is no longer scientifically defined after ESRD.