Abstract
Social desirability bias (SDB) has been a major concern in educational and psychological assessments when measuring latent variables because it has the potential to introduce measurement error and bias in assessments. Person-fit indices can detect bias in the form of misfitted response vectors. The objective of this study was to compare the performance of 14 person-fit indices to identify SDB in simulated responses. The area under the curve (AUC) of receiver operating characteristic (ROC) curve analysis was computed to evaluate the predictive power of these statistics. The findings showed that the agreement statistic outperformed all other person-fit indices, while the disagreement statistic , dependability statistic , and the number of Guttman errors also demonstrated high AUCs to detect SDB. Recommendations for practitioners to use these fit indices are provided.
Keywords: response bias, social desirability bias, factor mixture model, person-fit indices, receiver operating characteristic curve, the area under the curve
Since 1930, social desirability bias (SDB) has been considered a potential concern when measuring variables or latent constructs in psychological studies (Bernreuter, 1933), and it has been addressed in psychological and educational research (e.g., Leite & Nazari, 2020; Leng et al., 2020; Vésteinsdóttir et al., 2019). In prior studies, researchers have attempted to address SDB using three different approaches: administering a social desirability scale along with the focal scale of interest, reducing social desirability responding by manipulating test conditions, and using statistical methods to correct scores. However, these approaches either increase the respondent burden or are costly to the researcher in terms of research design or analysis complexity. Therefore, there is a need for low-cost methods to address SDB. This article addresses this need by evaluating whether a wide range of parametric and nonparametric person-fit statistics (e.g., Karabatsos, 2003) can be used to effectively identify responses affected by SDB.
Crowne and Marlowe (1960, p. 354), defined social desirability as “the need for subjects to respond in culturally sanctioned ways” and also “a need to be thought well of by others, a need for approval” (Crowne & Marlowe, 1964). Almost three decades later, Paulhus (1991) defined social desirability responding as “the tendency to give answers that make the respondent look good” (p. 17). SDB usually occurs when the context of an item is perceived as inappropriate in society, so respondents may not answer truthfully. They either systematically overreport or underreport their true attitudes, depending on the positive or negative content of survey/test items (Tourangeau et al., 2000). In survey studies to measure a construct, this type of bias in responses lies underneath the “common method variance” (Podsakoff et al., 2003), which is the variance due to measurement method and sources rather than variance related to the targeted construct (e.g., Johnson et al., 2011).
There are several social desirability scales, the most popular of which are the Marlowe–Crowne Social Desirability Scale (MCSDS; Crowne & Marlowe, 1960) and the Balanced Inventory of Desirable Responding (BIDR; Paulhus, 1984). Once SDB scores are obtained, the simplest method to evaluate the degree of SDB is calculating the correlation between the SDB scores and scores on the focal scale. Ferrando (2005) proposed a method based on confirmatory factor analysis (CFA), while Leite and Cooper (2010) developed a factor mixture model (FMM) to correct individual scores affected by SDB. These models assume a separate latent factor for SDB which influences item responses to the focal scale. The advantage of FMM over CFA is that the former is both item and person-centered, and it can evaluate the degree to which each person provided biased responses (Leite & Cooper, 2010). However, these approaches are costly as researchers need to administer two scales simultaneously and need a larger sample size as compared with the administration of one test (e.g., due to the complexity of models). In addition, administration of both the focal and SDB scales may be time-consuming, and respondents may feel exhausted toward the end of the testing period, thereby answering items carelessly (e.g., Nazari et al., 2021). Also, these methods cannot be applied to secondary data.
Another approach to reducing social desirability consists of manipulating different test conditions in an experimental setting. Methods using this approach include the randomized response technique (Warner, 1965), bogus pipeline (Jones & Sigall, 1971), the item count technique (Holbrook & Krosnick, 2010), eye-tracking (Kaminska & Foulsham, 2016), extended crosswise model (Heck et al., 2018), and audio computer-assisted self-interviewing (Stark et al., 2019). However, these methods cannot be applied to nonexperimental studies. Also, the design and administration of these methods are a burden on the researcher, and they cannot be used on the secondary data.
A third approach is to address SDB with statistical methods to correct scores without an SDB scale or an experimental manipulation. By introducing IRTree models, Böckenholt (2014) assumed that rating an item can generate multiple response processes based on both its content and response format. With the help of a tree structure, researchers can examine how people respond to different items in a variety of ways (i.e., different response styles) by modeling the processes involved in responding to the items (Böckenholt, 2014). Social desirability responding, if conceptualized as a response style, can be potentially addressed by the IRTree models.However, other researchers have conceptualized social desirability responding as having both a stable component that could be understood as a response style, and a situation specific component that is due to the interaction between examinee and test setting (Leite & Cooper, 2010).
Two studies investigated social desirability according to a cognitive-based approach within the item response theory (IRT) framework. Böckenholt (2014) proposed a retrieve–edit–select (RES) model, and Leng et al. (2020) proposed the retrieve–deceive–transfer (RDT) model to address the process for response editing. The former suggested that when people face sensitive questions in a questionnaire, they may modify the initial information they received before deciding between response options (Böckenholt, 2014). In the latter, Leng et al. (2020) stated that after retrieving information, the respondent may deceive himself or herself by adding positive or negative information to the initial knowledge, thereby transferring the answer to a more desirable higher or lower response option. The recently proposed RDT model is the enhanced version of RES, and it is based on strong assumptions such as equal threshold parameters across items and a multidimensional rating scale model. Furthermore, from a statistical point of view, it is difficult for applied researchers to implement this method with real data, and no statistical package is currently available. Wilcox (2017) added that with the use of these cutting-edge, robust techniques, researchers can get a better, more nuanced grasp of the data. However, the scientific community has been slow to adopt these enhanced methods, which may be due to unfamiliarity with the methods and unavailability of specific software.
In this study, we propose that person-fit indices can function as low-cost methods to detect SDB which are also applicable to secondary data. Given an established measurement model, the goal of person-fit or appropriateness measurement is to define individual response patterns as typical or atypical (Meijer & Sijtsma, 2001). These statistics have been used frequently to detect several response biases such as cheating, careless responding, lucky guessing, creative responding, and random responding (e.g., Beck et al., 2019; Dimitrov & Smith, 2006; Karabatsos, 2003; Sinharay, 2017; Tendeiro & Meijer, 2014). However, we found that no study examined the strength and predictive power of these statistics to detect SDB in responses. In contrast to previous methods, utilizing these indices is cost-effective as they do not require either administering an SDB scale accompanied by the focal scale or conducting an experimental manipulation to detect bias. Therefore, the objective of this study is to compare the ability of person-fit indices to detect SDB in individual responses using Monte Carlo simulations.
Person-Fit Indices
Most of the person-fit indices were created to test dichotomous items, although several have been expanded to test polytomous items as well (Tendeiro et al., 2016). Table 1 shows 14 frequently studied person-fit indices, together with a brief description of each index. Two of the 14 fit indices in Table 1 are parametric person-fit indices, which are used within the IRT framework to assess model fit at the individual level and determine the significance of test results (Embretson & Reise, 2013). These indices, in a sense, check the consistency of individuals’ item response vectors based on an IRT model, which is the key issue when seeking to flag particular individual responses that may have been biased (Embretson & Reise, 2013). The other 12 person-fit indices are nonparametric. Nonparametric person-fit indices are not computed based on an IRT model fit to the data; therefore, they have the advantage that they do not have to adhere to the same assumptions as parametric ones.
Table 1.
Person-Fit Indices.
| Person-fit index | Description |
|---|---|
| Nonparametric | |
| Personal point-biserial correlation ( ; Donlon & Fischer, 1968) | It is the correlation between the individual’s score and the item proportion-correct score. |
| Caution statistic ( ; Sato, 1975) | It is the complement of the two covariances ratio that measures to what extent an individual’s response deviates from a perfect response pattern. |
| Modified caution statistic ( ; Harnisch & Linn, 1981) | It is the modified version of the caution statistic, which ranges from zero to one. |
| Number of Guttman errors ( ; Meijer, 1994) | Guttman error occurs when an easy item is answered incorrectly and a hard item is answered correctly. |
| Normalized Guttman errors ( ; van der Flier, 1977) | It is the normalized version of the Guttman error which ranges from zero to one. |
| Agreement statistic ( ; Kane & Brennan, 1980) | It is the agreement between an individual’s responses on an item and proportion-correct score on that item. |
| Disagreement statistic ( ; Kane & Brennan, 1980) | |
| Dependability statistic ( ; Kane & Brennan, 1980) | |
| statistic ( ; van der Flier, 1980) | It is a global fit index that assumes invariant item ordering based on the proportion-correct score on items. |
| Standardized normal ( ; van der Flier, 1982) | It is the standardized normal version of . |
| Norm conformity index ( ; Tatsuoka & Tatsuoka, 1982, 1983) | It is the conformity of an individual’s response pattern in comparison with a criterion order such as item difficulty order. |
| statistic ( ; Sijtsma, 1986; Sijtsma & Meijer, 1992) | When an individual’s response is compared with the rest of the respondents, the measures the extent to which data complies with the Guttman model. |
| Parametric | |
| Standardized normal loglikelihood ( ; Drasgow et al., 1985) | It measures the standardized normal loglikelihood fit of an individual’s response based on an IRT model. |
| Corrected ( ; Snijders, 2001) | It is the corrected form of . |
Karabatsos (2003) compared 36 person-fit indexes to see how effective they were at detecting five different types of aberrant responses such as cheating, careless responding, lucky guessing, creative responding, and random responding. The results showed that the statistic (Sijtsma, 1986) and then statistic (Van Der Flier, 1982), caution statistic ( ; Sato, 1975), and modified caution statistic ( ; Harnisch & Linn, 1981) obtained the best predictive power or area under the curve (AUC) for detecting all the types of aberrant responses examined, while other indices such as the number of Guttman errors index ( ; Meijer, 1994) and standardized normal loglikelihood index ( ; Drasgow et al., 1985) showed fair AUC. Dimitrov and Smith (2006) replicated part of this study to detect guessing and cheating with and four other statistics. They found that outperformed other indices when the test length was 20 and 30 items. Another study was conducted by Tendeiro and Meijer (2014), which examined the parametric corrected index ( ; Snijders, 2001), nonparametric , normalized Guttman errors ( ; Van der Flier, 1977), probability of exceedance (PE; Van der Flier, 1980, 1982), , and statistics, to detect spuriously low, high, and mixed responding. They concluded that performed better across all manipulated conditions, while had low performance compared with , , , and . These findings were in contrast with Sinharay’s (2017) results with real datasets, which showed that there was no meaningful difference between the performance of and statistics. The index (Drasgow et al., 1985) also showed a good detection rate to detect lack of motivation when misfit is considerably large in response vectors (Conijn et al., 2014). Moreover, using a simulation study, Artner (2016) compared five well-known indices to detect guessing, cheating, careless behavior, distorting, and fatigue in responses. The results showed that nonparametric , , and outperformed parametric OUTFIT and INFIT (Linacre, 2002) using a Rasch model. Finally, Beck et al. (2019) utilized response time, instructed response items, and person-fit statistics such as G (Meijer, 1994), , , and , to detect inattentive responding, finding that had the greatest AUC among indices. In summary, most of the previous studies showed that had the best performance among a set of person-fit indices to detect a wide variety of aberrant response patterns.
Given that person-fit indices can potentially be used to detect SDB, the current study addresses the following research question: Can person-fit indices detect misfitted individuals stemming from SDB in scale responses under varying conditions of the number of items, sample size, class separation, and cross-loading between two factors?
The mentioned conditions were selected based on the conditions that were examined in previous research (e.g., Karabatsos, 2003; Leng et al., 2020; Rupp, 2013; Sinharay, 2015) and showed promising result for detecting different aberrant responding (e.g., careless responding, SDB, guessing). These conditions and their effects on different response biases will be discussed in “Manipulated Conditions” section in detail.
Method
A Monte Carlo simulation study was conducted to answer the research question by manipulating different conditions that may affect the performance of person-fit indices to detect SDB.
Population Model
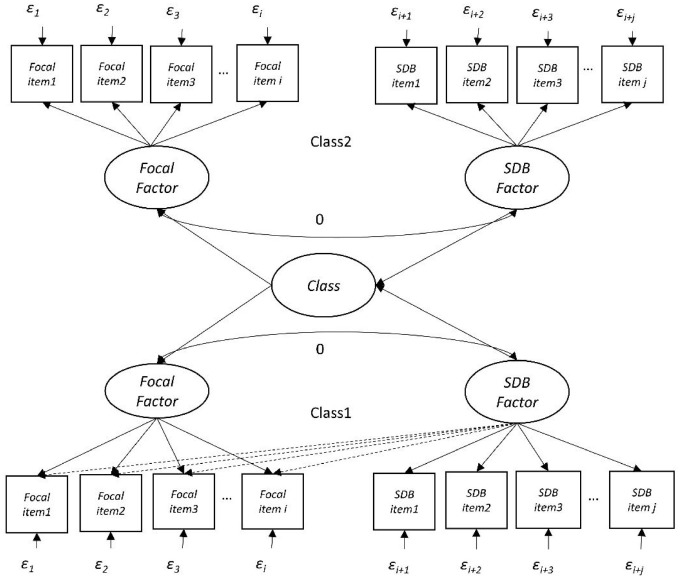
The FMM proposed by Leite and Cooper (2010) was selected as the population model to simulate SDB in responses, as manipulating the degree of bias was more feasible in FMM compared with CFA and IRT models. FMM was also preferable to CFA due to exploring both item and person dimensions. The population two-class FMM model consists of one class whose responses to the items of the focal factor were affected by the SDB factor, and one class whose responses to the focal factor were independent of the SDB factor. The focal factor is the latent variable measured by binary items of a hypothetical scale of interest to the researcher, while the SDB factor is the latent variable measured by items of an SDB scale. The population model is shown in Figure 1.
Figure 1.
Simulation Model Using SDB Factor and Focal Factor.
Note. SDB = social desirability bias.
For the items of both the focal and SDB scales, we assumed that there is a continuous response underlying the observed binary response . Therefore, a threshold is required to convert a continuous response to a binary response (Kaplan, 2008). We simulated dichotomous items because the most popular scale to detect SDB, the MCSDS, has dichotomous items, and was used in Leite and Cooper’s (2010) study. The rationale for socially desirable responding in dichotomous items is that individuals will be more likely to respond in a socially desirable direction (which can be endorsing or not endorsing the item, depending on the item’s wording) than expected from the level of the trait being measured. When focal and SDB factors are unidimensional, the matrix form of the equation is as follows (Leite & Cooper, 2010):
| (1) |
| (2) |
where and are assumed continuous responses for focal and SDB factors; and are intercepts of focal and SDB factors; and are factor loadings of two mentioned factors; and are factor scores, and and are residuals. In Equation 2, are thresholds (see Class 2 in Figure 1). When responses in the focal factor are affected by the SDB factor, the factor loadings in Equation 1 change to the following form:
| (3) |
where the second column of the matrix shows focal factor items are affected by (see dashed factor loadings in Class 1, Figure 1). The other terms in Equation 1 stay the same in Equation 3. The structural model explains the relationships between the latent variables and categorical latent variables, c (i.e., class; Lubke & Muthén, 2005).
| (3) |
where is focal factor score for the person i in class m; is the focal factor mean for class m; is the latent class, which is a binomial variable; and is the residual which follows a normal distribution with a mean of 0 and covariance matrix of (Muthén & Shedden, 1999).
To generate SDB scale items, the short form XX of the MCSDS (Strahan & Gerbasi, 1972) with dichotomous items was selected. This 20-item short form has been frequently used in previous research (e.g., Dawes et al., 2011; Fernandez et al., 2019; Fisher et al., 2012; Leite & Beretvas, 2005). The focal scale is a hypothetical scale with dichotomous items that will be detailed in the data generation section. As shown in Figure 1, Class 1 contains individuals with responses affected by SDB, which is illustrated by dashed cross-loadings. In this class, focal items are regressed on both focal and SDB factors, but SDB items are only regressed on the SDB factor (see Equation 3). In Class 2, with individuals not affected by SDB, there are no cross-loadings from the SDB scale to the focal scale, and the response vectors of individuals in this class are unbiased (see Equation 1).
Data Generation
To simulate the data for this study, Mplus 8.5 (Muthén & Muthén, 1998–2017) and the R statistical software version 4.0.3 (R Core Team, 2020) were used. To call Mplus from R, the MplusAutomation package (Hallquist & Wiley, 2018) was used. To facilitate setting the scale for both factors shown in Figure 1, the population value of the first factor loading of each factor was set to one. We assume that the SDB factor and focal factors are theoretically uncorrelated, so the population correlation between the two factors was set to zero. Except for the cross-loadings (dashed lines in Figure 1) that were manipulated to change from low to high, other population factor loadings of focal and SDB factors were set to 0.8. The population proportions of individuals in each class were set to be equal by setting the population logit of the two class proportions to zero (Muthén & Muthén, 1998–2017). Because of the long computation time for FMM, we generated 100 replications for each combination of simulated conditions, which is the number of replications frequently used in Monte Carlo studies of mixture models (e.g., Lubke & Muthén, 2007; Kim & Muthén, 2009).
Manipulated Conditions
The Monte Carlo simulation study had a fully crossed 3 × 3 × 3 × 3 factorial design, resulting in 81 independent simulated conditions with 100 datasets per condition. The manipulated conditions included three levels of sample size, three levels of test length (i.e., the number of items), three levels of SDB (i.e., size of cross-loadings), and three levels of class separation.
Sample Size
In previous person-fit studies, a sample size of 1,000 was simulated most frequently because of model complexity, the number of response categories, or other reasons (e.g., Rupp, 2013; Sinharay, 2015). Artner (2016) used 100 and 500 sample sizes for a Rasch model while Tendeiro and Meijer (2014) used a 1,000 sample size considering a three-parameter logistic (3-PL) model. To compute parametric person-fit indices, a two-parameter logistic (2-PL) IRT model (see “Analysis” section) was selected, and the minimum suggested sample size for this model is 500 (Crocker & Algina, 1986). Therefore, we selected 500 as a small sample size, 1,000 as a large sample size, and considered 750 to represent a medium sample size.
Test Length
In methodological literature about person-fit indices, there are a wide variety of test lengths that were considered. For example, Hong et al. (2021) examined 16, 32, and 64 items per latent trait; Tendeiro (2017) manipulated four scale lengths of 10, 20, 40, and 100; Artner (2016) included items sets of 50 or 25; and Sinharay (2015) tested three test length levels of 12, 30, and 60 items. In Karabatsos’s (2003) study, 17, 33, and 65 items were examined, but in Tendeiro and Meijer’s (2014) study, 15, 25, and 40 items were manipulated. In the current study, the number of items in SDB and focal scales was set to be equal, because it is unusual for researchers to administer a longer SDB scale than the focal scale. Therefore, we simulated conditions with focal and SDB scales with 10, 20, and 30 items each.
SDB
To generate different degrees of SDB, there is only one study to our knowledge that simulated SDB: Leng et al. (2020) introduced the RDT model with three latent traits, where the deceive trait is related to SDB. In their study, the model discrimination parameters (i.e., factor loadings) ranged from 0.5 to 2. In the current study, 0.1, 0.3, and 0.5 were selected for SDB cross-loadings to represent low, medium, and high levels of SDB in individual responses.
Class Separation
In a FMM, the distance between two classes can be measured by the multivariate Mahalanobis Distance (MD; Lubke & Muthén, 2007). Moreover, as MD considers covariances, standardized factor mean differences between classes can determine this distance to a large extent (Lubke & Muthén, 2007). In real data, the classes affected and not affected by SDB are not clearly separated, so we decided to consider a range of class separation from low to high. We expect improved class detection with a higher difference between factor means (Lubke & Muthén, 2007). Therefore, the means of two biased and unbiased classes were separated by 1, 2, and 3 standard deviations (SDs).
Analysis
We investigated the performance of 14 frequently used parametric and nonparametric person-fit statistics that showed promising results in previous research (see Table 1). All of these indices were available in the PerFit (Tendeiro et al., 2016) package of R statistical software (R Core Team, 2020). When 8,100 datasets were generated, the simulated data were divided into SDB and focal factor items, and the SDB items were discarded to keep only focal items. This is because SDB items are not needed in the calculation of person-fit indices.
To compute nonparametric person-fit indices, there is no need for an IRT model; however, to compute the parametric person-fit indices and , the 2-PL model was used. We chose the 2-PL model because factor loadings (which are equivalent to discrimination parameters; Kamata & Bauer, 2008) were manipulated. The 2-PL model is (Birnbaum, 1968) as follows:
| (4) |
where P is the probability of correct response for item i and person s, given θ, the latent ability of the individuals. b and a are item difficulties and item discriminations, respectively. Y represents the item responses and is a scaling constant.
To evaluate person-fit indices’ prediction results, we used receiver operating characteristic (ROC) curve analysis for each person-fit statistic, separately. For dichotomous data, the ROC curve relates a predictor’s sensitivity to its specificity (Hanley & McNeil, 1982). The capacity to recognize true SDB in responses (true positive rate) is referred to as sensitivity, whereas specificity refers to correctly identifying those responses that are not biased (true negative rate). ROC curves typically show “1-specificity,” which determines the Type I Error rate (false positive rate; Hanley & McNeil, 1982). The predictive power of the predictor or feature is represented by the AUC of a ROC curve, which varies from 0.5 to 1 from the identification line (i.e., the diagonal on the ROC), and different values of it can be interpreted to demonstrate the strength of a test. To interpret the AUC in the current study, we followed the academic point system (Tape, n.d.) guideline: AUC of 0.90 to 1 indicates an excellent test, 0.80 to 0.90 is regarded good, 0.70 to 0.80 is fair, AUC of 0.6 to 0.7 shows a poor test and 0.5 to 0.6 represents a fail test. For each simulation condition, the average of AUCs across 100 replications is reported.
The effect of the manipulated conditions on AUC was assessed using a four-way between-subjects analysis of variance (ANOVA). The generalized eta-squared (GES, ; Olejnik & Algina, 2003) was then calculated to reflect the size of effects. To interpret the effect sizes, we considered Cohen’s (1988) description of 0.02 as a small, 0.13 as a medium, and 0.26 as a large effect size for which is also appropriate for . In this study, the significant ANOVA factors with an effect size of 0.01 and higher were reported.
Results
The AUCs across 81 simulation conditions for 14 person-fit indices were calculated and averaged across 100 replications of each condition. This study aimed at identifying the strongest person-fit indices to detect SDB. The strongest indices are those with the highest predictive power in the classification of biased and unbiased responses which is represented by AUC. Therefore, to evaluate the strength of person-fit indices, we can compare the conditions that resulted in the highest AUC across all person-fit indices.
As shown in Table 2, the maximum AUC average for each person-fit index and the simulation factors that led to the maximum AUC were listed. 1 Overall, out of 14 person-fit statistics, five indices could detect SDB in responses with approximately 70% and greater AUC. One of these indices, , detected SDB similar to a fair test with about 70% AUC and the other four indices, namely, the disagreement statistic ( ; Kane & Brennan, 1980), , dependability statistic ( ; Kane & Brennan, 1980), and agreement statistic ( ; Kane & Brennan, 1980), detected bias similar to a good test with equal or greater than 80% AUC. The last two indices, and , reached 96.3% and 94.4% AUC, respectively, showing excellent discrimination ability. Norm conformity index ( ; Tatsuoka & Tatsuoka, 1982, 1983), standardized normal ( ; Van der Flier, 1982), , , , , , and personal point-biserial correlation index (r.pbis; Donlon & Fischer, 1968) could not discriminate between biased and unbiased responses. Because performed very well in previous studies of detection of aberrant response patterns, it was unexpected that it did not work for the detection of SDB.
Table 2.
Conditions With Max AUCs.
| Class separation (SD) | Cross-loading | No. of items | Sample size | Person-fit index | Max AUC mean |
|---|---|---|---|---|---|
| 3 | 0.1 | 30 | 500 | 96.3% | |
| 3 | 0.1 | 30 | 750 | 96.3% | |
| 3 | 0.1 | 30 | 1,000 | 96.3% | |
| 3 | 0.1 | 30 | 750 | 94.4% | |
| 3 | 0.1 | 30 | 1,000 | 94.4% | |
| 3 | 0.1 | 30 | 750 | 89.8% | |
| 3 | 0.1 | 30 | 1,000 | 89.8% | |
| 3 | 0.1 | 30 | 750 | 86.6% | |
| 3 | 0.1 | 10 | 1,000 | 70.4% | |
| 3 | 0.1 | 10 | 750 | 70.4% | |
| 3 | 0.1 | 10 | 1,000 | 69.1% | |
| 3 | 0.1 | 10 | 500 | 69.1% | |
| 3 | 0.1 | 10 | 750 | 69.1% | |
| 3 | 0.5 | 20 | 750 | 59.1% | |
| 3 | 0.5 | 20 | 750 | 59.0% | |
| 3 | 0.1 | 10 | 1,000 | 58.4% | |
| 3 | 0.5 | 10 | 500 | 53.5% | |
| 3 | 0.5 | 30 | 500 | 53.2% | |
| 3 | 0.5 | 10 | 500 | 52.9% | |
| 3 | 0.5 | 10 | 500 | 52.6% | |
| 2 | 0.1 | 30 | 500 | 52.0% | |
| 2 | 0.5 | 30 | 500 | 52.0% |
Note. = agreement statistic; = dependability statistic; = number of Guttman errors; = disagreement statistic; = normalized ; = corrected ; = statistic; = modified caution statistic; = standardized normal loglikelihood; = caution statistic; = personal point-biserial correlation; = statistic; = standardized normal ; = norm conformity index; AUC = area under the curve.
Furthermore, among indices with equal or greater than 70% AUC in Table 2, one index in the fair group (i.e., ) and three indices in the high predictive power group (i.e., , , and indices) showed a consistent pattern across manipulated factors. As expected, the conditions with the highest class separation (3 SD), and the lowest SDB (0.1) resulted in the highest AUCs across six indices, but we observed some differences across the number of items and sample size factors. More specifically, while with the lowest test length (10 items) and highest sample size (1,000) led to the highest AUC, , , and with the highest test length (30 items) and medium sample size (750) obtained the highest AUCs. Finally, with the highest test length (30 items) and lowest sample size (500) led to the highest AUC of 96.3% across all indices.
The next step of the analysis was to determine which combination of manipulated conditions significantly affects the AUC of person-fit indices using a four-way ANOVA. Among significant design factors with large enough effect sizes, those with the highest interaction level are reported. We expected the highest AUC in an ideal situation where sample size, the number of items, and class separation conditions were at the highest level, and the degree of bias was at the lowest level. That is the condition with 30 items, three SDs of class separation between class means, 0.1 degree of bias, and 1,000 sample size; however, not all the findings followed our expectation.
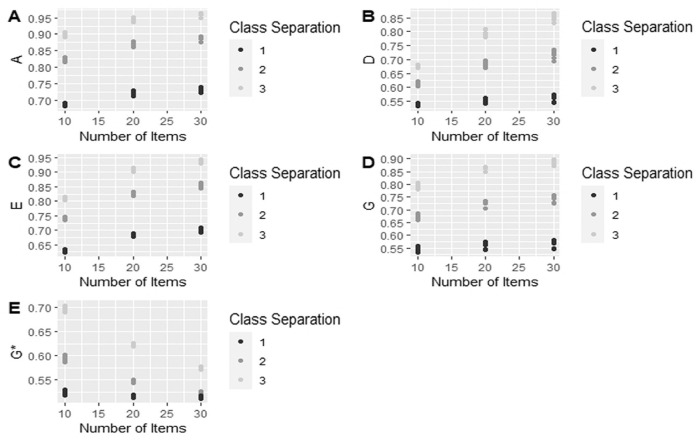
As shown in Table 3, all four person-fit statistics in the high predictive power group including , , , and showed a similar pattern of results, but with different effect sizes. The main effect of the size of cross-loading and two-way interaction of class separation by the number of items were the design factors with GES of . For the size of cross-loading, as it increased, AUC decreased. For example, we observed a lower AUC for with a cross-loading of 0.5 compared with the situation where the cross-loading was 0.3 or 0.1. The size of the main effect of the cross-loading varied across the fit index, with the G index showing a GES of 0.25, and showing a GES of 0.11, while and showed relatively small GES of 0.04 and 0.03, respectively. Regarding the interaction between class separation and the number of items, higher AUC was observed with higher levels of class separation and a higher number of items for , , , and . For example, AUC for was highest when the number of items was 30 and class means were 3 SDs apart (see Figure 2).
Table 3.
ANOVA Result and GES.
| PF statistic | Effect | GES |
|---|---|---|
| 0.11 | ||
| 0.04 | ||
| 0.04 | ||
| 0.20 | ||
| 0.25 | ||
| 0.31 | ||
| 0.03 | ||
| 0.27 | ||
| 0.44 |
Note. = number of items; = class separation; = cross-loading; PF = person-fit; GES = generalized eta-squared ( were reported), × indicates an interaction.
Figure 2.
Class Separation by the Number of Items Interaction Is Shown Across Five Person-Fit Indices.
Note. The y-axis is the area under the curve for each index.
Among five person-fit indices categorized as fair tests, the interaction effect between class separation and the number of items had a different pattern for than the other four indices. For the index, there was a two-way interaction of class separation by the number of items with a very large effect size of 0.44, showing that as the number of items decreased and class separation increased, the AUC increased. For example, the highest AUC was when the number of items was 10 and class separation was 3. For a complete ANOVA table, please see Appendix A.
Discussion and Conclusion
This study investigated a wide range of person-fit indices and offered valuable information about the ability of these statistics to detect SDB in responses. It contributes to the literature because, to the knowledge of authors, it is the first study that utilizes person-fit indices to detect SDB in a systematic simulation study. Moreover, given the importance of evaluating and monitoring SDB in both large-scale testings (e.g., scales administered within the Trends in International Mathematics and Science Study—TIMSS; Mullis & Martin, 2017), and measurements for academic research and personnel selection, this study can inform a host of measurement practices.
The results of this study lead to the recommendation of for the detection of SDB in item responses. This recommendation is anchored on the findings that showed a minimum AUC of 68.2% and a maximum AUC of 96.3% across all conditions. Also, for 72 out of 81 manipulated conditions, performed as a fair or higher-level test. Regarding the other nine conditions, the AUC was close to 70%. Therefore, the results show that this index could detect SDB across all study conditions. The second recommended index in this study was , which showed minimum and maximum AUC of 62.4% and 94.4%, respectively. This index’s strength was similar to , but with a few percent lower AUC and a lower number of simulated conditions with AUC of equal or greater than 70%. The third and fourth indices which showed strong performance were and , with an approximately similar range of AUC from 53% to 90%. Mean AUCs related to 45 out of 81 manipulated conditions were over the fair range for , but the number of covered conditions with fair predictive power was 26 for . In summary, all three person-fit statistics (i.e., , , and ) proposed by Kane and Brennan (1980) performed well in this study.
The three recommended person-fit indices were also successful in detecting other response biases in previous studies. For example, in Karabatsos’s (2003) study, overall, index detected random responding with the AUC of greater than 0.8, which is a good test. Moreover, index detected careless responding and index detected careless responding and lucky guessing as fair tests with AUC of greater than 0.7. index was also an excellent test to detect random responding with the AUC of more than 0.9. In another study, Nazari et al. (2021) used these three indices to detect careless responding in an applied study, and the results showed that with AUC of 69.1 was very close to being classified as a fair test.
For , , , and , class separation, cross-loading, and the number of items were important design factors to detect SDB. However, sample size did not influence the person statistics’ AUC to detect SDB. Regarding these indices, for most conditions that led to poor or failed AUCs, class separation was one. In agreement with what we expected, a larger difference between classes, lower degree of bias, and higher number of items led to higher AUC in person-fit statistics. The only exception was , where the lower number of items resulted in higher AUC. One unexpected finding was ’s poor performance to capture SDB by AUC of 52.9%, which was an ineffective test. In previous research (e.g., Artner, 2016; Beck et al., 2019; Dimitrov & Smith, 2006; Karabatsos, 2003; Sinharay, 2017; Tendeiro & Meijer, 2014), HT was frequently found to be a successful person-fit to capture aberrant responding. However, researchers did not attempt to address SDB in any of these studies.
The current implementation of the proposed methods and simulation study is based on dichotomous items, but existing SDB questionnaires often include polytomous items. This issue can be addressed by expanding this simulation study to cover polytomous items. For example, Emons (2008) simulated polytomous item responses based on the graded response model (e.g., Samejima, 1997). Alternatively, the current simulation can be extended to polytomous item responses after recoding each polytomous item response into binary codes. This is a reasonable approach according to the machine learning literature on the one-versus-all (OVA) approach to classification (e.g., Gao et al., 2021; Rifkin & Klautau, 2004).
It is noteworthy to say that the simulation design essentially created a multidimensional true parameterization that was unequal across different groups (classes). Ultimately, researchers would not know why a person-fit statistic identified a response as a misfitted pattern. A response may be flagged due to SDB, or it could be due to any other secondary dimension that was not modeled and that behaved differently over the classes. Therefore, the test content, the testing context, and the population tested may lead the researchers to hypothesize that SDB may be a problem. For example, one might expect SBD issues in personnel selection contexts when the stakes of the test results are high, or when attitude tests ask about sensitive topics without enough assurance of respondent anonymity. When the test administrators have reasons to believe that the test or testing context will elicit high SDB, they can apply the recommended person-fit indices to identify individuals who responded in a socially desirable way. Then, they may choose whether to remove or include the flagged responses in the subsequent analysis or decisions. For example, if researchers used the three recommended person-fit indices of , , and , small values of and , as well as large values of , may represent SDB in responses. However, to determine cutoffs for flagging individuals would require additional studies using an external measure, such as the MCSDS, or experimental manipulation of testing conditions. If the proportion of individuals with responses affected by SDB is large, it may be necessary to administer a social desirability scale (e.g., short form of MCSDS; Strahan & Gerbasi, 1972) or perform a manipulation of the testing conditions (e.g., extended crosswise model; Heck et al., 2018) to reduce SDB.
There are a variety of person-fit indices in the literature. For example, Karabatsos (2003) examined 36 different indices, but in this study, the most frequently studied statistics were used. Although person-fit indices can be used to detect SDB, they currently do not provide a way to correct responses for the effects of SDB. For that, methods that rely on the administration of an SDB scale, such as Leite and Cooper’s (2010) FMM, are needed. Also, multidimensional IRT models were developed to detect response styles (e.g., Falk & Cai, 2016), and these models could potentially be used to detect SDB without the need for administering an SDB scale. Another method that can be potentially used to detect SDB is Bayesian robust IRT outlier-detection model (Öztürk & Karabatsos, 2017).
In this study, based on a two-class model to simulate data, we assumed that some individuals respond in a socially desirable way while others do not. However, it might be possible that for a certain test condition, all individuals respond in a socially desirable way to different extents, corresponding to a one-class model.
The proposed methods of identifying SDB with person-fit indices are limited in that they only flag the complete response vector for a person as affected by SDB or not. However, it is possible that only a portion of an individual’s responses was biased, such as a few items with sensitive content within a larger survey. Therefore, there might be a potential for expanding the use of these person-fit indices as features or predictors in different machine learning classifiers to distinguish between biased and unbiased responses within an assessment and to explore the bias from multiple dimensions.
Appendix A.
Complete ANOVA Results.
| PF statistic | Effect | GES |
|---|---|---|
| 0.98 | ||
| 0.25 | ||
| 0.65 | ||
| 0.31 | ||
| 0.83 | ||
| 0.63 | ||
| 0.44 | ||
| 0.97 | ||
| 0.11 | ||
| 0.69 | ||
| 0.04 | ||
| 0.82 | ||
| 0.03 | ||
| 0.50 | ||
| 0.27 | ||
| 0.95 | ||
| 0.04 | ||
| 0.82 | ||
| 0.20 |
Note. = number of items; = class separation; = cross-loading; PF = person-fit; GES = generalized eta-squared ( were reported), × indicates an interaction.
Simulation and analysis codes are provided in the GitHub repository. https://github.com/SanazNazari/Person-Fit-Paper
Footnotes
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The authors received no financial support for the research, authorship, and/or publication of this article.
ORCID iDs: Sanaz Nazari  https://orcid.org/0000-0001-8209-5223
https://orcid.org/0000-0001-8209-5223
Walter L. Leite  https://orcid.org/0000-0001-7655-5668
https://orcid.org/0000-0001-7655-5668
References
- Artner R. (2016). A simulation study of person-fit in the Rasch model. Psychological Test and Assessment Modeling, 58(3), 531–563. https://lirias.kuleuven.be/retrieve/523896 [Google Scholar]
- Beck M. F., Albano A. D., Smith W. M. (2019). Person-fit as an index of inattentive responding: A comparison of methods using polytomous survey data. Applied Psychological Measurement, 43(5), 374–387. https://doi.org/10.1177%2F0146621618798666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernreuter R. G. (1933). Validity of the personality inventory. Personnel Journal, 11, 383–386. [Google Scholar]
- Birnbaum A. (1968). Some latent trait models and their use in inferring an examinee’s ability, contributed chapter. In Lord F. M., Novic M. R. (Eds.), Statistical theories of mental test scores (pp. 397–479). Addison-Wesley. [Google Scholar]
- Böckenholt U. (2014). Modeling motivated misreports to sensitive survey questions. Psychometrika, 79(3), 515–537. 10.1007/s11336-013-9390-9 [DOI] [PubMed] [Google Scholar]
- Cohen J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Lawrence Earlbaum Associates. [Google Scholar]
- Conijn J. M., Emons W. H., Sijtsma K. (2014). Statistic lz-based person-fit methods for noncognitive multiscale measures. Applied Psychological Measurement, 38(2), 122–136. [Google Scholar]
- Crocker L., Algina J. (1986). Introduction to classical and modern test theory. Holt, Rinehart and Winston. [Google Scholar]
- Crowne D. P., Marlowe D. (1960). A new scale of social desirability independent of psychopathology. Journal of Consulting Psychology, 24(4), 349–354. https://psycnet.apa.org/doi/10.1037/h0047358 [DOI] [PubMed] [Google Scholar]
- Crowne D. P., Marlowe D. (1964). The approval motive: Studies in evaluative dependence. Wiley. [Google Scholar]
- Dawes S. E., Palmer B. W., Allison M. A., Ganiats T. G., Jeste D. V. (2011). Social desirability does not confound reports of wellbeing or of socio-demographic attributes by older women. Ageing & Society, 31(3), 438–454. 10.1017/S0144686X10001029 [DOI] [Google Scholar]
- Dimitrov D., Smith R. M. (2006). Adjusted Rasch person-fit statistics. Journal of Applied Measurement, 7, 170–183. [PubMed] [Google Scholar]
- Donlon T. F., Fischer F. E. (1968). An index of an individual’s agreement with group-determined item difficulties. Educational and Psychological Measurement, 28(1), 105–113. https://psycnet.apa.org/doi/10.1177/001316446802800110 [Google Scholar]
- Drasgow F., Levine M. V., Williams E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. British Journal of Mathematical and Statistical Psychology, 38(1), 67–86. 10.1111/j.2044-8317.1985.tb00817.x [DOI] [Google Scholar]
- Embretson S. E., Reise S. P. (2013). Item response theory. Psychology Press. [Google Scholar]
- Emons W. H. (2008). Nonparametric person-fit analysis of polytomous item scores. Applied Psychological Measurement, 32(3), 224–247. 10.1177/0146621607302479 [DOI] [Google Scholar]
- Falk C. F., Cai L. (2016). A flexible full-information approach to the modeling of response styles. Psychological Methods, 21(3), 328–347. 10.1037/met0000059 [DOI] [PubMed] [Google Scholar]
- Fernandez E., Woldgabreal Y., Guharajan D., Day A., Kiageri V., Ramtahal N. (2019). Social desirability bias against admitting anger: Bias in the test-taker or bias in the test? Journal of Personality Assessment, 101(6), 644–652. 10.1080/00223891.2018.1464017 [DOI] [PubMed] [Google Scholar]
- Ferrando P. J. (2005). Factor analytic procedures for assessing social desirability in binary items. Multivariate Behavioral Research, 40(3), 331–349. 10.1207/s15327906mbr4003_3 [DOI] [PubMed] [Google Scholar]
- Fisher T. D., Moore Z. T., Pittenger M. J. (2012). Sex on the brain? An examination of frequency of sexual cognitions as a function of gender, erotophilia, and social desirability. Journal of Sex Research, 49(1), 69–77. 10.1080/00224499.2011.565429 [DOI] [PubMed] [Google Scholar]
- Gao X., He Y., Zhang M., Diao X., Jing X., Ren B., Ji W. (2021). A multiclass classification using one-versus-all approach with the differential partition sampling ensemble. Engineering Applications of Artificial Intelligence, 97, 104034. 10.1016/j.engappai.2020.104034 [DOI] [Google Scholar]
- Hallquist M. N., Wiley J. F. (2018). MplusAutomation: An R package for facilitating large-scale latent variable analyses in M plus. Structural Equation Modeling: A Multidisciplinary Journal, 25(4), 621–638. 10.1080/10705511.2017.1402334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanley J. A., McNeil B. J. (1982). The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology, 143(1), 29–36. 10.1148/radiology.143.1.7063747 [DOI] [PubMed] [Google Scholar]
- Harnisch D., Linn R. (1981). Analysis of item response patterns: Questionable test data and dissimilar curriculum practices. Journal of Educational Measurement, 18(3), 133–146. http://www.jstor.org/stable/1434737 [Google Scholar]
- Heck D. W., Hoffmann A., Moshagen M. (2018). Detecting nonadherence without loss in efficiency: A simple extension of the crosswise model. Behavior Research Methods, 50(5), 1895–1905. 10.3758/s13428-017-0957-8 [DOI] [PubMed] [Google Scholar]
- Holbrook A. L., Krosnick J. A. (2010). Social desirability bias in voter turnout reports: Tests using the item count technique. Public Opinion Quarterly, 74(1), 37–67. 10.1093/poq/nfp065 [DOI] [Google Scholar]
- Hong M., Lin L., Cheng Y. (2021). Asymptotically corrected person fit statistics for multidimensional constructs with simple structure and mixed item types. Psychometrika, 86, 464–488. 10.1007/s11336-021-09756-3 [DOI] [PubMed] [Google Scholar]
- Johnson R. E., Rosen C. C., Djurdjevic E. (2011). Assessing the impact of common method variance on higher order multidimensional constructs. Journal of Applied Psychology, 96(4), 744–761. https://psycnet.apa.org/doi/10.1037/a0021504 [DOI] [PubMed] [Google Scholar]
- Jones E. E., Sigall H. (1971). The bogus pipeline: A new paradigm for measuring affect and attitude. Psychological Bulletin, 76(5), 349–364. https://psycnet.apa.org/doi/10.1037/h0031617 [Google Scholar]
- Kamata A., Bauer D. J. (2008). A note on the relation between factor analytic and item response theory models. Structural Equation Modeling: A Multidisciplinary Journal, 15(1), 136–153. 10.1080/10705510701758406 [DOI] [Google Scholar]
- Kaminska O., Foulsham T. (2016). Eye-tracking social desirability bias. Bulletin of Sociological Methodology/Bulletin de Méthodologie Sociologique, 130(1), 73–89. https://doi.org/10.1177%2F0759106315627591 [Google Scholar]
- Kane M. T., Brennan R. L. (1980). Agreement coefficients as indices of dependability for domain-referenced tests. Applied Psychological Measurement, 4(1), 105–126. https://doi.org/10.1177%2F014662168000400111 [Google Scholar]
- Kaplan D. (2008). Structural equation modeling: Foundations and extensions (Vol. 10). SAGE. [Google Scholar]
- Karabatsos G. (2003). Comparing the aberrant response detection performance of thirty-six person-fit statistics. Applied Measurement in Education, 16(4), 277–298. 10.1207/S15324818AME1604_2 [DOI] [Google Scholar]
- Kim Y., Muthén B. O. (2009). Two-part factor mixture modeling: Application to an aggressive behavior measurement instrument. Structural Equation Modeling, 16(4), 602–624. https://doi.org/10.1080%2F10705510903203516 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leite W. L., Beretvas S. N. (2005). Validation of scores on the Marlowe-Crowne social desirability scale and the balanced inventory of desirable responding. Educational and Psychological Measurement, 65(1), 140–154. https://doi.org/10.1177%2F0013164404267285 [Google Scholar]
- Leite W. L., Cooper L. A. (2010). Detecting social desirability bias using factor mixture models. Multivariate Behavioral Research, 45(2), 271–293. 10.1080/00273171003680245 [DOI] [PubMed] [Google Scholar]
- Leite W. L., Nazari S. (2020). Marlowe-Crowne social desirability scale. In Zeigler-Hill V., Shackelford T. K. (Eds.), Encyclopedia of personality and individual differences. Springer; (pp. 2751–2753). 10.1007/978-3-319-24612-3_45 [DOI] [Google Scholar]
- Leng C. H., Huang H. Y., Yao G. (2020). A social desirability item response theory model: Retrieve–deceive–transfer. Psychometrika, 85(1), 56–74. 10.1007/s11336-019-09689-y [DOI] [PubMed] [Google Scholar]
- Linacre J. M. (2002). What do infit and outfit, mean-square and standardized mean. Rasch Measurement Transactions, 16(2), 878. [Google Scholar]
- Lubke G. H., Muthén B. O. (2005). Investigating population heterogeneity with factor mixture models. Psychological Methods, 10(1), 21–39. https://psycnet.apa.org/doi/10.1037/1082-989X.10.1.21 [DOI] [PubMed] [Google Scholar]
- Lubke G. H., Muthén B. O. (2007). Performance of factor mixture models as a function of model size, covariate effects, and class-specific parameters. Structural Equation Modeling, 14(1), 26–47. 10.1080/10705510709336735 [DOI] [Google Scholar]
- Meijer R. R. (1994). The number of Guttman errors as a simple and powerful person-fit statistic. Applied Psychological Measurement, 18(4), 311–314. https://doi.org/10.1177%2F014662169401800402 [Google Scholar]
- Meijer R. R., Sijtsma K. (2001). Methodology review: Evaluating person fit. Applied Psychological Measurement, 25(2), 107–135. https://doi.org/10.1177%2F01466210122031957 [Google Scholar]
- Mullis I. V., Martin M. O. (2017). TIMSS 2019 assessment frameworks. International Association for the Evaluation of Educational Achievement. [Google Scholar]
- Muthén B., Shedden K. (1999). Finite mixture modeling with mixture outcomes using the EM algorithm. Biometrics, 55(2), 463–469. 10.1111/j.0006-341X.1999.00463.x [DOI] [PubMed] [Google Scholar]
- Muthén L. K., Muthén B. O. (1998. –2017). Mplus user’s guide (8th ed.). Muthén & Muthén. [Google Scholar]
- Nazari S., Leite W. L., Huggins-Manley A. C. (2021). Detecting Careless Responses to Assessment Items in a Virtual Learning Environment Using Person-fit Indices and Random Forest. In Proceedings of the 14th International Conference on Educational Data Mining, 635–640. https://educationaldatamining.org/EDM2021/virtual/static/pdf/EDM21_paper_155.pdf
- Olejnik S., Algina J. (2003). Generalized eta and omega squared statistics: Measures of effect size for some common research designs. Psychological Methods, 8(4), 434–447. https://psycnet.apa.org/doi/10.1037/1082-989X.8.4.434 [DOI] [PubMed] [Google Scholar]
- Öztürk N. K., Karabatsos G. (2016). A Bayesian Robust IRT Outlier-Detection Model. Applied Psychological Measurement, 41(3), 195–208. doi: 10.1177/0146621616679394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulhus D. L. (1984). Two-component models of socially desirable responding. Journal of Personality and Social Psychology, 46(3), 598–609. https://psycnet.apa.org/doi/10.1037/0022-3514.46.3.598 [Google Scholar]
- Paulhus D. L. (1991). Measurement and control of response bias. In Robinson J. P., Shaver P. R., Wrightsman L. S. (Eds.), Measures of personality and social psychological attitudes (pp. 17–59). Academic Press. 10.1016/B978-0-12-590241-0.50006-X [DOI] [Google Scholar]
- Podsakoff P. M., MacKenzie S. B., Lee J. Y., Podsakoff N. P. (2003). Common method biases in behavioral research: A critical review of the literature and recommended remedies. Journal of Applied Psychology, 88(5), 879–903. 10.1037/0021-9010.88.5.879 [DOI] [PubMed] [Google Scholar]
- R Core Team. (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing. http://www.R-project.org/ [Google Scholar]
- Rifkin R., Klautau A. (2004). In defense of one-vs-all classification. The Journal of Machine Learning Research, 5, 101–141. https://dl.acm.org/doi/10.5555/1005332.1005336 [Google Scholar]
- Rupp A. A. (2013). A systematic review of the methodology for person fit research in item response theory: Lessons about generalizability of inferences from the design of simulation studies. Psychological Test and Assessment Modeling, 55(1), 3–38. [Google Scholar]
- Samejima F. (1997). Graded response model. In Handbook of modern item response theory (pp. 85–100). Springer. 10.1007/978-1-4757-2691-6_5 [DOI] [Google Scholar]
- Sato T. (1975). The construction and interpretation of SP tables. Meiji Tosho. [Google Scholar]
- Sijtsma K. (1986). A coefficient of deviance of response patterns. Kwantitatieve Methoden, 7(22), 131–145. https://research.tilburguniversity.edu/files/1030745/COEFFICI.PDF [Google Scholar]
- Sijtsma K., Meijer R. R. (1992). A method for investigating the intersection of item response functions in Mokken's nonparametric IRT model. Applied Psychological Measurement, 16(2), 149–157. 10.1177/014662169201600204 [DOI] [Google Scholar]
- Sinharay S. (2015). Assessment of person fit for mixed-format tests. Journal of Educational and Behavioral Statistics, 40(4), 343–365. https://doi.org/10.3102%2F1076998615589128 [Google Scholar]
- Sinharay S. (2017). How to compare parametric and nonparametric person-fit statistics using real data. Journal of Educational Measurement, 54(4), 420–439. 10.1111/jedm.12155 [DOI] [Google Scholar]
- Snijders T. A. (2001). Asymptotic null distribution of person fit statistics with estimated person parameter. Psychometrika, 66(3), 331–342. 10.1007/BF02294437 [DOI] [Google Scholar]
- Stark T. H., van Maaren F. M., Krosnick J. A., Sood G. (2019). The impact of social desirability pressures on whites’ endorsement of racial stereotypes: A comparison between oral and ACASI reports in a national survey. Sociological Methods & Research, 51(2), 605–631. https://doi.org/10.1177%2F0049124119875959 [Google Scholar]
- Strahan R., Gerbasi K. C. (1972). Short, homogeneous versions of the Marlow-Crowne social desirability scale. Journal of Clinical Psychology, 28(2), 191–193. [DOI] [Google Scholar]
- Tape T. (n.d.). The Area Under an ROC Curve. University of Nebraska Medical Center. http://gim.unmc.edu/dxtests/ROC3.htm [Google Scholar]
- Tatsuoka K. K., Tatsuoka M. M. (1982). Detection of aberrant response patterns and their effect on dimensionality. Journal of Educational Statistics, 7(3), 215–231. https://doi.org/10.3102%2F10769986007003215 [Google Scholar]
- Tatsuoka K. K., Tatsuoka M. M. (1983). Spotting erroneous rules of operation by the individual consistency index. Journal of Educational Measurement, 20(3), 221–230. http://www.jstor.org/stable/1434713 [Google Scholar]
- Tendeiro J. N. (2017). The lz (p)* person-fit statistic in an unfolding model context. Applied Psychological Measurement, 41(1), 44–59. https://doi.org/10.1177%2F0146621616669336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tendeiro J. N., Meijer R. R. (2014). Detection of invalid test scores: The usefulness of simple nonparametric statistics. Journal of Educational Measurement, 51(3), 239–259. 10.1111/jedm.12046 [DOI] [Google Scholar]
- Tendeiro J. N., Meijer R. R., Niessen A. S. M. (2016). PerFit: An R package for person-fit analysis in IRT. Journal of Statistical Software, 74(5), 1–27. 10.18637/jss.v074.i05 [DOI] [Google Scholar]
- Tourangeau R., Rips L. J., Rasinski K. (2000). The psychology of survey response. Cambridge University Press. [Google Scholar]
- Van der Flier H. (1977). Environmental factors and deviant response patterns. Basic problems in cross cultural psychology. Swets & Seitlinger. [Google Scholar]
- Van der Flier H. (1980). Vergelijkbaarheid van individuele testprestaties. Swets & Zeitlinger. [Google Scholar]
- Van der Flier H. (1982). Deviant response patterns and comparability of test scores. Journal of Cross-Cultural Psychology, 13(3), 267–298. https://doi.org/10.1177%2F0022002182013003001 [Google Scholar]
- Vésteinsdóttir V., Joinson A., Reips U. D., Danielsdottir H. B., Thorarinsdottir E. A., Thorsdottir F. (2019). Questions on honest responding. Behavior Research Methods, 51(2), 811–825. 10.3758/s13428-018-1121-9 [DOI] [PubMed] [Google Scholar]
- Warner S. L. (1965). Randomized response: A survey technique for eliminating evasive answer bias. Journal of the American Statistical Association, 60(309), 63–69. 10.1080/01621459.1965.10480775 [DOI] [PubMed] [Google Scholar]
- Wilcox R. (2017, April 27). New statistical methods would let researchers deal with data in better, more robust ways. The Conversation. https://theconversation.com/new-statistical-methods-would-let-researchers-deal-with-data-in-better-more-robust-ways-67981