Equidistant Response Options on Likert-Type Instruments: Testing the Interval Scaling Assumption Using Mplus

Abstract

The purpose of the present study was to provide the means to evaluate the “interval-scaling” assumption that governs the use of parametric statistics and continuous data estimators in self-report instruments that utilize Likert-type scaling. Using simulated and real data, the methodology to test for this important assumption is evaluated using the popular software Mplus 8.8. Evidence on meeting the assumption is provided using the Wald test and the equidistant index. It is suggested that routine evaluations of self-report instruments engage the present methodology so that the most appropriate estimator will be implemented when testing the construct validity of self-report instruments.

Since the pioneering work of Guttman, Thurstone, and Likert, several attempts to categorize the continuum of traits, skills, and abilities have been introduced (see Nunnally, 1978). Among the most prevalent are Likert-type scales (Likert, 1932) that usually engage a disagreement-to-agreement ordering. Thus, Likert-type data represent a categorical representation of a latent unidimensional continuous construct (Andrich, 1978b; Spratto, 2018). The present study deals with the inherent researcher-made assumption underlying these scales that adjacent options in ordered categorical schemes are equidistant (Henkel, 1975). In other words, the distance between strongly disagree and disagree is the same as the one between agree and strongly agree. Certainly, this is tentative and, should for that reason be, a testable assumption (Hensler & Stipak, 1979).

Figure 1 shows an equal and unequal spacing scheme using Likert-type disagree-to-agree scaling. As shown in the upper panel of Figure 1, the distance between adjacent disagree and agree options is fixed to 2.5 raw units of a ruler. This figure suggests that the conceptual distance between disagree and strongly disagree is the same as the one between agree and strongly agree. If, however, one considers that strong disagreements/agreements are positioned at the tails of a normally distributed latent variable describing the disagreement-to-agreement continuum, then one may favor the unequal spacing system shown in the lower panel of Figure 1, which suggests that more extreme responses (i.e., “strong” feelings) are less likely to occur compared with less extreme responses, thus, occupying less measurement space. If the above example is extended to the inclusion of a 6-point Likert-type scaling in which responses are absolute disagreement, major disagreement, minor disagreement, neither agree nor disagree, minor agreement, major agreement, and complete agreement, it is even harder to conceive equal conceptual spacing between response options as there aren’t any good reasons to suggest that the distance between absolute and major disagreement is the same as the one between major disagreement and minor disagreement. The latter likely represents a larger conceptual distance compared with the former.

Figure 1.

Assuming Equal Interval Scaling (Upper Panel) or Unequal (Lower Panel)

Note. The unequal threshold system suggests that the frequency of responses lessens as they become more extreme (strong disagreements or agreements). Upper panel: Equal distances between response options. Lower panel: Unequal distances between response options.

The necessity of verifying the “equal interval” assumption of Likert-type scaling systems stems from the unjustified use of parametric statistical methods using continuous estimators in the analyses of these data as they are oftentimes treated as being continuous. Based on the pioneering work of Stevens (1946), a salient difference between ordinal and interval measurement is that the latter assumes both rank ordering but also equal spacing. If the data do not satisfy equal interval scaling, parametric techniques assuming normality and interval measurement are invalid, resulting in the distortion of model fit statistics (Hutchinson & Olmos, 1998; Vigderhous, 1977). There is a solution to this potential problem: there are several analytical models that do not require the interval scaling assumption such as the graded response model (GRM, Muraki, 1992) or Andrich’s (1978a) model for polytomous responses. What is problematic is if the empirical study literature points to the misuse of proper analytical methodologies with categorical data when they are treated as being continuous (see Martens, 2005).

Here, an important distinction needs to be made which refers to the types of models employed. Using measured variables, tests of point estimates such as t-tests and ANOVA have shown robustness in assuming interval scaling (Gaito, 1980; Garifio & Perla, 2007). However, results from simulation studies using latent variable modeling have shown that modeling Likert-type data as continuous has been associated with biased parameter estimates as the continuous factor model is essentially misspecified when used with ordinal data (Beauducel & Herzberg, 2006; Rhemtulla et al., 2012), especially when the number of response options is small (Johnson & Creech, 1983. There is unequivocal evidence that asymmetric category thresholds bias the maximum likelihood estimator when being treated as symmetric (Babakus et al., 1987; DiStefano, 2002; Dolan, 1994; Forero et al., 2009; Green et al., 1997). For example, the simulation study by Beauducel and Herzberg (2006) showed that under all conditions of the confirmatory factor analysis (CFA) model (1 factor model with 5 items to 8 factor model with 40 items) number of items, number of categories (2–6) and sample sizes (250–1,000) the maximum likelihood (ML) estimator was inferior compared with the diagonally weighted least squares estimator. Even the robust estimators of ML (Satorra & Bentler, 1988, 1994; Yuan & Bentler, 1998; Yuan et al., 2011) showed biases in the presence of asymmetrical thresholds (Potthast, 1993; Rigdon & Fergusson, 1991). As the number of options increases to five or more, the bias becomes smaller as the ordered variables approach continuity (Johnson & Creech, 1983; B. O. Muthen & Kaplan, 1985; Rhemtulla et al., 2012; Sullivan & Artino, 2013; Zumbo & Zimmerman, 1993), although these studies have not focused on the distances across response options. This conclusion is in line with the observation of Bollen and Barb (1981) that a scaling system with 1–4 options will be weakly related to a latent construct compared with being measured in a continuous manner. Others have pointed to the inappropriateness of assuming rather than confirming the interval scaling assumption (Jakobsson, 2004; Jamieson, 2004; Knapp, 1990; O’Brien, 1979; Pohl, 1981; Spector, 1980). To evaluate whether validity studies “err” in that direction a systematic review of the literature was conducted in major counseling psychology journals as our present evaluation dealt with a well-known instrument in health and well-being, the Positive Youth Development Inventory (PYDS, Arnold et al., 2012). The goal of this review was to evaluate the extent to which studies ascertain construct validity using analytical means that are appropriate for continuous data, without testing whether ordered data satisfy interval scaling measurement. The present evaluation comes following early concerns that structural equation modeling (SEM) practices observed in counseling psychology journals do not engage in best practices as recommended by SEM experts (Martens, 2005). These results are briefly described in the next section.

A Review of Validity Studies in Counseling Psychology

A systematic review of the literature on the use of appropriate analytical methods with ordered data was conducted. Fifty-seven validity studies published between 2018 and 2021 from the journals: Measurement and Evaluation in Counseling and Development, Journal of Counseling and Development, Journal of Counseling Psychology, and Professional School Counseling met the criteria for inclusion in this brief review. The extraction procedure involved a person reading all titles, abstracts, and, subsequently, the manuscripts to verify appropriateness for inclusion and availability of pertinent data. Specific inclusionary criteria involved: (a) validation of an instrument, (b) use of a psychometrics model such as exploratory factor analysis, CFA, or item response theory (IRT), (c) use of a categorical/ordered scaling system, and (d) inclusion of information about the analytical methodology employed. Appropriate analytical methods involved IRT and CFA methodologies and estimators that accounted for the categorical nature of the data (e.g., maximum likelihood robust, weighted least squares mean and variance adjusted) or non-normality (e.g., Bayesian methodologies). As shown in Table 1, 33 of the published studies (57.9%) specifically mentioned methodologies that were appropriate for categorical/ordered data. Interestingly, 24 studies (42.1%) either did not mention or ignored the categorical nature of the data by assuming that data were continuous, meeting the assumption of equidistant measurement. Of these, 42.1% there is likely a large proportion that utilized inappropriate analytical methods. This raises serious concerns about the implicit assumption that ordered data (such as those utilizing Likert-type scales) can be treated as continuous, in that they meet the interval scaling assumption inherent in continuous data.

Table 1.

Description of Validity Studies, Scaling, and Analytical Methodologies

Study	Data scaling	Analytical method	Estimator	Appropriate for categorical data
Akdogan et al. (2018)	Likert	CFA	N.A.	No
Aldawsari et al. (2021)	Likert	CFA	N.A.	No
Autin et al. (2019)	Likert	CFA	N.A.	No
Bardoshi et al. (2019)	Likert	CFA	N.A.	No
Blau & DiMino (2019)	Likert	CFA	N.A.	No
Bloom & Dillman-Taylor (2020)	Likert	EFA	N.A.	No
Cho et al. (2018)	Likert	CFA	MLMV	Yes
Cimsir & Akdogan (2020)	Likert	CFA	MLR	Yes
Dillman-Taylor et al. (2019)	Likert	CFA	MLR	Yes
Erford et al. (2021)	Likert	CFA	WLSMV	Yes
Fu & Zhang (2019)	Likert	CFA	ML	No
Ganho-Avila et al. (2019)	Likert	CFA	MLR	Yes
Ghabrial & Andersen (2020)	Likert	CFA	ML	No
Ghosh et al. (2021)	Likert	CFA	WLSMV	Yes
Gonzalez et al. (2021)	Likert	CFA	N.A.	No
Greene (2019)	Likert	EFA	N.A.	No
Griffin et al. (2018)	Likert	CFA	MLR	Yes
Halamova et al. (2021)	Likert	IRT	MLR	Yes
Hiles-Howard et al. (2019)	Likert	CFA	ML	No
Johnson & Karcher (2019)	Likert	CFA	FIML	No
Johnson et al. (2021)	Likert	CFA	FIML	No
Kim et al. (2021)	Likert	CFA	FIML	No
Kivlighan et al. (2018)	Likert	CFA	Bayes	Yes
Lau et al. (2019)	Likert	CFA	ML	No
Lee et al. (2019)	Likert	CFA	N.A.	No
Lee et al. (2021)	Likert	CFA	WLSMV	Yes
Levant & Parent (2019)	Likert	IRT	N.A.	Yes
Levant et al. (2020)	Likert	CFA	MLR	Yes
Lim & Kim (2020)	Likert	CFA	WLSMV	Yes
Liu et al. (2018)	Likert	CFA	WLSMV	Yes
Lu et al. (2018)	Likert	CFA	Bollen-Stine	Yes
Ludlow et al. (2019)	Likert	IRT	JMLE	Yes
Luo et al. (2021)	Likert	CFA	ML	No
Martin et al. (2020)	Likert	CFA	WLSMV	Yes
Mazahreh et al. (2019)	Likert	CFA	Bollen-Stine	Yes
Moate et al. (2019)	Likert	CFA	MLR	Yes
Oh & Shillingofrd-Butler (2021)	Likert	CFA	MLR	Yes
Pederson et al. (2021)	Likert	CFA	N.A.	No
Perez-Rojas et al. (2019)	Likert	IRT	N.A.	Yes
Poynton et al. (2019)	Likert	IRT	N.A.	Yes
Pozza et al. (2019)	Likert	CFA	N.A.	No
Rowan-Kenyon et al. (2021)	Likert	CFA	Bollen-Stine	Yes
Shea et al. (2019)	Likert	CFA	MLR	Yes
Shin et al. (2018)	Likert	CFA	MLR	Yes
Simons (2018)	Likert	EFA	N.A.	No
Swank et al. (2020)	Nominal	CFA	WLSMV	Yes
Tadlock-Marlo & Hill (2019)	Likert	IRT	N.A.	Yes
TaeHyuk-Keum et al. (2018)	Likert	CFA	MLR	Yes
Toland et al. (2021)	Likert	IRT	ML-EAP	Yes
Trub et al. (2020)	Likert	CFA	FIML	No
Veronese & Pepe (2019)	Likert	CFA	N.A.	No
Waldrop et al. (2019)	Likert	CFA	WLSMV	Yes
Wang et al. (2019)	Likert	CFA	ML	No
Watson et al. (2019)	Likert	CFA	Bollen-stine	Yes
Watson et al. (2020)	Likert	CFA	ML	No
Xavier et al. (2019)	Likert	CFA	WLSMV	Yes
Young & Bryan (2018)	Likert	CFA	Bollen-Stine	Yes

Note. CFA = confirmatory factor analysis; N.A. = not available; EAP = Expected A posteriori; EFA = exploratory factor analysis; MLMV = maximum likelihood mean and variance adjusted; MLR = maximum likelihood robust; WLSMV = weighted least squares mean and variance adjusted; ML = maximum likelihood; IRT = item response theory; FIML = full information maximum likelihood; JMLE = joint maximum likelihood estimation.

The purpose of the present study was to evaluate the equal interval assumption when validating instruments using Likert-type scaling systems. Using the popular software Mplus 8.8 (Muthén & Muthén, 1998–2018) routines for evaluating interval scaling at the item level are provided in Appendix A. For that purpose, the GRM (Muraki, 1992) was utilized using the measurement of caring from the PYDS (Arnold et al., 2012).

Method

Participants

Data came from a random sample of 500 participants (from a total of 5,443) who took the PYDS as part of participating in online assessments via a governmental platform in the Kingdom of Saudi Arabia. Our choice to select a random sample was based on avoiding excessive levels of power and observing trivial, albeit significant effects. Using the MacCallum et al. (1996) approach, the power for a unidimensional CFA model with 8 indicators was 85% when contrasting an acceptable (i.e., RMSEA=0.05) from an unacceptable model (i.e., RMSEA=0.08). Furthermore, a Monte Carlo simulation was run to ensure the stability of the slopes and intercepts as per a 2PL model. Results indicated that using 500 replicated samples with n = 500 power levels were equal to 99% for discrimination parameters equal to 1 and intercept terms equal to 0.5. Coverage for these parameters ranged between 94.2% and 96.6%. Thus, our proposed sample size would likely result in unbiased estimates of model parameters without the burden of enhanced power levels.

Instrument

Arnold et al. (2012) developed the PYDS. The PYDS utilizes 55 items to assess six basic attributes, namely, Competence (14 items), Character (9 items), Connection (8 items), Caring (8 items), Confidence (9 items), and Contribution (7 items). Participants respond using a 4-point Likert-type scale anchored from 1 = strongly disagree to 4 = strongly agree. Using translation and back translation methodologies (Brislin, 1970), the original scale was translated into Arabic. To control for response bias (i.e., extreme response style, acquiescence, see Bolt & Johnson, 2009), developers of the Arabic version chose to reverse-code eight items. Validity studies have confirmed the factorial structure of the Arabic PYDS (Tsaousis et al., 2021). For the purposes of the present evaluation, the 8-item Caring domain was used that assesses a person’s proclivity to be empathic and caring toward others (see Appendix B). It consists of eight items that utilize a 4-point scaling system anchored between strongly disagree and strongly agree. The mid-response option that was available in the original version was deleted from the Arabic version of the scale in support of several criticisms raised about the necessity of the middle option and concerns about the midpoint response style.

Data Analysis: GRM to Test Simple Structures With Ordered Data

Given the polytomous nature of the data, the GRM (Muraki, 1992; Samejima, 1969) was deemed the appropriate choice for these data. Among polytomous models, there are two main categories: The different models that involve cumulative probabilities and the adjacent models. Adjacent models estimate the probability of moving from one response option to the next. However, because they are amenable to reversals and can result in the measurement of unstable parameters, especially with small samples (e.g., Spratto, 2018), they were not utilized here. Instead, we used the cumulative model in which the probability of responding to one category is contrasted against the sum of the options above it. For example, the probability of responding to Category 1 (e.g., strongly disagree) is contrasted with the probability of selecting any one of the categories above Category 1 (i.e., 2, 3, 4, or strongly disagree against the options disagree–agree–strongly agree).

The GRM represents an extension of the typical 2PL model, which has a single discrimination parameter (α_i) and a single item location (β_i). The extension involves the presence of thresholds equal to the number of categories−1 (termed β_iκ) and, thus, operating characteristic curves (OCCs) are fit for each threshold representing the boundary between two adjacent categories. The conditional probability of item endorsement is estimated as follows:

$$P(Y_{\mathrm{ij}}=1|a_i,b_{i\kappa })=\frac{e^{a_i({\theta }_j-{\beta }_{i\kappa })}}{1+e^{a_i({\theta }_j-{\beta }_{i\kappa })}},$$ (1)

Thus, the probability that person j will endorse the threshold (β_κ) of item i is a function of a single item discrimination parameter α_i and person’s j ability level theta (θ_j).

A visual examination of a sample item (Item 5 from the Caring subscale of the PYDS-see all items in Appendix B) is shown in Figures 2 and 3 to illustrate the merits of the cumulative logit model. Figure 2 displays an OCC and Figure 3 a category characteristic curve for Item 5 of the caring subscale. As shown in Figure 2, the first threshold was −2.56 suggesting that individuals with theta levels equal to −2.56 and below had a 50% chance to endorse strongly disagree. In other words, individuals with very low caring levels would strongly disagree with the statement that “Other people’s feelings matter to me.” Caring levels (theta) would have to be increased to −1.55 for individuals to have a 50% chance to select the disagree options (1 and 2), compared with the two agree options (3 and 4). Last, above zero thetas (i.e., θ =0.006) would be required for a person to select strongly agree compared with the three previous options.

Figure 2.

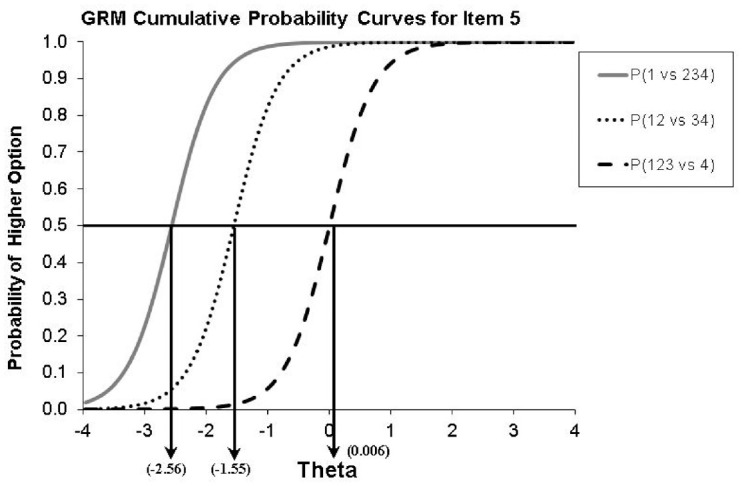
OCCs for Item 5 of the “Caring” Subscale of the PYDS With Category Boundary Locations b_1-i5 = −2.56, b_2-i5 = −1.55, and b_3-i5 = 0.006

Note. The vertical lines point to the theta estimate required by a person to have a 50% chance of responding in that category or higher. GRM = graded response model; OCCs = operating characteristic curves; PYDS = Positive Youth Development Scale.

Figure 3.

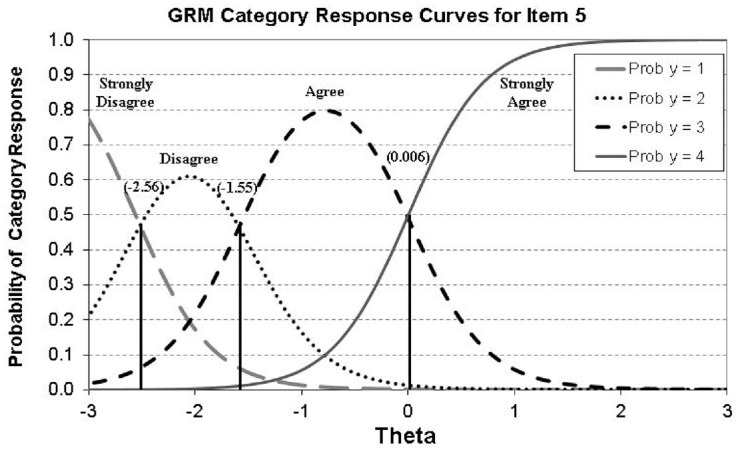
CCCs for Item 5 of the “Caring” Subscale of the PYDS (i.e., Other People’s Feelings Matter to Me)

Note. CCCs = category characteristic curves; GRM = graded response model; PYDS = Positive Youth Development Scale; T1 = theta required to respond disagree compared with strongly disagree; T2 = theta required to respond agree compared with disagree; T3 = theta required to respond strongly agree compared with agree.

Two analytical means were involved to assess the equidistance of the response options: the Wald test, and the equidistance index. The Wald test was employed to evaluate the equidistance hypothesis using a stepwise approach (testing one item at a time). The equidistance index proposed by Spratto (2018) was used as the difference of differences that is subtracting the difference between thresholds 1 versus 2 from 2 versus 3. A value of the index equal to zero would suggest equidistance among response options and satisfaction with the interval scaling assumption. Positive values of the index would suggest that the distance between Thresholds 2 and 3 is greater compared with the distance between Thresholds 1 and 2 and vice versa. Since the metric of the index is in logits, it is easy to understand the magnitude of non-equivalent thresholds but also to evaluate them using effect size indicators as suggested earlier (e.g., Dorans & Holland, 1992). For example, threshold differences within an item were termed small when <0.45 logits, medium when between 0.45 and 0.89 logits and large when ≥0.90 logits (see also Holland & Thayer, 1988; Zwick et al., 1999).

Testing the Equivalence of Thresholds: An Example Using the Construct of “Caring”

After fitting the GRM model to the data results indicated acceptable model fit (−2LL=6,703.68; M₂[244]=556.33, p<.001, RMSEA=0.05; AIC=6,767.68; BIC=6,902.55). Marginal reliability was equal to 0.81, which was acceptable. Figure 4 shows the Test Information Function in which the area of largest sensitivity is to the left of the figure (suggesting that the measure is highly sensitive to low levels of the latent trait).

Figure 4.

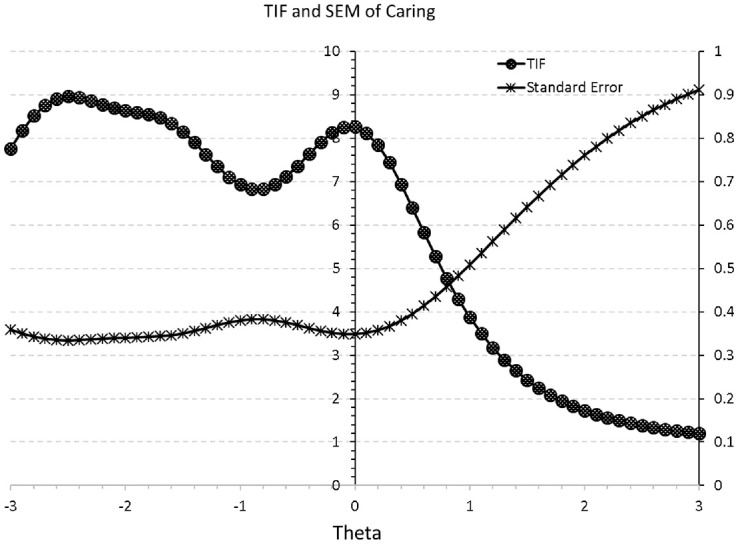
TIF and Conditional SEM of the Caring Subscale of the PYDS.

Note. The scaling at zero is for information and the secondary scaling is at +3 logits for SEM. PYDS = Positive Youth Development Scale; TIF = Test Information Function; SEM = Standard Error of Measurement.

After specifying equidistant thresholds, results indicated that all but two items failed to exhibit equal intervals (see Table 2) using the Wald test. The equidistant items were Numbers 4 and 8. Given that only 2/8 items (25%) showed equidistance in thresholds, the treatment of the current ordered data as continuous is prohibited. Further information was provided by the equidistance index. After subtracting 1–2 difference in thresholds from the 2–3 difference, results indicated that the distance between Thresholds 2 and 3 was larger compared with that of Thresholds 1 and 2, and this finding was consistent across all items but varied in magnitude. As shown in Table 2, there were three effects larger than large, three medium sized ones, and two that fall in the “small” range. This finding suggests that given the present sample and the current scale the distance between strongly disagree and disagree was smaller compared with the conceptual distance between the options agree and strongly agree. Thus, with the present Likert-type data, the assumption of interval scaling was violated. Consequently, in principle, the use of estimators in factor analytic models that do not account for the categorical nature of the data will be inappropriate and would hence likely lead to erroneous conclusions. Furthermore, the employment of estimators that account for non-normal, non-equidistant data needs to be utilized.

Table 2.

Equidistance Between Thresholds in the Caring Subscale of the PYDS.

Item	Discrimination	Threshold/SE		Diff. thresholds/SE of diff.		E.S. convention	Z-test	Wald test	df	Equidistance index
Item 1	1.866	−3.306	0.338	—	—	—	—	—	—	—
Threshold 1–2		−2.825	0.266	0.481	0.210	—	—	—	—	—
Threshold 2–3		−0.488	0.080	2.338	0.249	—	—	—	—	—
Diff-Thr. Item 1		—	—	−1.857	0.327	Large	−5.678***	32.241***	1	1.857
Item 2	1.992	−2.911	0.268	—	—	—	—	—	—	—
Threshold 1–2		−1.683	0.136	1.228	0.212	—	—	—	—	—
Threshold 2–3		0.098	0.074	1.781	0.143	—	—	—	—	—
Diff-Thr. Item 2		—	—	−0.554	0.233	Medium	−2.381*	5.670*	1	0.554
Item 3	1.061	−4.550	0.568	—	—	—	—	—	—	—
Threshold 1–2		−2.057	0.230	2.493	0.434	—	—	—	—	—
Threshold 2–3		0.770	0.129	2.828	0.295	—	—	—	—	—
Diff-Thr. Item 3		—	—	−0.335	0.398	Small	−0.841	0.708	1	0.335
Item 4	1.490	−3.324	0.344	—	—	—	—	—	—	—
Threshold 1–2		−2.288	0.218	1.036	0.227	—	—	—	—	—
Threshold 2–3		−0.266	0.085	2.021	0.207	—				—
Diff-Thr. Item 4		—	—	−0.986	0.277	Large	−3.564***	12.701***	1	0.985
Item 5	2.797	−2.563	0.212	—	—	—	—	—	—	—
Threshold 1–2		−1.552	0.112	1.011	0.174	—	—	—	—	—
Threshold 2–3		0.062	0.065	1.614	0.116	—	—	—	—	—
Diff-Thr. Item 5		—	—	−0.602	0.200	Medium	−3.009**	9.054*	1	0.602
Item 6	1.479	−3.421	0.354	—	—	—	—	—	—	—
Threshold 1–2		−1.999	0.188	1.421	0.260	—	—	—	—	—
Threshold 2–3		0.088	0.085	2.087	0.196	—	—	—	—	—
Diff-Thr. Item 6		—	—	−0.666	0.284	Medium	−2.345*	5.501*	1	0.666
Item 7	2.530	−2.609	0.226	—	—	—	—	—	—	—
Threshold 1–2		−1.804	0.135	0.806	0.170	—	—	—	—	—
Threshold 2–3		−0.030	0.067	1.774	0.137	—	—	—	—	—
Diff-Thr. Item 7		—	—	−0.968	0.207	Large	−4.676***	21.863***	1	0.968
Item 8	1.365	−2.747	0.270	—	—	—	—	—	—	—
Threshold 1–2		−1.343	0.138	1.404	0.194	—	—	—	—	—
Threshold 2–3		0.379	0.095	1.722	0.162	—	—	—	—	—
Diff-Thr. Item 8		—	—	−0.318	0.197	Small	—1.611	2.596	1	0.318

Note. The Wald tests run with 1 df in separate runs using Mplus 8.8. These results were supplemented with Z-tests and effect size conventions as described in the text. The equidistance index (Spratto, 2018) quantifies the difference of differences that is between pairs of adjacent thresholds (1, 2 vs. 2, 3). E.S. Conventions followed the guidelines of Dorans and Holland (1992) see also Lin and Lin (2013). df = degrees of freedom; Diff-Thr. = difference between adjacent thresholds; equidistance would be manifested with difference estimates equal to zero. PYDS = Positive Youth Development Scale.

^*p < .05. **p < .01. ***p < .001.

Concluding Remarks

The present study addresses a controversial issue in measurement, that of assuming that ordered data as Likert-type are, likely to possess the properties of continuous data. Among assumptions, that of interval scaling is one of the most prevailing as it defines continuous data. A systematic review of the literature including studies from the last 3 years in counseling psychology suggested that >40% of the studies engage parametric statistical models and assume that Likert-type data possess the properties of continuous data (particularly that of interval scaling). An analysis with real data from the construct of the caring subscale of the PYDS suggested that response categories were not equidistant and, consequently, data should not be analyzed using models that are appropriate for continuous data. The present study further provides the means to evaluate the interval scaling assumption that underlies continuous data using the popular software Mplus. Extension of the present study could include the creation of a modified GRM in which response options are equidistant but such an extension is currently not available in commercial statistical packages. The authors advise caution, however, when using the GRM model with small samples. For example, Jiang et al. (2016) showed that a sample size of n = 500 would suffice for most conditions they tested, producing good recovery of parameter estimates; an exception was very large models for which an n = 1,000 was recommended.

In the future, it will be important to evaluate factors that may alleviate the magnitude of threshold non-equivalence. For example, tangential item characteristics (Tourangeau et al., 2000), vague wording (Bass et al., 1974; Spratto, 2018), negatively worded items (Barnette, 2000; Coleman, 2013; Corwyn, 2000), emotionality elicited items (Tourangeau & Smith, 1996), the presence of a neutral option (Nowlis et al., 2002), clear labeling (Borgers et al., 2003), social presence (Tourangeau et al., 2003), and participant motivation (Krosnick, 1991), all contribute to some degree in altering participants’ response behaviors.

Appendix A.

Mplus 8.8 Syntax for Fitting the GRM Model to the Caring Subscale of the PYDS

Mplus Syntax	Explanation
TITLE: Fitting the GRM model and interval scaling	! Title of model
DATA: FILE IS ncare1.dat;	! Data file in ASCII format
VARIABLE: NAMES ARE y1-y8;	! Variable names
usevariables are y1-y8;	! Variables to be used in the model
categorical are y1-y8;	! Variables defined as categorical
analysis: ESTIMATOR = ML; Link is logit;	! Type of estimator
MODEL:	! Model command
f1 BY y1-y8* (Li1-Li8);	! Estimating slopes of one factor model
[y1$1-y8$1] (T1_i1-T1_i8);	! 1st threshold estimation of items 1–8
[y1$2-y8$2] (T2_i1-T2_i8);	! 2nd threshold estimation of items 1–8
[y1$3-y8$3] (T3_i1-T3_i8);	! 3d threshold estimation of items 1–8
f1* (Fvar);	! Variance of factor estimated at first
[f1*] (Fmean);	! Factor mean estimated at first
OUTPUT: Residual stdyx tech10;	! Additional evaluative information
Plot: Type is plot1; Type is plot2; Type is plot3;	! Requesting IRT plots
MODEL CONSTRAINT:	! Model constraint command
Fvar=1;	! Factor variance constrained to 1
Fmean=0;	! Factor mean constrained to 0
NEW(A_i1-A_i8 B1_i1-B1_i8 B2_i1-B2_i8 B3_i1-B3_i8	! Labels of newly created parameters
D12_i1-D12_i8 D34_i1-D34_i8	! Labels of threshold estimates
Dt1-Dt8);	! Labels of difference threshold estimates
DO(1, 8) A_i#=Li#*sqrt(Fvar);	! Estimating item discriminations
DO(1, 8) B1_i#=(T1_i#-(Li#*Fmean))/(Li#*sqrt(Fvar));	! Estimating 1st threshold levels in logit
DO(1, 8) B2_i#=(T2_i#-(Li#*Fmean))/(Li#*sqrt(Fvar));	! Estimating 2nd threshold levels in logit
DO(1, 8) B3_i#=(T3_i#-(Li#*Fmean))/(Li#*sqrt(Fvar));	! Estimating 3d threshold levels in logit
! Item 1	! For Item 1
D12_i1=B2_i1-B1_i1;	! Difference between thresholds 1 and 2
D34_i1=B3_i1-B2_i1;	! Difference between thresholds 2 and 3
.
.
! Item 8	! For Item 8
D12_i8=B2_i8-B1_i8;	! Difference between thresholds 1 and 2
D34_i8=B3_i8-B2_i8;	! Difference between thresholds 2 and 3
Model Test:	! Wald test for evaluating equivalence
0=D12_i1-D34_i1;	! between adjacent thresholds, i.e., 1
	! and 2 vs. 2 and 3 for the 1st item.
	! Wald tests for each item require
	! additional runs in Mplus.
	! Differences in thresholds using Z-tests
dt1=D12_i1-D34_i1;	! Difference threshold estimates in Item 1
dt2=D12_i2-D34_i2;	! Difference threshold estimates in Item 2
dt3=D12_i3-D34_i3;	! Difference threshold estimates in Item 3
dt4=D12_i4-D34_i4;	! Difference threshold estimates in Item 4
dt5=D12_i5-D34_i5;	! Difference threshold estimates in Item 5
dt6=D12_i6-D34_i6;	! Difference threshold estimates in Item 6
dt7=D12_i7-D34_i7;	! Difference threshold estimates in Item 7
dt8=D12_i8-D34_i8;	! Difference threshold estimates in Item 8

Note. More model test command runs need to follow for testing the equivalence in each item as one Wald test can be conducted at a time. Commands in the “Model Constraint” section are used to evaluate the interval scaling assumption. ASCII = American Standard Code for Information Interchange; GRM = graded response model; PYDS = Positive Youth Development Scale; ML = maximum likelihood; IRT = item response theory.

Appendix B.

Original Caring Items From the Positive Youth Development Scale

Please rate how strongly you agree or disagree with the following statements.	Strongly disagree	Disagree	Neither agree nor disagree	Agree	Strongly agree
1. When there is a need I offer assistance whenever I can	□	□	□	□	□
2. It is easy for me to consider the feelings of others*	□	□	□	□	□
3. I care about how my decisions affect other people*	□	□	□	□	□
4. I try to encourage others when they are not as good at something as me*	□	□	□	□	□
5. Other people’s feelings matter to me*	□	□	□	□	□
6. I can be counted on to help if someone needs me.	□	□	□	□	□
7. I care about the feelings of my friends*	□	□	□	□	□
8. When one of my friends is hurting, I hurt too.	□	□	□	□	□

Note. Note that the mid option (neither/nor) was not utilized in the Arabic version of the instrument with the number of options being only 4. *=code to signal freely estimated parameter