GillesPy2: A Biochemical Modeling Framework for Simulation Driven Biological Discovery

Abstract

Stochastic modeling has become an essential tool for studying biochemical reaction networks. There is a growing need for user-friendly and feature-complete software for model design and simulation. To address this need, we present GillesPy2, an open-source framework for building and simulating mathematical and biochemical models. GillesPy2, a major upgrade from the original GillesPy package, is now a stand-alone Python 3 package. GillesPy2 offers an intuitive interface for robust and reproducible model creation, facilitating rapid and iterative development. In addition to expediting the model creation process, GillesPy2 offers efficient algorithms to simulate stochastic, deterministic, and hybrid stochastic-deterministic models.

1. Introduction

In 1976, Dan Gillespie first presented the Stochastic Simulation Algorithm (SSA) (Gillespie, 1976, 1977), which allows for efficient and accurate simulation of discrete stochastic reaction systems. This method has gained wide popularity in the simulation of complex biological and biochemical systems, and is widely used in the field of computational systems biology. It has inspired a plethora of software packages which implement this method, and a family of algorithms that enhance and extend it. Our team has been part of the development of many of these algorithms and related software. In particular, we developed StochKit2 (Sanft et al., 2011) and later a Python 2 wrapper GillesPy (Abel et al., 2016), which we named in honor of Dan Gillespie. We have continued our algorithm and software development with the next generation of simulation software, GillesPy2, which has been completely rewritten and is stand-alone. Our design goals are to provide software that is easy to use by novices but powerful enough in performance and features for even the most advanced users. GillesPy2 is distributed and used as a Python 3 (Van Rossum and Drake, 2009) package, and the computationally expensive solvers are written in C++ (for maximum performance) and Python (for maximum compatibility). It provides simulation interfaces for stochastic and deterministic systems, as well as a novel hybrid method which can switch automatically between them. GillesPy2 aims to be a modeling and simulation package that can provide everything needed for building and solving any spatially homogeneous biochemical reaction system.

Stochastic modeling and simulation has become a powerful and impactful tool for the study of mathematical, biochemical, and biological systems (Gillespie et al., 2013; El Samad et al., 2005; Elowitz et al., 2002). In addition, it has made an impact in the fields of conservation ecology (Drawert et al., 2017, 2022) and epidemiology (Jiang et al., 2021; Drawert et al., 2017). The process of understanding such systems via modeling and simulation is iterative, akin to the scientific method: starting with observations and data, a user (modeler) first develops a mathematical model. Most biological and similar dynamic models, such as many ordinary differential equation (ODE) models, do not have analytical solutions and, therefore, are “solved” by simulation. These simulations are a form of experimentation that produce results and data that the modeler can compare to the original observations and data to further refine the model. This iterative process is captured in the schematic shown in Figure 1(A). Software is an essential tool in this workflow. The software needs to be simple to use, computationally efficient, and it should provide features to accommodate studying a wide variety of systems. For example, Figure 1 shows simulation results from a discrete stochastic model (B), a model with events (C), and a model with coupled discrete stochastic and continuous components (D). GillesPy2 provides an integrated Python 3 platform that is designed to meet the needs of modelers. A brief summary of the GillesPy2 capabilities is shown in the boxes around the schematic in Figure 1(A).

Figure 1:

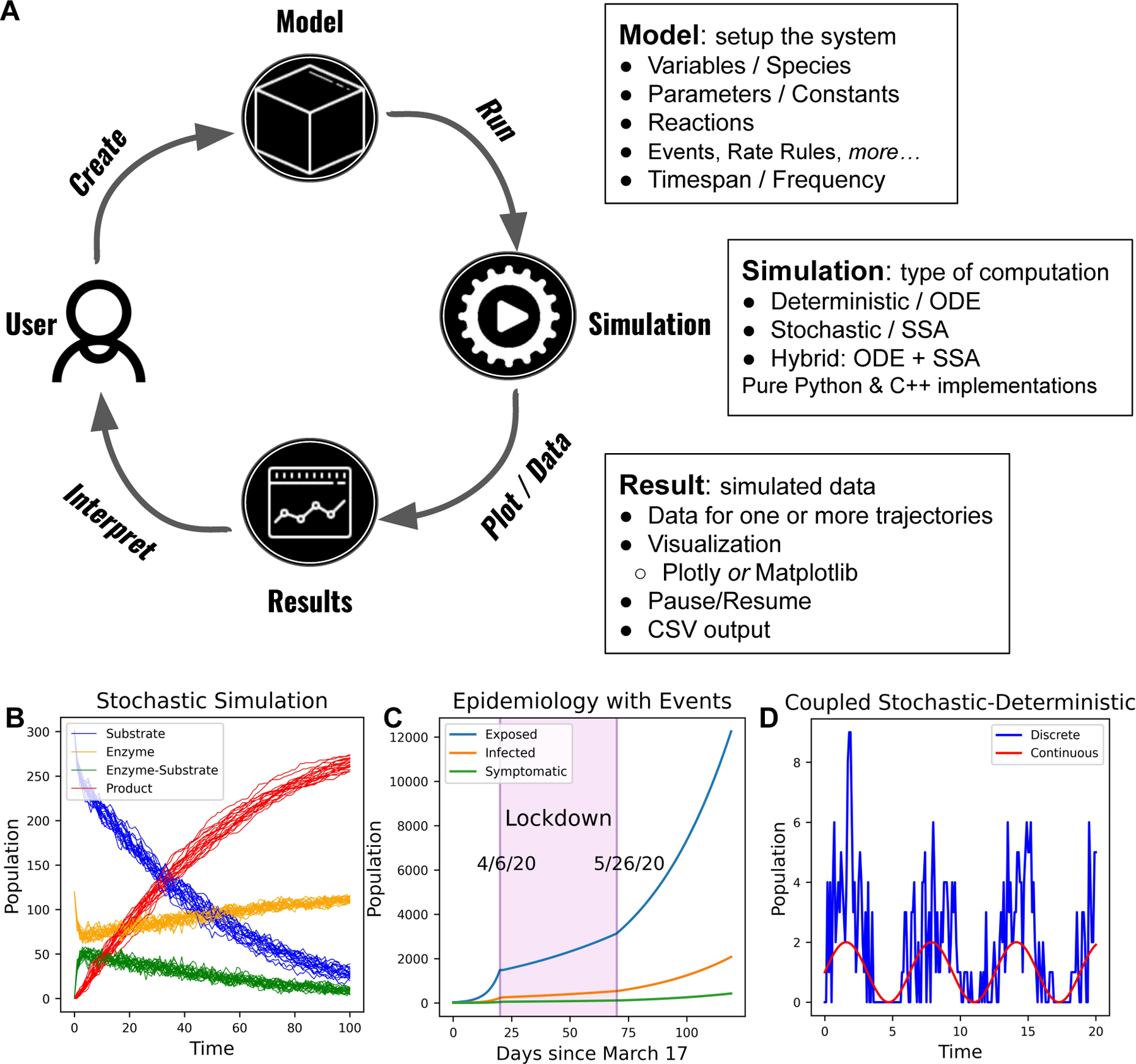
(A) Diagram representing the GillesPy2 workflow, and the three major components: Model, Simulation, and Result. (B) Simulation of the classic Michaelis-Menten model (Michaelis and Menten, 1913). (C) Simulation of Covid-19 infections in a population with lockdown and re-opening events. (D) Simulation of a discrete stochastic birth-death process coupled to a time-varying continuous variable. Visualizations of simulations were all performed with GillesPy2.

A number of software packages are kindred to GillesPy2. These include COPASI (Hoops et al., 2006), GillespieSSA (Pineda-Krch, 2008), StochPy (Maarleveld et al., 2013), PySB (Lopez and Garbett, 2014), Biosimulator.jl (Landeros et al., 2018), BioNetGen (Harris et al., 2016), Tellurium and libRoadRunner (Choi et al., 2018; Somogyi et al., 2015), and others. While a complete feature review is beyond the scope of this paper, each of these packages provides mechanisms for defining or importing models and/or simulating models within a particular programming language, integrated development environment, or graphical user interface. For example, COPASI features a graphical user interface that allows users to define models with multiple compartments using a comprehensive set of rate laws. GillespieSSA and Biosimulator.jl allow users to build and simulate biochemical models in the R and Julia languages, respectively. PySB implements rule-based modeling and BioNetGen implements structure-based modeling in Python. StochPy and Tellurium and libRoadRunner provide text-based interfaces for defining biochemical models that can be simulated and visualized in Python. GillesPy2 aims to provide a comprehensive and flexible collection of simulation methods in an easy-to-use package. It provides an intuitive object-oriented Application Programming Interface (API) for the development of well-mixed biochemical reaction models that can include stochastic, deterministic, or coupled components. GillesPy2 is designed to integrate with Jupyter notebooks. GillesPy2 is also the computational engine for our powerful web-based IDE, StochSS (Drawert et al., 2016).

The remaining sections of this manuscript are structured as follows. In Section 2 we discuss biological modeling and various methods of simulation. In Section 3 we present the Tau-Hybrid Simulation Algorithm. Section 4 describes how GillesPy2 was designed and implemented, including details on our novel hybrid simulation algorithm. Section 5 provides several examples of building and simulating models with GillesPy2. In Section 6, we illustrate the performance of GillesPy2 and how it fits into the software ecosystem of StochSS (Drawert et al., 2016). We end with our conclusions in Section 7.

2. Background

Biological systems feature dynamics that operate on a range of spatial and temporal scales. This leads to many different types of mathematical models, each with their own modeling assumptions and approximations. Furthermore, most models require software to simulate or “solve” them, and it can be difficult to separate model development from simulation and software. For example, creating an ODE model implicitly makes assumptions about the continuity of the state variables. In this section we describe the classes of models and the simulation algorithms that are utilized in GillesPy2.

2.1. Biological modeling

While there are many classes of biological models, here we consider models where the system state is a time-dependent vector of populations. For example, the populations could be numbers of molecules of different types in a biochemical simulation or populations of different species in an ecological model. The models’ populations change in time due to two primary mechanisms: discrete events and differential equations.

To demonstrate these mechanisms, consider the Michaelis-Menten reaction set (Michaelis and Menten, 1913)

$$\begin{gathered} R_1:A+B\stackrel{k_1}{\to }C \\ {R}_2:C\stackrel{k_2}{\to }A+B \\ {R}_3:C\stackrel{k_3}{\to }B+D. \end{gathered}$$ (1)

Reaction set (1) describes the enzyme-catalyzed conversion of substrate “A” into product “D” via enzyme “B”. The model state is the vector of the $N=4$ species’ populations $X\left(t\right)=\left[A\left(t\right),B\left(t\right),C\left(t\right),D\left(t\right)\right]$. The populations evolve via $M=3$ reactions, denoted $R_j$. For example, $R_1$ describes the binding of a molecule of A and a molecule of B into the complex C. Here, $k_i$ are rate constants that influence the rate at which the reactions are occurring. A complete model description requires values for the rate constants and initial populations defined at time $t=0$. We assume that reactions occur instantaneously.

The reaction set in (1) can be be formulated using reaction rate equations, as follows:

$$\begin{gathered} \frac{dA}{dt}=-k_{1}AB+k_{2}C \\ \frac{dB}{dt}=-k_{1}AB+k_{2}C+k_{3}C \\ \frac{dC}{dt}=k_{1}AB-k_{2}C-k_{3}C \\ \frac{dD}{dt}=k_{3}C. \end{gathered}$$ (2)

The model in (2) is deterministic and treats the populations as continuous quantities. This ODE model is appropriate if the effect of stochastic fluctuations is relatively small, which will generally be the case if all of the species populations are sufficiently large.

Alternatively, the reaction set in (1) could be formulated as a discrete stochastic system, where the populations are discrete and the reactions are random events. In the discrete stochastic representation, the evolution of the system state is probabilistic and can be described by the Chemical Master Equation (CME) (Gillespie et al., 2013):

$$\frac{\partial P\left(X,t\right)}{\partial t}\sum _{j=1}^M\left[a_j\left(X-v_j\right)P\left(X-v_j,t|X_0,t_0\right)-a_j\left(X\right)P\left(X,t|X_0,t_0\right)\right],$$ (3)

where $v_j$ is the stoichiometry vector that describes how the state variable $X\left(t\right)$ changes when reaction $R_j$ occurs (or fires), and $a_j$ is the propensity function that describes the rate at which $R_j$ is firing. The CME is huge. It contains one equation for each possible value of the population $X$. Thus, it cannot be solved directly for most models (Munsky and Khammash, 2006). Instead of solving the CME directly, the common alternative approach is to approximate the solution using Monte Carlo simulation.

The Systems Biology Markup Language (SBML) provides a way to describe many biological models such as the reaction set in (1) (Hucka et al., 2003). SBML uses tags to describe the Species and Reactions in a model. Reactions are comprised of Reactants (species that are consumed) and Products (species that are produced) and a KineticLaw, which may use Parameters, to describe differential equation or discrete stochastic state changes. SBML also defines other mechanisms such as rate rules and events. Rate rules describe additional differential equation state-change mechanisms, and events are state changes that happen when a condition known as a trigger occurs. For the purposes of this work, we will follow the SBML nomenclature and use the terms “reaction”, “rate rule”, and “event” to refer to the various state-change mechanisms in biological models.

We note that SBML includes several features that we will not consider. In particular, SBML defines Compartment components that define the region in which the species populations exist. Compartments can be used to describe spatially inhomogeneous models by tracking separate species populations within each compartment and by treating “diffusion” as a reaction that transfers populations between compartments. However, such spatial models can benefit from additional geometry information that SBML does not currently provide (however, an SBML spatial package is in development). Other modeling and simulation software is better suited to modeling systems that require detailed geometry information. In this work we consider only spatially homogeneous models.

2.2. Deterministic simulation

The theory for simulating ODE models is well established and mature (Ascher and Petzold, 1998). Numerically solving an initial value problem involves starting with the initial state, evaluating the derivatives, and repeatedly simulating over small, finite time intervals until an end time is reached. Algorithms exist that use dynamic step size selection to efficiently approximate the true solution. These algorithms can generally be categorized as explicit or implicit. Implicit methods perform better on models that exhibit stiffness, which arises in models that contain multiple timescales, as is common in biological systems. There are algorithms and software that can detect the presence of stiffness and choose an appropriate algorithm automatically (Petzold, 1983).

GillesPy2 uses the LSODA method (Petzold, 1983) for deterministic simulation. We use the implementation from the SciPy Python package (Virtanen et al., 2020) for the Python solvers, and the implementation from the SUNDIALS package (Hindmarsh et al., 2005) for the solvers implemented in C++. In addition, the Python solvers provide options for selecting other methods implemented by the SciPy package, which we recommend only for advanced users.

2.3. Stochastic simulation

Gillespie’s Stochastic Simulation Algorithm (SSA) generates statistically exact samples from the CME (3) (Gillespie et al., 2013). However, there are many variants of the SSA. The assumptions underlying the CME, namely the Markovian assumption and the spatially homogeneous assumption, require that each reaction type fires according to an exponential distribution. The original SSA direct method was derived naturally from the joint density:

$$Pr\left(\tau ,j|X,t\right)=a_j\left(X\right)e^{-{\sum }_{i=1}^M{a}_i\left(X\right)\tau },$$ (4)

where $Pr\left(\tau ,j|X,t\right)$ is the probability that reaction $R_j$ will fire in the infinitesimal interval $\left[t+\tau ,t+\tau +dt\right)$. Any algorithm that produces samples of the next reaction time $\tau$ and next reaction index $j$ from Eq. (4) can be used to generate samples of the CME. Therefore, the SSA is better viewed as a family of algorithms. Many algorithms have been proposed that use various data structures to achieve different performance and scaling properties (Gibson and Bruck, 2000; Slepoy et al., 2008; Ramaswamy et al., 2009; Mauch and Stalzer, 2011; Sanft and Othmer, 2015).

It is important to note that the time step size is not an algorithm parameter in the SSA. However, if the values of the propensities do not change much in a time step $\tau =\text{Δ}t$, then the number of firings of reaction $R_j$ can be well approximated as a Poisson random variable with mean $a_j\left(X\right)\tau$. This approximation is the basis for the Tau-Leaping simulation algorithm:

$$X\left(t+\tau \right)=X\left(t\right)+\sum _{j=1}^{M}Poisson\left(a_j\left(X\right)\tau \right)v_j,$$ (5)

where each Poisson is an independent Poisson random number. In practice, the step size $\tau$ is determined adaptively to control the error in the simulation (Gillespie, 1977; Cao et al., 2006).

When the populations are sufficiently large such that the mean of all the $Poisson$ random variables in (5) is large, then the Poisson random variables can be approximated as Normal random variables. If one makes this approximation and replaces the finite step size $\tau$ with the infinitesimal $dt$, the resulting algorithm is

$$X\left(t+dt\right)-X\left(t\right)=\sum _{j=1}^M\mathcal{N}\left(\mu =a_j\left(X\right)dt,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\sigma =\sqrt{a_j\left(X\right)dt}\right)v_j,$$ (6)

where each $\mathcal{N}\left(\mu ,\sigma \right)$ is an independent Gaussian random variate (Gillespie et al., 2013). Equation (6) is a stochastic differential equation known as the Chemical Langevin Equation (CLE). The CLE is often written as:

$$dX=va\left(X\right)dt+v\sqrt{a\left(X\right)}{\mathcal{N}}_M\left(\mu =0,\hspace{0.17em}\hspace{0.17em}\sigma =I\right)\sqrt{dt},$$ (7)

where $\nu$ is the stoichiometric matrix, $a\left(X\right)$ is the vector of propensities, and ${\mathcal{N}}_M$ is an $M$-dimensional normal random variable. In moving from Tau-Leaping to the CLE, the state $X$ transitions from a discrete population to a continuous population. It is interesting to note that as the population $X$ increases, the noise term becomes negligible and the CLE (7) approaches the reaction rate equation ODE, hence the ODE model arises in the large population (thermodynamic) limit of the discrete stochastic model (Kurtz, 1972).

2.4. Hybrid simulation

In this context we define hybrid modeling and simulation to be the simulation of a reaction system that includes both deterministic and stochastic components. This involves partitioning a model into two subsystems, where one is simulated deterministically and the other is simulated stochastically (Pahle, 2009; Helms et al., 2018). The partitioning can be based on the populations (i.e., large and small) or the reaction rates (i.e., fast and slow). Reactions that involve only large population species may be approximated as continuous, while reactions that fire less often or involve small population species can be simulated via an SSA variant or Tau-Leaping. With a hybrid model, one may gain computational performance while still capturing the stochasticity of the system (Ahmadian et al., 2017). On the other hand, hybrid simulation introduces computational overhead to maintain additional data structures, in which case the performance will typically be slower than specialized solvers for models that do not include both deterministic and stochastic components. In these situations, the benefit of hybrid simulation is to allow modelers more flexibility when defining their models by specifying whether a species should be simulated as only continuous, only discrete, or be able to switch between the two.

3. The Tau-Hybrid Simulation Algorithm

Here, we introduce our novel Tau-Hybrid simulation algorithm, which is a hybrid of ODE deterministic simulation of continuous species and the Tau-Leaping (Gillespie, 2001) method for stochastic simulation of discrete species. The Tau-Hybrid algorithm features two methods for combining continuous and discrete simulation: the coupling of discrete and continuous species in a reaction network, and the automatic switching of a species from discrete to continuous (and vice versa). It is important to note that in the case where all of the propensities of the system are dependent only on discrete state variables (no time-dependent propensities, or continuous species), this method is statistically equivalent to Tau-Leaping (note, it is not the same method).

3.1. Simulation of a coupled discrete-continuous system

We will first discuss the combined simulation method for coupled discrete and continuous species in a reaction network. We partition the reactions and species of the system. Reactions are either part of the deterministic (det) or stochastic (stoch) sets, species $S$ are either continuous $\left(S_c\in {ℝ}_0^{+}\right)$ or discrete $\left(S_d\in {\mathbb{Z}}_0^{+}\right)$. We evolve the state of the system $X\left(t\right)=\left[S_1,\mathrm{...},S_N\right]$ forward by continuously integrating the deterministic reactions and firing discontinuous jump events for the stochastic reactions. Reactions are deterministic if they consume and produce only continuous species, otherwise they are stochastic. The partitioning of the species as discrete or continuous can be done a priori by the modeler or automatically by the method (see next section).

We define the time evolution of the system due to the deterministic reactions as

$$\frac{d}{dt}{S}_i=\sum _j^{j\in det}{v}_{ij}{a}_j\left(X\left(t\right),t\right)$$ (8)

for all continuous species $i$. Note that in this formulation we are allowing propensity functions to be explicitly dependent on time. For stochastic reactions, we need to find the firing time $t_j$ for all reactions $j\in stoch$. We find this using the integral form of the next-reaction SSA as described in (Salis and Kaznessis, 2005):

$${\int }_{t_0}^{t_0+t_j}{a}_j\left(X\left(t\prime \right),t\prime \right)dt\prime +\text{log}\left(URN\right)=0,$$ (9)

where $t_0$ is the current time and $URN$ is an independent uniform random number $URN\in \left(0,1\right)$. Note that in the case where $a_j\left(X,t\right)$ is constant over the interval $\left[t_0,t_0+t_j\right]$ (i.e., discrete stochastic systems), this is simplified to: $t_j=\frac{-\text{log}\left(URN\right)}{a_j\left(X\right)}+t_0$, which is the time to the next reaction in the SSA method (Gillespie, 1976). Following the method in (Salis and Kaznessis, 2005) for solving (9), we define an indicator variable $r_j$ for each reaction $j\in stoch$. We forward integrate these variables to find the time $t_j$ at which $r_j=0$, which is the time at which the reaction fires. We do this by converting (9) to a differential equation initialized by an independent uniform random number:

$$\frac{d}{dt}{r}_j=a_j\left(X,t\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{r}_j\left|{}_{t=t_0}\right.=\text{log}\left(URN\right).$$ (10)

Note $r_j$ will always start negative since $\text{log}\left(URN\right)<0$, and $r_j$ is monotonically increasing since $a_j>\hspace{0.17em}=0$. The time at which $r_j$ crosses zero is then a statistically exact sample of the firing time of reaction $j$ for a jump process with time-varying intensity $a_j\left(X,t\right)$. If the numerical method used is an ODE solver to integrate (8) and (10) simultaneously, and using a root-finder to determine the reaction event times, we then have the hybrid ODE-SSA method as described in (Salis and Kaznessis, 2005).

However, integrating (8) and (10) with root-finding to find the reaction event times is quite computationally expensive. Following the idea from Tau-Leaping that tolerating a small amount of error can result in a large computational gain, instead of using root finding to determine the time of each reaction event, we take larger simulation steps by aggregating multiple firings of each stochastic reaction channel into a single event. All stochastic reaction channel firing events are processed at the end of each time step $\tau$. Over the time period $\left[t,t+\tau \right]$, deterministic reactions evolve the system using (8), and the reaction indicator variables $r_j$ evolve using (10) (however, the $r_j$ variables may now have positive values). At the end of each time step $\tau$ we examine each $r_j$. If it is positive, we determine the number of reaction events that have fired in the time step by finding the smallest number $n$ such that

$$\underset{n}{\text{arg}\hspace{0.17em}\text{min}}\left(r_j+\sum _1^n\text{log}\left(URN\right)\right)<0,$$ (11)

i.e., the sum of the log of $n$ samples of $URN$ until the value of $r_j$ becomes negative. Since the initial condition (10) after each firing is $\text{log}\left(URN\right)$, and we assume that $a_j\left(X,t\right)$ is constant over $\left[t,t+\tau \right]$, Eq. (11) can be efficiently implemented using the Poisson distribution:

$$n=1+Poisson\left(r_j\right),$$ (12)

for all reaction indicators $r_j$ that are positive at the end of an integration step. Once we know that reaction $j$ has fired $n$ times, we update the state: $X+=n{\nu }_j$, and then re-initialize $r_j=\text{log}\left(URN\right)$. In this way, the simulation continues time-discontinuously, integrating (8) and (10) from $t$ to $t+\tau$ and using (12) to update the state of the system at the end of the step. We call this hybrid Tau-Leaping/ODE simulation method the Tau-Hybrid Algorithm.

Figure 2 shows a visual representation of a simulation using the Tau-Hybrid algorithm. The populations of the two species are shown, along with the values of the reaction indicator variables. Note that the value of $r_3$ moves in straight lines between the discontinuous jumps that arise due to stochastic reactions firing. This is due to the propensity function being constant. In contrast, the value of $r_1$ moves in curved lines, with a positive second derivative. This is because the propensity function $a_1\left(X\right)$ depends on the population of $A$, which is continuously increasing. In this example, the value of $r_2$ is ignored, as it is a deterministic reaction. Thus, the value of $A$ changes continuously using the ODE integration over the step $\left[t,t+\tau \right]$, and then discontinuously (discretely) at the end of each step.

Figure 2:

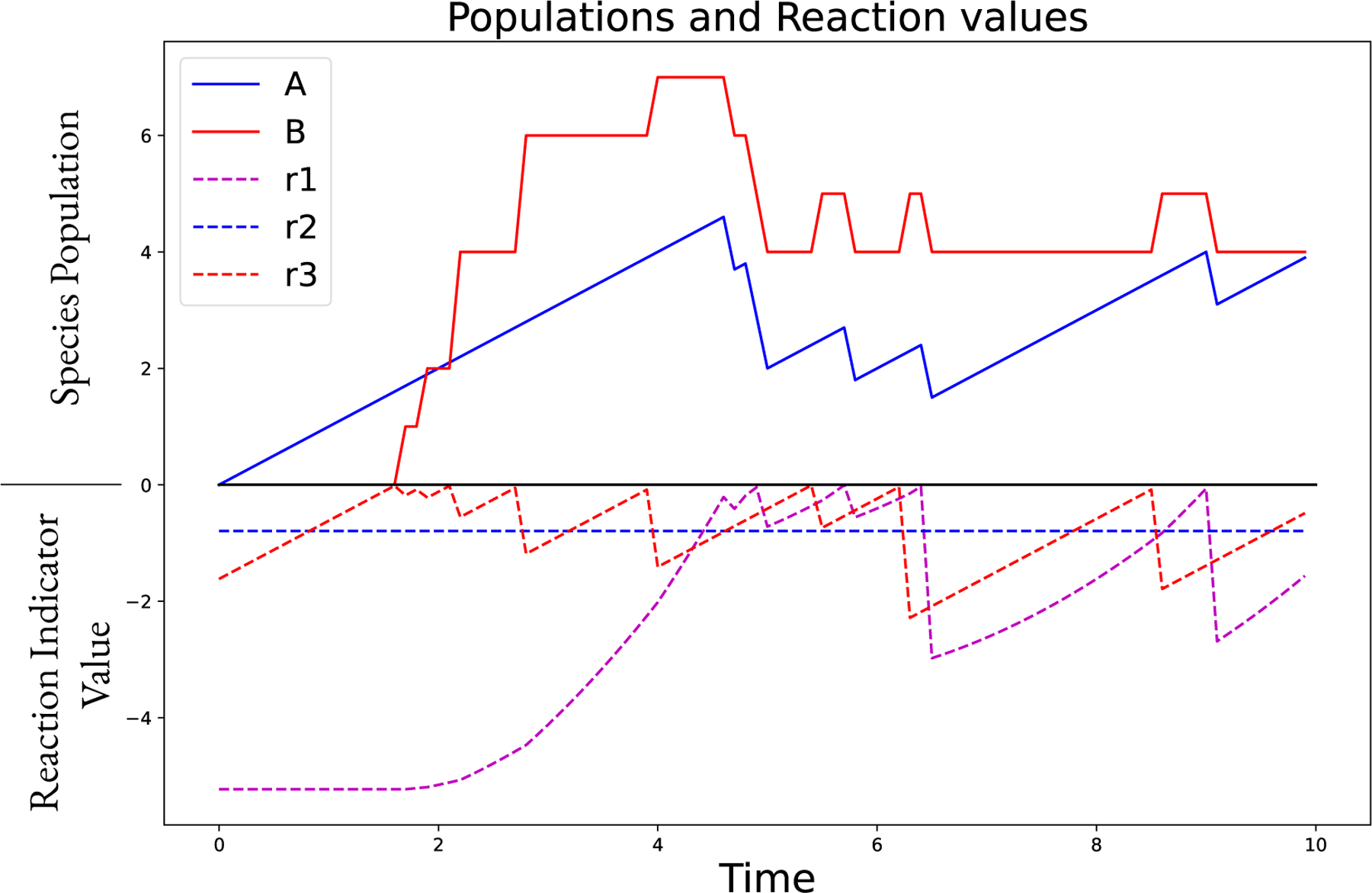
Visualization of the Tau-Hybrid simulation of a coupled discrete-continuous system. The model features three reactions: $R_1:A+B\to \varnothing$, $R_2:\varnothing \to A$, $R_3:\varnothing \to B$. The values of the reaction indicator variables, $r_1$, $r_2$, and $r_3$ are shown along with the populations of species $A$, which is set to be continuous, and species $B$, which is set to be discrete. The population of $B$ changes discretely when $r_1$ or $r_3$ fire, which occurs when their value crosses the $y = 0$ axis and becomes positive. We then use (11) to determine the number of times the reaction is fired and then reset the reaction indicator value to $\text{log}\left(URN\right)$ (a negative value). The reaction $R_2$ is simulated as deterministic because it depends only on species marked as continuous. Therefore, the indicator variable $r_2$ is ignored and the population of $A$ changes continuously. The population of $A$ also changes discretely when $R_1$ fires. The simulation $\tau$ step size is calculated adaptively, and the state of the simulation is sampled for output every 0.1 time units. All other options use the defaults (e.g., LSODA integrator).

3.2. Automatic switching between discrete and continuous species

Gillespie described how the different simulation regimes (e.g., stochastic vs. deterministic) relate to each other, and the assumptions at each level in Gillespie (2009). Using this as a foundation, we make the observation that for many discrete stochastic systems, it is important to keep track of the exact stochastic variations when the populations are relatively low. However, when the population of a discrete species is high, and the stochastic variation from the mean field trajectory is low, we can utilize the law of large number assumption and transition the discrete species into a continuous species with minimal loss of accuracy in the solution.

The Tau-Hybrid algorithm has two different methods for detecting when a species should be switched between discrete and continuous. The first is a simple population threshold value, where above this threshold the species is considered continuous and below the threshold the species is considered discrete. The second method uses the relative noise in the species simulation trajectory to determine whether the stochastic variation about the mean is more or less than an error tolerance. For this calculation we use an approximation of the coefficient of variation $\text{CV}=\sigma /\mu$, where $\sigma$ and $\mu$ are the standard deviation and mean value respectively. Related auxiliary quantities $\widehat{\sigma }$ and $\widehat{\mu }$ are approximated as part of the $\tau$ step size selection step outlined above, and as defined in (Cao et al., 2006), thus we use

$${\widehat{\mu }}_i=-\sum _j^M\sum _k^N{a}_j\left(X\right)\ast \text{Reactants}\left(k,j\right)+\sum _j^M\sum _k^N{a}_j\left(X\right)\ast \text{Products}\left(k,j\right)$$ (13)

$${\widehat{\sigma }}_i^2=-\sum _j^M\sum _k^N{a}_j\left(X\right)\ast \text{Reactants}{\left(k,j\right)}^2+\sum _j^M\sum _k^N{a}_j\left(X\right)\ast \text{Products}{\left(k,j\right)}^2$$ (14)

$${\widehat{CV}}_i=\sqrt{{\widehat{\sigma }}_i^2}/\left(S_i+{\widehat{\mu }}_i\right)$$ (15)

where Reactants $\left(k,j\right)$ is the number of species $k$ that are consumed by reaction $j$ (i.e., 2 for a bimolecular reaction, 0 if not involved). Similarly, Products $\left(k,j\right)$ is the number of species $k$ that are produced by reaction $j$. If ${\widehat{CV}}_i$ for species $S_i$ is less than the specified per-species tolerance, we mark the species continuous. We then examine each reaction $j$. If all of the reactants and products are marked as continuous then the reaction is marked deterministic, otherwise it is marked stochastic.

We also use the values from (13) and (14) in our implementation of the $\tau$ step size selection method (Cao et al., 2006)

$$\tau =\underset{i\in Reactants}{\text{min}}\left(\frac{\text{max}\left({\epsilon }_i{S}_i,1\right)}{\left|{\widehat{\mu }}_i\right|},\frac{\text{max}{\left({\epsilon }_i{S}_i,1\right)}^2}{{\widehat{\sigma }}_i^2}\right)$$ (16)

where Reactants is all species $k$ where Reactants $\left(k,j\right)>0$ for any reaction $j$, and $\epsilon$ is the error control parameter. We refer the reader to (Cao et al., 2006) for the complete derivation.

In the implementation of the $\tau$ step size selection method (Cao et al., 2006), to prevent species from going negative it is sometimes necessary to take a single SSA step (Step 9 in Algorithm 1). In our implementation, we check to see if any species are negative after all stochastic reactions have been processed for a given step. If a negative state is detected, then the system is restored to the state prior to the step and a new $\tau$ and the reaction $j\prime$ to fire is determined using the next-reaction SSA methodology by calculating

$${\tau }_j=\frac{-r_j\left(t\right)}{a_j\left(X\left(t\right),t\right)}$$ (17)

$$j\prime =\underset{j}{\text{arg}\hspace{0.17em}\text{min}}\left({\tau }_j\right)$$ (18)

for all $j\in stoch$. Using (18) we find $j\prime$, integrate the ODE system over $\left[t,t+{\tau }_{j\prime }\right]$, then fire a single $j\prime$ reaction. A complete description of the methods is given in Algorithm 1.

$$\overline{\underset{¯}{\begin{array}{l}\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm}}\hspace{0.17em}1:\text{Hybrid}\hspace{0.17em}\text{Tau}-\text{Leaping}\hspace{0.17em}\text{algorithm}\hspace{0.17em}(\text{hybrid}\hspace{0.17em}\text{of}\hspace{0.17em}\text{ODE}\hspace{0.17em}\text{and}\hspace{0.17em}\text{Tau}-\text{Leaping})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1:\hspace{0.17em}\hspace{0.17em}\text{Initialize}\hspace{0.17em}\text{state}\hspace{0.17em}X\left(t=0\right)\hspace{0.17em}\text{and}\hspace{0.17em}\text{each}\hspace{0.17em}{r}_j=\text{log}\left(URN\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2:\hspace{0.17em}\hspace{0.17em}\mathbf{\text{while}}\hspace{0.17em}\text{current}\hspace{0.17em}\text{time}<\text{simulation}\hspace{0.17em}\text{end}\hspace{0.17em}\text{time}\hspace{0.17em}\mathbf{\text{do}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}3:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Evaluate}\hspace{0.17em}\text{propensities}\hspace{0.17em}{a}_j\left(X\right)\hspace{0.17em}\text{at}\hspace{0.17em}\text{current}\hspace{0.17em}\text{state}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}4:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Find}\hspace{0.17em}{\widehat{\text{μ}}}_i,{\widehat{\text{σ}}}_i \&\hspace{0.17em}{\widehat{CV}}_i\hspace{0.17em}\text{for}\hspace{0.17em}\text{each}\hspace{0.17em}\text{species}\hspace{0.17em}\text{as}\hspace{0.17em}\text{in}\hspace{0.17em}\text{Eqs}.\hspace{0.17em}(13)–(15).\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}5: \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Select}\hspace{0.17em}\text{the}\hspace{0.17em}\text{step}\hspace{0.17em}\text{size}\hspace{0.17em}\text{τ}\hspace{0.17em}\text{according}\hspace{0.17em}\text{to}\hspace{0.17em}\text{Eq}.\hspace{0.17em}\left(16\right).\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}6: \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Identify}\hspace{0.17em}\text{continuous}/\text{discrete}\hspace{0.17em}\text{species}\hspace{0.17em}\text{and}\hspace{0.17em}\text{deterministic}/\text{stochastic}\hspace{0.17em}\text{reaction}\hspace{0.17em}\text{sets}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}7:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Integrate}\hspace{0.17em}\text{stochastic}\hspace{0.17em}\text{reaction}\hspace{0.17em}\text{indicator}\hspace{0.17em}\text{variables}\hspace{0.17em}{r}_j,\text{and}\hspace{0.17em}\text{deterministic}\hspace{0.17em}\text{species}\hspace{0.17em}\text{from}\hspace{0.17em}t\hspace{0.17em}\text{to}\hspace{0.17em}t+\text{τ}\hspace{0.17em}\text{using}\hspace{0.17em}\text{Eqs}.\left(8\right)\hspace{0.17em}\text{and}\hspace{0.17em}\left(10\right).\end{array}\hfill \\ \begin{array}{l}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}8:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Update}\hspace{0.17em}\text{state}\hspace{0.17em}\text{based}\hspace{0.17em}\text{on}\hspace{0.17em}\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{stochastic}\hspace{0.17em}\text{reaction}\hspace{0.17em}\text{firings}\hspace{0.17em}\text{using}\hspace{0.17em}\text{Eq}.\hspace{0.17em}\left(12\right).\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}9:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{if}}\hspace{0.17em}\text{no}\hspace{0.17em}\text{species}\hspace{0.17em}\text{have}\hspace{0.17em}\text{a}\hspace{0.17em}\text{negative}\hspace{0.17em}\text{population}\hspace{0.17em}\mathbf{\text{then}}\\ \hspace{0.17em}\hspace{0.17em}10: \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Store}\hspace{0.17em}\text{state}\hspace{0.17em}X\left(t+\text{τ}\right)=X,t=t+\text{τ}\\ \hspace{0.17em}\hspace{0.17em}11: \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{else}}\\ \hspace{0.17em}\hspace{0.17em}12: \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Reset}\hspace{0.17em}\text{state}\hspace{0.17em}X=X\left(t\right),\text{the}\hspace{0.17em}\text{state}\hspace{0.17em}\text{at}\hspace{0.17em}\text{the}\hspace{0.17em}\text{beginning}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{step}.\\ \hspace{0.17em}\hspace{0.17em}13: \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Using}\hspace{0.17em}\left(17\right)\hspace{0.17em}\text{and}\hspace{0.17em}\left(18\right),\hspace{0.17em}\text{Update}\hspace{0.17em}\text{state}\hspace{0.17em}\text{by}\hspace{0.17em}\text{firing}\hspace{0.17em}\text{a}\hspace{0.17em}\text{single}\hspace{0.17em}j\prime \hspace{0.17em}\text{reaction}:X\left(t+{\text{τ}}_{\text{j}\prime }\right) =v_{j\prime }+X\left(t\right),\text{and}\hspace{0.17em}\text{set}\hspace{0.17em}t=t+{\text{τ}}_{j\prime }.\\ \hspace{0.17em}\hspace{0.17em}14: \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{if}}\\ \hspace{0.17em}\hspace{0.17em}15:\hspace{0.17em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{while}}\end{array}\hfill \end{array}}}$$

4. GillesPy2 Design and Implementation

GillesPy2 is a Python 3 package that uses an object-oriented approach that provides an intuitive API for working with models, simulations, and results. In object oriented programming, classes describe the components of an object. GillesPy2 users create and manipulate objects via well documented methods (or “functions”). The primary classes in GillesPy2 are the Model, Solver, and Results classes, which are described in the subsections below.

4.1. Model class

A Model object consists of three primary components: species, parameters, and reactions. A GillesPy2 user can build a model by creating Species, Parameter, and Reaction objects and adding them to a Model object. This process is best described via a concrete example.

Consider the Michaelis-Menten reaction set from Eq. (1). A user can create the Species objects with the following simple Python 3 code snippet:

A = Species(name="A", initial_value=301)
B = Species(name="B", initial_value=120)
C = Species(name="C", initial_value=0)
D = Species(name="D", initial_value=0)

Similarly, one can define Parameters:

rate1 = Parameter(name="rate1", expression=0.0017)
rate2 = Parameter(name="rate2", expression=0.5
rate3 = Parameter(name="rate3", expression=0.1)

Species and Parameters are used to build the Reaction objects:

r1 = Reaction(name="r1", reactants={A: 1, B: 1}, products={C: 1}, rate=rate1)
r2 = Reaction(name="r2", reactants={C: 1}, products={A: 1, B: 1}, rate=rate2)
r3 = Reaction(name="r3", reactants={C: 1}, products={B: 1 , D: 1}, rate=rate3)

A user can then instantiate a Model object and add the Species, Parameters, and Reactions components to it:

michaelis_menten = Model()
michaelis_menten.add_species([A, B, C, D])
michaelis_menten.add_parameter([rate1, rate2, rate3])
michaelis_menten.add_reaction([r1, r2, r3])

Finally, to facilitate simulation, we define a TimeSpan that specifies the time points at which to keep data from a simulation:

michaelis_menten.timespan(TimeSpan(numpy.linspace(0, 100, 101)))

GillesPy2 models can include several additional features of the SBML Level 3 standard (Hucka et al., 2003), including rate rules, assignment rules, function definitions, and events.

4.2. Solvers

The base class for all GillesPy2 simulation algorithms is GillesPySolver, which provides an abstract “run” method that all subclasses (“Solvers”) must implement. However, GillesPy2 users are not required to have knowledge of particular Solvers or algorithms in order to run a simulation. GillesPy2 intelligently uses the properties of the Model and the user’s system to automatically select the appropriate Solver. Therefore, running a simulation of the Michaelis-Menten model defined above is as simple as:

results = michaelis_menten.run()

The above code will run a single stochastic simulation (or trajectory) using the SSA. To run an ensemble of several trajectories the code is:

results = michaelis_menten.run(number_of_trajectories=20)

The above code will generate a Results object containing simulation data similar to that shown in Figure 1(B).

GillesPy2 includes Solver classes for the SSA, Tau-Leaping, ODE, CLE, and Tau-Hybrid algorithms. Specifically, the SSA uses the direct method (Gillespie, 1977), Tau-Leaping uses the adaptive step-size algorithm from (Cao et al., 2006), ODE uses Sundials (Hindmarsh et al., 2005) or SciPy.integrate’s ode function (Virtanen et al., 2020), CLE uses an Euler-Maruyama method (McCauley, 2013) with dynamic step size chosen as in the Tau-Leaping method, and the Tau-Hybrid is implemented as described in Section 3. The default algorithm when a user calls the run() method will be the SSA unless the model includes Species designated as “dynamic” or “continuous” or if the model contains one or more of the following SBML features: rate rules, events, assignment rules, or function definitions, in which case the selected algorithm will be the Tau-Hybrid. The user can also manually select an algorithm, for example:

results = michaelis_menten.run(algorithm="Tau-Leaping")

Each algorithm (except the CLE) is implemented in two Solver classes, one written in Python and one written in C++. The rationale is that code written in C++, a compiled language, is faster than Python code. However, running C++ code requires a compiler. Therefore, GillesPy2, when selecting the particular Solver for a given algorithm, checks for an available C++ compiler and uses the C++ Solver if a compiler is accessible, otherwise it uses the Python implementation. A list of the available Solvers is shown in Table 1.

Table 1:

List of available Solvers in GillesPy2 as of version 1.7.0.

Algorithm	Implementation / Reference	Class Name	Language	Advanced Features
SSA	Direct Method / Gillespie, 1977	NumPySSASolver	Python
SSA	Direct Method / Gillespie, 1977	SSACSolver	C++
Tau-Leaping	Cao et al., 2006	TauLeapingSolver	Python
Tau-Leaping	Cao et al., 2006	TauLeapingCSolver	C++
ODE	LSODA∗ / Petzold, 1983	ODESolver	Python∗
ODE	LSODA∗ / Petzold, 1983	ODECSolver	C++∗
CLE	Euler-Maruyama / McCauley, 2013	CLESolver	Python
Tau-Hybrid	see Section 3	TauHybridSolver	Python	Event, RateRule, AssignmentRule, FunctionDefinition
Tau-Hybrid	see Section 3	TauHybridCSolver	C++	Event, RateRule

^∗The ODE solvers are wrappers to SciPy (Virtanen et al., 2020) (Python) and SUNDIALS (Hindmarsh et al., 2005) (C++) solvers. The ODE solvers use LSODA by default but other integrators can be chosen.

Users can override the default by instantiating a Solver object directly to have total control over the Solver. For example, a user with a C++ compiler could manually choose to use the Python SSA implementation to run an ensemble of the Michaelis-Menten model:

python_ssa = NumPySSASolver(model=michaelis_menten)
results = python_ssa.run(number_of_trajectories=20)

4.3. Simulation output and visualization

The GillesPy2 Solvers’ simulations return a Results object. A Results object contains a Python list of Trajectory objects, where each Trajectory contains a Python dictionary of the time array specified by the model’s timespan object and an array of values corresponding to those time points for each Species in the Model. The Results object is convenient for conducting analysis directly in Python.

The Results class provides several methods to facilitate common analysis tasks, including plotting and generating descriptive statistics. To plot a Results object, the syntax is:

results.plot()

If the results variable contained an SSA ensemble from the Michaelis-Menten model, the above statement will generate a plot similar to that in Figure 1(B). The default plot method uses the Python Matplotlib (Hunter, 2007) library. Users can generate a Plotly (Plotly Technologies Inc., 2015) graph with the plotplotly method. The methods average_ensemble and stddev_ensemble create a Trajectory object containing the means and standard deviations, respectively. The methods plot_mean_stdev and plotplotly_mean_stdev compute these statistics and plot them in a single call. Finally, users can export their Results by writing them to a file using the to_csv method.

5. Examples

In the following examples, we will look at the process of creating, simulating, and visualizing models with GillesPy2. All of the examples demonstrate the core benefit of GillesPy2’s object-oriented implementation: that of compartmentalization. Compartmentalization makes GillesPy2 easy to use by splitting the composition of a model into separate “building blocks”. Section 5.1 demonstrates the core components of a GillesPy2 model, Section 5.2 demonstrates events using an epidemic model, and the photosynthesis model in Section 5.3 demonstrates GillesPy2’s hybrid solver. All of the examples in this section are available in notebooks posted here: https://github.com/GillesPy2/GillesPy2_paper.

5.1. Predator-prey model

Lotka-Volterra models are a class of predator prey models often represented as ODEs (Lotka, 1920; Volterra, 1926). For example, the following set of ODEs can be used to described the population dynamics of a predator $F$ and prey $R$ (e.g., foxes and rabbits):

$$\begin{gathered} \frac{dF}{dt}=k_{2}FR-k_{3}F \\ \frac{dR}{dt}=-k_{2}FR+k_1. \end{gathered}$$ (19)

These ODEs can be converted into mechanistic reaction format:

$$\begin{gathered} R_1:\varnothing \stackrel{k_1}{\to }R \\ {R}_2:F+R\stackrel{k_2}{\to }2F \\ {R}_3:F\stackrel{k_3}{\to }\varnothing , \end{gathered}$$ (20)

where the empty set symbol is used when there are no reactants or products. In GillesPy2, these reactions are described with the following code:

R1 = Reaction (reactants={}, products={R: 1}, rate=k1
R2 = Reaction(reactants={R: 1, F: 1}, products={F: 2}, rate=k2)
R3 = Reaction(reactants={F: 1}, products={}, rate =k3)

For the parameter set $k_1=10$, $k_2=0.01$, $k_3=10$, the ODE model has an equilibrium point at $F=1000$, $R=1000$ (see Figure 3(B)). For non-zero populations away from the equilibrium point, the ODE system exhibits oscillations, as seen in Figure 3(A). Simulated stochastically, an initial population at the ODE equilibrium $\left(F=1000,R=1000\right)$ does not remain constant, as stochasticity pushes the system away from equilibrium and the system exhibits noisy oscillations as seen in Figure 3(C).

Figure 3:

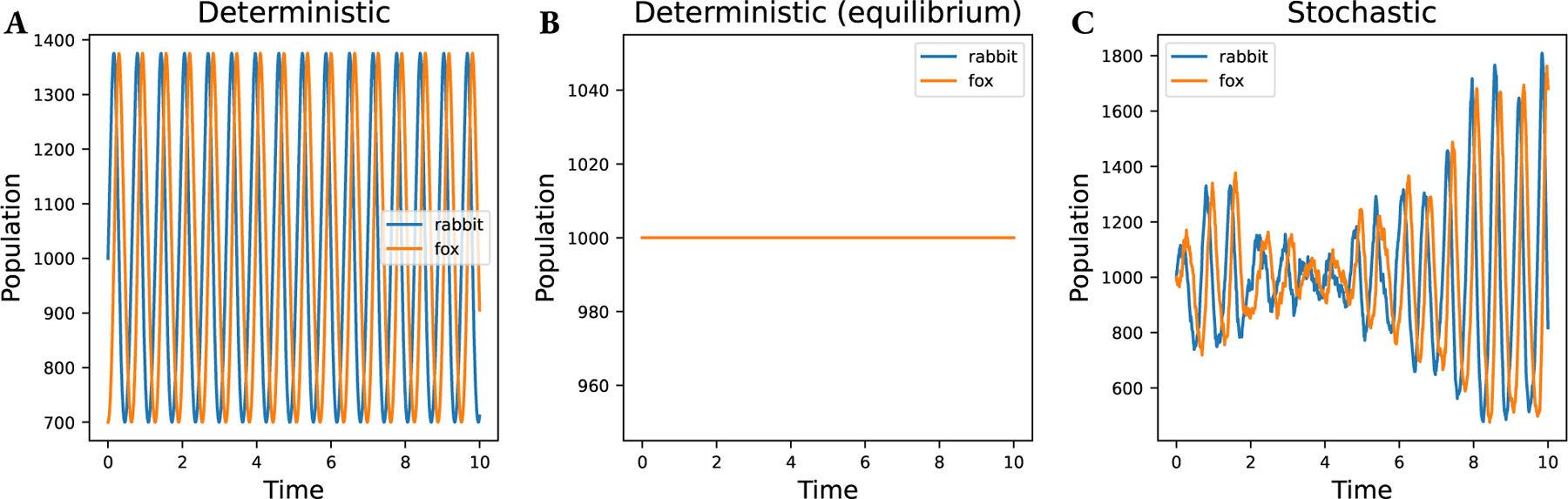
Simulations of the Predator-Prey model, as defined in (19) and (20). (A) deterministic (ODE) simulation from a non-equilibrium initial condition. (B) deterministic (ODE) simulation from the equilibrium initial condition. Note that the values never change. (C) stochastic simulation from the ODE equilibrium initial condition.

5.2. Epidemic model with events

Next we consider a variation of the standard SEIR epidemic model inspired by the early Covid-19 pandemic (Jiang et al., 2021). The species $S$, $E$, and $R$ correspond to susceptible, exposed, and recovered individuals, respectively. The total infected population is split into two categories: $I_1$ and $I_2$ corresponding to asymptomatic and symptomatic, respectively. Population $C$ are individuals who were silently cleared, meaning they were infected but never became symptomatic. Finally, $D$ is the number of deaths. The basic reaction set is as follows:

$$\begin{gathered} R_1:S+I_1\stackrel{k_e}{\to }{I}_1+E \\ {R}_2:S+I_2\stackrel{k_e}{\to }{I}_1+I_2 \\ {R}_3:E\stackrel{k_i}{\to }{I}_1 \\ {R}_4:I_1\stackrel{k_p}{\to }{I}_2 \\ {R}_5:I_1\stackrel{k_S}{\to }C \\ {R}_6:I_2\stackrel{k_r}{\to }R \\ {R}_7:I_2\stackrel{k_d}{\to }D. \end{gathered}$$ (21)

In this example we consider the effect of a societal “lockdown” to reduce virus transmission, as was common in the early months of the Covid-19 pandemic. To model a lockdown, we introduce two events. The first event triggers at time $t=20$ and modifies parameter $k_e$ by a value $q$ between 0 and 1 corresponding to the reduction in exposure due to the lockdown. The second event ends the lockdown at $t=70$ by modifying parameter $k_e$ by a value between $q$ and 1, where a value of 1 would simulate the population fully returning to pre-lockdown behaviors. An Event object is composed of an EventTrigger and an EventAssignment object. For example, the first event is added to the model as follows:

e1trigger = EventTrigger(expression="t >=20")
e1action = EventAssignment(variable=self.listOfParameters["k_e"], expression="q∗k_e0")
lockdown = Event(name="lockdown_start", trigger=e1trigger, assignments=[e1action])
self.add_event(lockdown)

Here “k_e0” is the nominal value of $k_e$. The Event’s trigger will become true at $t=20$, then the EventAssignment will be executed. The Event for ending the lockdown is defined similarly. This model was used to create part (C) in Figure 1.

5.3. Hybrid simulation of photosynthesis

To demonstrate the Tau-Hybrid solver, we have created an example model of photosynthesis based on (Whitmarsh and Covindjee, 1999). This model demonstrates the two major features of the Tau-Hybrid solver. The first feature is the ability to couple stochastic reactions to continuously changing variables. In this model, a RateRule is assigned to the variable “photons” to set its continuous value based on a derivative proportional to sin $\left(t\pi /12\right)$ to mimic the daily cycle of the sun. The domain of interest is a cell of a plant, though we do not explicitly model this. Instead, we simulate the diffusion of carbon dioxide, water, and oxygen into and out of the cell using purely deterministic reactions, with the steady-state being the initial condition of those quantities. The second feature we illustrate with this model is the ability for a reaction to be simulated stochastically at low populations and automatically switch the reaction to a continuous mode when the relative noise of the reactants and products falls below the threshold level. In this case, we have specified that the variable representing the carbohydrates in the model will switch when its relative noise is less than the default threshold of 0.03, using the following code:

Species(name="Carbohydrate", initial_value=0, mode="dynamic")

Alternatively, switching behavior can also be specified by a minimum population level parameter that changes the type from continuous to discrete when the species population drops below the specified threshold.

Figure 4 shows the results of the simulation of this model. The photons (green) change continuously with time. The carbohydrates (red) increase when Photons are high, and change discretely (taking only integer values) until $t\approx 17$. Each reaction event can be seen as a step increase in this variable. After $t\approx 17$, the Carbohydrates variable is simulated deterministically, and thus has smooth changes, though the qualitative behavior remains the same. Carbon dioxide (blue) and water (orange) are consumed in the photosynthesis reaction and oxygen (purple) is produced. Before $t\approx 17$ discontinuous jumps in their values correspond to reaction events. During this same time, the deterministic diffusion in/out reaction also changes the values continuously between reaction events.

Figure 4:

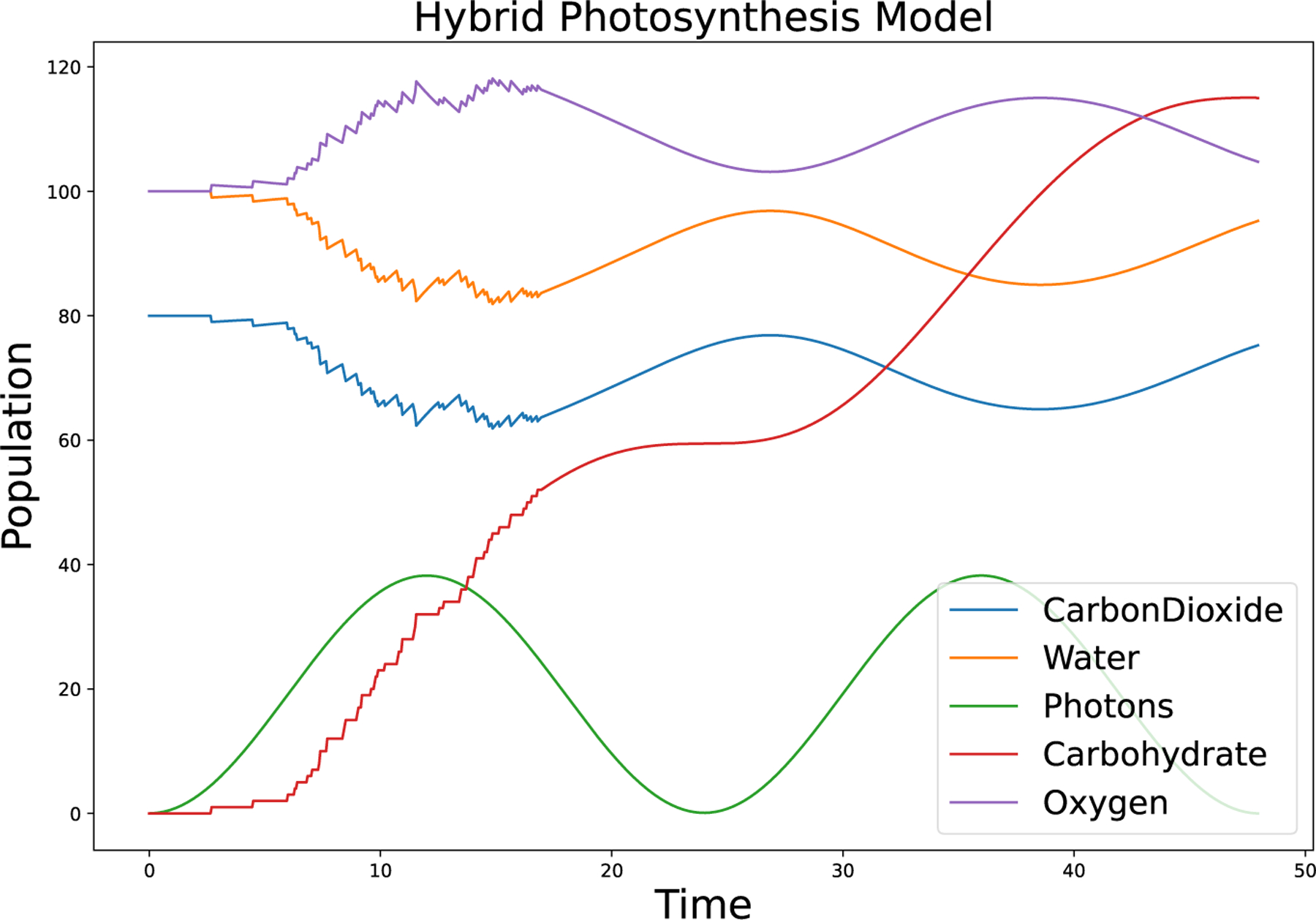
An example model showing hybrid ODE/SSA simulation. This model of photosynthesis, adapted from Whitmarsh and Covindjee (1999), couples an external time-varying input (sunlight, green) with a reaction network. Diffusion in and out of the volume of interest is simulated deterministically, while the reaction that creates sugars (carbohydrates, red) is stochastic when the population of carbohydrates is low (time < 17) and switches to deterministic after time ≈ 17 because the calculated noise crosses below the tolerance threshold.

This example demonstrates that the Tau-Hybrid solver allows the modeler to couple stochastic reactions with deterministic reactions and continuously time-varying inputs. It allows the modeler to specify whether a set of reactions should be stochastic, deterministic, or to switch between the two options based on specified thresholds. These features are applicable to a large class of models, as it is important to capture stochastic dynamics, however it is difficult to a priori determine which species and which reactions need to be simulated discretely, and which ones can be accurately simulated deterministically. GillesPy2’s Tau-Hybrid solver switches between these two modes automatically, giving the modeler an accurate and efficient simulation without requiring any extra knowledge.

6. Discussion

6.1. Performance

In GillesPy2 we provide a variety of solvers to our users, so that we may address as many different computational requirements as possible. GillesPy2 includes logic to choose the correct solver for the user automatically, by inspecting the features used in the model construction and testing if the C++ solver can be used in the current computation environment. This logic is contained in the “get_best_solver()” method. This method will return a C++ implementation over the Python counterpart, if supported. It will inspect the model for any advanced features (e.g., Event, Assignment Rules, Rate Rules, or Function Definitions) and returns the Tau-Hybrid solver if so, otherwise it returns the SSA Solver. These heuristics are appropriate for many situations, however we suggest that our users specify the solver that most closely fits their computational situation to maximize productivity. The SSA solvers have been optimized for performance in simulating stochastic systems, and as such does not support as many features. The ODE solvers have similarly for deterministic systems. However, the Tau-Hybrid solvers have been developed to simulate the most complex biochemical models by simultaneously solving ODE and SSA systems, thus it must do more work than either of them alone.

Understanding all of the performance characteristics of a simulation is a complex and multifaceted endeavor. To assist our readers in understanding the performance of GillesPy2, we present three analyses. In Figure 5, we compare the performance of the SSA, Tau-Hybrid, Tau-Leaping, and ODE solvers as a function of increasing system size by increasing the steady-state population, $X_0^{\ast } =X\left(t=0\right)$, in the birth-death model where $\varnothing \to X$ at rate $k\ast X_0^{\ast }$, and $X\to \varnothing$ at rate $k$ (e.g., $a_1\left(X\right)=k\ast X_0^{\ast }$ and $a_2\left(X\right)=k\ast X$). Both the C++ (A) and Python (B) implementations are analyzed. In Figure 6 we show separately total time (in A), initialization and compilation time (in B), and simulation run time (in C) as a function of the number of simulated trajectories. We see that in some fast-running simulations, the compilation time dominates the total time. In Table 2 we compare a set of common biochemical models with the GillesPy2 solvers, and additionally show the time for the simulation with StochKit2 (Sanft et al., 2011), for external comparison. Some entries are marked “N/A” if the solver does not possess the capabilities to correctly simulate the model. The models compared are: Decay $\left(S\to \varnothing ,S\left(0\right)=100\right)$, Dimerization $\left(2S_1\leftrightarrow S_2,S_1\left(0\right)=30\right)$, Michaelis-Menten (Michaelis and Menten, 1913), Genetic Toggle Switch (Gardner et al., 2000), Tyson 2-state Oscillator (Tyson, 1991), Vilar Oscillator (Vilar et al., 2002), a Multi-Event model (a test model with events), and an All-SBML-Features model (a test model that includes all supported SBML features: Event, Assignment Rules, Rate Rules, and Function Definitions).

Figure 5:

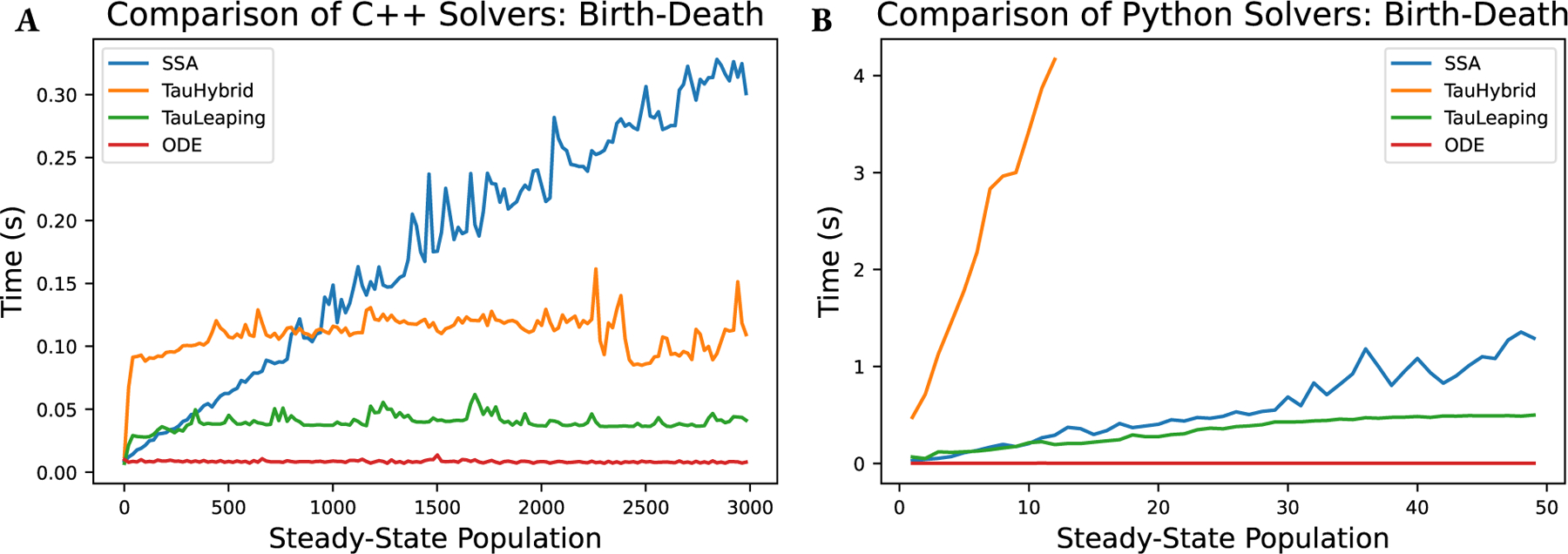
Comparison of solver performance for SSA, Tau-Hybrid, Tau-Leaping, and ODE solvers, for both the C++ implementations (A) and Python implementations (B). Performance is measured using a birth-death model across a range of steady-state conditions. This shows how performance of each solver changes as the system size increases. Note that the C++ solvers are significantly faster than the Python implementations, thus we compare them separately. Also note that the Tau-Leaping and Tau-Hybrid solvers are nearly flat with respect to system size, as expected since their performance scales with number of reaction channels. This is in contrast to the SSA which scales linearly with population size.

Figure 6:

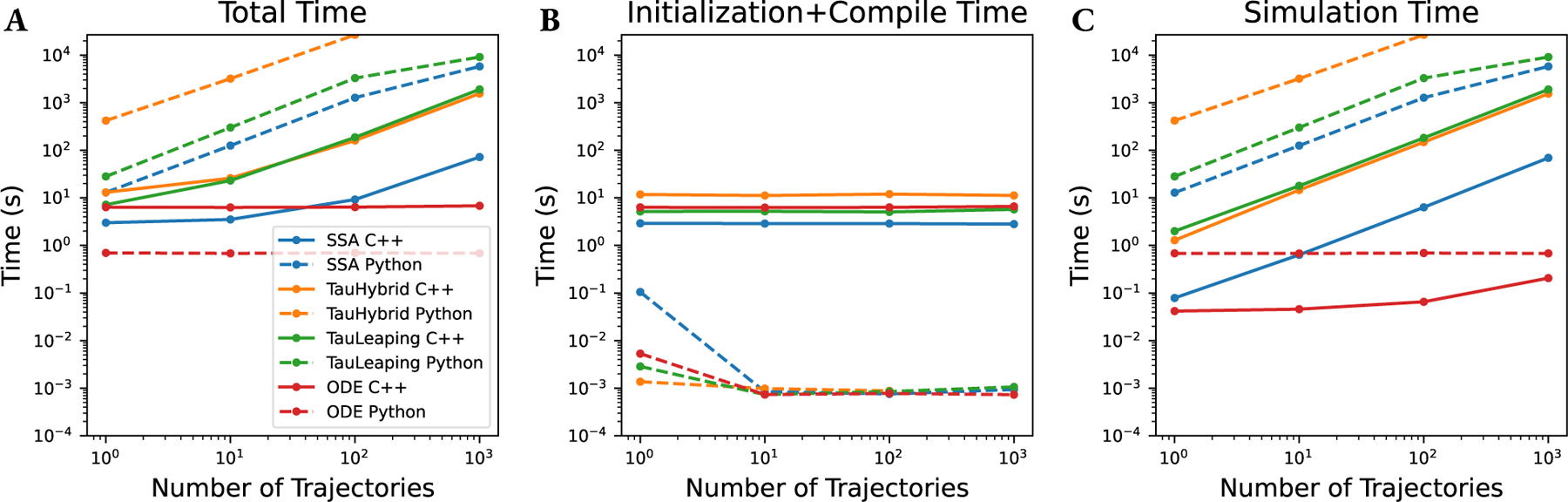
Performance analysis of GillesPy2 running the Vilar Oscillator (Vilar et al., 2002) model, showing (A) Total simulation time, (B) Compile time, and (C) Run time versus number of trajectories. Note that for the C++ solvers (solid lines), the compile time is a large fraction of the total time for fast-running simulations. The C++ solvers are all faster than their Python counterparts (dashed lines), however the relatively large compile time must be taken into account when considering the performance trade-offs of each solver.

Table 2:

Total simulation time (in seconds) comparison for GillesPy2 Solvers and StochKit2 (Sanft et al., 2011) for popular biochemical models. Times reported are the total time (compile + simulation) for a single trajectory. See Figure 6 for an example of performance versus ensemble size.

Model	SSA	SSA C++	Tau-Hybrid	Tau-Hybrid C++	Tau-Leaping	Tau-Leaping C++	StochKit2 (SSA)
Decay	0.00312	3.893	0.0610	16.292	0.00605	8.015	0.0406
Dimerization	0.00338	3.829	0.125	13.464	0.0132	7.493	0.0764
Michaelis-Menten	0.0654	4.573	0.797	17.010	0.0711	7.861	0.0743
Genetic Toggle Switch	0.0876	3.085	1.457	16.22	0.0885	6.800	7.623
Tyson 2-state Oscillator	21.16	3.164	303.1	14.29	22.16	6.807	6.984
Vilar Oscillator	15.29	3.167	299.5	14.42	31.72	8.301	0.223
Multi-Event model	N/A	N/A	0.246	16.22	N/A	N/A	N/A
SBML features model	N/A	N/A	0.586	N/A	N/A	N/A	N/A

6.2. Availability

GillesPy2 is open source software, available under the GNU General Public License (Version 3) (https://github.com/GillesPy2/GillesPy2/blob/main/LICENSE). Like many Python 3 packages, stable versions of GillesPy2 can be installed from PyPI via the Python “pip” command. It is also available on conda-forge.org for those using the Conda package manager. The source code and documentation can be downloaded from http://www.github.com/gillespy2/gillespy2. Users are encouraged to report bugs and request new features through the github repository’s web interface.

GillesPy2 is part of the StochSS ecosystem (Drawert et al., 2016). The StochSS organization encompasses multiple projects, including: StochSS Live (Jiang et al., 2021), SCIOPE (Scalable inference, optimization and parameter exploration) (Singh et al., 2020), and SpatialPy. GillesPy2 is the engine for all spatially homogeneous modeling and simulation services in StochSS. Through StochSS live, a Software-as-a-Service platform, users can create, simulate, and analyze models in a web browser.

7. Conclusion

GillesPy2 is an open source Python 3 package that provides biological modelers a set of user-friendly tools to facilitate their workflows. GillesPy2’s object-oriented design allows users to build, simulate, analyze, and improve their models using an intuitive set of classes and methods. The core solvers are written in C++ and Python for high performance and accessibility. The novel Tau-Hybrid implementation is compatible with several SBML model features, including events and rate rules. Additionally, GillesPy2 works well with Jupyter notebooks, facilitating open and reproducible science. In fact, all of the examples and code in this paper are available in notebooks posted at https://github.com/GillesPy2/GillesPy2_paper. All figures and data in this paper are based on GillesPy2 version 1.7.0.

For biological modelers who would like to use GillesPy2, a great place to start is the “Start_Here.ipynb” Jupyter notebook in the GillesPy2/examples folder. Users can start with a provided working example and then modify the code to develop their own model. The examples folder contains additional notebooks that showcase several different biochemical models and notebooks that demonstrate many GillesPy2 features. Users can also consult the extensive documentation on the web at https://gillespy2.readthedocs.io/. The documentation provides everything from a “Basic usage” page that walks through the basic workflow, to a complete API reference of all GillesPy2 classes and public methods. Through the user-friendly API, example notebooks, and extensive documentation, users can progress quickly from GillesPy2 beginners to experts who can utilize the powerful range of biochemical modeling, simulation, and analysis tools that are available in GillesPy2.