Abstract
Over the past century, understanding the nature of shock compression of condensed matter has been a major topic. About 20 years ago, a femtosecond laser emerged as a new shock-driver. Unlike conventional shock waves, a femtosecond laser-driven shock wave creates unique microstructures in materials. Therefore, the properties of this shock wave may be different from those of conventional shock waves. However, the lattice behaviour under femtosecond laser-driven shock compression has never been elucidated. Here we report the ultrafast lattice behaviour in iron shocked by direct irradiation of a femtosecond laser pulse, diagnosed using X-ray free electron laser diffraction. We found that the initial compression state caused by the femtosecond laser-driven shock wave is the same as that caused by conventional shock waves. We also found, for the first time experimentally, the temporal deviation of peaks of stress and strain waves predicted theoretically. Furthermore, the existence of a plastic wave peak between the stress and strain wave peaks is a new finding that has not been predicted even theoretically. Our findings will open up new avenues for designing novel materials that combine strength and toughness in a trade-off relationship.
Subject terms: Surfaces, interfaces and thin films; Mechanical properties
Introduction
Highly compressed states via shock waves have been essential for understanding various phenomena such as material synthesis1 and strengthening2, high-velocity impacts3, planet formation4, and inertial confinement fusion5. Material properties such as mechanical, optical, electrical, and magnetic ones change drastically on an ultrashort timescale when subjected to shock compression6,7. These studies have mainly used explosives, plate impacts and high-power lasers as shock drivers, mainly because such shock drivers can transiently create a thermodynamically steady and thermally equilibrium shocked state, i.e. the Hugoniot state8,9 in the material.
The femtosecond laser is a relatively new shock-driven tool that has been in use for about 20 years10–13. Direct femtosecond laser irradiation of a thin aluminium film produces a shock pressure of 100 to 300 GPa, depending on the laser intensity, estimated under the assumption of the Hugoniot state13. The femtosecond laser-driven shock wave in metal causes plastic deformation and, if the material has high-pressure phases, high-pressure phase transition, leaving unique traces such as unique dislocation structures14,15 and the high-pressure phase of iron16 that cannot be obtained by conventional compression techniques. Furthermore, the plastic deformation induced by direct femtosecond laser irradiation of metals has been applied to strengthen the metals as a new laser peening technique without any sacrificial overlay under atmospheric conditions, called dry laser peening (DLP)17,18, whereas conventional laser peening techniques using nanosecond pulsed lasers require sacrificial overlays such as protective coatings and plasma confinement media19–21.
Characteristics of the femtosecond laser-driven shock wave, such as shock profile and peak pressure, have been diagnosed experimentally using ultrafast pump and probe schemes10–13,22 such as ultrafast interferometry and ultrafast dynamic ellipsometry. Existing studies, except for Evans’ study13, have used a plasma confinement scheme, i.e. the pump laser passes through the glass substrate and irradiates the thin metal film deposited on the glass substrate, and the probe laser irradiates the free surface of the film. Although this scheme drives a shock wave and its characteristics have been thoroughly studied10–12, there is a concern that electrons and ions ejected from the metal during the early stage of the femtosecond laser irradiation may affect the shock formation due to preheating or plasma expansion because the laser-irradiated metal surface is the interface with the glass substrate and the ejected electrons and ions are confined in the interface23–26. Evans et al. measured the ultrafast behaviour of the backside of the metal when the pump laser was irradiated to the free surface of the metal and reported it to be driven by a shock pressure of 100 to 300 GPa assuming the Hugoniot state13. However, it is unclear whether the shock wave driven by direct femtosecond laser irradiation is applicable in the Hugoniot state. Furthermore, ultrafast interferometric and spectroscopic techniques can provide information on the ultrafast behaviour of laser-driven waves from nanometric order displacements with picosecond temporal resolution10–13,22. However, they cannot provide direct information on the lattice level behaviour, which is critical for understanding the elasto-plastic and phase transition behaviour under shock compression27–30.
Time-resolved X-ray diffraction (XRD) combined with laser-driven shock has been widely used to observe fast lattice behaviour31–34. X-rays from laser-produced plasma have mostly been used to study lattice behaviour such as structural phase transitions. The laser pulse duration is typically sub-nanoseconds or longer to produce a high X-ray flux, resulting in insufficient temporal resolution to observe lattice behaviour at the picosecond or femtosecond resolution. The X-ray free electron laser (XFEL) has successfully produced brilliant femtosecond X-ray pulses35,36. By combining an XFEL with an optical laser pulse, it is possible to investigate shock phenomena at femtosecond resolution30. The XFEL has been used to investigate shock compression states produced by a laser pulse with a pulse duration of sub-nanoseconds or longer30,37–39. In this case, the initial part of the laser pulse generates the plasma, while the rest of the laser pulse keeps the plasma stable by inverse bremsstrahlung, which pushes the material to form a steady shock wave, thereby creating a Hugoniot state20. However, in the case of direct femtosecond laser irradiation, there is no interaction between the ablation plasma and the laser pulse, as ablation occurs after the entire laser pulse has been deposited in the material40. For this reason, simulations have predicted that the mechanism of shock wave formation is different from that of conventional shock waves41. Because the femtosecond laser-driven shock wave behaves differently from conventional shock waves, unique microstructures14–16 are expected to be formed in materials by shock waves driven by direct femtosecond laser irradiation. However, the lattice behaviour of metals under shock compression driven by this direct femtosecond laser irradiation has never been investigated and remains experimentally unresolved.
In this study, we used the XFEL at SACLA36 to investigate the ultrafast lattice behaviour in iron directly irradiated by a femtosecond laser pulse. Iron was chosen as a reference material to evaluate the properties of shock waves driven by direct femtosecond laser irradiation, because iron is an important material in industrial and geoscientific fields and its behaviour under conventional shock compression has been thoroughly studied33,38,42–53.
Methods
Polycrystalline iron with a purity of 99.99% (Kojundo Chemical Laboratory Co., Ltd., 10 × 10 mm, 1 mm thickness) was used as the target material. It was annealed at 1123 K under a low pressure of 10–2–10–3 Pa for 1 h to remove the residual strain, and its surface was then mirror-finished using colloidal silica. The average grain size of the annealed iron was measured to be 63 µm using the electron backscatter diffraction method.
The pump-probe experiment was performed in the experimental hatch EH3 at the beamline BL3 of SACLA35. Figure 1 shows a schematic illustration of the experimental setup. Pump laser-pulses with a wavelength of 800 nm, pulse duration of 43 fs, pulse energy of 60 mJ, and contrast ratio of 10–6 (Coherent Inc., Hidra-100) irradiated the target surface with a spot diameter of 600 µm, corresponding to an average intensity of 4.9 × 1014 W/cm2, which is almost the same as the intensity for femtosecond laser-shock processing treatment14–18. The shock front propagates into the material normal to the surface. XFEL pulses with a duration of 10 fs and a photon energy of 10 keV with an energy spread of 5 × 10–3 irradiated the sample while maintaining spatial overlap with the pump laser. The glancing angle between the XFEL beam and the target surface was 20°, while the pump laser irradiated the target with a normal incidence. The XFEL beam was cut with a slit of 70 μm (vertical) × 300 μm (horizontal). The XFEL irradiation area over the sample surface is therefore 204 μm × 300 μm, which fits within the ϕ 600 μm pump laser irradiation area. Spatial overlap between pump and probe lasers was ensured by using a Ce:YAG, which fluoresce to both pump and probe lasers. The timing 0 was adjusted using optical delay line of the femtosecond laser so that the timing of the fluorescence generated by XFEL irradiation of Ce:YAG was located at the rise of the fluorescence generated by femtosecond laser irradiation of Ce:YAG. The XFEL and pump-laser pulses were synchronised in time with shot-to-shot fluctuation of sub-picosecond. The delay time τ of the XFEL pulse from the femtosecond laser pulse was varied using an optical delay line along the optical laser path. The probe depth of the 10 keV X-ray from the surface was 1.12 μm. A two-dimensional multi-port charge-coupled device (MPCCD) detector was positioned so that the normal line from the centre crossed the spot of the pump laser pulse on the target. Shot-to-shot XRD patterns were recorded using the MPCCD. The angle between the incident XFEL and the normal line of the detector was 36°. The distance between the spot and the detector, calibrated using a gold target, was 138.02 mm.
Figure 1.
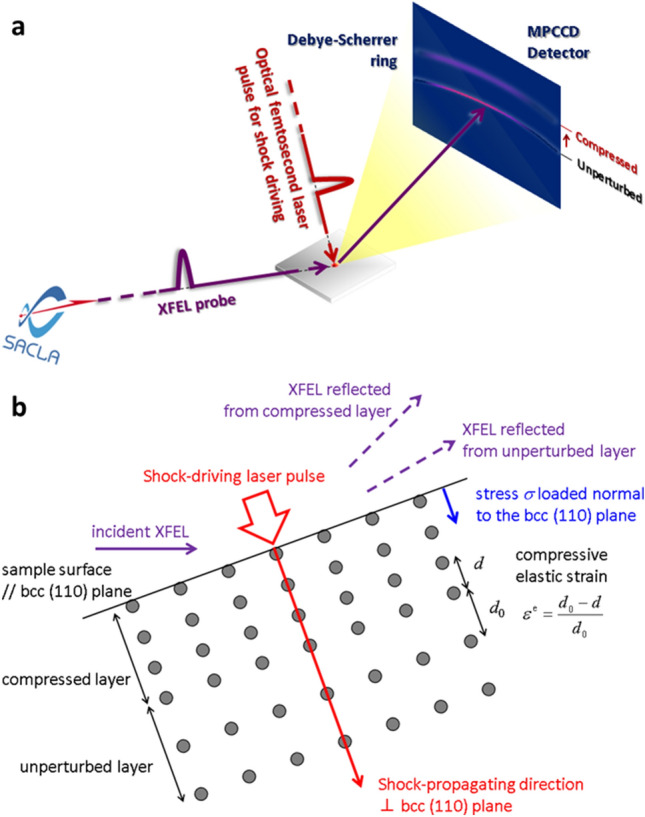
Schematic illustration of the optical femtosecond laser-pump and XFEL-probe experimental setup. (a) A pump-laser pulse is focused onto the 600 µm diameter spot on the iron surface. An XFEL pulse irradiates the sample maintaining a spatial overlap with the pump laser. Shot-to-shot XRD patterns are recorded with a two-dimensional MPCCD detector. (b) The sample surface is almost parallel to the bcc (110) plane of iron with a bcc structure. The direction of shock propagation is perpendicular to the bcc (110) plane, so stress σ is applied perpendicular to the plane. The diffracted X-ray beam from the compressed plane with the lattice spacing d is recorded at a higher angle than that from the unperturbed plane with the initial lattice spacing d0, where the compressive elastic strain εe is expressed by εe = (d0 – d)/d0.
Transmission electron microscopy (TEM: JEM-2010; JEOL) with an accelerating voltage of 200 kV was performed on femtosecond laser-driven shocked iron to observe its microstructure and lattice defects such as dislocations. To perform TEM, a small piece of the cross-section was extracted from the iron surface, and its thickness was reduced using a 30 keV focused Ga+ ion beam (FB-2000A; HITACHI). The sample surface was covered with tungsten before fabrication to prevent damage from ion beam bombardment. The dislocation density was estimated quantitatively using Ham's equation ρ = 2N/Lt, where ρ is the dislocation density, N is the number of intersections between dislocation lines and grid lines drawn on the TEM micrograph, L is the total length of the grid lines, and t is the thickness of the TEM sample54.
Results
Figure 2a to f show the typical diffraction patterns recorded at different delay times. The vertical direction in the figure represents the angle in the 2θ direction, and the circumferential direction of the diffraction ring represents the angle in the azimuthal δ direction. Figure 2a shows the unperturbed pattern recorded before pump-laser irradiation. A clear Debye–Scherrer ring was observed, indicating the Bragg peak for the (110) plane of iron with a body-centred-cubic (bcc) structure at 35.62°. The ring broadened slightly at τ = 10 ps (Fig. 2b). In Fig. 2c, the profile of this ring remained the same even at τ = 50 ps. However, an increased baseline intensity was observed in the higher-angle region of the initial Bragg peak, which became a distinct peak after τ = 70 ps (Fig. 2d to f). Subsequently, the peak shifts to a lower diffraction angle as the delay time increases.
Figure 2.
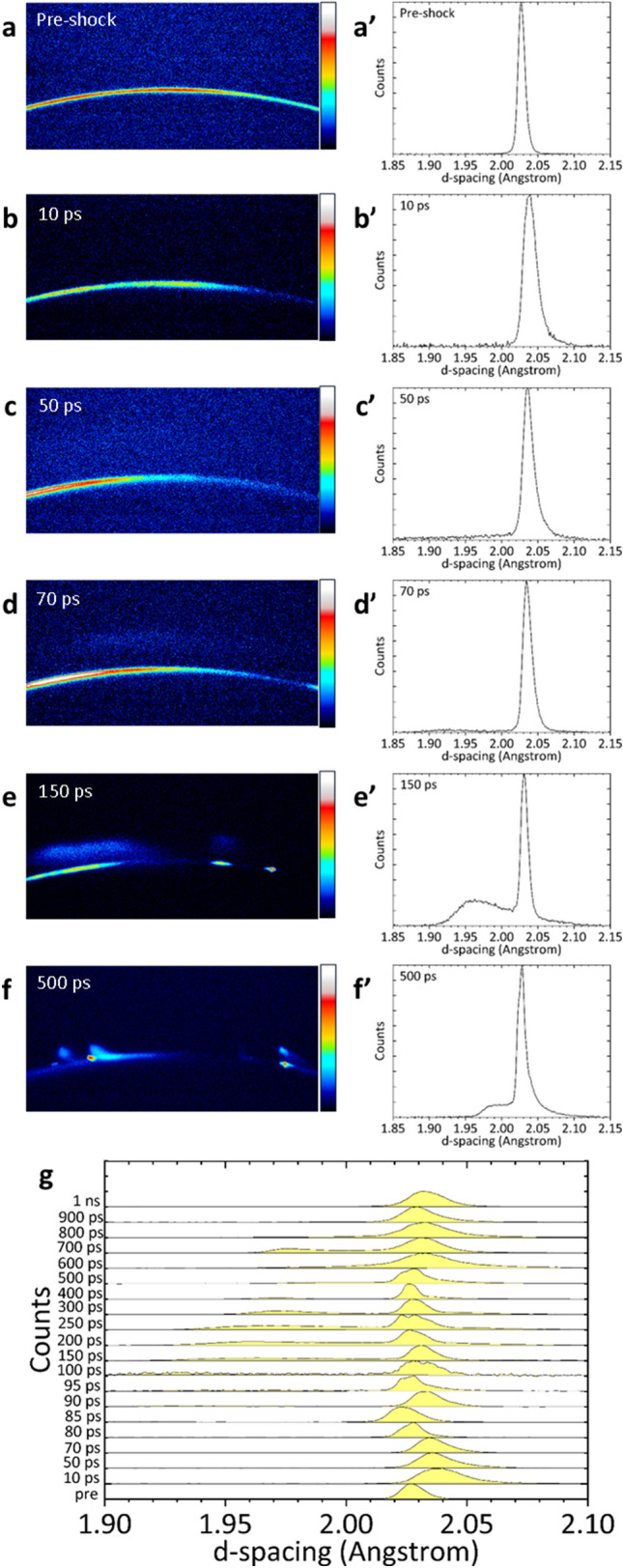
Diffraction patterns recorded at different delay times τ and the corresponding one-dimensional profiles. (a) The unperturbed pattern recorded before pump laser irradiation, pre-shocked state. A clear Debye–Scherrer ring indicates the Bragg peak for the (110) plane of iron with a bcc structure at 35.62°. (b) At τ = 10 ps, the ring becomes slightly wider. (c) At τ = 50 ps, an increase in baseline intensity in the higher angle region is observed relative to the initial Bragg peak. (d) At τ = 70 ps, a prominent new peak appears in the higher angle region. (e) At τ = 150 ps, the intensity of the new peak increases. (f) At τ = 500 ps, the peak shifts to a lower angle. This new peak indicates the Bragg one for the compressed bcc (110) plane. (a′–f′) are one-dimensional profiles corresponding to (a–f) where the XRD patterns obtained on the two-dimensional detector are intensity-integrated in the δ direction, 2θ is converted to d-spacing using λ = 2dsinθ relationships, where λ is the wavelength of the XFEL, d is a d-spacing of a lattice, θ is the Bragg angle, and the intensity is normalised to the maximum value. (g) One-dimensional profiles for a series of delay times.
One dimensional profiles at each delay time are shown in Fig. 2a′ to f′, corresponding to the two-dimensional patterns shown in Fig. 2a to f, where the XRD patterns obtained on the two-dimensional detector are intensity-integrated in the δ direction and 2θ is converted to d-spacing using the λ = 2dsinθ relationship, where λ is the wavelength of the XFEL, d is a d-spacing of the lattice, and θ is the Bragg angle. Furthermore, the intensity is normalised to the maximum value. The d-spacing of the (110) plane increases slightly at τ = 10 ps. The intensity of the peak on the compression side of the (110) plane increases at τ = 50 ps. As the intensity increases with time, it transforms into a new peak, which is the Bragg peak for the shock-compressed bcc (110) plane. This is the main target of our analysis.
Figure 2g shows one dimensional profiles for a series of delay times. The intensity of the new peak, which is significantly compressed compared to the initial peak, is low at τ = 50 ps, but it increases significantly from τ = 150 ps to 700 ps and decreases after τ = 800 ps.
Figure 3 shows the lattice spacing d of the shock-compressed bcc (110) plane and the corresponding nominal compressive elastic strain εe = (d0 – d)/d0 as a function of the delay time τ, where d0 is the initial lattice spacing of 2.0268 Å. The error bar shows the full width at half maximum (FWHM) in the fitting profile. Note that the direction normal to the lattice plane is nearly parallel to the direction of shock propagation normal to the surface. The lattice spacing in the shocked region decreases drastically to 1.88 Å at τ = 50 ps, corresponding to a compressive elastic strain εe of 7.19%. At τ = 10 ps, the peak from the shocked region is absent and lattice expansion is confirmed. Therefore, the compressive elastic strain rate from the initial state to 50 ps is 1.96 × 109 s−1.
Figure 3.
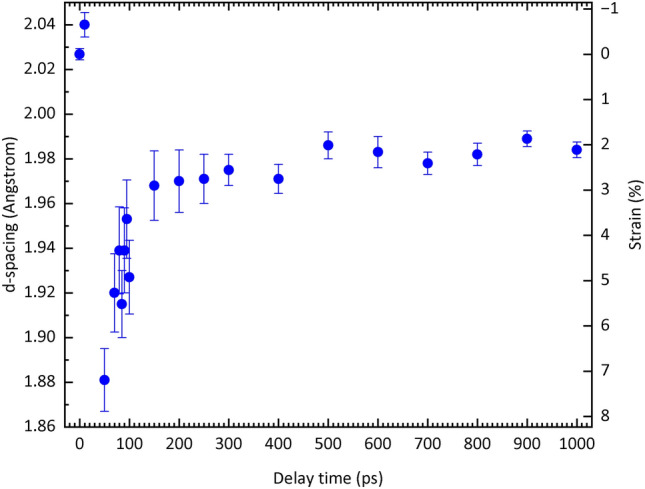
Temporal evolution of the lattice spacing d and the corresponding elastic strain εe for a shock-compressed bcc (110) plane. Lattice spacing d (blue dots) and the corresponding compressive elastic strain εe are shown. Error bars for the lattice spacing indicate the full width at half maximum (FWHM) of the Bragg peaks for the shock-compressed bcc (110) plane. The d-spacing increases at τ = 10 ps, presumably due to lattice expansion caused by the rapid energy transfer from the electrons in the higher energy state due to inverse bremsstrahlung to the lattice. The lattice spacing decreases drastically to 1.88 Å at τ = 50 ps, corresponding to an elastic strain εe of 7.19% at a compressive strain rate of 1.96 × 109 s−1. After τ = 50 ps, the lattice spacing starts to expand. The expansion rate is initially high (− 4.05 × 108 s−1 for 50 ps ≤ τ ≤ 150 ps), while it becomes moderate after 150 ps (− 9.29 × 106 s−1 for 150 ps ≤ τ ≤ 1 ns). The FWHM, which reflects the plasticity, increases between τ = 50 ps and 150 ps and then gradually decreases.
After τ = 50 ps, the lattice spacing in the shocked region begins to expand. The expansion rate is initially high, but becomes moderate after τ = 150 ps. The corresponding elastic strain rate is − 4.05 × 108 s−1 from τ = 50 ps to 150 ps and − 9.29 × 106 s−1 after τ = 150 ps. The peak width increases from τ = 50 ps to 150 ps, and then it gradually decreases.
Figure 4 shows the TEM image of shock-compressed iron within the probe depth of the XFEL pulse. This image shows high-density dislocations of the order of 1015 m−2 while the initial density is of the order of 1012 m−2, indicating severe plastic deformation is taking place.
Figure 4.
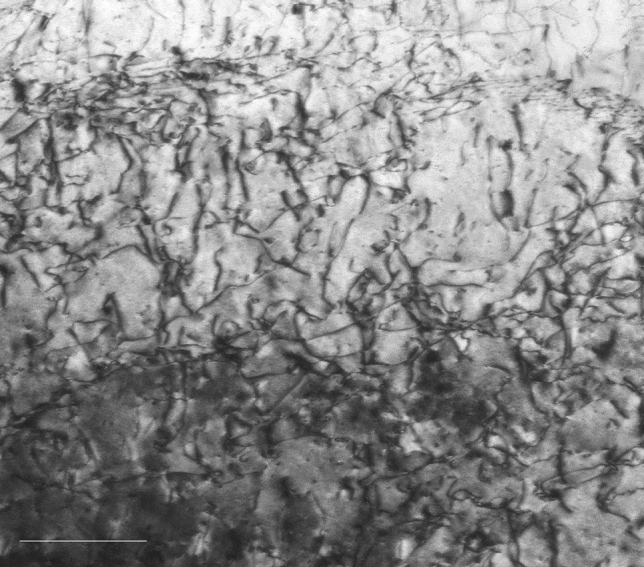
Transmission electron microscope image of shock-compressed iron within the probe depth of the XFEL pulse. The scale bar is 200 nm in length. This image shows high density dislocations, which is the trace of plastic deformation. The estimated dislocation density is of the order of 1015 m−2, while the initial density is of the order of 1012 m−2.
Discussion
The slight increase in the d-spacing of the bcc (110) plane at τ = 10 ps is considered to be due to lattice expansion caused by the rapid energy transfer from the electrons in the higher energy state due to inverse bremsstrahlung to the lattice24,40.
The stress under uniaxial elastic compression is expressed as σx = (C11 + C12 + 2C44) εxe/2, where x is the compression direction, C11, C12 and C44 are the elastic stiffness and εxe is the elastic strain along the compression direction. Assuming that the drastic change at τ = 50 ps is due to uniaxial elastic compression as in conventional shock compression, using C11 = 233.1 GPa, C12 = 135.44 GPa and C44 = 117.83 GPa at 300 K55 and the compressive elastic strain εe of 7.19% at τ = 50 ps, the stress σ loaded normal to the bcc (110) plane is 21.7 GPa. This is almost two orders of magnitude higher than the yield strength under static compression56. To confirm the validity of the uniaxial elastic compression assumption, this value of σ was compared with the yield stress obtained experimentally under high strain rate deformation47. For iron, the peak elastic precursor stress σE, which corresponds to the stress at the onset of plastic deformation, was measured up to the strain rate at the onset of plastic flow of 108 s−1 to obtain the relationship σE – βd–1/2 = 2.3 × 10–3 0.43, where β = 0.69 and d is the grain size47. The value of σE = 23 GPa was obtained by extrapolating the strain rate of 1.96 × 109 s−1 from τ = 10 ps to 50 ps obtained in this experiment and substituting d = 63 µm used in this experiment. These two values were in good agreement, indicating the suitability of the initial assumption that the drastic change at τ = 50 ps is due to uniaxial elastic compression in the same way as conventional shock compression.
Under conventional shock compression, the bcc to hcp phase transition of iron begins at 13 GPa and ends at 20 GPa42–53. The d-spacing of the (101) plane of the hcp structure in the Hugoniot state is 1.8825 Å at 13 GPa and 1.8648 Å at 20 GPa and that of the (100) plane is 2.1405 Å at 13 GPa and 2.1205 Å at 20 GPa. These peaks are not confirmed in Fig. 2a′ to f′, indicating that the femtosecond laser-driven shock wave does not induce the high pressure phase with the hcp structure at this time scale. The d-spacing of the bcc (110) plane is 1.9828 Å at 13 GPa and 1.9643 Å at 20 GPa45. These values agree well with the d-spacing values obtained in this experiment at τ = 1 ns and 150 ps, respectively. The decrease in elastic expansion strain rate and plasticity of the bcc structure after 150 ps may be influenced by the bcc to hcp phase transition. The sluggish phase transition of iron from bcc to hcp structure, despite its non-diffusive nature, remains an unresolved problem. The relaxation time of this transition depends on the shock pressure, i.e. with longer relaxation time at lower shock pressure, e.g. approximately 60 ns to 12 ns for the shock pressure of 17 GPa to 30 GPa44. As the peak stress measured in this experiment was 21.7 GPa, the shock wave required a relaxation time of at least 12 ns to complete the bcc to hcp phase transition. Therefore, no peaks of the hcp structure were observed during this measurement but could be observed later.
The width of the XRD peak qualitatively reflects the amount of plasticity or the number of lattice defects such as dislocations. The behaviour of the peak width, which increases from τ = 50 ps to 150 ps and then gradually decreases, is consistent with the observed plasticity trend, which also increases from τ = 50 ps to 150 ps and then gradually decreases. Therefore, the lattice behaviour shown in Fig. 3 can be interpreted as follows. At τ = 50 ps, a significantly large uniaxial elastic compression and many lattice defects are introduced, followed by a rapid elastic expansion up to τ = 150 ps and a gradual elastic expansion after τ = 150 ps with a decrease in the number of lattice defects. This behaviour is qualitatively consistent with an experimentally confirmed report that a shock-compressed material initially behaves as a purely elastic medium, eventually leading to plastic deformation57–59.
The shock pressure required for homogeneous nucleation of dislocations behind the shock front in iron is 8.6 GPa7. The peak elastic stress of 21.7 GPa for the femtosecond laser-driven shock wave estimated in this experiment was sufficiently higher than this value to allow the formation of the interface60 that allows a homogeneous nucleation of dislocations behind the femtosecond laser-driven shock front. The dislocation density at the interface at the shock pressure of 21.7 GPa was estimated to be 1.38 × 1016 m−2 (Supplementary Information). The elastic strain energy μρb2/2 of the dislocations was 3.3 × 107 J/m3, where μ is the shear modulus and b is the Burgers vector. Here, the most elastically compressed state at τ = 50 ps and the state with the largest peak width at τ = 80 ps are compared. As the stresses at τ = 50 ps and 80 ps were 21.7 GPa and 18 GPa and the corresponding elastic strains were 7.19% and 5.29%, respectively, the difference in elastic strain energy σε/2 was 3.4 × 107 J/m3, which agrees well with the value of the elastic energy of dislocations. The strain energy stored by the large elastic compression at τ = 50 ps was used to generate dislocations, which occurred from τ = 50 ps to 150 ps, resulting in the formation of the remaining high density dislocations observed in the directly femtosecond laser irradiated iron within the probe depth of the XFEL pulse, as shown in Fig. 4, where the dislocation density was estimated to be of the order of 1015 m−2, whereas the initial density was of the order of 1012 m−2.
The experimental results show that under femtosecond laser-driven shock compression the lattice was in a state of uniaxial elastic compression up to τ = 50 ps, an elasto-plastic hydrostatic compression or the Hugoniot state after τ = 150 ps, and an intermediate state between τ = 50 ps and 150 ps. This result is in good agreement with MD simulation results28, which show that when Cu was subjected to shock waves with rise times of 0 and 50 ps, it was initially in a state of uniaxial compression in the direction of shock wave propagation (one-dimensional compression), followed by a hydrostatic three-dimensional compression state to relax the uniaxial compression strain. Thus, the initial compression state caused by the shock wave driven by direct femtosecond laser irradiation is the same as that caused by conventional shock waves.
Based on these observations, we estimated the total strains in the compressed iron for 0 < τ ≤ 1 ns. The total strain εT is expressed as the sum of the elastic strain εe and the plastic strain εp, i.e. εT = εe + εp. In the initial region before τ = 50 ps under uniaxial elastic compression, εT = εe. After τ = 150 ps, is expressed as εT = 3εe due to the isotropic process (Supplementary Information). The stress at τ = 50 ps included only an elastic component of 21.7 GPa. As the material was in the Hugoniot state, the stresses of 19 GPa at τ = 150 ps and 14 GPa at τ = 1 ns were obtained after τ = 150 ps45.
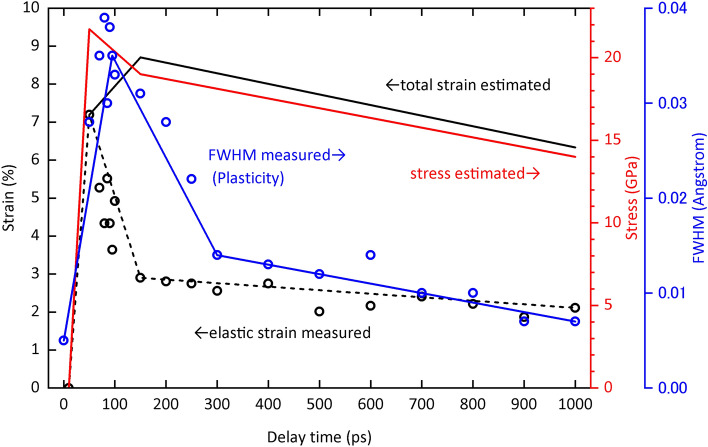
Figure 5 shows the measured elastic strain and FWHM of the diffraction peak, and the total strain and stress estimated from these measured data as a function of time, i.e. the temporal distribution of elastic, plastic, strain and stress waves, respectively. The time of maximum value of the temporal distribution of each wave is the earliest for stress and elastic waves, followed by plastic wave and then strain wave. It was theoretically predicted61 but shown here experimentally for the first time that the peaks of the stress and strain waves diverge with time, as significant dissipation and dispersion processes occur when the medium is subjected to compression or tension. Furthermore, the fact that the peak of the plastic wave lies between these stress and strain wave peaks is a new finding that has never been predicted theoretically. The findings of this study contribute to the understanding of the complex mechanisms of mechanics under shock compression, such as precursor decay anomaly and dynamic yielding, which have remained unanswered for the past 50 years57–59.
Figure 5.
Temporal evolution of measured elastic strain (black circles and dashed line), estimated total strain (solid line), estimated stress (red line), and measured FWHM of peaks (blue circles and line). The stress wave peak precedes the plastic wave peak, as indicated by the peak width of the diffraction pattern, followed by the strain wave peak. Although it was theoretically predicted that the peaks of the stress and strain waves would diverge with time, this has not been reported experimentally. Furthermore, it is a novel finding that the plastic wave peak is positioned between these deviations, which has never been predicted even theoretically.
In summary, using XFEL diffraction measurements, we have successfully demonstrated the complex behaviour of stress, strain and plasticity in iron subjected to the shock wave driven by direct femtosecond laser irradiation. It is not possible to determine directly from the results of this study whether these behaviours are unique to the material subjected to the femtosecond laser-driven shock wave or can also be caused by the conventional shock wave. However, it is worth investigating further as such ultrafast behaviours caused by conventional shock waves have not been reported before. After τ = 150 ps, the material is in the Hugoniot state despite the expansion process under compression, which means that there may be other unknown waves hidden. Therefore, the femtosecond laser-driven shock wave is a suitable tool to probe the nature behind and possibly within the shock front. Furthermore, these features can persist in the material, allowing unique events such as DLP17,18 and high-pressure phase quenching16 that would not be possible with conventional shock waves. Further research into the lattice behaviour under femtosecond laser-driven shock compression will open up new avenues for future applications of femtosecond lasers as shock drivers.
Supplementary Information
Acknowledgements
The authors wish to thank Y. Kohmura, Y. Isshiki, R. Kashiwabara, N. Matsuyama, H. Uranishi, K. Nakatsuka, Y. Kondo, S. Iketani, Y. Sato, M. Yamashita, R. Shiraishi, M. Yoshida, R. Takekuma, Y. Mori, N. Egashira, Y. Komatsubara, S. Inoue, N. Asaoka, A. Higuchi, S. Fujisawa, M. Hotta, Y. Tanaka, Y. Nagai, and the engineering staff of SACLA for their support for the experiments. We also wish to thank J. Wark for helpful discussions. The XFEL experiments were performed at the BL3 of SACLA with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal Nos. 2012A8053, 2012B8048, 2021B8031 and 2022A8031). This study was supported in part by MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) Grant No. JPMXS0118068348, JSPS KAKENHI Grant Nos. 19K22061 and 20H02048, JSPS core to core program on International Alliance for Material Science in Extreme States with High Power Laser, and X-ray Free Electron Laser Priority Strategy Program (MEXT), The Amada Foundation, The Light Metal Educational Foundation, Inc., Osawa Scientific Studies Grants Foundation, and Mazak Foundation.
Author contributions
T.S., T.M., Y.I., T.S., K.M. M.Y., T.T., K.T., O.S., K.A., Y.I., Y.T., T.O., T.S., T.S., N.N., Y.S., T.S., Y.S., T.H., T.M., T.Y., K.A.T., N.O. and R.K. performed the experiment. T.S., A.H., M.O., T.T., T.K., T.S., T.M. and M.S. performed the theoretical work. All authors discussed the results and commented on the manuscript.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-023-40283-6.
References
- 1.Erskine DJ, Nellis WJ. Shock-induced martensitic phase transformation of oriented graphite to diamond. Nature. 1991;349:317–319. [Google Scholar]
- 2.Tenaglia RD, Lahrman DF. Shock tactics. Nat. Photonics. 2009;3:267–269. [Google Scholar]
- 3.Kinslow R. High-Velocity Impact Phenomena. Academic Press; 1970. [Google Scholar]
- 4.Beck P, Gillet Ph, Goresy AE, Mostefaoui S. Timescales of shock processes in chondritic and martian meteorites. Nature. 2005;435:1071–1074. doi: 10.1038/nature03616. [DOI] [PubMed] [Google Scholar]
- 5.Drake RP. High-Energy-Density Physics: Fundamentals, Inertial Fusion, and Experimental Astrophysics. Springer; 2006. [Google Scholar]
- 6.Zel'dovich YB, Raizer YP. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Dover Publications; 2002. [Google Scholar]
- 7.Meyers MA. Dynamic Behavior of Materials. Wiley-Interscience; 1994. [Google Scholar]
- 8.Rankine WJM. On the thermodynamic theory of waves of finite longitudinal disturbance. Philos. Trans. R. Soc. Lond. 1870;160:277–288. [Google Scholar]
- 9.Hugoniot PH. Sur la propagation du mouvement dans les corps et spécialement dans les gaz parfaits (première partie) Journal de l'École Polytechnique. 1887;57:3–97. [Google Scholar]
- 10.Moore DS, McGrane SD, Funk DJ. Ultra-short laser shock dynamics. In: Horie Y, editor. Shock Wave Science and Technology Reference Library. Springer; 2007. pp. 47–104. [Google Scholar]
- 11.Moore DS. Shock physics at the nanoscale. J. Opt. Soc. Am. B. 2018;35:B1–B15. [Google Scholar]
- 12.Powell MS, Bowlan PR, Son SF, Bolme CA, Brown KE, Moore DS, McGrane SD. A benchtop shock physics laboratory: Ultrafast laser driven shock spectroscopy and interferometry methods. Rev. Sci. Instrum. 2019;90:063001. doi: 10.1063/1.5092244. [DOI] [PubMed] [Google Scholar]
- 13.Evans R, Badger AD, Falliès F, Mahdieh M, Hall TA, Audeberg P, Geindre J-P, Gauthier J-C, Mysyrowicz A, Grillon G, Antonetti A. Time- and space-resolved optical probing of femtosecond-laser-driven shock waves in aluminum. Phys. Rev. Lett. 1996;77:3359–3362. doi: 10.1103/PhysRevLett.77.3359. [DOI] [PubMed] [Google Scholar]
- 14.Matsuda T, Sano T, Arakawa K, Hirose A. Multiple-shocks induced nanocrystallization in iron. Appl. Phys. Lett. 2014;105:021902. [Google Scholar]
- 15.Matsuda T, Sano T, Arakawa K, Hirose A. Dislocation structure produced by an ultrashort shock pulse. J. Appl. Phys. 2014;116:183506. [Google Scholar]
- 16.Sano T, Mori H, Ohmura E, Miyamoto I. Femtosecond laser quenching of the e phase of iron. Appl. Phys. Lett. 2003;83:3498–3500. [Google Scholar]
- 17.Sano T, Eimura T, Kashiwabara R, Matsuda T, Isshiki Y, Hirose A, Tsutsumi S, Arakawa K, Hashimoto T, Masaki K, Sano Y. Femtosecond laser peening of 2024 aluminum alloy without a sacrificial overlay under atmospheric conditions. J. Laser Appl. 2017;29:012005. [Google Scholar]
- 18.Yoshida M, Nishibata I, Matsuda T, Ito Y, Sugita N, Shiro A, Shobu T, Arakawa K, Hirose A, Sano T. Influence of pulse duration on mechanical properties and dislocation density of dry laser peened aluminum alloy using ultrashort pulsed laser-driven shock wave. J. Appl. Phys. 2022;132:075101. [Google Scholar]
- 19.Clauer AH, Holbrook JH, Fairand BP. Shock Waves and High- Strain-Rate Phenomena in Metals. Plenum Publishing Corporation; 1981. pp. 675–703. [Google Scholar]
- 20.Fabbro R, Peyre P, Berthe L, Scherpereel X. Physics and applications of laser-shock processing. J. Laser Appl. 1998;10:265–279. [Google Scholar]
- 21.Sano Y, Obata M, Kubo T, Mukai N, Yoda M, Masaki K, Ochi Y. Retardation of crack initiation and growth in austenitic stainless steels by laser peening without protective coating. Mater. Sci. Eng. A. 2006;417:334–340. [Google Scholar]
- 22.Murzov S, Ashitkov S, Struleva E, Komarov P, Zhakhovsky V, Khokhlov V, Inogamov N. Elastoplastic and polymorphic transformations of iron at ultra-high strain rates in laser-driven shock waves. J. Appl. Phys. 2021;130:245902. [Google Scholar]
- 23.Schmidt V, Husinsky W, Betz G. Dynamics of laser desorption and ablation of metals at the threshold on the femtosecond time scale. Phys. Rev. Lett. 2000;85:3516–3519. doi: 10.1103/PhysRevLett.85.3516. [DOI] [PubMed] [Google Scholar]
- 24.Gamaly EG, Rode AV, Luther-Davies B, Tikhonchuk VT. Ablation of solids by femtosecond lasers: Ablation mechanism and ablation thresholds for metals and dielectrics. Phys. Plasmas. 2002;9:949–957. [Google Scholar]
- 25.Amoruso S, Bruzzese R, Vitiello M, Nedialkov NN, Atanasov PA. Experimental and theoretical investigations of femtosecond laser ablation of aluminum in vacuum. J. Appl. Phys. 2005;98:044907. [Google Scholar]
- 26.Dachraoui H, Husinskya W. Fast electronic and thermal processes in femtosecond laser ablation of Au. Appl. Phys. Lett. 2006;89:104102. [Google Scholar]
- 27.Kadau K, Germann TC, Lomdahl PS, Holian BL. Microscopic view of structural phase transitions induced by shock waves. Science. 2002;296:1681–1684. doi: 10.1126/science.1070375. [DOI] [PubMed] [Google Scholar]
- 28.Bringa EM, Rosolankova K, Rudd RE, Remington BA, Wark JS, Duchaineau M, Kalantar DH, Hawreliak J, Belak J. Shock deformation of fcc metals on subnanosecond timescales. Nat. Mater. 2006;5:805–809. doi: 10.1038/nmat1735. [DOI] [PubMed] [Google Scholar]
- 29.Zhakhovsky VV, Budzevich MM, Inogamov NA, Oleynik II, White CT. Two-zone elastic-plastic single shock waves in solids. Phys. Rev. Lett. 2011;107:135502. doi: 10.1103/PhysRevLett.107.135502. [DOI] [PubMed] [Google Scholar]
- 30.Milathianaki D, Boutet S, Williams GJ, Higginbotham A, Ratner D, Gleason AE, Messerschmidt M, Seibert MM, Swift DC, Hering P, Robinson J, White WE, Wark JS. Femtosecond visualization of lattice dynamics in shock-compressed matter. Science. 2013;342:220–223. doi: 10.1126/science.1239566. [DOI] [PubMed] [Google Scholar]
- 31.Wark JS, Whitlock RR, Hauer A, Swain JE, Solone PJ. Shock launching in silicon studied with use of pulsed x-ray diffraction. Phys. Rev. B. 1987;35:9391–9394. doi: 10.1103/physrevb.35.9391. [DOI] [PubMed] [Google Scholar]
- 32.Suggit MJ, Higginbotham A, Hawreliak JA, Mogni G, Kimminau G, Dunne P, Comley AJ, Park N, Remington BA, Wark JS. Nanosecond white-light Laue diffraction measurements of dislocation microstructure in shock-compressed single-crystal copper. Nat. Commun. 2012;3:1224. doi: 10.1038/ncomms2225. [DOI] [PubMed] [Google Scholar]
- 33.Kalantar DH, Belak JF, Collins GW, Colvin JD, Davies HM, Eggert JH, Germann TC, Hawreliak J, Holian BL, Kadau K, Lomdahl PS, Lorenzana HE, Meyers MA, Rosolankova K, Schneider MS, Sheppard J, Stölken JS, Wark JS. Direct observation of the a-e transition in shock-compressed iron via nanosecond X-ray diffraction. Phys. Rev. Lett. 2005;95:075502. doi: 10.1103/PhysRevLett.95.075502. [DOI] [PubMed] [Google Scholar]
- 34.Radousky HB, Armstrong MR, Goldman N. Time resolved x-ray diffraction in shock compressed systems. J. Appl. Phys. 2021;129:040901. [Google Scholar]
- 35.Emma P, Akre R, Arthur J, Bionta R, Bostedt C, Bozek J, Brachmann A, Bucksbaum P, Coffee R, Decker F-J, Ding Y, Dowell D, Edstrom S, Fisher A, Frisch J, Gilevich S, Hastings J, Hays G, Hering Ph, Huang Z, Iverson R, Loos H, Messerschmidt M, Miahnahri A, Moeller S, Nuhn H-D, Pile G, Ratner D, Rzepiela J, Schultz D, Smith T, Stefan P, Tompkins H, Turner J, Welch J, White W, Wu J, Yocky G, Galayda J. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics. 2010;4:641–647. [Google Scholar]
- 36.Ishikawa T, et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics. 2012;6:540–544. [Google Scholar]
- 37.Gleason AE, Bolme CA, Lee HJ, Nagler B, Galtier E, Milathianaki D, Hawreliak J, Kraus RG, Eggert JH, Fratanduono DE, Collins GW, Sandberg R, Yang W, Mao WL. Ultrafast visualization of crystallization and grain growth in shock-compressed SiO2. Nat. Commun. 2015;10:1038. doi: 10.1038/ncomms9191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hwang H, Galtier E, Cynn H, Eom I, Chun SH, Bang Y, Hwang GC, Choi J, Kim T, Kong M, Kwon S, Kang K, Lee HJ, Park C, Lee JI, Lee Y, Yang W, Shim S-H, Vogt T, Kim S, Park J, Kim S, Nam D, Lee JH, Hyun H, Kim M, Koo T-Y, Kao C-C, Sekine T, Lee Y. Subnanosecond phase transition dynamics in laser-shocked iron. Sci. Adv. 2020;6:eaaz5132. doi: 10.1126/sciadv.aaz5132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Okuchi T, et al. Ultrafast olivine-ringwoodite transformation during shock compression. Nat. Commun. 2021;12:4305. doi: 10.1038/s41467-021-24633-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chichkov BN, Momma C, von Nolte S, Alvensleben F, Tünnermann A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A. 1996;63:109–115. [Google Scholar]
- 41.Demaske BJ, Zhakhovsky VV, Inogamov NA, Oleynik II. Ultrashort shock waves in nickel induced by femtosecond laser pulses. Phys. Rev. B. 2013;87:054109. [Google Scholar]
- 42.Barker LM, Hollenbach RE. Shock wave study of the α↔ε phase transition in iron. J. Appl. Phys. 1974;45:4872–4887. [Google Scholar]
- 43.Brown JM, McQueen RG. Phase transitions, Grüneisen parameter, and Elasticity for shocked iron between 77 GPa and 400 GPa. J. Geophys. Res. 1986;91:7485–7494. [Google Scholar]
- 44.Boettger JC, Wallace DC. Metastability and dynamics of the shock-induced phase transitions in iron. Phys. Rev. B. 1997;55:2840–2849. [Google Scholar]
- 45.Brown JM, Fritz JN, Hixson RS. Hugoniot data for iron. J. Appl. Phys. 2000;88:5496–5498. [Google Scholar]
- 46.Sano Y, Sano T. Thermal properties of close-packed Fe up to 400 GPa determined using Hugoniot functions. Phys. Rev. B. 2004;69:144201. [Google Scholar]
- 47.Smith RF, Eggert JH, Rudd RE, Swift DC, Bolme CA, Collins GW. High strain-rate plastic flow in Al and Fe. J. Appl. Phys. 2011;110:123515. [Google Scholar]
- 48.Gunkelmann N, Bringa EM, Kang K, Ackland GJ, Ruestes CJ, Urbassek HM. Polycrystalline iron under compression: Plasticity and phase transitions. Phys. Rev. B. 2012;86:144111. [Google Scholar]
- 49.Wang SJ, Sui ML, Chen YT, Lu QH, Ma E, Pei XY, Li QZ, Hu HB. Microstructural fingerprints of phase transitions in shock-loaded iron. Sci. Rep. 2013;3:1086. doi: 10.1038/srep01086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Crowhurst JC, Reed BW, Armstrong MR, Radousky HB, Carter JA, Swift DC, Zaug JM, Minich RW, Teslich NE, Kumar M. The a⟶e phase transition in iron at strain rates up to ~109 s−1. J. Appl. Phys. 2014;115:113506. [Google Scholar]
- 51.Gunkelmann N, Bringa EM, Tramontina DR, Ruestes CJ, Suggit MJ, Higginbotham A, Wark JS, Urbassek HM. Shock waves in polycrystalline iron: Plasticity and phase transitions. Phys. Rev. B. 2014;89:140102. [Google Scholar]
- 52.Liu X, Mashimo T, Kawai N, Sano T, Zhou X. Isotropic phase transition of single-crystal iron (Fe) under shock compression. J. Appl. Phys. 2018;124:215101. [Google Scholar]
- 53.Hawreliak JA, Turneaurea SJ. Probing the lattice structure of dynamically compressed and released single crystal iron through the alpha to epsilon phase transition. J. Appl. Phys. 2021;129:135901. [Google Scholar]
- 54.Ham RK. The determination of dislocation densities in thin films. Philos. Mag. 1961;6:1183–1184. [Google Scholar]
- 55.Rayne JA, Chandrasekhar BS. Elastic constants of iron from 4.2 to 300 ºK. Phys. Rev. 1961;122:1714–1716. [Google Scholar]
- 56.Krafft JM, Sullivan AM, Tipper CF. The effect of static and dynamic loading and temperature on the yield stress of iron and mild steel in compression. Proc. R. Soc. Lond. A. 1954;221:114–127. [Google Scholar]
- 57.Taylor JW, Rice MH. Elastic-plastic properties of iron. J. Appl. Phys. 1963;34:364–371. [Google Scholar]
- 58.Taylor JW. Dislocation dynamics and dynamic yielding. J. Appl. Phys. 1965;36:3146–3150. [Google Scholar]
- 59.Kelly JM, Gillis PP. Dislocation dynamics and precursor attenuation. J. Appl. Phys. 1967;38:4044–4046. [Google Scholar]
- 60.Smith CS. Metallographic studies of metals after explosive shock. Trans. AIME. 1958;212:574–589. [Google Scholar]
- 61.Sano Y. Underdetermined system theory applied to qualitative analysis of response caused by attenuating plane waves. J. Appl. Phys. 1989;65:3857–3867. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.