Abstract
Humans and animals routinely infer relations between different items or events and generalize these relations to novel combinations of items. This allows them to respond appropriately to radically novel circumstances and is fundamental to advanced cognition. However, how learning systems (including the brain) can implement the necessary inductive biases has been unclear. Here we investigated transitive inference (TI), a classic relational task paradigm in which subjects must learn a relation (A > B and B > C) and generalize it to new combinations of items (A > C). Through mathematical analysis, we found that a broad range of biologically relevant learning models (e.g. gradient flow or ridge regression) perform TI successfully and recapitulate signature behavioral patterns long observed in living subjects. First, we found that models with item-wise additive representations automatically encode transitive relations. Second, for more general representations, a single scalar “conjunctivity factor” determines model behavior on TI and, further, the principle of norm minimization (a standard statistical inductive bias) enables models with fixed, partly conjunctive representations to generalize transitively. Finally, neural networks in the “rich regime,” which enables representation learning and has been found to improve generalization, unexpectedly show poor generalization and anomalous behavior. We find that such networks implement a form of norm minimization (over hidden weights) that yields a local encoding mechanism lacking transitivity. Our findings show how minimal statistical learning principles give rise to a classical relational inductive bias (transitivity), explain empirically observed behaviors, and establish a formal approach to understanding the neural basis of relational abstraction.
1. Introduction
Humans and animals have a remarkable ability to generalize to circumstances that are radically different from their prior experience. They are able to do so, in part, by learning relationships between different events or items and extending these relationships to novel combinations of components [1]. Such relational generalization is important across a broad range of domains: for example, subjects can reason about social relationships between individuals they have never seen interact [2–4], take a novel route between familiar locations [5], or apply familiar tools to novel problems [6]. Accordingly, relational cognition has been implicated in a variety of cognitive abilities, including social cognition [7], spatial navigation [8], and logical and causal cognition [9].
It is unclear how living subjects, and learning systems more generally, can learn the kinds of abstractions needed for relational generalization. To generalize from limited experience, subjects (whether they are humans, animals, or learning models) need an “inductive bias”: a disposition towards certain behaviors among the many that are consistent with past experience [10]. Much attention has been devoted to clarifying suitable inductive biases on standard statistical tasks, which require generalization to nearby data points (“near transfer” or “in-distribution generalization”) [11–16]. An important instance of such a “statistical inductive bias” is norm minimization, which selects the model parameters with the smallest weight norm and is at the core of many successful learning models [17–19]. Both theoretical and practical insights suggest that such a solution is likely to generalize well in distribution [20, 21]. In contrast, our understanding of how learning models perform relational tasks, which require generalization to radically different circumstances (“far transfer,” [22] “out-of-distribution generalization,” [23] or, more specifically, “generalization to the unseen” [24]), has been much more limited [25]. Addressing this gap is essential to understanding how living subjects perform these tasks.
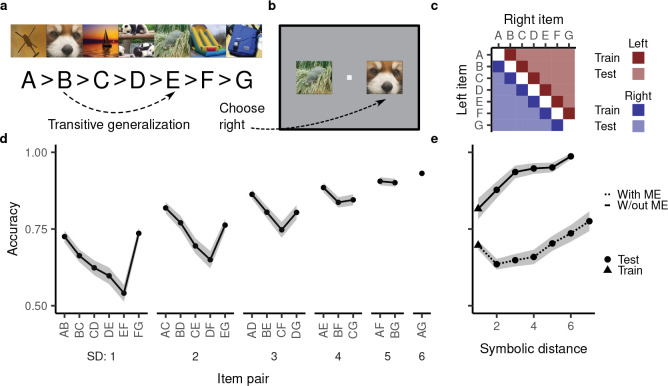
To investigate this question, we studied transitive inference [TI; Fig. 1a; 26–28], a classical cognitive task that tests if humans or animals can generalize transitively. In this task, subjects are presented with pairs of items (Fig. 1b) and must pick the “larger” item according to an implicit hierarchy (A > B > ·· · > G, Fig. 1a). Importantly, subjects are not informed of this task structure [cf. 29, 30] and, further, only receive feedback about the correct response on adjacent pairs (AB, BC,..., FG). Hence, they must infer the underlying relation and use transitive inference to determine the correct response to non-adjacent pairs (B > E, Fig. 1c).
Figure 1:
Transitive inference and behavioral patterns observed in subjects performing this task. a, Example stimuli taken from [31]. An example generalization (B > E) is highlighted. b, In a given trial, the subject is asked to choose between the two presented items. They are rewarded if the chosen item is “larger” according to the underlying hierarchy. This panel depicts a test trial where successful performance would consist in picking the item on the right. c, Schematic of the training and test cases. d, Example accuracy on all training and test cases (in this case by rhesus macaques). Terminal item, symbolic distance, and asymmetry effect are apparent in the plot. In the subsequent figures, we leave off the item pair labels but use the same ordering. Symbolic distance (SD) is the separation in the rank hierarchy. The data is reproduced from [31]. e, Symbolic distance effect with and without a memorization effect (ME). Data without ME reproduced from [31] and data with ME reproduced from [29]. Shaded regions in both panels indicate mean ± one standard error.
Notably, humans [32] and a variety of animals (ranging from monkeys [33, 34] and rodents [35] to wasps [36] and fish [37]) perform TI successfully. Moreover, they show consistent behavioral patterns (in their reaction time and accuracy, Fig. 1d), which may be informative of the underlying neural implementation. First, subjects’ performance improves with increasing separation in the hierarchy [“symbolic distance effect,” e.g. 32, 38–42]. Second, subjects’ performance tends to be better for trials involving more terminal (e.g. A and G) rather than more intermediate (e.g. D and E) items [“terminal item effect,” e.g. 31, 43–45]. Third, some studies indicate better performance on training trials (which have a symbolic distance of 1) than on test trials with a symbolic distance of 2 [29, 42, 46–48, Fig. 1e], a limited violation of the symbolic distance effect which we here refer to as the memorization effect. Finally, subjects’ performance is often better for item pairs towards the beginning of the hierarchy than item pairs towards the end (the “asymmetry effect,” which we do not address but return to in the discussion) [e.g. 29].
Many simple learning models have been shown to perform transitive inference. However, the inductive biases that give rise to this ability are not well understood. Various learning models associate a numerical “rank” with each presented item and choose whichever item has a higher rank [29, 31, 49–51]. Such models are pre-configured to generalize transitively and leave unclear how transitive generalization could arise from more basic learning principles. They also leave unclear how the brain, which is not constrained in this way [52], could implement TI. Intriguingly, several studies have found that generic neural networks can generalize transitively, suggesting that statistical learning principles can sometimes give rise to a suitable relational inductive bias [30, 53–55]. However, TI in neural networks has largely been studied through simulations, rather than analytically [cf. 56], raising the question of when and how statistical learning models can implement TI.
Here we show, via both analytical approaches and simulations, that a broad range of biologically relevant learning models generalize transitively and recapitulate the symbolic distance, terminal item, and memorization effect. We first consider models with “additive” representations that represent the two presented items independently, and show that they are constrained to implementing a transitive relation. If models additionally represent nonlinear conjunctions between items (as is important for many other tasks) but use norm minimization to determine their readout weights, they also generalize transitively. Remarkably, the same learning principle that underpins many instances of successful near transfer also enables this instance of successful far transfer. We further show that, for TI, the effect of a particular choice of internal representation can be characterized by a single scalar “conjunctivity factor.” Finally, we consider models which adapt their internal representation to a given task, an ability thought critical to human and animal cognition. Surprisingly, we find that this impairs performance on TI and leads to behavioral patterns that deviate from those in living subjects. Notably, this anomalous behavior is explained by the rich regime’s implementation of a different form of norm minimization, namely one over all weights in the network rather than just the readout weights.
At first glance, TI appears to be a complex task involving relational cognition and application of the transitive rule. Nevertheless, we can characterize a broad range of learning models performing this task in exact analytical terms, explaining how they give rise to the rich behavioral patterns observed in living subjects. In doing so, our investigation clarifies systematically how a learning principle that has largely been considered in the context of near transfer, also implements an important instance of far transfer and relational abstraction.
2. Model setup
We represent individual items as high-dimensional vectors. A trial input is a concatenation of the two vectors , corresponding to the two presented items. We generally consider a learning model which represents this input as a numerical vector (in the simplest case, this could be the input vector itself). The model then computes a linear readout from that representation: . A positive model output corresponds to , whereas a negative output corresponds to . We generally assume that is learned from the training trials, whereas remains fixed (for example arising from the representation in a neural network with random or pre-learned weights). In the final two sections, we investigate models that also learn .
Inputs where lie on the model’s decision boundary. Accordingly, a higher magnitude of the margin if or if corresponds to a larger distance from the decision boundary. We take this to indicate better performance, corresponding to higher choice accuracy and lower reaction time. This is a standard assumption in models of decision making [30, 57–59]. For example, in a drift diffusion model [60], the output determines the model’s drift rate. The higher the drift rate, the less susceptible the model is to noise (improving accuracy) and the faster it will cross its threshold (improving reaction time) [61].
3. Results
3.1. An additive representation yields transitive generalization
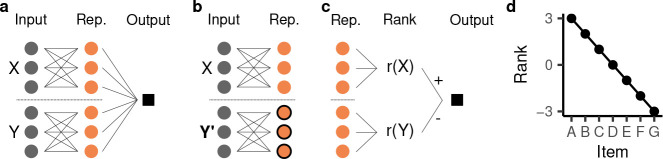
To perform TI, or indeed any kind of relational inference, a learning model’s representation of items and , , should reflect the fact that and are separate items. In the most extreme case, this would amount to an additive representation, where is a sum of two separate representations and . A simple instance of this is a model architecture where nodes respond exclusively either to or (Fig. 2a).
Figure 2:
An additive representation yields transitive generalization and the symbolic distance effect. a, Schematic illustration of an additive representation (rep.). The first three orange nodes represent the first item and the latter three represent the second item . b, Replacing the second item only results in changes to the highlighted half of the units. c, The readout weights of the model can be grouped into those pertaining to item and those pertaining to item . The model’s output can be understood as assigning a “rank” and to each item and then computing . d, Example of a model’s rank assignment.
A change in one of the two items will leave half of the additive representation unchanged (Fig. 2b), implementing a kind of compositionality [62]. A linear readout from an additive representation, , is a sum of responses to each individual item, , and therefore also additive. The consequences of this are especially clear in the case of a model without a choice bias, i.e. if (Appendix S1.1 considers the biased case). In this case, we know that , and, as a result, the model’s decision function can be expressed as
This means that the model necessarily learns to assign a scalar “rank” to each item, and computes its decision by comparing the two ranks (Fig. 2c):
Note that , i.e. the decision to choose the left item, is equivalent to .
As shown in previous work [e.g. 29, 31, 43], learning systems that are pre-configured to have such a ranking system yield both transitive generalization and the symbolic distance effect. This is because, to learn the training set, the model’s ranks must be monotonically decreasing:
As an example, if the model output has a margin of one for all inputs composed of adjacent items, the rank must decrease by one for each successive item (Fig. 2d). A monotonically decreasing rank directly implies that non-adjacent items are also ordered correctly and, consequently, that the model will generalize transitively. Further, item pairs with larger symbolic distance will have a larger difference in their ranks, giving rise to a symbolic distance effect.
Critically, and in distinction to previous work, the above model structure (additive representation) does not explicitly pre-configure or assume a ranking system. Rather, the above analysis shows that any learning model that implements an additive input representation necessarily implements a ranking system and thus encodes a transitive relation. Further, the above analysis makes no assumptions about how the model learns. As long as the model correctly classifies the training cases, it will correctly classify all test cases, i.e. transitively generalize, and it will exhibit a symbolic distance effect.1
3.2. A single scalar fully characterizes a broad range of relational representations
The above analysis indicates that an additive representation would enable the brain to perform TI. However, neural representations are not thought to be fully additive [63]. Indeed, non-additive representations (Fig. 3a) are important for learning relevant tasks across a broad range of domains and, with some differences in implementation, are known under a correspondingly broad range of names, including conjunctive [64] or configural [65] representations, nonlinear features, and representations with mixed selectivity [63]. We next asked whether and how non-additive representations can support transitive generalization.
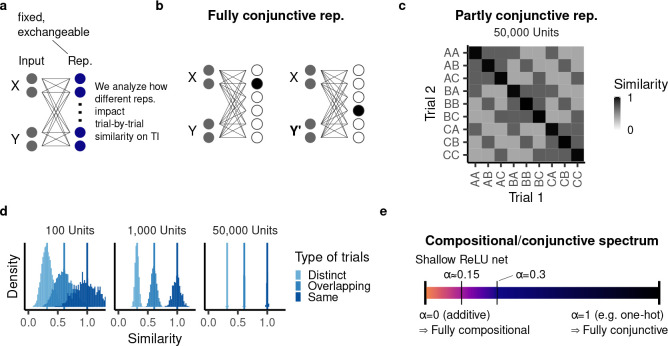
Figure 3:
Non-additive representations of TI cases. a, A non-additive representation encodes nonlinear interactions between items. b, A one-hot representation represents each combination of items by a distinct node. c, Representational similarity (cross-correlation) between a subset of trials in a ReLU network with 50,000 units. d, Representational similarity between all possible trials in networks with different numbers of hidden units, organized according to the type of trials. e, The conjunctivity factor characterizes a given representation according to how similarly it represents overlapping trials. Additive representations lie at one end of the spectrum, whereas one-hot representations lie at the other end.
To begin, consider the most extreme conjunctive case: a one-hot representation in which each composition of items is represented by a different hidden unit (Fig. 3b). In this case, a change in one of the two items yields a completely different representation. Such a model is able to memorize the training cases, but cannot generalize transitively.
Many representations, whether in the brain or in other learning systems, are neither fully conjunctive nor fully additive, but rather lie in between these two extremes [63, 66–69]. To characterize this spectrum formally, we considered the representational similarity between two trials and , as measured by their dot product, (leaving the representations fixed). We assumed that the representational similarity between two trials only depends on whether these trials are distinct ( and ), overlapping ( and or ), or identical ( and ) (Fig. 3c). We call this the “exchangeability assumption.”
The exchangeability assumption captures the fact that model behavior should not depend on the particular (i.e. arbitrary) hierarchy in which the set of items is arranged [70]. To promote exchangeability, we assumed that all input items are equally correlated with each other. In this case, most commonly used nonlinear representations of that input satisfy exchangeability as well. As a paradigmatic learning model, we considered a neural network with a ReLU nonlinearity and random weights. By determining the expected value of the representational similarity analytically (Appendix S1.3), we found that the network’s hidden layer, in expectation, satisfies the exchangeability assumption (Fig. 3c). This is because even though the hidden layer computes a nonlinear transformation, it partially inherits the input’s similarity structure [71]. In network simulations, the empirical representational similarity exhibits some variance around the expected value due to the random weight initialization. However, this variance vanishes as the network’s hidden layer becomes wider (Fig. 3d).
Under the exchangeability assumption, we found that for learning models that only modify their readout weights, a single scalar, which we call the “conjunctivity factor” , fully determines their TI task behavior, i.e. all models that have representations with the same exhibit the same behavior on TI (see Appendix S1.2). The conjunctivity factor is given by:
| (1) |
Here , , and are the similarity between identical, overlapping, and distinct pairs, respectively. Notably, we can extend the definition of the conjunctivity factor to non-exchangeable representations by taking the average over all identical, overlapping, or distinct pairs.
For an additive representation, half the units share their activation between different overlapping pairs. As a result, the similarity between overlapping pairs is halfway between that of distinct and that of identical pairs, corresponding to . At the other extreme, indicates that overlapping pairs are encoded in the model with equal similarity to each other as completely distinct pairs (as is the case for a one-hot representation). Consequently, systematically characterizes the spectrum from fully additive to fully conjunctive representations (Fig. 3e).
In most commonly used representations, overlapping trials are more similar to each other than distinct trials and therefore have an intermediate value for (“partly conjunctive” representations). This is because the input space represents overlapping trials as more similar than distinct trials and, as noted above, the hidden layer partly inherits the input’s similarity structure. Through analytical computation, we found that a random ReLU network with one hidden layer, for example, has ≈ 0.15 (Eq. (S28); Fig. 3c,d).
Importantly, the network giving rise to the representation could have an arbitrary number of layers; all we need to know is the conjunctivity factor of the network’s final layer. In fact, in Appendix S1.3, we compute the conjunctivity factor of neural networks with arbitrary depth, finding that increases with depth. Indeed, as the networks become deeper, eventually approaches one. However, if the connectivity structure is modified so a part of each layer is additive (but is, in turn, connected to the next layer’s conjunctive representation as well), can be reduced and, in fact, will eventually approach zero. This illustrates the crucial impact that network connectivity can have on representational structure.
For transitive inference, the conjunctivity factor raises two questions. First, how does > 0 affect TI behavior? Second, if the learning model’s internal representation is modifiable rather than fixed, how does this affect the conjunctivity factor and subsequent TI behavior?
3.3. Norm minimization and partly conjunctive representations yield transitive generalization
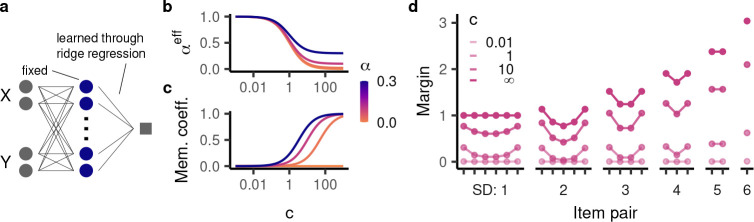
Unlike an additive representation, a representation with > 0 is not constrained to implementing a transitive relation. To understand how models with partly conjunctive representations perform on TI, we need to consider additional constraints. In particular, we analyzed models in which the learning of readout weights implements norm minimization (Fig. 4a), a paradigmatic statistical inductive bias (Fig. 4b). Under the exchangeability assumption, we were able to characterize model behavior on TI through exact analytical solutions. As noted above, to perform this analysis, we do not need to know the particular representation implemented, only its conjunctivity factor .
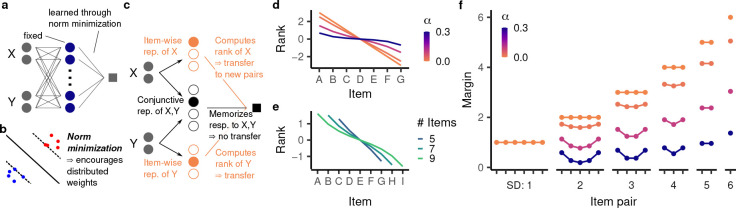
Figure 4:
We analyze the behavior of models having readout weights trained with norm minimization. a, Schematic illustration of the setup. b, Norm minimization implements a useful inductive bias for generalization to nearby data points. On categorization tasks, it determines the hyperplane separating the two categories with the maximal margin. c, Intuitively, a partly conjunctive representation is given by an item-wise representation of and concatenated with a fully conjunctive representation of and . The readout from the item-wise representations computes a rank for each item that transfers to overlapping pairs. The readout from the fully conjunctive representation memorizes a response to a given pair and does not transfer to overlapping pairs. Because norm minimization encourages distributed weights, it finds a solution that partly uses the item-wise representation and hence computes a rank. This leads to transitive generalization. d,e, The emergent rank representation at the end of training (Eq. 2) for (d) seven items and different values for ; and (e) and different numbers of items. f, For seven items and different values for , the corresponding margin for all trials. Item pairs are arranged by their position in the hierarchy, as in Fig. 1e.
On the training cases, the minimal norm model necessarily assigns a margin of ±1, as dictated by the desired output. On the test cases, however, our analysis revealed an intriguing emergent behavior: the model’s response to item pair invariably reflects a ranking system:
| (2) |
where is the total number of items (see Appendix S1.4.3 for the derivation of this result). This is remarkable as the model architecture is not constrained or pre-configured to implement a ranking system. Rather, the behavior is a consequence of the principle of norm minimization, operating on a partly conjunctive representation. Importantly, as implied by its ranking system, the model generalizes transitively (as long as overlapping trials are represented as more similar than distinct ones, i.e. ), and exhibits a symbolic distance effect.
For an intuition as to why a ranking system emerges, consider a particular class of representations having one-hot representations of the first and second item individually as well as their conjunction (Fig. 4c). This representation will have a conjunctivity factor of if the item-wise units are weighted by and the conjunctive units are weighted by . Changes in the item-wise unit weights correspond to changes in the model’s rank, as they generalize to overlapping trials. In contrast, changes in the conjunctive unit weights correspond to memorization, as they have no effect on overlapping trials (akin to a fully conjunctive representation). In principle, the model could learn the training set through pure memorization, i.e. changes in the conjunctive unit weights alone. However, because more distributed weights tend to have a smaller weight norm, norm minimization causes the model to learn the training premises by changing both the conjunctive unit weights (resulting in memorization) and the item-wise unit weights (resulting in transitive generalization). Thus, the partial conjunctivity is necessary for the existence of an item-wise population; the principle of norm minimization ascertains that this population is implicated in the learning process.
Beyond transitive generalization, the principle of norm minimization gives rise to several empirically observed behavioral patterns. The hyperbolic sine making up the rank expression compresses more intermediate items more strongly than more terminal items (Fig. 4d), thus giving rise to a terminal item effect (Fig. 4f). This effect becomes stronger for higher values of . A higher also compresses the ranking more strongly overall, leading to lower margins on the test set. As approaches one (the fully conjunctive case), the ranking becomes entirely flat and therefore no longer supports transitive generalization.
The form of the ranking also depends on the total number of items. Specifically, intermediate items are compressed more strongly when there are more items in total, an effect that is moreover dependent on . For , the ranking grows linearly with the number of items, whereas at higher values of , the model ranking’s overall range (between the first and last item) is almost invariant to the number of items (Fig. 4e).
Finally, when , the model assigns a larger margin to the training cases than specified by the ranking. Intuitively, this is because the conjunctive unit weights contribute to model behavior on the training cases, but do not transfer to the test cases. Since a higher compresses the ranks further, it leads to a higher discrepancy between training and test behavior. At a sufficiently high , the margin of the training cases is larger than that of the test cases with a small symbolic distance (Fig. 4f), giving rise to a memorization effect. While Ciranka et al. [29] explained this effect by fitting an explicit memorization parameter, our analysis reveals that it is an emergent consequence of having a nonlinear representation with sufficiently high conjunctivity factor. Notably, the fact that the memorization effect, according to our model, only arises in a subset of relational representations may explain why it is only occasionally observed in living subjects. In contrast, the symbolic distance and terminal item effect arise across the full spectrum of relational representations (except the fully conjunctive case) and indeed are also observed much more consistently in living subjects.
The above analytical solutions depend on the exchangeability assumption. In practice, the trials might be represented in a manner that violates this assumption. Indeed, we already saw that though randomly sampled features satisfy exchangeability in expectation, a model with insufficiently many of those features will have a non-exchangeable representation due to finite samples (Fig. 3d). In simulations (see Appendix S2.2), we found that a slight violation of exchangeability (e.g. resulting from a representation with many random features) does not change model behavior substantially. For larger violations (e.g. resulting from a representation with fewer random features), model behavior deviates from our theoretical account, but is still well approximated by it. Further, our account captured the average behavior across many models with a small number of random features almost exactly. This suggests that models with non-exchangeable representations behave differently from those with exchangeable representations but our analytical solutions can still be useful for understanding their behavior.
Our analysis demonstrates that norm minimization can explain not only transitive generalization, but also the symbolic distance effect, the terminal item effect (though only on test cases), and the memorization effect. We next characterize two popular statistical learning models implementing norm minimization: ridge regression and gradient flow, as applied to learning of network readout weights.
3.4. Learning through gradient flow or with weight regularization smoothly approaches the minimal norm solution
To see how the principle of norm minimization governs TI behavior across learning, we analyzed models with readout weights learned through either ridge regression [Fig. 5a; 17] or gradient flow, using mean squared error as the loss function (with the target response on the training cases being ±1). Ridge regression minimizes the sum of this loss and the squared -norm of the model weights, i.e.
Here, the regularization coefficient balances the weight penalty with the minimization of the loss function . Biologically, such weight regularization could, for instance, be implemented by mechanisms of synaptic homeostasis [72]. Gradient flow, on the other hand, assumes that a model minimizes by following the pointwise gradient exactly. This approximates gradient descent with a small learning rate, and is more amenable to formal analysis [73]. In this case, the learning duration determines how well the model has learned to minimize the loss function in the allotted time. At initialization, the model should be agnostic to all choices (i.e. output zero) and we therefore assumed that the weights are initialized at zero.
Figure 5:
TI behavior for models with a fixed representation and readout weights trained using regularized regression. a, Illustration of the setup. b,c, The (b) effective conjunctivity factor and (c) memorization coefficient as a function of the inverse regularization coefficient c. d, Generalization behavior for and different values of . The margins overall become larger as c increases.
The regularization coefficient and the learning duration play a similar role in the two learning models. With , the weight penalization is infinitely more important than the task-based component of the loss function and therefore the model weights are all zero. Similarly, at , the weights are initialized to zero. On the other hand, in the limit of infinite training , the model converges to the minimal norm solution determined in the section above [74]. This is also the case for the limit of models trained with increasingly small weight penalization [75]. Ridge regression and gradient flow are therefore two instances of common learning models which can perform TI by implementing the principle of norm minimization.
Going beyond these limits, we obtained exact solutions to model behavior for arbitrary or . For ridge regression (see Appendix S1.4.3), we found that the test behavior of a model with weight regularization and a given conjunctivity factor is equivalent to that of a model without weight regularization but a different conjunctivity factor. This “effective conjunctivity factor” eff depends on both and (see Lemma S1.4):
| (3) |
is generally higher (i.e. more conjunctive) than and, as becomes larger, gradually approaches from above (Fig. 5b). Thus, a model with smaller has a more compressed rank and a more pronounced terminal item effect.
On the training cases, the model’s performance is boosted compared to the rank difference, just like in the case of norm minimization. Specifically, its behavior is given by
| (4) |
i.e. a mixture of memorization (assigning a constant margin of ±1) and reliance on the ranking system. The balance between the two behaviors is specified by the “memorization coefficient” . starts out at zero, indicating no memorization and full reliance on the ranking system. As grows larger, increases as well (Fig. 5c). The smaller , the more strongly model behavior relies on the ranking. In particular, this partial reliance leads to a terminal item effect on the training cases in addition to the test cases (Fig. 5d). For , converges to 1, indicating full memorization as observed for the minimal norm solution.
For gradient flow, we found qualitatively similar solutions for model behavior (Appendix S1.4.4). In particular, the model’s behavior on test cases can be described by a ranking system throughout learning. Further, the model ranks gradually approach the minimal norm solution and, at earlier stages of training, have a more pronounced terminal item effect. Finally, the learning dynamics give rise to a transient terminal item effect on the training cases that vanishes as .
Humans and animals generally exhibit a terminal item effect on the training set. Our analysis suggests that this could be caused by either weight regularization or incomplete training (or both), arising from a mechanism that is related to but distinct from the mechanism giving rise to the terminal item effect on the test cases.
3.5. The conjunctivity factor exposes a tradeoff between learning transitive and non-transitive relational tasks
Our analysis thus far indicates that a higher conjunctivity factor generally yields worse performance on transitive inference. Indeed, if maximal generalization performance on TI were the sole aim, models with fully additive representations would be ideal. However, as noted above, humans and animals learn a broad range of relational tasks, not all of them transitive. Because models with fully additive representations are constrained to implementing a transitive relation, this makes partially conjunctive representations necessary (Fig. 6a).
Figure 6:
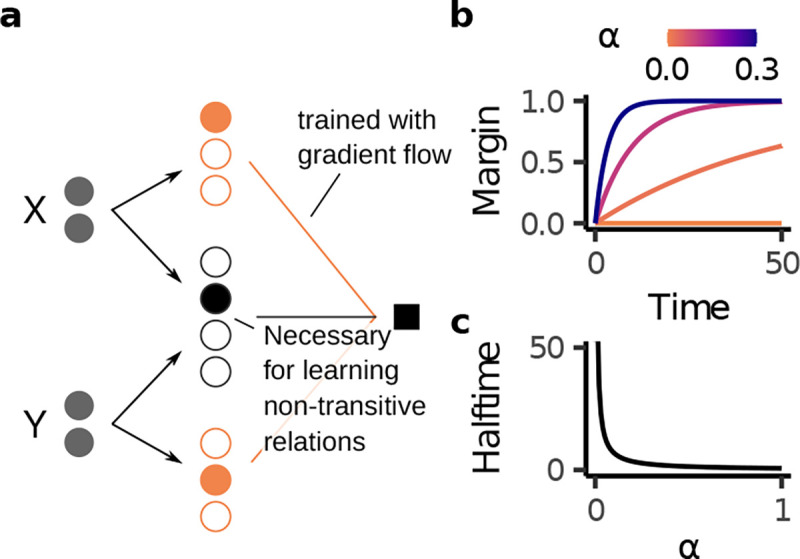
Behavior of models trained with readout weights trained through gradient flow on transverse patterning. a, Learning a non-transitive relation requires a conjunctive component. b, Margin over time for different values of . c, Halftime, i.e. time until the model reaches a margin of 0.5, as a function of the conjunctivity factor .
To investigate how different representational geometries change model behavior beyond transitive inference, we considered transverse patterning (“rock, paper, scissors” with more than three items, e.g.: A > B,B > C,...,F > G,G > A). Transverse patterning exemplifies a non-transitive relation and has been shown to be learned by both humans and various animals [34, 52, 76–79].
As with TI, we considered models with fixed, exchangeable representations with readout weights trained through gradient flow (Fig. 6a). We found that as long as , models were able to learn the task by relying on the conjunctive population. Further, by solving the learning dynamics of gradient descent analytically (see Appendix S1.6), we found that a higher leads to faster learning of the training trials (Fig. 6b,c). In contrast, on TI, a higher leads such models to have a smaller test margin. These behaviors highlights a potential tradeoff that imposes across different kinds of relations. In particular, our analysis predicts that subjects who are better at transitive inference should be slower to learn transverse patterning and vice versa.
One strategy for avoiding the tradeoff described above is representation learning. If models were able to adapt their internal representations to a given task, they could in principle learn an additive representation for TI and a non-additive representation for non-transitive relational tasks such as transverse patterning. We now investigate this hypothesis.
3.6. Neural networks with adaptive representations deviate from living subjects’ TI behavior
Deep neural networks, which learn by updating their internal weights, have become increasingly relevant both as artificial learning systems [80] and models of cognitive processes [81, 82]. Importantly, recent work has revealed that their generalization behavior fundamentally depends on the magnitude of their initial weights [83, 84]. For large initial weights, learning dynamics can be approximated by gradient flow on a particular fixed-feature model called the neural tangent kernel [NTK; 85, 86]. Thus, even though the network updates its internal weights, it effectively still relies on a fixed representation. Accordingly, this regime is often called “lazy” [83]. In contrast, neural networks initialized from sufficiently small values learn truly task-specific representations (“rich regime”). Broadly considered, adapting a model’s internal representation to a given task could address the competing demands imposed by the wide range of tasks subjects need to perform.
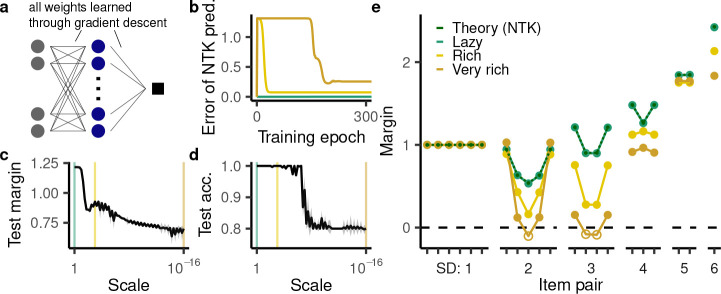
Indeed, the rich regime is seen as essential to the remarkable generalization capabilities of deep neural networks [83, 87, 88]. There is also widespread evidence that subjects adapt their representation to a given task [89, 90] and may do so similarly to deep neural networks trained in the rich regime [91]. In relational tasks, in particular, neural representations change to reflect how different items are related to each other [30, 92–96] and this may be essential for successful generalization on certain tasks [30, 97]. In light of this lazy vs. rich distinction and its potential relevance to biological learning, we investigated through simulations whether deep neural networks are suitable as a model of relational representation learning (Fig. 7a). Specifically, we trained neural networks from different scales of initialization using gradient descent (for details on training, see Appendix S2.3). In light of the important role played by the initialization scale, we covered a broad range of potential values, focusing on three representative values: 1 (resulting in lazy behavior), 10−3 (resulting in rich behavior), 10−16 (to characterize model behavior in the limit of small initialization).
Figure 7:
TI behavior in deep neural networks with modifiable representations. We considered twenty instances of a network with a ReLU nonlinearity and one hidden layer with 50,000 units, trained using mean squared error. Appendix S2.5 details other architectures, nonlinearities, and objective functions. Shaded regions indicate mean ± one standard deviation. (Note that some of the behaviors have sufficiently small variance that this shaded region may be invisible.) a, Illustration of network training. In contrast to the previous setups, the hidden layer weights were also trained using backpropagation. b, The mean squared error of the prediction made by the neural tangent kernel (NTK) at three different initialization scales (lazy: 1; rich: 10−3; very rich: 10−16). c,d, The (c) average test margin and (d) test accuracy as a function of initialization scale. The colored lines highlight the three representative values analyzed in more detail in panels b and e. e, TI performance according to our NTK-based prediction as well as of networks trained with backpropagation at the three representative scales.
In the lazy regime, we computed the NTK’s conjunctivity factor analytically (Appendix S1.5). For large initialization, the learning trajectory of neural networks trained with full weight updating is approximated by gradient flow on the fixed NTK representation. Hence we were able to use the gradient flow solutions determined in the previous sections to predict the network behavior over the course of training, finding a virtually perfect match with simulations in the case of wide neural networks (Fig. 7b,e, green line). Our account may therefore be able to explain why previous studies [53, 54] found empirically that feedforward neural networks generalize transitively.
Surprisingly, we found that networks trained in the rich regime performed worse at TI. They had a smaller test margin (Fig. 7c) and also made systematic errors on the cases CE, BE, and CF for a sufficiently small initialization scale (Fig. 7d,e, hollow points). Further, and in contrast to all learning models considered thus far, the behavior of neural networks in the rich regime was not consistent with a ranking system. This is apparent from the fact that the networks’ margin at a symbolic distance of three was smaller than at a symbolic distance of two (Fig. 7e). Importantly, in contrast to the previous limited violation of the symbolic distance effect, this cannot be explained by memorization as none of these cases are in the training set. Finally, the networks in the rich regime exhibited a violation of the terminal item effect at a symbolic distance of 4, a somewhat surprising pattern that no models examined thus far have exhibited. The networks’ unconvential behavior was not due to the specific setup considered here: we observed similar behavior for alternative activation functions (Fig. S5), alternative loss functions (Fig. S7a), and deeper networks (Fig. S7b). Further, the networks exhibited even more overtly idiosyncratic behavior for larger numbers of items, one striking behavioral pattern being a periodic (rather than monotonically increasing) symbolic distance effect (Fig. S6). These findings indicate that, for TI, representation learning in standard neural network does not necessarily confer the benefits of representation learning suggested in prior work.
3.7. The rich-regime networks implement a cooperative code that lacks a transitive inductive bias
Given that the rich regime has been found previously to improve generalization on other tasks, we sought to understand why it yields anomalous behavior on TI. To this end, we leveraged previous work indicating that lazy and rich regimes implement different forms of norm minimization: the lazy regime minimizes the -norm of the network’s readout weights, whereas the rich regime approximately minimizes the -norm of all weights in the network [98–100; but see 84, 101]. For the networks studied here, we found that the norm of all weights in a fully trained network is dramatically smaller for smaller scales of initialization (Fig. 8a). To clarify why norm minimization over all network weights is associated with an anomalous inductive bias (unlike norm minimization over readout weights, analyzed in the previous sections), we directly analyzed the computations performed by the rich-regime neural network.
Figure 8:
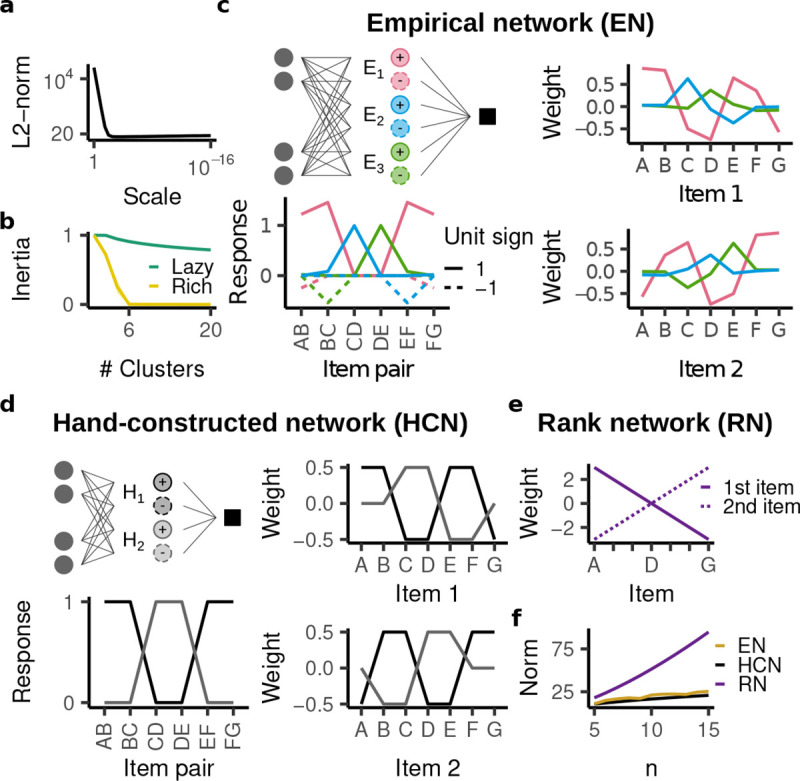
A mechanistic analysis of the rich regime’s inductive bias. All plots show the mean ± standard deviation across twenty random initializations. Standard deviation is too small to be visible. a, -norm of of all weights in the fully trained networks as a function of initialization scale. The rich regime yields much smaller norm. b, Inertia (i.e. proportion of explained variance) as a function of the number of clusters, for the lazy and rich network. Six clusters only leave 0.001% of the variance unexplained. c, The empirical network is therefore described by a network with six units, three with positive and three with negative responses. The right panels show the weights of the different units and the bottom panel shows how each units responds to the different training trials. Only units with positive readout weights are shown; the units with negative readout weights have the same structure but with Item 1 and 2 reversed. d, Analogous depiction of the hand-constructed network, which has four units. e, The rank network only has two units, but they span a much wider range. f, Weight norm of the empirical, hand-constructed, and rank network as a function of the number of items. The rank network has a much larger -norm, whereas the norm of the empirical network is similar to that of the hand-constructed network.
Prior studies [100, 102, 103] have found that minimization of the -norm over all network weights induces the networks’ hidden units to “specialize” into a low number of functionally distinct clusters with low -norm. To assess this possible structure, we performed k-means clustering with respect to the normalized weight vectors across all units, finding that in the rich regime, all 50,000 units of the network fall into just six clusters (Fig. 8b; details described in Appendix S3.3). In contrast, such a compact description was not apparent in the lazy regime. Remarkably, the six cluster centroids were extremely consistent between different random initializations (Fig. 8c).
We found that three of those centroids (“units”) were associated with positive readout weights, whereas the other three units were associated with negative readout weights. This is because the network has rectified activations in its hidden layer, which caused different units to specialize for trials with positive and negative labels. In examining hidden-layer weights, we focused on the positive units, which we denote by , , and (negative units are analogous, Fig. S10). Because we presented the network with concatenated onehot vectors, each weight entry corresponds to a different presented item and we identify each weight by its corresponding item. Note that items presented in the first and second position correspond to entirely distinct weights; we denote item in the first or second position by and , respectively.
We noticed two putative aspects of the underlying computation in the network: different units responded predominantly to a non-overlapping set of trials (“staggered response”; e.g. (pink) responded to AB, BC, EF, and FG, while (blue) responded to CD and (green) responded to DE; Fig. 8c, bottom left) and each unit encoded its corresponding trials by distributing positive weights across both items (“cooperative code”; e.g. to encode AB, assigned a positive weight to and ; Fig. 8c, right).
To see whether these two aspects could provide a sufficient explanation for the behavior in the rich-regime, we used them to hand-construct a simplified ReLU network (Fig. 8d). Specifically, the hand-constructed network has four hidden units, two with positive readout weights and two with negative readout weights. Again, we focus on those with positive readout weights, which we denote by and (see Fig. S9 for the analogous negative units). Note that we do not prove that the hand-constructed network actually learns the training trials with minimal -norm (though it has the lowest norm among all networks considered here). Rather, it serves as a useful construction to understand why the described computation yields both low norm and a non-transitive inductive bias.
Each unit in our construction implements a cooperative code, i.e. to encode its response to a trial, it distributes its weights equally between the two items. In particular, classifies trials AB and BC by assigning a weight of 0.5 to and as well as and . Because of the positive weights associated with these items, would also respond positively to trials BA, CB, and DC. Preventing this positive response requires negative weights associated with items , , and . However, because a negative weight is already associated with and , cannot classify trials CD and DE using a cooperative code. Thus, stays silent on these trials, which are instead encoded by (also using a cooperative code). This pattern explains the staggered responses observed in the empirical network. The interference from the negative weights associated with and prevents from classifying EF and FG, but these trials are no longer affected by interference with AB and BC and can therefore be encoded by . For TI variants with more than seven items, the two units would continue alternating in the same way, giving rise to periodic network weights (Fig. S9).
Intuitively, the coding scheme amounts to a set of local rules that support learning of the training trials, but do not generalize to the test trials. For example, because the cooperative code implemented in unit encodes a positive response to trials AB and EF, it also results in an incorrectly positive response on EB (see Fig. S9).
Critically, the hand-constructed network has a lower -norm because the cooperative code keeps the network weights in a range from −0.5 to 0.5. In contrast, a network using a ranking system would require weights in a range from to (Fig. 8e). As a result, its -norm is not only consistently larger, but also increases more quickly with increasing number of items (Fig. 8f).
Importantly, the staggered cooperative coding scheme is only norm-efficient because the hidden weights are followed by a rectifying nonlinearity. For example, takes on a value of −1 in response to CD. Without the rectification, would then have to compensate for the negative response to produce a positive label, which would require larger weights and thus would not be norm-efficient. However, because of the rectification following the hidden weights, remains silent on CD and requires no such compensation from . This explains why a cooperative and staggered coding scheme has a low -norm when all weights of the network are trained, but not when only the readout weights are trained.
The hand-constructed network illustrates how a constraint that imposes a low -norm on all network weights can give rise to anomalous behavior on transitive inference. As noted above, the empirical network implemented the same computational principles as the hand-constructed network, albeit in a slightly different way: approximately implemented , whereas and jointly approximated . These differences resulted in a somewhat higher, but qualitatively similar norm in the empirical network (Fig. 8f; see Appendix S3.3.3). In particular, the norm of both the empirical and the hand-constructed networks is systematically lower than that of the rank-network (Fig. 8f). Remarkably, the mechanism implemented by the empirical network is consistent across not only different random initializations but also different numbers of items : always approximates , whereas and jointly implement (Fig. S9f).
Our findings in this section may appear contrary to those of Nelli et al. [30], who also studied TI performance of neural networks, but found that the rich regime did not impair transitive generalization and further yielded an explicit rank representation in the hidden layer. We found that this was caused by a weight symmetry imposed on the hidden layer that constrains their networks to an additive internal representation (see Appendix S2.6). Indeed, our clustering analysis revealed that these networks approximately implemented the rank network (Fig. 8e) and the -norm of their weights was much higher than that of the unconstrained neural network (Fig. S10a). This further illustrates the misalignment between the rich regime’s norm minimization and a transitive inductive bias: architectural constraints that improve transitive generalization (here, weight symmetry) lead to a higher weight norm.
4. Discussion
We found that standard statistical learning models can perform transitive inference (TI) and recapitulate three empirically observed behavioral patterns (symbolic distance effect, terminal item effect, and memorization effect). The behavior of a given model is sufficiently captured by a single scalar “conjunctivity factor” , which characterizes the model’s internal representation (of task items) on a spectrum from fully compositional to fully conjunctive . For , the model is constrained to encoding a transitive relation. For partly conjunctive representations , the model is not constrained in this way, but the principle of norm minimization nevertheless yields transitive generalization. For fully conjunctive representations , the model cannot generalize transitively. Finally, we found that when representation learning is enabled in hidden layers, networks perform worse on TI and exhibit different behavioral patterns than living subjects. Through hand-constructed networks and a clustering-based analysis of empirical networks, we suggest that this anomalous behavior arises from the different form of norm minimization implemented by the rich regime.
Models of relational cognition often represent relations explicitly and are pre-configured to have a particular relational inductive bias [104–106]. In particular, alternative accounts of TI are either pre-configured to associate a rank (or value) with each item [29, 31, 49–51] or suggest that humans rely on abstract knowledge of transitivity [e.g. 31, 34, 107] (as implemented, for instance, in a cognitive map [108–110]). In contrast to these accounts, we took a “minimal principles” approach, representing nothing but the input itself (i.e. the two presented items). This perspective casts higher-level behavioral capacities (in this case transitive generalization) as emergent from minimally structured learning systems [111, 112]. Studies within this paradigm usually rely on simulations, which can leave the mechanisms for emergent behavior, such as generalization, unclear [cf. 113]. In contrast, our analytical account identifies the specific model components responsible for transitive generalization. This clarifies how the brain could implement relational generalizations without pre-configured representations or compositional constraints.
More generally, relational cognition likely relies on a wide range of learning mechanisms [114, 115]. The models considered here require repeated interleaved presentations of the training trials [116], suggesting learning mechanisms associated with prefrontal or higher-level association cortices. In contrast, other brain regions, such as the hippocampus, support rapid learning without the need for repeated trial presentations, presumably through the operation of memory re-activation (e.g. inferring that B > D by recalling that B > C and C > D) [117–120]. A recurrent neural network model with Hebbian plasticity (“REMERGE”) has been proposed to explain how a reactivation-based mechanism could support transitive generalization [121]. While this learning model does not recapitulate behavioral patterns such as the symbolic distance effect, it can explain how subjects may learn transitive inference from a minimal number of trials. Finally, whereas both the reactivation-based and statistical learning models described above rely on emergent inductive biases of the underlying learning mechanisms, learning systems can also develop relational inductive biases through structure learning or meta-learning [122, 123], which are associated with both hippocampus and prefrontal cortex [115, 124–126].
Which of these learning mechanisms is implicated in a particular TI task variant likely depends on factors such as the stimulus structure, how training trials are presented, and when test trials are presented. Subjects may also rely on a mixture of learning mechanisms on a single task. For example, trials could initially be encoded in the hippocampus but eventually be consolidated in prefrontal cortex [114, 127]. Creating more unified models of relational learning (e.g. fusing the REMERGE-model and our similarity-based mechanism, or incorporating structure learning) could shed further light on the interplay between different learning mechanisms on TI and their dependency on different task parameters such as stimulus presentation and training curriculum. Doing so may also allow closer investigation of proposed neural implementations of relational learning [117, 128].
With respect to similarity-based relational learning models, our account could be seen as an endpoint to a series of investigations of TI behavior: expanding upon previous studies [30, 53, 54], we show comprehensively that the principle of norm minimization enables any model with partly conjunctive representations to generalize transitively and further gives rise to naturalistic behavior on TI. Importantly, norm minimization is implicated not only in gradient flow and ridge regression (the examples we consider), but also a much broader range of learning models [129], including reinforcement learning [130]. Accordingly, the consistent behaviors many different animals exhibit on the task could be due to this shared, underlying learning principle. This is an alternative to the view that the ubiquity of TI stems from its ecological role in social cognition, in particular in animals which form hierarchies [131, 132], and the view that TI entails explicit reasoning.
Our results, while providing an alternative explanatory account of TI, should nevertheless be interpreted cautiously with regards to the basis of TI in living subjects, as our model is limited in a number of ways. In terms of behavioral predictions, it cannot account for the asymmetry effect, the observation that performance in living subjects is often better for items towards the start of the hierarchy (e.g. AB) than items towards of the end (e.g. FG) [29]. Further, our model does not generate predictions for what behavior we might expect from subjects that, after being trained on item pairs, are presented with three items at a time and expected to pick the largest item [33, 40, 133, 134]. Finally, our results do not speak to tasks testing for transitive inference in the form of a single question (e.g. “Alice is taller than Bob and Bob is taller than Chris. Who is taller, Alice or Chris?”) or after minimal training [26, 135]. Such a format likely requires a different mechanism from the one considered here and may be better understood as an instance of explicit reasoning.
These limitations, and extensions of TI, can inspire refining or expanding the statistical modeling approach. For example, Nelli et al. [30] found that conventional statistical learning models could not account for human behavior on a particular variant of TI [“list linking,” 136], but that a modification in which uncertainty is encoded could. More broadly, TI, with its rich and well-established set of empirical phenomena [e.g. 137–139], may serve as a useful model task to compare statistical learning models (and their failure modes) to human and animal behavior. For example, the lack of an asymmetry effect and the inability to perform the three-item task indicate what is lost by treating TI as a binary categorization task. A model that understands its decision as tied to one of the presented items (rather than as a choice between two arbitrary categories) may be able to better account for these behaviors [29]. Notably, better accounts of behavior within the TI framework may not only elucidate how subjects perform relational learning, but even inform more general models of statistical learning in living subjects.
Despite these potential limitations, our account still makes a set of falsifiable predictions that can produce evidence for or against the biological relevance of our insights. In particular, we identified the conjunctivity factor as a broadly important parameter for TI task behavior. Our account would predict that changes in should lead to a set of coordinated changes in behavior. For example, a stronger memorization effect should be associated with a weaker terminal item effect on the training cases (as both are caused by an increase in ). Observing that these different behavioral patterns indeed change in a coordinated manner (for example between different subjects performing the same task) may indicate that our theory can accurately describe behavior.
Changes in the conjunctivity factor may arise from inter-individual differences (different subjects may have representations that are best described by different values of ), but could also be introduced through experimental interventions. In particular, certain task variations may promote a representation of the input as either two separate items or a single conjunctive stimulus [140]; for example, presenting the two items in a common scene rather than as distinct stimuli may result in a higher . More broadly, this suggests that the conjunctivity factor may be a useful parameter for comparing subjects and TI task variants.
Beyond behavioral predictions, the conjunctivity factor also suggests a new approach for clarifying the neural basis of TI. On the one hand, perturbations in relevant neural areas, for example through lesions [78], may affect the conjunctivity factor. On the other hand, using neural recordings to estimate the empirical representational similarity [141] between distinct, overlapping, and identical trials could enable the estimation of an effective conjunctivity factor in a particular neural area. If differences in this estimated conjunctivity factor (either due to inter-individual differences or as a result of lesions) are associated with the corresponding behavioral differences predicted by our model, this may suggest a role for statistical learning as described here, and, in addition, that the recorded neural area is indeed involved in TI.
Intriguingly, past work suggests that a conjunctivity tradeoff – manifesting across different tasks – can be linked to a specific brain region. Lesions of the hippocampus have been found to impair generalization (but not the learning of training trials) in transitive inference (142; but see 143) and, in separate work, accelerate learning of transverse patterning [144], two effects that would both arise from an increased conjunctivity factor in our model. Notably, other studies indicate that hippocampal lesions can also impair learning of transverse patterning [145–147]. These differences appear to depend on whether items are presented together (e.g. together on a screen), in which case the hippocampus was not required for transverse patterning, or apart (e.g. in separate containers), in which case hippocampus was required. These results broadly suggest a role for hippocampus both in building representations of items presented separately [140] and in limiting the conjunctivity of items presented together.
Moreover, our findings on rich-regime neural networks performing worse on transitive inference may have important implications for machine learning, as deep neural networks have been observed to struggle with tasks involving compositional generalization more broadly [148–154]. A common strategy in attempting to address these shortcomings consists in training ever larger models on ever larger datasets [155]. Such models have shown impressive results on tasks such as natural language production [156, 157], but the overall scale and complexity of the training data, model, and learning algorithm make it difficult to attribute successful or unsuccessful generalization behaviors to specific components of the model [though see 158–161]. In contrast, TI is a particularly simple relational task on which deep networks exhibit non-naturalistic behavior. Our findings explain why the rich regime, which has a useful inductive bias on many different tasks, can give rise to such anomalous behavior on transitive inference. This can help in designing principled modifications to prevent such anomalous behavior – for example by adding additional training trials, regularizing the hidden layer to prevent a local encoding mechanism, or changing the connectivity structure of the network – and in this way improve our understanding of how relational learning is implemented [162–165]. Notably, the tools we employ to analyze the rich-regime behavior may also prove useful for analyzing neural networks trained on other tasks. At the same time, our analysis here was primarily empirical, but future work could provide an analytical characterization of the rich-regime solution [99, 100, 166].
Finally, transitive inference is a simple instance of compositional generalization, i.e. the ability to conceptualize prior experience in terms of components that can be re-configured in a novel situation [167, 168]. More broadly, compositional generalization has long been understood to be a crucial component for human-like learning and generalization [163], in large part due to the diversity and breadth of its applications: compositional generalization often involves the composition of many rules, relations, or attributes [163, 169–171]. The comparative simplicity of TI enabled us to identify how minimally structured learning systems can implement the inductive biases needed for this task. Our analysis provides a case study for how standard statistical inductive biases determine behavior on compositional tasks, in particular clarifying how representational structure (conceptualized through the conjunctivity factor ) impacts compositional generalization [172]. At the same time, TI certainly does not capture the complexity of most compositional task paradigms and future work should extend our formal analysis to a broader scope of compositional tasks. This would clarify the conditions under which standard statistical learning principles can explain compositional generalization and clarify challenging compositional motifs that require additional learning mechanisms.
In summary, we here investigated transitive inference, a task that tests for a fundamental logical capacity and has fascinated researchers across neuroscience and psychology for many decades. We derived exact mathematical equations describing the TI behavior of a large class of statistical learning models. This allowed us to understand systematically how these models can generalize compositionally, using TI as an example. Our theory provides a basis for using TI to investigate the neural structures implementing relational cognition. At the same time, our findings also suggest that TI, in its standard form, may not be sufficient to clarify relational inference abilities that require more than statistical learning. For this purpose, other relational tasks should be considered.
Supplementary Material
Acknowledgments
We are grateful to the members of the Center for Theoretical Neuroscience at Columbia University, the SueYeon Chung lab at Flatiron/NYU, and attendees at Cosyne 2023 and the Gatsby Tri-Centre Meeting 2023 for helpful comments. We thank Taiga Abe, Veronica Bossio, Tala Fakhoury, Ching Fang, Jeff Johnston, Erica Shook, Sharon Su, and Denis Turcu for detailed feedback. The work was supported by NSF 1707398 (Neuronex), Gatsby Charitable Foundation GAT3708, and NIH-R01MH111703.
Footnotes
A related paper [55] has come to our attention, in which the authors are concerned with a linear item representation. This is a special case of the additive representations here. Further, the authors derive an analytic solution for a specific learning algorithm, whereas we demonstrate a transitive constraint for a broader class of models.
References
- 1.Halford G. S., Wilson W. H. & Phillips S. Relational knowledge: the foundation of higher cognition. en. Trends in Cognitive Sciences 14, 497–505. ISSN: 1364-6613. https://www.sciencedirect.com/science/article/pii/S1364661310002020 (2023) (Nov. 2010). [DOI] [PubMed] [Google Scholar]
- 2.Cheney D. L., Seyfarth R. M. & Silk J. B. The responses of female baboons (Papio cynocephalus ursinus) to anomalous social interactions: Evidence for causal reasoning? Journal of Comparative Psychology 109, 134–141. ISSN: 1939-2087(Electronic),0735-7036(Print) (1995). [DOI] [PubMed] [Google Scholar]
- 3.Peake T. M., Terry A. M. R., McGregor P. K. & Dabelsteen T. Do great tits assess rivals by combining direct experience with information gathered by eavesdropping? Proceedings of the Royal Society of London. Series B: Biological Sciences 269. Publisher: Royal Society, 1925–1929. 10.1098/rspb.2002.2112 (2022) (Sept. 2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Paz-y-Miño C G., Bond A. B., Kamil A. C. & Balda R. P. Pinyon jays use transitive inference to predict social dominance. en. Nature 430. Number: 7001 Publisher: Nature Publishing Group, 778–781. ISSN: 1476–4687. https://www.nature.com/articles/nature02723 (2022) (Aug. 2004). [DOI] [PubMed] [Google Scholar]
- 5.Etienne A. S. & Jeffery K. J. Path integration in mammals. en. Hippocampus 14, 180–192. ISSN: 1098–1063. 10.1002/hipo.10173 (2022) (2004). [DOI] [PubMed] [Google Scholar]
- 6.Seed A. & Byrne R. Animal Tool-Use. en. Current Biology 20, R1032–R1039. ISSN: 0960-9822. https://www.sciencedirect.com/science/article/pii/S0960982210011607 (2022) (Dec. 2010). [DOI] [PubMed] [Google Scholar]
- 7.Baldwin M. W. Relational schemas and the processing of social information. Psychological bulletin 112, 461 (1992). [Google Scholar]
- 8.Tolman E. C. Cognitive maps in rats and men. Psychological Review 55, 189–208. ISSN: 1939-1471 (1948). [DOI] [PubMed] [Google Scholar]
- 9.Penn D. C. & Povinelli D. J. Causal cognition in human and nonhuman animals: A comparative, critical review. Annu. Rev. Psychol. 58. Publisher: Annual Reviews, 97–118 (2007). [DOI] [PubMed] [Google Scholar]
- 10.Mitchell T. M. The need for biases in learning generalizations (1980).
- 11.Krogh A. & Hertz J. A. Generalization in a linear perceptron in the presence of noise. en. Journal of Physics A: Mathematical and General 25, 1135. ISSN: 0305-4470. 10.1088/0305-4470/25/5/020 (2023) (Mar. 1992). [DOI] [Google Scholar]
- 12.Watkin T. L. H., Rau A. & Biehl M. The statistical mechanics of learning a rule. Reviews of Modern Physics 65. Publisher: American Physical Society, 499–556. 10.1103/RevModPhys.65.499 (2023) (Apr. 1993). [DOI] [Google Scholar]
- 13.Sollich P. Learning Curves for Gaussian Processes in Advances in Neural Information Processing Systems 11 (MIT Press, 1998). https://proceedings.neurips.cc/paper_files/paper/1998/hash/5cbdfd0dfa22a3fca7266376887f549b-Abstract.html (2023). [Google Scholar]
- 14.Liang T. & Rakhlin A. Just interpolate: Kernel “Ridgeless” regression can generalize. The Annals of Statistics 48. Publisher: Institute of Mathematical Statistics, 1329–1347. ISSN: 0090-5364, 2168–8966. 10.1214/19-AOS1849.full (2023) (June 2020). [DOI] [Google Scholar]
- 15.Jacot A., Simsek B., Spadaro F., Hongler C. & Gabriel F. Kernel Alignment Risk Estimator: Risk Prediction from Training Data in Advances in Neural Information Processing Systems 33 (Curran Associates, Inc., 2020), 15568–15578. https://proceedings.neurips.cc/paper/2020/hash/b367e525a7e574817c19ad24b7b35607-Abstract.html (2023). [Google Scholar]
- 16.Canatar A., Bordelon B. & Pehlevan C. Spectral bias and task-model alignment explain generalization in kernel regression and infinitely wide neural networks. en. Nature Communications 12, 2914. ISSN: 2041-1723. https://www.nature.com/articles/s41467-021-23103-1 (2023) (May 2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hoerl A. E. & Kennard R. W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 12, 55–67. ISSN: 0040-1706. 10.1080/00401706.1970.10488634 (2023) (Feb. 1970). [DOI] [Google Scholar]
- 18.Cortes C. & Vapnik V. Support-vector networks. en. Machine Learning 20, 273–297. ISSN: 1573-0565. 10.1007/BF00994018 (2022) (Sept. 1995). [DOI] [Google Scholar]
- 19.Soudry D., Hoffer E., Nacson M. S., Gunasekar S. & Srebro N. The implicit bias of gradient descent on separable data. Journal of Machine Learning Research 19, 1–57 (2018). [Google Scholar]
- 20.Krogh A. & Hertz J. A Simple Weight Decay Can Improve Generalization in Advances in Neural Information Processing Systems 4 (1991). https://proceedings.neurips.cc/paper/1991/hash/8eefcfdf5990e441f0fb6f3fad709e21-Abstract.html (2023). [Google Scholar]
- 21.Moody J. The Effective Number of Parameters: An Analysis of Generalization and Regularization in Nonlinear Learning Systems in Advances in Neural Information Processing Systems 4 (1991). https://proceedings.neurips.cc/paper/1991/hash/d64a340bcb633f536d56e51874281454-Abstract.html (2023). [Google Scholar]
- 22.Barnett S. M. & Ceci S. J. When and where do we apply what we learn?: A taxonomy for far transfer. Psychological Bulletin 128. Place: US Publisher: American Psychological Association, 612–637. ISSN: 1939-1455 (2002). [DOI] [PubMed] [Google Scholar]
- 23.Ye H. et al. Towards a Theoretical Framework of Out-of-Distribution Generalization in Advances in Neural Information Processing Systems 34 (Curran Associates, Inc., 2021), 23519–23531. https://proceedings.neurips.cc/paper/2021/hash/c5c1cb0bebd56ae38817b251ad72bedb-Abstract.html (2023). [Google Scholar]
- 24.Abbe E., Bengio S., Lotfi A. & Rizk K. Generalization on the Unseen, Logic Reasoning and Degree Curriculum June 2023. http://arxiv.org/abs/2301.13105 (2023). [Google Scholar]
- 25.Battaglia P. W. et al. Relational inductive biases, deep learning, and graph networks. arXiv preprint arXiv:1806.01261 (2018). [Google Scholar]
- 26.Piaget J. Judgment and reasoning in the child. Publisher: Harcourt, Brace; (1928). [Google Scholar]
- 27.Vasconcelos M. Transitive inference in non-human animals: An empirical and theoretical analysis. en. Behavioural Processes 78, 313–334. ISSN: 0376-6357. https://www.sciencedirect.com/science/article/pii/S0376635708000818 (2022) (July 2008). [DOI] [PubMed] [Google Scholar]
- 28.Jensen G. in APA handbook of comparative psychology: Perception, learning, and cognition, Vol. 2 385–409 (American Psychological Association, Washington, DC, US, 2017). ISBN: 978-1-4338-2352-7 978-1-4338-2353-4. [Google Scholar]
- 29.Ciranka S. et al. Asymmetric reinforcement learning facilitates human inference of transitive relations. en.Nature Human Behaviour 6, 555–564. ISSN: 2397-3374. https://www.nature.com/articles/s41562-021-01263-w (2022) (Apr. 2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nelli S., Braun L., Dumbalska T., Saxe A. & Summerfield C. Neural knowledge assembly in humans and neural networks. Neuron (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jensen G., Muñoz F., Alkan Y., Ferrera V. P. & Terrace H. S. Implicit Value Updating Explains Transitive Inference Performance: The Betasort Model. en. PLOS Computational Biology 11, e1004523. ISSN: 1553-7358. https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1004523 (2022) (Sept. 2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bryant P. E. & Trabasso T. Transitive Inferences and Memory in Young Children. en. Nature 232, 456–458. ISSN: 1476-4687. https://www.nature.com/articles/232456a0 (2022) (Aug. 1971). [DOI] [PubMed] [Google Scholar]
- 33.McGonigle B. O. & Chalmers M. Are monkeys logical? Nature 267, 694–696. ISSN: 1476-4687 (1977). [DOI] [PubMed] [Google Scholar]
- 34.Gillan D. J. Reasoning in the chimpanzee: II. Transitive inference. Journal of Experimental Psychology: Animal Behavior Processes 7, 150–164. ISSN: 1939-2184 (1981). [Google Scholar]
- 35.Davis H. Transitive inference in rats (Rattus norvegicus). Journal of Comparative Psychology 106, 342–349. ISSN: 1939-2087 (1992). [DOI] [PubMed] [Google Scholar]
- 36.Tibbetts E. A., Agudelo J., Pandit S. & Riojas J. Transitive inference in Polistes paper wasps. Biology Letters 15, 20190015. 10.1098/rsbl.2019.0015 (2022) (May 2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Grosenick L., Clement T. S. & Fernald R. D. Fish can infer social rank by observation alone. en. Nature 445, 429–432. ISSN: 1476-4687. https://www.nature.com/articles/nature05511 (2022) (Jan. 2007). [DOI] [PubMed] [Google Scholar]
- 38.Potts G. R. Storing and retrieving information about ordered relationships. Journal of Experimental Psychology 103, 431–439. ISSN: 0022-1015 (1974). [Google Scholar]
- 39.D’Amato M. R. & Colombo M. The symbolic distance effect in monkeys (Cebus apella). en. Animal Learning & Behavior 18, 133–140. ISSN: 1532-5830. 10.3758/BF03205250 (2022) (June 1990). [DOI] [Google Scholar]
- 40.McGonigle B. & Chalmers M. Monkeys are rational! The Quarterly Journal of Experimental Psychology Section B 45, 189–228. ISSN: 0272-4995. 10.1080/14640749208401017 (2022) (Oct. 1992). [DOI] [Google Scholar]
- 41.Merritt D., MacLean E. L., Jaffe S. & Brannon E. M. A comparative analysis of serial ordering in ring-tailed lemurs (Lemur catta). Journal of Comparative Psychology 121. Publisher: American Psychological Association, 363 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Scarf D. & Colombo M. Representation of serial order: A comparative analysis of humans, monkeys, and pigeons. en. Brain Research Bulletin. Special Issue:Brain Mechanisms, Cognition and Behaviour in Birds 76, 307–312. ISSN: 0361-9230. https://www.sciencedirect.com/science/article/pii/S0361923008000373 (2022) (June 2008). [DOI] [PubMed] [Google Scholar]
- 43.Von Fersen L., Wynne C. D., Delius J. D. & Staddon J. E. Transitive inference formation in pigeons. Journal of Experimental Psychology: Animal Behavior Processes 17. Publisher: American Psychological Association, 334 (1991). [Google Scholar]
- 44.Wynne C. D. L. Pigeon transitive inference: Tests of simple accounts of a complex performance. en. Behavioural Processes 39, 95–112. ISSN: 0376-6357. https://www.sciencedirect.com/science/article/pii/S0376635796000484 (2022) (Jan. 1997). [DOI] [PubMed] [Google Scholar]
- 45.Merritt D. J. & Terrace H. S. Mechanisms of inferential order judgments in humans (Homo sapiens) and rhesus monkeys (Macaca mulatta). Journal of Comparative Psychology 125. Publisher: American Psychological Association, 227 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Acuna B. D., Sanes J. N. & Donoghue J. P. Cognitive mechanisms of transitive inference. en. Experimental Brain Research 146, 1–10. ISSN: 1432-1106. 10.1007/s00221-002-1092-y (2022) (Sept. 2002). [DOI] [PubMed] [Google Scholar]
- 47.Van Elzakker M., O’Reilly R. C. & Rudy J. W. Transitivity, flexibility, conjunctive representations, and the hippocampus. I. An empirical analysis. en. Hippocampus 13, 334–340. ISSN: 1098-1063. 10.1002/hipo.10083 (2022) (2003). [DOI] [PubMed] [Google Scholar]
- 48.Wynne C. D. L. in Models of Action Num Pages: 40 (Psychology Press, 1998). ISBN: 978-0-203-77386-4. [Google Scholar]
- 49.Wynne C. D. L. Reinforcement accounts for transitive inference performance. en. Animal Learning & Behavior 23, 207–217. ISSN: 1532-5830. 10.3758/BF03199936 (2022) (June 1995). [DOI] [Google Scholar]
- 50.Couvillon P. A. & Bitterman M. E. A conventional conditioning analysis of ”transitive inference” in pigeons. Journal of Experimental Psychology: Animal Behavior Processes 18. Place: US Publisher: American Psychological Association, 308–310. ISSN: 1939-2184 (1992). [Google Scholar]
- 51.Jensen G., Terrace H. S. & Ferrera V. P. Discovering Implied Serial Order Through Model-Free and Model-Based Learning. Frontiers in Neuroscience 13. ISSN: 1662-453X. 10.3389/fnins.2019.00878 (2022) (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wynne C. D. L. Transverse patterning in pigeons. en. Behavioural Processes 38, 119–130. ISSN: 0376-6357. https://www.sciencedirect.com/science/article/pii/S0376635796000320 (2022) (Nov. 1996). [DOI] [PubMed] [Google Scholar]
- 53.De Lillo C., Floreano D. & Antinucci F. Transitive choices by a simple, fully connected, backpropagation neural network: implications for the comparative study of transitive inference. en. Animal Cognition 4, 61–68. ISSN: 1435-9448. 10.1007/s100710100092 (2022) (July 2001). [DOI] [Google Scholar]
- 54.Kay K. et al. Neural dynamics and geometry for transitive inference en. Pages: 2022.10.10.511448 Section: New Results. Oct. 2022. 10.1101/2022.10.10.511448v1 (2022). [DOI]
- 55.Antonio G. D., Raglio S. & Mattia M. Ranking and serial thinking: A geometric solution en. Pages: 2023.08.03.551859 Section: New Results. Aug. 2023. 10.1101/2023.08.03.551859v1 (2023). [DOI]
- 56.Carmesin H..−. & Schwegler H. Parallel versus sequential processing of relational stimulus structures. en. Biological Cybernetics 71, 523–529. ISSN: 1432-0770. 10.1007/BF00198470 (2022) (Oct. 1994). [DOI] [Google Scholar]
- 57.Bogacz R., Brown E., Moehlis J., Holmes P. & Cohen J. D. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. eng. Psychological Review 113, 700–765. ISSN: 0033-295X (Oct. 2006). [DOI] [PubMed] [Google Scholar]
- 58.Gold J. I. & Shadlen M. N. The Neural Basis of Decision Making. Annual Review of Neuroscience 30. eprint: 10.1146/annurev.neuro.29.051605.113038, 535–574. https://doi.org/10.1146/annurev.neuro.29.051605.113038 (2023) (2007). [DOI] [PubMed] [Google Scholar]
- 59.Churchland A. K. et al. Variance as a Signature of Neural Computations during Decision Making. English. Neuron 69. Publisher: Elsevier, 818–831. ISSN: 0896-6273. https://www.cell.com/neuron/abstract/S0896-6273(10)01087-1 (2023) (Feb. 2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ratcliff R. A theory of memory retrieval. Psychological Review 85, 59–108. ISSN: 1939-1471 (1978). [Google Scholar]
- 61.Ratcliff R. & McKoon G. The Diffusion Decision Model: Theory and Data for Two-Choice Decision Tasks. Neural Computation 20, 873–922. ISSN: 0899-7667. 10.1162/neco.2008.12-06-420 (2023) (Apr. 2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Frankland S. M. & Greene J. D. Two Ways to Build a Thought: Distinct Forms of Compositional Semantic Representation across Brain Regions. Cerebral Cortex 30, 3838–3855. ISSN: 1047-3211. 10.1093/cercor/bhaa001 (2023) (May 2020). [DOI] [PubMed] [Google Scholar]
- 63.Rigotti M. et al. The importance of mixed selectivity in complex cognitive tasks. en. Nature 497. Number: 7451 Publisher: Nature Publishing Group, 585–590. ISSN: 1476-4687. https://www.nature.com/articles/nature12160 (2022) (May 2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Rudy J. W. & O’Reilly R. C. Conjunctive representations, the hippocampus, and contextual fear conditioning. en. Cognitive, Affective, & Behavioral Neuroscience 1, 66–82. ISSN: 1531-135X. 10.3758/CABN.1.1.66 (2023) (Mar. 2001). [DOI] [PubMed] [Google Scholar]
- 65.Rescorla R. A. ”Configural” conditioning in discrete-trial bar pressing. eng. Journal of Comparative and Physiological Psychology 79, 307–317. ISSN: 0021-9940 (May 1972). [DOI] [PubMed] [Google Scholar]
- 66.Mante V., Sussillo D., Shenoy K. V. & Newsome W. T. Context-dependent computation by recurrent dynamics in prefrontal cortex. en. Nature 503, 78–84. ISSN: 1476-4687. https://www.nature.com/articles/nature12742 (2023) (Nov. 2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Komorowski R. W., Manns J. R. & Eichenbaum H. Robust Conjunctive Item–Place Coding by Hippocampal Neurons Parallels Learning What Happens Where. en. Journal of Neuroscience 29. Publisher: Society for Neuroscience Section: Articles, 9918–9929. ISSN: 0270-6474, 1529–2401. https://www.jneurosci.org/content/29/31/9918 (2023) (Aug. 2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.McKenzie S. et al. Hippocampal Representation of Related and Opposing Memories Develop within Distinct, Hierarchically Organized Neural Schemas. English. Neuron 83. Publisher: Elsevier, 202–215. ISSN: 0896-6273. https://www.cell.com/neuron/abstract/S0896-6273(14)00405-X (2023) (July 2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Fusi S., Miller E. K. & Rigotti M. Why neurons mix: high dimensionality for higher cognition. en. Current Opinion in Neurobiology. Neurobiology of cognitive behavior 37, 66–74. ISSN: 0959-4388. https://www.sciencedirect.com/science/article/pii/S0959438816000118 (2023) (Apr. 2016). [DOI] [PubMed] [Google Scholar]
- 70.Davis H. in Cognitive Aspects of Stimulus Control (Psychology Press, 1992). ISBN: 978-1-315-78910-1. [Google Scholar]
- 71.Cho Y. & Saul L. Kernel Methods for Deep Learning in Advances in Neural Information Processing Systems 22 (2009). https://papers.nips.cc/paper/2009/hash/5751ec3e9a4feab575962e78e006250d-Abstract.html (2022). [Google Scholar]
- 72.Turrigiano G. G. The Self-Tuning Neuron: Synaptic Scaling of Excitatory Synapses. English. Cell 135. Publisher: Elsevier, 422–435. ISSN: 0092-8674, 1097–4172. https://www.cell.com/cell/abstract/S0092-8674(08)01298-1 (2023) (Oct. 2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Saxe A., McClelland J. & Ganguli S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks in International Conference on Learning Representations (2014). [Google Scholar]
- 74.Gunasekar S., Lee J., Soudry D. & Srebro N. Characterizing implicit bias in terms of optimization geometry in International Conference on Machine Learning (PMLR, 2018), 1832–1841. [Google Scholar]
- 75.Ji Z., Dud´ık M., Schapire R. E. & Telgarsky M. Gradient descent follows the regularization path for general losses in Conference on Learning Theory (PMLR, 2020), 2109–2136. [Google Scholar]
- 76.Spence K. W. The nature of the response in discrimination learning. Psychological Review 59, 89–93. ISSN: 1939-1471 (1952). [DOI] [PubMed] [Google Scholar]
- 77.Alvarado M. C. & Rudy J. W. Some properties of configural learning: An investigation of the transversepatterning problem. Journal of Experimental Psychology: Animal Behavior Processes 18. Place: US Publisher: American Psychological Association, 145–153. ISSN: 1939-2184 (1992). [DOI] [PubMed] [Google Scholar]
- 78.Dusek J. A. & Eichenbaum H. The hippocampus and transverse patterning guided by olfactory cues. Behavioral Neuroscience 112, 762–771. ISSN: 1939-0084 (1998). [DOI] [PubMed] [Google Scholar]
- 79.Gao J., Su Y., Tomonaga M. & Matsuzawa T. Learning the rules of the rock–paper–scissors game: chimpanzees versus children. en. Primates 59, 7–17. ISSN: 1610-7365. 10.1007/s10329-017-0620-0 (2022) (Jan. 2018). [DOI] [PubMed] [Google Scholar]
- 80.LeCun Y., Bengio Y. & Hinton G. Deep learning. en. Nature 521, 436–444. ISSN: 1476-4687. https://www.nature.com/articles/nature14539 (2023) (May 2015). [DOI] [PubMed] [Google Scholar]
- 81.Richards B. A. et al. A deep learning framework for neuroscience. en. Nature Neuroscience 22, 1761–1770. ISSN: 1546-1726. https://www.nature.com/articles/s41593-019-0520-2 (2023) (Nov. 2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Saxe A., Nelli S. & Summerfield C. If deep learning is the answer, what is the question? en. Nature Reviews Neuroscience 22, 55–67. ISSN: 1471-0048. https://www.nature.com/articles/s41583-020-00395-8 (2023) (Jan. 2021). [DOI] [PubMed] [Google Scholar]
- 83.Chizat L., Oyallon E. & Bach F. On Lazy Training in Differentiable Programming in Advances in Neural Information Processing Systems 32 (2019). https://proceedings.neurips.cc/paper/2019/hash/ae614c557843b1df326cb29c57225459-Abstract.html (2023). [Google Scholar]
- 84.Woodworth B. et al. Kernel and Rich Regimes in Overparametrized Models en. in Conference on Learning Theory (July 2020), 3635–3673. https://proceedings.mlr.press/v125/woodworth20a.html (2023). [Google Scholar]
- 85.Jacot A., Gabriel F. & Hongler C. Neural tangent kernel: Convergence and generalization in neural networks. Advances in neural information processing systems 31 (2018). [Google Scholar]
- 86.Lee J. et al. Wide neural networks of any depth evolve as linear models under gradient descent. Advances in neural information processing systems 32 (2019). [Google Scholar]
- 87.Fort S. et al. Deep learning versus kernel learning: an empirical study of loss landscape geometry and the time evolution of the Neural Tangent Kernel in Advances in Neural Information Processing Systems 33 (2020), 5850–5861. https://proceedings.neurips.cc/paper/2020/hash/405075699f065e43581f27d67bb68478-Abstract.html (2023). [Google Scholar]
- 88.Vyas N., Bansal Y. & Nakkiran P. Limitations of the NTK for Understanding Generalization in Deep Learning arXiv:2206.10012 [cs]. June 2022. http://arxiv.org/abs/2206.10012 (2023).
- 89.Weinberger N. Dynamic regulation of receptive fields and maps in the adult sensory cortex. Annual review of neuroscience 18, 129–158 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Poort J. et al. Learning Enhances Sensory and Multiple Non-sensory Representations in Primary Visual Cortex. en. Neuron 86, 1478–1490. ISSN: 0896-6273. https://www.sciencedirect.com/science/article/pii/S0896627315004766 (2023) (June 2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Flesch T., Juechems K., Dumbalska T., Saxe A. & Summerfield C. Orthogonal representations for robust context-dependent task performance in brains and neural networks. en. Neuron 110, 1258–1270.e11. ISSN: 0896-6273. https://www.sciencedirect.com/science/article/pii/S0896627322000058 (2023) (Apr. 2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Van Opstal F., Fias W., Peigneux P. & Verguts T. The neural representation of extensively trained ordered sequences. en. NeuroImage 47, 367–375. ISSN: 1053-8119. https://www.sciencedirect.com/science/article/pii/S1053811909003838 (2023) (Aug. 2009). [DOI] [PubMed] [Google Scholar]
- 93.Hinton E. C., Dymond S., von Hecker U. & Evans C. J. Neural correlates of relational reasoning and the symbolic distance effect: involvement of parietal cortex. en. Neuroscience 168, 138–148. ISSN: 0306-4522. https://www.sciencedirect.com/science/article/pii/S0306452210004471 (2023) (June 2010). [DOI] [PubMed] [Google Scholar]
- 94.Constantinescu A. O., O’Reilly J. X. & Behrens T. E. J. Organizing conceptual knowledge in humans with a gridlike code. Science 352, 1464–1468. 10.1126/science.aaf0941 (2023) (June 2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Munoz F. et al. Learned representation of implied serial order in posterior parietal cortex. Scientific Reports 10. Publisher: Springer, 1–14 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Ramawat S. et al. Different Contribution of the Monkey Prefrontal and Premotor Dorsal Cortex in Decision Making During a Transitive Inference Task. en. Neuroscience 485, 147–162. ISSN: 0306-4522. https://www.sciencedirect.com/science/article/pii/S0306452222000276 (2023) (Mar. 2022). [DOI] [PubMed] [Google Scholar]
- 97.Whittington J. C. et al. The Tolman-Eichenbaum machine: unifying space and relational memory through generalization in the hippocampal formation. Cell 183, 1249–1263 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Nacson M. S., Gunasekar S., Lee J., Srebro N. & Soudry D. Lexicographic and depth-sensitive margins in homogeneous and non-homogeneous deep models in International Conference on Machine Learning (PMLR, 2019), 4683–4692. [Google Scholar]
- 99.Lyu K. & Li J. Gradient Descent Maximizes the Margin of Homogeneous Neural Networks in International Conference on Learning Representations (2020). https://openreview.net/forum?id=SJeLIgBKPS. [Google Scholar]
- 100.Chizat L. & Bach F. Implicit Bias of Gradient Descent for Wide Two-layer Neural Networks Trained with the Logistic Loss en. in Proceedings of Thirty Third Conference on Learning Theory ISSN: 2640-3498 (PMLR, July 2020), 1305–1338. https://proceedings.mlr.press/v125/chizat20a.html (2023). [Google Scholar]
- 101.Razin N. & Cohen N. Implicit Regularization in Deep Learning May Not Be Explainable by Norms in Advances in Neural Information Processing Systems 33 (2020), 21174–21187. https://proceedings.neurips.cc/paper/2020/hash/f21e255f89e0f258accbe4e984eef486-Abstract.html (2024). [Google Scholar]
- 102.Savarese P., Evron I., Soudry D. & Srebro N. How do infinite width bounded norm networks look in function space? in Proceedings of the Thirty-Second Conference on Learning Theory 99 (June 2019), 2667–2690. https://proceedings.mlr.press/v99/savarese19a.html. [Google Scholar]
- 103.Ongie G., Willett R., Soudry D. & Srebro N. A Function Space View of Bounded Norm Infinite Width ReLU Nets: The Multivariate Case in International Conference on Learning Representations (2020).
- 104.Glymour C. Learning, prediction and causal Bayes nets. en. Trends in Cognitive Sciences 7, 43–48. ISSN: 1364-6613. https://www.sciencedirect.com/science/article/pii/S1364661302000098 (2022) (Jan. 2003). [DOI] [PubMed] [Google Scholar]
- 105.Kemp C. & Tenenbaum J. B. The discovery of structural form. Proceedings of the National Academy of Sciences 105, 10687–10692. 10.1073/pnas.0802631105 (2022) (Aug. 2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Tenenbaum J. B., Kemp C., Griffiths T. L. & Goodman N. D. How to Grow a Mind: Statistics, Structure, and Abstraction. Science 331. Publisher: American Association for the Advancement of Science, 1279–1285. 10.1126/science.1192788 (2022) (Mar. 2011). [DOI] [PubMed] [Google Scholar]
- 107.Jacobs L. F. From movement to transitivity: the role of hippocampal parallel maps in configural learning. eng. Reviews in the Neurosciences 17, 99–109. ISSN: 0334-1763 (2006). [DOI] [PubMed] [Google Scholar]
- 108.De Soto C. B., London M. & Handel S. Social reasoning and spatial paralogic. Journal of Personality and Social Psychology 2, 513–521. ISSN: 1939-1315 (1965). [DOI] [PubMed] [Google Scholar]
- 109.Wilson R. C., Takahashi Y. K., Schoenbaum G. & Niv Y. Orbitofrontal Cortex as a Cognitive Map of Task Space. en. Neuron 81, 267–279. ISSN: 0896-6273. https://www.sciencedirect.com/science/article/pii/S0896627313010398 (2022) (Jan. 2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Behrens T. E. J. et al. What Is a Cognitive Map? Organizing Knowledge for Flexible Behavior. en. Neuron 100, 490–509. ISSN: 0896-6273. https://www.sciencedirect.com/science/article/pii/S0896627318308560 (2022) (Oct. 2018). [DOI] [PubMed] [Google Scholar]
- 111.McClelland J. L. et al. Letting structure emerge: connectionist and dynamical systems approaches to cognition. en. Trends in Cognitive Sciences 14, 348–356. ISSN: 1364-6613. https://www.sciencedirect.com/science/article/pii/S1364661310001245 (2022) (Aug. 2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Griffiths T. L., Chater N., Kemp C., Perfors A. & Tenenbaum J. B. Probabilistic models of cognition: exploring representations and inductive biases. English. Trends in Cognitive Sciences 14. Publisher: Elsevier, 357–364. ISSN: 1364-6613, 1879–307X. https://www.cell.com/trends/cognitive-sciences/abstract/S1364-6613(10)00112-9 (2022) (Aug. 2010). [DOI] [PubMed] [Google Scholar]
- 113.Saxe A. M., McClelland J. L. & Ganguli S. A mathematical theory of semantic development in deep neural networks. Proceedings of the National Academy of Sciences 116, 11537–11546 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.McClelland J. L., McNaughton B. L. & O’Reilly R. C. Why there are complementary learning systems in the hippocampus and neocortex: Insights from the successes and failures of connectionist models of learning and memory. Psychological Review 102, 419–457. ISSN: 1939-1471 (1995). [DOI] [PubMed] [Google Scholar]
- 115.Kumaran D., Hassabis D. & McClelland J. L. What Learning Systems do Intelligent Agents Need? Complementary Learning Systems Theory Updated. English. Trends in Cognitive Sciences 20, 512–534. ISSN: 1364-6613, 1879–307X. https://www.cell.com/trends/cognitive-sciences/abstract/S1364-6613(16)30043-2 (2024) (July 2016). [DOI] [PubMed] [Google Scholar]
- 116.Jensen G., Munoz F., Meaney A., Terrace H. S. & Ferrera V. P. Transitive inference after minimal training in rhesus macaques (Macaca mulatta). Journal of Experimental Psychology: Animal Learning and Cognition 47, 464 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Zeithamova D., Schlichting M. & Preston A. The hippocampus and inferential reasoning: building memories to navigate future decisions. Frontiers in Human Neuroscience 6. ISSN: 1662-5161. 10.3389/fnhum.2012.00070 (2024) (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Shohamy D. & Daw N. D. Integrating memories to guide decisions. Current Opinion in Behavioral Sciences 5, 85–90 (2015). [Google Scholar]
- 119.Tambini A. & Davachi L. Awake Reactivation of Prior Experiences Consolidates Memories and Biases Cognition. eng. Trends in Cognitive Sciences 23, 876–890. ISSN: 1879-307X (Oct. 2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Kurth-Nelson Z. et al. Replay and compositional computation. Neuron 111, 454–469 (2023). [DOI] [PubMed] [Google Scholar]
- 121.Kumaran D. & McClelland J. L. Generalization through the recurrent interaction of episodic memories: A model of the hippocampal system. Psychological Review 119, 573–616. ISSN: 1939-1471(Electronic),0033–295X(Print) (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Russin J., Zolfaghar M., Park S. A., Boorman E. & O’Reilly R. C. Complementary Structure-Learning Neural Networks for Relational Reasoning. CogSci... Annual Conference of the Cognitive Science Society. Cognitive Science Society (U.S.). Conference 2021, 1560–1566. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8491570/(2024) (July 2021). [PMC free article] [PubMed] [Google Scholar]
- 123.Miconi T. & Kay K. An active neural mechanism for relational learning and fast knowledge reassembly. bioRxiv. https://www.biorxiv.org/content/early/2023/09/04/2023.07.27.550739 (2023).
- 124.Wang J. X. et al. Prefrontal cortex as a meta-reinforcement learning system. Nature Neuroscience 21, 860–868 (2018). [DOI] [PubMed] [Google Scholar]
- 125.Whittington J. C. R., McCaffary D., Bakermans J. J. W. & Behrens T. E. J. How to build a cognitive map. en. Nature Neuroscience 25, 1257–1272. ISSN: 1546-1726. https://www.nature.com/articles/s41593-022-01153-y (2024) (Oct. 2022). [DOI] [PubMed] [Google Scholar]
- 126.Ambrogioni L. & Ólafsdóttir H. F. Rethinking the hippocampal cognitive map as a meta-learning computational module. English. Trends in Cognitive Sciences 27, 702–712. ISSN: 1364-6613, 1879–307X. https://www.cell.com/trends/cognitive-sciences/abstract/S1364-6613(23)00128-6 (2024) (Aug. 2023). [DOI] [PubMed] [Google Scholar]
- 127.Winocur G., Moscovitch M. & Bontempi B. Memory formation and long-term retention in humans and animals: Convergence towards a transformation account of hippocampal–neocortical interactions. Neuropsychologia. Animal Models of Amnesia 48, 2339–2356. ISSN: 0028-3932. https://www.sciencedirect.com/science/article/pii/S0028393210001624 (2024) (July 2010). [DOI] [PubMed] [Google Scholar]
- 128.Ramawat S. et al. The transitive inference task to study the neuronal correlates of memory-driven decision making: A monkey neurophysiology perspective. Neuroscience & Biobehavioral Reviews 152, 105258. ISSN: 0149-7634. https://www.sciencedirect.com/science/article/pii/S0149763423002270 (2024) (Sept. 2023). [DOI] [PubMed] [Google Scholar]
- 129.Telgarsky M. & Singer Y. A Primal-Dual Convergence Analysis of Boosting. Journal of Machine Learning Research 13 (2012). [Google Scholar]
- 130.Kumar A. et al. DR3: Value-Based Deep Reinforcement Learning Requires Explicit Regularization in International Conference on Learning Representations (2022). https://openreview.net/forum?id=POvMvLi91f.
- 131.Bond A. B., Kamil A. C. & Balda R. P. Social complexity and transitive inference in corvids. en. Animal Behaviour 65, 479–487. ISSN: 0003-3472. https://www.sciencedirect.com/science/article/pii/S0003347203921014 (2022) (Mar. 2003). [Google Scholar]
- 132.MacLean E. L., Merritt D. J. & Brannon E. M. Social complexity predicts transitive reasoning in prosimian primates. en. Animal Behaviour 76, 479–486. ISSN: 0003-3472. https://www.sciencedirect.com/science/article/pii/S0003347208002030 (2023) (Aug. 2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Harris M. & McGonigle B. A model of transitive choice. The Quarterly Journal of Experimental Psychology Section B 47. Publisher: Routledge; eprint: 10.1080/14640749408401362, 319–348. ISSN: 0272-4995. 10.1080/14640749408401362 (2023) (Aug. 1994). [DOI] [PubMed] [Google Scholar]
- 134.Bryson J. J. & Leong J. C. S. Primate errors in transitive ‘inference’: a two-tier learning model. en. Animal Cognition 10, 1–15. ISSN: 1435-9456. 10.1007/s10071-006-0024-9 (2023) (Jan. 2007). [DOI] [PubMed] [Google Scholar]
- 135.Halford G. S. Can young children integrate premises in transitivity and serial order tasks? Cognitive Psychology 16, 65–93. ISSN: 0010-0285. https://www.sciencedirect.com/science/article/pii/0010028584900045 (2023) (Jan. 1984). [Google Scholar]
- 136.Treichler F. R. & Van Tilburg D. Concurrent conditional discrimination tests of transitive inference by macaque monkeys: list linking. Journal of Experimental Psychology: Animal Behavior Processes 22, 105 (1996). [PubMed] [Google Scholar]
- 137.Gazes R. P., Chee N. W. & Hampton R. R. Cognitive mechanisms for transitive inference performance in rhesus monkeys: Measuring the influence of associative strength and inferred order. Journal of Experimental Psychology: Animal Behavior Processes 38. Place: US Publisher: American Psychological Association, 331–345. ISSN: 1939-2184(Electronic),0097–7403(Print) (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Lazareva O. F. & Wasserman E. A. Transitive inference in pigeons: Measuring the associative values of Stimuli B and D. en. Behavioural Processes 89, 244–255. ISSN: 0376-6357. https://www.sciencedirect.com/science/article/pii/S0376635711002403 (2023) (Mar. 2012). [DOI] [PubMed] [Google Scholar]
- 139.Jensen G., Alkan Y., Muñoz F., Ferrera V. P. & Terrace H. S. Transitive inference in humans (Homo sapiens) and rhesus macaques (Macaca mulatta) after massed training of the last two list items. Journal of Comparative Psychology 131. Place: US Publisher: American Psychological Association, 231–245. ISSN: 19392087(Electronic),0735–7036(Print) (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Eichenbaum H. The cognitive neuroscience of memory: An introduction (Oxford University Press, 2011). [Google Scholar]
- 141.Kriegeskorte N., Mur M. & Bandettini P. A. Representational similarity analysis — connecting the branches of systems neuroscience. Frontiers in systems neuroscience, 4 (2008). [DOI] [PMC free article] [PubMed]
- 142.Dusek J. A. & Eichenbaum H. The hippocampus and memory for orderly stimulus relations. Proceedings of the National Academy of Sciences 94. Publisher: National Acad Sciences, 7109–7114 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Basile B. M., Templer V. L., Gazes R. P. & Hampton R. R. Preserved visual memory and relational cognition performance in monkeys with selective hippocampal lesions. Science Advances 6, eaaz0484. 10.1126/sciadv.aaz0484 (2024) (July 2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Bussey T. J., Warburton E. C., Aggleton J. P. & Muir J. L. Fornix Lesions Can Facilitate Acquisition of the Transverse Patterning Task: A Challenge for “Configural” Theories of Hippocampal Function. en. Journal of Neuroscience 18. Publisher: Society for Neuroscience Section: ARTICLE, 1622–1631. ISSN: 0270-6474, 1529–2401. https://www.jneurosci.org/content/18/4/1622 (2023) (Feb. 1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Alvarado M. C. & Rudy J. W. Rats with damage to the hippocampal-formation are impaired on the transversepatterning problem but not on elemental discriminations. Behavioral Neuroscience 109. Place: US Publisher: American Psychological Association, 204–211. ISSN: 1939-0084 (1995). [DOI] [PubMed] [Google Scholar]
- 146.Rickard T. C. & Grafman J. Losing Their Configural Mind: Amnesic Patients Fail on Transverse Patterning.Journal of Cognitive Neuroscience 10, 509–524. ISSN: 0898-929X. 10.1162/089892998562915 (2022) (July 1998). [DOI] [PubMed] [Google Scholar]
- 147.Alvarado M. C. & Bachevalier J. Selective neurotoxic damage to the hippocampal formation impairs performance of the transverse patterning and location memory tasks in rhesus macaques. fr. Hippocampus 15. eprint: 10.1002/hipo.20037, 118–131. ISSN: 1098-1063. 10.1002/hipo.20037 (2022) (2005). [DOI] [PubMed] [Google Scholar]
- 148.Fodor J. A. & Pylyshyn Z. W. Connectionism and cognitive architecture: A critical analysis. Cognition 28, 3–71 (1988). [DOI] [PubMed] [Google Scholar]
- 149.Lake B. M., Salakhutdinov R. & Tenenbaum J. B. Human-level concept learning through probabilistic program induction. Science 350, 1332–1338. 10.1126/science.aab3050 (2022) (Dec. 2015). [DOI] [PubMed] [Google Scholar]
- 150.Shalev-Shwartz S. & Shashua A. On the Sample Complexity of End-to-end Training vs. Semantic Abstraction Training arXiv:1604.06915 [cs]. Apr. 2016. http://arxiv.org/abs/1604.06915 (2022).
- 151.Bender E. M. & Koller A. Climbing towards NLU: On Meaning, Form, and Understanding in the Age of Data in Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (July 2020), 5185–5198. https://aclanthology.org/2020.acl-main.463 (2022). [Google Scholar]
- 152.Klinger T. et al. A study of compositional generalization in neural models. arXiv preprint arXiv:2006.09437 (2020).
- 153.Summerfield C., Luyckx F. & Sheahan H. Structure learning and the posterior parietal cortex. en. Progress in Neurobiology 184, 101717. ISSN: 0301-0082. https://www.sciencedirect.com/science/article/pii/S0301008219303351 (2023) (Jan. 2020). [DOI] [PubMed] [Google Scholar]
- 154.Yuille A. L. & Liu C. Deep Nets: What have They Ever Done for Vision? en. International Journal of Computer Vision 129, 781–802. ISSN: 1573-1405. 10.1007/s11263-020-01405-z (2022) (Mar. 2021). [DOI] [Google Scholar]
- 155.Kaplan J. et al. Scaling laws for neural language models. arXiv preprint arXiv:2001.08361 (2020).
- 156.Brown T. et al. Language Models are Few-Shot Learners in Advances in Neural Information Processing Systems 33 (Curran Associates, Inc., 2020), 1877–1901. https://papers.nips.cc/paper/2020/hash/1457c0d6bfcb4967418bfb8ac142f64a-Abstract.html (2022). [Google Scholar]
- 157.Mahowald K. et al. Dissociating language and thought in large language models: a cognitive perspective arXiv:2301.06627 [cs]. Jan. 2023. http://arxiv.org/abs/2301.06627 (2023). [DOI] [PMC free article] [PubMed]
- 158.Saphra N. & Lopez A. Understanding learning dynamics of language models with SVCCA. arXiv preprint arXiv:1811.00225 (2018).
- 159.Tirumala K., Markosyan A. H., Zettlemoyer L. & Aghajanyan A. Memorization Without Overfitting: Analyzing the Training Dynamics of Large Language Models arXiv:2205.10770 [cs]. Nov. 2022. http://arxiv.org/abs/2205.10770 (2023).
- 160.Kandpal N., Deng H., Roberts A., Wallace E. & Raffel C. Large language models struggle to learn long-tail knowledge in International Conference on Machine Learning (PMLR, 2023), 15696–15707. [Google Scholar]
- 161.Grosse R. et al. Studying Large Language Model Generalization with Influence Functions arXiv:2308.03296 [cs, stat]. Aug. 2023. http://arxiv.org/abs/2308.03296 (2023).
- 162.Smolensky P. On the proper treatment of connectionism. en. Behavioral and Brain Sciences 11, 1–23. ISSN: 1469-1825, 0140–525X. https://www.cambridge.org/core/journals/behavioral-and-brain-sciences/article/abs/on-the-proper-treatment-of-connectionism/4B8871A82A932DB96D183AAC9C0CF037 (2023) (Mar. 1988). [Google Scholar]
- 163.Lake B. M., Ullman T. D., Tenenbaum J. B. & Gershman S. J. Building machines that learn and think like people. Behavioral and Brain Sciences 40 (2017). [DOI] [PubMed] [Google Scholar]
- 164.Kipf T., Fetaya E., Wang K.-C., Welling M. & Zemel R. Neural Relational Inference for Interacting Systems en. in Proceedings of the 35th International Conference on Machine Learning ISSN: 2640-3498 (PMLR, July 2018), 2688–2697. https://proceedings.mlr.press/v80/kipf18a.html (2022). [Google Scholar]
- 165.Hill F., Santoro A., Barrett D., Morcos A. & Lillicrap T. Learning to Make Analogies by Contrasting Abstract Relational Structure in International Conference on Learning Representations (2019). [Google Scholar]
- 166.Saxe A., Sodhani S. & Lewallen S. J. The Neural Race Reduction: Dynamics of Abstraction in Gated Networks en. in Proceedings of the 39th International Conference on Machine Learning (PMLR, June 2022), 19287–19309. https://proceedings.mlr.press/v162/saxe22a.html (2023). [Google Scholar]
- 167.Craik K. J. W. The Nature of Explanation (1943).
- 168.Frankland S. M. & Greene J. D. Concepts and Compositionality: In Search of the Brain’s Language of Thought. Annual Review of Psychology 71, 273–303. 10.1146/annurev-psych-122216-011829 (2023) (2020). [DOI] [PubMed] [Google Scholar]
- 169.Johnson J. et al. CLEVR: A Diagnostic Dataset for Compositional Language and Elementary Visual Reasoning in (2017), 2901–2910. https://openaccess.thecvf.com/content_cvpr_2017/html/Johnson_CLEVR_A_Diagnostic_CVPR_2017_paper.html (2023).
- 170.Ito T. et al. Compositional generalization through abstract representations in human and artificial neural networks arXiv:2209.07431 [q-bio]. Sept. 2022. http://arxiv.org/abs/2209.07431 (2023).
- 171.Lake B. M. & Baroni M. Human-like systematic generalization through a meta-learning neural network. en. Nature 623. Number: 7985 Publisher: Nature Publishing Group, 115–121. ISSN: 1476-4687. https://www.nature.com/articles/s41586-023-06668-3 (2023) (Nov. 2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Lepori M., Serre T. & Pavlick E. Break it down: Evidence for structural compositionality in neural networks. Advances in Neural Information Processing Systems 36 (2024). [Google Scholar]
- 173.Fukushima K. Visual Feature Extraction by a Multilayered Network of Analog Threshold Elements. IEEE Transactions on Systems Science and Cybernetics 5, 322–333. ISSN: 2168-2887 (Oct. 1969). [Google Scholar]
- 174.Maas A. L., Hannun A. Y., Ng A. Y., et al. Rectifier nonlinearities improve neural network acoustic models in Proc. icml 30. Issue: 1 (Atlanta, Georgia, USA, 2013), 3. [Google Scholar]
- 175.Tsuchida R., Roosta-Khorasani F. & Gallagher M. Invariance of Weight Distributions in Rectified MLPs arXiv:1711.09090 [cs, stat]. May 2018. http://arxiv.org/abs/1711.09090 (2022).
- 176.Tsuchida R., Roosta F. & Gallagher M. Richer priors for infinitely wide multi-layer perceptrons arXiv:1911.12927 [cs, stat]. Nov. 2019. http://arxiv.org/abs/1911.12927 (2022).
- 177.Han I. et al. Fast Neural Kernel Embeddings for General Activations arXiv:2209.04121 [cs, stat]. Sept. 2022. http://arxiv.org/abs/2209.04121 (2022).
- 178.Schölkopf B. The Kernel Trick for Distances in Advances in Neural Information Processing Systems 13 (MIT Press, 2000). https://proceedings.neurips.cc/paper/2000/hash/4e87337f366f72daa424dae11df0538c-Abstract.html (2024). [Google Scholar]
- 179.Hu G. Y. & O’Connell R. F. Analytical inversion of symmetric tridiagonal matrices. Journal of Physics A: Mathematical and General 29, 1511. 10.1088/0305-4470/29/7/020 (Apr. 1996). [DOI] [Google Scholar]
- 180.He K., Zhang X., Ren S. & Sun J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification in (2015), 1026–1034. https://openaccess.thecvf.com/content_iccv_2015/html/He_Delving_Deep_into_ICCV_2015_paper.html (2023).
- 181.R Core Team. R: A Language and Environment for Statistical Computing https://www.R-project.org/(R Foundation for Statistical Computing, Vienna, Austria, 2022). [Google Scholar]
- 182.Wickham H. ggplot2: Elegant Graphics for Data Analysis ISBN: 978–3-319–24277-4. https://ggplot2.tidyverse.org (Springer-Verlag; New York, 2016). [Google Scholar]
- 183.Pedersen T. L. patchwork: The Composer of Plots https://CRAN.R-project.org/package=patchwork (2022).
- 184.Paszke A. et al. in Advances in Neural Information Processing Systems 32 8024–8035 (Curran Associates, Inc., 2019). http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf. [Google Scholar]
- 185.Knuth D. E. Johann Faulhaber and sums of powers. en. Mathematics of Computation 61, 277–294. ISSN: 0025-5718, 1088-6842. https://www.ams.org/mcom/1993-61-203/S0025-5718-1993-1197512-7/(2024) (1993). [Google Scholar]
- 186.Böttcher A. & Grudsky S. M. Spectral properties of banded Toeplitz matrices (SIAM, 2005). [Google Scholar]
- 187.Gill J. The use of the sequence Fn(z)=fnf1(z) in computing fixed points of continued fractions, products, and series. en. Applied Numerical Mathematics 8, 469–476. ISSN: 0168-9274. https://www.sciencedirect.com/science/article/pii/016892749190109D (2023) (Dec. 1991). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.