Adopting standardized and reliable methodologies to accurately measure particle removal efficiency when developing fibrous materials for controlling airborne contamination is crucial. Here, we introduce well-established aerosol science and technology concepts often overlooked or misused in interdisciplinary studies developing new fibrous materials for particle filtration. We recommend best practices for experimental assessments and reporting to ensure a reliable evaluation of new airborne particle filtration media and technologies.
Subject terms: Characterization and analytical techniques, Chemical engineering, Pollution remediation, Biomedical engineering, Applied physics
Adopting standardized and reliable methodologies to accurately measure particle removal efficiency when developing fibrous materials for controlling airborne contamination is crucial. Here, the authors recommend best practices for experimental assessments and reporting to ensure a reliable evaluation of new airborne particle filtration media and technologies.
The origin of the term “PM” and its definition according to the US Code of Federal Regulations
Despite the growing concern about the health effects of exposure to airborne particles smaller than 1 μm, especially to those below 100 nm1–3, no widely recognized or established air quality standards define PM1 or PM0.1. The mass fraction of atmospheric particulate matter (PM) below 2.5 μm is composed mainly of particles smaller than 1 μm4, especially for urban aerosols. Fibrous filters performing well between the most penetrating particle size (MPPS) and 1 μm will also exhibit high efficiency below 100 nm due to the Brownian diffusion effect, which enhances particle capture efficiency as particle size decreases5. Hence, particle sizes between the MPPS and 1 μm represent the technological challenge for material scientists developing new fibrous filter media. The absence of air quality standards below 1 μm and 100 nm is a challenge for safeguarding public health from airborne PM.
US Federal Reference Method (FRM) 40 CFR Appendix J and L to Part 506–8 and European Standard EN 123419 define PM10 and PM2.5 as the PM penetrating a size-selective inlet with 50% efficiency at 10 μm and 2.5 μm aerodynamic diameters, respectively. The aerodynamic diameter is the diameter of a spherical particle with a density of 1000 kg m−3 with the same settling velocity (due to the force of gravity) as the measured particle. A particle having a specific aerodynamic diameter behaves aerodynamically like a water droplet with that diameter, regardless of its shape, density, or physical size5. Hence, the particle size defined by these methods depends on density and shape. For example, salt and iron particles having the same aerodynamic diameter will have different physical dimensions.
At the same time, the aerodynamic diameter is inappropriate to characterize smaller particles for which the force of gravity is negligible. The net transport does not depend on particle density5. For this reason, the physical diameter is more appropriate to characterize the behavior of particles smaller than 100 nm. Hence, a generic definition such as PM0.1 lacks specifications about whether the 0.1 µm size is aerodynamic or physical.
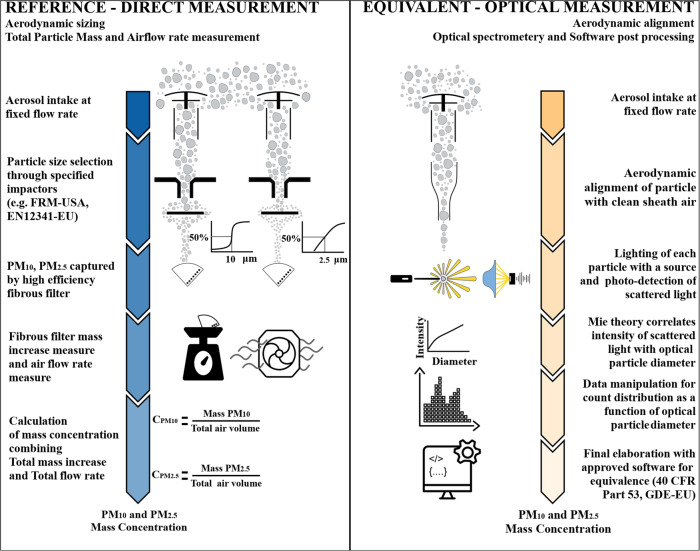
The result of a measurement according to an FRM is a mass concentration obtained by measuring the mass increase, i.e., the mass of particles captured, of a flat piece of high-efficiency filter material exposed to a specific airflow. This measurement approach is typically called gravimetric, and the geometry of the size-selective inlet strongly influences the results, as shown in Fig. 1, which compares the reference and equivalent methods measuring approaches for PM10 and PM2.5 values. The U.S. and European monitoring regulations7,8 outline the formal specifications for PM10 and PM2.5 reference method samplers and their measurement. FRMs and EN 12341 include the specifications of all components and operational airflow rate, together with the drawings of the size-selective impactors. A rigorous definition by describing it with words and numbers is otherwise too difficult.
Fig. 1. Schematization and comparison of the two methodologies used by government authorities for the environmental measurement of PM10 and PM2.5 concentrations.
On the left is the schematic of the reference method, based on the direct measurement of the mass increase of a filter material collecting the aerosol. The size-selective impactor specific for PM10 and PM2.5 selects the particles according to their aerodynamic diameter with an efficiency of 50%. On the right is the equivalent and indirect method schematic. It uses the optical measurement of light scattered by each particle when exposed to a collimated light beam (Mie theory) and without selective impactors, as in the reference methodology. The indirect measurement, combined with data post-processing through the software calibrated by the instrument manufacturer, is equivalent to the direct one if the deviation of the results is within the ±25% error band.
Many scientific papers10–19 use terms like PM0.3 and PM0.1 without defining them or assuming that they indicate the fraction of PM below a given size. This approach appears to replicate the statutory requirements to monitor ambient air that defines PM10 and PM2.5 with a similar definition (particles with an aerodynamic diameter equal to or less than 10 µm and 2.5 µm, respectively).
It is important to note that PM10 and PM2.5 rigorous definitions discussed above are not the same as the total amount of particles below 10 µm and 2.5 µm, respectively. The theory related to the operation of size-selective impactors explains the shape of the collection efficiency curve versus the particle size. An impactor is a device for selecting the particles collected on the filter material and weighed at the end of the measurement procedure. Some particles larger than the cut size will pass through the size-selective inlet. At the same time, some particles smaller than the cut size do not get through the impactor. Consequently, defining PM0.3 as the total number of particles below 0.3 µm may be intuitive, but it is not coherent with the definition of PM10 and PM2.5.
In addition, standard reference methods require one or more days of monitoring, and the prescribed measuring equipment is expensive. Hence, when quantifying PM to provide data with finer time resolution or cheaper devices, using a Federal Equivalent Method (FEM) is common. The 40 CFR Part 5320 (GDE for Europe21) describes how to validate FEMs, including appliances and techniques. In particular, they do not directly provide the mass concentration. Instead, they supply results calibrated against the reference methodology and respective instrumentation through an indirect measurement. The users can consider the measurement results equivalent to reference equipment when the accuracy is within ±25% over a specific period.
For example, optical spectrometers measure the number of particles as a function of their size. Using the data supplied by the optical instrument, it is possible to calculate the mass concentration of particles smaller than 2.5 μm (making assumptions about their shape and density) by integrating the area under the distribution function with an upper limit of 2.5 μm. Nevertheless, even using sophisticated instruments, we cannot consider such a result as an accurate mass concentration of PM2.5 according to its original definition without post-processing the measured data obtained from the optical instrument22.
This equivalent method does not adopt any gravimetric measurement or a sampling inlet determining the cut size of the particle distribution. Hence, the difference between the PM2.5 values provided by a reference method or instrument and other reported PM2.5 concentration values might be significant. The difference depends on the conversion between the measured data, i.e., the technology used to measure the particle concentration as a function of size and the calculated mass concentration. Under some conditions, the agreement between the two may be satisfactory. That is likely to occur if the sampled particles’ size, shape, material density, and relative humidity are close to those used for calibrating the instrument. However, the properties of the measured aerosol might deviate from the calibration assumptions. In this case, the agreement between the PM2.5 concentration provided by the alternative measurement method may differ considerably from the statutory value. Hence, it is crucial to calibrate optical spectrometers against gravimetric measurements using the same aerosol to be measured. Periodic recalibration is essential for maintaining reliable correlations.
Removal efficiency by filtration of a certain PM fraction
The recent COVID-19 pandemic highlighted the importance of fibrous materials with fine fibers for controlling airborne contamination. Air filtration media should ensure high efficiency of removal of airborne particles smaller than 1 µm. Scientists worldwide and in many disciplines are developing new technologies and materials claiming filtration performance adequate to control airborne bioaerosols and beyond.
Fibrous filtration efficiency is a function of particle size and other parameters23. Using the mass of particles below a certain threshold to determine the overall efficiency of a filter material is ambiguous because the measured data will depend on the distribution of the mass of particles as a function of their size. In other words, the same total particle mass, corresponding to various particle size distributions, will produce different removal efficiencies, i.e., filtration efficiency test data.
Measuring the total mass concentration upstream and downstream of the filter media through a photometer or a nephelometer can cause poor repeatability of the test data within the same lab if the particle size distribution is not strictly the same (the following section discusses this issue). The reproducibility of the test data among different labs is even more challenging when the labs use test equipment with various components supplied by other manufacturers. The same problem can arise when using turnkey equipment bought on the market. Especially in these situations, the researcher shall define and control in detail the particle size distribution to get repeatable and reproducible data. Such distribution should always be the same for a good agreement among laboratories and scientists.
Aerosol technology experts use the lognormal distribution to characterize most particle size distributions. The median of the distribution of mass is called the mass median diameter (MMD) to distinguish it from the count median diameter (CMD). The geometric standard deviation (GSD) replaces the standard deviation of the normal distribution and quantifies the dispersion of this distribution. One can fully identify the distribution by knowing the aerosol is distributed according to a lognormal distribution, its MMD and GSD, and determine the aerosol’s mass distribution as a function of the particle size.
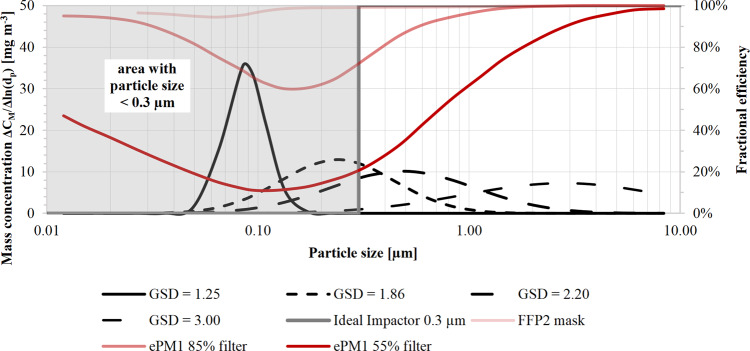
The example in Fig. 2 shows how different particle distributions can generate different efficiency test results using a lognormal particle size distribution. All black curves show the mass distribution as a function of the particle size of an aerosol characterized by identical CMD (75 nm, the mean value prescribed by 42 C.F.R. § 84.124), and total particle mass concentration (20 mg m−3). The different GSDs affect the shape of the particle distribution. In particular, the GSD varies from 1.25 (quasi-monodisperse aerosol) to 3.0 (polydisperse aerosol). This range is coherent with different applications of filter media. Indeed, a GSD equal to 1.25 is considered by ISO 29463-2:201125 as a monodisperse aerosol for testing HEPA filters. 42 C.F.R. § 84.1 prescribes a GSD below 1.86 for the N95 labeling. EN 13274-7:201926 specifies maximum GSD values of 2.2 and 3 when testing respiratory protective devices with paraffin oil and NaCl, respectively.
Fig. 2. Influence of particle size distribution on filtration efficiency.
The graph shows the particle size distributions of the mass concentration with CMD equal to 75 nm with four different GSDs (black lines have a GSD equal to 1.25, 1.86, 2.2, and 3, respectively). The distribution of mass concentration as a function of the particle size is lognormal. The mass concentration fraction is ΔCM/Δln(dp), where dp is the particle diameter. The gray area on the left represents all the particles with an equivalent size smaller than 0.3 µm. The red lines represent typical fractional efficiencies of FFP2 mask27, filter ePM1 85%28, and ePM1 55%28.
Figure 2 also depicts the efficiency by the particle size of three typical filter media, FFP227, ePM1 85%28, and ePM1 55%28. Once the filter efficiency by particle size is known (red curves in Fig. 2), we can calculate the overall mass efficiency (OME) across the entire particle size range using the equation:
| 1 |
where i = ith channel, n = total number of channels, Ei = efficiency at the ith channel, qm,i = mass concentration at the ith channel, = geometric mean of ith channel.
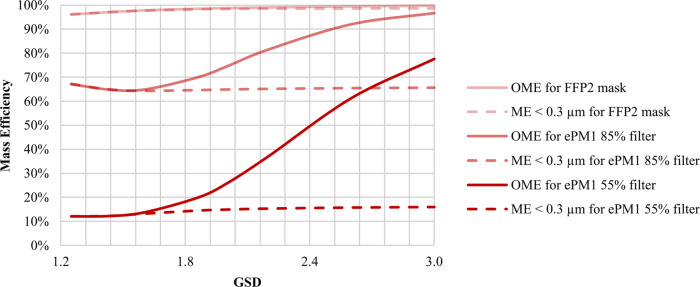
Table 1 shows, for each filter media, the GSD sensitivity analysis results of the OME and the mass efficiency (ME) for particles below 0.3 µm (equivalent diameter), as several authors usually assume for PM0.3 efficiency13–19. For better visualization, Fig. 3 summarizes the data in Table 1.
Table 1.
GSD sensitivity analysis results for different definitions of mass efficiency
| GSD 1.25 |
GSD 1.86 |
GSD 2.20 |
GSD 3.00 |
|
|---|---|---|---|---|
| Generated aerosol | ||||
| CMD [nm] | 75 | 75 | 75 | 75 |
| MMD [nm] | 87 | 238 | 484 | 2803 |
| GSD | 1.25 | 1.86 | 2.20 | 3.00 |
| Cumulative mass concentration [mg m−3] | 20 | 20 | 20 | 20 |
| FFP2 mask | ||||
| MPPS of filter [nm] | 65 | |||
| Efficiency at MPPS | 94.5% | |||
| Overall mass efficiency | 96.4% | 98.5% | 99.0% | 99.7% |
| Mass efficiency for particles <0.3 µm | 96.4% | 98.2% | 98.4% | 98.5% |
| ePM1 85% filter | ||||
| MPPS of filter [nm] | 134 | |||
| Efficiency at MPPS | 60.0% | |||
| Overall mass efficiency | 67.1% | 70.0% | 81.6% | 96.7% |
| Mass efficiency for particles <0.3 µm | 67.1% | 64.6% | 65.1% | 65.6% |
| ePM1 55% filter | ||||
| MPPS of filter [nm] | 110 | |||
| Efficiency at MPPS | 11.0% | |||
| Overall mass efficiency | 12.0% | 19.9% | 37.0% | 77.6% |
| Mass efficiency for particles <0.3 µm | 12.0% | 14.4% | 15.3% | 15.9% |
GSD, MMD, and CMD are linked by the equation MMD = CMD exp(3 ln2 GSD) for a lognormal distribution5. Increasing MMD or the dispersion of the test aerosols tends to overestimate the OME, driven by a higher concentration of larger particles that are easily captured. However, this phenomenon is less evident for filter media with high efficiency, like FFP2 masks. For instance, when the efficiency is close to 100% at MPPS, shifting the particle size distribution towards larger will not increase the efficiency appreciably. The underlying conceptual mistake remains hidden since the lowest efficiency is already nearly 100%. The same does not occur when testing filters with lower efficiency (ePM1 85% or ePM1 55%).
Fig. 3. Variation of the mass efficiency for the different filter media and varying the GSD.
The graph shows the efficiency differences. Note the impact of considering the entire size distribution (OME) versus only the fraction below 0.3 µm (ME < 0.3 µm) of a polydisperse test aerosol. Increasing the aerosol dispersion (e.g., increasing GSD from 1.2 to 3) results in a significant difference between OME and ME. Moreover, various filter media (FFP2 mask, ePM1 85%, and ePM1 55%) exhibit different effects. The difference between OME and ME < 0.3 µm increases when air filter efficiency decreases.
As expected from air filtration theory, the results show that increasing the aerosol dispersion increases the OME due to a higher mass concentration of larger particles (right tail of the lognormal distribution) which are easily captured. This effect is less relevant for high-efficiency filter media, such as the one used for FFP2 masks. Suppose the efficiency at the MPPS, i.e., the particle size corresponding to the maximum penetration, is nearly 100%. In that case, the shift toward particles easier to capture will not increase the efficiency because the lowest efficiency is already close to 100%.
This effect masks the conceptual mistake.
However, when measuring the performance of other standard filter media, the overall efficiency drastically changes. We show two relevant examples: ePM1 85% and ePM1 55% according to ISO 16890-1:201629. For ePM1 85%, as the GSD increases from 1.25 to 3, the OME increases from 67.1% to 96.7%, while it increases from 12.0% to 77.6% for ePM1 55%.
The overall efficiency approach does not provide insight into how the removal efficiency changes with particle size. One can use it to check the conformity requirements against a minimum efficiency or a maximum penetration, like for face masks. One can use it to compare the filtration performance of a new material against a benchmark or to evaluate the stability of filter media production quality. However, the particle size distribution of the test aerosol challenging the filter must be strictly fixed and well-known. Otherwise, researchers cannot compare the OME data obtained with different particle size distributions, as they are misleading or meaningless13,19,30–32.
In addition, OME cannot provide removal efficiency values at the MPPS, as shown in Table 1. We note that the values shown for the MPPS also depend on the airflow rate. The confusion between the efficiency at MPPS and at 0.3 µm comes probably from the definition of HEPA filter, proposed during the Second World War when Irvin Langmuir developed the hot DOP (Dioctyl-phthalate) test33 and described the challenge aerosol particles distribution with an MMD at 0.3 µm34. See also the following section’s discussion about the US Military Standard 282.
ISO 29463-3:201135 shows how to determine the MPPS on a flat media sheet and summarizes helpful information. The MPPS of most non-charged filter media is between 0.1 and 0.2 µm. The MPPS of charged filter media is much smaller, sometimes down to 40 nm. Hence, PM0.3 has nothing to do with the efficiency in correspondence to the MPPS. In general, measuring the overall efficiency will not provide the efficiency corresponding to a specific size unless the test aerosol is strictly monodisperse. In practice, air filtration test methods do not adopt this approach unless for calibration purposes with reference polystyrene PSL microspheres.
We also note that OME and PM0.3 are intrinsically different. OME considers all the particle sizes in the test aerosol challenging the filter, while PM0.3 data refer only to particles below the 0.3 µm threshold. When the test equipment cannot distinguish the particle size because the particle sensing instrument is a photometer, it will not provide the PM0.3 information unless all the particles of the challenging aerosol are smaller than 0.3 µm. Such a condition is impractical.
Finally, testing air filters and using a test aerosol with an MMD corresponding to a specific size does not imply obtaining the efficiency corresponding to that size or to the fraction of particles below that size. In fact, in the particle size distribution with a certain MMD, particles larger than the MMD contribute 50% of the mass to that size distribution.
Interpretation of the data provided by particle photometers vs. particle spectrometers
Optical instruments for measuring particle concentration are the most common particle-sensing instruments to assess air filtration performance. Light scattering is the physical phenomenon that correlates particles’ presence and size by detecting the scattered light’s intensity and angle. By solving Maxwell’s equations, the Mie theory calculates the scattering and absorption of light by a single spherical particle. The result is a function of the size, the refractive index, and the wavelength of the incident light. Consequently, the amount of scattered light is also a function of the type of light source and the particle’s chemical composition.
By analyzing one particle at a time, optical particle spectrometers generate a correlation between the intensity of the scattered signal and a single particle, enabling the determination of the particle’s size and, consequently, its volume and mass (see schematics of Fig. 1).
On the other hand, particle photometers analyze a group of particles simultaneously and do not allow for creating a correlation between the intensity signal and single particles. Instead, they generate a single signal for a group of particles that, in the case of a polydisperse aerosol, results from the interaction of the light source with a size range of particles that may be wide. This type of instrument correlates the amount of scattered light with the total particles’ volume, i.e., their total mass if their density is known. Photometers need calibration against the gravimetric measurement of aerosols of known size. The measurement accuracy of a photometer depends on whether the properties of the measured aerosol differ from those of the calibration aerosol. Indeed, most of the time, test rig manufacturers carry out suitable calibration procedures considering specific applications.
Using photometers cannot provide data referring to a specific particle size unless using a monodisperse aerosol. Hence, a test rig using photometers and a polydisperse aerosol cannot measure the filtration efficiency at the MPPS. These data are often crucial for assessing high-efficiency filter media.
In several countries, many assume that the efficiency of HEPA filters is measured at 0.3 μm particle size according to the US Military Standard 28236. Several experts include 0.3 μm in the definition of HEPA filter. However, 0.3 μm is the mass mean diameter of the aerosol specified by the US Military Standard 282, while the count mean diameter of this aerosol is around 0.18 μm (ISO 29463-225). Hence, testing a filter using an aerosol with a count mean diameter of 0.3 μm overestimates its efficiency. To avoid similar errors, one shall consider the complete particle size distribution, not its mean properties.
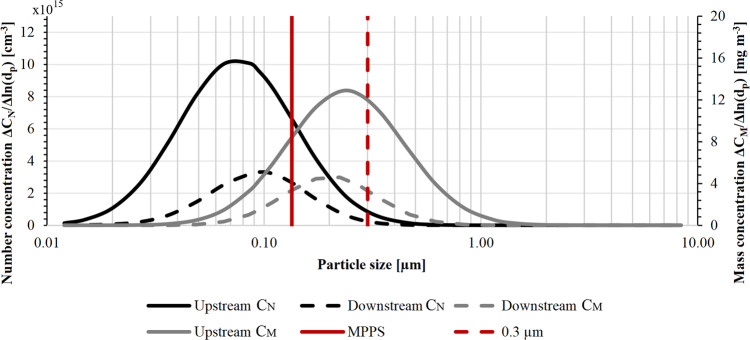
Figure 4 shows the count and mass distribution as a function of particle size of a test aerosol challenging an ePM1 85%29 filter. We note the clear difference between the mean values of the two distributions and the MPPS position in this specific case. The MPPS changes with the filtration velocity.
Fig. 4. Difference between the MPPS and the mass median diameter.
The graph shows the distribution of count concentration and mass concentrations (respectively, ΔCN/Δln(dp) and ΔCM/Δln(dp), where dp is the particle diameter) as a function of particle size of a test aerosol with a lognormal distribution. Solid lines represent the distributions of upstream number concentration (black) and mass concentration (gray), while dashed lines represent downstream distributions of an ePM1 85% filter. The vertical red lines indicate the distinct positions of the MPPS (solid line) and the mass median diameter (dashed line) at 0.3 µm. The MPPS is smaller than the mass median diameter, resulting in a higher efficiency value at 0.3 µm compared to the value at MPPS.
Concluding remarks and recommendations
Despite the growing concern about the health effects of exposure to the so-called PM1, PM0.3, or PM0.1, no established air quality standard exists for their definition. We discussed the implications of using these generic terms without accurately defining their meaning and showed their impact on the data describing air filtration performance. Table 2 suggests approaches to designing a correct experimental assessment so that researchers can compare new media and technology to existing ones with better reliability.
Table 2.
Overview of key points of concern when evaluating the filtration performance of novel filter media and recommendations to address them
| Points of Concern | Recommendations |
|---|---|
| Use of the term PMxx |
• Do not use the term PMxx to define an aerosol fraction below a specific size without specifying sampling, measurement, and experimental protocols in detail. • Remember their meaning when using PM10 and PM2.5 terms and relate them to reference methods. • Use aerodynamic and physical size within the appropriate range. • Report the particle size distribution used for the experiment, indicating how it was measured. |
| Approach for measuring air filter efficiency |
• Provide detailed information about the physical and chemical nature of the test aerosol. • The best methodology to understand and demonstrate fibrous filtration performance is measuring the efficiency as a function of the particle size. • Particle spectrometers can provide efficiency as a function of the particle size with a single test. • Photometers require challenging the filter with a monodisperse aerosol and measuring the reduction in particle concentration for one specific size. The procedure requires multiple tests as the investigated particle sizes. • If researchers are measuring a fixed polydisperse aerosol’s total particle number or mass, they must avoid expressing efficiency for specific PM fractions or at the MPPS. In this case, researchers can only compare filtration efficiency with benchmark media. • If possible, use a standardized test method following its qualification procedures. |
| Expressing air filter efficiency |
• Air filtration efficiency as a function of particle size is necessary for calculating the removed PMxx fraction. • To calculate the air filter efficiency for a specific PMxx fraction, use the procedure explained in ISO 16890-1. • Expressing air filtration efficiency with a single number (e.g., 90%) requires a detailed test aerosol characterization to ensure meaningfulness and reproducibility. |
| Use of the photometer |
• A photometer measurement using a polydisperse test aerosol cannot provide the efficiency corresponding to or below a specific particle size. • Single number efficiency obtained with a photometer is extremely sensitive to large particles in the tail of the particle size distribution. • Comparison among different filter media is valid only if the upstream distribution is identical. |
| Identification of MPPS and corresponding efficiency |
• A photometer measurement using a polydisperse challenge aerosol cannot identify the MPPS. • Do not combine a photometer with a polydisperse aerosol having an MMD equal to the MPPS to obtain the maximum penetration. • When using a spectrometer, the upstream distribution must cover the particle size range where the MPPS falls. • Associate the efficiency at the MPPS with the media velocity because the MPPS is a function of the airflow rate. |
Author contributions
Conceptualization: P.T., V.G., and J.M; Investigation: P.T., V.G., and J.M.; Visualization: V.G. and J.M.; Funding acquisition: P.T.; Writing—original draft: P.T. and V.G.; Writing—review and editing: P.T., V.G., and J.M.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Marval J, Tronville P. Ultrafine particles: a review about their health effects, presence, generation, and measurement in indoor environments. Build. Environ. 2022;216:108992. doi: 10.1016/j.buildenv.2022.108992. [DOI] [Google Scholar]
- 2.Ohlwein S, Kappeler R, Kutlar Joss M, Künzli N, Hoffmann B. Health effects of ultrafine particles: a systematic literature review update of epidemiological evidence. Int. J. Public Health. 2019;64:547–559. doi: 10.1007/s00038-019-01202-7. [DOI] [PubMed] [Google Scholar]
- 3.Kwon HS, Ryu MH, Carlsten C. Ultrafine particles: unique physicochemical properties relevant to health and disease. Exp. Mol. Med. 2020;52:318–328. doi: 10.1038/s12276-020-0405-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.John H. Seinfeld, S. N. P. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. (2016).
- 5.W.C. Hinds & Y. Zhu. Aerosol Technology. Properties, Behavior, and Measurement of Airborne Particles. (Wiley, 2022).
- 6.Gilliam, J. H. & Hall, E. S. Reference and Equivalent Methods Used to Measure National Ambient Air Quality Standards (NAAQS) Criteria Air Pollutants vol.1. I, 2016–2017 (2016).
- 7.Office of the Federal Register, N. A. and R. A. 40 CFR Appendix L to Part 50 - Reference Method for the Determination of Fine Particulate Matter as PM2.5 in the Atmosphere. Govinfo.Gov 74–118 (2001).
- 8.Office of the Federal Register, N. A. and R. A. 40 CFR Appendix J to Part 50 - Reference Method for the Determination of Particulate Matter as PM10 in the Atmosphere. Govinfo.Gov 73–78 (1999).
- 9.EN 12341: 2014 Ambient air—standard gravimetric measurement method for the determination of the PM10 or PM2,5 mass concentration of suspended particulate matter. 53 (2014).
- 10.Kim D, Jung S, Yoon C. Evaluation of airborne total suspended particulates and heavy metals in anodizing and electroplating surface treatment process. Sci. Rep. 2021;11:1–9. doi: 10.1038/s41598-021-01577-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang G, et al. Overcoming humidity-induced swelling of graphene oxide-based hydrogen membranes using charge-compensating nanodiamonds. Nat. Energy. 2021;6:1176–1187. doi: 10.1038/s41560-021-00946-y. [DOI] [Google Scholar]
- 12.Ryu, Y., Roh, S. & Joung, Y. S. Assessing the cytotoxicity of aerosolized carbon black and benzo [a] pyrene with controlled physical and chemical properties on human lung epithelial cells. Sci. Rep. 10.1038/s41598-023-35586-7 (2023). [DOI] [PMC free article] [PubMed]
- 13.Li Y, et al. Ultrafine, self-crimp, and electret nano-wool for low-resistance and high-efficiency protective filter media against PM0.3. J. Colloid Interface Sci. 2020;578:565–573. doi: 10.1016/j.jcis.2020.05.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Badran G, et al. Toxicological appraisal of the chemical fractions of ambient fine (PM2.5−0.3) and quasi-ultrafine (PM0.3) particles in human bronchial epithelial BEAS-2B cells. Environ. Pollut. 2020;263:1–12. doi: 10.1016/j.envpol.2020.114620. [DOI] [PubMed] [Google Scholar]
- 15.Geng Q, et al. Multi-component nanofiber composite membrane enabled high PM0.3 removal efficiency and in complex environment. J. Hazard. Mater. 2022;422:126835. doi: 10.1016/j.jhazmat.2021.126835. [DOI] [PubMed] [Google Scholar]
- 16.Li Y, et al. MOF-embedded bifunctional composite nanofiber membranes with a tunable hierarchical structure for high-efficiency PM0.3 purification and oil/water separation. ACS Appl. Mater. Interfaces. 2021;13:39831–39843. doi: 10.1021/acsami.1c09463. [DOI] [PubMed] [Google Scholar]
- 17.Liu H, Zhang S, Liu L, Yu J, Ding B. High-performance PM0.3 air filters using self-polarized electret nanofiber/nets. Adv. Funct. Mater. 2020;30:1–8. [Google Scholar]
- 18.Vishwakarma PK, et al. Multiwalled carbon nanotube-based freestanding filters for efficient removal of fine particulate matters (PM0.3), microplastics (MP0.3), and bioaerosols. ACS Appl. Nano Mater. 2022;5:9306–9318. doi: 10.1021/acsanm.2c01468. [DOI] [Google Scholar]
- 19.Huang Z, Dang C, Sun Z, Qi H. High-efficiency air filter media with a three-dimensional network composed of core-shell zeolitic imidazolate framework-8@tunicate nanocellulose for PM0.3 removal. ACS Appl. Mater. Interfaces. 2021;13:57921–57929. doi: 10.1021/acsami.1c17052. [DOI] [PubMed] [Google Scholar]
- 20.Federal Register. Revised Requirements for Designation of Reference and Equivalent Methods for PM2.5 and Ambient Air Quality Surveillance for Particulate Matter: Subpart F—Procedures for Testing Performance Characteristics of Class II Equivalent Methods for PM2.5. Fed. Regist. 40 CFR Parts 53 58 (1997).
- 21.EC Working Group on Guidance for the Demonstration of Equivalence. Guide to the Demonstration of Equivalence. 92 (2010).
- 22.UK Environment Agency. MCERTS: performance standard for indicative ambient particulate monitors. 20 https://www.gov.uk/government/publications/mcerts-performance-standard-for-indicative-ambient-particulate-monitors (2017).
- 23.Brown, R. C. Air Filtration. An Integrated Approach to the Theory and Applications of Fibrous Filters. (Pergamon, 2016).
- 24.Public Health, 42 CFR § 84.1. (2004).
- 25.ISO 29463-2:2011 High-efficiency filters and filter media for removing particles in air—Part 2: Aerosol production, measuring equipment and particle-counting statistics.
- 26.EN 13274-7:2019 Respiratory protective devices—Methods of test—Part 7: Determination of particle filter penetration.
- 27.Charvet A, et al. Impact of washing cycles on the performances of face masks. J. Aerosol Sci. 2022;160:105914. doi: 10.1016/j.jaerosci.2021.105914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Azimi P, Zhao D, Stephens B. Estimates of HVAC filtration efficiency for fine and ultrafine particles of outdoor origin. Atmos. Environ. 2014;98:337–346. doi: 10.1016/j.atmosenv.2014.09.007. [DOI] [Google Scholar]
- 29.ISO 16890-1:2016 Air filters for general ventilation—Part 1: Technical specifications, requirements and classification system based upon particulate matter efficiency (ePM).
- 30.Zuo F, et al. Free-standing polyurethane nanofiber/nets air filters for effective PM capture. Small. 2017;13:1–11. doi: 10.1002/smll.201702139. [DOI] [PubMed] [Google Scholar]
- 31.Zhang X, Xu Y, Zeng Y. Efficient, breathable and biodegradable filter media for face masks. Fibers Polym. 2023;24:1613–1621. doi: 10.1007/s12221-023-00178-9. [DOI] [Google Scholar]
- 32.Li L, Zuo Z, Japuntich DA, Pui DYH. Evaluation of filter media for particle number, surface area and mass penetrations. Ann. Occup. Hyg. 2012;56:581–594. doi: 10.1093/annhyg/mes034. [DOI] [PubMed] [Google Scholar]
- 33.Langmuir I. Report on Smokes and Filters. OSRD 865, Off. Sci. Res. Dev. Off. Tech. Serv. Washington DC (1942).
- 34.Slawski, J. W. Doe Handbook DOE-HDBK-1169-2003 Nuclear Air Cleaning Handbook. (U.S. Department of Energy, 2003).
- 35.ISO 29463-3:2011 High-efficiency filters and filter media for removing particles in air—Part 3: Testing flat sheet filter media.
- 36.MIL-STD-282 102.1. Department Of Defense Test Method Standard. Filter Units, Protective Clothing, Gas-Mask Components and Related Products: Performace Test methods. (1956).