The effect of average scores in reading, mathematics and science on innovation and income: A quantitative analysis for a group of countries

Abstract

The purpose of this paper is to The goal of this study is to empirically examine how innovation and income are affected by PISA scores—average scores in math, science, and reading. The specific objectives are threefold. First, we develop a conceptual model that describes the connection between income, innovation, and educational quality as determined by PISA scores. Second, we perform an empirical analysis to see if educational quality as assessed by the PISA scores has an impact on innovation.Third, we also test whether the PISA scores have a positive effect on income (GDP per capita). Using panel mode, we find that education quality has a significant and positive effect on innovation and income. Particularly high math test scores have been found to be an important subject that increases per capita income and innovation.

1. Introduction

According to endogenous theory, one of the key factors influencing development and growth is human capital, which takes the form of education and knowledge [1,2]. Based this theory, nations with higher educational systems and general knowledge may experience beneficial effects for their economic development and technological advancement. Besides, the human capital theory also views education as a key factor to accumulate human capital [3,4]. Pioneer work by Mincer [4] particularly focuses on how individual income and economic growth are determined by investment in education. Given the importance of education, this study particularly uses students' assessment scores from three core subjects mathematics, science and readings) as a measure of the quality of secondary education and empirically examines their impact on growth and innovation.

In recent decades, both knowledge in the form of education and innovation as technological progress, have been considered key factors to promote growth. Innovation is a multi-step process through which an economy successfully promotes, competes and differentiates itself from the rest of world, and the whole process is supported by science education [5,6]. The emergence of new ideas is strongly based on individual educational assessment [7,8]. The generation of such ideas requires a combination of critical thinking, cognitive skills and creative abilities [9,10]. Sharif [8] noted that high school students with better scores in mathematics and science could have a higher order of critical thinking. Manton et al. [11] claimed that education is a milestone for the development of cognitive skills. Further, they argue that education is expected to stimulate both knowledge and technology output and spike creativity levels at the country level. Thus, the existing knowledge will be further complemented by the introduction of novel ideas in further education [[11], [12], [13]].

All this implies that superior quality of education especially at the primary and secondary level is a springboard in the creation and generation of new ideas, which is the initial stage of the innovation process but ultimately affects the growth of a country. The studies already agreed that educational quality measured through grades increases productivity [6].

In this paper, we use quality of secondary education, which is measured by the average score in three core subjects as stated in the OECD Programme for International Student Assessment [14] survey. In this context, the PISA (Program for International Student Assessment) assessment spanned various levels of difficulty so that the entire pool of items measures performance across all component skills and across a broad range of contexts and student abilities [15]. PISA assessment focuses on students’ performance in three areas namely Mathematics, Reading and Science [16]. PISA scores serve as a proxy (albeit weakly) for the quality of secondary education, as it has been argued that educational inputs and their quality are strongly predictive of PISA scores across countries. It is also important to acknowledge that PISA scores have been criticized on account of their methodology [17]; their usefulness to policymakers [18]. At the same time, in some countries such as Germany, PISA scores have been able to bring about a transformation in the approach to educational policy, particularly highlighting the shift to an evidence-based approach [19]. The plus point of using PISA score is that it provides a magnitude of the cognitive knowledge of the individuals that affect the development and economic growth. Furthermore, It is suggested that having higher PISA scores can imply a greater likelihood of enrolment in higher education, and therefore skilled entry into the workforce. For example, Fischbach et al. [20], show that higher PISA scores in Luxembourg are strongly predictive of academic promotion as well as other productive educational outcomes. Indeed, Michaelowa [21] illustrates that there is a positive correlation between PISA scores and tertiary education outcomes. Thus, it is likely that a higher PISA score also means that more students enter higher education, and in turn, contribute to the skilled workforce of the country with innovative potential.

Although past studies do provide substantial evidence on the positive relationship between education, innovation and income growth. However, the effect of secondary educational quality, measured by assessment scores, on innovation and GDP per capita has been ignored. Furthermore, available research does not yield which particular subject has a greater impact on these. This paper puts forward a case for considering secondary educational quality measured by PISA score on innovation and GDP per capita. The specific research questions (and sub-questions) of this study are the following:

• •Can we construct a conceptual model based on literature that explains a bidirectional link between educational quality as measured by the PISA assessment score, innovation, and income?
• •
  Does educational assessment (as measured by PISA score) have a positive effect on innovation and income (GDP per capita)?

  • o
    Does the score in math, reading, or science have a greater impact on innovation and income?

Based on these questions, this study will test the following two hypotheses.

• •H1: educational quality positively affects innovation activity
• •H2: educational quality enhances income

Using panel data for 78 countries over the period 2012–2018, the results suggest that educational quality measured by PISA scores of three core subjects (mathematics, science and readings) positively affects both innovation and GDP per capita. Particularly, scores in mathematics is a proven to be a leading subject that contributes more towards a country's innovation and GDP per capita. These findings suggest that implementing policies to improve educational standards can increase levels of innovation and per capita income. It also emphasizes how important it is to raise educational standards in general. However, students who are proficient in math have greater levels of creativity and are better able to solve complicated problems.

The rest of the study is organized as follows: Section 2 presents the literature review and conceptual model related to secondary education, innovation and growth nexus. Methodology and Data are presented in Section 3. Section 4 offers results and discussion. Finally, Section 5 concludes the study.

2. Theoretical literature and conceptual model

This section is divided into three parts. The first part presents the review of selected studies related to the impact of education on innovation, while the second part focuses on the studies linked with education and growth. The third part builds a conceptual model based on the literature.

2.1. education and innovation

The definition of innovation includes introducing new products, processes, or organizational and marketing practices [22] and creating new business models and new sources of supply [[23], [24], [25]]. According to Lengyel et al. [26], undergraduate students have a concerning lack of mindfulness, sustainability literacy, universal values concerning nature and fellow humans, and system thinking. Menell and Scotchmer [27] consider innovation not as a one-time event but as a cumulative event when innovations follow the creative development work of others. In doing so, existing knowledge acts as input to ideation, modification, improvement, and invention [[28], [29], [30]]. Thus, one of the prerequisites for producing high-quality, innovative content is the ability to reach the burden of knowledge [31]. Quality education not only builds cognitive and non-cognitive skills but also increases entrepreneurship and economic growth [32]. Few studies also argued that higher education in science and engineering is the major predictor of innovation success (e.g., Refs. [[33], [34], [35], [36]]. On the other hand, Becker [3] and Mincer [4] pointed out that education is a main determinant for enhancing income and innovation through labour productivity. Advanced training in math and science is translated into socioeconomic success which is observed by many studies [[37], [38], [39]]. Chatterji [40] show that knowledge-intensive sectors of the economy are increasingly in need of skilled workers ready to create new inventions using new technologies along with developing business models for their commercialization. Further, they argued that underachievement of US high school students in math and science is a concern for innovation and long-term employment problems. Similarly, Augustine et al. [41] confirm that knowledge in science, technology, engineering and mathematics (STEM) significantly contributes to innovation.

With regards to secondary school education, Card and Giuliano [42,43] observe that access to quality education for talented K-12 schools significantly increases the flow of future innovators. In addition, certain types of educational programs appear to be particularly useful for innovation. This is supported by Bianchi and Giorcelli's [44], where the rise of interest in technical specialities due to STEM education in Italy in 1960 made a significant boost in patenting. A study by Moon et al. [45] describes that educational institutes are vital sources of innovation. Pertouz et al. [46] show a positive effect of educating top management on the number of patent applications.

With regards to cognitive skills, Knudsen et al. [47] and Cunha and Heckman [38] noted that the critical skills and knowledge that contribute to the accumulation of cognitive capital emerge early in learning and develop later in learning. Low performance at the secondary level could hinder the critical skills and knowledge required for success in higher education. Thus, high scores in secondary education indicate that the student can have a better competency to innovate in the future [48].

In recent decades, interest in innovativeness and creativity in education has grown exponentially [[49], [50], [51]]. Recently, Wangid et al. [52], show that high performance in math and science increases the student's thinking abilities and ability to solve complex problems for elementary school students.

2.2. Education and economic growth

Education is generally recognized as a key means of building human capital and is important for both individual and economic prosperity in general. Some of the basic research on the relationship between education and economic growth is the work of Schultz [53], Becker [3], and Mincer [4], in which education is essential for increasing income and productivity. Barro [54,55] also showed that education significantly affects economic growth in different countries. Barro confirmed a strong link between education and economic efficiency. This theory is also proven by Psacharopoulos and Patrinos [56].

However, it should be added that there is research on the relationship between economic growth and the level of education in certain countries. Agiomirgianakis et al. [57] investigated the links between human capital as measured by different levels of education and economic growth in Greece. He showed a clear relationship between primary and secondary education and economic efficiency gains and an inverse relationship of causal relationships - this is an exploratory relationship for higher education. A study of the relationship between economic growth and education in China in 1978–2004 by Kui [58] found that the improvement in economic performance comes at the expense of primary education. This is a key reason for further increase in the level of education. For example, Afzal et al. [59] studied this topic at all levels of education. The result showed that investment in education is vital to achieving higher economic performance. In addition, education can reduce poverty and improve the overall socioeconomic condition of society. A study by Delalibera and Ferreira [60] on the evolution of the human capital of American workers between 1961 and 2008 highlights that early childhood development is critical to productivity and formal education. Ogundari and Awokuse [61] looked at the relationship between education and economic performance. The result showed that the coefficients calculated for the participation rates in primary and secondary schools and the average duration of this process, used as education indicators, have a favourable and figuratively meaningful effect on improving economic performance.

In the literature, there is evidence that education contributes to economic growth as an indicator of human capital accumulation [1,62,63]. For example, Mankiw et al. [64] use the concept of Solow growth model and added human capital that is measured by education. Hanushek & Woessmann [65] identify three mechanisms by which education can influence economic growth: human capital leads to an increase in labour productivity and a higher equilibrium level of output; education reflects the possibility of increasing innovative potential through; education disseminates and transfer the knowledge needed to understand and process new information, as well as to successfully implement new technologies developed by others, which again promotes economic growth (see, for example, [[66], [67], [68]]. The claim that education is one of the key determinants of economic growth has led many economists to investigate whether such a correlation exists (see, for example, [8,[69], [70], [71]]. There are also studies on the relationship between education and economic growth. One of the first such studies is [72], who linked the cognitive skills score obtained from international student achievement tests before 1991 - the PISA score - with economic growth in 1960–1990. The sample included 31 countries with available data. Their study showed a link between economic growth and cognitive skills. Their general outcome framework has been replicated by a series of other studies using different tests and specifications and various measures of skill (see, [55,[73], [74], [75]]. Overall, the results confirm that the quality of education, as measured by cognitive skills tests, correlates with economic growth and matters more than just the number of school hours [76].

A key question for educators and policymakers is whether secondary education is valuable for innovation and economic growth. As we mentioned earlier, obtaining a quality education is fundamental to developing cognitive skills. Ultimately, it provides the intellectual capital for the prosperity of innovative industries and economic growth in general. The peculiarity of this study is that it includes the latest available data for analysis from 2012 to 2018. The sample consists of 78 countries, allowing one to study countries with developing and transition economies.

A crucial question for educators and politicians is whether the quality of education is valuable for innovation and economic growth. As we mentioned earlier, obtaining a high-quality secondary education is fundamental to the development of cognitive skills and, ultimately, provides intellectual capital for the prosperity of innovative industries in the country and economic growth in general.

Although the studies cited above provide enough evidence of the positive relationship between education, innovation and income growth. However, the empirical literature is silent about the impact of educational quality (measured by assessment in key subjects) on innovation and GDP per capita. Furthermore, available research does not yield which particular subject has a greater impact on these. Therefore, the current study will try to fill this gap by offering both a conceptual framework and empirical setup by using an econometric model.

2.3. Conceptual model of education, innovation and growth

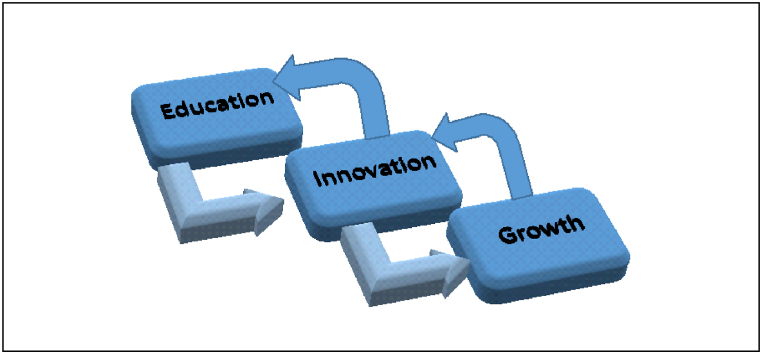
Based on the literature cited in Section 2, we try to build a conceptual model in Fig. 1 that shows a nexus between education, innovation and growth. Previous literature already supported a positive influence of innovation on economic growth and education on growth [1,2,4,25,[77], [78], [79], [80]]. However, very few studies have discussed the role of educational assessment, particularly math, science and readings, on innovation and growth. According to Fig. 1, quality of secondary education is the basis of both innovation and economic growth because of its direct and indirect (spillover) effects on the economy [[81], [82], [83]]. There is a bidirectional link between these three variables. For instance, initial direction goes from education to innovation and then to growth. The feedback effect goes from growth to innovation and education. According to Fig. 1, curved-down arrows show the effect of education on innovation and growth. Furthermore, it is also possible that if country's growth performance is high then innovation and educational quality will also be high. This effect is shown by using curved-up arrows from bottom to up.

Fig. 1.

Conceptual model of education-innovation-growth.

To measure the quality of secondary education, we use scores in three core subjects: science; math and reading. As cited above, knowledge in science is a key to improving scientific knowledge, improvement in innovation and ultimately affecting growth. For instance, Pradhan et al. [83], show a causal relationship between innovation and growth. Similarly, without mathematical knowledge, one cannot understand the complexity of scientific knowledge and technological advancements. Therefore, all three aspects of educational scores (science, math and readings) are important factors to boost innovation and hence growth. Our empirical part of the paper will analyse the quantitative measure of education on innovation and growth in Section 4.

3. Data and methodology

3.1. Data

Our data comes from three sources: 1) world development indicators from World Bank, 2) Programme for International Student Assessment (PISA) from OECD and 3) Knowledge and Technology output from Global Innovation Index (GII). Similarly, we have three main variables for our empirical analysis: quality of education, innovation and growth. The definition of each variable is as follows:

3.1.1. Educational quality

Student assessment scores are measured as the quality of education and the data is taken from PISA-OECD. The data on PISA scores is unbalanced, which consists of three different periods: 2012, 2015 and 2018. The cross-sectional units (countries) in each year are different but data is most reliable. In recent years, many countries have been focusing on PISA results because good PISA results are a major factor in improving the quality of the workforce and, ultimately, the country's overall economic performance, including innovation [48,75]. It is important to note that PISA scores are a useful standardized approximation of the quality of secondary education in a particular country. To assess the quality of education at the secondary level, the results of score values of the PISA assessment were used. This is a comparative assessment of mathematical, reading and science literacy. Tests were conducted for 15-year-old students. The results do not show the level of academic knowledge, but the level of functional literacy, that is, how much students can put their knowledge into practice, think logically, draw informed conclusions, interpret informational graphs and charts. PISA measures global competence and assesses student knowledge and skills. The survey is not only limited to the knowledge that can be derived from school curricula, but it also helps to determine the knowledge and skills necessary for successful adaptation in the modern world. The international scale has the following characteristics: the average value is 500 points; the standard deviation is 100. This means that about 2/3 of the students from the participating countries have results ranging from 400 to 600 points. We used the PISA scores from the available dataset of 2012, 2015 and the most recent of 2018. Specifically, we use students' assessment scores for 3 core subjects namely mathematics, science and reading.

The study included selected countries for which data were available for two other indicators: Knowledge and Technology Output and GDP per Capita. Data in the 2012 survey were collected from 35 participating countries, 2015–35, 2018–73. Therefore, the 35 countries in 2012 and 2015 are the same and in 2018 the number of countries grew to 73.

3.1.2. Innovation

Innovation is operationalized through innovative results in the form of new knowledge and technologies. To this end, we use Index Technology and Innovation output of the GII system [84,85], where the result of innovations is clearly defined: the amount of knowledge and technology output includes indicators such as scientific and technical articles, Researchers, patent applications, ISO 9001 quality certificates, and ICT. The GII model contains detailed data on innovation activity of 126 countries and territories of the world that constitutes 90.8% of the population worldwide and 96.3% of the world's GDP (bn PPP $). All the above-mentioned variables, traditionally considered the cornerstones of innovations, are covered by the results of knowledge and technology. The first sub-pillar is associated with the creation of knowledge which includes five indicators that are the result of inventive and innovative activities. These include patent applications filed by residents both at the national patent office and internationally through the PCT; utility model applications filed by residents at the national office; scientific and technical articles published in peer-reviewed journals; and number of articles (H-index) that have received at least 1 citation.

The second sub-pillar focuses on the impact of knowledge, contains statistics that emphasize the impact of innovation at the micro and macroeconomic levels or related factors: increased productivity, density of new companies, expenses on computer software, the number of issued certificates of compliance with ISO 9001 quality management systems and the measure of industrial production of high and medium technologies in the total volume of production.

The third sub-pillar considers the dissemination of knowledge which is a reflective image of knowledge. This subclause includes four statistics that are closely related to the high-tech content sectors or are key to innovation: intellectual property revenues as a percentage of total trade; net exports of high-tech goods as a percentage of total exports; export of ICT services as a percentage of total trade; and net outward FDI as a percentage of GDP (average for three years).

Economic growth is operationalized by per capita economic growth (PEG) derived from world development indicators (WDI) published by the World Bank. All variables are taken for recent available data from 2018 considering 73 overlapping countries. The list of countries, variables definition, summary statistics and data sources are reported in Appendix Tables A1 and A2.

3.2. Method and empirics

The technique and empirical findings are based on widely recognized endogenous growth theory, which asserts that human capital, as measured by knowledge and education, is an important component of economic development and growth [1,2]. The empirical link between education and earnings (growth) originates from Mincer [4]. Therefore, following their approaches, we divide our methodology into two types of analysis: 1) preliminary analysis, 2) Regression Analysis. Where preliminary analysis is based on a scatter plot of actual data, their correlation and Sobel test. On the other hand, regression analysis is based on econometric models. We used two methods of estimation: Pooled OLS and Panel regression using Fixed Effect (FE) method (for detail, see Refs. [2,55].

In our empirical analysis, we tried to analyse the impact of secondary education scores (Mathematics, Reading, Science) on innovation (knowledge and technology output). In this regard, we try to estimate the following equation (1) for our empirical analysis.

$$Innovation=f\left(PISAscores,growth\right)$$

$$Innovation=\alpha +{\beta }_1{readings}_1+{\beta }_2{Mathematics}_2+{\beta }_3{Science}_3+{\beta }_4{lnGDP}_{PC}+U$$ (1)

Where innovation is the dependent variable, PISA scores from Mathematics, Reading, Science are independent variable, lnGDP is the control variable and U is a random error term. And ${\beta }_1$, ${\beta }_2$, ${\beta }_3$, ${\beta }_4$ are parameters that need to be estimated. We can expect a positive sign for each parameter.

Similarly, we were also interested to see the impact of secondary education on GDP per capita. For that purpose, we try to estimate the following equation (2).

$${lnGDP}_{PC}=\alpha +{\beta }_1{Readings}_1+{\beta }_2{Mathematics}_2+{\beta }_3{XScience}_3+U$$ (2)

Where ${lnGDP}_{PC}$ (natural log of GDP is per capita) is used as a dependent variable and independent variables are the same as we used in equation (1). The empirical results are reported in the next Section 4.

4. Results

This section explains the results based on two approaches we used. First preliminary analysis results and second regression results.

4.1. Preliminary analysis

Table 1 reports the results correlation matrix for each variable. The correlation between innovation (R&D) and PISA scores from all 3 subjects (reading, math, science) is very high. Similarly, the correlation between GDP per capita and PISA scores for all subjects is positive and strong. This confirms that scores in readings, math and science positivity contribute to innovation and GDP per capita growth.

Table 1.

Correlation matrix.

	R&D	GDP_pc	Reading score	Math score	Science score	Average_score
R&D	1
GDP_pc	0.5955	1
Reading score	0.6267	0.5184	1
Math score	0.6434	0.5114	0.9388	1
Science score	0.6094	0.4825	0.9728	0.9624	1
Average_score	0.6357	0.5114	0.984	0.9814	0.9923	1

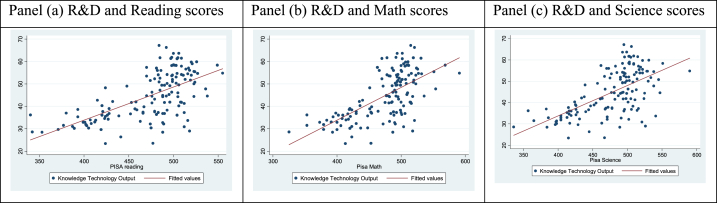
Fig. 2, Fig. 3 report the scatter plots of core variables. For instance, in Fig. 2 panel (a)–(c) represents the scatter plot between innovation and readings, innovation and math and innovation and science scores respectively. A linear fit for scatter plot is also presented, which shows a positive relationship between innovation and PISA scores (math, reading and science). Similarly, Fig. 3 (consists of 3 panels: a, b and c) shows the scatter plot between GDP and PISA scores for 3 subjects (reading, math, science), which also presents a significant relationship.

Fig. 2.

Scatter plot between Innovation and PISA cores in readings, math and science.

Fig. 3.

Scatter plot between GDP per capita and PISA cores in readings, math and science.

4.2. Regression results

To test our first hypothesis (H1: quality of secondary education positively affects innovation activity), we estimate equation (1) as shown in equation (1) in Section 3. Table 2 reports the results from 8 different specifications of equation (1) as shown in columns (1–8). Where columns 1–4 are based on pooled OLS estimation and Columns 5 to 8 are based on the Panel model by using Maximum likelihood estimation (MLE) techniques.

Table 2.

Impact of educational assessment on Innovation.

	Pooled OLS				Panel (MLE)
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
PISA reading	0.312***				0.311***
	(3.89)				(3.93)
PISA Math		0.352***				0.353***
		(4.61)				(4.66)
PISA Science			0.301***				0.302***
			(3.94)				(3.98)
PISA_average				0.334***				0.333***
				(4.27)				(4.31)
GDP per Capita	0.465***	0.447***	0.485***	0.455***	0.465***	0.447***	0.485***	0.455***
	(5.80)	(5.85)	(6.34)	(5.81)	(5.86)	(5.91)	(6.41)	(5.87)
N	143	143	143	143	143	143	143	143
R-sq	0.510	0.529	0.512	0.520
Wald statistics					Chi2(3) = 25.81 [0.0000]	Chi2(1) = 22.24 [0.0000]	Chi2(3) = 25.81 [0.0000]	Chi2(1) = 22.24 [0.0000]

Note: t statistics are in parentheses, standardized beta coefficients are reported after using robust standard error.

*, **, *** - significance of coefficients at 10%, 5%, and 1% levels, respectively.

To avoid multicollinearity between educational assessment scores (reading, math, science), we regress individual scores on innovation. We report standardized beta coefficients in the tables, which are easy to compare in size. Based on columns 1 to 4, all estimates are positive and significant; however, the size of the estimate of math (PISA math) is 0.353 which is greater than the reading and science scores. The effect of GDP per capita is also positive and significant on innovation. These results suggest that mathematic competencies are crucial for innovation performance. These findings are consistent with previous studies [8,45,46,86]. The impact of overall score (PISA average) is also positive and significant. It confirms that compare to individual subject scores, the overall average scores in these subjects positively affect innovation. These results also suggest that all three subjects are crucial to promoting innovation activities.

Columns 5 to 8 are based on Panel model by using MLE method that takes care of observable heterogeneity across countries, therefore, is considered a better estimation procedure. The effect of the mathematic score is again positive, greater than reading and science scores and consistent with OLS estimates. Similarly, the effect of average PISA score is highly significant with a positive sign.

Both estimation procedure confirms that all three subjects are crucial to enhance innovation performance; however, the effect of mathematic knowledge is more important than the others alone. These findings are robust across two different estimation techniques (OLS and Panel MLE).

To test our second hypothesis (H2: quality of secondary education increases GDP Per capita), we estimate equation (2) as shown in Section 3. The results are reported in Table 3, where the dependent variable is the natural log of GDP per capita.

Table 3.

Impact of educational assessment on GDP per capita.

	Pooled OLS				Panel (MLE)
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
PISA reading	0.602***				0.308***
	(10.87)				(3.68)
PISA Math		0.651***				0.418***
		(8.51)				(5.43)
PISA Science			0.614***				0.284***
			(8.53)				(3.47)
PISA_average				0.663***				0.381***
				(9.27)				(4.71)
N	143	143	143	143	143	143	143	143
R-sq	0.457	0.424	0.403	0.440
Wald statistics					Chi2(3) = 25.81 [0.0000]	Chi2(1) = 22.24 [0.0000]	Chi2(3) = 25.81 [0.0000]	Chi2(1) = 22.24 [0.0000]

Note: t statistics are in parentheses, standardized beta coefficients are reported after using robust standard error.

*, **, *** - significance of coefficients at 10%, 5%, and 1% levels, respectively.

Similar to Table 2, columns 1–4 are based on pooled OLS estimation and Columns 5 to 8 are based on Panel model by using Maximum likelihood estimation (MLE) techniques that take care of observable heterogeneity across countries, therefore, considered a better estimation procedure. Based on columns 1 to 4, all estimates are positive and significant; however, the size of the estimate of math (PISA math) is 0.651 which is greater than reading and science scores. These results again confirm the importance of math for innovation and are consistent with the literature (see, Sharif, 2019; Moon et al., 2019; Pertuze et al., 2019, Reyes, 2018). The results based on Panel (MLE) in Columns 5–8, show positive and significant effects of all educational assessments on GDP per capita. The effect of mathematics scores is again greater than reading and science scores. Both estimation techniques show that all three subjects are essential for improving innovation performance, but math knowledge has a greater impact than other subjects do.

4.3. Robustness check

We estimate our core models using the Mundlak procedure as a robustness check and to address the potential endogeneity issue between innovation, educational assessment scores, and GDP per capita (see, [87]. The Mundlak model calculates random-effects regression models by incorporating group-means of variables in independent variables that vary across groups. Mundlak [87] proposed the procedure as a way to relax the random-effects estimator's assumption that the observed variables are uncorrelated with the unobserved variables. Therefore, using this technique provides an alternative method for dealing with the potential endogeneity problem for our core variables. The results are reported in Table 4. Columns 1 to 4 report the effect of different educational assessment scores in reading, math, science and average on innovation while the effect same variables on GDP per capita are reported in columns 5–8. The over results are robust with those reported in Table 2, Table 3 The scores in mathematics (PISA math) consistently have a greater impact on both innovation and GDP per capita which again confirms the importance of mathematics. To summarize, our core results appear to be robust to different estimation techniques that account for endogeneity.

Table 4.

Robustness check for the effect of educational assessment on Innovation and GDPpc.

	Innovation				GDP per capita
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
PISA reading	0.074***				0.005***
	(3.89)				(4.59)
PISA Math		0.080***				0.007***
		(4.61)				(5.70)
PISA Science			0.070***				0.005***
			(3.87)				(4.22)
PISA_average				0.078***				0.006***
				(4.27)				(5.18)
GDP per Capita	5.877***	5.642***	0.485***	5.743***
	(5.80)	(5.86)	(6.34)	(5.81)
N	143	143	143	143	143	143	143	143
R-sq	0.51	0.53	0.51	0.512	0.456	0.424	0.403	0.441
group	78	78	78	78	78	78	78	78

Note: t statistics are in parentheses, standardized beta coefficients are reported after using robust standard error.

*, **, *** - significance of coefficients at 10%, 5%, and 1% levels, respectively.

5. Conclusion and policy recommendation

The main purpose of this paper was to analyse the impact of secondary educational assessment scores (educational quality (measured by assessment) on innovation and GDP per capita. For that purpose, we utilize both qualitative and quantitative approaches to investigate the impact of education quality on innovation and GDP per capita. Concerning qualitative analysis, we try to build a conceptual model that is based on theoretical and empirical literature. The conceptual model shows a strong link between the quality of secondary education, innovation and per capita growth.

With regard to the quantitative approach, we use secondary data consists of 78 countries over the period 2012–2018, and empirically investigate the impact of secondary education on innovation and GDP per capita. Particularly, we try to test two hypothesis: H1) quality of secondary education positively affect innovation activity, H2) quality of secondary education increase GDP Per capita. Both hypotheses (H1 and H2) are accepted in our empirical part and support the followings:

First, concerning H1, the effect of math score is positively affecting innovation performance. Individual scores in science and reading also have a significant impact on innovation but the size of the effect is smaller than the effect of math on innovation. However, average scores from all three subjects (math, reading and science) do have a positive impact on innovation. It means all three subjects are crucial to enhance innovation performance but the effect of mathematics is more important than science and reading scores. Second, related to H2, it is accepted that average scores in three subjects have positive and significant effects on GDP per capita. Similar to H1, the effect of mathematics is greater than the effect of reading and science on GDP per capita. Based on these results, it is confirmed that the quality of secondary education measured by mathematical scores is highly relevant for both innovation performance and income level (GDP per capita). In our robustness section, we use the Mundlak procedure to deal with the potential endogeneity issue. Our main findings seem to be robust to other technique that takes care of endogeneity.

The study's findings provide obvious suggestions for policies to raise income levels and innovative activities by enhancing educational quality. For instance, it is undoubtedly crucial to improve education overall, with a focus on mathematics, as this will help students develop their innovative skills while also improving their ability to solve complex problems on their own. Therefore, the focus of authority should be on offering math-related training and courses to teachers working in primary schools. Additionally, enhancing the standard of education with a math emphasis encourages innovation in the nation and raises GDP per capita, a measure of standard of living.

Despite the aforementioned findings, this study includes future research directions. For example, further research could be expanded by categorizing countries based on their level of development and innovation performance and then analysing which subjects are most important to their innovation and growth performance. Furthermore, while the current study focuses on primary education, the analysis can be expanded by focusing on assessments from higher secondary or college education. The limitation of this study is that we do not currently have a complete data set for a larger sample. Future studies along these lines, once the relevant data is available, can help improve the results and their implications.

Author contribution statement

Amjad Naveed: Conceived and designed the experiments; Performed the experiments; Wrote the paper.

Aziza Zhuparova: Collected the data; Performed the experiments; Analyzed and interpreted the data.

Muhammad Ashfaq: Collected the data; Performed the experiments; Analyzed and interpreted the data.

Abdul Rauf: Analyzed and interpreted the data; wrote the paper.

5.1. Data availability statement

Data will be made available on request.

Additional information

No additional information is available for this paper.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

Table A1.

List of countries in the sample

Albania	Germany	Panama
Argentina	Greece	Peru
Australia	Hong Kong, China	Philippines
Austria	Hungary	Poland
Azerbaijan	Iceland	Portugal
Belarus	Indonesia	Qatar
Belgium	Ireland	Romania
Bosnia and Herzegovina	Israel	Russia
Brazil	Italy	Saudi Arabia
Brunei	Japan	Serbia
Bulgaria	Jordan	Singapore
Canada	Kazakhstan	Slovak Republic
Chile	Korea, Republic of	Slovakia
China	Latvia	Slovenia
Colombia	Lebanon	South Korea
Costa Rica	Lithuania	Spain
Croatia	Luxembourg	Sweden
Cyprus	Malaysia	Switzerland
Czech Republic	Malta	Thailand
Czechia	Mexico	Turkey
Denmark	Moldova	Ukraine
Dominican Republic	Montenegro	United Arab Emirates
Estonia	Netherlands	United Kingdom
Finland	New Zealand	United States
France	North Macedonia	Uruguay
Georgia	Norway	Switzerland

Table A2.

Summary Statistics of variables used in Regression

Variable	definition	source	Obs	Mean	Std. Dev.	Min	Max
innovation	Knowledge and technology output	OECD and INSEAD Cornell; World Intellectual Property Organization	143	44.76783	10.57402	23.4	67.2
PISA reading	PISA Score in Reading	OECD	143	473.8112	44.83035	340	555
PISA math	PISA Score in Mathematics	OECD	143	474.9371	46.64055	325	591
PISA science	PISA Score in Science	OECD	143	477.1678	45.17306	336	590
lgdppc	GDP per Capita	WorldBank Data	143	10.12267	0.837426	8.156247	11.65

Data consist of 73 countries for three different periods: 2012, 2015 and 2018.