Abstract
We evaluate neural network (NN) coarse-grained (CG) force fields compared to traditional CG molecular mechanics force fields. We conclude that NN force fields are able to extrapolate and sample from unseen regions of the free energy surface when trained with limited data. Our results come from 88 NN force fields trained on different combinations of clustered free energy surfaces from four protein mapped trajectories. We used a statistical measure named total variation similarity to assess the agreement between reference free energy surfaces from mapped atomistic simulations and CG simulations from trained NN force fields. Our conclusions support the hypothesis that NN CG force fields trained with samples from one region of the proteins’ free energy surface can, indeed, extrapolate to unseen regions. Additionally, the force matching error was found to only be weakly correlated with a force field’s ability to reconstruct the correct free energy surface.
I. INTRODUCTION
Coarse-grained (CG) molecular dynamics (MD) is a tool to complement experiments.1,2 A CG model can be considered a “reduced model” as not all degrees of freedom are considered explicitly. The objective is to eliminate irrelevant atomic details to gain computational advantages.3 According to Noid,4 CG models provide a foundation for most scientific efforts by focusing on “essential” features of a system. CG MD enables the sampling of thermodynamic systems at larger spatial and temporal scales, which are inaccessible at the all-atom resolution. As a result, CG MD is often used to study phenomena such as protein folding and multi-protein structure assemblies.5,6 CG modeling is implicitly based on the separation of timescales between molecular motions. Therefore, this provides a practical alternative to uncover the underlying Hamiltonian of the reduced models at these length scales.7 Works by Kidder, Szukalo, and Noid,8 Jin et al.,9 Noid,10 Saunders and Voth,11 and Brini et al.12 provide fundamental perspectives on CG modeling.
A CG model consists of two main components: (1) CG representation (mapping) and (2) CG force field (FF). The first is a projection of the all-atom system into a reduced, “coarser” representation. A CG site can be identified as a pseudo-atom and should ideally encapsulate the average physicochemical characteristics of a given group of atoms.4,13 More discussions on selecting a suitable CG representation and their impact can be found in Refs. 2, 3, and 13–17. Next, a CG FF is a potential energy function that approximates the interactions between these pseudo-CG atoms. Ideally, a CG FF should capture eliminated atomistic-level details.4,18 A CG FF must be able to compute any equilibrium property that is expressed as an ensemble average of the CG coordinates.19 For this reason, a CG FF can be thought of as a potential of mean force (PMF).3,4,20 Foley, Shell, and Noid3 highlighted that a CG PMF is a configuration-dependent free energy function, which should ideally preserve structural and thermodynamic properties at the lower resolution. Finding a fitting approximation of this PMF is one of the key challenges associated with CG modeling. Furthermore, since a CG model averages over atomistic configurations, CG models are less transferable to different thermodynamic state points.4,10,11,21 Thermodynamic inconsistency between atomistic and CG resolutions, parameterization of the CG FFs, and the choice of CG representation are a few factors that contribute to the limited transferability in CG modeling. According to Noid,10 these fundamental challenges arise due to the lack of understanding of the relationship between atomistic and CG models.
Traditionally, two common approaches are used in developing CG FFs: (1) bottom-up approaches2,22 and (2) top-down approaches.11 A bottom-up approach relies on information from fine-grained (atomistic) models to approximate the PMFs, while a top-down approach aims to reproduce macroscopic properties.3,4,23 However, the objective of both these approaches is that a CG model must reflect the “correct physics” of the atomistic system.4 However, parameterizing a CG FF to approximate the behavior of an atomistic system is often a tedious and iterative task.
With the recent advances of deep learning, researchers have begun to focus on utilizing neural networks (NNs) in CG modeling. Work in Ref. 13 is an example that demonstrates CG mapping generation can be automated by training a graph neural network (GNN) based on human knowledge. Additionally, NNs are being used as atomistic MD FFs24–27 and CG FFs to study biomolecular systems.20,28–31 The main assumption behind CG FF development is that CG FFs can extrapolate to unseen regimes of the configurational space when parameterized/trained with limited data. However, little to no studies have investigated if this assumption is valid for NN CG FFs when compared to physics-informed traditional CG FFs. To address this research gap, we aim to evaluate the extrapolating capability of NNs as CG FFs.
Often, a NN CG FF is trained by minimizing the force matching error [shown in Eq. (1)]. This refers to the squared error between mapped forces (atomistic forces mapped to CG atoms) and CG forces, which are computed from the predicted CG coordinates,32,33
| (1) |
Here, M is the mapping matrix that scales N atomistic coordinates into n CG coordinates. represents the gradient of the learned free energy function (effective CG forces), where m are the CG variables. Instantaneous CG forces mapped from the all-atom trajectory are represented by the last term in Eq. (1). Note that, although NNs have shown to be promising as molecular FFs,34–36 their training is highly dependent on the availability of useful data.33,37 Generally, the applicability of NNs raises an open question of “how well can these NN FFs extrapolate beyond training data.” Another important challenge using NNs as CG potential is the lack of interpretability when compared with traditional FFs that are parameterized on empirical data. Therefore, Zeni et al.37 explained that it is not trivial whether NN potentials are able to exploit the extrapolation regime, specifically when the atomistic potential energy surface (PES) is smoothened by CG representations.
In this work, we aim to investigate the extrapolating capabilities of NN CG potentials and the impact of the amount of data used in training. We aim to discuss whether NNs are, indeed, apt to be used in the place of traditional, physics-informed models. Finally, we question if force matching by itself is adequate to benchmark the performance of trained CG FFs. To study these research questions, we selected four (mini)proteins based on structural properties:38 (1) a folded protein: P-element somatic inhibitor miniprotein (PDB ID:2BN6),39 (2) a half-folded protein: Miniature Esterase (PDB ID: 1V1D),40 (3) a small fast-folding protein near its melting point: Trp-cage (PDB ID: 2JOF),41 and (4) a disordered protein: β-amyloid peptide residues 10–35 (PDB ID: 1HZ3).42
First, we conducted atomistic simulations for these miniproteins with GROMACS software and mapped the trajectories to generate reference CG trajectories. These mapped protein trajectories were next projected onto a low-dimensional free energy space (FES) with time-structure independent component (IC) analysis.43–45 Next, the FES was clustered using a Markov State Model (MSM) based approach to identify four states (conformations). Various subsamples from these states were selected systematically to train NN CG FFs CGSchNet20,29 and TorchMD-Net.36 We trained 88 NN FFs in total (11 CGSchNet FFs and 11 TorchMD-Net FFs for each of the four proteins). Finally, we proceeded to produce CG simulations from each FF and to evaluate the performances of the trained FFs. We used a metric named total variation similarity46,47 (TVS) given in Eq. (2) to compare the similarity between the mapped and CG FES,
| (2) |
| (3) |
| (4) |
The term in Eq. (2) measures the maximum possible distance between the mapped and CG FES over the measurable space Ω. ϕ is the maximizer in Eq. (2) that represents the mapped space. ζ given in Eq. (3) is a penalty term that accounts for the probability of the CG trajectory explored beyond the regions of the mapped trajectory. As shown in Eq. (4), π defines the total explored space by the CG trajectory. We use the TVS metric to evaluate the performance of CG FFs because it is a system-agnostic metric. Therefore, TVS can be used to compare different CG models with dissimilar FFs and CG representations.
II. METHODS
A. Simulation methods
1. All-atom simulations
For each protein, all-atom MD simulations were conducted with the AMBER99SB*-ILDN force field48,49 and TIP3P water model50 with neutralizing potassium ions added. All simulations were performed in GROMACS 2020.4.51 Minimization and equilibration were performed according to a standard protocol,52 which involves up to 50 000 steps of steepest descent minimization, followed by 100 ps of NVT equilibration with backbone atoms restrained. For each protein, 15 µs long NPT simulations were produced at T = 300 K for 2BN6, T = 290 K for 1V1D, T = 350 K for 2JOF, and T = 310 K for 1HZ3. These temperatures were selected empirically to ensure that simulation temperature is below the melting point of each protein except for 2JOF.40,42,53,54 For 2JOF, we selected a slightly higher temperature to sample from both folded and non-folded states. Production simulations used a 2 fs time step, a 1 nm cutoff for electrostatics, the v-rescale thermostat55 with a 0.1 ps time constant, and a Parrinello–Rahman barostat56 using a 2 ps time constant. From these production runs, training data frames were generated by restarting from fixed points along these trajectories using the same MD parameters, but with velocities resampled for each run. Starting points for restart trajectories were checkpoint files separated every 50 ns starting after 2.5 μs. From these 250 checkpoint files, four 10 ns simulations were performed, where positions and forces were saved in double precision every 20 ps. Each frame was then treated for periodic boundary conditions to make the molecules whole GROMACS.
To map atomistic trajectories to the CG representations, MDAnalysis software57,58 and “fast_forward” software tools59 were used. The latter is a specific CG mapping tool designed for MARTINI modeling. MDAnalysis software was used for mapping the trajectories for other CG models found in this study. α-carbon CG representation was used for NN-based CG modeling. For MARTINI and OpenAWSEM, their respective mapping schemes were used.60–63
2. CG simulations
We selected two NN CG FFs: CGSchNet29 and TorchMD-Net.36 After training CGSchNet and TorchMD-Net models, each FF was used to conduct NVT CG simulations with Langevin dynamics at the same temperatures as the all-atom simulations (300, 290, 350, and 310 K). A time step of 2 fs was used for all FFs. For all NN CG simulations, each protein residue was represented by their α-carbons (one-bead mapping). Each CG trajectory was initiated from a centroid configuration randomly selected from the testing states/clusters. For example, if a NN was trained from frames with clusters labeled as 1–3, then the starting configuration was from cluster 4. We used this approach to avoid the impact of the starting configuration during the CG production. With CGSchNet FFs, we were only able to run 50 independent trajectories in the range 0.02–0.2 ns. Most simulations were not stable beyond 0.2 ns. In contrast, with TorchMD-Net, we were able to generate 2 ns long CG trajectories with ten replicas. See the supplementary material for further details. To perform NVT CG simulations with the MARTINI FF, we employed Gō-like models in combination with the MARTINI3 model64 following the standard protocol.65 Each MARTINI3 simulation was run for 10 ns with a time step of 20 fs using GROMACS software at constant temperatures as all-atom simulations. Explicit water was used to solvate the protein system; see the supplementary material for further details. For CG simulations with the OpenAWSEM FF, we used Langevin dynamics at constant temperatures (similar to the previous simulations). Each CG simulation was run for 1 ns with a time step of 2 fs. Again, the standard simulation protocol was followed.66 The CG mappings used in MARTINI3 and OpenAWSEM analyses were the default mappings associated with MARTINI60 and AWSEM62 FFs. CG simulations for both these FFs were initiated from their crystal structure configurations. Simulations from MARTINI and OpenAWSEM FFs were stable and ran to completion. More details can be found in the supplementary material.
B. Clustering the configuration space
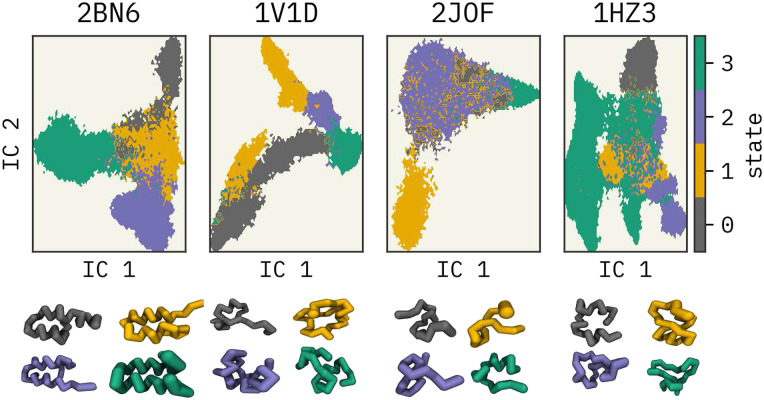
First, all-atom trajectories of 2BN6,39 1V1D,40 2JOF,41 and 1HZ342 miniproteins were mapped into a CG representation, where each residue was represented with its α-carbon atom. MDAnalysis57,58 software was used for the mapping. We used the same configuration mapping operator for force mapping as well. A reader may find more work on force mapping in Refs. 67 and 68. Then, each mapped trajectory was clustered into four states based on a Hidden-Markov State Model (HMSM)69,70 using the PyEMMA python library, as described in Refs. 71 and 72. See Fig. 1. These can be thought of as metastable states of the miniproteins. Finally, configurations (snapshots from the trajectory) from various subsets of the clustered states were used for training separate FFs. Note that the number of frames per cluster was not equal after the assignment.
FIG. 1.
Four clusters of the miniproteins in the low-dimensional space projected using the TICA method.43 P-element somatic inhibitor miniprotein (PDB ID:2BN639), Miniature Esterase (PDB ID: 1V1D40), Trp-Cage miniprotein (PDB ID:2JOF41), and β-amyloid peptide residues 10–35 (PDB ID: 1HZ342) were used in this study. The centroid configuration of each cluster is illustrated at the bottom with their respective colors.
As mentioned previously, protein FES was clustered into four states based on a Hidden-MSM. In general, MSMs are used for analyzing dynamic data from MD simulations.73,74 Four main steps are involved in building an MSM: (1) featurization, (2) dimensionality reduction, (3) clustering, and (4) estimation of the transition matrix.75 This workflow is illustrated in the supplementary material, Fig. S1. The use of MSM on approximating observables from MD simulations is extensively discussed in the literature.76–80
We selected the α-carbon pairwise distances to featurize the mapped trajectories in the dimensionality reduction task. Time-lagged independent component analysis (TICA)43–45,81 was used for this step. Next, these projected spaces were discretized using K-means82 clustering to estimate an initial Markov State Model (MSM). 50, 75, 75, and 200 cluster centers were used for 2BN6, 1V1D, 2JOF, and 1HZ3 miniproteins, respectively. These cluster numbers were selected based on the VAMP2 scores.83 These are the sums of singular values of the symmetrized MSM transition matrix; see the supplementary material. Respective lags of 100, 100, 100, and 10 were selected to build the MSMs. Lags were selected such that the implied timescales were constant with the statistical error (see the supplementary material). Furthermore, we validated the MSMs using Chapman–Kolmogorov tests (see the supplementary material).84,85 Finally, HMSMs were estimated based on the reference MSMs where each trajectory was clustered into four coarser groups where each frame of the trajectories was assigned to a cluster. Christoforou et al.86 described an HMSM as a “kinetic” coarse-graining model, which groups the microstates identified by the k-means clustering algorithm. We followed a similar approach as Christoforou et al.86 to cluster the projected configurational space. Figure 1 illustrates the four clusters of reduced-dimensional spaces along the first two independent components (IC1 and IC2) identified by TICA43 and their centroid configurations. Further details for this procedure are given in the supplementary material.
C. Training force fields and running CG simulations
In this study, we selected two NN CG FFs: CGSchNet29 and TorchMD-Net.36 CGSchNet29 is a modified version of the CGNet model,20 which learns the CG FES based on the force-matching approach. In the CGNet model, inputs are hand-selected features, such as bond distances, angles, and dihedral angles. However, in the CGSchNet model, the features are “learned” during training by leveraging the SchNet model.26,87 Additionally, TorchMD-Net36 provides state-of-the-art graph neural network (GNN) and equivariant transformer (ET) based NN potentials for molecular simulations. In this work, we used TorchMD-Net’s GNN model for training CG FFs since the performance from both models was similar. The main difference between CGSchNet and TorchMD-Net architectures arises from input featurization where the CGSchNet model uses SchNet features and the TorchMD-Net model embeds the atom types into a fixed embedding. Both architectures are built on the PyTorch88 model builder. A technically oriented reader may find further detail on the differences between the two models in their open source GitHub repositories: https://github.com/coarse-graining/cgnet and https://github.com/torchmd/torchmd. Note that we used TorchMD30 Python API for performing CG MD simulations using the TorchMD-Net trained FFs. The CGSchNet tool is equipped with its own Python scripts for performing simulations.
The key objective of this work is to investigate if NN CG FFs are able to extrapolate and sample from unseen regions of the reference FES. Therefore, during training, we subsampled different sets of identified clusters and trained multiple independent FFs per miniprotein (listed in Table I). For example, to train “FF1,” we used 75% of clusters, those labeled as 2–4—data from cluster 1 were withheld. Note that the labels were generated randomly. The number of frames for each cluster was kept constant through downsampling to match the minimum number of frames among the four states to avoid oversampling from one cluster. The total number of frames used during training was 123 456, 258 676, 63 364, and 204 332 for 2BN6, 1V1D, 2JOF, and 1HZ3 miniproteins, respectively. Hyperparameters used in training and train-validation error plots can be found in the supplementary material. Finally, the trained FFs were used to produce CG simulations (see Sec. II A). Note that, due to the smoothness of the underlying CG FES, a similar amount of sampling is obtained in these “ns” long simulations as compared to the original microseconds of training data.
TABLE I.
Cluster combinations used for training.
| Cluster percentage | 100% | 75% | 50% | 25% |
|---|---|---|---|---|
| FF label: Clusters used in training | FF0: 1,2,3,4 | FF1: 2,3,4 | FF5: 1,2 | FF7: 1 |
| FF2: 1,3,4 | FF8: 2 | |||
| FF3: 1,2,4 | FF6: 3,4 | FF9: 3 | ||
| FF4: 1,2,3 | FF10: 4 |
III. RESULTS AND DISCUSSION
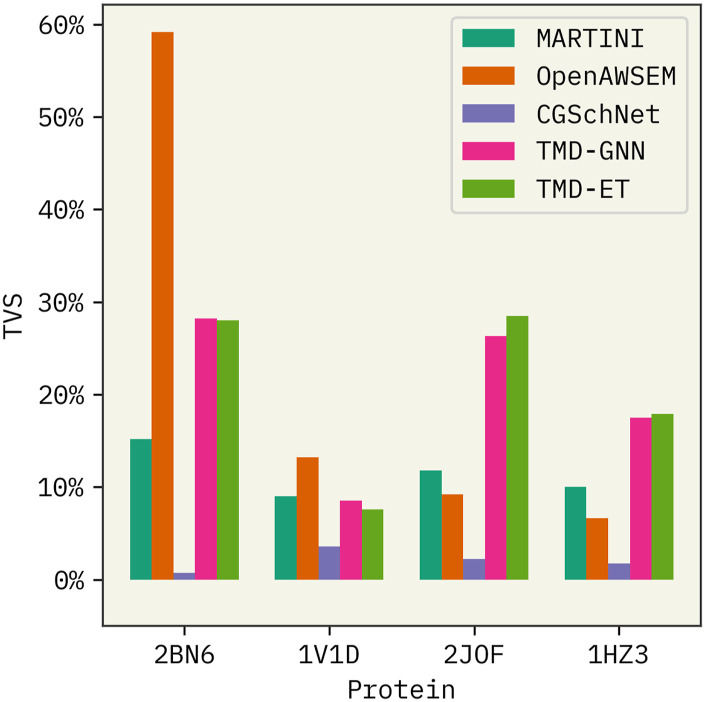
First, we compared the performances of FF0 from CGSchNet and TorchMD-Net (trained with data from all four clusters) with state-of-the-art physics-informed FFs MARTINI60,61 and OpenAWSEM.63 MARTINI is possibly the most popularly used FF for generating CG simulations89 of lipids,90,91 proteins,92,93 sugars,94 and other biomolecules.95,96 OpenAWSEM is the implementation of the AWSEM62 CG FF for proteins within the graphics processing unit (GPU)-compatible OpenMM framework. AWSEM contains physics-informed many-body effects and employs an implicit solvent environment.62 This FF has been successfully applied to study protein structure prediction.97–99
Based on the comparison illustrated in Fig. 2, we observe the following. (a) Performance of the OpenAWSEM FF decreases significantly with the increasing structural disorder of the miniproteins, whereas MARTINI3 is not affected. (b) CGSchNet has the lowest overall performance among all four FFs. (c) TorchMD-Net’s performance is comparable among all four proteins regardless of the structural disorder. (d) TorchMD-Net’s GNN and ET model demonstrate similar performances.
FIG. 2.
Comparison of CGSchNet and TorchMD-Net potentials with state-of-the-art methods MARTINI and OpenAWSEM. TMD-GNN and TMD-ET refer to the TorchMD-Net’s graph neural network and equivariant transformer models. Higher TVS refers to the high similarity between the mapped and CG free energy surfaces in the projected TICA spaces. 100% data were used to train the latter two FFs. PDB IDs of the four protein systems used are shown in the x axis.
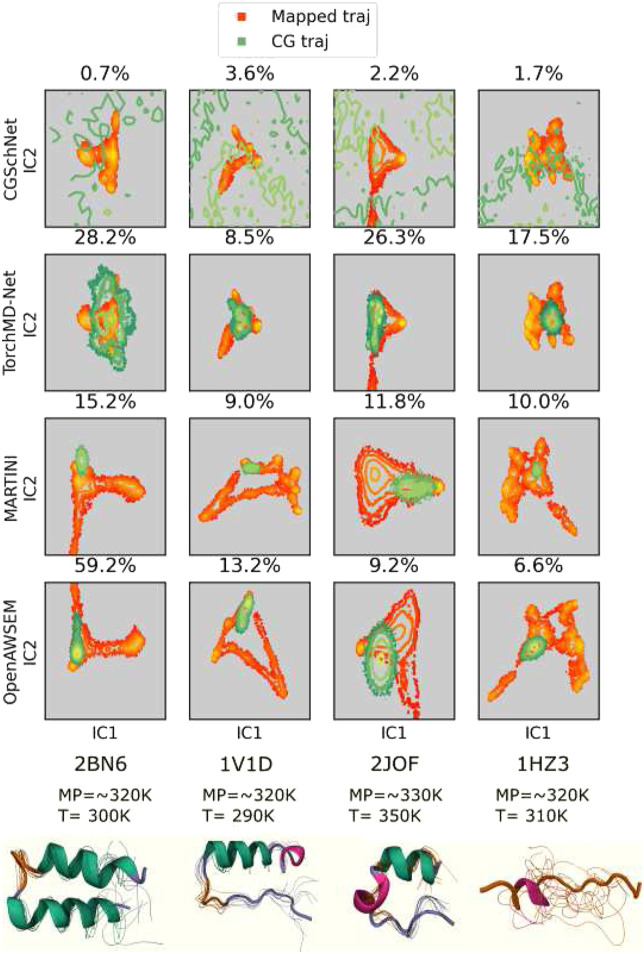
First, CG trajectories from all four FF0 force fields were projected onto the first two independent components (ICs) identified for the mapped trajectory with TICA. The similarity between the reference and CG FES was calculated with TVS;46,47 see Eq. (2). The configurational space explored by the protein is histogrammed in the two-dimensional projected space of TIC1 and TIC2 with a resolution of 100 bins in each direction. TVS values are computed over the area spanned by both atomistic and CG models. This metric evaluates the performance of the CG models with respect to the atomistic references. At the bottom of Fig. 3, the cartoon representations of the four miniproteins and 20 frames from the mapped trajectories are shown. The structural disorder of the proteins increases from left to right in Fig. 3 (1HZ3 has the highest disorder).38 Note that the reference FES of MARTINI and OpenAWSEM FFs is visually dissimilar to the reference FES from the two NN FFs due to differences in the CG representations. The FES (projected space) is a function of the CG representations. In CGSchNet and TorchMD-Net models, each amino acid residue was represented with their α-carbons, while in MARTINI and OpenAWSEM, their default mappings (four heavy atoms to 1 CG atom) were used.60,63 Additionally, in the supplementary material, Fig. 13, we provide a comparison of the four FFs, where MARTINI and OpenAWSEM trajectories were also mapped to a one-bead representation. The center-of-geometry of each residue was used for this task. While TVS can be used to quantitatively compare the FF performances with respect to the reference trajectories, S13 provides a better visual comparison.
FIG. 3.
Mapped and CG FES from FF0–FFs trained with all four states. Top: projected miniprotein mapped and CG trajectories from CGSchNet, TorchMD-Net, MARTINI, and OpenAWSEM FFs. Total variation similarity (TVS) between the mapped and CG FES is annotated as a percentage. Higher TVS indicates higher similarity. Bottom: cartoon representations of miniprotein reference trajectories annotated with approximate melting and simulation temperatures. P-element somatic inhibitor miniprotein (PDB ID:2BN6), Miniature Esterase (PDB ID: 1V1D), Trp-cage miniprotein (PDB ID:2JOF), and β-amyloid peptide residues 10–35 (PDB ID: 1HZ3) were used in this study. Conformational ensembles are 20 random frames after a weighted iterative alignment following the procedure of Ref. 100.
We observed that CG trajectories from CGSchNet FFs explore a broader region in their 2D FES beyond the reference trajectory, resulting in lower TVS scores. This observation can be interpreted as CGSchNet-FF0 having a tendency to explore physically non-meaningful regions. This could explain why CG simulations from CGSchNet FFs did not run to completion for all 44 simulations. Total trajectory times were between 0.02 and 0.2 ns, and none of the CG simulations were stable beyond 0.2 ns. Although we attempted to improve the performance of CGSchNet FFs with hyperparameter tuning, we were unsuccessful in our attempts. While we were able to minimize the “over extrapolation” by increasing the friction term in Langevin dynamics, the overall performance was not significantly improved. Wang et al.20 stated that a prior energy term was added to their GNN architecture to avoid sampling from physically non-meaningful regions. Therefore, we expect that by optimizing the prior term, CGSchNet may be improved. However, we did not attempt to alter the initial architecture, as this was beyond the scope of our work.
In comparison, we were able to produce longer, stable simulations for 2 ns each with TorchMD-Net. Note that 2 ns in CG coordinates are comparable to the microsecond length scale of the atomistic simulations. Furthermore, we observe in Fig. 3 that TorchMD-Net is able to explore the mapped trajectory while avoiding physically non-meaningful regions. This demonstrates NNs provide a promising playground for the development of CG FFs. With these observations, we conclude that TorchMD-Net outperforms CGSchNet and its performance is consistent across all four proteins with varying degrees of disorder. These observations raise the following question: “does the model architecture significantly impact the performance of an FF?” To answer this non-trivial question, we compared the performances of TorchMD-Net’s GNN and ET models. Based on the results in Fig. 2, we note that both GNN and ET models have almost identical TVS values. This suggests that the role of the model architecture does not play a significant role in the overall behavior. However, further investigations are needed to establish a profound conclusion. We did not pursue to answer this question, as the main aim of this work is to investigate if CG NN-FFs are able to extrapolate. Therefore, we conclude with hyperparameter tuning and architectural changes that the performance of the FFs can be improved.
Additionally, TorchMD-Net’s performance is comparable to MARTINI and OpenAWSEM FFs when trained with all available data. It can also be seen in Fig. 3 that CG trajectories from MARTINI and OpenAWSEM FFs tend to be localized around the starting configurations, unlike TorchMD simulations. We expect that this restricted sampling of MARTINI and OpenAWSEM FFs can be improved by increasing the CG simulation length. However, note that TorchMD-Net simulations can explore the reference FES more within the same timescale. Furthermore, OpenAWSEM is seemingly affected by the structural changes of the miniproteins, while the NN CG FFs are indifferent. This is a noteworthy observation as one of the main challenges in the field of CG modeling is limited transferability. Based on these observations, we conclude that NN CG FFs can satisfactorily learn the physicochemical behaviors of the underlying systems, and they are not yet utilized to the full capacity. While NNs provide advantages such as ease of training, conventional empirical FFs are better at capturing physical knowledge. Therefore, we can be hopeful that NN can be integrated with empirical CG models to expand the boundaries of research.
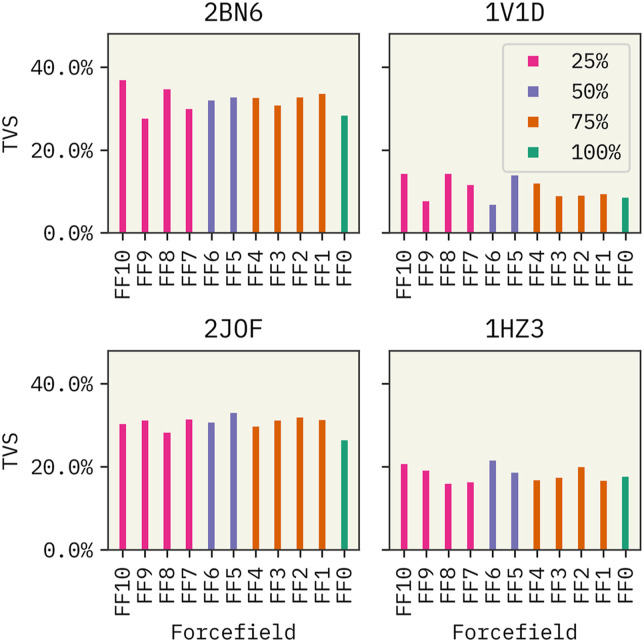
Next, we proceeded to focus on the impact of training data on the performance of TorchMD-Net FFs. Results from the CGSchNet model were not included here due to the poor performance observed previously. See the supplementary material for CGSchNet results. First, we tested the sensitivity of the TorchMD-Net FF0 model on training data. We trained two separate FF0 models for each miniprotein with 500 000 frames and downsampled frames (123 456, 258 676, 63 364, and 204 332 frames for 2BN6, 1V1D, 2JOF, and 1HZ3, respectively). As shown in Fig. S12 of the supplementary material, the overall performance of the models did not improve significantly when the models were trained with more data. Note that the results shown in Fig. 4 are from models trained downsampled data clusters. Surprisingly, we observed that the percentage of clusters used in training is not correlated with the extrapolation ability of the FFs. For example, we see that the TVS of FF0 trained with data from all four states is comparable to FF7-10 trained with data from only one cluster. These observations validate the hypothesis that CG FFs can, indeed, extrapolate beyond the available knowledge and that having large amounts of training data does not necessarily improve performance. Fu et al.32 arrived at a similar conclusion where they observed that the performance of learned NN FFs cannot be improved by increasing the amount of training data. Stocker et al.101 stated that one way of improving the robustness of NN FFs is by including distorted and off-equilibrium conformations during training.
FIG. 4.
Impact of the amount of data in training of TorchMD-Net FFs. Labels of the FFs indicate the percentage of states used in training. See Table I.
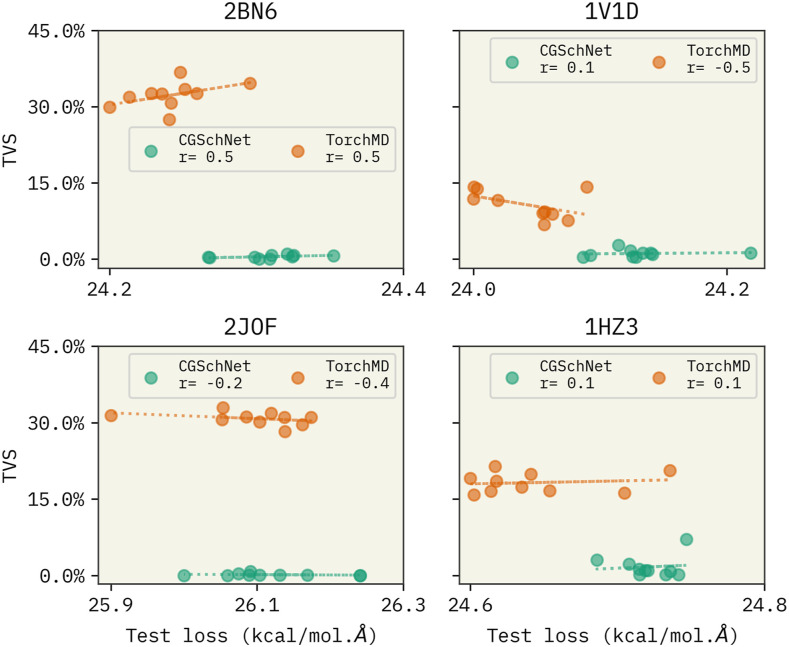
Another important observation was that during the training, we observed that both CGSchNet and TorchMD-Net had similar validation errors. This led us to expect similar performances from both NN architectures. However, their performances varied drastically in the simulation phase. We faced difficulty in conducting stable, long simulations with CGSchNet unlike with TorchMD-Net. Baffled by this, we had the following question: “is the force matching error a suitable benchmark?” Our observations align with the findings by Fu et al.,32 who showed that machine learning FFs with a lower force matching error are not an indication of the performance. They showed that learned FFs can fail to reproduce simulation-based observables, such as radial distribution functions, and to produce stable simulations. To further investigate this question, we compared the force matching error (validation error) from all CGSchNet and TorchMD-Net FFs with their respective TVS values. Our results shown in Fig. 5 indicate that, although the force matching errors from both CGschNet TorchMD-Net models only differ by ±0.2 kcal/(mol Å), their TVS differs by ∼20%. This indicates that there is only a weak correlation between force matching error and the FF’s performance as measured by TVS. Therefore, we conclude that the force matching error should not be the only benchmark when developing FFs, and it can be misleading.32,102
FIG. 5.
Variation of TVS with the force matching error of all CGSchNet and TorchMD-Net FFs. The x axis denotes the average force matching error of the last three epochs. TVS indicates the similarity between mapped and CG trajectories from the trained FFs.
IV. CONCLUSIONS
Based on our results, we observe that TorchMD-Net trained with limited data is comparable to the two physics-informed FFs: MARTINI60 and OpenAWSEM.63 Unlike CGSchNet, TorchMD-Net FFs strictly explore physically meaningful regions of the FES as captured by the mapped trajectories indicating. This shows that TorchMD-Net FFs learned the underlying physics of the reference system compared to CGSchNet. We also observe that the amount used in training does not impact the overall performance of FFs trained with TorchMD-Net for proteins with varying degrees of protein disorder. This lessens the need to generate long-scale atomistic trajectories with millions of data frames, which are already time and resource expensive. Mainly, we observe that while NN FFs are unaffected by the availability of data, they are able to extrapolate to unseen regions of the FES. When compared with empirical FFs MARTINI and OpenAWSEM, TorchMD-Net has significant advantages—ease of training, exploring a large region of the reference FES within a short time span, and robustness to the structural disorder of miniproteins. Additionally, we find that force matching error NN of CG FF is not strongly correlated with a model’s accuracy. This highlights the need to explore a better benchmark for FF training. We are hopeful that NN CG FFs can be further improved with hyperparameter and architectural optimization.
SUPPLEMENTARY MATERIAL
We have included methodologies, data, and results used during training and conducting CG simulations and the following figures and tables in the supplementary material. Figure S1: meta-state assignment workflow. Figure S2: discretized reduced 2D configurational spaces with k-means centers and implied timescale plots. Figures S3–S6: Chapman–Kolmogorov tests for proteins 2BN6, 1V1D, 2JOF, and 1HZ3. Figure S7: train and validation error plots of TorchMD-Net trained FFs. Figure S8: train and validation error plots of CGSchNet trained FFs. Figure S9: mapped and CG FES of the trained TorchMD-Net’s GNN FFs. Figure S10: mapped and CG FES of the trained TorchMD-Net’s ET FF0. Figure S11: total energy during CG simulations from TochMD-Net FF0. Figure S12: impact on training data. Figure S13: one-bead representations of all force fields. Figure S14: timeseries plots for the 2BN6 protein. Figure S15: timeseries plots for the 1V1D protein. Figure S16: timeseries plots for the 2JOF protein. Figure S17: timeseries plots for the 1HZ3 protein. Figure S18: performance of all CGSchNet FFs. Figure S19: mapped and CG FES of the trained CGSchNet FFs. Table S1: parameters used in cluster assignment of mapped trajectories. Table S2: hyperparameters used for training TorchMD-Net force fields. Table S3: hyperparameters used for training CGSchNet force fields. Table S4: CG simulations parameters: trained TorchMD-Net FFs. Table S5: CG simulations parameters: trained CGSchNet FFs.
ACKNOWLEDGMENTS
This research was supported by the National Institutes of Health through Award Nos. R35GM137966 (for G.P.W. and A.D.W.) and R35GM138312 (for G.M.H.). This work was supported, in part, through the NYU IT High Performance Computing resources, services, and staff expertise, and simulations were partially executed on resources supported by the Simons Center for Computational Physical Chemistry at NYU (SF Grant No. 839534). We would also like to thank Fabian Grünewald of the University of Groningen and Nicholas E. Charron at Freie Universität Berlin for assistance with Martini3 and CGSchNet.
Note: This paper is part of the JCP Special Topic on Machine Learning Hits Molecular Simulations.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Author Contributions
Geemi P. Wellawatte: Conceptualization (equal); Data curation (equal); Formal analysis (equal); Investigation (equal); Methodology (equal); Writing – original draft (equal); Writing – review & editing (equal). Glen M. Hocky: Data curation (equal); Investigation (equal); Resources (equal); Supervision (equal); Validation (equal); Writing – original draft (equal); Writing – review & editing (equal). Andrew D. White: Conceptualization (equal); Supervision (equal); Validation (equal).
DATA AVAILABILITY
The data that support the findings of this study are available within the article and its supplementary material.
REFERENCES
- 1.Ayton G. S. and Voth G. A., “Simulation of biomolecular systems at multiple length and time scales,” Int. J. Multiscale Comput. Eng. 2, 291 (2004). 10.1615/intjmultcompeng.v2.i2.80 [DOI] [Google Scholar]
- 2.Izvekov S. and Voth G. A., “A multiscale coarse-graining method for biomolecular systems,” J. Phys. Chem. B 109, 2469–2473 (2005). 10.1021/jp044629q [DOI] [PubMed] [Google Scholar]
- 3.Foley T. T., Shell M. S., and Noid W. G., “The impact of resolution upon entropy and information in coarse-grained models,” J. Chem. Phys. 143, 243104 (2015). 10.1063/1.4929836 [DOI] [PubMed] [Google Scholar]
- 4.Noid W. G., “Perspective: Coarse-grained models for biomolecular systems,” J. Chem. Phys. 139, 090901 (2013). 10.1063/1.4818908 [DOI] [PubMed] [Google Scholar]
- 5.Kmiecik S., Gront D., Kolinski M., Wieteska L., Dawid A. E., and Kolinski A., “Coarse-grained protein models and their applications,” Chem. Rev. 116, 7898–7936 (2016). 10.1021/acs.chemrev.6b00163 [DOI] [PubMed] [Google Scholar]
- 6.Voynov V. and Caravella J. A., Therapeutic Proteins: Methods and Protocols (Springer, 2012). [Google Scholar]
- 7.Clementi C., “Coarse-grained models of protein folding: Toy models or predictive tools?,” Curr. Opin. Struct. Biol. 18, 10–15 (2008), part of Special Issue: Folding and binding/Protein-nucleic acid interactions. 10.1016/j.sbi.2007.10.005 [DOI] [PubMed] [Google Scholar]
- 8.Kidder K. M., Szukalo R. J., and Noid W. G., “Energetic and entropic considerations for coarse-graining,” Eur. Phys. J. B 94, 153 (2021). 10.1140/epjb/s10051-021-00153-4 [DOI] [Google Scholar]
- 9.Jin J., Pak A. J., Durumeric A. E. P., Loose T. D., and Voth G. A., “Bottom-up coarse-graining: Principles and perspectives,” J. Chem. Theory Comput. 18, 5759–5791 (2022). 10.1021/acs.jctc.2c00643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Noid W. G., “Systematic methods for structurally consistent coarse-grained models,” in Biomolecular Simulations: Methods and Protocols, edited by Monticelli L. and Salonen E. (Humana Press, Totowa, NJ, 2013), pp. 487–531. [DOI] [PubMed] [Google Scholar]
- 11.Saunders M. G. and Voth G. A., “Coarse-graining methods for computational biology,” Annu. Rev. Biophys. 42, 73–93 (2013). 10.1146/annurev-biophys-083012-130348 [DOI] [PubMed] [Google Scholar]
- 12.Brini E., Algaer E. A., Ganguly P., Li C., Rodríguez-Ropero F., and van der Vegt N. F. A., “Systematic coarse-graining methods for soft matter simulations – A review,” Soft Matter 9, 2108–2119 (2013). 10.1039/c2sm27201f [DOI] [Google Scholar]
- 13.Li Z., Wellawatte G. P., Chakraborty M., Gandhi H. A., Xu C., and White A. D., “Graph neural network based coarse-grained mapping prediction,” Chem. Sci. 11, 9524–9531 (2020). 10.1039/d0sc02458a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chakraborty M., Xu C., and White A. D., “Encoding and selecting coarse-grain mapping operators with hierarchical graphs,” J. Chem. Phys. 149, 134106 (2018). 10.1063/1.5040114 [DOI] [PubMed] [Google Scholar]
- 15.Chakraborty M., Xu J., and White A. D., “Is preservation of symmetry necessary for coarse-graining?,” Phys. Chem. Chem. Phys. 22, 14998–15005 (2020). 10.1039/d0cp02309d [DOI] [PubMed] [Google Scholar]
- 16.Empereur-Mot C., Pesce L., Doni G., Bochicchio D., Capelli R., Perego C., and Pavan G. M., “Swarm-CG: Automatic parametrization of bonded terms in MARTINI-based coarse-grained models of simple to complex molecules via fuzzy self-tuning particle swarm optimization,” ACS Omega 5, 32823–32843 (2020). 10.1021/acsomega.0c05469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang Z., Lu L., Noid W. G., Krishna V., Pfaendtner J., and Voth G. A., “A systematic methodology for defining coarse-grained sites in large biomolecules,” Biophys. J. 95, 5073–5083 (2008). 10.1529/biophysj.108.139626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ponder J. W. and Case D. A., “Force fields for protein simulations,” in Protein Simulations, Advances in Protein Chemistry (Academic Press, 2003), Vol. 66, pp. 27–85. [DOI] [PubMed] [Google Scholar]
- 19.Köhler J., Chen Y., Krämer A., Clementi C., and Noé F., “Flow-matching: Efficient coarse-graining of molecular dynamics without forces,” J. Chem. Theory Comput. 19, 942 (2022); arXiv:2203.11167 (2022). 10.1021/acs.jctc.3c00016 [DOI] [PubMed] [Google Scholar]
- 20.Wang J., Olsson S., Wehmeyer C., Pérez A., Charron N. E., de Fabritiis G., Noé F., and Clementi C., “Machine learning of coarse-grained molecular dynamics force fields,” ACS Cent. Sci. 5, 755–767 (2019). 10.1021/acscentsci.8b00913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Durumeric A. E., Charron N. E., Templeton C., Musil F., Bonneau K., Pasos-Trejo A. S., Chen Y., Kelkar A., Noé F., and Clementi C., “Machine learned coarse-grained protein force-fields: Are we there yet?,” Curr. Opin. Struct. Biol. 79, 102533 (2023). 10.1016/j.sbi.2023.102533 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Reith D., Pütz M., and Müller-Plathe F., “Deriving effective mesoscale potentials from atomistic simulations,” J. Comput. Chem. 24, 1624–1636 (2003). 10.1002/jcc.10307 [DOI] [PubMed] [Google Scholar]
- 23.Jarin Z., Newhouse J., and Voth G. A., “Coarse-grained force fields from the perspective of statistical mechanics: Better understanding of the origins of a MARTINI hangover,” J. Chem. Theory Comput. 17, 1170–1180 (2021). 10.1021/acs.jctc.0c00638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Behler J. and Parrinello M., “Generalized neural-network representation of high-dimensional potential-energy surfaces,” Phys. Rev. Lett. 98, 146401 (2007). 10.1103/physrevlett.98.146401 [DOI] [PubMed] [Google Scholar]
- 25.Thaler S. and Zavadlav J., “Learning neural network potentials from experimental data via differentiable trajectory reweighting,” Nat. Commun. 12, 6884 (2021). 10.1038/s41467-021-27241-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schütt K. T., Sauceda H. E., Kindermans P.-J., Tkatchenko A., and Müller K.-R., “SchNet–A deep learning architecture for molecules and materials,” J. Chem. Phys. 148, 241722 (2018). 10.1063/1.5019779 [DOI] [PubMed] [Google Scholar]
- 27.Smith J. S., Isayev O., and Roitberg A. E., “ANI-1: An extensible neural network potential with DFT accuracy at force field computational cost,” Chem. Sci. 8, 3192–3203 (2017). 10.1039/c6sc05720a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Majewski M., Pérez A., Thölke P., Doerr S., Charron N. E., Giorgino T., Husic B. E., Clementi C., Noé F., and De Fabritiis G., “Machine learning coarse-grained potentials of protein thermodynamics,” arXiv:2212.07492 (2022). [DOI] [PMC free article] [PubMed]
- 29.Husic B. E., Charron N. E., Lemm D., Wang J., Pérez A., Majewski M., Krämer A., Chen Y., Olsson S., de Fabritiis G., Noé F., and Clementi C., “Coarse graining molecular dynamics with graph neural networks,” J. Chem. Phys. 153, 194101 (2020). 10.1063/5.0026133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Doerr S., Majewsk M., Pérez A., Krämer A., Clementi C., Noe F., Giorgino T., and Fabritiis G. D., “TorchMD: A deep learning framework for molecular simulations,” arXiv:2012.12106[physics.chem-ph] (2020). [DOI] [PMC free article] [PubMed]
- 31.Zhang L., Han J., Wang H., Car R., and E W., “DeePCG: Constructing coarse-grained models via deep neural networks,” J. Chem. Phys. 149, 034101 (2018). 10.1063/1.5027645 [DOI] [PubMed] [Google Scholar]
- 32.Fu X., Wu Z., Wang W., Xie T., Keten S., Gomez-Bombarelli R., and Jaakkola T., “Forces are not enough: Benchmark and critical evaluation for machine learning force fields with molecular simulations,” arXiv:2210.07237 (2022).
- 33.Noé F., Tkatchenko A., Müller K.-R., and Clementi C., “Machine learning for molecular simulation,” Annu. Rev. Phys. Chem. 71, 361–390 (2020). 10.1146/annurev-physchem-042018-052331 [DOI] [PubMed] [Google Scholar]
- 34.Khorshidi A. and Peterson A. A., “Amp: A modular approach to machine learning in atomistic simulations,” Comput. Phys. Commun. 207, 310–324 (2016). 10.1016/j.cpc.2016.05.010 [DOI] [Google Scholar]
- 35.Chmiela S., Tkatchenko A., Sauceda H. E., Poltavsky I., Schütt K. T., and Müller K.-R., “Machine learning of accurate energy-conserving molecular force fields,” Sci. Adv. 3, e1603015 (2017). 10.1126/sciadv.1603015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Thölke P. and De Fabritiis G., “Equivariant transformers for neural network based molecular potentials,” in The Tenth International Conference on Learning Representations (ICLR 2022) (OpenReview.net, 2022).
- 37.Zeni C., Anelli A., Glielmo A., and Rossi K., “Exploring the robust extrapolation of high-dimensional machine learning potentials,” Phys. Rev. B 105, 165141 (2022). 10.1103/physrevb.105.165141 [DOI] [Google Scholar]
- 38.Robustelli P., Piana S., and Shaw D. E., “Developing a molecular dynamics force field for both folded and disordered protein states,” Proc. Natl. Acad. Sci. U. S. A. 115, E4758–E4766 (2018). 10.1073/pnas.1800690115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ignjatovic T., Yang J.-C., Butler J., Neuhaus D., and Nagai K., “Structural basis of the interaction between P-element somatic inhibitor and U1-70k essential for the alternative splicing of P-element transposase,” J. Mol. Biol. 351, 52–65 (2005). 10.1016/j.jmb.2005.04.077 [DOI] [PubMed] [Google Scholar]
- 40.Nicoll A. J. and Allemann R. K., “Nucleophilic and general acid catalysis at physiological pH by a designed miniature esterase,” Org. Biomol. Chem. 2, 2175–2180 (2004). 10.1039/b404730c [DOI] [PubMed] [Google Scholar]
- 41.Barua B., Lin J. C., Williams V. D., Kummler P., Neidigh J. W., and Andersen N. H., “The Trp-cage: Optimizing the stability of a globular miniprotein,” Protein Eng., Des. Sel. 21, 171–185 (2008). 10.1093/protein/gzm082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang S., Iwata K., Lachenmann M., Peng J., Li S., Stimson E., Lu Y. a., Felix A., Maggio J., and Lee J., “The Alzheimer’s peptide aβ adopts a collapsed coil structure in water,” J. Struct. Biol. 130, 130–141 (2000). 10.1006/jsbi.2000.4288 [DOI] [PubMed] [Google Scholar]
- 43.Molgedey L. and Schuster H. G., “Separation of a mixture of independent signals using time delayed correlations,” Phys. Rev. Lett. 72, 3634–3637 (1994). 10.1103/physrevlett.72.3634 [DOI] [PubMed] [Google Scholar]
- 44.Naritomi Y. and Fuchigami S., “Slow dynamics of a protein backbone in molecular dynamics simulation revealed by time-structure based independent component analysis,” J. Chem. Phys. 139, 215102 (2013). 10.1063/1.4834695 [DOI] [PubMed] [Google Scholar]
- 45.Schultze S. and Grubmüller H., “Time-lagged independent component analysis of random walks and protein dynamics,” J. Chem. Theory Comput. 17, 5766–5776 (2021). 10.1021/acs.jctc.1c00273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Verdú S., “Total variation distance and the distribution of relative information,” in 2014 Information Theory and Applications Workshop (ITA) (IEEE, 2014), pp. 1–3. [Google Scholar]
- 47.Chen T. and Kiefer S., On the Total Variation Distance of Labelled Markov Chains (Association for Computing Machinery, New York, 2014). [Google Scholar]
- 48.Best R. B. and Hummer G., “Optimized molecular dynamics force fields applied to the helix–coil transition of polypeptides,” J. Phys. Chem. B 113, 9004–9015 (2009). 10.1021/jp901540t [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lindorff-Larsen K., Piana S., Palmo K., Maragakis P., Klepeis J. L., Dror R. O., and Shaw D. E., “Improved side-chain torsion potentials for the Amber ff99SB protein force field,” Proteins 78, 1950–1958 (2010). 10.1002/prot.22711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., “Comparison of simple potential functions for simulating liquid water,” J. Chem. Phys. 79, 926–935 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 51.Abraham M. J., Murtola T., Schulz R., Páll S., Smith J. C., Hess B., and Lindahl E., “GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers,” SoftwareX 1–2, 19–25 (2015). 10.1016/j.softx.2015.06.001 [DOI] [Google Scholar]
- 52.See http://www.mdtutorials.com/gmx/lysozyme/index.html for GROMACS standard protocol.
- 53.Chmiel N. H., Rio D. C., and Doudna J. A., “Distinct contributions of KH domains to substrate binding affinity of drosophila P-element somatic inhibitor protein,” RNA 12, 283–291 (2006). 10.1261/rna.2175706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhou R., “Trp-cage: Folding free energy landscape in explicit water,” Proc. Natl. Acad. Sci. U. S. A. 100, 13280–13285 (2003). 10.1073/pnas.2233312100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bussi G., Donadio D., and Parrinello M., “Canonical sampling through velocity rescaling,” J. Chem. Phys. 126, 014101 (2007). 10.1063/1.2408420 [DOI] [PubMed] [Google Scholar]
- 56.Parrinello M. and Rahman A., “Polymorphic transitions in single crystals: A new molecular dynamics method,” J. Appl. Phys. 52, 7182–7190 (1981). 10.1063/1.328693 [DOI] [Google Scholar]
- 57.Michaud-Agrawal N., Denning E. J., Woolf T. B., and Beckstein O., “MDAnalysis: A toolkit for the analysis of molecular dynamics simulations,” J. Comput. Chem. 32, 2319–2327 (2011). 10.1002/jcc.21787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gowers R. J., Linke M., Barnoud J., Reddy T. J., Melo M. N., Seyler S. L., Dotson D. L., Domanski J., Buchoux S., Kenney I. M., and Beckstein O., “MDAnalysis: A Python package for the rapid analysis of molecular dynamics simulations,” in Proceedings of the 15th Python in Science Conference (SciPy2016), 11–17 July 2016, Austin, TX, pp. 98–105. 10.25080/majora-629e541a-00e [DOI]
- 59.“Fastforward github,” https://github.com/fgrunewald/fast_forward.
- 60.Marrink S. J., de Vries A. H., and Mark A. E., “Coarse grained model for semiquantitative lipid simulations,” J. Phys. Chem. B 108, 750–760 (2004). 10.1021/jp036508g [DOI] [Google Scholar]
- 61.Marrink S. J., Risselada H. J., Yefimov S., Tieleman D. P., and de Vries A. H., “The MARTINI force field: Coarse grained model for biomolecular simulations,” J. Phys. Chem. B 111, 7812–7824 (2007). 10.1021/jp071097f [DOI] [PubMed] [Google Scholar]
- 62.Davtyan A., Schafer N. P., Zheng W., Clementi C., Wolynes P. G., and Papoian G. A., “AWSEM-MD: Protein structure prediction using coarse-grained physical potentials and bioinformatically based local structure biasing,” J. Phys. Chem. B 116, 8494–8503 (2012). 10.1021/jp212541y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Lu W., Bueno C., Schafer N. P., Moller J., Jin S., Chen X., Chen M., Gu X., Davtyan A., de Pablo J. J., and Wolynes P. G., “OpenAWSEM with Open3SPN2: A fast, flexible, and accessible framework for large-scale coarse-grained biomolecular simulations,” PLoS Comput. Biol. 17, e1008308 (2021). 10.1371/journal.pcbi.1008308 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Poma A. B., Cieplak M., and Theodorakis P. E., “Combining the MARTINI and structure-based coarse-grained approaches for the molecular dynamics studies of conformational transitions in proteins,” J. Chem. Theory Comput. 13, 1366–1374 (2017). 10.1021/acs.jctc.6b00986 [DOI] [PubMed] [Google Scholar]
- 65.Martini3 tutorial,” http://cgmartini.nl/index.php/2021-martini-online-workshop/tutorials/564-2-proteins-basic-and-martinize-2\#GoProteins.
- 66.“Openawsem github,” https://github.com/npschafer/openawsem.
- 67.Ciccotti G., Kapral R., and Vanden-Eijnden E., “Blue moon sampling, vectorial reaction coordinates, and unbiased constrained dynamics,” ChemPhysChem 6, 1809–1814 (2005). 10.1002/cphc.200400669 [DOI] [PubMed] [Google Scholar]
- 68.Krämer A., Durumeric A. E. P., Charron N. E., Chen Y., Clementi C., and Noé F., “Statistically optimal force aggregation for coarse-graining molecular dynamics,” J. Phys. Chem. Lett. 14, 3970–3979 (2023). 10.1021/acs.jpclett.3c00444 [DOI] [PubMed] [Google Scholar]
- 69.Baum L. E. and Petrie T., “Statistical inference for probabilistic functions of finite state Markov chains,” Ann. Math. Stat. 37, 1554–1563 (1966). 10.1214/aoms/1177699147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Rabiner L., “A tutorial on hidden Markov models and selected applications in speech recognition,” Proc. IEEE 77, 257–286 (1989). 10.1109/5.18626 [DOI] [Google Scholar]
- 71.Scherer M. K., Trendelkamp-Schroer B., Paul F., Pérez-Hernández G., Hoffmann M., Plattner N., Wehmeyer C., Prinz J.-H., and Noé F., “PyEMMA 2: A software package for estimation, validation, and analysis of Markov models,” J. Chem. Theory Comput. 11, 5525–5542 (2015). 10.1021/acs.jctc.5b00743 [DOI] [PubMed] [Google Scholar]
- 72.Zwanzig R., “From classical dynamics to continuous time random walks,” J. Stat. Phys. 30, 255–262 (1983). 10.1007/bf01012300 [DOI] [Google Scholar]
- 73.Pande V. S., Beauchamp K., and Bowman G. R., “Everything you wanted to know about Markov state models but were afraid to ask,” Methods 52, 99–105 (2010), part of Special Issue: Protein Folding. 10.1016/j.ymeth.2010.06.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Husic B. E. and Pande V. S., “Markov state models: From an art to a science,” J. Am. Chem. Soc. 140, 2386–2396 (2018). 10.1021/jacs.7b12191 [DOI] [PubMed] [Google Scholar]
- 75.Kolloff C. and Olsson S., “Machine learning in molecular dynamics simulations of biomolecular systems,” arXiv:2205.03135 (2022).
- 76.Noé F., Horenko I., Schütte C., and Smith J. C., “Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states,” J. Chem. Phys. 126, 04B617 (2007). 10.1063/1.2714539 [DOI] [PubMed] [Google Scholar]
- 77.Noé F., “Probability distributions of molecular observables computed from Markov models,” J. Chem. Phys. 128, 244103 (2008). 10.1063/1.2916718 [DOI] [PubMed] [Google Scholar]
- 78.Chodera J. D. and Noé F., “Probability distributions of molecular observables computed from Markov models. II. Uncertainties in observables and their time-evolution,” J. Chem. Phys. 133, 09B606 (2010). 10.1063/1.3463406 [DOI] [PubMed] [Google Scholar]
- 79.Buchete N.-V. and Hummer G., “Coarse master equations for peptide folding dynamics,” J. Phys. Chem. B 112, 6057–6069 (2008). 10.1021/jp0761665 [DOI] [PubMed] [Google Scholar]
- 80.Schütte C., Noé F., Lu J., Sarich M., and Vanden-Eijnden E., “Markov state models based on milestoning,” J. Chem. Phys. 134, 05B609 (2011). 10.1063/1.3590108 [DOI] [PubMed] [Google Scholar]
- 81.Pérez-Hernández G., Paul F., Giorgino T., De Fabritiis G., and Noé F., “Identification of slow molecular order parameters for Markov model construction,” J. Chem. Phys. 139, 015102 (2013). 10.1063/1.4811489 [DOI] [PubMed] [Google Scholar]
- 82.Lloyd S., “Least squares quantization in PCM,” IEEE Trans. Inf. Theory 28, 129–137 (1982). 10.1109/tit.1982.1056489 [DOI] [Google Scholar]
- 83.Wu H. and Noé F., “Variational approach for learning Markov processes from time series data,” J. Nonlinear Sci. 30, 23–66 (2020). 10.1007/s00332-019-09567-y [DOI] [Google Scholar]
- 84.Prinz J.-H., Wu H., Sarich M., Keller B., Senne M., Held M., Chodera J. D., Schütte C., and Noé F., “Markov models of molecular kinetics: Generation and validation,” J. Chem. Phys. 134, 174105 (2011). 10.1063/1.3565032 [DOI] [PubMed] [Google Scholar]
- 85.Papoulis A., “Bayes’ theorem in statistics and Bayes’ theorem in statistics (reexamined),” in Probability, Random Variables, and Stochastic Processes, 2nd ed. (McGraw-Hill, NY, 1984), pp. 38–114. [Google Scholar]
- 86.Christoforou E., Leontiadou H., Noé F., Samios J., Emiris I. Z., and Cournia Z., “Investigating the bioactive conformation of Angiotensin II using Markov state modeling revisited with web-scale clustering,” J. Chem. Theory Comput. 18, 5636–5648 (2022). 10.1021/acs.jctc.1c00881 [DOI] [PubMed] [Google Scholar]
- 87.Schutt K., Kessel P., Gastegger M., Nicoli K., Tkatchenko A., and Muller K.-R., “SchNetPack: A deep learning toolbox for atomistic systems,” J. Chem. Theory Comput. 15, 448–455 (2018). 10.1021/acs.jctc.8b00908 [DOI] [PubMed] [Google Scholar]
- 88.Paszke A., Gross S., Massa F., Lerer A., Bradbury J., Chanan G., Killeen T., Lin Z., Gimelshein N., Antiga L., Desmaison A., Kopf A., Yang E., DeVito Z., Raison M., Tejani A., Chilamkurthy S., Steiner B., Fang L., Bai J., and Chintala S., “PyTorch: An imperative style, high-performance deep learning library,” in Advances in Neural Information Processing Systems 32, edited by Wallach H., Larochelle H., Beygelzimer A., d’Alché Buc F., Fox E., and Garnett R. (Curran Associates, Inc., 2019), pp. 8024–8035. [Google Scholar]
- 89.Bruininks B. M. H., Souza P. C. T., and Marrink S. J., “A practical view of the Martini force field,” in Biomolecular Simulations: Methods and Protocols (Springer, NY, 2019), pp. 105–127. [DOI] [PubMed] [Google Scholar]
- 90.Marrink S. J. and Mark A. E., “The mechanism of vesicle fusion as revealed by molecular dynamics simulations,” J. Am. Chem. Soc. 125, 11144–11145 (2003). 10.1021/ja036138+ [DOI] [PubMed] [Google Scholar]
- 91.Marrink S. J. and Mark A. E., “Molecular dynamics simulation of the formation, structure, and dynamics of small phospholipid vesicles,” J. Am. Chem. Soc. 125, 15233–15242 (2003). 10.1021/ja0352092 [DOI] [PubMed] [Google Scholar]
- 92.Monticelli L., Kandasamy S. K., Periole X., Larson R. G., Tieleman D. P., and Marrink S.-J., “The MARTINI coarse-grained force field: Extension to proteins,” J. Chem. Theory Comput. 4, 819–834 (2008). 10.1021/ct700324x [DOI] [PubMed] [Google Scholar]
- 93.de Jong D. H., Singh G., Bennett W. F. D., Arnarez C., Wassenaar T. A., Schafer L. V., Periole X., Tieleman D. P., and Marrink S. J., “Improved parameters for the Martini coarse-grained protein force field,” J. Chem. Theory Comput. 9, 687–697 (2013). 10.1021/ct300646g [DOI] [PubMed] [Google Scholar]
- 94.López C. A., Bellesia G., Redondo A., Langan P., Chundawat S. P., Dale B. E., Marrink S. J., and Gnanakaran S., “MARTINI coarse-grained model for crystalline cellulose microfibers,” J. Phys. Chem. B 119, 465–473 (2015). 10.1021/jp5105938 [DOI] [PubMed] [Google Scholar]
- 95.Uusitalo J. J., Ingólfsson H. I., Akhshi P., Tieleman D. P., and Marrink S. J., “Martini coarse-grained force field: Extension to DNA,” J. Chem. Theory Comput. 11, 3932–3945 (2015). 10.1021/acs.jctc.5b00286 [DOI] [PubMed] [Google Scholar]
- 96.de Jong D. H., Liguori N., van den Berg T., Arnarez C., Periole X., and Marrink S. J., “Atomistic and coarse grain topologies for the cofactors associated with the photosystem II core complex,” J. Phys. Chem. B 119, 7791–7803 (2015). 10.1021/acs.jpcb.5b00809 [DOI] [PubMed] [Google Scholar]
- 97.Chen X., Chen M., and Wolynes P. G., “Exploring the interplay between disordered and ordered oligomer channels on the aggregation energy landscapes of α-synuclein,” J. Phys. Chem. B 126, 5250–5261 (2022). 10.1021/acs.jpcb.2c03676 [DOI] [PubMed] [Google Scholar]
- 98.Chen X., Chen M., Schafer N. P., and Wolynes P. G., “Exploring the interplay between fibrillization and amorphous aggregation channels on the energy landscapes of tau repeat isoforms,” Proc. Natl. Acad. Sci. U. S. A. 117, 4125–4130 (2020). 10.1073/pnas.1921702117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Zheng W., Tsai M.-Y., Chen M., and Wolynes P. G., “Exploring the aggregation free energy landscape of the amyloid-β protein (1–40),” Proc. Natl. Acad. Sci. U. S. A. 113, 11835–11840 (2016). 10.1073/pnas.1612362113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Klem H., Hocky G. M., and McCullagh M., “Size-and-shape space Gaussian mixture models for structural clustering of molecular dynamics trajectories,” J. Chem. Theory Comput. 18, 3218 (2022). 10.1021/acs.jctc.1c01290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Stocker S., Gasteiger J., Becker F., Günnemann S., and Margraf J. T., “How robust are modern graph neural network potentials in long and hot molecular dynamics simulations?,” Mach. Learn.: Sci. Technol. 3, 045010 (2022). 10.1088/2632-2153/ac9955 [DOI] [Google Scholar]
- 102.Schaarschmidt M., Riviere M., Ganose A. M., Spencer J. S., Gaunt A. L., Kirkpatrick J., Axelrod S., Battaglia P. W., and Godwin J., “Learned force fields are ready for ground state catalyst discovery,” arXiv:2209.12466 (2022).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
We have included methodologies, data, and results used during training and conducting CG simulations and the following figures and tables in the supplementary material. Figure S1: meta-state assignment workflow. Figure S2: discretized reduced 2D configurational spaces with k-means centers and implied timescale plots. Figures S3–S6: Chapman–Kolmogorov tests for proteins 2BN6, 1V1D, 2JOF, and 1HZ3. Figure S7: train and validation error plots of TorchMD-Net trained FFs. Figure S8: train and validation error plots of CGSchNet trained FFs. Figure S9: mapped and CG FES of the trained TorchMD-Net’s GNN FFs. Figure S10: mapped and CG FES of the trained TorchMD-Net’s ET FF0. Figure S11: total energy during CG simulations from TochMD-Net FF0. Figure S12: impact on training data. Figure S13: one-bead representations of all force fields. Figure S14: timeseries plots for the 2BN6 protein. Figure S15: timeseries plots for the 1V1D protein. Figure S16: timeseries plots for the 2JOF protein. Figure S17: timeseries plots for the 1HZ3 protein. Figure S18: performance of all CGSchNet FFs. Figure S19: mapped and CG FES of the trained CGSchNet FFs. Table S1: parameters used in cluster assignment of mapped trajectories. Table S2: hyperparameters used for training TorchMD-Net force fields. Table S3: hyperparameters used for training CGSchNet force fields. Table S4: CG simulations parameters: trained TorchMD-Net FFs. Table S5: CG simulations parameters: trained CGSchNet FFs.
Data Availability Statement
The data that support the findings of this study are available within the article and its supplementary material.