Assessment of atmospheric emissivity models for clear-sky conditions with reanalysis data

Abstract

Atmospheric longwave downward radiation (L_d) is one of the significant components of net radiation (R_n), and it drives several essential ecosystem processes. L_d can be estimated with simple empirical methods using atmospheric emissivity (ε_a) submodels. In this study, eight global models for ε_a were evaluated, and the best-performing model was calibrated on a global scale using a parametric instability analysis approach. The climatic data were obtained from a dynamically consistent scale resolution of basic atmospheric quantities and computed parameters known as NCEP/NCAR reanalysis (NNR) data. The performance model was evaluated with monthly average values from the NNR data. The Brutsaert equation demonstrated the best performance, and then it was calibrated. The seasonal global trend of the Brutsaert equation calibrated coefficient ranged between 1.2 and 1.4, and the K-means analysis identified five homogeneous zones (clusters) with similar behavior. Finally, the calibrated Brutsaert equation improved the R_n estimation, with an error reduction, at the worldwide scale, of 64%. Meanwhile, the error reduction for each cluster ranged from 18 to 77%. Hence, Brutsaert’s equation coefficient should not be considered a constant value for use in ε_a estimation, nor in time or location.

Introduction

Thermal atmospheric emissivity (ε_a) is a parameter mainly used to estimate the atmospheric downward longwave radiation (L_d), which is used to determine net radiation (R_n). In this way, the R_n plays a significant role in modeling natural phenomena such as vegetation evapotranspiration rates, snowmelt, and frost occurrence¹. The longwave radiation emitted by the atmosphere occurs at wavelengths between 4 and 100 μm in the electromagnetic spectrum and is influenced mainly by water vapor, carbonic anhydride, ozone, and clouds².

The L_d is one of the significant components of the R_n model applied to forests³, affecting several essential ecosystem processes, such as photosynthetic rate, plant respiration, and primary productivity. However, the L_d term is not easy to measure. Although pyrgeometers are used to measure it, their high cost^4,5 often limits their inclusion in automatic weather stations.

Then, the L_d term can be estimated using simple empirical methods adjusted based on direct measurements to solve this problem. In this regard, the literature shows that reliable estimations of L_d can be obtained using a statistical adjustment or calibration based on measured air temperature and relative humidity data measured at the surface (at screen height). However, local calibration is required⁶ for accurate results. Another approach is to use radiosonde data and atmospheric radiative transfer models, but this information limits their application to a specific date and place^7–13.

Although an extensive database is needed, estimating ε_a through statistical models could be significantly improved using different parameterizations based on atmospheric conditions. This database should be able to represent a range of atmospheric conditions for every location in the world to decrease the error of statistical estimations of ε_a.

Therefore, local calibrations of the coefficients involved in the empirical ε_a models are necessary. Research indicates that the majority of equations used to estimate ε_a are only valid for clear-sky days, reaching more accurate results when considering daily or climatological averages. Clear-sky days are defined by the absence of visible clouds in the sky. In this sense, the clear-sky conditions are defined when the clear-sky index (Global solar radiation/Extraterrestrial solar radiation) is approximately greater than 0.9^14,15. In order to achieve this, it is possible to use existing databases such as NCEP/NCAR reanalysis to obtain more accurate estimations of the emissivity at the Earth’s surface^16,17.

According to the literature, using semiempirical approaches to estimate ε_a has inherent errors linked to instrument-based measurement deviation or uncertainty. Therefore, the use of a properly calibrated ε_a model is a viable alternative for estimating more accurately at specific locations using meteorological variables such as air temperature and relative humidity^6,18–20. In this regard, there is plenty of information in the literature about the estimation of R_n using empirical and semiempirical ε_a models based mainly on ground-based instruments for specific locations of different roughness surfaces worldwide^20–36.

In this study, the performance of eight models was evaluated to determine their accuracy in the estimation of atmospheric emissivity for different locations worldwide. Climatic data from NCEP/NCAR reanalysis (NNR) were obtained from a dynamically consistent scale resolution of basic atmospheric quantities and computed parameters. Among the evaluated models, the one with the best statistical performance was calibrated on a global scale using a parametric instability analysis approach. In this way, one of the main contributions of the study at hand was to improve the R_n computation over homogeneous latitude areas globally, reducing the need for local calibration of atmospheric emissivity.

Information derived from NCEP/NCAR reanalysis data (NNR)

Exploratory analysis for the NCEP/NCAR reanalysis data (1948–2020) across the world revealed that the air temperature (t_a) varied between – 37 °C and 49 °C, with an average of 17 °C. Additionally, the actual vapor pressure (e_a) values ranged from 0.01 to 21.9 kPa with an average value of 5.02 kPa; meanwhile, ε_a averaged 0.73 and varied between 0.34 and 0.97. Moreover, the variable with the most significant variation coefficient was t_a, presenting a value of 447.7%, e_a with 107.6%, and ε_a reached an 18.5% variation.

Figure 1 shows the observed values of ε_a obtained using the NNR data throughout the year’s seasons. In Fig. 1, a spatial pattern can be seen due to the formation of homogeneous groups or units (clusters) based on latitude. Moreover, this trend was also observed on a monthly scale (data not shown). These clusters have temporal variability related to atmospheric dynamics. Additionally, ε_a presents homogeneous values overseas and in oceans; likewise, the poles show the same trend but with different absolute values. On the continents, ε_a have variations related to the topography, land use, and closeness to seas and oceans. That trend was also observed in other study³⁷, which indicated that uncertainties in the computation of land surface temperature, can be highly influenced by the spatial variability of the ground.

Figure 1.

Maps of climatological world atmospheric emissivity (ε_a) for (a) winter, (b) spring, (c) summer, and (d) autumn, calculated from NCEP/NCAR reanalysis data. This figure was obtained with R software⁸³.

At the spatial resolution scale of the NNR, climatological variables merely correspond to a spatial trend as the NNR's spatial estimate being approximately 250 km. Comparing this data with surface weather station networks at this resolution is difficult since they correspond merely to an average in each grid element or “pixel”^38,39. However, several studies have established the agreement between grid and ground-based observations for variables such as solar radiation, air temperature, relative humidity, precipitation, and pressure⁴⁰. Wind speed exhibits the largest biases in space recorded, compared with other reanalysis products like ERA-40, ERA-Interim, or ERA5. Although the NNR presents significant differences, the spatial calculation resolution is different, adding additional elements, and making it challenging to make direct comparisons^38,40–44. It is noteworthy that evapotranspiration calculated from NNR data is comparable to those calculated from observations at most weather stations^39,45.

Performance of atmospheric emissivity models

Descriptive analysis for the ε_a evaluation using the eight models is presented in Table 1. This table shows that the estimated values of ε_a were between 0.22 and 0.99, and the average values ranged from 0.61 to 0.83. Moreover, the Bastiaanssen model exhibited the lowest variation, with a variation coefficient of 1.1%; meanwhile, the Brutsaert model showed the highest variation coefficient, with a value of 28.1%. The other models obtained an intermediate variation with values from 6.4 to 20.1%.

Table 1.

Descriptive statistics of estimated atmospheric emissivity (dimensionless) for each model.

Model	Minimum	Maximum	Median	Average	Standard deviation	Variation coefficient (%)
Bastiaanssen	0.71	0.76	0.76	0.75	0.0083	1.1
Prata	0.67	0.85	0.71	0.72	0.0512	7.1
Idso	0.70	0.89	0.74	0.75	0.0480	6.4
Brutsaert	0.22	0.85	0.66	0.61	0.1701	28.1
Idso and Jackson	0.74	0.99	0.82	0.83	0.0737	8.9
Swinbank	0.37	0.89	0.68	0.66	0.1330	20.1
Brunt	0.61	0.83	0.69	0.69	0.0627	9.1
Angstrom	0.65	0.82	0.72	0.72	0.0602	8.3

Table 2 presents the performance of the eight models, showing that the minimum and maximum values of the root mean square error (RMSE) were 0.097 and 0.216, respectively. Meanwhile, the coefficient of determination (r²) ranged from 0.45 to 0.69, while the Akaike information criterion (AIC) presented a minimum value of − 2,354,713 and a maximum of − 1,745,909. Considering all statistical parameters such as systematic error (BIAS), mean absolute error (MAE), RMSE, normalized RMSE (nRMSE), coefficient of determination (r²), index of agreement (d) and AIC, the Idso and Jackson model presented the poorest performance (BIAS = 0.097, MAE = 0.143, RMSE = 0.216, nRMSE = 34%, r² = 0.45, d = 0.25, and AIC = − 1,745,909), while the ε_a Brutsaert model had the best performance (BIAS = − 0.127, MAE = 0.128, RMSE = 0.152, nRMSE = 23.9%, r² = 0.76, d = 0.80, and AIC = − 2,354,713).

Table 2.

Comparative statistics for the performance of the eight models for estimating atmosphere emissivity, using processed NCEP/NCAR reanalysis data.

Model	BIAS	MAE	RMSE	nRMSE	r2	d	P	AIC
Bastiaanssen	0.019	0.099	0.131	20.6	0.50	0.23	**	− 1,996,608
Prata	− 0.011	0.084	0.103	16.2	0.57	0.68	**	− 1,949,235
Idso	0.020	0.076	0.105	16.6	0.59	0.65	**	− 1,973,122
Brutsaert	0.127	0.128	0.152	23.9	0.69	0.80	**	− 2,354,713
Idso and Jackson	0.097	0.143	0.216	34.0	0.45	0.25	**	− 1,745,909
Swinbank	− 0.070	0.089	0.108	17.0	0.66	0.85	**	− 2,058,430
Brunt	− 0.041	0.088	0.101	16.0	0.64	0.75	**	− 2,058,430
Angstrom	− 0.010	0.079	0.097	15.3	0.60	0.74	**	− 2,018,959

BIAS, MAE and RMSE are the systematic error, mean absolute error, and root mean square error, respectively. The units are dimensionless. nRMSE is the normalized root mean square and corresponds to a percentage. r² is the coefficient of determination, and d is the index of agreement (dimensionless). The AIC is the Akaike information criterion (dimensionless).

Global calibration for the best model

The better performance of the Brutsaert model for estimating ε_a simplifies the global calibration process, considering that only one parameter remains dependent, so that the exponent’s hypothesis is invariant.

Supplementary Fig. 1 shows the seasonal behavior of ε_a, revealing a consistent linear and positive regression with (e_a/t_a), independent of the season. The plot shows two separated data tendencies during the winter season with the upper right side of the graph being the most important as it concentrates more points over a linear trend.

Only a trend was evident for the spring season, with a higher concentration of points from 0.7 to 1.0. For the summer months, the graph presents the most irregular linear regression of all seasons, with the cluster of points concentrated in the top portion of Supplementary Fig. 1c, in a range of 0.8 to 1.0.

Finally, in the autumn season, two linear regressions can be identified with different slopes. However, the most important trend is located in the upper portion of the graph, where ε_a are concentrated in a range from 0.8 to 1.0.

The performance summary of the parametric instability analysis through the geographically weighted regression (GWR) of the spatial variation for Brutsaert equation parameters, is presented in Supplementary Table 1. The negative BIAS values show that the GWR coefficients underestimated the spatial variability of the Brutsaert equation parameters. Furthermore, the BIAS depicted a random behavior. The monthly mean RMSE was approximately 0.022 (dimensionless) with an estimation error of 1.5%. The RMSE values for autumn and winter were above the mean, while the RMSE values for spring and summer were below the mean.

As a result, the months that were closer to the average maximum temperature showed a more accurate estimation of the parameters in the Brutsaert equation compared to the colder months near the average minimum temperature. AIC values showed a similar pattern to RMSE; thus, warmer months resulted in a better AIC value than colder months. The Nash–Sutcliffe efficiency (NSE) index, d, and r² indices had values near 1, indicating a good fit of the GWR coefficients for each month.

Figure 2 shows the global seasonal trend of calibrated Brutsaert model coefficient and the cluster resulting from the K-means analysis. The calibrated coefficient value ranged between 1.2 and 1.4, considering the four seasons and the five zones with similar behavior. In this sense, the Brutsaert model coefficient did not present a unique value for the entire world. The predominant zone was related to the Ecuador line, which covered a critical zone of the study area.

Figure 2.

World spatial distribution of the calibrated coefficient of Brutsaert for (a) winter, (b) spring, (c) summer, and (d) autumn. Additionally, the homogeneous areas or clusters are presented (e), referenced for the Northern Hemisphere. This figure was obtained with R software⁸³.

Additionally, the austral and boreal zones presented differentiation from the rest of the world. The monthly mean empirical coefficient of the Brutsaert model is shown in Supplementary Table 2. Moreover, the performance of the uncalibrated and calibrated Brutsaert equations in computing net radiation for each cluster is presented in Table 3. Here, a RMSE reduction was observed at a worldwide scale of 64%, while in Cluster 2, a RMSE decrease of approximately 77% was observed. However, Cluster 3, which mainly represents a significant portion of the land, only reached an RMSE reduction of 18%.

Table 3.

Comparison of statistical indices for evaluating the Brutsaert equation effect on net radiation computation.

Zone	Model	BIAS (W m–2)	MAE (W m–2)	RMSE (W m–2)	nRMSE (%)	NSE	d	r2
Cluster 1	Uncalibrated Brutsaert’s	– 37.5	37.5	40.1	46.4	0.78	0.95	0.99
	Calibrated Brutsaert’s	− 4.5	6.1	7.5	8.7	0.99	1.00	1.00
Cluster 2	Uncalibrated Brutsaert’s	− 26.9	27.1	30.9	36.3	0.87	0.97	0.99
	Calibrated Brutsaert’s	− 2.3	5.5	7.0	8.2	0.99	1.00	0.99
Cluster 3	Uncalibrated Brutsaert’s	− 3.8	9.1	11.4	22.5	0.95	0.99	0.96
	Calibrated Brutsaert’s	1.7	7.2	9.3	18.2	0.97	0.99	0.97
Cluster 4	Uncalibrated Brutsaert’s	− 16.9	17.1	20.1	25.8	0.93	0.98	0.99
	Calibrated Brutsaert’s	7.6	9.0	10.6	13.6	0.98	1.00	0.99
Worldwide	Uncalibrated Brutsaert’s	− 15.2	18.1	23.6	32.0	0.90	0.98	0.97
	Calibrated Brutsaert’s	− 0.2	6.5	8.4	11.3	1.00	1.00	0.99

BIAS, MAE, and RMSE are the systematic error, mean absolute error, and root mean square error, respectively. The nRMSE is the normalized root mean square error, and its unit is %. The NSE is the Nash–Sutcliffe model efficiency index, d is the index of agreement, and r² is the coefficient of determination (dimensionless). The information is only presented for four out of the five clusters.

It is important to note that the spatial resolution of the model used is approximately 250 km, which allows the calculation of meteorological variables that correspond to large climatic regions across the Earth.

The spatial configuration of the variables is influenced by factors such Earth's topography, oceans, and land surface cover, which affects variables such as albedo and surface emissivity. The Seasonal dependence is strongly associated with the Earth's trajectory in its solar orbit, affecting the incident energy of short and long waves, adjusting to the solar declination^29,46,47.

Improvements of estimated net radiation

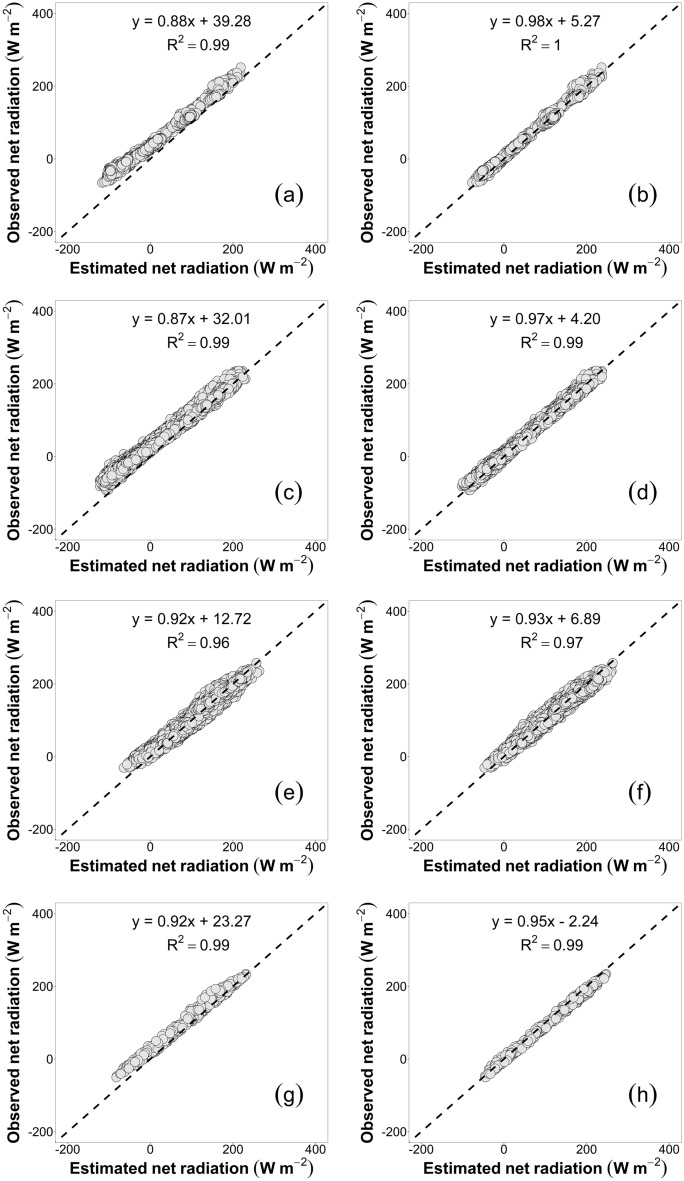
In high latitudes (C1 in Fig. 2), a calibrated Brutsaert model coefficient demonstrated good agreement between the observed and estimated values of R_n (Fig. 3b) values using a calibrated Brutsaert model coefficient (Cluster 1 in Table 3). Low error values were observed for BIAS, MAE, and RMSE, − 4.5, 6.1, and 7.5 W m^–2, respectively.

Figure 3.

Comparison of net radiation computed using uncalibrated (a,c,e,g) and calibrated (b,d,f,h) Brutsaert’s equation in the estimated worldwide clusters: Cluster 1 (a,b); Cluster 2 (c,d); Cluster 3 (e,f); and Cluster 4 (g,h).

At the same time, the NSE, d, and the r² had values close to 1.0 and a value of nRMSE equal to 8.7%. In this context, estimated R_n for latitudes greater than 60° N under all-sky conditions from MODIS imagery, was validated using data from 82 sites and eight different observation networks²⁷.

These authors found acceptable accuracy values of RMSE ranging between 15.04 and 23.66 W m^–2, whereas the values of r² and BIAS were between 0.51 and 0.85 and between − 0.08 and 0.27 W m², respectively. However, for Alaska’s Arctic tundra summer conditions (at USA sites Fen, Tussock, and Heath, the latitude of 68° N), the estimated R_n for all-sky conditions aligned well with the observed values, presenting an average RMSE of 23 W m^–2 and r² value equal to 0.99 using the remote sensing thermal-based two-source energy balance model⁴⁸.

Errors were found using a similar value for the original Brutsaert coefficient (1.25 ± 0.009), which was consistent with our study for summer condition (S Table 1). When estimating the R_n in the geographic areas corresponding to Cluster 2 (Table 3), latitudes are between 40 and 60°N (C2 in Fig. 3), and lower errors were observed, with values of 49, 10, and 7% for BIAS, MAE and RMSE, respectively. Simulations of R_n in different zones, locations, and vegetation surfaces have been performed within a range of latitudes³⁴, 41–60°N in Canada (Eloria, Ontario, with a latitude of 43°N) using an empirical R_n-Model observed an average MAE, r² and d of approximately 28 W m^–2, 0.98 and 0.99, respectively. At the same latitude but different locations in Avignon, France³⁰ (latitude 43°N), the R_n was evaluated using a semiempirical model based on Stefan–Boltzmann under grass cover, observing a RMSE of 34 W m^-2 with a calibrated Brutsaert’s coefficient of 1.31.

Also, the R_n has been estimated for clear-sky and all-wave net radiation combined visible and shortwave infrared (VSWIR) and thermal infrared (TIR) remote sensing data at a location in Montana, USA (Fort Peck, latitude 48° N)⁴⁹, observing that the component-based approach presented a BIAS, RMSE and r² of 76.7, 2.0 and 0.87, respectively. Using a direct estimation approach, the BIAS, RMSE, and r² values were 52.3, − 1.5, and 0.94, respectively. Furthermore, R_n estimations from solar shortwave radiation measurements and conventional meteorological observations (or satellite retrievals) were conducted at 24 different sites⁵⁰. Three of these sites were located at latitudes over 42° N (Fort Peck, MT in grass cover; Sioux Falls, SD in grass cover; and Wind River, WA in temperate evergreen forest cover). Thus, the errors obtained at those sites were 17.2, 20.8, and 16.0 W m^–2 for RMSE and 3.5, 2.6, and 4.6 W m^–2 for BIAS, respectively. For mid-latitudes (C3 in Fig. 3), the estimation of R_n (Fig. 3f), using a calibrated Brutsaert’s coefficient (Cluster 3 in S Table 2), presented a statistical mean deviation lower than 9.3 W m^–2. The evaluation of the different R_n models presented in the literature worldwide are mainly inserted between latitudes 42°N and 40°S. In this context, R_n was estimated using MODIS data for clear sky days with an empirical ε_a equation^51,52, and this study covered most of Oklahoma and the southern part of Kansas, USA (latitude from approximately 34.5°to 38.5°N and longitude from 95.3° to 99.5°W).

Thus, the comparison between observed and simulated R_n presented 59 W m^–2, 74 W m^–2, and 0.89 for BIAS, RMSE, and r², respectively. On the other hand, for the climate of Baghdad, Iraq (latitude 33°N) in natural prairie grass, there was a good agreement between observed and estimated R_n with a simple empirical approach for all clear skies⁵³, with an average RMSE value equal to 28 W m^–2 and r² value of 0.984.

However, in a semiarid climate covered by sparse vegetation near Tabernas⁵⁴, Almería, Spain (37°N) good agreement was obtained between the observed and simulated R_n, with a mean RMSE value of 47 W m^–2 and r² value of 0.96. In another study conducted on an olive vegetation surface in southwestern Sicily, Italy (37°N)⁵⁵, an RMSE value of 35.4 W m^–2 was obtained in the R_n. They used a semiempirical model based on the Stefan–Boltzmann law that included estimating longwave radiation incorporating the original Brutsaert’s coefficient value. Furthermore, in a wetland in the Paynes Prairie Preserve (29° N) in north-central Florida, USA⁵⁶, the R_n was estimated using GOES satellite data. Thus, the R_n was best characterized when the GOES solar and GOES longwave radiation products were combined, reaching average RMSE, NSE, and r² values equal to 14.1 W m^–2, 0.92, and 0.95, respectively.

In another experience, in the Upper Blue Nile Basin, Ethiopia (7.5°–12.5° N)⁵⁷ the R_n distribution was estimated from satellite MODIS and automatic weather station, obtaining a reduction in the mean bias (MB) and RMSE values of 76.43 and 17.71%, respectively, by implementing the new recalibrated Brutsaert equation.

Furthermore, the solar shortwave radiation data and meteorological observations (or satellite retrievals) from 24 different sites (USA and China) were used to estimate R_n⁵⁰, where 21 of them were in latitudes between 32° and 41°N under various land covers (grass, pastures, wheat, rangeland, crop, forest, native prairie, and desert). Across all sites and land covers, the BIAS varied between 19.7 and 27.8 W m^–2, while the RMSE ranged from 12.8 to 21.0 W m^–2.

For grass cover, a semiempirical model based on the Stefan–Boltzmann law was evaluated to estimate R_n in Talca, Chile (35°S)³⁰, obtaining an RMSE of 42 W m^–2 with a calibrated Brutsaert’s ε_a coefficient equal to 1.31. Furthermore, for olive tree cover (Pencahue Valley site, Pencahue, Chile, latitude 35°S and CIFA Experimental Station site, Córdoba, Spain, latitude 37.8°N) and vineyard cover (Pencahue Valley site, Pencahue, Chile, latitude 35°S), the estimation of R_n was observed with RMSE and MAE values below 45.0 and 31.0 W m^–2, respectively^25,35,36. For latitudes from 41°S to 60°S (C4 in Fig. 3), the estimation of R_n (Fig. 3h), using a calibrated Brutsaert’s coefficient (Cluster 4 in Table 3), presented a statistical mean deviation lower than 10.6 W m^–2.

In this case, there is limited literature about the estimation of R_n in southern latitudes. Thus, the approaches presented in this study are promising for improving the estimation of R_n by incorporating a calibrated Brutsaert’s ε_a equation coefficient, broken down by homogeneous latitudes separated into five zones around the world (Figs. 2e and 3). Additionally, the errors found in this study are lower and similar in the same case compared to those found in the existing literature. In this sense, it is necessary to further evaluate ε_a estimates under a larger number of land cover types, different vegetation architectures of surface roughness lengths, and other characteristics than the Brutsaert ε_a equation coefficient values obtained in this research.

Conclusions

A spatially explicit approximation method for calculating atmospheric emissivity (ε_a) has been investigated to improve the estimation of downward longwave radiation during the day and further enhance radiation calculations.

The study evaluated eight models globally to estimate air emissivity using the NCEP/NCAR Reanalysis database, which corresponds to spatial trends in each variable used, mainly due to the calculation resolution, which is 2.5° in latitude and longitude. The results showed that the Brutsaert ε_a model had the best performance (BIAS = − 0.127, MAE = 0.128, RMSE = 0.152, nRMSE = 23.9%, r² = 0.76, d = 0.80, AIC = – 2,354,713), and it was calibrated using geographically weighted regression (GWR) for global use.

The calibrated values considerably improved the calculation of the components of the surface energy balance, reducing calculation errors in net radiation from 25.2 W m^–2 (nRMSE = 32.6%) to 8.6 W m^–2 (nRMSE = 12.0%). The study indicates that the Brutsaert ε_a model should not be considered to have a constant coefficient value in time or space. It is advisable to use the coefficients found in this work to minimize errors when calculating net radiation. Using a sinusoidal equation or spline-type interpolation to reproduce the temporal variability of the coefficients for each day of the year is recommended when using the average monthly coefficients of the Brutsaert equation to estimate the emissivity of the atmosphere at a daily level.

Methods

Due to the different climatic conditions, the entire world was used as the study area to achieve an adequate model evaluation and calibration. Observed climatic data were obtained from a dynamically consistent scale resolution of basic atmospheric quantities and computed parameters known as NCEP/NCAR reanalysis data (NNR). These data were produced by the US National Centers for Environmental Predictions (NCEP) and the National Center for Atmospheric Research (NCAR) based in Boulder, CO, USA¹⁶.

NCEP/NCAR reanalysis data

The NNR data of global climatic information cover the period from 1948 to the present. Its spatial resolution is 2.5° longitude and 2.5° latitude with a temporal resolution of one month, one day, or six hours, and diagnosed diabatic heating of 17 vertical isobaric levels from 1000 to 10 hPa^58–60. The NNR data were developed by the synergy of processes such as quality control, assimilation, interpolation, observed data acquired by ground and sea stations, planes, satellites, and atmospheric soundings, together with simulations of atmospheric general circulation models using the Climate Data Assimilation System (CDAS)⁵⁸.

The data used in this research were based on the “Surface” and “Surface flux” sections and their upward solar radiation flux.

Atmospheric emissivity parameterizations

Below are the equations used to estimate ε_a with meteorological variables such as t_a and actual vapor pressure (e_a). The exception is the Bastiaanssen model²¹ because it estimates ε_a at a daily scale for any condition of cloudiness, only depending on atmospheric transmissivity (τ_sw). The Bastiaanssen model was calibrated⁶¹ and used in the satellite-based energy balance for mapping evapotranspiration with an internalized calibration (METRIC) model⁶². The eight evaluated models are the following^{2,12,13,21,52,63–65}:

$${\epsilon }_a=\text{0.85}{\left(-,\text{Ln},\left({\tau }_{\mathit{sw}}\right)\right)}^{0.09},$$

$${\epsilon }_a=1-\left(1,+,\xi \right)·e^{-\sqrt{\text{1.2}+\text{3.0}·\xi }},$$

$${\epsilon }_a=\text{0.70}+\text{0.0000595}·e_a·e^{\left(1500,/,T_a\right)},$$

$${\epsilon }_a=1.24·{\left(e_a,/,T_a\right)}^{\frac{1}{7}},$$

$${\epsilon }_a=1-\text{0.261}·e^{-\text{0.000777}·(273-T_a{)}^2},$$

$${\epsilon }_a=\text{0.0000092}·{\left(T_a\right)}^2,$$

$${\epsilon }_a=\text{0.605}+\text{0.048}·\sqrt{e_a},$$

$${\epsilon }_a=\text{0.83}-\text{0.18}·1{\text{0}}^{-\text{0.067}·e_a},$$

where ε_a is the atmospheric emissivity (dimensionless) for clear-sky conditions based on air temperature (T_a, K), water vapor pressure (e_a, hPa), atmospheric transmissivity (τ_SW, dimensionless), and altitude (z, meters above sea level). The z was obtained from the WorldClim data⁶⁶ with a spatial resolution of 1 km. Moreover, e_a was estimated as follows^29,67:

$$e_a=6.108·\left(\frac{\mathit{RH}}{100}\right)·e^{\left(\frac{17.27·t_a}{t_a+237.3}\right)},$$

where e_a is the actual water vapor pressure (hPa), t_a is the air temperature (°C), and RH is the relative humidity (%). Also, the τ_SW and ξ were calculated according to:

$${\tau }_{\text{sw}}=\text{0.75}+\text{0.00002}·z,$$

$$\xi =\text{46.5}·\left(e_a,/,t_a\right),$$

The observed values of ε_a were calculated as follows:

$${\mathrm{\epsilon }}_{\mathrm{a}}=\frac{L_d}{\mathrm{\sigma }·{\mathrm{T}}_{\mathrm{o}}^4},$$

where T_o corresponds to the average temperature of the whole air profile (K) measured by a meteorological station, and L_d is the atmospheric longwave downward radiation (W m^–2).

For this study, the T_o and L_d data was obtained from the reanalysis databases. On the other hand, the estimated values of ε_a from the eight models were calculated using t_a and RH obtained from the same reanalysis databases.

The evaluation of the goodness of fit for each model was conducted using the monthly average values of the NCEP/NCAR reanalysis (NNR) data.

Statistical analysis

The evaluation of the goodness of fit for each model was conducted using the monthly average values of the NNR data through the determination of the systematic error⁶⁸ (BIAS), mean absolute error⁶⁸ (MAE), root mean square error⁶⁸ (RMSE), normalized root mean square error⁶⁹ (nRMSE), and coefficient of determination⁷⁰ (r²) (Table 3). Additionally, the index of agreement (d) was used^70–75, as well as the Akaike information criterion (AIC)^76–78. Also, the Nash–Sutcliffe efficiency (NSE) index⁷⁹ was used, and it can range from − ∞ to 1. An efficiency of 1 (NSE = 1) corresponds to a perfect match of modeled data to the observed data. An efficiency of 0 (NSE = 0) indicates that the model predictions are as accurate as the mean of the observed data, whereas an efficiency less than zero (NSE < 0) occurs when the observed mean is a better predictor than the model. Essentially, if the model efficiency is closer to 1, the model is more accurate. NSE is equivalent to the coefficient of determination (r²), thus ranging between 0 and 1.

Global calibration

The ε_a model with the best performance was adjusted globally using geographically weighted regression (GWR). For this analysis, the dependent variable was ε_a, and the independent variables were e_a and T_a. The GWR was carried out using NNR data, where information on each pixel was extracted from the grids, generating a vector type point layer for every month.

The GWR is based on weighted least squares⁸⁰, considering the distance between each point, and it is described with the following equation^80–82:

$$y_i=a_0\left(u_i,,,v_i\right)+{\sum }_k{a}_k\left(u_i,,,v_i\right)x_{\mathit{ik}}+{\delta }_i,$$

where (u_i, v_i) corresponds to the coordinates of the ith point in the space, y_i is the dependent variable value, x is the kth independent variable in the ith point, a₀ and a_k are the regression parameters in the ith point, and δ_i is the error in the ith point. The a_k(u_i, v_i) coefficients were estimated as follows:

$$a_k\left(u_i,,,v_i\right)={\left[X^T,·,W,\left(u_i,,,v_i\right),·,X\right]}^{-1}·X^T·W\left(u_i,,,v_i\right)·Y,$$

where the dependent and independent variables are in the Y and X matrices, respectively.

All calculations, statistical analyses, and figures were processed using R software⁸³ and the libraries “raster”⁸⁴, “rgdal”⁸⁵, “hexbin”⁸⁶, “hydroGOF”⁸⁷, “topmodel”⁸⁸, and “GWmodel^89,90.

Net radiation improvements

R_n was computed at a global scale to evaluate the impact of the ε_a calibrated model on the traditional method of calculating net radiation. The R_n is the sum of downward (incoming) and upward (outgoing) shortwave and longwave radiation, which is also a measure of the available energy at an underlying surface. It is also the fundamental parameter that governs the climate of the planetary boundary layer and is the driving force for processes such as evapotranspiration, air and soil heating, and photosynthesis. The net radiation over the terrestrial surface can be calculated as follows²¹:

$$R_n=\left(1,-,\alpha \right)R^{\downarrow }+L^{\downarrow }-L^{\uparrow }-\left(1,-,{\epsilon }_s\right)L^{\downarrow },$$

where R_n is the estimated net radiation (W m^-2); R^↓ is the downward shortwave solar radiation (W m^–2); L^↓ and L^↑ are the downward and upward longwave radiation, respectively (W m^–2); α is the surface albedo (dimensionless); and ε_s is the surface emissivity (dimensionless). The components of the incoming and outgoing longwave radiation, respectively, are given by:

$$L^{\downarrow }={\epsilon }_a\sigma T_a^4,$$

$$L^{\uparrow }={\epsilon }_s\sigma T_s^4,$$

where ε_a is atmospheric emissivity (dimensionless); T_a is air temperature (K); T_s is the land surface temperature (K), which was obtained from the monthly mean MOD11C3 product⁹¹; and σ is the Stefan–Boltzmann constant (5.67 × 10^–8 W m^–2 K^–4).

ε_s can be calculated from a simple linear regression using the normalized difference vegetation index or NDVI⁹², which is necessary to estimate the land surface temperature (LST). The values of ${\mathrm{\epsilon }}_{\mathrm{s}}$ were calculated as follows²⁵:

$${\epsilon }_s=0.9585+0.0357·NDVI,$$

where the NDVI is obtained from the monthly mean MOD13A3 product⁹³.

ε_a is determined according to Brutsaert’s⁶⁴ method, where the observed R_n was computed with the shortwave and longwave radiation from the NCEP/NCAR reanalysis. Meanwhile, the estimated R_n was obtained using the uncalibrated and calibrated parameters of Brutsaert’s equation and calculating the longwave radiation using $L^{\downarrow }$ and $L^{\uparrow }$ equations.

Author contributions

L.M.S and S.O.F conceived the study. L.M.S. designed the research. L.M.S., C.R.B. and G.F.J. did the computations. L.M.S, S.O.F, C.R.B., J.L.C, M.C.B., J.N.R., R.L.O., and G.F.J. analyzed the results. L.M.S and C.R.B. wrote the paper with comments from S.O.F, J.L.C, S.W., F.T., M.C.B., J.N.R., and R.L.O.

Data availability

The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-023-40499-6.