Abstract
This reflection on the evolution of methods and data in historical demography argues that we can still find inspiration and guidance in the work of the founders of our discipline. Historical demography is in the midst of a transition from a data-poor to a data-rich environment. Previous generations relied on demographic models to squeeze as much information as possible from the small amounts of data available. Today we live in a new era of large data sets and regression models. Researchers are creating both regional and international historical data sets of unprecedented size and depth. When examined closely, however, the methods that we use now make the same simplifying assumptions that generated the key advances of earlier generations. As we transition to new methods, demographic insight must inform our analyses and enrich our conclusions.
In its first issue the Journal of Interdisciplinary History published Pierre Goubert’s account of a new approach to historical demography that originated in France in the 1950s. This “demographic revolution” brought together historians, statisticians, and demographers who used new methods to create a “scientific demographic history”.1
This article examines the development of historical demography from the 1950s to the present by examining the development of its methods. It is not intended as a rigorous or comprehensive intellectual history of the field, but rather as an appreciation of the extraordinary resourcefulness of the scholars who revolutionized our field during this period. I will be focusing on a few influential methodological developments, and I will omit many important substantive contributions. For those who want a more comprehensive overview of historical demography I recommend A Global History of Historical Demography, the 50th anniversary issue of Annales de Démographie Historique, and Gutmann and Merchant in the Handbook of Population.2
Viewing historical demography from a methodological perspective, I will examine two important transitions and the links between them. From the late-1950s to the mid-1980s, which I will call the “classic” period of historical demography, there was an explosion of interest in historical demography. The expansion of research during this period involved the application of new methods that were rooted in mathematical demography. These tools assume that regularities in demographic processes can be observed and modelled, and they create new ways to analyze historical sources. At this time historical data were scarce and expensive to acquire, and data collection was an important component of almost all research projects. We benefit today from databases started during this period. This generation of research was also characterized by intense scrutiny of sources. Great care was taken to evaluate the quality of sources and to understand potential biases.
In the 1980s historical demography began a reorientation from reconstructing trends to the study of socio-economic differentials in demographic behaviors. The most important contributions of the earlier generation had been aggregate-level reconstructions of trends in population sizes, fertility, and mortality. These trends were often interpreted in a framework derived from Malthus and Demographic Transition Theory. The next generation of research paid much more attention to individual level analysis presented in a statistical rather than demographic framework. This work emphasized differences within societies due to socio-economic status, ethnicity, and community and to life course models highlighting the importance of gender and age. In part, this was due to changes in computer technology, new multi-variate statistical models, and the emergence of large data collections.
I will also show that there is an underlying continuity between the statistical methods used today and the demographic models used in the classical period. Although they are expressed in estimated coefficients and standard errors, statistical models are also based on simplifying assumptions about the phenomena being described. In particular, Event History Analysis makes the same assumptions about regularities in demographic behaviors as demographic projection and Stable Population Theory. Unfortunately, this underlying continuity is not always understood, and some of the important lessons of the classic generation have been forgotten. I will show why those principles are still important.
Demographic Models in Classic Historical Demography
From the mid-1950s to the mid-1980s historical demography was completely transformed by new methods that traced the demographic history of Europe in unprecedented detail and resulted in new ways of thinking about that history. These methods were new applications of techniques of mathematical demography that had been perfected in the early twentieth century. Louis Henry and Ansley Coale, who were central figures in both historical demography and contemporary demography, also published textbooks on demographic methods. This section discusses four methods that supported important findings during this pivotal period: the Singulate Mean Age at Marriage, Family Reconstitution, the European Fertility Project indices, and Back Projection.
Singulate mean age at marriage
In 1956 John Hajnal identified a distinctive European pattern of marriage characterized by high average ages at marriage and high proportions never marrying. Hajnal showed that this pattern divided Europe into two zones with the “European Marriage Pattern” northwest of a line running from Trieste to St. Petersburg. Moreover, he argued that late marriage had been common in northwest Europe for at least two centuries, a point that he expanded in later writing. Hajnal’s evidence for this discovery relied on a statistic that he had described earlier, the singulate mean age at marriage (SMAM), which could be easily calculated from census data. Although the calculation of SMAM appears simple, Hajnal showed that it was derived from the Life Table and Stable Population Theory.3
By the 1970s the Northwest European Marriage Pattern had become a central concept in historical demography. Peter Laslett called attention to the correlation between the geography of late marriage and the prevalence of nuclear family households. Since Le Play sociological theorists often argued that the modern pattern of small households was a product of the Industrial Revolution, which promoted individualism and weakened patriarchal authority. Laslett showed that small families were common in England and elsewhere in Northwest Europe for at least two centuries before the Industrial Revolution, and he suggested that causation went from the culture of small families to individualism and economic innovation rather than the reverse. E.A. Wrigley described the importance of late marriage in a Malthusian world of limited resources and stagnant technology. Malthus had assumed a limited economy in which population growth inevitably leads to poverty, and he saw only two ways to bring population and resources into balance: the positive check of high mortality or the prevent restraint of late marriage. Wrigley and Schofield argued that the positive check was no longer important in seventeenth-century England, which had come to rely on late marriage and migration to cities and colonies.4
The remarkable achievement of SMAM is that it estimates an average age at marriage without any data on marriages. SMAM uses only population counts by marital status and age from a single census. Hajnal’s innovation involved seeing the similarity between proportions never married by age and the proportion of survivors in a Life Table. A Life Table describes the history of a hypothetical cohort of births, who experience a set of age-specific probabilities of dying. Starting with an arbitrary number of births we compute the number who die in each year of life (), the number of survivors at each birthday (), and the number of ‘person-years’ of life lived at each age (). The expectation of life at birth ( or average age at death) is computed by summing “person-years” of life and dividing by the number of births. Stable Population Theory shows that the Life Table can also be interpreted as a stationary population in which the number of births exactly equals the number of deaths. Under this interpretation the column can be understood as the number of people alive in the interval between age x and x+1. Hajnal draws an analogy between the proportion never married at each age in a census and the proportion of people surviving at each age in a stationary population. In his hypothetical stationary population the number of never married people “born” at age 15 exactly equals the number who will marry (i.e. “die”) by age 50.5
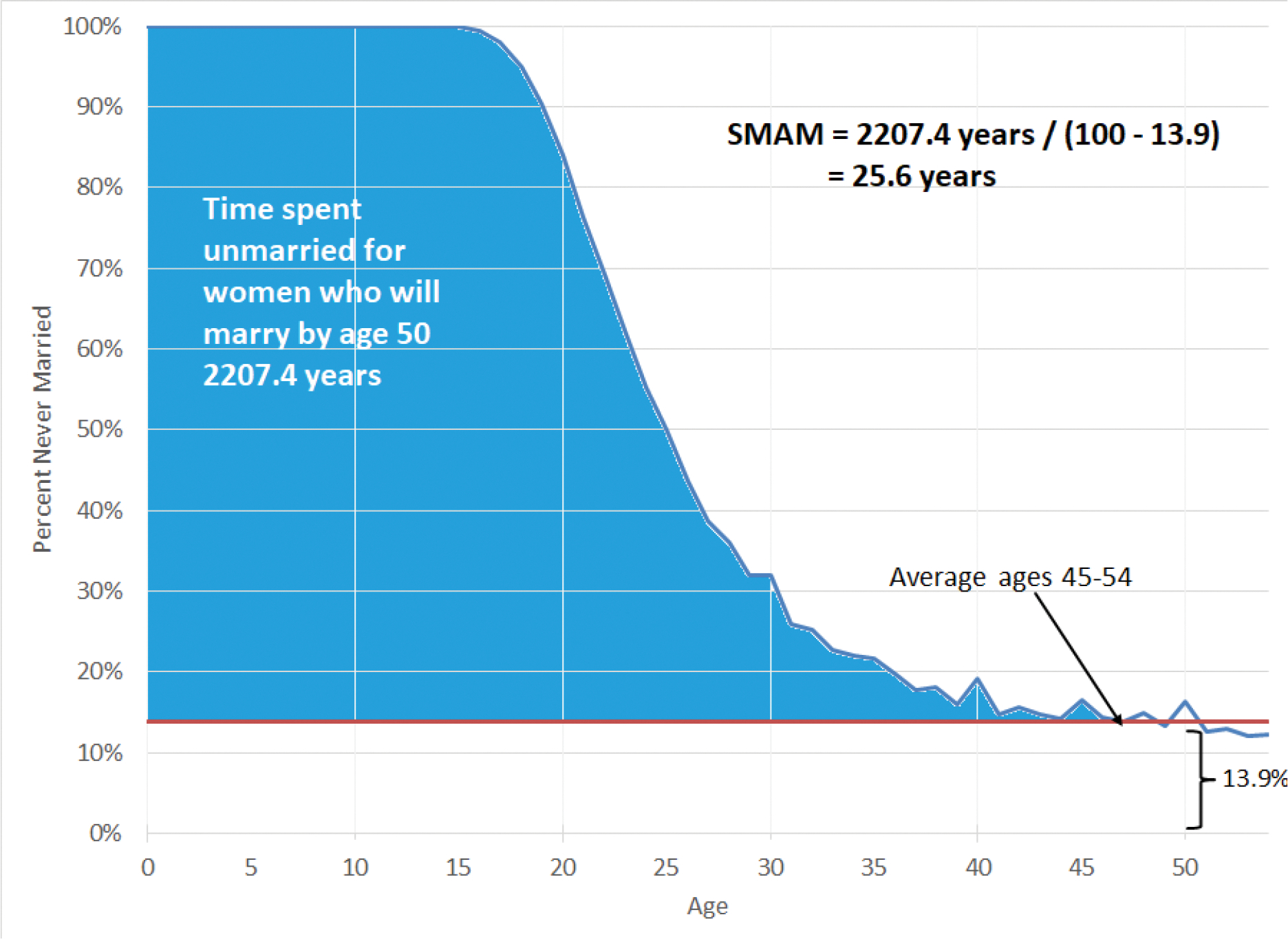
This is illustrated in Figure 1 with proportions married for women in France in 1853. The proportion of never married decreases with age, because those who marry cannot return to the status of never married. If this were a true cohort, i.e. the same group of women at each age, the curve would only decrease, but it is not. Women at ages 30, 40, and 50 in 1853 were born in 1823, 1813, and 1803 respectively. Hajnal is assuming that they all married at the same rate, but discrepancies are possible as we see at older ages in Figure 1. SMAM also assumes that no first marriages occur after age 50, but this is an approximation too.
Figure 1.
Proportion Women Who Were Single by Age, France, 1851
Source: Inter-university Consortium for Political and Social Research. Social, Demographic, and Educational Data for France, 1801–1897. Ann Arbor, MI: Inter-university Consortium for Political and Social Research [distributor], 1992–02-16. https://doi.org/10.3886/ICPSR00048.v1.
If the survival curve in Figure 1 was depicting mortality, it would fall to zero around age 100, but this curve will never reach zero. Everyone dies, but some people never marry. To compute an average age at marriage Hajnal must subtract those who will never marry from the starting cohort. He estimates this proportion from those who are unmarried at ages 45 to 54. Then, he computes an adjusted survival curve describing those who had not married yet as a proportion of those who will eventually marry.
Hajnal interprets the area under the curve in Figure 1 as average person-years lived by never-married women. Since there are no marriages under age 15, every woman contributes 15 years to the number of years lived before marriage. Above age 15 some women are married, and the contributions of these ages are scaled downward to the proportion or women who remained unmarried. In Figure 1 there is a horizontal line at 13.9%, which is the proportion of never married women at ages 45–55. The area between the curve and this line is 2207.4 years, which needs to be divided by the proportion who ever married (100 – 13.9) to get SMAM, average years lived before marriage.
By recognizing the analogy between the Life Table and the age distribution of never married women, Hajnal was able to use census data to estimate a cohort measure (average age at marriage) from cross-sectional data. Since it is not a true cohort measures, SMAM is affected by trends in marriage ages, and it can be very sensitive to migration in local populations. For historical demography Hajnal provided both a powerful new tool and an important pattern in need of explanation.
Family Reconstitution
Sølvi Sogner dates the founding of historical demography as a discipline to Louis Henry’s presentation of Family Reconstitution at the 1960 International Congress for Historical Sciences meeting in Stockholm. The historical study of populations was not new in 1960, but Henry had added a new level of scientific rigor. For the first time historical demographers could estimate demographic rates with the same precision as contemporary demographers, and they could apply this method to the enormous quantity of parish registers available in archives and churches across Europe and similar records around the world. The Fleury and Henry manual provided a detailed plan for conducting these studies that was copied in hundreds monographs, published and unpublished. Family Reconstitution set off a wave of new research across Europe, North and South America, and Japan. 6
Rosental argues that Henry’s contribution goes beyond the method of Family Reconstitution itself. All of the components used in Family Reconstitution were already available before Henry became involved. Even the Family Reconstitution Form had been invented independently by Swedish demographer Hannes Hyrenius more than a decade earlier. Henry provided a conceptual framework that put historical research at the center of demographic research. In monographs and manuals Henry and his co-authors demonstrated a broad range of techniques for reconstructing demographic patterns including but by no means limited to Family Reconstitution. While Henry’s own interest in using historical data to inform demographic models was clearly stated, he made alliances with archivists, historians, and “passionate amateurs” who could use Family Reconstitution for their own purposes.7
Henry actively sought partnerships with other disciplines. At the end of his study of the leading families of Geneva he wrote:
Much closer collaboration between demographers and historians is also necessary. The demographer left to himself can furnish only results; he can certainly, as we have done, indicate interpretations suggested by the relationships that he observes among diverse phenomena. It remains to be seen whether these interpretations accord with what is already known in political, economic, and social history and, if not, to propose others. This task belongs to historians.8
For historians Henry was offering not only scientific precision, but also a new set of tools and rigorous tests for evaluating the quality of historical sources. Even Pierre Goubert, who had responded sharply to Henry’s criticism of his own work, eventually endorsed Family Reconstitution. Henry was successful both in obtaining funding for his projects and in asserting his leadership within France and international organizations.9
By 1958 Henry had launched the Enquête Henry, a demographic database of randomly selected French parishes. Forty parishes were fully reconstituted, and baptisms, burials, and marriages were collected in a larger sample for aggregate analysis without record linkage. The latter were used to reconstruct the population of France by age and sex back to 1740. Results of the family reconstitutions were published in four regional studies, and they show substantial regional differences in the level of fertility in the early eighteenth century.10
Henry had turned to historical data because he could not find contemporary data with the level of detail he required for estimating and projecting fertility. As demographers were struggling to understand the Baby Boom, Henry started a series of publications aimed at more sophisticated ways to measure fertility. For example, his models distinguish between the effects of increasing secondary sterility and decreasing fecundity on the level of fertility at older ages. Early in this project he saw the need for data on “natural fertility,” fertility “of a population making no conscious effort towards birth control,” that would allow him to distinguish the role of choice from the effects of biology. The first Family Reconstitution studies of Geneva and Crulai were mined for empirical results shedding light on natural fertility. As data accumulated, he recognized that the level of fertility varied considerably among populations that were not practicing family limitation, and that cultural and environmental conditions play an important role. In 1961 Henry gave a more nuanced definition of natural fertility:11
We can term as natural the fertility which exists or has existed in the absence of deliberate birth control. The adjective “natural” is admittedly not ideal but we prefer it to “physiological” since the factors affecting natural fertility are not solely physiological: social factors may also play a part – sexual taboos for example, during lactation. Some of these factors may result in a reduction of fertility but this cannot be considered a form of birth control. Control can be said to exist when the behavior of the couple is bound to the number of children already born and is modified when this number reaches a maximum which the couple does not want to exceed: it is not the case for a taboo concerning lactation, which is independent of the number of children already born.12
Thus, for Henry the opposite of natural fertility is birth control used to terminate childbearing after reaching a target family size. The reconstitution of families in the Genevan bourgeoisie provided an opportunity to document this pattern. Henry found increasing evidence of fertility control starting with couples married between 1650 and 1699. Beginning with this cohort age-specific fertility rates started to fall, the average age at last birth decreased, and completed family sizes decreased. The family reconstitutions strongly suggested that couples had begun aiming for small families. Fertility rates at younger ages remained constant, as did the length of the interval between the first and second birth. Birth intervals became wider at higher parities, but he noted that this was mostly due to the last and next to last intervals. Henry attributed these longer birth intervals to failed attempts to stop in an era when birth control was often ineffective. Moreover, Henry noted that the onset of fertility decline coincided with increased out-migration and reductions in marriage, which suggested economic adversity.13
Natural fertility was criticized almost immediately, and it has remained one of the most contentious concepts in historical demography. However, most of this debate is about explaining the transition to low fertility and not about the questions that motivated Henry. As explanations shifted from socio-economic to cultural (see below), the “natural fertility hypothesis” became part of the debate about what initiates family limitation. On one side, a strict interpretation of “natural fertility” was taken to imply that fertility decline depended upon the spread of knowledge and attitudes favorable to birth control. The other side maintains that European couples already knew how to control fertility, and the key change was a new preference for small families.14
Family Reconstitution solved a well-known problem with the parish registers: How do we use counts of births, deaths, and marriages when we do not know the size of the population? The standard way to compute demographic rates is to divide the number of events (births, deaths, marriages, migrants) by the average number of people who could have experienced the event. The latter is usually estimated from population counts in a census. Henry’s solution was to use a different denominator, person-years of experience, which is a basic feature of the Life Table. A Life Table can be interpreted as the history of a hypothetical cohort of births. The age-specific death rate in the Life Table, , is the ratio of deaths between ages x and x+n and the number of person-years lived by the cohort in this age interval. In contemporary populations we approximate by dividing counts of deaths by the mid-year population at ages x to x+n. Henry recognized that person-years lived could be estimated directly from the parish registers without a census. If we can link a person’s date of birth/baptism to her date of death/burial, we can compute the number of person-years lived in each age of her life. Thus, we can compute age-specific death, fertility, and nuptiality rates without a census.
The Fleury and Henry manual presented simple paper forms and step-by-step procedures for performing a family reconstitution study. All baptisms, marriages, and burials are transcribed to color-coded slips of paper, sorted, and then assembled into families. A family begins with a marriage, and it includes the husband, wife, and their children. When all of the events associated with a family have been assembled, they are transferred to a Family Reconstitution Form (FRF) as in Figure 2. Information about the husband and wife is at the top of the form. Children are listed in order in the central columns below their parents. A table on the left is divided into age groups for recording the mother’s time at risk and number of births for computing age-specific fertility rates. Family reconstitution began as a manual process, and it resisted computerization for a long time.15
Figure 2.

Family Reconstitution Form
Source: E. A. Wrigley, David Edward Charles Eversley and Peter Laslett, An Introduction to English Historical Demography, from the Sixteenth to the Nineteenth Century with Contributions by W. A. Armstrong and Lynda Ovenall, (New York, 1966), 126.
Data quality was a central concern for Henry and his co-authors. They were acutely aware of the limitations of the parish registers, and they went to great lengths to evaluate their sources. The first chapter in Henry’s Manuel de démographie historique is “Vérification des données.” His technical manuals offer tools for detecting and estimating missing events. Fertility rates in each of the regional reports on the Enquête Henry are adjusted to correct for births that were not reported as baptisms.16
The central problem in Family Reconstitution is the handling of incomplete life histories. Incomplete histories are a difficult problem, because the parish registers did not record migration. Almost all Family Reconstitution studies are local, because searching for people over a wider area is difficult and expensive, and even families who moved to an adjacent parish will have incomplete histories. We only know that a person was present in community when an event (birth, marriage, burial) was recorded for them or a close family member. Migration took place sometime after the last recorded event, but there is no way to know how long the family were present before they moved away.
Fleury and Henry recognized that the use of incomplete histories could bias the analysis of family reconstitution data, and they introduced strict rules for selecting which families should be included. Family histories can only be used in an analysis when the event ending the history is unrelated to the subject of the analysis. If the analysis is about fertility, family histories that end with a birth or the death of a child must be excluded, because they will over-estimate the level of fertility. Statisticians now call this principle “non-informative censoring”.17
We can illustrate this problem by imagining a population consisting of couples with only two fertility patterns. Suppose that some couples have a birth every three years, and the rest have a birth every five years. Assume also that there are the same proportion of out-migrants in each group, and that the timing of migration is random with respect to childbearing. The last event that we observe in the migrant families will be a birth or the death of a child, because the husband and wife will die somewhere else. Under these assumptions, the average time between the last observed birth and the migration date will be longer in the families with long birth intervals than among those with short birth intervals. By construction the maximum time between last birth and migration will be five years for couples with longer birth intervals instead of three years for the short interval couples. This is time that should be included in the denominator of the fertility rate, because the couple could have had a birth in the study area during this time. However, we cannot measure the time between last birth and migration, because migration was not recorded in the parish registers. If we use the date of the last observed birth to close family histories, we will be excluding more time at risk from the low fertility couples than from the high fertility couples. Consequently, the fertility rates that we compute will be too high.
Unfortunately, this important principle was asserted but not explained in the seminal texts on Family Reconstitution. Fleury and Henry made the point in this way:
As the date of the end of union holds an essential place in the study of fertility, it is only usable when it is known independently of any document, death or marriage in particular, concerning the children; not respecting this rule favors the most fertile families and leads to an over-estimation of fertility.18
Since the Henry manuals were never translated into English, the most detailed account of Family Reconstitution appeared in Wrigley, Eversley, and Laslett. They gave this version of the same point:
…it is clear that evidence from this FRF could not be used in the study of marital fertility. The continued residence of the family in the parish is known only because of the baptism and burial of children. The burial of the parents is not recorded in the register. If they had been childless nothing would have been known about them after their marriage and they would not have been included in any study of marital fertility. If families whose residence in the parish is known only from entries about their children in the baptism and burial registers are included in the calculation of marital fertility rates, the rates which result will be higher than the true rates. 19
Even if it was not fully explained, the prohibition of informative censoring was embedded in the rules and procedures for dating the end of observation of the family. The period of observation for the analysis of fertility is usually closed by the date of death of the spouse that died first. A census or tax document showing that the couple were present in the study area may be used to close observation when the couple died somewhere else. However, when the last document pertaining to the family is a baptism, child death, or marriage of a child, the end of observation is considered “open,” and the family cannot be used in computing fertility rates. The computation of age-specific fertility rates also requires both the date of marriage and the age of the mother, which is usually obtained by linking to her baptism. These dates will not be available if the couple migrated into the study area after marrying somewhere else. More than half of the families in a parish are usually excluded from fertility analysis because they lack dates required to begin or end observation. Thus, Family Reconstitution describes the sedentary population who spent their entire lives in a single parish.20
The European Fertility Project
The European Fertility Project under the direction of Ansley Coale was one of the first “big data” projects in historical demography. Conceived as a test of Demographic Transition Theory, the European Fertility Project was designed to measure the impact of economic development on fertility decline in nineteenth-century Europe. Under the influence of books like The Population Bomb, concern about the rapid growth of population in Africa and Asia had spread from academic and policy circles to the general public. Coale’s earlier work had shown how rapid population growth could inhibit economic development. Demographic Transition Theory stressed the impact of industrialization and urbanization on the costs of children and attitudes about large families, and demographers debated whether fertility decline was possible without economic development.21
Coale and his associates set out to map patterns of economic development and fertility by using the abundant records of censuses and vital registration available for Europe from the middle of the nineteenth century. Most countries had published annual counts of births, marriages, and deaths as well as decennial counts of population by age and sex at the provincial and often the district level, and these publications were easily available in libraries on both sides of the Atlantic. The European Fertility Project collected and digitized these data for all of Europe from Ireland to Russia. Books and articles were published on fourteen countries, and the implications of the project were described in an influential summary volume.22
The findings of the European Fertility Project had far-reaching impacts in contemporary as well as historical demography. Maps, like Figure 3, dramatically undermined the assumption that industrialization, urbanization, and demographic change moved together, as described in Demographic Transition Theory. France stands out clearly in Figure 3 as the early leader in fertility decline. The fertility transition in England, which was the first industrialized country in the world, lagged France by at least half a century. Paul Demeny anticipated this result in the early years of the project in an article showing that fertility decline in Hungary, one of the least industrial areas in nineteenth-century Europe, was almost simultaneous with the decline in England. The distinctive imprint of French borders in Figure 3 also points to the unexpected importance of national and linguistic boundaries in fertility decline. Ron Lesthaeghe showed that the timing of fertility decline varied systematically between pairs of villages on opposite sides of the border between Flemish- and French-speakers in Belgium. The importance of language had also been anticipated in a study of Spain by William Leasure, whose PhD adviser was Ansley Coale.23
Figure 3.

Timing of Fertility Decline in Europe
Source: Ansley J. Coale and Susan Cotts Watkins, The Decline of Fertility in Europe: The Revised Proceedings of a Conference on the Princeton European Fertility Project (Princeton NJ, 1986).
The evidence produced by the European Fertility Project turned attention away from socio-economic explanations of fertility decline toward the study of attitudes and culture. Coale did not dismiss the importance of socio-economic factors, but he also emphasized knowledge and attitudes about birth control. Knodel and van de Walle suggested that the diffusion of information and attitudes toward favorable toward birth control played a key role in the fertility transition. These conclusions were important in the contemporary debate between those who advocated family planning programs in high fertility countries and others who argued for the necessity of economic development.24
Maps like Figure 3 are derived from new measures of fertility developed for the European Fertility Project. The data available to the project posed a familiar problem for demographic research. Aggregate measures, like the crude birth rate (births divided by total population), are sensitive to differences in age, sex, and marital status distributions across populations. Places with early marriage and young populations are likely to have higher crude birth rates than places with late marriage and older populations. Demographers prefer to solve this problem by computing age-specific birth rates separately for married and unmarried women, which can then be summarized by a weighted average. These computations require tables of births by age and marital status of mother as well as census counts of all women by age and marital status. The European Fertility Project had the latter but not the former. National statistical offices rarely published births by age of mother in the nineteenth century. So, Coale turned to a technique that was well known to demographers and actuaries, Indirect Standardization.
Indirect Standardization assumes that the age-specific rates of a population of interest are a constant proportion of the age-specific rates in a reference population. This assumption can be represented as
| (1) |
where
is the age specific fertility rate for age in population ,
is the age specific fertility rate for age in a standard population (), and
is a constant for all age groups.
Under this proportionality assumption we can solve for a multiplier or index () that can be used to convert rates in the standard population to rates in the population of interest.25
The solution involves calculating the expected number of births that would have occurred in the standard population if it had the same age distribution as the population of interest. The formula is
| (2) |
where
is the number of women at age in population ,
is the total number of births to all women in population , and
is the total number of births that women in population would have had if they had the fertility rates in the standard () population.
Although they did not have age-specific fertility rates, the European Fertility Project did have the total number of births, which is the numerator in Equation 2, and the number of women at each age required to compute the denominator. The Project used age-specific fertility rates of the Hutterites, an American religious sect known for their high fertility, as the standard in these calculations. In addition, the Project ingeniously devised an equation separating the effects of marriage, illegitimate fertility, and fertility within marriage.
| (3) |
where
= Index of overall fertility,
= Index of marital fertility (relative to the Hutterites),
= Index of non-marital fertility, and
= Index of marriage.
All of these indexes are scaled to Hutterite fertility, including the illegitimacy and marriage measures. An index of marital fertility () of .7 implies that married women were having children at 70% the rate of Hutterite married women. The index of marriage () is not a pure measure of marriage patterns. Age groups are weighted by their level of fertility in the Hutterite population, so an index of marriage () of .6 implies that marriage patterns reduced the potential fertility of the population by 40%.
As we will see, the proportionality assumption behind the European Fertility Project indices continues to play a central role in historical demography. It is based on confidence that demographic processes follow patterns determined by biological and social regularities. Coale was one of the foremost developers of demographic measurement techniques based on this assumption. There are certainly occasions when the assumptions behind indirect standardization are not acceptable, and the methods used by the European Fertility Project to date fertility transitions have been questioned. Nevertheless, the European Fertility Project fertility indexes enabled comparisons of fertility and marriage across time and space on an unprecedented scale.26
Back Projection
In 1985 the JIH published a special issue examining the implications of The Population History of England 1541–1875. The Population History of England was much more than an incremental addition to knowledge about the size of the English population. Wrigley and Schofield presented annual estimates of the full range of demographic indicators for population size, age structure, mortality, fertility, and nuptiality. Underlying this work was a powerful new technique, Back Projection, with a fully articulated demographic model. Back Projection is an extension of Inverse Projection, a method invented by Ronald D. Lee 67 that used well known demographic tools in a new way.27
As mentioned above, Wrigley had been describing demographic history in terms of the Malthusian model since the 1960s, and he drew particular attention to the potential role of late marriage in moderating the rate of population growth and the recurrence of subsistence crises. The Population History of England provided evidence that population growth reduced the standard of living, as Malthus claimed, but it argued that poorer living conditions reduced marriage in a way that dampened the cycle of growth and crisis. Wrigley and Schofield also added a new element to the history of modern population growth. The standard account attributed the beginning of modern population growth in the eighteenth century to a decrease in mortality, partly due to the absence of bubonic plague. The back projection estimates showed an increase in fertility during the eighteenth century as well. Wrigley and Schofield argue that rising fertility was due to an increase in marriage, which began as a Malthusian response to rising wages. However, the early development of manufacturing in England loosened Malthusian constraints and sustained higher marriage and fertility rates into the nineteenth century. David Weir demonstrated that this increase in marriage was due to a decrease in permanent celibacy not to younger ages at marriage.28
In demographic terms Back Projection operates in the opposite direction of the European Fertility Project indices and SMAM. Where Coale and Hajnal used population counts from censuses to estimate events (births, marriages), Wrigley and Schofield used events (births and deaths) to estimate population counts for a time before censuses were conducted. The conventional approach to population projection is the “cohort component” method. A projection begins with a baseline population divided into subgroups by age and sex. In each period the subgroups are multiplied by selected mortality, fertility, and out-migration rates to calculate numbers of deaths, births, and migrants, which determine the population at the beginning of the next period. Thus, a projection consists of a known starting population and a set of hypothetical rates. Lee inverted this procedure by using numbers of births, deaths and migrants to estimate rates. Lee’s Inverse Projection finds a set of rates that produces the observed number of events.29
At its heart Inverse Projection uses a simplifying assumption about demographic rates that is a variant of Indirect Standardization. Lee reduced the universe of possible demographic rates by considering sets of rates that could be identified by a single parameter. For fertility he assumed that the age-specific fertility rates in any time period are all proportional to a set of standard rates, i.e. the same assumption as the European Fertility Project shown above in Equation 1. For mortality Lee used a model in which rates are related by a linear model where
| (4) |
where
is the death rate in age group at time ,
and are constants depending only on age, and
is a constant depending only on time period.
This model has the same property that we saw in Equation 2. It is possible to solve for by using the total number of deaths, the constants ( and ), and the number of people at each age. Thus, Lee is able to turn a single number, total deaths, into a set of age-specific rates for each period. These rates are applied to the starting population to estimate deaths at each age and the surviving population at the end of the period.30
As its name implies, Back Projection is a modification of inverse projection that operates backwards in time. The assumptions in Inverse Projection are straightforward, but back projection requires additional assumptions, which were described by Jim Oeppen in the original volume. Lee criticized the assumptions in Back Projection, but he reproduced most of the results in The Population History of England using Inverse Projection. Oeppen later developed a more general version back projection that integrates more data in the calculations.31
The Cambridge Group shared the attention to data quality that we find in Henry’s work. The first 154 pages of The Population History of England 1541–1871 is devoted to evaluating data quality and correcting for problems. Not to be outdone, the Cambridge Group family reconstitution volume has five appendices on data quality as well as numerous discussions in the text.32
Models in Historical Demography Today
In the 1990s historical demography entered a new phase that differed in important ways from the work of the pioneers like Henry, Hajnal, Coale, Wrigley, and Schofield. The types of models used in historical demography shifted from demographic to statistical. Where key features of earlier research can be linked to Life Tables and Stable Population Theory, multiple regression became the dominant organizing framework. Regression was not new in quantitative historical research, but several developments allowed it to assume new importance in historical demography: changing research questions, easier access to individual-level data, and new methods.
First, the focus of research in historical demography shifted away from long-run trends in national populations toward differences within populations. On one hand, this was a tribute to the success of the previous generation of studies. Henry’s team at INED had reconstructed population dynamics in France back to 1740, and the Cambridge Group had taken England back to 1541. While there could still be debate about the quality and the meaning of those estimates, they were widely accepted. On the other hand, the study of differential experiences by class, race, and ethnicity has a long history in demography, and it was never absent from historical demography. In the 1980s and 1990s studies focusing on socio-economic differences became much more common. Simon Szreter assigns an important role to sub-national “communication communities” that have both social and geographic dimensions. 33
Second, large-scale databases and comparative projects became much more important. Family Reconstitution created a template for village studies that could be completed by a solitary scholar. The operations of transcribing the original documents and linking individuals to families were done on paper, and computers were only used for the final calculation of tables if at all. Even the European Fertility Project was organized as a series of single-author national monographs. This began to change in the 1980s as new computer technology dramatically reduced the cost of collecting and analyzing historical data. Instead of transcribing documents to paper coding forms and then to punch cards, data could be typed directly into inexpensive personal computers. Flexible database software reduced the costs of managing data and allowed consistency checks to be built into data entry programs. New technology accelerated a trend toward larger databases intended for broad research programs, such as the Programme de Recherche en Démographie Historique in Quebec, the Demographic Data Base at the University of Umeå, the Utah Population Database, the Historical Sample of the Netherlands, and the TRA Project in France. In 1999 the North Atlantic Population Project was formed to create comparative samples of historical population censuses based on the model established by the Integrated Public Use Microdata Series led by Steven Ruggles in the U.S. The new databases welcomed researchers to study a wide range of questions.34
An important subset of these databases focused on population registers, which have important advantages for demographic analysis. The key difference between parish registers and population registers is explicit reporting of migration in the latter. Population registers are not exempt from the principles that motivated Henry’s rules for Family Reconstitution, but the availability of clear dates for entry and exit from observation allows the experiences of migrants to be analyzed. Population registers also tend to have more socio-economic information than parish registers. Since they were usually maintained for administrative rather than religious reasons, population registers often have consistent reporting of occupations. In addition, population registers are organized as lists of individuals within households, which allows for the dynamic study of co-residence. Etienne van de Walle demonstrated the advantages of population registers in studies of the Belgian village of La Hulpe. Since then historical demographers have used population registers or similar documents from Belgium, China, Italy, Japan, Korea, Netherlands, Taiwan, Russia, and Sweden.35
Third, technology for statistical analysis, especially Event History Analysis, was catching up to the needs of historical demographers interested in comparative analysis. Tables of age-specific rates can be used for simple comparisons, but they quickly become unwieldy as the number of dimensions (time period, marital status, occupation, urban/rural residence, etc.) increases. Statisticians were developing regression models allowing for multiple explanatory variables in the 1970s, but they did not become available in general purpose statistics packages, like SAS and Stata, until the late 1980s and 1990s. In particular, the Cox proportional hazards model allowed historical demographers to examine the effects of individual-level characteristics, like occupation and family size, on demographic events.36
The Eurasia Project on Population and Family History illustrates all of these trends. The Eurasia Project grew out of a 1994 meeting called by Akira Hayami to discuss methods of analysis for historical population registers. The outcome was a comparative study of demographic responses to economic stress in five societies (Belgium, China, Italy, Japan, and Sweden) that produced three comparative volumes and dozens of papers at international meetings and conferences. The questions addressed by the Eurasia Project were not new. In fact, they can be traced in a direct line back to Malthus. But these questions were posed in new ways.37
The shift from long-run trends to individual-level comparisons can be seen in the Eurasia Project’s focus on individuals within families. The statistical model used in the Eurasia Project was an extension of the Cox proportional hazards model to allow the inclusion of annual grain prices with time lags as community-level variable. The statistical model included both individual (e.g. age, sex, relationship to household head) and household (size, occupation of household head, numbers of children, working-age adults, and elderly), and attributes were interacted with the price variables to examine the effects of these characteristics on responses to economic hardship.38
Many previous studies had shown that fertility, mortality, and marriage responded to fluctuations in harvests and food prices in pre-industrial populations, including Dorothy Thomas’s pioneering work, and this had been the subject of a chapter by Ron Lee in the Cambridge Group Back Projection volume. The Eurasia Project took demographic responses for granted and asked: Who in the family was most affected by hard times in different family systems? Malthusian theory predicts that mortality responses to prices should have been weaker in the “low pressure” European populations, and anthropological theories suggest stronger biases against females in the Asian families. But the results were rarely simple. Overall, death rates in the European communities were as susceptible to high prices as in the Chinese and Japanese case studies. However, status within households tended to be more important in the Asian cases. For example, high prices and competition with other members of the household (e.g. grandparents) were more harmful to girls (ages 2–14) than to boys in the Asian families.39
The most important differences between Europe and Asia were in the areas of nuptiality and fertility. Malthus was correct in emphasizing the importance of late marriage in Europe, but he dismissed the idea that Asians could be controlling family size by regulating their reproduction. Both the Chinese and Japanese families in the Eurasia Project were using infanticide in deliberate ways. Tsuya and Kurosu show clearly that Japanese couples not only limited family size, but also selected the order in which boys and girls were born. As a result, the number of births per couple was very similar between East and West, but population growth was lower in the Asian populations because of higher mortality. When population growth increased, Europeans often responded with migration before they adopted fertility control, as in our Belgian case study. 40
Over the course of the Eurasia Project the Cox model went from a novelty to a standard tool for historical demographers. The JIH supported the diffusion of Event History Analysis by publishing an issue devoted to papers resulting from the ICPSR summer course on Longitudinal Analysis in Historical Demography created by Myron Gutmann and myself.41
Event History Analysis as a Demographic Model
When Event History Analysis appears in a publication, it is usually described in the same way as other regression models with tables of estimated coefficients for explanatory variables. If we look below the surface, however, we find that Event History Analysis is built on the same tools that were used by Hajnal, Henry, Coale, Wrigley, and Schofield. In the case of the Cox proportional hazards model, there is no need to speculate on its debt to the Life Table. Cox himself made the connection in the first of his two seminal articles “Regression Models and Life Tables.” We can go beyond this to point out that proportional hazards models, like the Cox model, are also a form of Indirect Standardization.42
Event history models are usually expressed in terms of the hazard function for an event. Hazard rates are conditional probabilities that the event will occur at a moment in time as measured from some starting point. For example, the risk of dying varies by time since birth (age). It is high immediately after birth, decreases to a minimum in late childhood, and then rises (sometimes irregularly) into old age. Since the risk is not constant, most event history models cannot be subsumed into simpler statistical models assuming constant risks, like a Poisson process or Markov chain. The hazard rate of a Life Table is a well-known quantity called the “force of mortality,” which is designated by and related to the mortality rate by this equation:
| (5) |
in which is the age-specific death rate for ages to .43
Estimation procedures for event history models usually involve simplifying assumptions, the most common of which is proportional hazards. The Cox proportional hazards model simplifies the model in this way
| (6) |
where
is the hazard rate at time t for an individual with explanatory variables
is hazard function for a standard individual, and
are parameters describing the effects of the explanatory variables.
The Cox model is a proportional hazards model, because an explanatory variable has the same proportional effect on the hazard rate regardless of time (). The proportional hazards assumption in Equation 6 is the same as the proportionality assumption that we saw in Indirect Standardization given in Equation 1. Both models assume that a standard set of age specific rates, in Equation 1 and in Equation 6, are modified proportionally by a case-specific index, Ii and . In other words, the Cox model is an elaborate form of Indirect Standardization.
Event history models are also similar to demographic models in the way that they focus on transition rates rather than average duration times. The expectation of life in a Life Table is equal to the average age at death. Following a cohort from birth until everyone has died works well for studies of fruit flies, but it is rarely feasible for human populations. However, we can calculate death rates by age from vital registration and census data, and these rates can be treated as the experience of a hypothetical cohort. The Life Table is an accounting tool for translating age-specific transition rates into expectation of life and numbers surviving at each age in this hypothetical cohort. Event History Analysis faces the same challenge. How can we compute the average survival of cancer patients if some of them are still alive? The answer is to focus on hazard rates, which can be computed at each point where we have data. Censored cases, patients who have not died, are used in the computation of the hazard rate until the time (duration) where they were last observed. Omitting censored cases will overestimate the hazard rate and underestimate the time lived by survivors. This is the same bias that Henry warned against when he created the rules for Family Reconstitution.
Lessons Forgotten
The apparent similarity between Event History Analysis and other regression models has had unfortunate consequences, because some authors seem to be unaware of the lessons of classic studies in historical demography. In particular, a number of published fertility studies use Family Reconstitution datasets that are biased, because they include family histories terminated with births or child deaths. These publications violate Henry’s rules for Family Reconstitution, and they produced biased results that are misinterpreted as new findings.
In a series of articles Jan Van Bavel claimed to be using Event History Analysis to detect evidence of birth spacing. Van Bavel is not alone in arguing that previous methods for detecting birth control do not reliably distinguish between stopping and spacing. He also criticizes Okun’s simulation study for not testing for situations where both stopping and spacing are present. But when Van Bavel proposes an alternative way to study birth spacing, he goes awry by focusing on closed birth intervals: “Secondly, a duration model could be developed for all closed birth intervals, representing the determinants of birth spacing and again including age and attained parity as two of the covariates.” In another paper he explained his intended analysis this way: “In this paper, the question asked is: given that another birth has occurred, what are the covariates of the length of the past birth interval?” Unfortunately, the method that he chose, Cox regression, does not answer that question. In fact, Cox regression does not look at the lengths of birth intervals at all. It analyzes transition rates, and by including only closed birth intervals Van Bavel omitted time at risk that should have been included in those rates. Selecting intervals that end in a birth, the event of interest, is a clear example of informative censoring, which leads to biased results.44
Event history models are estimated from duration-specific transition rates that compare the number of events to the number of women at risk at a moment in time. The Cox model actually ignores time altogether by using the order of events without considering the amount of time between them. By computing duration-specific rates event history models can include information from censored histories, i.e. histories that have not experienced the event. If we are studying birth intervals, the denominator of the hazard rate should include all women who were at risk of a birth, including those whose birth intervals were censored by migration or sterility. This piece-wise approach to the hazard function is the way that life tables are constructed, and it underlies the computation of age-specific fertility rates in Family Reconstitution. When informative censoring is correlated with explanatory variables, such as age and birth order, these variables do not ‘control’ for the effects of those variables, rather the estimated coefficients of these variables reflect the biases in the data. Omitting incomplete birth intervals does not make the model estimate the lengths of completed birth intervals, it produces biased estimates of the hazard rates.45
We can see the consequences of violating the rules of Family Reconstitution in Table 1. This table shows age-specific fertility rates computed from family reconstitutions based on six German village genealogies collected by John Knodel. The first two columns, labeled “Henry rules,” are computed using the strict rules described in the Henry manuals. Families are only included if we observe the death of at least one spouse or another event unrelated to childbearing, such as a census or divorce. The columns labelled “Incomplete histories” use only families that are excluded by the Henry rules. “Incomplete histories” end with a birth or the death of a child, because the family moved somewhere else before one of the spouses died. The columns labeled “Closed intervals” include all intervals that end in a birth which are drawn from intervals in both the “Henry rules” and the “Incomplete histories” columns.46
Table 1.
Age-specific Fertility Rates Calculated in Three Ways by Time Period, Six German Village Genealogies
| Henry rules | Incomplete histories | Closed intervals | ||||
|---|---|---|---|---|---|---|
| Age | Before 1875 | After 1875 | Before 1875 | After 1875 | Before 1875 | After 1875 |
|
| ||||||
| 15–19 | 0.400 | 0.383 | 0.596 | 0.711 | 0.443 | 0.589 |
| 20–24 | 0.454 | 0.428 | 0.559 | 0.472 | 0.498 | 0.539 |
| 25–29 | 0.396 | 0.356 | 0.472 | 0.384 | 0.454 | 0.471 |
| 30–34 | 0.343 | 0.263 | 0.431 | 0.341 | 0.424 | 0.420 |
| 35–39 | 0.267 | 0.192 | 0.435 | 0.372 | 0.415 | 0.444 |
| 40–44 | 0.137 | 0.078 | 0.520 | 0.449 | 0.499 | 0.527 |
| 45–49 | 0.019 | 0.008 | 0.463 | 0.567 | 0.784 | 0.928 |
Source: George Alter, “From Data Scarcity to Data Abundance,” Ann Arbor, MI: Inter-university Consortium for Political and Social Research [distributor], 2019–03–29. https://doi.org/10.3886/E109127V1
Violating the rules of Family Reconstitution has dramatic effects on the calculation of age-specific fertility rates, especially at older ages. The rates computed correctly show fertility decreasing with age, and the fertility transition after 1875 reduces rates at older ages more than at younger ages. Both of these features are absent when the rules are violated. As Henry warned, the inclusion of birth intervals with informative censoring over-estimates birth rates. The bias is greatest at older ages, because more time at risk is lost due to incomplete intervals.
Event history methods, including the Cox proportional hazards model (see Table 2), produce the same biased results as the simpler calculations in Table 1. When family histories end with informative censoring, the estimated coefficients for age do not decrease as we know they should. When only closed birth intervals are used, the estimated coefficients in Table 2 imply that the birth rates of women over age 45 were the same as those of women aged 25–29. This bias will also affect other variables if they are correlated with the process creating informative censoring. In particular, birth order (parity) is highly correlated with age, and we should expect birth rates and hazard rates computed on data with informative censoring to be biased too. Evidence of this bias is in the Cox regression estimates published by Van Bavel. In his 2004 study the relative risk of a birth above age 40 compared to under 25 is reported as 0.56, 1.03, and .94 for the 1830, 1850, and 1864 generations respectively. This would mean that women over age 40 were having children at the same rate as those under 25. Van Bavel and Kok suggest that the absence of age effects in this model is due to the control of marital duration, which is an indicator of coital frequency, but Wood estimates that most of the decrease in fecundability after age 35 is due to physiological changes.47
Table 2.
Relative Risks of a Birth by Age from Cox Proportional Hazards Regression Calculated in Three Ways by Time Period, Six German Village Genealogies
| Henry rules | Incomplete histories | Closed intervals | ||||
|---|---|---|---|---|---|---|
|
|
||||||
| Age | Before 1875 | After 1875 | Before 1875 | After 1875 | Before 1875 | After 1875 |
|
| ||||||
| 15–19 | 1.00 | 0.53 | 3.10 | 2.00 | 1.04 | 0.97 |
| 20–24 | 1.17 | 1.07 | 1.20 | 1.13 | 1.19 | 1.09 |
| 25–29 | ref. | ref. | ref. | ref. | ref. | ref. |
| 30–34 | 0.84 | 0.78 | 0.83 | 0.92 | 0.86 | 0.88 |
| 35–39 | 0.63 | 0.64 | 0.78 | 0.97 | 0.75 | 0.91 |
| 40–44 | 0.31 | 0.30 | 0.70 | 1.12 | 0.71 | 0.96 |
| 45–49 | 0.07 | 0.06 | 0.61 | 1.09 | 0.94 | 1.53 |
| Observations | 78,868 | 47,942 | 3,458 | 12,556 | 64,566 | 39,575 |
| Births | 14496 | 8,110 | 827 | 3,168 | 15,101 | 9,945 |
| Time at risk | 57284.76 | 43,327 | 1,950 | 9,652 | 36,869 | 24,007 |
Source: Alter, “From Data Scarcity to Data Abundance.”
When we understand that the Cox model compares duration-specific rates and not the lengths of completed intervals, Van Bavel’s claim that he is measuring spacing falls apart. As I will show in the next section, the Cox model cannot distinguish between stopping and spacing, and a change in stopping will usually violate the proportional hazards assumption in the model. Unfortunately, this erroneous interpretation of the Cox model has been adopted by others, like Cinnirella, Klemp, and Weisdorf who also base their analysis on only closed birth intervals.48
Avoiding informative censoring does impose substantial costs on family reconstitution, because Henry’s rules typically remove between 40 and 60 percent of family histories from analysis. Fialova, Tesarkova and Kuprova compare the strictest version of Henry’s selection rules to an “extended” sample in which the family history ends with a birth only when no other event is available. Their dataset drops from 5,588 to 1,290 observations when the stricter rules are applied. Fialova and her colleagues see the same patterns in both samples, but the magnitudes of coefficients estimated by the Cox model are sometimes very different. Alternatives to dropping incomplete family histories involve much more complicated computations. Jonker and van der Vaart developed a maximum likelihood approach, and Alter, Devos, and Kvetko show that migration dates can be imputed in some situations.49
These comments are not meant to reject the idea that intentional postponement of births may have been important in historical populations. (See for example Reher and Sanz-Gimeno.) The point here is methodological not substantive. Van Bavel has done very innovative work on the fertility transition and other topics, and his hypotheses about associations between birth spacing and other variables may turn out to have merit. But we can only evaluate those hypotheses when our methods fit both the data and the question. Publications based on these flawed methods betray a loss of knowledge previously shared by historical demographers as well as a misunderstanding of the new tools that Event History Analysis has provided. The old tools, like the Life Table, can guide us in using new tools more effectively.50
Moving Forward with Old and New Tools
The issue of stopping and spacing provides an example of the benefits of combining old and new models of historical demography. Figure 1 which is used above to illustrate Hajnal’s Singulate Mean Age at Marriage also shows how we can distinguish stopping and spacing in fertility histories. Compare Figure 1 to Figure 4. These are both survival curves. In Figure 1 the height of the curve is the proportion of women who survived from birth to each age without marrying. The curve in Figure 4 is the proportion of women who have not yet given birth to their next child. The methods used to obtain the curves are somewhat different. Figure 1 plots percentages by marital status from a census. The survival curves in Figure 4 were estimated with the Kaplan-Meier procedure. But both figures show processes in which a part of the population never experiences the event of interest, i.e. marriage or childbirth.51
Figure 4.

Kaplan-Meier Survival Curves for Women Who Have Not Given Birth by Time Since Last Birth and Time Period, Six German Village Genealogies (Source: Alter, “From Data Scarcity to Data Abundance.”)
The fact that some people will never marry or have another birth distinguishes nuptiality and fertility from the analysis of mortality and from most event history methods. The curves in both Figures 1 and 4 become flat before reaching zero. Hajnal used the flat part of the curve to measure the percentage of women who will never marry. We can use the height of the curve in Figure 4 to measure stopping, and, like Hajnal, we can adjust the curve to measure spacing by subtracting the proportion who stop. Using the Kaplan-Meier estimate of uncompleted birth intervals after 15 years as our measure of stopping, we can compute an adjusted survival curve for completed birth intervals. The computation of average birth intervals is slightly different from the way that SMAM is estimated, because the Kaplan-Meier curve corresponds to the number of survivors at an exact age (lx) in the Life Table. Results for the data in Figure 4 are shown in Table 3.
Table 3.
Measures of Stopping and Spacing in Six German Village Genealogies
| Percent of birth intervals not completed | Average length of completed birth intervals | |||
|---|---|---|---|---|
|
|
||||
| Before 1875 | After 1875 | Before 1875 | After 1875 | |
|
|
||||
| All | 10% | 17% | 2.64 | 2.65 |
| Number of previous births | ||||
| 1 | 3% | 8% | 2.36 | 2.44 |
| 2 | 5% | 14% | 2.52 | 2.66 |
| 3 | 7% | 15% | 2.61 | 2.73 |
| 4 | 8% | 18% | 2.60 | 2.76 |
| 5 | 13% | 20% | 2.61 | 2.75 |
| 6 | 14% | 25% | 2.68 | 2.56 |
| 7 | 22% | 25% | 2.70 | 2.49 |
Source: Alter, “From Data Scarcity to Data Abundance.”
Table 3 suggests that the German fertility transition involved an increase in stopping from 10% to 17% of all birth intervals with no change in the average birth interval. This is somewhat misleading, because stopping also changes the distribution of birth intervals by birth order and age of mother. Women who stop after two children are never at risk of third, fourth, or fifth births. For this reason, it is more informative to analyze birth intervals separately by parity for historical data as in the work of Reher, Sandstrom, Sanz-Gimeno and van Poppel and Casterline and Odden for contemporary data. When we look at stopping and spacing by number of previous births, the picture is a little different. Stopping increased more among women with 2–6 children than among those with 1 or 7. Average lengths of birth intervals increased slightly at lower parities, but birth intervals became shorter for women with 6 or 7 children.52
Figure 4 should also be seen as a warning that common event history methods cannot be used to distinguish between stopping and spacing. The Cox model has no way of identifying stopping and spacing separately. Assuming that the baseline hazard rate goes to zero at some point (i.e. the survival curve becomes horizontal), a proportional increase in the hazard rate will result in shorter birth intervals and fewer open intervals, i.e. less spacing and less stopping. A decrease in the hazard rate at all durations will increase spacing and increase stopping. The model does not allow stopping and spacing to move independently, as we see in Figure 4 and Table 3. Moreover, the survival curves in Figure 4 cross, which cannot happen if hazard rates change proportionally at all durations. In other words, birth intervals were changing in ways that violated the proportional hazards assumption in the Cox model.53
Fortunately, there are ways to estimate models with explanatory variables that affect stopping and spacing separately. The Cure Model also known as the Split Population Model is a type of mover-stayer model with an event history component. When a new medical treatment is introduced, some of the population are “cured” and will not die of the disease. Even those who die may live longer because of the treatment. The Cure Model has two branches for estimating the effects of explanatory variables on the “cure fraction” and on the timing of transitions separately. The “cure fraction” is analogous to the proportion who never marry or never have another birth. There have only been a few applications of the Cure Model in demography including work in historical demography by Anjelique Janssens. 54
Another promising development is the introduction of sequence analysis to historical demography. Sequence analysis describes a life history as a trajectory composed of states marked by important events (starting school, leaving home, marriage, childbirth). Differences between individuals can be ranked in terms of the similarity of the types, order, and timing of events in their lives, which makes it possible to identify clusters of individuals with similar experiences. Unlike event history analysis, which focuses on a single event, sequence analysis considers all of the events in a life history. Bras and Schumacher use this approach to study the effect of age gaps between husbands and wives on childbearing trajectories. They find that more egalitarian relationships were more conducive to fertility control.55
Conclusion
In 1996 Coale and Trussell reviewed the development of demographic models and commented on recent changes in demographic research.
The decline in the use of demographic models coincides with the increasing availability of the wealth of survey data collected by the World Fertility Survey and the successor Demographic and Health Surveys. These data are frequently used -- without any comparison with demographic models to assess their validity -- to analyse individual, not aggregates behaviour. The techniques demographers use to analyse these data are increasingly the techniques of statistics, particularly event-history analysis. While the trend toward the use of sophisticated statistical models appropriate for the problem to be analysed and the data that are available is healthy, the trend toward accepting demographic survey data at face value is not.56
A similar development was occurring in historical demography at the same time. There has been a trend away from aggregate analysis based on demographic models toward statistical analysis of individual level data. As a participant in and promoter of this trend, I am not arguing against it. New questions, data, and techniques are healthy developments in any field of inquiry. However, I do agree with Coale and Trussell that much is lost if we forget the lessons of earlier generations. I have tried to show that demographic models can provide deeper insight into statistical models, and there is no substitute for understanding the processes that we are studying. We should be particularly skeptical of research that emphasizes statistical significance for results that make no demographic or biological sense.
The classic generation of historical demography left us an important legacy. Their work should be studied not only for the important results that they achieved, but also for their sophisticated understanding of demographic processes and their obsession with data quality.
Acknowledgment:
I am very grateful for helpful comments on earlier drafts from Göran Broström, Myron Gutmann, and Emily Merchant.
References
- 1.Goubert Pierre, Historical Demography and the Reinterpretation of Early Modern French History: A Research Review The Journal of Interdisciplinary History, 1 (1970), 37–48 [Google Scholar]
- 2.Fauve-Chamoux Antoinette, Bolovan Ioan and Sogner Sølvi (eds.), A Global History of Historical Demography: Half a Century of Interdisciplinarity, (Bern, 2016); [Google Scholar]; Boudjaaba Fabrice, Gourdon Vincent, Oris Michel, Robin Isabelle and Trévisi Marion, “50 ans De Démographie Historique : Bilan Historiographique D’une Discipline En Renouvellement,” Annales de Démographie historique, 129 (2015), 7–8; [Google Scholar]; Gutmann Myron P. and Merchant Emily Klancher, Historical Demography, in Poston Dudley (ed.), Handbook of Population, forthcoming). [Google Scholar]
- 3.Hajnal John, “European Marriage Patterns in Perspective, In Population in History: Essays in Historical Demography,” in Glass DV and Eversley David Edward Charles (eds.), (Chicago, 1965), 101–143; [Google Scholar]; Hajnal John, “Two Kinds of Preindustrial Household Formation System,” Population and Development Review, 8 (1982), 449–494; [Google Scholar]; Hajnal John, “Age at Marriage and Proportions Marrying,” Population Studies, 7 (1953), 111–136. [DOI] [PubMed] [Google Scholar]
- 4.Laslett Peter, “Characteristics of the Western Family Considered over Time,” Journal of Family History, 2 (1977), 89–115; [Google Scholar]; Le Play Frédéric, L’Organisation de la Famille Selon Le Vrai Modèle Signalé par l’Histoire de Toutes les Races et de Tous les Temps (Paris, 1895); [Google Scholar]; Laslett Peter, “Size and Structure of the Household in England over Three Centuries,” Population Studies, 23 (1969), 199–223; [DOI] [PubMed] [Google Scholar]; Laslett Peter, “The Comparative History of Household and Family Journal of Social History,” 4 (1970), 75–87; [Google Scholar]; Wrigley EA, Population and History (New York, 1969); [Google Scholar]; Malthus Thomas R., An Essay on the Principle of Population, as It Affects the Future Improvement of Society. With Remarks on the Speculations of Mr. Godwin, M. Condorcet, and Other Writers (London,, 1798); [Google Scholar]; Wrigley EA and Schofield RS, The Population History of England, 1541–1871 : A Reconstruction (London, 1981); [Google Scholar]; Schofield Roger S., “Through a Glass Darkly: The Population History of England as an Experiment in History,” The Journal of Interdisciplinary History, 15 (1985), 571–593. [Google Scholar]
- 5.Preston Samuel H., Heuveline Patrick and Guillot Michel, Demography : Measuring and Modeling Population Processes (Oxford; ; Malden, Mass., 2001), xiii, 291 p. [Google Scholar]
- 6.Sogner Sølvi, “Historical Demography in Norway 1960–2010, In A Global History of Historical Demography: Half a Century of Interdisciplinarity,” in Fauve-Chamoux Antoinette, Bolovan Ioan and Sogner Sølvi (eds.), (Bern, 2016); [Google Scholar]; Fleury Michel and Henry Louis, Des Registres Paroissiaux a L’histoire De La Population: Manuel De Dépouillement Et D’exploitation De L’état Civil Ancien, (Paris, 1956), 142–144; [Google Scholar]; Le Mée René, “De La Naissance De La Démographie Historique À L’enquête Henry Population (French Edition),” 50 (1995), 1475–1487; [Google Scholar]; Fauve-Chamoux Antoinette, Bolovan Ioan and Sogner Sølvi, A Global History of Historical Demography: Half a Century of Interdisciplinarity, (Bern, 2016). [Google Scholar]
- 7.Rosental Paul-André, “The Novelty of an Old Genre: Louis Henry and the Founding of Historical Demography,” Population, 58 (2003), 103–136; [Google Scholar]; Terrisse Michel, “Aux Origines De La Méthode De Reconstitution Des Familles. ‘Les Suédois D’estonie’,” De Hannes Hyrenius Population (French Edition), 30 (1975), 143–155; [Google Scholar]; Rosental Paul-André, L’intelligence Démographique (Paris, 2003). [Google Scholar]
- 8.Henry Louis, Anciennes Familles Genevoises; Étude Démographique: Xvie-Xxe Siècle, (Paris, 1956), 232; translated by author, emphasis in original. [Google Scholar]
- 9.Henry Louis, “Une Richesse Démographique En Friche: Les Registres Paroissiaux,” Population (French Edition), 8 (1953), 281–290; [Google Scholar]; Goubert Pierre, “Une Richesse Historique En Cours D’exploitation: Les Registres Paroissiaux,” Annales. Histoire, Sciences Sociales, 9 (1954), 83–93; [Google Scholar]; Rosental Paul-André, “Thirteen Years of Thinking: From Population History to Historical Demography (France 1945–1958),” Population, 51 (1996), 1211–1238; [Google Scholar]; Fauve-Chamoux Antoinette, “Historical Demography and International Network Developments (1928–2010),” in A Global History of Historical Demography: Half a Century of Interdisciplinarity,” in Fauve-Chamoux Antoinette, Bolovan Ioan and Sogner Sølvi (eds), (Bern, 2016), 15–66. [Google Scholar]
- 10.Séguy Isabelle, Colençon H, Méric C and le Sager F, La Population De La France De 1670 À 1829 : L’enquête Louis Henry Et Ses Données (Paris, 2001), xvi, 208; [Google Scholar]; Henry Louis and Blayo Yves, “La Population De La France De 1740 a 1860,” Population (French Edition), 30 (1975), 71–122; [Google Scholar]; Blayo Yves, “Mouvement Naturel De La Population Française De 1740 a 1829,” Population (French Edition), 30 (1975), 15–64. [Google Scholar]; Henry Louis, “Fécondité Des Mariages Dans Le Quart Sud-Ouest De La France De 1720 À 1829 (I),” Annales (1972), 612–640; [Google Scholar]; Henry Louis, “La Fécondité Des Mariages Dans Le Quart Sud-Ouest De La France, De 1720 À 1829 (Suite),” Annales (1972), 977–1023; [Google Scholar]; Houdaille Jacques and Henry Louis, “Fécondité Des Mariages Dans Le Quart Nord-Ouest De La France De 1670 À 1829,” Population (1973), 873–924; [Google Scholar]; Houdaille Jacques, “La Fécondité Des Mariages De 1670 À 1829 Dans Le Quart Nord-Est De La France,” Annales de Démographie historique (1976), 341–391; [PubMed] [Google Scholar]; Henry Louis, “Fécondité Des Mariages Dans Le Quart Sud-Est De La France De 1670 À 1829,” Population (1978), 855–883; [Google Scholar]; Bideau Alain and Bardet Jean-Pierre, “Une Géographie Très Contrastée,” in Dupâquier Jacques, Sauvy Alfred and Le Roy Ladurie Emmanuel (eds.), Histoire De La Population Française (Paris, 1988), 364–372. [Google Scholar]
- 11.Rosental, “Novelty of an Old Genre,” 103–136.; [Google Scholar]; Henry Louis, On the Measurement of Human Fertility: Selected Writings of Louis Henry (Amsterdam, New York,, 1972), xix, 228; [Google Scholar]; Henry Louis, “Fondements Théoriques Des Mesures De La Fécondité Naturelle,” Revue de l’Institut International de Statistique / Review of the International Statistical Institute, 21 (1953), 135–151. [Google Scholar]
- 12.Henry Louis, “Some Data on Natural Fertility,” Eugenics Quarterly, 8 (1961), 81–91. [DOI] [PubMed] [Google Scholar]
- 13.Henry Louis, Anciennes Familles Genevoises, 71–110, 178–179. [Google Scholar]
- 14.Goubert, “Une Richesse Historique “; [Google Scholar]; Gutmann and Merchant, “Historical Demography,” ; [Google Scholar]; Knodel John E. and van de Walle Etienne, “Lessons from the Past: Policy Implications of Historical Fertility Studies,” Population and Development Review, 5 (1979), 217–245; [Google Scholar]; Coale Ansley J., “The Demographic Transition Reconsidered,” International Population Conference, Liege 1973 (Liege, Belgium, 1973), 53–72; [Google Scholar]; McLaren Angus, Reproductive Rituals: The Perception of Fertility in England from the Sixteenth Century to the Nineteenth Century (London, New York, 1984); [Google Scholar]; Bengtsson Tommy and Dribe Martin, “Deliberate Control in a Natural Fertility Population: Southern Sweden, 1766–1864,” Demography, 43 (2006), 727–746; [DOI] [PubMed] [Google Scholar]; Alter George, “Theories of Fertility Decline: A Non-Specialist’s Guide to the Current Debate on European Fertility Decline,” in Tilly Louise, Gillis John R. and Levine David (eds.), The European Experience of Declining Fertility, 1850–1970 (Cambridge, MA, 1992), 13–27; [Google Scholar]; Guinnane TW, “The Historical Fertility Transition: A Guide for Economists,” Journal of Economic Literature, 49 (2011), 589–614; [Google Scholar]; Carlsson Gosta, “Decline of Fertility - Innovation or Adjustment Process,” Population Studies-a Journal of Demography, 20 (1966), 149–174. [DOI] [PubMed] [Google Scholar]
- 15.Fleury and Henry, Des Registres Paroissiaux.
- 16.Henry Louis, Manuel De Démographie Historique (Genève, Paris, 1967), xii, 148; [Google Scholar]; Henry Louis, Techniques D’analyse En Démographie Historique (Paris, 1980), 177; [Google Scholar]; Henry Louis and Blum Alain, Techniques D’analyse En Démographie Historique (Paris, 1988); [Google Scholar]; Henry, “Fécondité des Mariages dans le Quart Sud-Ouest (I)”; [Google Scholar]; Henry, “La Fécondité des Mariages dans le Quart Sud-Ouest (Suite)”; [Google Scholar]; Houdaille and Henry, “Fécondité des Mariages dans le Quart Nord-Ouest”; [PubMed] [Google Scholar]; Houdaille, “La Fécondité des Mariages dans le Quart Nord-Est”; [PubMed] [Google Scholar]; Henry, “Fécondité Des Mariages dans le Quart Sud-Est.” [Google Scholar]
- 17.Kalbfleisch JD and Ross L Prentice, The Statistical Analysis of Failure Time Data (New York, 1980), 195–196. [Google Scholar]
- 18.Fleury Michel and Henry Louis, Nouveau Manuel De Dépouillement et d’Exploitation de l’État Civil Ancien (Paris, 1965), 183; author’s translation. [Google Scholar]
- 19.Wrigley Eversley and Laslett, An Introduction to English Historical Demography, 148. [Google Scholar]
- 20.Henry, Techniques d’Analyse, 67–69; [Google Scholar]; Ruggles Steven, “The Limitations of English Family Reconstitution: English Population History from Family Reconstitution 1580–1837,” Continuity and Change, 14 (1999), 105–130; [DOI] [PubMed] [Google Scholar]; Wrigley EA, “The Effect of Migration on the Estimation of Marriage Age in Family Reconstitution Studies,” Population Studies-a Journal of Demography, 48 (1994), 81–97; [DOI] [PubMed] [Google Scholar]; Levine David, “Reliability of Parochial Registration and Representativeness of Family Reconstitution,” Population Studies-a Journal of Demography, 30 (1976), 107–122; [PubMed] [Google Scholar]; Ruggles Steven, “Migration, Marriage, and Mortality - Correcting Sources of Bias in English Family Reconstitutions,” Population Studies-a Journal of Demography, 46 (1992), 507–522; [DOI] [PubMed] [Google Scholar]; Kasakoff Alice B. and Adams John W., “The Effect of Migration on Ages at Vital Evejnts- a Critique of Family Reconstitution in Historical Demography,” European Journal of Population-Revue Europeenne De Demographie, 11 (1995), 199–242. [DOI] [PubMed] [Google Scholar]
- 21.Merchant Emily R., Prediction and Control: Global Population, Population Science, and Population Politics in the Twentieth Century [Electronic Resource], PhD, University of Michigan; (Ann Arbor, 2015), 336–345. [Google Scholar]; Ehrlich Paul R., The Population Bomb (San Francisco, 1969); [Google Scholar]; Coale Ansley J. and Hoover Edgar Malone, Population Growth and Economic Development in Low-Income Countries : A Case Study of India’s Prospects (Princeton NJ, 1958). [Google Scholar]
- 22.Coale Ansley J. and Watkins Susan Cotts, The Decline of Fertility in Europe: The Revised Proceedings of a Conference on the Princeton European Fertility Project (Princeton NJ, 1986). [Google Scholar]
- 23.Demeny Paul, “Early Fertility Decline in Austria-Hungary: A Lesson in Demographic Transition,” Daedalus, 97 (1968), 502–522; [PubMed] [Google Scholar]; Lesthaeghe Ron J., The Decline of Belgian Fertility, 1800–1970 (Princeton NJ, 1977); [Google Scholar]; Leasure J. William, “Factors Involved in the Decline of Fertility in Spain 1900–1950,” Population Studies, 16 (1963), 271–285. [Google Scholar]
- 24.Coale, “The Demographic Transition Reconsidered”; [Google Scholar]; Hodgson Dennis, “Orthodoxy and Revisionism in American Demography,” Population and Development Review, 14 (1988), 541–569; [Google Scholar]; Hodgson Dennis, “Demography as Social Science and Policy Science,” Population and Development Review, 9 (1983), 1–34; [Google Scholar]; Merchant, Prediction and Control. [Google Scholar]
- 25.Shryock Henry S., Siegel Jacob S. and Stockwell Edward G., The Methods and Materials of Demography (New York, 1976), 285. [Google Scholar]
- 26.Coale Ansley J., Demeny Paul George and Vaughan Barbara, Regional Model Life Tables and Stable Populations (New York, 1983); [Google Scholar]; Coale Ansley J. and McNeil DR, “Distribution by Age of Frequency of First Marriage in a Female Cohort,” Journal of the American Statistical Association, 67 (1972), 743–749; [DOI] [PubMed] [Google Scholar]; Coale Ansley J. and Trussell T. James, “Model Fertility Schedules - Variations in Age Structure of Childbearing in Human Populations,” Population Index, 40 (1974), 185–258; [PubMed] [Google Scholar]; Guinnane, Okun BS and Trussell, “What Do We Know About the Timing of Fertility Transitions in Europe,” Demography, 31 (1994), 1–20. [PubMed] [Google Scholar]
- 27.Schofield Roger S. and Wrigley E. Anthony, “Population and Economy: From the Traditional to the Modern World,” The Journal of Interdisciplinary History, 15 (1985), 561–569; [Google Scholar]; Wrigley and Schofield, The Population History of England; [Google Scholar]; Lee Ronald D., “Estimating Series of Vital Rates and Age Structures from Baptisms and Burials: A New Technique, with Applications to Pre-Industrial England,” Population Studies, 28 (1974), 495–512. [PubMed] [Google Scholar]
- 28.Wrigley and Schofield, The Population History of England, 438–443, 473–476; [Google Scholar]; Weir David R., “Rather Never Than Late: Celibacy and Age at Marriage in English Cohort Fertility, 1541–1871,” Journal of Family History, 9 (1984), 340–354. [PubMed] [Google Scholar]
- 29.Preston Heuveline and Guillot, Demography, 119–127; [Google Scholar]; Lee Ronald D., “Inverse Projection and Back Projection: A Critical Appraisal, and Comparative Results for England, 1539 to 1871,” Population Studies, 39 (1985), 233–248. [DOI] [PubMed] [Google Scholar]
- 30.Lee, “Estimating Series of Vital Rates and Age Structures.” [PubMed]
- 31.Wrigley and Schofield, The Population History of England, 715–738; [Google Scholar]; Lee Ronald D., “Inverse Projection and Back Projection: A Critical Appraisal, and Comparative Results for England, 1539 to 1871,” Population Studies, 39 (1985), 233–248; [DOI] [PubMed] [Google Scholar]; Oeppen Jim, “Back Projection and Inverse Projection: Members of a Wider Class of Constrained Projection Models,” Population Studies, 47 (1993), 245–267. [Google Scholar]
- 32.Wrigley and Schofield, The Population History of England; [Google Scholar]; Wrigley EA, Davies RS, Oeppen JE and Schofield RS, English Population History from Family Reconstitution, 1580–1837 (Cambridge, U.K. ;, New York, 1997). [DOI] [PubMed] [Google Scholar]
- 33.Henry Louis and Blayo Yves, “La Population De La France De 1740 a 1860,” Population (French Edition), 30 (1975), 71–122; [Google Scholar]; Blayo Yves, “La Proportion De Naissances Illégitimes En France De 1740 a 1829,” Population (French Edition), 30 (1975), 65–70; [Google Scholar]; Blayo Yves, “La Mortalité En France De 1740 a 1829,” Population (French Edition), 30 (1975), 123–142; [Google Scholar]; Wrigley and Schofield, The Population History of England; [Google Scholar]; Szreter Simon, Fertility, Class and Gender in Britain, 1860–1940 (Cambridge England ; New York, 1996), 546–547; [Google Scholar]; Garrett Eilidh, Reid Alice and Szreter Simon, Changing Family Size in England and Wales : Place, Class, and Demography, 1891–1911 (Cambridge, 2001). [Google Scholar]
- 34.Ruggles Steven, Roberts Evan, Sarkar Sula and Sobek Matthew, “The North Atlantic Population Project: Progress and Prospects,” Historical Methods: A Journal of Quantitative and Interdisciplinary History, 44 (2011), 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gutmann Myron P. and van de Walle Etienne, “New Sources for Social and Demographic History: The Belgian Population Registers,” Social Science History, 2 (1978), 121–143; [PubMed] [Google Scholar]; van de Walle Etienne, “Household Dynamics in a Belgian Village, 1847–1866,” Journal of Family History, 1 (1976), 80–94; [DOI] [PubMed] [Google Scholar]; Van de Walle Etienne and Blanc Olivier, “Registre De Population Et Démographie: La Hulpe,” Population et Famille, 36 (1975), 113–128; [Google Scholar]; Alter George, Family and the Female Life Course: The Women of Verviers, Belgium, 1849–1880 (Madison, Wis., 1988); [Google Scholar]; Lee James Z. and Campbell Cameron, Fate and Fortune in Rural China: Social Organization and Population Behavior in Liaoning, 1774–1873 (Cambridge, U.K, New York, 1997); [Google Scholar]; Kertzer David I., Family Life in Central Italy, 1880–1910 : Sharecropping, Wage Labor, and Coresidence (New Brunswick, N.J., 1984), xvii, 250; [Google Scholar]; Cornell Laurel L. and Hayami Akira, “The Shumon-Aratame-Cho - Japan Population Registers,” Journal of Family History, 11 (1986), 311–328; [Google Scholar]; Hayami Akira, Kinsei Noson No Rekishi-Jinkogakuteki Kenkyu (a Historical Demographic Study of Agricultural Villages in Early Modern Japan) (Tokyo, 1973); [Google Scholar]; Smith Thomas C., Eng Robert Y. and Lundy Robert T., Nakahara: Family Farming and Population in a Japanese Village, 1717–1830 (Stanford, Calif., 1977); [Google Scholar]; Lee Sangkuk and Lee Wonjae, “Strategizing Marriage: A Genealogical Analysis of Korean Marriage Networks,” The Journal of Interdisciplinary History, 48 (2017), 1–19; [Google Scholar]; Janssens Angelique, Family and Social Change : The Household as a Process in an Industrializing Community (Cambridge, 1993); [Google Scholar]; Van Poppel Frans and Mandemakers Kees, “Differential Infant and Child Mortality in the Netherlands: First Results of the Historical Sample of the Population of the Netherlands,” in Bideau Alain, Desjardins Bertrand and Brignoli Héctor Pérez (eds.), Infant and Child Mortality in the Past (Oxford, 1997), 276–300; [Google Scholar]; Engelen Theo, Shepherd John Robert and Yang Wen-Shan (eds.), Death at the Opposite Ends of the Eurasian Continent: Mortality Trends in Taiwan and the Netherlands, 1850–1945 2011); [Google Scholar]; Blum Alain and Troitskaja Irina, “Mortality in Russia During the Eighteenth and Nineteenth Centuries. Local Assessments Based on the Revizii,” Population, 51 (1996), 303–328; [Google Scholar]; Bengtsson Tommy, “The Vulnerable Child. Economic Insecurity and Child Mortality in Pre-Industrial Sweden. A Case Study of Västanfors, 1757–1850,” European Journal of Population, 15 (1999), 117–151; [Google Scholar]; Brändström Anders and Sundin Jan, “Infant Mortality in a Changing Society: The Effects of Child Care in a Swedish Parish 1820–1894,” in Brändström Anders and Sundin Jan (eds.), Tradition and Transition: Studies in Microdemography and Social Change (Umeå, 1981), 67–104. [Google Scholar]
- 36.Gutmann Myron P. and Alter George, “Family Reconstitution as Event-History Analysis,” in Reher David Sven and Schofield Roger (eds.), Old and New Methods in Historical Demography (Oxford, 1993), 159–177; [Google Scholar]; Cox David R., “Regression Models and Life Tables,” Journal of the Royal Statistical Society, 74 (1972), 187–220; [Google Scholar]; Cox David R., “Partial Likelihood,” Biometrika, 62 (1975), 269–276. [Google Scholar]
- 37.Bengtsson Tommy, Campbell Cameron and Lee James Z., Life under Pressure: Mortality and Living Standards in Europe and Asia, 1700–1900 (Cambridge, Mass., 2004); [Google Scholar]; Tsuya Noriko O., Feng Wang, Alter George and Lee James Z., Prudence and Pressure : Reproduction and Human Agency in Europe and Asia, 1700–1900 (Cambridge, Mass., 2010); [Google Scholar]; Lundh Christer and Kurosu Satomi, Similarity in Difference: Marriage in Europe and Asia, 1700–1900 (Cambridge, Mass., 2014). [Google Scholar]
- 38.Bengtsson Tommy, “Combined Time-Series and Life Event Analysis: The Impact of Economic Fluctuations and Air Temperature on Adult Mortality by Sex and Occupation in a Swedish Mining Parish, 1757–1850,” in Reher David Sven and Schofield Roger (eds.), Old and New Methods in Historical Demography (Oxford, New York, 1993), 239–258. [Google Scholar]
- 39.Thomas Dorothy Swaine, Social Aspects of the Business Cycle (New York, 1927); [Google Scholar]; Thomas Dorothy Swaine, Social and Economic Aspects of Swedish Population Movements, 1750–1933 (New York, 1941); [Google Scholar]; Lee Ronald D., “Short-Term Variation: Vital Rates, Prices, and Weather,” in Wrigley EA and Schofield RS (eds.), The Population History of England, 1541–1871 : A Reconstruction (London, 1981), 356–401; [Google Scholar]; Galloway Patrick R., “Basic Patterns in Annual Variations in Fertility, Nuptiality, Mortality, and Prices in Pre-Industrial Europe,” Population Studies: A Journal of Demography, 42 (1988), 275–302; [DOI] [PubMed] [Google Scholar]; Bengtsson Campbell and Lee, Life under Pressure, 68–82, 341–343. [Google Scholar]
- 40.Malthus, An Essay on the Principle of Population (1798, 1826); [Google Scholar]; Tsuya Noriko O. and Kurosu Satomi, “Family, Household, Reproduction in Northeastern Japap, 1716 to 1870,” in Tsuya Noriko O., Feng Wang, Alter George and Lee James Z. (eds.), Prudence and Pressure : Reproduction and Human Agency in Europe and Asia, 1700–1900 (Cambridge, Mass., 2010), 249–286; [Google Scholar]; Oris Michel, Alter George and Servais Paul, “Prudence as Obstinate Resistance to Pressure: Marriage in Nineteenth-Century Rural Eastern Belgium,” in Lundh Christer and Kurosu Satomi (eds.), Similarity in Difference: Marriage in Europe and Asia, 1700–1900 (Cambridge, Mass., 2014), 261–294. [Google Scholar]
- 41.Gjerde Jon and McCants Anne, “Individual Life Chances, 1850–1910: A Norwegian-American Example,” The Journal of Interdisciplinary History, 30 (1999), 377–405; [Google Scholar]; McQuillan Kevin, “Family Composition and Remarriage in Alsace, 1750–1850,” The Journal of Interdisciplinary History, 33 (2003), 547–567; [Google Scholar]; Alter George, Gutmann Myron P., Leonard Susan Hautaniemi and Merchant Emily R., “Introduction: Longitudinal Analysis of Historical-Demographic Data,” The Journal of Interdisciplinary History, 42 (2012), 503–517. [Google Scholar]
- 42.Gutmann and Alter, “Family Reconstitution as Event-History Analysis”;; Cox, “Regression Models and Life Tables.”
- 43.Preston Heuveline and Guillot, Demography, 59. [Google Scholar]
- 44.Van Bavel Jan and Kok Jan, “Birth Spacing in the Netherlands. The Effects of Family Composition, Occupation and Religion on Birth Intervals, 1820–1885,” European Journal of Population-Revue Européenne De Démographie, 20 (2004), 119–140; [Google Scholar]; Van Bavel Jan and Kok Jan, “The Role of Religion in the Dutch Fertility Transition: Starting, Spacing, and Stopping in the Heart of the Netherlands, 1845–1945,” Continuity and Change, 20 (2005), 247–263; [Google Scholar]; Van Bavel Jan and Kok Jan, “A Mixed Effects Model of Birth Spacing for Pre-Transition Populations Evidence of Deliberate Fertility Control from Nineteenth Century Netherlands,” History of the Family, 15 (2010), 125–138; [Google Scholar]; Van Bavel Jan, “Deliberate Birth Spacing before the Fertility Transition in Europe: Evidence from Nineteenth-Century Belgium,” Population Studies-a Journal of Demography, 58 (2004), 95–107; [DOI] [PubMed] [Google Scholar]; Van Bavel Jan, “Detecting Stopping and Spacing Behaviour in Historical Demography. A Critical Review of Methods,” Population (English Edition), 59 (2004), 117–128; [Google Scholar]; Okun BS, “Evaluating Methods for Detecting Fertility-Control - Coale and Trussells Model and Cohort Parity Analysis,” Population Studies-a Journal of Demography, 48 (1994), 193–222; [Google Scholar]; Anderton DL and Bean LL, “Birth Spacing and Fertility Limitation - a Behavioral-Analysis of a 19th-Century Frontier Population,” Demography, 22 (1985), 169–183; [PubMed] [Google Scholar]; Okun BS, “Distinguishing Stopping Behavior from Spacing Behavior with Indirect Methods,” Historical Methods, 28 (1995), 85–96. [Google Scholar]
- 45.Box-Steffensmeier Janet M. and Jones Bradford S., Event History Modeling : A Guide for Social Scientists (New York, 2004), 51. [Google Scholar]
- 46.Knodel John E., Demographic Behavior in the Past a Study of Fourteen German Village Populations in the Eighteenth and Nineteenth Centuries (Cambridge England, New York, 1988). [Google Scholar]
- 47.Bavel Van, “Deliberate birth spacing before the fertility transition in Europe,” 103; [DOI] [PubMed] [Google Scholar]; Bavel Van and Kok, “Birth spacing in the Netherlands,” 131; [Google Scholar]; Wood James W., Dynamics of Human Reproduction Biology, Biometry, Demography (New York, 1994), 315. [Google Scholar]
- 48.Cinnirella Francesco, Klemp Marc and Weisdorf Jacob, “Malthus in the Bedroom: Birth Spacing as Birth Control in Pre-Transition England,” Demography, 54 (2017), 413–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Fialova Ludmila, Tesarkova Klara H. and Kuprova Barbora, “Determinants of the Length of Birth Intervals in the Past and Possibilities for Their Study: A Case Study of Jablonec Nad Nisou (Czech Lands) from Seventeenth to Nineteenth Century,” Journal of Family History, 43 (2018), 127–156; [Google Scholar]; Jonker Marianne A. and van der Vaart Aaad W., “Estimation of Average Mortality under Censoring and Truncation,” Journal of Population Research, 22 (2005), 49–62; [Google Scholar]; Jonker Marianne A. and van der Vaart Aaad W., “Correcting Missing-Data Bias in Historical Demography,” Population Studies-a Journal of Demography, 61 (2007), 99–113; [DOI] [PubMed] [Google Scholar]; Alter George, Devos Isabelle and Kvetko Alison, “Completing Life Histories with Imputed Exit Dates: A Method for Historical Data from Passive Registration Systems,” Population, 64 (2009), 327–353. [Google Scholar]
- 50.Reher DS and Sanz-Gimeno A, “Rethinking Historical Reproductive Change: Insights from Longitudinal Data for a Spanish Town,” Population and Development Review, 33 (2007), 703–727; [Google Scholar]; Van Bavel Jan, “Diffusion Effects in the European Fertility Transition: Historical Evidence from within a Belgian Town (1846–1910),” European Journal of Population-Revue Europeenne De Demographie, 20 (2004), 63–85. [Google Scholar]
- 51.Kaplan Edward L and Meier Paul, “Nonparametric Estimation from Incomplete Observations,” Journal of the American Statistical Association, 53 (1958), 457–481. [Google Scholar]
- 52.Reher David S., Sandstrom Glenn, Sanz-Gimeno Alberto and van Poppel Frans W. A., “Agency in Fertility Decisions in Western Europe During the Demographic Transition: A Comparative Perspective,” Demography, 54 (2017), 3–22; [DOI] [PMC free article] [PubMed] [Google Scholar]; Casterline John B. and Odden Colin, “Trends in Inter-Birth Intervals in Developing Countries 1965–2014,” Population and Development Review, 42 (2016), 173–194. [Google Scholar]
- 53.Reher Sandstrom, Sanz-Gimeno and van Poppel, “Agency in Fertility Decisions”, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gray Edith, Evans Ann, Anderson Jon and Kippen Rebecca, “Using Split-Population Models to Examine Predictors of the Probability and Timing of Parity Progression,” European Journal of Population-Revue Europeenne De Demographie, 26 (2010), 275–295; [Google Scholar]; Li Lei and Choe Minja K., “A Mixture Model for Duration Data: Analysis of Second Births in China,” Demography, 34 (1997), 189–197; [PubMed] [Google Scholar]; Yamaguchi Kazuo, “Mover-Stayer Models for Analyzing Event Nonoccurrence and Event Timing with Time-Dependent Covariates: An Application to an Analysis of Remarriage,” (eds.), Sociological Methodology, 28 (1998), 327–361; [Google Scholar]; Yamaguchi Kazuo and Ferguson Linda R., “The Stopping and Spacing of Childbirths and Their Birth-History Predictors - Rational-Choice Theory and Event-History Analysis,” American Sociological Review, 60 (1995), 272–298; [Google Scholar]; Janssens Angelique, Labouring Lives: Women, Work and the Demographic Transition in the Netherlands, 1880–1960 (Bern, 2014). [Google Scholar]
- 55.Ritschard Gilbert and Oris Michel, “Life Course Data in Demography and Social Sciences: Statistical and Data-Mining Approaches,” in Levy René, Ghisletta Paolo, Le Goff Jean-Marie, Spini Dario and Widmer Eric (eds.), Towards an Interdisciplinary Perspective on the Life Course (Amsterdam ; Boston, 2005), 283–314; [Google Scholar]; Abbot Andrew, “Sequences of Social Events: Concepts and Methods for the Analysis of Order in Social Processes,” Historical Methods, 16 (1983), 129–147; [Google Scholar]; Bras Hilde and Schumacher Reto, “Changing Gender Relations and Declining Fertility: An Analysis of Spousal Age Differences and Women’s Childbearing Trajectories in Zeeland, the Netherlands, 1812–1911,” Demographic Research (forthcoming). [Google Scholar]
- 56.Coale Ansley J. and Trussell James, “The Development and Use of Demographic Models,” Population Studies-a Journal of Demography, 50 (1996), 469–484. [DOI] [PubMed] [Google Scholar]


