Abstract
震颤是肢体一种非自主和重复性的摆动动作,在基于功能性电刺激 (FES) 的震颤抑制系统中可将其视为周期性扰动信号。因此,利用重复控制器调节施加在相应肌肉上的FES强度和时间,从而产生与震颤运动反相的肌肉力矩,是震颤抑制的一种可行手段。目前,大多数基于FES的重复控制系统都假设震颤是固定的单一频率信号,但实际上震颤可能是多频率信号,且震颤频率也会随时间变化。本文从频率角度对意向性震颤患者数据进行分析,提出了内模切换的自适应重复控制器来抑制不同频率的腕关节震颤。仿真和试验结果表明,所提出的并联多内模和串联高阶内模切换的自适应重复控制对多频率和单频率震颤信号可实现平均84.98%的抑制效果,比传统单内模重复控制器和基于滤波的反馈控制器在震颤抑制性能上均有明显提高。因此本文所提基于FES的自适应重复控制方法可以更为有效地解决意向性震颤患者腕部震颤问题,为患者后续运动功能障碍的康复提供有效的技术支撑。
Keywords: 功能性电刺激, 震颤抑制, 串联高阶内模, 并联多内模, 自适应重复控制
Abstract
Tremor is an involuntary and repetitive swinging movement of limb, which can be regarded as a periodic disturbance in tremor suppression system based on functional electrical stimulation (FES). Therefore, using repetitive controller to adjust the level and timing of FES applied to the corresponding muscles, so as to generate the muscle torque opposite to the tremor motion, is a feasible means of tremor suppression. At present, most repetitive control systems based on FES assume that tremor is a fixed single frequency signal, but in fact, tremor may be a multi-frequency signal and the tremor frequency also varies with time. In this paper, the tremor data of intention tremor patients are analyzed from the perspective of frequency, and an adaptive repetitive controller with internal model switching is proposed to suppress tremor signals with different frequencies. Simulation and experimental results show that the proposed adaptive repetitive controller based on parallel multiple internal models and series high-order internal model switching can suppress tremor by up to 84.98% on average, which is a significant improvement compared to the traditional single internal model repetitive controller and filter based feedback controller. Therefore, the adaptive repetitive control method based on FES proposed in this paper can effectively address the issue of wrist intention tremor in patients, and can offer valuable technical support for the rehabilitation of patients with subsequent motor dysfunction.
Keywords: Functional electrical stimulation, Tremor suppression, Series high-order internal model, Parallel multiple internal models, Adaptive repetitive control
0. 引言
意向性震颤也称运动性震颤,是一种非自主、有节律、交替性的肌肉收缩和放松,通常发生在有目标意图的上肢运动中,且当肢体接近目标物时震颤幅度显著增大[1]。因此,震颤患者无法完成精准的上肢和手部运动,如饮食、穿衣、书写等,严重影响其生活质量[2]。传统的震颤抑制手段主要有药物治疗和外科手术两种。药物的长期服用会产生药品依赖性,且会带来副作用[3]。侵入性手术治疗,如立体定向丘脑切开术[4]、立体定向苍白球切开术[5]和深脑部电刺激[6]等,具有一定的手术风险和并发症,且费用昂贵。
随着机电一体化技术的发展,辅助式震颤抑制手段受到越来越多的重视[7-8]。其中,功能性电刺激(functional electrical stimulation,FES)因其具有便携性、低成本、非创伤性等特点在康复医疗领域应用非常广泛[9-11]。FES是一种人工电刺激,可以直接激活运动神经元使肌肉收缩,达到运动功能恢复和重建的目的。利用FES抑制震颤是通过设计闭环反馈控制系统产生适当的电脉冲信号刺激相关肌肉,使之产生与震颤运动相反的肌肉力矩,从而实现震颤幅度的减小。Prochazka等[12]最早提出了基于滤波的反馈控制器,并通过试验对三种类型的单频震颤分别达到73%、62%和38%的震颤抑制效果。Zhang等[13]使用基于FES的神经振荡器结合比例积分微分(proportional integral derivative,PID)控制器,仿真实现90%的震颤抑制率。Taheri等[14]利用高通滤波器和反演法估计震颤力矩,在手臂关节模拟器上评估所提出的算法,取得了97.5%~99.2%震颤抑制。张伟等[15]提出了前馈控制与线性二次型控制相结合的复合控制策略,通过仿真实现了多自由度震颤幅值约94%的抑制效果。
由于震颤是肢体一种节律性、交替性摆动动作,是肌肉非自主、重复性的收缩和放松,故在震颤抑制控制系统中可将其视为周期性扰动信号。因此,基于内模原理的重复控制器比上述传统基于滤波的反馈控制器在震颤抑制效果方面更显著[16-18]。然而,现有基于重复控制的震颤抑制研究中通常假设震颤为固定的单一频率信号,但实际患者的震颤信号可能具有多频率特点[19-20],且峰值频率也不是固定的。并联多内模重复控制对于多频率周期性干扰信号具有很好的抑制性能[20-22]。Zhang等[20]针对多频震颤信号设计并联多内模重复控制方案,试验结果表明可实现平均81.23%的震颤抑制。Kurniawan等[21]针对伺服电机多频干扰的有效抑制设计了并联多内模重复控制器,并通过仿真验证了控制器的有效性。文献[22]利用多内模重复控制方法实现了所有特征谐波的提取和跟踪,提高了有源滤波器的动态响应特性。但以上研究并没有考虑峰值频率变化对控制性能的影响,由于患者震颤信号频率的个体差异性和时变性等特点,本文将并联多内模结构和串联高阶内模结构结合,提出了针对不同震颤频率特点的内模切换自适应重复控制(adaptive repetitive control,A-RC)策略。与以往基于重复控制的震颤抑制相关研究相比,本文的主要创新之处如下:
(1)提出了基于哈默斯坦(Hammerstein)模型结构的手腕肌骨模型及其快速参数辨识方法,并期望通过搭建的手腕震颤抑制实验平台验证模型的有效性。
(2)针对意向性患者震颤信号频率特性的个体差异性和时变性,结合线性化控制设计了并联多内模和串联高阶内模切换的A-RC控制器,分析了闭环系统稳定性,提出基于频率修正逆的重复控制补偿器构造方法。
(3)利用搭建的手腕震颤抑制实验平台,通过健康参与者的诱发性震颤抑制试验和意向性患者的手腕震颤抑制试验,以期验证所提A-RC方法的可行性和有效性。
1. 方法
1.1. 手腕肌骨模型
为了设计刺激强度和刺激时间精准调节的A-RC控制器,首先需要建立手腕肌骨模型。手腕肌骨模型由肌肉模型和骨骼模型组成。非线性Hammerstein模型由于其结构简单,便于震颤抑制控制器的设计,被广泛应用于基于FES的肌肉建模中[23]。Hammerstein模型由静态非线性招募特性和线性动态模型组成,前者表现肌肉的激活特性,后者表现肌肉对电刺激信号的收缩响应。而骨骼模型的建立通常描述为线性刚体动力学(rigid body dynamics,RBD)模型。
本文主要研究手腕屈伸运动时的震颤抑制。腕部屈伸运动主要由桡侧腕伸肌(extensor carpi radialis, ECR)和桡侧腕屈肌(flexor carpi radialis,FCR)驱动桡骨实现。因而,根据Hammerstein模型结构,构造了FCR和ECR的非线性肌肉招募特性fFCR(uFCR)、fECR(uECR)和线性肌肉收缩动态特性GFCR(z)、GECR(z) ,以及骨骼线性刚体动力学模型GRBD(z)。电刺激手腕肌骨模型如图1所示,其中uFCR(k)和uECR(k)是电刺激输入信号,y(k)为手腕屈伸运动角度输出信号。wFCR(k)和wECR(k)为招募特性的输出, 为作用在骨骼系统上的肌肉总力矩。d(k)可以看作是由于震颤引起的干扰信号。
为作用在骨骼系统上的肌肉总力矩。d(k)可以看作是由于震颤引起的干扰信号。
图 1.
Electrically stimulated wrist musculoskeletal model
电刺激手腕肌骨模型
为简化模型结构和参数辨识过程,将uFCR(k)、uECR(k)分别等效为如式(1)、式(2)所示的单一输入 :
:
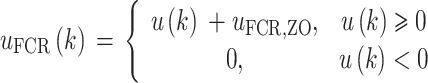 |
1 |
 |
2 |
其中,uFCR,ZO和uECR,ZO是FCR和ECR肌肉招募特性的死区阈值,根据试验设置为50 μs。由于典型的招募特性包括初始死区、单调递增区和饱和区,进而等效非线性招募特性输出w(k)与输入u(k)可以通过如式(3)所示的静态映射关系表示:
 |
3 |
其中,umax是最大电刺激输入脉宽,为避免过强电刺激输入造成肌肉收缩时的不适感,本文最大脉宽设置为300 μs [24]。 和
和  分别为FCR和ECR肌肉的非线性招募特性,
分别为FCR和ECR肌肉的非线性招募特性, 和
和  分别为
分别为  和
和 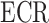 肌肉的招募特性死区阈值。
肌肉的招募特性死区阈值。 为等效的桡侧肌肉非线性招募特性。化简后的非线性招募特性f (u(k))在工作区间
为等效的桡侧肌肉非线性招募特性。化简后的非线性招募特性f (u(k))在工作区间  是连续且递增的,如式(4)所示:
是连续且递增的,如式(4)所示:
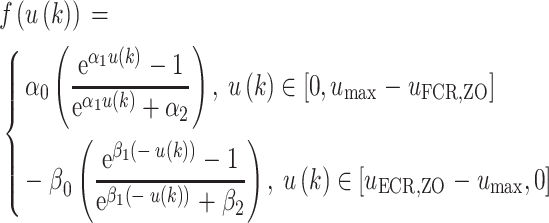 |
4 |
其中,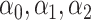 以及
以及  分别为FCR和ECR 肌肉需要识别的非线性标量参数;e为指数函数。
分别为FCR和ECR 肌肉需要识别的非线性标量参数;e为指数函数。
由于相似的肌群具有相似的线性收缩特性[25],因而FCR和ECR动态特性近似为 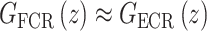 ,可用GL(z)表示。人体骨骼动力学可以建模为刚体动力学GRBD(z),其中阻尼和弹性函数都可以看作线性函数[26]。故,等效的线性动态肌骨模型
,可用GL(z)表示。人体骨骼动力学可以建模为刚体动力学GRBD(z),其中阻尼和弹性函数都可以看作线性函数[26]。故,等效的线性动态肌骨模型  如式(5)所示:
如式(5)所示:
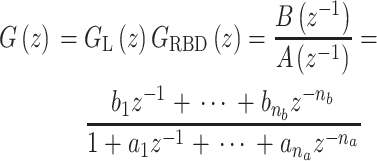 |
5 |
其中,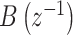 和
和  分别为等效线性肌骨模型数学表达式的分子和分母,
分别为等效线性肌骨模型数学表达式的分子和分母, 和
和 分别是
分别是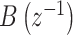 的阶数和待辨识的参数,
的阶数和待辨识的参数,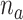 和
和 分别是
分别是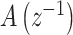 的阶数和待辨识的参数。
的阶数和待辨识的参数。
1.2. 控制器设计
由于腕关节肌骨模型具有固有的非线性,首先设计线性化控制器 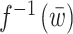 ,在此基础上设计A-RC控制器C(z)以抑制不同类型的腕部震颤,提高手腕对参考轨迹的跟踪性能。基于FES的闭环震颤抑制系统控制框图如图2所示,其中r(k)为指定的跟踪参考位置,e(k)为手腕实际运动位置与参考位置的偏差,
,在此基础上设计A-RC控制器C(z)以抑制不同类型的腕部震颤,提高手腕对参考轨迹的跟踪性能。基于FES的闭环震颤抑制系统控制框图如图2所示,其中r(k)为指定的跟踪参考位置,e(k)为手腕实际运动位置与参考位置的偏差,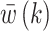 为控制器C(z)的输出。
为控制器C(z)的输出。
图 2.
FES based closed-loop tremor suppression control diagram
基于FES的闭环震颤抑制控制框图
1.2.1. 线性化控制器设计
由于电刺激肌骨模型具有复杂的非线性因素,且非线性主要表现在静态招募特性,因而采用线性化控制器补偿肌骨模型中的招募非线性,线性化控制器 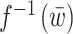 如式(6)所示:
如式(6)所示:
 |
6 |
1.2.2. A-RC控制器设计
重复控制是基于内模原理的一种控制方法。内模原理指出,如果在稳定的闭环系统中包含外部周期性信号的数学模型,系统就能够实现对周期性信号的无静差跟踪或抑制。本文根据患者震颤数据的分析,设计了内模切换的A-RC控制器。经过线性化之后,等效的闭环控制系统框图如图3所示,H(z)是提高闭环系统稳定性和动态性能的重复控制补偿器。自适应调节器根据傅里叶变换得到的震颤数据频域特性调节内模结构,实现并联多内模或串联高阶内模的自适应选择,即根据震颤信号频域分析结果,调节内模结构的数学模型,以实现对不同震颤患者最佳的震颤抑制效果。
图 3.
Equivalent closed-loop tremor suppression system diagram
等效的闭环震颤抑制系统框图
其中,A-RC控制器C(z)如式(7)所示:
 |
7 |
其中,补偿器H(z)如式(8)所示:
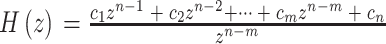 |
8 |
H(z)包含n个零点,其位置由系数c1, c2, ···, cn确定,并在原点引入n − m个极点。自适应内模结构 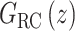 由m条并联支路构成,Wq为第q条内模支路增益,q = 1, 2, ···, m。其中,第q条高阶内模支路
由m条并联支路构成,Wq为第q条内模支路增益,q = 1, 2, ···, m。其中,第q条高阶内模支路 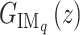 如式(9)所示:
如式(9)所示:
 |
9 |
其中, 为一个周期的采样次数,
为一个周期的采样次数,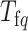 为震颤信号的周期,
为震颤信号的周期, 为采样周期,
为采样周期, (p = 1, 2, ···, n)是第p阶支路增益。
(p = 1, 2, ···, n)是第p阶支路增益。
1.2.3. 稳定性分析
定理1:在A-RC控制器的作用下,选择控制增益 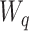 、
、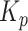 和补偿器
和补偿器  使得闭环控制系统特征多项式的根均在单位圆内,如式(10)所示:
使得闭环控制系统特征多项式的根均在单位圆内,如式(10)所示:
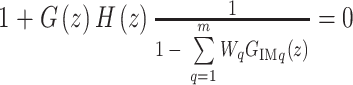 |
10 |
那么,如图3所示的闭环控制系统是渐近稳定的,且能够完全抑制  周期的扰动。尤其是,选择
周期的扰动。尤其是,选择  ,则当
,则当  时,
时,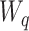 需要满足如式(11)所示:
需要满足如式(11)所示:
 |
11 |
证明:根据图(3)可得误差  、参考输入
、参考输入  和扰动
和扰动  之间的关系如式(12)所示:
之间的关系如式(12)所示:
 |
12 |
将式(7)带入式(12),则闭环系统的特征多项式如式(13)所示:
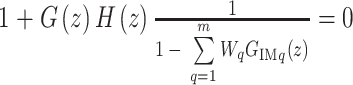 |
13 |
当特征多项式的根都在单位圆内时,则闭环反馈控制系统是渐近稳定的。特别地,当  时,式(13)可写为如式(14)、式(15)所示:
时,式(13)可写为如式(14)、式(15)所示:
 |
14 |
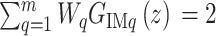 |
15 |
为了有效抑制震颤,需要选择重复控制器的内模结构  在震颤信号基波和谐波处增益无穷大,即
在震颤信号基波和谐波处增益无穷大,即 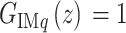 ,令
,令 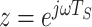 从而得到离散系统的频率响应,其中,
从而得到离散系统的频率响应,其中,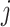 表示虚数单位,
表示虚数单位, 为角频率,那么如式(16)所示:
为角频率,那么如式(16)所示:
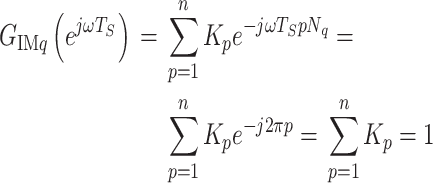 |
16 |
故当选择  ,
, 时,有
时,有  ,这时第
,这时第  条内模支路增益
条内模支路增益 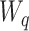 选择满足
选择满足 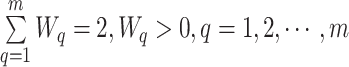 。
。
证明完毕。
1.2.4. 补偿器H(z)设计
在实际中,由于手腕肌骨模型参数的不确定性和模型单位圆外可能存在零点等因素,补偿器H(z)无法通过  得到。因此,本文采用频率修正逆重复控制方法来获得补偿器H(z)的阶数和参数[20, 27]。即适当选择式(8)中的参数c=[c1, c2,…, cn]T来最小化以下成本函数J,从而实现
得到。因此,本文采用频率修正逆重复控制方法来获得补偿器H(z)的阶数和参数[20, 27]。即适当选择式(8)中的参数c=[c1, c2,…, cn]T来最小化以下成本函数J,从而实现 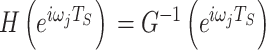 的频率响应。成本函数J如式(17)所示:
的频率响应。成本函数J如式(17)所示:
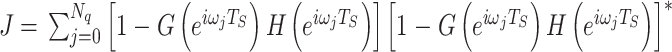 |
17 |
其中,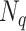 为一个周期的采样次数,i表示虚数单位,
为一个周期的采样次数,i表示虚数单位, 是从零到奈奎斯特的一组离散频率,
是从零到奈奎斯特的一组离散频率,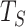 为采样周期,*表示复共轭。
为采样周期,*表示复共轭。
2. 仿真与试验验证
在试验验证环节,招募4名健康参与者和4名意向性震颤患者。健康参与者编号为No.1~No.4,3男1女,平均年龄为(28.25 ± 8.54)岁。震颤患者来自郑州大学第五附属医院康复科,编号为No.5~No.8,3男1女,平均年龄为(43.25 ± 10.90)岁。试验中8位受试者均签署书面知情同意书,且已通过郑州大学伦理审查,伦理审批编号为No.ZZURIB2019-004。基于搭建的手腕震颤抑制实验平台,每位受试者首先进行手腕肌骨模型参数辨识试验,然后根据辨识的模型参数设计相应控制器,进而开展手腕震颤数据采集和震颤抑制试验。
2.1. 实验平台
基于FES的腕部震颤抑制实验平台如图4所示。震颤抑制实验平台由轮椅改装而成,其中手臂支架是固定的,前端的U型手掌支撑夹板运动范围被限制在± 80°之内,这符合手腕屈伸的运动范围。试验时受试者舒适、放松地坐在实验平台的轮椅上,右前臂放于手臂支架,右手放在U型手掌支撑夹板中间。受试者的前臂用绑带固定,以防止产生除手腕屈伸平面外其他任何自由度的运动。支架外侧设计扇形角度标尺,方便受试者跟踪指定的参考位置。实时的手腕屈伸运动角度数据由编码器(E6B2-CWZ6C,深圳布瑞特科技有限公司,中国)测量,其中编码器的轴与U型手掌支撑夹板的转轴通过直径比为1∶1的齿轮连接。仿真系统平台dSPACE(Microlabbox 1202, dSPACE Inc.,德国)实现手腕角度数据和控制信号的实时传输,为控制算法的开发和验证提供支持。最终的控制信号由电刺激仪(4 CHANNEL STIMULATOR, Odstock Medical Ltd.,英国)输出。本文电刺激信号的频率、电流幅值和最大脉宽设置分别为40 Hz、20 mA和300 μs,并且可以根据受试者对电刺激信号强弱的不同反应,利用电刺激仪上每个通道的电位器调节信号的大小。
图 4.
Experimental platform for wrist tremor suppression
腕部震颤抑制实验平台
在临床试验之前,对健康参与者进行控制方案的可行性测试是必要的步骤。因此,在实验平台上嵌入直流电机(VDM08SGN24-60-1800/JB5G12T,北京微特微电机制造有限公司,中国),利用电机来模拟震颤信号。其原理是U型手掌支撑夹板与电机同轴,当电机产生输出转矩时,可直接带动U型手掌支撑夹板动作。因此,通过软件设置震颤频率和幅度,电机驱动器(ESCON50/5,maxon motor Inc.,匈牙利)驱动电机运转即可输出相应的转速和角度。这样,健康参与者的手腕会产生不自主的屈伸运动,即得到诱发性震颤信号。
2.2. 手腕肌骨模型参数辨识
手腕肌骨模型的参数辨识基于输入/输出数据集[u, y],利用迭代最小二乘法获得,整个辨识过程大约2 min左右。输入信号u(k)为0.2~4.0 Hz、脉冲宽度为300 μs的不同频率正弦信号。y(k)为编码器测量的手腕屈伸运动的角度数据。在参数辨识过程中,受试者手腕运动是由输入的电刺激信号驱动,而不是自主运动产生。为了计算模型的拟合度,定义最佳拟合比  如式(18)所示:
如式(18)所示:
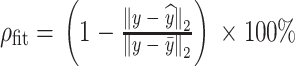 |
18 |
其中,y为实测输出, 为模型模拟输出。y的均值用
为模型模拟输出。y的均值用 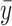 表示。一般来说
表示。一般来说  值越高,参数辨识的精度越高,但模型阶数也越高。在本文中,
值越高,参数辨识的精度越高,但模型阶数也越高。在本文中,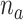 和
和  的值[即
的值[即  中
中 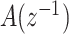 和
和 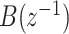 的阶数]从4~10进行选取。以受试者No.1为例,其最佳拟合率如图5所示。相对低阶模型的最佳拟合率为62.06%(
的阶数]从4~10进行选取。以受试者No.1为例,其最佳拟合率如图5所示。相对低阶模型的最佳拟合率为62.06%( 和
和 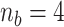 ),相对高阶模型的最佳拟合率最高为67.94%(
),相对高阶模型的最佳拟合率最高为67.94%( 和
和 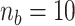 )。当
)。当 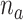 和
和 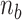 在4~10之间取值时,最佳拟合率变化并不明显。因此,为了减少辨识计算量、简化控制器设计,本文选取了
在4~10之间取值时,最佳拟合率变化并不明显。因此,为了减少辨识计算量、简化控制器设计,本文选取了  。
。
图 5.
The best fit rate of participant No.1’s wrist model
受试者No.1手腕模型最佳拟合率
2.3. 震颤信号分析
利用搭建的实验平台采集意向性震颤患者No.5~No.8手腕屈伸运动时伴随的震颤数据,如表1所示。
表 1. Data of Patients No.5~No.8.
患者No.5~No.8数据
| 患者编号 | 性别 | 年龄 | 频率特点 | 峰值频率/Hz |
| No.5 | 男 | 49 | 单一频率 | 2.2 |
| No.6 | 女 | 29 | 单一频率 | 2.4 |
| No.7 | 男 | 41 | 多频率 | 2.3,2.5 |
| No.8 | 男 | 54 | 多频率 | 2.2,2.4 |
具体的采集方法为:让意向性震颤患者右手通过屈伸手腕自主地跟踪一个指定的参考轨迹,指定的参考轨迹类似于一些简单的日常任务,例如,屈伸手腕以达到一个特定的角度。患者需要通过自主屈伸手腕跟踪参考轨迹,产生的运动跟踪轨迹为黑色虚线。由于震颤的存在,实际手腕运动的跟踪轨迹会偏离指定的参考轨迹。如图6所示,通过随机选择的患者No.5和No.7的跟踪轨迹数据时频图可以看到,自主运动的频率范围低于1 Hz,且在20 s和40 s手腕有自主屈伸动作时,功率谱密度增强。意向性震颤频率范围主要在2~5 Hz之间[1, 28],本文采集的意向性震颤频率在2~3 Hz之间,且震颤频率随时间会有稍许的变化,如患者No.5震颤信号时频图40 s之后,震颤频率明显降低。
图 6.

Frequency analysis of tremor signals in patient No.5 and No.7
震颤患者No.5和No.7震颤信号频率分析
通过对患者No.5和No.7跟踪轨迹信号分析可得,患者No.5为单频率震颤信号,而患者No.7为多频率震颤信号。对于单频率或多频率的震颤信号,通过自适应调节器选择切换不同的重复控制器内模结构,即通过傅里叶变换得到最大振幅对应的震颤频率(frequency corresponding to peak amplitude,FPA),如患者No.5的FPA为2.2 Hz,患者No.7的FPA为2.3 Hz。若其余频率振幅均小于FPA的80% (患者No.5没有超过FPV的80%的震颤频率,故归类为单频率震颤信号),则选择单一支路的高阶内模结构(图3中q = 1);若震颤频率幅值中有高于80%的FPA频率(患者No.7在2.5 Hz处的震颤幅值超过FPV的80%,故归类为多频率震颤信号),则选择并联内模结构(图3中q > 1),因为震颤频率的振幅越大,对患者的影响越大。
2.4. 仿真测试
在本小节中,使用受试者No.1的手腕模型验证提出的A-RC方法对周期性震颤抑制的有效性,并将并联多内模结构和串联高阶内模结构切换的A-RC方法与单周期重复控制方法(single periodic repetitive control,SP-RC)[16]和传统的基于高通滤波器的比例积分控制方法(proportional integral control algorithm based on high pass filter,PI-HPF)[12]进行比较。根据震颤信号的单频率或多频率特点,将仿真测试分为以下两个环节。
2.4.1. 仿真环节1结果与分析
仿真测试环节1中,震颤信号d(k)采用频率为2 Hz、幅值为1的正弦信号。采样周期TS为0.005 s,因此A-RC控制器q = 1,选择单一支路的串联高阶内模结构。W1 = 1,内模延时周期N1 = 100,p = 2,K1 = 2,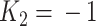 。对于单周期重复控制器,图3中q = 1,W1 = 1,N1 = 100,p = 1且K1 = 1。重复控制器补偿器H(z)由频率修正逆算法得到。采用临界比例度法确定了PI-HPF调节器的参数(P = 36.82,I = 1.4),高通巴特沃斯滤波器阶数为6,截止频率为1.2 Hz。设定参考输入r(k)为零,输出y(k)在干扰d(k)的作用下跟踪参考信号。
。对于单周期重复控制器,图3中q = 1,W1 = 1,N1 = 100,p = 1且K1 = 1。重复控制器补偿器H(z)由频率修正逆算法得到。采用临界比例度法确定了PI-HPF调节器的参数(P = 36.82,I = 1.4),高通巴特沃斯滤波器阶数为6,截止频率为1.2 Hz。设定参考输入r(k)为零,输出y(k)在干扰d(k)的作用下跟踪参考信号。
根据采集的患者震颤数据频谱分析可得,震颤信号的峰值频率随时间会产生稍许变化,故在仿真环节进行蒙特卡洛实验,以验证所提控制器对于频率变化的周期性震颤信号的抑制效果。令震颤信号d(k)在峰值频率±5%的范围内随机波动(即1.9~2.1 Hz随机变化),控制器参数不变,进行100次仿真实验,如图7所示。图7左侧图为仿真环节1中不同控制器下一次仿真测试的跟踪误差结果,PI-HPF方法的控制输入相对于两个重复控制器(A-RC和SP-RC)小一些,但是震颤抑制效果最差,因而验证了对于周期性扰动信号重复控制器的优越性。对比A-RC和SP-RC两种重复控制方法,在震颤峰值频率有所变化的情况下(设定2 Hz,实际2.05 Hz),本文所提的A-RC控制器跟踪误差信号最小,震颤抑制效果最佳。
图 7.

Tracking error and control input under different controllers
不同控制器下的跟踪误差和控制量
通过以下两个指标来量化各控制方法在震颤抑制方面的性能。
(1)均方根误差(root mean square error,RMSE)的计算公式如式(19)所示:
 |
19 |
其中,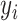 为输出信号,
为输出信号, 为参考信号,n为测试的总样本数。
为参考信号,n为测试的总样本数。
(2)震颤抑制率(tremor suppression rate,TSR)如式(20)所示:
 |
20 |
其中, 是输入信号
是输入信号 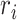 和输出信号
和输出信号 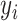 的偏差。
的偏差。 为震颤信号对跟踪角度的影响。
为震颤信号对跟踪角度的影响。 是输入信号
是输入信号  和
和 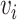 之间的偏差。
之间的偏差。 与
与  的比值为震颤抑制性能。
的比值为震颤抑制性能。
仿真环节1蒙特卡洛实验的统计结果如图8左侧图所示。PI-HPF方法受震颤信号频率变化影响最小,其次是本文所提的A-RC方法,而SP-RC方法最差。但PI-HPF方法的RMSE均值(0.357)却远远大于A-RC和SP-RC方法。SP-RC方法的RMSE均值为0.095,本文所提A-RC方法RMSE均值仅为0.043。RMSE 均值越小,意味着跟踪误差越小。在TSR的统计指标中,A-RC方法、SP-RC 方法和PI-HPF方法TSR均值分别为93.90%,85.26%和49.58%,TSR指标越大,震颤抑制效果越好。因此,本文所提的A-RC方法对于单频率变化的周期性震颤信号具有最佳的抑制效果。
图 8.

Statistical results of Monte Carlo trials
蒙特卡洛实验统计结果
2.4.2. 仿真环节2结果与分析
在仿真测试环节2中,震颤信号d(k)采用频率为2 Hz和2.5 Hz,幅值为1和0.8的叠加正弦信号。A-RC控制器切换到并联多内模结构,q = 2,W1 = W2 = 0.5,内模延时周期分别为N1 = 100和N2 = 80,K1 = K2 = 0.5,其余参数与仿真环节1一致。对于SP-RC控制器和PI-HPF控制器参数均不变。
在不同控制器下系统跟踪误差如图7仿真环节2所示,控制量和仿真环节1的结果类似,PI-HPF方法的控制量最小,A-RC和SP-RC方法的控制量相差不大。但是SP-RC方法的跟踪误差和仿真环节1相比有明显增加,因为单内模结构只能抑制内模中已有的周期性信号,而对于2.5 Hz的信号无法抑制。相比较而言,本文所提的A-RC方法可以实现多频率扰动信号的完全抑制。利用蒙特卡洛实验讨论在震颤频率变化情况下,控制器对于多频率震颤信号的抑制性能。震颤信号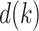 在峰值频率±5%的范围内波动,100次仿真测试的统计结果如图8仿真环节2所示。从统计结果分析来看,PI-HPF和SP-RC方法的RMSE均值接近,分别为0.408和0.394,这说明在震颤频率变化的情况下,这两个方法的稳态跟踪误差大,TSR指标仅为48.36%和50.21%,无法实现多频率震颤信号的抑制。而本文所提的A-RC控制器,利用其并联多内模结构,在频率变化的情况下,稳态误差小,TSR均值可达90.27%,即实现对多频率震颤信号的良好抑制。
在峰值频率±5%的范围内波动,100次仿真测试的统计结果如图8仿真环节2所示。从统计结果分析来看,PI-HPF和SP-RC方法的RMSE均值接近,分别为0.408和0.394,这说明在震颤频率变化的情况下,这两个方法的稳态跟踪误差大,TSR指标仅为48.36%和50.21%,无法实现多频率震颤信号的抑制。而本文所提的A-RC控制器,利用其并联多内模结构,在频率变化的情况下,稳态误差小,TSR均值可达90.27%,即实现对多频率震颤信号的良好抑制。
2.5. 试验验证
试验验证也分为两个阶段,第一阶段在健康参与者身上开展诱发性震颤抑制试验,用以评价所提控制方法的可行性。第二阶段招募意向性震颤患者进行震颤抑制验证试验,进一步验证所提方法的有效性。
2.5.1. 试验阶段1结果与分析
在试验阶段1中,通过震颤抑制实验平台产生诱发性震颤。为了防止肌肉疲劳,每个受试者的电刺激时长不超过20 min。4名健康参与者需要完成以下三个测试:
测试1(test 1,T1):自主地屈伸手腕跟踪参考轨迹,此测试无诱发性震颤和电刺激输入。
测试2(test 2,T2):自主地屈伸手腕跟踪参考轨迹,但此测试加入诱发性震颤信号。
测试3(test 3,T3):在具有诱发性震颤和功能性电刺激输入的情况下,自主屈伸手腕跟踪指定参考轨迹(每位受试者在同一控制器下进行3次T3试验)。
为了更好地对比不同控制器下T3的试验结果,将诱发震颤设置为多频震颤,频率为2 Hz和2.5 Hz。受试者No.1在不同控制器作用下其中一次试验的手腕运动轨迹和电刺激控制输入信号如图9所示。
图 9.

Wrist angular position and electrical stimulation level of participant No.1 under different controllers
受试者No.1在不同控制器下的手腕角度位置和电刺激信号
如图9中的T3手腕跟踪轨迹所示,3种不同的控制器均可以不同程度地实现诱发性震颤的抑制,但本文所提的A-RC方法的T3运动轨迹相对参考轨迹的偏离程度最小,具有最佳的震颤抑制效果。其次是SP-RC控制器,PI-HPF控制器的震颤抑制性能最差。对于电刺激控制输入,PI-HPF控制器产生的电刺激控制输入信号相对重复控制器要小一些,但震颤抑制性能差。A-RC控制器和SP-RC控制器的电刺激输入信号相差不大,结合T3的手腕运动轨迹可得本文所提A-RC方法具有震颤抑制的性能优势。如图10所示,受试者No.1在不同控制器下T3的跟踪轨迹时频图也可以得到相同的结论。在不同控制器作用下,多频率震颤信号的功率谱密度在震颤频率处均有不同程度的下降。其中,本文所提A-RC方法的功率谱密度下降最为明显,其次是SP-RC方法,而PI-HPF方法对于周期性震颤信号的抑制作用最差。
图 10.

The time-frequency diagram of tracking trajectory of participant No.1 under different controllers
参与者No.1在不同控制器下跟踪轨迹的时频图
试验环节采用与仿真环节相同的性能指标。如式(19)所示,RMSE值用于量化T3( )与T1(
)与T1( )的之间的偏离程度。如式(20)所示,
)的之间的偏离程度。如式(20)所示, 是T3(
是T3(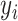 )与T1(
)与T1( )之间的偏差。
)之间的偏差。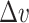 是T2(
是T2(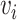 )与T1(
)与T1( )之间的偏差。其余三位健康参与者也得到了相似的试验结果,统计结果如图11所示。
)之间的偏差。其余三位健康参与者也得到了相似的试验结果,统计结果如图11所示。
图 11.

Statistical results of experiment with four participants
四位健康参与者试验统计结果
四位健康参与者RMSE均值A-RC方法最小为1.34,而SP-RC方法为3.12,PI-HPF方法为3.58,这一试验结果与仿真结果类似。通过TSR值可以更为直观地判断每种控制方法对周期性震颤信号的抑制情况,如图11所示四位健康参与者在本文所提的A-RC方法下震颤抑制性能显著提升,四位健康参与者TSR均值为87.59%,比SP-RC方法和PI-HPF方法均有明显提升。
2.5.2. 试验阶段2结果与分析
本阶段招募意向性震颤患者开展震颤抑制试验,定义以下三个测试试验:
测试4(test 4,T4):将指定参考轨迹提供给患者,患者不需任何动作。
测试5(test 5,T5):患者自主地屈伸手腕跟踪参考轨迹,此测试无FES信号。
测试6(test 6,T6):在FES作用下患者自主屈伸手腕跟踪参考轨迹(同一控制器下患者需进行3次T6试验)。
随机选择患者No.5和No.7的T6跟踪轨迹时频图如图12所示。从时频图可以看到,本文所提的A-RC方法,对于单频率震颤和多频率震颤均有很好的抑制效果,在震颤频率处的功率谱密度均有明显下降,比PI-HPF方法在震颤抑制性能方面有明显提升。而SP-RC方法对于周期性震颤信号也有一定的抑制作用,但效果相对不佳。患者试验环节也采用相同的性能指标。如式(19)所示,RMSE值用于量化T6(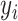 )与T4(
)与T4( )的之间的偏离程度。如式(20)所示,
)的之间的偏离程度。如式(20)所示, 是T6(
是T6( )与T4(
)与T4( )之间的偏差。
)之间的偏差。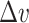 是T5(
是T5(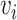 )与T4(
)与T4( )之间的偏差。患者No.5和No.7的量化试验统计结果如图13所示。
)之间的偏差。患者No.5和No.7的量化试验统计结果如图13所示。
图 12.

The time-frequency diagram of T6 tracking trajectory of patients No.5 and No.7 under different controllers
患者No.5和No.7在不同控制器下T6跟踪轨迹的时频图
图 13.

Statistical experimental results of intention tremor patients
意向性震颤患者试验统计数据
如图13所示,患者震颤抑制试验结果与第1阶段健康参与者的结果类似。A-RC方法对于单频率和多频率,且频率存在微变的震颤均有很好的抑制作用。A-RC方法实现平均82.53%的单频震颤和82.21%多频震颤抑制,而SP-RC方法和PI-HPF方法对于这两种类型震颤的抑制率仅分别为71.22%、58.31%和67.88%、52.33%。
3. 结论
本文提出一种基于FES的A-RC方法来抑制腕关节意向性震颤。首先建立了非线性Hammerstein结构的手腕肌骨模型,提出了自动、快速的参数辨识算法,在搭建的手腕震颤抑制实验平台完成了肌骨模型的参数辨识。其次,根据辨识的每位受试者肌骨模型设计相应的线性化控制与反馈A-RC相结合的控制器,并根据患者震颤频率特点自动选择重复控制内模结构,分析了闭环系统稳定性,并利用频率修正逆算法实现了重复控制补偿器的构造。最后,通过健康参与者诱发性震颤抑制试验和意向性患者震颤抑制试验验证了本文提出的A-RC策略,其平均震颤抑制率可达84.98%,比传统单内模重复控制和基于滤波的反馈控制均有明显提高。
重要声明
利益冲突声明:本文全体作者均声明不存在利益冲突。
作者贡献声明:张赞主要负责数据收集与分析、算法程序设计以及论文编写;霍本岩主要负责试验素材收集;刘艳红、楚冰和Owens David Howard主要负责试验指导、数据分析指导以及论文审阅修订。
伦理声明:本研究通过了郑州大学伦理委员会的审批(批文编号:No.ZZURIB2019-004)。
Funding Statement
国家重点研发计划(2020YFB1313701);国家自然科学基金项目(62103376,62003309) ;河南省引智计划项目(GZS2019008)
National Key Research and Development Project; National Natural Science Foundation of China; Outstanding Foreign Scientist Support Project in Henan Province
References
- 1.Saifee T A Tremor. British Medical Bulletin. 2019;130(1):51–63. doi: 10.1093/bmb/ldz017. [DOI] [PubMed] [Google Scholar]
- 2.王宇卉 解读2017年国际帕金森病和运动障碍学会震颤工作组共识声明之震颤的分类. 世界临床药物. 2018;39(7):433–440. doi: 10.13683/j.wph.2018.07.001. [DOI] [Google Scholar]
- 3.Smits E J, Tolonen A J, Cluitmans L, et al Graphical tasks to measure upper limb function in patients with Parkinson’s disease: validity and response to dopaminergic medication. IEEE Journal of Biomedical and Health Informatics. 2017;21(1):283–289. doi: 10.1109/JBHI.2015.2503802. [DOI] [PubMed] [Google Scholar]
- 4.Fukutome K, Kuga Y, Ohnishi H, et al What factors impact the clinical outcome of magnetic resonance imaging-guided focused ultrasound thalamotomy for essential tremor? Journal of Neurosurgery. 2020;134(5):1618–1623. doi: 10.3171/2020.2.JNS192814. [DOI] [PubMed] [Google Scholar]
- 5.Eisenberg H M, Krishna V, Elias W J, et al MR-guided focused ultrasound pallidotomy for Parkinson’s disease: safety and feasibility. Journal of Neurosurgery. 2020;135(3):792–798. doi: 10.3171/2020.6.JNS192773. [DOI] [PubMed] [Google Scholar]
- 6.梅加明, 牛朝诗, 熊赤, 等 苍白球或丘脑毁损术后帕金森病脑深部电刺激术疗效分析及策略. 中国现代神经疾病杂志. 2020;20(12):1045–1049. [Google Scholar]
- 7.Zahedi A, Zhang B, Yi A, et al A soft exoskeleton for tremor suppression equipped with flexible semiactive actuator. Soft Robotics. 2021;8(4):432–447. doi: 10.1089/soro.2019.0194. [DOI] [PubMed] [Google Scholar]
- 8.Pascual-Valdunciel A, Hoo G W, Avrillon S, et al Peripheral electrical stimulation to reduce pathological tremor: a review. Journal of Neuroengineering and Rehabilitation. 2021;18(1):33. doi: 10.1186/s12984-021-00811-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shin H, Hawari M A, Hu X Activation of superficial and deep finger flexors through transcutaneous nerve stimulation. IEEE Journal of Biomedical and Health Informatics. 2021;25(7):2575–2582. doi: 10.1109/JBHI.2020.3041669. [DOI] [PubMed] [Google Scholar]
- 10.Li Y, Yang X , Zhou Y, et al. Adaptive stimulation profiles modulation for foot drop correction using functional electrical stimulation: a proof of concept study. IEEE Journal of Biomedical and Health Informatics 2020;25(1):59–68. doi: 10.1109/JBHI.2020.2989747. [DOI] [PubMed] [Google Scholar]
- 11.李嘉莹, 赵丽, 边琰, 等 电刺激辅助下肢运动想象特征分类以增强康复训练研究. 生物医学工程学杂志. 2021;38(3):425–433. doi: 10.7507/1001-5515.202007004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Prochazka A, Elek J, Javidan M Attenuation of pathological tremors by functional electrical stimulation I: method. Annals of Biomedical Engineering. 1992;20(2):205–224. doi: 10.1007/BF02368521. [DOI] [PubMed] [Google Scholar]
- 13.Zhang D, Poignet P, Widjaja F, et al Neural oscillator based control for pathological tremor suppression via functional electrical stimulation. Control Engineering Practice. 2011;19(1):74–88. doi: 10.1016/j.conengprac.2010.08.009. [DOI] [Google Scholar]
- 14.Taheri B, Case D, Richer E Robust controller for tremor suppression at musculoskeletal level in human wrist. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2014;22(2):379–388. doi: 10.1109/TNSRE.2013.2295034. [DOI] [PubMed] [Google Scholar]
- 15.张伟, 张定国, 刘建荣 基于功能性电刺激的腕关节多自由度震颤抑制仿真研究. 生物医学工程学杂志. 2015;32(2):423–429. [PubMed] [Google Scholar]
- 16.Copur E H, Freeman C T, Chu B, et al Repetitive control of electrical stimulation for tremor suppression. IEEE Transactions on Control Systems Technology. 2019;27(2):540–552. doi: 10.1109/TCST.2017.2771327. [DOI] [Google Scholar]
- 17.Verstappen R J, Freeman C T, Rogers E, et al. Robust higher order repetitive control applied to human tremor suppression//IEEE International Symposium on Intelligent Control, Croatia: IEEE, 2012: 1214-1219.
- 18.Freeman C T, Sampsonb P, Burridgeb J H, et al Repetitive control of functional electrical stimulation for induced tremor suppression. Mechatronics. 2015;32:79–87. doi: 10.1016/j.mechatronics.2015.10.008. [DOI] [Google Scholar]
- 19.Kovács A, Kiss M, Pintér N, et al Characteristics of tremor induced by lesions of the cerebellum. Cerebellum. 2019;18(4):705–720. doi: 10.1007/s12311-019-01027-3. [DOI] [PubMed] [Google Scholar]
- 20.Zhang Z, Chu B, Liu Y, et al Multiperiodic repetitive control for functional electrical stimulation-based wrist tremor suppression. IEEE Transactions on Control Systems Technology. 2022;30(4):1494–1509. doi: 10.1109/TCST.2021.3111107. [DOI] [Google Scholar]
- 21.Kurniawan E, Afandi M I, Suryadi. Repetitive control system for tracking and rejection of multiple periodic signals//2017 International Conference on Robotics, Automation and Sciences (ICORAS), Malaysia: IEEE, 2017. DOI: 10.1109/ICORAS.2017.8308058.
- 22.Xu Q, Hu Z, Wu J, et al. Fast control strategy of APF based on improved DFT algorithm and repetitive control with multiple control frequency in synchronous rotation coordinates//22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin: CES, 2019. DOI: 10.1109/icems.2019.8922157.
- 23.Sa-e S, Freeman C T, Yang K Iterative learning control of functional electrical stimulation in the presence of voluntary user effort. Control Engineering Practice. 2020;96:104303. doi: 10.1016/j.conengprac.2020.104303. [DOI] [Google Scholar]
- 24.Lyons G M, Leane G E, Clarke M M, et al An investigation of the effect of electrode size and electrode location on comfort during stimulation of the gastrocnemius muscle. Medical Engineering & Physics. 2004;26(10):873–878. doi: 10.1016/j.medengphy.2004.08.003. [DOI] [PubMed] [Google Scholar]
- 25.Colacino F M, Emiliano R, Mace B R Subject specific musculoskeletal parameters of wrist flexors and extensors estimated by an EMG-driven musculoskeletal model. Medical Engineering & Physics. 2012;34(5):531–540. doi: 10.1016/j.medengphy.2011.08.012. [DOI] [PubMed] [Google Scholar]
- 26.Curtin M, Lowery M M Musculoskeletal modelling of muscle activation and applied external forces for the correction of scoliosis. Journal of NeuroEngineering and Rehabilitation. 2014;11:52–63. doi: 10.1186/1743-0003-11-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Longman R W On the theory and design of linear repetitive control systems. European Journal of Control. 2010;16(5):447–496. doi: 10.3166/ejc.16.447-496. [DOI] [Google Scholar]
- 28.Bhatia K P, Bain P, Bajaj N, et al Consensus statement on the classification of tremors. From the task force on tremor of the international Parkinson and movement disorder society. Movement Disorders. 2018;33(1):75–87. doi: 10.1002/mds.27121. [DOI] [PMC free article] [PubMed] [Google Scholar]







