Exploring the structural acrobatics of fold-switching proteins using simplified structure-based models

Abstract

Metamorphic proteins are a paradigm of the protein folding process, by encoding two or more native states, highly dissimilar in terms of their secondary, tertiary, and even quaternary structure, on a single amino acid sequence. Moreover, these proteins structurally interconvert between these native states in a reversible manner at biologically relevant timescales as a result of different environmental cues. The large-scale rearrangements experienced by these proteins, and their sometimes high mass interacting partners that trigger their metamorphosis, makes the computational and experimental study of their structural interconversion challenging. Here, we present our efforts in studying the refolding landscapes of two quintessential metamorphic proteins, RfaH and KaiB, using simplified dual-basin structure-based models (SBMs), rigorously footed on the energy landscape theory of protein folding and the principle of minimal frustration. By using coarse-grained models in which the native contacts and bonded interactions extracted from the available experimental structures of the two native states of RfaH and KaiB are merged into a single Hamiltonian, dual-basin SBM models can be generated and savvily calibrated to explore their fold-switch in a reversible manner in molecular dynamics simulations. We also describe how some of the insights offered by these simulations have driven the design of experiments and the validation of the conformational ensembles and refolding routes observed using this simple and computationally efficient models.

Introduction

Proteins are molecules that can fold in the three-dimensional space to reach, in most cases, a single structure that is referred to as native state. Sequences that fold into these structures are evolutionarily constrained to maintain such folding capabilities (Gilson et al. 2017), whose chemistry in space gives rise to what we recognize as their molecular function, i.e., their role as reaction catalysts, molecular switches, signal receptors, molecular motors, or proton pumps.

Surprisingly, some proteins seemingly defy the canonical idea of one sequence—one fold—one function, by having a single amino acid sequence that switches between more than one thermodynamically favorable structure, each with its own functional role. These are called metamorphic or fold-switching proteins (Lella and Mahalakshmi 2017), as they experience drastic changes in secondary and tertiary—and, in some cases, quaternary—structure, altering the topology of their folded structures in a reversible manner within relevant biological timescales of milliseconds (Zuber et al. 2019) to seconds (Tyler et al. 2011). In most cases, these structural acrobatics between two topologically dissimilar native states are triggered by environmental changes, such as interactions with binding partners or changes in pH or redox states (Murzin 2008).

Most known proteins displaying a metamorphic behavior are implicated in paramount biological processes, with their fold-switch having strong functional consequences for the fitness of their source organism (Artsimovitch and Ramírez-Sarmiento 2022). Two examples are the master regulator of enterobacterial virulence factors RfaH (Artsimovitch and Knauer 2019) and the periodicity-determining protein KaiB in the cyanobacterial circadian clock (Chang et al. 2015) (Fig. 1). The metamorphosis of these two proteins is drastic, involving a structural rearrangement of around 30–50% of their sequence length. Moreover, their involvement in crucial cellular processes makes their fold-switch an exquisite regulatory process of their biological function. Importantly for this review, a notable feature of both proteins is that they are relatively small, having less than 200 residues in their polypeptide chain, which makes them suitable to explore the details of their transformation mechanism in silico.

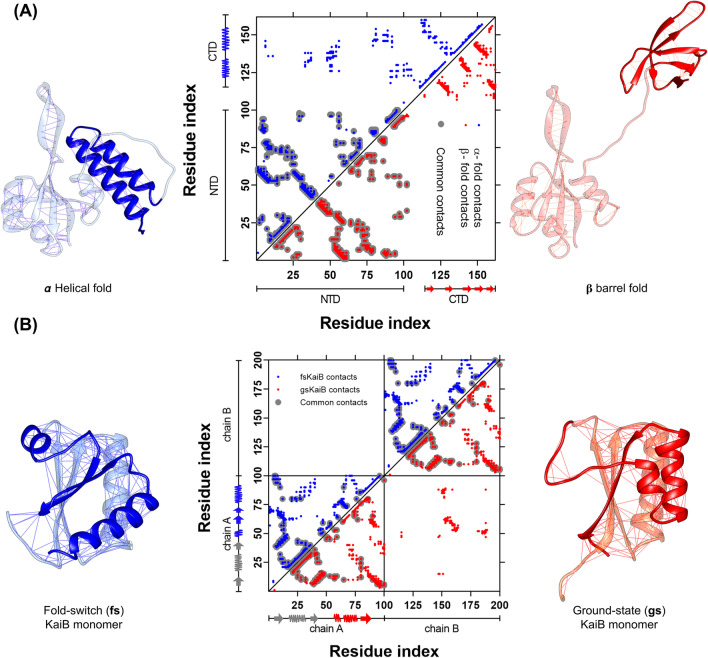
Fig. 1.

Topological rearrangement due to the fold-switch of the metamorphic proteins RfaH and KaiB. A Cartoon representation of full-length RfaH, with the C-terminal domain (CTD) folded as an α-helical hairpin (PDB 5OND, blue) or a β-barrel (PDB 2LCL, red), with the lines on each structure representing the native contacts. The middle panel shows the residue pair contact map for each native state of RfaH CTD, with the upper left triangle corresponding to the native contacts in the α-helical fold (blue) and the lower right triangle to the β-barrel fold. The interdomain contacts can be seen in the upper part of the contact map. B Cartoon representation of the KaiB monomer in the fold-switch (fs) state (PDB 5JYT, blue) and the ground-state (gs) fold (PDB 1VGL, red), with the lines on each structure representing the native contacts, highlighting the C-terminal half of the monomer that experiences the topological rearrangement. The middle panel shows the residue pair native contact map for each native state, with the upper left triangle corresponding to the native contacts in the fs state (blue) and the lower right triangle to the gs fold (red). Common contacts between both folds are shown in gray. Given that the gs fold is only observed in KaiB dimers or tetramers, the lower right square presents the intermolecular interactions between adjacent subunits in the KaiB dimer

RfaH is a non-essential transcription factor mostly found in enterobacteria (Wang et al. 2020) that regulates the expression of pathogenicity-related genes; hence, it behaves as a virulence factor. The solved crystal structures of Escherichia coli RfaH (PDB 2OUG and 5OND) show that it consists of two domains, commonly referred to as N-terminal (NTD, 100 residues) and C-terminal domains (CTD, 51 residues), being connected by a 11-residue linker and establish extensive interdomain interactions (Belogurov et al. 2007). The NTD folds as an α/β sandwich that hides an RNA polymerase (RNAP) binding site at its interface with the interacting CTD, which is forming an α-helical hairpin (PDB 2OUG and 5OND, Fig. 1A) (Belogurov et al. 2007). These interdomain interactions prevent it from binding the RNAP spontaneously, constituting an autoinhibited state. Nevertheless, this state is relieved upon RfaH recruitment to transcription elongation complexes paused at a specific hairpin-forming DNA sequence named ops (Zuber et al. 2018), triggering the breakage of the interdomain interactions and the fold-switch of its CTD into a small β-barrel (PDB 6C6S, Fig. 1A) (Kang et al. 2018). This structural rearrangement in RfaH allows to couple transcription and translation, by enabling CTD binding to the ribosomal protein S10 (Zuber et al. 2019).

The metamorphosis of the 108-residue long KaiB regulates the cyanobacterial circadian clock, composed also by KaiA and KaiC (Chang et al. 2015). The KaiABC protein clock is the simplest biological clock known, which is ATP/ADP dependent and insensitive to light. The subjective day physiology is dictated by the auto-phosphorylation of KaiC, which is stimulated by KaiA binding to its CII domain (Kim et al. 2008). The metamorphosis of KaiB plays a key role by transforming its structure from a ground-state (gs) homotetramer composed of two asymmetric dimers, where each monomer has a topology βαββααβ (PDB 1VGL, Fig. 1B) (Iwase et al. 2005), into a monomeric thioredoxin-like fold-switched (fs) state (PDB 5JYT, Fig. 1B) (Tseng et al. 2017) with a topology βαβαββα, which is able to bind to the N-terminal domain of the phosphorylated KaiC and to KaiA (Chang et al. 2015). In this scenario, KaiA binds to fsKaiB and promotes the auto-dephosphorylation of KaiC, thus leading to the subjective cyanobacterial night physiology.

It comes as no surprise that, even for small metamorphic proteins such as RfaH and KaiB, determining their experimental fold-switching mechanism is a huge endeavor as the triggers for the transformation are quaternary complexes of hundreds of kilodaltons in mass. Molecular dynamics (MD) simulations provide a complementary approach to gain insights into the molecular mechanism of their metamorphosis, as they can explore the atomic details of such large-scale structural changes while also setting the ground for new hypotheses that can be tested through wet lab experiments, including structural and mutagenic approaches. However, although efforts to model the refolding processes of RfaH in the all-atom scale have been successful (Gc et al. 2014, 2015; Li et al. 2014; Bernhardt and Hansmann 2018; Joseph et al. 2019; Appadurai et al. 2021), their adoption for simulating other—often bigger—metamorphic systems is challenged by the high computational costs of these conventional MD simulations, requiring enhanced sampling methods that do not ensure a thorough exploration of the refolding landscape or reaching the fully folded native states.

In this regard, simplified structure-based models (SBMs) (Noel and Onuchic 2012), which are rigorously footed on the energy landscape theory of protein folding and the minimal frustration principle (Bryngelson et al. 1995), are an attractive toolbox to study fold-switching (Ramírez-Sarmiento et al. 2015; Rivera et al. 2022) and other types of large-scale structural rearrangements, such as domain motions (Whitford et al. 2007), prion protein misfolding (Singh et al. 2012), and pre-to-post structural transitions in viral surface proteins (Lin et al. 2014; Dodero-Rojas et al. 2021).

In this review, the general use of SBMs as an ideal toolbox to study fold-switching proteins is presented. First, we will briefly describe how these models are constructed, followed by their reported use in two of the most extensively studied metamorphic proteins, RfaH and KaiB, and how these simulations unveil their refolding mechanism and source new hypotheses for experimental validation.

General features of structure-based models (SBMs)

SBMs are native-centric simulation models inspired by the principle of minimal frustration (Bryngelson and Wolynes 1987), an essential element that distinguishes natural proteins from random heteropolymers, according to which protein sequences are selected throughout protein evolution to maximize their ability to fold quickly. In such scenario, frustrated residue interactions that conflict with the native state are minimized, leading to smooth funnel-shaped folding energy landscapes with a clear preference for a single energy minimum corresponding to the native state (Bryngelson et al. 1995).

The crucial elements of the energy landscape theory of protein folding, namely, the minimally frustrated contacts that drive folding through a smooth funneled energy landscape, can be captured in a MD simulation model by obtaining the residue pairs that are in spatial proximity in the structure of the native state of a given protein and using them as an explicit component of its potential energy function (Noel and Onuchic 2012). These short-range, attractive “interactions” are calculated from an initial structure, either experimentally solved (Berman et al. 2000), computationally modeled (Kuhlman and Bradley 2019), or, more recently, predicted using state-of-the-art artificial intelligence strategies (Jumper et al. 2021); hence the name structure-based model.

Since these SBMs simplify and approximate the distribution of stabilizing enthalpy in the native state provided by short range interactions and density of native contacts in different regions of the protein regardless of their physicochemical nature (Noel and Onuchic 2012), a solvent is no longer a requirement for these models and the number of non-bonded interactions to be computed is dramatically reduced. Moreover, although the set of all native contacts in a protein, also known as contact map, is calculated using distance cutoffs over the heavy atom distances in the native structure, the granularity of these models can be reduced from all-atom (Whitford et al. 2009) to coarse-grained representations (Clementi et al. 2000), further reducing the number of particles in the simulation system and, in consequence, the number of non-bonded interactions is even lower and the MD simulations become even more computationally efficient. The most typical, extensively used coarse-grained SBM corresponds to a single bead per residue centered at the coordinates of the α-carbon (Clementi et al. 2000), which corresponds to a ~10-fold reduction in the number of atoms in comparison to an all-atom representation of the protein structure. It is worth mentioning at this point that we will focus on coarse-grained SBMs in this review, as they have been the most used for the study of metamorphic proteins.

In a typical coarse-grained SBM, both bonded and non-bonded interactions in the potential energy function of these models are extracted from the initial native structure, with interactions that maintain the covalently bonded structure of the protein—bonds, angles, dihedrals—being treated with harmonic potentials, whereas non-bonded interactions are treated as either attractive (in the case of native contacts) or repulsive (in the case of non-native contacts, i.e., all residue pairs that are not part of the contact map) through different potentials. The functional form of the potential energy function is:

$$V_{\mathit{CG}}=\sum _{\mathit{bonds}}{\epsilon }_r{\left(r,-,r_0\right)}^2+\sum _{\mathit{angles}}{\epsilon }_{\theta }{\left(\theta ,-,{\theta }_0\right)}^2+\sum _{\mathit{dihed}}{\epsilon }_D{F}_D\left(\varphi ,-,{\varphi }_0\right)+\sum _{\mathit{contacts}}{\epsilon }_{C}C\left(r_{\mathit{ij}},,,{r_0}^{\mathit{ij}}\right)+\sum _{non-contacts}{\epsilon }_{\mathit{NC}}{\left(\frac{{\sigma }_{\mathit{NC}}}{r_{\mathit{ij}}}\right)}^{12}$$ 1

where the dihedral potential F_D is:

$$F_D\left(\varphi \right)=\left[1,-,cos,\left(\varphi \right)\right]+\frac{1}{2}\left[1,-,cos,\left(3,\varphi \right)\right]$$ 2

In these equations, r₀, θ₀, ϕ₀, and r₀^ij are reference bond distances, angles, dihedral torsions, and contact distances obtained from the input structure. The strengths of these interactions have been extensively calibrated, corresponding to the homogeneous values ε_r = 100ε, ε_θ = 40ε, ε_ϕ = ε_C = ε_NC = ε, upon setting the energy scale to ε = k_BT = 1. Also, an appropriate excluded volume radius (σ_NC) of 4 Å is given to all residues to avoid chain crossings during MD simulations using SBMs.

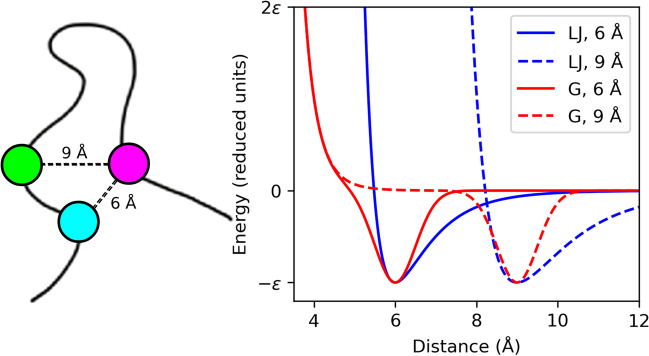
All native residue pair interactions in these models are given attractive potentials with their energy minima defined at the contact distance r₀^ij observed in the input structure, with a sequence separation between residue pairs ∣i − j ∣  > 3. The initial coarse-grained SBMs utilized a 12-10 Lennard-Jones (LJ) type potential due to the availability of LJ potentials in most simulation packages:

$$C_{\mathit{LJ}}\left(r_{\mathit{ij}},,,{r_0}^{\mathit{ij}}\right)=5{\left(\frac{r_0^{\mathit{ij}}}{r_{\mathit{ij}}}\right)}^{12}-6{\left(\frac{r_0^{\mathit{ij}}}{r_{\mathit{ij}}}\right)}^{10}$$ 3

However, these LJ potentials have the issue that the excluded volume for all native contacts moves with the energy minima (Fig. 2). Therefore, a Gaussian attractive potential has been recently developed to overcome this limitation, which enables the excluded volume to be fixed at a given radius (here, 4 Å) independently of the contact distance (Lammert et al. 2009):

$$C_G\left(r_{\mathit{ij}},,,{r_0}^{\mathit{ij}}\right)=\left[\left(1,+,{\left(\frac{{\sigma }_{\mathit{NC}}}{r_{\mathit{ij}}}\right)}^{12}\right),\left(1,+,G,\left(r_{\mathit{ij}},,,{r_0}^{\mathit{ij}}\right)\right),-,1\right]$$ 4

$$G\left(r_{\mathit{ij}},,,{r_0}^{\mathit{ij}}\right)=-exp\left[-,{\left(r_{\mathit{ij}},-,{r_0}^{\mathit{ij}}\right)}^2,/,\left(2,{\sigma }^2\right)\right]$$ 5

Fig. 2.

Graphic representation of native contact potentials used in SBMs. A scheme of the native contacts for two residue pairs forming native contacts at distances of 6 and 9 Å is shown on the left, and the corresponding 12-10 Lennard-Jones (LJ, blue) and Gaussian (G, red) contact potentials are plotted on the right. For the Gaussian potential presented herein, a well width of 0.5 Å and a fixed excluded volume radius of 4 Å were set for both native contacts, demonstrating the utility of Gaussian potentials to set custom yet homogenous excluded volumes for all native interactions in an SBM

where σ is the width of the attractive Gaussian term (0.5 Å) and the depth of the Gaussian minimum corresponds to ε (Fig. 2).

These SBMs can be obtained using the SMOG (Structure-based Models in GROMACS) webtool (Noel et al. 2010) or the SMOG2 standalone, downloadable version of the software (Noel et al. 2016), freely available at https://smog-server.org. Both tools take a given PDB file, which typically requires some pre-processing prior to using the SMOG software, and generate the coordinate and topology files with all bonded and non-bonded LJ or Gaussian interactions required for follow-up MD simulations. SMOG2 introduces more flexibility to users, by including several tools for formatting the PDB files before inputting them into SMOG, as well as enabling the creation and use of additional non-bonded potentials (e.g., elastic network models, Debye-Hückel electrostatic interactions) and force fields (e.g., support for simulations with ions, glycans), which are constantly developed by the SMOG user community.

The name of these tools for generating SBMs is quite deceiving, as now they not only generate the proper files for running MD simulations on GROMACS (Abraham et al. 2015), but also for other popular MD simulation packages such as NAMD (Phillips et al. 2020), LAMMPS (Thompson et al. 2022), and OpenMM (Eastman et al. 2017) using OpenSMOG (de Oliveira et al. 2022). The website also includes tutorials for running MD simulations in GROMACS and OpenMM. For Gaussian contact potentials, custom-modified versions of GROMACS (Abraham et al. 2015) that include these potentials are also available for download at the SMOG website to run such simulations.

Simulations are typically run at several temperatures around the folding temperature of the system (T_F) to obtain the free-energy profile of the folding reaction as a function of different reaction coordinates, such as the fraction of native contacts (Q), which are obtained using Perl scripts readily available on the SMOG server website (Noel et al. 2010) or the tool “g_kuh” from the SMOG-enhanced version of GROMACS (Noel et al. 2016); or the root mean square deviation (RMSD) against the initial structure as reference (Clementi et al. 2000), using the weighted histogram analysis method (WHAM) (Kumar et al. 1992) that is also included as part of the SMOG2 package (Noel et al. 2016). It is worth noting that neither RMSD nor Q alone may capture the full complexity of a protein’s conformational landscape, and both depend on knowing the native structures and the nature of the protein system under study. Sometimes it is useful to take subsets of native contacts to better explore the conformational landscape of a metamorphic protein. For example, the experimental knowledge of the interdomain contacts of RfaH as crucial for controlling its fold-switch (Tomar et al. 2013) enabled to use the interdomain native contacts to better display its refolding landscape (Ramírez-Sarmiento et al. 2015). Similarly, for KaiB we utilized the subset of contacts that were unique to either native state to better explore its fold-switch (Rivera et al. 2022). Additional analysis techniques and reaction coordinates (Chong and Ham 2018) may be necessary to be explored to gain a complete understanding.

From protein folding to fold-switching using SBMs

The SBMs described above can be defined as single-basin models: even in the scenario that these simulations step into intermediate states as in the case of three-state folding proteins (Clementi et al. 2000; Levy et al. 2004), the global energy minima to be reached is explicitly defined in the Hamiltonian to correspond to a single native state.

These SBMs can be expanded to simulate the refolding of metamorphic proteins, in which there is interconversion between two dissimilar native states, by explicitly adding the information of both states in the Hamiltonian, what is also known as a dual-basin SBM. These approaches have been used in the past to simulate other conformational changes, such as the domain motions in several enzymes (Okazaki et al. 2006; Whitford et al. 2007) and the formation of amyloid structures by prion proteins (Singh et al. 2012). In fact, these dual-basin models can be, in principle, further expanded into more general “multi-basin” SBMs (Okazaki et al. 2006).

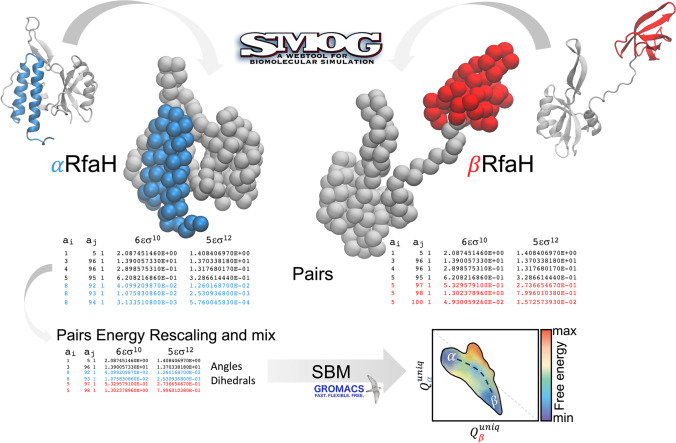
A scheme of how to generate a dual-basin coarse-grained SBM for simulating the refolding of a metamorphic protein is presented in Fig. 3. First, the coordinate and topology files of both native states are required. Then, residue pair contacts that are unique to each native state must be merged into a single contact map. As expected, it is possible that some of the residue pairs forming native contacts in each state are the same, in which case some decisions must be made. The simplest scenario corresponds to the spatial distances between these common residue pairs being similar for both native states, in which case keeping only one of such interactions in the contact map suffices. But if the spatial distance varies significantly, then both contact distances must be informed in the potential energy function. As can be gathered from Fig. 2, this is a complex problem when utilizing LJ potentials, since the excluded volume moves along with the minima, meaning that for a residue pair with two contact distances, the largest distance will inform an excluded volume that will overcome the energy minima of the shortest distance. A rule of thumb would be that LJ potentials can be used only if: (i) the number of contacts between common residue pairs for both native states is small and (ii) the changes in distance between these native contacts are small. Otherwise, the Gaussian potential, in which a homogeneous excluded volume can be used for all contacts, is the most recommended option. In fact, these single-basin contact potentials can be further expanded into dual-basin contact potentials centered at two energy minima by adding another Gaussian into its functional form:

$$C_{\mathit{DB}}\left(r_{\mathit{ij}},,,r_A^{\mathit{ij}},,,r_B^{\mathit{ij}}\right)=\left[\left(1,+,{\left(\frac{{\sigma }_{\mathit{NC}}}{r_{\mathit{ij}}}\right)}^{12}\right),\left(1,+,G,\left(r_{\mathit{ij}},,,r_A^{\mathit{ij}}\right)\right),\left(1,+,G,\left(r_{\mathit{ij}},,,r_B^{\mathit{ij}}\right)\right),-,1\right]$$ 6

Fig. 3.

Scheme of the generation of a dual-basin coarse-grained SBM for simulating the refolding of RfaH using LJ potentials. The granularity of the simulation system is reduced to a single bead centered at the α-carbon of each residue, and the residue pair contact map from the topology files of each state is taken as an input to resolve which contacts are unique to each state (blue and red) and which ones are formed by common residue pairs at similar or different distances (black), to be combined into a single potential energy function. Since combining these contacts does not ensure reversible refolding, the strength ε_C of the contacts of one of the native states must be rescaled to enable such reversibility. Once residue pair interactions are mixed and rescaled, and angles and dihedrals that specify each native state are also included, MD simulations enable to observe many refolding transitions and obtain the free energy landscape connecting both native states, indicated as α and β in the contour map, within a reasonable computing time of a few weeks

These Gaussian potentials can be even further expanded into multi-basin potentials.

Merging the bonded and non-bonded contributions of each native state into a single Hamiltonian might lead to the observation of just one of these two states during the simulation. This is because each native state, with its uneven distribution and number of native contacts, has different folding temperatures and stabilities. For example, the combination of the native contact potentials of both RfaH folds led to the observation of the autoinhibited state of RfaH alone, without refolding into the active state (Ramírez-Sarmiento et al. 2015). For dual-basin models of metamorphic proteins, it becomes also necessary to rescale the strength ε_C of the contact potentials of one of the native states to enable the simulation of reversible refolding transitions (Fig. 3). A rule of thumb to determine whether such step is necessary is to run simulations of the single-basin SBMs and checking whether there is a large gap in the folding temperature of both systems, and to rescale the strength ε_C based on the proportion of native contacts between both states (Rivera et al. 2022).

Caution must also be taken when combining the information for bonded interactions into a single potential energy function. While bond distances are unlikely to vary significantly, such that they can be retrieved from only one native state, this is not the case for angles and dihedral torsions, which can be quite different when there are significant changes in secondary and tertiary structure, as in the case of metamorphic proteins. From our experience, we merge only those angles and dihedrals where the absolute difference between both native states is bigger than 10°, which are typically only located in the fold-switching region. It is worth noting that this mixing of dihedral angles from both native states is not ideal, as the combination of dihedrals leads to their averaging at a dihedral angle in the midpoint of the two angles, which could lead to artifactual configurations. Alternatively, dual-basin angle potentials (Giri Rao et al. 2016) and dual-basin dihedral potentials (Lin et al. 2014) are also a possibility to avoid cancelation of their energy minima.

For a hands-on deep dive into the generation and use of dual-basin models, our research group recently released a collection of tutorials on molecular modeling and simulation for execution on the cloud (Engelberger et al. 2021), available at https://github.com/pb3lab/ibm3202, with one of such tutorials being the generation of a coarse-grained dual-basin SBM to simulate the large-scale domain motions of adenylate kinase according to a previous research work (Whitford et al. 2007).

In the following sections, we will illustrate how these fundamentals for the generation of dual-basin SBMs were utilized to explore the refolding landscapes of RfaH and KaiB, looking under the computational microscope for the structural features of their metamorphic transitions and for potential intermediate states along the fold-switching route.

Dual-basin simulations of RfaH fold-switch match experimental observations

RfaH regulates the transcription and translation of otherwise poorly translated genes, such as foreign genes and distal genes in long operons, by inhibiting Rho action and enabling physical coupling between RNAP and the ribosome (Belogurov et al. 2009). To avoid spurious binding to RNAP, RfaH action is controlled by a large-scale conformational change from an autoinhibited state, in which the CTD is folded as an α-helical hairpin tightly bound to the RNAP-binding site in the NTD, into an active state in which interdomain interactions are lacking and the CTD is folded as the canonical β-barrel conformation that is conserved across all NusG-like transcription factors (Burmann et al. 2012).

The dramatic all-α to all-β refolding of RfaH in the context of the full-length protein has been described using dual-basin SBMs based on LJ potentials (Ramírez-Sarmiento et al., 2015), by merging the bonded and non-bonded interactions derived from the experimental structure of full-length RfaH in the autoinhibited state obtained by X-ray crystallography (PDB 2OUG) (Belogurov et al. 2007) and the NMR solution structure of the isolated CTD in the β-barrel conformation (PDB 2LCL) (Burmann et al. 2012). To simulate the fold-switch of this domain in the context of the full-length protein, the coordinate and topology parameters for the NTD were taken from the autoinhibited state, and all other parameters for the CTD were combined into a single Hamiltonian. Moreover, since the NTD was expected to remain unchanged in light of experimental evidence, particularly that it is well-conserved in all NusG family members irrespective of the topology of the CTD, all its native contacts were treated with harmonic potentials instead of 12-10 LJ potentials, such that the NTD was not allowed to undergo unfolding and only the CTD would be refolded or unfolded as a function of temperature (Ramírez-Sarmiento et al., 2015).

Once the dual-basin SBM of RfaH was generated, it was observed that the α-helical hairpin was not completely bound to the NTD, with the ends of the helices being disordered (Ramírez-Sarmiento et al. 2015). Given that the relaxation times observed for the NTD and CTD domains in the full-length protein were informative of tight interdomain interactions, it was decided to reduce the sequence separation between residue pairs in contact from ∣i − j ∣  > 3 to ∣i − j ∣  > 2 to successfully increase the stability of the helical structure by increasing the number of native contacts involved in α-helical structures. Also, dihedrals involving the linker between domains (residues 101–114) were disregarded, since they were modeled as a loop due to its absence in the structure of the autoinhibited state of RfaH (PDB 2OUG).

In total, 106 contacts from the α-folded CTD, 166 contacts from the β-folded, and 80 interdomain contacts between RfaH NTD and CTD were included in the final dual-basin SBM. Of these contacts, only 19 residue pairs in contact in the native state were found to be shared between the α- and β-folded CTD, which were counted only once and given the native distance of the α-folded CTD. This choice of contact distance was made such that the separation between the autoinhibited and active states of RfaH in terms of the number of native contacts formed upon reaching each native basin was maximized (Ramírez-Sarmiento et al. 2015).

The final dual-basin SBM exhibited 100% of the population in the autoinhibited state below T_F. However, if the interdomain interactions were turned off by removing them from the topology file or making their strength ε_C = 0, the dual-basin SBM was exclusively folded as a β-barrel below T_F. These thermodynamics were in full agreement with what was captured in NMR experiments (Burmann et al. 2012): (i) when the CTD is bound to the NTD, the folding conformation of the CTD is an α-hairpin; (ii) when the CTD is released from the NTD by protease cleavage of the linker connecting both domains, the CTD becomes a β-barrel.

Both NMR experiments on an RfaH mutant (E48S) that disrupts an interdomain salt bridge (Burmann et al. 2012) and domain-swapping experiments in which the sequence ordering of the NTD and CTD was inverted (Tomar et al. 2013) suggested that the refolding of RfaH from the autoinhibited to the active state was controlled by interdomain contacts. Hence, it came as no surprise that the decrease of the strength of the interdomain contacts in our dual-basin SBM for RfaH by ~50% led to the reversible all-α to all-β refolding of RfaH with both states in 1:1 equilibrium (Ramírez-Sarmiento et al. 2015). Such simulations resembled the 1:1 equilibrium observed for the E48S mutant of RfaH in NMR experiments (Burmann et al. 2012). Since the β-barrel buries many of the residues involved in forming the interdomain contacts that stabilize the α-folded CTD upon refolding (Fig. 4), decreasing the strength of these interdomain contacts destabilizes the autoinhibited state of RfaH more than the β-folded CTD (Ramírez-Sarmiento et al. 2015).

Fig. 4.

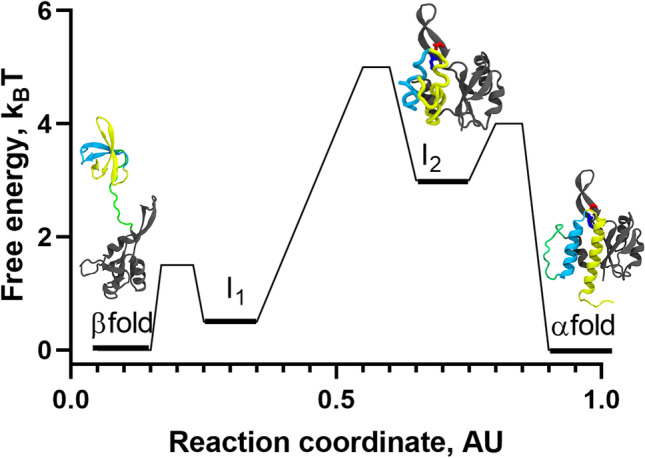
Refolding landscape of RfaH obtained from MD simulations at interdomain contact strength of 50% using a coarse-grained dual-basin SBM. The protein structures in cartoon representation correspond to the native and intermediate states observed during the refolding simulations. The NTD (100 residues) is colored gray, whereas the first and second helix of the CTD (51 residues) are colored in cyan and yellow, respectively, and the 11-residue linker connecting both domains is colored green. Based on the contact map for I₁, which contains many of the native contacts of the β-folded CTD, it is likely that it structurally belongs to the β-fold energy minimum according to β/I₁ ⇄ I₂ ⇄ α. The reaction coordinate was created to project the complex refolding landscape of RfaH in two dimensions

As mentioned above, by controlling the strength of these interdomain contacts in the simulations we can observe RfaH regions associated with transient and partial unfolding resembling the all-α or all-β CTD structures. In fact, it was observed that the native states of RfaH are connected by two obligated intermediate states comprising a mixture of native contacts from both folds (Fig. 4). In one of such intermediates, termed I₂, the CTD remains interacting with the NTD through the tip of its α-helical hairpin, which prevents the CTD from entirely unfolding, whereas the ends of the α-helical hairpin are unfolded. A second intermediate, termed I₁, exhibited a higher number of native contacts from the active state with a higher probability of being formed, particularly those located between strands β3–β4 and β1–β5. Both intermediates were found to be relatively unstable compared to the autoinhibited and active states of RfaH, and can undergo rapid conformational changes towards the native basins. Overall, these features enabled to propose a refolding landscape for RfaH following a three-state folding process β/I₁ ⇄ I₂ ⇄ α, mostly due to the low transition state barrier and free-energy difference connecting β and I₁ (Fig. 4).

Recent experiments using hydrogen-deuterium exchange mass spectrometry (Ramirez-Sarmiento and Komives 2018) to localize the structural flexibility of different regions of RfaH enabled to successfully validate the existence of I₂ in solution, in which the ends of the α-helical hairpin are more solvent-accessible than the tip of the hairpin in the full-length protein under native conditions (Galaz-Davison et al. 2020). These results, and the good agreement between prior experimental evidence for RfaH and the set of simulations performed with the dual-basin SBM at different interdomain contact strengths, demonstrate how these simplified models show a consistent picture of the refolding landscape of metamorphic proteins.

Double-basin SBM simulations unveil the relevance of dimer dissociation during the transformation of KaiB

KaiB regulates the rhythmicity of the KaiABC clock by not only fold-switching the C-terminal half of its structure, but also by changing its quaternary state from a homotetramer (gsKaiB) to a monomeric thioredoxin-like fold (fsKaiB) (Kitayama et al. 2003; Chang et al. 2015). Exploring the metamorphosis of a protein whose structural acrobatics alters its oligomerization state is not as trivial as for a monomeric protein like RfaH, and determining the switching landscape of KaiB can help to understand the relevance of oligomers in other metamorphic proteins such as selecase (López-Pelegrín et al. 2014). Here, we describe the steps of constructing a dual-basin SBM of KaiB recently utilized by our research group to understand its fold-switch (Rivera et al. 2022).

To simulate the fold-switch of KaiB, the crystallographic structure of a single-point mutant (C64T) gsKaiB (PDB 1VGL) (Iwase et al. 2005) and the NMR structure of quintuple-point mutant (A8Y/A29N/A89G/R91D/A94Y) fsKaiB (PDB 5JYT) (Tseng et al. 2017) were mutated back to restore the wild-type sequences and then used as inputs for generating coarse-grained single-basin SBM models that were later combined into a dual-basin model. To reduce the added complexity of the simulations provided by the changes in quaternary structure driven by the KaiB fold-switch, only the dimeric state of gsKaiB (gs₂) was used due to four reasons: (i) gsKaiB forms a homotetramer of two asymmetrical dimers (Iwase et al. 2005); (ii) the dimer is sufficient to sustain the biological role of KaiB in vitro (Murakami et al. 2012; Iida et al. 2015); (iii) the available structures of KaiB lack structural information at the ends of their polypeptide chain, crucial for stabilizing the tetramer (Iida et al. 2015); (iv) the monomers within the dimer show no significant structural differences, compared to the monomers within the tetramer (Garces et al. 2004).

An uneven number of native contacts per monomer in the gsKaiB dimer may lead to a higher probability of unfolding of one subunit over the other, which is why chain B was replaced by chain A after structural superposition (α-carbon root mean square deviation = 0.615 Å), making the structure symmetrical and with both monomers with identical native bond lengths, angles, dihedrals, contacts, and contact distances. Finally, for consistency of the number of atoms and residues on the models, the switching of KaiB was simulated as gs₂ ⇄ 2fs. Hence, we used a SBM of the fsKaiB state in which the fs monomer was duplicated and placed 50 Å away from the initial one (i.e., 2fs), ensuring that protein-protein interactions were only calculated from the gsKaiB dimer.

As a result of the generation of the single-basin SBM using these preprocessed structures, 287 and 289 monomer contacts were obtained for fs and gs₂, respectively, and 76 interface contacts for gs₂ (Fig. 1B). Among these protein-protein contacts, 3 were asymmetrically formed, which is why they were symmetrized in the final gs₂ configuration so that each monomer contributed the same number of contacts and interacting residue pairs to the dimer stability. These were the final single-basin SBMs that were used for generation of a dual-basin SBM for KaiB.

The dual-basin SBM was generated by merging the Hamiltonians from gs₂ and 2fs into a single energy function, using gs₂ as ground state (Rivera et al. 2022). Regarding the bonded interactions (Eq. 1), while bonds were taken from gs₂ as the ground state, native angles from both 2fs and gs₂ were savvily merged, by only considering those with an absolute difference between the gs₂ and 2fs bigger than 10° (102 angles); otherwise, the potential for the angle was represented only for the angle potential of gs₂. A similar strategy was used for dihedrals, where only those involved in the fold-switching region (residues 51–100) were considered for merging into a dual-basin SBM, whereas all others were taken from gs₂.

In contrast to the strategy used with RfaH, in which the native contacts of a whole domain were treated with harmonic potentials (Ramírez-Sarmiento et al. 2015), all native interactions in KaiB were given attractive Gaussian potentials. By examining the residue pairs forming native contacts on each state, it was determined that 189 intramolecular per subunit and 76 intermolecular contacts were unique to gs₂, whereas 187 contacts per monomer were unique to 2fs, for which we used single-basin Gaussian potentials (Eq. 4). For all other residue pairs that form native contacts in both native states, a dual-basin Gaussian potential (Eq. 6) was given only if the difference in contact distances for these residue pairs in gs₂ and 2fs was larger than 20%, corresponding to 41 contacts. All other 59 contacts were treated with single-basin Gaussian potentials using the topology parameters from gs₂. Finally, as gs₂ had more contacts (654) than 2fs (574), reversible fold-switching of KaiB was ensured by balancing the energy contributions of each native states in the dual-basin model by rescaling the depth of the Gaussian minimum for all contacts in 2fs by the ratio of native contacts between gs₂ and 2fs (~1.13).

The simulations of the gs₂ ⇄ 2fs fold-switch were challenging due to the added complexity of dimer dissociation during the refolding process on a simulation system that lacks solvent molecules and periodic boundary conditions. In this regard, the proximity of the protein subunits was ensured by adding a harmonic restraint between the centers of mass of each monomer, using either a soft (k = 1.0 ε·nm⁻²) or a stiff (k = 4.0 ε·nm⁻²) spring constant. Then, after running simulations at 26 different temperatures around T_F for 5 × 10⁹ steps, heat capacity and free-energy profiles were obtained using the WHAM method (Kumar et al. 1992).

The simulations with dual-basin SBMs effectively explored the refolding landscape of gs₂ ⇄ 2fs and exhibited two peaks in heat capacity, corresponding to two folding temperatures termed T_F1 and T_F2. By analyzing the refolding landscape of KaiB as a function of the proportion of native monomer contacts unique to the fs and gs folds, it was determined that the KaiB fold-switch occurred at T_F1, with a transition state of ~7 k_BT comprising about 30% and 50% of the unique contacts from fs and gs, respectively. When we associated the changes of unique contacts with dimer contacts, we demonstrated that the fold-switch from gsKaiB dimer to fsKaiB monomer is mediated by a scarcely populated gs monomer, with a free-energy barrier of dissociation (gs₂ ⇄ 2gs) ~10 k_BT (Fig. 5). Moreover, despite that the dual model explores the formation of a fraction of the dimer contacts expected for the gsKaiB dimer in the context of the fs fold, this is an off-pathway metastable state of high energy that does not lead to gs₂.

Fig. 5.

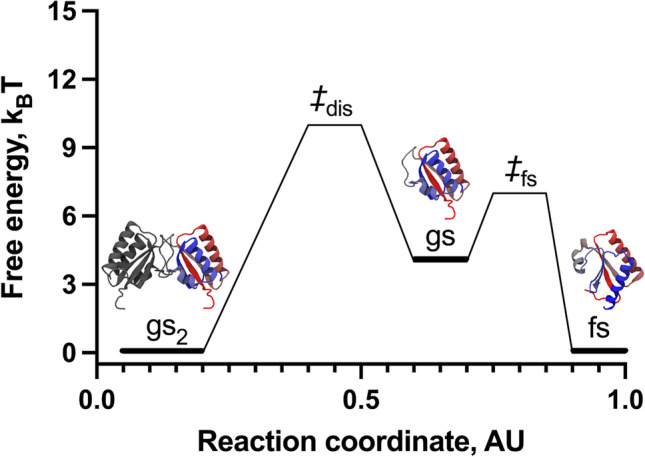
Refolding landscape of KaiB obtained from MD simulations using a coarse-grained dual-basin SBM. The protein structures in cartoon representation correspond to the native and intermediate states observed during the refolding simulations. The reaction coordinate was created to project the complex refolding landscape of KaiB in two dimensions

Lastly, analyzing the population fractions of all states, namely, gs₂, gs, fs, and the unfolded state, as a function of temperature, we determined that the dissociation of gsKaiB dimer into its monomers leads to the concurrent fold-switch into the fs monomer. Hence, the accumulation of fsKaiB occurs on the detriment of gsKaiB and confirmed that T_F2 corresponds to the folding temperature of the fsKaiB monomer preceding unfolding. Based on these results using dual-basin SBMs, we determined that the dimer dissociation is the rate limiting step of the fold-switch of KaiB, which follows the pathway gs₂ ⇄ 2gs ⇄ 2fs (Fig. 5).

To further understand the thermodynamics of KaiB fold-switching, MD simulations using the confine-convert-release (CCR) method (Roy et al. 2014) were performed to determine the transformation energies following the refolding pathway suggested by our dual-basin SBM. In these CCR simulations, which employ empirical force fields with implicit solvation, it was confirmed that the main energy cost of KaiB fold-switching is the transformation of gs₂ → 2gs, and once KaiB is in the monomeric state the transformation towards fs is highly favorable. This observation is in good agreement with SBM, where the dissociation of the dimer is the limiting step for the fold-switch (Rivera et al. 2022).

These computational observations led to the design of experiments using size exclusion chromatography and hydrogen-deuterium exchange mass spectrometry (HDXMS) (Ramirez-Sarmiento and Komives 2018) on a KaiB mutant that accelerates the KaiABC clock periodicity by 2 h (R75C) (Qin et al. 2010). This mutant populated dimeric and monomeric species, and its local flexibility across different peptides observed by HDXMS strongly suggested that the secondary structure of R75C resembled fsKaiB (Rivera et al. 2022). Therefore, the computational results were well correlated with experimental observations, in which the fold-switch of KaiB is highly related to the dissociation of the dimer.

Beyond SBM: other computational approaches to study fold-switching proteins

Since the explosion of highly accurate methods for protein structure prediction such as AlphaFold2 (Jumper et al. 2021), OmegaFold (Wu et al. 2022), RosettaFold (Baek et al. 2021), and ESMFold (Lin et al. 2023), obtaining an initial structure for performing folding trajectories has become a much simpler task. Nevertheless, most of these prediction tools alone are insufficient to sample deeper features of the protein free energy landscape, and their use using default settings has proven to be insufficient to predict the native states of metamorphic proteins (Chakravarty and Porter 2022), needing specific manual inputs for accessing structural heterogeneity (Wayment-Steele et al. 2022). However, even in the presence of multiple structures, the connectivity and energy barriers between them are missing; hence, a MD approach is still better suited to provide the desired transformation process.

When faced with solving a folding or fold-switching problem, one can rely on several MD tools with different degrees of complexity. The simpler approach is to only solve this as a geometric topological problem, where a change in native contacts is taking place, and this is the coarse-grained SBM approach (Ramírez-Sarmiento et al. 2015; Rivera et al. 2022), which is described in detail throughout this review.

An alternative that considers the complexity of side chain packing corresponds to the all-atom SBM (Whitford et al. 2009), in which every heavy atom is represented, and every atom-atom native contact is considered as an attractive interaction. One can then move onto models that are not entirely structure-based, such as AWSEM (Davtyan et al. 2012), that considers a structure-biasing term among all its knowledge-based potentials, and has been already used for studying deep structural changes (Chen et al. 2016; Galaz-Davison et al. 2021).

Finally, a myriad of enhanced-sampling MD approaches have been developed and utilized for studying fold-switching of metamorphic proteins using atomistic representations (Bernhardt and Hansmann 2018; Joseph et al. 2019; Appadurai et al. 2021; Seifi and Wallin 2021; Wang et al. 2022). These methods have been extensively reviewed by us in the past (Artsimovitch and Ramírez-Sarmiento 2022), yet none of them compares to the simplicity and sampling efficiency of SBM while providing similar or equivalent answers.

Conclusions

The fold-switching landscape of monomeric and oligomeric metamorphic proteins can be unveiled using computationally efficient dual-basin SBMs, in turn enabling to predict novel residues that can potentially impair or favor fold-switching due to their involvement in the stability of the tertiary and/or quaternary structure of their native states or in reaching the transition state that separates each native basin.

By making observations from these computational simulations and finding clues in the conformational ensembles captured over time, we can also learn about the characteristics of potential intermediate states on the route of fold-switching and the structural features that would enable their discrimination in properly designed and well-thought experiments. An exemplar case is the determination that the NTD-bound intermediate state of RfaH, described as the melting of the ends of the α-helical CTD hairpin, has been experimentally demonstrated using hydrogen-deuterium exchange mass spectrometry (Galaz-Davison et al. 2020).

While most fold-switching simulations of metamorphic proteins have been performed using coarse-grained SBM, there is still the need for atomistic representations of these refolding phenomena. In this regard, the SMOG webtool also enables the generation of all-atom SBMs that incorporate all heavy atoms of a given protein structure (Whitford et al. 2009), and has been used for simulating proteins that have been engineered to switch between folds (Sutto and Camilloni 2012). Further use of such all-atom models to simulate refolding of metamorphic proteins, and of other higher-granularity models that incorporate side chain β-carbons alongside physics- and knowledge-based potentials (Galaz-Davison et al. 2021), will further enable to understand the steric effects of side chain packing during protein refolding and to generate estimates of the relevance of local energetic frustration (Rausch et al. 2021) emerging from sequence variations and non-native interactions (Parra et al. 2015).

Author contributions

All authors wrote the manuscript and prepared the figures. C.A.R-S. reviewed the manuscript. M.R. and C.A.R-S. conceptualized and led the work.

Funding

This work was funded by the National Agency for Research and Development (ANID) through Fondo de Desarrollo Científico y Tecnológico (FONDECYT 1201684 to C.A.R-S.; FONDECYT 3190731 to M.R.) and ANID Millennium Science Initiative Program (ICN17_022). J.G. and P.G-D. were supported by ANID Doctoral Scholarships (PFCHA 21212113 and 21181705, respectively).

Data availability

The software used to generate the contact maps in Fig. 1 and the contact pairs listed in Fig. 3 is publicly available at https://smog-server.org. The structures to generate this data are publicly available in the Protein Data Bank under accession codes 2OUG, 5OND, and 2LCL for RfaH and 1VGL and 5JYT for KaiB. The free energy data used to generate the schematic free energy landscapes in Figs. 4 and 5 is publicly available in the articles by Ramirez-Sarmiento et al. (2015) and Rivera et al. (2022).

Code availability

Not applicable.

Declarations

Ethical approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.