Abstract
Background
Accurate analysis of quantitative PET data plays a crucial role in studying small, specific brain structures. The integration of PET and MRI through an integrated PET/MR system presents an opportunity to leverage the benefits of precisely aligned structural MRI and molecular PET images in both spatial and temporal dimensions. However, in many clinical workflows, PET studies are often performed without the aid of individually matched structural MRI scans, primarily for the sake of convenience in the data collection and brain segmentation possesses. Currently, two commonly employed segmentation strategies for brain PET analysis are distinguished: methods with or without MRI registration and methods employing either atlas-based or individual-based algorithms. Moreover, the development of artificial intelligence (AI)-assisted methods for predicting brain segmentation holds promise but requires further validation of their efficiency and accuracy for clinical applications. This study aims to compare and evaluate the correlations, consistencies, and differences among the above-mentioned brain segmentation strategies in quantification of brain metabolism in 18F-FDG PET/MR analysis.
Results
Strong correlations were observed among all methods (r = 0.932 to 0.999, P < 0.001). The variances attributable to subject and brain region were higher than those caused by segmentation methods (P < 0.001). However, intraclass correlation coefficient (ICC)s between methods with or without MRI registration ranged from 0.924 to 0.975, while ICCs between methods with atlas- or individual-based algorithms ranged from 0.741 to 0.879. Brain regions exhibiting significant standardized uptake values (SUV) differences due to segmentation methods were the basal ganglia nuclei (maximum to 11.50 ± 4.67%), and various cerebral cortexes in temporal and occipital regions (maximum to 18.03 ± 5.52%). The AI-based method demonstrated high correlation (r = 0.998 and 0.999, P < 0.001) and ICC (0.998 and 0.997) with FreeSurfer, substantially reducing the time from 8.13 h to 57 s on per subject.
Conclusions
Different segmentation methods may have impact on the calculation of brain metabolism in basal ganglia nuclei and specific cerebral cortexes. The AI-based approach offers improved efficiency and is recommended for its enhanced performance.
Keywords: Magnetic resonance imaging, Positron emission tomography, Metabolism, Artificial intelligence
Introduction
Accurate analysis of quantitative positron emission tomography (PET) data plays a crucial role in studying small, specific brain structures. For instance, investigations of abnormalities in the hippocampus in Alzheimer’s disease, localization of the epileptogenic zone in epilepsy, and delineation of lesion distribution in patients with brain tumors or ischemic stroke [1–4]. Magnetic resonance imaging (MRI) has high soft-tissue contrast and image resolution, facilitating localization and segmentation of brain regions of interest (ROIs) in individual subjects. Consequently, the integration of PET and MRI through an integrated PET/MR system presents an opportunity to leverage the benefits of precisely aligned structural MRI and molecular PET images in both spatial and temporal dimensions, thereby enhancing the value of such studies [5–8].
However, in many clinical workflows, PET studies are often performed without the aid of individually matched structural MRI scans, primarily for the sake of convenience in the data collection and brain segmentation possesses. Currently, two commonly employed segmentation strategies for brain PET analysis are distinguished: methods with or without MRI registration and methods employing either atlas-based or individual-based algorithms [9]. These strategies can be implemented using well-established brain automatic analysis tools, including statistical parametric mapping (SPM) [10], FMRIB software library (FSL) [11], and FreeSurfer [12]. While the previous studies have compared morphological parameters derived from structural MRI using these methods, none have specifically examined the impact of MRI segmentation when registered to PET, nor have they compared these results with regional standardized uptake values (SUV) obtained solely from PET data. Moreover, the development of artificial intelligence (AI)-assisted methods for predicting brain segmentations holds promise but requires further validation of their efficiency and accuracy for clinical applications [13, 14].
The present study aims to apply the three pairs of segmentation strategies to quantitative brain PET studies and assess their respective effects on calculating brain metabolism. To accomplish this, we employed the gold-standard tracer 18F-FDG, acquired precisely matched PET and MRI images using an integrated PET/MR system. The three pairs of segmentation methods considered are as follows: (1) methods with or without MRI registration employing SPM and denoted as “SPM_MRI_ATL” and “SPM_PET_ATL,” respectively; (2) atlas-based or individual-based methods with or without MRI registration using FSL, and referred to as “FSL _MRI_ATL,” “FSL _MRI _IND,” “FSL _PET_ATL,” and “FSL_PET_IND”; and (3) methods with or without AI assistance using FreeSurfer, and denoted as “Neural Network” and “FreeSurfer.” By comparing the relationships, consistencies, and differences between SUVs derived from these segmentation methods, we aim to elucidate whether these strategies significantly impact the calculation of brain metabolism. Furthermore, we hypothesize that specific brain regions may be influenced differently by various segmentation methods and postulate that AI-assisted approaches could offer time-saving benefits and thus be preferable for brain PET analysis.
Materials and method
Subjects and data acquisition
The brain PET/MR images of the 40 healthy volunteers (23 males and 17 females, age range: 31 to 66 years) were scanned using an integrated 3.0 T PET/MR scanner (uPMR 790; UIH). All subjects were injected intravenously with 3.7 MBq/kg 18F-FDG tracer. The MRI and PET list mode data were acquired 30 min (38 ± 11.5 min) after the injection, started with a 5-min scan of ultra-short echo time MRI sequence for PET attenuation correction. The structural MRI images were obtained using a three-dimensional (3D) T1-weighted (T1w) sequence (repetition time = 7.86 ms, echo time = 3.2 ms, inversion time = 750 ms, flip angle = 10°, number of slices = 288, voxel sizes = 1.0 × 1.0 × 1.0 mm3, matrix size = 256 × 230, echo train length = 160, scan time = 266 s). The PET images were reconstructed with the ordered subset-expectation–maximization (OSEM) algorithm during a 24-min scan (3 iterations and 20 subsets with time of flight (TOF) and point spread function (PSF), matrix size = 256 × 256, field of view (FOV) = 25.6 cm, voxel size = 1.0 × 1.0 × 1.0 mm3). SUVs were calculated by the default settings in the workstation as:
where decay factor = exp(− 0.693 × wait time/radionuclide half-life).
Templates and atlases
Commonly used methods of brain segmentation are voxel-based morphometry (VBM) and surface-based morphometry (SBM), which have different templates and atlases. VBM adopts the ICBM152 template proposed by the International Consortium for Brain Mapping (ICBM) [15]. The standard MRI template, with a voxel size of 1 mm × 1 mm × 1 mm and a matrix of 182 × 182 × 218, is provided by FSL [11]. The standard PET template, with a voxel size of 1 mm × 1 mm × 1 mm and a matrix size of 182 × 200 × 215, was provided by Darkner Sune of the University of Copenhagen (https://staticcuris.ku.dk/portal/files/55751238/MNI152_PET_1mm.nii). SBM adopts the Desikan-Killiany atlas [16] proposed by Rahul S. Desikan et al., with a voxel size of 1 mm × 1 mm × 1 mm and a matrix size of 256 × 256 × 256. Thirty-two brain regions and 68 cortical brain regions were specified. Then, they were mapped to 21 whole-brain regions and 48 cortical brain regions of the Harvard–Oxford brain atlas.
Brain segmentation process
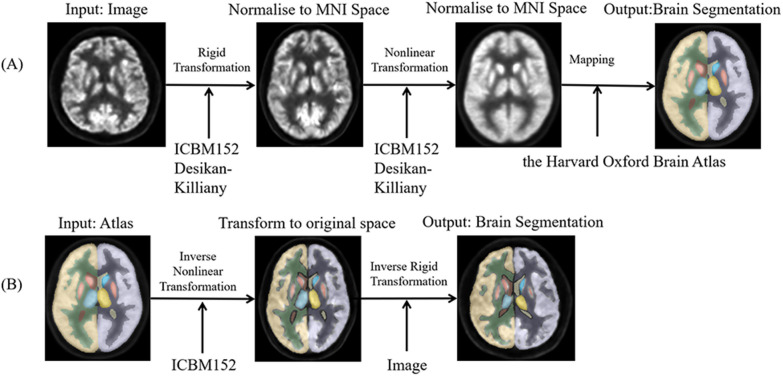
In the atlas-based segmentation approach, the segmentation problem is reduced to an image registration problem. Image registration was performed in two steps (shown in Fig. 1A). First, the image to be segmented was rigidly registered to the standard brain template so that they are roughly aligned. Then, we used a nonlinear registration algorithm to complete the fine registration. We used large deformation differential homeomorphism [17] to register the new input image to the brain template, and the presegmented atlas was used to obtain the segmentation of the input image in the MNI152 space. Another method is individual-based segmentation (shown in Fig. 1B). The segmentation result obtained in the MNI152 space as described above is transformed to the original individual image space through the mathematical inverse transform operator to obtain the segmentation result of the original input image. It should be noted that this segmentation method is not done directly in the individual image space.
Fig. 1.
Block diagram of atlas-based (A) and individual-based (B) segmentation
For the methods named “SPM_MRI_ATL” and “SPM_PET_ATL,” data processing was performed by using VBM-DARTEL [15] of SPM, based on MATLAB R2018b (MathWorks). First, we segmented the white matter (WM), gray matter (GM), and cerebrospinal fluid of each subject. The unified segmentation algorithm in SPM, which combined tissue classification, bias correction, and image registration in the same generative model, was used. Then, we created a brain template for this group of people (DARTEL template). Afterward, we normalized the images to Montreal Neurological Institute (MNI) space with smoothing under the parameter Gaussian full width at half maximum (FWHM) set to “8 8 8”. For the methods named “FSL_MRI_ATL,” “FSL_MRI_IND,” “FSL_PET_ATL,” and “FSL_PET_IND,” linear registration was completed by using FMRIB’s Linear Image Registration Tool of the FSL, and nonlinear registration was completed by using FMRIB’s Nonlinear Image Registration Tool of the FSL (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/). SIENAX from FSL was used to first extract brain and skull images from input data of a single full head. Images were then affine registered to the MNI152 space.
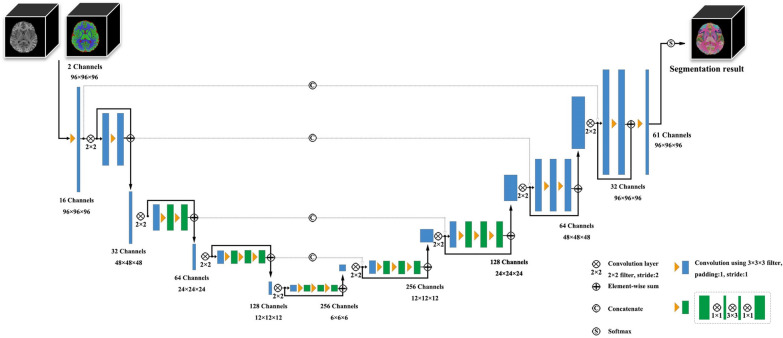
The process of FreeSurfer includes intensity normalization, Talairach spatial registration, skull dissection, white matter segmentation, smoothing of mosaic surfaces, and automatic topology correction. The tessellated surface was used as the starting point of the deformable surface algorithm to find the white matter and then the pial boundary. For the method with assistance from AI named Neural Network, images were processed with a previously established VB-Net toolkit [18] in a standard pipeline, including intensity correction, AC-PC alignment, skull stripping, tissue segmentation, and brain parcellation [16]. This toolkit is a deep learning-based framework with encoder, decoder, and bottleneck layers, and the architecture of VB-Net is shown in Fig. 2. Over 1800 MRI images from the publicly available Consortium for Reliability and Reproducibility (CoRR) were used as training data [19]. See Table 1 for processor configurations.
Fig. 2.
The architecture of the VB-Net method for brain ROI segmentation. VB-Net consists of two input channels, which are the original MRI images, and the segmentation maps of gray matter, white matter, and cerebrospinal fluid obtained from the VBM analysis of SPM. VB-Net consists of four levels with an encoding path followed by four levels of the corresponding decoding path. On the left side of the network, the encoding path reduces the size of the input by downsampling. The network was divided into four blocks, which comprise several convolutional blocks and residual blocks. A skip connection was introduced to improve the segmentations, and bottleneck layers were introduced to decrease the memory consumption. Similarly, on the right side of the network, the decoding path recovered the semantic segmentation image by deconvolution
Table 1.
Server information
| Server Information | ||
|---|---|---|
| Hardware Environment | CPU | Intel(R) Xeon(R) CPU E5-2640 v4 @ 2.40 GHz |
| Number of Cores | 80 Cores | |
| RAM | 252 GB | |
| Hard Disk | 1 TB | |
| Software Environment | Operating System | Linux Version 3.10.0-862.el7.x86_64 |
| Application | MATLAB 2018b | |
Statistical analysis
All data were descripted as mean ± standard deviation. Pearson correlation analysis was used to determine the correlation coefficients between SUVs derived from different methods in all ROIs [20]. The homogeneity of variance was tested by Jarque–Bera test. Multiway analysis of variance was used to analyze the most possible variance source generating the variances in brain SUV calculations [21]. We considered three possible factors: SUVs from different volunteers, SUVs from different brain regions, and SUVs derived by using different brain segmentation methods. The intraclass correlation coefficient (ICC) was used to quantify the consistency among the three pairs of segmentation strategies. To measure the differences between each pair of the two given strategies (for example, methods with MRI registration as strategy A, while methods without MRI registration as strategy B), we calculated the percentage of difference value as follows: 2 × (SUVA-SUVB)/(SUVA + SUVB) × 100%.
Results
Correlations between SUVs obtained by different segmentation methods
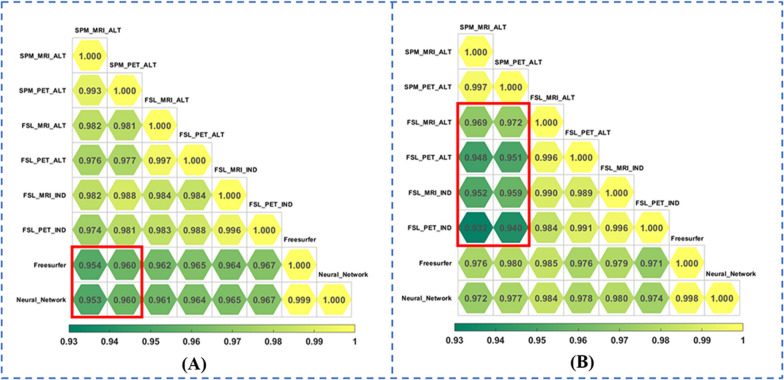
Eight brain segmentation methods were performed and their performances were compared (shown in Fig. 3). Strong correlations among different methods of whole-brain segmentation (r = 0.953 to 0.999, P < 0.001) and cerebral cortex segmentation (r = 0.932 to 0.998, P < 0.001) are illustrated in Fig. 4. At the whole-brain level, comparatively weaker correlations (r = 0.953 to 0.960) were found among atlas-based SPM, individual-based FreeSurfer and Neural Network methods (highlighted in Fig. 4A), while at the cerebral cortex level, comparatively weaker correlations (r = 0.932 to 0.972) were found between SPM and FSL with either atlas- or individual-based methods (highlighted in Fig. 4B).
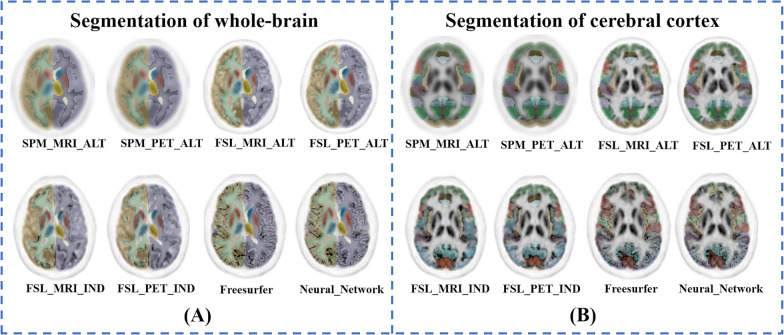
Fig. 3.
The segmentation results of different methods overlaid on the PET images of one subject. A The results at the whole-brain level, and B depicts the results at the cerebral cortex level. Different methods produced brain segmentations with similar appearances. The methods based on SPM and FSL divided the cortical brain regions into block-shaped areas that contain cerebrospinal fluid; in contrast, the method based on FreeSurfer and Neural Network divided the cortical brain regions into surface-shaped areas that do not contain cerebrospinal fluid
Fig. 4.
The Pearson correlation coefficients of SUVs calculated by eight different segmentation methods in the 21 brain regions at the whole-brain level (A) and 48 cortical regions at the cerebral cortex level (B)
Possible sources of variation in the calculation of brain SUVs
The possible sources of variation in the calculation of SUVs were explored (shown in Table 2). At the whole-brain level, the results showed that variances among brain regions (F = 26,140.6) > variances among subjects (F = 22,590.5) > variances among methods (F = 1003.1), while at the cortical brain level, the results showed that variances among subjects (F = 50,963.4) > variances among methods (F = 4233.2) ≈ variances among brain regions (F = 4098.6).
Table 2.
Multifactor analysis of variance in the calculation of SUVs at the whole-brain and cerebral cortex levels
| Source | Sum Sq | d.f | Mean Sq | F | P value | |
|---|---|---|---|---|---|---|
| Whole-brain level | Brain regions | 29,234.7 | 20 | 1461.7 | 14,265.0 | < 0.001 |
| Subjects | 39,571.9 | 39 | 1014.7 | 9902.1 | < 0.001 | |
| Methods | 857.3 | 7 | 122.5 | 1195.2 | < 0.001 | |
| Brain region × Subject | 5103.8 | 780 | 6.54 | 63.9 | < 0.001 | |
| Brain region × Method | 1947.4 | 140 | 13.9 | 135.7 | < 0.001 | |
| Subject × Method | 163.6 | 273 | 0.6 | 5.8 | < 0.001 | |
| Error | 559.5 | 5460 | 0.1 | |||
| Total | 77,438.1 | 6719 | ||||
| Cerebral cortex level | Brain region | 22,250.2 | 47 | 473.4 | 4261.8 | < 0.001 |
| Subject | 137,029.7 | 39 | 3513.6 | 31,630.8 | < 0.001 | |
| Method | 3329.5 | 7 | 475.6 | 4282.0 | < 0.001 | |
| Brain region × Subject | 6336.7 | 1833 | 3.5 | 31.1 | < 0.001 | |
| Brain region × Method | 2164.6 | 329 | 6.6 | 59.2 | < 0.001 | |
| Subject × Method | 682.8 | 273 | 2.5 | 22.5 | < 0.001 | |
| Error | 1425.3 | 12,831 | 0.1 | |||
| Total | 173,218.8 | 15,359 |
Sum Sq. sum of square; d.f. degree of freedom; Mean Sq. mean square; and F F value
Consistencies and differences among the three pairs of segmentation strategies
For the above-mentioned three pairs of segmentation strategies, we evaluated the consistency among methods with or without MRI data registration, methods with atlas-based or individual-based algorithms, and methods with or without AI assistance using FreeSurfer. For methods with MRI (SPM_MRI_ATL, FSL_MRI_ATL, FSL_MRI_IND, FreeSurfer, and Neural Network) or without MRI (SPM_PET_ATL, FSL_PET_ATL, and FSL_PET_IND) registration, we further divided them according to whether their segmentation algorithm was atlas-based (SPM_MRI_ATL, FSL_MRI_ATL, SPM_PET_ATL, and FSL_PET_ATL) or individual-based (FSL_MRI_IND, FSL_PET_IND, FreeSurfer, and Neural Network), and vice versa.
As illustrated in Table 3, stronger ICCs between methods with MRI and without MRI registration were found at the whole-brain level (0.951 to 0.985) than those at the cerebral cortex level (0.924 to 0.975). The mean difference in SUVs among 21 whole-brain regions was 3.43 ± 2.31%. Brain regions with mean difference over 1 standard deviation from mean value (5.74%) were in the bilateral caudate (right, 8.54 ± 1.76%; left, 7.48 ± 1.57%) and right putamen (5.98 ± 1.16%). The mean difference in SUVs among 48 cerebral cortex regions was 3.01 ± 1.68%. Cortical regions with mean difference over 1 standard deviation from mean value (4.69%) were in the planum temporale (8.77 ± 2.50%), occipital fusiform gyrus (6.90 ± 2.18%), anterior division of the temporal fusiform cortex (6.64 ± 2.98%), planum polare (6.36 ± 2.67%), posterior division of the superior temporal gyrus (5.67 ± 1.66%), and frontal pole (5.20 ± 2.46%).
Table 3.
The consistencies of regional brain SUVs among the three pairs of segmentation strategies at the whole-brain and cerebral cortex level
| The consistencies among different methods | With or without MRI registration | With atlas- or individual-based algorithms | With or without AI | |||||
|---|---|---|---|---|---|---|---|---|
| With atlas-based algorithms | With individual-based algorithms | All | With MRI registration | Without MRI registration | All | |||
| Whole-brain level | ICC | 0.984 | 0.951 | 0.985 | 0.963 | 0.936 | 0.970 | 0.998 |
| LB | 0.962 | 0.884 | 0.964 | 0.913 | 0.851 | 0.928 | 0.995 | |
| UB | 0.994 | 0.980 | 0.994 | 0.985 | 0.973 | 0.987 | 0.999 | |
| Cerebral cortex level | ICC | 0.974 | 0.924 | 0.975 | 0.741 | 0.879 | 0.819 | 0.997 |
| LB | 0.954 | 0.869 | 0.956 | 0.582 | 0.795 | 0.699 | 0.995 | |
| UB | 0.985 | 0.957 | 0.986 | 0.846 | 0.930 | 0.894 | 0.998 | |
ICC intraclass correlation coefficients, UB and LB the upper bound and lower bound of 95% confidential interval
Higher ICCs between methods with atlas-based or individual-based algorithms were found at the whole-brain level (0.936 to 0.970) than at the cerebral cortex level (0.741 to 0.879). The mean difference in SUVs among 21 whole-brain regions was 6.04 ± 2.79%. Brain regions with mean difference over 1 standard deviation from mean value (8.83%) were in the bilateral caudate (right, 10.38 ± 5.07%; left, 11.50 ± 4.67%), cerebral cortex (right, 9.26 ± 1.94%; left, 10.15 ± 2.20%), and right lateral ventricle (10.90 ± 3.71%). The mean difference in SUVs among 48 cerebral cortex regions was 7.79 ± 3.85%. Cortical regions with mean difference over 1 standard deviation from mean value (11.64%) were in the anterior division of the temporal fusiform cortex (18.03 ± 5.52%), occipital pole (16.13 ± 4.40%), inferior and superior division of the lateral occipital cortex (14.33 ± 3.64%, 13.03 ± 3.88%), frontal pole (13.89 ± 6.68%), anterior division of the supramarginal gyrus (12.68 ± 2.85%), anterior division of the middle temporal gyrus (12.65 ± 2.71%), and pars triangularis of the inferior frontal gyrus (12.09 ± 3.00%).
The ICCs between methods with or without AI assistance using FreeSurfer were 0.998 and 0.997, respectively, at the whole-brain level and cerebral cortex level. The mean difference in SUVs among 21 whole-brain regions was 1.85 ± 1.09%; no region had a difference greater than 5%. The mean difference in SUVs among 48 cerebral cortex regions was 1.17 ± 0.53%; no region had a difference greater than 3%. We further compared the average time cost for analyzing one subject by using FreeSurfer and the “Neuronal Network.” The former required 8.13 h for one subject on average, while the latter required 57 s on average. The computation time cost for the training steps of “Neuronal Network” was about 3.5 days.
Discussion
In our study, we conducted an analysis of brain metabolism using eight different segmentation methods with PET and MRI images acquired from integrated PET/MR system. While prior research has explored the impact of volumetric software (FSL vs. SPM vs. FreeSurfer) on MRI data, our study contributes by examining the potential influence of these morphological methods on PET analysis [22–25]. Overall, strong correlations were found among all methods at both the whole-brain and cerebral cortex levels, indicating their consistent performance and robust interrelationships. However, relatively weaker correlations were found between SUVs derived by VBM-based and SBM-based methods, as well as between SPM and FSL specially at the cerebral cortex level. Given that both SPM and FSL are VBM-based approaches, this finding suggests that VBM introduces greater variability in cortical PET calculations compared to SBM. Previous studies have indicated that while VBM can detect similar group differences as SBM in morphological studies, they may yield different regional statistics under certain conditions. SBM has demonstrated its suitability for capturing brain changes over time in longitudinal performance [26]. Additionally, the selection of analysis method (SPM vs. FSL vs. FreeSurfer) has been shown to impact different brain components [23]. For instance, in patients with multiple sclerosis, SBM exhibited greater robustness in GM volumes across different scanners compared to VBM and proved to be a viable alternative for WM segmentations [24]. In patients with cognitive impairment, all methods were capable of detecting decreased GM and WM volumes, while SBM yielded larger GM and smaller WM volumes than VBM [25]. Consequently, we propose that the choice of VBM-based or SBM-based methods may exert a limited yet specific influence to PET analysis.
Additionally, our findings highlight that variability attributed to subject and brain region factors surpassed that associated with the segmentation method. This finding underscores the necessity of employing individualized quantitative in brain metabolism research. Previous studies have emphasized the significance of considering individual differences among subjects and brain regions. For example, inter-subject variability of the cerebral cortex was significantly correlated with the degree of evolutionary cortical expansion and was also related to the variability in sulcal depth rather than cortical thickness [27]. The strength of association between brain function and structure also varied across the cortex [28]. Novel approaches have been developed to map brain activity at the individual level, effectively capturing the variability across subjects [29, 30]. Consequently, we suggest that it is especially crucial to select an SBM-based segmentation pipeline with MRI registration for PET studies, to minimize errors arising from individual differences.
Furthermore, our investigation revealed that brain regions demonstrating greater difference were located in the bilateral basal ganglia nuclei (especially in the caudate) and several cerebral cortexes in the temporal lobe, occipital lobe, and frontal lobe. Notably, differences resulting from utilization of individual atlas use (6.04 ± 2.79% to 7.79 ± 3.85%) exceeded those arising from MRI matching (3.01 ± 1.68% to 3.43 ± 2.31%). This finding bears considerable significance for clinical studies focusing on the physiological processes and pathological states within these above-mentioned regions. For example, the basal ganglia constitute essential components of complex distributed networks interconnected with specialized cortical areas, thereby contributing to distributed processing of higher-order cognitive functions and behaviors—an aspect of particular relevance in the context of neurodegeneration diseases [31]. The accumbens is involved in modulating information from the amygdaloid complex to the basal ganglia, mesolimbic dopaminergic regions, mediodorsal thalamus, and prefrontal cortex, which are all implicated in cognitive, emotional, and psychomotor functions [32]. Hence, we infer that it is necessary to calculate SUVs using methods incorporating precise structural registration and individual segmentation when examining the function of these brain regions.
In our analysis, FreeSurfer with or without AI assistance showed very high consistency at both the whole-brain level and cerebral cortex level, and the AI-based “Neuronal Network” shortened the processing time for analyzing one subject from an average of 8.13 h to 57 s. The clinical value of FreeSurfer has been verified in the detection of cortical abnormalities in patients with neurodegenerative diseases [13], schizophrenia [33, 34], bipolar disorder [35], and anisometropic amblyopia [36]. However, a notable drawback of FreeSurfer is extensive processing time, which is commonly range from 10–20 h for one subject, thereby greatly limiting its clinical applicability. Rapid AI-assisted postprocessing methods have been preliminarily employed in quantitative brain PET studies for the diagnosis of Parkinson’s disease and dementia subjects [37, 38]. Furthermore, deep learning techniques have been developed to predict FreeSurfer segmentations of MRI and have been established and applied in a model of Alzheimer’s disease [13, 14]. Our results further provide evidence for the high efficiency and clinical convenience of AI-based FreeSurfer methods in quantitative PET study. If this method could be applied to other populations in the future, it should continuously be optimized due to the increasing amount of training data.
As a limitation of our study, the small sample size and the lack of strict age restrictions for the subjects may have influenced the calculation of SUVs by different segmentation methods. The basic conditions of subjects (such as age and gender) may also influence SUV calculation of brain PET by different segmentation methods, which could be further verified by large-scale, multi-center, and longitudinal studies in the future. Additionally, inclusion of patients with abnormal metabolism in specific brain areas, such as Alzheimer’s disease or brain tumors, would help assess whether segmentation methods could influence the identification of lesions. Thus, the accuracy comparisons between different methods could be further discussed in specific population and clinical applications, such as subjects with various neurological conditions or age groups.
Conclusions
In conclusion, our study evaluated various methods for analyzing brain metabolism using precisely matched PET and MRI data obtained from an integrated PET/MR system. We found relatively strong correlations between all methods. However, some method comparisons demonstrated insufficient consistency (with minimum correlation coefficient of 0.741) and significant differences (up to 18.03%) in several brain regions. Consequently, methods incorporating MRI registration (particularly those employing SBM) and individual-based algorithms may enhance the accuracy of SUV calculations in studies focusing on these regions. Furthermore, we presented a time-saving AI-based method that optimized SBM for PET/MR analysis. Our study has the potential to benefit radiologists and clinicians seeking more efficient and targeted methods for brain PET analysis.
Acknowledgements
Not applicable.
Abbreviations
- SUV
Standardized uptake values
- AI
Artificial intelligence
- SPM
Statistical parametric mapping
- FSL
FMRIB software library
- ICC
Intraclass correlation coefficient
- 3D T1w
Three-dimensional T1-weighted
- OSEM
Ordered subset-expectation–maximization
- TOF
Time of flight
- PSF
Point spread function
- FOV
Field of view
- VBM
Voxel-based morphometry
- SBM
Surface-based morphometry
- ICBM
International Consortium for Brain Mapping
- GM
Gray matter
- WM
White matter
- MNI
Montreal Neurological Institute
- FWHM
Full width at half maximum
Author contributions
JL contributed to conceptualization, supervision, and project administration; ZW and FS were involved in methodology; ZW and J-MY provided software; YS and Y-SZ contributed to validation; YS and ZW were involved in formal analysis and writing—original draft preparation; Y-SZ contributed to investigation; B-XC and H-WY were involved in data curation; YS contributed to writing—review and editing; YS and Y-YY were involved in visualization; and YS and JL contributed to funding acquisition.
Funding
This work was supported by the Beijing Natural Science Foundation (Grant Number 7224334), National Natural Science Foundation of China (Grant Number 82130058), HuiZhi Ascent Project of Xuanwu Hospital (Grant Number HZ2021ZCLJ005).
Availability of data and materials
The datasets generated during the current study are available from the corresponding author on reasonable request.
Declarations
Ethics approval and consent to participate
All procedures performed in studies involving human participants were approved by the ethical standards of the committee of Xuanwu Hospital, Capital Medical University, and performed in accordance with the ethical standards as laid down in the 1964 Declaration of Helsinki and its later amendments or comparable ethical standards. Written informed consent was obtained from all individual participants included in the study.
Consent for publication
Written informed consent was obtained from the patient for publication of this study and accompanying images.
Competing interests
The authors have no relevant financial or non-financial interests to disclose.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Yi Shan and Shao-zhen Yan have contributed equally to this work.
References
- 1.Cui B, Zhang T, Ma Y, Chen Z, Ma J, Ma L, et al. Simultaneous PET/MRI imaging of cerebral blood flow and glucose metabolism in the symptomatic unilateral internal carotid artery/middle cerebral artery steno-occlusive disease. Eur J Nucl Med Mol Imaging. 2020;47:1668–1677. doi: 10.1007/s00259-019-04551-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Song S, Cheng Y, Ma J, Wang L, Dong C, Wei Y, et al. Simultaneous FET-PET and contrast-enhanced MRI based on hybrid PET/MR improves delineation of tumor spatial biodistribution in gliomas: a biopsy validation study. Eur J Nucl Med Mol Imaging. 2020;47:1458–1467. doi: 10.1007/s00259-019-04656-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yan S, Zheng C, Cui B, Qi Z, Zhao Z, An Y, et al. Multiparametric imaging hippocampal neurodegeneration and functional connectivity with simultaneous PET/MRI in Alzheimer's disease. Eur J Nucl Med Mol Imaging. 2020;47:2440–2452. doi: 10.1007/s00259-020-04752-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Guo K, Wang J, Wang Z, Wang Y, Cui B, Zhao G, et al. Morphometric analysis program and quantitative positron emission tomography in presurgical localization in MRI-negative epilepsies: a simultaneous PET/MRI study. Eur J Nucl Med Mol Imaging. 2022;49(6):1930–1938. doi: 10.1007/s00259-021-05657-w. [DOI] [PubMed] [Google Scholar]
- 5.Heiss WD. The potential of PET/MR for brain imaging. Eur J Nucl Med Mol Imaging. 2009;36(Suppl 1):S105–S112. doi: 10.1007/s00259-008-0962-3. [DOI] [PubMed] [Google Scholar]
- 6.Disselhorst JA, Bezrukov I, Kolb A, Parl C, Pichler BJ. Principles of PET/MR imaging. J Nucl Med. 2014;55:2S–10S. doi: 10.2967/jnumed.113.129098. [DOI] [PubMed] [Google Scholar]
- 7.Chen Z, Jamadar SD, Li S, Sforazzini F, Baran J, Ferris N, et al. From simultaneous to synergistic MR-PET brain imaging: a review of hybrid MR-PET imaging methodologies. Hum Brain Mapp. 2018;39:5126–5144. doi: 10.1002/hbm.24314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen S, Gu Y, Yu H, Chen X, Cao T, Hu L, et al. NEMA NU2-2012 performance measurements of the united imaging uPMR790: an integrated PET/MR system. Eur J Nucl Med Mol Imaging. 2021 doi: 10.1007/s00259-020-05135-9. [DOI] [PubMed] [Google Scholar]
- 9.Demir M, Toklu T, Abuqbeitah M, Cetin H, Sezgin HS, Yeyin N, et al. Evaluation of PET scanner performance in PET/MR and PET/CT systems: NEMA tests. Mol Imaging Radionucl Ther. 2018;27:10–18. doi: 10.4274/mirt.97659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ashburner J, Friston KJ. Unified segmentation. Neuroimage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- 11.Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 12.Fischl B. FreeSurfer. Neuroimage. 2012;62:774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kim J, Lee M, Lee MK, Wang SM, Kim NY, Kang DW, et al. Development of random forest algorithm based prediction model of Alzheimer's disease using neurodegeneration pattern. Psychiatry Investig. 2021;18:69–79. doi: 10.30773/pi.2020.0304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.McClure P, Rho N, Lee JA, Kaczmarzyk JR, Zheng CY, Ghosh SS, et al. Knowing what you know in brain segmentation using Bayesian deep neural networks. Front Neuroinform. 2019;13:67. doi: 10.3389/fninf.2019.00067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lancaster JL, Tordesillas-Gutierrez D, Martinez M, Salinas F, Evans A, Zilles K, et al. Bias between MNI and Talairach coordinates analyzed using the ICBM-152 brain template. Hum Brain Mapp. 2007;28:1194–1205. doi: 10.1002/hbm.20345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- 17.Beg MF, Miller MI, Trouvé A, Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. Int J Comput Vis. 2005;61:139–157. doi: 10.1023/B:VISI.0000043755.93987.aa. [DOI] [Google Scholar]
- 18.Hua R, Huo Q, Gao Y, Sui H, Zhang B, Sun Y, et al. Segmenting brain tumor using cascaded V-nets in multimodal MR images. Front Comput Neurosci. 2020;14:9. doi: 10.3389/fncom.2020.00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zuo XN, Anderson JS, Bellec P, Birn RM, Biswal BB, Blautzik J, et al. An open science resource for establishing reliability and reproducibility in functional connectomics. Sci Data. 2014;1:140049. doi: 10.1038/sdata.2014.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Adler J, Parmryd I. Quantifying colocalization by correlation: the Pearson correlation coefficient is superior to the Mander's overlap coefficient. Cytometry A. 2010;77:733–742. doi: 10.1002/cyto.a.20896. [DOI] [PubMed] [Google Scholar]
- 21.Theodorsson-Norheim E. Kruskal–Wallis test: BASIC computer program to perform nonparametric one-way analysis of variance and multiple comparisons on ranks of several independent samples. Comput Methods Programs Biomed. 1986;23:57–62. doi: 10.1016/0169-2607(86)90081-7. [DOI] [PubMed] [Google Scholar]
- 22.Martin P, Bender B, Focke NK. Post-processing of structural MRI for individualized diagnostics. Quant Imaging Med Surg. 2015;5:188–203. doi: 10.3978/j.issn.2223-4292.2015.01.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Heinen R, Bouvy WH, Mendrik AM, Viergever MA, Biessels GJ, de Bresser J. Robustness of automated methods for brain volume measurements across different MRI field strengths. PLoS ONE. 2016;11:e0165719. doi: 10.1371/journal.pone.0165719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Guo C, Ferreira D, Fink K, Westman E, Granberg T. Repeatability and reproducibility of FreeSurfer, FSL-SIENAX and SPM brain volumetric measurements and the effect of lesion filling in multiple sclerosis. Eur Radiol. 2019;29:1355–1364. doi: 10.1007/s00330-018-5710-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fellhauer I, Zollner FG, Schroder J, Degen C, Kong L, Essig M, et al. Comparison of automated brain segmentation using a brain phantom and patients with early Alzheimer's dementia or mild cognitive impairment. Psychiatry Res. 2015;233:299–305. doi: 10.1016/j.pscychresns.2015.07.011. [DOI] [PubMed] [Google Scholar]
- 26.Clarkson MJ, Cardoso MJ, Ridgway GR, Modat M, Leung KK, Rohrer JD, et al. A comparison of voxel and surface based cortical thickness estimation methods. Neuroimage. 2011;57:856–865. doi: 10.1016/j.neuroimage.2011.05.053. [DOI] [PubMed] [Google Scholar]
- 27.Mueller S, Wang D, Fox MD, Yeo BT, Sepulcre J, Sabuncu MR, et al. Individual variability in functional connectivity architecture of the human brain. Neuron. 2013;77:586–595. doi: 10.1016/j.neuron.2012.12.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Langs G, Wang D, Golland P, Mueller S, Pan R, Sabuncu MR, et al. Identifying shared brain networks in individuals by decoupling functional and anatomical variability. Cereb Cortex. 2016;26:4004–4014. doi: 10.1093/cercor/bhv189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cooper SR, Jackson JJ, Barch DM, Braver TS. Neuroimaging of individual differences: a latent variable modeling perspective. Neurosci Biobehav Rev. 2019;98:29–46. doi: 10.1016/j.neubiorev.2018.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang D, Buckner RL, Fox MD, Holt DJ, Holmes AJ, Stoecklein S, et al. Parcellating cortical functional networks in individuals. Nat Neurosci. 2015;18:1853–1860. doi: 10.1038/nn.4164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Riva D, Taddei M, Bulgheroni S. The neuropsychology of basal ganglia. Eur J Paediatr Neurol. 2018;22:321–326. doi: 10.1016/j.ejpn.2018.01.009. [DOI] [PubMed] [Google Scholar]
- 32.Mavridis I. The role of the nucleus accumbens in psychiatric disorders. Psychiatriki. 2015;25:282–294. [PubMed] [Google Scholar]
- 33.Jessen K, Rostrup E, Mandl RCW, Nielsen MO, Bak N, Fagerlund B, et al. Cortical structures and their clinical correlates in antipsychotic-naive schizophrenia patients before and after 6 weeks of dopamine D2/3 receptor antagonist treatment. Psychol Med. 2019;49:754–763. doi: 10.1017/S0033291718001198. [DOI] [PubMed] [Google Scholar]
- 34.Kong L, Herold CJ, Zollner F, Salat DH, Lasser MM, Schmid LA, et al. Comparison of grey matter volume and thickness for analysing cortical changes in chronic schizophrenia: a matter of surface area, grey/white matter intensity contrast, and curvature. Psychiatry Res. 2015;231:176–183. doi: 10.1016/j.pscychresns.2014.12.004. [DOI] [PubMed] [Google Scholar]
- 35.Lyoo IK, Sung YH, Dager SR, Friedman SD, Lee JY, Kim SJ, et al. Regional cerebral cortical thinning in bipolar disorder. Bipolar Disord. 2006;8:65–74. doi: 10.1111/j.1399-5618.2006.00284.x. [DOI] [PubMed] [Google Scholar]
- 36.Liang M, Xiao H, Xie B, Yin X, Wang J, Yang H. Morphologic changes in the visual cortex of patients with anisometropic amblyopia: a surface-based morphometry study. BMC Neurosci. 2019;20:39. doi: 10.1186/s12868-019-0524-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Piccardo A, Cappuccio R, Bottoni G, Cecchin D, Mazzella L, Cirone A, et al. The role of the deep convolutional neural network as an aid to interpreting brain [(18)F]DOPA PET/CT in the diagnosis of Parkinson's disease. Eur Radiol. 2021;31:7003–7011. doi: 10.1007/s00330-021-07779-z. [DOI] [PubMed] [Google Scholar]
- 38.Song TA, Chowdhury SR, Yang F, Dutta J. Super-resolution PET imaging using convolutional neural networks. IEEE Trans Comput Imaging. 2020;6:518–528. doi: 10.1109/tci.2020.2964229. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated during the current study are available from the corresponding author on reasonable request.