A method is proposed for transforming unit cells for a group of crystals so that they all appear as similar as possible to a selected cell.
Keywords: lattice matching, Delaunay, Delone, Niggli, Selling
Abstract
A method is proposed for choosing unit cells for a group of crystals so that they all appear as nearly similar as possible to a selected cell. Related unit cells with varying cell parameters or indexed with different lattice centering can be accommodated.
1. Introduction
A common problem in crystallography is to provide a list of the unit cells of several (or many) crystals so that they can be visually compared, making it easier to identify meaningful clusters of crystals of related morphology. Collections of experimental unit-cell parameters have been created based on similarity of morphology [for example, see Donnay et al. (1963 ▸)] and, in recent years, the clustering of unit cells from the myriad of images in serial crystallography has become increasingly important (Keable et al., 2021 ▸). We have created a method to group unit cells to serve these needs and have addressed this problem in the space S 6 (Andrews et al., 2019b ▸).
2. Background and notation
2.1. The space S 6
Andrews et al. (2019b ▸) introduced the space S 6 as an alternative representation of crystallographic lattices. The space is defined in terms of the ‘Selling scalars’ used in Selling reduction (Selling, 1874 ▸) and by Delaunay (1932 ▸; note that in his later publications, Boris Delaunay used the more accurately transliterated version of his surname, Delone) for the classification of lattices. A point s in S 6 is defined by
where d = −a − b − c. As a mnemonic to remember the order, the terms involve, in order, α, β, γ, a, b, c.
2.2. Similarity
In Euclidean geometry, two objects are described as ‘similar’ if they are identical except for a scale factor; see Euclid’s work as translated by Heath (1956 ▸) and a longer description in Wikipedia (https://en.wikipedia.org/w/index.php?title=Similarity_(geometry)&oldid=1097100366). In crystallography, we can say that all face-centered cubic unit cells are similar (assuming that they are in the same presentation). On the other hand, not all primitive orthorhombic unit cells are similar. In a metric space, we refer to two objects as ‘approximately similar’ if the distance between them after scaling to the same size is, in some sense, small, e.g. commensurate with the experimental errors in determination of the unit cells. The algorithm below attempts to find the representation of one cell that is nearest to similar to some other cell. For a given reference cell, the probe cell will be transformed to other choices of unit cell that would generate the probe’s lattice and the closest match to the reference will be chosen for the result. Finally, the lattice centering of the reference cell will be restored (if necessary).
3. Algorithm
We start with a collection of experimental unit cells. From among them, we select or create the ‘reference’ cell; that is, the one to which all the rest will be matched as closely as possible.
We transform the reference cell by many operations in the course of exploring alternative lattice representations. For each newly generated lattice representation, we accumulate the transformations needed to convert back to the original reference cell. All of these operations are performed in S 6. (The alternative space, G 6, is less convenient because the G 6 fundamental unit is non-convex.) To avoid duplication, for each step we only accumulate transformations that have not already been found.
To begin, each input cell is transformed to the S 6 representation and then Selling-reduced [see Delaunay (1932 ▸) and Andrews et al. (2019a ▸), the latter of which discusses the lesser complexity of Selling reduction and includes pseudocode]. As there is a need to be able to reverse the reduction, the reduction transformation is saved for use in later stages.
The following transformations of the reference will be done in three stages.
First, the 24 S 6 reflections are applied (Andrews et al., 2019b ▸) and the results stored. The store of S 6 vectors and their generating matrices holds 24 entries each at that point.
Because the 24 operations defining reflection are unitary, and in S 6 they are simply perturbations of the six values, they retain the values and signs of the six values, simply rearranging the six scalars.
Next, the boundary (reduction) transformations (Andrews et al., 2019b ▸) are applied to the results of the previous step. The 24 reflections are then applied again. In each step, only newly found results are stored. These last two steps are repeated at least once in order to gain better coverage of possibly useful transformations. The counts of entries for each iteration are 24, 1566, 45 876 and finally 1 016 726. Three iterations, i.e. 45 876 entries, have been sufficient in test cases to date.
Although the six scalars are all negative for Selling-reduced unit cells, the boundary transformations are not unitary and so do not retain the six negative values.
Finally, all the accumulated transformed representations of the reference cell must be rescaled and the saved transformations inverted. The S 6 vectors are all scaled to the same length (see Section 4) and the transformation matrix attached to each vector is inverted, thereby yielding the operation to return a lattice to the vicinity of the original reference cell. For more efficient searching in this final step, it is helpful to use a nearest-neighbor search function such as NearTree (Andrews & Bernstein, 2016 ▸).
4. Why must the S 6 vectors be scaled?
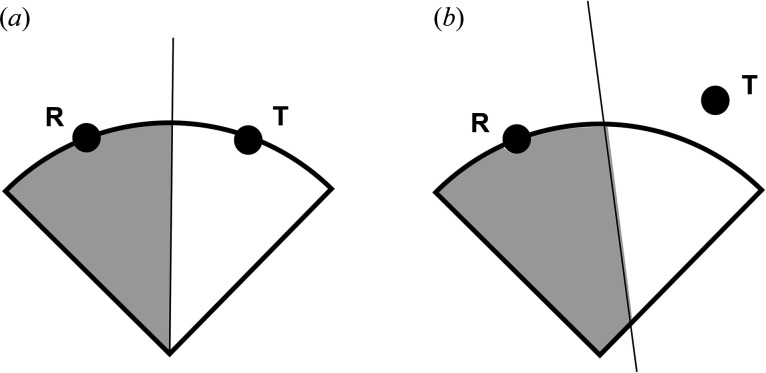
All similar lattices lie on lines that go through the origin of S 6. Fig. 1 ▸ shows the distinction between the case where the transformed points are all scaled to be at the same distance from the origin as the reference point [Fig. 1 ▸(a)] and the case where they are not [Fig. 1 ▸(b)]. Fig. 2 ▸ illustrates the way in which scaling all the reference points to the same 6-spherical surface defines the zones of approximate similarity. Any non-zero scale factor will produce the same correct result. In S 6 the reflections maintain the distance from the origin but the boundary transformations may not. To repeat: the only way to guarantee that the separation line for two regions goes through the origin is to have all the points at the same radius.
Figure 1.
(a) The case where the transformed point T has been scaled to be at the same distance from the origin as the reference point R. (b) Point T has not been scaled, and some areas are incorrectly assigned to point R. In each panel, the straight line between points R and T separates the regions closer to each of the points.
Figure 2.
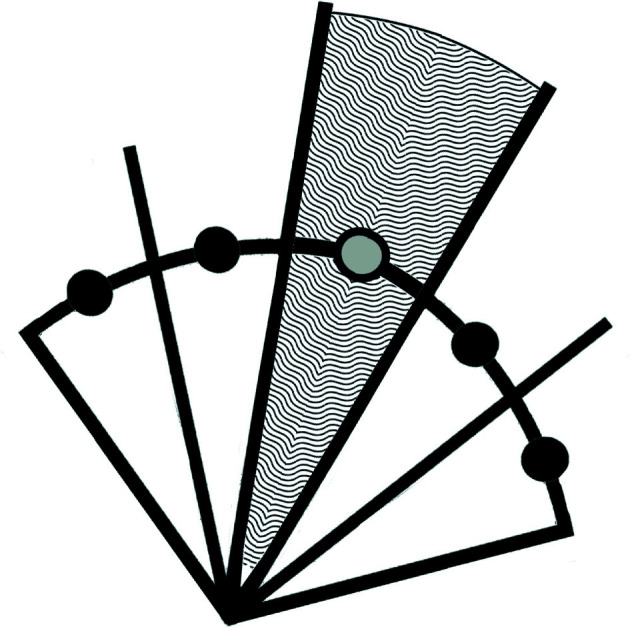
A two-dimensional example of the geometry for determining similarity. Each transformed copy of the reference cell is normalized to a constant length in the chosen space (here S 6). Each transformed and normalized cell then defines a zone in which every point in that zone is closer to the transformed and normalized cell defining that zone than it is to the transformed and normalized cell defining any other zone. In this example, each point within the textured zone (which extends to infinity) is closer to the gray-centered point than it is to any of the black points.
5. Angular measure of fit
Because the measure of similarity is independent of scale, projecting points onto a spherical surface does not modify the similarity. The angle between a probe point and the reference point is a meaningful measure of how similar the two points are.
6. Generating the approximation
The following operations are performed for each of the probe lattices in the original list. For a given probe lattice, the closest approximation among all of the transformed reference points is found. If there are multiple representations of the reference point that are equally close, then all should be examined. For the case of multiples, a method must be used to find the preferred one. For our purposes, we have found it convenient to choose the one for which the unreduced G 6 distances to the transformed reference are the smallest. Other choices might be useful for other purposes.
Once the preferred result has been found, the corresponding inverted transformation is used to place the vector in the region of the original reduced reference cell. Finally, the inverse of the reduction operation that was performed on the reference cell is used to create the best match to the original reference. If it is desirable to restore lattice centering, then that operation must also be performed; the search returns a primitive representation of the unit cell.
7. Examples
7.1. A rhombohedral example
Le Trong & Stenkamp (2007 ▸) cite several structures for phospholipase A2 (krait neurotoxin) that were reported as different structures but were actually all the same structure (Bernstein et al., 2020 ▸). Expanding their search using the program SAUC (McGill et al., 2014 ▸), we find a total of six structures, four of which are identical in two pairs. Table 1 ▸ lists the unit cells as reported in the Protein Data Bank (PDB; Bernstein et al., 1977 ▸; Berman et al., 2000 ▸). In Tables 2 ▸, 3 ▸ and 4 ▸, the first entry in each table is used as the reference, and the following five entries are matched as closely as possible to the presentation of the reference cell. In Table 2 ▸, a rhombohedral presentation with PDB ID 1dpy was chosen as the reference. In Table 3 ▸, a C-centered cell with PDB ID 1g2x was chosen as the reference. In Table 4 ▸, the hexagonal cell 1u4j was chosen as the reference. In each case, the probe cells were returned in the same presentation, including lattice centering as the reference cell. So the resulting centerings were hR, mC and hP, respectively, for each matched cell, regardless of the input centering, which had been determined by crystallographic analysis.
Table 1. Unit cells of phospholipase A2 from the PDB.
Table 2. The data of Table 1 ▸ matching a rhombohedral reference; the reference cell is highlighted in bold.
| PDB ID | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Fit (°) |
|---|---|---|---|---|---|---|---|
| 1dpy | 57.98 | 57.98 | 57.98 | 92.02 | 92.02 | 92.02 | 0 |
| 1fe5 | 57.980 | 57.980 | 57.980 | 92.020 | 92.020 | 92.020 | 0 |
| 1g0z | 57.020 | 57.020 | 57.020 | 90.395 | 90.395 | 89.605 | 2.11 |
| 1g2x | 57.106 | 57.106 | 57.100 | 89.752 | 90.248 | 90.270 | 2.11 |
| 1u4j | 57.020 | 57.020 | 57.020 | 90.395 | 90.395 | 89.605 | 2.11 |
| 2osn | 57.100 | 57.100 | 57.100 | 90.250 | 90.250 | 89.750 | 2.11 |
Table 3. The data of Table 1 ▸ matching a monoclinic reference; the reference cell is highlighted in bold.
| PDB ID | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Fit (°) |
|---|---|---|---|---|---|---|---|
| 1g2x | 80.95 | 80.570 | 57.10 | 90 | 90.35 | 90 | 0 |
| 1dpy | 83.42999 | 80.53835 | 57.98115 | 87.0908 | 89.9992 | 90.00114 | 3.14 |
| 1fe5 | 83.42999 | 80.53835 | 57.98115 | 87.0908 | 89.9992 | 90.00114 | 3.14 |
| 1g0z | 80.91861 | 80.35937 | 57.02143 | 89.9996 | 90.5644 | 90.00144 | 0.09 |
| 1u4j | 80.91861 | 80.35937 | 57.02143 | 89.9996 | 90.5603 | 90.00144 | 0.09 |
| 2osn | 80.92799 | 80.57842 | 57.10254 | 90.0002 | 90.3502 | 89.99745 | 0.01 |
Table 4. The data of Table 1 ▸ matching a hexagonal reference; the reference cell is highlighted in bold.
| PDB ID | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Fit (°) |
|---|---|---|---|---|---|---|---|
| 1u4j | 80.36 | 80.36 | 99.44 | 90 | 90 | 120 | 0 |
| 1dpy | 83.4287 | 80.5380 | 101.5974 | 91.6597 | 90 | 121.195 | 4.30 |
| 1fe5 | 83.4287 | 80.5380 | 101.5974 | 91.6597 | 90 | 121.195 | 4.30 |
| 1g0z | 80.3600 | 80.3600 | 99.4400 | 90 | 90 | 120 | 0 |
| 1g2x | 80.5809 | 80.5809 | 99.3468 | 90.0138 | 89.986 | 120.009 | 0.09 |
| 2osn | 80.5752 | 80.5752 | 99.3307 | 90 | 90 | 120 | 0.08 |
7.2. Adenosine receptor A2A
Unit cells were determined automatically from frames from serial-crystallography data collection for adenosine receptor A2A, PDB ID 5nlx (Weinert et al., 2017 ▸).
Three example unit cells were chosen from several hundred indexed data frames. Two are C-centered and one is primitive. Table 5 ▸ gives the reported data, and Tables 6 ▸, 7 ▸ and 8 ▸ are the approximate similarity matches.
Table 5. Adenosine receptor A2A, PDB ID 5nlx, unit cells as reported.
| Serial No. | Center | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) |
|---|---|---|---|---|---|---|---|
| 1 | C | 39.741 | 183.767 | 140.649 | 90 | 90 | 90 |
| 2 | P | 40.160 | 142.899 | 92.417 | 90 | 102.480 | 90 |
| 3 | C | 180.613 | 40.156 | 142.737 | 90 | 90.017 | 90 |
Table 6. Adenosine receptor A2A, approximating a C-centered cell.
The reference cell is highlighted in bold. Centering in parentheses indicates the lattice centering before matching.
| Serial No. | Center | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Fit (°) |
|---|---|---|---|---|---|---|---|---|
| 1 | C | 39.741 | 183.767 | 140.649 | 90 | 90 | 90 | 0 |
| 2 | (P) | 40.160 | 180.467 | 142.899 | 90 | 90 | 89.931 | 1.37981 |
| 3 | C | 40.156 | 180.613 | 142.737 | 89.983 | 90 | 90 | 1.30423 |
Table 7. Adenosine receptor A2A, approximating a primitive cell.
The reference cell is highlighted in bold. Centering in parentheses indicates the lattice centering before matching.
| Serial No. | Center | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Fit (°) |
|---|---|---|---|---|---|---|---|---|
| 2 | P | 40.160 | 142.899 | 92.417 | 90 | 102.480 | 90 | 0 |
| 1 | (C) | 39.741 | 140.649 | 94.008 | 90 | 102.21 | 90 | 1.37981 |
| 3 | (C) | 40.156 | 142.73 | 92.512 | 89.983 | 102.535 | 90 | 0.08374 |
Table 8. Adenosine receptor A2A, approximating a C-centered cell.
The reference cell is highlighted in bold. Centering in parentheses indicates the lattice centering before matching.
| Serial No. | Center | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Fit (°) |
|---|---|---|---|---|---|---|---|---|
| 3 | C | 180.613 | 40.156 | 142.737 | 90 | 90.017 | 90 | 0 |
| 1 | C | 183.767 | 39.741 | 140.649 | 90 | 90 | 90 | 1.31 |
| 2 | (P) | 180.467 | 40.160 | 142.899 | 90 | 90 | 89.930 | 0.07 |
7.3. Points along a line in S 6
Tables 9 ▸ and 10 ▸ present two views of artificial data. A line of points in S 6 was created from the C-centered [80.95, 80.95, 57.10, 90, 90.35, 90] to the A-centered [57.10, 80.95, 80.95, 90, 90, 90.35] representation of the same cell of phospholipase A2. The series of intervening points interpolated in S 6 are shown in Table 9 ▸ (each as the reduced unit cell except for the endpoints) and the lattice-matched results are shown in Table 10 ▸.
Table 9. A line of unit cells generated by interpolating between the first and last points in S 6 .
| Center | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) |
|---|---|---|---|---|---|---|
| C | 80.95 | 80.95 | 57.1 | 90 | 90.35 | 90 |
| P | 57.24 | 57.24 | 80.68 | 129.50 | 94.21 | 90 |
| P | 57.24 | 57.24 | 80.68 | 124.46 | 98.26 | 90 |
| P | 57.24 | 57.24 | 80.68 | 119.70 | 102.36 | 90 |
| P | 57.24 | 57.24 | 80.68 | 115.16 | 106.52 | 90 |
| P | 57.24 | 57.24 | 80.68 | 110.78 | 110.78 | 90 |
| P | 57.24 | 57.24 | 80.68 | 106.53 | 115.16 | 90 |
| P | 57.24 | 57.24 | 80.68 | 102.36 | 119.70 | 90 |
| P | 57.24 | 57.24 | 80.68 | 98.26 | 124.46 | 90 |
| P | 57.24 | 57.2 | 80.68 | 94.209 | 129.50 | 90 |
| A | 57.10 | 80.95 | 80.95 | 90 | 90 | 90.35 |
Table 10. A list of the same cells in the same order as Table 9 ▸ after transformation to match approximately with the reference cell, which is highlighted in bold.
| a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Fit (°) |
|---|---|---|---|---|---|---|
| 80.950 | 80.950 | 57.100 | 90 | 90.350 | 90 | 0 |
| 80.680 | 88.685 | 57.240 | 86.171 | 94.210 | 95.086 | 5.687 |
| 80.680 | 95.7216 | 57.240 | 83.0450 | 98.260 | 99.564 | 12.17 |
| 80.680 | 102.287 | 57.240 | 80.280 | 102.360 | 103.547 | 19.35 |
| 80.680 | 108.450 | 57.240 | 77.787 | 106.520 | 107.167 | 27.08 |
| 80.677 | 114.284 | 57.240 | 75.499 | 110.775 | 110.520 | 35.10 |
| 80.680 | 108.450 | 57.240 | 77.780 | 106.530 | 107.167 | 27.09 |
| 80.680 | 102.287 | 57.240 | 80.280 | 102.360 | 103.547 | 19.35 |
| 80.680 | 95.722 | 57.240 | 83.045 | 98.260 | 99.564 | 12.17 |
| 80.680 | 88.685 | 57.200 | 86.172 | 94.209 | 95.086 | 5.70 |
| 80.950 | 80.950 | 57.100 | 90 | 90.350 | 90 | 0 |
In Table 10 ▸, the first line is the reference cell, which is also the C-centered cell in the first row of Table 9 ▸. The final cell is the same cell but in the A-centered presentation. The points between are equally spaced in S 6 between those two centered points. Table 9 ▸ presents the list of points as generated and Table 10 ▸ lists the same cells in the lattice-matching presentation. Because the initial cell was C-centered, the following cells are also in that presentation, although the intermediate cells are not C-centered.
7.4. Examples from the PDB
The program SAUC (McGill et al., 2014 ▸) was used to query the PDB. The search started from the C-centered unit cell of PDB entry 1rgx (resistin) requesting the nearest 50 cells; 26 unique cells resulted. Because there was no limit on how far the points could be from the probe, some cells differ significantly from the search cell. The results are listed in Table 11 ▸ in their published representation. Table 12 ▸ lists the same cells in the same order as in Table 11 ▸, but with the same lattice centering as 1rgx, which is the first, reference, entry.
Table 11. Unit cells from the PDB.
Cells listed are nearest the C-centered cell of 1rgx and keeping only one representative of each protein type. The search was performed using the program SAUC.
| PDB ID | Center | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) |
|---|---|---|---|---|---|---|---|
| 1rgx | C | 49.021 | 52.475 | 96.609 | 90 | 96.53 | 90 |
| 1r8m | P | 33.429 | 95.775 | 33.665 | 90 | 101.67 | 90 |
| 2fxo | P | 40.157 | 41.867 | 97.795 | 91.11 | 92.73 | 107.18 |
| 4rne | C | 37.656 | 54.197 | 95.677 | 90 | 90 | 90 |
| 3mgd | C | 57.933 | 56.341 | 99.721 | 90 | 98.86 | 90 |
| 5yo3 | C | 40.328 | 50.126 | 94.237 | 90 | 90 | 90 |
| 4gzn | C | 40.218 | 60.641 | 96.119 | 90 | 90 | 90 |
| 3vvw | C | 195.72 | 37.420 | 40.280 | 90 | 94.66 | 90 |
| 4bhv | P | 33.078 | 33.621 | 99.138 | 90 | 96.75 | 90 |
| 3ihu | C | 54.646 | 79.135 | 103.244 | 90 | 102.08 | 90 |
| 5wou | C | 36.429 | 53.884 | 94.219 | 90 | 90 | 90 |
| 3nhm | C | 56.616 | 40.408 | 99.617 | 90 | 102.28 | 90 |
| 5k2l | P | 29.130 | 29.130 | 94.257 | 90 | 90 | 90 |
| 3t47 | P | 26.152 | 94.356 | 29.196 | 90 | 97.19 | 90 |
| 4ruv | P | 31.376 | 31.376 | 94.804 | 90 | 90 | 90 |
| 5ed9 | C | 86.371 | 34.743 | 99.839 | 90 | 101.49 | 90 |
| 1sip | C | 32.180 | 62.520 | 95.760 | 90 | 90 | 90 |
| 2sam | C | 62.700 | 32.200 | 96.100 | 90 | 90 | 90 |
| 1ytj | C | 62.300 | 32.100 | 96.300 | 90 | 90 | 90 |
| 4hhx | C | 34.790 | 73.610 | 95.900 | 90 | 90 | 90 |
| 3w92 | P | 31.760 | 33.552 | 94.998 | 90 | 90 | 90 |
| 167d | P | 33.200 | 33.200 | 96.040 | 90 | 90 | 120 |
| 4qeg | P | 31.237 | 31.237 | 93.848 | 90 | 90 | 90 |
| 2ygg | C | 200.700 | 38.350 | 34.100 | 90 | 91.35 | 90 |
| 1oz7 | P | 37.966 | 95.258 | 42.611 | 90 | 112.58 | 90 |
| 6nfs | P | 30.584 | 34.753 | 94.679 | 90 | 90 | 90 |
Table 12. Data in Table 11 ▸ best matched to PDB entry 1rgx; the reference cell is highlighted in bold.
| PDB ID | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Fit (°) |
|---|---|---|---|---|---|---|---|
| 1rgx | 49.021 | 52.475 | 96.609 | 90 | 96.53 | 90 | 0 |
| 1r8m | 42.374 | 52.020 | 95.775 | 90 | 90 | 90.41 | 2.67 |
| 2fxo | 48.706 | 66.020 | 97.795 | 89.04 | 93.21 | 87.50 | 3.07 |
| 4rne | 37.656 | 54.197 | 95.677 | 90 | 90 | 90 | 3.80 |
| 3mgd | 57.933 | 56.341 | 99.721 | 90 | 98.86 | 90 | 2.91 |
| 5yo3 | 40.328 | 50.126 | 94.237 | 90 | 90 | 90 | 2.84 |
| 4gzn | 40.218 | 60.641 | 96.119 | 90 | 90 | 90 | 3.86 |
| 3vvw | 54.979 | 54.979 | 99.633 | 86.02 | 100.74 | 85.78 | 3.90 |
| 4bhv | 47.165 | 47.165 | 99.138 | 85.27 | 94.73 | 89.07 | 2.71 |
| 3ihu | 54.646 | 79.135 | 103.244 | 90 | 102.08 | 90 | 5.07 |
| 5wou | 36.429 | 53.884 | 94.219 | 90 | 90 | 90 | 4.01 |
| 3nhm | 56.616 | 40.408 | 99.617 | 90 | 102.28 | 90 | 4.39 |
| 5k2l | 41.196 | 41.196 | 94.257 | 90 | 90 | 90 | 2.65 |
| 3t47 | 41.563 | 36.677 | 94.356 | 90 | 90 | 83.65 | 2.91 |
| 4ruv | 44.372 | 44.372 | 94.804 | 90 | 90 | 90 | 2.54 |
| 5ed9 | 46.548 | 67.682 | 99.839 | 82.70 | 100.65 | 107.73 | 5.82 |
| 1sip | 35.158 | 57.508 | 95.760 | 90 | 90 | 84.31 | 4.83 |
| 2sam | 35.242 | 57.582 | 96.10 | 90 | 90 | 84.20 | 4.83 |
| 1ytj | 35.042 | 57.348 | 96.30 | 90 | 90 | 84.36 | 4.86 |
| 4hhx | 40.709 | 63.858 | 95.90 | 90 | 90 | 80.10 | 4.63 |
| 3w92 | 46.200 | 46.200 | 94.998 | 90 | 90 | 86.86 | 2.75 |
| 167d | 33.20 | 57.504 | 96.040 | 90 | 90 | 90 | 5.26 |
| 4qeg | 44.176 | 44.176 | 93.848 | 90 | 90 | 90 | 2.54 |
| 2ygg | 51.318 | 51.318 | 102.166 | 82.83 | 98.954 | 96.71 | 3.40 |
| 1oz7 | 44.886 | 67.078 | 95.258 | 90 | 90 | 82.86 | 4.45 |
| 6nfs | 46.294 | 46.294 | 94.679 | 90 | 90 | 82.70 | 2.99 |
8. Summary
A method is proposed for transforming unit cells for a group of crystals so that they all appear as similar as possible to a selected cell. The search for cells similar to the reference cell is done using the reduced cell and comparing with other possible unit cells nearby in the space S 6. At the end, the lattice centering of the reference cell is restored.
9. Availability of code
The C++ code for lattice matching in S 6 is available on github.com at https://github.com/duck10/LatticeRepLib.git.
Acknowledgments
Careful copy-editing and corrections by Frances C. Bernstein are gratefully acknowledged. Our thanks to Jean Jakoncic and Alexei Soares for helpful conversations and access to data and facilities at Brookhaven National Laboratory. We thank Ronald Stenkamp for pointing us to the paper by Le Trong & Stenkamp (2007 ▸). We gratefully acknowledge Jörg Standfuss for permission to use the adenosine receptor A2A data. Richard Gildea helped in securing data for examples.
Funding Statement
Funding for this research was provided in part by: US Department of Energy, Office of Biological and Environmental Research and Office of Basic Energy Sciences (grant Nos. KP1607011 and DE-SC0012704, and in earlier years grant No. DE-AC02-98CH10886); US National Institutes of Health (grant No. P30GM133893, and in earlier years grant Nos. P41RR012408, P41GM103473, P41GM111244, R01GM117126 and 1R21GM129570); and in earlier years Dectris Ltd.
References
- Andrews, L. C. & Bernstein, H. J. (2016). J. Appl. Cryst. 49, 756–761. [DOI] [PMC free article] [PubMed]
- Andrews, L. C., Bernstein, H. J. & Sauter, N. K. (2019a). Acta Cryst. A75, 115–120. [DOI] [PMC free article] [PubMed]
- Andrews, L. C., Bernstein, H. J. & Sauter, N. K. (2019b). Acta Cryst. A75, 593–599. [DOI] [PMC free article] [PubMed]
- Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res. 28, 235–242. [DOI] [PMC free article] [PubMed]
- Bernstein, F. C., Koetzle, T. F., Williams, G. J. B., Meyer, E. F. Jr, Brice, M. D., Rodgers, J. R., Kennard, O., Shimanouchi, T. & Tasumi, M. (1977). J. Mol. Biol. 112, 535–542. [DOI] [PubMed]
- Bernstein, H. J., Andrews, L. C., Diaz, J. A. Jr, Jakoncic, J., Nguyen, T., Sauter, N. K., Soares, A. S., Wei, J. Y., Wlodek, M. R. & Xerri, M. A. (2020). Struct. Dyn. 7, 014302. [DOI] [PMC free article] [PubMed]
- Delaunay, B. N. (1932). Z. Kristallogr. 84, 109–149.
- Donnay, J. D. H., Donnay, G., Cox, E. X., Kennard, O. & King, M. V. (1963). Editors. Crystal Data: Determinative Tables, 2nd ed. Buffalo: American Crystallographic Association.
- Heath, T. L. (1956). Translator. The Thirteen Books of Euclid’s Elements, 2nd ed., unabridged. North Chelmsford, Massachusetts, USA: Courier Corporation.
- Keable, S. M., Kölsch, A., Simon, P. S., Dasgupta, M., Chatterjee, R., Subramanian, S. K., Hussein, R., Ibrahim, M., Kim, I.-S., Bogacz, I., Makita, H., Pham, C. C., Fuller, F. D., Gul, S., Paley, D., Lassalle, L., Sutherlin, K. D., Bhowmick, A., Moriarty, N. W., Young, I. D., Blaschke, J. P., de Lichtenberg, C., Chernev, P., Cheah, M. H., Park, S., Park, G., Kim, J., Lee, S. J., Park, J., Tono, K., Owada, S., Hunter, M. S., Batyuk, A., Oggenfuss, R., Sander, M., Zerdane, S., Ozerov, D., Nass, K., Lemke, H., Mankowsky, R., Brewster, A. S., Messinger, J., Sauter, N. K., Yachandra, V. K., Yano, J., Zouni, A. & Kern, J. (2021). Sci. Rep. 11, 21787.
- Le Trong, I. & Stenkamp, R. E. (2007). Acta Cryst. D63, 548–549. [DOI] [PubMed]
- McGill, K. J., Asadi, M., Karakasheva, M. T., Andrews, L. C. & Bernstein, H. J. (2014). J. Appl. Cryst. 47, 360–364. [DOI] [PMC free article] [PubMed]
- Selling, E. (1874). J. Reine Angew. Math. 1874(77), 143–229.
- Weinert, T., Olieric, N., Cheng, R., Brünle, S., James, D., Ozerov, D., Gashi, D., Vera, L., Marsh, M., Jaeger, K., Dworkowski, F., Panepucci, E., Basu, S., Skopintsev, P., Doré, A. S., Geng, T., Cooke, R. M., Liang, M., Prota, A. E., Panneels, V., Nogly, P., Ermler, U., Schertler, G., Hennig, M., Steinmetz, M. O., Wang, M. & Standfuss, J. (2017). Nat. Commun. 8, 542. [DOI] [PMC free article] [PubMed]