Viscous-capillary entrainment on bioinspired millimetric structure for sustained liquid transfer

Abstract

Liquid entrainment with a solid architecture passing through the fluid-fluid interface is ubiquitous and widely used in industrial processes as a liquid transfer method. Besides liquid properties, solid structures play a core role in entrainment. Although the influence of its macroscopic curvatures and microscale roughness has attracted years of research, the effect and potential of the commonly seen millimetric structures have not been sufficiently explored and exploited. Here, we demonstrate enhanced liquid entrainment on the millimetric structured surface by the co-effect of viscosity and capillarity for sustained liquid transfer of small deviation, including high-quantity uptake and practically operational drainage with small and relatively uniform droplet dripping time of varied liquid viscosities. With the overall process of viscous-capillary entrainment, we achieve stable cyclical arrayed liquid transport, showing its potential for sustained liquid transfer in intractable situations in laboratory, industry, and even daily life.

Millimetric structure achieves enhanced and stable liquid uptake and drainage by viscous-capillary entrainment.

INTRODUCTION

Liquid entrainment occurs when a solid architecture passes through the interface of two fluids, forming either liquid droplets or film on the solid surface. However, from the practical perspective, the whole entrainment process, including the liquid uptake with a solid surface withdrawn from a liquid bath and the liquid drainage after the withdrawal, still lacks overall concern, understanding and control. As entrainment phenomenon is ubiquitous in nature, such as nectar feeding by dipping with tongues (1–5) and water entraining while aquatic animals are leaping out (6), and widely applied in industrial processes across various scales, such as film coating on devices and products (7–9), the investigation and control of the liquid entrainment is important for industrial applications and, therefore, has raised broad interests for scientific research (10–15). Since Goucher and Ward’s pioneering work of the liquid entrainment dynamics on metal strips and wires in 1922 (10), extensive fundamental studies have been made to understand the liquid uptake process by entrainment on solid surfaces. The classic works of Landau and Levich (16) and then Derjaguin (17) quantified the thickness of the liquid film entrained by a flat plate withdrawn at a constant speed, which is now referred to as the LLD theory (18). Modifications were then made to consider different regimes and factors, such as expansion and correction terms (19), inertial effect (20), shape and confinement of liquid bath (21, 22), and rheological properties of liquid (23). However, the consideration of the different aspect of the process, the liquid drainage after uptake, was relatively few and rarely integrated with the liquid uptake process in the practical view.

Besides liquid properties, surface macroscopic curvatures influence the overall pressure gradient during the liquid entrainment (10), and microscale roughness can trap the liquid and change the friction state (24–26). However, the role of millimetric structure in the liquid entrainment process has not received adequate attention, although natural creatures have been found to take advantage of millimetric structure to enhance the liquid entrainment in some everyday situations, such as nectar feeding by bees and bats with their hairy tongues (Fig. 1A) (27, 28). The lack of research is partly due to a lack of fabrication method and the complexity of dynamic effects involved at the millimetric scale. With the development of advanced manufacturing in recent years, such as three-dimensional (3D) printing, chemical and optical etching, and precision sculpting, the millimetric structured surfaces are designed and applied to open fluidics (29–31), thermal control (32, 33), and wet state adjustment (34, 35) to achieve higher efficiency than macro- or microstructures. Therefore, an in-depth study on the dynamic properties of the bio-inspired millimetric structure–modified entraining will lead to insight into the one-century-old question of liquid entrainment and provide possibilities for liquid transfer.

Fig. 1. Liquid entrained by rod with arrayed millimetric structures.

(A) Honey bee and glossophagine bat feed on nectar (left) with the help of their millimetric hairy tongues (right). (B) Schematic of a rod with periodic millimetric spiky plates. (C) Micro-CT images of a 3D-printed rod in the front (i) and cross-section (ii) views, with its axial plate distance D, plate angle α, axis radius R, and plate height H being marked out (1.5 mm, 30°, 1.0 mm, and 1.0 mm shown here, respectively). (D) Experimental setup for observation and measurement of liquid entrainment. The rod is withdrawn by the lifter from the liquid bath at a constant speed U, and the process is recorded by the high-speed camera. The balance measures the mass before the immersion and after the withdrawal of the rod. The coordinate origin is placed at the surface of the liquid bath (z = 0). (E) Typical process: a rod with α of 30° or 150° was withdrawn from the liquid bath (silicone oil with a viscosity of 100 mPa·s) at a constant speed of 18.00 mm s⁻¹ and entrained the oil. Sequence images go as four typical states from left to right: initial state, liquid uptake state, rod-bath separated state, and liquid drainage (droplet dripping) state. (F) Liquid uptake capacity of the millimetric structured rod (red) or bare rods (black) represented by the average volume of the entrained liquid per unit length along the rod’s axial direction (inset). Photo credit of bee image in (A): Z. Dong, Chinese Academy of Sciences. Bat image in (A) reproduced with permission from (1). The data are shown as mean ± SD (N = 3), and the error bar represents SD. Note that some errors are smaller than the size of the symbol.

Here, we demonstrate the whole entrainment process and the millimetric structure enhanced liquid entrainment. We perform theoretical analysis and reveal a co-effect of viscosity and capillarity at the millimetric scale that improves the quantity and robustness of the entrainment. The co-effect dominates the entraining processes during and after the withdrawal of solid surface, leading to liquid uptake with high quantity and small deviation, as well as liquid drainage and droplet dripping with operationally high frequency and small differences between liquids with varied viscosities. The fundamental understandings of the whole uptake and drainage process are integrated and applied to stable cyclical fetching, transporting, and depositing of viscous liquids from confined space, showing its potential for sustained liquid transfer in intractable situations and providing broader guidance for the assessment and design of liquid clinging and coating on the uneven surfaces in daily life, laboratory operation, and industrial production.

RESULTS

Liquid entrainment on millimetric structured rod

To mimic the millimetric structure enhanced nectar-feeding process by bees and bats (1–5) (Fig. 1A), we abstracted their tongues with hairy structures as a solid rod periodically surrounded by millimetric spiky plates (Fig. 1B). The rod sample was computer-aided designed and prepared by 3D printing for controllable bottom-up fabrication (fig. S1A, Materials and Methods). The total length L of the rod was set at a scale of 10² mm, and the radius R at 1.0 mm for millimetric structured rods and 1.0 and 2.0 mm for bare rods. L was more than an order of magnitude larger than R to weaken the boundary effects at the top and bottom sides. Spiky plates were periodically distributed around the central axis of the rod. Micro-computed tomography (micro-CT) images (fig. S1B) demonstrate the 3D-printed rod in the front (Fig. 1Ci) and cross-sectional views (Fig. 1Cii). Parameters, including the axial plate distance D ∈ {1.0, 1.5, 3.0, 6.0, 12.0, 24.0, >30.0} mm and the angle α ∈ [15°, 165°] between the plate and the central axis, were varied to investigate the liquid entrainment ability, and the plate height H = 1.0 mm was fixed to keep the “outer” radius, (R + H), unchanged. The layer-by-layer printing process endowed the periodically distributed plates with sliced microgrooves at an interval of 10¹ μm (fig. S1C). Silicone oils with viscosities η of ~100 and ~1000 mPa·s were used as the entrained liquid. The silicone oils have a similar surface tension γ of ~21.1 mN m⁻¹ (21.11 ± 0.02 mN m⁻¹ for silicone oil-100 and 21.13 ± 0.06 mN m⁻¹ for silicone oil-1000; see table S1), which can completely wet the rod in the experiment (fig. S1D).

With the customized experimental setup (Fig. 1D), a millimetric structured rod was slowly immersed into a silicone oil bath and then withdrawn by a vertical lifter at a constant speed U ∈ [1.00, 18.00] mm s⁻¹. Then, the capillary number, Ca = ηU/γ, ranged from 10⁻² to 10⁰ in the experiment. Note that the over-small Ca (approaching 10⁻²) led to only a thin liquid film wrapping the rod surface, and the over-large Ca (approaching 10⁰) resulted in the over-thick film that “buried” the structure. Thus, the range of Ca in the experiment covered the millimetric structure–dominated regime we are interested in and matched the range of conventional concerns (fig. S2). While being withdrawn from the liquid bath (Fig. 1E), rods with downward plates (top images in Fig. 1E for α = 30°) and upward plates (bottom images for α = 150°) had unexpectedly the similar effect on the volume and shape of the entrained liquid, which indicates the absence of the influence of gravity on the structure’s effect on the liquid entrainment. In both downward and upward plate conditions, the plates held the entrained liquid to occupy a large space around the rod and shaped periodic menisci on the air-liquid interface. We term this process as the liquid uptake.

As shown in Fig. 1F, the liquid uptake on a millimetric structured rod surpassed the quantity and robustness of even that on a thick bare rod with the same outer radius of R + H = 2.0 mm, not to mention the thin bare rod with a radius of R = 1.0 mm. Here, $\overline{S}$ = m/ρl represents the average volume of the entrained liquid by the uptake process per unit length along the rod’s axial direction (inset in Fig. 1F), where m and ρ are the mass and density of the entrained liquid, respectively, and l is the length of the part of the rod that entrains the liquid. At a medium Ca of ~0.1, the quantity of liquid taken by the structured rod was about four times that by the thin bare rod. Also, when the Ca decreased from 10⁰ to 10⁻², the quantity by the structured rod decreased by a factor of ~5, while the factor was of ~15 for the thin bare rod, showing a better robustness of the structured rod against the deviation of liquid viscosity or withdrawal speed.

After the whole rod and entrained liquid left the bath, the liquid drained, and droplets dripped in a time scale of ~10⁰ s. This process is termed liquid drainage. Compared to the upward plate condition (α = 150°), the last group of downward plates (α = 30°) at the bottom of the rod held the draining liquid. The shrinking neck of the liquid filament was pinned by the apex of the downward plates but could slip down along the upward plates (fig. S3). Therefore, the filament of downward plate condition between the droplet and the entrained liquid became thicker, and the droplet dripping time was larger (Fig. 1E). The millimetric structure reshapes the entrained liquid surface in both the liquid uptake and drainage processes, and its influences on these processes will be investigated in order.

Liquid uptake by the co-effect of viscosity and capillarity

Figure 2 shows the dependency of meniscus morphology on the spiky plate space that reshapes it. Optical (Fig. 2A) and micro-CT (Fig. 2B) images manifest that, during the liquid uptake process, the entrained liquid was held by the apexes of the plates and formed periodic hammock-shaped concave menisci (Fig. 2C), whose curvature determines the capillary pressure on the liquid-air interface (18). To demonstrate the mechanism of liquid uptake by entrainment, the dimensionless average entraining cross-section $\overline{S}$/R² with varied structure parameters (Fig. 2, D and E) was derived and shown in Fig. 2 (F and G).

Fig. 2. Entrainment dynamics of the liquid uptake process.

(A) Optical and (B) micro-CT images of the entrainment (A) for silicone oil of 100 mPa·s at high withdrawal speed and (B) for cured wax at low withdrawal speed. (C) Schematics of the shape of the entrained liquid surface corresponding to the images in (B) one-to-one. (D to G) Experimental designs (D and E) and results (F and G) of the quantity of liquid uptake by entrainment of varied plate number density n_a and n_c (D and F) and angle α (E and G) under different Ca. The experimental liquids were silicone oils, which are ~100 mPa·s for the data points on the left side in (F) and (G), and ~1000 mPa·s on the right. The plate number densities n_a,0 and n_c,0 shown in (D) are equal to 1/1.5 mm⁻¹ and 10/2π, respectively. The “plate number density” of a bare rod with a radius equal to R can be defined as zero (black circle). The optical images between (D) and (E) are examples to show the liquid uptake with different structure parameters. The formula in (F) shows the theoretical estimation of entrainment quantity. The short solid lines with the power of 2/3 and 1/2 represent the scaling laws according to the Landau-Levich-Derjaguin theory. The inset in (G) shows the negative correlation between the quantity of entrained liquid and sinα under different Ca. Note that this inset is performed under the linear coordinates, unlike the logarithmic coordinates in (F) and (G). Data in (F) and (G) are shown as mean ± SD (N = 3), and the error bar represents SD. Note that some errors are smaller than the size of the symbol.

First, the influence of the size of spiky plate space on the meniscus formation was investigated. The number densities of the plates in both axial (n_a = 1/D) and circumferential (n_c = plate number/2π in the circumferential cross-section view) directions of the rod were varied to change the space size (Fig. 2D). $\overline{S}$/R² is positively correlated with the number density (Fig. 2F). The change of n_a and n_c sharply modifies the axial and circumferential curvatures of the liquid surface. With the decrease of the plate number density, curved menisci mainly exist near the plates, while the liquid surface tend to be flat when far away from the plates (inset in Fig. 2F). This distinction of liquid surface shape is relevant to the characteristic scale of capillary effect, i.e., capillary length κ⁻¹ = (γ/ρg)^1/2 (18) (~1.5 mm for the silicone oil, which is approximately equal to 1/n_a,0), where g is the gravitational acceleration of 9.8 m s⁻². For example, the entrained liquid becomes nearly a uniform film in the broad space between two groups of plates when n_a decreases to about 1/6 mm⁻¹ (D ~ 4κ⁻¹), and the entrainment can be decomposed into the plate-entrained domain and bare rod–entrained domain in practical terms (fig. S4, purple triangle in Fig. 2, D and F). The concave meniscus leads to the supplementary negative capillary pressure on the liquid surface (18). Therefore, the size of the millimetric space between plates regulates the liquid entrainment by controlling the curvatures of the entrained liquid surface and thus the capillary pressure on it, which can provide additional support for the liquid. In a broad sense, the “plate number density” of a bare rod with a radius equal to R can be defined as zero, on which the behavior of liquid uptake by entrainment is back to the Landau-Levich theory (16) as h₀Γ_ch ~ Ca^2/3, where h₀ is the thickness and Γ_ch is the total characteristic curvature of the flat liquid film.

Besides the space size, the effect of the space shape is then considered. Rods with varied angle α between the central axis and the plate were tested (Fig. 2E). As Fig. 2G shows, consistent with the unexpected qualitative observation shown in Fig. 1E, $\overline{S}$/R² of two supplementary angles show uniformity with the relative differences less than 6%. Taking α = 30° and 150° as a pair of examples, they result in plate spaces with the same shape but different directions. Therefore, gravity has little influence on the effect of plates on the meniscus shape and then the entrainment. It will be discussed later that gravity influences the liquid entrainment by the overall flow between the plates as the Bond number Bo = ρgR²/γ ~ 10⁰ (Materials and Methods, table S2). For the effect of plates, the different shape of the millimetric space between plates controls the meniscus and then the liquid uptake. $\overline{S}$/R² is negatively correlated with sinα (inset of Fig. 2G), indicating the stronger geometrical constraint on the liquid by the long and narrow space. The similar uptake quantity of rods with different plate arrangements and the notable difference between different plate shapes also support the conclusion that the plate angle–controlled space shape and the characteristic space size dominate the liquid uptake (fig. S5). Small sinα enhances not only the quantity of the liquid uptake but also its robustness: from the experimentally fitted scaling of 2/3 at α = 90°, approaching the Landau-Levich theory (16), to that of 1/3 at α = 15°, approaching the completely trapped situation for microstructure, in which the scaling continuously decreases with Ca and finally approaches zero (26). Therefore, a rod with small sinα can better resist the perturbation of withdrawal speed deviation in practical operations.

The positive effect of the supplementary negative capillary pressure on the liquid uptake is further proved by the experiments with different wettability of both the liquid (by adding surfactant) and the solid (by gas-phase fluorination of the rod) (fig. S6). With the surfactant sodium dodecyl sulfate (SDS) added to low down the surface tension of the liquid, the entraining quantity is less than that without surfactant (fig. S6, A and B). It is opposite to the result in previous research on the smooth solid surface that the surfactant makes the entrained liquid thicker (25, 36, 37). Meanwhile, the fluorinated rod is partially but not completely wetted by the silicone oil with a static contact angle of ~71.5°, and it takes up less liquid than the untreated rod (fig. S6C). It is consistent with the previous research that the harder the liquid wets the solid, the harder it can be entrained (14, 18), ruling out the possibility that the unusual results in fig. S6 (A and B) is caused by the wetting effect between liquid and solid. These two phenomena support our idea that the reversed capillary pressure gradient plays a core role to drive but not resist the entrainment. Liquid with smaller surface tension results in smaller capillary pressure and is less entrained.

Considering the order of magnitude of all characteristic lengths is controlled by the millimetric structure with the dimension of 10⁰ mm, the idealized framework of liquid uptake by entrainment on the millimetric structured rod is performed by the situation of our interests relevant to the competition among viscosity, capillarity, gravity, and inertia. With all length variables and parameters being nondimensionalized by R, we could then nondimensionalize the governing equations (38), η∆v − γ∇Γ + ρg = ρ(v · ∇)v, into

$$\mathrm{Ca}{\text{Δ}}^{\ast }{\mathit{v}}^{\ast }-{\mathrm{\nabla }}^{\ast }{\text{Γ}}^{\ast }+\mathrm{Bo}(-{\mathit{e}}_z)=\mathrm{We}({\mathit{v}}^{\ast }\cdot {\mathrm{\nabla }}^{\ast }){\mathit{v}}^{\ast }$$ (1)

where v* = v/U and Γ* = ΓR are the dimensionless flow velocity and surface curvature, respectively. The dimensionless coordinates are defined as x* = x/R, y* = y/R, and z* = z/R, and e_z represents the unit vector along the z direction, which points to the opposite direction of gravity (g = −ge_z). The capillary number, Ca = ηU/γ ~ 10⁻² to 10⁰, compares the viscous effect with the capillary effect; Bond number, Bo = ρgR²/γ ~ 10⁰, shows gravity versus capillarity; and Weber number, We = ρU²R/γ ~ 10⁻⁴ to 10⁻² << 1, contrasts the effect of inertia versus capillarity. Therefore, the inertial term in Eq. 1 could be neglected.

Examining the remaining terms in Eq. 1 reveals the physical picture of the process. The viscous force upon the liquid between the plate array is enhanced by the new solid-liquid interface on the rod originating in the structure (26, 39) and yields a larger magnitude of the first term in Eq. 1. The capillary pressure gradient provides a driving force for entrainment here rather than resistance on the bare rod because of the negative characteristic principal curvature radii of the meniscus between plates (R_a and R_c, controlled by n_a and n_c in axial and circumferential directions, respectively) (fig. S7). Although gravity is found to have little influence on the liquid behavior on the plates, it influences the overall flow between the plates and acts as the resistance throughout. With the assumption that $\overline{S}$ is approximately proportional to h_m, the minimum distance between the meniscus and the side wall of the central axis, Eq. 1 then yields

$$\frac{\overline{S}}{R^2}\sim \frac{1}{\sqrt{\frac{1}{\mathrm{Ca}}(\mathrm{Bo}-{\text{Φ}}^{\ast }{n}_{\mathrm{a}}^{\ast })-{{\text{Ψ}}^{\ast }}^{-2}{n_{\mathrm{c}}}^2}}$$ (2)

where the dimensionless structure parameter Φ* ~ Γ_bath* − Γ_plate* represents the curvature difference of the meniscus at the bath-entrainment transition zone, Γ_bath*, and the meniscus between plates, Γ_plate*, and Ψ* = R* + H* is the dimensionless outer radius of the structured rod. Detailed theoretical estimation is performed in Materials and Methods. Equation 2 tells that the capillary number, Ca, and the millimetric structure parameters, n_a and n_c, enhance $\overline{S}$, in accordance with what Fig. 2F shows. When to the large Ca limit, because of the enlargement of entraining quantity, the characteristic size of liquid grows, the capillary effect by structure subsides, and the Bond number, Bo, goes even much larger, so the growth rate of entrainment will not burst to infinity but approach the Derjaguin theory (17) with the power of Ca of 1/2. At small Ca, the entraining quantity keeps the trend of the power of ~1/2 rather than 2/3 (16). The millimetric structure dramatically decreases the power of Ca compared to the Landau-Levich condition (16) or the rough surfaces (25), which decreases it from 2/3 to about 0.6. Therefore, the entraining quantity decreases more slowly with the reduction of Ca, showing higher robustness against the deviation of mechanical condition. In short summary, the co-effect of the enhanced viscous force and the reversed capillary pressure gradient originating in the millimetric structure improves the liquid entrainment on the solid surface and resists the perturbation of withdrawal condition, leading to an enhanced liquid uptake with high quantity and small deviation.

Unfixed meniscus and dynamic capillary effect between plates with liquid retreat

An unforeseen result remains to be clarified: The effect of α becomes more significant and $\overline{S}$/R² diverges at small Ca conditions (Fig. 2G). As sinα increases, the entraining quantity decreases and the power of Ca gradually grows to even ~2/3. It can be explained by the liquid retreat phenomenon during the liquid uptake shown in Fig. 3. The principal part of the entrained liquid retreats from the apex of plate, along the plate to the central axis, changing the volume of entrained liquid and the shape of its meniscus (Fig. 3A). Image tracking shows the evolution of the meniscus (Fig. 3B). We number the menisci from top to bottom along the central axis of the rod. The first meniscus, contiguous to the wetting zone on the top of the whole entrained liquid, is initially near the apex but retreats swiftly. Away from the wetting zone, the retreat is relatively slight but still exists (fifth/seventh/ninth meniscus, for example). Figure 3C shows that a thin liquid film holds its ground on the plate, while the “bulk” part of the liquid retreats (movie S1). Therefore, between the millimetric plates, the liquid initially entrained from the liquid bath is overloaded and thus pulled away by the tendency of drainage, and can still wrap up the plates because of a “secondary entrainment” on every single plate (Fig. 3D). The meniscus between plates is unfixed, unlike assumed above.

Fig. 3. Retreat of entrained liquid.

(A) Optical observation of liquid retreat from the apex of plates during the liquid uptake process. (B) Deformation and retreat of the air-liquid menisci (counted vertically from the top of the entrained liquid to the bottom) with time (insets) and position (data points). Time interval of the timelines in the insets is 1000 ms. (C) X-ray image that shows the thinning of the “secondary” entrained liquid film on the plates. (D) Schematics of the retreat process. The liquid between plates is pulled by the tendency of drain under gravity, leaving secondary films behind. (E) Retreat differential of the upper and lower part of the bulk of the meniscus (ninth meniscus as an example here), estimated by the size ∆_z of the optical shadow (marked by the dotted circles in the insets) originating in the curved surface that reflects the light. The represented rods of α = 30°, n_a = n_a,0, n_c = n_c,0, and H = 1.0, 1.5, 2.0 mm were withdrawn from the silicone oil of viscosity of ~1000 mPa·s at a constant speed of 2.00 mm s⁻¹.

What changes during the liquid uptake process is not only the position of the meniscus but also its shape. The retreat is not perpendicular to the central axis of the rod but toward the plate-axis corner (insets in Fig. 3B and movie S1). To magnify and demonstrate the specific retreat behavior, rods with longer plates were then tested to leave more space for liquid to retreat (Fig. 3E). The change of the optical shadow (insets in Fig. 3E; ∆_z is the shadow’s axial size) was measured to estimate the retreat differential of the upper and lower part of the bulk part of meniscus (distinguished from the secondary entrained film) between two plates. The dimensionless size ∆_z/D decreases with the withdrawal process of the rod, demonstrating that the lower part of the meniscus retreats faster than the upper part, and the retreat is toward the corner of the plate and central axis. The chord of the meniscus changes with a tendency from approximately parallel to the central axis (chord length scales as D) to approximately perpendicular to the plates (chord length scales as Dsinα). Therefore, the curvature of the meniscus decreases dramatically during the retreat, and smaller sinα, that is, more negative curvature, can provide larger capillary pressure to resist the retreat, struggling to keep liquid in shape. This effect explains the significant effect of α and divergence of $\overline{S}$/R². For large sinα, when to the small Ca limit, the liquid between the plates cannot be effectively held and thus wraps the solid surface like a liquid film. This thin film–like entrainment mode approaches what the classic works discussed (16, 17). At particularly small Ca of ~10⁻², the liquid entrainment of large sinα (α = 90°, for example) approaches the Landau-Levich law with a power of 2/3. For small sinα, the large contact area of the liquid to plate and the strong capillary force resist the drainage and retreat, weakening the flow between two axially arranged plates. This state is more consistent with the ideal model of Eq. 2 and can obtain larger entraining quantity.

The overload and drainage of the initially entrained liquid do attribute to the millimetric scale of the structure. However, because of the incessant retreat during the withdrawal process of the rod, the curvature of the meniscus at larger z is smaller than that at a lower place (Fig. 3, B and E). The capillary pressure at larger z is more negative, providing additional force from lower menisci to upper ones. Therefore, the effect of the unfixed meniscus and dynamic capillary force resists liquid drainage in a self-adapted mode of negative feedback. This self-adapted mode will produce a special droplet dripping effect on the millimetric structured surface.

Fast liquid drainage and uniform droplet dripping on millimetric structure

The uptake and drainage of liquid, which run through the whole process during and after the withdrawal of the solid surface, are all dominated by the liquid entrainment dynamics and modified by the millimetric structure (Fig. 4A). Actually, by transforming the coordinate system, the process of liquid uptake from the bath is equivalent to that of liquid drainage from a solid surface. In contrast with the easy drainage from the unstructured surface and firmly trapped state on the microstructured surface (40), liquid drainage from the millimetric structured surface shows a moderate and self-adapted mode, in which the retreat and drainage do exist but are resisted by the evolution of meniscus of the retreating liquid and the liquid accumulation and droplet formation at the bottom of the rod.

Fig. 4. Droplet dripping after withdrawal.

(A) Sequence images showing the liquid uptake and drainage process on the rod of α = 30° with silicone oil of viscosity of ~100 mPa·s and withdrawal speed of 18.00 mm s⁻¹. (B) First droplet dripping time. Colors represent different rod morphologies (bare and structured) and liquid viscosities (~100 and 1000 mPa·s). The arrows indicate the dripping time differences between liquids with varied viscosities. (C) First (square), second (diamond), and third (circle) droplet dripping times of silicone oils of ~100 mPa·s (red) and ~1000 mPa·s (blue) on the rod of α = 30°. The black solid line represents the trend of the power of −1. The red and blue solid lines are the fitted lines of the data of first droplet of silicone oil-100 and silicone oil-1000 with the power of ~−1.00 and ~−1.10, respectively. The dashed lines are the fitted lines of the data of second droplet with the power of ~−1.30 and ~−1.07. The dotted lines are those of third droplet with the power of ~−2.02 and ~−1.22. (D) First droplet dripping volume after the rod and entrained liquid totally separate from the liquid bath. Different colors represent different rod morphologies (bare and structured) and liquid viscosities (~100 and 1000 mPa·s). (E) First (square), second (diamond), and third (circle) droplet dripping volumes of silicone oils of ~100 mPa·s (red) and ~1000 mPa·s (blue) on the rod of α = 30°. Note that some errors are smaller than the size of the symbol. Data in (B) to (E) are shown as mean ± SD (N = 3), and the error bar represents SD. Note that some errors are smaller than the size of the symbol.

From the practical point of view of liquid obtaining and usage, we measured the droplet dripping time, Δt, after the rod and entrained liquid totally separated from the liquid bath to evaluate the liquid drainage from the withdrawn surface (Fig. 4B). The dripping time is negatively correlated with the withdrawal speed, because higher speed leads to a larger uptake quantity and the entrained liquid is, therefore, easier to drain after the separation. The most attractive phenomenon is that, compared to the bare rod, the millimetric structured rod not only shortens the dripping time but also decreases its difference between varied liquid viscosities, |Δt_{100 mPa·s} − Δt_{1000 mPa·s}| (Fig. 4B). For an uptake-drainage process, although higher viscosity η tends to increase the friction and restrain liquid dripping, it enhances the uptake quantity, resulting in smaller velocity gradient (thus decreases the friction), and therefore promoting liquid dripping. These two opposite effects reach a good balance at the millimetric scale, and the capillary pressure between plates further reduces the relative influence of viscous force, resulting in the uniform droplet dripping time for varied viscosity. Both the first and second droplet dripping times are correlated with the withdrawal speed with an approximately uniform trend of the experimental scaling of ~−1 for the structured rod (fitted as −1.00 and −1.30 for the first and second droplet of silicone oil-100, and −1.10 and −1.07 for those of silicone oil-1000, respectively) (Fig. 4C), providing the feasibility to unify the dripping time for liquid of different viscosities. The third droplet shows a notable deviation from the first and second ones. The deviation can also be found in the second droplet of silicone oil-100 at a small withdrawal speed. This phenomenon results from the volume deduction of the remaining liquid on the rod. What is more, consistent with the observation in Fig. 1E, the rod with downward plates (α = 30°) results in a slightly larger dripping time, because its last group of plates at the rod bottom can better hold the draining liquid and the filament between the droplet and the entrained liquid will be thicker. This slight distinction provides a way for further fine-tuning of dripping time. As counted, the droplet dripping time in Fig. 4 (B and C) is shortened by the structured rods and of order 10⁰ to 10¹ s, a convenient time interval for one to operate with common mechanical motion parameters in practical applications, whereas the dripping on a bare rod with the speed of 10⁰ mm s⁻¹ requires minutes of waiting (table S3).

The volume of the droplet, V, was then investigated. As shown in Fig. 4 (D and E), liquid viscosity significantly influences the droplet volume, unlike the uniform dripping time on the structured rod. It also influences the effect of withdrawal speed on the volume. The structure plays a core role as well. Under the same liquid viscosity and withdrawal speed, the droplet volume of the structured rod with downward plates (α = 30°) is larger than that with upward plates (α = 150°). The bare rod with a radius of 2.0 mm obtains the largest droplet, and the 1.0-mm bare rod shows the smallest.

There are two key processes that dominate the dripping volume of the droplet: the accumulating of liquid from the side wall of the rod to the bottom, and the formation and breakup of the liquid neck and filament (Fig. 4A). The first process depends on the quantity of entrained liquid and the resistance to the liquid drainage from the rod, both of which are influenced by the withdrawal speed and the structure of the rod. As Fig. 4E shows, the volume of the former droplet is slightly larger than the latter one because of the larger quantity of the remaining liquid. However, its influence is not as significant as that of the viscosity, which controls the second process. The second process is also influenced by the shape and area of the rod. The 2.0-mm bare rod has the largest and most sound bottom to hold the liquid, and the bottom of rod with downward plates is larger than that with upward plates (Fig. 1E and fig. S3) but not as sound as the bare rod. As shown in Fig. 4D, the volume-speed curve is mainly shaped by the liquid viscosity and then translated by the structure of the rod. Therefore, with different liquid viscosities, the bare rod has neither uniform dripping time nor uniform dripping volume. On the contrary, the structured rod can obtain droplets with different volume under uniform time.

Viscous-capillary entrainment by millimetric structure as a liquid transfer method

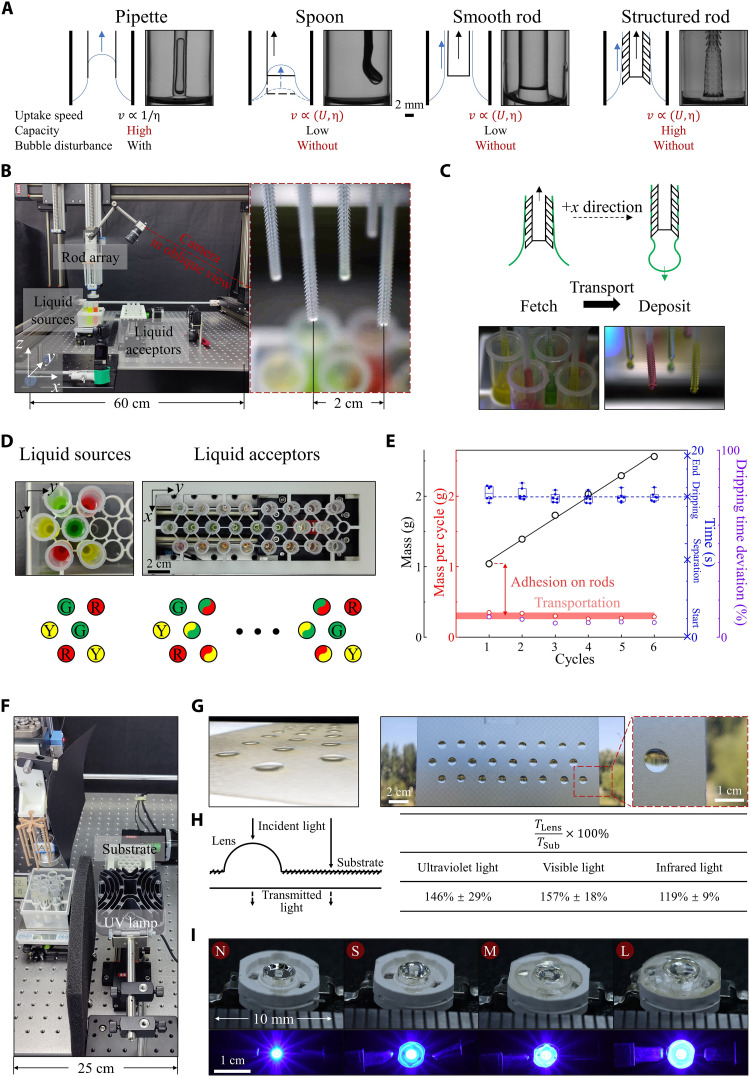
Liquid uptake and drainage together enable a liquid transfer method with special properties. As common intuition goes, the viscous effect is undesirable in general liquid transfer processes, such as the flow in a pipe following the Hagen-Poiseuille law (38). On the contrary, during the withdrawal process of a solid surface from the liquid bath, the quantity of the entrained liquid is positively correlated with viscosity. Therefore, from the practical perspective, the dip-withdrawal operation as a liquid uptake method is to transfer high-viscosity liquid in a long narrow space. On this occasion, general tools like pipettes (active suction with low inner pressure) or spoons (to support liquid from below) are restricted (Fig. 5A). For example, the pipette is limited by high viscosity and low vacuum degree and with bubbles generated during suction or pressure release. The confined space limits the capacity of the spoon to support liquid from below. By contrast, in the solid withdrawal process, the liquid is entrained by the side wall of the solid with a speed depending on the withdrawal speed. Compared to a widely used smooth glass rod with weak entrainment and significantly influenced by confinement effects (22), a structured rod can entrain much more liquid with the help of additional capillary pressure between structures. Therefore, the insight of the liquid entrainment by structured surface provides a facile way for viscous liquid transfer (Fig. 5).

Fig. 5. Liquid transfer by an array of millimetric structured rods.

(A) Liquid uptake by a pipette, spoon, smooth glass rod, and millimetric structured rod. (B) Apparatus (left) and rod array (right) for dyed glycerol transport test. (C) Transfer process: fetching, transporting, and depositing liquid. (D) Transfer and final mixed state of the dyed glycerol. Glycerol dyed green, yellow, and red was fetched, transported, and deposited from the liquid sources to the liquid acceptors. (E) Mass change (left axes) of liquid sources during the repeating process (black) and the unit mass change per cycle (red). The black solid represents a linear fit of the experimental data in black. The first right axis (blue) tells the time nodes in one cycle: the start of the cycle and rod array descending (0 s), rod array separating from liquid sources (~8.13 s), droplets dripping (~15.10 s, box plots, blue dotted line), and the end of the cycle (~19.47 s). The elements of the box plots: whiskers for maximum and minimum values, edges of the boxes for first and third quartiles, and midlines for median. The second right axis (purple) shows the relative dripping time deviation in each cycle. The rod array included six rods in the experiment. (F) Apparatus for the transfer and curing of the UV-curable resin. The substrate was made of printed resin or cured PDMS. (G) Transparent cured resin droplets on a rough rigid printed resin substrate. The substrate itself is not transparent because of its surface roughness, and one can see the background through the cured droplets. (H) Transmittance measurement of the substrate with (T_Lens) or without (T_Sub) lens. (I) Blue LED chips are covered by cured resin droplets with small (S), medium (M), and large (L) sizes, showing different lighting effects. The letter N represents no droplet for comparison.

DISCUSSION

The liquid entrainment enhanced by the millimetric structure has unique superiority as the liquid transfer method in some intractable situations. A modularized apparatus for sustained liquid transfer was performed (Fig. 5B). A programmable multi-axis displacement table held a detachable array of structured rods, the core component, and could move vertically and horizontally at the set speeds and distances. The liquid sources consisted of well-arranged 10-ml centrifuge tubes with tested liquid inside. The liquid acceptors were installed on a single-axis mobile platform and could move in ±y direction to imitate conveyor belts in the industry. The rod array fetched, transported, and deposited liquid from the sources to the acceptors (Fig. 5C).

First, we took glycerol as the example liquid, which is a high-viscosity liquid frequently used for standard study (41). Controlled by the multi-axis displacement table, the rod array cyclically transferred the dyed glycerol from the liquid sources to the liquid acceptors (Fig. 5D and movie S2). The liquid acceptors (1.5-ml centrifuge tubes) were controlled by the single-axis mobile platform, moving in −y direction in a square-wave mode to match the liquid transfer period, ensuring that the following next cycle droplets drip just right into the successive liquid acceptors. Glycerol dyed in different colors was steadily deposited together by the programmed transfer (Fig. 5D). As shown in Fig. 5E, the cycling process was stable, with a dripping time deviation of ~9% among rods in one cycle and ~3% among cycles, and the mass of transferred liquid in one cycle of 0.30 ± 0.04 g (0.05 ± 0.01 g for each rod on average in this experiment). This transferred liquid quantity (~2.4 × 10² μl) matches the quantity range of the widely used commercial positive displacement pipettes (42) and can be easily adjusted by changing the number of detachable rods. The residual amount on the rod array was of a constant value of 0.74 ± 0.04 g, which would not grow in the cycling process and, therefore could be neglected after enough cycles.

With aforesaid verification of method feasibility and stability, we then dispensed photosensitive resin in place of glycerol by the same apparatus plus an ultraviolet (UV) lamp (Fig. 5F). A substrate made of the same resin (3D-printed) (Fig. 5G) or polydimethylsiloxane (PDMS; thermal cured) (fig. S8) was placed on the single-axis mobile platform in advance. The resin droplets dripped on the substrate and were quickly cured under the UV light at the short time interval between two transfer cycles. An array of cured resin droplets was achieved and increased the transmittance of the rough resin substrate by ~50% for UV and visible light and ~20% for infrared light (Fig. 5H). Thus, the cured droplets could perform as an array of lenses to see the deformed images of objects behind (natural scenery in Fig. 5G and light matrix in fig. S8D). One step further and we placed the unpackaged blue light-emitting diode (LED) chips in advance. The resin droplets straightly dripped on and covered the LED chips, and were then cured under the UV lamp. LED chips covered with droplets of different sizes resulted in different lighting effects. Without cured resin covering, the main lighting area was localized around the chip (Fig. 5I and fig. S9N). By contrast, the light was refracted when passed through the cured resin, and the main lighting area expanded (Fig. 5I and fig. S9, S, M, and L). The apparatus can easily manipulate the droplet size (Materials and Methods). Therefore, batch fabrication, packaging, and modification of lenses, chips, or other similar devices can be achieved in the way of facile operation with the enhanced liquid entrainment method (43, 44).

In conclusion, we investigate the influence of the millimetric structure on the liquid entrainment by a withdrawn solid. The co-effect of the enhanced viscous friction and reversed capillary pressure gradient enhance the entrainment's quantity and robustness. The retreat and secondary entrainment on the structure modifies the shape and behavior of the liquid, resulting in a moderate and self-adapted entraining mode to manipulate the drainage and dripping of the entrained liquid. The viscous-capillary entrainment provides enhanced liquid uptake with high quantity and small deviation, as well as liquid drainage and droplet dripping with operationally high frequency and small differences between liquids with varied viscosities. As a proof of concept, the millimetric structured surface is arrayed and applied to fetching, transporting, and depositing viscous liquid from a confined space in a facile and sustained way. These results will contribute to the design of liquid collecting and dispensing methods, and potentially to the liquid control technology for various applications (45, 46). In contrast with routine methods, the viscous-capillary entrainment on the withdrawn millimetric structured surface ensures sustained liquid transfer with high quantity, frequency, and robustness, and is suitable for some intractable situations or even special operations. For example, one could collect liquid with unknown composition from an opaque and confined space for further detection. In a broader view of understanding, controlling, and using liquid entrainment dynamics, uneven surfaces with millimetric morphology are ubiquitous, from toys being painted and nasopharyngeal swabs for virus testing (47), to tracks with lubricant and tires through a puddle (48, 49), and even intestinal villi absorbing nutrients (50). Relative motion often occurs between these surfaces and liquid droplet, flow, bath, and water body, requiring analysis from the perspective of liquid entrainment. Therefore, our work can provide broader inspiration for the assessment of liquid clinging or material coating on uneven surfaces in daily life, laboratory operation, and industrial production.

MATERIALS AND METHODS

Chemicals

Silicone oils (PDMS) with the viscosity of ~100, ~1000, and ~30,000 mPa·s and glycerol were purchased from Aladdin (China) and of analytical reagent grade. The surfactant SDS was purchased from Shanghai You Yang Industrial (China) with the purity of 95%. Water was deionized from Milli-Q equipment with a resistance of 18.2 megohm·cm. The photosensitive resin (Basic Clear, 405 nm, GOPRINT, China) was used as transferred liquid shown in Fig. 5 (F to I). The same resin was used for 3D printing to prepare the substrate shown in Fig. 5G, and the substrate shown in fig. S8 was made of PDMS (Sylgard-184 silicone elastomer, Dow Corning, USA).

Sample preparation

The bare (radius of 1.0 and 2.0 mm) and millimetric structured (central axis radius R = 1.0 mm) rod samples with varied plate angle α = 15°, 30°, 60°, 90°, 120°, 150°, and 165°, axial plate number density n_a/n_a,0 = 3/2, 1, 1/2, 1/4, 1/8, 1/16, and <1/20 (n_a,0 = 1/1.5 mm⁻¹), circumferential plate number density n_c/n_c,0 = 1/2, 1 (n_c,0 = 10 per 2π), and plate height (by changing the plate length) H = 1.0, 1.5, and 2.0 mm were designed with 3ds Max Software (Autodesk) and fabricated with photosensitive resin (Clear, FSL3D, China) by a digital light processing (DLP) 3D printer (PhoenixPro 3D Printer, FSL3D, China) with xy-plane resolution of 50 μm and z-axis resolution of 25 μm. The plate thickness is 0.2 mm, and the axial distance of plate D equals 1/n_a. The samples were then cleaned in the detergent (Processing Kit, GOPRINT, China) by an ultrasonic cleaner for 3 min and postcured in pure water under UV light (405 nm) for 3 min (Wash & Cure Plus, ANYCUBIC, China). The fluorinated rod used in the experiment shown in fig. S6C was obtained by being treated with O₂ plasma (DT-03, Suzhou OPS Plasma Technology, China) at 200 W for 5 min and then fluorinated in a vacuum dryer oven at 80°C with 1H,1H,2H,2H-perfluorodecyltrimethoxysilane (Sigma-Aldrich, China) for 6 hours. The detachable scaffolds (with slots to ensconce rods and mortise-tenon joints to connect each slot) and rods shown in Fig. 5 were fabricated with photosensitive resin (Red Wax, 405 nm, GOPRINT, China; Basic Clear, 405 nm, GOPRINT, China) by a liquid crystal display (LCD) 3D printer (Sonic Mini 8K, Phrozen, China) with xy-plane resolution of 22 μm and z-axis resolution of 20 μm and assembled as needed.

Micro-CT characterization and x-ray imaging

Micro-CT images of the rods (shown in Fig. 1C and fig. S1B) were taken under 25-kV and 193-μA x-ray with no filter, and at the resolution of 1.00 μm, rotation step/rotation angle of 0.1°/180.0°, and exposure of 3072 ms (Skyscan 1272, Bruker, USA). The raw data were then reconstructed into tomographic images with NRecon software (Bruker, USA) and postprocessed with CTAn software (Bruker, USA). Finally, the images were transformed into a 3D model with the volume rendering software CTVox (Bruker, USA) for characterization from different views.

The orthodontic wax used in the experiment shown in Fig. 2 was melted in advance under 60°C to 65°C in our experiment. When a rod was withdrawn from it, the entrained wax swiftly solidified on the rod surface. Since the liquid retreat speed was ~10⁻² mm s⁻¹, the dynamics of the entrainment (that is to say, its shape) can be “frozen” by the solidified wax (10) and then characterized by micro-CT (Skyscan 1272, Bruker, USA) under 30-kV and 180-μA x-ray with no filter, and at the resolution of 2.00 μm, rotation step/rotation angle of 0.1°/180.0°, and exposure of 2609 ms. The raw data were then processed with NRecon (Bruker, USA), CTAn (Bruker, USA), and CTVox software (Bruker, USA).

Details of the retreat dynamics of the meniscus were recorded by x-ray imaging (Skyscan 1272, Bruker, USA) at the spatial resolution of 1.00 μm and temporal resolution of about 8 frames per minute under 40-kV and 180-μA x-ray with no filter (shown in Fig. 3C). The x-ray image recorded the liquid draining state just after the withdrawal and is shown as circumstantial evidence for the existence of the thin film.

SEM characterization of the rod sample

The detailed morphology of the rod sample was observed by a scanning electron microscope (SEM) at the acceleration voltage of 10 kV and low vacuum mode (QUANTA FEG 250, FEI, USA). The rod sample was mounted on an aluminum stub with copper tape and coated with a thin layer of platinum by an ion sputter at 10 mA for 60 s (MC1000, Hitachi, Japan).

Silicone oil wetting behavior on the plate surface

The wetting behavior of the silicone oil on the plate surface was characterized. A single 10 mm × 10 mm × 3 mm (length × width × height) plate was 3D-printed slantly with an angle of 30° to match the printing state of the plates on rod. The plate was horizontally placed, and the wetting process of a 2.0-μl silicone oil droplet of ~100 mPa·s on its surface was recorded at room temperature (LSA 100, LAUDA Scientific, Germany).

Characterization of the tested liquids

Physical properties (viscosity, surface tension, and density) of the tested liquids in our experiments (silicone oils, glycerol, and Basic Clear photosensitive resin) were characterized (table S1). The viscosity was characterized by a cone-plate viscometer (DV-II+ Pro, Brookfield, USA) and a concentric viscometer (NDJ-9S, LICHEN, China; for silicone oil-30000 only). The surface tension was characterized by pendant drop method with a surface analyzer (LSA 100, LAUDA Scientific, Germany). Each reported datum was derived by at least three independent trials at room temperature. The density of liquids with high viscosity was obtained by measuring the liquid mass of varied volume and performing linear regression with five independent points for each datum, and the density of liquids with low viscosity (water or aqueous solutions) was obtained by averaging the five independent measurements of mass of constant volume (ME204, METTLER TOLEDO, Switzerland).

Experimental setup

As Fig. 1D shows, the experimental setup for fundamental observation of the liquid uptake and drainage processes includes a 3.5-cm deep liquid bath in a 6.5 cm × 6.5 cm (length × width) acrylic box, a motorized vertical mobile device (ESM 301, MARK-10, USA) as a lifter to vertically immerse the rod sample into the liquid bath and withdraw the sample from it at the constant speed, and a high-speed camera (i-SPEED 3, OLYMPUS, Japan or Wave, Freefly Systems, USA) with a lens (AT-X M100 PRO D Macro, Tokina, Japan) at a horizontal distance of ~10 cm from the rod to record the processes from the side view. An electronic balance (ME204, METTLER TOLEDO, Switzerland) is also included to measure the mass change of the liquid bath during the experiment.

For the liquid transfer demonstration shown in Fig 5, the detachable array of structured rods is installed on a programmable multi-axis displacement apparatus (homemade with five RXP45, one RXS60, and one RXSN40 modules, QRXQ, China). The rods connect to each other with detachable mortise-tenon joints. Therefore, the distance between rods can be manipulated easily to match that between liquid sources. In the experiments, the distance between two rods is set to 2 cm. The liquid sources are 10-ml centrifuge tubes with tested liquid inside. The liquid acceptors are 1.5-ml centrifuge tubes for glycerol transfer, 3D-printed resin/cured PDMS substrate for lens array preparation, and blue LED chips for chip package, respectively. The liquid acceptors are installed on a single-axis mobile platform (RXP45, QRXQ, China) and can move in ±y direction to imitate conveyor belts in industry. The rod array is initially 10 cm above the liquid sources, and the distance between the liquid sources and acceptors is set to 15 cm. Four cameras are used to record the transfer process from different views: Osmo Pocket, DJI, China from the front view; D750, Nikon, Japan (with a lens of AF-S DX NIKKOR 55-300mm f/4.5-5.6G ED VR, Nikon, Japan) from the oblique-front view; TG-5, OLYMPUS, Japan from the side view; U3-3060CP-C-HQ Rev.2.2, iDS, Germany (with a lens of VT-LEM2514CBMP8, Vision Datum, China) from the oblique-side view.

Observation and measurement of liquid uptake by entrainment

The tested rod was carefully immersed into the liquid bath to a depth of 3.0 cm (20 times of 1/n_a,0 = 1.5 mm) without visible bubble entrained (fig. S10) and then withdrawn by the motorized vertical mobile device (ESM 301, MARK-10, USA) at the constant speed U ranging from 1.00 to 18.00 mm s⁻¹ (approaching 1100 mm min⁻¹, the maximum speed the device could attain). The whole withdrawal process was recorded from the side view by a high-speed camera (i-SPEED 3, OLYMPUS, Japan) with a lens (AT-X M100 PRO D Macro, Tokina, Japan) at 1000 fps for silicone oils of ~100 and ~1000 mPa·s. Especially, the whole withdrawal and dripping processes shown in Fig. 1E were recorded by a high-speed camera (Wave, Freefly Systems, USA) with a lens (AT-X M100 PRO D Macro, Tokina, Japan) at 1000 fps for silicone oil of ~100 mPa·s and withdrawal speed of 18.00 mm s⁻¹. The electronic balance (ME204, METTLER TOLEDO, Switzerland) was used to obtain the entrained liquid mass by measuring the mass difference of the liquid bath before the rod immersion and after the withdrawal. Each reported measurement was an average of three independent trials.

Observation of liquid retreat

Details of the retreat dynamics of the meniscus were recorded by a high-speed camera (Wave, Freefly Systems, USA) with a lens (FF 24 mm F14 2X Macro Probe, LAOWA, China) at 100 fps (shown in Fig. 3A). The optical images to investigate the retreat process in Fig. 3 (B and E) were recorded at 1000 fps (i-SPEED 3, OLYMPUS, Japan with a lens of AT-X M100 PRO D Macro, Tokina, Japan). The data were extracted from the videos by an open source tracking software (Tracker, Open Source Physics).

Observation of droplet dripping

The droplet dripping process of entrained liquid after withdrawal and total separation from the liquid bath shown in Fig. 4A was recorded by a high-speed camera (i-SPEED 3, OLYMPUS, Japan) with a lens (AT-X M100 PRO D Macro, Tokina, Japan) at 1000 fps for silicone oils of ~100 mPa·s and withdrawal speed of 18.00 mm s⁻¹. The dripping processes of varied liquid viscosity and withdrawal speed were recorded by a high-speed camera (Wave, Freefly Systems, USA) with a lens (AT-X M100 PRO D Macro, Tokina, Japan) at 500 and 100 fps for small and large dripping time, respectively. The first droplet dripping time, Δt, was derived from the optical video by subtracting the moment of total separation of entrained liquid and liquid bath from the moment of droplet dripping. The second (third) droplet dripping time was derived by subtracting the moment of first (second) droplet dripping from that of second (third) droplet dripping. The tested liquid was of high viscosity and would form a long filament between the dripped droplet and the liquid on rod. Therefore, the droplet dripping moment was defined to be the moment when the droplet fell 1.5 cm (about 10 times of the capillary length of silicone oils) from the rod bottom to enable comparison. Each reported measurement was an average of three independent trials.

Liquid transfer

The detachable array of structured rods was controlled by the programmable multi-axis displacement apparatus (homemade with five RXP45, one RXS60, and one RXSN40 modules, QRXQ, China) to cyclically fetch, transport, and deposit the viscous liquids. The liquid acceptors were controlled by the single-axis mobile platform (RXP45, QRXQ, China) and moved in ±y direction to match the liquid transfer process by the rod array. The glycerol was dyed green, yellow, and red with food colorants. An electronic balance underneath was used to display the total mass change of liquid in the centrifuge tubes during experiments. The unit mass change (red circle in Fig. 5E) of the nth cycle was derived by subtracting the (n + 1)th total mass change from the nth one, assuming that the mass of liquid entrained by the withdrawn rod array in each cycle was constant.

The photosensitive resin (Basic Clear, 405 nm, GOPRINT, China) used in Fig. 5 (F to I) was cured by 405-nm UV light at the interval of the transfer process. The same resin was used for 3D printing to prepare the substrate shown in Fig. 5G, and the substrate shown in fig. S8 was made of PDMS (Sylgard-184 silicone elastomer, Dow Corning, USA). The PDMS pre-polymer and curing agent were mixed with a mass ratio of 10:1 and then cured under 80°C for 6 hours. The substrates had a thickness of ~10² μm. A handheld light transmittance meter (CT-23, Hangzhou CHNSpec Technology, China) was used to measure the transmittance of infrared (940 nm), visible (530 nm), and UV (365 nm) light through the 3D-printed resin substrate with (T_Lens in Fig. 5H) and without (T_Sub) resin lenses in at least three different positions. The results with lenses (T_Lens) were then divided by those of substrate (T_Sub) to show the relative transmittance in Fig. 5H.

The unpacked blue LED chips were purchased from SuZhou Uking Photoelectric Technology Co. Ltd. (China) and tested under a constant voltage of 3 V. The medium-sized resin droplet (M) can be obtained with a single transfer cycle, while the large sized one (L) requires more cycles for one chip. The small sized one (S) can be obtained by the entrained liquid on rod slightly touching the chip. The curing process of the resin, though released heat, showed no apparent damage to the chips.

The liquid transfer processes were recorded by cameras from different views (Osmo Pocket, DJI, China at 50 fps; D750, Nikon, Japan at 60 fps with a lens of AF-S DX NIKKOR 55-300mm f/4.5-5.6G ED VR, Nikon, Japan; TG-5, OLYMPUS, Japan at 25 fps; U3-3060CP-C-HQ Rev.2.2, iDS, Germany at 24 fps with a lens of VT-LEM2514CBMP8, Vision Datum, China). The lighting effects of LED shown in Fig. 5I and fig. S9 were captured by a camera (D7500, Nikon, Japan) with a lens (AF-S DX NIKKOR 55-300mm f/4.5-5.6G ED VR, Nikon, Japan), and it should be mentioned that the pictures in fig. S9 were captured with an orange filter.

Theoretical estimation of liquid entrainment

For the incompressible and steady flow, the Navier-Stokes equations go as

$$\mathrm{\eta }\text{Δ}\mathit{v}-\mathrm{\nabla }p+\mathrm{\rho }\mathit{g}=\mathrm{\rho }(\mathit{v}\cdot \mathrm{\nabla })\mathit{v}$$ (3)

For the condition we focus on, the pressure gradient ∇p originates in the capillary pressure gradient γ∇Γ by assuming that the surface tension γ is constant. With all length variables and parameters being nondimensionalized by the radius of central axis of rod, R, it allows us to nondimensionalize the equations as given in Eq. 1.

We could then neglect the inertial term in the equation and get an asymptotic expression by a scaling argument

$$\mathrm{Ca}(\frac{1}{{h_{\mathrm{m}}^{\ast }}^2}+\frac{{n_{\mathrm{c}}}^2}{{(R^{\ast }+H^{\ast })}^2})+(\frac{1}{R_{\mathrm{a}}^{\ast }}+\frac{1}{R_{\mathrm{c}}^{\ast }}-{\mathrm{\kappa }}^{\ast }+\frac{1}{R^{\ast }+H^{\ast }})n_{\mathrm{a}}^{\ast }\sim \mathrm{Bo}$$ (4)

where h_m is the minimum distance between the meniscus and the side wall of the central axis of rod, and the viscous terms in Eq. 4 represent the viscous friction on the liquid with the boundaries of the side wall of the central axis and the plates, respectively. The boundary of the plates is a virtual boundary. Considering that the concave meniscus forms at the center of four neighboring plates, the flow mainly takes place in this position, and the liquid between two axially arranged plates has weaker flowability. Therefore, the plates of the same column at the axial direction can be assumed to integrate with each other to form a wall-like virtual boundary. For the capillary terms, −R_a ~ −D = −1/n_a and −R_c ~ −(R + h_m)/[1/sin(1/2n_c) − 1] are the characteristic principal curvature radii of the meniscus between plates in axial and circumferential directions, respectively. κ, as mentioned in the main text, represents the characteristic curvature of the capillary length, κ⁻¹ = (γ/ρg)^1/2. Therefore, the characteristic principal curvatures of the meniscus at the transition zone between the entrained liquid and the liquid bath scale as −κ and 1/(R + H) in vertical and horizontal directions, respectively. The Bond number acts as the gravitational term, for gravity influences the overall flow between the plates but not the liquid behavior on the plates. All length variables and parameters are nondimensionalized by R as well and then marked with superscript asterisks. If we assume that the meniscus between plates is supported by the apex of the plate and R_c is constant and scales as (R + H) tan(1/2n_c), the equation can be further simplified and yield

$$h_{\mathrm{m}}^{\ast }\sim \frac{1}{\sqrt{\frac{1}{\mathrm{Ca}}(\mathrm{Bo}-{\text{Φ}}^{\ast }{n}_{\mathrm{a}}^{\ast })-{{\text{Ψ}}^{\ast }}^{-2}{n_{\mathrm{c}}}^2}}$$ (5)

where the dimensionless structure parameter Φ* = 1/D* + [tan(1/2n_c) + 1]/(R* + H*) − κ* ~ Γ_bath* − Γ_plate* represents the curvature difference of the meniscus at the bath-entrainment transition zone and that between the plates, and Ψ* = R* + H* is the dimensionless outer radius of the structured rod. The capillary number Ca and axial plate number density n_a* enhance the entrainment, while Bo plays the opposite role. With the assumption that $\overline{S}$ is approximately proportional to h_m and controlled by these parameters as $\overline{S}$ ~ Rh_m, we derive

$$\frac{\overline{S}}{R^2}\sim \frac{1}{\sqrt{\frac{1}{\mathrm{Ca}}(\mathrm{Bo}-{\text{Φ}}^{\ast }{n}_{\mathrm{a}}^{\ast })-{{\text{Ψ}}^{\ast }}^{-2}{n_{\mathrm{c}}}^2}}$$ (6)

which indicates that the effects of viscosity (presented by Ca) and the millimetric structure parameters enhance the liquid entrainment. When to the large Ca limit, since h_m* enlarges fast, the characteristic size grows and Bo goes even much larger than Ca, so this result is back to the Derjaguin theory (h₀Γ_ch ~ Ca^1/2) (17). One may notice that when n_a* is extremely large, the term (Bo − Φ*n_a*) will be negative. In this condition, the liquid between plates is almost trapped because of the capillary effect, whose behavior should be described by the double-layer model for the microstructure but not the millimetric one we discuss here (26, 28).

Supplementary Materials

This PDF file includes:

Figs. S1 to S10

Tables S1 to S4

Legends for movies S1 and S2

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 and S2