Patient-specific, mechanistic models of tumor growth incorporating artificial intelligence and big data

Abstract

Despite the remarkable advances in cancer diagnosis, treatment, and management that have occurred over the past decade, malignant tumors remain a major public health problem. Further progress in combating cancer may be enabled by personalizing the delivery of therapies according to the predicted response for each individual patient. The design of personalized therapies requires patient-specific information integrated into an appropriate mathematical model of tumor response. A fundamental barrier to realizing this paradigm is the current lack of a rigorous, yet practical, mathematical theory of tumor initiation, development, invasion, and response to therapy. In this review, we begin by providing an overview of different approaches to modeling tumor growth and treatment, including mechanistic as well as data-driven models based on “big data” and artificial intelligence. Next, we present illustrative examples of mathematical models manifesting their utility and discussing the limitations of stand-alone mechanistic and data-driven models. We further discuss the potential of mechanistic models for not only predicting, but also optimizing response to therapy on a patient-specific basis. We then discuss current efforts and future possibilities to integrate mechanistic and data-driven models. We conclude by proposing five fundamental challenges that must be addressed to fully realize personalized care for cancer patients driven by computational models.

1. INTRODUCTION

Over the past three decades remarkable advances in cancer diagnosis, treatment, and management of malignant tumors have resulted in a 33% overall reduction in cancer mortality [131], yet the incidence of many cancers continues to increase and cancer remains a major public health problem worldwide. Shifting the clinical management of these diseases towards personalized therapies that account for the intra- and inter-tumor heterogeneity in treatment response could further improve patient outcomes. However, it is not typically known a priori how a patient’s tumor physiology, genotype, and phenotype will influence response to a particular therapeutic regimen. Thus, the current clinical paradigm for personalized therapeutic regimens relies on post hoc assessment of tumor response after some or all of the therapy has been delivered. Unfortunately, this approach potentially exposes patients to invasive biopsies, weeks or months of ineffective therapy, and off-target toxicities. Personalized therapies guided by a patient’s predicted outcome rather than their observed or assessed outcome could avoid these ineffective therapies and their side effects and dramatically improve patient outcomes [164]. To design personalized therapies guided by predicted patient response requires a deep understanding of the underlying biology embedded within a practical (i.e., actionable) mathematical theory capable of rigorously characterizing the dominant processes determining the individual’s response to a particular set of interventions. Without a mathematical theory rooted in known cancer biology, we are left with trial and error (albeit, perhaps, from well-informed large population-based studies) to select the optimal therapeutic regimen for a given patient. In fact, there has been enormous effort to develop mathematical descriptions of the disease from the genetic to tissue scales [163, 27, 37] in the growing field of mathematical or computational oncology [5, 119].

Mathematical models that attempt to incorporate the underlying mechanisms of tumor biology can provide readily interpretable solutions that enable the systematic investigation of alternative treatment strategies in silico to estimate their efficacy, safety, and overall impact on tumor response, thereby helping the treating physicians to make well-informed (high-risk) decisions. To fully realize the potential of mechanistic mathematical models to guide care on a patient-specific basis, models need to be initialized and integrated with patient-specific data that is practically available in the routine clinical setting. While there is hardly a scarcity of mathematical models describing tumor initiation, growth, invasion, and response [27, 5], a historical (and lingering) challenge has been that many of these models rely on parameters that are difficult or impossible to assign or calibrate based on readily-available data. Some of the barriers to progress have been the lack of quantitative biological assays for directly measuring model parameters or the necessity of highly-invasive (or impractical) means to measure quantities of interest [76]. Therefore, in the development of a clinically-relevant mechanistic modeling framework, it is important to determine the quantities of interest that can be measured at the spatial and temporal scales necessary to personalize the key biological components of the mechanistic model. Fortunately, in parallel to the advances of the clinical management of cancer, there has been substantial growth in the development of mathematical models that can be initialized and personalized via patient-specific data [76, 14, 58, 41, 68, 105] through either direct measurement or model calibration and therefore might serve as tools enabling personalized therapy.

On the opposite side of the computational spectrum from mechanism-based models, are the methods of artificial intelligence (AI) and “big data”. While the potential of AI to positively impact healthcare is difficult to deny, there are fundamental limitations of the AI-only approach that may restrict its ability to hasten the arrival of truly personalized medicine. In particular, the AI approach relies on data sets that may fail to capture unique individual patient conditions and are not truly representative of a diverse patient population [129]. These issues are exacerbated when trying to identify an optimal therapy for a particular patient’s tumor subtype and physiological conditions—all of which can exist outside of the available training data. However, AI may serve a complementary role with mechanistic modeling in realizing personalized medicine through, for example, relating large quantities of ‘omic’ data to mechanistic model parameters, reducing the computational burden, or parsing mechanistic model forecasts to select optimal therapies [119, 13].

In this review we discuss topics from theory to application that may help realize personalized medicine in oncology. Clinically-relevant models of tumor growth have been and will continue to be driven by the available data. Thus, we first describe the available data across scales. Second, we introduce mathematical models based on biological mechanisms and data-driven models facilitated by AI. Third, we discuss how mechanistic models have the potential to identify optimal interventions and treatments. Fourth, we describe how mechanistic models and AI can be synergistically combined to advance the fields of personalized cancer management and treatment. Finally, we conclude by identifying five fundamental and currently unmet challenges to realizing truly personalized care for cancer patients.

2. DATA AVAILABILITY ACROSS SCALES

2.1. Microscopy approaches for informed diagnostics

Traditional pathological examination of tissue samples has been performed under a bright-field microscope by highly trained laboratory personnel. However, a new era of digital pathology is evolving towards digitized whole-slide images where the whole prepared slide is scanned with an automated scanning microscope [108]. The availability of these detail-rich digital files has facilitated the rise of computer aided/assisted diagnosis (CAD) which aims to increase speed, accuracy, and sensitivity in the diagnosis of breast cancer and other malignancies [72]. CAD relies on the digitization of whole-slide images of prepared tissue sections that are usually stored in a high-resolution format. However, large files are challenging for centers to store and manage. These data can also be sensitive to center-based and user-based perturbations. Labor-intensive staining of the slides introduces variation between laboratories, creates heterogeneity in samples and can influence diagnostic model training and performance on unseen data known as domain shift [97]. Domain shift represents a significant problem in the computer automated pathology realm [78]. Core needle biopsy histology has shown promise in controlling domain shift but is still not ready for clinical application [112]. Currently, histological analysis of tumor sections by pathology professionals remains the gold standard diagnostic technique for solid tumors [72]. There remains a need for large, high-fidelity data sets from tissue samples to train cancer cell detection in samples for screening patients, monitoring disease progression, and interoperative tumor margin applications. Attenuated Total Reflection Fourier Transform Infrared (ATR-TFIR) spectroscopy represents a potential resource in training machine learning models to detect cancer cells. ATR-FTIR has shown promise as a high-throughput method of detecting biochemical changes in malignant cells [85, 47]. ATR-FTIR is a biochemical analysis method that can discriminate a sample’s unique spectra of lipids, proteins, carbohydrates, and nucleic acids. These spectra, a biochemical “fingerprint” of the sample, represent a large training dataset with potential to couple with machine learning to offer reliable quantitative information readily usable by computational models.

2.2. Medical imaging

Medical imaging is central to the clinical management of cancer patients as it is used for screening, diagnosis and staging, guiding interventions, assessing response, and long-term surveillance. It is widely available and a trusted data source capable of delivering longitudinal, non-invasive (with the exception of the administration of exogeneous contrast agents or radiotracers), and spatially resolved measurements of tumor biology. These characteristics make medical imaging an exceptional candidate for informing mechanistic tumor models [93].

Magnetic resonance imaging (MRI) [61] and positron emission tomography (PET) [69] have emerged as the primary modalities for informing patient-specific models of tumor growth and response at the tissue scale. In the routine clinical setting, MRI can achieve a spatial resolution of 1–2.5 mm isotropic with a temporal resolution of seconds to minutes, whereas PET may achieve a spatial resolution ranging from 2.5 to 5 mm isotropic with a temporal resolution of minutes to hours. MRI is capable of quantitatively characterizing anatomy and underlying physiology of the tissue of interest, while PET can report on a range of molecular and metabolic features via a wide range of radiotracers. Since anatomical imaging provides information about the structure and extent of the tumor, it plays a crucial role in the assessment of treatment response across disease sites [40, 151]. For mathematical modeling applications, anatomical images are essential for defining the computational domain, assigning boundary conditions, and identifying the extent of disease both before and during treatment. Physiological or molecular imaging techniques report on an array of parameters frequently incorporated into mechanism-based models including: a) cellularity, via diffusion-weighted MRI (DW-MRI) [109]; b) vascularity and perfusion, via dynamic contrast-enhanced MRI (DCE-MRI) [106, 114]; c) hypoxia, via 18F-fluoromisonidazole PET [117]; and d) glucose metabolism, via 18F-flourodeoxyglucose PET [28]. Mapping these tumor characteristics in three dimensions and across time facilitates patient-specific, tissue-scale modeling as the mechanism-based mathematical models frequently explicitly incorporate such quantities of interest. It is important to note that heterogeneity in these parameters can have great influence on patient response; for example, perfusion or tissue oxygenation are well-established indicators of the efficacy of systemic- and radio-therapy. A patient-specific model capable of predicting how these quantities change in space and time could provide guidance to many clinical management strategies across oncology [141]. Therefore, accurate measurement and characterization of the evolution of these properties via mechanistic mathematical modeling may be essential to optimizing treatment strategies and, subsequently, treatment outcomes on a patient-specific basis.

2.3. Informing on the totality of molecular processes

Tumors are comprised of dynamic, heterogenous cell populations which change as the cancer progresses [70]. These changes not only allow cells to seed and colonize new tissues, but they also alter the response of tumor cells to therapeutics. Precision analysis of these mixed cell populations poses a substantial hurdle as bulk sequencing of cells (i.e., all of the cells simultaneously) results in population averaging [159], and can limit insight into how the mixed cell populations interact to facilitate metastasis and drug resistance. Single cell methods of characterizing individual tumor cells overcome this challenge and provide rich datasets on the cell’s genome, epigenome, proteome, or transcriptome [123]. Single cell genomic sequencing approaches such as the widely-adopted scRNA-seq can provide information about tumor cell population heterogeneity and how cell populations change with growth and metastasis [55]. Multiomics approaches that allow for the profiling of multiple “omes” in an individual cell are rising in popularity [107]. As the amount of multimodal data extracted from singular cells is increasing, cellular labeling methods such as molecular barcoding become increasingly important to tie data back to its source [107, 62]. Despite the increasing complexity of data able to be extracted from each cell, omics data are inherently static as the cell must be lysed [55, 147]. Therefore, data that could have been gleaned from dynamic processes suffers. Deployment of machine learning algorithms on omics datasets generated from patient samples as the disease progresses represents a significant opportunity for patient-specific medicine.

3. MATHEMATICAL MODELS

3.1. Mechanistic and data-driven: Two types of models to fight cancer

Finding a mathematical model that faithfully reproduces the spatiotemporal dynamics of a tumor may be considered the ultimate goal of tumor modeling. However, there are numerous examples in tumor modeling (and other fields of science) showing that, even if that ultimate goal is not achieved, careful development of parsimonious models can provide remarkable insight and useful approximations [23].

Mechanistic models are based on first principles and hypotheses generated from observations. In cancer modeling, first principles include physics principles like conservation of mass and biological principles like the concept of homeostasis. Observations include medical images, pathological information obtained from microscopy, genomic and proteomic information, and clinical data. Data-driven models are consistent with observations, but cannot be derived from first principles. The purpose of data-driven models is to enable prediction. Mechanistic models are used to increase our understanding of a phenomenon, but they can also be used for prediction after calibration. The distinction between mechanistic and data-driven models goes back many years [102]. Historically, scientists have favored mechanistic over data-driven or phenomenological models. However, recent literature has seen a more vigorous debate. The unprecedented growth of data-driven models is fueled by AI, and our increasing ability to collect, fit, and extrapolate large amounts of data. This growth is driven by advances in hardware and software, including tensor processing units (i.e., a circuit specifically designed to accelerate AI workloads) and machine learning algorithms.

3.2. Data-driven models

3.2.1. The AI paradigm

AI, and its most recent and exciting subset, deep learning, has permeated virtually every aspect of modern life. Medicine has been no exception: Based on PubMed data, the number of publications that use the terms “deep learning” or “neural network” has increased by a factor of ~10 in the last 5 years. The most common application of AI is image classification. Therefore, it is not surprising that quantitative techniques for deep learning-based image analysis have gained momentum in medicine. The reasons for the explosion of AI in medical imaging are multifold, but two facets deserve especial attention: a pressing and consistent clinical need, and the convergence of computational innovations with interdisciplinary collaborations. These facets are particularly well highlighted in the context of the cancer continuum, from diagnosis and detection to treatment and management of malignant lesions. Given the heterogeneity and dynamic nature of cancers, medical advances have focused on earlier screening and detection, and preferential removal of lesions using a subset or a combination of surgery, chemotherapy, radiation therapy, immunotherapy, and/or targeted therapy, to improve survival. Here, we describe the two arms of the tumor progression continuum where AI has shown significant success, namely, diagnosis and treatment assessment, as well as a more emerging application intended to predict diagnostic endpoints.

3.2.2. AI for cancer diagnosis

Initial cancer detection and staging today employs a variety of noninvasive or minimally-invasive imaging technologies as described in Sect. 2.2. The diagnostic gold standard for most cancers, however, remains the biopsy. A biopsy presents a non-negligible degree of invasiveness to the patient regardless of cancer type, as sample tissue must be extracted from the body for grading [90]. Given the minimally invasive nature of the aforementioned imaging modalities already a part of the clinical workflow, there has been a proliferation of AI-based algorithms, many of which claim to interpret imaging scans at the level of expert clinicians. In breast cancer, a quantitative image analysis technique for detection of Human epidermal growth factor receptor 2 (HER2) has received FDA approval [44, 16, 140]. The goal of a HER2-directed image analysis platform is to detect and quantify HER2 membranous IHC staining, providing critical information to guide treatment. In prostate cancer, Paige [115] is the first AI-based pathology product to receive FDA approval for in vitro diagnostic use to detect cancer in prostate biopsies. In brain cancer, the release of annotated, open-source datasets, such as the Multimodal Brain Tumor Segmentation Challenge (BraTS) [99, 8, 12, 11, 10] has spearheaded the generation of AI models for tumor segmentation, which is essential for planning surgical and radiation treatments. Segmentation of primary brain tumors has been often performed with 3D U-Nets and their variations [121]. Notably, the winners of the 2020 BRATS challenge used an architecture named “No NewNet” to emphasize that a standard U-Net coupled with thorough training and optimization continues to achieve state-of-the-art results [64].

3.2.3. AI for cancer progression assessment

AI approaches aimed at assessing tumor progression can be categorized into radiomics and deep learning. Radiomics involves the extraction of quantitative imaging features and subsequent analysis using statistical and machine learning methods, while deep learning focuses on training deep neural networks to automatically learn patterns and relationships directly from raw medical image data [148]. Current radiomics and deep learning applications can be delineated into three overarching areas: a) Preprocessing, which consists of approaches to automate image acquisition and spatiotemporal registration [167, 46]; b) Analysis, which includes anatomical segmentation, volumetric quantification, extraction of parameter maps from diffusion or perfusion imaging, and groupwise population analyses [64, 30]; and c) Interpretation, which can be framed as an image classification process that includes identifying tumor subtypes, radiogenomics, response assessment, and survival prediction [9, 53]. The longitudinal measurement of lesion burden is an important aspect of tumor progression assessment that is well-suited for AI. Even though volumetric measurement is ideal to assess lesion burden, proxy measures, such as RANO (Response Assessment in Neuro-Oncology) for gliomas are often used. The tool AutoRANO, which uses the outputs of a segmentation model that can run on post-operative images, aims at automating RANO measurements [30]. Other tumor types have also seen promising advances in this area [111]. Another aspect of tumor progression assessment where AI has shown promising results is the automatic delineation of tumor subtypes and molecular markers from medical images. The correlation between imaging features and specific gene expressions of tumors is termed radiogenomics. A priori knowledge of the mutational status of known oncogenic drivers together with radiographic suspicion of a neoplasm may favor prompt intervention, as well as targeted therapy. Some of the most promising advances in radiogenomics have enabled delineation of the Isocitrate Dehydrogenase (IDH) mutation status in gliomas [29], and the Epidermal Growth Factor Receptor (EGFR) status in non-small cell lung cancer [36].

Finally, survival analysis, which is used in cohort and other longitudinal studies to estimate the time it takes for a specific event to happen, has incorporated radiomics, deep learning, and a combined utilization of both approaches in various tumor types. In the case of gliomas, for example, reference [9] put forth a three-step framework for predicting overall survival, which involved segmenting data, extracting radiomic features, and utilizing a survival prediction model. The aim was to classify patients into three survival groups (short-term, mid-term, and long-term) and provide predictions for their overall survival [110].

3.2.4. AI for outcome prediction

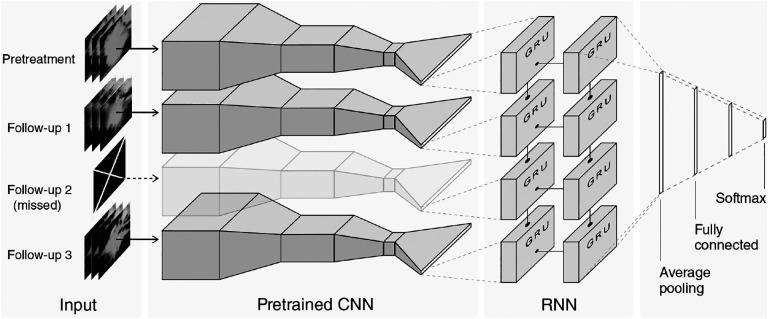
While tumors are dynamic biological systems, influenced by their microenvironment and other factors, most AI algorithms have concentrated on developing imaging markers for a single time point. Contemporary deep learning techniques, such as recurrent neural networks (RNN), which have been successfully employed in video classification and natural language processing, have the potential to incorporate longitudinal data [51, 39]. However, these advanced computational approaches have been relatively underutilized in the field of radiology. Recently, an algorithm combining convolutional neural networks (CNNs) and RNNs has shown success predicting the survival and pathologic response of patients with non-small cell lung cancer by integrating pretreatment and follow-up CT images [161]. In particular, this algorithm predicted two-year overall survival with AUC = 0.74. Fig. 1 shows the network architecture, where the pretrained CNN is a ResNet. While acquiring enough longitudinal data to train this type of networks is very challenging (n=107 patients were required for training) in cancer, this research highlights the potential of AI for outcome prediction.

Figure 1: Data-driven model predicting outcome in lung cancer patients.

The input to the model is a sequence of longitudinal CT images from an individual patient that includes a pretreatment CT and several follow-up images. The network architecture is composed of a ResNet convolutional neural network (CNN) that was pretrained on the ImageNet database. Each input CT, corresponding to data at one timepoint, is fed into a CNN. The pretrained CNN is followed by a recurrent neural network (RNN) with gated recurrent units (GRU). The network is able to handle missing scans by masking the output of the CNN to skip the timepoint. After the GRU, the network uses averaging and fully-connected layers to prevent overfitting. The final softmax layer provides a binary classification output. Reproduced with permission from [161].

3.2.5. Fundamental Limitations

The explosion of AI in elucidating tumor biology, while promising, has brought forth a number of key concerns. These limitations include dataset level limitations such as data variability, noise, poor quality and limited availability of large amounts of data, as well as model brittleness and lack of interpretability or explainability of the model [15].

Most current AI models continue to be highly dependent on the training dataset. These datasets are often limited in size and are frequently homogeneous. Data heterogeneity continues to be a key hindrance to the generalizability of deep learning models. Within real world clinical oncology data, this heterogeneity can come in several forms, such as different image capture devices, patient populations or inter-tumor heterogeneity. There is a paucity of current work towards the creation of clinical-domain-specific yet generalizable AI models. AI models also frequently struggle with cases that deviate significantly from the patterns seen in the training data, a phenomenon described as out-of-distribution data [4, 43]. Modeling tumor growth often requires approaches that are patient specific, and an AI-only solution is likely insufficient to capture the high patient-level variability in tumor growth.

Additionally, deep learning models are frequently considered as “black boxes” owing to the minimal transparency in how these models arrive at predictions [88]. This makes translating deep learning model predictions to clinical settings difficult [145]. These models frequently have complex architectures and operate via multiple layers of interconnected neurons, which makes understanding the reasoning behind their predictions difficult. This limits the ability to gain insights into the specific mechanistic patterns that drive tumor growth and the molecular makeup of the tumor micro-environment, and limits the reliability of AI-generated results.

3.3. Mechanistic models

The main mechanisms underlying the development of a tumor and the effect of treatments are described with mathematical models, which are usually written in terms of time-resolved ordinary differential equations (ODEs) or spatiotemporally-resolved partial differential equations (PDEs) and agent-based models. In general, the choice of each formulation paradigm is subject to the scale of the tumor-specific phenomena to be captured by the model (e.g., cell-cell interactions in the tumor microenvironment, chemotherapeutic response at organ scale, metastasis over the body), as well as the available data types, and their level of spatiotemporal resolution (e.g., cellular versus organ scale, and daily versus yearly measurements) [76, 100, 93]. Here, we focus on models based on ODEs and PDEs, but agent-based models also have a rich literature and are important to investigate the spatiotemporal evolution of a tumor and its microenvironment at cellular level [100].

3.3.1. Mechanistic models based on ODEs

ODE models have been broadly leveraged to describe the temporal dynamics of tumor burden and its response to treatment both in preclinical and clinical scenarios. These models are posed in terms of variables that can be repeatedly measured over time during the experimental protocol or the clinical management of the tumor, such that these longitudinal datasets can be used to inform the model. There are three common choices for these variables. First, tumor volume is an established metric for monitoring therapeutic response that can be readily determined, for example, using anatomic imaging data in (pre)clinical settings (e.g., X-ray CT, and T1- and T2-weighted MRI) and also calipers in animal models [87, 166, 132]. Second, the tumor cell count is a common metric of tumor malignancy and therapeutic response that can be measured, for instance, using in vivo ADC maps derived from DWI-MRI and automated microscopy techniques during in vitro experiments [76, 162]. Finally, some tumor-specific biomarkers can serve as surrogates for tumor growth and response to treatment, such as the blood serum levels of the Prostate-Specific Antigen (PSA) in the clinical management of prostate cancer [24, 134, 91].

The formulation of ODE models usually features a term describing tumor growth and one or more terms characterizing the effects of treatments on tumor dynamics [20, 165, 87]. For instance, radiotherapy is usually represented as an instantaneous reduction of the tumor burden on the dates of each radiation dose, although this approach can also be extended to a hybrid formulation with a continuous term accounting for the delay in tumor cell death since the exposure to radiation [91, 166]. In general, drug-based therapies use a hybrid formulation to represent the treatment: the discrete component represents the delivery of drug doses while continuous terms may account for a diverse host of mechanisms, such as a dose-dependent death rate, early and late effects of the drugs, drug interactions, and the time-resolved change of drug concentration during treatment [87, 24, 162]. For example, an ODE model to describe the temporal dynamics of tumor growth and response to chemotherapy in terms of the total tumor cell count (N) can be written as

$$\frac{dN}{dt}=\rho N(1-\frac{N}{K})-\alpha N{U}_0\sum _i{e}^{-\beta (t-t_i)}\mathscr{H}(t-t_i).$$ (1)

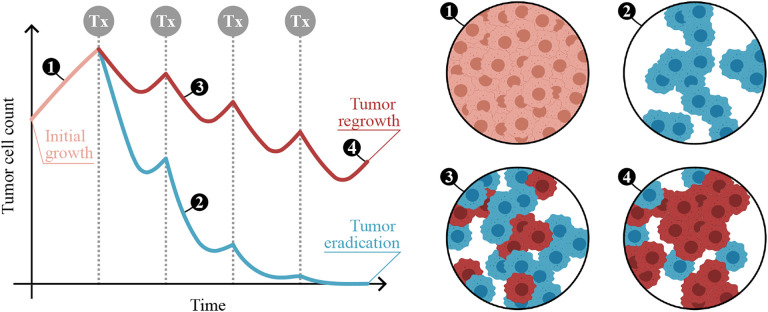
The first term on the right-hand side of Eq. 1 represents tumor growth with a logistic term, in which ρ is the net tumor cell proliferation rate and K is the tissue carrying capacity (i.e., the maximally admissible tumor cell burden). The second term on the right-hand side formulates the tumor cell-killing effect of a drug, where α is the rate of drug-induced tumor cell death, U₀ is the delivered drug dose, β is the drug’s decay rate, t_i are the times of drug delivery, and H(t − t_i) is a Heaviside function activated at the treatment times. Figure 2 illustrates the result of an ODE model of tumor growth and response to cytotoxic therapy (e.g., chemotherapy, radiotherapy).

Figure 2: ODE modeling of tumor growth and treatment response.

(Left) Example of the outcome of an ODE model describing the temporal dynamics of tumor cell count under a certain cytotoxic therapy. Vertical dotted lines indicate the times of treatment (Tx) delivery. An initial period of untreated growth is represented in light orange, and two alternative scenarios of therapeutic response are considered after treatment onset. The blue curve represents a situation in which the therapeutic regimen effectively kills all tumor cells. The red curve corresponds to a scenario in which the tumor resumes growth after the last therapy dose. This situation may be motivated by different causes, such as the existence of a subset of treatment-resistant cells in the original tumor, the development of chemoresistance or an inadequate treatment regimen for this specific tumor. (Right) Snapshots numbered 1 to 4 provide insight into the tumor cells status in different situations. In these snapshots, light orange cells represent untreated cells, blue cells are effectively treated and will ultimately die, and red cells survive to the chosen therapy and continue proliferating. This figure was partially created using BioRender.

ODE models of tumor growth and therapeutic response can also be extended to a multicompartment formulation that can accommodate, for example, multiple cell types [134, 24], different therapeutic responses [162, 91], several imaging-identified intratumoral regions with prognostic significance (e.g., tumor habitats with distinct cellularity and vascularization) [132], or other variables affecting tumor dynamics and eligible as treatment targets (e.g., tumor vascularity, reactive oxygen species) [87, 20]. Consequently, these multicompartment models consist of a set of ODEs informed by one or more of the aforementioned time-resolved data types.

The main advantage of ODE models is that they require minimal computational resources, which facilitates the execution of multiple simulations in short times. This advantage is pivotal to enable a fast computational evaluation of multiple therapeutic regimens and find an optimal treatment for each individual [87, 162, 24]. Additionally, the reduced computational cost of ODE models also facilitates the quantification and propagation of uncertainties in the data to the ensuing forecasts of tumor growth and therapeutic response [87]. Importantly, uncertainty quantification is key to derive clinically-actionable modeling results supporting clinical decision-making, such as probabilistic risks and survival odds [24, 166]. However, the main limitation of ODE models is their inherent lack of spatial resolution, which limits their ability to capture intratumor heterogeneity and its driving role in tumor development and therapeutic response.

3.3.2. Mechanistic models based on PDEs

PDE models constitute a natural extension of ODE models to accommodate spatially-resolved mechanisms at tissue and organ scale in both preclinical and clinical scenarios (see Fig. 3). There are three main paradigms to describe tumor growth and therapeutic response with PDE models. First, advection-diffusion-reaction models are usually posed in terms of tumor cell density [157, 57, 89, 35, 154, 6] or tumor cell volumetric fraction [139, 79]. The formulation of these models is obtained by combining two types of phenomena: (i) a mobility mechanism, which is generally represented by a flux featuring diffusive and advective processes within an elastic [157, 57, 89, 35] or poroelastic medium [6, 139, 79], and (ii) a collection of reaction terms representing local tumor cell mechanisms, such as proliferation, death, metabolism, therapeutic response, and phenotypic change of tumor cells [165, 86, 93]. Second, phase-field models are governed by the minimization of a functional featuring all types of energy interacting in the tumor growth problem (e.g., internal energy, kinetic energy, interfacial energy between tumor and healthy tissues, elastic energy), wherein the tumor is represented by a variable identifying the regions occupied by cancerous tissue [94, 33, 45, 86, 160, 153]. The resulting PDE model is completed with a collection of reaction terms as those mentioned above, and may also feature advection [45, 153]. Third, biomechanical models describe tumor growth in terms of the nonlinear volumetric deformation of the host tissue by leveraging a combination of poroelasticity and multiplicative splitting to separate the elastic and growth-dependent components of the deformation [21, 135, 142]. In these models, the constitutive definition of the main stretches in the growth deformation gradient introduces the description of tumor growth and therapeutic response using reaction-based formulations.

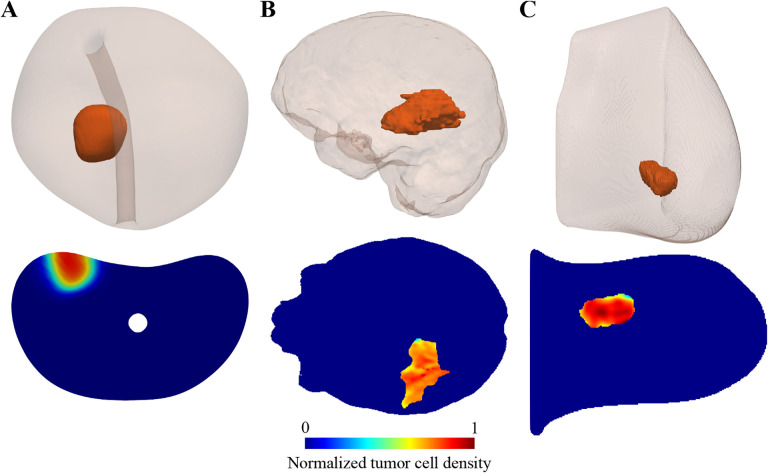
Figure 3: PDE modeling of tumor growth and treatment response.

This figure illustrates the outcome of three patient-specific PDE models that have been developed to predict prostate cancer growth during active surveillance (panel A) [92], response of high-grade glioma to chemoradiation (panel B) [57], and breast cancer response to neaodjuvant therapy (panel C; images courtesy of Dr. Chengyue Wu) [157]. Each panel shows a 3D visualization of the patient’s tumor within the affected organ on top, along with an axial section showing the map of normalized tumor cell density calculated with the PDE model.

According to the description of the three types of PDE models provided above, their formulation can accommodate the time-resolved terms appearing on the right-hand side of ODE models into reaction terms with a spatiotemporal definition. This feature enables the representation of intratumoral heterogeneities, for example, using proliferation maps calibrated from longitudinal imaging data [157, 57, 154], adjusting growth in terms of the local availability of nutrients or the local vascularization [122, 6, 94, 33, 59, 139], and characterizing therapeutic response based on the local tumor burden [165, 35, 157, 57], nutrient availability [6, 120], tumor-supporting vasculature [60, 57, 136], and drug concentration in the tissue [157, 142]. The description of these phenomena driving tumor growth can be further enriched by extending a baseline PDE model to include other key spatiotemporal mechanisms represented by additional PDEs, such as the effect of tumor-driven mechanical deformation of the host tissue and the effect of mechanical stress on tumor dynamics [57, 157, 94, 135, 6, 154], nutrient and drug transport in the tissue [142, 94, 45, 6], the production of key substances (e.g., angiogenic factors, matrix-degrading enzymes or biomarkers) [94, 136, 153, 142, 45], blood flow in the native vascular network [160, 45, 79], and the development of angiogenesis [160, 79, 59]. Similar to ODE models, PDE models can also adopt a multicompartmental formulation to accommodate several tumor cell types with different phenotypes or therapeutic response (e.g., normoxic, hypoxic, and necrotic cells; sensitive and resistant cells to a given treatment; surviving and irreversibly-damaged cells after a therapeutic dose) [136, 153, 122, 45], various non-tumor cell and tissue types (e.g., healthy cells, vascular tissue, extracellular matrix) [59, 79, 160, 153], as well as multiple solid and liquid phases included in the problem (e.g., interstitial water and extracellular matrix) [79, 135, 139, 6, 45, 153].

To illustrate the formulation of PDE-based models of tumor growth and treatment response discussed herein, let us consider the extension of the ODE model in Eq. 1 to a spatiotemporal framework given by

$$\frac{\partial N}{\partial t}=\nabla \cdot (\mathbf{\text{D}}\nabla N)+\rho N(1-\frac{N}{K})-\alpha N{U}_0\sum _i{e}^{-\beta (t-t_i)}\mathscr{H}(t-t_i).$$ (2)

In Eq. 2, the first term on the right-hand represents the mobility of the tumor cell density N(x, t) with a diffusion process governed by the tumor cell diffusivity tensor D(x,t), which can vary spatiotemporally (e.g., due to tumor-induced tissue deformation) or represent preferential directions of growth. The second and third terms on the right-hand side of Eq. 2 are reaction terms matching those in Eq. 1. However, now parameters governing tumor cell proliferation and drug effects may adopt a spatiotemporal definition (e.g., ρ(x, t), α(x, t)).

PDE models are primarily informed by imaging data that, if collected at several time points, provide a spatiotemporal characterization of the tumor dynamics enabling model initialization, calibration, and regular update. Anatomic imaging data types, such as CT, T1-W MRI, and T2-W MRI (with and without contrast), have been extensively used to define a computational model of the 3D geometry of the tumor and its host organ from their corresponding imaging-based segmentations [94, 89, 157, 57, 6]. These imaging data can also be employed to define spatial maps of mechanical properties for the different tissues or anatomic zones in the host organ [157, 57, 94]. Additionally, anatomic imaging data have been proposed to define tumor cell density maps, for example, by combining T1-W and T2-W MRI data [35] or using pre-contrast and post-contrast CT data [154]. Quantitative imaging data types can also provide measurements of tumor morphology, but these imaging types can further probe tumor biology properties that are not accessible with anatomic imaging. For example, ADC maps derived from DW-MRI have been used to define tumor cell density maps [157, 57, 92], while DTI constitutes the main data type to inform preferential directions of growth [49, 6]. DCE-MRI can inform the vascular compartments of the model (e.g., the main vascular network in the host tissue or tumor-supporting vasculature formed due to angiogenesis) [59, 156] as well as local perfusion, which can be leveraged as a surrogate for the relative availability of therapeutic agents and nutrients [157]. Additionally, DCE-MRI has also been proposed to perform tumor segmentation [59, 86, 157] and to define tumor cell densities of multiple tumor cell phenotypes according to nutrient availability [122]. PET data can provide a host of biological information to inform PDE models depending on the specificity of the radiotracer, such as tumor cell density maps [89], the local level of hypoxia to inform tumor cell radiosensitivity [120] and the tumor metabolic activity to inform proliferation rates [154]. In preclinical settings, while MRI and PET data can be collected from animal models [59, 73, 61], photoacoustic and microscopy imaging techniques also enable to collect spatially-resolved data from cell cultures and tissue samples [76, 160, 139]. Moreover, the spatial integration of the fields representing the location and amount of cellular types and the concentration of key substances over the host organ anatomy can provide scalar values comparable to common clinical measurements and key problem-specific quantities of interest (e.g., tumor volume, global cell counts, blood levels of a biomarker like PSA, global amount of a nutrient or a growth factor or vascularity) [94, 92, 160, 157, 57]. Hence, these scalar measurements, which traditionally inform ODE models, can also be used to constrain PDE models as well.

Therefore, the main advantage of PDE models is their ability to provide a robust and flexible description of tumor growth and treatment response at tissue and organ scale over timeframes ranging from weeks to years. Nevertheless, their mathematical formulation also introduces two main limitations. First, their numerical solution demands more computational resources. Hence, the comparatively larger computational cost of PDE models may require ancillary methods to accelerate their simulation in applications requiring an elevated number of model simulations, such as treatment optimization or uncertainty quantification [86, 98, 89, 93]. The usual approaches to overcome this limitation include the development of fast and problem-specific solvers, as well as the deployment of reduced order modeling or scientific machine learning techniques [93, 89, 3, 144]. Second, PDE models that operate at tissue scale cannot resolve mechanisms specifically happening at cellular scale (e.g., cell-cell-interactions, asymmetric cell division, epithelial to mesenchymal transition, multiple phenotypes evolving with the local microenvironment and applied therapy). To address this limitation, hybrid multiscale models can introduce discrete agents in PDE models to characterize some of these cell-scale mechanisms at tissue scale (e.g., tip endothelial cells driving angiogenesis, epithelial to mesenchymal transition, taxis phenomena); see [160, 142, 37, 163].

3.3.3. Limitations

Beyond the limitations discussed thus far, the mathematical models described in this section are inherently constrained by the hypotheses underlying the formulation of the mechanisms participating in the model. These assumptions ultimately govern the number of parameters, variables, and equations constituting the model formulation and characterizing its complexity. Ideally, the complexity of ODE models and PDE models should be balanced with the spatiotemporal availability of data required to robustly calibrate them and render meaningful and accurate predictions. Model selection techniques can identify the optimal model formulation among a pool of candidates with increasing model complexity [57, 93, 86]. Preliminary models to describe a specific type of tumor growth or therapeutic response usually start with a simple formulation capturing essential mechanisms (e.g., tumor cell mobility and net proliferation). The analysis and comparison of model simulations and available datasets can then reveal potential mechanisms that play a driving role in tumor growth and treatment action. Hence, the model can be extended to include these mechanisms, provided that there exists sufficient data to still perform a robust calibration of the new model. This path towards mechanistic model discovery has paved the way to several model hierarchies, which provide an increasingly deeper insight in the biophysical processes underlying tumor growth and therapeutic response [93, 86, 57]. Additionally, the recent application of machine learning techniques to model discovery has resulted in data-driven methods capable of identifying the mathematical formulation of ODE and PDE models [101, 25], which show promise to identify hidden mechanisms underlying tumor and therapeutic dynamics as well as to improve model selection.

4. MECHANISTIC MODELS ALLOW FOR OPTIMIZING INTERVENTIONS

Multiple patient-specific mechanistic models have been shown to enable the personalized forecast of tumor growth and therapeutic response. Thus, these models provide an practical in silico framework to investigate alternative monitoring and treatment strategies to those prescribed initially to each individual patient [93, 89, 91, 24]. In particular, these models could be exploited to perform an n=1 clinical study, where the outcomes of a range of clinical interventions are quantitatively assessed using computer simulations of the personalized model to rigorously and systematically optimize the monitoring and treatment of each patient’s tumor. In this section, we discuss two approaches that have shown promise to achieve these challenging goals: optimal control theory (OCT) and digital twins.

4.1. Optimal control theory

OCT is an established framework to optimize the state of a dynamical system through the action of external forces, which are systematically adjusted to achieve a particular goal of interest [84, 93, 124]. The dynamics of the system is described by means of a mechanistic model, whose main variables are termed state variables, while the external forces are termed controls or control variables. The calculation of the controls is governed by the minimization of a functional involving quantities of interest calculated in terms of the state and the control variables. This optimization problem is posed over a certain timeframe of interest, such that the terms in the functional can be calculated over the whole time period via (spatio)temporal integration to introduce the desired target dynamics. The functional terms can also be posed at the time horizon to define their terminal target value (i.e., an endpoint control). In the first case, the integrand usually features a linear or a quadratic formulation. The linear case leads to controls that switch between their minimum and maximum admissible value (i.e., a bang-bang control), whereas the quadratic case results in controls that smoothly adjust their value within their admissible range to the dynamics of the state variable (i.e., a continuous control). While the admissible range of the controls determines their minimal and maximal value at each timepoint, the OCT problem may further feature an isoperimetric constraint that limits the total value of a control variable over time.

In the context of cancer, OCT has been employed to find optimal treatment regimens that maximize tumor control with minimal toxicities [84, 93, 124]. Since these OCT applications have been mainly developed at tissue or organ scale, they usually rely on mechanistic models that are posed in terms of ODEs and PDEs. The state variables usually correspond to the tumor volume [87, 19], the total tumor cell count [93], the tumor cell density [35], the tumor phase field [33], and key substances related to tumor dynamics [33, 63]. The control variables can represent the treatments (e.g., the radiation or drug dosage delivered in each treatment session) [35, 87, 63] or their dose-dependent effects on tumor dynamics (e.g., therapeutically-induced tumor cell death) [33, 22, 124, 19]. Regarding the formulation of the functional, the endpoint terms usually aim at minimizing the tumor burden at the prescribed time horizon [33, 22, 19, 124], although this goal can also be achieved dynamically over the OCT problem timeframe by leveraging (spatio)temporally-resolved integral terms [33, 22, 63, 87]. A clinically-admissible dosage range is usually defined to limit the amount of treatment delivered in every instant (e.g., the radiation or drug dose fraction) [35, 33, 19], and the OCT functional usually incorporates additional (spatio)temporally-resolved integral terms that seek to minimize the total dosage under the optimal regimen [33, 87, 124]. Additionally, isoperimetric constraints can further bound the total amount of a therapeutic agent delivered over the OCT problem timeframe [87, 84, 19]. Figure 4 provides an example of the OCT framework in the context of designing optimal, personalized chemotherapy regimens.

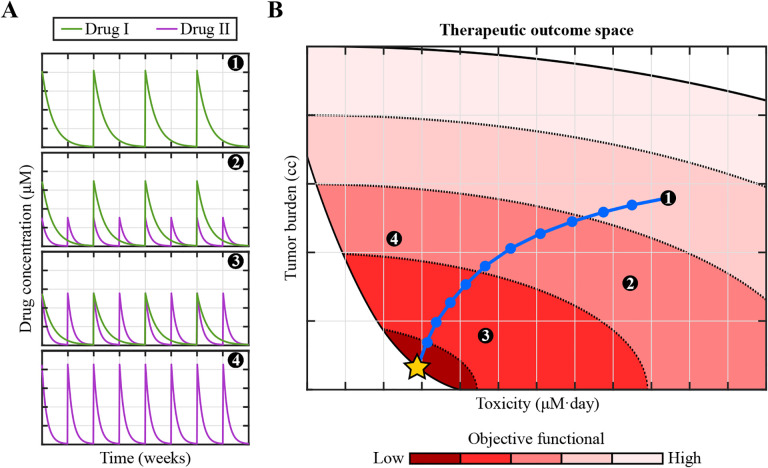
Figure 4: Optimal control theory enables the design of personalized cancer treatments.

Let us assume that we have a validated, personalized mechanistic model of tumor growth and treatment response. The standard-of-care treatment for this tumor consists of chemotherapy using drug I (delivered every two weeks), drug II (delivered weekly), or a combination of both drugs. (A) Temporal changes of the concentration in blood of either drug during the course of four illustrative standard-of-care chemotherapeutic regimens. (B) Space of therapeutic outcomes spanned by the tumor burden (e.g., the tumor volume) and the treatment toxicity (e.g., the total cumulative exposure to both drugs) calculated at a fixed time after the conclusion of chemotherapy by leveraging the personalized mechanistic model for any admissible combination of drugs I and II [67, 33, 156]. An objective functional combining the tumor burden and the toxicity further assesses the performance of each treatment regimen (color mapping in panel B), such that low values of this functional identify treatments achieving large tumor burden reductions while entailing low toxicity. OCT usually involves an iterative algorithm whereby, starting from a standard-of-care regimen, each iteration adjusts the treatment towards an improved performance. The iterative strategy is represented by circles in the blue path, which starts in standard-of-care regimen 1 and ends in the optimal treatment for this scenario (golden star).

Several studies have shown that OCT is a promising framework to maximize treatment outcomes while minimizing the amount of therapeutic agents delivered to the patient, thereby minimizing potential toxicities and side-effects. For example, OCT has been leveraged to investigate optimal radiation plans for glioblastoma [35], optimal combinations of cytotoxic and antiangiogenic therapies in solid tumors at the metastatic stage [19] and advanced prostate cancer [33], optimal combinations of chemotherapy and HER2-targeted therapy for HER2+ breast cancer [87], optimal hormonal treatments for advanced prostate cancer [63], and optimal drug regimens for neodjuvant chemotherapy of locally advanced breast cancer [156]. Nevertheless, a main limitation of OCT is that the resulting optimal control variables may correspond to therapeutic regimens that are not possible to achieve in the clinic. For example, the on-off treatment regimen resulting from a bang-bang control may require maintaining a maximal concentration of a therapeutic for unfeasible times, while the smooth concentration dynamics obtained with a continuous control may not correspond to any known and clinically-validated therapeutic agent [33, 22, 93]. Mathematical adjustments to the problem formulation may contribute to palliate these issues, such as defining the control as a timepoint therapeutic agent source within an ODE or PDE modeling its interaction with tumor dynamics and its natural decay [87, 63]. Alternatively, if the eligible treatments for an individual patient constitute a limited set of options, the OCT framework can be employed to evaluate each of them separately and choose the one rendering best results in terms of tumor control and total dosage of the therapeutic agent [156]. Additionally, OCT can also be applied in a two-step strategy, whereby the resulting theoretical controls can serve as basis to define clinically feasible optimal therapies achieving comparable treatment outcomes as the parent OCT solution [33, 22]. In the future, the development of new biochemical technologies enabling the control of local delivery and tissue concentration of drugs [31, 38] as well as the production of therapeutic drugs with pharmacokinetics and pharmacodynamics tailored to each individual patient [65, 126] may open a new opportunity to apply OCT for the personalized design of treatment regimens. However, the clinical translation of OCT frameworks will still constitute a dramatically bigger challenge than that of patient-specific models for tumor forecasting because OCT would produce novel treatment regimens that may have not been assessed within a clinical study. Hence, the computationally-derived therapies obtained via OCT would require a close monitoring to control treatment response, toxicity, and the well-being of every patient in the treatment arm, which can be extremely difficult to balance and maintain during a clinical study.

4.2. Digital twins

A digital twin can be defined as a virtual representation of a physical object (e.g., a human organ) by means of a computational model that is continuously informed by object-specific measurements to enable decision-making about the physical object based on its current and future status (e.g., health or response to external agents) [103, 158, 118, 137]. The initial setup of a digital twin usually requires data characterizing the properties of the constituents of the physical object (e.g., physiological features or geometry). Then, periodic or continuous measurements of the physical object status enable the updating of the parameterization of the computational models at the core of the digital twin and, hence, assess the integrity and quality of performance of the physical object. Computational forecasts obtained with the updated models enable the projection of the behavior of the digital twin in the future, which can inform about potential adjustments to the physical object operation that are required to optimally maintain its health and satisfactory performance. Likewise, the response of the physical object to external actions can be optimized by further exploiting the computational forecasts of the underlying models (e.g., the delivery of a drug to control the tumor). Central to the construction of a digital twin is the selection of metrics that robustly and accurately characterize its status and performance. These metrics need to be readily calculated from the computational models by using the measurements from the physical object and serve in the decision-making process. Probabilistic digital twins cast these technologies in a Bayesian framework that enables to account for the uncertainty in the incoming data and model predictions [75, 158], thereby allowing for a richer risk-based optimization of the physical object status and performance than digital twins based on deterministic approaches.

In the context of medicine, digital twins have been developed to address several procedures [103, 158], such as the planning of surgeries and interventions [96, 26, 103, 34], the convection-enhanced delivery of drugs to treat brain tumors and neurological disorders [155, 150], and the control of blood levels of glucose in diabetic patients [125, 82]. The success of biomechanistic models to recapitulate and predict the growth and treatment response of different types of tumors in individual patients motivates the development of digital twins for applications in clinical oncology [158, 56]. In particular, digital twins have been proposed as a promising computational environment to effectively translate these models to the clinic and guide biological discovery in the preclinical setting. For instance, preliminary efforts have shown the application of digital twins in monitoring and predicting the response of breast cancer to neoadjuvant therapy in individual patients [157], experimental planning to investigate the mechanical cues underlying tumor growth in vitro [139], and investigating the combination of chemotherapy and antiangiogenic therapy in xenograft animal models [52]. As an example, Fig. 5 provides an overview of a prototype of a digital twin to optimally monitor and design neaodjuvant chemohterapy for breast cancer. In the future, increased access to data and computational resources may contribute to the development of these pioneering digital twin prototypes towards a technology that can be assessed in a clinical trial for its ultimate deployment as a predictive, personalized decision-making technology to guide the oncological management of tumors [158, 56].

Figure 5: Digital twins provide a practical computational framework to optimally manage cancer monitoring and treatment on a patient-specific basis.

Personalized digital twin framework for neoadjuvant chemotherapy (NAC) of breast cancer [157, 158]. The physical twin represents the patient’s tumor and the host organ, while the digital twin consists of a model that describes the spatiotemporal dynamics of tumor growth and treatment response. The formulation of the digital twin requires the definition of three key quantities in the physical space and another three key quantities in the digital space. First, the physical state (S_i) describes the physiology and local anatomy of the patient at time t_i. The only information available on the physical state is provided by the observational data (O_i), which offer a limited and indirect assessment of the physical twin (e.g., via imaging, biomarker, and omics data). The calibration of the model constituting the digital twin to the observational data enables the determination of the digital state at time t_i (D_i). The calibrated model enables the calculation of quantities of interest (Q_i) for the design of each therapeutic cyle of the treatment (e.g., terminal total tumor cell count or volume, toxicity or time to progression). The rewards (R_i) quantify the performance of a candidate therapeutic regimen on the basis of the current observational data, digital state, and the corresponding quantities of interest. The formulation of the rewards usually enables the definition of an optimization problem to find the best treatment plan for each patient, which would then be delivered to the patient as a control input (U_i). Finally, the digital twin can be progressively updated as new data from the patient becomes available, which would enable the personalized adjustment of the treatment plan to optimize therapeutic outcomes. The image for the physical twin was created using BioRender, and the image of the digital twin is courtesy of Dr. Chengyue Wu.

5. MECHANISTIC MODELS INCORPORATING AI

Given the limitations of stand-alone AI and mechanistic models, it is essential to consider the potential of combining both approaches. This opens up new avenues for improved understanding of tumor growth and development of personalized treatment strategies [98, 18, 57]. Below we describe a few possibilities to incorporate AI into mechanistic models.

5.1. Parameter identification and initialization

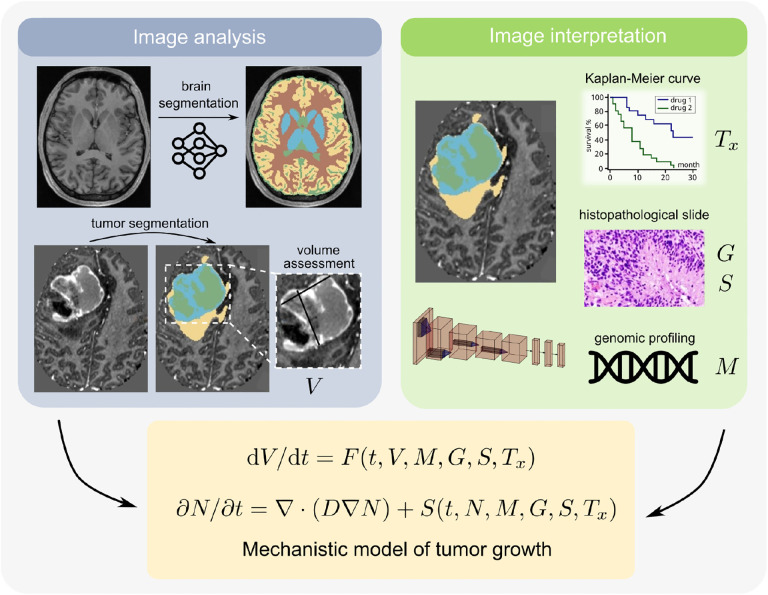
One key drawback of AI and machine learning approaches designed to assess tumor growth and dynamics is overfitting to the training set, which can be largely attributed to a combination of sparse clinical data that is limited by a patient’s presentation, and suboptimal methodological approaches. Solid tumors exhibit substantial inter- and intra-tumor heterogeneity, and AI models frequently fail to capture the full complexity and extent of this heterogeneity. This can be addressed by generating patient-specific, mechanistic models of tumor dynamics which are initialized and parameterized by data obtained using deep neural networks trained on a larger training set. These parameters could be the volumetric quantification outputs of deep learning segmentation models, as well as classification models designed to identify other contributors to tumor growth and regression, which may include but are not limited to oncogenic driver/molecular marker status of tumors, any therapeutic treatment administered and the corresponding dose response, as well as the grading and staging of disease; see Fig. 6. A wide range of input data can be utilized to identify these parameters, such as genetic profiles, imaging results and clinical history. The parameters can be fed into a mechanistic model based on ODEs [20, 165] or PDEs [157, 57, 93]. Upon training on a sufficiently large dataset, these segmentation or classification networks can be used to run inference on individual patients, and generate initial patient-specific parameters for the mechanistic models. The mechanistic models can subsequently be run to forecast tumor growth at various time points, as well as assess treatment response and shed light on other diagnostically and prognostically meaningful variables. This integration allows for more personalized tumor growth predictions and treatment planning that accounts for inter-patient variability.

Figure 6: Initializing mechanistic models with parameters from AI models.

Potential approach to combine mechanistic models with AI models in a clinical scenario relevant to brain cancer. We propose to utilize trained glioma segmentation models [110] for volumetric quantification of tumors [left], while classification networks can be used for oncogenic driver/molecular marker status prediction (M), histopathological grading and staging of the neoplasm (G, S), and assess treatment response (Tx) [right]. Each of these can serve as parameters and inputs to the patient-specific mechanistic model, which can take the form of and ODE or a PDE.

5.2. Surrogate modeling

Surrogate models serve as approximations of complex mechanistic models and are particularly useful (1) when fast solving is required due to minimal time, and (2) when many simulations are required, such as in the case of conducting uncertainty analyses [133]. AI and deep learning can be utilized to develop surrogate models that approximate the behavior of mechanistic models. These surrogate models can be trained on the outputs of mechanistic models, which enables the AI model to learn the mapping between the input parameters of the mechanistic model and the corresponding mechanistic model predictions. The recent explosive growth of neuro-symbolic AI [48] is particularly relevant in the context of surrogate modelling: architectures such as transformers [77, 138] offer both predictive accuracy and computational efficiency that are crucial elements to creating a surrogate model. Once trained, surrogate models can provide tumor growth predictions or conduct extensive simulations with prognostic value.

In the first case, a critical situation where fast solving is essential is in surgical procedures, where quick tumor growth predictions are required to inform surgical decision making. Surrogate models can quickly generate predictions of tumor response to different therapeutic interventions, enabling real-time decision-making. These predictions can subsequently be used by surgeons to guide their specific surgical approach and optimize patient outcomes.

Uncertainty analysis, in the oncology space, involves quantifying the impact of uncertain parameters on tumor dynamics. In situations where uncertainty analysis or sensitivity analysis requires running multiple simulations, AI models can be used to construct surrogate models that can efficiently handle the computational load. Conceptually, this is analogous to the creation of a digital twin [158] with the notable difference that the computations are performed by a neural network. AI models can also enhance the efficiency of uncertainty quantification methods such as Monte Carlo simulations or optimization algorithms.

The effectiveness of surrogate models relies on the availability of high-quality data and accurate mechanistic models. Sufficient training data, covering diverse patient cases, is necessary to ensure that surrogate models capture the heterogeneity of tumor growth. The underlying mechanistic models also need to be carefully validated and refined to accurately represent the corresponding biological processes. Ultimately, the integration of AI and mechanistic models requires individuals with expertise in both domains to come together and effectively optimize their interactions.

5.3. Biology-informed neural networks

Recent research has shown that AI algorithms have achieved a noteworthy level of success predicting patient outcome and other prognostic endpoints using sequences of longitudinal images for a single patient [161]. However, longitudinal images for a single patient are rarely available in standard-of-care cancer protocols, and it is unlikely that they will become available in the near future. One way to alleviate this challenge is combining these purely data-driven approaches with a biomechanistic model. Physics-informed neural networks (PINNs) [116], and their extension to medical sciences, namely biology-informed neural networks (BINNs), [80, 81] constitute an ideal mathematical framework to accomplish this combination. The recent emergence of recurrent neural networks in medical sciences [161] offers an opportunity for the development of BINNs that couple machine learning with evolutive mechanistic models based on PDEs. For example, the recurrent neural network illustrated in Fig. 1 could be enhanced by adding to the loss function a term that penalizes deviations from solutions to a biomechanistic PDE with uncertain parameters. We believe this is a very promising area of future research. The framework of BINNs can also be exploited to the discovery of hidden biomechanistic PDEs following an approach similar to that illustrated in [116].

6. FIVE FUNDAMENTAL CHALLENGES

6.1. Predicting metastasis

Despite major advances in cancer diagnosis and treatment, the vast majority of cancer deaths are the result of metastatic disease [130, 7, 152]. During metastasis, tumor cells interact with multiple distinct microenvironments to facilitate the process of leaving the primary tumor site and forming discontinuous secondary masses. Due to the high morbidity rate, there has been a growing emphasis on developing model systems that specifically study metastasis. However, many of these model systems equate the process of cell motility and invasion to metastasis. This assumption is incorrect [54]. Recent studies have demonstrated that cells with high invasive capacity typically are only capable of seeding distal tissues and are not capable of completing the metastatic cascade [54, 74, 127]. It is becoming increasingly clear that models must account for cellular plasticity to predict metastasis. To help bring clarity to this issue 4 key hallmarks of metastasis have recently been defined and include [149]: (i) the ability to modulate both the secondary premetastatic site and the local primary tumor microenvironment, (ii) cellular plasticity, (iii) motility and invasion, and (iv) the ability to colonize new tissues [149]. The need to understand the dynamics at both the primary site and metastatic site creates a data challenge in that metastatic tissues are not commonly collected from patients, which limits the ability to use omic-based approaches to study the dynamics of the tissue. Furthermore, metastasis is a rare event, which limits the pool of cell lines and animal model systems available for data collection. Recent advances in microphysiological systems [143, 146, 42] and ex vivo cultures [71] provide a promising route in which the dynamic events that occur during metastasis can be studied under controlled setting to inform in silico models. These platforms allow for systematic evaluation of cellular heterogeneity [127, 95, 128], tissue histological factors that affect migration [113] as well as mechanical forces within metastatic tissues and their effect on cell seeding and colonization [42].

6.2. Reliability of the predictions

The last few decades have witnessed an increase in the sophistication of computational tumor models which has been driven by the growth of our scientific understanding of tumor biology and computer power. Transferring highly-complex models to the clinic requires very high levels of model reliability and robustness. To ensure reliability in safety-critical applications like treatment planning, uncertainties in parameters, initial and boundary conditions, numerical approximations as well as the natural stochasticity of the system must be quantified. Uncertainty quantification techniques, including sensitivity analysis, parameter estimation, Bayesian inference, probabilistic modeling, and Monte Carlo simulations, help assess reliability, explore outcomes, and estimate confidence intervals [24, 166]. In tumor growth modeling, uncertainty quantification aids in understanding model limitations and uncertainties, improving decision-making in treatment planning, and guiding prognosis assessment. It also enhances model robustness and generalizability, driving refinement and improvement of modeling approaches.

6.3. Practicality of the predictions

There are several key barriers on both the computational and clinical fronts that limit practical or clinically-actionable predictions. On the computational front, predictions based on medical imaging currently require multiple manual or semi-automated steps to prepare patient data for modeling. These steps include tumor and tissue segmentation, verification of image registration, definition of the computational domain, and incorporating clinical notes and treatment schedules. Although automated approaches could potentially be used for many of these tasks, their ability to handle variations in data quality, data type, and treatment effects need to be demonstrated. An additional computational challenge is calibration and personalization of mathematical models of tumor growth in a timely fashion. Depending on the number of parameters, the size of the computational domain, and the calibration approach, models could take greater than a day for a single calibration [68]. Reduced order modeling approaches have the potential to address this barrier [17].

On the clinical front, it is crucial for model predictions of optimal therapeutic regimens be made available within a clinically-actionable time frame. These predictions should also recommend regimens that are reasonable for patients to complete and can be readily integrated into clinical workflows. Moreover, while confidence in the use of mathematical modeling in the guiding of patient care is growing, it is important for models to recommend optimal regimens that do not deviate greatly outside of what clinicians would typically select or are comfortable for delivering. Thus, close collaboration with clinicians from the earliest stages of a given study is absolutely required. Radiotherapy provides guidance on how to proceed as there are many approaches for personalizing dose maps based on imaging data [66]; for example, potential treatment regimens could be limited to dose escalation or de-escalation simply within the tumor region of interest rather than deviation from the standard-of-care treatment schedule.

6.4. Incorporating multiscale data into models

We contend that in the next decade, tumor modeling will continue to be driven by data availability. Arguably, the most successful models will be those with greatest ability to integrate more data types consistently in a reliable and systematic manner. Genomic, proteomic, microscopy and imaging data have different nature and come at different length scales which poses a formidable task to modelers. Models that incorporate all these data types will necessarily be complex and difficult to interpret. The lack of interpretability is inherent to multiscale models with emerging behavior that arises from the interactions between components at different scales. These emergent properties may not be directly observable or intuitive at individual scales, making it difficult to identify and transfer the underlying mechanisms that give rise to them. Therefore tumor models incorporating multiscale data will require extensive validation, verification and uncertainty quantification. Also, the standard approach to determine model parameters in engineering and physics has been to design a specific experiment that would reveal the value of a single parameter. This strategy is likely to be unsuccessful in tumor models that incorporate multiscale data. However, given the current progress in inverse problems fueled by machine learning, we envision algorithms capable of identifying all parameters at once, given large amounts of data. Another critical challenge to be overcome is finding an adequate scale separation and a systematic way to transfer data and model outputs across scales.

6.5. Consistency and bias

A desirable characteristic of any predictive model is consistency of predictions. Consistency, or repeatability refers to the ability of a model to generate near-identical predictions for the same patient under identical conditions, ensuring that the model produces precise, reliable outputs in the clinical setting. AI models in the existing literature frequently suffer from a lack of reliability due to overfitting: multiple images obtained from the same patient under similar or identical settings tend to result in different model outcomes. A number of approaches have been utilized to address this concern, such as dedicated optimization of models for repeatability [1], loss function optimization [2], and Monte Carlo (MC) dropout [83]. Linking AI model predictions with patient-specific, mechanistic models can make modeling of tumor dynamics more patient specific and thus more consistent within each patient.

Another key concern with AI and “big data” is the issue of bias. Frequently, training data is not representative of patient-level heterogeneity or variability that is encountered with real-world clinical data. Recent work has reported systemic biases in AI model predictions and lead to categorically biased recommendations [50, 104]. Given that AI model recommendations are intended to be a part of clinical-decision making flow-diagrams, an incorrect, unreliable or biased model prediction would lead to a particular cascade of undesirable downstream clinical actions, that might significantly jeopardize the health and safety of a patient, and put their lives at risk. Combining patient-level mechanistic models with AI model predictions addresses the issue of bias to some extent by accounting for the patient-level heterogeneity. However, the AI models that are used for parameter initialization or as surrogate models can still output biased predictions, if not trained on a sufficiently large and multiply heteregoneous dataset.

DEEP LEARNING SEGMENTATION WITH nnU-Net.

The nnU-Net is a segmentation method that utilizes deep learning to automatically adapt to new tasks by configuring various components such as preprocessing, network architecture, training, and post-processing. The process involves incorporating fixed parameters, interdependent rules, and empirical decisions to make key design choices. By initially extracting the “dataset fingerprint” and applying heuristic rules, nnU-Net generates three distinct configurations of U-Net: a 2D U-Net, a 3D U-Net operating at the original image resolution, and a 3D U-Net cascade. In the cascade, the first U-Net operates on down-sampled images, and the second U-Net is trained to enhance the segmentation maps produced by the first U-Net at full resolution [64].

GROWTH OF NEURO-SYMBOLIC AI.

Symbolic machine learning involves the manipulation of symbols during a discrete search process to find the optimal representation for solving a specific classification or regression task. By combining neural and symbolic AI architectures, neuro-symbolic AI aims to tackle the inherent strengths and weaknesses of both approaches. This integration results in a robust artificial intelligence system that possesses the ability to reason, learn, and perform cognitive modeling tasks effectively. Large language models (LLM) such as GPT-3 utilize neuro-symbolic AI, which uses transformers as their architecture.

Transformers:

Transformers employ a self-attention mechanism to capture contextual relationships between words or tokens, enabling them to generate high-quality language representations. They have become the backbone of numerous Natural Language Processing (NLP) applications, computer vision and multi-modal processing, and have been prevalently adopted as the state-of-the-art architecture for training LLMs.

IMPROVING REPEATABILITY OF DEEP LEARNING MODELS.

Recent work has shed light onto the importance of consistency and repeatability of deep learning model predictions as a crucial and optimizable task [1, 2, 83]. Model hyperparameters such as the loss function and the model architecture can be chosen based on model performance on key repeatability metrics such as weighted kappa [32]. In particular, recent work has shown that focal loss, which is a modulated form of cross-entropy loss, and Monte Carlo dropout [2, 83], which is a model regularization technique involving training and testing a neural network with dropout, can improve repeatability of model predictions.

SUMMARY POINTS.

1. Mechanistic or biology-based models of tumor growth and responseprovide “interpretable” model predictions whose model parameters are rooted in the key components of tumor biology.

2. AI has shown success in cancer diagnosis and treatment responseassessment, but models are complex and lack interpretability.

3. Quantitative medical imaging techniques are clinically feasible and report on underlying tumor biology.

4. Optimal control theory can be applied to enable the design of personalized cancer treatments that balances multiple constraints.

5. Digital twin approaches can be to applied optimally manage cancermonitoring and treatment on a patient-specific basis.

6. AI approaches, such as deep learning segmentation and radiogenomicclassification, can be used to identify and initialize input parameters for mechanistic models.

7. AI models can serve as surrogate models that approximate the behavior of mechanistic models, particularly when fast solving is required and when many simulations need to be performed (e.g., for uncertainty analysis).

8. While the combination of AI with mechanistic models represents apromising advance, limitations such as metastasis prediction, multiscale data incorporation, lack of consistency, and bias need to be considered.

Glossary

AI

Artificial Intelligence

CAD

Computer Aided/Assisted Diagnosis

ATR-TFIR

Attenuated Total Reflection Fourier Transform Infrared

MRI

Magnetic resonance imaging

PET

Positron Emission Tomography

DW-MRI

Diffusion weighted MRI probes water diffusion

DCE-MRI

Dynamic contrast-enhanced MRI measures tissue perfusion and permeability

scRNA-seq

Single-cell RNA sequencing, a powerful tool for studying gene expression at the level of individual cells

HER2

Human epidermal growth factor receptor 2; overexpression is associated with breast cancer invasiveness

BraTS

Multimodal Brain Tumor Segmentation Challenge

Radiomics

A data-driven approach for extracting features from imaging data

RANO

Response Assessment in Neuro-oncology

Radiogenomics

Methodology that combines radiomics features from medical images with genomic data from high-throughput sequencing

CNN

Convolutional Neural Network

RNN

Recurrent Neural Network

ADC

Apparent diffusion coefficient; measure of water diffusion from DW-MRI

T1-W MRI

T1-weighted MRI anatomical image

T2-W MRI

T2-weighted MRI anatomical image

PSA

Prostate-specific antigen, a biomarker of prostate cancer

DTI

Diffusion tensor imaging; an imaging technique that measures anisotropic diffusion of water in tissue