Abstract
Antimicrobial peptides (AMPs) are a promising alternative to antibiotics for mitigating bacterial infections, in light of increasing bacterial resistance to antibiotics. However, predicting, understanding, and controlling the antibacterial activity of AMPs remain a significant challenge. While peptide intramolecular interactions are known to modulate AMP antimicrobial activity, peptide intermolecular interactions remain elusive in their impact on peptide bioactivity. Herein, we test the relationship between AMP intermolecular interactions and antibacterial efficacy by controlling AMP intermolecular hydrophobic and hydrogen bonding interactions. Molecular dynamics simulations and Gibbs free energy calculations in concert with experimental assays show that increasing intermolecular interactions via interpeptide aggregation increases the energy cost for the peptide to embed into the bacterial cell membrane, which in turn decreases the AMP antibacterial activity. Our findings provide a route for predicting and controlling the antibacterial activity of AMPs against Gram-negative bacteria via reductions of intermolecular AMP interactions.
Antimicrobial peptides (AMPs) have received much attention in light of increasing antimicrobial resistance to common small-molecule antibacterial drugs. AMPs exhibit unique modes of antibacterial action and can even be effective against certain antibiotic-resistant bacterial strains.1,2 AMPs interact with and embed into bacterial cell membranes,3 leading to bacterial death. Recent research on AMPs has centered on structure–function relationships,4,5 and studies found that properties of individual peptides, such as hydrophobicity, charge, and amphipathicity, can affect the activities of AMPs. In addition to the intrinsic properties of individual AMPs, intermolecular interactions between AMPs could also affect antibacterial activity of the resulting peptide formulation. For example, amyloid-β peptide, a natural antibiotic that protects the brain from infection,6 kills bacteria in its monomeric form, but antibacterial activity is lost when high-order peptide oligomeric aggregates are formed.7 Evidence such as amyloid-β loss-of-function upon oligomerization exemplifies the need to consider interpeptide interactions in the design of AMPs. However, the relationships between the intermolecular properties of AMPs (eg., self-aggregation) and antibacterial activity remain elusive.
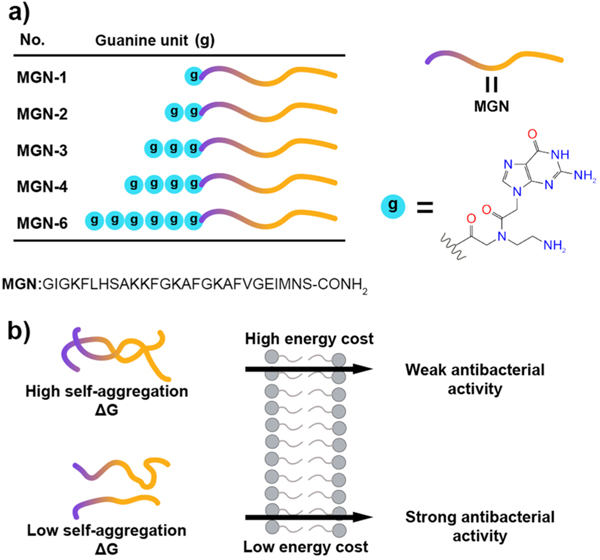
Theoretical studies have recently shown that AMPs have an increased propensity to assume random coil configurations in solution with a low tendency to have a defined structure, when compared to non-AMPs.8 Thus, theory suggests that AMPs have a higher propensity for nonspecific intermolecular interactions that could lead to oligomerization and aggregation. As such, we explored the relationship between peptide aggregation propensity and the resulting antibacterial activity of AMPs with parallel theoretical and experimental studies. To this end, we chose magainin II (MGN) as our model AMP to study the relationship between self-aggregation and antibacterial activity. MGN II is a naturally occurring polypeptide that binds to the bacterial membrane and kills bacteria by disrupting membrane integrity.9 Evidence suggests peptide self-aggregation is mainly determined by intermolecular interactions such as hydrogen bonds, electrostatic forces, hydrophobic interactions, and π–π stacking.10 Therefore, fine-tuning the self-aggregation propensity of AMPs requires precise control over these interactions. We chose to test the effect of peptide self-aggregation on MGN II antimicrobial activity by controlling intermolecular interactions between individual MGN II peptide units. On the basis of our previous work,11 guanine was chosen as an ideal monomer for linking MGN II peptides together via hydrogen bonding and hydrophobic interactions between peptides.12 This strategy allows us to test MGN II activity without disrupting the native MGN-2 sequence, while promoting interpeptide aggregation through interguanine interactions. To test our hypothesis, we developed a strategy in which 1 through 6 guanine units were synthesized into to the N-terminus of the MGN II peptide (Figure 1a) to generate MGNs with different self-aggregation propensities based on the different numbers of N-terminal guanine units. We hypothesized that increased peptide self-aggregation propensity decreases the AMP’s antibacterial activity, which can be explained by the increased energy cost of the peptide embedding into the cell membrane (Figure 1b). For an AMP to embed into the cell membrane, it must overcome interactions with itself and with other peptides, and these self- and cross-interactions may significantly affect the internalization propensity of peptides and thus their antibacterial activities.
Figure 1.
(a) Guanine-modified peptides were studied as an AMP self-aggregation model. Different numbers of guanine units were attached to the peptide N-terminus as shown. Cyan balls represent guanine units. MGN represents magainin II. (b) The relationship between self-aggregation, and aggregation Gibbs free energy, of AMPs and their antibacterial activities.
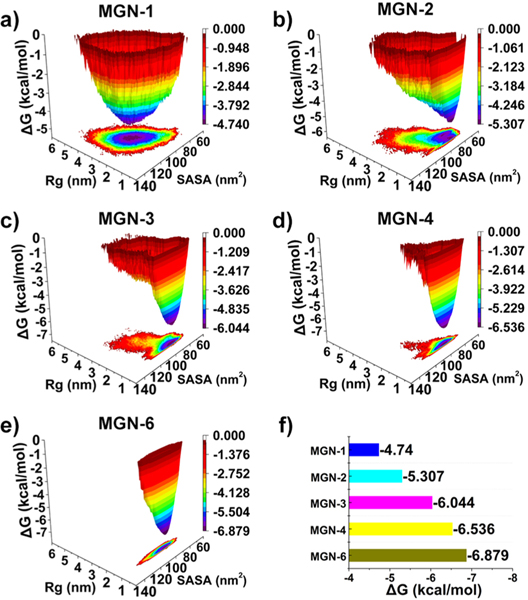
To test our hypothesis, molecular dynamics (MD) simulations were performed to compare the aggregation Gibbs free energy difference between Guanine-tagged antibacterial peptide systems with differing aggregation propensities. Comparing the aggregation Gibbs free energy difference between peptides with small sequence differences is normally a very challenging task; thus we implemented a simple but effective strategy inspired by DNA denaturation.13 At higher temperatures, more stable aggregates are less likely to disaggregate. For the unmodified MGN II peptide and the guanine-modified MGNs, a rapid decrease in solvent-accessible surface area (SASA) indicated the formation of aggregates (Figures S1 and S2a). We observe that, MGN-1, similar in structure to the unmodified MGN II peptide, can quickly disaggregate, as evidenced by the further increase in SASA. Wide fluctuations in SASA usually suggest the aggregates are not stable, while small SASA fluctuations indicate relatively high interpeptide stability.14 To visualize the detailed structures of the self-assembled AMPs, cluster analysis was applied to obtain the structure with the highest probability for each system. As shown in Figure S2b, guanine units of MGN-1 mostly interact with MGN-II peptide sequence scaffolds. For the other guanine-tagged MGN peptides, guanine units interact with each other via hydrogen bonding and hydrophobic interactions promoting inter-peptide interactions. Next, we plotted the free energy landscape of the system using the radius of gyration (Rg) for guanine units and SASA values for the peptides (Figure 2a–e). The free energy landscapes show that increasing the number of guanine units narrows the free energy wells, indicating that peptide aggregates become more compact with increasing guanine content. For stable assemblies, the Rg of guanine units adopt a narrow distribution, while the distribution of SASA values is wide, suggesting guanine units form a stable core within the aggregate, while the MGN-II peptide forms a surrounding shell that is relatively flexible. Increasing the number of guanine units decreases the self-assembly Gibbs free energy from −4.740 kcal/mol to −6.879 kcal/mol (Figure 2f), indicating that the aggregated state becomes increasingly stable with increasing number of guanine units. As such, our MD simulations establish a quantitative relationship between the aggregation propensity of peptides and the calculated aggregation Gibbs free energy of MGNs.
Figure 2.
(a–e) Free energy landscape of the MGNs as a function of radius of gyration (Rg) for guanine and solvent-accessible surface area (SASA) of MGNs. (f) Aggregation Gibbs free energy of MGNs.
We synthesized guanine-tagged peptides to study MGNs experimentally. Peptides were synthesized by solid phase peptide synthesis (SPPS)15 and purified by high-performance liquid chromatography (HPLC; Tables S1–S5; Figures S3–S7). Circular dichroism (CD) spectra (Figure S8) show that the MGNs self-assemble, as evidenced by the negative Cotton effect at ∼230 nm.16 In the near-UV region (240–320 nm), CD signals mainly reflect guanine–guanine interactions and guanine–MGN II peptide interactions.17 For MGN-6, guanine units are most likely to form G-quadruplexes due to strong interactions between guanine units.18 Overall, the results of CD experiments are in good agreement with our MD simulations.
Next, antibacterial assays were carried out as described previously for AMPs19 to investigate the antibacterial activities of the guanine-modified MGNs. MGN-1 displayed the highest antibacterial efficacy, with MIC50 values of 1.0 μM, 7.6 μM, and 18.6 μM against Escherichia coli, Acinetobacter baumannii, and Citrobacter freundii, respectively (Table 1), similar to that of the unmodified MGN II peptide as previously reported.20 The MIC50 value of MGN-6 against these three Gram-negative bacteria was higher than 30.4 μM in all cases, and activity against E. coli was barely detectable, even at the highest MGN-6 concentration, whereas E. coli was most sensitive to MGN-1 among the three organisms tested. This phenomenon of decreasing antibacterial activity may be related to the self-assembling propensity of MGNs. Antimicrobial peptide aggregates exhibit less antibacterial efficacy, and much like Aβ peptides discussed above, lose their protective antibiotic function upon aggregation.
Table 1.
MIC50 of MGNs to Escherichia coli (E. coil), Acinetobacter baumannii (A.), and Citrobacter freundii (C. freundii)
| MIC50 (μM) |
|||||
|---|---|---|---|---|---|
| pathogens | MGN-1 | MGN-2 | MGN-3 | MGN-4 | MGN-6 |
| E. coil | 1.0 | 1.8 | 12.5 | 19.4 | >30.4 |
| A. baumanmii | 7.6 | 10.5 | 16.9 | 17.7 | >30.4 |
| C. freundii | 18.6 | 20.3 | 22.9 | 24.7 | >30.4 |
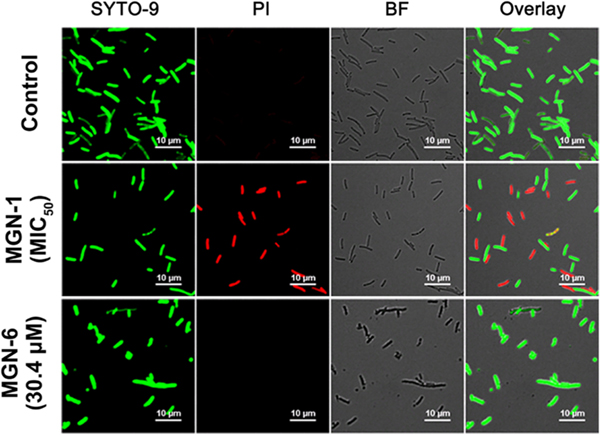
The antibacterial mechanisms of MGN-1 and MGN-6 were examined with confocal laser scanning microscopy (CLSM) and a LIVE/DEAD BacLight bacterial viability test.21 Upon cellular exposure to fluorescent dyes, the green fluorescent SYTO-9 dye crosses the intact membrane, whereas the red fluorescent propidium iodide enters bacterial cells through lesions in the membrane. As shown in Figure 3, both red (dead) and green (live) signals are observed in bacteria incubated with MGN-1 at its MIC50 concentration. In contrast, for bacteria incubated with MGN-6 at 30.4 μM (highest concentration tested in the antibacterial assay), only green (live) signal is observed. These results suggest that MGN-1 has a stronger ability to disrupt the cell membrane integrity than that of MGN-6. These phenomena may be related to the increased energy cost of aggregated peptides to embed into and disrupt the bacterial cell membrane.
Figure 3.
Confocal laser scanning microscope (CLSM) images of E. coli cells incubated with 1.0 μM MGN-1 (MIC50 of MGN-1) and 30.4 μM MGN-6 (the maximum tested concentration of MGN-6) at 37 °C for 1 h and stained with a LIVE/DEAD BacLight bacterial viability assay for 15 min in Mili-Q water. Channel 1 (green), excitation = 488 nm, emission = 500–550 nm; channel 2 (red), excitation = 561 nm, emission = 570–620 nm.
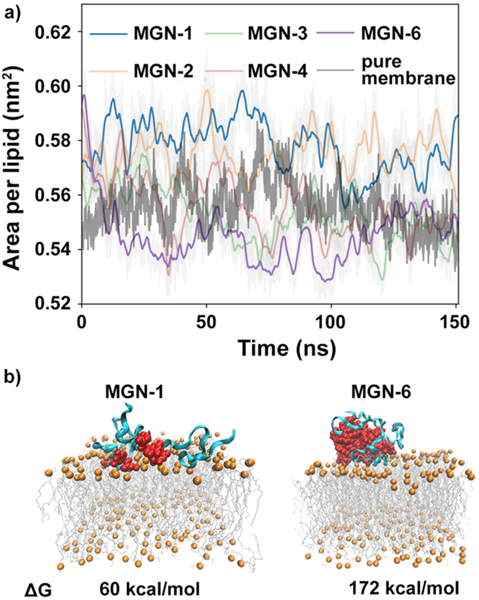
Next, we determined the energy cost of imbedding a peptide into the membrane using a simple membrane model of the bacterial cell membrane22–24 with MD simulations. Our model membrane is chosen based on prior studies that have shown that, for AMPs, similar MD results can be obtained with a model membrane as with natural complex membranes.25 Our starting structures comprised MGN1 through MGN6, each with four peptides constituting the aggregate. We first carried out simulations (150 ns) to probe the interaction between membranes and peptide aggregates, and to obtain an equilibrated starting structure for further simulation. The peptide aggregates attached to the membrane within the first 50 ns of simulation (Figure S11). We note that with increasing numbers of guanine units, the z-distance between peptide aggregates and the membrane also increases, further suggesting peptides are less likely to interact with and subsequently enter the membrane with increased intermolecular aggregation. Once on the membrane, the aggregates are stable except for the aggregates formed by MGN-1. MGN-1 has the lowest aggregation propensity, and thus the structure of the aggregates is relatively flexible. (Figures S12 and S13). By analyzing the surface area occupied per lipid of the simulated systems (Figure 4a), we found that area per lipid is the largest for MGN-1 interactions with the cell membrane. Area per lipid in the presence of MGN-6 is similar to the area per lipid of pure membrane in the absence of peptides. Previous studies have shown that an increase in area per lipid of a bilayer yields a decrease in the membrane bending modulus, suggesting that the membrane deforms more easily.26,27 Thus, MGN-1 has the strongest ability to disrupt membrane integrity, while MGN-6 shows little effect on the membrane deformability. The permeation Gibbs free energy of a single peptide embed into the membrane was calculated using the umbrella sampling method.28 To generate the windows for the umbrella sampling simulation, steered MD (SMD) simulations were carried out with a very slow pulling rate (0.1 nm/ns). This slow pulling rate enabled us to draw the peptide cluster into the membrane without dissociation of the pulled peptide from the aggregate. As such, the permeation Gibbs free energy measured is a contribution from the small pulled peptide rearrangement within its aggregated cluster, in addition to imbedding into the membrane. The starting structure for the SMD simulation was the snapshot of the unbiased simulation at 50 ns, at which time each of the aggregates were attached to the membrane (Figure 4b and Figure S17). SMD generated 37 windows, and each window was simulated for 50 ns in the umbrella sampling simulation. The permeation Gibbs free energy increased from 60 to 172 kcal/mol upon increasing the number of attached guanine units on MGN peptides from 1 to 6 (Figure 4b, Figure S17). Thus, our MD simulations suggest the peptide must overcome the self-interaction energy with adjacent peptides as it permeates the membrane. Furthermore, MD simulations show that increasing the number of guanine units will increase peptide–peptide interactions, thus increasing the permeation Gibbs free energy, as corroborated by our experimental studies with bacterial viability upon exposure to MGN-1 and MGN-6 AMPs.
Figure 4.
(a) Time evolution of the surface area per lipid in the presence or absence of an MGN aggregate. MGN-1, blue line; MGN-2, orange line; MGN-3, green line; MGN-4 pink line; MGN-6, violet line; pure membrane without peptides, gray line. (b) Permeation Gibbs free energy of MGN-1 and MGN-6. Starting structures of MGNs aggregates attached to the membrane for SMD simulation. The MGN II peptide scaffold is colored cyan, guanine units are colored red, and lipids are orange and gray.
On the basis of our theoretical and experimental results, we find that the antibacterial activity of MGNs is correlated with their aggregation propensity. More precisely, upon increasing the intermolecular interaction propensity of MGNs, the antibacterial efficacy is decreased. We implemented our experimental strategy to test the antimicrobial activity of another AMP, cecropin A-melittin (CAM). CAM is a hybrid peptide with the sequence KWKLFKKIGAVLKVL-NH2, which we implemented to test the broad-scale applicability of our results in another antimicrobial peptide test case. We synthesized two peptides, CAM-1 and CAM-6 (Tables S6–S7; Figures S18–S19), with 1 and 6 guanine units as with our MGN tests, and tested CAM-1 and CAM-6 antibacterial activities as described above. We observed that, similar to results obtained with MGN II peptides, CAM-1 also showed greater antimicrobial activity than CAM-6 against several strains of Gram-negative bacteria (Table 2). The consistent trend between AMP intermolecular interaction strength and antimicrobial activity for both guanine-modified MGN II and CAM peptides suggests that our understanding of the relationship between intermolecular peptide interactions and antimicrobial activity may be generalizable to other AMPs. For natural AMPs, there are two additional examples previously reported showing that our hypothesis may be generalizable. One such example is related to the PSMα3 peptide. A mutant form of PSMα3, F3A, shows decreased aggregation propensity, but increased antibacterial activity.29,30 Another example is related to the Temporin L peptide. Its mutant, the G10L peptide, also shows increased aggregation propensity but decreased antibacterial activity.31
Table 2.
Activity of CAM-1 and CAM-6 against Gram-negative bacteria
| MIC50 (μM) |
|||
|---|---|---|---|
| peptides | E. coli | A. baumanmii | C. freundii |
| CAM-1 | 2.4 | 3.9 | 4.4 |
| CAM-6 | 27.9 | 19.9 | >36.4 |
In conclusion, through a combination of theoretical and experimental approaches, we establish a relationship between the intermolecular interaction strength and antibacterial activity of AMPs. By introducing different numbers of guanine units, interactions between MGNs can be finely controlled by increasing aggregation propensity, which in turn determines MGN antibacterial activity. Increasing aggregation between MGNs increases the energy cost of the peptide to embed into the bacterial cell membrane, which decreases antibacterial activity. Our method was demonstrated for two unrelated AMP systems: MGN and CAM antimicrobial peptides. These findings provide a fundamental guiding principle for the design and modification of therapeutically active AMPs.
Supplementary Material
ACKNOWLEDGMENTS
This work was supported by a Burroughs Welcome Fund Career Award at the Scientific Interface (CASI), the Foundation for Food and Agricultural Research (FFAR), and a Beckman Foundation Young Investigator Award (M.P.L.). M.P.L. is a Chan-Zuckerberg Biohub Investigator. We thank the NSFC (91529101, 21572057, and 21778017) for financial support. R.Z. thanks the China Scholarship Council for financial support. We also thank the Swedish National Infrastructure for Computing (SNIC) for providing computational resources for Project SNIC 2016-1-343 and SNIC201634-43.
Footnotes
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.biochem.8b00052.
Simulation details, experimental details (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Fox JL (2013) Nat. Biotechnol. 31, 379–382. [DOI] [PubMed] [Google Scholar]
- (2).Chellat MF, Raguž L, and Riedl R. (2016) Angew. Chem., Int. Ed. 55, 6600–6626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Brogden KA (2005) Nat. Rev. Microbiol. 3, 238–250. [DOI] [PubMed] [Google Scholar]
- (4).Porter EA, Weisblum B, and Gellman SH (2005) J. Am. Chem. Soc. 127, 11516–11529. [DOI] [PubMed] [Google Scholar]
- (5).Schmitt MA, Weisblum B, and Gellman SH (2004) J. Am. Chem. Soc. 126, 6848–6849. [DOI] [PubMed] [Google Scholar]
- (6).Soscia SJ, Kirby JE, Washicosky KJ, Tucker SM, Ingelsson M, Hyman B, Burton MA, Goldstein LE, Duong S, Tanzi RE, and Moir RD (2010) PLoS One 5, e9505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Kumar DKV, Choi SH, Washicosky KJ, Eimer WA, Tucker S, Ghofrani J, Lefkowitz A, McColl G, Goldstein LE, Tanzi RE, and Moir RD (2016) Sci. Transl. Med. 8, 340ra72–340ra72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Torrent M, Andreu D, Nogués VM, and Boix E. (2011) PLoS One 6, e16968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Matsuzaki K, Murase O, Fujii N, and Miyajima K. (1996) Biochemistry 35, 11361–11368. [DOI] [PubMed] [Google Scholar]
- (10).Cai C, Lin J, Lu Y, Zhang Q, and Wang L. (2016) Chem. Soc. Rev. 45, 5985–6012. [DOI] [PubMed] [Google Scholar]
- (11).Yao D, Lin Z, and Wu J. (2016) ACS Appl. Mater. Interfaces 8, 5847–5856. [DOI] [PubMed] [Google Scholar]
- (12).Peters GM, and Davis JT (2016) Chem. Soc. Rev. 45, 3188–3206. [DOI] [PubMed] [Google Scholar]
- (13).Wartell RM, and Benight AS (1985) Phys. Rep. 126, 67–107. [Google Scholar]
- (14).Raschke TM, Tsai J, and Levitt M. (2001) Proc. Natl. Acad. Sci. U. S. A. 98, 5965–5969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Coin I, Beyermann M, and Bienert M. (2007) Nat. Protoc. 2, 3247–3256. [DOI] [PubMed] [Google Scholar]
- (16).Hauser CAE, Deng R, Mishra A, Loo Y, Khoe U, Zhuang F, Cheong DW, Accardo A, Sullivan MB, Riekel C, Ying JY, and Hauser UA (2011) Proc. Natl. Acad. Sci. U. S. A. 108, 1361–1366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Karabencheva-Christova TG, Carlsson U, Balali-Mood K, Black GW, and Christov CZ (2013) PLoS One 8, e56874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Masiero S, Trotta R, Pieraccini S, De Tito S, Perone R, Randazzo A, and Spada GP (2010) Org. Biomol. Chem. 8, 2683–2692. [DOI] [PubMed] [Google Scholar]
- (19).Chen L, Zhu Y, Yang D, Zou R, Wu J, and Tian H. (2015) Sci. Rep. 4, srep06860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Zhang W, He J, Wu J, and Schmuck C. (2017) Bioconjugate Chem. 28, 319–324. [DOI] [PubMed] [Google Scholar]
- (21).Wenzel M, Chiriac AI, Otto A, Zweytick D, May C, Schumacher C, Gust R, Albada HB, Penkova M, Kramer U,¨ Erdmann R, Metzler-Nolte N, Straus SK, Bremer E, Becher D, Brötz-Oesterhelt H, Sahl H-G, and Bandow JE (2014) Proc. Natl. Acad. Sci. U. S. A. 111, E1409–E1418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Kwon B, Waring AJ, and Hong M. (2013) Biophys. J. 105, 2333–2342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Tu Y, Lv M, Xiu P, Huynh T, Zhang M, Castelli M, Liu Z, Huang Q, Fan C, Fang H, and Zhou R. (2013) Nat. Nanotechnol. 8, 594–601. [DOI] [PubMed] [Google Scholar]
- (24).Mani R, Cady SD, Tang M, Waring AJ, Lehrer RI, and Hong M. (2006) Proc. Natl. Acad. Sci. U. S. A. 103, 16242–16247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Faust JE, Yang P-Y, and Huang HW (2017) Biophys. J. 112, 1663–1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Szleifer I, Kramer D, Ben-Shaul A, Roux D, and Gelbart WM (1988) Phys. Rev. Lett. 60, 1966–1969. [DOI] [PubMed] [Google Scholar]
- (27).Stevens MJ (2004) J. Chem. Phys. 121, 11942–11948. [DOI] [PubMed] [Google Scholar]
- (28).Lyu Y, Xiang N, Zhu X, and Narsimhan G. (2017) J. Chem. Phys. 146, 155101. [DOI] [PubMed] [Google Scholar]
- (29).Cheung GYC, Kretschmer D, Queck SY, Joo H-S, Wang R, Duong AC, Nguyen TH, Bach T-HL, Porter AR, DeLeo FR, Peschel A, and Otto M. (2014) FASEB J. 28, 153–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Zheng Y, Joo H-S, Nair V, Le KY, and Otto M. (2017) Int. J. Med. Microbiol.. DOI: 10.1016/j.ijmm.2017.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Mangoni ML, Carotenuto A, Auriemma L, Saviello MR, Campiglia P, Gomez-Monterrey I, Malfi S, Marcellini L, Barra D, Novellino E, and Grieco P. (2011) J. Med. Chem. 54, 1298–1307. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.