Extending arterial stiffness assessment along the circumference using beam-steered ARFI and wave-tracking: A proof-of-principle study in phantoms and ex vivo

Abstract

Background

To fully quantify arterial wall and plaque stiffness, acoustic radiation force impulse (ARFI)-induced wave-tracking along the entire vessel circumference is desired. However, attenuation and guided wave behavior in thin vessel walls limits wave-tracking to short trajectories. This study investigated the potential of beam-steered ARFI and wave-tracking to extend group velocity estimation over a larger proportion of the circumference compared to conventional 0° ARFI-induced wave-tracking.

Methods

Seven vessel-mimicking polyvinyl alcohol cryogel phantoms with various dimensions and compositions and an ex vivo human carotid artery were imaged in a dedicated setup. For every 20⁰ phantom rotation, transverse group wave velocity measurements were performed with an Aixplorer Ultimate system and SL18–5 transducer using 0⁰/20⁰/−20⁰-angled ultrasound pushes. Transmural angular wave velocities were derived along 60⁰-trajectories. A 360⁰-angular velocity map was composed from the top-wall 60⁰-trajectories 0°-data, averaged over all physical phantom rotations (reference). For each phantom rotation, 360⁰-angular velocity maps were composed using 0°-data (0⁰-approach) or data from all angles (beam-steered approach). Percentages of rotations with visible waves and relative angular velocity errors compared to the reference map as function of the circumferential angle were determined for both approaches.

Results

Reference 360°-angular velocity maps could be derived for all samples, representing their stiffness. Beam-steering decreased the proportion of the circumference where waves were untraceable by 20% in phantoms and 10% ex vivo, mainly at 0° push locations. Relative errors were similar for both approaches (phantoms: 10–15%, ex vivo: 15–35%).

Conclusion

Beam-steering enables wave-tracking along a higher proportion of the wall circumference than 0⁰ ARFI-induced wave-tracking.

Graphical Abstract

1. Introduction

With a global incidence of 7.63 million per year, ischemic stroke is a leading cause of death and disability [1]. Carotid arteriosclerosis underlies 10–20% of ischemic strokes [2]. Current stroke risk stratification and treatment planning in carotid plaques are based on stenosis degree [3], [4]. However, there is increasing evidence that plaque composition is of great importance in stroke risk prediction, regardless of the stenosis degree [5], [6]. Lipid-rich plaques with a thin cap are rupture-prone, whereas fibrous or calcified plaques have a low rupture risk [7]. Because lipid is less stiff than fibrous tissue, plaque stiffness could elucidate its composition [8].

Tissue stiffness can be determined using ultrasound shear wave elastography (SWE) [9]. In SWE, an acoustic radiation force impulse (ARFI), also called a push pulse, is applied to induce shear waves that propagate perpendicular to the push pulse. The propagation speed of the ARFI-induced wave is directly related to the tissue stiffness. Higher shear wave velocities correspond to stiffer tissues [10]. SWE has been developed for large, homogeneous tissues such as the liver and breasts [10]. The conversion from ARFI-induced wave velocities to tissue elasticity in carotid arteries is more complicated because not all assumptions for stiffness estimation are valid since arteries are thin, heterogeneous, and anisotropic [11], [12], influencing the wave propagation pattern. Nevertheless, multiple studies have shown the ability of arterial SWE to assess plaque vulnerability, as defined based on neurological symptoms [13], [14], [15], [16], [17], [18], histology [19], [20], [21], [22], American Heart Association classification of atherosclerotic plaques, plaque progression [18], or echogenicity [13], [15], [20], [23].

Prior studies mainly performed ARFI-induced wave velocity measurements in the longitudinal vessel direction [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], whereas these measurements in the transverse plane could be complementary or beneficial. In the longitudinal view, stiffness can only be estimated and visualized in the anterior and posterior walls. Plaque formation outside the imaging plane may thus be overlooked [25]. Moreover, it is impossible to appreciate the vessel wall elasticity entirely when only imaging longitudinally because the vessel wall shows anisotropic mechanical behavior [12]. ARFI-induced wave propagation velocities in a transversal plane could provide additional or more optimal information on the mechanical function of arteries because it provides a different mode of wave propagation [22]. In the longitudinal view, the waves propagate in the axial vessel direction as guided waves following the arterial and intravascular plaque structure [11], [22]. In the transverse view, waves propagate unobstructed through the plaque as an embedded inclusion rather than as a waveguide [22], [26], [27]. Additionally, the technique can only be extended to 3D in the transversal direction, using a multi-slice approach [28].

Although ARFI-induced wave velocity estimations in a transverse plane could enable stiffness estimation for the entire wall circumference, its application is still complicated. Multiple studies showed the feasibility to assess ARFI-induced wave propagation along the transverse vessel cross-section in phantoms and in ex and in vivo (carotid) arteries [22], [25], [26], [29], [30], [31], [32], [33]. Additionally, differences in velocities of these waves were detectable in plaque phantoms between the soft plaque and stiff wall [25] and in vivo between vulnerable and stable carotid plaques [22]. However, these studies only investigated wave velocity estimation along a short trajectory. ARFI-induced wave-tracking along the entire circumference is limited. The waves are guided along the wall circumference as their wavelength is larger than the vessel wall thickness [11], [27], [31], [34], [35]. Moreover, the waves attenuate quickly in real arteries [9], [25], [33], making them only trackable for a short trajectory. Therefore, eccentric plaques cannot be fully evaluated. This is unfavorable because eccentric plaques are associated with an increased risk of ipsilateral stroke compared to concentric plaques [36]. With electronic beam-steering, it is possible to perform ARFI-induced wave velocity measurements at oblique angles [37], [38], [39]. This approach could enable wave velocity estimation for other segments of the transverse arterial cross-section and, thus, provide a solution for stiffness estimation for a higher proportion of the vessel circumference.

This study aims to determine the feasibility, performance, and added value of beam-steered ARFI and wave-tracking for wave velocity estimation along the entire wall circumference compared to traditional 0⁰ transverse ARFI and wave-tracking. Its performance was evaluated in vessel-mimicking phantoms and an ex vivo human carotid artery.

2. Materials and methods

2.1. Phantom production

Seven vessel-mimicking phantoms with different compositions and geometries were manufactured to evaluate the performance of beam-steered compared to 0°-only ARFI and wave-tracking for wave velocity estimation along the entire circumference. Phantoms were produced using a mixture of polyvinyl alcohol (PVA) (Mw 130.0, 99% hydrolyzed, Sigma-Aldrich, Zwijndrecht, the Netherlands), demineralized water, and ethylene glycol (VWR Chemicals, Amsterdam, the Netherlands) in varying ratios (Table 1). PVA solutions were heated to 85–90 ⁰C for approximately three hours while continuously stirring with a magnetic bar until the PVA was completely dissolved. Silica gel particles (Merck Kieselgel 60, 0.063–0.100 mm, Boom B.V., Meppel, the Netherlands) were added for the last few minutes. A lower concentration of scatterers was used in soft (0.5%) than in stiff phantom parts (1.3–2.0%) to ensure that both parts were distinguishable in B-mode images. PVA solutions were cooled to 50 ⁰C before pouring and rested approximately two hours after pouring to allow air bubbles to escape. Freeze-thaw cycles consisted of 16 hours of freezing at − 23 ⁰C and 8 hours of thawing at room temperature (∼21 ⁰C).

Table 1.

Phantom properties. D_bore,wall = bore-diameter in stainless-steel mold for vessel wall production, D_rod,wall = rod-diameter for vessel wall production, D_rod,plaque= rod-diameter for plaque production, PVA = polyvinyl alcohol, DMW = demineralized water, Eth. glyc. = ethylene glycol, Sci = silica gel, FTC = freeze-thaw cycles.

N	Phantom	Dbore,wall (mm)	Drod,wall (mm)	Drod,plaque (mm)	PVA-stiff/ soft (wt%)	DMW-stiff/ soft (wt%)	Eth. glyc. stiff/ soft (wt%)	Sci-stiff/ soft (wt%)	FTC-stiff/ soft (n)
1	Thin half-half	10	7	-	10/8	53/55%	35/37%	1.3/0.5%	3/2
2	Thick half-half	13	7	-	10/8	53/55%	35/37%	1.3/0.5%	3/2
3	Thin plaque	10	7	5	10/8	53/55%	35/37%	2.0/0.5%	2/1
4	Thick plaque	13	10	7	10/8	53/55%	35/37%	2.0/0.5%	2/1
5	Thin eccentric	10	5	-	10/-	53/ - %	35/ - %	2.0/ - %	2/-
6	Thick eccentric	13	7	-	10/-	53/ - %	35/ - %	2.0/ - %	2/-
7	Concentric	13	5	-	10/-	53/ - %	35/ - %	2.0/ - %	2/-

Phantoms were created using stainless-steel molds with a cylindrical bore and stainless-steel rods with various dimensions (Table 1 and Fig. 1). Phantoms 1 and 2, further referred to as half-half phantoms, consist of one half with soft and one half with stiff material, as seen transversally, along the entire phantom length. An initial version of the stiff half was formed by filling one mold-half in horizontal position with a 10 wt% PVA solution. The mold was closed after concentric placement of a rod inside and freeze-thawed once in horizontal position. The soft phantom half was added by pouring a hot (∼85 ⁰C) 8 wt% PVA solution into the remaining empty, flat-lying mold half, which was pre-heated to ∼40 ⁰C to stimulate PVA cross-linking between both phantom halves. The mold was then closed and freeze-thawed twice in upright position. Phantoms 3 and 4, the so-called ‘plaque’ phantoms, consist of a soft ‘plaque’ layer inside a stiff ‘outer wall’ layer with an eccentric lumen along the entire phantom length. To produce the outer wall, molds with a concentrically placed rod with a 2–3 mm larger diameter than the final lumen were filled with a 10 wt% PVA solution and freeze-thawed once upright. Plaques were created by filling the outer wall with the 8 wt% PVA solution, eccentrically placing the rod with a diameter as large as the final lumen, and freeze-thawing it upright once again. Finally, three homogeneous phantoms (phantoms 5, 6, and 7) were produced by pouring a 10 wt% PVA solution into the mold with the eccentric or concentric placement of the rod and freeze-thawing it twice. Excess material on either side of the phantom, where the two mold halves come together, was cut aqay as much as possible.

Fig. 1.

Schematic overview of a) the phantom mold and rod used to produce the b) vessel-mimicking polyvinyl alcohol cryogel phantoms (only the homogeneous concentric phantom is shown for visualization purposes) with c) an overview of the phantom transverse cross-sections (as similar over the entire phantom length) with their corresponding dimensions.

2.2. Measurement setup

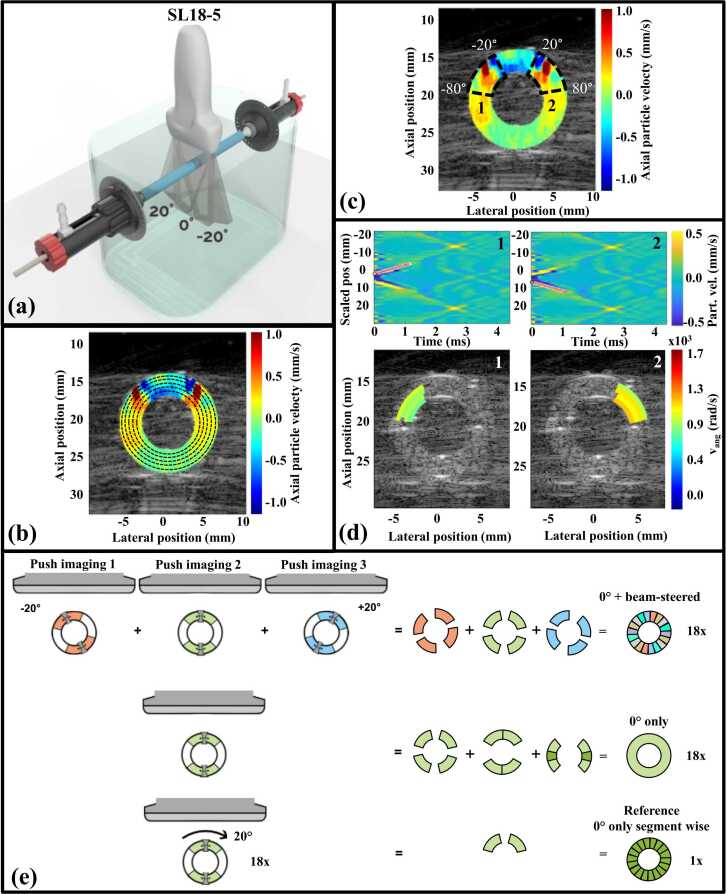
As shown in Fig. 2a, phantoms were mounted in a custom-made water tank setup enabling vessel rotation and longitudinal stretching. The in- and outlet of the setup were attached to a water column that could be elevated to pressurize the phantom. Phantoms were pre-stretched in the longitudinal and radial direction by 15% longitudinal stretching and ∼8 mmHg pressurization, respectively. All measurements were performed at room temperature (∼21 ⁰C).

Fig. 2.

Data acquisition and data processing. (a) Measurement setup allowing vessel rotation and elongation; (b) definition of wave-tracking ellipses within the vessel wall every 0.5 mm over the wall thickness; (c) subdivision of the wall circumference in 60⁰-segments (only −20° to −80° and 20–80° segments are shown for visualization purposes) with (d) manual tracking of the wave propagation in spatiotemporal maps for the − 20⁰ to − 80⁰ segment (1) and the 20–80° segment (2) per tracking ellipse (top) with a visualization of the angular velocities over all ellipses in the corresponding segments (bottom, only one ellipse is shown for visualization purposes); (e) construction of 360⁰ angular velocity maps for individual top and bottom wall pushes or supersonic pushes based on a combination of 0° and beam-steered acquisitions (top row), based on 0° acquisitions only (middle row), or reference map based on the −20° to −80° and 20° to 80° top segments of the supersonic push (bottom row).

2.3. Acquisitions settings

Measurements were performed using the fully programmable research mode of an Aixplorer Ultimate ultrasound system (Hologic®, SuperSonic™ Imagine, Aix-en-Provence, France) with an SL18–5 transducer. The transducer was positioned transversally above the vessel. The phantom was physically rotated 360⁰ in 20⁰-steps. For every phantom rotation, beam-steered ARFI-induced wave acquisitions were performed at −20⁰, 0⁰, and 20⁰ angles. The center of the vessel was manually selected, and single ultrasonic pushes (f_c 5 MHz, 150 µs, F-number 2) centered at the top or bottom wall or a supersonic push covering the top, lumen, and bottom wall (three 150-μs pushes, interspaced by 5–6 mm distance, with 15-μs pause between pushes) were applied. Also for beam-steered push pulse transmissions, the center of the vessel was targeted, resulting in pushes in the top and bottom walls located next to the 0⁰ push locations. After a 50-µs break, plane wave acquisitions were performed (70 frames, pulse repetition frequency 14 kHz, Welch apodization) for wave-tracking. The plane wave transmission angle was set equal to the angle of the corresponding push pulse. The acquisition angle was always 0⁰, independent of the push pulse angle. IQ data were stored for offline analysis.

2.4. Axial displacement estimation

Post-processing was performed using MATLAB 2021a (The MathWorks, Natick, MA, USA). Data were beamformed using delay-and-sum beamforming with an F-number of 0.875 and 70% Hamming apodization on a 0⁰ grid with a 100-μm sampling distance axially and laterally. Elliptical region-of-interests (ROI) were manually drawn along the outer and inner wall of the transversal phantom cross-section to segment the vessel wall at 0° phantom rotation. For all other phantom rotations, the ROI was rotated with the corresponding rotation angle and, if needed, translated to cover the vessel wall. Axial displacements were calculated on a Cartesian grid for the entire ROI using a two-dimensional Loupas’ estimator [40] with kernel sizes of 13 axial points x 3 time frames. Additionally, spatial filtering was performed using a median filter of 3 × 3 ultrasound pixels that moved pixel-wise. Next, axial motion maps were recalculated on an ellipsoidal grid. The grid consisted of multiple ellipses whose radius increased in 0.1-mm steps from the lumen to the outer wall interface. Ellipses were circumferentially sampled at 0.1° angular increment. For each coordinate, axial displacements were calculated using bilinear interpolation. Next, this highly sampled ellipsoid grid was downsampled in the radial direction to a lower-resolution grid by applying a moving 1D 5-point median filter. This led to smoothened axial displacements for tracking ellipsoids every 0.5 mm over the entire wall thickness (Fig. 2b). Resulting filtered axial particle velocities on the ellipsoidal grid were visualized over time in a movie.

2.4.1. 360⁰ angular velocity maps

The spatiotemporal maps for each ellipse and each phantom rotation were subdivided into 60°-segments (Fig. 2c). One observer selected the start and end position of the wave when visible, i.e. when the traveling wave could be distinguished from the background (particle velocity difference ≥1 mm/s). Together with the corresponding time coordinates in every segment, this provided a (group) wave velocity estimate for that segment part (Fig. 2d). Because a constant angular speed over all ellipses was expected [29], angular wave velocities (in rad/s) were calculated instead of true wave velocities (in m/s). Subsequently, as a surrogate of a stiffness map, 360⁰ angular velocity maps were derived for every phantom rotation using two approaches: I) based on 0° acquisitions only and II) based on compounding of 0° and beam-steered acquisitions. Separate maps for the two approaches were derived for data obtained using single push foci in the top and bottom wall or using supersonic pushing. A reference 360⁰ angular velocity map was calculated by averaging the velocities of the two upper 60°-segments (−20° to −80° and 20–80°) of the 0°-supersonic acquisitions over all phantom rotations (Fig. 2e).

2.5. Phantom stiffness estimation

Longitudinal 0⁰ ARFI-induced wave-tracking data were also acquired for all physical 20⁰ phantom rotations using single top and bottom wall or supersonic pushes using the same acquisition and post-processing settings as the 0⁰ transverse measurements. In a sample of the physical phantom rotations (0°, 80°, 180°, and 260°), wave propagations were manually tracked. For these data, dispersion curves, i.e. wave propagation velocity as a function of wave frequency, were estimated using a 2D Fast Fourier Transform analysis and peak detection as previously described [30], [41], [42]. Dispersion curves were fit to a theoretical leaky Lamb-wave model following the method of Bernal et al. [41] to estimate the stiffness, i.e. Young’s modulus. The cut-off frequency f_c (in Hz) for fitting was calculated as [34]:

$$f_c=0.304(1/h)\sqrt{(E/3\rho )}{(R/h)}^{-0.934}$$ (1)

with phantom wall thickness h in m, mass density ρ in kg/m³, Young’s modulus E in Pa, and inner radius R in m. In this equation, the Young’s modulus was first approximated by an initial curve fitting, and phantom dimensions were determined from compounded B-mode images assuming a speed of sound of 1490 m/s in water. The vessel diameter was calculated as the average diameter in lateral and axial directions because of the (slight) ellipsoidal vessel shape. The mean stiffness over all rotations and pushes was taken as the stiffness estimate. Appendix A shows an example of a stiffness estimation.

2.6. Ex vivo carotid

To evaluate our method in a real vessel, we included a carotid artery with an atherosclerotic plaque. This carotid was excised from a human body donated to science, obtained from the Preparatory of the Department of Anatomy, Radboud University Medical Center, Nijmegen, the Netherlands. The sample was extracted ten hours post-mortem and included the common, internal, and external carotid arteries (total length 12.5 cm). The vessel was mounted in the same setup as the phantoms, attached to both sides, and stretched by 10% to obtain its original length in situ. A pump was attached to the in- and outlet of the setup. The vessel was pressurized to ∼65 mmHg using a mechanical pressure regulator. A 0.9% saline solution was used as filling of the water tank and as pressurization fluid to prevent the vessel wall from swelling. The same measurements as in phantoms were performed in transverse and longitudinal cross-sections at the cross-section with maximum plaque thickness (as identified on the ultrasound image). After the measurements, the vessel was stored in 37% formaldehyde for 24 hours. The vessel was then cut into 5-mm sections that were sliced into 4-μm thick histology slides. To determine the plaque composition, different histological stainings were applied at the location of transverse ultrasound measurements, including Hematoxylin & Eosin (calcifications, lipid cores, thrombus, and overall phenotype), Masson’s Trichome (collagen and thrombus), CD68 (macrophages), and SM-1 stainings (smooth muscle cells).

2.7. Statistics

The performance of the 0⁰ and beam-steered approaches was quantified as a function of the circumferential phantom angle, seen from the 0° top push location, using two metrics: I) the percentage of 360⁰ angular velocity maps over all physical phantom rotations with a visible wave, and II) the median relative error with respect to thereference angular velocity map averaged over all phantom rotations. The first metric was calculated per sample; the latter per approach, combining the values over all phantoms (except for the ex vivo sample). To calculate the median error, angular velocity values per phantom were only considered when > 10% of all rotational maps had a visible wave for that circumferential angle, i.e. number of values > 10% of 3–8 tracking ellipses* 19 phantom rotations. To get an indication on the error distribution across the thickness of the phantoms, we also calculated the median error over all phantoms for the trajectories on the luminal side of the central trajectory (n = 1–3), the central trajectory itself (n = 1, or n = 2 in case of an even number of trajectories), and the remaining outer trajectories (n = 1–3).

3. Results

3.1. Phantom properties

Table 2 shows the phantom dimensions and stiffness as estimated from the B-mode images and dispersion curves, respectively. Some phantoms with similar characteristics (PVA-concentration and freeze-thaw cycles) differ in stiffness: the thick half-half phantom is stiffer than the thin half-half phantom (185/130 versus 80/45 kPa), and the thin eccentric phantom is stiffer than the other homogeneous phantoms (90 versus 50 kPa).

Table 2.

Phantom dimensions and stiffness. D_outer, D_inner, and D_plaque = diameter of the outer vessel wall, vessel lumen (without plaque), and vessel lumen with plaque, respectively.

N	Phantom	Douter (mm)	Dinner (mm)	Dplaque (mm)	Stiffness stiff/ soft (kPa)
1	Thin half-half	11.7	9.5	-	80/45
2	Thick half-half	12.0	7.3	-	185/130
3	Thin plaque	10.2	7.0	5.7	120/50
4	Thick plaque	13.2	10.0	7.9	120/65
5	Thin eccentric	9.7	5.1	-	90
6	Thick eccentric	13.0	7.0	-	50
7	Concentric	13.6	6.4	-	50

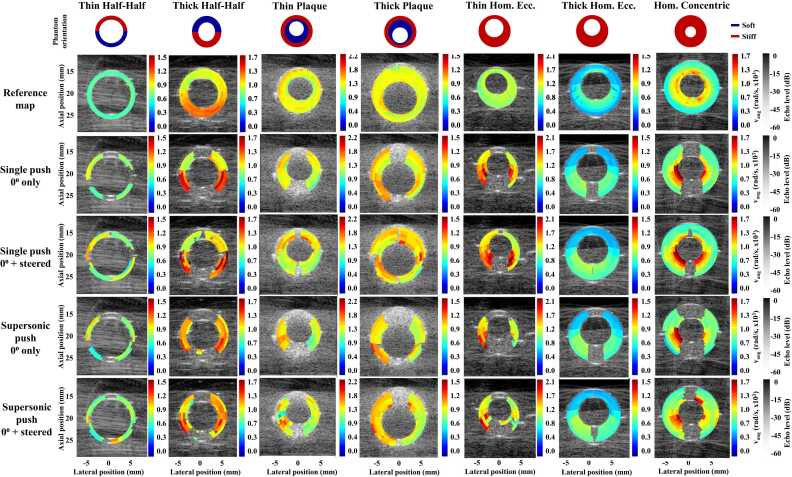
3.2. Reference 360° angular velocity maps

Fig. 3 displays the 360⁰ reference angular velocity maps for all phantoms. These maps represented the overall phantom stiffness with similar values in phantoms with similar stiffness. However, the stiffness contrast between the soft and stiff phantom parts could not be observed in the thin half-half and thick plaque phantoms. Additionally, velocities (unexpectedly) increased from the outer wall to the lumen interface in homogeneous phantoms.

Fig. 3.

Reference 360⁰ velocity maps (1^st row) and example of 360⁰ angular wave velocity maps for half-half phantoms and plaque phantoms per compounding method (2^nd to 5^th row). All color maps are scaled to 7.5 m/s divided by the center ellipse radius. V_ang = angular velocity; Hom = homogeneous; Ecc. = eccentric.

3.3. Performance of 0° and compounded approach

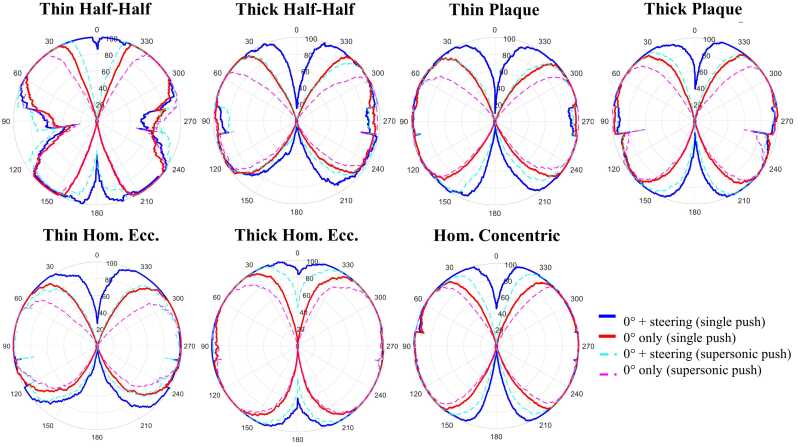
Fig. 3 shows 360⁰ angular velocity maps for the different approaches of all phantoms at 0° phantom rotation. Beam-steering enabled wave-tracking for a higher proportion of the circumference than 0°-only acquisitions in all phantoms. Averaged over all phantom rotations, the regions along the circumference where waves could not be tracked decreased by 20% using beam-steering (0–20%) compared to the 0⁰-only approach (20–40%) (Fig. 4). Angular wave velocity estimation was especially enabled using beam-steering in the segments corresponding to the 0° push locations. Additionally, supersonic push acquisitions showed a lower proportion of the circumference with possible wave-tracking than single push acquisitions (50–70% versus 70–80%). Median relative errors over all phantoms compared to the reference maps were approximately 10–15% in segments with visible waves for all approaches (Fig. 5). No substantial differences between approaches or along the wall circumference were observed. Over the phantom thickness, similar errors are observed for the 0-degree and beam-steered approach, and for the single and supersonic pushes, with one exception. For the inner trajectories the single push with steering performs worse than the supersonic push approach in the anterior wall (top segment of the plot). Furthermore, it is observed that errors increase in the posterior wall for all methods for the outer trajectories, which is less observed in the inner and middle trajectories.

Fig. 4.

Percentage of rotational maps with a visible wave as seen from the push location averaged over all phantom rotations for all approaches for all phantoms.

Fig. 5.

Median (solid line) and 25th and 75th percentile (dashed lines) relative error (in %) of the 0°-only and the compounded 0⁰ and beam-steered single-push approach (top row) and of the 0⁰-only and the compounded 0⁰ and beam-steered supersonic push approach (bottom row) compared to the gold-standard angular velocities as seen from the push location over all phantoms over all trajectories (1^st column), for the trajectories on the luminal side of the central trajectory (2^nd column), the central trajectory itself (in case of an even number two center trajectories, 3^rd column), and the remaining outer trajectories (4^th column).

3.4. Ex vivo carotid artery

Fig. 6 shows the ex vivo results. Atherosclerosis is found along the entire wall circumference but is most prominent in the bottom wall (140–160⁰ location). The reference 360⁰ angular velocity map shows heterogeneity in wave velocities along the wall circumference. Compared to the rest of the vessel wall (800–1100 rad/s ∼3–4.5 m/s), some lower values are observed in the medial/plaque layer at 160–180⁰ location (∼400 rad/s ∼1.5 m/s), whereas higher values are seen in the luminal side of the wall at 330–360⁰ location (1200–1600 rad/s ∼5–6.5 m/s). Longitudinally, group wave velocities were also lower in the bottom plaque region than in the surrounding wall (∼2 m/s versus ∼10 m/s, respectively). Histology showed a stable, collagen-rich plaque. Although there was some variation in histological composition along the wall circumference, no clear morphological substrate for variations in angular velocities could be found. The proportion of the wall circumference where waves were visible was smaller in the ex vivo sample than in phantoms. However, beam-steering decreased the proportion of the circumference where waves could not be tracked by approximately 10% (beam-steered approach: 60–65%; 0°-only approach: 50%), mainly at the 0° push locations. The median relative error compared to the reference map was higher for both approaches in the ex vivo sample than in phantoms, namely 15–35%.

Fig. 6.

Overview of the ex vivo sample with (a) a picture of the specimen in the longitudinal direction and (b) a picture of the transverse vessel cross-section at the location of wave velocity estimations with atherosclerosis along the entire vessel wall; (c) Masson’s Trichome Staining with collagen in the atherosclerotic regions and surrounding smooth vessel cells of the arterial wall; (d) CD68 staining coloring macrophages in the atherosclerotic regions; (e) SM-1 staining coloring actine in the vessel wall myofibroblasts and smooth muscle cell; (f) Hematoxylin & Eosin staining with collagen in the plaque region and smooth muscle cells in the surrounding vessel wall; (g) zoomed region of the top wall; (h) zoomed region of the bottom wall; B-mode ultrasound images of the sample in (i) longitudinal and (j) transverse direction; 360⁰ angular velocity maps of the single-push (k) 0⁰ only and (l) compounded 0⁰ and beam-steered acquisitions; 360⁰ angular velocity maps of the supersonic push (m) 0⁰ only acquisitions (n) compounded 0⁰ and beam-steered acquisitions; (o) the reference 360⁰ angular velocity map; (p) the percentage of rotational maps with a visible wave as seen from the push location; (q) the median relative error (in %) compared to 360⁰ reference maps over the entire wall circumference at 0° physical rotation. MTS = Masson’s Trichome Staining, H&E = Hematoxylin & Eosin, SMC = smooth muscle cells, SSI push = supersonic push.

4. Discussion

ARFI-induced wave velocity estimation along the vessel wall circumference is challenging due to attenuation and guided wave behavior in thin vessel walls. We introduced a dedicated setup to obtain ARFI-induced wave velocity images over the entire circumference by rotating the sample under investigation over 360⁰ as well as by obtaining these images using one static orientation of the sample. The rotated acquisitions were compounded to one image and served as the reference maps. These maps enabled us to evaluate and quantify the performance of ARFI-induced wave imaging methods using a static orientation of the samples with and without beam-steering, as rotation is also impossible in vivo. Both approaches were evaluated in vessel-mimicking phantoms and an ex vivo human carotid artery. Beam-steering increased the proportion of the circumference where waves could be tracked in phantoms by approximately 20% compared to 0°-only acquisitions, mainly at the 0° push locations. The relative error compared to reference maps was similar for beam-steered and 0°-only approaches (10–15%). In the ex vivo sample, similar results were found but in this case the increment in the proportion of the circumference with possible wave-tracking was smaller (circa 10%), and median relative errors were higher (15–35%).

360⁰ angular velocity maps, derived from transverse ARFI-induced wave velocity estimations, could be used as surrogate maps of arterial wall composition. To our knowledge, we are the first to derive full 360° angular velocity maps, which represented overall phantom stiffness. However, they did not perfectly represent wall stiffness yet. For the half-half phantoms, the stiffness contrast between both halves could be observed in the thick but not in the thin-walled phantom. This could be related to the lower stiffness and stiffness contrast in the thin (80 versus 45 kPa) compared to the thick half-half phantom (185 versus 130 kPa), resulting in lower angular wave velocity differences. Furthermore, the differential ability for stiffness is lower in the transverse than in the longitudinal view [22], [43], with a geometry-dependent effective wave speed resolution of 0.5 m/s [43]. Moreover, we only analyzed group velocities, which provide a less accurate stiffness quantification than phase velocities [22], [29], [41], [43], [44], [45]. Phase velocity analysis could improve the sensitivity but is not trivial because the waves propagate along paths with different curvatures for each frequency. Further research on optimal post-processing methods is needed to assess and improve the sensitivity of transverse ARFI-induced wave velocity estimations.

The lack of a velocity contrast between the soft plaque and the stiff wall in the thick plaque phantom could be explained by the circumferential wave propagation pattern. We assumed guided behavior in all phantoms resulting in equal angular velocities for all tracking ellipses, as described by Guo et al. [29]. However, waves propagate differently in thick phantom (parts) with shape factors, i.e. the ratio between the inner radius and the wall thickness, ≤ 1.5 [27], [31], [35], [46]. Therefore, the assumption of guided circumferential wave propagation is probably (partly) violated. This can already be observed in the 360⁰ velocity maps of the thick homogeneous phantoms where angular velocities unexpectedly increase towards the lumen interface (Fig. 3). Waves seem to propagate laterally until they are guided downwards when reaching the outer wall interface (Supplementary video 1–7). When visualizing the true wave velocities, not the angular velocities, the homogeneity of the 360⁰ velocity maps improves for the thicker phantoms (phantom 6 and 7) and the contrast between the stiff wall and soft plaque in the soft plaque phantoms seems clearer (phantom 3 and 4) (Appendix B). However, more sophisticated physics-based models should be developed to correctly convert angular or true wave velocities to tissue stiffness in geometric variations, such as varying wall thickness. This is even more challenging for anisotropic, multi-layered vessel walls [12], [47].

Supplementary material related to this article can be found online at doi:10.1016/j.csbj.2023.08.024.

The following is the Supplementary material related to this article Video S1, Video S2, Video S3, Video S4, Video S5, Video S6, Video S7.

.

Similar but heterogeneous angular velocities in the ex vivo vessel wall and plaque could be related to plaque composition and vesssel wall inhomogeneity but are difficult to correlate with histology. The stiffness of collagen-rich stable plaques is higher and more alike the surrounding wall stiffness compared to lipid-rich plaques that have rupture-prone features [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23]. As the included plaque was stable, its stiffness could indeed be similar to the vessel wall. Nevertheless, a morphological substrate for angular velocity variation in the plaque or surrounding vessel wall was not observed. However, physiological variation in angular velocities along the wall circumference is unknown. The vessel wall is known to be inhomogeneous [11], but 360⁰ angular velocity maps of healthy carotids are needed as a reference for our results. Additionally, an underlying morphological substrate could have been missed. We experienced substantial deviations in histological composition over slices located slightly further (∼50 µm) in the sample. We observed, amongst others, calcifications in another slice, not seen in the included histological slices. These varying histological compositions will be averaged in the ARFI-induced wave velocity estimate because the elevational resolution of the ultrasound beam is in the order of 1–2 mm. Therefore, another morphological substrate than the obtained histology slices will have affected the observed wave velocity patterns.

Observed hampered wave-tracking close to the push location is mainly related to the echoes originating from the ultrasound push. These echoes saturate the probe immediately after the push and render plane wave imaging for tracking infeasible for a short period of time. Previous studies on transverse ARFI-induced wave velocity estimations only investigated traditional, 0° acquisitions [22], [25], [26], [29], [30], [31], [32], [33]. These studies showed that waves could be induced using ARFI, traveling along (part of) the phantom or arterial circumference. However, they only analyzed wave velocities over a short trajectory near the push location but never assessed the extent of this “blind area”. We observed that this area covers up to 30° of the circumference. This blind area is even wider for supersonic than for single push acquisitions as the push duration and, with that, the first moment of saturation-free imaging is longer.

Beam-steered acquisitions could provide insight into wave propagation at the 0⁰ push locations because the corresponding push locations spatially differ. Beam-steering indeed decreased the blind area for wave-tracking along the wall circumference in phantoms (∼20%) and ex vivo (∼10%) at the 0° push locations. The smaller decrease observed ex vivo could be attributed to the higher angular wave velocities than in phantoms (800–1200 rad/s versus 500–1000 rad/s), leading to a larger segment wherein waves travel during the “dead” time. This can also be observed in the thick half-half phantom where the increment in the proportion of the circumference where waves can be tracked is lower in the stiff than in the soft phantom half. Nevertheless, wave-tracking was still infeasible in the entire push beam region, possibly due to overlapping blind areas of beam-steered and 0° acquisitions. Translating the push next to or to the vessel boundary, as performed by Marlevi et al. [43], could enable wave-tracking in the push location. However, this is not applicable in this study without surrounding tissue. Furthermore, different push settings (e.g. lower F-number or shorter push duration), steering angles, tracking segment sizes or positions, or a shorter break after the push could improve wave-tracking in these regions [48], [49]. However, future studies have to further explore optimal acquisition settings.

Attenuation and waveguide behavior limit wave-tracking in the side walls of the vessel circumference. The waves barely attenuate in phantoms but rapidly attenuate in vivo due to the tissue viscosity and the presence of surrounding tissue in the latter [9], [25], [33], limiting wave-tracking far from the push beam region. Moreover, the waves are guided along the wall circumference due to the thin vessel geometry [11], [27], [31], [34], [35], resulting in a dominant lateral displacement in the side walls. Nevertheless, wave-tracking in the side walls was already feasible in most phantoms using 0° push acquisitions. This could be related to the (thick/asymmetric) wall geometry, leading to continuous axial displacements in the side walls. However, wave propagation in asymmetric or irregular phantoms should be determined.

Beam-steering could improve wave-tracking in the side walls. Due to the oblique acquisition angles, the propagation trajectory towards the side walls is naturally shorter, and there are continuous axial displacements in the side walls. However, beam-steering did not improve (half-half phantom) or even deteriorate (ex vivo) wave-tracking in the side walls. This may be related to the lower force induced by beam-steered than 0° pushes with the same voltage, i.e. 20–30% reduced mechanical index as we observed in safety measurements in the context of another study (unpublished). Therefore, induced axial displacements are lower, making them more challenging to track. Increasing the push voltage of beam-steered acquisitions could be advantageous but is not always configurable in practice. Furthermore, for perfectly circumferentially guided waves, the particle motion will remain perpendicular to the lumen-wall interface [11], [27], [31], [34], [35]. Therefore, the measurable axial component of the wave will drop as a function of the circumferential angle following a cosine function. Without attenuation, the maximal amplitude will drop 50% after having traveled 60 degrees. Because this is also the case in the beam-steered approach, the waves remain difficult to track in the side walls. Tracking radial instead of axial displacement using an alternative approach, such as proposed by He et al. [26], or using two ultrasound probes [33] could improve wave-tracking in the side walls but should be investigated using beam-steered acquisitions. Higher relative errors in some segments could be of importance for (in vivo) vascular application. Increasing errors in the posterior wall for the outer trajectories can be caused by a lower signal in the posterior wall resulting from attenuation further from the transducer [9], leading to a lower amplitude of the push pulse, or from attenuation of the wave amplitude with propagation along the circumference [9], [25], [33]. Furthermore, the higher propagation velocities in the outer circles can induce higher measurement errors in these trajectories. Higher errors in the anterior wall for the single push beam-steered approach compared to the supersonic push approach in the inner circles could be related to the lower push energy below the focus in the single push scenario. Therefore, the initiated wavefront is less of a perfect plane as compared to the wave induced by the elongated supersonic push scenario. This phenomenon could be affirmed in the acquired particle velocity movies. Nevertheless, similar relative errors of beam-steering and 0° approaches compared to the reference maps emphasize its applicability for circumferential wave-tracking.

Limitations of this study should be considered when interpreting the results. Measurements were performed in water. Surrounding tissue in vivo will increase wave attenuation and could influence wave propagation [22], [43]. Moreover, only one ex vivo sample was included. Therefore, the performance of beam-steered transverse ARFI-induced wave velocity estimations with different plaque geometries and compositions could not be assessed. Besides, excess phantom material on either side of the phantom, where both mold halves come together, could not be completely removed without breaking the phantom. This excess material could (probably minimally) influence the wave propagation behavior. However, its exact influence should be further studied using simulations. Furthermore, only one person performed the manual tracking as it is time-consuming. Automatic wave-tracking would greatly facilitate its development, reproducibility, and in vivo applicability. Additionally, acoustic output limits, stated by the International Electrotechnical Commission [50] or Food- and Drug Administration [10] were not considered for applications in this study. However, the acoustic output should be reduced for in vivo applications by, for example, lowering the push voltage, which could impede wave-tracking. Furthermore, many artifacts were observed in the B-mode phantom measurements. As these images are based on 0⁰ plane wave acquisitions, we expect the artifacts to mainly result from sidelobes and reflections from the (phantom) vessel wall-water boundary and the bottom of the water tank, not to be present in vivo. B-mode images could be improved using more filtering and smoothening. This was not performed in the current study as beamformed raw IQ data was used for motion estimation, not the post-processed imaging data. Furthermore, plane wave compounding could be used to improve the B-mode image quality. Though, previous studies in the longitudinal imaging view showed that a higher frame rate is more important for accurate ARFI-induced wave-tracking than image quality [51]. A higher frame rate is probably of even greater importance in the transverse imaging view because the circumferential propagation leads to more in plane decorrelation, restricting the size of kernels used for motion estimation and filtering. Additionally, coherent compounding can alter the visual appearance of the ARFI-induced wave front when dispersion is at play, as present in the phantoms used [52]. Therefore, we opted out to apply any compounding. Additionally, there is a trade-off between beam-steering angle and artifacts. In case of beam-steering, grating lobes can be induced on an array with an element pitch larger than half the ultrasound wavelength [53], possibly impeding wave-tracking results. However, comparative studies on wave-tracking using different steering-angles have not been performed yet, but should be performed to find optimal steering angles for circumferential wave-tracking. The same counts for the length and start and end points of the wave-tracking trajectories. However, the presence of such artifacts should be further evaluated in vivo. Therefore, further research using beam-steered ARFI-induced wave velocity measurements applying lower push voltages using ultrasound arrays with smaller lambda-to-pitch ratios in vivo is needed to fully evaluate its performance.

5. Conclusion

We proposed a method to compile 360° angular velocity maps representative of arterial wall composition. Beam-steering enabled the visualization of a higher proportion of the vessel wall circumference compared to 0°-only acquisitions, which could improve vascular health assessment. Further improvement in the quantification of 360⁰ stiffness maps is needed for in vivo application.

CRediT authorship contribution statement

Judith Pruijssen: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Validation, Visualization, Writing – original draft preparation & Editing. Stein Fekkes: Resources, Methodology, Writing – review & editing. Jan Menssen: Software, Writing – review & editing. Chris de Korte: Methodology, Supervision, Writing – review & editing. Rik Hansen: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Visualization, Supervision, Writing – review & editing.

Declaration of Competing Interest

None.

Appendix A

Example of stiffness estimation for the soft (left column) and stiff half (right column) of the thick half-half phantom, both when located at the top of the phantom (i.e. 0⁰ (left) and 180⁰ phantom rotation (right)) with a top wall push with B-mode image of the vessel (1^st row); selection of the region-of-interest (green rectangle) and tracking line in the middle of the vessel wall (black, dotted line) for particle velocity estimation in the upper wall (2^nd row); the corresponding spatiotemporal maps with wave-tracking for the wave traveling to the left and the right (3^rd row); and dispersion curve fitting (4^th row, only the dispersion curve of the wave traveling to the left is shown for visualization purposes), The black circles correspond to the measured phase velocity per frequency, the red lines to the dispersion curve following the theoretical leaky Lamb-wave model fit from the calculated cut-off frequency to fit the curve as visualized using the white dashed line. Settings for the theoretical model for the soft wall were: wall thickness 2.3 mm, inner radius 3.7 mm, stiffness 125 kPa, cut-off frequency 547 kPa; for the stiff wall: wall thickness 2.4 mm, inner radius 3.6 mm, stiffness 177 kPa, cut-off frequency 666 kPa. The amplitude is normalized by dividing all values by the maximum amplitude value.

.

Appendix B

360⁰ angular wave velocity maps based on 60⁰ segments (20–80° and −20° to −80°) of the 0° supersonic push acquisitions without correction for the length of the tracking ellipses within the vessel wall. Shape factors, i.e. ratio inner radius and wall thickness, per phantom wall are stated below the velocity maps.

.

Data Availability

The data that support the findings of this study are available from the corresponding author, Judith Pruijssen, upon reasonable request.