Hypermetabolic Cerebellar Connectome in Alzheimer's Disease

Abstract

Introduction:

Regional hypermetabolism in Alzheimer's disease (AD), especially in the cerebellum, has been consistently observed but often neglected as an artefact produced by the commonly used proportional scaling procedure in the statistical parametric mapping. We hypothesize that the hypermetabolic regions are also important in disease pathology in AD.

Methods:

Using fluorodeoxyglucose (FDG)-positron emission tomography (PET) images from 88 AD subjects and 88 age-sex matched normal controls (NL) from the publicly available Alzheimer's Disease Neuroimaging Initiative database, we developed a general linear model-based classifier that differentiated AD patients from normal individuals (sensitivity = 87.50%, specificity = 82.95%). We constructed region–region group-wise correlation matrices and evaluated differences in network organization by using the graph theory analysis between AD and control subjects.

Results:

We confirmed that hypermetabolism found in AD is not an artefact by replicating it using white matter as the reference region. The role of the hypermetabolic regions has been further investigated by using the graph theory. The differences in betweenness centrality (BC) between AD and NL network were correlated with region weights of FDG PET-based AD classifier. In particular, the hypermetabolism in cerebellum was accompanied with higher BC. The brain regions with higher BC in AD network showed a progressive increase in FDG uptake over 2 years in prodromal AD patients (n = 39).

Discussion:

This study suggests that hypermetabolism found in AD may play an important role in forming the AD-related metabolic network. In particular, hypermetabolic cerebellar regions represent a good candidate for further investigation in altered network organization in AD.

Impact statement

Cerebellar hypermetabolism is a commonly observed characteristic of Alzhiemer's disease (AD) neurodegeneration in neuroimaging studies. However, whether cerebellar hypermetabolism is relevant to disease progression or whether it is an artefact of proportional scaling is controversial. In this study, we developed a general linear model-based classifier for AD by using the white matter mean for image scaling. We demonstrate that cerebellar hypermetabolism is a robust neuroimaging feature of AD. Further, hypermetabolism in the cerebellum is associated with an increase in the betweenness centrality of this region, indicating an important role of the cerebellum in changes in brain connectivity during AD.

Introduction

Alzheimer's disease (AD) is the most common form of dementia affecting 5.8 million people in the United States alone (Alzheimer's Association, 2019). AD is a neurodegenerative disorder marked by an irreversible, progressive decline in cognitive capabilities, leading to the deterioration of memory and thinking skills (Dá Mesquita et al., 2016). Fluorodeoxyglucose (FDG) positron emission tomography (PET) has often been used to approximate synaptic activity (Lin et al., 2008), and thus the decreased FDG uptake in the key anatomical regions has been commonly accepted as an imaging biomarker for AD and the mild cognitive impairment (MCI) due to AD (i.e., prodromal AD [PAD]; McConathy and Sheline, 2015). A lot of effort has been invested to standardize FDG PET readings, including the machine learning approach that minimizes human errors and subjective differences. Utilizing the Alzheimer's Disease Neuroimaging Initiative (ADNI; http://adni.loni.usc.edu/about; Toga and Crawford, 2015) database (i.e., a longitudinal multicenter study involving combined efforts of multiple research centers across North America), several studies have established quantitative biomarkers that may aid in AD diagnosis (Chen et al., 2016; Partovi et al., 2017; Shaffer et al., 2013; Yamane et al., 2014; Yao et al., 2010; Zhang and Shen, 2012).

AD is typically characterized by hypometabolism (decline in FDG uptake) in medial–frontal lobes, posterior cingulum, and temporal lobes when compared with age–gender matched normal controls (NL; McConathy and Sheline, 2015; Teune et al., 2014). Hypermetabolism in AD has also been consistently reported in some brain regions, including the cerebellum, but it is often neglected in AD diagnosis (Borghammer et al., 2009; Buchert et al., 2005). Some studies have suggested that hypermetabolism is observed in neurodegenerative disorders on account of different signal intensity normalization procedures (e.g., global mean normalization; Borghammer et al., 2008, 2009). In addition, these hypermetabolic regions (e.g., cerebellum and pons) are not traditionally perceived as key anatomical structures that are affected by AD; although recent studies demand reconsideration of their positions (Jacobs et al., 2018; Miyazawa et al., 2010). It has been suggested that the cerebellum has an integral contribution to cognitive and neuropsychiatric deficits in AD (Jacobs et al., 2018).

The graph theory is an analytic approach that investigates the hierarchy of nodal structure within a network, for example, identifying the hub of the information transfer (Khazaee et al., 2015; van Diessen et al., 2014). Using the graph theory analysis on the brain metabolic network, we have revealed an important contribution of hypermetabolic anatomical structures, including the cerebellum in the pathological network formulation in Parkinson's disease (Ko et al., 2018). To our knowledge, this has not been explicitly investigated in AD. To address this issue, we explored the topographical relationship between the disease-related metabolic status (hypermetabolism vs. hypometabolism) of different regions identified in the FDG PET-based AD classifier (FAC) and their functional hubness measured by betweenness centrality (BC).

In the current study, we investigated the role of hypermetabolic regions, such as the cerebellum in the AD metabolic network. We validated the relevance of hypermetabolism observed in AD patients by using the mean of white matter for intensity normalization (proportional scaling). Using BC as a measure of hubness of the regions, we investigated the significance of each region in the information flow within the AD metabolic network (Brandes, 2001). We also examined the longitudinal metabolic changes via FDG uptake in regions with increased hubness in the AD metabolic network.

To validate whether our results are dependent on different brain parcellation approaches, the analysis has been repeated with two different parcellation schemes: automated anatomical labeling (AAL, the most widely used brain parcellation method; Lancaster et al., 2000) and 268-node functional atlas generated via group-wise spectral clustering (an atlas based on functional homogeneity within each subunit; Finn et al., 2015; Shen et al., 2013).

Materials and Methods

Subjects

Data used in the preparation of this article were obtained from the ADNI database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), PET, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. The study was conducted after Institutional Review Board approval at each site. Written informed consent was obtained from study participants or authorized representatives.

The ADNI database comprised 1000 subjects, including 200 Alzheimer's patients (AD), 200 NL subjects, and 600 MCI subjects. Based on the availability of FDG PET and MRI scans at baseline, 116 AD patients were selected from the ADNI cohort. All PET and MRI images were visually inspected by V.G. Subjects were excluded if images did not cover the entire cerebellum or showed any noticeable abnormalities. Twenty-eight AD subjects that had partial scans of cerebellar regions were excluded. Hence, finally we selected 88 AD patients by using this selection protocol for AD network analysis and biomarker derivation (Fig. 1). Out of the 154 NL subjects with available PET and MRI scans, 127 remained NL after a follow-up of 3 years. Similarly, 88 age–sex matched NL1 were selected from the 127 stable NL subjects for comparative network analysis. Demographic details of subjects included in the study from ADNI cohort are mentioned in Table 1.

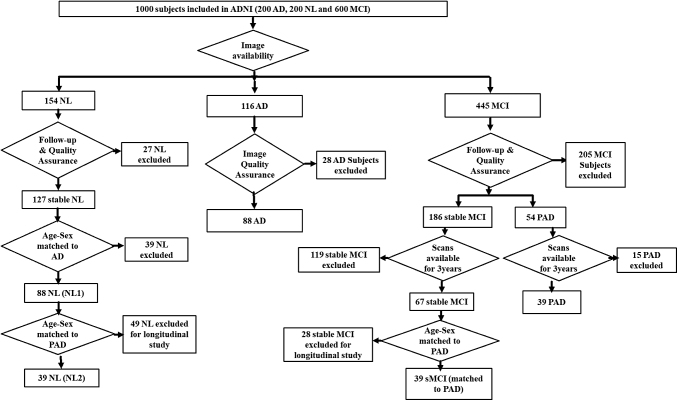
FIG. 1.

Subject selection protocol. ADNI database comprised 1000 subjects, including 200 AD patients, 200 NL subjects, and 600 MCI subjects. Based on availability of PET and MRI scans, 116 AD patients were selected. Twenty-eight AD patients were excluded after image quality assurance, such as the inclusion of whole cerebellum in PET scans. Finally, 88 AD patients were selected for biomarker derivation and network analysis. Follow-up duration was neglected for AD, as dementia was already present at the time of screening in the subjects. Out of the 154 NL subjects with available PET and MRI scans, 127 remained NL after a follow-up of 3 years. Eighty-eight age–sex matched NL subjects were selected from the 127 stable NL subjects. Of the 445 MCI subjects for which PET and MRI scans were available, based on a follow-up period of at least 3 years, 186 remained stable MCI and 54 converted to AD (PAD). Thirty-nine PAD subjects had scans available at three time points (conversion year, 1 year before conversion, and 2 years before conversion). For longitudinal FDG-SUR analysis, 39 age–sex matched stable MCI and NL subjects were selected that had scans available at three time points. AD, Alzheimer's disease; ADNI, Alzheimer's Disease Neuroimaging Initiative; FDG, fluorodeoxyglucose; MCI, mild cognitive impairment; MRI, magnetic resonance imaging; NL, normal controls; PAD, prodromal AD; PET, positron emission tomography; sMCI, stable MCI; SUR, standard uptake ratios.

Table 1.

Demographic Data for Patients

	AD	NL1	p *	PAD	sMCI	NL2	p **
Number of patients	88	88		39	39	39
Age	75.23 ± 7.29 (63–92)	74.66 ± 8.32 (56–90)	0.625	74.52 ± 7.47 (60–87)	73.91 ± 8.16 (59–90)	72.96 ± 8.83 (63–88)	0.479
Sex (M:F)	55:33	54:34	0.878	25:14	24:15	23:16	0.367
MMSE	23.6 ± 2.2 (20–26)	28.8 ± 1.1 (26–30)	0.544	26.7 ± 2.3 (24–30)	27.9 ± 1.6 (24–30)	28.9 ± 1.0 (26–30)	0.285

Mean ± standard deviation (minimum–maximum).

^* Independent t-test between AD versus NL1.

^** One-way ANOVA across PAD, sMCI, and NL2.

AD, Alzheimer's disease; ANOVA, analysis of variance; F, female; M, male; MMSE, mini-mental state exam; NL1, normal subjects matched for AD; NL2, normal subjects matched for PD; PAD, prodromal AD; sMCI, stable mild cognitive impairment matched for PAD.

To investigate the metabolic changes happening before AD diagnosis in the key anatomical regions, the longitudinal study data of the MCI subjects included in the ADNI database were analyzed. The MCI subjects were further divided into two categories: stable MCI (sMCI), subjects who remained MCI after a follow-up period of >3 years and PAD, MCI subjects who developed Alzheimer's later during the follow-up period (Knopman et al., 2003; Petersen, 2009). Of the 445 MCI subjects for which PET and MRI scans were available, based on a follow-up period of at least 3 years, 186 remained sMCI and 54 converted to AD (PAD). Overall, 39 PAD subjects (n = 39) were selected for whose scans were available at three time points (conversion year, 1 year before conversion, and 2 years before conversion; Fig. 1). Of the 186 overall sMCI subjects, 39 age–sex matched sMCI subjects that had FGD PET and MRI scans available at three consecutive points were selected. Similarly, of the 88 NL1, 39 NL2 were selected among whose PET and MRI images are available at baseline and 2-year follow-up. It should be noted that NL2 is a subgroup of NL1.

Image acquisition

The FDG PET and structural MRI images were retrieved from the Laboratory of Neuroimaging database in a format under which images had been preprocessed coregistration, averaging, and standardization. The detailed procedure for FDG PET images can be found at: http://adni.loni.usc.edu/methods/pet-analysis-method/pet-analysis/#pet-pre-processing-container. Similarly, the detailed procedure for structural MRI images can be found at: http://adni.loni.usc.edu/methods/mri-tool/mri-analysis.

Image preprocessing

FDG PET images were preprocessed by using standard parameters using statistical parametric mapping 12 (SPM12) software. FDG PET images were coregistered to structural MRI images by using rigid body transformation in SPM12. CAT12 was used to segment structural MRI images and generate forward deformation fields from MRI used in normalization. The coregistered FDG PET images were normalized by warping to the standard Montreal Neuroimaging Institute space using forward deformation fields. The normalized images were subsequently smoothed by using an 8 × 8 × 8 mm Gaussian filter.

FDG PET-based AD classifier

The preprocessed FDG PET images were proportionally scaled to the WM mean, which was the average FDG uptake value within each individual's white matter (WM) mask that has been generated from the segmentation step. Linear regression (Y = β × X + C; where X is the dummy variable used for group classification, Y is the subject's observed image, β is the slope of the regression model, and C is the constant) was performed for each voxel within the whole brain mask. The whole brain mask was produced by combining the gray matter and white matter masks from each subject's segmented structural MRIs and used as an inclusive mask, as previously described (Katako et al., 2018).

Using this regression model, the β map was constructed. The dot product between the reconstructed image (i.e., FAC) and each individual's proportionally scaled images within the brain mask was defined as the subject score, and it was used to differentiate AD versus NL1. To evaluate the effect of overfitting and selection bias, we performed a 10-fold cross-validation on the AD versus NL1 dataset (Poldrack et al., 2020). Subject pools were divided into 10 bins, and then 10 FACs were constructed by using 90% of the subjects (training set). The resulting FACs were used to classify the reserved testing set (10% of the subjects). This was repeated 10 times without overlapping testing sets (Katako et al., 2018).

The AAL atlas was masked with the whole brain mask, as described earlier. Pons were added to the original AAL atlas, as described elsewhere (Ko et al., 2018). The mean values of each of the 118 regions of interest were extracted from the FDG PET images of all subjects, and then they were proportionally scaled to the WM mean. Using the same regression model used in voxel-based analysis, slope coefficient β was calculated for all regions of interest (ROIs). The β value for each ROI is referred to as that ROI's FAC region weight. We used a 10-fold cross-validation as used in voxel-based analysis to test the predictive accuracy of the ROI-based method. Based on their β values (β > 0 or β < 0) and Bonferroni corrected p values for the model [p < (0.05/number of ROIs)], regions are classified as hypermetabolic or hypometabolic, respectively. Regions with p > 0.05/number of ROIs were classified as non-significant (NS). To test the reproducibility and interchangeability of voxel-based versus ROI-based FAC, topographical similarity was evaluated by Pearson's correlation. For this, the mean of β values from each ROI was extracted from the voxel-based β map.

AD network analysis using graph theory

The normalized metabolic activity with respect to WM mean in all ROIs was used to generate a region × region correlation matrix for the AD group and NL1 group separately (Tatsuoka, 2016). The absolute r values were ranked, and undirected unweighted adjacency matrices were generated at varying cost thresholds (1–50%; Hosseini et al., 2012). Minimum network density is defined as the minimum cost at which all nodes become fully connected in brain networks of both groups and it was found to be at 16%. To compare the overall network efficiency between AD and NL1, we computed characteristic path length (L) and clustering coefficient (C) at varying cost thresholds of 16–25% (Lovejoy and Loch, 2003; Watts and Strogatz, 2011). L is a measure of the average shortest path length between all pairs of nodes in a network, and represents the efficiency of interaction of different nodes in a network. C is the fraction of the node's neighbors that are, in turn, nearest neighbors of each other and it represents the resiliency of the network. To test for statistical significance of the group differences between AD and NL1 groups in C and L, a non-parametric permutation test with 1000 iterations was used, as previously described (Ko et al., 2018). The difference between AD and NL1 groups is deemed statistically significant if it lies outside 95% confidence interval of permutation distribution (two-tailed; Bernhardt et al., 2011).

To compare the relative nodal importance within the constructed graphs of AD versus NL1, we computed BC as a measure of hubness of each region in the network for the cost threshold range 16–25% (Freeman, 1977). BC is the fraction of all shortest paths in the network that contain a given node, and it approximates the role of a region in information transfer through the network. Nodes with high values of BC participate in a large number of shortest paths, and thus they play a significant role in information transfer acting as “hubs” in the network.

The correlations between regional β from FAC and their corresponding BC were evaluated by computing Pearson product–moment correlation coefficient (Ko et al., 2018). The regional BCs were averaged within 16–25% cost range, and then they were z-scored within each group (AD and NL1); then, the group difference was computed within each region. The regional β values defined in FAC were also z-scored, and the difference in z-scored β values was computed between AD and NL1 groups.

Longitudinal changes in FDG standard uptake ratios

To examine the metabolic relevance of the regions identified as AD-related pathological hubs in BC measures, we investigated the longitudinal changes in FDG standard uptake ratios (SUR) referenced to WM mean in PAD, sMCI, and NL2 subjects who were repeatedly scanned over a period of 2 years. To examine the comparative metabolic changes in regions according to their hubness as observed in the AD network, we divided regions into three groups based on their BC: regions with significantly high hubness (normalized difference in BC of ROI >2), regions with significantly low hubness (normalized difference in BC of ROI < −2), and regions with NS change in hubness (|normalized difference in BC of ROI | < 2). Similarly, based on their β values and Bonferroni corrected p values for the analyses, regions were classified as hypermetabolic, hypometabolic, and metabolically NS regions.

To examine the differences in FDG-SUR between regions identified as hubs in AD progression as compared with non-hub regions, we evaluated the interaction effect of ROI group and time between different scans by using repeated-measures analysis of variance in PAD, sMCI, and NL groups separately. To examine the effects of using different brain parcellation schemes on FAC and the graph theory network measures, we repeated all analyses with a 268-node functional atlas (Finn et al., 2015) by using the same procedure as used with AAL-based analyses. The parcellation image is publicly available on the BioImage Suite NITRC page (https://www.nitrc.org/frs/?group_id=51).

Results

FDG PET-based AD classifier

Using a general linear model analysis on 88 AD patients and 88 age–sex matched healthy controls, we derived voxel-based and ROI-based FAC (Katako et al., 2018). The β map is characterized by a decline in FDG uptake (or hypometabolism) in medial–frontal lobes, posterior cingulum, precuneus, inferior–parietal, and temporal lobes (Fig. 2). It also shows increased FDG uptake (hypermetabolism) in the cerebellum, paracentral lobule, and pons (Fig. 2).

FIG. 2.

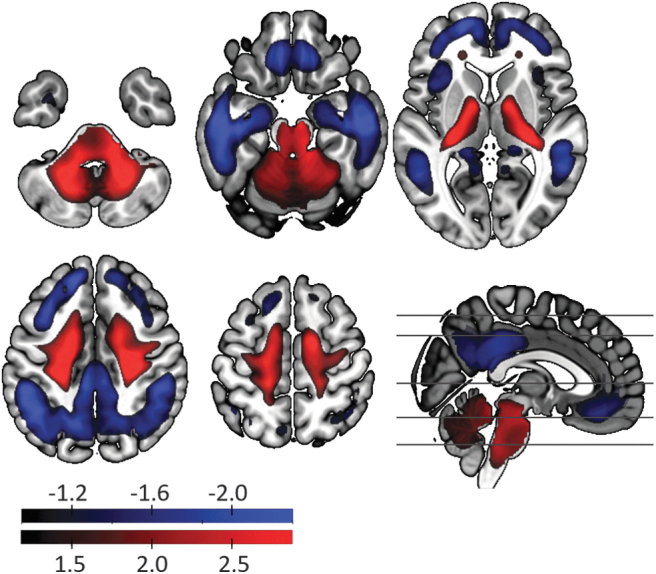
FAC. AD classifier FAC is characterized by the hypometabolism (shown in blue) in medial–frontal lobes, posterior cingulum, precuneus, inferior–parietal, and temporal lobes. Hypermetabolism (shown in red) is observed in the cerebellum, paracentral lobule, and pons in AD. The voxel-wise coefficient (voxel-weights of FAC) was z-scored to the mean and standard deviation of the whole-brain. FAC, FDG PET-based AD classifier.

The voxel-based FAC demonstrated excellent sensitivity (87.50%) and specificity (82.95%) in the classification of AD versus NL1 subjects. This was preserved in a 10-fold cross-validation with high sensitivity (84.09%) and specificity (80.95%), suggesting the minimal effects of overfitting. The ROI-based FAC had almost identical metabolic topology with high topographical similarity between two classifiers (r = 0.9720, p = 8.92E-75). Slightly less performance was achieved with ROI-based FAC (sensitivity of 71.59% and specificity of 86.39%; 10-fold cross-validation sensitivity of 79.55% and specificity of 77.27%).

AD metabolic network profile

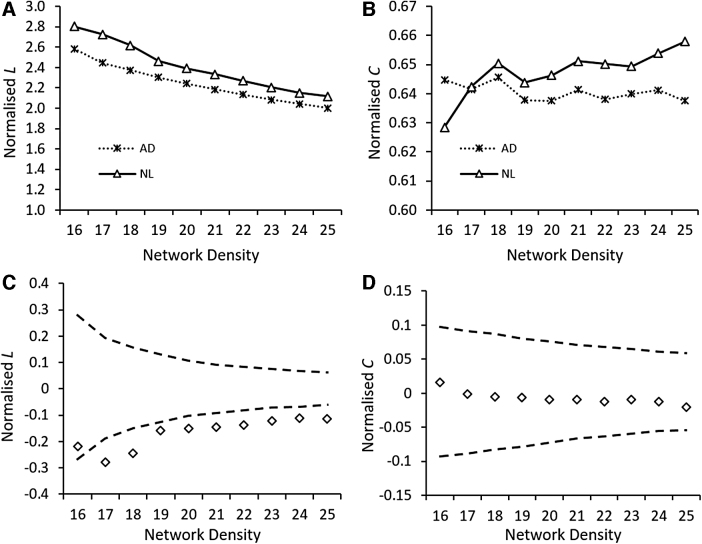
Overall, the L in the AD metabolic network was lower than the L in the NL1 metabolic network over the network density range of 16–25% (Fig. 3A). The decrease in L was statistically significant over the examined network density range by 1000 permutations (Fig. 3C). This is indicative of increased global efficiency in the AD network for information transfer. On the contrary, C in the AD metabolic network was not statistically different from the C in the NL1 metabolic network over the network density range of 16–25% (Fig. 3D).

FIG. 3.

Group differences in characteristic path length (L) and clustering coefficient (C) as a function of network density. The changes in L (A) and C (B) of the AD and NL1 network over the network density range of 16–25%. Group differences in L (C) and C (D) between AD and NL1 network over a network density range of 16–25%. The gray lines indicate a 95% confidence interval defined by a permutation test with 1000 permutations. The + marker shows the difference between NL1 and AD networks (i.e., NL1_metric – AD_metric); the + marker falling outside the confidence interval shows network densities at which between-group differences are significant. The positive values of + indicate NL1_metric > AD_metric, whereas the negative values of + indicate NL1_metric < AD_metric.

Hubness correlates with abnormal AD metabolic topography

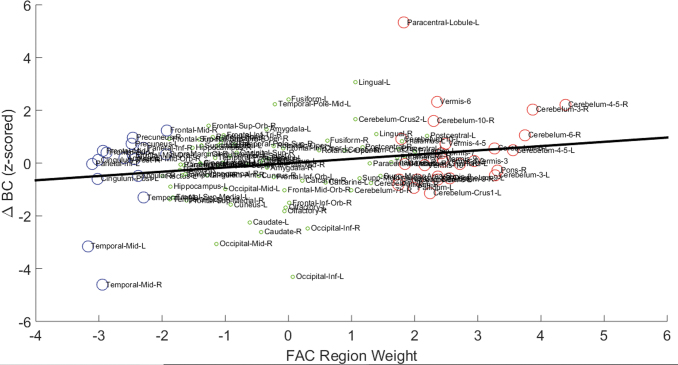
We compared the association between the difference in BC between AD and NL networks (deltaBC) and the FAC region weight for each anatomical parcellation (Fig. 4). The deltaBC and FAC weight for each ROI can be found in Supplementary Table S1. Analysis revealed that the cerebellum, paracentral lobule, mid-temporal pole, and lingual gyrus showed significantly higher BC in the AD network than the NL1 network. Conversely, the caudate, inferior occipital, mid-occipital, and mid-temporal pole had significantly lower BC in the AD network as compared with the NL1 network. These group differences in BC were significantly correlated with β (a measure of increased/decreased FDG uptake in these regions) in FAC (r = 0.254, p < 0.005; Fig. 4). This suggests that the hub regions (high BC) of the AD brain network generally demanded more energy consumption whereas the peripheral brain regions (low BC) in the AD brain network were associated with decreased glucose metabolism.

FIG. 4.

Correlation between FAC region weights and BC of regions. The region weights of regions on FAC are plotted on x-axis, whereas the normalized difference in BC between AD and NL networks is plotted on y-axis. The regions are delineated by using AAL. The regions shown by red circles are identified as hypermetabolic on the AD metabolic pattern, whereas the ones shown in blue are identified as hypometabolic on FAC. The regions denoted by green circles are the ones that do not undergo significant metabolic change in AD. A significant correlation (r = 0.254, p < 0.005), shown by a solid black line, exists between region weights of regions on FAC and their corresponding BC values. BC, betweenness centrality.

The relationship between hubness and abnormal AD metabolic topography was replicated when a 268-node functional atlas was used as an alternate parcellation scheme (r = 0.125, p = 0.04; Supplementary Fig. S1). The functional atlas used here is produced by using a group-wise graph theory-based parcellation scheme for node definition in network analysis. This suggests that this relationship is not sensitive to how brain regions are defined in a brain parcellation atlas.

Longitudinal changes of FDG-SUR in hub versus non-hub regions

We investigated the longitudinally measured changes in FDG-SUR to compare metabolism in the regions with positive ΔBC (>2; regions that showed higher BC in AD vs. NL1), regions with NS ΔBC (<2 and ≥2; regions that showed similar BC in AD vs. NL1), and regions with negative ΔBC (≤2; regions that showed lower BC in AD vs. NL1) in NL2, sMCI, and PAD. Significant main effects of time were observed in all three groups (NL2, sMCI, and PAD; p < 0.001). Significant interaction effects between time and brain regions (divided by ΔBC) were observed only in PAD (F[4,152] = 10.962, p = 7.764E-08; Fig. 5). In particular, the hub regions of the AD network with high ΔBC showed increased metabolism over time (p = 0.001, post hoc Bonferroni). The metabolic changes in regions with negative ΔBC and NS ΔBC were not significant (p > 0.147, post hoc Bonferroni). No significant interaction effect was observed between time and brain regions in NL2 (F[2,73] = 1.144, p = 0.324) or sMCI (F[4,152] = 0.706, p = 0.589).

FIG. 5.

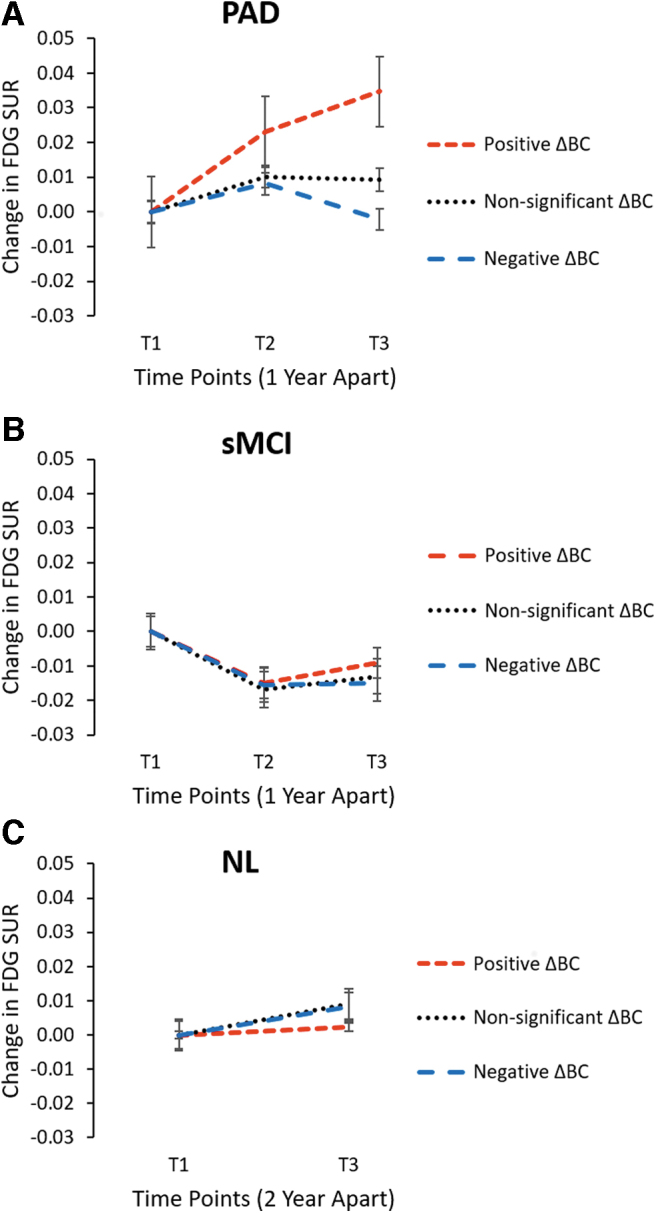
Longitudinal changes in FDG-SUR. The overall averaged changes in FDG-SUR in the high ΔBC regions (shown by dotted red line), NS ΔBC regions (shown by dotted black line), and low ΔBC regions (shown by dotted blue line). The high, NS, and low ΔBC regions were determined based on BC differences between AD and NL1 shown in Figure 5 (ΔBC >2, −2 < ΔBC <2, ΔBC < −2, respectively). (A) In the PAD subjects, there is a significant difference in averaged FDG-SUR between three groups with a significant interaction effect of ROI group and time (F[4,152] = 10.962, p = 7.764E-08). The metabolism increases significantly in “hub” regions in PAD subjects near conversion to AD. (B) In the sMCI subjects, there is no significant difference in averaged FDG-SUR between three ROI groups (F[4,152] = 0.706, p = 0.589). (C) In the NL2 subjects, there is no significant interaction effect of ROI group and time (F[2,73] = 1.144, p = 0.324). ROI, region of interest; NS, non-significant.

Discussion

Conventional practices of FDG PET reading for AD diagnosis have focused on hypometabolism in key anatomical regions (Katako et al., 2018; Teune et al., 2014). Hypermetabolism observed in AD is often dismissed as an artefact arising due to use of global mean for normalization in traditional studies (Borghammer et al., 2009). There is increasing evidence from anatomical and neuroimaging studies, which is leading to a paradigm shift in the role of hypermetabolic regions in neurodegenerative diseases (Miyazawa et al., 2010). Emerging evidence suggests that the hypermetabolism observed in AD patients is an integral part of AD pathophysiology (Apostolova et al., 2018). Using WM mean for signal normalization under the assumption that the overall activity in the WM is not significantly altered in AD, we confirmed that hypermetabolism observed in AD is not an artefact that is merely induced by the global signal normalization.

In further graph theory analysis on the metabolic network, we observed a statistically significant decrease in L in the AD metabolic network when compared with NL1, whereas the changes in C were not statistically significant between the two groups. The phenomena of decreasing L and unchanging C is a well-described characteristic in Watts–Strogatz smallworld model (Watts and Strogatz, 2011), where it was explained as such that a network becomes a small world (and more cost-efficient) when there is more “randomness” in the re-wiring process. The random rewiring of the connections in a network introduces shortcuts among nodes, resulting in decreased L while maintaining C, thus making AD whole-brain network “small-world like” (Lovejoy and Loch, 2003; Saramäki et al., 2007).

A resting-state fMRI study of AD subjects found that decreased path length is directly associated with lower mini-mental state exam (MMSE) scores, suggesting that an increase in the random topology of a graph is associated with worse cognitive functioning (Tijms et al., 2013b). Maintaining the balance of short path length and high clustering in the AD network suggests an evolutionary optimization of the equilibrium between information segregation (represented by nodes forming particular clusters) and information integration (represented by interactions among clusters; Tijms et al., 2013a). The regional changes associated with this increased “randomness” (N.B. it should be noted that we are not implying that the brain network rewiring is happening in a random fashion, but it refers to the opposite of the regular network in Watts–Strogatz model) can be investigated by understanding which regions gained hubness (the new important functional node).

The BC for each node quantifies the hubness of that node by incorporating connectivity information from the whole network (Arendt, 2009). Brain regions acting as hubs make information processing in the network more efficient, thereby increasing the robustness of the network toward random failure (Albert et al., 2000). Cerebellar lobules, paracentral lobule, and lingual gyrus were the key regions associated with increased hubness in the AD network as compared with controls. The increased hubness may reflect the adaptive role of these regions (via increased recruitment) in AD patients to limit the clinical consequences of loss of functionality in large-scale networks associated with high-level cognition in AD patients.

Recent research on the functional topology of the cerebellum has implicated the cerebellum in the modulation of many distributed networks, including cognitive, emotional, and autonomic functions (reviewed in Schmahmann, 2019). Previous brain imaging studies have established the integral role of the cerebellum in the modulation of cognition and emotion, suggesting its contribution to cognitive and neuropsychiatric deficits in AD (Jacobs et al., 2018). The cerebellum is reported to be associated with cerebral sensorimotor regions and higher-order cognitive regions via feedback projections through thalamus (Schmahmann, 1998). These connections suggest cerebellar involvement in cognitive processes, and the observation that these connections retain their functional capacity in early stages of AD may explain the increased hubness in cerebellar regions in AD patients. Our results have supported the assertion that cerebellar hypermetabolism in AD is not an artefact resulting from the whole-brain mean proportional scaling of FDG-PET images. In addition, we have shown that many of these hypermetabolic cerebellar regions increase in BC in AD. If feed-forward and feedback pathways of the posterior cerebellum are relatively spared in AD-related neurodegeneration, the observed increase in metabolism and BC hubness could be interpreted as a compensatory mechanism.

The paracentral lobule and lingual gyrus are associated with sensorimotor and visual information integration, respectively. The increased metabolism and hubness in these regions are commonly identified in neurodegenerative disorders, including AD (He et al., 2008). It has been reported that the hyperactivity in the paracentral lobule is associated with delusional thinking, which is present in 31% of AD patients (Nemoto et al., 2010; Stone et al., 2015; Zhao et al., 2016). The lingual gyrus has been implicated in anxiety and depression, which is present in 39–42% of AD patients (Couvy-Duchesne et al., 2018; Zhao et al., 2016). These neuropsychiatric symptoms may have worsened during the PET center visits, which may explain the observed increase in hubness of lingual gyrus in the AD network when compared with NL.

We observed a significant decrease in the hubness of a few hypometabolic regions in the AD network, which may be a direct consequence of corticocortical dysconnectivity (Stone et al., 2015). These regions (middle temporal, occipitotemporal, and caudate) have been well documented to be affected in AD (Nemoto et al., 2010; Zhao et al., 2016). The loss of local centrality in these regions has been found to be strongly related with the cognitive decline in AD patients (Couvy-Duchesne et al., 2018). Thus, decreased BC paired with decreased metabolism in the mid-temporal region, inferior occipital region, and caudate may be explained by the loss of neuronal function and potentially accompanied by atrophy (Yao et al., 2010).

It must be noted that the level of correlation between changes in BC and glucose metabolism was very weak (r = 0.25), although it was statistically significant. The significance was primarily driven by a few hypermetabolic and hypometabolic nodes paired with increased and decreased BC, respectively, as described earlier. However, the majority of the brain regions showed preserved BC level in AD compared with NL1; whereas apparent metabolic changes have been consistently observed (Tijms et al., 2013b). This may be caused by relative insensitivity of BC measurement, the statistical significance of which was conservatively tested with 1000 permutations (Hosseini et al., 2012). It should be also noted that the AD individuals that were included in the ADNI project had very early stage AD (MMSE score ranges from 20 to 26), and thus it may be possible that these regions retained some level of functional connectivity despite decreasing neuronal glucose metabolism (Convit et al., 2000).

To understand the functional relevance of the regions with a significant increase in hubness (high ΔBC regions) or significant decrease in hubness (negative ΔBC regions) in AD development, the longitudinal metabolic changes were compared in PAD, sMCI, and NL2. When divided by ΔBC of AD versus NL1 networks, the regions with high ΔBC (which included cerebellar lobules, left lingual gyri, paracentral lobule) are the only regions that showed significant metabolic changes (increased) over the 3 years of the follow-up period in PAD, which was not observed in sMCI or NL2. This suggests that the progressive regional metabolic increases associated with increased hubness precede AD diagnosis at least by 1 year and that it may be involved with rapid symptom worsening that can be observed 1 year before the clinical diagnosis.

Conclusion

The present study suggests that hypermetabolism observed in AD is not an artefact of using global mean in signal normalization; instead, it suggests that hypermetabolism might be an integral component of AD pathology, especially in the early stage of the disease. There is rich, but under-appreciated literature, documenting cerebellar hypermetabolism in AD and the role of the cerebellum in AD pathology. This study suggests that more research is needed to understand the cause of hypermetabolism in AD and potentially investigate the role of the cerebellum in neuropathology and disease progression in AD.

The disruption in large-scale structural and functional neuronal networks in AD causes the network to become more random, resulting in an evolutionary optimization of the balance of information segregation and information integration. Within this framework, we propose that the cerebellum is more than a silent bystander in the pathophysiology of AD. We suggest a robust model where the loss of hubness in cortical regions observed in AD patients is paralleled by an increase in the hubness of cerebellar regions, with the possible adaptive role to limit the clinical consequences of tissue damage associated with AD.

Authors' Contributions

Conceptualization, J.H.K., V.G.; Methodology and investigation, J.H.K., V.G.; Writing—original draft, V.G.; Writing—review and editing, J.H.K., S.B.; Funding acquisition, J.H.K.; Supervision, J.H.K.

Author Disclosure Statement

The authors declare no conflict of interest.

Funding Information

The funding for this project was provided by the Natural Sciences and Engineering Research Council of Canada, Mitacs, Canada Foundation for Innovation, and University of Manitoba.

Supplementary Material

Supplementary Table S1

Supplementary Figure S1