Abstract
Imaging the dynamic behavior of neuromodulatory neurotransmitters in the extracelluar space that arise from individual quantal release events would constitute a major advance in neurochemical imaging. Spatial and temporal resolution of these highly stochastic neuromodulatory events requires concurrent advances in the chemical development of optical nanosensors selective for neuromodulators in concert with advances in imaging methodologies to capture millisecond neurotransmitter release. Herein, we develop and implement a stochastic model to describe dopamine dynamics in the extracellular space (ECS) of the brain dorsal striatum to guide the design and implementation of fluorescent neurochemical probes that record neurotransmitter dynamics in the ECS. Our model is developed from first-principles and simulates release, diffusion, and reuptake of dopamine in a 3D simulation volume of striatal tissue. We find that in vivo imaging of neuromodulation requires simultaneous optimization of dopamine nanosensor reversibility and sensitivity: dopamine imaging in the striatum or nucleus accumbens requires nanosensors with an optimal dopamine dissociation constant () of 1 μM, whereas above 10 μM are required for dopamine imaging in the prefrontal cortex. Furthermore, as a result of the probabilistic nature of dopamine terminal activity in the striatum, our model reveals that imaging frame rates of 20 Hz are optimal for recording temporally resolved dopamine release events. Our work provides a modeling platform to probe how complex neuromodulatory processes can be studied with fluorescent nanosensors and enables direct evaluation of nanosensor chemistry and imaging hardware parameters. Our stochastic model is generic for evaluating fluorescent neurotransmission probes, and is broadly applicable to the design of other neurotransmitter fluorophores and their optimization for implementation in vivo.
Keywords: Fluorescent probes, neurochemical imaging, nanosensor kinetics, stochastic simulation, dopamine, striatum, neuromodulation
Graphical Abstract
INTRODUCTION
Diffuse volume transmission constitutes an important element of neuronal signaling for certain neurotransmitters such as acetylcholine, dopamine, norepinephrine, and serotonin. While classical neurotransmission is confined to communication between the pre- and postsynaptic neuron, and is mediated by fast acting ligand-gated ion channels, neuromodulation employs slower acting metabotropic receptors that exhibit a high level of extrasynaptic expression.1 Thus, modulatory neurotransmitter activity extends well beyond the synapse. As a consequence, neuromodulators such as dopamine influence a population of neurons beyond the synapse, enabling a single neuron to modulate the activity of a larger network of neuronal cells. It is therefore of great interest to develop tools to observe and quantify the release, diffusion, and reuptake of neuromodulatory neurotransmitters such as dopamine, where the spatial and temporal dynamics observed in the brain extracellular space (ECS) can be directly linked to receptor activation, neuronal activity, and behavior.
Among the most prominent dopaminergic systems are the nigrostriatal, mesocortical, and mesolimbic projections. Small clusters of dopamine neuron cell bodies located in the substantia nigra pars compacta (SNc) make extensive connections with the medium spiny neurons (MSN) of the dorsal striatum, forming the nigrostriatal pathway.2 This pathway is responsible for controlling fine motor movements and its dysfunction underlies the pathology of Parkinson’s disease.3 Axons of dopaminergic cell bodies in the ventral tegmental area project into the nucleus accumbens and the prefrontal cortex, forming the mesolimbic and mesocortical pathways, respectively.2 These systems play significant roles in cognitive control of behavior and reward processing, and their dysfunction contributes to the pathology of depression, addiction, schizophrenia and attention deficit hyperactivity disorder (ADHD), among others.4–8 In all of these systems, neuromodulation, as opposed to neurotransmission, is the primary mode of influence. This diffusion-mediated transport of dopamine in the ECS is also known as volume transmission.9
One of the most ambitious pursuits in neuroscience is elucidating the relationship between neurons, neural circuits, behavior, and disease.10 Successful chronic and real-time recording of neurotransmitter mediated chemical signaling would be a decisive step in that direction.11 Current methods to measure the dynamics of dopamine volume transmission in ECS lack the spatial and/or temporal resolution of relevance to study neuromodulation. Voltammetry and amperometry are electrode-based methods used to record the presence of neuromodulators via redox chemistries, yet require penetration of the brain tissue and only assay neurotransmitter concentration at one point in space. Optical probes include cell-based neurotransmitter fluorescent-engineered reporters (CNiFERs) that have been engineered to express a chimeric dopamine receptor and a genetically encoded calcium indicator.12 CNiFERs utilize slow G-protein coupled receptor (GPCR) responses and thus do not report millisecond or micrometerscale neurotransmitter activity. Fluorescent false neurotransmitters (FFNs) fluorescently label dopaminergic vesicles and provide single release site resolution but do not report neurotransmitter concentrations in ECS.13–15 Calcium imaging can show bouton activity in dopamine axons preceding release but tell us little about extracellular dopamine concentration.15 In sum, existing methods are insufficient to enable reliable measurements of dopamine and other modulatory neurotransmitters in the ECS with the necessary spatial and temporal resolution to be commensurate with physiological function. As a result, the theoretical framework developed to date has served primarily to describe the local, not global, dynamics of neurotransmission. Recent advances in new optical probes that report changes in extracellular dopamine concentrations in real time with significant spatial information warrant a thorough theoretical study of how such optical reporters of ECS neurotransmitter concentrations should be designed and implemented in vivo for recording fast dynamic processes.
Herein, we generate a theoretical framework with which to evaluate fluorescent probes designed to record the dynamics of modulatory neurotransmitters in the ECS under ex vivo and in vivo imaging conditions. We develop a model to probe the spatiotemporal profiles of dopamine in the striatum accounting for the stochasticity of dopamine quantal release, diffusivity, and reuptake, combined with fluorescent nanosensor kinetics and microscope imaging parameters. We implement our model in the context of nanoparticle-based near-infrared fluorescent nanosensors for dopamine16–18 and develop appropriate neurochemical and imaging boundary conditions under which imaging of fast dynamics of dopamine neuromodulation can be accomplished for in vivo relevant spatial and temporal scales. Our results show that the process of dopaminergic neuromodulation occurs on characteristic time scales on the same order as exposure times used to optimize fluorescence imaging, thereby introducing temporal distortions in dopamine recordings. Therefore, when we optimize sensor–analyte binding interactions, a phenomenon emerges in which only sensors with kinetics parameters in a small critical window become feasible for in vivo imaging of fast dynamic processes. We probe these phenomena in the spatial domain as well. With physiologically relevant in vivo firing behavior of striatal dopamine neurons, we show that optimally selected sensor kinetics and imaging frame rates can capture behavior-relevant dynamics of phasic release in the dorsal striatum, with the necessary temporal resolution and signal-to-noise ratio (SNR) to distinguish individual transient events elicited by dopamine release and reuptake.
RESULTS AND DISCUSSION
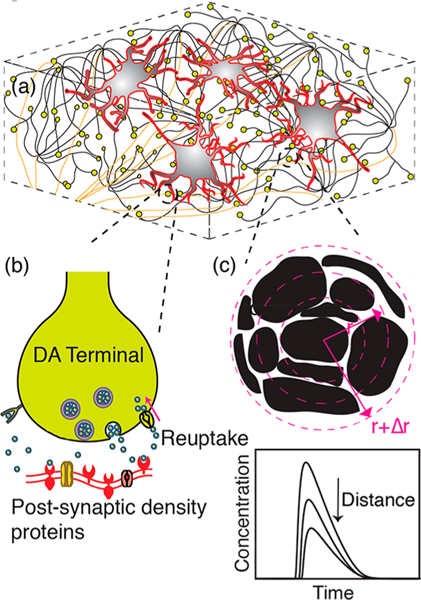
We model the diffusion driven dynamics of dopamine in the ECS of striatal tissue by numerically solving the diffusion equation with dopamine source and sink terms. Dopamine sources are the quantal releases from dopaminergic terminals within a defined simulation volume, while the reuptake of dopamine from the ECS acts as a sink. Reuptake parameters are assumed to be uniform throughout the simulation volume. We set the simulation volume as a cubic block of striatal tissue comprised of evenly interspaced dopamine terminals. A schematic of striatal tissue model with dopamine terminals depicted as yellow spheres is shown in Figure 1a. We use the nigrostriatal projection as a model system owing to its critical role in reward and reinforcement, addictive behavior, habit formation, and its implications for motor neuron disorders, such as Parkinson’s disease. Furthermore, the nigrostriatal system is well described in the literature, providing requisite physiological parameters relevant to dopaminergic neurotransmission with which to implement our model.
Figure 1.
Schematic of dopamine model. (a) Dorsal striatum with medium spiny neurons (MSN, red contours/gray body), dopamine terminals (yellow), and projection axons (tan) from SNc. (b) Magnified view of an individual dopamine terminal forming a synapse onto a dendritic shaft of MSN. Dopamine release: An action potential causes a dopamine-containing vesicle to release dopamine into the synaptic cleft. Dopamine encounters postsynaptic receptor proteins, triggering further downstream neuronal processes. Dopamine reuptake: DATs clear dopamine from the ECS to be recycled. (c) Space discretization around a dopaminergic terminal representing tortuous morphology of brain tissue. Black represents tissue surrounded by void ECS. Concentric circles depict simulation volume elements. Inset graph: Dopamine concentration fluctuates in space and time as a result of release, diffusion, and reuptake.
Simulation Volume.
Dopamine terminals are the source of dopamine in our simulation, and dopamine transporters (DATs) drive dopamine reuptake. To elucidate the spatiotemporal dynamics of dopamine concentration in the ECS, we define our simulation space as a 1000 μm3 () volume of striatal neural tissue containing 100 dopaminergic terminals. Terminals are arranged in a periodic lattice structure filling the simulation volume. The structural and functional parameters of our simulation volume are summarized thus: (i) the density of dopaminergic terminals in the striatum, (ii) probability of dopamine release upon membrane depolarization, (iii) amount of dopamine released per quanta (per vesicle fusion), (iv) effective diffusivity of dopamine in tissue, and (v) dopamine reuptake kinetics by DATs. A summary of parameter values and literature sources is provided in Table 1.
Table 1.
Values of Simulation Parameters and Literature Sources
| parameter | value | ref |
|---|---|---|
| dopaminergic terminal density in the dorsal striatum () |
0.1 μm−3 | 22 |
| dopamine molecules released per quanta () | 5000 | 28, 52 |
| terminal release probability () | 0.06 | 13, 14, 25, 56 |
| Effective diffusivity () | 322 μm2·s−1 | 28, 34 |
| void fraction of striatal tissue () | 0.21 | 35 |
| maximum reuptake rate () | 4.1 μm·s−1 | 36 |
| Michaelis–Menten constant () | 0.21 μm | 36 |
Model Representation of Dopamine Terminals.
We define dopamine terminals as the boutons of axonal projections from the SNc into the dorsal striatum (Figure 1a). Cell bodies of dopaminergic neurons of the nigrostriatal pathway are located in the SNc and their axonal projections ascend into the dorsal striatum and make connections with dendritic spines or dendritic shafts of MSNs.19–21 These ascending axonal tracts are notable for their high terminal density, where each axon is estimated to make on the order of 400 000 connections in the striatum.22–24 A dopaminergic terminal contains a cluster of vesicles in close proximity to symmetric membrane densities, forming dopaminergic synapses with MSNs (Figure 1b). Asymmetric synapses also constitute a minority of synaptic configurations, in which case long-range effects of neuromodulation will dominate over local synaptic effects.1,20 Our simulation considers these sites as point release sources in a three-dimensional space. We recreate the neuroanatomy within the simulation volume as described in previous computational studies.25–28
Dopamine Release Sites and Probability of Release.
Neurotransmitter release occurs at release sites within synapses. We execute our model for which each dopamine terminal possesses a single release site29 (Figure 1b), where dopamine release probability per action potential per terminal is set to 6%.15,25 The probability of quantal release is a function of the size of the readily releasable pool (RRP) in proportion to the total pool size which encompasses the RRP, the recycling, and reserve pools.30 For dopaminergic activity in striatum, the low dopamine release probability is further supported by experimental results, which reveal that many dopamine terminals remain “silent” during stimulation.13,14 We assume a constant probability of release and quantity of release in the simulation, although some temporal and spatial heterogeneities have been reported.13,31,32 Furthermore, membrane depolarization, which drives neurotransmitter release, is mitigated by voltage-gated sodium channel activity which remain inactive for ~10 ms following an action potential.33 Thus, we impose a constraint in our simulation to limit sequential dopamine release events to occur at intervals greater than 10 ms per terminal, for a 100 Hz maximum release rate for any given terminal. Despite this maximum release rate, the low probability of release makes it such that the 100 Hz boundary condition is rarely encountered in our simulations
Simulation of Release, Diffusion, and Reuptake.
Our simulation of dopamine concentration in the ECS invokes the equation of change for species conservation surrounding a dopaminergic terminal27
| 1 |
where represents spatial () and temporal () variation in dopamine concentration, and and represent quantal release of dopamine into the ECS and reuptake by DATs, respectively. is the effective diffusivity of dopamine in tissue after accounting for tortuosity of brain tissue.34,35 We solve this governing equation at each dopamine release terminal using finite difference method, and obtain the solution for temporal and spatial dopamine dynamics resulting from release from one dopamine terminal. Striatal tissue is composed of approximately 1 terminal per 10 μm3.22,24 With this terminal density, we determine the temporal profile of dopamine concentration resulting from the activity of all terminals included in the simulation volume of interest as described in Methods. Lastly, we discretize the governing equation to solve it numerically, since no known analytical solutions exist for this equation. The difference equation is written in spherical coordinates as forward difference in time and central difference in space.
Quantal Release.
In eq 1, represents quantal dopamine release following vesicle fusion25 and is represented by
| 2 |
where represents the number of dopamine molecules released per exocytosis event and represents Avogadro’s number. The parameter assumes a value of 1 or 0 based on a release probability . A release event increases the concentration of the first spatial element of the simulation volume (Figure 1c) by an amount represented by
| 3 |
This is the volume element immediately surrounding the location of the dopamine release site (Figure 1b, c). The parameter accounts for porosity of brain tissue.27 We use a Gaussian probability density function to determine the spatial distribution of dopamine immediately after release, normalized to ensure that only 5000 () molecules of dopamine are released per quanta (Table 1). Dopamine spillover after quantal release is instantaneous.28 Thus, a quantal release event affects the concentration of volume elements away from the center of the release site by an amount equal to the increase in the center of the release site (eq 3) scaled by an exponential decay term, . This exponential term is a function of the distance of the volume element from the center of the release site , where represents the spatial index, , representing each volume element in the simulation. The sum of this exponential scaling term over the spatial indices gives rise to the normalization constant, 1.386. Firing frequency () sets the number of action potentials over a given simulation period. The temporal distribution of action potentials over the simulation time period, , is modeled as a Poisson distribution with mean a firing rate of . is a delta function in time and ensures that release can only occur during an action potential firing event with a binary probability .
Dopamine Reuptake.
Reuptake of dopamine from the ECS occurs via DATs. In our model, we assume a uniform distribution of DATs in the simulation volume and model dopamine reuptake with a Michaelis–Menten rate equation with parameters and and in a medium of porosity .27,36
| 4 |
Dopamine saturation must be taken into account especially for simulation regions in close proximity to a terminal, where dopamine concentration immediately following a release can be very high. This nonlinear expression allows for saturation of the dopamine reuptake process at high physiological dopamine concentrations, corresponding to the case of substrate saturation.
Single Terminal Behavior.
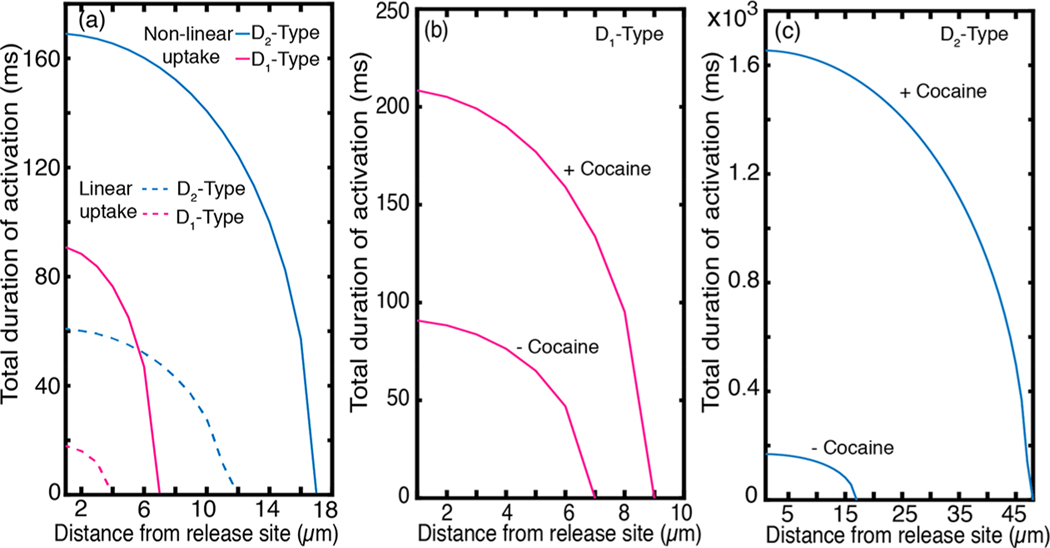
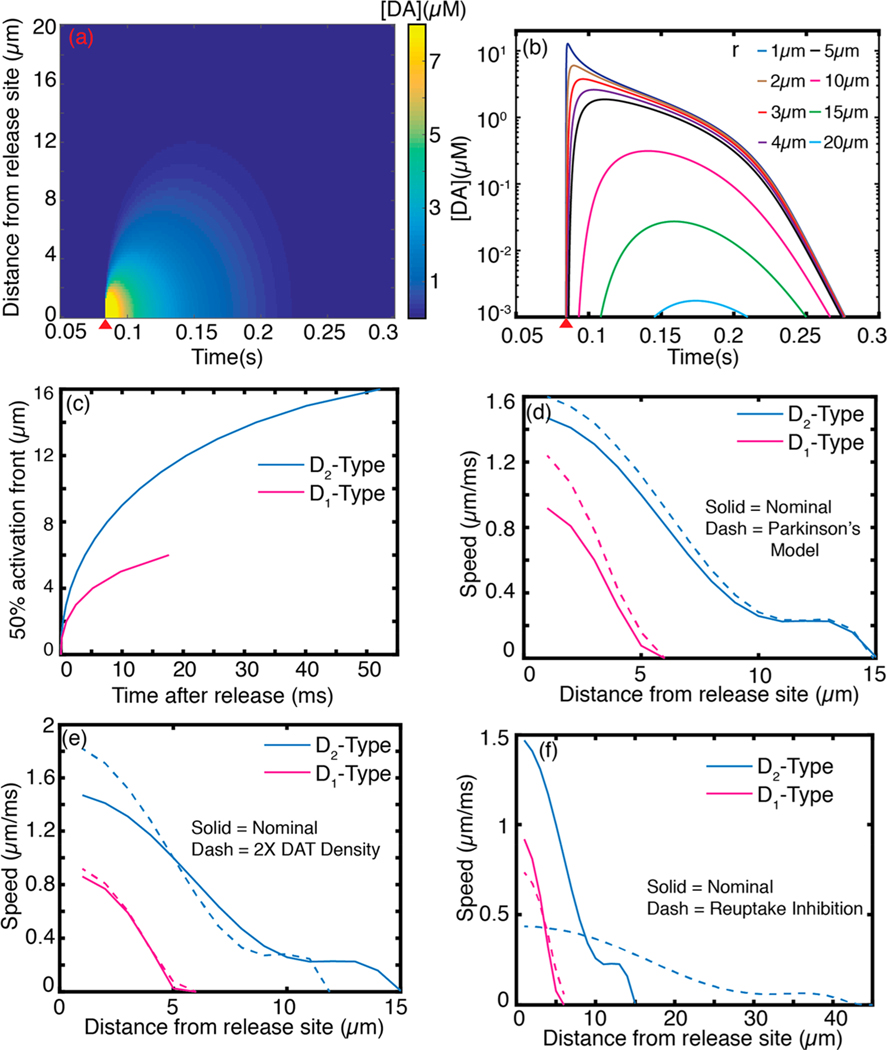
The spatiotemporal dynamics of dopamine in the ECS following release from a single terminal influences dopamine receptors within the diffusion volume prior to dopamine reuptake. Dopamine is the primary endogenous ligand for two dopamine receptor subclasses: -type and -type receptors, with binding affinities of 1 μM and 10 nM, respectively.28,37 We define the sphere of influence of a quantal release of dopamine after release from a terminal based on these activation values.28 Our simulation shows that for a single quantal release from a terminal, the sphere of influence on low affinity -type receptors and high affinity -type receptors is 7 and 17 μm, respectively (Figure 3a). The spatiotemporal dynamics of a quantal release from a single terminal over a 20 μm radial distance shown in Figures 2a,b, 3a, and S1, is consistent with prior studies that show that dopamine diffuses from synaptic termini in quantities that overflow the synaptic cleft, giving rise to dopamine volume transmission.26,28
Figure 3.
Nonlinear computation of receptor activation by dopamine diffusion. (a) Sphere of influence of a single dopaminergic terminal over - and -type receptors. Time over which the of each receptor type is exceeded is plotted as a function of distance from the terminal. - type receptors are insensitive to quantal release at 7 μm radial distance beyond the release site, whereas -type receptors can be influenced by a single quantal release through a radial distance of 17 μm. The duration during which the of each receptor type is exceeded decreases monotonically with distance. Broken lines represent spheres of influence of linear uptake kinetics with the nominal and values listed in Table 1. (b) Effect of dopamine reuptake blocker, cocaine, on sphere of influence of -type receptors, plotted as receptor activation duration as a function of distance from release site. (c) Same competitive inhibition effect on -type receptor activation. Cocaine increases the sphere of influence on -type receptors dramatically.
Figure 2.
Spatiotemporal dopamine dynamics following a single action potential driven quantal release of dopamine. (a) Dopamine concentration profile evolution following a single quantal release as a function of distance and time. Red wedge indicates quantal dopamine release. (b) Dopamine spatial concentration profile at varying distances from release site. (c) Front (instance where is exceeded) of dopamine receptor activation following dopamine release for (pink) and (blue) type receptors. (d) Propagation speed of - and -type receptor activation after a quantal release obtained from first derivative of (c) (solid trace) compared with propagation speed obtained with porosity and tortuosity of ECS in Parkinson’s disease. (e) Nominal propagation speeds compared with speeds computed with DAT density increased by a factor of 2. (f) Nominal propagation speeds compared with speeds in which dopamine clearance is competitively inhibited.
Dopamine propagation from the center of the synaptic cleft occurs on short time scales relative to dopamine diffusive effects. Our simulation shows that the activation for both and -type receptors within the sphere of influence of a terminal are exceeded within 50 and 20 ms of dopamine release, respectively (Figure 2c). Furthermore, we compute the speed of propagation of receptor activation as a function of distance from the release site (Figure 2d, solid). The -type receptor activation wavefront (10 nM dopamine) moves forward at peak speeds approaching 1.5 μm·ms−1 and slows to 0 μm·ms−1 as a function of distance from the release site. Similarly, we observe peak propagation speeds of 1 μm·ms−1 for -type receptor activation (1 μM dopamine). Our simulations provide estimates for speeds of dopamine volume transmission, and the time dependence of dopamine’s activity on distal receptors from the release point. As expected, dopamine volume propagation speeds we compute for - and -type receptors is four to 5 orders of magnitude slower than reported speeds of electrical signal propagation in nerve fibers.33,38 To our knowledge, this is the first quantitative report on the speed of chemical signaling of dopamine in the dorsal striatum.
We studied the effect of varying simulation parameters on the speed of signal propagation in the striatum. Changes in morphology of the ECS in disease states and under hypoxic conditions could affect dopamine volume transmission. Brain tissue afflicted by Parkinson’s disease shows changes in the tortuosity and porosity of the ECS morphology, where porosity and tortuosity decrease by 33% and 5%, respectivly.39 When such parameters are varied in our simulation, we observe modest increases in the speed of propagation for both and receptor types, with the effect being slightly higher for -type receptors (Figure 2d). We next explored the anisotropy of volume transmission that could arise from heterogeneous DAT expression. When we double the density of DATs, we observe enhanced transmission speeds for -type receptors for proximal regions that are colocalized with high DAT expressions, and slower transmission speeds for distal sites and a correspondingly reduced overall sphere of influence (Figure 2e). On the other hand, competitive inhibition of DATs by cocaine slows the speed of -type receptor activation and increases the activation sphere of influence (Figures 2f and 3c). Combined, these results suggest that anisotropy in dopamine neuromodulation could in part be driven by heterogeneities in capacity for dopamine clearance in the striatum. In regions close to the release site (<5 μm), high DAT expression creates a concentration gradient driving force that speeds up the activation of colocalized receptors, whereas reuptake inhibition slows the speed of volume transmission.
Nonlinear reuptake kinetics we defined in eq 4 is sometimes approximated by a linear expression of the form .27 While a linear approximation of dopamine reuptake facilitates an analytical solution for the governing equation, linearization creates significant deviation from dopamine dynamic behavior obtained with nonlinear reuptake kinetics (Figure 3a). The impact of the linear approximation on dopamine reuptake kinetics arises from neglecting the fact that DATs in close proximity to the releasing terminal are saturated and can only clear dopamine at a maximum rate of . The linear approximation overestimates uptake in regions proximal to the point of dopamine release, resulting in different linear versus nonlinear reuptake kinetics. Our model implements nonlinear reuptake kinetics with a Michaelis–Menten rate equation, and enables us to calculate the spatial sphere of influence with the biologically relevant influence of saturating dopamine reuptake proximal to the release site. Indeed, our results show the spatial sphere of influence with linear uptake is only half of that obtained with nonlinear kinetics for D1-type receptors (Figure 3a). To demonstrate the importance of treating the reuptake kinetics as a nonlinear saturable process, we compared the linear model at nominal and values (Table 1) with a nonlinear model in which was increased by a factor of 10 (equivalent to increasing the density of DATs by an order of magnitude) and found the two dynamic behaviors to be comparable (Figure S2). Our results exemplify the importance of treating dopamine clearance from ECS as a nonlinear process, especially when spatial and temporal domains are simultaneously considered, and provide a quantitative comparison between linear and nonlinear reuptake on the dynamics of dopamine in ECS.
Certain psychostimulants act by competitively binding to DATs and modulating dopamine clearance rate from the ECS. We demonstrate the applicability of our model to probe the neurophysiology of dopaminergic systems by testing the effect of dopamine reuptake inhibition by cocaine. Cocaine has been shown to increase the affinity parameter in eq 4, , from 0.21 to 8 μM.40 Our simulation shows that inhibition of dopamine reuptake by cocaine increases the duration of -type receptor activation by up to 2-fold and that of -type receptors by up to 6-fold (Figure 3b, c). The spatial spheres of influence from a quantal release increase from 7 to 9 μm, and from 17 to 47 μm, for - and -type receptors, respectively. Our results suggest that competitive inhibitors—whether therapeutic or abusive—have drastic effects on the dopamine sphere of influence for a singular dopamine terminal, the extent of which is best demonstrated when we model dopamine reuptake as a nonlinear process.
Many-Terminal Behavior.
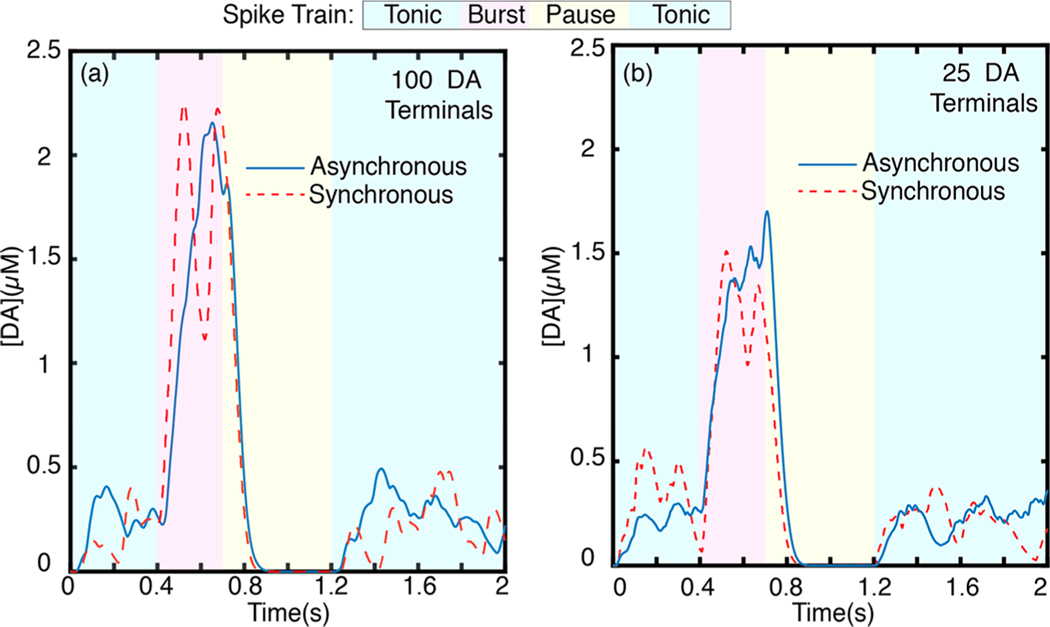
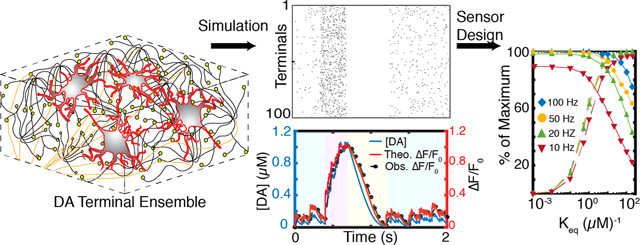
Dynamic dopamine behavior at a point in the striatal ECS is influenced by the behavior of active terminals in the vicinity. Dopaminergic neurons exhibit slow tonic and fast burst firing activity.41,42 A burst in firing activity correlates with reward reinforcement as a response to salient events, whereby striatal dopamine neurons burst in spike trains of 4–7 spikes per burst event at a spiking frequency of 20 Hz.41,43,44 Conversely, a pause in firing is correlated with response to adverse events or withdrawal of an expected reward. Tonic activity underlies dopaminergic activity at rest.41–44 We implement our model to calculate dopamine concentrations in a volume of striatal brain tissue for a simulated spike train of physiological relevance. To account for the neurologically relevant case of collective multiterminal activity, we extend our model to employ spatiotemporal summation of solutions from each terminal surrounding of a point of interest in the ECS (Methods). To this end, we evaluate spatiotemporal dopamine dynamics at a point of interest surrounded by 100 dopamine terminals (Figure 4a) and, separately, at a point surrounded by 25 terminals (Figure 4b) arranged at uniformly spaced cubic lattice points, with no terminal located closer than 2 μm to the point of interest. The terminal spacing of each cluster is based on density parameter defined in Table 1. We chose an extrasynaptic point located at least 2 μm from the closest terminal to avoid capturing the dominant behavior of synaptic dopamine hot spots in which behavior is dominated by the firing activity of the closest terminal. We simulate a 2 s spike train representative of phasic firing behavior by implementing our model over four distinct firing regimes (Figure 4). The simulated firing frequency and duration is chosen based on experimentally observed in vivo spiking activity of dopaminergic neurons:41,43 we simulate an ensemble of dopaminergic neurons undergoing a 4 Hz tonic firing rate for to , followed by a 20 Hz burst firing regime for to , followed by a 0.5 s pause (0 Hz) until . For the last 0.8 s of the simulation, we return to a 4 Hz tonic firing regime. Note that each firing rate is the mean of a Poisson distribution of firing rates among the ensemble, as we described in preceding sections and in Methods. The simulation ensemble size is commensurate with experimental fast scan cyclic voltammetry (FSCV) assays where the carbon fiber electrode samples dopamine overflow from a region encompassing ~100 dopaminergic terminals.45,46
Figure 4.
Dopamine concentration evolution profile for a simulated volume. (a) Dopamine dynamics at an extrasynaptic point surrounded by (a) 100 and (b) 25 phasically firing dopaminergic neurons with asynchronous firing (blue trace, solid) and synchronous firing (red trace, dashed). Each trace represents the average of independent simulation runs.
We present results from a cluster of 100 dopaminergic terminals and 25 dopaminergic terminals firing phasically with the above-described spike train to highlight how the underlying functional connectivity of terminals can result in different spatiotemporal dopamine behavior. While the firing activity of an individual or a pair of dopaminergic neurons is well studied, the number of terminals in a phasically firing ensemble is not well understood.43,47 We predict that functional or subfunctional connectivity influences the size of phasically firing ensembles and their synchrony.43 As such, we simulate a spike train from a phasically firing cluster of 100 dopaminergic terminals (Figure 4a) compared to a cluster of 25 dopaminergic terminals (Figure 4b) firing synchronously or asynchronously. Dopamine release is a highly stochastic process and the results presented here are average behavior from separate runs of our simulation. We present individual simulation runs and run average for the 100 terminal asynchronous firing case in Figure S3. In both terminal clusters, asynchronous firing results in a more temporally homogeneous concentration profile. Synchronous firing concentration profiles exhibit sharp dopamine concentration transients in all firing regimes (Figure 4). Peak dopamine concentration during burst phase is modestly higher for the 100 terminal cluster, and its scale and diffusion also has a larger spatial extent. Tonic dopamine concentration levels, however, are roughly the same for both the 100 and 25 terminal clusters. For both simulated terminal cluster sizes, tonic asynchronous firing gives rise to a steady basal dopamine level whereas synchronous firing does not. The pause in firing following burst firing activity clears dopamine from the ECS in both cases; complete clearance is achieved within 150 ms of the onset of pause in firing. The observation that tonic dopamine concentrations are mediated by uncorrelated, asynchronous firing is in agreement with prior studies, which show that tonic activity gives rise to the basal dopamine level measured in ECS.8 It is worth noting the concentration profile depicted in Figure 4 measures dopamine for a singular point in ECS. Of relevance to the spatial and temporal limitations of existing experimental tools to probe brain neurotransmission, we implement our model for space averaged dopamine dynamics, as detailed below.
Dopamine Nanosensors in the Striatal ECS.
Of relevance to fluorescent probes for measuring neurotransmitter concentrations in the ECS,16 our model captures spatial evolution of dopamine in the ECS, in addition to the temporally relevant information obtained from FSCV. Nanoparticle based optical probes hold great promise for probing volume transmission dynamics in the ECS in a space and time-resolved manner. First, nanoparticles can fit into the intricate porous and tortuous morphology of the ECS, allowing them proximate access to synaptic and extrasynaptic locations to record dynamic concentration behavior. Second, their diffusive distribution over large volumes of the ECS provides much needed spatial information. Here, we develop a model of the sensor’s fluorescence modulation in response to dynamic analyte behavior. In particular, we evaluate the dynamic range of a carbon nanotube-based dopamine nanosensor, previously validated for dopamine responsivity in vitro.16,48 Briefly, the polymer–nanotube conjugate nanosensor contains a surface environment with active recognition sites for dopamine.16,49 The reversible adsorption of individual dopamine molecules onto the nanosensor recognition sites increases the quantum efficiency of the nanotubes, causing a brightening and thus providing a fluorescent recognition signal. Denoting the total number of dopamine binding sites as L, the free (dopamine unbound) sites as *, the dopamine-bound sites as , and free dopamine molecules as DA, we establish equilibrium conditions for reversible dopamine adsorption to an ensemble of nanosensor binding sites in the ECS:
| 5 |
The first expression represents the dopamine active site balance and the second approximates that the dopamine adsorption process equilibrates on relatively short time scales compared to dopamine diffusion time scales in tissue. We define equilibrium constant, , for the dopamine–sensor binding process as
| 6 |
We next substitute the equilibrium constant into the site balance equation to derive an expression for the dopamine nanosensor fluorescent response as follows:
| 7 |
| 8 |
We note that the increase in nanosensor fluorescence intensity is directly proportional to bound active sites . Thus, the expression for change in intensity normalized against initial nanosensor fluorescence can be represented as
| 9 |
The additional fitting parameter, , is introduced to account for dopamine binding cooperativity.
Temporal Resolution Is Determined by Nanosensor Kinetics and Imaging Frame Rate.
Nanosensor technologies to measure neurotransmitters in the ECS must capture hundred millisecond-scale dopamine release and clearance, as shown by our simulations. Temporally resolved neurotransmitter measurements with FSCV need only account for temporal sampling rates, which are achieved with a high scan rate voltammogram. Conversely, for nanosensors with fluorescence readouts, both temporal and spatial sampling rates will influence the measurement signal-to-noise, due to hardware limitations in fast sampling rates. Our simulations above set the physiologically relevant dopamine spatiotemporal dynamics in the striatum. Henceforth, we consider nanosensor performance limitations that are imposed by imaging hardware and binding kinetics. While our model can be implemented generically for any fluorescence probe including calcium dyes, CNiFERs, and FFNs, among others, we focus on dopamine measurements in the striatal ECS using near-infrared fluorescent dopamine nanosensors.16 During video-rate fluorescence imaging, substantive deviations from theoretical nanosensor response profiles are likely to be encountered owing to the short time scales over which dopamine is released into and cleared from the ECS. Specifically, quantal release and related dopamine dynamic behavior occurs on similar time scales as the exposure time used in conventional fluorescence microscopy (tens to hundreds of milliseconds). We must therefore account for the temporal distortion imposed on nanosensor response by imaging hardware. The nanosensor observed using a video-rate fluorescence imaging is evaluated as
| 10 |
where is the observed nanosensor response when imaging by fluorescence microscopy, and is the theoretical nanosensor response function (eq 9). is the camera exposure time and is inversely related to the nominal frame rate of imaging.
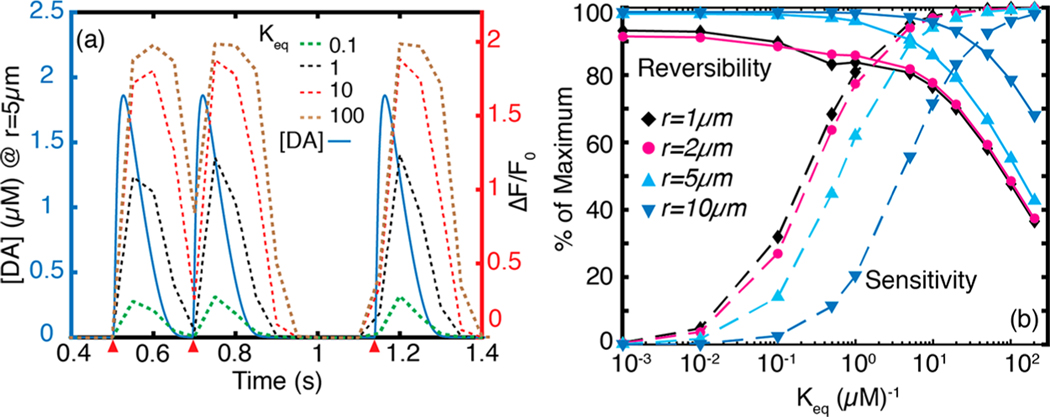
To optimize nanosensor performance, we tuned several parameters in the dopamine nanosensor model (eq 9). Our goal is to determine which nanosensor parameters will enable us to resolve dopamine dynamics of physiological relevance in the striatum. The equilibrium constant (), the proportionality factor (), and the cooperativity parameter () are intrinsic to the nanosensor and can be tuned to optimize nanosensor performance. The parameter weighs the nanosensor quantum yield toward the imaging SNR. Higher corresponds to stronger turn-on response () and improves SNR over the entire physiological dopamine concentration range. is a measure of the affinity between the nanosensor and dopamine analyte. High (or low dissociation constant, ) improves nanosensor response at low concentrations of dopamine, but also leads to quicker nanosensor saturation. On the other hand, low results in a nanosensor that is unresponsive to low concentrations of dopamine. Thus, to maximize the dynamic range of the dopamine nanosensor for the range of experimentally relevant dopamine concentrations of 30 nM to 10 μM31,50,51 we sought to identify nanosensor parameters that are amenable to capturing in vivo endogenous dopamine dynamics. First, we set a 5% lower-limit at the spatial boundary of the -type receptor sphere of influence (17 μm), and this fixes . We set the cooperativity factor , which has been shown to represent our concentration range in experimental nanosensor calibrations16 yielding a sigmoidal response curve representative of a Langmuir surface. Fixing and , we vary over several orders of magnitude and determine to be optimal for a fluorescent nanosensor, which balances nanosensor reversibility and sensitivity according to biologically imposed boundary conditions. To evaluate reversibility, we simulated nanosensor response to two quantal release events located 0.2 s apart from the same terminal (Figure 5a). We define reversibility as the fall in nanosensor intensity during clearance of the first quantal release, divided by rise in intensity in response to the first quantal release. The parameter sets maximum nanosensor response, and we define sensitivity as the measured peak divided by . With these definitions, we varied over 5 orders of magnitude to develop the parameter maps shown in Figures 5b and 6a, b. High values enhance sensitivity, enabling the nanosensor to turn-on at low dopamine concentrations. However, high values cause nanosensor to saturate rapidly and adversely impact nanosensor reversibility (Figure 5). On the other hand, low values have very good reversibility but reduced sensitivity. At , we observe that the nanosensor both responds instantaneously to quantal dopamine release, and also captures dopamine reuptake kinetics to accurately discern between two quantal release events 0.2 s apart. Thus, we identify as optimal for imaging dopamine dynamics in the dorsal striatum, in which the fastest sequential quantal release events occur at least 0.2 s apart during tonic firing.42,52
Figure 5.
Effect of nanosensor parameter on performance. (a) Dynamics of three quantal release events (red wedges) imaged using nanosensors for which varies over 3 orders of magnitude. The first two quantal releases are located 0.2 s apart. Plots of for a 20 Hz frame rate (eq 10) corresponding to each value are plotted in dashes. At , the nanosensor affinity for dopamine is too strong, which adversely affects reversibility. The second release event cannot be resolved. Peak values increase with increasing . At low values, the nanosensor shows high reversibility but poor sensitivity. (b) Parameter space for reversibility and sensitivity at , and 10 μm from release site corresponding to a 20 Hz imaging frame rate. High dopamine concentrations proximal to the release site yield high percent nanosensor sensitivity. However, maintaining good nanosensor reversibility suffers proximal to the release site.
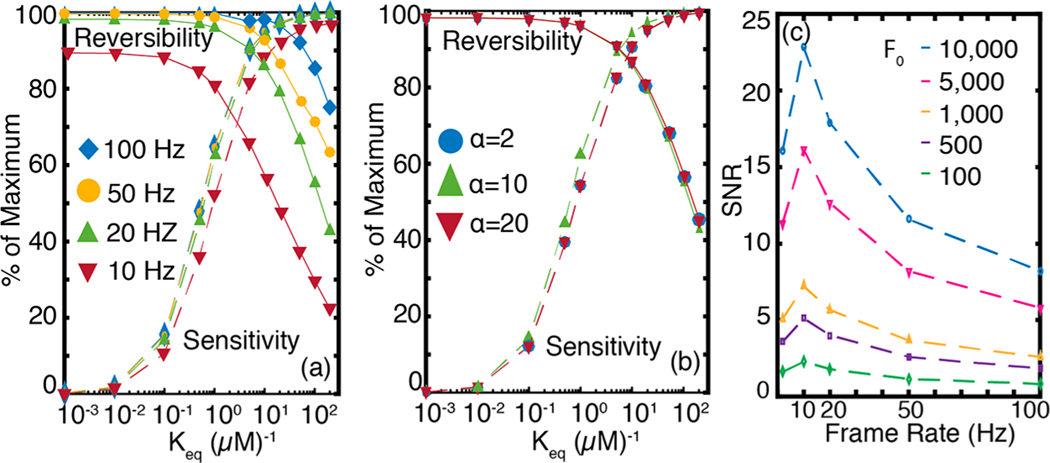
Figure 6.
Nanosensor sensitivity, reversibility, and signal-to-noise ratio, probed for varying frame rates, nanosensor chemistries, and baseline nanosensor fluorescence. (a) Nanosensor parameter space for frame rates ranging from 10 to 100 Hz with . Lower frame rates adversely impact reversibility and sensitivity but improve SNR (panel c). (b) Nanosensor parameter space for nanosensor turn-on response parameter ranging from 2 to 20. Nanosensor parameter space is largely insensitive to varying . (c) SNR shows strong dependence on frame rate (abscissa) and baseline intensity (, dashed traces) of the nanosensor. As frame rate increases, SNR passes through a maximum at 10 Hz and monotonously decreases afterward. The baseline fluorescence intensity is varied from 100 to 10 000 and corresponds to the 2 Hz frame rate, and units of are arbitrary. For definition of , see eq 11.
The parameter space we developed to optimize spatiotemporal signal acquisition of dopamine nanosensors with various values can now allow us to test how camera frame rates affect the nanosensor reversibility and sensitivity parameter space. We stress that the following imaging frame rate analysis is generic to other fluorescent probes for neuromodulation. As we show in Figure 6a, fast imaging frame rates are needed if the nanosensor binds the dopamine analyte too strongly (large ) to temporally resolve the two quanta released 0.2 s apart. Therefore, we conclude that an optimal frame rate is a necessary but not sufficient condition to resolve the temporal heterogeneities of dopamine dynamics in the striatum. The nanosensor’s chemical responsivity and adsorption/desorption kinetics, combined with the imaging hardware limitations, both contribute to the spatiotemporal profiles of dopamine evolution that can be captured. Corresponding to the 1 μM−1 optimal we identified previously, a 20 Hz imaging rate offers the best reversibility (Figure 6a) and SNR (Figure 6c). When sequential release events faster than 0.2 s apart are considered, the reversibility curves shift toward nanosensors with lower in a manner similar to that observed for imaging close to the release site (Figure 5b). Therefore, recording of faster dynamic events demands nanosensors with lower , and comes with an opportunity cost of low sensitivity (Figure 5b) and higher noise (Figures 6c and S4). The second chemical parameter of the nanosensor, the turn-on response parameter , has little effect on nanosensor sensitivity and reversibility (Figure 6b), and which we set at .
Nanosensor Fluorescence and Imaging Frame Rate Considerations for Optimizing Signal-to-Noise Ratio.
The observed nanosensor signal () takes into account the relationship between hardware (frame rate and instrument noise), and nanosensor chemistry (nanosensor fluorescent signal, sensitivity, and reversibility parameters). During optical imaging of fast dynamic events, frame rates cannot be made arbitrarily faster because of their adverse impact on SNR. Here, we provide an analysis to include noise into the observed signal, . To elucidate how hardware and nanosensor chemistry contribute to SNR, we consider the peak signal from a nanosensor with optimal kinetic parameters of and responding to a single quantal release of dopamine at a radial distance of . The mathematical derivation of noise for is provided in Methods. We consider the primary contribution of noise to the SNR to be Poisson noise (also known as shot noise) and do not take into account other sources of noise inherent to the imaging system such as read noise, which can be significant at high frame rates. Our analysis confirms that SNR is inversely related to frame rate and imaging frame rate should be carefully selected to optimize SNR in conjunction with the competing interest of maintaining high temporal resolution (Figure 6c). Furthermore, we identify the baseline fluorescence intensity (brightness) of the nanosensor, , as an important parameter that influences SNR. SNR varies directly with and nearly inversely with frame rate, with a local maximum at 10 Hz (Figure 6c). The observed maximum at 10 Hz arises from the diffusion induced broadening of a quantal release (Figure 2b). For experiments wishing to optimize the temporal resolution of multiple dopamine release events, selection of a nanosensor with strong baseline fluorescence in combination with higher frame rates that achieve a decent fluorescence SNR is recommended.
The surprisingly strong dependence of SNR on warrants closer examination. depends on variables that are intrinsic to the fluorophore and to the imaging system as follows:
| 11 |
where represents frame rate, is the fluorophore number density, is the excitation light source intensity, and is the absorption cross section of the fluorophore. The last two terms in eq 11 represent the quantum yield of the fluorophore () and the photon collection efficiency of the imaging system (). The direct dependence of SNR on arises from noise filtering effects that originate from counting large numbers of photons, which inherently reduces Poisson noise. Thus, SNR optimization can be accomplished by tuning the fluorophore’s photophysical and chemical properties such as absorption cross-section, quantum yield, and analyte specificity. Two saturation regimes are worth noting: a neurotransmitter analyte saturation regime and a photon saturation regime. For the neurotransmitter concentration regime: the fluorophore number density, N, contributes to improved SNR only as long as the neurotransmitter analyte concentration does not become limiting. If the number of active binding sites on the nanosensor exceeds available analyte molecules, the relationship between N and SNR will deviate from that shown in Figure 6c. For the photon limiting regime: SNR will increase proportional to excitation intensity I, so long as photobleaching or fluorophore saturation does not dominate the imaging process. These latter effects demonstrate the importance of choosing optimal fluorophore excitation sources.
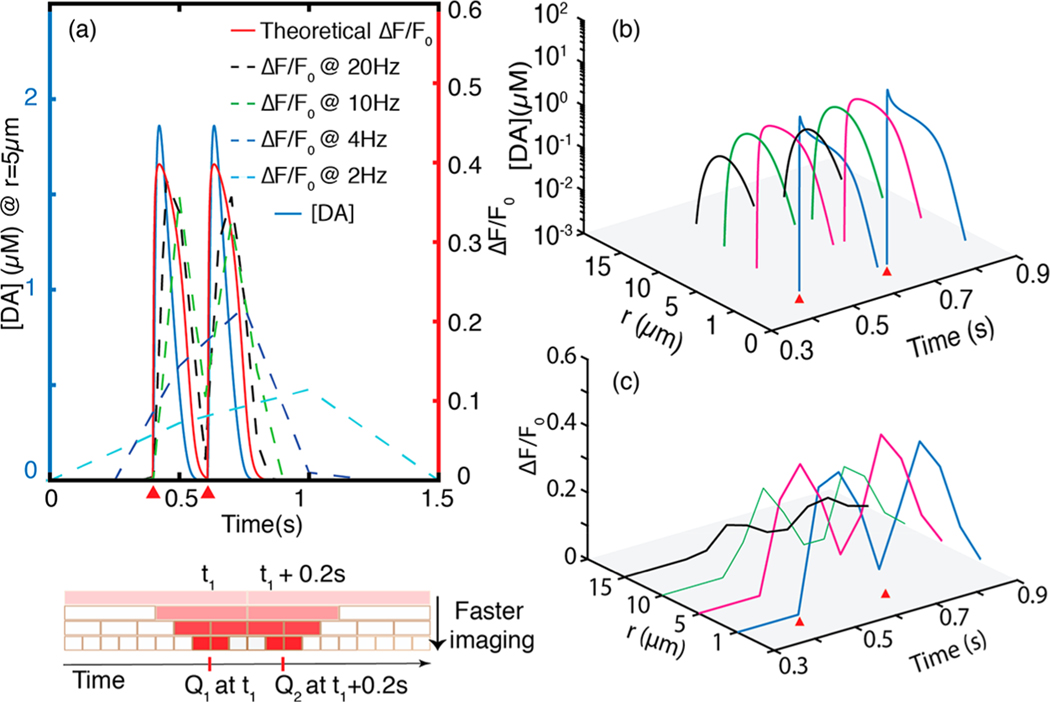
We implemented the nanosensor performance evaluation paradigm we developed previously to the dopamine nanosensor described by Kruss et al.16 that has a value of 2.31 μM−1 and of 0.55. We probe dopamine concentrations at several distances from a terminal within the -type and -type receptor spheres of influence. Consistent with our results above, the spatiotemporal dependence of dopamine concentration evolution and corresponding nanosensor response requires a 20 Hz frame rate to discriminate between two sequential release events occurring 0.2 s apart (Figure 7a). When camera exposure times are incorporated into our model, we indeed find that longer exposure times decrease the nanosensor fluorescence response recorded by the camera. As a result, the recorded spatial and temporal responsivity of the dopamine nanosensor underestimates the physiological dopamine concentration, and misses the true temporal release by overestimating the peak dopamine release time (Figure 7a). We compare the discrepancy between true nanosensor response and imaged nanosensor response for 2, 4, 10, and 20 Hz frame rates. The ability of a nanosensor to capture single terminal quantal release is compromised at frame rates below 2 Hz, where observed nanosensor response is only 20% of the predicted peak response, and could introduce a time-delay of up to 0.5 s. Conversely, when imaging with a 20 Hz frame rate, 95% of the nanosensor fluorescence response is captured, and time-delay of no more than 50 ms is introduced between the quantal release event and the nanosensor response. Considering that there is diffusion induced temporal distortion of 30 ms at (Figure S1), this temporal delay at 20 Hz imaging becomes negligible. For the dual quantal events located 0.2 s apart corresponding to tonic activity, a 20 Hz frame rate can indeed identify the two events (Figure 7). Conversely, both a 2 and 4 Hz frame rate enables the nanosensor to record a spike in local dopamine concentration, but cannot discern that this spike is a result of two distinct quantal release events (Figure 7a). However, because the peak turn-on response of the sensor is only , the farthest sphere of detection set by a of at least 5%, is 15 μm (Figure 7c).
Figure 7.
Temporal resolution of single and dual quantal dopamine release events. (a) Faster imaging frame rates enable resolution of quantal release events. As imaging frame rate increases, the observed nanosensor response to dopamine more accurately captures the theoretical nanosensor response. Red wedge indicates time of quantal release. Bottom panel: schematic shows how faster imaging more precisely localizes temporal position of a quantal release. Color gradient is to scale, showing the relative to the theoretically expected at each frame rate. (b) Dopamine concentration evolution of a dual quantal release of dopamine separated in time. Discrimination between two quantal releases improves as one moves away from release site. Red wedges show times of quantal release positioned 0.2 s apart. (c) Nanosensor response to the dual quantal release presented in (a) and (b) imaged with a 20 Hz frame rate. Evolution of the two releases can be imaged up to 15 μm away from the release site with of ≥5%.
The preceding analyses show that diffusion of dopamine out of the synaptic cleft and into the brain ECS can be detected by nanosensors located up to 17 μm away from the terminal with of 5% or more when sensor kinetics and imaging frame rates are optimally selected. Furthermore, we exemplify how nanosensors can be implemented to image temporal heterogeneities of dopamine dynamics, provided imaging hardware with sufficiently high frame rates. Specifically, frame rates of 20 Hz resolve multiple quantal releases that occur during tonic firing. In general, for optimal values, quantal releases located ms apart require camera exposure times of less than to be resolved. However, imaging frame rates cannot be increased infinitely to fully recapitulate the temporal profile of dopamine release and an optimization needs to be carried out in consideration of nanosensor SNR. While improving SNR, slower frame rates decrease nanosensor response () and introduce significant temporal distortion on the measured dopamine response profile.
Optimal Nanosensor Kinetic and Imaging Parameters can Record Behavior-Relevant Dopamine Dynamics for in vivo Applications.
The optical readout from nanosensors located in the striatal ESC will report the space-averaged dopamine dynamics resulting from terminals in the volume surrounding the nanosensor. In practice, we wish to sample the cumulative behavior of dopamine over a region of interest in the ECS for parameters relevant to our nanosensor. Our model fluorescent single-walled carbon nanotube sensors, with a 250 nm length and 1 nm width, diffuse through the ECS as rigid rods, and sample ECS subdomains on a short characteristic time scale of 200 ms.53 As such, the ensemble fluorescence modulation of optical nanosensors reflects average dopamine concentration. We simulate the ensemble fluorescence modulation of nanotube nanosensors in the ECS by averaging dopamine concentration over the simulation volume as described in Methods.
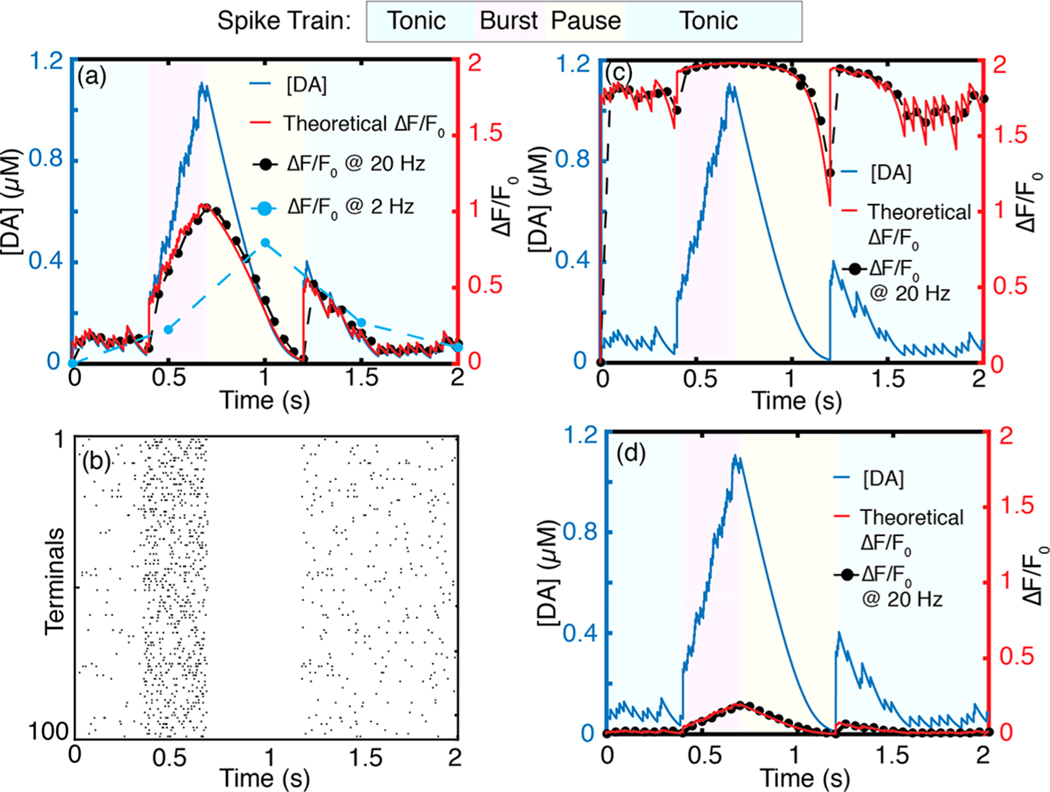
The volume averaged dopamine dynamics corresponding to 100 terminals firing phasically is shown in Figures 8a, b and S6. We define the phasic firing regime over a 2 s simulation with the physiologically relevant spike train defined in Figure 4: A 4 Hz tonic firing rate for to , a 20 Hz burst firing regime for to , a 0.5 s pause (0 Hz) until , and a 4 Hz tonic firing regime for 1.2–2.0 s. Our simulation shows that when neurons fire asynchronously (Figure 8b) tonic dopamine concentrations in the ECS fluctuate between 10 nM and 100 nM (Figure 8a, blue regions). Conversely, synchronous firing of terminals (Figure S6b) gives rise to transient dopamine concentrations in the ECS that range from 200 nM to 300 nM, with no basal levels between the peaks (Figure S6a, blue regions). The average tonic dopamine concentration in the striatal ECS obtained with our model is 50 nM (Figure S5), in agreement with results from prior computational studies25 and experimental measurements.54,55
Figure 8.
Volume averaged concentration profiles of 100 phasically firing dopamine terminals. (a) Dopamine concentration profile in which terminals fire asynchronously and corresponding sensor response of theoretical, 20 and 2 Hz video-rate frame rates with and . (b) Raster plot of asynchronous firing activity corresponding to (a). (c) Same asynchronous activity imaged with a sensor with . The high nanosensor–analyte affinity results in nanosensor saturation at low (tonic) levels of dopamine (d) Same asynchronously activity imaged with a sensor with . The low nanosensor–analyte affinity results in decreased nanosensor sensitivity, with an exemplary burst firing event resulting in only 10% of the nanosensor peak .
This confirms that basal striatal dopamine is mediated by random, uncorrelated firing from dopaminergic terminals belonging to different neurons as opposed to correlated tonic firing. The volume averaging result is consistent with our simulations of many-terminal behavior presented in the previous section (Figure 4), validates our volume-averaging model, and corroborates previous experimental hypotheses about the nature of basal dopamine in the striatum originating from asynchronously firing neurons.
We next compute the ensemble dopamine nanosensor response profile for the theoretical versus practical cases of video-rate fluorescence imaging. We implement our results for a 20 Hz imaging frame rate identified previously as optimal for capturing striatal dopamine dynamics with optimal nanosensor parameters , . During a firing burst that lasts 0.3 s, volume-averaged concentration rises to ~1 μM for both synchronous and asynchronous firing. These results represent space-averaged concentrations; locally, concentrations are heterogeneous and can be higher than the volumetric averages computed here (Figure 4a). Corroborating our prior results, imaging at 20 Hz, one can capture transient peaks during tonic firing in addition to the global concentration peak caused by a burst firing (Figures 8a and S6). Furthermore, all behaviorally relevant spiking regimes can be resolved, including the 0.5 s pause following the burst firing. At an imaging frame rate of 2 Hz, one can only resolve the concentration increase caused by burst firing; neither transient activity during tonic firing nor the pause following burst firing can be resolved (Figure 8a). High affinity nanosensors saturate at tonic dopamine levels (Figure 8c), whereas nanosensors with low dopamine affinity result in low (Figure 8d).
CONCLUSIONS
The ECS constitutes an interconnected, porous, and tortuous milieu that pervades neural tissue and serves as the medium through which neurons communicate with each other by way of neurochemical signaling. Our work quantifies the spatial and temporal nature of dopamine neuromodulation with the dorsal striatum as a model system, and provides the requisite imaging and nanosensor kinetic parameters necessary to record chemical signaling in real time in vivo. Dopamine chemical signaling involves significant spillover of dopamine molecules from the synaptic cleft into the ECS, and a complex dynamic behavior arises as a consequence of release and simultaneous diffusion and reuptake. This work elucidates the dynamics by use of a rigorous, nonlinear stochastic simulation, validated against existing experimental and computational literature. We show that the overflow of dopamine can be detected with optical probes placed in the ECS when proper imaging and kinetic parameters are chosen. A parameter space encompassing nanosensor kinetics and imaging frame rate is developed, whereby optimal nanosensor Kds are identified for imaging neuromodulation in the striatum, or nucleus accumbens, and prefrontal cortex, and 20 Hz is identified as the optimal fluorescence imaging frame rate to capture dopamine neuromodulatory dynamics. Our work can be used to guide new nanosensor development, or to characterize those already developed. We use generic receptor–ligand nanosensor kinetics, making the results of our work broadly applicable to neurochemical imaging in the brain ECS. Furthermore, the model of the striatum developed here can be easily adapted to explore dynamics in other dopaminergic systems, such as the prefrontal cortex or the nucleus accumbens, or to study analogous volume transmission phenomena of monoamines such as norepinephrine and serotonin. The simulation is modular and can be efficiently adapted to investigate broader variety phenomena that involve neurotransmitter dynamics such as pharmacokinetics of therapeutic agents and brain disease states.
METHODS
Dopamine Release Sites and Probability of Release.
Our model is implemented to study spatiotemporal profiles of neurotransmitter release from synapses. As such, our model is implemented with parameters and boundary conditions relevant to experimentally validated neuronal processes. Central synapses of the nervous system such as those found in the striatum contain a single release site, as comprehensively reviewed in Stevens.29 During an action potential, a single quantal release of dopamine occurs with a certain probability , at each terminal (Figure 1b). Dreyer et al.25 calculate probability of 6% based on studies of neurotransmitter release using FFNs13,14 and the dopamine content of striatal tissue.56 As such, our model sets the probability of dopamine release to 6% per action potential per terminal, consistent with experimental observations, and that this release probability remains constant for the simulation time course.
Simulation of Release, Diffusion, and Reuptake.
Our simulation of dopamine concentration in the ECS invokes the equation of change for species conservation surrounding a dopaminergic terminal27
We solve the governing equation, eq 1, individually for each dopamine terminal, and superimpose temporal solutions of the governing equation to determine dopamine dynamics at any location within the simulation volume. Thus, the temporal change in dopamine concentration at any point in the ECS is the sum of the dopamine dynamics contributed by all terminals in the point of interest vicinity. We note that the error introduced by summing the nonlinear reuptake term is negligible: dopamine reuptake approximates linear behavior at sites distant from a release point, where the spatial summation occurs. For our simulation of dopamine release, diffusion, and reuptake, we use radial steps, , of 0.2 μm and time steps, , of 0.02 ms, which yield stable solutions over a wide range of biological parameters.
Discretization Scheme and Boundary Conditions.
The model implements finite differences to solve the governing equation (eq 1). We take advantage of dopamine diffusion symmetry and isotropy to reduce the problem into 1D in spherical coordinates such that the distance from the release site, , is the only spatial domain in the model. Symmetry at the site of a release site serves as a boundary condition for our numerical solution, and is used to calculate dopamine concentration at the center of the simulation volume. We provide details of the discretization scheme below.
The left-hand side of the governing eq 1 can be written in difference form as
| 12 |
where indices and represent discrete steps in space and time, respectively.
To cast the right-hand side of eq 1 in difference form, we first expand the Laplacian:
| 13 |
and discretize the first and second spatial derivatives as follows:
| 14 |
| 15 |
Using these difference equations and leaving the release and uptake terms as and , respectively, we can write an explicit equation for as (eq 16):
| 16 |
where .
The uptake term is written explicitly in space as a Michaelis–Menten rate expression, and the quantal release term () is handled as described previously:
| 17 |
| 18 |
We discretize the symmetry boundary condition as follows. First, we note that the governing equation as becomes
| 19 |
where we used L’Hopital’s rule to evaluate the limit. The spatial and temporal derivatives of eq 19 are discretized using eqs 12 and 14 and then evaluated for (center), yielding:
| 20 |
Simulation Algorithm.
At each simulation time step, the algorithm determines whether an action potential will invade a terminal based on a Poisson probability distribution with mean firing rate . If there is a firing event, a quantal release of dopamine will occur based on a release probability, , by toggling the binary variable between 1 (release) and 0 (no release). If a quantal release of dopamine occurs, dopamine concentration in the volume immediately surrounding the terminal () will be incremented by an amount in eq 3. Increments at subsequent volume elements are scaled as , a factor that follows directly from a Gaussian probability density function. Once dopamine reuptake is determined, dopamine concentration at the location in space is decreased by an amount equal to the computed reuptake term. Because the discretized governing equation (eq 16) fails for (), where it becomes a singularity, we set Neumann’s symmetry principle at as a boundary condition and use it to compute concentration at the center (eq 20). We construct our simulation volume such that the effects of dopamine depletion at any point in space will result from dopamine reuptake by DATs within the simulation volume. Thus, we implement the Dirichlet boundary condition to enable modeling of dopamine reuptake effects at any distance from the center of the release site. Determining the exact location of this boundary requires solving the governing equation first, with a free boundary condition. We therefore set dopamine concentration to 0 when dopamine reuptake is higher than the available dopamine concentration at any given location from release point as described by Berger et al.57 for the diffusion and uptake of oxygen in tissue. The simulation is implemented using MATLAB 2016a.
Volume-Averaged Dopamine Dynamics.
The dynamics from many terminals averaged over the volume encompassing the terminals is computed as follows:
| 21 |
where is the volume averaged concentration of dopamine at time , is concentration at time , and is the time index of the simulation. is the number of terminals in the simulation volume . Terminals depolarize at designated times , where is the same for all terminals during synchronous firing and different for each terminal during asynchronous firing. The firing frequency sets the number of action potentials during a given simulation period. A Poisson distribution with a known mean firing rate sets the distribution of action potentials over the simulation time. Synchrony in firing activity is a reflection of the underlying functional connectivity of the ensemble. Synchronous firing (depolarization), however, does not mean all terminals release dopamine simultaneously; release of dopamine at each terminal is probabilistic and independent as per prior experimental literature,15,58 and thus set to 6% in our simulations. Note also that where is the density of dopamine terminals (Table 1) and is the simulation time step . The volume averaging as defined in eq 21 is valid only for large enough ensembles where diffusive flux out of the volume can be neglected. This is true if the volume is larger than the length scale of dopamine diffusion from a terminal. For small ensemble volume averaging, diffusive flux out of the volume needs to be taken into account because the length scale of the volume is smaller than the diffusion length scale of dopamine (Figure S5).
Signal-to-Noise Ratio.
The noise on the signal is related to the noise on and . Using uncertainty propagation rules, we have
| 22 |
where is the noise on our signal . We use noise of and on and , respectively, for Poisson limited imaging. Experimental results suggest signal-to-noise ratio will also scale with the imaging technique implemented, whereby nonlinear excitation of nanosensors will increase SNR due to reduced photon absorption and scattering in brain tissue.59
Supplementary Material
ACKNOWLEDGMENTS
We thank members of the Wilbrecht, and Feller laboratories for insightful discussions. We thank the Molecular Graphics and Computation Facility at UC Berkeley College of Chemistry (NIH S10OD023532) for access to the computing facility during this work.
Funding
This work was supported by a Burroughs Wellcome Fund Career Award at the Scientific Interface (CASI), the Simons Foundation, a Stanley Fahn PDF Junior Faculty Grant with Award # PF-JFA-1760, and a Beckman Foundation Young Investigator Award (M.P.L.). M.P.L. is a Chan Zuckerberg Biohub investigator. A.G.B. acknowledges the support of an NSF Graduate Research Fellowship and UC Berkeley Chancellor’s Fellowship.
Footnotes
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acschemneuro.7b00193.
Peak dopamine concentration as a function of release site; nonlinear uptake with at 41 μM·s−1 compared to linear uptake with at 4.1 μM·s−1; averaging simulation runs; dependence of SNR on the sensor parameter ; volume-averaged behavior of simulation runs; synchronous activity of 100 terminals (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Yung KKL, Bolam JP, Smith AD, Hersch SM, Ciliax BJ, and Levey AI (1995) Immunocytochemical localization of D 1 and D 2 dopamine receptors in the basal ganglia of the rat: light and electron microscopy. Neuroscience 65, 709–730. [DOI] [PubMed] [Google Scholar]
- (2).Trimble M. (2002) Molecular neuropharmacology, a foundation for clinical neuroscience. J. Neurol., Neurosurg. Psychiatry 73, 210. [Google Scholar]
- (3).Davie CA (2008) A review of Parkinson’s disease. Br. Med. Bull 86, 109–127. [DOI] [PubMed] [Google Scholar]
- (4).Kalivas PW, and Volkow ND (2005) The neural basis of addiction: a pathology of motivation and choice. Am. J. Psychiatry 162, 1403–1413. [DOI] [PubMed] [Google Scholar]
- (5).Li D, Sham PC, Owen MJ, and He L. (2006) Meta-analysis shows significant association between dopamine system genes and attention deficit hyperactivity disorder (ADHD). Hum. Mol. Genet 15, 2276–2284. [DOI] [PubMed] [Google Scholar]
- (6).Cabib S, and Puglisi-Allegra S. (1996) Stress, depression and the mesolimbic dopamine system. Psychopharmacology 128, 331–342. [DOI] [PubMed] [Google Scholar]
- (7).Weinberger DR (1987) Implications of normal brain development for the pathogenesis of schizophrenia. Arch. Gen. Psychiatry 44, 660–669. [DOI] [PubMed] [Google Scholar]
- (8).Grace AA (1991) Phasic versus tonic dopamine release and the modulation of dopamine system responsivity: a hypothesis for the etiology of schizophrenia. Neuroscience 41, 1–24. [DOI] [PubMed] [Google Scholar]
- (9).Agnati LF, Zoli M, Strömberg I, and Fuxe K. (1995) Intercellular communication in the brain: wiring versus volume transmission. Neuroscience 69, 711–726. [DOI] [PubMed] [Google Scholar]
- (10).Alivisatos AP, Andrews AM, Boyden ES, Chun M, Church GM, Deisseroth K, Donoghue JP, Fraser SE, Lippincott-Schwartz J, Looger LL, et al. (2013) Nanotools for neuroscience and brain activity mapping. ACS Nano 7, 1850–1866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Garris PA (2010) Advancing neurochemical monitoring. Nat. Methods 7, 106–108. [DOI] [PubMed] [Google Scholar]
- (12).Muller A, Joseph V, Slesinger PA, and Kleinfeld D. (2014) Cell-based reporters reveal in vivo dynamics of dopamine and norepinephrine release in murine cortex. Nat. Methods 11, 1245–1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Gubernator NG, Zhang H, Staal RGW, Mosharov EV, Pereira DB, Yue M, Balsanek V, Vadola PA, Mukherjee B, Edwards RH, et al. (2009) Fluorescent false neurotransmitters visualize dopamine release from individual presynaptic terminals. Science 324, 1441–1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Pereira DB, Schmitz Y, Meszá ros J, Merchant P, Hu G, Li S, Henke A, Lizardi-Ortiz JE, Karpowicz RJ Jr, Morgenstern TJ, et al. (2016) Fluorescent false neurotransmitter reveals functionally silent dopamine vesicle clusters in the striatum. Nat. Neurosci 19, 578–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Sames D, Dunn M, Karpowicz RJ Jr, and Sulzer D. (2013) Visualizing neurotransmitter secretion at individual synapses. ACS Chem. Neurosci 4, 648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Kruss S, Landry MP, Vander Ende E, Lima BMA, Reuel NF, Zhang J, Nelson J, Mu B, Hilmer A, and Strano M. (2014) Neurotransmitter detection using corona phase molecular recognition on fluorescent single-walled carbon nanotube sensors. J. Am. Chem. Soc 136, 713–724. [DOI] [PubMed] [Google Scholar]
- (17).Salem DP, Landry MP, Bisker G, Ahn J, Kruss S, and Strano MS (2016) Chirality dependent corona phase molecular recognition of DNA-wrapped carbon nanotubes. Carbon 97, 147–153. [Google Scholar]
- (18).Beyene AG, Demirer GS, and Landry MP (2016) Nanoparticle-Templated Molecular Recognition Platforms for Detection of Biological Analytes. Current protocols in chemical biology, 197–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Freund TF, Powell JF, and Smith AD (1984) Tyrosine hydroxylase-immunoreactive boutons in synaptic contact with identified striatonigral neurons, with particular reference to dendritic spines. Neuroscience 13, 1189–1215. [DOI] [PubMed] [Google Scholar]
- (20).Gerfen CR (1988) Synaptic organization of the striatum. J. Electron Microsc. Tech 10, 265–281. [DOI] [PubMed] [Google Scholar]
- (21).Arluison M, Dietl M, and Thibault J. (1984) Ultrastructural morphology of dopaminergic nerve terminals and synapses in the striatum of the rat using tyrosine hydroxylase immunocytochemistry: a topographical study. Brain Res. Bull 13, 269–285. [DOI] [PubMed] [Google Scholar]
- (22).Doucet G, Descarries L, and Garcia S. (1986) Quantification of the dopamine innervation in adult rat neostriatum. Neuroscience 19, 427–445. [DOI] [PubMed] [Google Scholar]
- (23).Oorschot DE (1996) Total number of neurons in the neostriatal, pallidal, subthalamic, and substantia nigral nuclei of the rat basal ganglia: a stereological study using the cavalieri and optical disector methods. J. Comp. Neurol 366, 580–599. [DOI] [PubMed] [Google Scholar]
- (24).Iversen LL (2010) Dopamine handbook, Oxford University Press, Oxford, UK. [Google Scholar]
- (25).Dreyer JK, Herrik KF, Berg RW, and Hounsgaard JD (2010) Influence of phasic and tonic dopamine release on receptor activation. J. Neurosci 30, 14273–14283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Arbuthnott GW, and Wickens J. (2007) Space, time and dopamine. Trends Neurosci. 30, 62–69. [DOI] [PubMed] [Google Scholar]
- (27).Nicholson C. (2001) Diffusion and related transport mechanisms in brain tissue. Rep. Prog. Phys 64, 815. [Google Scholar]
- (28).Rice ME, and Cragg SJ (2008) Dopamine spillover after quantal release: rethinking dopamine transmission in the nigrostriatal pathway. Brain Res. Rev 58, 303–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Stevens CF (2003) Neurotransmitter release at central synapses. Neuron 40, 381–388. [DOI] [PubMed] [Google Scholar]
- (30).Rosenmund C, and Stevens CF (1996) Definition of the readily releasable pool of vesicles at hippocampal synapses. Neuron 16, 1197–1207. [DOI] [PubMed] [Google Scholar]
- (31).Cragg SJ (2003) Variable dopamine release probability and short-term plasticity between functional domains of the primate striatum. J. Neurosci 23, 4378–4385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Trevathan JK, Yousefi A, Park HO, Bartoletta JJ, Ludwig KA, Lee KH, and Lujan JL (2017) Computational Modeling of Neurotransmitter Release Evoked by Electrical Stimulation: Nonlinear Approaches to Predicting Stimulation-Evoked Dopamine Release. ACS Chem. Neurosci 8, 394–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Phillips R, Kondev J, Theriot J, and Garcia H. (2012) Physical biology of the cell; Garland Science. [Google Scholar]
- (34).Nicholson C. (1995) Interaction between diffusion and Michaelis-Menten uptake of dopamine after iontophoresis in striatum. Biophys. J 68, 1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Rice ME, and Nicholson C. (1991) Diffusion characteristics and extracellular volume fraction during normoxia and hypoxia in slices of rat neostriatum. J. Neurophysiol 65, 264–272. [DOI] [PubMed] [Google Scholar]
- (36).Ross SB (1991) Synaptic concentration of dopamine in the mouse striatum in relationship to the kinetic properties of the dopamine receptors and uptake mechanism. J. Neurochem 56, 22–29. [DOI] [PubMed] [Google Scholar]
- (37).Richfield EK, Penney JB, and Young AB (1989) Anatomical and affinity state comparisons between dopamine D 1 and D 2 receptors in the rat central nervous system. Neuroscience 30, 767–777. [DOI] [PubMed] [Google Scholar]
- (38).Kusano K. (1966) Electrical activity and structural correlates of giant nerve fibers in Kuruma shrimp (Penaeus japonicus). J. Cell. Physiol 68, 361–383. [Google Scholar]
- (39).Sykova E, and Nicholson C. (2008) Diffusion in brain extracellular space. Physiol. Rev 88, 1277–1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Jones SR, Garris PA, and Wightman RM (1995) Different effects of cocaine and nomifensine on dopamine uptake in the caudate-putamen and nucleus accumbens. J. Pharmacol. Exp. Ther 274, 396–403. [PubMed] [Google Scholar]
- (41).Grace AA, and Bunney BS (1984) The control of firing pattern in nigral dopamine neurons: burst firing. J. Neurosci 4, 2877–2890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Grace AA, and Bunney BS (1984) The control of firing pattern in nigral dopamine neurons: single spike firing. J. Neurosci 4, 2866–2876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Hyland BI, Reynolds JNJ, Hay J, Perk CG, and Miller R. (2002) Firing modes of midbrain dopamine cells in the freely moving rat. Neuroscience 114, 475–492. [DOI] [PubMed] [Google Scholar]
- (44).Schultz W. (1998) Predictive reward signal of dopamine neurons. J. Neurophysiol 80, 1–27. [DOI] [PubMed] [Google Scholar]
- (45).Wong-Lin K, and Nakamura K. (2015) Neurobiological circuit function and computation of the serotonergic and related systems, Frontiers Media SA. [Google Scholar]
- (46).Zachek MK, Takmakov P, Moody B, Wightman RM, and McCarty GS (2009) Simultaneous decoupled detection of dopamine and oxygen using pyrolyzed carbon microarrays and fast-scan cyclic voltammetry. Anal. Chem 81, 6258–6265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Venton BJ, Zhang H, Garris PA, Phillips PEM, Sulzer D, and Wightman RM (2003) Real-time decoding of dopamine concentration changes in the caudate–putamen during tonic and phasic firing. J. Neurochem 87, 1284–1295. [DOI] [PubMed] [Google Scholar]
- (48).Zhang J, Landry MP, Barone PW, Kim J-H, Lin S, Ulissi ZW, Lin D, Mu B, Boghossian AA, Hilmer AJ, et al. (2013) Molecular recognition using corona phase complexes made of synthetic polymers adsorbed on carbon nanotubes. Nat. Nanotechnol 8, 959–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Bisker G, Dong J, Park HD, Iverson NM, Ahn J, Nelson JT, Landry MP, Kruss S, and Strano MS (2016) Proteintargeted corona phase molecular recognition. Nat. Commun 7, 10241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Cragg SJ, Hille CJ, and Greenfield SA (2000) Dopamine release and uptake dynamics within nonhuman primate striatum in vitro. J. Neurosci 20, 8209–8217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Jones SR, O’Dell SJ, Marshall JF, and Wightman RM (1996) Functional and anatomical evidence for different dopamine dynamics in the core and shell of the nucleus accumbens in slices of rat brain. Synapse 23, 224–231. [DOI] [PubMed] [Google Scholar]
- (52).Pothos EN, Davila V, and Sulzer D. (1998) Presynaptic recording of quanta from midbrain dopamine neurons and modulation of the quantal size. J. Neurosci 18, 4106–4118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Godin AG, Varela JA, Gao Z, Danne N, Dupuis JP,´ Lounis B, Groc L, and Cognet L. (2016) Single-nanotube tracking reveals the nanoscale organization of the extracellular space in the live brain. Nat. Nanotechnol 12, 238. [DOI] [PubMed] [Google Scholar]
- (54).Ngo KT, Varner EL, Michael AC, and Weber SG (2017) Monitoring Dopamine Responses to Potassium Ion and Nomifensine by in vivo Microdialysis with Online Liquid Chromatography at One-Minute Resolution. ACS Chem. Neurosci 8, 329–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Gu H, Varner EL, Groskreutz SR, Michael AC, and Weber SG (2015) In vivo Monitoring of Dopamine by Microdialysis with One-Minute Temporal Resolution Using Online Capillary Liquid Chromatography with Electrochemical Detection. Anal. Chem 87, 6088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Bannon MJ, Michaud RL, and Roth RH (1981) Mesocortical dopamine neurons. Mol. Pharmacol 19, 270–275. [PubMed] [Google Scholar]
- (57).Berger AE, Ciment M, and Rogers JCW (1975) Numerical solution of a diffusion consumption problem with a free boundary. SIAM Journal on Numerical Analysis 12, 646–672. [Google Scholar]
- (58).Sudhof TC (2004) The synaptic vesicle cycle. Annu. Rev. Neurosci 27, 509. [DOI] [PubMed] [Google Scholar]
- (59).Del Bonis-O’Donnell JT, Page RH, Beyene AG, Tindall EG, McFarlane IR, and Landry MP Molecular Recognition of Dopamine with Dual Near Infrared Excitation-Emission Two-Photon Microscopy. bioRxiv 145912, 10.1101/145912 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.