Abstract
Patterns of crowd behavior are believed to result from local interactions between pedestrians. Many studies have investigated the local rules of interaction, such as steering, avoiding, and alignment, but how pedestrians control their walking speed when following another remains unsettled. Most pedestrian models assume the physical speed and distance of others as input. The present study compares such “omniscient” models with “visual” models based on optical variables. We experimentally tested eight speed control models from the pedestrian- and car-following literature. Walking participants were asked to follow a leader (a moving pole) in a virtual environment, while the leader's speed was perturbed during the trial. In Experiment 1, the leader's initial distance was varied. Each model was fit to the data and compared. The results showed that visual models based on optical expansion () had the smallest root mean square error in speed across conditions, whereas other models exhibited increased error at longer distances. In Experiment 2, the leader's size (pole diameter) was varied. A model based on the relative rate of expansion () performed better than the expansion rate model (), because it is less sensitive to leader size. Together, the results imply that pedestrians directly control their walking speed in one-dimensional following using relative rate of expansion, rather than the distal speed and distance of the leader.
Keywords: pedestrian following, optical expansion, visual control of locomotion
Introduction
A number of pedestrian models have been developed to characterize the interactions between walking humans. For example, the dominant Social Force Model and its variants (Helbing & Molnar, 1995; Lakoba, Kaup, & Finkelstein, 2005; Yu, Chen, Dong, & Dai, 2005) take the distance and velocity of objects and other pedestrians as input to compute the acceleration of the simulated agent. Velocity-based models of collision avoidance (Berg, Lin, & Manocha, 2008; Guy, Lin, & Manocha, 2010; Van Den Berg, Guy, Lin, & Manocha, 2011) calculate the velocity space (set of velocities) that will lead to collisions, then find a velocity outside the space based on some optimization criteria. However, physical variables such as distance and velocity are not directly available to human observers, nor is there evidence that pedestrian interactions are governed by hypothesized forces or global optimization. Such “omniscient” phenomenological models are approximations of pedestrian movements but do not offer plausible explanations of human behavior grounded in the perceptual coupling between individuals. Pedestrian interactions are likely based on optical variables and governed by control laws for locomotion (Warren, 2006).
In this article, we focus on one-dimensional (1D) pedestrian following, in which a follower walks behind a leader and regulates their speed to stay with the leader. One-dimensional following is a phylogenetically ancient behavior dating to the Cambrian explosion, as revealed by fossils of trilobites processing in single file, coupled via mechanoreception (Vannier et al., 2019). Models of pedestrian following are often inspired by car-following models of vehicular traffic (Brackstone & McDonald, 1999; Wilson & Ward, 2011), which are based on physical variables (variable names appear in Table 1, models in the left two columns of Table 2; see Rio, Rhea, & Warren, 2014, for detailed descriptions). For example, the follower could maintain a constant distance from the leader (Kometani & Sasaki, 1958), maintain a distance that increases with speed (Herman, Montroll, Potts, & Rothery, 1959; Pipes, 1953), use a linear combination of distance and speed (Helly, 1959), or match the leader's speed (Lee & Jones, 1967). Lemercier et al. (2012; Fehrenbach et al., 2015) proposed that pedestrian followers use the ratio of speed difference to leader distance to control their speed, similar to the car-following model of Gazis, Herman, and Rothery (1961), with an explicit time delay between leader and follower. The model was able to reproduce stop-and-go waves that are commonly observed in dense one-way pedestrian traffic. Bruneau, Dutra, and Pettré (2014) subsequently proposed a model in which the speed of the follower is based on the predicted future distance of the leader, which can also replicate stop-and-go waves. However, these pedestrian models are again omniscient, relying on the leader's physical distance and/or speed as input.
Table 1.
Variable names used in this article.
| Notation | Meaning |
|---|---|
| xf | Position of follower |
| Δx | Distance between follower and leader |
| Speed of follower | |
| Speed difference between leader and follower | |
| Acceleration of follower | |
| θ | Visual angle of leader from the perspective of follower |
| Rate of expansion (RE) | |
| Relative rate of expansion (RRE) | |
| d 0 | Initial distance between leader and follower |
| Δv | Speed perturbation of leader |
Table 2.
Tests of the nine models in Experiment 1. Note: Parameter values and BIC values were acquired by fitting the models to all perturbation trials (n = 696), while minimizing the RMSE on speed. BIC values were computed based on Equation 1. The models were also tested using leave-one-subject-out cross-validation, in which each model was trained on 11 participants and tested on the one left out until all combinations of training set and test set were used. The test results (mean and standard deviation of RMSE) of 12 iterations of cross-validation are shown in the table. The letters in the superscript of BIC values indicate the rank of model based on BIC, whereas those in the superscript of cross-validation error indicate Duncan group in Duncan's multiple range test. τ in Lemercier et al. (2012) was capped at 1 s because a reaction time longer than 1 s is unlikely for a human pedestrian.
| Model | Equation | Parameters | BIC | Mean RMSE (m/s) |
|---|---|---|---|---|
| Relative rate of expansion (RRE) | b = 0.920 | −3,182a | 0.092 (SD = 0.049)a | |
| Ratio | c = 1.810 | −3,162b | 0.091 (SD = 0.053)a | |
| M = −0.052 | ||||
| L = 1.509 | ||||
| Rate of expansion (RE) | b = 8.463 | −3,136c | 0.091 (SD = 0.056)a | |
| Linear | c 1 = 0.255 | −3,043d | 0.102 (SD = 0.054)b | |
| c 2 = 0.010 | ||||
| a = −6.946 | ||||
| b = 10.665 | ||||
| Speed | c = 0.219 | −3,021e | 0.105 (SD = 0.054)b | |
| Lemercier et al. (2012) | τ = 1.000 | −3,008f | 0.102 (SD = 0.056)b | |
| c = 2.466 | ||||
| γ = 1.439 | ||||
| Speed-based distance (SBD) | c = 0.026 | −2,494g | 0.144 (SD = 0.087)c | |
| a = −17.461 | ||||
| b = 19.750 | ||||
| Distance | c = 0.004 | −2,355h | 0.152 (SD = 0.096)d | |
| Null | None | −2,355h | 0.154 (SD = 0.101)d |
Rio et al. (2014) tested a variety of omniscient physical models against data on following in pedestrian dyads and found that the simple speed-matching model fit the human data as well as or better than other models. In this model, the follower's acceleration () is proportional to the difference between the speed of the leader and the follower (), and the gain parameter (c) is fit to the data:
| (1) |
Rio et al. (2014) also proposed a visual control law in which the follower adjusts their speed to cancel the leader's optical expansion and contraction (cf. Andersen & Sauer, 2007; Lee & Jones, 1967, for car following). Specifically, the follower's acceleration is proportional to the rate of change in the leader's visual angle (), and the gain parameter (b) is fit to the data:
| (2) |
This rate of expansion (RE) model did not fit their data quite as well as the physical speed-matching model, but there are two possible reasons it may have fallen short.
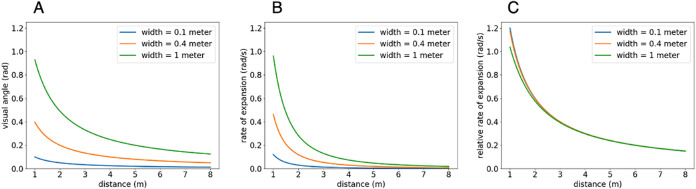
First, the theoretical advantage of the RE model is that it exploits the nonlinearity of visual angle, which decreases with distance (d) as tan−1(1/d) (see Figure 1A). Whereas the speed-matching model is independent of leader distance, the rate of expansion decreases nonlinearly with distance (Figure 1B). Consequently, the RE model inherently depends on the leader's distance (Ducourant et al., 2005) without explicitly recovering physical distance. It is possible that the speed-matching model fit the data better because the range of distances tested by Rio et al. (2014) was small (1–4 m), and a larger distance range might produce a distance effect consistent with the RE model. Second, the RE model predicts an asymmetric response to leader acceleration and deceleration. For a given initial distance, decelerating decreases the leader's distance, producing a higher expansion rate, whereas accelerating increases the leader's distance, producing a lower contraction rate. Rio et al. (2014) did not report this asymmetry in their first experiment with a human leader, perhaps because the leader's acceleration and deceleration were uncontrolled. But in a second experiment with a virtual leader, they reported a significant asymmetry in the follower's response: Speed changes were twice as large to leader deceleration as to leader acceleration. In the present study, we tested a larger range of distances and also controlled the acceleration/deceleration of the leader using virtual reality (VR).
Figure 1.
(A) The visual angle of the leader (θ) increases nonlinearly as distance decreases, at a rate that depends on leader size. (B) Similarly, the rate of change in visual angle (optical expansion, ) increases nonlinearly as distance decreases and also depends on size. (C) The RRE () also increases nonlinearly but is less dependent on size. Graphs are computed with a constant relative speed between leader and follower ().
A limitation of the RE model is the fact that the rate of expansion depends on not only the leader's distance and relative speed but also its size: For a given relative speed and distance, an object with a larger diameter generates a higher rate of expansion or contraction at the follower's eye (Figure 1B). We thus test an alternative model based on the relative rate of expansion (RRE) (Wagner, 1982). The RRE normalizes expansion rate () by the visual angle (θ) of the leader, thus partially compensating for variation in leader size (Figure 1C):
| (3) |
Note that RRE is the inverse of the time-to-contact variable τ (assuming the small angle approximation) (Lee, 1976). The τ variable is a poor control variable for following, however, for as the follower brings the rate of expansion to zero, τ goes to infinity. Its inverse is more useful, for RRE ∼ 0 indicates successful following, RRE < 0 indicates falling behind the leader, RRE > 0 indicates gaining on the leader, and RRE >> 0 indicates an imminent collision. The relative rate of expansion thus increases with temporal “immediacy.”
In Experiment 1, we compared the speed-matching and RE models by varying the leader's distance over a larger range (1–6 m) and controlling the leader's speed perturbation (± 0.3 m/s). If distance influences the follower's response, the RE model should show a higher goodness of fit than the speed-matching model and vice versa. In Experiment 2, we compared the RE and RRE models by varying the diameter of the leader (0.2, 0.6, 1.0 m) while controlling the speed perturbation (± 0.3 m/s). If leader size influences the follower's response, the RRE model should fit the data better than the RE model and vice versa. We also compared six physical models using the data from both experiments: speed matching, constant distance, speed-based distance (SBD), linear combination, ratio, and Lemercier models (see Table 2). Finally, we did not investigate the role of binocular disparity or vergence angle here, which can contribute to time-to-contact judgments (Gray & Regan, 1998; Heuer, 1993) and ball catching (Rushton & Wann, 1999; Savelsbergh, Whiting, & Bootsma, 1991). Previously, Rio et al. (2014) dissociated disparity and vergence from optical expansion and found little influence of the former variables on pedestrian following, possibly because optical expansion dominates responses to objects larger than the interpupillary distance (Rushton & Wann, 1999).
Experiment 1
Method
Participants
Twelve students from Brown University (four males, eight females) participated in the experiment. All participants had normal or corrected-to-normal vision. The protocol was approved by Brown University's Institutional Review Board, in accordance with the Declaration of Helsinki. Informed consent was obtained from all participants, who were paid for their participation.
Apparatus
The experiment was conducted in the Virtual Environment Navigation Laboratory (VENLab) at Brown University. Participants walked freely in a 11-m × 9-m area while immersed in a virtual environment presented in a head-mounted display (HMD; Oculus Rift CV1, Oculus VR, Long Beach, California, USA). The HMD provided stereoscopic viewing with a 94 H × 93 V binocular field of view (Okreylos, 2016), resolution of 1,080 × 1,200 pixels in each eye, and a refresh rate of 90 Hz. Displays were generated on an MSI VR One backpack PC (New Taipei City, Taiwan; weight 3.3 kg) at a frame rate of 90 fps, using the Vizard 5 3D animation package (WorldViz, 2014). Head position was recorded at a sampling rate of 90 Hz by a hybrid inertial-ultrasonic tracking system (IS-900; Intersense, Billerica, MA, USA). Head orientation was tracked by the built-in inertial sensor of the HMD. Head position and orientation were used to update the display with a latency estimated to be less than 50 ms.
Displays
The virtual environment consisted of a ground plane with a granite texture and a blue sky; a blue home pole (radius 0.12 m, height 1.35 m) with a granite texture on the ground plane, where participants started each trial; a stationary red orientation pole (radius 0.2 m, height 3 m) that appeared in front of the participant, which participants faced before the trial began; and a moving green leader pole (radius 0.2 m, height 2 m) that appeared during the trial, which served as the leader in the following task (see Figure 2).
Figure 2.

Virtual display of the leader pole from the participant's viewpoint.
Procedure
Prerecorded instructions were played through the HMD's built-in headphones at the beginning of the experiment. A session began with four self-paced walking trials, in which the participant simply walked to the red orientation pole in the virtual environment at their preferred speed, allowing us to measure their normal walking speed. The participant then received four practice trials to learn the following task. These preexperimental trials helped participants adapt to walking in VR and rescale perceived distance in the virtual environment (Mohler, Creem-Regehr, & Thompson, 2006; Richardson & Waller, 2007). They were followed by 90 experimental trials.
In both practice and experimental trials, participants were asked to “walk behind the green pole as if you were following someone down the street, while trying to keep a constant distance.” This instruction was intended to encourage participants to keep up with the leader pole and was also used by Rio et al. (2014). Their observation that distance was not actually held constant is consistent with reliance on some other control variable. Participants were not told how closely or quickly to follow the pole.
At the beginning of each trial, the participant stood at the blue home pole and faced the red orientation pole (see Supplementary Movie S1). After 3 s, the green leader pole appeared (1, 3, or 6 m in front of them) and immediately started to move away from the participant on a straight path at a constant initial speed (1.2 m/s), while the prerecorded instruction “begin” was played over the headphones. After a random interval (3−4 s), a speed perturbation (−0.3, 0, or +0.3 m/s) was applied to the leader pole, with an average acceleration of 1 m/s2. After the perturbation, the leader pole moved at a new constant speed (0.9, 1.2, or 1.5 m/s) until the end of the trial. The trial ended when the participant had walked for 12.2 m or 12 s, whichever came first. The blue home pole then reappeared nearby and the participant walked to it, which triggered the next trial.
Design
Experiment 1 had a within-subject factorial design: 3 initial distance (do = 1, 3, 6 m) × 3 speed perturbation (∆v = −0.3, 0, +0.3 m/s), yielding nine conditions. There were 10 repetitions in each condition, for a total of 90 trials, which were presented in different random order for each participant.
Data processing
The time series of the participant's head position in the horizontal plane was recorded, which was reduced to a unidimensional trajectory along the axis of leader motion. Given that there were minor fluctuations in sampling rate, the unidimensional data were then linearly interpolated to 90 Hz to ensure equal time intervals between frames. The time series for each trial was then filtered using a fourth-order low-pass Butterworth filter (1 Hz cutoff) to reduce anterior-posterior oscillations due to the step cycle and tracker noise. To eliminate endpoint error caused by the filter, each time series was extended by 2 s using linear extrapolation before filtering and was truncated by 3 s after filtering. The filtered time series of position were then differentiated to produce a time series of speed for each trial, which provided the data for model fitting. Dependent variables for statistical analysis included the participant's final speed (the mean speed in the last 2 s) and final distance from the leader (the mean distance in the last 2 s), as well as final speed difference with the leader (mean difference in speed during the last 2 s) on each trial. Twenty out of 1,080 trials (1.85%) were excluded due to tracking failures.
Statistical analysis
To analyze the relationships between independent and dependent variables, linear mixed-effects regression analyses were performed in R (R Core Team, 2019) and lme4 (Bates, Mächler, Bolker, & Walker, 2015). The advantage of a linear mixed-effects model is that it has higher statistical power, partials out individual differences, and is robust to missing data (Baayen, Davidson, & Bates, 2008). Visual inspection of residual plots did not reveal any obvious deviations from homoscedasticity or normality. P values were obtained from Wald chi-squared test.
Model fitting and comparison
Only trials in which the speed of the leader pole was perturbed (−0.3 and +0.3 m/s) were used for model fitting because trials with no speed perturbation drive model parameters to zero. To avoid initial and final transients, we fit the follower's speed time series from 0.5 s before the perturbation to 5.5 s after the perturbation in each trial. Based on these criteria, 696 trials were used in the fitting procedures, while 11 were excluded for being shorter than 5.5 s after the perturbation.
Two fitting procedures were used to serve different goals. Numerical optimizations were achieved by a derivative-free method (Lagarias, Reeds, Wright, & Wright, 1998) for both procedures. The first procedure searched for the optimal parameter values over all trials; although this procedure introduces the risk of overfitting, it allows us to have a set of optimal parameters. Overfitting will be addressed by model comparisons using the Bayesian information criterion (BIC) because it penalizes models that have more free parameters (i.e., higher chance of overfitting). The nine candidate models in Table 2 were fit to and tested on the time series of follower speed for all trials, including a null model that made no response to the leader. Each trial was simulated using the optimal parameter values for a model, the mean squared error between the model time series and human time series was computed for each trial, and the mean squared error (MSE) was computed over all n trials. The BIC (Equation 4) was used to penalize models based on the number of free parameters (k). The BIC value indicates the overall goodness of fit for each model, and models can be compared by computing the difference in BIC scores, where a ∆BIC of 2–6 indicates positive evidence, 6–10 strong evidence, and > 10 very strong evidence in favor of the lower BIC.
| (4) |
The second fitting procedure used leave-one-subject-out cross-validation to avoid overfitting and allowed frequentist model comparisons. The nine candidate models were fit to the time series of speed for 11 participants and were tested on the data from the 12th participant. This procedure was repeated 12 times, such that each participant was left out and tested once. In the test, each trial was simulated using the parameter values from fitting the other 11 participants, and the root mean squared error (RMSE) between the model time series and human time series was computed. This resulted in a mean RMSE for each subject in each condition, which was compared using frequentist statistical tests. Note that the RMSE does not penalize free parameters.
Results
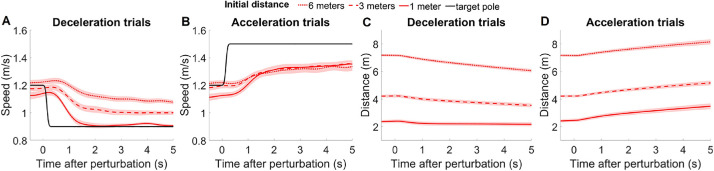
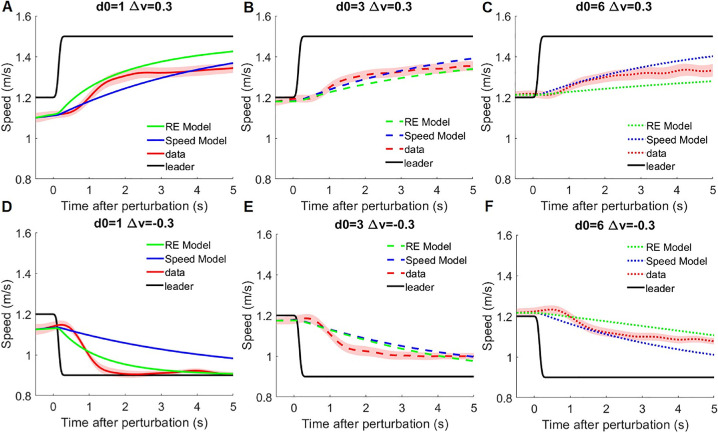
Mean time series of speed for each condition appear in Figures 3A, B. It is apparent that the participant's response decreased with leader distance on deceleration trials (Panel A) and was greater on deceleration trials than acceleration trials (Panel B).
Figure 3.
Mean participant time series in Experiment 1. Time series of speed on (A) deceleration (n = 355) and (B) acceleration (n = 341) trials. Time series of distance from leader on (C) deceleration and (D) acceleration trials. Black curves indicate the leader's speed, red curves indicate participant responses at each initial distance, and shading indicates 95% confidence intervals computed on all trials. All time series are aligned at the time of perturbation.
Final states
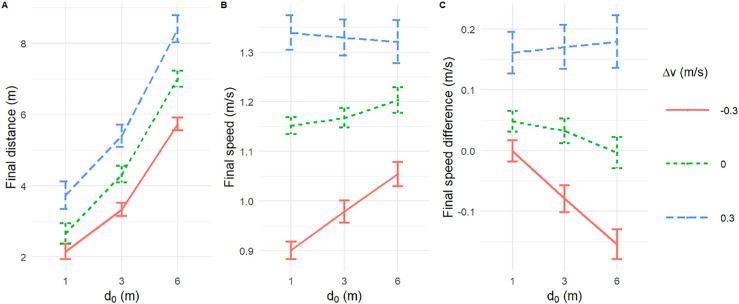
The follower's mean final distance, final speed, and final speed difference with the leader are plotted for each experimental condition in Figure 4. A linear mixed-effects regression, in which initial distance (d0) and speed perturbation (∆v) were fixed-effect predictors and subject was a random effect, was used to analyze each of the three dependent variables. The results reveal significant effects of initial distance, speed perturbation, and their interaction on all final states, all p < 0.001 (see Table 3).
Figure 4.
Mean final states in Experiment 1. (A) final distance to leader, (B) final speed of follower, and (C) final speed difference between follower and leader as a function of initial distance (do) and speed perturbation (Δv). In C, positive values mean that the leader was faster than the follower. Error bars represent the standard error of the mean (SEM).
Table 3.
The results of the Wald chi-squared test on fixed effects on final states in Experiment 1. ***p < 0.0001.
| Dependent variable | d 0 | Δv | d 0 × Δv |
|---|---|---|---|
| Final distance | χ 2(2, N = 1,060) = 669.74*** | χ 2(2, N = 1,060) = 115.13*** | χ 2(4, N = 1,060) = 148.16*** |
| η 2 = .98 | η 2 = .85 | η 2 = .13 | |
| Final speed | χ 2(2, N = 1,060) = 21.57*** | χ 2(2, N = 1,060) = 103.95*** | χ 2(4, N = 1,060) = 208.84*** |
| η 2 = .64 | η 2 = .83 | η 2 = .17 | |
| Final speed difference | χ 2(2, N = 1,060) = 21.79*** | χ 2(2, N = 1,060) = 73.48*** | χ 2(4, N = 1,060) = 208.80*** |
| η 2 = .64 | η 2 = .77 | η 2 = .17 |
Trials with greater initial distance showed greater final distance (Figure 4A). There was also a significant effect of initial distance on final speed (Figure 4B red curve): Closer distances tended to produce slower final speeds. However, this effect did not occur when the leader sped up (blue curve), yielding a significant distance by speed perturbation interaction. This asymmetry will be considered further below. Finally, the difference between the final speed of the follower and the leader grew with initial distance (Figure 4C), as revealed by the significant distance effect. This effect was largely due to leader deceleration (red curve), yielding a significant interaction. Participants thus did not match the speed of the leader, except in the constant-speed control condition.
On deceleration trials (red curves), final distance was smaller (Figure 4A) and final speed was slower but depended on initial distance (Figure 4B). Acceleration trials (blue curves) showed greater final distance (Figure 4A) and faster final speed (Figure 4B). Thus, our manipulations on initial distance and speed perturbation effectively influenced the participants’ behavior.
Response asymmetry
The results for walking speed revealed an asymmetry in the response to leader acceleration and deceleration (Figures 3A, B and Figures 4B, C). Although the leader increased and decreased speed by the same amount, participants had a larger response to deceleration than acceleration, especially at smaller initial distances, consistent with the asymmetry in the rate of optical expansion and contraction. A linear mixed-effects regression was performed on the absolute value of the follower's speed adjustment, with initial distance (d0) and leader speed perturbation (∆v = −0.3 and +0.3 m/s only) as fixed effects and subject as a random effect. There was a significant main effect of leader acceleration/deceleration (Figure 5), confirming the asymmetry in the magnitude of the follower's response (χ2 =7.60, p < 0.01, η2 = .39). There was also a main effect of initial distance (χ2 =49.42, p < 0.01, η2 = .77). The interaction was not significant (χ2 = 4.31, p = 0.12).
Figure 5.
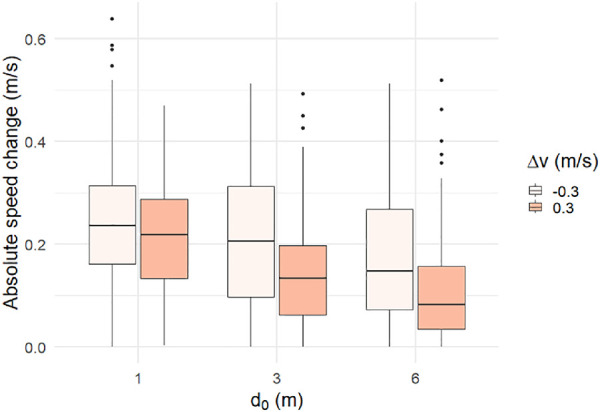
The asymmetry in absolute speed change of participants in response to the leader's deceleration (light bars) or acceleration (dark bars) (∆v) in Experiment 1.
Finally, despite instructions to follow the leader at a constant distance, the actual following distance increased by the time of the speed perturbation and was generally not maintained after perturbation (Figures 3C, D), except when the initial distance was 1 m and the leader decelerated.
Model comparisons
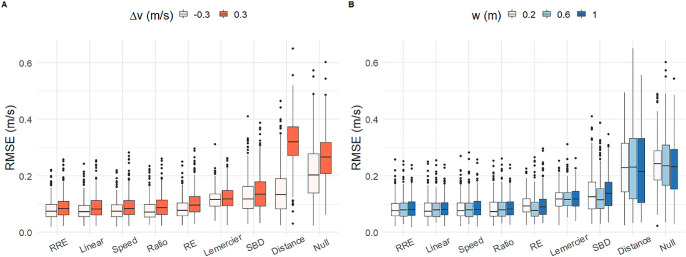
Results from the two fitting procedures appear in the right two columns of Table 2. Based on BIC (lower is better), the ranking of models is RRE < Ratio < RE < Linear < Speed < Lemercier < SBD < Distance = Null. For all inequalities, ∆BIC > 10, indicating very strong evidence in favor of this ordering.
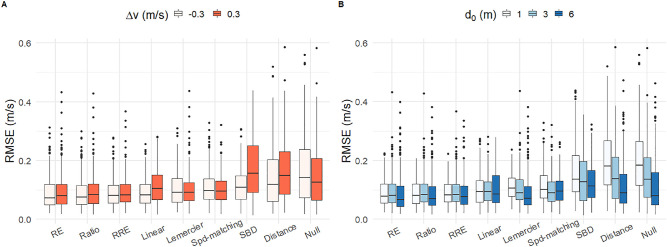
Similar results were found for the mean RMSE from cross-validation (right column of Table 2; smaller is better), confirmed by frequentist tests (Figure 6). A one-way analysis of variance (ANOVA) on RMSE revealed a main effect of model, F (8, 6,255) = 102.26, p < 0.0001, η2 = 0.116. Duncan's multiple range test (de Mendiburu, 2019) showed the following RMSE ranking: (RE, RRE, Ratio) < (Speed, Linear, Lemercier) < SBD < (Null, Distance), where all inequalities are p < 0.05.
Figure 6.
Box plots of RMSE for each model from leave-one-subject-out cross-validation in Experiment 1. (A) RMSE on acceleration (red) and deceleration (pink) trials. (B) RMSE in each initial distance condition. The heavy black bar is the median, boxes represent the interquartile range, and vertical whiskers represent the range of the data excluding outliers (black dots), which were defined as lying outside 1.5 times the interquartile range.
The purpose of Experiment 1 was to compare the RE and speed-matching models, because Rio et al. (2014) found that these two models best explained their data. We thus compared them in a linear mixed-effect regression with model, initial distance (d0), and speed perturbation (∆v) as fixed effects and subject as a random effect. The results revealed (a) a significant main effect of model, χ2(1, N = 696) = 31.32, p = 0.020, η2 = 0.02; (b) a Model × d0 interaction, χ2(2, N = 696) = 7.83, p = 0.020, η2 < 0.01; (c) a Model × ∆v interaction, χ2(1, N = 696) = 5.26, p = 0.022, η2 < 0.01; and (d) a three-way interaction of Model × d0 × ∆v, χ2(2, N = 696) = 24.73, p < 0.0001, η2 = 0.02. The Model × d0 interaction indicates that the difference between the RE model and speed-matching model depends on d0: The speed-matching model shows larger error than the RE model, especially when d0 is 1 or 6 m, which is due to its distance invariance (Figure 7).
Figure 7.
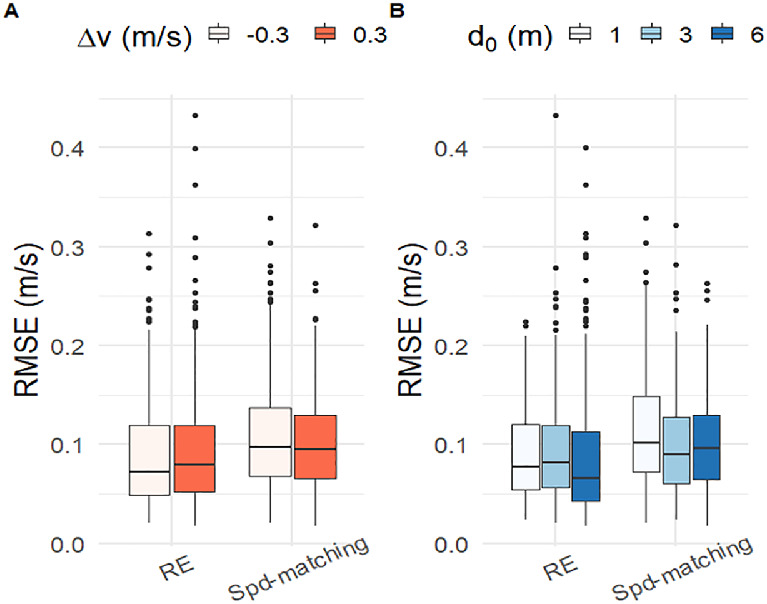
Box plots of RMSE highlighting the effects of (A) speed perturbation and (B) initial distance on the RE and speed-matching models. Data are the same as Figure 6.
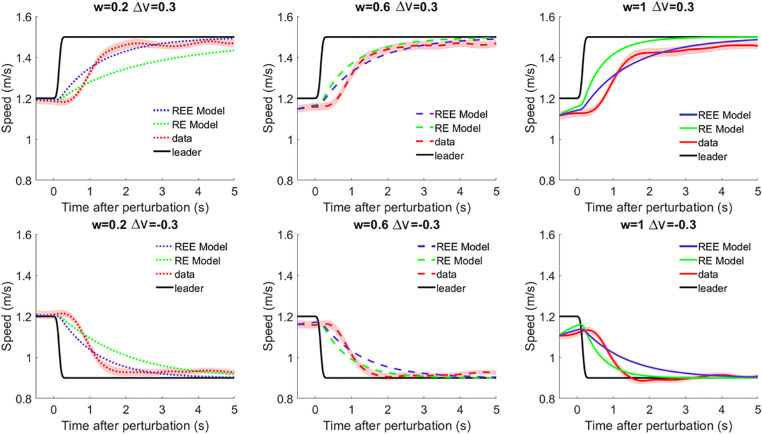
The mean time series of speed for the speed-matching model and the RE model in each condition (Figure 8) reveal why the speed-matching model has a poorer fit. The predictions of the RE model (green curves) vary with initial distance, whereas the speed-matching model (blue curves) makes similar predictions across conditions (compare columns in Figure 8). For the speed-matching model, minimizing error at the middle distance (d0 = 3, panels B,E) means increasing error at short (d0 = 1, panels A,D) and long (d0 = 6, panels C,F) distances, because the behavior of participants changed with distance.
Figure 8.
The real and predicted mean time series of speed in Experiment 1. D0 is initial distance, and ∆v is speed perturbation. The shading indicates 95% confidence intervals for the human data. The predictions of the RE model are distance dependent, whereas those of the speed-matching model are not.
Discussion
The RE, RRE, and ratio models describe pedestrian following better than other models. They can predict the speed of pedestrians across different conditions without changing parameter values. In contrast, the speed-matching model makes very similar predictions at different following distances, which does not match the behavior of the participants. This was not observed in Rio et al. (2014) because the range of following distances used in their experiments was not large enough to reveal the limitation of the speed-matching model.
Although distance can influence following behavior, it did not do so as described by the distance model or the SBD model. Participants did not maintain the initial distance from the leader, nor did they maintain a distance that increases with their speed. Moreover, linearly adding a distance term to the speed-matching model (linear model) did not significantly improve the performance. The data and fitting results from Experiment 1 suggest a nonlinear relationship between distance and following behavior.
The models that use nonlinear forms of distance are the RE, RRE, ratio, and Lemercier models. The Lemercier model is a version of the ratio model with a constant delay or reaction time, but it had a lower goodness of fit. Although a delay can be observed in the data, it is not a constant value. In particular, the delay is shorter at smaller distances than at larger distances; we suspect this is due to lower rates of optical expansion/contraction at greater distances. In addition, whereas the Lemercier model does not consider the speed of the follower, the ratio model takes it into account. The RE and RRE models both rely on the change in visual angle, which is a nonlinear function of distance and depends on the relative speed of leader and follower. Not only do they predict behavior as well as the ratio model, but they have a more concise form with only one free parameter compared to three. Given that humans rely on vision, they also offer biologically plausible control laws for pedestrian following. In contrast, the ratio model is omniscient, relying on distance, absolute speed, and relative speed, variables that are not immediately available in vision and are not accurately perceived.
Experiment 2
The RE model is sensitive to the size of the leader, because the optical expansion rate depends on the leader's visual angle, for a given distance and speed. The model thus predicts that a larger leader will produce a stronger response in the follower, all other things being equal (Figure 1B). This size dependance is attenuated by the RRE model because the expansion rate is normalized by the visual angle (Figure 1C); in effect, RRE specifies the immediacy of a collision in time at the current relative speed. Experiment 1 did not strongly distinguish these models because the leader pole was a constant size, so they made similar predictions after parameter fitting. In Experiment 2, we tested the models by manipulating the size (diameter) of the leader pole.
Method
Participants
Twelve students from Brown University, five males and seven females who had not participated in Experiment 1, participated in Experiment 2. All participants had normal or corrected-to-normal vision. The protocol was approved by Brown University's Institutional Review Board, in accordance with the Declaration of Helsinki. Informed consent was obtained from all participants, who were paid for their participation.
Apparatus and displays
The equipment and displays were the same as in Experiment 1, with two exceptions. First, the diameter (i.e., width) of the leader pole was manipulated (0.2, 0.6, or 1 m), while its height was 3 m in all trials. Second, the initial distance of the leader pole was held constant at 2 m.
Procedure and design
The instructions and procedure were the same as before. Experiment 2 had a within-subject factorial design: 3 leader width (0.2, 0.6, 1 m) × 3 speed perturbation (−0.3, 0, +0.3 m/s), yielding nine conditions. There were 10 repetitions in each condition, for a total of 90 trials, presented in a different random order for each participant. A test session lasted about 40 min.
Data processing and model fitting
The data were processed as in Experiment 1. Thirty-six (3.33%) out of 1,080 trials were excluded due to tracking failures. The data used for model fitting were the time series of follower's speed from 0.5 s before the perturbation to 5.5 s after the perturbation in each trial. Only trials with a speed perturbation (n = 694) were used for model fitting, after removing 26 trials that were shorter than 5 s after perturbation. Participants’ final speed (the average speed in the last 2 s) and final distance to the leader pole (the average distance in the last 2 s) were calculated for each time series. Models were fitted and tested using the same procedures as in Experiment 1.
Results
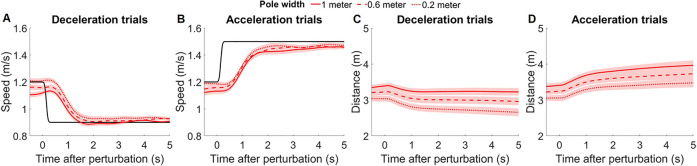
Mean time series of speed and distance in each condition appear in Figure 9. Leader size (separate curves) clearly influenced the participant's distance from the leader (Panels C, D), but had little influence on the participant's speed (Panels A, B). The latter result is contrary to the RE model, but was predicted by the RRE model.
Figure 9.
Mean participant time series in Experiment 2. Time series of speed on (A) deceleration (n = 346) and (B) acceleration (n = 351) trials. Time series of distance from leader on (C) deceleration and (D) acceleration trials. Black curves indicate leader speed, red curves indicate participant responses in each width condition, and shading indicates 95% confidence intervals. All time series are aligned at the time of perturbation.
Final states
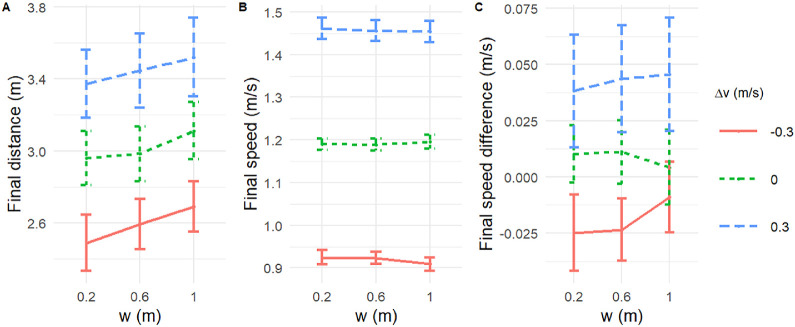
The mean final distance, final speed, and final speed difference between the participant and the leader are plotted as a function of leader width in Figure 10. A linear mixed-effect regression with leader width (w) and speed perturbation (∆v) as fixed effects and subject as a random effect revealed a significant effect of leader width on final distance (p < 0.001) (Table 4). Specifically, distance increased with the width of the leader (Figure 10A); this effect cannot be explained by a constant visual angle, for the mean final angle was four times larger with a 1-m width than a 0.2-m width in each speed perturbation condition. In contrast, there was no effect of leader width on final speed or final speed difference (Figures 10B, C). This finding is inconsistent with the RE model, in which the speed response depends on leader size, but consistent with the RRE model, in which the response is normalized by leader visual angle.
Figure 10.
Mean final states in Experiment 2. (A) final distance to (the near surface of) leader, (B) final speed of follower, and (C) final speed difference between follower and the leader, as a function of leader width (w) and speed perturbation (∆v). In C, positive values on the ordinate mean that the leader was faster than the follower. Error bars represent the SEM.
Table 4.
The results of the Wald chi-squared test on fixed effects on final states in Experiment 2. ***p < 0.0001.
| w | Δv | w × Δv | |
|---|---|---|---|
| Final distance | χ 2(2, N = 1,044) = 23.72 *** | χ 2(2, N = 1,044) = 63.68 *** | χ 2(4, N = 1,044) = 1.18 |
| η 2 = .52 | η 2 = .83 | ||
| Final speed | χ 2(2, N = 1,044) = 1.15 | χ 2(2, N = 1,044) = 2173.35 *** | χ 2(4, N = 1,044) = 6.19 |
| η 2 = .99 | |||
| Final speed difference | χ 2(2, N = 1,044) = 1.16 | χ 2(2, N = 1,044) = 23.23 *** | χ 2(4, N = 1,044) = 6.19 |
| η 2 = .55 |
On the other hand, the speed perturbation had a significant effect on all final states, confirming that it effectively influenced behavior. In particular, participants followed at a closer distance when the leader slowed down than when the leader sped up (Figure 10A). Participants also walked slower when the leader decelerated than when the leader accelerated (Figure 10B), resulting in a slower and faster speed than the leader, respectively (Figure 10C). However, the w × ∆v interaction was not significant for any final state.
Following speed and distance
As is apparent from the mean time series (Figure 9), the width of the leader did not influence participants’ speed response (panels A, B) but did affect the distance of participants from the leader (panels C, D). Once again, participants did not maintain the initial distance of 2 m to the leader, nor did they keep a constant distance after perturbation.
Model comparisons
Results from the two fitting procedures are shown in Table 5. Based on BIC (lower is better), the ranking of models is RRE < (Ratio = Linear) < Speed < RE < Lemercier < SBD < Null < Distance. For all inequalities, ∆BIC > 8, indicating strong evidence in favor of this ranking.
Table 5.
Tests of the nine models in Experiment 2. Note: Parameter values and BIC values were acquired by fitting the models to all perturbation trials (n = 694), while minimizing the RMSE on speed. BIC values were computed based on Equation 1. The models were also tested using leave-one-subject-out cross-validation, in which each model was trained on 11 participants and tested on the one left out until all combinations of training set and test set were used. The test results (mean and standard deviation of RMSE) of 12 iterations of cross-validation are shown in the table. The letters in the superscript of BIC values indicate the rank of model based on BIC, whereas those in the superscript of cross-validation error indicate Duncan group in Duncan's multiple range test. τ in Lemercier et al. (2012) was capped at 1 s because a reaction time longer than 1 s is unlikely for a human pedestrian.
| Model | Equation | Parameters | BIC | Mean RMSE (m/s) |
|---|---|---|---|---|
| Relative rate of expansion (RRE) | b = 2.629 | −3,289a | 0.086 (SD = 0.038)a | |
| Ratio | c = 3.698 | −3,281b | 0.088 (SD = 0.040)a | |
| M = −1.760 | ||||
| L = 1.014 | ||||
| Linear | c 1 = 0.894 | −3,281b | 0.087 (SD = 0.038)a | |
| c 2 = −0.035 | ||||
| a = 2.080 | ||||
| b = 0.652 | ||||
| Speed | c = 0.831 | −3,267c | 0.087 (SD = 0.039)a | |
| Rate of expansion (RE) | b = 20.443 | −3,141d | 0.095 (SD = 0.043)b | |
| Lemercier et al. (2012) | τ = 1.000 | −2,863e | 0.121 (SD = 0.039)c | |
| c = 1.833 | ||||
| γ = 0.796 | ||||
| Speed-based distance (SBD) | c = 2.644 | −2,647f | 0.137 (SD = 0.066)d | |
| a = 1.231 | ||||
| b = 1.746 | ||||
| Null | None | −1,887g | 0.238 (SD = 0.097)f | |
| Distance | c = 0.011 | −1,868h | 0.231 (SD = 0.120)e |
The mean RMSE for each model (smaller is better) from leave-one-subject-out cross-validation appears in Figure 11. One-way ANOVA on RMSE revealed a main effect of model, F (8, 6,237) = 636.2, p < 0.0001, η2 = 0.449. Duncan's multiple range test (de Mendiburu, 2019) showed the following ranking of models: (RRE, Speed, Linear, Ratio) < RE < Lemercier < SBD < Distance < Null, where inequalities are p < 0.05 (means and standard deviations are shown in Table 5).
Figure 11.
Box plots of RMSE for each model from leave-one-subject-out cross-validation in Experiment 2. (A) RMSE on acceleration (red) and deceleration (pink) trials. (B) RMSE in each leader width condition.
To compare the RE and RRE models, a linear mixed-effect regression was performed on RMSE with model, leader width (w), and speed perturbation (∆v) as fixed effects and subject as a random effect. It revealed a significant main effect of model, χ2(1, N = 694) = 23.39, p < 0.001, η2 = 0.02; a model × w interaction, χ2(2, N = 694) = 7.92, p = 0.019, η2 < .01; and a significant model × ∆v interaction, χ2(1, N = 694) = 9.52, p = 0.002, η2 < .01. It can be seen from Figure 11B that the difference between the RE and RRE model depends on w. The error of the RE model is larger than that of the RRE model, especially when w is 0.2 m or 1 m, due to the RE model's sensitivity to the size of the leader pole.
Mean time series for simulations of the RE and RRE models in each leader acceleration/deceleration condition (Figure 12) reveal that the RE model overreacted to the large leader (w = 1 m, right) and underreacted to the small leader (w = 0.2 m, left). The RRE model overcame this sensitivity by normalizing the expansion/contraction rate with the visual angle of the leader.
Figure 12.
The real and predicted mean time series of speed in Experiment 2. D0 is initial distance. ∆v is speed perturbation. The shading indicates the 95% confidence intervals for the human data. The predictions of the RE model change with the width of the leader pole, whereas those of the RRE model do not to the same degree.
Discussion
Experiment 2 found that the width of the leader did not influence the participant's speed in 1D following. Speed responses to the leader did not change significantly based on its diameter, at least over the range of 0.2 to 1.0 m. Whereas the RE model was sensitive to this range of leader size, the RRE model normalized the expansion rate by the leader's visual angle and thus had a smaller error.
Note that the final distance did vary with the width of the leader. Figure 10A shows that the final distance to the near surface of the leader increased as the width of the leader increased. This is due to differences in speed after initial acceleration. The time series of speed in Figures 9A, B show that participants’ average speed before the perturbation was lower when the leader was larger, which caused a greater distance at the time of perturbation. This reluctance to get close to a larger object could be a result of safety concerns or the limited field of view in the HMD. However, the width of the leader did not influence how participants changed speed in response to the perturbation. Therefore, the width of the leader influenced final distance but not final speed.
Experiment 2 also replicated the results of Rio et al. (2014), because it tested only one initial distance. They found that the speed-matching, ratio, and linear models all performed at a comparable level, with a significantly lower RMSE than the RE, distance and speed-based distance models. We find that the RRE model is also comparable to these omniscient models by the frequentist criterion, but it has the smallest RMSE overall and performs the best by the BIC because it has only one free parameter. The RRE model does not rely on separate inputs of distance and speed but on an optical variable that depends on both. Therefore, it is free from assumptions about the accuracy of distance and speed perception. The RRE model thus offers a biologically plausible explanation of how human pedestrians use visual information to control walking speed while following a leader.
General discussion
Pedestrian-following behavior
The present study showed that the speed control of pedestrian following depends on the distance and speed, but not the size, of the leader. Although participants were asked to maintain a constant following distance, the actual distance varied. When the leader accelerated to 1.5 m/s, participants did not fully match that speed, which caused the distance to increase; conversely, when the leader decelerated to 0.9 m/s, participants also did not fully match that speed until the distance decreased to less than 3 m. In addition, the present study replicated the asymmetry in the response to leader deceleration and acceleration reported by Rio et al. (2014): Participants exhibited a greater change in speed when the leader slowed down than when the leader sped up. This asymmetry was greater at closer leader distances because the rate of expansion was higher, given the same deceleration. Finally, the follower's speed does not depend on leader size (over a range of 0.2–1.0 m), contrary to the prediction of the RE model but consistent with the RRE model.
We note that the human data have a sigmoidal speed profile in response to the leader's change in speed, whereas all the models produce an instantaneous speed change (Figures 8, 12). This contributed to visible prediction errors. The discontinuous change in speed is due to the fact all the models are second-order models, which control instantaneous acceleration. In the future, use of third-order models could reduce this error by controlling the derivative of acceleration (jerk). Such an approach would allow the model to generate a gradual change in speed similar to the sigmoidal speed profile of the human data.
Models of pedestrian following
Previously, Rio et al. (2014) reported that the speed-matching model approximated the human data more closely than the RE model, at least over a small range of leader distance (1–4 m). However, the present Experiment 1 found that both the RE and RRE models perform better than the speed-matching model when tested on a wider range of distances (1–6 m). Moreover, the follower's speed is better predicted by the RRE than the RE model in both of the present experiments. When the size of the leader was varied in Experiment 2, the error of the RE model increased, whereas the error of the RRE model remained smaller than all other models, with ∆BIC indicating strong evidence in favor of RRE.
The closest competitor to the RRE model is the ratio model. However, it is predicated on physical rather than optical variables and has three free parameters as opposed to one. The ratio model takes leader distance, follower speed, and speed difference as input and is thus omniscient. In addition, the optimal value for each of its three parameters differed between Experiment 1 and Experiment 2, for reasons that are hard to interpret. In contrast, the RRE model takes one optical variable and its rate of change as input, and its one free parameter has a straightforward interpretation as the gain or sensitivity of speed control. Most important, the RRE model provides a biologically plausible explanation of speed control based on vision, whereas the ratio model presumes that distance and speed are accurately perceived.
Conclusions
The RRE model explains speed control in pedestrian following better than the eight other models tested in the present study. The model generalizes over a range of leader distances, speeds, and sizes. Most important, it provides a concise, vision-based explanation of 1D pedestrian following, which can be applied to related problems such as two-dimensional following, or controlling heading and speed in the horizontal plane (Dachner & Warren, 2017), and collective crowd motion (Dachner, Wirth, Richmond, & Warren, 2022).
Supplementary Material
Acknowledgments
Supported by NSF BCS-1431406, NIH R01-EY029745.
Commercial relationships: none.
Corresponding author: Jiuyang Bai.
Email: jiuyang_bai@alumni.brown.edu.
Address: Department of Cognitive, Linguistic, and Psychological Sciences, Box 1821, Brown University, Providence, RI 02912, USA.
References
- Andersen, G. J., & Sauer, C. W. (2007). Optical information for car following: The driving by visual angle (DVA) model. Human Factors, 49, 878–896. [DOI] [PubMed] [Google Scholar]
- Baayen, R. H., Davidson, D. J., & Bates, D. M. (2008). Mixed-effects modeling with crossed random effects for subjects and items. Journal of Memory and Language, 59(4), 390–412. [Google Scholar]
- Bates, D., Mächler, M., Bolker, B., & Walker, S. (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48, 10.18637/jss.v067.i01. [DOI] [Google Scholar]
- Berg, J. Van den, Lin, M., & Manocha, D. (2008). Reciprocal velocity obstacles for real-time multi-agent navigation. In 2008 IEEE International Conference on Robotics and Automation (pp. 1928–1935). Pasadena, CA: IEEE. [Google Scholar]
- Brackstone, M., & McDonald, M. (1999). Car-following: A historical review. Transportation Research Part F, 2, 181–196. [Google Scholar]
- Bruneau, J., Dutra, T. B., & Pettré, J. (2014). Following behaviors: A model for computing following distances. Transportation Research Procedia, 2, 424–429. [Google Scholar]
- Dachner, G., & Warren, W. H. (2017). A vision-based model for the joint control of speed and heading in pedestrian following. Journal of Vision, 17(10), 716, 10.1167/17.10.716. [DOI] [Google Scholar]
- Dachner, G. C., Wirth, T. D., Richmond, E., & Warren, W. H. (2022). The visual coupling between neighbors explains local interactions underlying human ‘flocking’. Proceedings of the Royal Society B, 289, 20212089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Mendiburu, F. (2019). Agricolae: Statistical procedures for agricultural research [Computer software manual], https://CRAN.R-project.org/package=agricolae.
- Ducourant, T., Vieilledent, S., Kerlirzin, Y., & Berthoz, A. (2005). Timing and distance characteristics of interpersonal coordination during locomotion. Neuroscience Letters, 389, 6–11. [DOI] [PubMed] [Google Scholar]
- Fehrenbach, J., Narski, J., Hua, J., Lemercier, S., Jelic, A., Appert-Rolland, C., & Degond, P. (2015). Time-delayed follow-the-leader model for pedestrians walking in line. Networks and Heterogeneous Media, 10, 579–608. [Google Scholar]
- Gazis, D. C., Herman, R., & Rothery, R. W. (1961). Nonlinear follow the leader models of traffic flow. Operations Research, 9, 545–567. [Google Scholar]
- Gray, R., & Regan, D. (1998). Accuracy of estimating time to collision using binocular and monocular information. Vision Research, 38, 499–512. [DOI] [PubMed] [Google Scholar]
- Guy, S. J., Lin, M. C., & Manocha, D. (2010). Modeling collision avoidance behavior for virtual humans. In van der Hoek, W., Kaminka, G. A., Lespérance, Y., Luck, M., Sen, S. (Eds.), Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems (AA-MAS 2010), May 10-14, 2010, Toronto, Canada (Vol. 2, pp. 575–582).
- Helbing, D., & Molnar, P. (1995). Social force model for pedestrian dynamics. Physical Review E, 51(5), 4282. [DOI] [PubMed] [Google Scholar]
- Helly, W. (1959). Simulation of bottlenecks in single lane traffic flow. In Herman, R. C. (Ed.), Proceedings of the Symposium on Theory of Traffic Flow (pp. 207–238). New York, NY: Elsevier. [Google Scholar]
- Herman, R., Montroll, E., Potts, R., & Rothery, R. (1959). Traffic dynamics: Analysis of stability in car following. Operations Research, 7, 86–106. [Google Scholar]
- Heuer, H. (1993). Estimates of time-to-collision based on changing size and changing target vergence. Perception, 22, 549–563. [DOI] [PubMed] [Google Scholar]
- Kometani, E., & Sasaki, T. (1958). On the stability of traffic flow. Journal of the Operations Research Society of Japan, 2, 11–26. [Google Scholar]
- Lagarias, J. C., Reeds, J. A., Wright, M. H., & Wright, P. E. (1998). Convergence properties of the Nelder–Mead simplex method in low dimensions. SIAM Journal on Optimization, 9(1), 112–147. [Google Scholar]
- Lakoba, T. I., Kaup, D. J., & Finkelstein, N. M. (2005). Modifications of the Helbing-Molnar-Farkas-Vicsek social force model for pedestrian evolution. Simulation, 81(5), 339–352. [Google Scholar]
- Lee, D. N. (1976). A theory of visual control of braking based on information about time-to-collision. Perception, 5(4), 437–459. [DOI] [PubMed] [Google Scholar]
- Lee, J., & Jones, J. (1967). Traffic dynamics: Visual angle car following models. Traffic Engineering and Control, 8, 348–350. [Google Scholar]
- Lemercier, S., Jelic, A., Kulpa, R., Hua, J., Fehrenbach, J., Degond, P., & Pettré, J. (2012). Realistic following behaviors for crowd simulation. In Computer Graphics Forum (Vol. 31, No. 2pt2, pp. 489–498). Oxford, UK: Blackwell Publishing Ltd. [Google Scholar]
- Mohler, B. J., Creem-Regehr, S. H., & Thompson, W. B. (2006). The influence of feedback on egocentric distance judgments in real and virtual environments. In Fleming, R., Kim, S. (Eds.), Proceedings of the 3rd Symposium on Applied Perception in Graphics and Visualization (pp. 9–14). New York, NY, USA: Association for Computing Machinery. [Google Scholar]
- Okreylos. (2016). Optical properties of current vr hmds, http://doc-ok.org/?p=1414.
- Pipes, L. A. (1953). An operation analysis of traffic dynamics. Journal of Applied Physics, 24, 274–281. [Google Scholar]
- R Core Team. (2019). R: A language and environment for statistical computing [Computer software manual], https://www.R-project.org/. [Google Scholar]
- Richardson, A. R., & Waller, D. (2007). Interaction with an immersive virtual environment corrects users’ distance estimates. Human Factors, 49(3), 507–517. [DOI] [PubMed] [Google Scholar]
- Rio, K. W., Rhea, C. K., & Warren, W. H. (2014). Follow the leader: Visual control of speed in pedestrian following. Journal of Vision, 14(2), 4, 10.1167/14.2.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rushton, S. K., & Wann, J. P. (1999). Weighted combination of size and disparity: A computational model for timing a ball catch. Nature Neuroscience, 2, 186–190. [DOI] [PubMed] [Google Scholar]
- Savelsbergh, G. J. P., Whiting, H. T. A., & Bootsma, R. J. (1991). Grasping tau. Journal of Experimental Psychology: Human Perception and Performance, 17, 315–322. [DOI] [PubMed] [Google Scholar]
- Van Den Berg, J., Guy, S. J., Lin, M., & Manocha, D. (2011). Reciprocal n-body collision avoidance. In Pradalier, C., Siegwart, R., Hirzinger, G. (Eds.), Robotics Research: The 14th International Symposium ISRR (pp. 3–19). Berlin, Heidelberg: Springer Berlin Heidelberg. [Google Scholar]
- Vannier, J., Vidal, M., Marchant, R., El Hariri, K., Kouraiss, K., Pittet, B., & Martin, E. (2019). Collective behaviour in 480-million-year-old trilobite arthropods from Morocco. Scientific Reports, 9(1), 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner, H. (1982). Flow-field variables trigger landing in flies. Nature, 297(5862), 147–148. [Google Scholar]
- Warren, W. H. (2006). The dynamics of perception and action. Psychological Review, 113, 358–389. [DOI] [PubMed] [Google Scholar]
- Wilson, R. E., & Ward, J. A. (2011). Car-following models: Fifty years of linear stability analysis–a mathematical perspective. Transportation Planning and Technology, 34(1), 3–18. [Google Scholar]
- WorldViz. (2014). Vizard 5, https://www.worldviz.com/vizard-virtual-reality-software.
- Yu, W., Chen, R., Dong, L., & Dai, S. (2005). Centrifugal force model for pedestrian dynamics. Physical Review E, 72(2), 026112. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.