Abstract
Background
X-ray is an effective measure in the diagnosis of coronavirus disease 2019. However, it suffers from low visibility and poor details. A plausible solution is to decompose the captured images and enhance the details. The bilateral weighted least square model can be an effective tool for this task. However, it is highly computationally expensive.
Method
In this article, we propose an efficient algorithm for the bilateral weighted least square model. We approximate the bilateral weight with the bilateral grid and then incorporate it into the optimization model. This significantly reduces the number of variables in the linear system. Therefore, the model can be efficiently solved. We employ the proposed algorithm to decompose the input X-rays into base and detail layers. The detail layers are then boosted and added back to the input to derive the detail-enhanced results.
Results
The subjective results indicate that our method achieves higher contrast than the best-performing method ( , , ). Furthermore, our method is highly efficient. It takes 0.92 s to process a 720P color image on an Intel i7-6700 CPU. The objective results derive from the chi-square test indicate that subjects hold more positive attitudes toward our detail-enhanced images than the original X-ray images ( , , ).
Conclusion
We have conducted extensive experiments to evaluate the proposed image detail enhancement method. It can be concluded that (1) our method could significantly improve the visibility of the X-ray images. (2) our method is fast and effective, thus facilitating real applications.
Keywords: X-ray image, detail enhancement, coronavirus disease 2019, bilateral weighted least square
Introduction
The coronavirus disease 2019 (COVID-19) is extremely contagious due to the high basic reproduction number (R0).1–4 During the last three years, it has spread rapidly across the world. The booming development of COVID-19 has imposed a heavy burden on the control of the disease. Even though the impact of the virus is being alleviated, the number of reported reinfections is increasing.5–7 A timely diagnosis of COVID-19 could prevent the spread of the virus. However, the dominant variants8,9 of COVID-19 are characterized by a range of clinical signs of asymptomatic infection,10,11 which complicates the diagnosis.
Chest radiography (X-ray) is an essential measure for human experts to diagnose COVID-19 disease.12,13 Moreover, researchers have also attempted to investigate deep learning-based approaches for the diagnosis of COVID-19. Comprehensive studies of these methods can be found in existing surveys.14,15 However, due to the low dynamic range and contrast of the X-ray images, subtle but meaningful details may be challenging to identify for both humans and machines. Therefore, it is critical to enhance the details so that the visibility of the X-ray images can be improved.
Detail enhancement refers to the process to enhance the details of images. It can be leveraged to improve the clarity of X-ray images. The early attempts on this task are based on the histogram equalization and its variants, such as the adaptive histogram equalization, 16 contrast limited adaptive histogram equalization,17,18 and normalized contrast limited adaptive histogram equalization. 19 The Histogram equalization-based methods could promote the image details, but they may also increase the contrast of noise and suppress the contrast of meaningful structures.
Recent methods for detail enhancement mostly rely on image decomposition with edge-aware smoothing filters, such as the bilateral filter,20,21 anisotropic diffusion filter, 22 guided filter,23,24 soft clustering filter, 25 reconstruction filter, 26 filter, 27 generalized smoothing filter, 28 and weighted least square filter. 29 The decomposition-based methods consider the pixels in the neighborhood during the enhancement process, thus could alleviate the problems of the histogram equalization-based methods.
It is worth noting that, among the decomposition-based methods, the weighted least square (WLS) filter 29 is shown to be particularly useful for detail manipulation, that is, it can significantly enhance the details without causing the gradient reversal or halo artifacts. However, the weighted design only involves the range, making it less edge-aware. Moreover, similar to many methods based on global optimization, it is highly time-consuming, as it requires to solve a linear system with a large inhomogenous Laplacian coefficient matrix.
With the booming advancement of the deep learning technique, we are seeing significant progress in the field of medical data/image processing, such as COVID-19 prediction, 30 segmentation of cervical cytology, 31 thyroid 32 and iris, 33 pulse extraction, 34 and breast cancer detection. 35 Different from these researches, our objective is to enhance the details of the COVID-19 chest X-ray images, thus aiding the diagnosis. We intend to develop a method that is not learning-based, and can be more stable and interpretable.
To facilitate our objective, we develop a novel decomposition-based image detail enhancement method, where we extract the detail layer, boost it, and add it back to the input image. The main contributions of this article are:
We propose a bilateral WLS model for the task of the X-ray image detail enhancement. The bilateral weighted scheme involves not only the range, but also the domain, thus can be more edge-aware.
We propose a fast solution to our bilateral WLS model, where we approximate the bilateral weight with the bilateral grid. This significantly reduces the size of the problem, thus can be highly efficient.
We have conducted subjective and objective experiments to evaluate our method. The subjective results show that our method achieves better contrast than existing methods. The objective results indicate that our method can improve the visibility of COVID-19 chest X-ray images.
The rest of the article is organized as follows. In the “Literature review” section, we summarize relevant methods. The “Method” section covers the details of the proposed method. Both objective and subjective experiments are presented in the “Experimental settings” section and both objective and subjective evaluations are presented in the “Experimental results” section. We discuss the proposed model in the “Discussion” section. Finally, we conclude the article and present future directions of research in the “Conclusion and future work” section.
Literature review
The most important step in our detail enhancement method is image decomposition. In this section, we will focus on various smoothing filters for image decomposition, which can be mainly divided into two categories, namely local and global methods. The former ones are based on explicitly define filter kernels, while the latter ones are based on sophisticated global optimization models.
Local methods
The bilateral filter 36 is perhaps the most prevalent non-linear filter for edge-preserving smoothing. It consists of a spatial kernel and a range kernel. Both of the two kernels are mostly Gaussian functions that are used to penalize pixels that are distant in space and range. Even though there are various artifacts, such as halos and gradient reversals, the bilateral filter is still effective in practice. The main impediment is the high computational cost.
Over the last decade, researchers have made various attempts to improve the efficiency of the bilateral filter. Most of the methods are built upon range quantization,37,38 range decomposition,39,40 or spatial subsampling. 27 These strategies significantly accelerate the bilateral filter, but they may not be able to improve the quality of image decomposition over the naive bilateral filter.
Another popular local method is the guided image filter. 23 The basic assumption in the work is that there exist local linear relations between the corresponding patches of the output and guidance images. Based on this assumption, the authors build a set of local linear regression problems that have closed-form solutions. The guided image filter can be computed efficiently. However, it suffers from severe halo artifacts in image decomposition.
In order to alleviate the halo artifacts that haunt the guided image filter, various strategies have been proposed, such as the anisotropic guided filter, 24 the weighted guided filter with steering kernel, 41 and the soft clustering guided filter. 42 These strategies all focus on the weighted averaging operation in the final step. These variants of guided filter significantly suppress the halo artifacts. However, the improvement is at the cost of sacrificing efficiency.
Global methods
The WLS filter 29 is the pioneering work for global image decomposition. It seeks to minimize the loss between the input and output regularized by the WLS of the output gradients. The model is shown to be particularly useful for detail enhancement, as it alleviates the halo and gradient reversal artifacts. However, the absence of the domain in the weighted design limits its edge-aware power. Furthermore, it can be time-consuming to solve. Though there exist separable 1D approximations,43,44 they may introduce severe streak artifacts.
The reconstruction model 26 optimizes the fidelity term regularized by the gradient reconstruction loss. The regularization enforces the sparsity of the output gradients, thus better facilitating edge awareness. The authors propose a novel mapping function to compress the small gradients while preserving large gradients, which further promote the edge awareness. However, the lack of the weighted scheme limits its performance.
The iterative least square filter 45 explores a non-convex penalty for regularization. It optimizes the fidelity term regularized by the generalized Charbonnier penalty on the gradients. The non-convex penalty function accommodates the gradient distribution of natural images. Therefore, the filter achieves promising performance on various tasks. Furthermore, it is highly efficient. However, it is inclined to the compartmentalization artifacts in detail enhancement.
The generalized smoothing filter 28 is designed to provide a framework for various edge-aware image processing tasks. The model is based on a novel truncated Huber penalty function, which is friendly to weak edges. Therefore, the resultant filter is strongly edge-aware. However, it tends to sharpen the salient edges, thus may be subject to the gradient reversal artifacts. Moreover, the piece-wise objective function can be computationally expensive to solve.
Different from existing optimization-based image decomposition methods that impose gradient regularization, the soft clustering filter 25 models the task as image clustering similar to super-pixel segmentation. The partition matrix derived from the clustering process is then leveraged to construct the affinity matrix for image decomposition. The method accommodates a variety of applications, yet it may not be able to protect thin structures.
From the above discussion, we see that the local methods are mostly fast, but they suffer from poor quality. Moreover, the global methods suffer from artifacts in detail enhancement except for the WLS filter, which on the other hand, is time-consuming to solve. In this article, we propose a global method for image decomposition based on the bilateral WLS model. We consider not only the range, but also the domain in the weighted design, thus can be more edge-aware. Furthermore, we propose a fast solution to our model based on the bilateral grid. 38
Proposed method
Bilateral WLS model
The bilateral WLS model seeks to minimize the summed squared error regularized by the bilateral weighted norm of the gradients. The objective function of the model is
| (1) |
where is the bilateral affinity between pixels and and it is formally defined as
| (2) |
where and are the spatial and range bandwidths, respectively, which are used to control the amount of smoothing. Different from the weighted scheme in the original WLS model 29 that considers only the range, the bilateral weight scheme incorporates both the range and domain, thus is deemed to be more edge-aware.
Rewriting equation (1) into the matrix form, we have
| (3) |
where is the degree matrix derived from . Specifically, is a diagonal matrix, where the th diagonal entry is the sum of the entries in the th row of . is the inhomogeneous Laplacian matrix. The fidelity term ensures that the filtering output does not deviate too far from the input . The regularization term enforces that the output must be smoothed. The parameter balances the two seemingly contradicting terms.
Taking the derivative of equation (3) to , and let it be zero, we have
| (4) |
where is the identity matrix. Equation (4) is computationally expensive to solve, as it is a linear system with a large sparse coefficient matrix.
Efficient solver
Directly solving equation (4) can be time-consuming. Inspired by the bilateral grid, 38 which is essentially a fast approximation of the bilateral filter, we propose a fast solver to the bilateral WLS model. According to the idea of the bilateral grid, the bilateral weight can be approximated as:
| (5) |
where stands for the splat matrix, and it is for hard quantization, where the entries can be either 0 or 1. is a matrix, where is the number of pixels and is the number of grids. indicates that pixel belongs to the grid and indicates otherwise. The range and domain values are quantized into grids. The matrix can then be derived by checking which grid the domain and range values of each pixel fall in. is the matrix for the high-dimensional spatial-invariant Gaussian filtering. is the slice matrix, and it is the transpose of .
Based on equation (5), equation (3) can be approximated as
| (6) |
where is the degree matrix derived from . Specifically, is a diagonal matrix, where the th diagonal entry is the sum of the entries in the th row of .
We introduce an auxiliary variable , and let
| (7) |
Assume the number of pixels and grids are and ( ), ( column vector) is in fact the grid representation of ( column vector), then equation (6) becomes
| (8) |
To solve the optimization problem shown in equation (8), we take the partial derivative to and let it be zero, then we have
| (9) |
where is a diagonal matrix, where each diagonal entry is the number of pixels in the corresponding grid, thus it can be evaluated efficiently. Note that equation (9) is also a linear system akin to equation (3). However, since contains much fewer unknowns than , it can be much easier to solve, namely
| (10) |
In this article, we leverage the preconditioned conjugate gradient algorithm 46 to solve the linear system.
When is solved, we can derive by a simple matrix–vector multiplication according to equation (7), namely
| (11) |
Since the matrix is for hard quantization, the output may exhibit blocky artifacts. In order to eliminate the artifacts, we further apply the domain transform filter 47 on the results derived from the optimization model. The domain transform filter is extremely fast ( ), so it has a neglectable influence on the running time.
System model
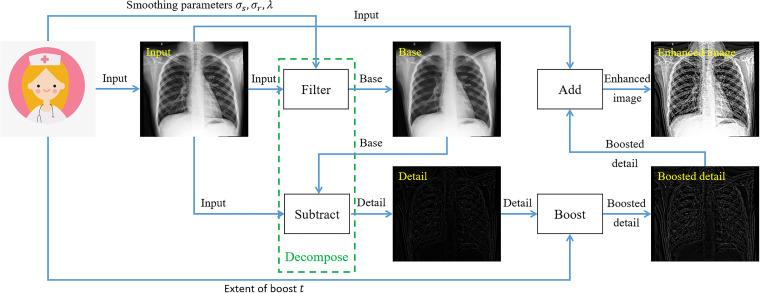
To achieve detail enhancement, the input X-ray image is firstly decomposed into the base and detail layers with our fast bilateral WLS filter. The detail layer is then boosted ( ) and added back to the input image to derive the detail-enhanced result. The flowchart of our enhancement method is shown in Figure 1.
Figure 1.
The flowchart of the proposed X-ray image detail enhancement method.
Our detail enhancement process can be mainly divided into three steps, which are detailed as follows:
Derive the base layer with the bilateral weighted least filter described in the previous sections.
- Extract the detail layer by subtracting the base layer from the input image , as shown below:
(12) - The detail layer is then boosted and added back to the input image to derive the detail-enhanced image, that is,
where is a scalar specifying the extent of boost. Throughout this article, we set . Our detail enhancement method can be sketched as Algorithm 1.(13)
Algorithm 1.
X-ray image detail enhancement
| Input: image , parameters , , , ; |
| 1: Solve equation (11) for the base layer |
| 2: Derive the detail layer with equation (12); |
| 3: Derive the enhanced image with equation (13); |
| Output: enhanced image ; |
Our detail enhancement method is highly efficient. Assume that the number of pixels and grids are and , and the number of iterations of the preconditioned conjugate gradient algorithm 46 is , deriving the base layers by solving equation (11) takes time. Deriving, boosting, and adding back the detail layer are element-wise operations, so the running time is . Therefore, the overall time complexity of our detail enhancement method is . On the other hand, if we derive the base layer by solving equation (4), it would take . Considering that in practice , our method could significantly accelerate the detail enhancement process.
Experimental settings
We have conducted both objective and subjective experiments to evaluate the proposed X-ray image detail enhancement method. In this section, we will detail the experimental settings from these two aspects.
Objective evaluation
Metrics
For objective evaluation, we leverage the contrast measure as the objective metric to evaluate the quality of the detail-enhanced X-ray images, as shown below
| (14) |
where and are the intensities of neighboring pixels. is the absolute difference between and , that is,
| (15) |
is the probability distribution of the absolute difference . The contrast measure is a nice indicator of the visibility and the amount of details in an X-ray image.
Furthermore, we record and compare the running time (measured in seconds) of various methods on images with varying resolutions. Note that the running time of all methods is collected on a modern desktop with an Intel i7-6700 CPU, an Nvidia GTX 1070, and 16 GB memory. The running time could be an essential criterion to validate the practicability of the proposed method.
Dataset
The objective evaluation is conducted on the COVID-19 chest X-ray image dataset. 48 The dataset is initially developed to advance the detection of COVID-19 using chest X-rays. It contains 317 X-ray images in total, which can be mainly divided into three categories, that is, COVID-19, viral pneumonia, and normal chest X-rays. Our method is not learning-based and it does not require training. We test our method on the 61 images in the test dataset.
Methods
We compare the proposed method to a variety of prevalent methods. The full names, abbreviations, and references of all the methods involved in this experiment can be found in Table 1. We use the official implementations of these methods, which are provided by the authors. For the parameter settings, we best tune the parameters based on the recommended values for all methods.
Table 1.
Brief of the methods in our experiment.
| Method | Reference | Abbreviation |
|---|---|---|
| Fast bilateral filter | Paris and Durand 38 | FBF |
| Guided image filter | He et al. 23 | GIF |
| Domain transform filter | Gastal and Oliveira 47 | DTF |
| Mutual structure filter | Shen et al. 49 | MSF |
| Weighted least square | Farbman et al. 29 | WLS |
| Anistropic diffusion | Liu and Gong 50 | AD |
| Smoothing sharpening filter | Deng et al. 51 | SSF |
| Iterative least square | Liu et al. 45 | ILS |
| reconstruction filter | Yang et al. 26 | L1RF |
| General smoothing filter | Liu et al. 28 | GSF |
| Soft clustering filter | Liu et al. 25 | SCF |
| Ours | - | Ours |
Subjective evaluation
Procedure
For the subjective evaluation, we conduct a user study to validate the effectiveness of the proposed method. We invite a total of 36 doctors to participate in our user study. We randomly choose 20 X-ray images from the COVID-19 chest X-ray image dataset 48 and then enhance the detail of the images with our method. The doctors are required to observe and analyze 10 original X-ray images, and the other 10 detail-enhanced X-ray images, through a 32-inches monitor with 2K resolution.
After carefully observing all of the 20 images, the doctors are required to provide responses to a questionnaire, which includes the following questions:
I think the images are clear for diagnosis.
I think the images contain adequate details.
I am satisfied with the presented images.
We adopt a five-point Likert scale 52 for the answers to the questions. The doctors need to choose responses from the following: strongly disagree (SD); disagree (D); neutral (N); agree (A); and strongly agree (SA). The ratings for the choices are 1, 2, 3, 4, and 5, respectively.
Grouping information
The 36 doctors are from the departments of respiratory, emergency, and geriatrics. There are 15 males and 21 females. They are randomly divided into two groups, namely the control and the treatment groups. The doctors in the control group are presented with the original X-ray images, and the doctors in the treatment group are presented with the detail-enhanced X-ray images derived from our method. We divide the 20 pairs of X-ray images into two image sets, that is, S1 and S2, with 10 pairs in each set. The control group observing image set S1 is the treatment group observing image set S2. The treatment group observing image set S2 is the control group observing image set S1. In this way, all subjects are exposed to both the original X-ray images and the detail-enhanced image. The detailed arrangement can be found in Table 2.
Table 2.
Grouping information.
| Set | Group | Mode | No. of subjects |
|---|---|---|---|
| rowspan="2" align="*"S1 | Control | X-ray images | 18 |
| Treatment | Enhanced X-rays | 18 | |
| rowspan="2" align="*"S2 | Control | X-ray images | 18 |
| Treatment | Enhanced X-rays | 18 |
The number of subjects.
The control group observing image set S1 is the treatment group observing image set S2.
The treatment group observing image set S1 is the control group observing image set S2.
Research hypotheses
Through the user study, we want to find out the answers to the following research questions:
What were the perceived clarity of the original X-ray images and the detail-enhanced X-ray images?
What were the perceived details of the original X-ray images and the detail-enhanced X-ray images?
What were the satisfaction levels provided by the original X-ray images and the detail-enhanced X-rays?
The corresponding research hypotheses are as follows:
-
H1.
The detail-enhanced X-ray images derived from our method are clearer than the original X-ray images.
-
H2.
The detail-enhanced X-ray images derived from our method contain more details than the original X-ray images.
-
H3.
The detail-enhanced X-ray images derived from our method improve the satisfaction levels over the original X-ray images.
Data collection and analysis
The doctors’ responses to the questionnaire are used to validate hypotheses H1, H2, and H3 in our user study. We printed the questions on paper so that it would be convenient for collecting the responses. The doctors are required to provide their responses by filling in their answers on the papers.
We record the number of subjects choosing each answer for each of the questions in the questionnaire. We leverage the chi-square test to study hypotheses H1, H2, and H3, as the measurements are discrete variables, and the purpose is to test whether the number of individuals in different categories fits a null hypothesis.
Experimental results
Objective evaluation
Quality
Table 3 shows the contrast measures of the original X-ray images and the enhanced images derived with various methods. The contrast measures are averaged over the entire testing dataset. It can be observed that enhancing the X-ray images with any one of the methods could significantly promote the contrast measures. However, among all the methods involved in this experiment, our method achieves the highest contrast for all the three categories of X-ray images. Therefore, our method could better improve the clarity and details in the X-ray images.
Table 3.
Contrast measures of the detail-enhanced X-ray images derived with various methods.
| Method | COVID-19 | Normal | Viral pneumonia |
|---|---|---|---|
| Input | 75.54 | 32.66 | 55.34 |
| FBF | 408.97 | 320.34 | 496.48 |
| GIF | 326.63 | 275.17 | 393.82 |
| DTF | 384.84 | 310.56 | 471.71 |
| MSF | 401.63 | 395.47 | 479.14 |
| WLS | 346.86 | 274.67 | 409.78 |
| AD | 349.83 | 287.25 | 461.92 |
| SSF | 407.93 | 327.70 | 498.09 |
| ILS | 427.23 | 358.15 | 484.33 |
| L1RF | 389.88 | 312.62 | 459.09 |
| GSF | 395.00 | 313.63 | 475.17 |
| SCF | 410.09 | 403.34 | 531.38 |
| Ours | 442.30 | 426.40 | 564.51 |
FBF: fast bilateral filter; GIF: guided image gilter; DTF: domain transform filter; MSF: mutual structure filter; WLS: weighted least square; AD: anistropic diffusion; SSF: smoothing sharpening filter; ILS: iterative least square; L1RF: reconstruction filter; GSF: general smoothing filter; SCF: soft clustering filter.
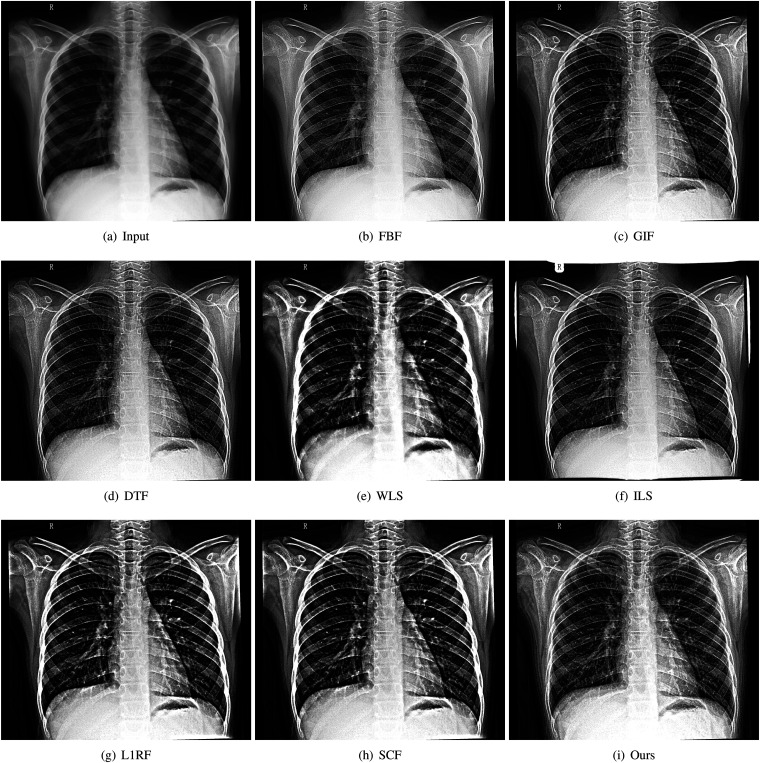
The superiority of the proposed method can be also validated from the qualitative comparisons in Figure 2. We observe that enhancing the images with any method could improve the clarity, as any one of the enhanced images has a clearer appearance than the input X-ray image. However, the image derived with our method demonstrates even more details than that of fast bilateral filter (FBF), guided image gilter (GIF), domain transform filter (DTF), and iterative least square (ILS). Furthermore, our filter tends to better preserve the intensity of the original X-ray image compared to WLS, soft clustering filter (SCF), and reconstruction filter (L1RF) (see the black areas).
Figure 2.
Qualitative comparisons on medical image detail enhancement: (a) input, (b) FBF, (c) GIF, (d) DTF, (e) WLS, (f) ILS, (g) L1RF, (h) SCF, and (i) ours. FBF: fast bilateral filter; GIF: guided image gilter; DTF: domain transform filter; WLS: weighted least square; ILS: iterative least square; L1RF: reconstruction filter; SCF: soft clustering filter.
Efficiency
To further validate the practicality of our method, we compare its running time (measured in seconds) to that of other methods. Note that all the recorded time is averaged over 10 runs. As shown in Table 4, our method is highly efficient. It takes 0.92 seconds to process a 720P image, enabling interactive image processing. Through comparison, we can see that our method is faster than most of the methods involved in our experiments. DTF, FBF, GIF, and SCF achieve better efficiency than our method. However, our method delivers much better image quality, as demonstrated in the previous subsection. Finally, our method significantly improves the efficiency of WLS.
Table 4.
Running time of various methods under different resolutions (measured in seconds).
| Method | |||
|---|---|---|---|
| FBF | 0.04 | 0.25 | 0.85 |
| GIF | 0.05 | 0.26 | 0.87 |
| DTF | 0.01 | 0.06 | 0.15 |
| MSF | 0.30 | 1.34 | 4.35 |
| WLS | 0.45 | 1.92 | 6.03 |
| AD | 0.92 | 4.19 | 15.05 |
| SSF | 0.08 | 0.18 | 0.42 |
| ILS | 0.15 | 0.55 | 1.63 |
| L1RF | 0.07 | 0.32 | 1.08 |
| GSF | 2.46 | 9.65 | 31.51 |
| SCF | 0.06 | 0.27 | 0.88 |
| Ours | 0.06 | 0.30 | 0.92 |
FBF: fast bilateral filter; GIF: guided image gilter; DTF: domain transform filter; MSF: mutual structure filter; WLS: weighted least square; AD: anistropic diffusion; SSF: smoothing sharpening filter; ILS: iterative least square; L1RF: reconstruction filter; GSF: general smoothing filter; SCF: soft clustering filter.
Subjective evaluation
Image clarity
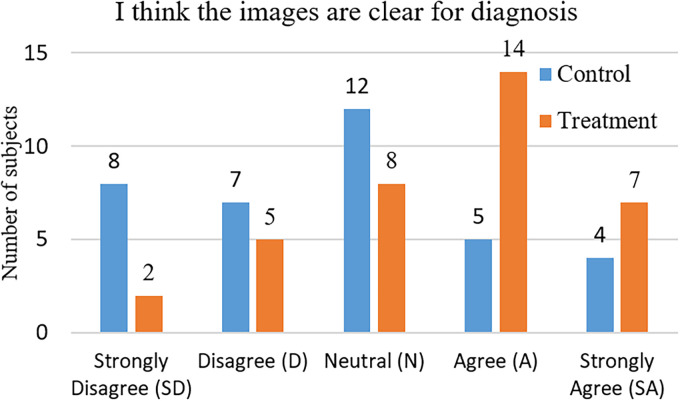
Figure 3 demonstrates the subjects’ responses to the question “I think the images are clear for diagnosis.” Their ratings from 1 to 5 are used to evaluate the clarity of the images. The results are analyzed with the chi-square test as shown in Table 5. We observe that the subjects in the treatment group (presented with the detail-enhanced images) hold a more positive attitude ( ) toward the clarity of the images than that of the control group (presented with the original X-ray images). Furthermore, we observe that the difference between the perceived image clarity of the two groups is significant ( , , is the probability of the difference being insignificant). The above findings support hypothesis H1, that is, our detail-enhanced X-ray images show better clarity than the original X-ray images.
Figure 3.
Subjects’ responses to the question “I think the images are clear for diagnosis.”
Table 5.
Chi-square test result for the perceived image clarity (degree of freedom = 4).
| Control | Treatment | Expect | ||
|---|---|---|---|---|
| SD (1) | 8 | 2 | 5 | 3.6 |
| D (2) | 7 | 5 | 6 | 0.33 |
| N (3) | 12 | 8 | 10 | 0.8 |
| A (4) | 5 | 14 | 9.5 | 4.26 |
| SA (5) | 4 | 7 | 5.5 | 0.82 |
| Total | 36 | 36 | 36 | 9.81 |
| Mean rating | 2.72 | 3.53 |
SD: strongly disagree; D: disagree; N: neutral; A: agree; SA: strongly agree.
Image details
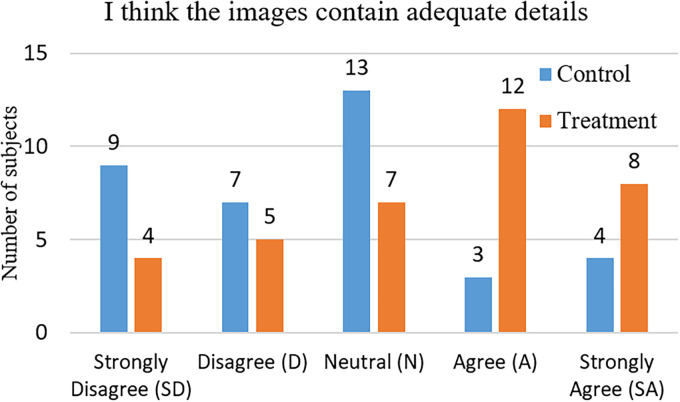
Figure 4 illustrates the subjects’ responses to the question “I think the images contain adequate details.” Their ratings from 1 to 5 are used to evaluate the details of the images. The results are analyzed with the chi-square test as shown in Table 6. It can be observed that the average ratings about the details of the image in the treatment group (presented with the detail-enhanced images) are higher ( ) than that of the control group (presented with the original X-ray images). Moreover, we observe that the difference between the perceived image details of the two groups is significant ( , ). The above findings support hypothesis H2, that is, our detail-enhanced X-ray images contain more adequate details than the original X-ray images.
Figure 4.
Subjects’ responses to the question “I think the images contain adequate details.”
Table 6.
Chi-square test result for the perceived image details (degree of freedom = 4).
| Control | Treatment | Expect | ||
|---|---|---|---|---|
| SD (1) | 9 | 4 | 6.5 | 1.92 |
| D (2) | 7 | 5 | 6 | 0.33 |
| N (3) | 13 | 7 | 10 | 1.8 |
| A (4) | 3 | 12 | 7.5 | 5.4 |
| SA (5) | 4 | 8 | 6 | 1.33 |
| Total | 36 | 36 | 36 | 10.78 |
| Mean rating | 2.61 | 3.42 |
SD: strongly disagree; D: disagree; N: neutral; A: agree; SA: strongly agree.
Satisfaction level
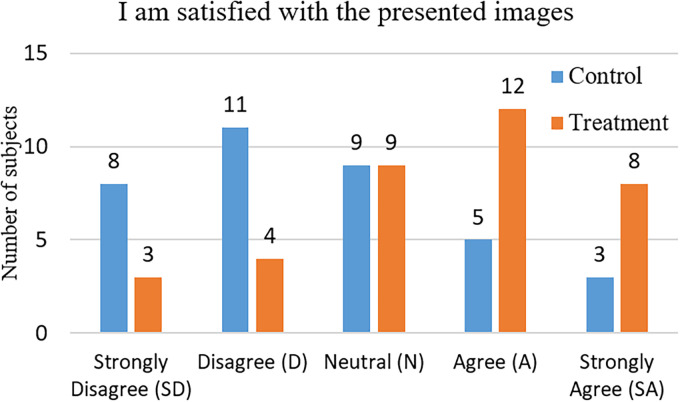
The subjects’ responses to the question “I am satisfied with the presented images” are shown in Figure 5. The subjects’ ratings from 1 to 5 are used to evaluate the satisfaction level provided by the images. The results are studied with the chi-square test as demonstrated in Table 7. It can be observed that the satisfaction levels of the subjects in the treatment group (presented with the detail-enhanced images) are higher ( ) than that of the control group (presented with the original X-ray images). Furthermore, we observe that the difference between the satisfaction levels of the two groups is significant ( , ). The above findings support hypothesis H3, that is, the satisfaction levels provided with our detail-enhanced X-ray images are better than that provided with the original X-ray images.
Figure 5.
Subjects’ responses to the question “I am satisfied with the presented images.”
Table 7.
Chi-square test result for the perceived satisfaction levels (degree of freedom = 4).
| Control | Treatment | Expect | ||
|---|---|---|---|---|
| SD (1) | 8 | 3 | 5.5 | 2.27 |
| D (2) | 11 | 4 | 7.5 | 3.27 |
| N (3) | 9 | 9 | 9 | 0 |
| A (4) | 5 | 12 | 8 | 2.88 |
| SA (5) | 3 | 8 | 5.5 | 2.27 |
| Total | 36 | 36 | 36 | 10.69 |
| Mean rating | 2.56 | 3.5 |
SD: strongly disagree; D: disagree; N: neutral; A: agree; SA: strongly agree.
Discussion
In this article, we propose a novel and efficient method to enhance the details of images and explore the COVID-19 chest X-ray image dataset 48 as an example to demonstrate the effectiveness of the proposed method. In fact, our method essentially defines a general framework for image detail enhancement, that is, besides the X-ray images, our method can be potentially applied to an even broader range of images, such as computed tomography images, magnetic resonance imaging images, or even natural images. More studies need to be conducted to evaluate our method in enhancing other types of images. Our method is implemented on the CPU, which processes 720P images at interactive rates. It would be beneficial to implement the proposed method on GPU so that it can achieve real-time enhancement for 720P images.
Due to the lack of ground truth labels, we leverage the contrast measure for objective evaluation of the proposed image detail enhancement method. The contrast measure is a good indicator of the details and clarity. However, it does not reflect artifacts or degradation generated in the enhancing process. More efforts need to be spent to build a dataset with ground truth labels for X-ray image detail enhancement. The ground truth labels can be obtained with more extensive user studies, where human experts are invited to select the best-looking images from a set of detail-enhanced images derived from a variety of methods. In this way, one can study the quality of the detail-enhanced images in a more objective sense, using measures such as peak noise-to-signal ratio and structure similarity.
The proposed method can be used to enhance the details of the X-ray images. It can be beneficial to down-streaming diagnosis tasks conducted by either machines or human experts. However, the tones of images are not involved in this article. The X-ray images suffer from low dynamic range. Therefore, the tone can be also important to the visibility of the X-ray images. More studies need to be done to consider the tones of the X-ray images in order to further improve the clarity. Possible directions can be the HDR tone mapping operator 20 and the tone manipulation method. 53 It would be interesting to investigate the proposed fast WLS filter in the tasks of tone mapping and manipulation to see how it can be applied to further improve the visibility of the X-ray images.
The proposed solution to the optimization model shown in equation (11) is highly efficient. However, it is based on the approximation with the bilateral grid, which is essentially a hard quantization technique. Therefore, the results of our filter may exhibit blocky artifacts. Even though the artifacts can be eliminated by post-processing with the domain transform filter, degradation in the quality of the results may be introduced. It would be also interesting to investigate soft quantization or clustering techniques to approximate or define the affinity matrix in the weighted scheme, so that the results can be free of blocky artifacts without post-processing. Possible ways to achieve this objective can be the approximation of the bilateral affinity with spatial subsampling 21 or the soft clustering affinity. 25
Conclusion and future work
X-ray images can be essential to the diagnosis of COVID-19, which has brought significant impacts on our lives. However, the original X-ray images may suffer from low dynamic range and low contrast, which would hinder the diagnosis by either human experts or machine learning methods. Aiming at improving the clarity of the X-ray images, we propose an efficient method to enhance the details of the X-ray images. The proposed enhanced method is based on image decomposition with the bilateral WLS model. In order to efficiently solve the model, we propose to approximate the bilateral weight matrix with the bilateral grid so that the large sparse linear system would be simplified into a linear system with much fewer unknowns.
We have conducted extensive experiments to evaluate the proposed X-ray image detail enhancement method. Both objective and subjective evaluations are leveraged in our experiment. For the objective evaluation, we analyze the contrasts of the enhanced images derived with different methods. It is shown that our method could achieve higher contrast than the methods being compared. Furthermore, we compare the running time of different methods in deriving the enhanced images. Our method can process 720P 3-channel images at interactive rates on an i7-6700 CPU. For the subjective evaluation, we conduct a user study that involves 36 doctors. The chi-square test results indicate that the ratings of our detail-enhanced X-ray images are significantly higher than that of the original X-ray images. Therefore, we draw that our method could significantly improve the visibility of the X-ray images. Moreover, it can be applied to real practice, as it is efficient and effective.
Based on the discussion in the previous section, we summarize the future directions of research as follows:
We only apply our detail enhancement method in X-ray images, more studies need to be conducted to evaluate our method on a broader range of images.
In order for a more objective evaluation, more efforts need to be spent to build a dataset with ground truth labels for X-ray image detail enhancement.
The proposed method only deals with the details, more studies need to be carried out to investigate the tone manipulation techniques20,53 to further improve the clarity.
Our fast solution is based on a hard quantization technique, that is, the bilateral grid, more studies need to be conducted to explore affinity designs with soft quantization 21 or clustering. 25
Acknowledgements
We would like to thank all participants for their time and efforts in our user study.
Footnotes
Contributorship: Conceptualization: YY and WB; data curation: WB and YY; methodology: WB and YY; formal analysis: WB and YY; supervision: YY; validation: YY; writing–original draft: WB; writing–review and editing: YY.
Consent statement: Patient consent was not required for the present manuscript, as the COVID-19 image dataset in this study is publicly available.
The author(s) declared no potential conflicts of interest with respect to the research, authorship and/or publication of this article.
Ethical approval: Not applicable.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This project was funded by National Natural Science Foundation of China (Ref: 61402205), China Postdoctoral Science Foundation (Ref: 2015M571688), Jiangsu University (Ref: 13JDG085), and Jiangsu Province Elderly Health Project (Ref: LD2021039).
Guarantor YY.
ORCID iD: Yang Yang https://orcid.org/0000-0001-8782-4819
References
- 1.Alimohamadi Y, Taghdir M, Sepandi M. The estimate of the basic reproduction number for novel coronavirus disease (Covid-19): a systematic review and meta-analysis. J Prev Med Public Health 2020; 53: 151–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Elsaid M, Ayman M, Nguyen H. R0 of Covid-19 and its impact on vaccination coverage: compared with previous outbreaks. Hum Vaccin Immunother 2021; 17: 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Prada J, Maag L, Siegmund L. et al. Estimation of r0 for the spread of SARS-CoV-2 in germany from excess mortality. Sci Rep 2022; 12: 17221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chinazzi M, Davis J, Ajelli M. et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (Covid-19) outbreak. Science 2020; 368: 395–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tenforde M, Olson S, Self W. et al. Effectiveness of Pfizer-biontech and moderna vaccines against Covid-19 among hospitalized adults aged greater or equal to 65 years – United States, January–March 2021. MMWR Morb Mortal Wkly Rep 2021; 70: 674–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Antonelli M, Pujol JC, Spector TD. et al. Risk of long Covid associated with delta versus omicron variants of sars-cov-2. Lancet 2022; 399: 2263–2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Notarte KI, Catahay JA, Velasco J. et al. Impact of Covid-19 vaccination on the risk of developing long-Covid and on existing long-Covid symptoms: a systematic review. EClinicalMedicine 2022; 53: 101624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Organization WH. Tracking SARS-CoV-2 variants. https://www.who.int/activities/tracking-SARS-CoV-2-variants/. Accessed March 25, 2023.
- 9.Organization WH. Summary of variant surveillance. https://covid.cdc.gov/covid-data-tracker/variant-summary. Accessed March 25, 2023.
- 10.Wang B, Andraweera P, Elliott S. et al. Asymptomatic SARS-CoV-2 infection by age: a global systematic review and meta-analysis. Pediatr Infect Dis J 2023; 42: 232–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kronbichler A, Kresse D, Yoon S. et al. Asymptomatic patients as a source of Covid-19 infections: a systematic review and meta-analysis. Int J Infect Dis 2020; 180–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Habas E, Said A, Ramzee Abdul Aziz AF. et al. Chest X-ray findings and hyponatremia in Covid-19 pneumonia patients. Qatar Med J 2022; 2022: 34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cozzi D, Albanesi M, Cavigli E. et al. Chest x-ray in new coronavirus disease 2019 (Covid-19) infection: findings and correlation with clinical outcome. Radiol Med 2020; 125: 730–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nayak S, Nayak D, Sinha U. et al. Application of deep learning techniques for detection of Covid-19 cases using chest X-ray images: a comprehensive study. Biomed Signal Process Control 2021; 64: 102365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhou T, Liu F, Lu H. et al. A review of deep learning imaging diagnostic methods for Covid-19. Electronics 2023; 12: 1167. [Google Scholar]
- 16.Öktem H, Egiazarian KO, Niittylahti J. et al. An approach to adaptive enhancement of diagnostic X-ray images. EURASIP J Adv Signal Process 2003; 2003: 430–436. [Google Scholar]
- 17.Qiu J, Li H, Zhang T. et al. Automatic X-ray image contrast enhancement based on parameter auto-optimization. J Appl Clin Med Phys 2017; 18: 218–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wu S, Zhu Q, Yu S. et al. Multiscale X-ray image contrast enhancement based on limited adaptive histogram equalization. In International Conference on Internet Multimedia Computing and Service, 2013, pp. 231–236. DOI: 10.1145/2499788.2499793. [DOI]
- 19.Koonsanit K, Thongvigitmanee S, Pongnapang N. et al. Image enhancement on digital X-ray images using n-clahe. In Biomedical Engineering International Conference, 2017, pp. 1–4. DOI: 10.1109/BMEiCON.2017.8229130. [DOI]
- 20.Durand F, Dorsey J. Fast bilateral filtering for the display of high-dynamic-range images. ACM Trans Graph 2002; 21: 257–266. [Google Scholar]
- 21.Yang Y, Xiong Y, Cao Y. et al. Fast bilateral filter with spatial subsampling. Multim Syst 2022; 29: 435–446. [Google Scholar]
- 22.Septiana L, Lin KP. X-ray image enhancement using a modified anisotropic diffusion. In International Symposium on Bioelectronics and Bioinformatics, 2014, pp. 1–4. DOI: 10.1109/ISBB.2014.6820940. [DOI]
- 23.He K, Sun J, Tang X. Guided image filtering. IEEE Trans Pattern Anal Mach Intell 2013; 35: 1397–1409. [DOI] [PubMed] [Google Scholar]
- 24.Ochotorena CN, Yamashita Y. Anisotropic guided filtering. IEEE Trans Image Process 2020; 29: 1397–1412. [DOI] [PubMed] [Google Scholar]
- 25.Yang Y, Hui H, Zeng L. et al. Edge-preserving image filtering based on soft clustering. IEEE Trans Circuits Syst Video Technol 2022; 32: 4150–4162. [Google Scholar]
- 26.Yang Y, Zheng H, Zeng L. et al. L1-regularized reconstruction model for edge-preserving filtering. IEEE Trans Multimedia 2022. DOI: 10.1109/TMM.2022.3171686. [Google Scholar]
- 27.Yang Y, Tang L, Zeng L. et al. L0 image smoothing via iterating truncated L1 gradient regularization. J Electron Imaging 2022; 31: 053016. [Google Scholar]
- 28.Liu W, Zhang P, Lei Y. et al. A generalized framework for edge-preserving and structure-preserving image smoothing. IEEE Trans Pattern Anal Mach Intell 2022; 44: 6631–6648. [DOI] [PubMed] [Google Scholar]
- 29.Farbman Z, Fattal R, Lischinski D. et al. Edge-preserving decompositions for multi-scale tone and detail manipulation. ACM Trans Graph 2008; 27: 67. [Google Scholar]
- 30.Liao Z, Lan P, Fan X. et al. SIRVD-DL: a COVID-19 deep learning prediction model based on time-dependent SIRVD. Comput Biol Medicine 2021; 138: 104868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu G, Ding Q, Luo H. et al. Cx22: a new publicly available dataset for deep learning-based segmentation of cervical cytology images. Comput Biol Medicine 2022; 150: 106194. [DOI] [PubMed] [Google Scholar]
- 32.Yu M, Han M, Li X. et al. Adaptive soft erasure with edge self-attention for weakly supervised semantic segmentation: thyroid ultrasound image case study. Comput Biol Medicine 2022; 144: 105347. [DOI] [PubMed] [Google Scholar]
- 33.Chen Y, Gan H, Chen H. et al. Accurate iris segmentation and recognition using an end-to-end unified framework based on madnet and dsanet. Neurocomputing 2023; 517: 264–278. [Google Scholar]
- 34.Zhao C, Wang H, Chen H. et al. Jamsnet: a remote pulse extraction network based on joint attention and multi-scale fusion. IEEE Trans Circuits Syst Video Technol 2023; 33: 2783–2797. [Google Scholar]
- 35.Din NMU, Dar RA, Rasool M. et al. Breast cancer detection using deep learning: datasets, methods, and challenges ahead. Comput Biol Medicine 2022; 149: 106073. [DOI] [PubMed] [Google Scholar]
- 36.Tomasi C, Manduchi R. Bilateral filtering for gray and color images. In International Conference on Computer Vision, 1998, pp. 839–846. DOI: 10.1109/ICCV.1998.710815. [DOI]
- 37.Gastal ESL, Oliveira MM. Adaptive manifolds for real-time high-dimensional filtering. ACM Trans Graph 2012; 31: 33:1–33:13. [Google Scholar]
- 38.Paris S, Durand F. A fast approximation of the bilateral filter using a signal processing approach. Int J Comput Vis 2009; 81: 24–52. [Google Scholar]
- 39.Nair P, Chaudhury KN. Fast high-dimensional bilateral and nonlocal means filtering. IEEE Trans Image Process 2019; 28: 1470–1481. [DOI] [PubMed] [Google Scholar]
- 40.Nair P, Gavaskar RG, Chaudhury KN. Compressive adaptive bilateral filtering. In International Conference on Acoustics, Speech and Signal Processing, 2020, pp. 2078–2082. DOI: 10.1109/ICASSP40776.2020.9053275. [DOI]
- 41.Sun Z, Han B, Li J. et al. Weighted guided image filtering with steering kernel. IEEE Trans Image Process 2020; 29: 500–508. [DOI] [PubMed] [Google Scholar]
- 42.Li L, Guo X, Feng W. et al. Soft clustering guided image smoothing. In International Conference on Multimedia and Expo, 2018, pp. 1–6. DOI: 10.1109/ICME.2018.8486448. [DOI]
- 43.Min D, Choi S, Lu J. et al. Fast global image smoothing based on weighted least squares. IEEE Trans Image Process 2014; 23: 5638–5653. [DOI] [PubMed] [Google Scholar]
- 44.Liu W, Chen X, Shen C. et al. Semi-global weighted least squares in image filtering. In International Conference on Computer Vision, 2017, pp. 5862–5870. DOI: 10.1109/ICCV.2017.624. [DOI]
- 45.Liu W, Zhang P, Huang X. et al. Real-time image smoothing via iterative least squares. ACM Trans Graph 2020; 39: 28:1–28:24. [Google Scholar]
- 46.Shewchuk JR. An introduction to the conjugate gradient method without the agonizing pain. Technical report, USA, 1994. DOI: 10.5555/865018. [DOI]
- 47.Gastal ESL, Oliveira MM. Domain transform for edge-aware image and video processing. ACM Trans Graph 2011; 30: 69. [Google Scholar]
- 48.RAIKOTE P. Covid-19 image dataset. https://www.kaggle.com/datasets/pranavraikokte/covid19-image-dataset, 2023.
- 49.Shen X, Zhou C, Xu L. et al. Mutual-structure for joint filtering. Int J Comput Vis 2017; 125: 19–33. [Google Scholar]
- 50.Liu J, Gong X. Guided depth enhancement via anisotropic diffusion. In Pacific-Rim Conference on Multimedia, 2013, pp. 408–417. DOI: 10.1007/978-3-319-03731-8_38. [DOI]
- 51.Deng G, Galetto F, Al-nasrawi M. et al. A guided edge-aware smoothing-sharpening filter based on patch interpolation model and generalized gamma distribution. IEEE Open J Signal Process 2021; 2: 119–135. [Google Scholar]
- 52.Likert R. A technique for the measurement of attitudes. Arch Psychol 1932; 140: 1–55. [Google Scholar]
- 53.Guo X, Li Y, Ling H. LIME: low-light image enhancement via illumination map estimation. IEEE Trans Image Process 2017; 26: 982–993. [DOI] [PubMed] [Google Scholar]