Abstract
Prediction of movement intentions from electromyographic (EMG) signals is typically performed with a pattern recognition approach, wherein a short dataframe of raw EMG is compressed into an instantaneous featureencoding that is meaningful for classification. However, EMG signals are time-varying, implying that a frame-wise approach may not sufficiently incorporate temporal context into predictions, leading to erratic and unstable prediction behavior.
Objective:
We demonstrate that sequential prediction models and, specifically, temporal convolutional networks are able to leverage useful temporal information from EMG to achieve superior predictive performance.
Methods:
We compare this approach to other sequential and frame-wise models predicting 3 simultaneous hand and wrist degrees-of-freedom from 2 amputee and 13 non-amputee human subjects in a minimally constrained experiment. We also compare these models on the publicly available Ninapro and CapgMyo amputee and non-amputee datasets.
Results:
Temporal convolutional networks yield predictions that are more accurate and stable () than frame-wise models, especially during inter-class transitions, with an average response delay of 4.6 ms () and simpler feature-encoding. Their performance can be further improved with adaptive reinforcement training.
Significance:
Sequential models that incorporate temporal information from EMG achieve superior movement prediction performance and these models allow for novel types of interactive training.
Conclusions:
Addressing EMG decoding as a sequential modeling problem will lead to enhancements in the reliability, responsiveness, and movement complexity available from prosthesis control systems.
Keywords: Electromyographic (EMG), stability, latency, sequence, amputee, reinforcement, temporal convolutional network (TCN), ED-TCN
I. Introduction
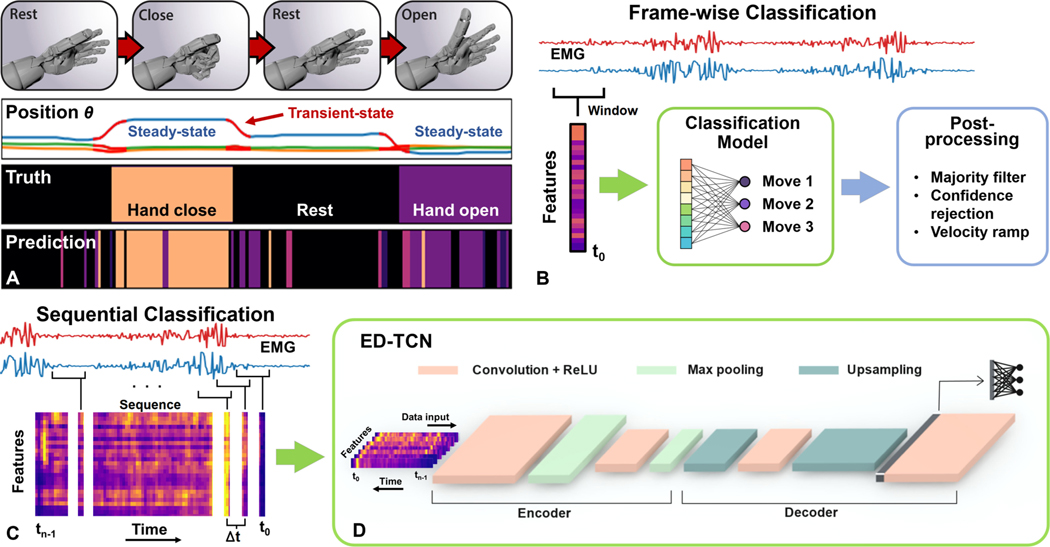
The fundamental objective of myoelectric prosthesis control for upper-limb amputees is to determine a user’s intended arm and hand movement actions from the corresponding electromyographic (EMG) muscle activation signals [1]. EMG movement prediction is often performed with a frame-wise sliding window approach where a short window of the raw EMG signal is individually compressed into a feature representation that spatially encodes discrete movement classes. In ideal cases, such as during steady-state muscle contractions, prediction models like linear discriminant analysis [2], support vector machines [3], and spatial convolutional networks [4] can reliably decode many movement class patterns from EMG feature representations [5]. However, these models can also exhibit unstable or erratic prediction behavior (Fig. 1A), especially during transient-states when the user transitions between movement classes [6], [7].
Fig. 1.
(A) As a user transitions from one steady-state movement pattern to another, EMG classification models can exhibit erratic prediction behavior. (B) Frame-wise classification of EMG signals, wherein movement intentions are predicted from the most recent feature-extraction window, or frame, of EMG. Frame-wise models lack a mechanism for factoring longer-term temporal information into their predictions. (C) Sequential classification of EMG signals, wherein consecutive frames provide additional temporal information to a model. (D) With ED-TCN, the convolutional encoder-decoder framework learns latent temporal patterns which can improve prediction accuracy and stability.
Improving the error-tolerance and stability of frame-wise models has become a focal point of EMG movement decoding research. Majority voting among consecutive predictions [1] can stabilize the prediction stream but also causes response delay. Methods like confidence-based rejection [8], [9] and ensemble voting among binary classifiers [10] have been used to improve accuracy and stability by suppressing the output of uncertain and potentially erratic predictions. A velocity ramp procedure has been used to both improve stability and apply a proportional output to movement predictions [11]. Adaptive models have been developed to enhance condition-tolerance with sparse representations [12] and to intelligently update movement class boundaries in real-time [13], [14]. These methods all demonstrate that EMG movement prediction is a difficult problem where, in all but the most ideal cases, erratic and unstable behavior does arise and must be mitigated or suppressed to achieve reliable prosthesis control. Furthermore, to improve amputee satisfaction and prosthesis embodiment, a major clinical goal is to keep response delays below 100 ms [15]. The post-processing methods and optimal window sizes [16] required to stabilize predictions often exceed this bound. Our present inquiry is to determine if stability and response time can be improved with under-utilized aspects of EMG signals.
Frame-wise classification of time-series data like EMG is, in the Bayesian sense, a naive process wherein single feature windows are predicted independently (Fig. 1B), lacking an encoding mechanism for longer-range temporal information. As has been demonstrated with Hidden Markov Models in speech recognition [17] and EMG movement prediction [18], prior temporal information can be relevant for the prediction of time-series data. For example, prediction of a word from speech audio can be done more accurately by using a contextual language model [17]. Herein, we use the term sequential models to broadly refer to models that leverage temporal sequences of consecutive data-frames in their predictions (Fig. 1C). Sequential models such as long short-term memory (LSTM) recurrent neural networks [19] have achieved state-of-the-art results in many time-series prediction applications like speech recognition [20] and EMG movement decoding [21]. Recurrent networks have also been used for movement prediction from primate cortical signals [22].
We began this investigation to explore the benefits of using sequential models for EMG movement prediction. In our prior work [23], sequential models indeed increased accuracy, but a model architecture called temporal convolutional networks (TCN) [24] yielded other benefits warranting further exploration. In addition to being more accurate, TCN predictions were very stable, producing smooth, clean transitions between classes [23]. Furthermore, TCN models are highly interpretable [24], [25] and can be trained many times faster than LSTM [24], [26]. Herein, we focus on an enhanced TCN model called encoder-decoder temporal convolutional networks (ED-TCN) [26] for EMG movement prediction that are more accurate and stable than prevailing models, with reduced prediction latency. We present our results in two contexts:(i) public databases using standard movement-cue protocols, and (ii) a minimally constrained subject-driven experiment. We also demonstrate how a subject might continue to significantly improve performance with adaptive reinforcement training.
II. Methods
A. Encoder-Decoder Temporal Convolutional Networks
Single-layer TCNs can learn hidden temporal patterns [24], smoothed via temporal-dimension convolution filters, and have demonstrated superior results on video recognition datasets [24], [26], [27] and our own prior work in EMG decoding [23]. ED-TCN [26] was developed as a temporal variation of SegNet [28], a powerful encoder-decoder framework for image segmentation that smoothly delineates object boundaries by employing max-pooling operations in the encoder to down-sample the image prior to up-sampling in the decoder. Similarly, ED-TCN is an encoder-decoder framework, using temporal max-pooling and up-sampling layers to deeply connect multiple TCN layers (Fig. 1D), designed to smoothly delineate temporal class boundaries for video activity recognition.
Each layer in the encoder has a corresponding layer in the decoder, and we found that a depth of 2 layers per network provided a good balance between accuracy and stability. Each encoding layer is defined by , where is the number of convolutional filters in the -th layer and is the number of time-steps. is dependent on the sequence length of the input, , and is shortened with max pooling operations in each encoding layer and lengthened with up-sampling operations in each decoding layer. Through preliminary testing, we chose the number of filters for the first layer, for the second, and filter length . is the feature dimension of the input. The output of each encoding layer is a set of temporal feature maps produced when the collection of filters for that layer, where , is convolved with the output of the previous layer:
| (1) |
where is a bias term. Rectified linear unit (ReLU) activations [29] are applied to each element, and 2-point temporal max pooling is performed. Each decoding layer, , up-samples the feature maps by factor 2, performs temporal convolution with a decoder filter bank, and applies element-wise ReLU activations. The final decoder output is fed to a fully-connected time-distributed layer with softmax activation [30] to produce class probabilities, , at each time, :
| (2) |
where and are the weight matrix and bias, respectively, of the fully connected layer. All ED-TCN layers are trained together in end-to-end fashion, and training can be greatly accelerated with multicore GPUs.
1). Measuring Model Stability:
In our previous work [23], we defined a stability metric to complement accuracy by quantifying how inclined a model is to predicting erratic inter-class switches and transitions that were not intended by the human subject. Given a vector representing a series of consecutive predictions, we count how many times the prediction model switches its class output:
| (3) |
where is an equivalence indicator. After computing , and computing from a ground truth vector , our prediction stability metric is defined as
| (4) |
Accuracy estimates a model’s true probability of success as , whereas stability estimates the probability that a model’s inter-class transitions are based on a subject’s intent.
To avoid fully relying on our own metric, we computed the edit score [31] which penalizes incorrect class order and over-segmentation in a prediction sequence while ignoring minor timing shifts. Edit score is defined as
| (5) |
where and are formed by removing repeated consecutive labels from vectors and , and is normalized Levenshtein or edit distance [32]. For example, if the vector then , and finds the fraction of insertions, deletions, and replacements needed to convert into . We also computed the score [33], which is the harmonic mean of precision and recall.
B. Experiment Set-Up
1). Experimental Considerations for Sequential Models:
It is important to examine how a standard experimental approach might influence sequential models. Typically, a subject is shown a movement cue for a specified amount of time, performs the movement, and this process repeats for a given set of cues. Each aspect of this approach– the cues, their order, and their duration– is constrained by the experiment. Subjects are often restricted to class transitions to and from a neutral “rest” class [6], [7], [34] in part because the number of transitions grows combinatorially with the number of classes. Sequential models learn temporal relationships and, if care is not taken, they may learn specific experimental constraints. For example, an experiment restricted to 3 s duration classes into and out of “rest” may teach a sequential model that movements always last for 3 s, and inter-class transitions involving “rest” are the only type that can occur. Thus, the model might learn distorted, experiment-centric relationships but fail to learn more generalizable temporal and transition information.
In our field, the terms stability and responsiveness are only meaningful insofar as they relate to a human subject’s volition or intent. Since we are evaluating these concepts, we preferred that our experimental data originate from a subject’s voluntary choices rather than from his delayed responses to movement cues. The unique properties of sequential models inspired and allowed us to pursue new subject-driven approaches to experimentation. For completeness in our comparisons, we also report results on two public EMG databases, Ninapro [34] and CapgMyo [35], collected with more traditional experimental approaches.
2). Human Subjects:
Our experiments were conducted with protocols approved by the Johns Hopkins Medicine Institutional Review Boards. 13 non-amputee and 2 transradial amputee subjects participated in these experiments. Amputee subjects were familiar with EMG movement prediction, whereas most non-amputee subjects were unpracticed or unfamiliar. Non-amputee subjects (10 male, 3 female) were ages 23.4 ± 3.0 years. The specific traits of amputee subjects were:
| ID | Age | Sex | Status | Amputation | Time | Residual |
|---|---|---|---|---|---|---|
| A1 | 49 yr | M | unilateral | right transradial | 16 yr | 18 cm |
| A2 | 54 yr | M | unilateral | right transradial | 16 yr | 14 cm |
3). Data Acquisition, Feature Extraction, and Visualization:
Eight channels of raw EMG sampled at 200 Hz were obtained from a Myo Armband (Thalmic Labs, Ontario, Canada) placed around the circumference of the forearm. For frame-wise models, a sliding window of 150–250 ms is considered optimal [16] so 200 ms windows with 25 ms step-size were used to extract time-domain (TD5) features from the raw EMG signals: mean absolute value (MAV), waveform length, variance, slope sign change, and zero crossings [1]. We note that EMG signals are often recorded above a 1 kHz threshold to prevent raw signal aliasing, and this threshold may be necessary to discriminate fine motor movements like individual fingers. However, when classifying gross motor movements like those in our experiments, features extracted from the 200 Hz Myo Armband have yielded performance similar to that of recording systems sampling at ≥ 1 kHz [36], [37]. We also demonstrate that our results are consistent on data recorded with high sampling rates from two public EMG databases.
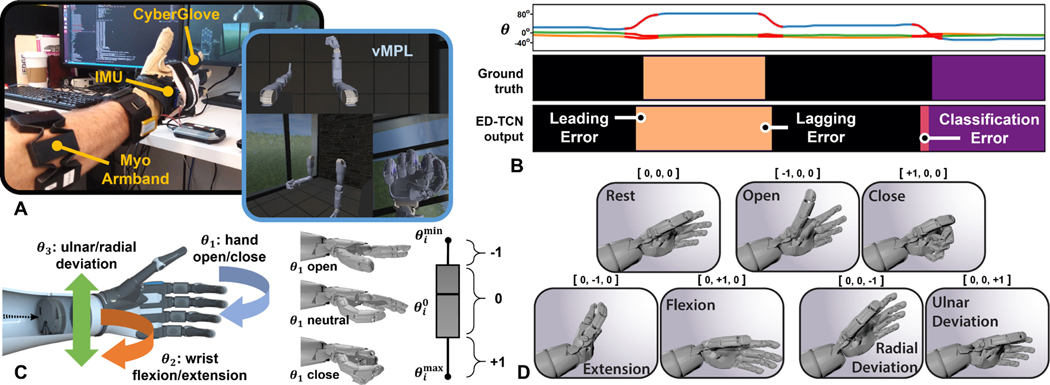
Angular hand position data were recorded with the Cyberglove II (CyberGlove Systems LLC, San Jose, CA). Angular wrist position data were recorded with 9-axis MPU-9150 inertial sensors (InvenSense, San Jose, CA), one mounted on the back of the subject’s hand and referenced to another which was placed under the computer display (Fig. 2A). We created a user interface to control the virtual Modular Prosthetic Limb (vMPL) developed by the Johns Hopkins University Applied Physics Laboratory [38]. The vMPL environment approximates the physical Modular Prosthetic Limb (MPL) by incorporating its dynamic properties such as mass and momentum. This interface provided subjects with a real-time display of their hand and wrist movements, and it provided us with visual confirmation that subject movements and positional recordings were in correspondence. Non-amputee subjects wore all sensors on either their left or right arm depending on subject preference. To demonstrate the feasibility of our methods for unilateral amputee subjects A1 and A2, we recorded EMG signals from their residual amputated limb and recorded position data from their intact limb while they mirrored their intended movements to establish a synchronous ground truth. To visually aid amputees, their movements were flipped horizontally and displayed in the vMPL environment on their amputated side.
Fig. 2.
(A) Each subject donned a Myo Armband, CyberGlove, and inertial sensors (IMU) for EMG and hand/wrist positional recording. The vMPL environment provided a real-time display of each subject’s hand/wrist movements. (B) Example sequence of 3-DOF joint angles , the corresponding automated encoding into ground truth class labels, and the class prediction output of ED-TCN. Three error types are evident from this example: leading, lagging, and classification errors. The first two are timing related, whereas the latter is unintentional movement. Our stability metric penalizes only the last error type, whereas the accuracy metric penalizes all three. (C) The movement classes are based on 3 hand and wrist DOFs. For each , we determined a rest position , maximum angle , and minimum angle . Each DOF is converted from its continuous joint position into a class label (−1, 0, or +1). (D) The class labels for each DOF were combined into a ternary encoding representing one of 27 possible simultaneous 3-DOF movement classes– the seven shown and their combinations.
4). Automated Class Label Encoding:
By automating the labeling of ground truth movement classes, there was neither a need for any movement-cue presentation during our experiments nor a need to offset the variable reaction-time delays resulting from a movement-cue approach. Subjects were first asked to explore for 40 s their full range of motion in each of 3 degrees-of-freedom (DOF) representing hand and wrist movements– hand close/open, wrist flexion/extension, and radial/ulnar deviation–while outer boundary positions , , and rest position were determined for each (Fig. 2B–C). Class thresholds along each DOF were set at 50% of the distance from to and (Fig. 2C). Thus, at every 25 ms time-step, each DOF is labeled with either +1, 0, or −1. By combining these labels for each of the three DOFs, we create a ternary class encoding representing 33 = 27 classes of simultaneous 3-DOF movements (Fig. 2D).
To determine when a subject was in a transient-state, we first computed the normalized position of each . We applied a 3-point causal moving average filter to each then computed position magnitude . Velocity was computed with backward difference , and we deemed threshold suitable to define the transient-state (highlighted in red in Fig. 2B and throughout). We emphasize that transient-states were used for the purpose of results analysis, not model training.
5). Model Comparison and Results Analysis:
To obtain our results, we compared ED-TCN with the following sequential and frame-wise models:
| TCN: | Temporal convolutional network [23], , |
| LSTM: | Long short-term memory network [19], 64 nodes |
| LDA: | Linear discriminant analysis [2] |
| -NN: | -nearest neighbors [39], |
| SVM: | Support vectors [3], Gaussian radial basis, , |
| Tree: | Decision tree [40], split by Gini index, all leaves pure |
| ANN: | Artificial neural network [41], 3 layers x 5 tanh nodes |
ED-TCN, TCN, and LSTM sequential models were trained with cross-entropy loss. Compared to LSTM, ED-TCN and TCN models trained about 2 and 18 times faster, respectively. LDA, SVM, and ANN were chosen due to their frequent use in EMG movement prediction literature. Decision tree and -NN were chosen and parameterized to highlight the effect of over-fitting on stability. We independently tested all sequential models using sequences of MAV, TD5, and raw EMG. Of these, the sequential models achieved the best results using MAV sequences– a point we will discuss in more detail. For our results, we focused on the best-performing model/feature pairings: MAV sequences were used for sequential models and TD5 features were used for frame-wise models. All models were constrained to be strictly causal such that predictions were based on EMG information available at prediction time. Thus, each model’s prediction delay is limited only by model properties and window size.
Computations were performed with a Quadro K2200 GPU (NVIDIA, Santa Clara, CA) using common Python 3.6.8 modules and the following open-source packages: Keras [42] and Temporal Convolutional Networks [43]. Performance distributions were not assumed to be Gaussian; therefore, all statistical -values were computed with Kruskall-Wallis one-way variance analysis [44]. Figure error bars and shaded regions represent standard error of the mean.
6). Parameterizing Sequential Models:
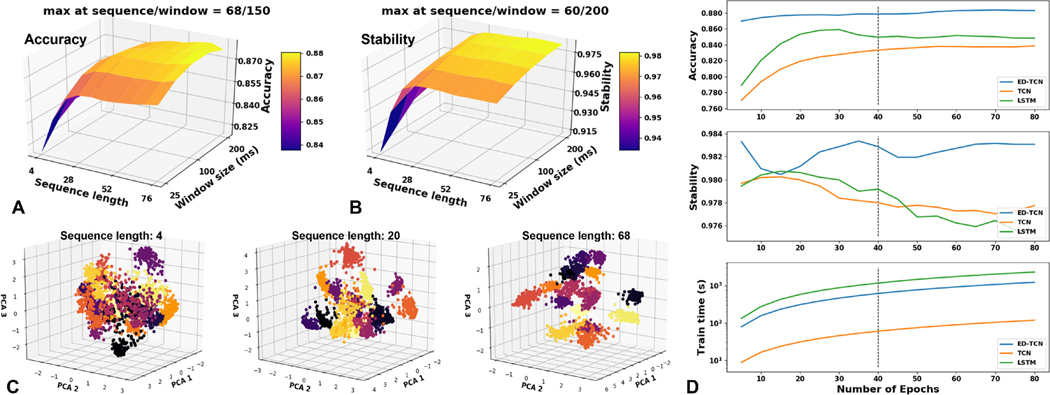
Parameter selection is a major factor governing the performance of sequential models. To illustrate, we executed parameter sweeps using subject 1’s data from the public Ninapro Database 2 [34] and generated performance curves for our models to determine their optimal window sizes, sequence lengths, and number of training epochs (Fig. 3). We define an epoch as a single pass through the training data while model weights are learned. Increasing the epochs can improve test performance up to a point, but could eventually over-fit the training data. The training and testing data used to obtain optimal parameters are shown in Table I, and we chose parameters to maximize test-data accuracy.
Fig. 3.
Parameter-tuning ED-TCN to determine optimal window size, sequence length, and number of training epochs. Final parameters used for Ninapro and CapgMyo public datasets are shown in Table I, and parameters used for our experiments are shown in Table II. (A) Importantly, sequential models demonstrated that the inclusion of sequence data improved accuracy while reducing the model’s dependence on window size, and (B) model stability was generally improved with longer sequences and larger windows. (C) Principle component projection of the latent temporal class patterns learned by ED-TCN when trained on different sequence lengths (18 classes shown). The added temporal data taught ED-TCN to better organize classes into distinct and separable clusters. (D) Accuracy, stability, and training time as a function of epochs. For this subject, ED-TCN outperformed other models after only 5 epochs.
TABLE I.
Model Parameters Used for Public Databases
| Database | Model† | Features | Window | Sequence | Epochs |
|---|---|---|---|---|---|
| Ninapro | ED-TCN | MAV | 150 ms | 68 | 40 |
| Train: reps 1,3,5,6 | TCN | MAV | 200 ms | 20 | 40 |
| Test: reps 2,4 | LSTM | MAV | 100 ms | 60 | 40 |
| Tuned on subject 1 | Frame-wise | TD5 | 200 ms | 1 | – |
|
| |||||
| CapgMyo | ED-TCN | MAV | 100 ms | 4 | 100 |
| Train: first 67% | TCN | MAV | 50 ms | 28 | 100 |
| Test: last 33% | LSTM | MAV | 100 ms | 44 | 100 |
| Tuned on subject 9 | Frame-wise | TD5 | 200 ms | 1 | – |
A prediction time-step of was used for all models. Batch size: 100.
Importantly, Fig. 3 shows that EMG decoding accuracy and stability is improved by the inclusion of sequential information (Fig. 3A–B). Furthermore, we show that the abstract temporal feature maps learned by ED-TCN (output at layer ) are heavily influenced by the length of feature sequences provided to the network (Fig. 3C). Up to a point, additional sequence information allowed sequential models like ED-TCN to better organize class data into distinct and separable clusters within an abstract temporal feature-space. Taken together, these observations suggest that the EMG decoding problem might be better served by treating it as a sequential modeling problem with its accompanying considerations.
C. Performance on Public Databases
We began our investigations by testing model performance on the publicly available Ninapro [34] and CapgMyo [35] databases of class-dense, channel-dense EMG data sampled at ≥1 kHz with standard movement-cue experiment procedures. Ninapro Databases 2 and 3 (exercises 1 and 2) contains 40 non-amputee and 11 amputee subjects, respectively, performing 6 repetitions (reps) of 41 movement classes. EMG signals were recorded with 12 channels sampled at 2 kHz while hand position data were recorded with a Cyberglove. CapgMyo Database C contains 10 non-amputee subjects performing 13 movement classes for ten consecutive trials. High-density EMG signals were recorded with 128 channels sampled at 1 kHz, though no hand position data were recorded.
For Ninapro Database 2, we used a process similar to our experiments to determine transient-state periods. However, instead of joint-angles, we used raw 22-channel Cyberglove data, at each time-step, smoothed with a 17-point Hanning window, to quantify “position” magnitude . A measure of “velocity” was found by calculating the central-difference . We chose to represent transient phases.
Model parameters in Table I were determined from parameter sweeps using data from Ninapro subject 1 and CapgMyo subject 9. These subjects were selected for parameter tuning simply because theirs were the first data we processed. Parameters were chosen to maximize test data accuracy. After determining these parameters, we then trained and tested the prediction models on every subject. Class labels in these datasets are ordered lowest to highest so we randomized the data batch order to prevent sequential models from learning the label ordering.
D. 3-DOF Simultaneous Movement Experiment
All 13 non-amputee and 2 amputee subjects participated in this experiment. Each subject participated in a 15 min introductory session wherein the 3-DOF movements and combinations were explained. The subjects then practiced performing these discrete movement classes with consistent suddenly-initiated muscle contractions to avoid making inter-class transitions gradually like those used for proportional velocity experiments. Once the subject was comfortable performing the movements, the experiment was initiated.
For 6 min, while EMG and hand/wrist positional data were recorded, each subject explored 3-DOF simultaneous movements. The subjects were instructed that they could perform the movements in any preferred order and duration less than 5 s while EMG and position data were recorded. The constraint on duration was to allow the subject to have ample opportunity to explore as many movement combinations as desired. As discussed in Section II-B1, this minimally constrained exploration process helped to ensure that data sequences were formed naturally from each subject’s specific intent, rather than as responses to experiment-driven movement cues. A trade-off for allowing this freedom was that subjects were not guaranteed to perform all 27 movements nor in a balanced manner, which we will address in our results and discussion. To obtain our results (Fig. 5), we used the first 3 min of each subject’s EMG and position data to train various sequential (batches randomized) and frame-wise prediction models, and those models were tested on the last 3 min of data. Model parameters in Table II were determined from parameter sweeps using experiment training and testing data from a subject who was excluded from our final results.
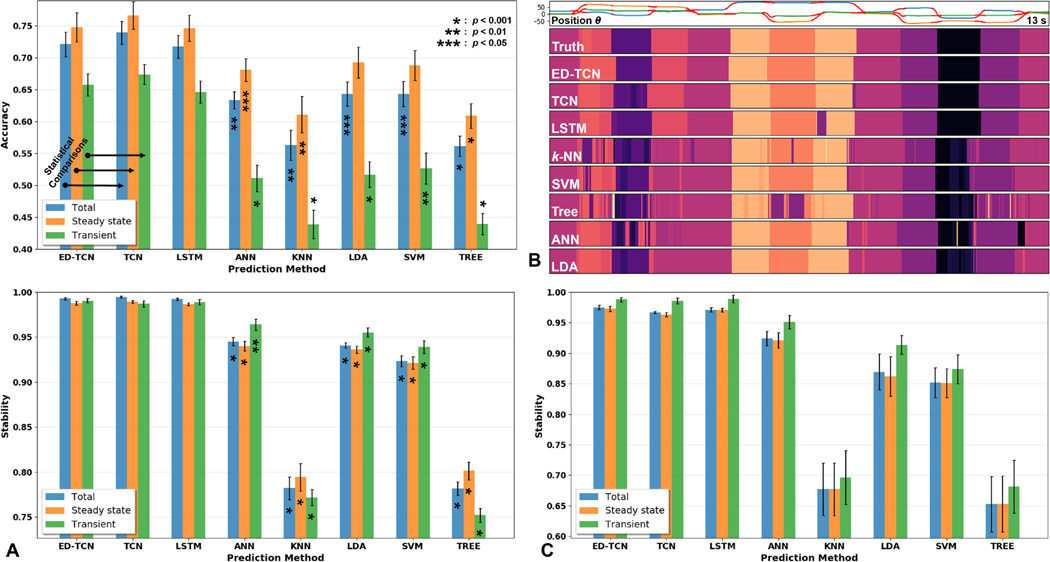
Fig. 5.
Comparative analysis of ED-TCN with other models from our 3-DOF simultaneous movement experiment. Statistical -values are based on comparing ED-TCN performance during steady-state and transient phases of movement with the corresponding like-colored aspects of other models. (A) Prediction accuracy and stability for 13 non-amputee subjects. Sequential models achieved higher accuracy with sequences of MAV than frame-wise models with TD5 features. (B) Example prediction output behaviors of sequential and frame-wise models. The sequential models are visibly more stable than frame-wise models, smoothly transitioning between classes. Video S1 shows an extended animated version of this sequence for multiple models in the vMPL environment. (C) Each model’s prediction stability profile for 2 amputee subjects generally matched those for non-amputee subjects.
TABLE II.
Model Parameters Used for Experiments
| Type | Model† | Features | Window | Sequence | Epochs |
|---|---|---|---|---|---|
| Train: first 3 min | ED-TCN | MAV | 125 ms | 56 | 15 |
| Test: last 3 min | TCN | MAV | 125 ms | 56 | 15 |
| Tuned on an | LSTM | MAV | 125 ms | 52 | 15 |
| excluded subject | Frame-wise | TD5 | 200 ms | 1 | – |
A prediction time-step of was used for all models. Batch size: 24.
E. Adaptive Reinforcement Experiment
We performed two variations of an adaptive reinforcement experiment: (i) A2 and 12 non-amputee subjects (9 male, 3 female) performed 3-DOF independent movements involving only the 7 movement classes shown in Fig. 2D and (ii) 7 non-amputee subjects (6 male, 1 female) performed 3-DOF simultaneous movements involving all 27 movement class combinations. Subjects decided which experiment variation(s) to perform based on their preference or experience during the previous experiment. With this experiment, we sought to understand how unguided human-machine interaction with the ED-TCN model affected performance (e.g. would reinforcement drive a sequential model toward a subject-specific optimum?). In clinical settings, an experimenter or clinician might coach a user over time to perform consistent muscle activations in order to achieve a certain performance level. We wanted to, instead, invert and perhaps automate this approach by studying if reinforcement training a sequential model like ED-TCN can improve performance over time by adapting to an unguided user’s preferred or evolving muscle activations.
The experiment was sectioned into twenty-six consecutive 18 s trials for a total experiment time of 8 min. Beyond their initial 15 min introduction and experience with the first experiment, subjects were not provided any guidance on how to improve their classification performance. As before, subjects explored movements in any order they desired for the experiment duration. However, at the end of each trial, the data obtained from that trial was used to reinforce the ED-TCN model with a batch update. Specifically, the ED-TCN model was first trained with the data from trial 1 for 40 epochs and trial 1 data was discarded. The model was then tested for the next 18 s trial, after which the subjects were able to see the model’s classification predictions compared to ground truth labels for new data obtained during that trial (Fig. 6A top). The ED-TCN model, with the weights learned as of that moment, was then trained with the data from trial 2 for 40 epochs, trial 2 data was discarded, and this process repeated for the remaining twenty-four trials. The 18 s trial interval was chosen to be long enough to allow subjects time to explore a variety of movements but short enough that inter-trial update time was minimal. Theoretically, in a single trial the model weights may get trapped in local minima on a noisy contour, but each trial update alters this noise profile, freeing the weights to gravitate toward a global and/or evolving minimum.
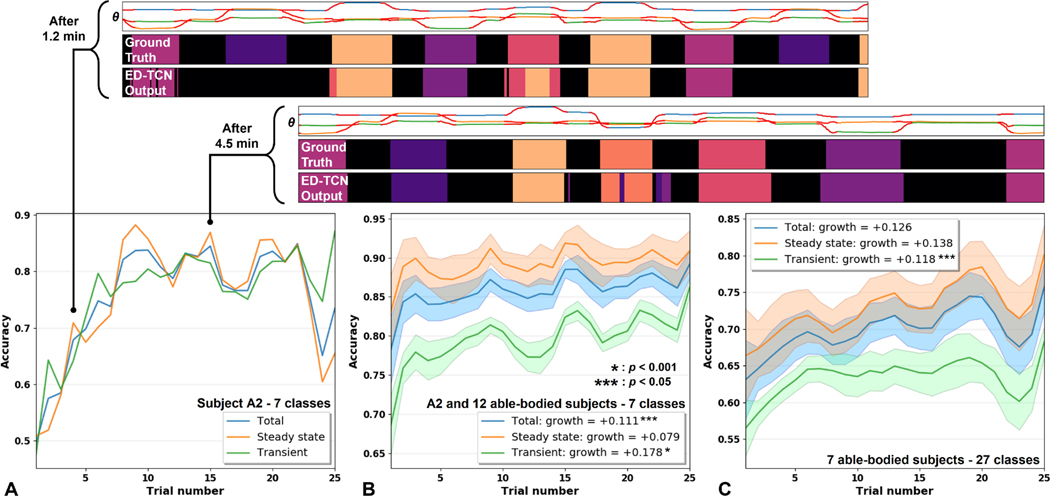
Fig. 6.
The evolution of ED-TCN’s transient-state, steady-state, and total accuracy during our reinforcement experiment. (A) Amputee subject A2 performed 3-DOF independent (7 classes) movements. ED-TCN output is very stable, even early in the training period (top), but accuracy continuously improves. A movement class which was not correctly predicted early in the experiment (dark purple) was eventually learned by the model. A2 established ground truth by mirroring movements with his intact limb, yet his timing was well-synchronized with model predictions. (B) Subject A2 and 12 non-amputee subjects performed 3-DOF independent (7 classes) movements. (C) 7 non-amputee subjects performed 3-DOF simultaneous (27 classes) movements. Across subjects, there was a consistent and significant upward trend in accuracy during the experiment, especially in transient-states. There was also an oscillating effect similar to that of an under-damped system, which we suspect is due to our using a full 40 training epochs after each trial. If the model was over-trained on the previous 18 s of data, performance may have been temporarily reduced due to the “unlearning” of some older information. Most learned information was retained after each trial, though the overall learning rate might be improved with fewer epochs per trial.
III. Results
A. Public Database Results
Model performance results for the class-dense Ninapro data and the channel-dense CapgMyo data are shown in Table III and Fig. 4. Of the sequential and frame-wise models, ED-TCN was the most accurate and stable model by a significant margin (), especially during transient movements (+18.6% over SVM, ). In fact, ED-TCN metrics during transient phases were higher than the total metrics of nearly all other models. The macro scores for ED-TCN and SVM were 0.790 and 0.596, respectively (). We tested raw EMG, TD5, and MAV inputs for sequential models. Raw EMG resulted in a large performance reduction, more training data, and longer training times for our models. MAV slightly outperformed TD5 (statistically insignificant) and required fewer training epochs, which is why we selected MAV features for all sequential models. On the CapgMyo data, ED-TCN performance was optimized with sequences of length 4 indicating that high spatial resolution reduced its reliance on temporal information.
TABLE III.
Comparison of Sequential and Frame-Wise Model Performance on Public Databases
| Sequential models (MAV) |
Frame-wise models (TD5) |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Database | Metric | ED-TCN† | TCN | LSTM | LDA | –NN | SVM | Tree | ANN |
| Ninapro Database 2 | Total accuracy | 0.827 | 0.752 * | 0.785 * | 0.652 * | 0.598 * | 0.691 * | 0.490 * | 0.557 * |
| 41-class, 40 non-amputee subjects | Total stability | 0.984 | 0.973* | 0.960* | 0.902* | 0.733* | 0.910* | 0.936* | 0.874* |
| 12-channel EMG, 2 kHz | Transient accuracy | 0.784 | 0.710* | 0.755** | 0.528* | 0.473* | 0.598* | 0.259* | 0.369* |
| Exercises 1 and 2 | Transient stability | 0.970 | 0.938* | 0.938* | 0.809* | 0.610* | 0.817* | 0.876* | 0.751* |
| Edit Score | 0.432 | 0.307* | 0.234* | 0.109* | 0.044* | 0.119* | 0.033* | 0.079* | |
|
| |||||||||
| Ninapro Amputee Database 3 | Accuracy | 0.635 | 0.564 | 0.574 | 0.502 | 0.433*** | 0.521 | 0.394** | 0.441*** |
| 41-class, 11 amputee subjects | Stability | 0.955 | 0.959 | 0.923*** | 0.859* | 0.631* | 0.890** | 0.503* | 0.885*** |
| Edit Score | 0.238 | 0.214 | 0.147*** | 0.081* | 0.032* | 0.104** | 0.023* | 0.053** | |
|
| |||||||||
| CapgMyo HD-EMG Database C | Accuracy | 0.944 | 0.893* | 0.888* | 0.909* | 0.873* | 0.883* | 0.777* | 0.868* |
| 13-class, 10 non-amputee subjects | Stability | 0.993 | 0.987* | 0.986* | 0.992 | 0.941* | 0.975* | 0.973* | 0.979* |
Method for statistical comparison.
p < 0.001.
p < 0.01.
p < 0.05.
The highest metrics are in bold. Also note the underlined comparison.
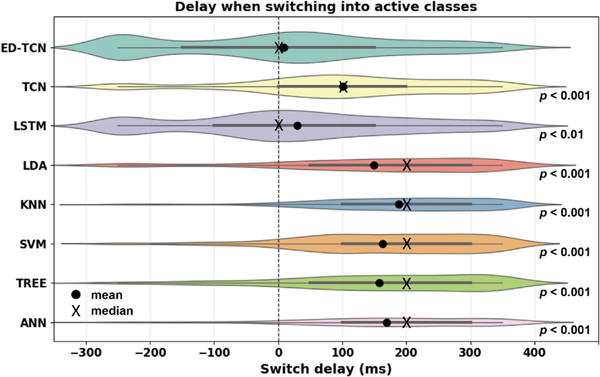
Fig. 4.
The prediction delay of each model in producing stable and correct transitions into active movement classes were computed for all subjects in Ninapro Database 2. ED-TCN’s average prediction delay was 4.6 ms. The area of each model’s “violin” plot is proportionate to the number of correct transitions it produced (distribution tails are extrapolated slightly for visualization purposes only). Frame-wise model delays were governed predominantly by the window size, whereas the temporal information learned by sequential models allowed them to predict faster than their window size would otherwise dictate.
Using test data from all subjects in Ninapro Database 2, we also computed the prediction delay required for each model to produce stable and correct inter-class transitions (Fig. 4). For each transition occurring in the test data at time , we recorded the output predictions of each model across the 1 s interval . If a model produced 8 correct predictions within the interval we recorded the time of the eighth correct prediction. For a perfectly-timed stable transition, would occur at . Therefore, we subtracted this term to compute the prediction delay time, . Aggregating the delays for all models, ED-TCN yielded an average stable and correct transition delay of 4.6 ms, significantly less than other models ( for LSTM, for all others).
B. 3-DOF Simultaneous Movement Results
Model performance results from this experiment are shown in Fig. 5 and Table IV. Video S1 shows an extended version of the sequence in Fig. 5B for multiple models animated in the vMPL environment. A trade-off of experimenting with subject-determined movements was that subjects may not perform all movements and some may be used disproportionately. Out of the 27 available movements, subjects explored 18.13 ± 3.50 during the training period and 18.07 ± 3.45 during the testing period, with 16.47 ± 3.34 classes overlapping both. ED-TCN was significantly more accurate than frame-wise models (worst-case ), especially in transient-states (worst-case ). Consistent with our Ninapro results, ED-TCN metrics during transient phases were higher than the total metrics of all frame-wise models. ED-TCN was significantly more stable () than frame-wise models. Unlike our Ninapro and CapgMyo results, differences among sequential models for this task were not significant. To address potential class imbalance issues, we also applied synthetic minority over-sampling [45] to artificially balance frame-wise data and weighted cross-entropy loss to train sequential models. These pre-processing methods did not significantly affect performance metrics for our data. Macro scores for ED-TCN and SVM were 0.436 and 0.342, respectively. Edit scores were 0.558 and 0.277, respectively (). Finally, we show a comparative analysis (Table IV) of SVM and LDA performance when appended with two post-processing filters: confidence rejection [9] and majority voting [2].
TABLE IV.
Frame-Wise Post-Processing Results
| Model | Total accuracy | Transient accuracy | Total stability | Added delay | Reject rate |
|---|---|---|---|---|---|
| SVM | 0.643 | 0.527 | 0.923 | – | – |
| SVM+CR (0.7)† | 0.665 | 0.559 | 0.990 | – | 0.316 |
| SVM+MV (5)‡ | 0.663 | 0.573 | 0.978 | +100 ms | – |
|
| |||||
| LDA | 0.643 | 0.517 | 0.941 | – | – |
| LDA+CR (0.7) | 0.589 | 0.523 | 0.988 | – | 0.519 |
| LDA+MV (5) | 0.666 | 0.579 | 0.978 | +100 ms | – |
|
| |||||
| ED-TCN | 0.721 | 0.658 | 0.993 | – | – |
C. Adaptive Reinforcement Results
Adaptive reinforcement experiment results are shown in Fig. 6 and Video S2 shows a real-time online implementation of the procedure. Given that ED-TCN stability was high even from minimal training (Fig. 3D), we report only the evolution of accuracy during this experiment. Subjects began this experiment directly after our first, and we observed that results from the first experiment (Fig. 5A) were similar those of this experiment around trial 7 (Fig. 6C). For all subjects, accuracy increased steadily throughout the experiment, dramatically in some cases, and was still increasing at the end of 8 min. For example, amputee subject A2 was able to improve his transient-state accuracy by 38.9% (Fig. 6A). Subjects performing the 7-class sequential movement experiment variation (Fig. 6B) achieved an average total accuracy improvement of 11.1% () and an average transient-state improvement of 17.8% (). Subjects performing the 27-class simultaneous variation (Fig. 6C) achieved total accuracy improvement of 12.6% and an average transient-state improvement of 11.8% ().
IV. Discussion
Prediction stream instability is a major problem in continuous EMG classification, especially during inter-class movement transitions, because it produces spastic jittery outputs that can hinder the control of prosthetic devices. We demonstrate these effects for various prediction models on the vMPL arm (Video S1). Efforts to stabilize the prediction stream with post-processing methods like thresholding and output suppression [9] are particularly useful in that they do not cause appreciable delays, whereas majority voting methods [2] can introduce perceptible delays (Table IV). We focused our examination on the inherent stability and responsiveness of prediction models, and demonstrated that ED-TCN is an impressive model for EMG-based movement classification and minimizes any need for post-processing. Specifically, ED-TCN provides significantly more stable and accurate predictions than other sequential and frame-wise models (Table III), achieving this performance with an average response delay of only 4.6 ms (Fig. 4), with easily visible improvements occurring during transient movements (Fig. 5B). The smoothing effect of convolutions helps to stabilize predictions for both TCN models, but ED-TCN’s inclusion of temporal pooling and up-sampling layers to connect multiple TCNs gives it a significant improvement over LSTM and TCN on large datasets that are dense in output classes (Ninapro) or dense in input dimensions (CapgMyo). Absent these conditions, we recommend using the leaner TCN model defined in our prior work [23]. Models with large architectures like ED-TCN can overfit smaller datasets such as those from our experiments [46], possibly explaining TCN’s small testing accuracy improvement in our 3-DOF experiment (Fig. 5A). Though all three sequential models performed similarly in our experiment, with dramatic improvements over the frame-wise models, there are reasons one might prefer TCN models over LSTM. For one, TCN models tend to train much faster, with previous literature [24], [26] reporting an order of magnitude improvement in training times over LSTM. We report that both TCN models trained faster than LSTM (Section II-B5), and Fig. 3D shows that ED-TCN can achieve superior performance after only a few training epochs. Furthermore, information learned with TCN models is highly interpretable [24], [25] such that, generally speaking, if the input features are intuitive to interpret then the information learned from TCN will be as well. We leave it to readers to weigh the balance of equities and develop a model preference according to their needs.
We elected to pursue minimally constrained subject-driven approaches to experimentation to better capture temporal information from each subject’s volitional intent. In many standard experiment set-ups, subjects are reacting to presented movement cues as opposed to proactively performing the movements and transitions of their choice. We discussed how restricting these variables might inhibit sequential models by teaching them distorted temporal relationships (Section II-B1). Such restrictions are understandable because they ensure every movement class is equally represented and make the experiment more tractable. It would be burdensome to ask human subjects to perform all possible inter-class transition combinations (702 for 27 classes), yet these transitions are where performance accuracy is at its lowest (Fig. 5A, 6C and Table III). After only 3 min of subject-driven exploration, sequential models learned to predict movement transitions stably and accurately compared to the frame-wise models (Fig. 5), indicating that they may be better suited for generalizing to a large variety of inter-class transition relationships. For high-stability models, transient-state predictions were less accurate, as expected, but slightly more stable than steady-states. These differences indicate that more instability occurs during pre-transition muscle activation or post-transition recovery than during the actual transition itself. Examples of pre- and post-transition instability are evident in Fig. 5B.
The frame-wise models benefited most from the TD5 feature set [1], [2], which is a compressed but informative short-term (200 ms) temporal representation of EMG. However, sequential models exhibited equivalent or better performance with only MAV sequences than with TD5 or raw EMG and required considerably less training. This result suggests that the latent temporal relationships within MAV sequences are very informative and, importantly, that the information contained within the EMG signal itself has been under-utilized. We do not imply that MAV is the “best” feature for EMG prediction; we simply emphasize that sequential models learned meaningful temporal relationships and achieved superior performance from only a single feature type. Of the TD5 features, MAV is least affected by sampling rate, which may explain why our experimental results from the 200 Hz Myo Armband are consistent with results from sampling at 1 kHz (Table III). MAV is also a very interpretable feature from biological standpoint since it is linked directly to the intensity of the underlying muscle contractions. Because TCN models are intuitive to interpret given interpretable inputs [24], [25], analysis of the learned temporal MAV relationships (Fig. 3C) may yield important insights about muscle recruitment patterns and movement synergies. We note that the parameter values used herein were selected from a single subject and do not contend they are the optimal values, only that a diligent effort was made to identify a set of parameters from which reasonable inferences could be made about our results. Though we also computed results (not shown) optimizing for each subject individually, we found that those results were not significantly different. The sequential models did not appear to be overly sensitive to minor changes in sequence and window parameters.
In the adaptive reinforcement experiment, the subjects continued to improve performance and incorporate previously unseen classes into model predictions despite receiving no additional instructions (Fig. 6 and Video S2). Video S2 also demonstrates the feasibility of online prosthesis control using our methods. Amputee subject A2 was able to improve his accuracy during transient movements by nearly 40%, though he did have a performance drop in trial 24 due to a temporary distraction (Fig. 6A). Whereas the aggregated performance trends increased, we also observed a notable oscillation effect (Fig. 6B–C). This phenomenon may be related to the interplay of the subject adaptation and consequent model adaptation, and oscillations might be dampened by reducing the number of training epochs per trial. A potential research direction would be to investigate how such human-machine interaction affects the learning rates of prosthesis users. We speculate that continued interaction would eventually capture many inter-class transitions and unique subject habits. Hypothetically, the subject could revisit the reinforcement procedure at his leisure for refinement until converging on a subject-specific optimal prediction model.
V. Conclusion
We have demonstrated that TCN models incorporate temporal information from EMG to achieve highly stable, responsive, and accurate movement prediction when compared with other sequential and frame-wise models, especially during movement transitions. The frame-wise approach is in some ways an unnatural method of predicting dynamic time-varying signals like EMG because our limbs are often in motion, not simply discretely jumping between fixed steady-state positions at regular intervals. We want readers of this work to come away, not just with a specific prediction model, but with a concept: that movement decoding from EMG is better represented as a sequential problem requiring a new set of considerations and experiment designs. The models themselves will evolve and today’s leading-edge methods will become obsolete, so encouraging researchers to think about the problem in a new way is our overarching goal. Addressing EMG decoding as a sequential modeling problem will lead to enhancements in the reliability, responsiveness, and movement complexity available from prosthesis control systems, pushing us further toward the ultimate goal of achieving restorative natural upper-limb function for amputees.
Supplementary Material
Acknowledgment
We thank the Johns Hopkins Applied Physics Laboratory (JHU/APL) for making available the vMPL, developed under their Revolutionizing Prosthetics program and based upon work supported by the Defense Advanced Research Projects Agency (DARPA) under Contract No. N66001-10-C-4056. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of DARPA and JHU/APL. We thank the human subjects who participated in this study and our colleagues Dr. Brock Wester, Robert Armiger, Dr. Colin Lea, Tae Soo Kim, and Dr. Austin Reiter.
This work was supported by the Johns Hopkins University Applied Physics Laboratory Graduate Research Fellowship.
Contributor Information
Joseph L. Betthauser, Department of Electrical and Computer Engineering, The Johns Hopkins University, Baltimore, MD 21218 USA
John T. Krall, Department of Biomedical Engineering, The Johns Hopkins University
Shain G. Bannowsky, Department of Biomedical Engineering, The Johns Hopkins University
György Lévay, Infinite Biomedical Technologies, LLC.
Rahul R. Kaliki, Infinite Biomedical Technologies, LLC
Matthew S. Fifer, Research and Exploratory Development Department, Johns Hopkins University Applied Physics Lab
Nitish V. Thakor, Department of Biomedical Engineering, The Johns Hopkins University, and Department of Electrical and Computer Engineering, The Johns Hopkins University
References
- [1].Hudgins B, Parker P, and Scott R, “A new strategy for multifunction myoelectric control,” IEEE Trans. Biomed. Eng, vol. 40, no. 1, pp. 82–94, Jan. 1993. [DOI] [PubMed] [Google Scholar]
- [2].Englehart K. and Hudgins B, “A robust, real-time control scheme for multifunction myoelectric control,” IEEE Trans. Biomed. Eng, vol. 50, no. 7, pp. 848–854, Jul. 2003. [DOI] [PubMed] [Google Scholar]
- [3].Amari S. and Wu S, “Improving support vector machine classifiers by modifying kernel functions,” Neural Netw., vol. 12, no. 6, pp. 783–789, 1999. [DOI] [PubMed] [Google Scholar]
- [4].Atzori M, Cognolato M, and Muller H, “Deep learning with convolutional neural networks applied to electromyography data: A resource for the classification of movements for prosthetic hands,” Front. Neurorobot, vol. 10, 2016, Art. no. 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Yang D. et al. , “Dynamic hand motion recognition based on transient and steady-state EMG signals,” Int. J. Humanoid Rob, vol. 9, pp. 1250007–1250018, 2012. [Google Scholar]
- [6].Kanitz G, Cipriani C, and Edin B, “Classification of transient myoelectric signals for the control of multi-grasp hand prostheses,” IEEE Trans. Neural Syst. Rehabil. Eng, vol. 26, no. 9, pp. 1756–1764, Sep. 2018. [DOI] [PubMed] [Google Scholar]
- [7].Lorrain T, Jiang N, and Farina D, “Influence of the training set on the accuracy of surface EMG classification in dynamic contractions for the control of multifunction prostheses,” J. NeuroEng. Rehabil, vol. 8, no. 1, 2011, Art. no. 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Scheme E, Hudgins B, and Englehart K, “Confidence-based rejection for improved pattern recognition myoelectric control,” IEEE Trans. Biomed. Eng, vol. 60, no. 6, pp. 1563–1570, Jun. 2013. [DOI] [PubMed] [Google Scholar]
- [9].Robertson J, Scheme E, and Englehart K, “Effects of confidence-based rejection on usability and error in pattern recognition-based myoelectric control,” IEEE J. Biomed. Health. Inf, vol. 23, no. 5, pp. 2002–2008, Sep. 2019. [DOI] [PubMed] [Google Scholar]
- [10].Scheme E, Englehart K, and Hudgins B, “Selective classification for improved robustness of myoelectric control under nonideal conditions,” IEEE Trans. Biomed. Eng, vol. 58, no. 6, pp. 1698–1705, Jun. 2011. [DOI] [PubMed] [Google Scholar]
- [11].Simon A. et al. , “A decision-based velocity ramp for minimizing the effect of misclassifications during real-time pattern recognition control,” IEEE Trans. Biomed. Eng, vol. 58, no. 8, pp. 2360–2368, Aug. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Betthauser J. et al. , “Limb position tolerant pattern recognition for myoelectric prosthesis control with adaptive sparse representations from extreme learning,” IEEE Trans. Biomed. Eng, vol. 65, no. 4, pp. 770–778, Apr. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Amsuss S. et al. , “Self-correcting pattern recognition system of surface EMG signals for upper limb prosthesis control,” IEEE Trans. Biomed. Eng, vol. 61, no. 4, pp. 1167–1176, Apr. 2014. [DOI] [PubMed] [Google Scholar]
- [14].Zhu X. et al. , “Cascaded adaptation framework for fast calibration of myoelectric control,” IEEE Trans. Neural Syst. Rehabil. Eng, vol. 25, no. 3, pp. 254–264, Mar. 2017. [DOI] [PubMed] [Google Scholar]
- [15].Farrell T. and Weir R, “The optimal controller delay for myoelectric prostheses,” IEEE Trans. Neural Syst. Rehabil. Eng, vol. 15, no. 1, pp. 111–118, Mar. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Smith L. et al. , “Determining the optimal window length for pattern recognition-based myoelectric control: Balancing the competing effects of classification error and controller delay,” IEEE Trans. Neural Syst. Rehabil. Eng, vol. 19, no. 2, pp. 186–192, Apr. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Rabiner L. and Juang B, “An introduction to hidden markov models,” IEEE ASSP Magazine, vol. 3, pp. 4–16, Jan. 1986. [Google Scholar]
- [18].Chan A. and Englehart K, “Continuous myoelectric control for powered prostheses using hidden Markov models,” IEEE Trans. Biomed. Eng, vol. 52, no. 1, pp. 121–124, Jan. 2005. [DOI] [PubMed] [Google Scholar]
- [19].Hochreiter S. and Schmidhuber J, “Long short-term memory,” Neural Comput., vol. 9, pp. 1735–1780, 1997. [DOI] [PubMed] [Google Scholar]
- [20].Graves A. and Schmidhuber J, “Framewise phoneme classification with bidirectional LSTM and other neural network architectures,” Neural Netw., vol. 18, no. 5, pp. 602–610, 2005. [DOI] [PubMed] [Google Scholar]
- [21].Xia P, Hu J, and Peng Y, “EMG-based estimation of limb movement using deep learning with recurrent convolutional neural networks,” Artif. Organs, vol. 42, pp. E67–E77, 2018. [DOI] [PubMed] [Google Scholar]
- [22].Gallego J. et al. , “Neural manifolds for the control of movement,” Neuron, vol. 94, no. 5, pp. 978–984, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Betthauser J. et al. , “Stable electromyographic sequence prediction during movement transitions using temporal convolutional networks,” in Proc. IEEE/EMBS Conf. Neural Eng, 2019, pp. 1046–1049.
- [24].Lea C. et al. , “Segmental spatiotemporal CNNs for fine-grained action segmentation,” in Proc. Comput. Vis, 2016, pp. 36–52.
- [25].Kim T. and Reiter A, “Interpretable 3D human action analysis with temporal convolutional networks,” in Proc. 2017 IEEE Conf. Comput. Vision Pattern Recognition Workshops (CVPRW), Jul. 21–26, 2017, doi: 10.1109/CVPRW.2017.207. [DOI] [Google Scholar]
- [26].Lea C. et al. , “Temporal convolutional networks for action segmentation and detection,” in Proc. IEEE Conf. Comput. Vis. Pattern Recogn., CVPR, 2017, pp. 1003–1012. [Google Scholar]
- [27].Bai S, Kolter J, and Koltun V, “An empirical evaluation of generic convolutional and recurrent networks for sequence modeling,” arXiv: 1803.01271v2, 2018.
- [28].Badrinarayanan V, Kendall A, and Cipolla R, “SegNet: A deep convolutional encoder-decoder architecture for image segmentation,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 39, no. 12, pp. 2481–2495, Dec. 2017. [DOI] [PubMed] [Google Scholar]
- [29].Hahnloser R. et al. , “Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit,” Nature, vol. 405, pp. 947–951, 2000. [DOI] [PubMed] [Google Scholar]
- [30].Luce R, Individual Choice Behavior: A Theoretical Analysis. New York, NY, USA: Wiley, 1959. [Google Scholar]
- [31].Lea C, Vidal R, and Hager G, “Learning convolutional action primitives for fine-grained action recognition,” in Proc. IEEE Int. Conf. Robot. Autom., 2016, pp. 1642–1649. [Google Scholar]
- [32].Levenshtein V, “Binary codes capable of correcting deletions, insertions, and reversals,” Soviet Phys., vol. 10, no. 8, pp. 707–710, 1966. [Google Scholar]
- [33].Ortiz-Catalan M. et al. , “Offli ne accuracy: A potentially misleading metric in myoelectric pattern recognition for prosthetic control,” in Proc. Conf. Eng. Med. Biol. Soc., 2015, pp. 1140–1143. [DOI] [PubMed] [Google Scholar]
- [34].Atzori M. et al. , “Electromyography data for non-invasive naturally-controlled robotic hand prostheses,” Sci. Data, vol. 1, 2014, Art. no. 140053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Geng W. et al. , “Gesture recognition by instantaneous surface EMG images,” Sci. Rep, vol. 6, 2016, Art. no. 36571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Pizzolato S. et al. , “Comparison of six electromyography acquisition setups on hand movement classification tasks,” PLoS One, vol. 12, no. 10, 2017, Art. no. e0186132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Mendez I. et al. , “Evaluation of classifiers performance using the Myo armband,” in Myoelectric Controls and Upper Limb Prosthetics Symposium, MEC, p. ID98, 2017. [Google Scholar]
- [38].Ravitz A. et al. , “Revolutionizing prosthetics–Phase 3,” Johns Hopkins APL Tech. Dig, vol. 31, no. 4, pp. 366–376, 2013. [Google Scholar]
- [39].Cover T. and Hart P, “Nearest neighbor pattern classification,” IEEE Trans. Inf. Theory, vol. 13, no. 1, pp. 21–27, Jan. 1967. [Google Scholar]
- [40].Breiman L, Classification and Regression Trees. New York, NY, USA: Routledge, 1984. [Google Scholar]
- [41].Tsuji T. et al. , “Pattern classification of time-series EMG signals using neural networks,” Int J. Adapt. Control Signal Process, vol. 14, no. 8, pp. 829–848, 2000. [Google Scholar]
- [42].Chollet F, Keras, GitHub repository, 2018. [Online]. Available: https://github.com/keras-team/keras
- [43].Lea C, TCN, GitHub repository, 2018. [Online]. Available: https://github.com/colincsl/TemporalConvolutionalNetworks
- [44].Kruskall W. and Wallis W, “Use of ranks in one-criterion variance analysis,” J. Amer. Stat. Assoc, vol. 47, no. 260, pp. 583–621, 1952. [Google Scholar]
- [45].Chawla N. et al. , “SMOTE: Synthetic minority over-sampling technique,” J. Artif. Intell. Res, vol. 16, no. 1, pp. 321–357, 2002. [Google Scholar]
- [46].Krizhevsky A, Sutskever I, and Hinton G, “ImageNet classification with deep convolutional neural networks,” ACM Commun., vol. 60, no. 6, pp. 84–90, 2017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.