Computational exploration and characterization of potential calcium sensitizing mutations in cardiac troponin C

Abstract

Calcium-dependent heart muscle contraction is regulated by the cardiac troponin protein complex (cTn), and specifically by the N-terminal domain of its calcium binding subunit (cNTnC). cNTnC contains one calcium binding site (site II), and altered calcium binding in this site has been studied for decades. It has been previously shown that cNTnC mutants which increase calcium sensitization may have therapeutic benefits, such as restoring cardiac muscle contractility and functionality post myocardial infarction events. Here we computationally characterized eight mutations for their potential effects on calcium binding affinity in site II of cNTnC. We utilized two distinct methods to estimate calcium binding: adaptive steered molecular dynamics (ASMD) and thermodynamic integration (TI). We observed a sensitizing trend for all mutations based on the employed ASMD methodology. The TI results showed excellent agreement with experimentally known calcium binding affinities in wildtype cNTnC. Based on the TI results, five mutants were predicted to increase calcium sensitivity in site II. This study presents an interesting comparison of the two computational methods, which have both been shown to be valuable tools in characterizing the impacts of calcium sensitivity in mutant cNTnC systems.

Graphical Abstract

Introduction

Cardiac troponin (cTn) is a regulatory protein of calcium-dependent muscle contraction and relaxation. The cTn complex is comprised of three subunits: troponin T (cTnT), troponin I (cTnI), and troponin C (cTnC). The N-terminal region of cTnT interacts with tropomyosin (Tm) and anchors the protein complex to the thin filament, while its C-terminus forms interactions with both cTnI and cTnC ^{1, 2}. cTnI is an extremely flexible protein that acts as an inhibitory subunit for actomyosin interaction ³. cTnC is a dumbbell-shaped protein with globular terminal domains linked by a long central helix ^{4, 5}. The terminal domains consist of two helix-loop-helix (EF-hand) motifs, respectively. The C-terminal domain (cCTnC) contains two high-affinity binding sites (site III and site IV) for Ca²⁺ and Mg²⁺ ions; under physiological conditions these sites are constantly occupied by either ion. cCTnC, the structural domain of the cTnC subunit, facilitates key interactions related to anchoring the protein to the remaining cTn complex and the thin filament ⁶. In contrast, the N-terminal domain of cTnC (cNTnC) contains only one active binding site, site II ⁷. cNTnC is frequently referred to as the regulatory domain, due to the conformational change the complex undergoes once a calcium ion binds to site II. The conformational change results in the exposure of the cNTnC hydrophobic patch (cNTnC residues 20, 23, 24, 26, 27, 36, 41, 44, 48, 57, 60, 77, 80, and 81) which promotes binding of the cTnI switch peptide, thereby facilitating disassociation of cTnI from actin. As a result, Tm moves along the thin filament and exposes the myosin binding site. Myosin is then able to bind to actin forming a cross-bridge, a key step in muscle contraction.

Cardiac muscle contractility and function has been shown to be affected by mutations in cNTnC that alter the calcium sensitivity of site II. The mutational effect (sensitizing or desensitizing) depends on the identity and location of the substituted amino acid ⁷. There are several examples of previous attempts to rationally design and characterize calcium sensitivity altering mutants within the hydrophobic patch of the cNTnC. For instance, Tikunova and Davis designed five glutamine calcium sensitizing mutations (F20Q, V44Q, M45Q, L48Q, and M81Q) ⁷. Others have deigned calcium desensitizing mutations, such as I61Q ⁸ and D73N ⁹. The notable success of L48Q to restore cardiac muscle contractility and functionality post myocardial infarction (MI) event makes mutated cNTnC structures a promising option for treating heart failure via gene therapy techniques^10,11. In addition to mutations modulating the calcium affinity of cNTnC, small molecules bound to the hydrophobic patch also exhibit a similar effect ^12,13,14,15. However, there is a lack of exploration of calcium sensitizing mutations in the loop regions of the two EF-hand motifs. In order to bridge this gap, we explore several presumed calcium sensitizing mutations and characterize their effects via the computational methods adaptive steered molecular dynamics and thermodynamic integration.

Adaptive steered molecular dynamics (ASMD), developed by Hernandez and co-workers ¹⁶, functions similarly to traditional steered molecular dynamics (SMD). In both techniques, a pseudo particle applies a steering force in order to move along the predetermined reaction coordinate at a particular velocity. The nonequilibrium work conducted on the system during the simulation can be related to the difference in free energy between the initial and final states ¹⁷. However, the benefit of the ASMD methodology, is that the reaction coordinate can be separated into N smaller stages. For each stage, the Jarzynski average (JA)¹⁸ is calculated over the specified number of individual trajectories. The individual nonequilibrium trajectory’s work that most closely matches the JA serves as the initial position for the next sequential stage of the reaction coordinate. ASMD has been demonstrated to significantly reduce the number of nonequilibrium trajectories required to converge the potential mean force (PMF) compared to traditional SMD ^19,20. Thermodynamic integration (TI) is an alchemical method utilized to determine the relative binding affinity of ligand to receptor ^21,22,23,24. TI relates two states (initial and final) via a coupling parameter, $\lambda$, through a series of intermediate stages. $\lambda =0$ corresponds to the initial state and $\lambda =1$ corresponds to the final state. At each $\lambda$ window a molecular dynamics simulation is performed to generate an ensemble of structures. The total energy of the system is taken to be its potential energy, and the derivative of the energy with respect to $\lambda$ is utilized to calculate the free energy difference.

In a previous work, we developed an ASMD protocol to characterize the calcium binding affinity of site II in wildtype cNTnC, several known sensitizing mutations (F20Q, V44Q, M45Q, L48Q, and M81Q), and two desensitizing mutations (I61Q and D73N) ²⁵. We successfully predicted the correct calcium binding affinity trends of those mutations compared to wildtype. Much work has also been done to study the dynamics and energetics of the hydrophobic patch opening and the potential effect of mutations in this region ^{26,27,28,29,30,31,32,33}. Additionally, the dynamics and effects of mutations in other parts of the cTn complex, particularly cTnI, have been explored ^{34,35,36,37,38,39,40,41}. Finally, thermodynamic integration has been previously applied to study calcium and magnesium binding to site II ^{42, 43}. In this work, we rationally explore several presumed Ca²⁺ sensitizing mutations based on protein stability point mutation predictions and characterize their effects with ASMD and TI. We hope that this publication will be able to serve as a guide for potential future protein design studies. Furthermore, our work serves as an interesting comparison between ASMD and TI methods for predicting calcium binding affinities.

Methods

Identification of Explored Mutations based on Predicted Protein Stability

In order to predict protein stability, we used the Cologne University Protein Stability Analysis Tool (CUPSTAT) ^44,45,46. This program makes use of structural environment-specific atom potentials and torsion angles to predict the difference in free energy of unfolding ($\Delta \Delta G_{unfolding}$) between wild-type and mutant proteins. CUPSTAT was utilized to exhaustively predict all possible single point mutations in the wildtype cNTnC subunit. In order to identify mutations that could possibly cause increased calcium sensitivity, we sought mutants that destabilized the closed conformation, while concurrently stabilizing the open conformation of the cNTnC hydrophobic patch. In order to model the different states of calcium-bound cNTnC (closed and open) we used NMR models of the protein obtained from the Protein Data Bank (PDB). The most representative models of PDB IDs 1AP4 ⁴⁷ and 2KFX ⁴⁸ were used to model the closed and open patch conformations respectively. 2KFX was selected to model the open conformation of Ca²⁺-bound cNTnC since this structure was obtained in absence of the cTnI switch peptide, making this the best model for comparison to 1AP4. However, the initial structure of 2KFX was determined with the known inhibitor W7 bound in the hydrophobic patch, therefore the ligand was removed prior to any computational analysis. We focused on mutations in the loop I and loop II regions and immediately adjacent residues. Eight mutations of interest were identified: D33H, D33M, L41W, V72D, V72N, F74E, F74R, and F77I.

Adaptive Steered Molecular Dynamics (ASMD)

The representative protein conformation of PDB 1AP4 served as the model for wildtype cNTnC and the base model from which all mutations were constructed using the protein mutagenesis tool in PyMOL ⁴⁹. The N-terminal domain of cTnC has served as the blueprint for many impactful studies evaluating the role and influence of wildtype and mutant cardiac troponin in muscle contraction ^{8, 26, 27, 28, 29, 39, 50, 51, 52}. Although the cNTnC model is rather simplistic to capture the function of the entire troponin complex in context of the muscle tissue, many experts in the field have utilized cNTnC to study the dynamics and calcium binding properties of site II. The initial protein structures for molecular dynamics of the wildtype and mutants models were solvated, minimized, and equilibrated as described in our previous work ²⁵. For the point mutations located in loop I (D33H, D33M, and L41W), the ASMD pulls were calculated based on the distance between the center of mass of the $\alpha$ carbons in the residues Ser69, Gly70, and Thr71 and the initial position of the Ca²⁺ ion. Hereafter, we will refer to this center of mass point as COM 1. The initial distance between COM 1 and the calcium ion was determined for all systems using the CPPTRAJ ⁵³ distance function. The ASMD simulations were performed for a total distance of 20 Å, using a force constant of 7.2 kcal mol⁻¹ Å⁻² and a pulling speed of 0.5 Å/ns. All ASMD simulations were split into ten stages, and each stage was simulated for 4 ns (nstlim=2,000,000) with 50 trajectories per stage. For mutations located in loop II and adjacent (V72D, V72N, F74E, F74R, and F77I), we observed increased flexibility in the loop region resulting in the calcium ion being driven into the adjacent helices (helix C and D) while conducting ASMD pulls based on COM 1. Therefore, to compensate for this effect we employed a new center of mass point (COM 2) based on the $\alpha$ carbons in the residues Asp67, Gly68, Ser69, Gly70, and Thr71. Similar to the mutations located in loop I, the distance between the starting position of the Ca²⁺ ion and COM 2 served as the initial distance for the ASMD simulations. Additionally, simulations based on this center of mass point were performed for a total distance of 20Å utilizing a force constant of 7.2 kcal mol⁻¹ Å⁻², pull speed of 0.5 Å/ns, and 50 trajectories per stage The initial distance for these systems was also obtained using the distance function of CPPTRAJ. The wildtype cNTnC system PMF was determined based on both center of mass points. Additionally, the PMF of the wildtype system was obtained utilizing a pulling speed of 0.1 Å/ns and the reaction coordinate partitioned into 20 stages. Each stage was simulated for 10 ns (nstlim=5,000,000) with 50 individual trajectories per stage. Upon completion of the SMD pulls for any stage (N) of the simulation, the JA was calculated via the “ASMD.py” script provided by Hernandez and colleagues in the AMBER Advanced Tutorial 26. The final coordinates of the trajectory whose work most closely matched the JA were used to initialize the subsequent stage (N+1) of the simulation. All ASMD simulations were performed with the GPU implementation of PMEMD⁵⁴ from the AMBER18⁵⁵ package.

Thermodynamic Integration (TI)

Similar to the protocol for the ASMD simulations, the representative model of PDB 1AP4 served as the model for wildtype cNTnC, and the base from which all mutations where created in PyMOL using the protein mutagenesis tool. The wildtype and all mutant systems were prepared in the following manner. The individual models were solvated in a 12Å TIP3P ⁵⁶ water box and neutralized with Na⁺ ions via the tLeap module of AMBER18. The protein was described with the forcefield ff14SB⁵⁷. In order to complete the thermodynamic cycle, a system containing the Ca²⁺ ion was prepared using the tLeap module and solvated in a 12Å TIP3P water box. Simulations were conducted under NPT conditions using the Berendsen barostat ⁵⁸ and periodic boundary conditions. The system was minimized for 2000 cycles and heated to 300 K using the Langevin thermostat ⁵⁹ over 500 ps prior to the 5 ns production with a time step of 2 fs. The SHAKE algorithm was employed to constrain all bonds involving hydrogen atoms, and the Particle Mesh Ewald method⁶⁰ was utilized to calculate electrostatic interactions of long distances with a cutoff of 10 Å.

The alchemical thermodynamic cycle used for ligand binding has been detailed previously by Leelananda and Lindert ⁶¹. In this implementation of TI, the method consisted of three steps for ligand (Ca²⁺) in protein: introduction of harmonic distance restraints, removal of electrostatic interactions, and removal of van der Waals forces. However, for the ligand in water system only two steps were necessary: removal of electrostatic interactions and removal of van der Waals forces. The specific distance restraints for all systems were calculated with the CPPTRAJ distance function. Restraints were created based on the distance between the Ca²⁺ ion and the following atoms: ASP67 CG, SER69 OG, and THR71 OG1. The coupling parameter $(\lambda )$ increased incrementally by 0.1 from 0.0 – 1.0 for each transitional step of the thermodynamic cycle. During each simulation, $\text{dV}∕\mathrm{d}\lambda$ values were collected every 2 ps resulting in 5000 data points per transitional step of $\lambda$ for further analysis. The Multistate Bennett Acceptance Ratio (MBAR)⁶² was used to calculate the relative free energies of the simulations across all values of $\lambda$. Finally, analytical free energy $(\Delta G)$ corrections were made to account for the introduction of the distance restraints as described previously⁴². For each system, five independent TI runs were performed and the results averaged.

Results and Discussion

Prediction of Potential Calcium Sensitizing Mutations.

The Cologne University Protein Stability Analysis Tool (CUPSTAT) was employed to exhaustively predict the protein stability resulting from all possible single point mutations in the wildtype cNTnC subunit. We were particularly interested in mutations in the loop regions that were predicted to destabilize the closed conformation (model based on PDB 1AP4) while simultaneously predicted to stabilize the open conformation (model based on PDB 2KFX). We hypothesized that the stabilization of the open conformation will correlate with a lower free energy of hydrophobic patch opening and/or a slower Ca²⁺ disassociation rate $(k_{off})$, thereby leading to an increase in calcium sensitivity. Based on this line of thinking, we filtered the CUPSTAT predictions focusing on cases where torsion angles of the mutated residue were favorable in both open and closed conformations. The CUPSTAT predictions of all mutants that met these criteria are available in Table S1, where the bolded rows denote the mutations that were selected for simulations. We further narrowed the results for in silico characterization based on a predicted $\Delta \Delta G_{unfolding}$ less than −0.7 kcal/mol, thus focusing our studies on the following mutations: D33H, D33M, L41W, V72N, F74E, F74R, and F77I. Although the mutation V72D did not meet our cutoff criteria ($\Delta \Delta G_{unfolding}=-0.56$ kcal/mol), it was rationally selected for further analysis as we speculated that the inclusion of an additional negatively charge residue in the coordination sphere of site II might cause a divalent cation (i.e. Ca²⁺) to bind more tightly. Therefore, we ultimately selected eight potential calcium sensitizing mutations (D33H, D33M, L41W, V72D, V72N, F74E, F74R, and F77I) for further characterization via adaptive steered molecular dynamics and thermodynamic integration methods.

Characterization and Comparison of Potential Ca²⁺ Sensitizing Mutations with Adaptive Steered Molecular Dynamics and Thermodynamic Integration.

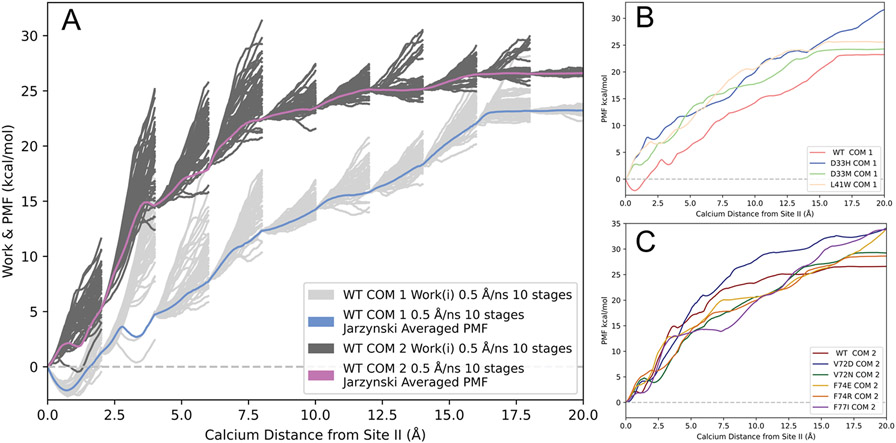
We simulated Ca²⁺ binding in cNTnC wildtype and mutant structures based on the CUPSTAT predictions with ASMD and TI. It has been well established that the accuracy of ASMD can be improved via two ways: using an increasingly slow pull speed and increasing the number of trajectories per stage ^{19,20, 25}. In our previous work, we examined two different pull speeds and three different numbers of trajectories per stage. Ultimately, we settled on a pull speed of 0.5 Å/ns and 50 trajectories per stage (tps). Here, we explored the impact of an even slower velocity for wildtype cNTnC with the reaction coordinate separated into 20 stages. Figure S1 depicts two different JA PMFs of the wildtype cNTnC that differ by their pulling velocities and the number of stages that the reaction coordinate was segmented into (0.5 Å/ns with 10 stages and 0.1 Å/ns with 20 stages). We found the JA PMFs of these two simulations to be rather similar to one another (difference of only ~ 4kcal/mol). We considered this difference to be insignificant as the two PMFs overlapped in several of the individual work traces. These results supported our choice of pull speed (0.5 Å/ns) and number of stages (10) for ASMD of the mutations, as these parameters were less computationally expensive in comparison. Additionally, based on these results we hypothesize that when comparing PMFs at significantly slow pull velocities, the number of trajectories per stage has a more substantial impact on the accuracy of ASMD compared to the speed of the pull.

Figure 1A depicts two different JA PMFs of wildtype cNTnC that differed by the center of mass points for pulling calcium away from its initial bound position in site II. The JA PMF and the individual work traces for cNTnC based on COM 1 (identical to that published in our previous work) are depicted in light blue and light gray, respectively. For mutations located in and adjacent to loop II (V72D, V72N, F74E, F74R, and F77I), we observed increased flexibility in the loop region due to the substitution of larger residues. Upon visualizing the trajectories of the loop II mutant systems based on COM 1, we found that the calcium ion was being driven into the adjacent helices (helix C and D) leading to significantly higher PMFs. To remedy this biologically irrelevant occurrence, we created a new center of mass point, COM 2 (as described in the Methods section). The cNTnC system based off of COM 2 was simulated with a pull speed of 0.5 Å/ns, the reaction coordinate split into 10 stages, and 50 tps. The JA PMF and individual work traces for the ASMD pull based off of COM2 are depicted in Figure 1A as violet and dark gray, respectively. While the PMF for this system was slightly higher than that of the cNTnC system based on COM 1 for multiple calcium distances, there was overlap between the PMFs and both converged to a similar free energy. Figure 1B depicts the JA PMFs of wildtype and loop I mutant cNTnC structures based on COM 1. Figure 1C displays the JA PMFs of wildtype and loop II mutant cNTnC structures based on COM 2.

Figure 1.

ASMD PMFs of Ca²⁺–bound wildtype and mutant cNTnC systems. All PMFs were obtained at constant NPT conditions. (A) The PMFs of wildtype cNTnC obtained using two different center of mass points. The PMF for the system (pull speed of 0.5 Å/ns and 10 stages) based on COM 1 is shown as the light blue line and the work traces $W({\xi }_t^i)$ for the 50 individual trajectories in each stage are shown in light grey lines. The PMF for the system (pull speed of 0.5 Å/ns and 10 stages) based on COM 2 is shown as the violet line and the work traces $W({\xi }_t^i)$ for the 50 individual trajectories in each stage are shown in dark grey lines. (B) JA PMFs of Ca²⁺ binding to wildtype cNTnC and loop I mutations based on COM 1 and a pull speed of 0.5 Å/ns, the reaction coordinate separated into 10 stages, and 50 individual trajectories per stage. (C) JA PMFs of Ca²⁺ binding to wildtype cNTnC and loop II mutations based on COM 2 and a pull speed of 0.5 Å/ns, the reaction coordinate separated into 10 stages, and 50 individual trajectories per stage.

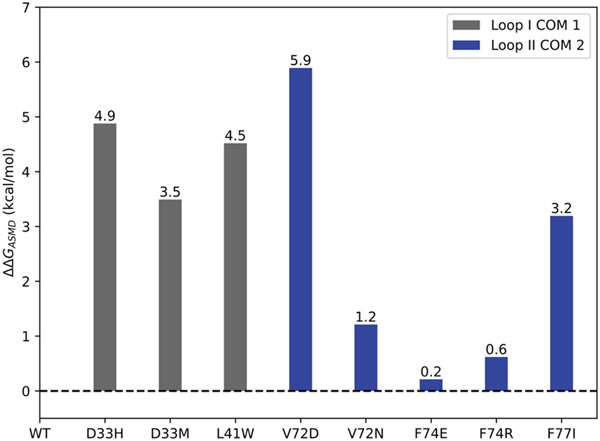
The $\Delta \Delta G$ values calculated from the ASMD simulations ($\Delta \Delta G_{ASMD}$) for all of the predicted sensitizing mutations followed the anticipated trend. Mutant V72D showed the greatest increase in predicted binding affinity with a $\Delta \Delta G_{ASMD}$ of 5.9 kcal/mol. Mutations D33H, D33M, L41W, and F77I all showed a significant predicted increase in calcium binding with $\Delta \Delta G_{ASMD}$ values of 4.9 kcal/mol, 3.5 kcal/mol, 4.5 kcal/mol, and 3.2 kcal/mol respectively. Mutant V72N showed a moderate increase in predicted calcium binding with an $\Delta \Delta G_{ASMD}$ of 1.2 kcal/mol. Finally, the mutants F74E and F74R showed only a slight increase of calcium binding with $\Delta \Delta G_{ASMD}$ values of 0.21 kcal/mol and 0.62 kcal/mol, respectively. The $\Delta \Delta G_{ASMD}$ values between wildtype cNTnC and all single mutant cNTnC systems are summarized in Figure 2. $\Delta \Delta G_{ASMD}$ was calculated using the following equation, indicating that all mutants were predicted to bind calcium more strongly than wildtype (positive $\Delta \Delta G_{ASMD}$ values):

$$\Delta \Delta G_{ASMD}=\Delta G_{mutant}-\Delta G_{wildtype}$$

Figure 2.

Relative $\Delta \Delta G_{ASMD}$ values between mutant and wildtype cNTnC structures as predicted by ASMD. $\Delta G_{ASMD}$ values of Ca²⁺ binding were obtained from the respective PMFs at a distance of 15 Å from the calcium ion’s initial bound position in site II.

In our previous work, we have shown that the ASMD method significantly overestimates the relative free energy of calcium binding. Therefore, we additionally characterized the wildtype and mutant systems by means of thermodynamic integration.

Thermodynamic integration (TI) was performed in quintuplicate and averaged for wildtype and all proposed mutant cNTnC structures. Figure 3 illustrates a schematic version of the thermodynamic cycle implemented in our TI protocol. For all systems of ligand-bound protein and ligand in solvent, an ensemble of structures at each $\lambda$ step was generated via a 5ns molecular dynamics simulation. In our application of the TI protocol the ligand of interest was the calcium ion. In Figures S2-S10, we provide plots of the $\partial V∕\partial \lambda$ values of the thermodynamic cycle for each simulated cNTnC system. The kinetics of calcium binding to the wildtype form of cNTnC have been previously described by Hazard and colleagues ⁶³, via IAANS fluorescence titrations. The authors report the $K_D$ of Ca²⁺ for wildtype cTnC site II as 3 ± 1 μm ($\Delta G=-7.5\pm 0.2$ kcal/mol). We found our relative free energy of calcium binding based on TI $\Delta G_{TI}$ to be in good agreement with the experimental value for the wildtype system ($\Delta G_{TI}=-7.2\pm 1.2$ kcal/mol). The $\Delta G_{TI}$ and $\Delta \Delta G_{TI}$ values for wildtype and mutant cNTnC structures are provided in Table 1. All simulated mutant systems had either a negative $\Delta \Delta G_{TI}$ effect (indicating increased predicted calcium binding affinity) or no effect. Mutant L41W was predicted to have the greatest effect on calcium binding with a $\Delta G_{TI}=-9.6\pm 0.9$ kcal/mol and $\Delta \Delta G_{TI}=-2.4\pm 0.3$ kcal/mol. Mutants F77I and F74R had the next largest impacts on predicted calcium binding affinity with $\Delta G_{TI}$ values of −8.6 ± 1.0 kcal/mol ($\Delta \Delta G_{TI}=-1.4\pm 0.2$ kcal/mol) and −8.5 ± 0.5 kcal/mol ($\Delta \Delta G_{TI}=-1.3\pm 0.7$ kcal/mol), respectively. Mutants F74E and V72D showed moderate increases in predicted calcium binding affinity with $\Delta G_{TI}$ values of −8.1 ± 1.5 kcal/mol ($\Delta \Delta G_{TI}=-0.9\pm 0.4$ kcal/mol) and −8.0 ± 1.7 kcal/mol ($\Delta \Delta G_{TI}=-0.8\pm 0.5$ kcal/mol), respectively. Mutations D33H and D33M showed relatively small differences in $\Delta G_{TI}$ compared to wildtype with $\Delta G_{TI}$ values of −7.6 ± 0.9 kcal/mol ($\Delta \Delta G_{TI}=-0.4\pm 0.3$ kcal/mol) and −7.3 ± 1.6 kcal/mol ($\Delta \Delta G_{TI}=-0.1\pm 0.5$ kcal/mol), respectively. Therefore, we believe that these mutations would have an insignificant impact on the calcium sensitivity of site II. The TI results for mutant V72N suggested that this mutant had no effect on calcium binding affinity, with $\Delta G_{TI}=-6.8\pm 0.7$ kcal/mol and $\Delta \Delta G_{TI}=0.4\pm 0.5$ kcal/mol.

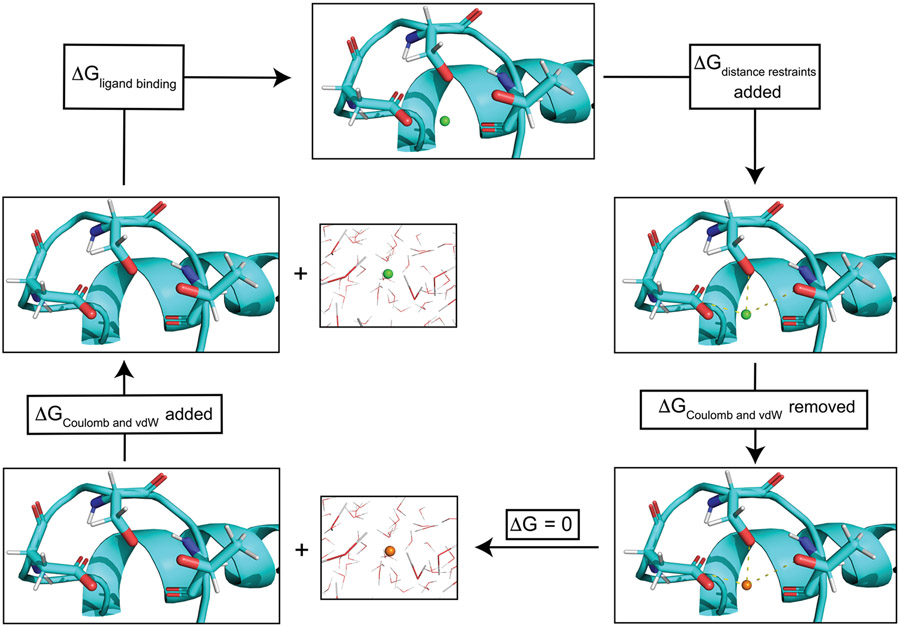
Figure 3.

Schematic thermodynamic cycle for thermodynamic integration calcium binding free energy calculation. cNTnC site II is shown in cyan with side chains of residues ASP67, SER69, and THR71 explicitly shown. When the ligand (Ca²⁺) is depicted as a green sphere, coulombic and vdW interactions with the chemical environment are present. However when the ligand is depicted as an orange sphere these nonbonded interactions are removed. The first step was to add harmonic distance restraints (depicted as dashed yellow lines) between the ligand and protein. These restraints prevent the ligand from leaving site II during the course of the simulation once the coulombic and vdW forces were removed. Next the coulombic and vdW interactions of the ligand were removed, and the ligand was subsequently removed from the protein system and placed into a water box. The coulombic and vdW interactions of the ligand were then restored to the ligand in the water box. Summing the free energy changes along the thermodynamic cycle resulted in the protein–ligand binding free energy. All systems were simulated in explicit solvent.

Table 1.

Thermodynamic integration results of calcium binding

cNTnC Structure	$\Delta {\mathit{G}}_{\mathit{TI}}(\mathit{kcal}∕\mathit{mol})$	$\Delta \Delta {\mathit{G}}_{\mathit{TI}}(\mathit{kcal}∕\mathit{mol})$
WT	−7.2 ± 1.2	-
D33H	−7.6 ± 0.9	−0.4 ± 0.3
D33M	−7.3 ± 1.6	−0.1 ± 0.5
L41W	−9.6 ± 0.9	−2.4 ± 0.3
V72D	−8.0 ± 1.7	−0.8 ± 0.5
V72N	−6.9 ± 0.7	0.4 ± 0.5
F74E	−8.1 ± 1.5	−0.9 ± 0.4
F74R	−8.5 ± 0.5	−1.3 ± 0.7
F77I	−8.6 ± 1.0	−1.4 ± 0.2

While ASMD has been shown previously to predict the correct trends of mutants altering calcium binding affinity, the method is prone to error. The loop region of site II is highly flexible and during the SMD trajectory the direction is likely to shift as it is dependent on the center of mass between alpha carbon atoms of multiple residues. If the loop region shifts dramatically, the calcium ion could be driven into the adjacent helices, thereby greatly increasing the energy of the PMF. Therefore, we believe this method to be suited for instances where the ASMD pull is dependent on more stable secondary structure (i.e., $\alpha$ helix or $\beta$ sheet) which experiences less inherent dynamic motion. In regards to calculating calcium binding in site II of the cNTnC system, thermodynamic integration seems to be a more appropriate choice to correctly predict the relative free energy of binding. We found excellent agreement between our predicted $\Delta G_{TI}$ and that of reported experimental $\Delta G$ for the wildtype cNTnC. Additionally, for all systems (wildtype and mutant) we observed a relatively low standard deviation between the five independent TI trials. Therefore, we have more confidence in the predicted $\Delta \Delta G_{TI}$ of the proposed mutant systems. Based on the TI predictions, we suggest that mutants L41W, V72D, F74E, F74R, and F77I might exhibit a measurable calcium sensitizing effect. While we did not experimentally confirm the proposed mutations, we have previously simulated the correct trends in calcium binding affinity of sensitizing mutations (F20Q, V44Q, L48Q, M81Q) and desensitizing mutations (I61Q and D73N) utilizing the ASMD methodology ²⁵. Additionally, we have used TI to accurately obtain the relative binding affinity for wildtype cNTnC and mutant D67A/D73A for calcium and magnesium ions ⁴², as well as the relative binding affinity of Mg²⁺ for several calcium sensitizing mutations such as L48Q and hypertrophic cardiomyopathy associated mutants Q50R and C84Y ⁴³.

It is important to note that increased calcium sensitization of the myofilament and the cardiac troponin T subunit has been linked to cardiac arrhythmias ^64,65,66,67. In cases of increased sensitization, the relaxation of cardiac muscle was impaired. However, the proposed sensitizing mutations in this work were intended to target the disease state (i.e., congestive heart failure) in which an individual exhibits a decreased sensitivity towards calcium binding. As such, they might be able to restore cardiac contractility and functionality post an initial loss of function.

Conclusion

We performed an exhaustive prediction of protein stability for all possible single point mutations in the cNTnC system, using the CUPSTAT webserver. Based on these results we studied eight mutations focused in cNTnC’s loop regions (loop I and loop II): D33H, D33M, L41W, V72D, V72N, F74E, F74R, F77I. We computationally characterized the effects of the mutations on altering calcium binding affinity via two methods: adaptive steered molecular dynamics and thermodynamic integration. With regards to the ASMD method, we showed that one reaches a convergence point, for this system, with increasingly slow pull speeds. Additionally, for instances where ASMD parameters are based on disordered regions, alternative methods may be more appropriate. Thermodynamic integration provided predictions to be in good agreement with experimentally determined calcium binding affinity for site II in wildtype cNTnC. Furthermore, the predicted $\Delta \Delta G_{TI}$ of proposed mutations were in a much more realistic range with the greatest $\Delta \Delta G_{TI}$ observed for mutant L41W (−2.372 ± 0.270 kcal/mol). Therefore, based on the TI results, we predict mutants L41W, V72D, F74E, F74R, and F77I to have a potential sensitizing effect on calcium binding affinity. We plan to experimentally validate these results and elucidate the impacts of the mutations on the K_D of calcium binding in future works. In addition to experimental validation, in future work, we plan to simulate the proposed mutations in context of the whole troponin complex or even parts of thin filament. We believe this work will serve as a starting point for future design and characterization of novel mutations with therapeutic benefits.