Stoichiometry Controls the Dynamics of Liquid Condensates of Associative Proteins

Abstract

Multivalent associative proteins with strong complementary interactions play a crucial role in phase separation of intracellular liquid condensates. We study the internal dynamics of such “bond-network” condensates comprising two complementary proteins via scaling analysis and molecular dynamics. We find that when stoichiometry is balanced, relaxation slows down dramatically due to a scarcity of alternative binding partners following bond breakage. This microscopic slow-down strongly affects the bulk diffusivity, viscosity, and mixing, which provides a means to experimentally test this prediction.

Protein-rich liquid condensates, also known as membraneless organelles, have recently emerged as an important paradigm for intracellular organization [1–3]. The molecular mechanisms involved in condensate phase separation [4] include weak interactions between intrinsically disordered regions of proteins, interactions with RNA and DNA, and specific protein-to-protein complementary interactions. Here, we focus on the latter mechanism, often described in terms of “sticker-and-spacer” models [5], where strongly interacting complementary “stickers” are separated by flexible “spacers,” which have little to no interactions. In a simple case, only two species are involved with complementary sticker domains [Fig. 1(a)], and the condensate liquid consists of a dynamically rearranging network of these bound domains [Fig. 1(b)]. This paradigm of a binary mixture of complementary proteins has been observed in membraneless organelles such as the algal pyrenoid [6], as well as in artificial systems [7].

FIG. 1.

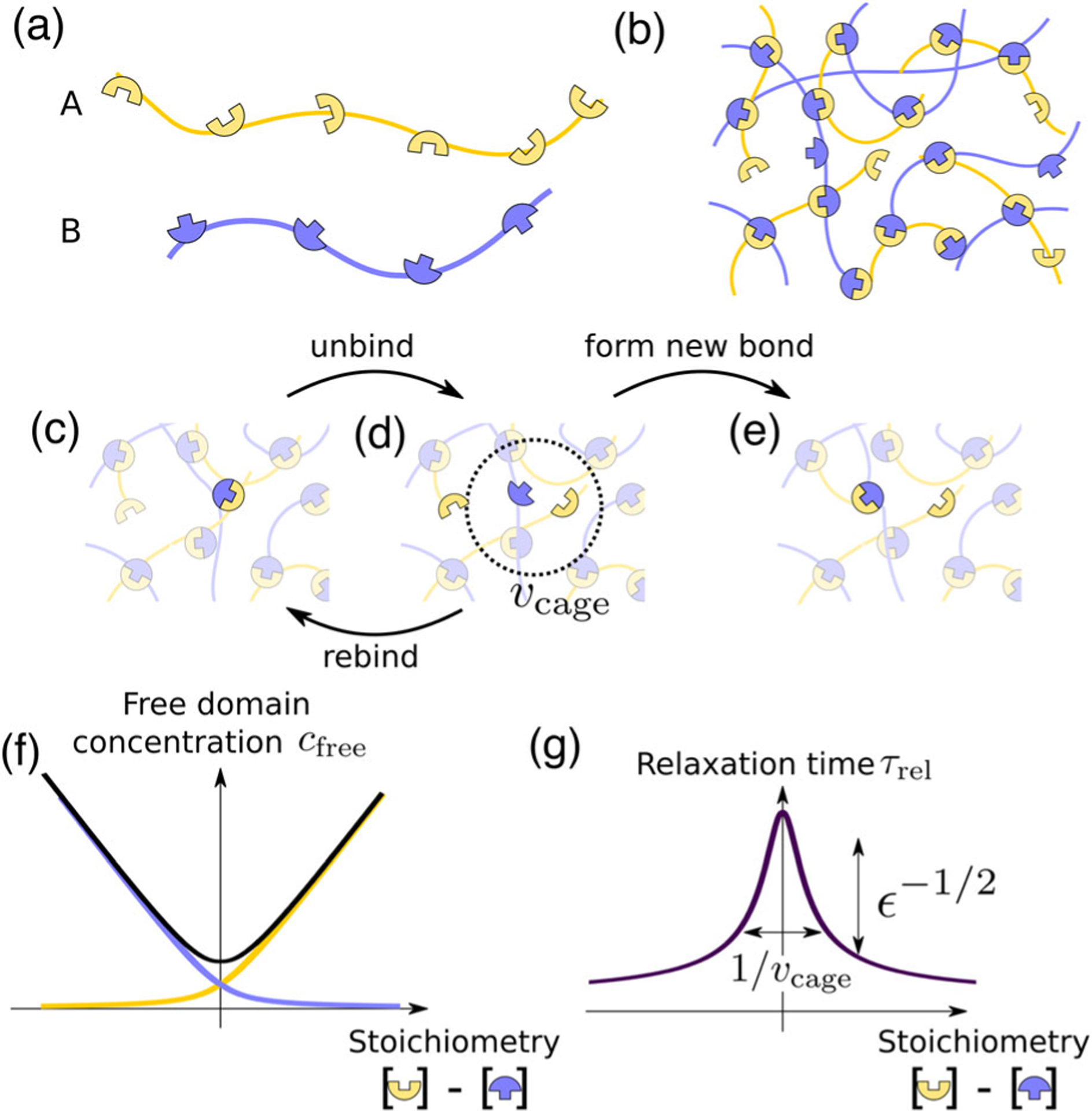
Stoichiometry controls the bond relaxation time of multivalent associative proteins. (a) Sketch of associative multivalent proteins, with complementary domains separated by flexible linkers. (b) Strong yet reversible binding between proteins leads them to condense into a network with most possible bonds formed. (c)–(e) Schematic of the bond relaxation mechanism. When two initially bound domains (c) unbind, the two are caged in a small volume $v_{\text{cage}}$ (d). Two events can then occur: the initially bound domains can rebind, or, if a free domain is within reach, a new bond may form (e), which is the system’s basic relaxation mechanism. (f) Concentration of unbound domains $c_{\text{free}}$ of both types as a function of stoichiometry difference. (g) Relaxation time [Eq. (1)] corresponding to the process of unbinding and then rebinding with a new partner (c)–(e), as a function of stoichiometry difference. Here, $ϵ=e^{-\mathrm{\Delta }F}$.

Recent studies show that such binary liquids differ in their properties from usual, nonbiological liquids: for instance, their valence sensitively controls their phase boundary through a “magic number” effect [6,8,9], and they can exhibit long-lived metastable clusters prior to macroscopic phase separation [10]. The equilibrium phase transitions of these systems, which are to be distinguished from gelation [11] and bond-percolation [12] transitions, are well characterized. Little is known, however, about the bulk dynamical properties of these liquids. It is expected that these liquids will inherit some properties of associative polymers—a class of materials characterized by long chains with sparse sticky sites [13]. In these materials, relaxation is slowed down by the attachment-detachment dynamics of binding sites, resulting in sticky reptation [14]. Indeed, it has been experimentally observed that a sparsity of free binding sites can significantly slow the dynamics [15]. However, the corresponding role of attachment-detachment dynamics has not yet been considered in liquid protein condensates.

We theoretically study the bulk relaxation mechanisms of liquids consisting of a binary mixture of multivalent complementary proteins [Figs. 1(a) and 1(b)]. We show that the strong specificity of interactions results in a finely tuned response to changes in composition—a property that cells might exploit to dynamically adapt the mixing properties of condensates. We first present a simple kinetic model that predicts a strong dependence of the relaxation time of bonds on composition of the liquid: at equal stoichiometry of complementary domains, we anticipate a sharp peak in the relaxation time. We then employ molecular dynamics (MD) simulations to confirm these predictions and show their striking consequences for bulk diffusivity and viscosity. Finally, we demonstrate that this effect strongly affects the mixing dynamics of droplets of different compositions, and propose experiments to test our predictions.

We consider the dense phase of multivalent proteins of two different types, denoted $A$ and $B$ [Fig. 1(a)], where each domain can bind to one and only one domain of the complementary type. The free energy favoring formation of such a bond is $\mathrm{\Delta }F$, with a corresponding unbinding Arrhenius factor $ϵ=\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{\Delta }F)$ (we set $k_{B}T=1$ throughout). We consider the strong-binding regime, i.e., $ϵ\ll 1$, in which almost all possible bonds are formed [Fig. 1(b)]. However, over sufficiently long times, bonds still break and rearrange, the system relaxes, and the system can flow as a liquid. We investigate here the dependence of this relaxation time on the Arrhenius factor $ϵ$ and on the composition of the liquid.

In the strong-binding regime, relaxation is controlled by individual bond breaking [Fig. 1(c)]. This process is slow and thermally activated, occurring at a dissociation rate $k_d=ϵ/{\tau }_0$ where ${\tau }_0$ is a microscopic relaxation time, and these events are rapidly followed by rebinding. However, the two newly unbound complementary domains are part of the network, and thus are not free: they remain confined and diffuse only in a small volume $v_{\text{cage}}$ around their initial position [Fig. 1(d)]. This caging volume is determined by the length and flexibility of linkers. Subsequent to a bond breaking, there is a high probability the two former partners will rebind to each other, thus negating the effect of the bond break on relaxation. Only if either of the two finds a new, unbound partner within the cage volume [Fig. 1(e)] does the initial break contribute to relaxation and liquidity.

The effective relaxation time can be approximated as ${\tau }_{\text{rel}}=1/\left(\left(|p{k}_d|\right)\right)$, where $p$ is the probability that either domain finds a new partner instead of rebinding the former, i.e., $p\approx n/(1+n)$, where $n$ is the number of free domains in $v_{\text{cage}}$. Assuming that the local density of free domains in $v_{\text{cage}}$ is on average the same as in the whole system, we can then express $n=v_{\text{cage}}{c}_{\text{free}}$ in terms of the concentration $c_{\text{free}}=c_A+c_B$ of unbound domains in the system, where we denote by $c_A$ and $c_B$ the respective concentration of free domains of each type. We define the stoichiometry difference $\delta =c_A-c_B$ as the difference between these concentrations (which depends only on the overall composition, not on the fraction bound), and $c_{AB}$ as the concentration of bound domain pairs. We assume that the linkers are sufficiently flexible to consider the binding state of each domain of a protein as independent of the others, and thus treat the binding-unbinding process as a well-mixed solution. The dissociation equilibrium reads $K_d=c_A{c}_B/c_{AB}$, with $K_d$ the dissociation constant. We thus have $c_{\text{free}}=\sqrt{{\delta }^2+4K_d{c}_{AB}}$. The concentration of free domains thus exhibits a global minimum at $\delta =0$ [Fig. 1(f)].

We relate the dissociation constant to the Arrhenius factor for unbinding, writing $K_d=ϵ/v_0$ where $v_0$ is a molecular volume. Indeed, $K_d=k_d/k_a$ where the dissociation rate $k_d=ϵ/{\tau }_0$ is proportional to the Arrhenius factor, assuming that the association rate $k_a$ is independent of the binding strength. We can thus express the relaxation time as

$${\tau }_{\text{rel}}=\frac{{\tau }_0}{ϵ}\left(1+\frac{1}{v_{\text{cage }}\sqrt{{\delta }^2+4ϵc_{AB}/v_0}}\right).$$ (1)

When $n\ll 1$, i.e., for strong binding when there are few available partners within reach, the second term in Eq. (1) dominates the relaxation time. In particular, ${\tau }_{\text{rel}}$ exhibits a sharp maximum at $\delta =0$, whose magnitude scales as ${\tau }_{\text{rel}}\propto {ϵ}^{-3/2}$. This scaling reflects the probability of coincident dissociation events: neither of the two domain types is in excess with respect to the other, and so rebinding to a new partner is conditioned on finding another thermally activated unbound domain within $v_{\text{cage}}$. The concentrations of such unbound domains are $c_A=c_B=\sqrt{K_d{c}_{AB}}\propto {ϵ}^{1/2}$. In contrast, for $\delta \gg 1/v_{\text{cage}}$ such that $n\gg 1$, binding to a new partner is fast and essentially independent of $\delta$, so that ${\tau }_{\text{rel}}\propto {ϵ}^{-1}$. This scaling behavior is our central prediction, and is illustrated in Fig. 1(g).

We employ MD simulations to test our theoretical predictions for the relaxation time [Eq. (1)]. Specifically, we model the system schematized in Figs. 1(a) and 1(b) using a bead-spring representation, where only the binding domains are simulated explicitly [Fig. 2(a)]. Binding between complementary domains is modeled by a soft attractive potential minimized when the beads fully overlap, while strong repulsion between beads of the same type prevents the formation of multiple bonds involving the same domain (see Methods). The mean linker length between domains sets the unit of length, while the unit of time is chosen to be the average time it takes for a free domain to diffuse a unit length. We simulate only the dense phase of this phase-separating system [Fig. 2(b)]. The control parameters are the binding free energy $\mathrm{\Delta }F$ and the stoichiometric difference $\delta =c_A-c_B$, while the total concentration of domains $c_{\text{tot}}$ is held fixed. Simulations are performed using lammps [16,17] (see Methods).

FIG. 2.

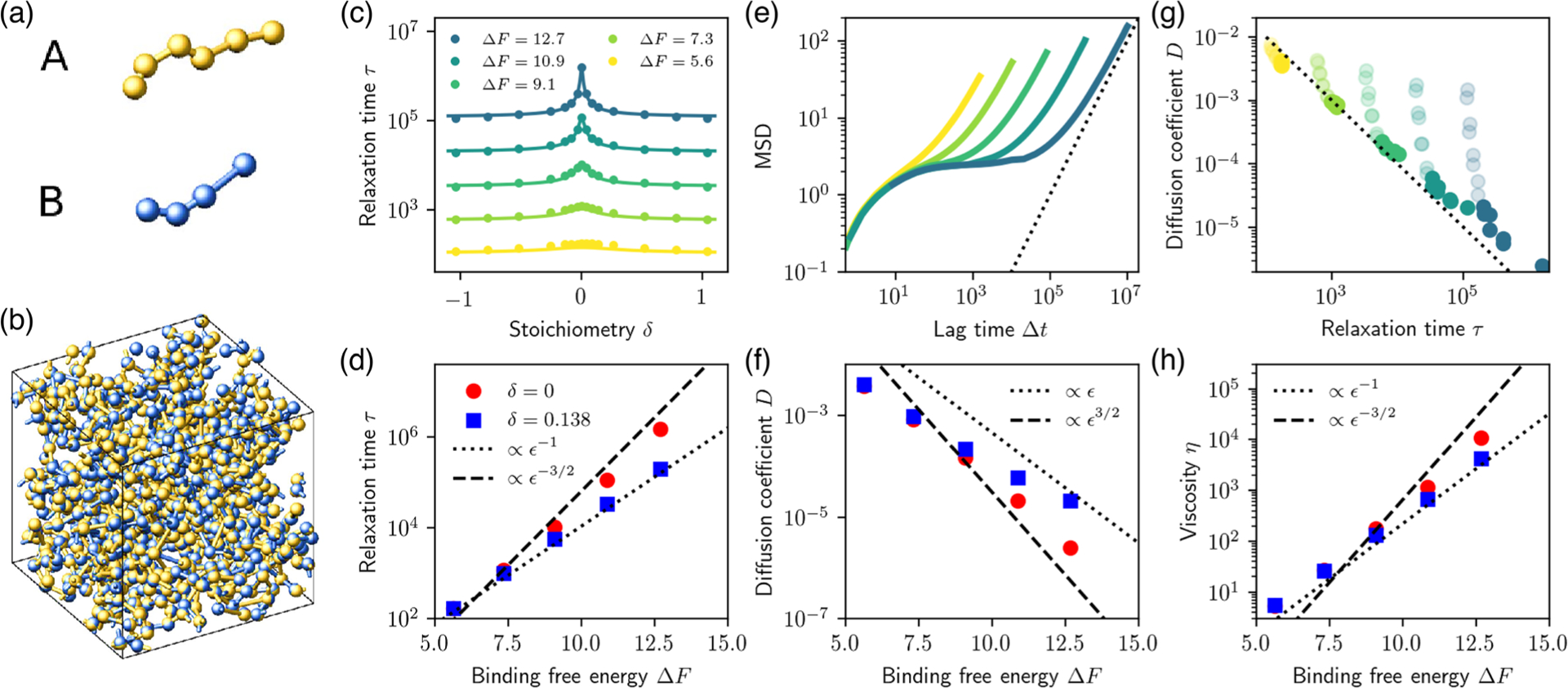
MD simulations reveal the importance of stoichiometry to the dynamical properties of the condensate. (a) MD model for the multivalent associative proteins. Colored spheres represent $A$ and $B$ domains. (b) Representative snapshot of the dense, network-forming liquid condensate. (c) Bond relaxation time (see text) as a function of stoichiometry for different binding strengths. Symbols indicate MD simulations; solid curves indicate theory [Eq. (1)] with $c_{AB}$ estimated assuming full binding of the minority domains and with fitted values $v_{\text{cage}}=11.4,\mathrm{ }{v}_0=0.4$, and ${\tau }_0=0.37$. (d) Bond relaxation time ${\tau }_{\text{rel}}$ as a function of binding strength is consistent with predicted scaling for both equal and unequal stoichiometries [Eq. (1), Fig. 1(g)]. (e) Mean squared displacement (MSD) of individual domains as a function of time reveals diffusive scaling (dashed line) at long times (here $\delta =0$). (f) Diffusion coefficient of the minority species as a function of binding strength at equal and unequal stoichiometry. (g) Longtime diffusion coefficient plotted against bond relaxation time, for all values of $\delta$ and $\mathrm{\Delta }F$. The dotted black line indicates $D\propto {\tau }_{\mathrm{r}\mathrm{e}\mathrm{l}}^{-1}$. Transparent circles correspond to systems where one component is in large excess, $\left|\delta \right|>0.2c_{\text{tot}}$. (h) Viscosity, obtained using the Green-Kubo relation, as a function of binding strength, reflects the scaling of the bond relaxation time (d).

We first study the relaxation of individual bonds. To quantify this relaxation, we compute the bond adjacency matrix $A_{ij}\left(t\right)$, where $A_{ij}\left(t\right)=1$ if at time $t$ the distance between the center of domains $i$ and $j$ is within the attractive interaction range $r_c$, and 0 otherwise. We first obtain the average autocorrelation function of this matrix, $C\left(\mathrm{\Delta }t\right)={⟨{\sum }_{i,j} A_{ij}\left(t\right)A_{ij}(t+\mathrm{\Delta }t)⟩}_t$, where the sum runs over all pairs of complementary domains, and then extract the bond relaxation time $\tau$ by integration of the normalized autocorrelation, $\tau ={\int }_0^{\mathrm{\infty }} C\left(\mathrm{\Delta }t\right)d\mathrm{\Delta }t/C\left(0\right)$. The resulting relaxation time $\tau$ is plotted in Fig. 2(c). These values are in good agreement with the theoretical prediction of Eq. (1), and in particular exhibit a clear maximum at equal stoichiometry $(\delta =0)$. The magnitude and sharpness of the peak increases with the binding free energy $\mathrm{\Delta }F$. Furthermore, we confirm in Fig. 2(d) that for strong enough binding $\tau$ scales as ${ϵ}^{-3/2}=\mathrm{e}\mathrm{x}\mathrm{p}(3\mathrm{\Delta }F/2)$ at equal stoichiometry, and as ${ϵ}^{-1}=\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{\Delta }F\right)$ at unequal stoichiometry. Thus, the relaxation time increases much faster with $\mathrm{\Delta }F$ at equal stoichiometry. For longer chains, the relaxation peak is strengthened as network caging is more efficient, while the peak disappears for monomers (see Supplemental Material [18]).

How does this sizable difference in relaxation times influence macroscopic condensed-phase properties such as diffusivity and viscosity? To answer these questions, we first monitor the mean squared displacement (MSD) of individual binding domains of the minority species as a function of lag time [Fig. 2(e)]. Several distinct regimes are apparent in the MSD: short times correspond to bond-level vibrations. At intermediate times, the plateau reveals caging of binding sites due to the well-bonded character of the network. Finally, the longtime scaling $\mathrm{M}\mathrm{S}\mathrm{D}\propto \mathrm{\Delta }t$ is diffusive, confirming that the system behaves as a liquid. We extract the longtime diffusion coefficient from these simulations, and find that its variations directly reflect those of the bond relaxation time over several orders of magnitude, with approximately $D\propto 1/\tau$ [Fig. 2(g)]. Indeed, the product $D\tau$ exhibits much smaller variations than either $D$ or $\tau$ (see Supplemental Material [18]). Thus, slow bond relaxation within the connected network dominates the diffusive properties of the system. Note that at large stoichiometry differences $\left[\left|\delta \right|>0.2c_{\text{tot}}\right.$, transparent symbols in Fig. 2(g)], the large number of unbound sites results in a loose network with possible disconnected clusters, and these scaling laws do not apply.

Turning to the viscosity $\eta$, which we measure using the Green-Kubo relation between viscosity and equilibrium stress fluctuations [19], we observe similarly that it reflects the variations of the bond relaxation time, with approximately $\eta \propto \tau$ [Fig. 2(h)]. The macroscopic transport properties of this binary liquid thus directly reflect the highly stoichiometry-dependent molecular relaxation mechanism (Fig. 1): in the strong-binding regime, the viscosity of the liquid noticeably increases near equal stoichiometry.

Our predictions for the dependence of bulk transport on the stoichiometry of the associative protein condensate have experimentally testable consequences. For instance, by preparing a homogeneous droplet and tagging all domains on one side by fluorescently bleaching them, one could measure the mixing dynamics as a function of composition. We simulate the relaxation of the composition profile for this case by putting in contact two simulation boxes [Figs. 3(a) and 3(b)]. We monitor the relaxation of the tagged composition difference between the two halves of the simulation box [Fig. 3(c)] and extract the relaxation time by exponentially fitting the decay curve [Fig. 3(d)]. Consistent with our equilibrium analysis, we find that mixing is substantially faster when one species is in excess [Fig. 3(d), squares] than when stoichiometry is balanced [Fig. 3(d), circles].

FIG. 3.

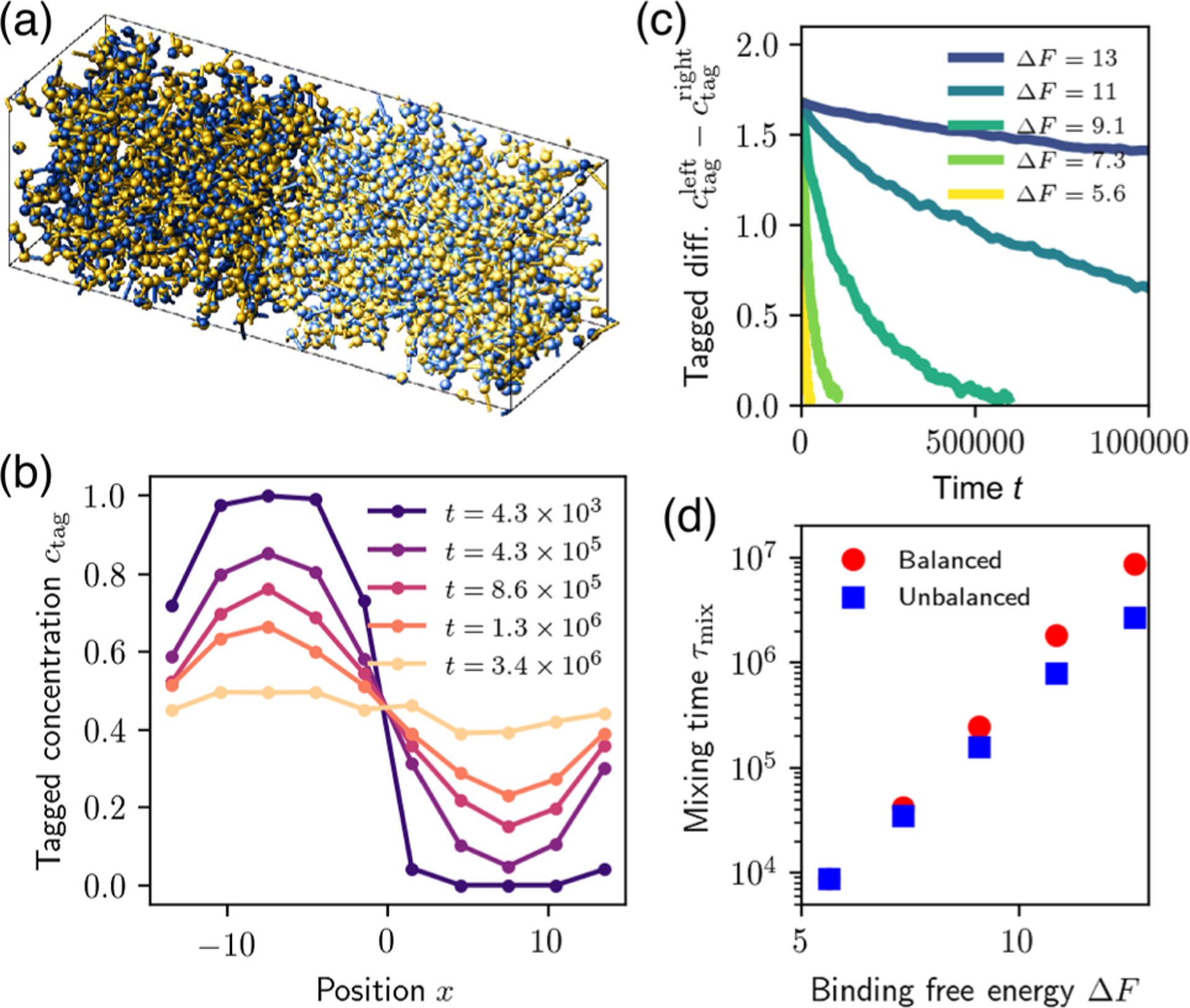
Composition controls mixing rate near equal stoichiometry. (a) Snapshot of an MD simulation with initially tagged particles on the left side of the box. (b) Normalized concentration profiles for tagged particles along the long axis at different times, for equal stoichiometry $\delta =0$, showing slow relaxation towards the homogeneous state. (c) Relaxation of the tagged concentration difference between the two half-boxes, for different binding free energies. (d) Equilibration time as a function of binding strength. The unbalanced case has $\delta =0.14$.

In this Letter, we investigated the dynamics of proteinrich condensates characterized by strong, specific interactions between complementary binding sites. Our theoretical analysis of the molecular-level relaxation mechanisms in these liquids suggests a strong composition dependence: near equal stoichiometry of complementary binding sites, the dynamics of the liquid dramatically slows down. This slowing is due to the lack of free binding sites at equal composition, which leads to a predominance of rebinding following bond breaks. We confirmed this mechanism through molecular dynamics simulations and showed that it controls the equilibrium diffusivity and viscosity of the liquid network.

The molecular-level connectivity relaxation of protein liquids through binding-unbinding events is generally not directly accessible in experiments. By contrast, our predictions for macroscopic transport quantities are readily testable, for instance using engineered protein condensates such as the SUMO-SIM [7] and SH3-PRM [20] systems. The reported dissociation constant of SUMO-SIM domains is $K_d\approx 10\mu \mathrm{M}$ [7], which for a binding domain of diameter 1 nm corresponds to a binding energy of $13k_{B}T$. Our simulations thus suggest a sizable tenfold decrease in diffusivity for such systems near equal stoichiometry. Our predictions would also hold in other liquids characterized by strong specific interactions, such as DNA nanoparticles [21]. In such systems, the effect of composition on diffusivity could be observed using fluorescence recovery after photobleaching [22] as in Fig. 3 or nanoparticle tracking [23], while our predictions for viscosity could be tested by passive or active microrheology [24], with predicted mixing dynamics also testable by monitoring the shape relaxation of merging droplets [25].

While the dynamics of protein condensates can be regulated by many factors, such as density [25,26], salt concentration, and the presence of RNA [27], our work highlights the possibility that cells can also fine-tune the mechanical and dynamical properties of their membraneless organelles through small changes in composition. Importantly, while in this study we have focused on the dense phase and used component stoichiometry as a control variable, in multicomponent phase-separated systems there is a subtle interplay between overall composition and dense-phase composition [7,28]. Beyond controlling the timescale of internal mixing and merging of droplets, stoichiometry-dependent slowing could also be involved in the recently characterized aging of viscosity [29] and could impact the exchange rates of “clients”—constituents of condensates that do not contribute directly to phase separation [3]. Overall, we have shown that high specificity liquids have unusual physical properties [30] and provide novel avenues that cells could use to regulate their phaseseparated bodies.

Methods.—

Molecular dynamics simulations are performed using the March 2020 version of lammps [16]. Proteins of types $A$ and $B$ are represented by bead-spring multimers with, respectively, six and four binding domains (chosen with different valency to avoid magic-number effects associated with the formation of stable dimers [6,8,9]). Simulations of Langevin dynamics are done using the standard lammps combination of commands “fix_nve” and “fix_langevin,” with energy normalized so that $k_{B}T=1$, mass of domain 1, and a damping parameter 0.5. Links between domains in a given protein are modeled as finite extensible nonlinear elastic bonds, with interaction potential $E\left(r\right)=-0.5K{R}_0^2\mathrm{l}\mathrm{o}\mathrm{g}\left[1-{\left(r/R_0\right)}^2\right]$ as a function of bond elongation $r$, with coefficients $K=3$ and $R_0=3$. Interaction between domains of the same type are given by a repulsive truncated Lennard-Jones potential, $E\left(r\right)=4\epsilon \left[(\sigma /r{)}^{12}-(\sigma /r{)}^6\right]$ with $\epsilon =1,\mathrm{ }\sigma =0.6$, and cutoff at $R=2^{1/6}\sigma$. The linker potential and the repulsion between neighboring domains lead to a mean linker length one which sets the unit of length. Binding between complementary domains occurs via a soft potential, $E\left(r\right)=A\left[1+\mathrm{c}\mathrm{o}\mathrm{s}\left(\pi r/r_c\right)\right]$ for $r<r_c$, with cutoff $r_c=0.3$. Energy is minimized when domains fully overlap, and Lennard-Jones repulsive interaction between domains of the same type ensured that binding is one-to-one. The interaction strength $A$ is related to the binding free energy by $\mathrm{\Delta }F=\mathrm{l}\mathrm{n}\left({\int }_0^{r_c} 4\pi r^2{e}^{-E\left(r\right)}dr/\left(4\pi r_c^3/3\right)\right)$. We set the average time it takes for an unbound domain to diffuse a unit length to be the unit of time, ${\tau }_0=1$. The simulation time step is $\delta t=0.005$. We simulate only the dense phase, with periodic boundary conditions (box size: ${10}^3$ for Fig. 2, $30\times 10\times 10$ for Fig. 3) and density typical of a demixed droplet with free surface. The total concentration $c_{\text{tot}}=1.73$ of domains is kept fixed while the stoichiometry $\delta$ is varied.

To ensure equilibration of the system, the attraction strength $A$ is annealed from zero to its final value over one bond relaxation time $\tau$. The system then evolves for another $4\tau$, prior to measurements performed over $10\tau$. In Fig. 2, measurements of $\tau ,\mathrm{ }\mathrm{M}\mathrm{S}\mathrm{D}$, and $D$ have $N=10$ repeats; measurements of $\eta$ have $N=100$ repeats. Statistical error bars are smaller than the symbol size. In Fig. 3, the system is initially annealed with walls separating the two halves of the system, with different labels for domains in either side. At $t=0$, the walls are removed and mixing starts.