Abstract
The interaction between cavitation bubbles and particles is essential for the operational performance many kinds of fluid machineries. In the present paper, jet dynamics and shock waves induced by the cavitation bubble collapsing near two spherical particles are numerically investigated based on OpenFOAM. The numerical scheme is validated by the experimental data obtained based on our high-speed camera cavitation system. Our results reveal that bubble split induced by annular jet is the primary feature during bubble collapsing with four typical cases defined. For the jet formation, the localized high pressure produced at the bubble split point is the main reason and the split point also serves as the source of the shock waves shown by the numerical schlieren. Furthermore, the nondimensional bubble-particle distance is the most paramount parameter influencing the jet phenomenon (e.g. jet velocity).
Keywords: Cavitation bubble dynamics, Particle-bubble interaction, Jet dynamics, Shock waves
1. Introduction
The interaction between cavitation bubbles and particles has a profound impact on the operational performance and safety of fluid machinery [1], [2], [3]. The interaction mechanisms between particles and cavitation bubbles are of great importance for the enhanced mechanical performance and safety of the fluid machinery [4], [5]. In the present paper, we employ an open source CFD package OpenFOAM [6] to simulate the behaviors of cavitation bubble between spherical particles.
OpenFOAM has been widely employed to study the dynamics of cavitation bubbles with a brief review given below. Koch et al. [7], [8] have developed a numerical model of gas bubble considering liquid compressibility to study the jet dynamics near a rigid wall and a solid cylinder, respectively. Yin et al. [9] considered the thermodynamic model for revealing the interaction of bubble pairs. In subsequent research [10], the phase-change model was further considered to investigate the dynamic behavior of the cavitation bubble during the rebound stage near the flat wall, and the jet dynamics during the rebound stage. Hence, OpenFOAM serves as a powerful tool for the investigation of the complex bubble phenomenon (especially the jet and shock wave dynamics).
The nondimensional distance between the cavitation bubble and the structures (e.g. rigid walls, particles, free surfaces, etc.) plays a crucial role in determining the bubble dynamics (e.g. shape of the bubble interface evolution). For a single rigid wall, as the distance between the bubble and the wall increases the bubble collapses from a non-spherical to a spherical shape [11]. Zhang et al. [12] developed a theoretical model to predict the bubble dynamics near different structures. For cavitation bubble dynamics near complex structures (free surface and rigid wall), Zhang et al. [13] found that the bubble splits into two toroidal bubbles during the late collapse stage near the free surface, as well as at some distance from the rigid wall. Previously, for cavitation bubble dynamics near particles, our group [14] experimentally investigated the effects of spherical particles on the laser-induced cavitation bubble. Based on various kinds of dynamics observed during the bubble collapse, three typical cases were identified together with criteria for the classification given: mushroom-shaped collapse, pear-shaped collapse, and spherical collapse. For the multiple particles, the phenomenon will be more complex with variations of the distances between the particles and the bubble [15]. Zhang et al. [16] shows that uneven pressure distributions around cavitation bubbles is one of the reasons for their non-spherical collapse. Li et al. [17] shows that the distance between the suspended sphere and the bubble affects the shape change of the bubble and founds that the sphere will be pushed away and attracted, respectively, during the growth and collapse of the bubble. Li et al. [18] further investigated the acceleration effect of bubble on the particle based on the boundary element method. Zheng et al. [19] found that the bubble experiences spherical collapse when the nondimensional distance of particle-movable particle is greater than 1. However, the jet and shock wave dynamics during collapsing process of cavitation bubble near multi-particles still requires further exploration.
Jet phenomenon during the non-spherical collapse of cavitation bubble near a wall has been extensively investigated by many researchers. When the cavitation bubble collapses near the wall, Bußmann et al. [20] showed three kinds of jet mechanisms (needle, mixed, and regular jets), corresponding to the nondimensional distances of 0–0.2, 0.2–0.24, and 0.24–0.9, respectively. Lechner et al. [21], [22] conducted a numerical investigation of the cavitation bubble dynamics near a rigid wall, and found that the jet velocity during the cavitation bubble collapse is about 100 m/s for a nondimensional distance of 0.24 to 3.0. Through experiments and simulations, Zhang et al. [23] found that when the nondimensional distance is between 1 and 3, the bubble forms a reflected jet in the rebound stage. And, the maximum height of the reflected jet increases first and then decreases with the increase of the nondimensional distances. Sun et al. [24] found that a rigid wall with a gas entrapping hole can change the direction of motion of the bubble and the jet morphology, thus effectively reducing cavitation on the wall surface. Li et al. [25], [26] found that cavitation bubble near the free surface and vertically rigid wall has four jet behaviors, namely, 'formally downward jet', 'annular collapse', 'horizontal jet' and 'weak jet'. For jet dynamics near a single particle, with the increase of the distance between the cavitation bubble and the particle, Zevnik and Dular [27] observed the transition of the jet from a fast, thin, annular shape to a spherical shape. For the experimental research, our group [15] conducted high-speed photography experiments to observe the growth and the collapse of cavitation bubble between two particles. However, due to the high velocity of the jet, it is still challenging to observe it entirely through experiments.
Shock waves generated by the bubble collapsing play an important role on the bubble-particle interactions [28]. Additionally, there exists a significant correlation between the shock waves and the jet. Johnsen and Colonius [29] discovered that a precursor wave precedes the water-hammer shock wave. Iloreta et al. [30] and Calvisi et al. [31] found that the impact of reflected shock waves could affect the growth and the subsequent collapse of cavitation bubbles near a rigid wall. Wen et al. [32] reported that the compressed liquid surrounding the bubble was the main reason for the shock wave generated during the collapse of the bubble. Yang et al. [33] found that the bubble collapse induces a re-entrant jet and a shock wave generated within the cavitation bubble refracting on the bubble inner wall. Tian et al. [34] numerically investigated the jet and shock waves generated by near-wall bubble. Based on the numerical schlieren method, which is also used to show the flow as well as the turbulent structure [35], [36], [37], when the jet impinges on the wall, the shear flow will tear the toroidal bubble and generate two toroidal shock waves. Zevnik and Dular [27] conducted a numerical study of a cavitation bubble near a rigid particle. They show that the shock wave generated by the collapse of the cavitation bubble initially hits the particle, generating a reflecting tensile pressure wave propagating in the liquid. The propagation of the shock wave observed by Geng et al. [38] at the beginning of the growth of the bubble can be divided into two regions, i.e., the sharp decay region and the non-decay region.
From literature review, the cavitation bubble dynamics near a single particle or rigid wall have been extensively studied. However, there is still limited understanding of the collapsing behavior, jet dynamics, and shock wave mechanisms (the generation and propagation of waves).
In the present paper, numerical and experimental research on the cavitation bubble dynamics near multiple particles are demonstrated with a focus on the jet and shock wave dynamics. The rest of the paper is organized as follows. Section 2 introduces the numerical method together with validations by our experimental results. Section 3 provides detailed discussions on the evolution of bubble shapes with four kinds of cases defined. Section 4 discusses the jet dynamics in terms of annular jet generations and jet velocities. Section 5 examines the generation and propagation of shock waves during the cavitation bubble collapse. Section 6 concludes our primary findings with a focus on the jet and shock wave dynamics.
2. Numerical method and validation
2.1. Numerical method
A compressible two-phase flow model was employed to simulate the bubble dynamics between two particles with Volume of Fluid (VOF) method for capturing the bubble interface. It was assumed that the bubble contains vapor without non-condensable gas. Due to the small size and short oscillation period of the bubble, the effect of gravity was neglected. During the multi-period oscillation process of the bubble, high temperature will be generated and mass transfer occurs [10]. Hence, our model considers both the thermodynamic and phase-change model.
The VOF model employs volume fraction (α) to describe the distribution of liquid (subscript l) and vapor (subscript v) in the fluid domain. Therefore, the continuity equation for the bubble-liquid system is:
| (1) |
where the density field , and are the densities of the liquid and vapor, respectively. and are the volume fraction of liquid and vapor, respectively. The velocity field , and are the velocity of liquid and vapor, respectively. is mass transfer rate.
The momentum equation is:
| (2) |
with
| (3) |
where, is pressure; is viscous stress tensor; dynamic viscosity . In this study, dynamic viscosity of liquid , dynamic viscosity of vapor , represents unit tensor. The surface tension acting on the liquid-vapor interface , where is surface tension coefficient, is obtained from the volume fraction by smoothing it over a finite region around the interface using Lafaurie filter. [39], [40].
In VOF, the volume fraction is solved with the transport equation [10], [41]:
| (4) |
where is the relative velocity between two phases and acts as an artificial compressible term, , ensuring a sharp interface [42].
The energy equation is [10]
| (5) |
where T is temperature; heat capacity of liquid and vapor and , respectively; and are the thermal conductivity of liquid and vapor, respectively. Kinematic energy .
A cavitation model is introduced to account for the vaporization and condensation effects during the growth and collapse stages of cavitation bubble. The Schnerr-Sauer cavitation model [43] is derived based on the Rayleigh-Plesset equation [44] of classical cavitation dynamics. It has been analyzed and verified in the non-spherical collapse of cavitation bubble [10], [45], [46]. In Appendix A, we compared the Schnerr-Sauer [43] and Kunz [47] cavitation model, demonstrating minor discrepancies. Hence, we ultimately choose the Schnerr-Sauer model for the present research. In the Schnerr-Sauer cavitation model, condensation rate and evaporation rate are given as:
| (6) |
where, the cavitation nuclei radius is expressed as:
| (7) |
where is the number of nuclei per cubic meter. Volume fraction of the nucleation site expressed as:
| (8) |
where is the nucleation site diameter.
In order to close the equations, the equations of state (EOS) of liquid and vapor are introduced. It is assumed that the vapor is an ideal gas, and the EOS expressed as:
| (9) |
where Rv denotes the vapor constant.
The liquid is assumed to be an ideal liquid, and the EOS is:
| (10) |
when T = 0, the density of the liquid in this study, is the liquid constant.
2.2. Numerical implementation
In the simulation, numerical scheme for time related terms is solved by a first-order bounded implicit Euler scheme. And, the pressure and velocity gradient terms were solved using Gauss linear scheme and the convection terms are solved a second-order Gaussian TVD scheme. The Laplacian terms are solved by Gauss linear with linear corrected and a corrected surface normal gradient schemes are employed.
Stabilized preconditioned bi-conjugate gradient solver (PBiCGStab) with diagonal incomplete LU (DILU) was employed for the matrix solver of pressure, velocity, temperature, and volume fractions. For solving the velocity-pressure coupling, the pressure implicit with splitting of operator (PISO) algorithm was employed. The convergence residual for pressure, velocity, temperature, and volume fractions were set as .
2.3. Experimental set-up
To verify the numerical model mentioned above, high-speed photography experiments of laser-induced cavitation bubble between two spherical particles were conducted. For the purpose of position control, the spherical particles were fixed on the tip of two needles, which were connected to a three-dimensional displacement platform. A digital delay generator was used to control the laser generator to produce a cavitation bubble near the two particles. At the same time, the delay generator simultaneously controls the high-speed camera to capture photographs of the dynamic oscillations of the cavitation bubble. For more details of the experimental system, readers can refer to our previously published paper [15].
2.4. Validations
2.4.1. Validation via the laser-induced bubble experiment near two particles
Fig. 1 shows the schematic representation of computation domain for cavitation bubble located near two particles (a) and the illustration of the mesh with local mesh refinement (b). Fig. 1(a) shows the computational domain, with the left side representing the entire domain and the right side presenting a local magnification around the double particles along with description of parameters. The simulation was based on a 5° wedge (bule region in Fig. 1(a)) axisymmetric model, with the Y-axis as the axis of symmetry. And, Rp and Rmax represent the particle radius and the maximum bubble radius. Here, for the simplicity, two particles are of the same size. The distance between the particle and the bubble center is represented as l. The bubble center was situated at the origin of the coordinate. To ensure that the quality of the numerical simulations, the boundary of the computational domain was set to be 60Rmax. For accurate capture of the liquid-vapor interface, a localized refinement was implemented in the region surrounding the bubble. Specifically, a circular refinement region with a center at origin and a radius of 4Rmax was selected, as indicated by the blue auxiliary lines in Fig. 1(a). Furthermore, we quantified the level of refinement in terms of the distance between adjacent nodes along line 1 in Fig. 1(a), which served as a baseline for defining the mesh size. For convenience of analysis, several dimensionless parameters are defined as follows:
| (11) |
| (12) |
| (13) |
where denotes the nondimensional distance between the particle surface and the bubble center. denotes the ratio of the particle radius to the maximum radius of the bubble. In addition, the particle radius in this paper is 1.5 mm. is the nondimensional time. is the time when the bubble reaches its minimum volume in the first period.
Fig. 1.
The schematic representation of computation domain for cavitation bubble located in the middle of two particles (a) and 2D illustration of the mesh with local mesh refinement (b).
The initial moment of laser-induced cavitation bubble is with high temperature and high pressure, leading to a rapid growth of the bubble [10]. Therefore, during simulation, the initial bubble radius (Rini) is 0.2 mm, with an initial temperature and pressure inside the bubble of 593.8 K and 50.7 MPa, respectively. The liquid temperature is 300 K, with a pressure of 101325 Pa. The velocity inside and outside of the bubble is assumed to be still. An adaptive local time-stepping with a maximum Courant number of 0.3 was employed for all simulations.
In the simulation, the particle surface is considered as a wall. Therefore, the boundary conditions for the pressure and velocity of the particle surface are fixed pressure flux and no slip, respectively, and the temperature and volume fraction are zero gradient, respectively. The boundary conditions for velocity, temperature and volume fraction at the outlet are zero gradient, and the pressure is the wave transmissive outflow condition. If not specified, all simulation results in this paper use the above initial and boundary conditions. For mesh independence and model validation, the experimental results for γ = 0.908, η = 0.938, Rmax = 1.60 mm were used.
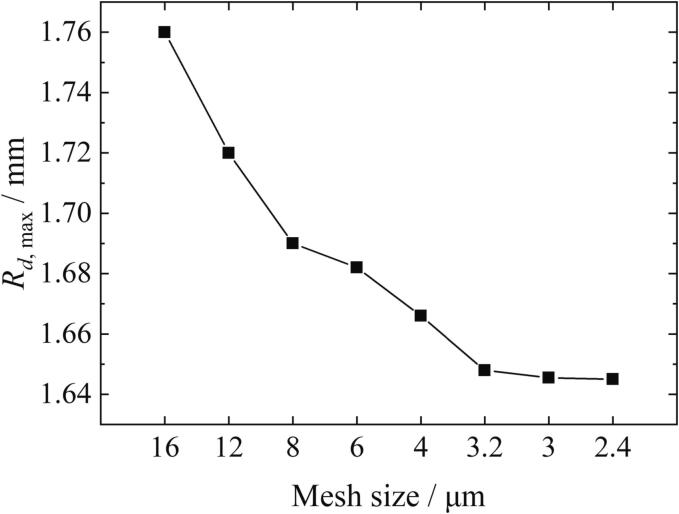
Fig. 2 shows the simulation results for eight different mesh sizes. Rd, max denotes the distance between the intersection of the bubble wall with the Y = 0 plane and the bubble center when the bubble reaches its maximum volume. Since l < Rmax, the particles limit the development of the bubble in the vertical direction and the bubble will develop farther in the horizontal direction. Therefore, Rd, max > Rmax. When the mesh size reaches 3 μm, continuing to reduce the mesh size has little effects on the simulation results, but it will significantly increase the computational cost. Therefore, this paper chooses 3 μm as the mesh size.
Fig. 2.
The mesh-independence for different mesh sizes. The mesh size is defined as the distance between two adjacent nodes on line 1 in Fig. 1. γ = 0.908, η = 0.938, Rmax = 1.60 mm.
Fig. 3 illustrates a comparison between the simulated and experimental bubble shapes at different time. The accuracy of the numerical model in reproducing the evolution process of the bubble shape with time in the experiment is quite evident. Additionally, Fig. 4 presents the variation of Rd with time in the first period, and Rd represents the distance between the intersection point of the bubble wall and the Y = 0 plane and the bubble center. Clearly, the numerical model can accurately predict the size and shape variations of the cavitation bubble observed in the experiment.
Fig. 3.
Comparison of bubble shapes between the present numerical results (top) and experimental results (bottom). Red, blue and gray in the numerical results indicate liquid, bubble and particles, respectively. γ = 0.908, η = 0.938, Rmax = 1.60 mm.
Fig. 4.
Comparison between simulations and experimental results of the variation of Rd with time. The simulation results are recorded every microsecond, resulting in a total of 330 data. γ = 0.908, η = 0.938, Rmax = 1.60 mm.
2.4.2. Validation via the theoretical results of bubble dynamics near a wall
In this section, results of bubble dynamics for numerical and theoretical model near a solid wall are compared. A theoretical model [12] that considered fluid compressibility, internal pressures of the bubble, surface tension, and viscosity was used to calculate the radius variation of the bubble near a solid wall.
According to the Ref. [12], the bubble is located at a distance of d = 2.02Rmax (Rmax = 0.768 mm) from the solid wall. Fig. 5 illustrates the computational domain (60Rmax × 60Rmax) and mesh configuration used for the numerical simulation. The region (4Rmax × 4.5Rmax) near the bubble with the minimum mesh of 3 µm is refined for better capturing the cavitation bubble motion. The initial pressure inside the bubble is 4 MPa, and the other boundary conditions and initial conditions are the same as in Section 2.4.1.
Fig. 5.
The computational domain and mesh configuration.
Fig. 6 compares the results of the present simulation with the theoretical and experimental results from the literature data in Ref. [12]. During the first period, the variation of bubble radius predicted by the present numerical model is in good agreement with the theoretical and experimental results. During the rebound phase, the numerical model does not take into account the non-condensable gas inside the bubble and therefore underestimates the radius variation.
Fig. 6.
Comparison of the present simulated bubble radius over time with literature data in Ref. [12].
3. Bubble dynamics
3.1. Temporal evolutions of bubble shapes
This section examines the impact of the nondimensional particle-bubble distance on the evolution of the bubble shape. The shape evolution of cavitation bubble during the first period can be categorized into four cases with details given as follows.
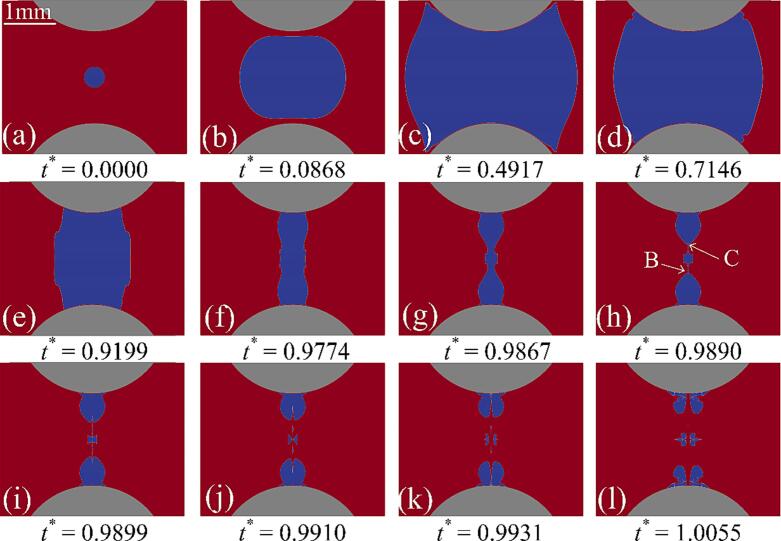
Fig. 7 illustrates the temporal evolution of the bubble shape for Case 1 (γ = 0.502, η = 0.938 was chosen as a representative result). Initially, the pressure inside the bubble exceeds that of the surrounding liquid, causing the bubble to expand. As shown in Fig. 7(b), the presence of particles at the top and bottom of the bubble limits its expansion and forces the bubble to expand laterally. In Fig. 7(c), the bubble reaches maximum volume. As shown in Fig. 7(d), at the onset of the collapse, necks appear at the top and bottom of the bubble near the particles. Fig. 7(d – f) indicate that the necks shrink at a faster rate than the rest of the bubble. The intersection of the necks leads to the split of the bubble into a toroidal sub-bubble enclosing a cylindrical one, as depicted in Fig. 7(g). The toroidal sub-bubble collapses and disappears shortly, while at the equatorial position of the remaining bubble, a depression appears and evolves into an annular jet. Fig. 8 shows the detailed process of cavitation bubble split by the necks and the generation of annular jet with the split point marked as A. in Fig. 7(h), the annular jet moves towards the bubble center and, meets at the bubble center, ultimately splits the bubble into two sub-bubbles (an upper and a lower bubble). Following this process, sub-bubble jets appear in the opposite directions, each pointing towards the nearest particles. In Fig. 7(k), the jet eventually reaches the surface of the particle.
Fig. 7.
Temporal evolution of the bubble shapes for case 1 during the first period. Red, blue and gray indicate liquid, bubble and particles, respectively. γ = 0.502, η = 0.938, Rmax = 1.60 mm.
Fig. 8.
Detailed demonstrations of the process shown Fig. 7(g). Red and blue indicate liquid and bubble, respectively. A indicates the position of the bubble split by the necks.
Fig. 9 shows the change of bubble shape with time for Case 2 (γ = 0.564, η = 0.938 was chosen as a representative result). The growth stage (Fig. 9(a – c)) and early collapse phase (Fig. 9(d and e)) exhibit a similar evolution of bubble shape over time as observed in Fig. 7 at γ = 0.502. However, in Fig. 9(h), during the subsequent collapse, the upper and lower necks of the bubble split the bubble into three sub-bubbles (upper, middle, and lower ones) at locations B and C along the axis of symmetry. After the bubble was split, directional jets were observed in both upper and lower sub-bubble. In Fig. 9(k), the sub-bubbles were penetrated by the jets, ultimately reaching the particles' surface by Fig. 9(l). Furthermore, as depicted in Fig. 9(j), following the splitting of the bubble, two opposing jets originate from the top and bottom tips of the middle-bubble, directed towards its center. Subsequently, the jets penetrate the middle-bubble, resulting in the formation of an outward-expanding annular jet. In Fig. 9(k), the middle-bubble reaches its minimum volume, priors to the upper and lower sub-bubble, before subsequently rebounding.
Fig. 9.
Temporal evolution of the bubble shape for Case 2 during the first period. Red, blue and gray indicate liquid, bubble and particles, respectively. In subfigure h, locations B and C lie on the symmetry axis and represent the points where bubble split. γ = 0.564, η = 0.938, Rmax = 1.60 mm.
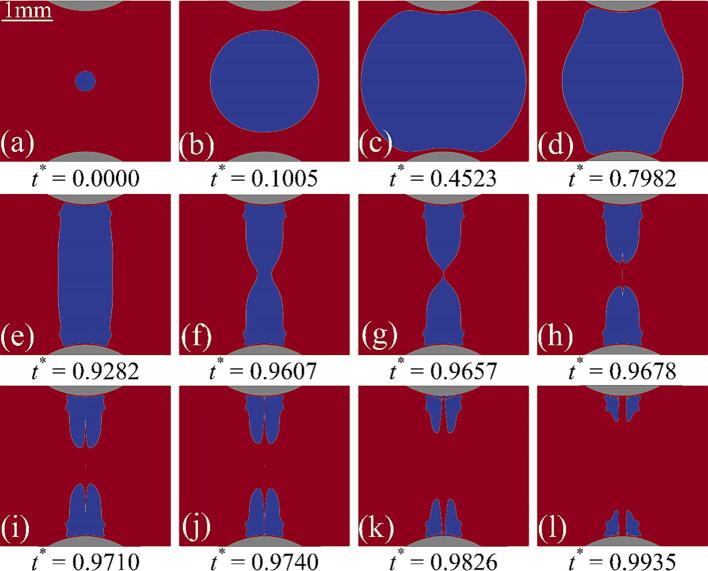
Fig. 10 illustrates the evolution of the bubble shape as a function of time for Case 3 (γ = 0.878, η = 0.938 was chosen as a representative result). From Fig. 10(a – c), the bubble undergoes a growth phase. Even though the bubble is under the influence of the particles, the increase in distance between the bubble and the particles results in a shape that differs from that of Fig. 7, Fig. 9. When the bubble begins to collapse, it does not exhibit the necks seen in Fig. 7, Fig. 9. In Fig. 10(e), the spherical bubble transforms into a cylindrical shape, and subsequently undergoes a central depression resulting in an annular jet as depicted in Fig. 10(f). In Fig. 10(g), the annular jet intersects at the center of the bubble, causing it to be split into upper and lower sub-bubble, and producing two opposite jets pointing towards the nearest particles, respectively. As illustrated in Fig. 10(j), the jets continue towards the particles until they reach it, penetrating the upper and lower sub-bubble, respectively. Ultimately, the bubble reaches its minimum volume, as illustrated in Fig. 10(l).
Fig. 10.
Temporal evolution of the bubble shape for Case 3 during the first period. Red, blue and gray indicate liquid, bubble and particles, respectively. γ = 0.878, η = 0.938, Rmax = 1.60 mm.
Fig. 11 presents the temporal evolution of bubble shape under the condition of Case 4 (γ = 1.066, η = 0.938 was chosen as a representative result). In this case, the distance between the particles and the bubble is slightly larger than Rmax. As illustrated in Fig. 11(c), the bubble grows to its maximum volume with a liquid film between the bubble and the particle, and the thickness of the liquid film is greater than the cases 1–3. From Fig. 11(c – d), the upper and lower ends of the bubble continue to move towards the particles while the middle part has begun to shrink. In Fig. 11(e), the middle of the bubble has experienced significant shrinkage, while the upper and lower portions have only contracted a short distance towards the center. In Fig. 11(f), an annular jet emerges in the middle, and the reflected jets towards the center of the bubble. As shown in Fig. 11(g), the annular jet intersects the center of the bubble and splits it into two sub-bubbles, which subsequently produce jet towards the particles. Ultimately, in Fig. 11(i), the jets and the reflected jets converge and penetrate the bubbles.
Fig. 11.
Temporal evolution of the bubble shape for Case 4 during the first period. Red, blue and gray indicate liquid, bubble and particles, respectively. γ = 1.066, η = 0.938, Rmax = 1.60 mm.
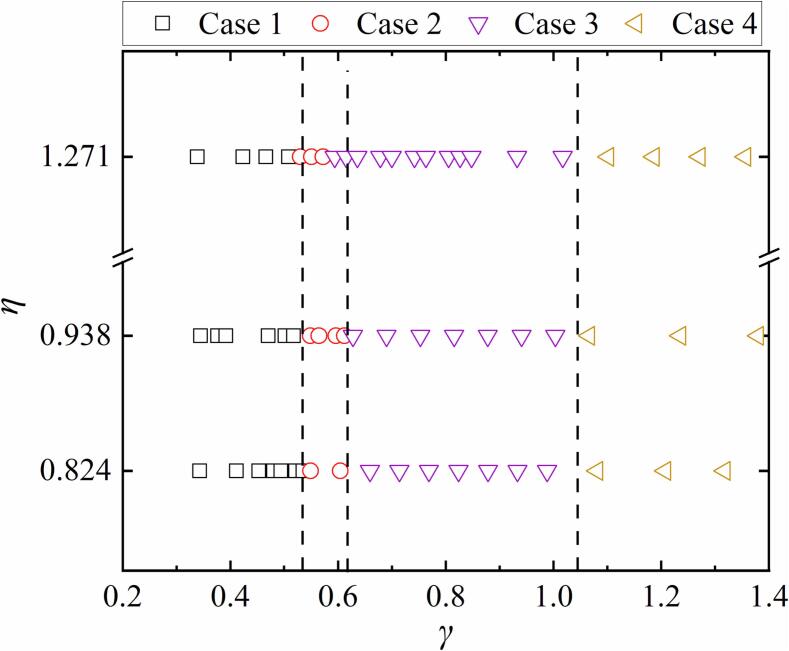
Fig. 12 shows the categorization of bubble collapse behaviors. The study identified four cases: Case 1, which occurred within 0.3< γ <0.515; Case 2 within 0.515< γ <0.605; Case 3 within 0.601 < γ < 1.02; Case 4 within 1.02< γ <1.40. When γ >1.4, bubble collapses in a spherical shape and no jet appears during the collapse.
Fig. 12.
Categorization of four cases of the evolution of bubble shape in terms of γ and three . The marked three black dashed lines indicate the critical values that distinguish the bubble collapse dynamics into four cases.
3.2. Evolution mechanism of bubble shapes
To gain a deeper comprehension of the collapse dynamic of cavitation bubble between two particles, the collapse mechanism is analyzed through studying the pressure and velocity distribution in the region surrounding the bubble during its collapse stage.
Fig. 13 displays the pressure and velocity fields near the bubble during its collapse stage for Case 1. In Fig. 13(a), the local high-pressure regions appear near the upper and lower ends of the bubble during the initial collapse stage, marked by a red circle. The high pressure in this region is the main reason for neck appearances. As the bubble shrinks, the necks still shrink at high speed. As shown in Fig. 13(d), at the same time, the pressure at the necks is higher than other positions, leading to a small part of the bubble being split. Fig. 13(e) illustrates the formation of a pressure wave resulting from the bubble split. The propagation of the wave is discernible from Fig. 13(e – h). More discussions about the emergence and propagation of pressure waves or shock waves are discussed in Section 5.
Fig. 13.
Pressure field (left of each subfigure) and velocity field (right of each subfigure) for Case 1. White areas in velocity field belong to the bubble. Black lines indicate the bubble walls, and vector arrows indicates the size and direction of the flow velocity. γ = 0.502, η = 0.938, Rmax = 1.60 mm.
Fig. 14 displays amplified views of the pressure and velocity fields surrounding the cavitation bubble depicted in Fig. 13(g – l). The local high pressure resulting from the bubble splitting accelerates the middle part of bubble to the center, forming an annular jet. In Fig. 14(b), the bubble was split into two sub-bubbles by the annular jet, creating a high-pressure region at the splitting position. Such pressure causes the upper and lower sub-bubble to produce directional jets towards the particles, with a liquid velocity as high as 418.4 m/s. As the upper and lower sub-bubble collapse towards the particles, the pressure and velocity near the directional jet gradually decrease. From Fig. 14(e – f), the jet continuously hit the particle surface, causing the pressure on the surface to be as high as 77971.5 KPa.
Fig. 14.
Zoom-in details of Fig. 11(g) ∼ (l).
Fig. 15 shows the pressure and velocity distribution during the first period of bubble collapse for Case 2. In Fig. 15(a), the velocity vector lines reveal an interesting phenomenon where liquid near the middle of the bubble flow towards the bubble and causes it to shrink inward, while the liquid near the particles continues to flow outside the bubble. As progresses, the velocity of the liquid near the necks, formed by local high pressure, becomes slightly higher than the velocity at other positions. In Fig. 15(b – d), a high-pressure area becomes noticeable near the middle of the bubble.
Fig. 15.
Pressure field (left of each subfigure) and velocity field (right of each subfigure) for Case 2. White areas in velocity field belong to the bubble. Black lines indicate the bubble walls, and vector arrows indicates the size and direction of the flow velocity. γ = 0.564, η = 0.938, Rmax = 1.60 mm.
Fig. 16 shows localized features of Fig. 13(d – i) to offer a clearer understanding of the field around the cavitation bubble. In Fig. 16(a) the pressure distribution inside the bubble is noticeably uneven, with substantially higher pressure noticed in the center than in the upper and lower sections. In Fig. 16(b), the bubble splits into three parts as a result of the uneven pressure distribution, creating localized high-pressure areas where the bubble split. The upper and lower high-pressure areas cause the bubbles to form jet pointing to the particles. At the same time, the two high-pressure regions lead to opposing jets at the upper and lower of the middle-bubble. Finally, after penetrating the middle-bubble, the opposing jets produce annular jets that point towards the outside of the middle-bubble. In Fig. 16(e), according to the velocity vector lines, the liquid around the bubble flows towards the exterior of the bubble, indicating that the middle-bubble has entered the rebound stage. Furthermore, in Fig. 16(c), the shock waves generated from the centers of the two high-pressure aeras are visible, and the propagation and interference process that is easily observable in Fig. 16(c – f).
Fig. 16.
Zoom-in details of Fig. 13 (d) ∼ (i).
Fig. 17 depicts the pressure and velocity distribution of the bubble first period collapse stage for Case 3. In Fig. 17(a), the bubble grows in the upper and lower parts while the middle part begins its collapse. In Fig. 17(b), the pressure in the middle of the bubble becomes higher than that on the upper and lower sides, therefore the middle part of the bubble collapses at the fastest speed. In Fig. 17(c), a clear high-pressure region emerges near the middle of the bubble. And in Fig. 17(d), the pressure increases further, and a detectable depression in the middle is formed (e.g. annular jet). The annular jet reaches the center of the bubble, leading to liquid pressure and velocity with values of 56321.1 KPa and 184.3 m/s, respectively. The high-pressure liquid splits the bubble into upper and lower sub-bubble, and drives the two sub-bubbles to produce jets. At the same time, the splitting of the bubble generates a shock wave.
Fig. 17.
Pressure field (left of each subfigure) and velocity field (right of each subfigure) for Case 3. White areas in velocity field belong to the bubble. Black lines indicate the bubble walls, and vector arrows indicates the size and direction of the flow velocity. γ = 0.878, η = 0.938, Rmax = 1.60 mm.
Fig. 18 illustrates the pressure and velocity distribution during the first period collapse process for Case 4. The middle of bubble collapse process shares similarities with that of Fig. 17. In Fig. 16(c), the pressure at the upper and lower ends of the bubble is higher than the surrounding liquid's pressure. As a result, the upper and lower ends collapse towards the center of the bubble. From Fig. 18(c – d), the liquid pressure around the upper and lower ends continues to increase, leading to the formation of an inward concave reflected jets. In Fig. 18(h), the jet combines with the reflected jet to puncture the upper and lower sub-bubbles. Subsequently, the jet drives some little sub-bubbles toward the particles, and impacts the particle surface.
Fig. 18.
Pressure field (left of each subfigure) and velocity field (right of each subfigure) for Case 4. White areas in velocity field belong to the bubble. Black lines indicate the bubble walls, and vector arrows indicates the size and direction of the flow velocity. γ = 1.066, η = 0.938, Rmax = 1.60 mm.
4. Jet dynamics
Fig. 19 shows the contraction velocity in the middle of the bubble for cases 1 to 4 with respect to nondimensional time. When 0.5< t* <0.95, the bubble shrinkage velocity exhibits a consistent pattern (e.g. gradually increases over time) across the four cases.
Fig. 19.
Shrinkage velocity of the middle of the bubble with time for four cases. γ = 0.502, 0.564, 0.878 and 1.066, η = 0.938 were selected as representative results for Cases 1–4, respectively. v indicates the contraction velocity in the middle of the bubble. P1–P4 correspond to (a), (c), (d) and (g) in Fig. 6, respectively.
For case 1 (e.g. γ = 0.502, η = 0.938), as the bubble necks approaches the Y = 0 plane, the shrinkage of the bubble in that collapse direction is inhibited, causing the velocity to peak for the first time at point P1 (corresponds to Fig. 8(a)). When the upper and lower necks intersect, the contraction velocity of the toroidal bubble reaches a minimum, signifying the point P2 in Fig. 19 (corresponds to Fig. 8(c)). Subsequently, an annular jet (P3 point in Fig. 19, corresponds to Fig. 8(d)) develops, with the annular jet velocity reaching 139.796 m/s, which is 3.12 times than point P1. Initially, the velocity of the annular jet decreases gradually and reaches its lowest value at point P4 (corresponds to Fig. 8(g)). Afterward, it starts increasing gradually, and the velocity at the end of the annular jet is 129.465 m/s. For Case 2 (e.g. γ = 0.564, η = 0.938), the necks split the bubble into three parts on the axis of symmetry, with the small pressure difference between the inside and outside of the middle bubble, thereby decreasing the growth of the shrinkage velocity. For Case 3 (e.g. γ = 0.878, η = 0.938) and Case 4 (e.g. γ = 1.066, η = 0.938) show similar collapse process. The contraction velocity of the bubble increased sharply, reaching 134.335 m/s and 114.237 m/s, respectively.
Fig. 20 depicts the annular jet velocities corresponding to different γ at three Rmax. For Case 1, as γ increases, the velocity of the annular jet gradually increases. However, for Case 2, the velocity is the smallest, the main reason is the small pressure difference between the inside and outside of the middle bubble. As γ increases, the velocity of the annular jet gradually increases. When γ is approximately 0.95, the annular jet velocity reaches its maximum, and then decreases.
Fig. 20.
Annular jet velocity as function of γ at three . The corresponding γ ranges for the Cases 1–4 are labeled at the top.
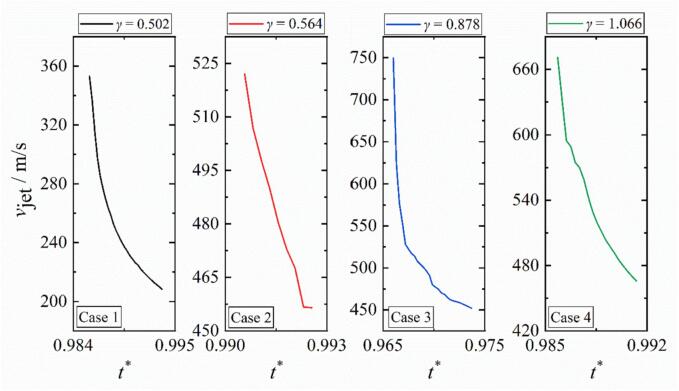
Fig. 21 illustrates the variation of jet velocity with time for Cases 1–4. For all cases, the velocity variation of the jet exhibits similar tendencies, beginning with a high velocity and gradually decreasing. This phenomenon is attributed to the high pressure at the location of the jet, which provides it with significant kinetic energy. However, as the cavitation bubble collapses, the pressure differential between the inside and outside of the cavitation bubble reduces, which causes a consistent decrease of jet velocities.
Fig. 21.
Jet velocity with time for four cases. γ = 0.502, 0.564, 0.878 and 1.066, η = 0.938 were selected as representative results for Cases 1–4.
Fig. 22 quantitatively analyzes the jet dynamics for the four cases through the nondimensional jet impact volume (V*=Vjet/Vmax), the nondimensional jet impact time difference (∇t*=(tjet-tc)/tc) and the jet impact velocity vjet. Where tjet, Vjet and vjet represent the time, bubble volume and jet velocity when the jet penetrates the bubble.
Fig. 22.
The variation of nondimensional quantities with γ when the jet penetrates the cavitation bubble. The corresponding γ ranges for the Cases 1–4 are labeled at the bottom.
The variations of V* and ∇t* exhibit similar changes with increasing γ. In both Case 1 and Case 2, V* decrease gradually with increasing γ, indicating an intensification of the collapse of the bubble. The decrease of ∇t* indicate that the time difference between jets impact and bubble collapse diminishes. Especially, when 0.5< γ <0.6, ∇t* < 0.01, the jet impingement and bubble collapse occur almost simultaneously. In Case 1, the annular jet compresses the bubble to a greater extent, therefore the jet velocity gradually decreases and reaches the minimum value at γ ≈ 0.5.
In Case 3 and Case 4, the distance between the particles and the bubble increases, providing more time for the jet development. Therefore, V* and ∇t* continuously increase and reach their maximal values at γ ≈ 0.82. Continuously increasing γ, the influence of particles on the bubble becomes weaker. Hence, V* and ∇t* gradually decrease. The effect of γ on the jet velocity is relatively small in Case 3 and Case 4.
5. Shock waves
This section employs the numerical schlieren method to analyze the process of shock wave emergence and propagation. The schlieren value is calculated using the expression exp(−k|∇ρ|/max(|∇ρ|)) [36], where k is an adjustable parameter.
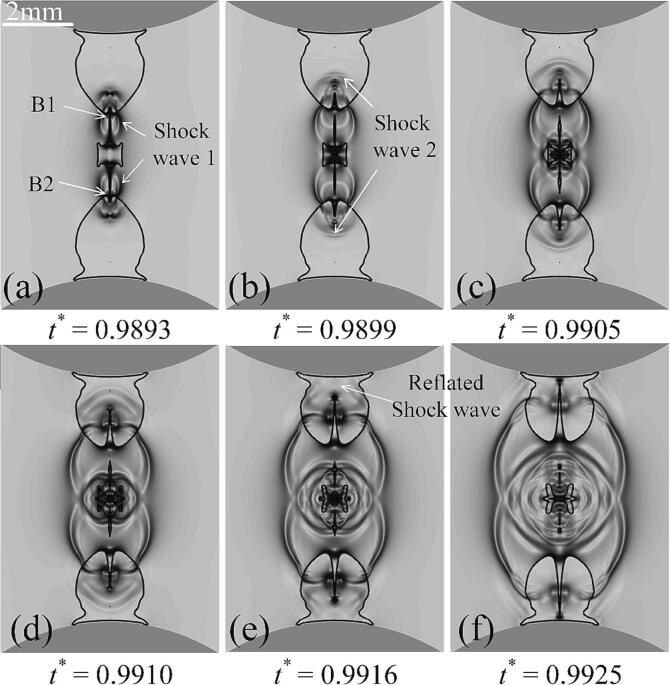
Fig. 23 presents the numerical schlieren resulting from the interaction between bubble and particles for Case 1. In Fig. 23(a), Shock wave 1, is located outside the bubble, while Shock wave 2 is positioned inside it. Due to the axisymmetric of the model, shock waves 1 and 2 are shape as “annular shock wave”. According to Fig. 14, we infer that Shock wave 1 caused by the necks splitting the bubble. Specifically, split point is the wave source of Shock wave 1. In Fig. 23(c), Shock wave 2 reflects near the annular jet's tail and interferes near location A. In addition, the collapse of toroidal bubbles induces the generation of Shock wave 3. In Fig. 23(d), the reflected wave becomes visible, along with the propagating waves after interference. Fig. 23(f) illustrates the shock wave generated due to bubble splitting, and Shock wave 5 generated at the front of the jets. Fig. 23(f) ∼ (i) clearly shows the propagation of the Shock wave 5 inside the bubble and its reflection by the particles.
Fig. 23.
The emergence, propagation and interaction of shock waves for Case 1 obtained by numerical schlieren. Black lines indicate the bubble walls. γ = 0.502, η = 0.938, Rmax = 1.60 mm.
Fig. 24 depicts the numerical schlieren of the bubble-particles interaction for Case 2. In Fig. 24(a), the upper and lower necks split the bubble into three sub-bubbles at B1 and B2, giving rise to two shock waves with the same properties and are identified as Shock wave 1. In Fig. 24(b), Shock wave 2, caused by the upper and lower sub-bubble, propagates in the direction of the particles, and reflects on the particles surface before jets reached. In Fig. 24(e), we can clearly observe the reflected wave of Shock wave 2. As the middle-bubble is continuously punctured by the jet, shock waves generation is clearly observed from Fig. 24(c – e). Furthermore, shock waves produced by the collapse of the middle-bubble and the Shock wave 2 have complex interference.
Fig. 24.
The emergence, propagation and interaction of shock waves for Case 2 obtained by numerical schlieren. Black lines indicate the bubble walls. γ = 0.564, η = 0.938, Rmax = 1.60 mm.
Fig. 25 illustrates the shock waves for Case 3 obtained by numerical schlieren. In Fig. 25(a), Shock wave 1 generated at the splitting point due to cavitation bubble split by the annular jet. At the same time, the jet induces a Shock wave 2 inside the cavitation bubble and propagates in the direction of the particles. In Fig. 25(g), Shock wave 2 reaches the particle surface and is subsequently reflected. As shown in Fig. 25(h), the reflected wave reflected wave passes through the jet. And a series of shock waves are generated when the jet impacts the particles.
Fig. 25.
The emergence, propagation and interaction of shock waves for Case 3 obtained by numerical schlieren. Black lines indicate the bubble walls. γ = 0.878, η = 0.938, Rmax = 1.60 mm.
Fig. 26 illustrates the shock waves for Case 4 obtained by numerical schlieren. Similar to Fig. 26, shock waves appear at the position of bubble splitting and at the front of the jet of sub-bubbles. However, no shock waves appear at the front of the reflected jet. Fig. 26(c) indicate that Shock wave 2 arrives at the tip of the reflected jets before the jets does. When the jet penetrates the sub-bubbles, a precursor wave appears in the front of the penetrating location. In Fig. 26(f), a water-hammer shock wave is produced after the jets penetrate the sub-bubbles. The water-hammer shock wave spreads almost spherically to the surrounding area and moves towards the particle after merging with Shock wave 1. In Fig. 26(h), the merged shock wave interferes with the reflected wave, which is the precursor wave reflected by the particles.
Fig. 26.
The emergence, propagation and interaction of shock waves for Case 4 obtained by numerical schlieren. Black lines indicate the bubble walls. γ = 1.066, η = 0.938, Rmax = 1.60 mm.
6. Conclusions
In this research, a compressible two-phase model based on the finite volume method and volume of liquid was used to simulate the dynamics of cavitation bubble near two spherical particles. The numerical model was validated through experimental results, which confirmed its high accuracy and ability to reproduce the shape evolution of cavitation bubble observed in the experiment. We focus on the temporal evolution of the bubble shape near two particles and its underlying evolutionary mechanism, and quantitatively analyze the jet characteristics. Finally, the shock wave generated by cavitation collapse is qualitatively analyzed. Several main findings are concluded as follows:
-
(1)
During the collapse stage, the cavitation bubble is split by the annular jet, resulting in another jet toward the particles from the split point.
-
(2)
The jet begins with a high velocity due to the high pressure generated by the cavitation bubble splitting, but the jet velocity gradually decreases with the bubble collapse process.
-
(3)
For all cases, the shock waves generated by cavitation bubble splitting propagate inside and outside the bubble. While the jet produces shock waves inside the bubble. Especially, in case 4, the water hammer shock waves generated by the jet will merge with the shock wave generated by the bubble splitting and then impact the particle surface.
In future work, more complex cavitation bubble-particle models will be investigated by numerical simulations. And the effect of the cavitation model on the multi-period oscillations of cavitation bubbles will be considered.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This research was financially supported by the National Natural Science Foundation of China (Project Nos.: 51976056 and 52076215).
Contributor Information
Jiaxin Yu, Email: yujiaxin1012@foxmail.com.
Yuning Zhang, Email: yuning.zhang@foxmail.com.
Appendix A. Comparison between the Schnerr-Sauer and Kunz cavitation model
In order to investigate the effect of the cavitation model on cavitation bubble dynamics, the numerical results of the Schnerr-Sauer and Kunz cavitation models were compared. The Condensation rate and evaporation rate for the Kunz cavitation model [29] were expressed as:
| (11) |
where both the condensation coefficient and the evaporation coefficient are set to 1; 2 m/s is the free-flow velocity; is the characteristic time scale, where L = 1.7 mm is the feature length.
Fig. A1 illustrates a comparison between the two cavitation models and experimental results in the first period. The two cavitation models exhibit similar results during the bubble growth stage and the early stages of collapse. However, a slight difference is observed in the later stage of the collapse. We argue that the effect of the cavitation model on the cavitation bubble dynamics during the first period can be neglected.
Fig. A1.
Comparison of Schnerr-Sauer cavitation model, Kunz cavitation model and experiment of Rd. Rd represents the distance between the intersection point of the bubble wall and the Y = 0 plane and the bubble center. Rmax = 1.60 mm, l = 1.97 mm.
References
- 1.J. Satoh, K. Usami, T. Okamura. Basic study of coupled damage caused by silt abrasion and cavitation erosion: experiments with submerged water jets, JSME International Journal Series 2 - Fluids Engineering Heat Transfer Power Combustion Thermophysical Properties. 34. (1991). 292-297.
- 2.Zhang Y.N., Zhang Y.N., Qian Z.D., Ji B., Wu Y.L. A review of microscopic interactions between cavitation bubbles and particles in silt-laden flow. Renewable and Sustainable Energy Reviews. 2016;56:303–318. [Google Scholar]
- 3.Zhang W., Zhu B. Risk assessment of erosive aggressiveness due to the condensation shock by numerical simulation. Journal of Hydrodynamics. 2022;34:200–206. [Google Scholar]
- 4.Cui P., Zhang A.M., Wang S., Khoo B.C. Ice breaking by a collapsing bubble. Journal of Fluid Mechanics. 2018;841:287–309. [Google Scholar]
- 5.Yin J.Y., Zhang Y.X., Zhu J.J., Lv L., Li S.D. Numerical investigation of the interactions between a laser-generated bubble and a particle near a solid wall. Journal of Hydrodynamics. 2021;33:311–322. [Google Scholar]
- 6.Weller H.G., Tabor G., Jasak H., Fureby C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Computers in Physics. 1998;12:620–631. [Google Scholar]
- 7.Koch M., Lechner C., Reuter F., Kohler K., Mettin R., Lauterborn W. Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM. Computers and Fluids. 2016;126:71–90. [Google Scholar]
- 8.Koch M., Rosselló J.M., Lechner C., Lauterborn W., Mettin R. Dynamics of a laser-induced bubble above the flat top of a solid cylinder—Mushroom-shaped bubbles and the fast jet. Fluids. 2022;7:2. [Google Scholar]
- 9.Yin J., Zhang Y., Zhu J., Zhang Y., Li S. On the thermodynamic behaviors and interactions between bubble pairs: A numerical approach. Ultrasonics Sonochemistry. 2021;70 doi: 10.1016/j.ultsonch.2020.105297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yin J.Y., Zhang Y.X., Zhu J.J., Lv L., Tian L. An experimental and numerical study on the dynamical behaviors of the rebound cavitation bubble near the solid wall. International Journal of Heat and Mass Transfer. 2021;177 [Google Scholar]
- 11.Yang Y.X., Wang Q.X., Keat T.S. Dynamic features of a laser-induced cavitation bubble near a solid boundary. Ultrasonics sonochemistry. 2013;20:1098–1103. doi: 10.1016/j.ultsonch.2013.01.010. [DOI] [PubMed] [Google Scholar]
- 12.Zhang A.M., Li S.M., Cui P., Li S., Liu Y.L. A unified theory for bubble dynamics. Physics of Fluids. 2023;35 [Google Scholar]
- 13.Zhang A.M., Cui P., Wang Y. Experiments on bubble dynamics between a free surface and a rigid wall. Experiments in fluids. 2013;54:1–18. [Google Scholar]
- 14.Zhang Y.N., Chen F.P., Zhang Y.N., Zhang Y.X., Du X.Z. Experimental investigations of interactions between a laser-induced cavitation bubble and a spherical particle. Experimental Thermal and Fluid Science. 2018;98:645–661. [Google Scholar]
- 15.Zheng X.X., Wang X.Y., Lu X., Yuan J., Zhang Y.N., Zhang Y.N. Experimental research on the collapse dynamics of the cavitation bubble near two spherical particles. Journal of Mechanical Science and Technology. 2023;37:2451–2460. [Google Scholar]
- 16.Zhang J., Du Y., Liu J., Sun Y., Yao Z., Zhong Q. Experimental and numerical investigations of the collapse of a laser-induced cavitation bubble near a solid wall. Journal of Hydrodynamics. 2022;34:189–199. [Google Scholar]
- 17.Li S., Han R., Zhang A.M. Nonlinear interaction between a gas bubble and a suspended sphere. Journal of Fluids and Structures. 2016;65:333–354. [Google Scholar]
- 18.Li S., Zhang A., Wang S., Han R. Transient interaction between a particle and an attached bubble with an application to cavitation in silt-laden flow. Physics of Fluids. 2018;30 [Google Scholar]
- 19.Zheng Y., Chen L., Liang X., Duan H. Numerical Study of the Interaction between a Collapsing Bubble and a Movable Particle in a Free Field. Water. 2020;12:3331. [Google Scholar]
- 20.Bußmann A., Riahi F., Gkce B., Adami S., Barcikowski S., Adams N. Investigation of cavitation bubble dynamics near a solid wall by high-resolution numerical simulation. Physics of Fluids. 2023;35:1–22. [Google Scholar]
- 21.Lechner C., Lauterborn W., Koch M., Mettin R. Fast, thin jets from bubbles expanding and collapsing in extreme vicinity to a solid boundary: A numerical study. Physical Review Fluids. 2019;4 [Google Scholar]
- 22.Lechne C., Lauterborn W., Koch M., Mettin R. Jet formation from bubbles near a solid boundary in a compressible liquid: Numerical study of distance dependence. Physical Review Fluids. 2020;5 [Google Scholar]
- 23.Zhang M., Chang Q., Ma X., Wang G., Huang B. Physical investigation of the counterjet dynamics during the bubble rebound. Ultrasonics Sonochemistry. 2019;58 doi: 10.1016/j.ultsonch.2019.104706. [DOI] [PubMed] [Google Scholar]
- 24.Sun Y., Yao Z., Wen H., Zhong Q., Wang F. Cavitation bubble collapse in a vicinity of a rigid wall with a gas entrapping hole. Physics of Fluids. 2022;34 [Google Scholar]
- 25.Li S.M., Zhang A.M., Wang Q.X., Zhang S. The jet characteristics of bubbles near mixed boundaries. Physics of Fluids. 2019;31 [Google Scholar]
- 26.Li S.M., Zhang A.M., Cui P., Li S. Y.L Liu, vertically neutral collapse of a pulsating bubble at the corner of a free surface and a rigid wall. Journal of Fluid Mechanics. 2023;962:A28. [Google Scholar]
- 27.Zevnik J., Dular M. Cavitation bubble interaction with a rigid spherical particle on a microscale. Ultrasonics Sonochemistry. 2020;69 doi: 10.1016/j.ultsonch.2020.105252. [DOI] [PubMed] [Google Scholar]
- 28.Lauterborn W., Kurz T. Physics of bubble oscillations. Reports on Progress in Physics. 2010;73(10) [Google Scholar]
- 29.Johnsen E., Colonius T. Numerical simulations of non-spherical bubble collapse. Journal of Fluid Mechanics. 2009;629:231–262. doi: 10.1017/S0022112009006351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Iloreta J.I., Fung N.M., Szeri A.J. Dynamics of bubbles near a rigid surface subjected to a lithotripter shock wave. Part 1. Consequences of interference between incident and reflected waves. Journal of Fluid Mechanics. 2008;616:43–61. [Google Scholar]
- 31.Calvisi M.L., Iloreta J.I., Szeri A.J. Dynamics of bubbles near a rigid surface subjected to a lithotripter shock wave. Part 2. Reflected shock intensifies non-spherical cavitation collapse. Journal of Fluid Mechanics. 2008;616:63–97. [Google Scholar]
- 32.Wen H., Yao Z., Zhong Q., Tian Y., Sun Y., Wang F. Energy partitioning in laser-induced millimeter-sized spherical cavitation up to the fourth oscillation. Ultrasonics Sonochemistry. 2023;95 doi: 10.1016/j.ultsonch.2023.106391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yang X., Liu C., Wan D., Hu C. Numerical study of the shock wave and pressure induced by single bubble collapse near planar solid wall. Physics of Fluids. 2021;33:1–22. [Google Scholar]
- 34.Tian L., Zhang Y.X., Yin J.Y., Lv L., Zhang J.Y., Zhu J.J. Study on the liquid jet and shock wave produced by a near-wall cavitation bubble containing a small amount of non-condensable gas. International Communications in Heat and Mass Transfer. 2023;145 [Google Scholar]
- 35.Uzun A., Malik M.R. Wall-resolved large-eddy simulations of transonic shock-induced flow separation. AIAA Journal. 2019;57:1955–1972. [Google Scholar]
- 36.Huai W.X., Zhang J., Katul G.G., Cheng Y.G., Tang X., Wang W.J. The structure of turbulent flow through submerged flexible vegetation. Journal of Hydrodynamics. 2019;31:274–292. [Google Scholar]
- 37.J. Dumon, N. Gourdain, L. Michel. Fluid-structure interaction between a composite aileron and a turbulent flow at transonic conditions, In Proceedings of the 53rd 3AF International Conference on Applied Aerodynamics. Salon de Provence, France. 26 March 2018.
- 38.Geng S., Yao Z., Zhong Q., Du Y., Xiao R., Wang F. Propagation of shock wave at the cavitation bubble expansion stage induced by a nanosecond laser pulse. Journal of Fluids Engineering. 2021;143 [Google Scholar]
- 39.Zemach C. A continuum method for modeling surface tension. Journal of Computational Physics. 1992;100:335–354. [Google Scholar]
- 40.Lafaurie B., Nardone C., Scardovelli R., Zaleski S., Zanetti G. Modelling merging and fragmentation in multiphase flows with SURFER. Journal of Computational Physics. 1994;113(1):134–147. [Google Scholar]
- 41.Zeng Q., Gonzalez-Avila S.R., Ohl C.D. Splitting and jetting of cavitation bubbles in thin gaps. Journal of Fluid Mechanics. 2020;896:A28. [Google Scholar]
- 42.Weller H. A new approach to VOF-based interface capturing methods for incompressible and compressible flow. Report TR/HGW/04, OpenCFD Ltd. 2008 [Google Scholar]
- 43.Schnerr G.H., Sauer J. ICMF; New Orleans USA: 2001. Physical and Numerical Modeling of Unsteady Cavitation Dynamics. [Google Scholar]
- 44.Plesset M.S., Prosperetti A. Bubble dynamics and cavitation. Annual Review of Fluid Mechanics. 1977;9(1):145–185. [Google Scholar]
- 45.Duan H., Chen L., Liang X. Numerical study of the emission of acoustic energy of single collapsing vapor bubble near a rigid wall. Water. 2022;14:455. [Google Scholar]
- 46.T. Wang, L. Chen. Thermodynamic Behavior and energy transformation mechanism of the multi-period evolution of cavitation bubbles collapsing near a rigid wall: a numerical study. Energies. 16. (2023). 1048.
- 47.Medvitz R.B., Kunz R.F., Boger D.A. Performance Analysis of cavitating flow in centrifugal pumps using multiphase CFD. Journal of Fluids Engineering. 2002;124:377–383. [Google Scholar]