An optimal Fe–C coordination ensemble for hydrocarbon chain growth: a full Fischer–Tropsch synthesis mechanism from machine learning

Abstract

Fischer–Tropsch synthesis (FTS, CO + H₂ → long-chain hydrocarbons) because of its great significance in industry has attracted huge attention since its discovery. For Fe-based catalysts, after decades of efforts, even the product distribution remains poorly understood due to the lack of information on the active site and the chain growth mechanism. Herein powered by a newly developed machine-learning-based transition state (ML-TS) exploration method to treat properly reaction-induced surface reconstruction, we are able to resolve where and how long-chain hydrocarbons grow on complex in situ-formed Fe-carbide (FeC_x) surfaces from thousands of pathway candidates. Microkinetics simulations based on first-principles kinetics data further determine the rate-determining and the selectivity-controlling steps, and reveal the fine details of the product distribution in obeying and deviating from the Anderson–Schulz–Flory law. By showing that all FeC_x phases can grow coherently upon each other, we demonstrate that the FTS active site, namely the A-P5 site present on reconstructed Fe₃C(031), Fe₅C₂(510), Fe₅C₂(021), and Fe₇C₃(071) terrace surfaces, is not necessarily connected to any particular FeC_x phase, rationalizing long-standing structure–activity puzzles. The optimal Fe–C coordination ensemble of the A-P5 site exhibits both Fe-carbide (Fe₄C square) and metal Fe (Fe₃ trimer) features.

By using a machine-learning-based transition state (ML-TS) exploration method, we here resolve where and how long-chain hydrocarbons grow on in situ-formed Fe-carbide (FeC_x) surfaces in Fischer–Tropsch synthesis.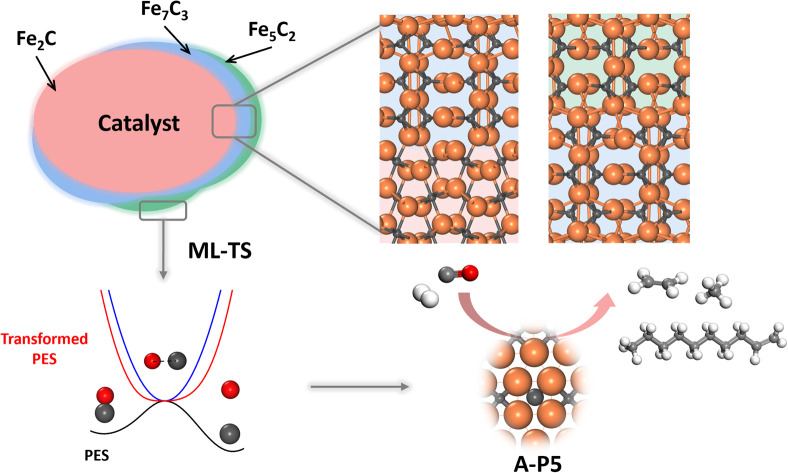

1. Introduction

Fe-based Fischer–Tropsch synthesis (FTS) is a key technology to convert syngas (H₂ and CO mixtures) to long-chain hydrocarbons.¹ The reaction is operated at high temperature (423–623 K) and high pressure (2–3 MPa, H₂/CO = 1–2)^2–5 using iron oxides or/and hydroxides as the catalysts that are in situ activated under a reductive gas flow for 2–24 h. The catalytic active phase has been long believed to be pertinent to complex carbon-containing Fe phases, i.e. iron-carbides (FeC_x),^6–10 where at least five bulk phases with different Fe : C ratios and two different Fe–C local coordination patterns were reported,^11–17 namely triangular prismatic (TP) coordination for θ-Fe₃C, χ-Fe₅C₂ and Fe₇C₃ phases and the octahedral (Oct) coordination for ε-carbides, ε′-Fe_2.2C, and ε-Fe₂C. Despite the great importance of Fe-based FT technology and more than a century of research, it remains largely elusive on where and how the long-chain hydrocarbons grow under the reaction conditions. New techniques are called for to clarify the in situ catalyst structural evolution and its dynamic coupling with FT reactions.

The product distribution of Fe-based FTS generally satisfies the Anderson–Schulz–Flory distribution^11–14 with a fairly large chain growth probability factor α, 0.4–0.7 from different experiments^3,4,15,16 and the unwanted CH₄ yield is 10–30% in products. By measuring the CH₄ yield, steady-state isotopic transient kinetic analysis (SSITKA)^17–19 has provided some key clues for the active phase. For example, Chai et al.¹⁹ showed that the adsorbed C species derived from CO occurring at a low concentration of active sites (10%) contribute to 90% of the total activity with an average rate constant of 1.47 × 10⁻³ s⁻¹, while the rest of the activity originates from the lattice C of FeC_x (the rate constant is 3.23 × 10⁻⁴ s⁻¹). While these experiments suggest the C from CO and the lattice C in FeC_x could follow distinct pathways to generate hydrocarbons, the other possibility that the surface structures are dynamic and active C species diffuse and exchange frequently on the surface cannot be excluded.

To clarify the nature of the active C species on catalyst surfaces, a series of surface-sensitive characterization techniques have been utilized to probe FeC_x structures under near-ambient pressure conditions (<700 mbar). By using the C 1s photoelectron spectra, Shipilin et al.⁹ distinguished the near-surface C species on an Fe(110) single crystal having both TP and Oct coordination that show peaks at 283.6 and 283.3 eV, respectively. With increasing time and temperature, these surface C species can lead to hydrocarbons as detected from the increasing mass spectrometry (MS) signal of the methyl radical at 550 mbar (H₂/CO = 1 and 10). This conclusion from surface science experiments agrees with previous studies under FTS conditions that both TP (triangular prism) and Oct (octahedron) FeC_x bulk phases characterized by X-ray diffraction (XRD) and Mössbauer spectroscopy are active.^15,20–25 However, which type of Fe–C coordination is more active remains controversial. Zhao et al.²⁵ reported that Fe₅C₂ (TP coordination) is the most active phase in terms of initial CO conversion (35%) compared to Fe₇C₃ and Fe₂C at 543 K and 3 MPa. However, Xu et al.²¹ found that ε-carbides (Oct coordination) prepared by the on-site carbidization of rapidly quenched skeletal iron (RQ Fe) exhibit superior initial activity for CO conversion (43 mol_CO mol_Fe⁻¹ h⁻¹) to an Fe₅C₂-dominant RQ Fe catalyst (10 mol_CO mol_Fe⁻¹ h⁻¹) by 75% at 443 K.

On the other hand, theoretical studies generally do not support experimental FTS findings on the hydrocarbon formation rate.^26–34 By using density functional theory (DFT) calculations on an Fe–B₅ site from an Fe-terminated Fe₅C₂(100) model, Cheng et al.²⁶ showed that CO dissociation can proceed with a barrier of 0.79 eV,³³ but the effective barriers of C hydrogenation to CH₄ and C–C coupling (C + CH₃) are very high, ∼1.9 eV. Even on bulk-truncated FeC_x surfaces^27,30,31 with a mixed Fe/C termination, the barriers for CH₄ formation or C–C coupling are still unexpectedly high, for example, 2.18 eV for CH₄ formation by Pham et al.³¹ and >2.34 eV for C–C coupling by Yin et al.³⁰ on Fe₅C₂(510). The theoretical turnover frequencies (TOFs) from these calculated barriers are thus at least two orders of magnitude lower for methane and long-chain hydrocarbon formation compared to those from experiments. This may stem from the incorrect active-site model utilized in theoretical studies considering that the in situ catalyst structure may well deviate from the bulk-truncated surfaces from FeC_x crystals. Indeed, by using machine-learning atomic simulations^35,36 to explore thermodynamically stable FeC_x bulk phases and surfaces, we recently demonstrated that most FeC_x surfaces will undergo reconstruction under reaction conditions, leading to the surface Fe : C ratio deviating largely from the bulk ratio. As a result, the surface C vacancies are commonly available, which, as exemplified on the Fe₅C₂(510) surface, can dissociate CO molecules with a low barrier (1.11 eV). It is thus expected that the FeC_x surfaces reconstructed dynamically under reaction conditions are the key to reconciling puzzles on FT hydrocarbon formation.

Here we aim to clarify the hydrocarbon formation mechanism on FeC_x catalysts under FTS conditions. For this purpose, we develop a machine-learning-based transition-state (TS) exploration technique, ML-TS, that is able to expedite efficiently the exploration of the vast FT hydrocarbon reaction network on a series of FeC_x surfaces, featuring an intimate coupling of the reaction pattern sampling with surface structure global optimization. With millions of structures and thousands of pathways determined, we show that the CO activation and C–C coupling to grow long-chain hydrocarbons occur favorably on the same active site, a planar five-Fe-atom site, originating from reconstructed FeC_x terraces. Our results rationalize the long-standing controversies on the FTS active site and the reaction kinetics.

2. Methods

2.1. Machine-learning-based transition state exploration (ML-TS)

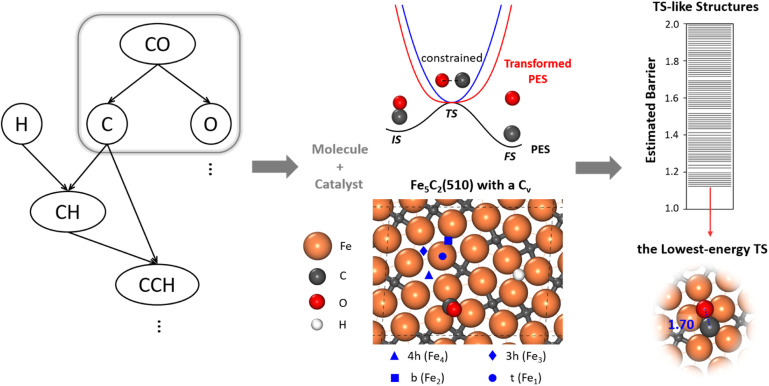
To allow for efficient coupling between reaction pathway search and the catalyst surface structure dynamics, i.e. reaction-induced surface reconstruction, this work develops an ML-TS method based on our previously developed stochastic surface walking (SSW) global optimization using the global neural network (G-NN), as shown in Fig. 1 for the scheme of the methodology. Briefly, the ML-TS combines the reaction coordinate constraining technique and the fast global structure exploration of the SSW-NN method. The reaction coordinate is fixed via the bias potential approach, which is widely utilized in enhanced molecular dynamics (MD) for visiting the TS region of the potential energy surface (PES).

Fig. 1. Scheme of the machine-learning-based transition state exploration. A likely reaction map (Left) is first generated, which provides the reaction patterns of elementary reactions. For CO dissociation, the C–O distance of a reacting [C–O] molecule is constrained at the typical C–O distance of the CO dissociation TS via the bias potential energy of a simple harmonic oscillator (middle, blue line). The TS in the real PES (black line) is thus converted to the minimum of the transformed PES (red line). After the sampling, we use the CBD method to locate the TSs from the TS-like candidates (right). The top view of Fe₅C₂(510) with a C vacancy in a p(2 × 1) supercell is also shown to illustrate the catalyst, with the typical adsorption sites labelled, including 4-fold hollow (4h, Fe₄), 3-fold hollow (3h, Fe₃), bridge (b, Fe₂) and top (t, Fe₁) sites. The color scheme for atoms is as follows: Fe: orange, C: gray, O: red, and H: white.

In the ML-TS simulation, a likely reaction map is first generated as shown on the left side of Fig. 1, which provides the reaction patterns of elementary reactions. For a target reaction involving a bond making/breaking between two atoms A and B, a series of SSW global optimization tasks are performed in parallel, with the A–B distance in each task being fixed at a TS-like distance. Taking CO dissociation as an example, the C–O distance of a reacting [C–O] complex is fixed via the harmonic oscillator bias potential (blue line in Fig. 1) at a set of predefined values, i.e. 1.60, 1.80 and 2.00 Å (the typical C–O distance window at TSs), in different SSW tasks. The force constant of the harmonic oscillator is set as 100 eV Å⁻², which is large enough to maintain the fixed distance during SSW simulations. In this way, the TS region on the original PES (black line) is transformed to a minimum region on the modified PES (red line), whereas the original PES minima, the initial state (IS) and the final state (FS) are no longer the minima. By using ML-TS, a large number of TS-like structures on different surface structures can be collected thanks to the great efficiency of G-NN potential for PES evaluation and the SSW method for structural configuration exploration. For the low-energy TS-like candidates obtained from ML-TS simulations, the single-ended TS search method—the constrained Broyden dimer (CBD) method,^37,38 is then utilized to locate exactly the TS structure. The lowest barrier of the reaction on the catalyst surface is thus obtained, which takes into account the degrees of freedom from both molecular configurations and the surface structure reconstruction. An example of ML-TS simulation for finding the likely TS structures with different molecular configurations that adapt to different surface reconstruction patterns is given in Fig. S3 and S4.†

All ML-TS simulations were conducted using the LASP code³⁹ (Large-scale Atomic Simulation with neural network potential, http://www.lasphub.com/#/lasp/laspHome) developed by our group, which implements G-NN potential^40,41 training and SSW structural search.^42,43 The SSW-NN method has been utilized for studying complex catalytic structures and reaction pathways.^44–47

2.2. G-NN potential

Our G-NN potential follows the atom-centered NN potential architecture,^48,49 where the input layer utilized the power-type structure descriptor (PTSD).⁴¹ Different from other machine learning potentials, G-NN potential was generated by iteratively fitting the DFT global PES data obtained from the SSW global PES sampling. In this work, the quaternary-element Fe–C–H–O G-NN potential first utilized in our previous work³⁵ is updated via the iterative self-learning to better account for the global PES of long-chain hydrocarbon reactions on FeC_x surfaces. More details on the G-NN generation and the SSW-NN method can be found in ESI Section 1.1.†

The final Fe–C–H–O training data set consists of 38 755 structures and is openly accessible from the LASP website (see the web page link (ref. 50)). The Fe–C–H–O G-NN contains 382 136 parameters in total. The Fe element is represented by 529 PTSDs (310 two-body, 179 three-body, and 40 four-body PTSDs), while each of the other elements (C/H/O) is represented by 535 PTSDs (316 two-body, 179 three-body, and 40 four-body PTSDs). The root-mean-square (RMS) errors for the energy and the force of the G-NN potential are 4.155 meV per atom and 0.113 eV Å⁻¹, respectively. The Fe–C–H–O G-NN potential is openly available on the LASP website (see the web page link (ref. 51)). The important low-energy structures from SSW-NN calculations have been further examined by using DFT calculations, and the benchmark results are detailed in ESI Table S2,† which showed that the energy RMS error is 1.18 meV per atom for important minima and TSs. The accuracy is good enough for the SSW global PES search to find low-energy minima and TSs.

2.3. DFT calculations

All key energetics reported in this work were verified using plane-wave DFT calculations, as implemented in the VASP (Vienna Ab initio Simulation Package) code.⁵² The electron–ion interaction was represented by the projector augmented wave (PAW) potential. The exchange-correlation potential utilized was the GGA-PBE,⁵³ and the kinetic energy cutoff was 450 eV. Spin polarization has also been considered in all DFT calculations. The first Brillouin zone k-point sampling adopted the Monkhorst–Pack scheme with an automated mesh determined by 25 times the reciprocal lattice vectors. The energy and force criteria for the convergence of the electron density and structure optimization were set at 5 × 10⁻⁶ eV and 0.05 eV Å⁻¹, respectively. It should be mentioned that we have confirmed all important minima and pathways by DFT calculations, and thus, unless otherwise specifically mentioned, all energetics data reported in this work are from DFT calculations.

2.4. Surface modeling and microkinetics simulations

In modeling the molecular adsorption and reactions, at least two bottom layers of FeC_x were fixed and the top two surface layers were relaxed together with adsorbed molecules. As an illustration, the top view of Fe₅C₂(510) with a C vacancy in a p(2 × 1) supercell is shown in Fig. 1, with the typical adsorption sites being labelled, including 4-fold hollow (4h), 3-fold hollow (3h), bridge (b) and top (t) sites which consist of Fe₄, Fe₃, Fe₂ and Fe₁ sites, respectively. The other surface structures are shown in Fig. S2.†

The surface free energy (γ) is computed using the following eqn (1):

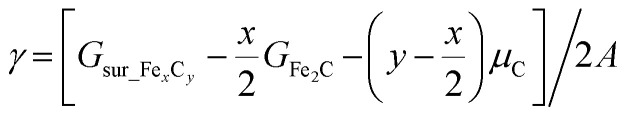1

where G_{sur_FexCy} and G_Fe2C denote the free energy of the surface and η-Fe₂C (the most stable FeC_x bulk phases at a carbon chemical potential (μ_C) of −6.90 eV), respectively, and the C atom contribution (y − x/2), if required, is to balance the equation with respect to μ_C = −6.90 eV. For the eight surfaces considered in this work (η-Fe₂C(111), o-Fe₇C₃-II(071), χ-Fe₅C₂(510), θ-Fe₃C(031), χ-Fe₅C₂(021), χ-Fe₅C₂(111), θ-Fe₃C(102) and θ-Fe₃C(131)), their surface free energy is computed to be 1.83, 2.03, 2.09, 2.13, 2.14, 2.25, 2.26 and 2.34 J m⁻², respectively.

The free energy profile for the reaction pathway was obtained based on the DFT energetics, as described previously.^35,54 For all reaction intermediates on the surfaces, the vibrational zero-point-energy (ZPE) was corrected by performing vibrational frequency analysis, and for the gas phase molecules, the entropy terms from standard thermodynamics data were also amended with T = 523 K, P = 2.5 MPa, and H₂/CO = 2. These kinetics data were then utilized for microkinetics simulation.

With the overall pathways, we build a microkinetic model to compute the steady-state rate. The ordinary differential equations of all reactions are solved using the backward differentiation formula method,⁵⁵ and the solution is further polished by Newton's method optimization.⁵⁶ The corrections for the gas-phase CO (−0.17 eV), H₂O (+0.15 eV) and CO₂ (−0.13 eV) free energies are adopted to match the enthalpy changes for the gas-phase reactions. To correct the coverage dependence of the adsorption energy, the linear relationship between the adsorption free energies of CO and H and the total surface coverage of the Fe site 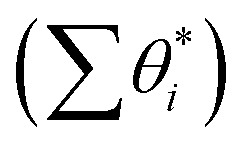are established based on the DFT energetics (see Fig. S1†). More details can be found in ESI Section 1.3.†

3. Results

3.1. CO activation on FeC_x surfaces

Let us first recall the major results on the thermodynamics of FeC_x bulk phases from our previous work.³⁵ By using the C chemical potential, μ_C, to derive the relative stability of FeC_x bulk phases, we showed that multiple FeC_x bulk phases grow under FTS conditions. FeC_x bulk phases at four Fe : C ratios (Fe₃C, Fe₅C₂, Fe₇C₃, and Fe₂C) form at the early stage of FTS when the CO conversion is low (−7.2 eV < μ_C < −6.6 eV), while Fe₅C₂, Fe₇C₃, and Fe₂C are favorable carbide bulk phases under the typical steady-state conditions where olefin is the major product of FTS (μ_C < −7.2 eV).

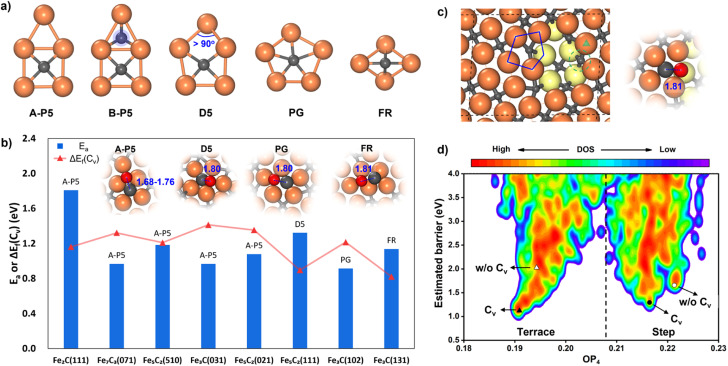
While many surfaces have been proposed as possible reaction sites,⁵⁷ we here follow our previous work,^35,36 which lists eight surfaces as the most likely reaction sites, namely θ-Fe₃C(031), θ-Fe₃C(102), θ-Fe₃C(131), χ-Fe₅C₂(510), χ-Fe₅C₂(111), χ-Fe₅C₂(021), o-Fe₇C₃-II(071) and η-Fe₂C(111). These surfaces are thermodynamically stable (low surface free energy) under reaction conditions and able to adsorb both CO molecules and H atoms. We thus first explored the CO activation step on these eight FeC_x surfaces. These surfaces expose at least six distinguishable local Fe–C bonding patterns, and five of them, namely A-type planar five-fold site (A-P5), B-type planar five-fold site (B–P5), distorted five-fold site (D5), pentagon (PG) and folded rectangle (FR), are shown in Fig. 2a. Because of the great variety of surface sites and the possibility of further surface reconstruction, the identification of the best reaction site is not feasible with traditional TS search methods that rely on the manual guess of the reaction coordinate and are difficult to cope with the large surface structural change.

Fig. 2. CO dissociation on FeC_x surfaces. (a) Five major types of Fe–C local bonding patterns (reaction sites) on eight surfaces. A-P5: A-type planar five-fold site, B-P5: B-type planar five-fold site, D5: distorted five-fold site, PG: pentagon, and FR: folded rectangle. (b) The lowest CO dissociation barrier (E_a) and the C vacancy formation energy (ΔE_f(C_v)) of the corresponding C site from SSW-NN on each stable FeC_x surface. Top views of TSs for the C-vacancy mediated CO dissociation on four types of sites are shown in the inset. The surface on the x axis is ordered by the surface free energy (γ) referring to η-Fe₂C and μ_C = −6.90 eV. (c) Top view of a defective Fe₅C₂(510) surface. The Fe atoms in the second layer are colored in yellow. The TS of CO dissociation with the lowest barrier on the step edge is shown on the right. The green triangle denotes the most stable adsorption site of CO in the presence of a C vacancy (the green dashed line denotes the C-vacant site). (d) PES contour plot for the estimated barrier of CO dissociation using the TS-like candidates collected from ML-TS on the terrace and step of Fe₅C₂(510) with or without a C vacancy. The y-axis is the estimated barrier referring to the most stable CO adsorption state of the four different surface models. The x-axis is the structure order parameter with l = 4 (OP₄). The TSs with the lowest barrier for the four different models are marked with triangles and circles. C_v denotes the surface model with a C vacancy.

By using the fully automated ML-TS method, we are able to visit all the likely pathways for CO activation on different surfaces, as described in Section 2.1, where the likely surface evolution in response to CO activation is taken into account. Not only CO direct dissociation on thermodynamically stable surfaces but also CO dissociation on surfaces with C vacancies and with an additional H atom is considered. The surface C vacancy is modeled by extracting surface C atoms in simulations; the additional H atom on surfaces is utilized to examine the feasibility of H-assisted CO activation. In total, more than 10⁵ minima structures were visited for eight surfaces with at least 10 000 minima collected for each surface.

Our ML-TS results show that the lowest-energy pathway of CO activation on all eight FeC_x surfaces shares the same mechanism, being the C-vacancy mediated CO dissociation. The barrier of the H-assisted CO dissociation channel is higher than that of the C-vacancy mediated CO direct dissociation on all eight surfaces (see ESI Fig. S6† for the example on an Fe₅C₂(510) surface). The CO dissociation requires firstly the formation of a C vacancy followed by C–O bond breaking at the surface C void center where the C-end of the CO molecule sits. The C vacancy can be generated by surface reconstruction (e.g. a lattice C diffuses into the subsurface, see Fig. S4†), or via the hydrogenation of surface C to CH_x that subsequently diffuses out the original site. We summarized in Fig. 2b the energetics for the C vacancy formation ΔE_f(C_v) (red) and the reaction barrier of CO dissociation E_a (blue), where the surfaces are ordered by surface free energy from left to right (x-axis). The corresponding geometries of CO dissociation at the C vacancy are also indicated in the inset of Fig. 2b, including A-P5, D5, PG and FR. A-P5 sites are the most active on five surfaces, including Fe₂C(111), Fe₇C₃(071), Fe₅C₂(510), Fe₃C(031), and Fe₅C₂(021). D5, PG and FR are the best sites for CO dissociation at Fe₅C₂(111), Fe₃C(102) and Fe₃C(131), respectively. More structural details of these surface sites can be found in Fig. S2.†

Fig. 2b shows that except Fe₂C(111) which has a too-high CO dissociation barrier (>1.8 eV), the other seven surfaces do have both low ΔE_f(C_v) (0.82–1.41 eV) and low E_a in CO dissociation (0.97–1.32 eV). Therefore, it is not feasible to exclude the possibility of these surfaces as the active site for FTS. Nevertheless, we recall that Fe₇C₃(071) and Fe₅C₂(510) have much lower surface free energies (<2.10 J m⁻²) compared to the other five surfaces, i.e. Fe₃C(031), Fe₅C₂(021), Fe₅C₂(111), Fe₃C(102) and Fe₃C(131) (2.13, 2.14, 2.25, 2.26 and 2.34 J m⁻², respectively). These two surfaces, Fe₇C₃(071) and Fe₅C₂(510), have similar close-packed surface bonding patterns, that is, the closely linked metal-like three-fold Fe₃ sites separated by four-coordinated planar C atoms (Fe-carbide feature), as shown in Fig. 1 and S2.† The higher surface stability of Fe₇C₃(071) and Fe₅C₂(510) would lead to their higher population in catalysts. In addition, comparing these two surfaces, the Fe₅C₂(510) surface has a smaller periodicity (4.99 Å × 12.68 Å with γ = 93.45° vs. 4.96 Å × 35.69 Å with γ = 90° in Fe₇C₃(071)) due to the smaller bulk lattice of Fe₅C₂ bulk and thus the Fe₅C₂(510) surface is at first selected for studying the FT mechanism in detail.

Now we have a closer examination of the ML-TS results for CO activation on Fe₅C₂(510), which comprise the pathways on both the terrace and the defected sites of Fe₅C₂(510). The stepped Fe₅C₂(510) is modeled by the global minimum structure from an Fe₅C₂(510) surface missing 0.15 monolayer (ML) Fe atoms (three Fe atoms per p(2 × 1) supercell), as found by SSW-NN (shown in Fig. 2c), which exposes step edges with Fe₄-square and Fe₅-pentagon coordinated C atoms. From 41 120 minima in total and 2071 distinct minima of the likely TSs collected from SSW-NN data, we can plot the E–OP contour map for the PES of CO activation in Fig. 2d, where the y-axis is the estimated barrier for CO activation calculated by referencing the fixed TS-like C–O geometry at different surface sites with respect to the most stable CO adsorption state and the x-axis is the structure fingerprint using the Steinhart order parameter with the degree l = 4 (OP₄).⁵⁸

From the E–OP plot we can distinguish the structures between the terrace and step: the structures from stepped Fe₅C₂(510) have larger OP₄ values (mostly >0.21) while those from the terrace are mostly located in the lower OP₄ region (0.19–0.21). The CO activation at the stepped sites (right side in Fig. 2d) is generally more difficult than that on the terrace site (left side in Fig. 2d). The lowest barriers of CO activation are 1.18, 2.17, 1.27 and 1.77 eV (DFT-PBE) for the terrace with and without a C vacancy (triangles in Fig. 2d), and the stepped sites with and without a C vacancy (circles in Fig. 2d), respectively. Obviously, the Fe₅C₂(510) terrace is the most active site for CO dissociation and the presence of stepped sites does not bring down the barrier.

CO dissociation on the Fe₅C₂(510) terrace occurs at the A-P5 site, as shown in Fig. 2a. It consists of an Fe₄C square neighbored by an edge-sharing Fe₃ hollow site, which in total has five planar Fe atoms. The C atom is protruding, leading to a positive torsion angle of the C–Fe bond with respect to each Fe–Fe bond in the Fe₄C square. In the presence of the C vacancy in A-P5, CO adsorbs on the top of one of the Fe atoms in the vacant Fe₄ square (see Fig. S5†). The TS of CO dissociation shows a geometry where the C-end fills the Fe₄ square and the O-end induces new bonding with the three adjacent planar Fe atoms, with the C–O distance being 1.70 Å (inset in Fig. 2b).

It might be mentioned that there is another quite similar P5 site, namely the B-P5 site (Fig. 2a) in Fe₂C(111), but it is much poorer in the activity for CO dissociation. The major difference is that an extra C atom locates beneath the Fe₃ hollow site (blue shadow in Fig. 2a), which apparently poisons the whole B-P5 site.

For the stepped Fe₅C₂(510), the CO dissociation at the step-edge site is kinetically less favored—even with a C vacancy, the dissociation barrier is still higher than that on the terrace site. This can be attributed to the too-stable CO adsorption state at the step edge, as shown in Fig. S5,† where the CO molecule adsorbs on the top site of an Fe atom at the edge (green triangle in Fig. 2c) near the vacant stepped Fe₄ square (green dashed line in Fig. 2c). The adsorbed CO is 0.45 eV more exothermic compared to the CO at the terrace site. The TS at the step edge is at the Fe₅ pentagon (blue line in Fig. 2c), where the C-end is located at the Fe₅ stepped site between the first and second layers and the O-end links with three adjacent Fe atoms on the edge (two in the first layer and one in the second layer) with the C–O distance being 1.81 Å.

It is of interest to compare our results with previous theoretical studies for CO activation. Previous studies show that the CO activation mechanism varies on FeC_x surfaces,^33,57,59,60 for example, direct dissociation on the Fe site of Fe₅C₂(111̄)⁵⁷ and H-assisted CO dissociation via an HCO intermediate on the Fe site of Fe₅C₂(010),⁵⁹ with barriers being 1.22 and 0.96 eV, respectively. Nevertheless, both Fe₅C₂(111̄) and Fe₅C₂(010) are not thermodynamically stable surfaces under FT conditions. On the other hand, the FeC_x-terminated bulk-truncated surfaces are generally utilized as the catalyst model without considering the likely surface reconstruction and the presence of C vacancies. Our ML-TS results show that eight FeC_x active site candidates have the same CO activation pathway—C-vacancy mediated CO dissociation. For surfaces such as Fe₅C₂(510) and Fe₅C₂(021) where surface reconstruction is not dramatic, our results are consistent with the literature. In particular, He et al.⁵⁹ and Chen et al.⁶⁰ reported the CO dissociation barriers of 1.18 and 1.03 eV on unreconstructed Fe₅C₂(510) and Fe₅C₂(021), respectively (1.18 and 1.08 eV from our ML-TS). These results and our large-scale ML-TS exploration of FeC_x surfaces conclude that the best CO dissociation channel involves 4-fold Fe hollow sites^61,62 identified here as A-P5 sites that are present on several stable FeC_x surfaces (Fe₇C₃(071), Fe₅C₂(510), Fe₃C(031) and Fe₅C₂(021)).

3.2. C–C coupling pathways

We then explored the C–C coupling pathways on the Fe₅C₂(510) terrace starting from C₂ hydrocarbon formation. In total, fourteen possible reaction patterns, including CH_x coupling CH_x + CH_y and CO-assisted coupling CH_x + CO (x, y = 0–3), are considered by ML-TS. More than 1.4 × 10⁵ minima structures were visited with 10 000 minima collected for each pattern. The main results are listed in Table 1, including the reaction site, TS geometry, the C–C distance in TS (d_C–C) and the effective energy barrier (E_a) of each reaction pattern.

The effective energy barriers for different C–C coupling pathways on Fe₅C₂(510)^a.

	Reaction site	TS geometry	d C–C (Å)	E a (eV)
C + CH	A-P5	4h + 3h	2.22	0.48 (0.48)
C + CH2	A-P5	4h+3h	1.91	0.87
C + CH3	Fe4	4h + t	2.07	1.13
CH + CH	A-P5	4h + 3h	2.10	0.38 (0.43)
CH + CH2	A-P5	4h + 3h	1.84	0.77
CH + CH3	Fe4	4h + t	1.91	1.39
CH2 + CH2	A-P5 + Fe3	b + b	2.06	0.99
CH2 + CH3	A-P5	3h + t	2.11	0.84
C + CO	Fe4	4h + t	1.61	1.34
CH + CO	Fe3	3h + t	1.72	0.96
CH2 + CO	Fe3	3h + t	1.75	1.05
CH3 + CO	Fe1	t + t	1.81	1.45

^aListed data include the reaction site, TS geometry, C–C distance in TS (d_C–C) and the effective energy barrier (E_a) with respect to the most exothermic state preceding the coupling reaction. The data in parenthesis are ZPE-corrected E_a. Fe₄, Fe₃ and Fe₁ denote the site consisting of an Fe₄ square, Fe₃ triangle and Fe₁ single atom. The TS geometry is indicated as 4h (4-fold hollow site), 3h (3-fold hollow site), b (bridge) and t (top).

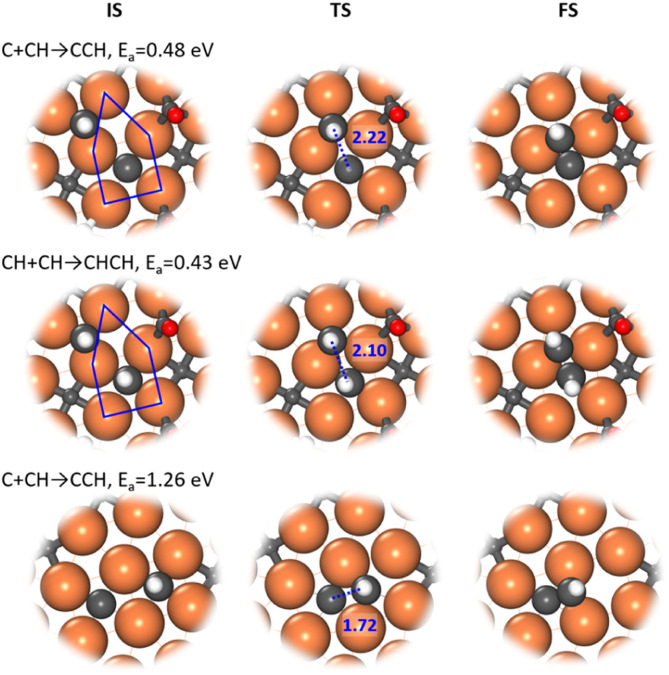
Our ML-TS results show that the CO-assisted chain growth is not favored, but the two lowest-energy pathways of chain growth both belong to CH_x coupling with barriers below 0.5 eV, i.e. C + CH and CH + CH, occurring similarly at the A-P5 site (Fig. 3). At the TS, the Fe₄-square coordinated C or CH reacts with another CH on the planar Fe₃ hollow site. The C–C distance at the TSs of C + CH and CH + CH is 2.22 and 2.10 Å, respectively. CH + CH has the lowest reaction barrier of 0.43 eV, which is 0.05 eV lower than that of C + CH. Nevertheless, the exothermicity of the CCH formation is larger (−0.24 eV) than that of CHCH (−0.01 eV). The final CCH and CHCH fragments achieve a similar adsorption geometry at the A-P5 site, where one C or CH is located in the Fe₄ square and the linked CH situates at the Fe₃ triangle with the C–C distance being 1.41 and 1.45 Å, respectively.

Fig. 3. Enlarged local view for the structure snapshots (IS, TS and FS) from the low-energy channel of C + CH and CH + CH reactions (top two panel) and a high-energy channel of the C + CH reaction. Blue lines in ISs outline the A-P5 site.

In fact, all of the CH_x + CH_y pathways prefer to occur at the A-P5 site, although the other C–C coupling pathways have higher reaction barriers (above 0.76 eV). Generally, one CH_x coordinates with two to four Fe atoms in the Fe₄ square of A-P5 and the other coming CH_y is situated at the top, bridge or 3-fold hollow site in or around the A-P5 at the TS (see Fig. S7†). On the other hand, most CH_x + CO pathways occur at the Fe₃ triangle and Fe₁ single atom in the 3-fold hollow site, while the C + CO reaction occurs at the Fe₄ square (Fig. S7†).

It is worth mentioning that the C–C coupling pathway is very sensitive to the surface site geometry due to the bonding competition of two reacting C-containing moieties. From our ML-TS search, the surface structure is indeed dynamic in response to the diffusion of CH_x and the creation and recovery of the C vacancy. This may explain why the previous theoretical studies did not identify energetically favorable C–C coupling pathways on Fe₅C₂(510). For example, Yin et al.³⁰ found that the coupling barriers of CH_x + CH_y on Fe₅C₂(510) are >2.3 eV using a surface model with C vacancies left, but our results show that the surface with C vacancies healed is much better for C–C coupling (<1.4 eV). Pham et al.³¹ investigated similar C + CH and CH + CH occurring at two neighboring Fe₄ squares from two A-P5 sites on Fe₅C₂(510) and found that the barriers are ∼1.27 eV. Our ML-TS data for the barriers of the direct coupling between two CH_x species at two Fe₄ squares are indeed similar (Fig. 3), being 1.26 and 1.28 eV for C + CH and CH + CH, respectively.

3.3. Overall mechanism of FTS

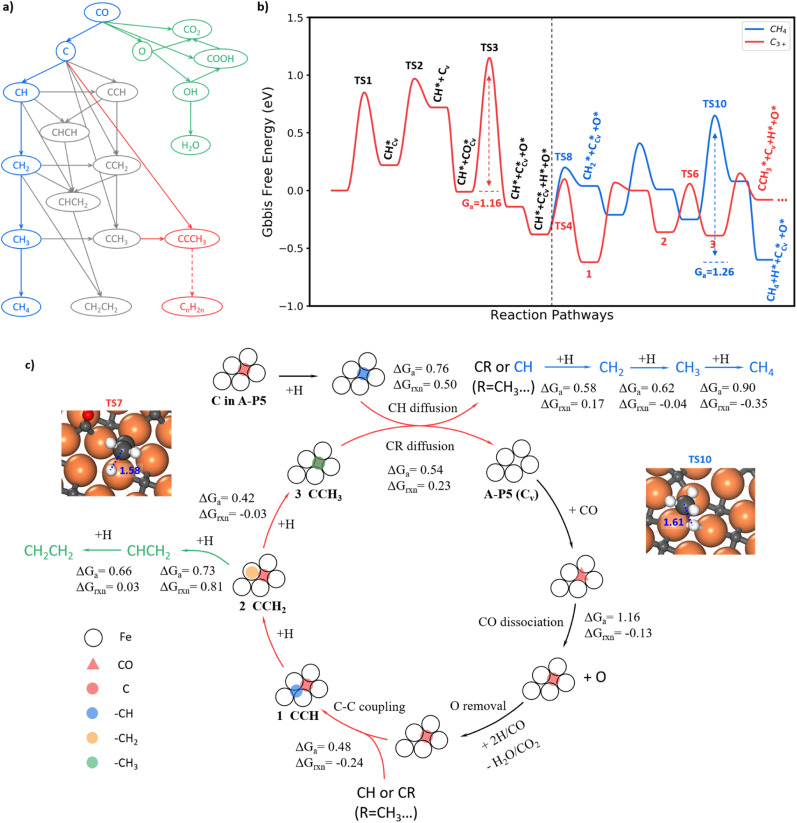
With the knowledge of the lowest energy pathways of CO activation and C–C coupling, we can now simplify the full reaction network of FTS as shown in Fig. 4a for producing CH₄, C₂H₄ and C₃₊. This map allows for a further ML-TS to explore the overall mechanism of FTS. In addition to the already-investigated CO dissociation and C–C coupling reactions, there are more than 30 elementary steps to explore in order to complete the reaction network. In order to consider the possible surface coverage effects on the kinetics, 9 key reactions are examined at one low (mixed 0.05 ML CO + 0.05 ML H) and two medium (mixed 0.20 ML CO + 0.05 ML H and 0.25 ML H) coverages.

Fig. 4. Full FTS mechanism. (a) Key reactions pruned from the FTS reaction network for producing CH₄, C₂H₄ and C₃₊. (b) Free energy profile for CH₄ and C₃₊ formation on Fe₅C₂(510). The reaction conditions are set at T = 523 K, P = 2.5 MPa, and H₂/CO = 2 for computing the free energies. The blue line is the hydrogenation route of CH to CH₄. The red line is the chain propagation route starting from the coupling between C and CH. The asterisk indicates the adsorption state and C_v denotes the carbon vacancy on the surface. (c) The scheme of the reaction mechanism for CH₄, C₂H₄ and long-chain product formation on Fe₅C₂(510). ΔG_a and ΔG_rxn denote the Gibbs free energy barrier and reaction energy of some key steps. The blue, green and red arrows indicate the pathway for CH₄, C₂H₄ and C₃₊ product formation. The red triangle denotes the CO molecule on the A-P5 site. The red, blue, orange and green circles denote C, –CH, –CH₂ and –CH₃ species, respectively. The structure snapshots for the TS of CCH₂ + H (TS7) and CH₃ + H (TS10) are also shown.

Fig. 4b summarizes the lowest free energy profile for CH₄ formation and chain propagation to C₃₊ on Fe₅C₂(510) at a representative medium coverage, mixed 0.20 ML CO and 0.05 ML H. The results of other coverages are listed in ESI Table S4.† The left side of the energy profile in Fig. 4b starts from the surface C vacancy formation via the C hydrogenation and then CH diffusion. A coming CO adsorbs at the C vacancy of the A-P5 site and dissociates with a barrier of 1.16 eV (TS3). After that, an O atom is left on the surface and the reaction pathways of O removal are discussed in ESI Fig. S8–S10.† The right side of the energy profile displays two pathways about how CH reacts after its diffusion out from the Fe₄ site, including (i) CH hydrogenation to CH₄ (blue line) and (ii) chain growth initiated by CH coupling with C to produce C₃₊ (red line). The overall FTS mechanism for carbon chain initiation, propagation, and termination to CH₄ and C₂H₄ is shown in Fig. 4c.

Briefly, the chain initiation starts from the hydrogenation of the C atom in the A-P5 site. After the CH diffusion from the A-P5 site, CH couples with the C, a monomer of chain propagation, at the A-P5 site or goes through hydrogenation to form CH₄. By step-wise hydrogenation after C–C coupling, the CCH species converts to a new CR species (R = –CH₃ in this case) and is ready for the next chain propagation. Alternatively, the CCH species can undergo continuous hydrogenation to CH₂CH₂ that desorbs from the surface to terminate the chain growth. During the chain propagation, the carbon vacancy of the A-P5 site can be recovered by CO direct dissociation on it and then O can be removed as H₂O or CO₂. The participation of the lattice C from FeC_x bulk in FTS is unlikely—our results show that the barrier of lattice C diffusion from the subsurface to the surface C vacancy is 1.81 eV, much higher than that of CO dissociation. It indicates that the C source of FTS products is mainly the surface C atoms at the active A-P5 sites that can dynamically exchange with CO.

In the following, we will elaborate on the lowest energy reaction pathway for CH₄, C₂H₄ and C₃₊ production in FTS.

CH₄ is formed via the continuous hydrogenation of CH species at the Fe₃ hollow site with an overall barrier of 1.26 eV (blue line in Fig. 4b). The elementary free energy barrier is increasingly higher as more hydrogen attaches, being 0.58, 0.62 and 0.90 eV for the hydrogenation of CH, CH₂ and CH₃, respectively. The TS for the step with the highest barrier, CH₃+H, is illustrated in the inset of Fig. 4c (TS10), where CH₃ stands on the Fe top site and H is located at the bridge site below CH₃ with a C–H distance of 1.61 Å.

C₂H₄ formation (see Fig. S11†) mainly results from the step-wise hydrogenation of CCH around the A-P5 site with an overall barrier of 1.14 eV. The CCH is hydrogenated first to CCH₂ and then to CHCH₂ at the A-P5 site. The final hydrogenation step, CHCH₂ + H, occurs with the highest overall barrier of 1.14 eV, where the CH-end of CHCH₂ shifts to a surface Fe₃ site to react with a coming H.

The FT chain propagation occurs most favorably via the chain intermediate of the CR pattern (R is a hydrogen atom or a saturated alkyl group such as CH₃, and so on) reacting with a surface C monomer. The pathway for C₂ to C₃ as an example is illustrated in Fig. 4b, where a C₂ species (CCH) grows to a C₃ species (CCCH₃). The step-wise hydrogenation of CCH in the A-P5 site results in the formation of CCH₂ and then CCH₃, which have the barriers of 0.69 and 0.42 eV, respectively. It should be noted that the hydrogenation of CCH₂ to CCH₃ has an overall barrier of 0.69 eV (with respect to CCH, state 1, in Fig. 4b), which is 0.30 eV lower than the barrier of CCH₂ hydrogenation to CHCH₂. The hydrogenation of CCH₂ to CCH₃ occurs at the Fe atom bonding with the CH₂ end, which has a C–H distance of 1.58 Å at the TS7 (geometry shown in the inset of Fig. 4c). As the C₂ chain intermediate, CCH₃ has a similar reaction profile to CH. Specifically, the CCH₃ species diffuse and leave the C vacancy after the hydrogenation, which has a barrier of 0.54 eV (0.22 eV lower than CH diffusion). The subsequent coupling between C and CCH₃ needs to overcome a barrier of 0.53 eV, which is 0.05 eV higher than that of C + CH, and finally, a C₃ chain intermediate, CCCH₃, is yielded.

The chain growth mechanism via the C + CR pattern is not unique to the Fe₅C₂ surface as a similar pattern was identified on Ru metal surfaces.⁶³ It implies that the atomic C could generally be the most reactive species for chain growth on FT catalyst surfaces. In addition, the SSITKA experiments on carbided Fe catalysts by Govender et al.^64–66 detected only one kind of H-D mixed C₂ product – C₂H₁D₅ following the switch from H₂/CO to D₂/CO, suggesting the presence of CCH intermediates in C₂₊ hydrocarbon formation. They also observed that the MS signal of C₂H₁D₅ has a similar tailing to that of CH₁D₃ detected in CH₄ formation, which supports the C–CH coupling mechanism in producing C₂ products.

We may also emphasize that not only the surface structure but also the in situ coverage effects of coadsorbates (e.g., C and H atoms and CO molecules)^28,34 are important to FTS kinetics. From our results, at the medium coverage, mixed 0.20 ML CO + 0.05 ML H, CH₄ and CH₂CH₂ formation do have comparable overall barriers (1.26 and 1.14 eV), but a too-low or too-high CO or H coverage will change markedly the selectivity. At a low coverage (mixed 0.05 ML CO + 0.05 ML H) or a relatively high H coverage (0.25 ML H), the barriers of C–C couplings are 0.15–0.25 eV higher while the overall barrier for CH₄ formation varies within 0.1 eV. In the literature, Zhang et al.²⁸ studied the reaction mechanism of CH₄ and CH₂CH₂ formation on unreconstructed Fe₅C₂(510) covered with a layer of H atoms (0.55 ML with respect to surface Fe atoms). Their results showed that the barrier of CH₄ formation is quite low, being only 0.80 eV, while the C–C coupling pathway (CH₂ + CHO) has a higher barrier of 1.10 eV, which is not consistent with the experimental fact that CH₄ is a minor product under FTS conditions.

3.4. Microkinetics

With the quantitative data on the reaction energy and barrier of elementary steps, including CO activation, C hydrogenation, C–C coupling and O removal, we are in the position to derive the kinetics of the whole FTS reaction cycle. Based on the DFT energies, we perform microkinetics simulation to evaluate the reaction rate. The simulation is performed under the typical FTS conditions from 523 to 623 K (interval of 25 K), where the pressures for the gas-phase CO, H₂ and each product (including hydrocarbons from C₁ to C₈, CO₂ and H₂O) are set at 0.83, 1.67 and 0.1 MPa, respectively.

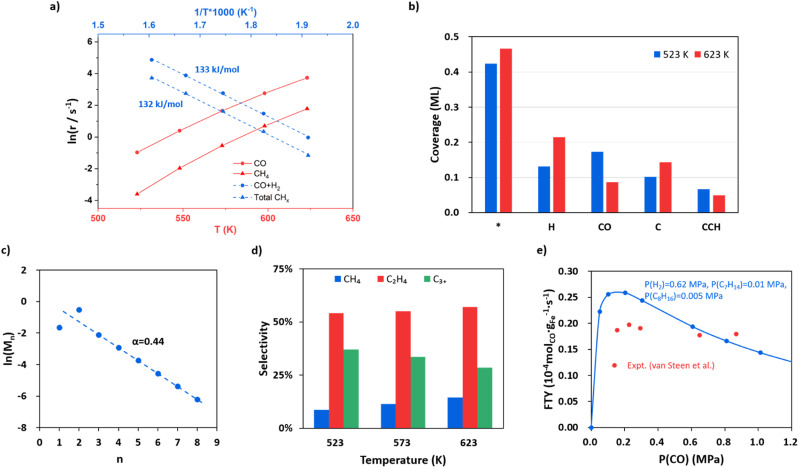
Fig. 5a (the red lines) indicates that the CO consumption and CH₄ formation rates increase 109 and 217 times from 523 to 623 K. The O-consumption is via H₂O and CO₂ formation, where the formation of H₂O is increasingly preferred over CO₂ from 523 to 623 K (Fig. S14†). The calculated CO consumption rate at 548 K is 1.49 s⁻¹ (see Fig. 5a). According to the exposure area of the (510) facet from the Wulff construction of Fe₅C₂ nanoparticles (Fig. S13†), we obtained a theoretical iron time yield (FTY, moles of CO converted to hydrocarbons per gram of Fe per second) of 3.4 × 10⁻⁴ mol_CO g_Fe⁻¹ s⁻¹ (see ESI Section 5.1 for estimation in detail), which is consistent with the experimental values, i.e. 2.3 × 10⁻⁴ mol_CO g_Fe⁻¹ s⁻¹ for single-phase Fe₅C₂ nanoparticles (∼20 nm) at 543 K.²⁵ We also note that the theoretical FTY is 10 times larger than that of the traditional composite catalysts prepared from iron oxide,^2,3 which is apparently because of less concentration of active sites in composite catalysts compared to the pure-phase Fe₅C₂ catalyst. By evaluating the degree of rate control (DRC)⁶⁷ of each elementary step (see ESI Table S7†), the rate-determining step for FT activity (r_CO+H2) at 523 K is determined to be CO dissociation (r_net = 3.1 × 10⁻¹ s⁻¹) with the highest DRC of +0.41. The hydrogenation steps of CCH₂, CHCH, and CHCH₂ to ethene are also slow steps contributing to the overall rate.

Fig. 5. FTS kinetics from microkinetics simulation based on DFT energetics on Fe₅C₂(510) under typical reaction conditions, where pressures are 0.83, 1.67 and 0.1 MPa for CO, H₂ and each product (including hydrocarbons, CO₂ and H₂O), respectively. Two types of reaction sites, the Fe site (*) and the C vacant site ($), are set at a ratio of 10 : 3 (0.77 : 0.23). (a) The steady-state rates in ln(r) as a function of temperature for CO consumption and CH₄ formation and the apparent activation energy for CO + H₂ and total hydrocarbons. (b) Steady-state surface coverage of the main species on Fe₅C₂(510) at 523 K and 623 K. (c) Plot for fitting the chain growth probability factor. (d) The product distributions at 523, 573 and 623 K. (e) Influence of CO partial pressure on FTY. The data from our simulation and the experiment by van Steen et al.⁷⁰ are denoted in blue and red, respectively.

The apparent activation energy is obtained by fitting the rate in ln(r) against the reciprocal of temperature as shown in Fig. 5a blue lines. The overall syngas consumption (CO + H₂) has an apparent activation energy of 133 kJ mol⁻¹, which can be largely attributed to the rate-determining step, CO dissociation. The overall hydrocarbon formation has a similar activation energy of 132 kJ mol⁻¹, while the formation of long-chain products, such as C₅H₁₀ and C₈H₁₆, has lower apparent activation energies (113 and 82 kJ mol⁻¹, respectively, see Fig. S15†), suggesting that the formation of chain intermediate CR species becomes increasingly important compared to the monomer (atomic C) formation. Our results are in agreement with the experimental kinetics observation that the apparent activation energy decreases with increasing carbon number.^68,69

Fig. 5b shows the steady-state surface coverage of key species at 523 and 623 K. The symbols * and $ denote the Fe site and the C vacant site, respectively. The surface is mainly covered by H, CO and atomic C at the surface vacancy (C$), which have coverages of 0.13, 0.17 and 0.10 ML at 523 K, respectively. The coverage of the CO molecule adsorbed at the surface C vacancy is 1.03 × 10⁻² ML, contributing to 6% of the total coverage of CO. Compared to that at 523 K, the coverage of CO at 623 K decreases obviously by 50% (to 8.59 × 10⁻² ML) while the coverage of H increases by 63% (to 0.22 ML), which is apparently because of the sharper reduction of the differential adsorption energy for CO at higher coverages (see the adsorption free energy-coverage plot in Fig. S1†). The coverage of C$ is generally 424 times higher than the coverage of CH$—at 523 K the coverage of C$ and CH$ is 0.10 and 2.40 × 10⁻⁴ ML respectively. This leads to the major C–C coupling channel being CH* + C$ instead of CH*+CH$, although the effective barrier of CH* + C$ is 0.05 eV higher than that of CH* + CH$.

For evaluating the product selectivity, we calculate the distribution of the hydrocarbons using eqn (2) (CO₂ is not included):

2

ln(M_n) = (n − 1)ln α + ln(1 − α) 3

α = r_p/(r_p + r_t) 4

and thus, the chain growth probability factor α from the Schulz formula (eqn (3)) can be obtained, where n is the carbon number of hydrocarbons and M_n is the molar ratio of hydrocarbons with carbon number n. The α value is determined by the rates of chain propagation (r_p) and chain termination (r_t) as shown in eqn (4).

Fig. 5c shows that as the chain grows longer, the product distribution drops exponentially as indicated by the Anderson–Schulz–Flory distribution (the fitted line), whereas the initial two products, CH₄ and C₂H₄, are either below or higher than the predicted value of the Anderson–Schulz–Flory distribution. The lower CH₄ distribution is due to a different active site for methyl hydrogenation to CH₄ (Fe₃ site) with a higher overall barrier of 1.26 eV. The chain growth probability factor α is fitted to be 0.44 at 523 K, which is at the lower limit of those obtained from experiments (α = 0.4–0.7 for Fe-based catalysts with mainly the Fe₅C₂ component).^2–4,15,22 The product distributions at 523, 573 and 623 K are also shown in Fig. 5d. The selectivity to C₂H₄ is the highest among the hydrocarbon products, which is ∼55%, and remained largely constant as the temperature increases. The selectivity to CH₄ increases as the temperature goes higher, from 9% at 523 K to 14% at 623 K, and the selectivity of C₃₊ products drops from 37% at 523 K to 29% at 623 K.

Following the derivation of eqn (4) (see ESI Section 5.2†), we found that the α value is determined by the rates of the hydrogenation of CCHR to CCH₂R and CH₂CHR, not by those of the C–C coupling steps. Specifically, there are three selectivity-controlling steps, corresponding to CH₄ and C₂₊ product formation. The first one is the hydrogenation of CH₃ (CH₃* + H* − > CH₄ + 2*). The other two are the hydrogenation and diffusion of CCHR species, CCHR$ + H* − > CHCHR$ + * and CHCHR$ + * − > CHCHR* + $, which are the steps prior to the chain termination in forming olefin. This can be rationalized as follows. In FTS the C–C coupling step is always faster than the chain termination steps via deep hydrogenation, which is also evidenced by the high coverage of the final states of C–C coupling, such as CCH$ and CCCH₃$ (6.64 × 10⁻² and 2.92 × 10⁻² ML at 523 K) compared to those of deep-hydrogenation intermediates (coverages of CCH₂$ and CCHCH₃$ are 6.43 × 10⁻⁵ and 2.83 × 10⁻⁵ ML, respectively). The variation of the C–C coupling barrier is thus not critical to the overall selectivity. Instead, the chain termination rate controlled by the CCHR hydrogenation steps determines the probability of chain growth.

The influence of CO and H₂ partial pressure on the FTY at 548 K has also been analyzed and the results are shown in Fig. 5e for CO and ESI Fig. S16† for H₂. In Fig. 5e the pressures are set at 0.62, 0.01, 0.005 and 0.1 MPa for H₂, C₇H₁₄, C₈H₁₆ and the other products, respectively. The FTY (also see ESI Section 5.1† for the calculation) is found to be positively correlated with CO pressure when the CO pressure is low (<0.2 MPa), but decreases as the CO pressure goes above 0.2 MPa. Similarly, the reaction order of CO (Fig. S17†) is positive at a CO pressure lower than 0.2 MPa and then becomes negative with increasing CO pressure. When the CO partial pressure is higher than 0.6 MPa, the reaction order of CO is −0.63. The former is caused by the enhanced CO adsorption at the C vacancy, and the latter is due to the difficulty to create the C vacancy (inhibition of hydrogenation) with decreased H coverages. The trend is consistent with the experimental data from van Steen et al.⁷⁰ as also shown in the figure (red points). The FTY gradually increases with increasing H₂ partial pressure with a H₂ reaction order of 0.66 (Fig. S17†).

Interestingly, our kinetic model has a different mechanism from most previous kinetic models,^68,70,71 which assume that the FTS chain grows via the CH₂ or COH₂ monomer, and these monomers are produced from the surface atomic C or CO species. In their model, the rate-determining step was set to be the production of the monomer, e.g. the hydrogenation of C. In order to reproduce the observed positive correlation between CO pressure and the FTS rate at low CO pressure,^68,70,72 these kinetic models have to parameterize the endothermicity for atomic C formation or CO adsorption. However, from our results, the CO adsorption at surface C vacancies and the subsequent atomic C formation (CO dissociation) are both exothermic. It is the endothermic C vacancy formation (CH diffusion) that leads to the pressure-dependent FTS rate.

4. Discussions

4.1. The most active A-P5 site for FTS

From our microkinetics results, the A-P5 site on Fe₅C₂(510) is proven to be the key reaction site for FTS, where the two key elementary steps, CO dissociation and C–CH coupling, occur. Considering that the A-P5 sites are also present on other FeC_x surfaces, it is of interest to compare the activity of A-P5 sites on different surfaces, which should provide important insights into the correlation between FTS activity and the FeC_x phases. By analyzing the stable surfaces of FeC_x phases, we can identify 3, 8, 8, 6, 5 and 7 kinds of A-P5 sites on Fe₂C(111), Fe₇C₃(071), Fe₅C₂(510), Fe₅C₂(021), Fe₃C(031) and Fe₃C(102), respectively, which are slightly different in their neighboring environment. We, therefore, studied the key elementary steps relating to CO dissociation on all these A-P5 sites and the data for the best A-P5 site on each surface are summarized in Table 2. These key elementary steps include the hydrogenation of the four-fold C of A-P5 sites, the CH diffusion out from the A-P5 site, and the CO direct dissociation at the C vacancy. More details of the structures are shown in ESI Table S8.†

The free energetics and Fe–C coordination for the most favorable CO dissociation channels on six surfaces, all on A-P5 sites^a.

Surface	G a(TS1) (eV)	G a(TS2) (eV)	G a(TS3) (eV)	CN(A-P5)	ΔCN
Fe2C(111)	0.88	0.78	2.06	2.06	0.09
Fe7C3(071)	0.86	1.04	1.24	1.55	−0.15
Fe5C2(510)	0.88	0.98	1.31	1.59	−0.14
Fe5C2(021)	0.70	1.14	1.14	1.44	−0.21
Fe3C(031)	0.90	1.16	1.11	1.47	−0.13
Fe3C(102)	0.83	1.40	1.44	1.41	−0.33

^aThe listed data include the effective free energy barriers of C hydrogenation to CH, CH diffusion and CO dissociation (corresponding to TS1, TS2 and TS3 in Fig. 4b), the average Fe–C coordination number of five Fe atoms in the A-P5 site (CN(A-P5)) and the change of CN for the Fe atoms at the A-P5 site coordinated with CH before and after its diffusion (ΔCN).

We found that for the hydrogenation of C to CH, all A-P5 sites have similar low barriers (TS1, 0.70–0.90 eV), while the barrier of the other two reactions (TS2 and TS3, 0.78–1.44 eV) are sensitive to the surface, which are thus the focus of our analysis.

Fe₂C(111) is notably poor in dissociating CO, where the barrier of CO activation is much higher than that on the other surfaces (above 2.05 eV), and Fe₃C(102) has the second highest barrier of 1.44 eV. On the other hand, Fe₇C₃(071), Fe₅C₂(510), Fe₅C₂(021) and Fe₃C(031) have relatively low barriers (1.14–1.31 eV). We also note that only in Fe₃C(031) the barrier of CO dissociation (1.11 eV) is slightly lower than that of the CH diffusion (1.16 eV). Except that, the CO dissociation is generally the step with the highest barrier (text in bold in Table 2).

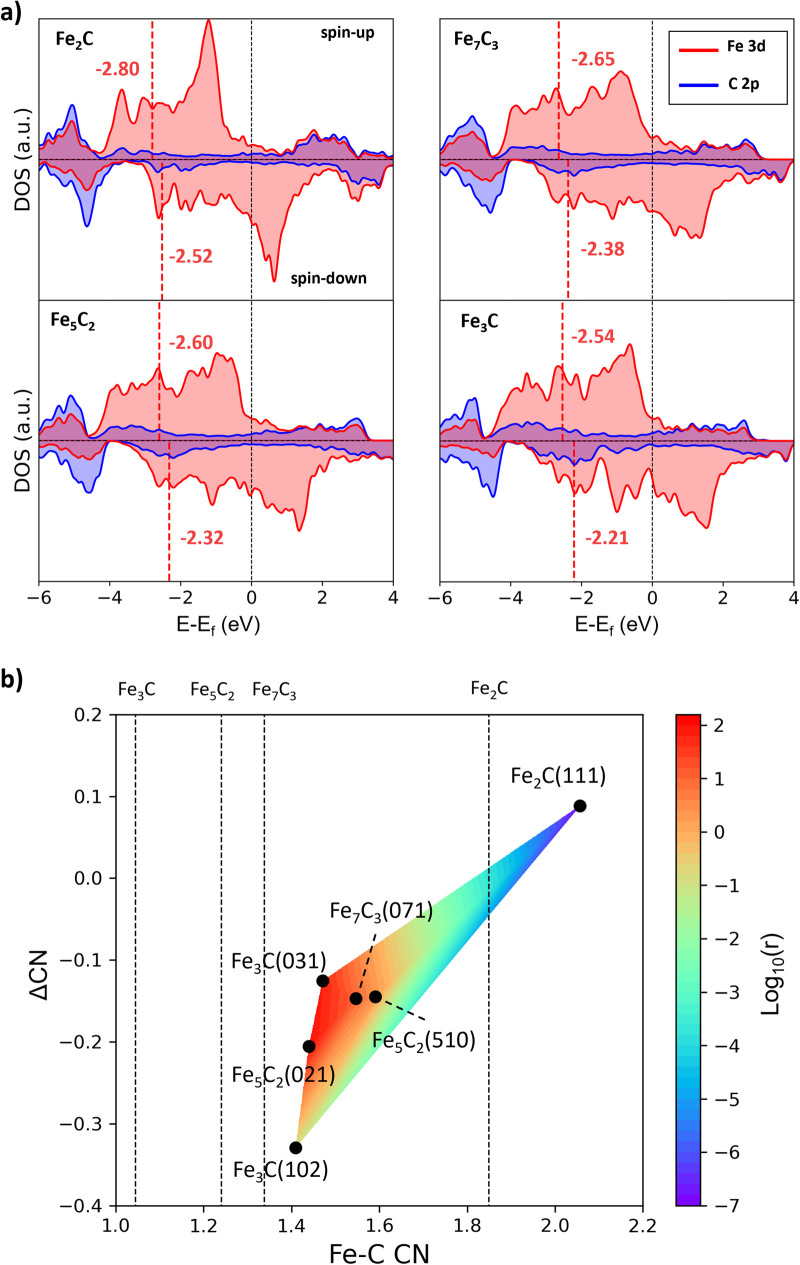
To gain insights into the activity difference between these A-P5 sites, we first analyze the electronic structure of four FeC_x bulk phases, i.e. Fe₃C, Fe₅C₂, Fe₇C₃ and Fe₂C. The projected electronic density of states (DOS) onto Fe 3d and C 2p is shown in Fig. 6a, where with increasing C content in FeC_x, the Fe d-band center (ε_d) shifts downward with respect to the Fermi level, namely from −2.54 (spin-up) and −2.21 (spin-down) eV for Fe₃C to −2.80 (spin-up) and −2.52 (spin-down) eV for Fe₂C. This reflects the passivation of Fe d-states by neighboring C atoms. The Fe atoms in Fe₂C are the most saturated and thus the least active, and the Fe atoms in Fe₃C are the most active with the highest ε_d value. Considering that the monotonic behavior of the bulk ε_d differs from the observed CO dissociation activity that peaks at several Fe₃C, Fe₅C₂, and Fe₇C₃ surfaces, it can be concluded that the bulk ε_d alone is not able to rationalize the activity, which should be surface structure sensitive.

Fig. 6. The bulk electronic structure of FeC_x and activity vs. Fe–C coordination contour plot. (a) Projected DOS on Fe 3d (red) and C 2p (blue) states of four FeC_x bulk phases. The position of the Fe d-band center (ε_d) is denoted by the red vertical line. (b) Contour map for the activity of A-P5 sites with the Fe–C CN and ΔCN as the x-axis and y-axis. The color indicates the CO dissociation rate (log₁₀(r)) calculated using the highest effective barrier in Table 2. The average Fe–C CN of the four bulk phases is also shown by the vertical line.

One step further, we design a structure descriptor, the Fe–C coordination number (CN) as described in eqn (5), which can better distinguish the subtle structural change of the A-P5 site on different surfaces:

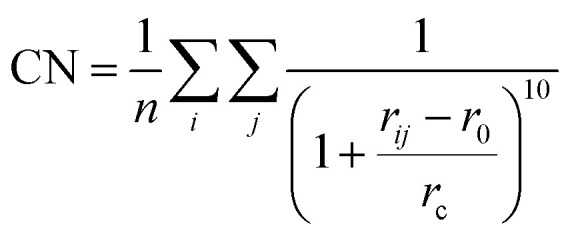5

ΔCN = CN_FS − CN_IS 6

where i is the selected Fe atom on the surface site and j is the neighboring C atom within the cutoff radius r_c (2.50 Å). r_ij is the distance between i and j, and r₀ is set at 1.80 Å. n is the total number of the involved Fe atoms. By using eqn (5), we compute two quantities to represent the environment of the A-P5 site related to CO dissociation and CH diffusion: (i) CN(A-P5), the average CN of five Fe atoms in the A-P5 site considering that the CO dissociating TS bonds with all five Fe atoms of the A-P5 site; (ii) ΔCN, the change of the average CN for the Fe atoms coordinated with CH before (CH at the four-fold hollow site of Fe₄, CN_IS in eqn (6)) and after its diffusion (CH at the three-fold hollow site of Fe₃, CN_FS in eqn (6)). The ΔCN thus measures the homogeneity of the Fe bonding environment of the A-P5 site, which affects the diffusion barrier of CH. Our results for CN(A-P5) and ΔCN are also listed in Table 2. By correlating the barriers with the CN values, we found that a smaller CN(A-P5) is beneficial to lowering the CO dissociation barrier, and the larger ΔCN can promote CH dissociation (see ESI Fig. S18† for the linear fitting of the data). For example, Fe₂C(111), which has the largest ΔCN and CN(A-P5), has the smallest barrier of CH diffusion (0.78 eV) and the largest barrier of CO dissociation (2.06 eV).

Based on the CN(A-P5) and ΔCN data, we can plot a contour map for the activity of the A-P5 sites in Fig. 6b. The color indicates the rate (log₁₀(r)) calculated from the Arrhenius equation using the highest effective barrier of each site. We found that for the sites with high activity (region dominated by red in Fig. 6b), i.e. Fe₃C(031), Fe₅C₂(510), Fe₅C₂(021) and Fe₇C₃(071), both CN(A-P5) and ΔCN are at the medium values (1.44–1.59 and −0.21–−0.13), neither too large nor too small. The negative ΔCN suggests that the Fe₃ of the A-P5 site (CN_FS) needs to have a lower Fe–C CN compared to the Fe₄ of the A-P5 site (CN_IS).

It should be emphasized that all the A-P5 sites on the six surfaces have larger CNs than that of the corresponding bulk phases (the vertical lines indicate the CNs of FeC_x bulk, which are 1.85, 1.34, 1.24 and 1.04 for Fe₂C, Fe₇C₃, Fe₅C₂ and Fe₃C, respectively). This is due to the surface reconstruction where C tends to aggregate onto the FeC_x surface and the surface Fe : C ratio turns out to be close to 2 for stable surfaces.

From the map, pure Fe₃C, Fe₅C₂, and Fe₇C₃ can be good FT catalysts by themself. Fe₃C, however, is thermodynamically unstable under the FT conditions of producing olefins (μ_C < −7.2 eV). On the other hand, since the best A-P5 site has a medium CN (∼1.5), in between the values of the bulk CN of Fe₇C₃ and Fe₂C, for a typical FT catalyst synthesized from iron oxide, a fractional presence of Fe₂C in situ formed under reaction conditions could be a good indicator for the presence of the active surface with a large enough CN (compared to metallic Fe). The active surfaces are not limited to a single bulk phase of FeC_x, but can be Fe₃C, Fe₅C₂ and Fe₇C₃ surfaces that grow upon Fe₂C bulk phases. Indeed, Wang et al.⁷³ used extended X-ray absorption fine structure spectroscopy (EXAFS) and X-ray absorption near edge structure (XANES) techniques to analyze the Fe–C coordination and iron oxidation state of their prepared Fe catalysts (mixtures of χ-Fe₅C₂, Fe₃O₄ and amorphous FeC_x), and they found that the catalyst with a too low bulk iron oxidation state and Fe–C coordination number turns out to be less active to FTS.

4.2. FeC_x active sites in composite FTS catalysts

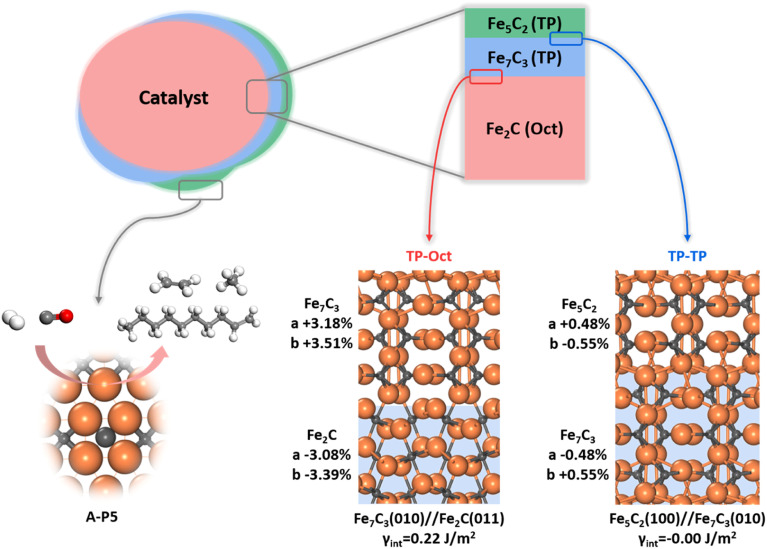
Since multiple FeC_x phases coexist in FTS, it is of significance to answer how they attach with each other. Naturally, if one phase can grow upon another phase readily, forming a coherent solid–solid interface, the exact nature and amount of the bulk phase would be less important as to the surface-active site. This picture of the FTS active site can be schematically drawn in Fig. 7, where the most thermodynamically stable Fe₂C under reaction conditions is the dominated carbide bulk phase and the other carbide phases with lower Fe : C ratios, i.e. Fe₇C₃ and Fe₅C₂, grow upon Fe₂C via the possible solid–solid junctions. The facets with active A-P5 sites, i.e. Fe₅C₂(510), Fe₅C₂(021) and Fe₇C₃(071), can always expose no matter the amount of bulk Fe₂C phases.

Fig. 7. FTS active site model. Different FeC_x phases grow coherently upon the thermodynamically most stable Fe₂C bulk phase and the active site can be created after surface reconstruction under reaction conditions. Two representative interface structures obtained from the ML-interface method, i.e. Fe₂C(011)//Fe₇C₃(010) (TP-Oct) and Fe₇C₃(010)//Fe₅C₂(100) (TP–TP), are shown.

To determine the possible interface between different FeC_x phases, we have attempted to utilize the ML-interface⁷⁴ to build the junction using the most stable surface of four bulk phases, i.e. Fe₃C(010), Fe₅C₂(100), Fe₇C₃(010) and Fe₂C(011), since we notice that they have similar atomic arrangement and lattice parameters (a = 4.69, 4.54, 4.52, 4.47 Å and b = 5.14, 4.96, 4.99 and 5.03 Å for Fe₂C(011), Fe₇C₃(010), Fe₅C₂(100) and Fe₃C(010), respectively). Our results show that these four FeC_x phases can indeed form a coherent interface with each other, which have both low interfacial energy (<0.22 J m⁻²) and low strain (<5%).

Fig. 7 also highlights the two types of coherent interfaces identified by the ML-interface, differing in the Fe–C coordination patterns at the junction, namely TP–TP and TP-Oct junctions. The other interface structures can be found in ESI Fig. S19.† We note that TP-Oct interfaces have larger interfacial energies (0.12–0.22 J m⁻²) and strain (3–5%) compared to TP–TP (−0.00–0.02 J m⁻² and 0.5–1.6%). The favorable energetics and the low strain confirm that the interfaces between these FeC_x phases are thermodynamically stable and well likely present during FTS. For the TP-Oct junction, the lattice of the TP phase is expanded by 3–5% while the lattice of Fe₂C is compressed. For the TP–TP junction, one direction of the TP lattice is expanded and the other one is compressed. Interestingly, based on the interface model, the lattices of Fe₇C₃ and Fe₅C₂ in two directions grown on Fe₂C will be expanded by 3.18 and 3.51% and 3.68 and 2.95%, respectively. Specifically, after the Fe₅C₂ lattice expansion, the CN(A-P5) and ΔCN of Fe₅C₂(510) decrease from 1.59 to 1.49 and −0.14 to −0.16, respectively, both shifting towards the better activity region (see Fig. 6b). This implies that the local Fe–C CN can be further tuned by the carbide phase evolution during FTS, which may further boost the FT activity.

It should be mentioned that a few tens of atomic layers in Fe-based catalysts have been characterized by surface-sensitive techniques recently. Shipilin et al.⁹ observed the coexistence of TP- and Oct-carbides on an Fe(110) single-crystal surface at various temperatures and gas compositions (e.g., at 548 K (H₂/CO = 4) or 485 and 506 K (H₂/CO = 1 and 2) from 85 to 700 mbar) by C 1s XPS, while only Fe₃C (TP carbide) can be detected by surface XRD at 623 K and 150 mbar (H₂/CO = 4). This finding supports that TP- and Oct-carbides can grow upon each other, which is in agreement with our theoretical model for the active site—the active site on the reconstructed surface may well be different from that derived from dominant FeC_x bulk phases. Importantly, our model could rationalize the intriguing experimental findings that virtually all FeC_x bulk phases were suggested to be the active phase as characterized by in situ XRD and Mössbauer spectroscopy. On the other hand, it should be emphasized that the surface phases are complex in FTS experiments. In particular, the presence of iron oxides is well confirmed by XPS^10,15 and X-ray absorption spectroscopy,⁷⁵ which might be due to the incomplete carburization during the activation and the oxidation by H₂O and CO₂ products. The iron oxides may well contribute to the FT activity, specifically in the O cycle. The interplay between oxides and carbides needs further investigation.

5. Conclusion

This work develops an ML-TS reaction exploration method to resolve the FTS reaction network, focusing on CO activation and C–C coupling. The ML-TS method explores thousands of pathway candidates and identifies low-energy pathways on FeC_x surfaces by taking into account the degrees of freedom of both molecular configurations and the surface structure dynamics at finite coverages. The complex nature of FeC_x surfaces is reflected by four bulk phases, a number of energetically degenerate stable surfaces and at least six types of surface sites with distinguishable Fe–C local bonding patterns.

The active site is revealed to be an A-P5 site abundant on several stable Fe₃C(031), Fe₅C₂(510), Fe₅C₂(021) and Fe₇C₃(071) surfaces, which consists of five Fe atoms with an Fe₄C carbide square neighbored by an edge-sharing Fe₃ metal-like hollow site. We show that both CO activation and C–C coupling can occur on the A-P5 site. On the A-P5 site of Fe₅C₂(510) CO activation occurs via C-vacancy-mediated direct dissociation with a barrier of 1.16 eV, and the lowest-energy pathway for C–C coupling is C + CH with a low barrier of only 0.48 eV.

Microkinetics simulation based on the first principles kinetics data show that the FTY on Fe₅C₂(510) is 3.4 × 10⁻⁴ mol_CO g_Fe⁻¹ s⁻¹ and the chain growth probability factor α is 0.44. The rate-determining step is CO dissociation, and the selectivity-controlling steps are determined to be the hydrogenation reactions prior to the chain termination in forming methane and olefin.

We also show that an optimal Fe–C CN ensemble is required to achieve the highest FT activity, where the CN(A-P5) and ΔCN are at the medium values (1.44–1.59 and −0.21–−0.13). The negative ΔCN suggests the Fe₃ metal-like part of the A-P5 site needs to have a lower Fe–C CN compared to the other Fe₄ part. The active site Fe–C CN(A-P5) could be much higher than the corresponding bulk values, suggesting that the active site does not necessarily relate to the bulk phase. The active-site–bulk structure independence is further confirmed by the fact that all FeC_x phases can achieve coherent interfaces with each other with either TP–TP or TP-Oct low-energy interfaces.

Data availability

The LASP code, Fe–C–H–O G-NN potential and the training data set are available on the LASP website (http://www.lasphub.com/).

Author contributions

Z.-P. L. and C. S. conceived the project and contributed to the design of the calculations and analyses of the data. Q.-Y. L. carried out most of the calculations and wrote the draft of the paper. D. C. wrote the ML-TS/lasp code. All authors discussed the results and commented on the manuscripts.

Conflicts of interest

The authors declare no competing financial interests.