Predictive overfitting in immunological applications: Pitfalls and solutions

ABSTRACT

Overfitting describes the phenomenon where a highly predictive model on the training data generalizes poorly to future observations. It is a common concern when applying machine learning techniques to contemporary medical applications, such as predicting vaccination response and disease status in infectious disease or cancer studies. This review examines the causes of overfitting and offers strategies to counteract it, focusing on model complexity reduction, reliable model evaluation, and harnessing data diversity. Through discussion of the underlying mathematical models and illustrative examples using both synthetic data and published real datasets, our objective is to equip analysts and bioinformaticians with the knowledge and tools necessary to detect and mitigate overfitting in their research.

Introduction

Machine learning (ML) and statistical modeling have become important tools in modeling medical data and prediction of disease outcomes and vaccination responses in immunological research.^1–5 However, the application of ML algorithms necessitates caution. A common occurrence in misusing ML algorithms is overfitting, which arises when a predictive model fits well to training data but performs poorly on new data due to excessive model complexity.^6,7 The implications of overfitting in medical research can result in the erroneous publication of immunological markers that are highly predictive on the training data but generalize poorly to untouched test datasets. Put another way, overfitted models perform well in their respective studies, but do not generalize to novel datasets. To this end, recognizing and avoiding common pitfalls that can lead to overfitting in contemporary immunological research is of paramount importance.

This review delves into the prevalent scenarios that contribute to overfitting and then presents strategies to counteract its effects. We structure the content into three primary themes:

• The double-edged nature of model complexity.

• Reliable model evaluation.

• Harnessing data diversity.

Our objective is to provide analysts and bioinformaticians with the concepts and tools required to detect and circumvent overfitting in their modeling and analysis endeavors, informed by the latest advances in statistics and machine learning.

Double-edged nature of model complexity

Model complexity, which quantifies the complexity of a model and its fit to the training data, is a crucial concept in understanding the phenomenon of overfitting. A predictive model’s complexity increases with increased number of independent features, such as analytes. Model complexity also increases when a more intricate model architecture is used, such as comparing linear regression to a deep neural network. Modern immunological studies have enabled access to a vast array of tens of thousands of analytes. In addition, off-the-shelf machine learning tools have facilitated easy access to non-linear modeling for capturing the interactive effects among biological processes.⁸ Both of these trends have given rise to more complex and flexible models and reduce the training errors which measure the estimation error of the response on the training data. However, a flexible model does not always lead to improved prediction accuracy on new data (referred to as test data) not used during model fitting.

On the one hand, a more complex model might have a smaller test error which measures the prediction error of the response on the untouched test data. This is achieved by reducing the model bias which measures the distance between the expected/average estimated models and the underlying true model. Here, the averaging of the estimated models is done across models constructed using repeated regenerations of training data. On the other hand, it is important to note that fitting a more complex model also introduces a higher model variance in the prediction function. That is, if the training data were regenerated independently, the resulting fitted model could differ substantially. This interplay between model complexity, model bias, and model variance is commonly referred to as the bias-variance tradeoff. This offers a clear mathematical perspective on how model complexity affects the prediction performance on novel test data: while an overly simplified model might fail to capture strong predictive relationships and lead to underfitting, excessively high model complexity can cause the model to overfit by excessively fitting to the noise in the training data, thereby compromising its performance (Figure 1a).

Figure 1.

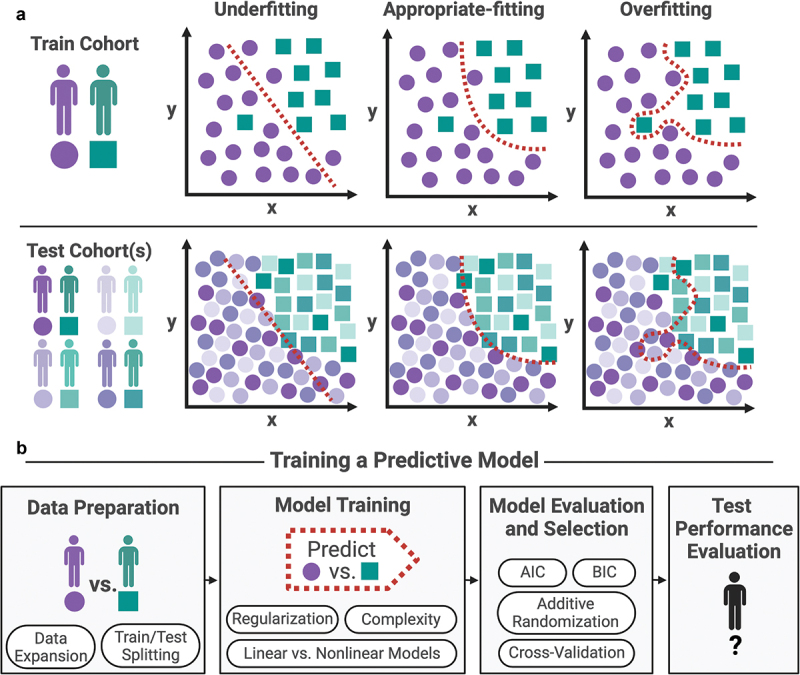
(a) Examples of underfitting, appropriate-fitting, and over-fitting a machine learning model to a training cohort. Underfitting oversimplifies the relationship between predictive features whereas over-fitting fails to generalize to novel test cohorts that were not used to train the machine learning model. (b) Schema for effective training of a predictive model, including data preparation, model training, model evaluation and selection, and finally test performance evaluation. Tools for good machine learning practice provided are further explored in the manuscript.

The effects of underfitting and overfitting become evident when evaluating the model on novel datasets. For instance, if we employ ordinary least squares (OLS) to fit a linear regression model with an equal or greater number of features than the features in the training dataset, the model can usually perfectly explain the response in the training cohort. However, such models often fail to generalize well when predicting outcomes for new test samples. The same overfitting issue may happen when adopting a highly non-linear model. Another example described in a study by Peng et al.⁹ involves the use of support vector regression to forecast COVID-19 cases in severely affected countries, employing both linear and non-linear predictive models. While the non-linear fit demonstrated superior performance during training, it was the linear fit that achieved the best results on the test data. These two examples emphasize the need for caution when employing machine learning models in medical decision-making.

Finally, to illustrate the issue of overfitting in the immunological application, we present Example 2.1 where xgboost^10,11 was employed to identify common immune signatures that predict antibody responses using a recently curated database.

Example 1.

Consider the identification of common PBMC transcriptomics signatures for predicting antibody responses across 13 different vaccines by Fourati et al.,⁷ covering live viruses, inactivated viruses, and glycoconjugate vaccines, collected by the Human Immunology Project Consortium (HIPC) as the Immune Signature Data Resources.¹⁴ We demonstrate the phenomenon of overfitting by constructing models with varying complexity using the 500 most variable genes to separate high-responder (267 participants) from low-responder (265 participants) groups, defined from discretizing maximum fold change antibody responses (day 28/day 0). To evaluate how well the model generalizes to new test samples, we split the data into the training set and the validation set, with the model trained using only the training and classification accuracies recorded for both the training and the validation. This scheme was repeated five times, and results were averaged to increase the evaluation stability. The classification accuracy is measured by area under the receiver operating characteristic (AUROC), with higher value indicating better classification. Figure 2 displays the training AUROC and validation AUROC of prediction models trained from xgboost over the training rounds, with the tree depth being 1 or 6. At each training round, xgboost constructs a tree of depth 1 or 6 to improve the current fit and aggregate the newly constructed tree into the prediction model to increase model complexity. As the training rounds increased, the predictions within training samples achieved high accuracy, with AUROC improving for both tree depths. However, the validation AUROC is much lower. Selecting a model with highest training AUROC can lead to overfitting where the validation AUROC is worse compared to earlier training rounds. Furthermore, the model with a tree depth of 6 quickly overfitted from the inclusion of highly non-linear. It achieved almost perfect training AUROC but achieved worse validation AUROC than the simpler xgboost model with a tree depth of 1.

Figure 2.

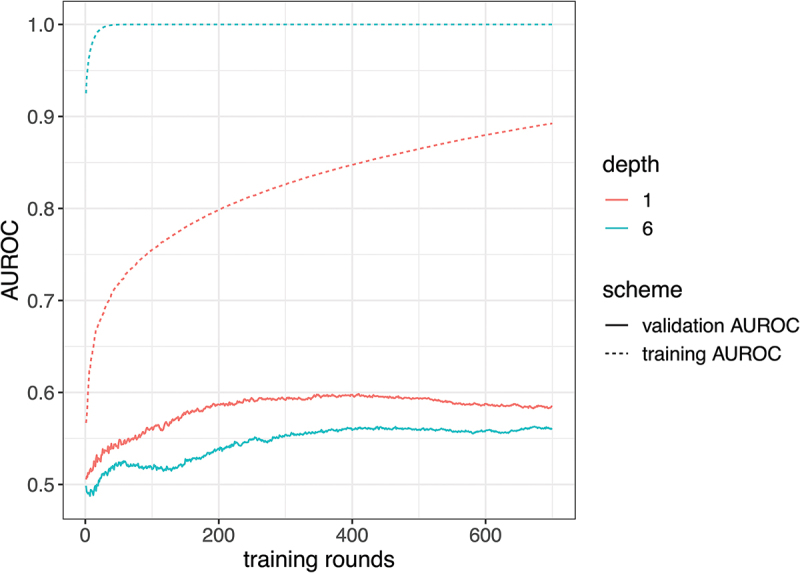
Training AUROC and validation AUROC for predicting high/low responders (y-axis) using xgboost against the training rounds (x-axis). It shows the model performances in training or cross-validation as the training rounds increased (increased model complexity) and compares the prediction performance when using trees with depth being 1 (low non-linearity) or 6 (high non-linearity).

Ideally, the objective is to construct a model that strikes a favorable tradeoff between model bias and model variance, thereby achieving an appropriate level of fitting for good prediction performance on the test samples (Figure 1a). In this review, we discuss three important aspects of good practices for appropriate model fitting: model training, model selection, and evaluation (Figure 1b). Finally, we review the utilization of data diversity and its application to avoiding overfitting.

Model complexity reduction

Learning the available strategies to effectively control or reduce model complexity is an important step in taking full advantage of the wide array of machine learning tools. Here, we review model complexity reduction approaches based on regularization and dimensionality reduction.

Regularization

Regularization is one of the most widely used techniques for reducing the model complexity of prediction models. Given a loss function, which is the user-specified objective that measures the goodness of model fit, e.g., mean-squared error is the loss function for OLS, the standard regularization involves adding a penalty term to the loss function to discourage the model from learning overly complex patterns. As a concrete example, let $x_i$ and $y_i$ be the observed $p$ analytes and response for training sample $i$, with $i=1,\dots ,n$, for $n$ total samples. Regularized linear regression considers the following regularized loss function:

$$L_{\lambda }\left(\beta \right)=\frac{1}{2}\sum _{i=1}^n{\left(x_i\beta -y_i\right)}^2+\lambda J\left(\beta \right),$$

where $\beta$ is a vector contains the coefficients of the linear model and ${\beta }_{\mathrm{j}}$ is the coefficient for analyte $j$ for $j=1,\dots p$, and $J\left(\beta \right)$ is the regularization or penalty term to encourage simpler $\beta$, thus, a less complex model. $\lambda$ is the amount of penalty included, with larger $\lambda$ favoring a simpler model. Some of the popular forms for $J\left(\beta \right)$ are listed below.

• Best subset selection defines $J\left(\beta \right)={\sum }_{j=1}^p{\left|{\beta }_j\right|}^0$ with ${\left|{\beta }_j\right|}^0$ being 0 if ${\beta }_j$ is 0 and 1 otherwise. It penalizes the number of non-zero entries in $\beta$. The problem of best subset selection can be difficult to solve in general.¹² There have been many approximation algorithms for this purpose. For example, forward stepwise selection can be seen as a greedy algorithm for the best subset selection.¹³

• Ridge (or ${\mathrm{l}}_2$) regularization defines $J\left(\beta \right)={\sum }_{j=1}^p{\left|{\beta }_j\right|}^2$ as the square sums of entries in $\beta$.¹⁴

• Lasso (or ${\mathrm{l}}_1$) regularization defines $J\left(\beta \right)={\sum }_{j=1}^p\left|{\beta }_j\right|$ to penalize sum of the absolute values of entries in $\beta$

¹⁵

In the family of penalty loss $J\left(\beta \right)={\sum }_{j=1}^p{\left|{\beta }_j\right|}^{\alpha }$ that penalizes the ${\alpha }^{th}$ power of $\left|{\beta }_j\right|,$the lasso penalty with $\alpha =1$ is a special case because it is the turning point where we can encourage sparsity (a small number of non-zero entries in $\beta$) while being able to solve the problem effectively. That is, when $\alpha \le 1$, sparsity is encouraged in $\beta$, but it is difficult to solve the general problem exactly for all $\alpha <1$.

There are other types of regularization penalties proposed by statisticians. For example, the elastic net penalty¹⁶ considers a mixture of lasso penalty and ridge penalty to encourage sparsity and the co-selection of highly correlated features, which can be desirable in immunological applications for interpretation.¹⁷ The grouped lasso penalty encourages the co-selection of features from the same group specified by the users.¹⁸

The idea of regularization through penalty losses is also applicable to other non-linear machine learning techniques, such as boosting and neural networks. In addition, regularization does not only come in the form of penalty losses. For example, dropout is a popular and effective technique to prevent overfitting in neural networks.¹⁹ At each updating step during training, a percentage of nodes and connections from the neural network are randomly dropped. This can also be viewed as training with an adaptive regularizer that incorporates the effect of artificial feature noising.²⁰

Early stopping is another technique used to train machine learning models, including boosting and neural networks, to prevent overfitting by stopping the training process before the model starts to overfit the training data.^7,21 This procedure can be viewed as a form of implicit regularization with effects similar to ridge regularization in some cases.^22,23

Dimension reduction

Dimension reduction can also be an effective way to reduce model complexity and is commonly used in contemporary immunological studies. It has been one of the main techniques for working with high-dimensional immune profiles, such as high-dimensional transcriptomics or complex multi-omics observations.^24–26 Dimension reduction addresses the challenge of high dimensionality by constructing low-dimensional factors to capture data variation from available omics. These factors can be used for both biological interpretation and prediction tasks of interest (Figure 3).^27,28 Working with low-dimensional factors helps to alleviate potential overfitting issues because the number of features, and therefore model complexity, is reduced.

Figure 3.

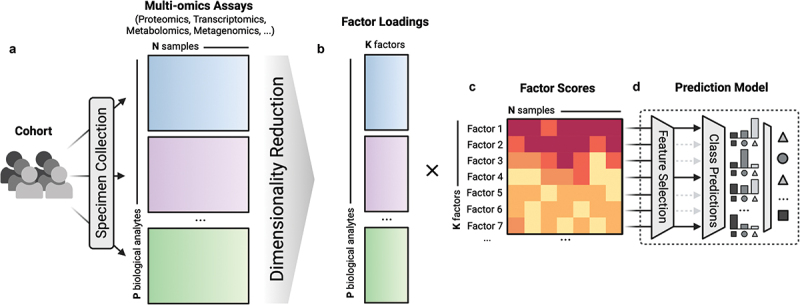
An illustration workflow of multi-omics dimensionality reduction. (a) Multi-omics assays are profiled from the same cohort, resulting in multi-omics profiles for the same N samples. (b) P biological analytes are condensed via dimensionality reduction into the construction of low-dimensional factors, consisting of factor loadings and factor scores. Factor loadings are coefficients that indicate which biological analytes are contributing to construction of the each factor. (c) All N samples from the cohort are assigned a score for each of the K factors, resulting in the factor scores matrix. (d) The resulting factor scores can be used as machine learning features to predict responses of interest in a prediction model.

Matrix factorization provides core concepts for dimension reduction with high-dimensional data and serves as the foundation of many dimension reduction tools for omics and multi-omics analyses in immunological studies. Suppose we have collected observations for $p$ analytes across $n$ samples and denote the observed matrix as $X\in {ℝ}^{n\times p}$ for these $n$ samples and $p$ analytes. The number of analytes, $p,$ is often large. The central goal of matrix factorization is to approximate $X$ by the product of$a$ factor matrix $U\in {ℝ}^{n\times K}$ and a loading matrix $V\in {ℝ}^{p\times K}$ for some $K$ much smaller then $p:$

$$X\approx U{V}^{\mathrm{\top }}.$$

The factor matrix is constructed for capturing the variation across $n$ samples using $K$ factors (columns in $U$), and the loadings matrix describes each factor’s influence on the analytes (columns in V). For example, in gene expression analysis, it can identify groups of genes that may be involved in underlying biological processes or functions, with factors capturing the variation of these processes across samples.

Widely used matrix factorization techniques principal component analysis (PCA) and single-value decomposition (SVD)^29,30 derive $U$ such that $U$ can explain the maximum amount of variance across features in $X$. Non-negative matrix factorization (NMF) requires additionally that $U$ and $V$ contain only non-negative values, which was originally proposed to work with image data where this non-negativity constraint leads to better interpretability.³¹ The sparse PCA algorithm imposes that columns in $V$ have sparse non-zero entries, which can lead to higher quality estimation in high dimensions and often improved interpretability by highlighting a smaller set of features for each factor.³² There are many other variants of PCA for dimension reduction that could prove useful in analyzing omics data, such as hub-feature identification which identifies a small subset of hub-features as drivers of the systematic level changes^33,34 and autoencoder methods for dimension reduction with non-linear model architectures.³⁵

Of note, the concept of matrix factorization is frequently combined with co-expression networks in omics analysis.^36,37 For instance, the widely used weighted correlation network analysis (WGCNA)³⁸ approach first identifies modules as non-overlapping subsets of co-expressed genes or other features and uses the eigenvectors for genes from each module to capture variability of features in the given module.

Given the increasing availability of large-scale multi-omics data, it is crucial to perform dimension reduction appropriately with multi-omics observations. While matrix factorization approaches can be directly applied after concatenating features from different omic assays, this is generally not advisable due to the varying dimensionality and data properties from different technologies. For example, instead of using WGCNA on concatenated data, it has been suggested to perform a two-step procedure where we first apply WGCNA to individual omics assays and align different assays as a second step.³⁹

Many popular matrix-factorization-based approaches have been developed for dimension reduction with multi-omics data, such as JIVE⁴⁰ as a generalization of PCA, jNMF and iNMF as generalizations of NFM.^41–43 Multi-omics integration methods based on Bayesian factor models have also gained popularity, which enables flexible modeling of different omic data types and introduction of suitable priors. Multi-omics integration tools like iCluster,⁴⁴ iClusterBayes,⁴⁵ and MOFA^46,47 employ such Bayesian factor models.

A different perspective for dimension reduction is taken by Canonical correlation analysis (CCA),⁴⁸ which extracts factors to capture co-varying patterns between two matrices instead of aiming for the maximization of explained variance as in matrix factorization. This idea can be useful by connecting different types of omics together to form a more comprehensive picture of the underlying biology. For instance, Li et al.²⁸ linked metabolomic profiles with transcriptomic profiles using CCA to gain an improved understanding of vaccination response. This concept has been generalized to work with multiple data blocks simultaneously, and we consider all methods based on the generalization of CCA as belonging to the generalized CCA (GCCA) family. GCAA has motivated the development of several multi-omics integration methods such as multiple co-inertia analysis (MCIA),^49,50 regularized GCCA (rGCCA),^51,52 and multi-block sparse CCA (msCCA).⁵³

In this direction, supervised dimension reduction techniques have been proposed to identify factors predictive of responses of interest.^54–59 In multi-omics analysis, for example, DIABLO⁵⁸ includes the response matrix as another assay in dimension reduction using GCCA, while SPEAR⁵⁹ prioritizes the construction of factors in a Bayesian multi-omics factor model. To some extent, we can view supervised dimension reduction as preventing overfitting by using regularization to deviate from the meaningful data variation directions.

Reliable model evaluation and selection

In the previous section, we discussed many popular techniques for model complexity reduction, which can effectively avoid overfitting. Equally important is the reliability of model evaluation, crucial for parameter tuning, model selection, and understanding the prediction model and its usefulness. In this section, we will review model evaluation methods and discuss potential pitfalls.

AIC, BIC, and additive randomization

Akaike Information Criterion (AIC)⁶⁰ jointly considers the goodness-of-fit and model complexity, measured by the number of parameters in the model:

$$\mathrm{A}\mathrm{I}\mathrm{C}=-\frac{2}{n}\cdot \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{i}\mathrm{k}+2\cdot \frac{s}{n},$$

where $loglik$ is the achieved log-likelihood summed over all $n$ training samples, and $s$ is the number of parameters used to characterize model training. For instance, if we consider a linear regression model where the noise follows a standard normal distribution, then, $\frac{2}{n}\cdot \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{i}\mathrm{k}$ becomes the mean-squared error in OLS and $s$ is the number of features used in the linear model. In this case, the AIC statistic is equivalent to Mallow’s $C_p$ statistic,⁶¹ whose expectation is unbiased for the prediction error. In general, the AIC aims to achieve this unbiasedness. Hence, by design, lower AIC statistics indicate better fitting of models, which can be very useful for selecting among competing models.

However, AIC may not always achieve this goal in practice. One significant issue in using AIC is determining $s$, as it is common that the number of parameters appearing in the trained model, does not always reflect the actual complexity of the model’s training process.

Bayesian Information Criterion (BIC)⁶² adopts a similar form to AIC, with more penalization on $s$:

$$\mathrm{B}\mathrm{I}\mathrm{C}=-\frac{2}{n}\cdot \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{i}\mathrm{k}+p\cdot \frac{s}{n},$$

where $p$ is the total number of parameters. Since $p>2$ in most settings, it penalizes complex models more heavily and favors the selection of simpler models compared to AIC. Despite the similarity between BIC and AIC, BIC has a different motivation. Approximately, selection of the model with minimum BIC is equivalent to choosing the model with the largest posterior probability in the Bayesian framework.⁶³

Determining $s$ to reflect the model complexity can be challenging at times, even in the linear regression setting as demonstrated in Example 3.1.

Example 2:

Suppose that $x\in {\mathbb{R}}^{1000}$ is a vector contains 1000 features, where each feature $x_j$ is generated from a standard normal distribution for $j=1,\dots ,1000$, and the response $y=x_1{\beta }_1+$ $\epsilon$ depends only on the value of the first feature. Independent noise $\left(\epsilon \right)\hspace{0.17em}$is then generated from a standard normal distribution. Figure 4a,b show training errors, AIC, BIC, and prediction errors as well as error estimates from the additive randomization method (see later) for forward stepwise selection with subset size $0\le s\le 10$, averaged over 10 random repetitions.

Figure 4.

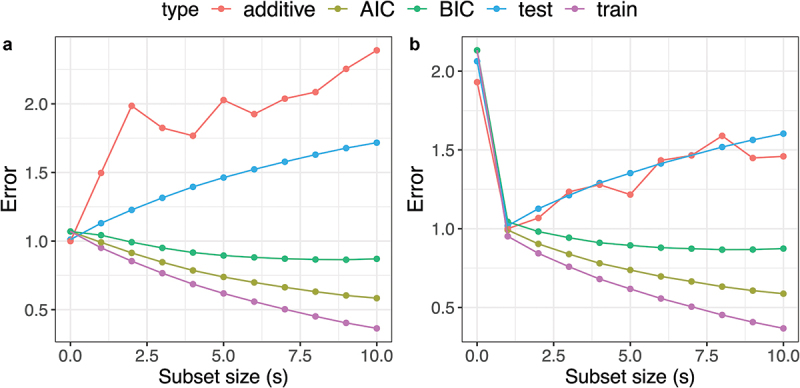
A comparison of error estimate from additive randomization (denoted as “additive”), AIC, BIC, the true prediction error (denoted as “test”), and training error (denoted as “train”) in example 2. Panels a and B shows the results for $\beta =0$ and $\beta =1,$ respectively as we vary the subset size ($s)$. The prediction performance in this example is not able to be tracked by the training error, AIC or BIC.

The issue with using AIC and BIC in Example 2 arises from the fact that the model at each subset size $s$ is not fixed but adaptively constructed and selected from the data, which is common with high-dimensional data. Following the endeavor of AIC to perform a fair evaluation of the bias-variance trade-off, the additive randomization method⁶⁴ was proposed to measure the prediction performance among competing models regardless of complex training and selection procedures. The core idea of additive randomization is to construct randomized responses $y^{+}$ and $y^{-}$ as shown below,

$$y^{+}=y+\alpha \omega =\mu +\epsilon +\alpha \omega ,y^{-}=y-\frac{1}{\alpha }\omega =\mu +\epsilon -\frac{1}{\alpha }\omega ,$$

where $\mu =\mu \left(x\right)$ is the underlying signal depending on the feature value $x$, and $\omega$ is additional additive noise from a standard normal distribution generated by the analyst, which is used in the construction of responses $y^{+}$ and $y^{-}$ after multiplying by the scalers $\alpha$ and $\frac{1}{\alpha }$ respectively. This particular form of construction guarantees the mutual independence between $y^{+}$ and $y^{-}$. Motivated by such an observation, the additive randomization method uses $y^{+}$ for all model training, while using $y^{-}$ to measure the model predictive performance and select a final model with the smallest loss using $y^{-}$. It is worth noting that only the relative loss values here are meaningful, as the absolute loss calculated from using $y^{-}$ does not resemble the true prediction error. In Figure 4, we have shifted the loss estimated with additive randomization such that the best model corresponds to a value of 1. Unlike AIC and BIC, the evaluations from using additive randomization successfully identified the model with the best prediction performance in both experiment settings. The drawbacks of the additive randomization are threefold: (1) it is currently only applicable to linear regression problems with Gaussian data, (2) it requires knowledge of the noise distribution, and (3) the randomization renders higher variability, as seen in Figure 4.

Cross-validation

Cross-validation (CV) is a widely used technique for assessing the performance of machine learning models and model selection to prevent overfitting.^65,66 Its popularity can be attributed to its conceptual simplicity, improvement of data utilization efficiency over sample-splitting, and wide applicability to all types of supervised machine learning models.

CV starts by dividing the training samples into $K$ disjoint subsets (folds) randomly, usually of roughly equal size. For each fold $K$, CV evaluates the prediction accuracy of a training procedure by fitting it on the remaining $\left(K-1\right)$ folds. For example, we may fit a Lasso regularized linear regression with penalty $\lambda$ to the remaining $\left(K-1\right)$ folds, with $\widehat{{\beta }^{-k}}$ being the estimated regression coefficient. Then, for each sample $i$, suppose it in fold $k\left(i\right)$, let $\left(x_{n+1},y_{n+1}\right)$be its associated feature value and response. We then calculate the squared error loss with ${\mathrm{l}}_i^{-k\left(i\right)}={\left(y_i-x_i^{\mathrm{\top }}\widehat{{\beta }^{-k\left(i\right)}}\right)}^2$ for all $k=1,\dots ,K$. The CV error is defined by pooling together all cross-validated errors ${\mathrm{l}}_i^{-k\left(i\right)}$:

$$\widehat{\mathrm{E}\mathrm{r}{\mathrm{r}}^{CV}}=\frac{1}{n}{\sum }_{i=1}^n{\mathrm{l}}_i^{-k\left(i\right)}.$$

The CV error $\widehat{\mathrm{E}\mathrm{r}{\mathrm{r}}^{CV}}$ is used as the evaluation for the trained model. By selecting a model with a small CV error from a set of competing models, we can select a relatively good model among them and mitigate overfitting. While AIC, BIC, and additive randomization estimate the prediction error with fixed feature values, CV aims to estimate the expected test error on new data as the both the features and response are independently generated together.^7,67

A common choice for the number of folds is $K=5$ or $K=10$ as suggested by Kohavi et al.⁶⁸ However, practitioners may want to use a larger $K$, even leave-one-out cross-validation which treats each sample as its own fold in CV, when the sample size $n$ is small. The fold number $K$ indicates a different kind of bias-variance tradeoff: when $K$ is large, the per-fold model in CV has a comparable training sample size as the original model, thus, CV induces less learning bias due to reduced sample size; however, when $K$ is large, the model similarity across folds becomes increased, and $\widehat{\mathrm{E}\mathrm{r}{\mathrm{r}}^{CV}}$ has increased variability for estimating the expected test error.⁷

Practitioners should exercise caution when applying CV. Firstly, the estimated CV error of the selected model can be biased and an underestimation of the actual test error due to selection, especially when the space of candidate models is large.⁶⁹ Guan and Tibshirani⁷⁰ proposed a randomized CV, which combines CV with the idea of additive randomization, enabling unbiased test error estimation after arbitrary selection in the CV procedure. Secondly, careless application of CV can fail even for model selection purposes. This often happens if there is unintended information leakage, in which data information from the validation set is not perfectly hidden from practitioners during the training and leaked to practitioners during model training. Here, we demonstrate that information leakage invalidates CV under two most encountered settings in practice: (1) Explicit information leakage due to using response (e.g., feature filtering) outside the CV loop, and (2) Implicit information leakage due to unaccounted sample structure.

We first demonstrate that information leakage can happen when preprocessing steps occur before CV. Example 3 is a simple demonstration built upon section 7.10.2 from Hastie et al.⁷ which highlights the danger of severe overfitting caused by analysis steps (e.g., feature filtering) outside of the CV loop.

Example 3:

Suppose we have $n=50$ samples with half from class 1 and the other half class 2. Suppose we have $p=5000$ quantitative features, such as gene expression levels, that are independently generated from the standard Gaussian distribution and are independent of the class assignment. Consider the following invalid but typical CV analysis strategy: (1) perform feature filtering by selecting $d$ features with the largest associations with the response, (2) construct a one-nearest neighbor classifier (1NN) using the selected features. This CV scheme is invalid because the feature filtering step has used all data before CV is carried out. Since the data contains pure noise, we expect the test error to be 50%. However, as we vary $d\in \left\{10,50,100,500,1000,2000,3000,4000,5000\right\}$, CV classification errors from step 2 are much lower than 50% when we adopt the feature filtering scheme and let $d$ be smaller than 5000 (Figure 5a).

Figure 5.

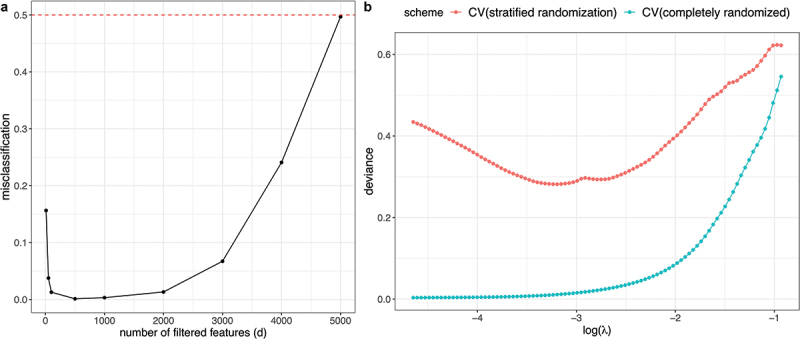
A) CV evaluation using 1NN with feature filtering as described in example 3. The x-axis shows the number of remaining features after filtering (d) with $d=5000$ representing no-filtering, and the y-axis shows the misclassification error using CV. The actual test error should be 0.5 (red dashed line), which is much higher than the CV error in the presence of strong filtering (small $d$). B) CV evaluation with different randomization schemes using the lipidomic breast cancer dataset in example 4. The x-axis shows the logarithm of lasso penalty ($\lambda$), and the y-axis is the deviance loss. The achieved deviance when using CV with the stratified randomization grouped by patient id (in red) is considerably higher than that from using CV with the completely randomized scheme (in turquoise).

When applying CV, it is also crucial to understand sample structures that may contribute to potential information leakage sources and account for them. Example 4 illustrates the importance of accounting for the sample structure when performing CV. In this example, a completely random splitting of samples into different folds results in an invalid CV scheme.

Example 4:

The lipidomic breast cancer data from the lab of Livia Schiavinato Eberlin at UT Austin consist of 806 features measured on 15,359 pixels in tissue images from 24 breast cancer patients, and this data is used by Guan et al.³⁷ The pixels are divided into two classes, the normal class and the cancer class, and we fit a regularized logistic regression model using each procedure. In this example, randomly splitting CV folds is an invalid scheme since pixels from the same patient reveal patient-specific information, and the resulting CV errors are over-optimistic for test error evaluation on samples from a new patient. Instead, a better CV scheme is to consider the stratified population structure and randomly split samples based on their patient ids. Indeed, we observe that the CV errors using random sample splitting to be much smaller than that using random patient-id splitting (Figure 5b), as a result of sample associations from the same patient.

Apart from such population stratification as demonstrated in Example 4, the random sample splitting scheme is also often invalid for time series data where the noises from nearby time points are often correlated. In this case, randomly sampling long blocks consisting of consecutive time points can usually alleviate this problem.^71,72

These examples highlight the importance of the proper implementation of cross-validation. For practitioners who utilize CV in their research, it is beneficial to think about the following questions when designing the CV scheme instead of blindly using the default choice:

1. Are the samples independent or are they correlated with each other? If samples are correlated with each other, correlated samples should be grouped together when constructing the CV folds, such as samples from the same patient, samples from consecutive time, etc.

2. Has the information from the response been used outside of the CV loop? Any analysis utilizing the response itself is not allowed outside the CV loop. For example, if we use feature filtering as a preprocessing step before feeding data into the machine learning model, this must also be done using only samples excluding the fold under evaluation.

To further guard against potential negligence of using CV, alternative model-free approaches such as permutation-based analysis can be employed.⁷³ Lu et al.⁷⁴ used a random permutation approach to assess the degree to which their modeling approach was susceptibly overfitting and raised the alert of over-training if the prediction accuracy is much better than random guess.

Finally, it is always beneficial to set aside a separate test dataset to mimic future independent observations. Similarly as in CV, the test dataset aims to contain independent samples from the remaining training data, for example, samples from the same patient are not shared by the test dataset and the training. Once set aside, the test dataset should not be used during the entire pipeline consisting of training, evaluation, model selection, and comparisons, and is only used for the final validation (Figure 1b). Evaluations on this independent test set can provide a reliable assessment of model performance, and huge discrepancy between CV error and the prediction error on the test set can help raise concerns about the adopted CV scheme.

Note that even if our cross-validation or other evaluations are not overfitted toward the noise, there is no guarantee that we will always achieve the same level of accuracy on a future dataset. For instance, the prediction errors on the test set could still be significantly smaller than the prediction error on a future dataset. This situation can arise if the future data introduce new sources of variation that were not present in the training data. For instance, measurements collected on COVID-19 infected patients in 2020 may not completely reflect the biology of new variants of interest, and a model trained on medical data collected from one hospital might not generalize well to another hospital.

Utilization of data diversity

The lack of reproducibility in generalizing discoveries to novel datasets is an issue that has been well recognized by the scientific community.⁷⁵ Here, we ask the question: Can we mitigate overfitting toward certain environments to improve the prediction model’s generalizability to underrepresented or new environments?

In many instances, the prediction accuracy can increase significantly by increasing the volume of the training dataset. The power of data expansion goes beyond prediction improvement solely based on the volume boosting. Previously, it has been shown that a suitable meta-analysis of multi-cohorts’ study can enhance the reproducibility of signature discovery via hypothesis testing.⁷⁶ Similarly, the diversity of data could play a critical role in improving the generalization of the model to under-represented environments. For example, Fourati et al.⁵ and Hagan et al.⁷⁷ considered the problem of identifying common immune signatures predictive of antibody response among 13 different vaccinations, leading to signatures with increased generalization potential.

Apart from data expansion efforts, we may further consider adapting machine learning approaches to explicitly utilize data diversity. Standard model training criteria involve empirical risk minimization (ERM), which aims to achieve overall high accuracy on another independently and identically generated test cohort, e.g., the test cohort behaves similarly as the training data with some newly generated data noise. However, models from ERM may perform poorly on certain subgroups of samples due to heterogeneous subpopulation structure and inclusion of non-generalizable predictive relationships.^78–81 Alternatively, we can construct models that favor uniformly good performance across different subpopulations rather than focusing on overall accuracy, often referred to as distributional robust optimization (DRO).^81–86

Below, we describe a standard DRO where we find the model parameter $\hat{\beta }$to minimize the loss ($\underset{\beta }{\mathrm{m}\mathrm{i}\mathrm{n}}$) in the worst subpopulation or group ($\underset{g\in G}{\mathrm{m}\mathrm{a}\mathrm{x}}$):

$$\widehat{\beta }=\underset{\text{β}}{\text{argmin}}\underset{g\in G}{\max }\frac{1}{\left|{ℐ}_g\right|}\underset{i\in {ℐ}_g}{{{\displaystyle \sum }}^{\text{}}}{\ell }_{\beta }\left(x_i,y_i\right)+\mathcal{J}\left(\text{β}\right)$$

where $g\in G$ represents the group assignment, ${\mathcal{J}}_g$ contains samples in group $g$, $\left|{\mathcal{J}}_g\right|$ is the size of ${\mathcal{J}}_g$, $\beta$ is the model parameter, $J\left(\beta \right)$ is some regularization penalty on the parameter $\beta$, ${\mathrm{\ell }}_{\beta }\left(x_i,y_i\right)\hspace{0.17em}$is the achieved loss at sample $i$ with model parameter $\beta$. The above $minmax$ formulation enables predictions with more uniform performance across groups. This DRO framework has been used in linear and other more flexible models such as neural networks and is effective for robust classification against distributional changes, including future changes in the test cohort, and helps identify invariant or generalizable predictive relationships across different populations. Example 5 demonstrates this desirable property of DRO over ERM in a simulated example.

Example 5:

Consider a classification task where the response is $y\in \left\{0,1\right\}$, the hidden group is $g\in \left\{0,1\right\}$. Given the class label $y$and the group assignment $g$, the observed feature values $x$ are from a 10-dimensional Gaussian distribution. The first dimension of $x$separates the two response classes in the same way and the second and third dimensions have opposite effects for samples from the two groups. We generate the samples with 90% of them from group 1 and 10% of them from group 2 and predict $y$ using feature $x$. Figure 6a shows the boxplots of predicted probability of $y=1$ separately for the two groups using an ERM model and a DRO model, which minimizes the worst group performance.⁸⁵ For samples from group 2, the ERM model achieves no better accuracy than random guessing, even though it achieves high classification accuracy in group 1. In contrast, the DRO model performs similarly well in both groups. The estimated model coefficients are shown in Figure 6b, with the ERM model depending heavily on all three features and the DRO model largely dependent on the first invariant feature.

Figure 6.

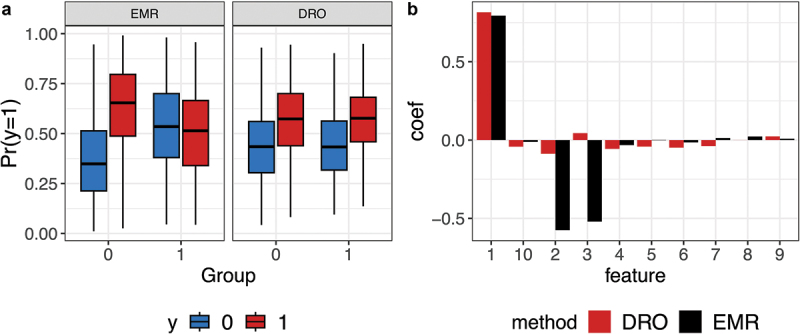
Illustrative example comparing ERM and DRO. Data are generated using example 5 with a signal-to-noise ratio of 1 for the prediction task. There are two groups, with 90% samples from group 1 and 10% from group 2. In the underlying model, the first feature separates the two classes invariantly, but the second and third features have opposite effects on samples from the two groups. A) Boxplots of predicted probability for $y=1$ using the ERM and the DRO models separately for the two groups. B) Estimated model coefficients (y-axis) for both the DRO and ERM models.

The idea of explicitly utilizing population diversity for robust learning has not been widely exploited in medical studies, with only a few works adopting this modern learning scheme. For example, Yang et al.⁸⁷ considered robust COVID-19 risk predictions across sex and ethnicity, opening opportunities for novel analysis in this direction.

Discussion

When applying machine learning methods to predictive tasks in immunological and other biomedical applications, researchers need to be aware of both the strengths and limitations of these methods. Overfitting is one common issue encountered during the construction of prediction models in contemporary applications, which often deal with complex and high-dimensional data. Gaining a thorough understanding of the causes behind overfitting, the associated challenges, and cutting-edge strategies for diagnosis and mitigation is critical for appropriately applying various techniques.

Traditional perspectives on overfitting typically assume that training and test samples exhibit similar characteristics. In practice, however, test samples might follow different patterns than the training counterparts. In such situations, it becomes increasingly important to develop models that can capture invariant relationships, which can be more effectively achieved by leveraging the diversity of populations within the training data. Although discussions on this topic are currently limited, recognizing this crucial aspect of research could lead to significant advancements, particularly in light of the growing international efforts to conduct large-scale studies spanning multiple environments, as exemplified by various study centers, cohort populations, and responses of interest.^88–91

Funding Statement

The work was supported by the National Institute of Allergy and Infectious Diseases under the Award numbers U19AI089992 and U01AI167892, and the National Science Foundation under the Award Number DMS2310836.

Disclosure statement

SHK receives consulting fees from Peraton. All other authors declare that they have no competing interests.