A Hybrid Structure-Based Machine Learning Approach for Predicting Kinase Inhibition by Small Molecules

Abstract

Kinases have been the focus of drug discovery programs for three decades leading to over 70 therapeutic kinase inhibitors and biophysical affinity measurements for over 130,000 kinase-compound pairs. Nonetheless, the precise target spectrum for many kinases remains only partly understood. In this study, we describe a computational approach to unlocking qualitative and quantitative kinome-wide binding measurements for structure-based machine learning. Our study has three components: (i) a Kinase Inhibitor Complex (KinCo) data set comprising in silico predicted kinase structures paired with experimental binding constants, (ii) a machine learning loss function that integrates qualitative and quantitative data for model training, and (iii) a structure-based machine learning model trained on KinCo. We show that our approach outperforms methods trained on crystal structures alone in predicting binary and quantitative kinase-compound interaction affinities; relative to structure-free methods, our approach also captures known kinase biochemistry and more successfully generalizes to distant kinase sequences and compound scaffolds.

Introduction

Mammalian kinases make up a large family of enzymes that bind ATP and catalyze phosphotransfer to a protein or small molecule substrate. Among the set of approximately 700 human proteins having structures associated with kinase activity, 544 have a highly conserved Protein Kinase Like (PKL) three-dimensional fold.¹⁻³ These kinases have diverse functions in the regulation of cell division, migration, morphology, and metabolism, and many are components of multienzyme signal transduction cascades.⁴ Multiple kinases involved in cell signaling networks are mutated or differentially expressed in human disease, often serving as driver mutations in cancer.⁵ As a result, kinases have been the focus of intense drug development efforts. Most kinase inhibitors are ATP-competitive molecules that interact with the ATP binding site although some, generally referred to as “allosteric inhibitors”, bind outside the catalytic site.^6,7

Due to the conserved structure of the ATP binding site, small molecule kinase inhibitors commonly inhibit kinases other than the one they were designed to target (we will refer to the intended or most commonly accepted target as the “nominal target”).^8,9 For example, crizotinib was developed as an inhibitor of the MET tyrosine kinase but was later found to also inhibit ALK, and this later activity enabled its approval for advanced or metastatic nonsmall-cell-lung-cancers carrying ALK fusion genes.¹⁰ A complete understanding of the target spectrum of kinase inhibitors is rarely achieved in preclinical development, and the polypharmacology of many approved therapeutics is only discovered after they are in widespread use.⁸ It would nonetheless be highly advantageous were preclinical drug development programs able to accurately predict the full spectrum of kinases that a particular small molecule is likely to bind and use this information as part of in silico compound optimization.

A variety of experimental assays are available to measure interactions between kinase inhibitors and their kinase targets at the kinome scale. These include several different types of competitive binding assays that measure binding to ATP-like scaffolds in the presence and absence of a small molecule inhibitor of interest. For example, binding of native kinases present in cell extracts to bead-bound ATP scaffolds can be assayed using mass spectrometry and binding of libraries of recombinant kinases to scaffolds can be measured using PCR.¹¹⁻¹⁴ These assays are relatively expensive to perform, and different methods do not return identical results, emphasizing the importance of computational approaches to data fusion and interpretation. Multiple methods have been described for predicting interactions between proteins and small molecules,^15,16 including ones that consider the ligand alone (“ligand-based”) or the ligand in combination with the target protein.¹⁷

Ligand-based methods are usually developed for a single target protein by abstracting away target structure and are thus only suitable for proteins that have already been profiled against a substantial number of compounds.¹⁸ For proteins with limited compound affinity data, more general models that utilize information from multiple protein-compound complexes are preferable. Models integrating target information can be further subdivided into those that utilize the 3D atomic structure of the target protein (“structure-based”) and ones that do not (“structure-free“).¹⁹ Structure-free methods can be effective at predicting kinase-ligand affinity but lack geometrical and chemical interpretability; such models infer protein sequence and compound features favorable for binding based on co-occurrences in a data set but generate relatively little insights into structural features of protein-compound interaction.^20,21

Structure-based models predict binding affinities directly from experimentally determined or predicted structures of protein-compound cocomplexes using either physics-based force fields or machine-learned energy functions. Physics-based methods, such as free energy perturbation, often produce highly accurate predictions but require substantial computing resources, complicating large-scale in silico screening.²² Machine learning-based methods are fast but have traditionally struggled to generalize to compounds or proteins whose structures deviate substantially from those in training sets.¹⁸ Many previous well-performant machine learning-based methods rely on precalculated complex features to represent the protein–ligand complex,²³⁻²⁶ and most are generic models not adapted to a specific target family.²⁷ However, due to advances in deep learning, numerous approaches have been developed in the past few years to represent protein–ligand complexes as point clouds, grids, and graphs and infer, based on data, interaction motifs important for affinity prediction.²⁸⁻³² Irrespective of their architectural details, all such models require measured binding affinities as well as structures of the corresponding complexes as input.¹⁹ They infer the relationship between input (structure) and output (binding affinity) using neural networks that uncover recurring structural motifs predictive of binding affinity.¹⁸ Given that the number of experimental cocrystal structures currently available in the public domain is orders of magnitude smaller than the number of binding affinity measurements, structure-based modeling has historically faced a data imbalance problem that has limited its applicability and utility.³³

Predicted structures of protein–ligand complexes provide one way to overcome the lack of experimental structural data. These methods are rapidly becoming as accurate as experimentally determined structures, at least for single domains, and attempts have been made to use predicted structures in a limited manner, for example by docking the structures of chemical ligands, derived from their experimentally determined poses in other cocomplexes, into apo structures of proteins of interest.³⁴ Kinase-small molecule affinity data derived from profiling methods^9,12,13,35 have been underutilized as a resource for machine learning in large part because the data are heterogeneous, spanning quantitative binding constants (derived from fits to dose response curves) and qualitative binary labels (e.g., “disassociation constant ≥ 10 μM”). While qualitative binary labels do not permit direct comparison of binding affinities, they do provide valuable data on the selectivity of kinase inhibitors as well as upper and lower bounds on their affinity.³⁶ Furthermore, qualitative data are far more abundant than quantitative data due to the high expense of measuring full dose response curves. This suggests the likely value of integrating qualitative and quantitative data in a way that simultaneously extracts the maximum information possible from both. In contrast, existing ML models generally use one form of data or the other or binarize quantitative data to merge them with binary data, losing continuous-valued quantitation in the process. Overcoming the challenges inherent in combining qualitative and quantitative affinity data in ML model training is thus of fundamental importance.

In this study, we developed a machine learning approach to modeling the interactions between kinases and ATP-competitive inhibitors. Our approach introduces two advances to address the twin challenges of limited structural data and heterogeneous binding affinity. First, we describe the Kinase Inhibitor Complexes data set KinCo (https://lsp.connect.hms.harvard.edu/ikinco/) that contains experimental binding constants and predicted atomic structures for over 130,000 kinase-compound pairs. KinCo makes it possible to utilize nearly all publicly available kinase-compound affinity data for structure-based machine learning even when experimental structural data is unavailable. Second, we introduce a novel loss function that makes it possible to integrate qualitative and quantitative binding measurements without the loss of information during model training. We couple this loss function with a new training regimen that successively optimizes KinCo structures by using an iterative model building scheme. Compared to models trained exclusively on crystal structures, KinCo-trained models have an expanded scope of prediction, modeling kinases currently inaccessible to other methods. Through a rigorous training/test set partitioning scheme, we demonstrate that our new models outperform existing ones in predicting binary kinase-compound interactions and binding affinity values as well as better recapitulate expected biochemical behavior. We also show that our structure-based models generalize better to distant kinase sequences and compound scaffolds when compared with existing structure-free models. These advances set the stage for the further development of ML-based methods to predict kinase inhibitor selectivity. All the code for data set generation and model training is available on https://github.com/labsyspharm/KinCo.

Results

KinCo: A Structure-Affinity Data Set for Kinase-Compound Interactions

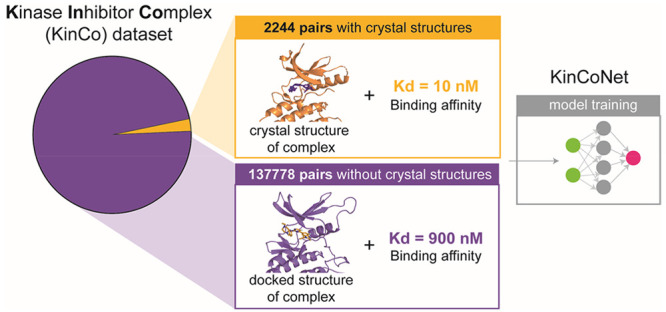
As a first step in creating a data set that pairs experimental and predicted protein structures with kinase-compound binding affinities, we searched the PDBBIND2018 database,³⁷ which combines affinity measurements with cocrystal structures for 170 human proteins having a Protein Kinase Like (PKL) domain. This yielded ∼2,000 kinase-ligand pairs that we will refer to as the “PDBBIND-kinase” data set. Since PDBBIND-kinase covers only 31% of all PKL kinases, we also mined Drug Target Commons (a crowd-sourcing platform for sharing data on drug-target interactions; DTC)³⁸ which includes quantitative and qualitative activities of drug compounds on human kinases along with bioactivity measurements. These are typically formatted as a percent inhibition value (of kinase activity) or binding constant. We collected 130,000 unique kinase-compound pairs from DTC with measured binding constants (either K_i values measured by kinase activity or K_d values measured using a competition binding assay) (Figure 1A). We refer to kinase-compound pairs with binding constants derived from DTC as the DTC-kinase set (see GlossaryTable). The DTC-derived data set exceeded PDBBIND-kinase in size by 2 orders of magnitude and covers more than twice as many kinases (378 kinases, 70% of all PKL kinases) but, to the best of our knowledge, has not yet been used for structure-based modeling, likely due to the absence of corresponding structural data.

Figure 1.

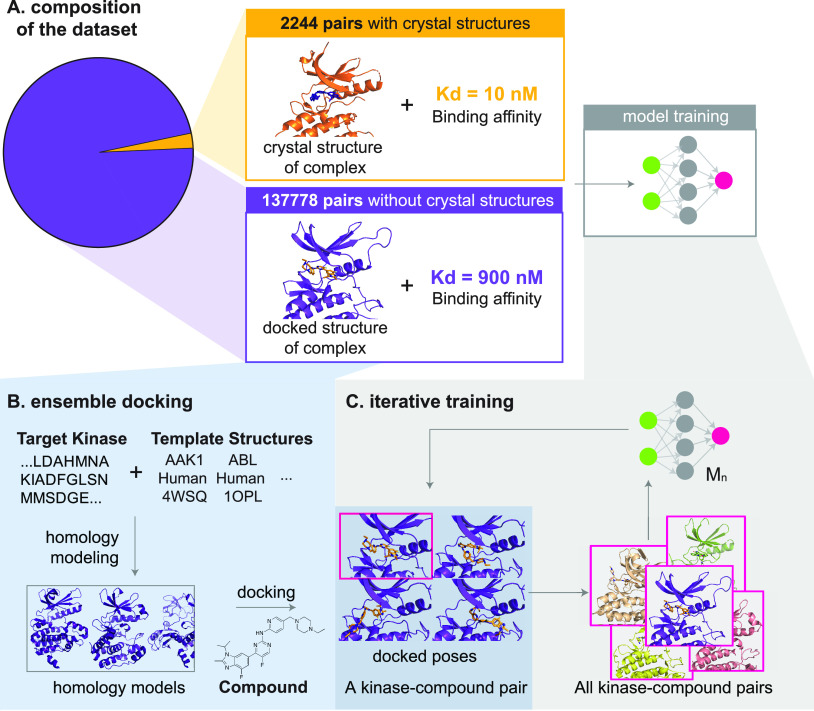
Composition of the data set and generation of KinCo. (A) Composition of the data set. DTC contains over 130,000 kinase-compound pairs with a binding constant but without a corresponding crystal structure (green), and PDBBind2018-kinase contains 2244 kinase-compound pairs with binding affinities matched with a crystal structure (orange). To mobilize the kinome-wide binding constants in DTC, we applied docking and iterative training to train structure-based affinity prediction models. (B) Docking workflow. Homology models were created for each target kinase, starting from its sequence using all mammalian kinase structures as templates. Homology models whose template kinase shares over 40% sequence identity with the target kinase were selected, and the compound was docked into each of the selected homology models. This docking workflow resulted in over 11,000 docked poses in various conformations of the kinases for each kinase-compound pair. KinCo consists of over 137,000 kinase-compound pairs with such docked poses and the corresponding experimental binding constant for the pairs. (C) Iterative training. The scoring function in Autodock Vina was used to select the pose with the highest predicted binding affinity as the representative structure for each kinase-compound pair, and the docked pose was matched with the corresponding experimental binding affinity to train the first iteration model KinCoNet-M₁. KinCoNet-M₁ was used to predict the poses with the highest binding affinity, which were used to train the second iteration model KinCoNet-M₂. This iterative training process could be repeated n times to train model KinCoNet-M_n.

To enable use of DTC-kinase data in structure-based modeling, we generated homology models for all kinases in the data set with the Ensembler pipeline.³⁹ This homology modeling pipeline generates many putative conformations for every kinase in our data set, enabling downstream models to consider an ensemble of thousands of kinase-compound conformations, including ones reflective of binding-induced fit. In future work, it might be possible to extend the approach by using molecular dynamics to generate additional conformations and to exploit AlphaFold2 structures followed by a repeat of the docking approach described here.

After in silico structures were generated, we docked every compound in our data set into every homology model using QVina, a fast variant of AutoDock Vina,^40,41 thereby generating an ensemble of docked poses (Figure 1B). The resulting KinCo data set includes >137,000 unique kinase-compound pairs with >10,000 docked poses per pair, each with a different conformation of a kinase-compound complex. For example, the docked poses of CDK2-staurosporine included both the monomeric and active CDK2 cocomplexes (i.e., kinase bound to Cyclin A). We retained those poses in which a compound was bound to a known inhibitory site (e.g., the ATP binding site) and those in which a compound was bound to a previously unknown or peripheral sites, delegating to downstream modeling the task of determining real versus spurious binding pockets and their relative affinities (we use an iterative training regimen to identify relevant poses, as described below). All KinCo homology models are publicly available at https://lsp.connect.hms.harvard.edu/ikinco/ to facilitate future structure-based modeling efforts.

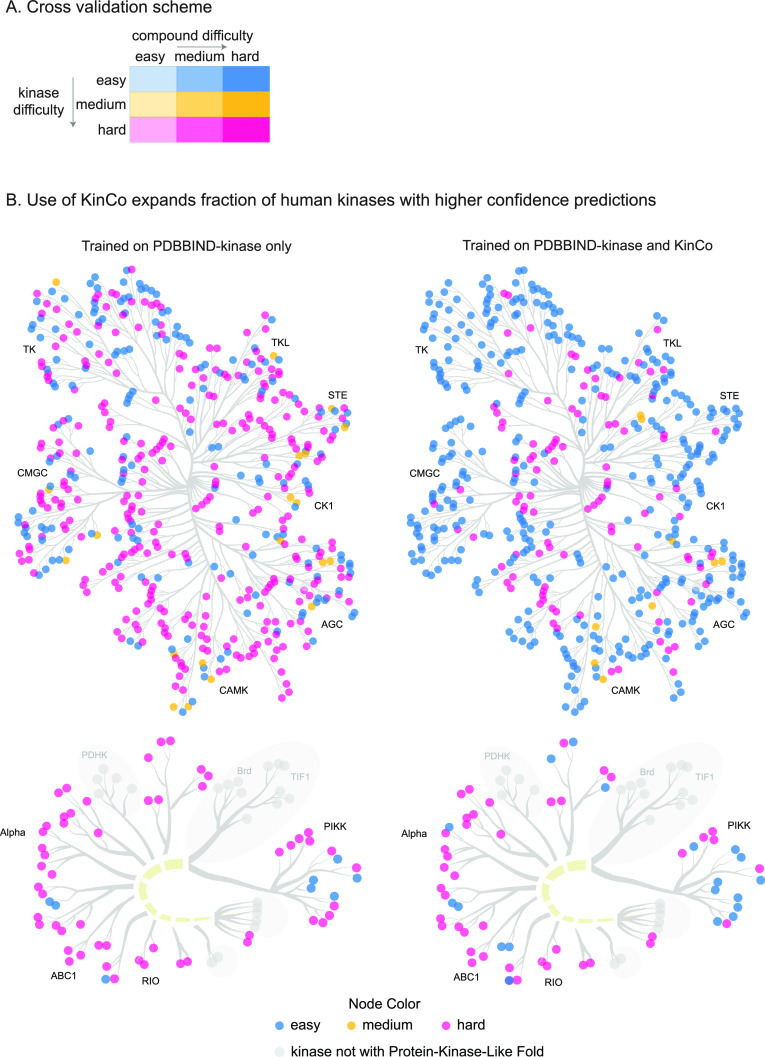
To enable the use of KinCo in machine learning, we partitioned the data into training, validation, and test sets based on sequence and chemical similarity. Existing structure-based models typically assess generalized performance (relative to the training set) on either chemically distant compounds or sequence-dissimilar proteins. We evaluated these forms of generalization individually and in combination. Adapting a procedure outlined previously,⁴² we first generated three test sets (validation sets were treated identically) in which kinases in the test set had decreasing sequence identity to those in the training set: an easy kinase set (one in which the training and test sets consisted of identical kinases), a medium difficulty set (a training set in which the kinases in the two sets were nonidentical and had <95% sequence identity with the test set), and a hard kinase set (<87% sequence identity with test set). We then subdivided each of these test sets into three subsets (for a total of nine test sets overall) by ranking the small molecules by chemical similarity, as measured using Tanimoto scores. This generated an easy compound set (training compounds with ≤ 0.8 Tanimoto similarity to test set), a medium difficulty compound set (training compounds with ≤ 0.6 Tanimoto similarity to test set), and a hard compound set (training compounds with ≤ 0.4 Tanimoto similarity to test set) (Figure 2A). Some chemical scaffolds had many more derivatives in the set of known kinases inhibitors resulting in nonuniform sampling of chemical space. We therefore clustered compounds based on Morgan fingerprint and then sampled one representative from each cluster to ensure that the test set more evenly captured data across chemical space. Table S1 shows the sizes and compositions of the training, validation, and test sets. This process is illustrated in Figure S1.

Figure 2.

Partition of validation and test sets and expanding of the prediction scope for kinases. (A) Partition of validation and test sets. Nine validation and test sets were constructed with increasing kinase difficulty (indicated by color) and compound difficulty (indicated by opacity) as approximated by sequence identity and Tanimoto similarity, respectively. Five independent partitions were performed, and model performance on the test set from each partition was reported. (B) Including KinCo for training expands prediction scope for kinases. Kinases in the data set in the easy, medium, and hard categories were identified based on their similarity to the kinases from PDBBind2018-kinase (left) or in KinCo and PDBBind2018-kinase (right). Kinases with a different protein fold from protein kinases are colored in gray and not included in the data set.

To visualize the impact of including kinase-compound pairs lacking experimental structures on the breadth of kinases that can be modeled, we computed the sequence identities of all known kinases to those in PDBBIND-kinase and KinCo. We colored kinases by their sequence similarity and projected them onto the kinome tree (Figure 2B). Compared to training on crystal structures alone, KinCo substantially increased the number of kinases considered to be easier to predict, thereby expanding the number of kinases for which modeling can make reliable binding inferences (Figure S2). Exemplar kinases and compounds in the training set along with their nearest neighbors in the test set as well as the distributions of kinase and compound similarity are shown in Figure S3.

Two-Sided Loss Function

Supervised machine learning models are trained by minimizing a loss function that computes the deviation between the ground truth measurements and model predictions. Designing suitable loss functions is key to building models that fully utilize available data. As previously noted, binding affinity data for kinase-compound pairs are derived from a diverse set of biochemical assays and include both quantitative estimates of K_d (e.g., imatinib binds ABL1 with a K_d of 0.0015 μM) as well as qualitative labels (e.g., imatinib does not bind ULK3 or K_d > 10 μM). For quantitative measurements, the mean squared error (MSE) is a suitable loss function that directly captures how much predicted affinities deviate from experimental ones. For qualitative labels, the situation is more complicated, as these labels can best be understood as inequality relationships (e.g., K_d ≥ 10 μM for negative labels) that cannot be evaluated using the MSE. To leverage binary labels in conjunction with quantitative affinities, we devised a two-sided loss function (see Methods, eq 1) in which quantitative values were scored using the MSE and binary labels were handled as follows: if the label was negative (K_d ≥ 10 μM) and the model predicted K_d to be greater than 10 μM, then the loss function was set to zero, i.e., no penalty was incurred; on the other hand, if the model predicted K_d to be lower than 10 μM, the loss function computed the MSE between the predicted K_d and preset threshold value (10 μM in the current work, a value that corresponds to the most commonly used threshold between binding and nonbinding). The reasoning behind this approach is that, given a negative label and the way in which assays are commonly performed, the highest K_d expected is 10 μM, and so model predictions of tighter binding (K_d < 10 μM) is penalized in proportion to the deviation from the threshold value. We applied the same logic to positive labels but in the reverse direction. As a result, our two-sided loss function enables downstream models to utilize both qualitative and quantitative data for training.

Iterative Training Regimen

In KinCo, each kinase-compound pair is associated with a large number of putative docked poses. To train machine learning models that predict kinase-compound affinities, a mechanism is needed to select one or more poses per kinase-compound pair for training purposes. To do this, we introduced an iterative training strategy that alternates between (i) using (ranked) poses to train kinase-compound affinity models and (ii) using the trained affinity models to rerank poses for subsequent training iterations, in a process akin to expectation-maximization algorithms.⁴³ Our approach was inspired by student self-distillation in image recognition, in which data sets are augmented by applying predicted labels to images lacking ground truth labels.⁴⁴ A similar idea was successfully used by AlphaFold2⁴⁵ to build a more performant protein structure prediction model by training it on predictions made by an earlier model. In our case, poses were first ranked using Autodock Vina energies, and the lowest energy pose was selected for each kinase-compound pair. An initial model, which we termed M₁, was then trained on these poses. For this, we used a model architecture based on 3D convolutional neural networks that was previously applied to protein-drug binding,⁴⁶ but our iterative approach is broadly applicable to any machine learning model. Since M₁ was capable of predicting kinase-compound affinities, we used it to rerank the full set of poses in KinCo and thereby infer new lowest energy poses. These poses were then used to train a new model M₂, and the process continued until a final model M_k is trained (Figure 1C). In our experiments, we set k = 2. This approach was enriched for true binding poses by repeatedly using trained models to rank and select the highest ranked poses. This was helpful for positively labeled data but did not address negative data in which poses ought to correspond to the ensemble of unbound states. To tackle this, we augmented negatively labeled kinase-compound pairs with poses in which compounds were bound to sites far away from the active site; such pairs are presumed to be low affinity (allosteric inhibition is not covered by our model, largely because the necessary metadata are missing).

Training on KinCo Structures Improves Kinase-Compound Interaction Prediction

We combined the iterative training approach described above with our two-sided loss function to train a 3D convolutional neural network on KinCo. As a proof of concept, we adapted the Pafnucy⁴⁶ architecture to KinCo (Figure 3), although KinCo is agnostic to any specific structure-based model architectures. The resulting KinCoNet model is focused on predicting kinase-compound affinities, but we first pretrained it on all protein–ligand complexes in PDBBIND2018 so that it learned a general understanding of the biophysics of protein-compound interaction. We have previously found that this type of pretraining on general features of protein biophysics improves model performance. We then created five validation and test sets by applying the partitioning scheme described above. We used the validation sets to identify the optimal hyperparameters (Table S2) and then determine the performance of the model on the test sets.

Figure 3.

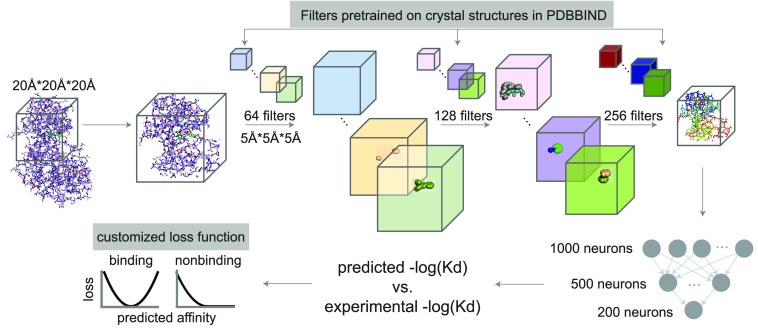
Adapted model architecture. The 3D convolutional neural network is adapted from Pafnucy:⁴⁶ we applied 3 layers of 3D convolution with 64, 128, and 256 filters with a filter size of 5 Å * 5 Å * 5 Å. Each convolution layer is followed by a max pool layer with a 2 Å * 2 Å * 2 Å patch. The output of the last convolution layer is concatenated and passed through a fully connected neural network with 1000, 500, and 200 neurons to predict the binding affinity. We also customized Pafnucy with the following modifications (highlighted in gray rectangles): the convolutional filters were initialized with parameters pretrained using crystal structures across all protein families in PDBBind2018. The MSE-based customized loss function between the prediction and experimental values was adopted to include qualitative data.

First, we assessed whether training on homology structures in KinCo improved the performance relative to training on experimental structures alone. We compared the Area Under the Receiver Operating Characteristics Curve (AUC) of KinCoNet (using one and two training iterations, resulting in KinCoNet-M₁ and KinCoNet-M₂, respectively) with two baseline models: (i) ExperimentalNet, an adapted version of the KinCoNet architecture trained exclusively on 16,000 experimentally determined protein–ligand complexes in PDBBIND2018, and (ii) Vina, the scoring function used by AutoDock Vina. KinCoNet-M₁ and KinCoNet-M₂ achieved overall AUC values of 0.81 and 0.79, respectively, when considering all kinase-compound pairs in all test sets. Both models outperformed ExperimentalNet (AUC = 0.74) and Vina (AUC = 0.68) by substantial margins, demonstrating the utility of including KinCo structures in model training (Table 1). Training on KinCo resulted in the biggest performance improvement for kinases in the easy category (AUC of 0.87 for KinCoNet-M₁ and KinCoNet-M₂ as opposed to 0.79 for ExperimentalNet) and for compounds in the easy and medium categories, which showed an improvement in AUC of about 0.06 in both cases relative to ExperimentalNet. We conclude that KinCo-trained models work better by expanding the set of kinases that meet the definition of the easy category; this includes kinases lacking experimental structures.

Table 1. Comparison of AUROC between models^a.

	Overall AUROC
Difficulty	ExperimentalNet	Vina	KinCoNet-M1	KinCoNet-M2
	0.74 ± 0.02	0.68 ± 0.01	0.81 ± 0.02	0.79 ± 0.02

	AUROC by kinase difficulty
Kinase difficulty	ExperimentalNet	Vina	KinCoNet-M1	KinCoNet-M2
easy	0.79 ± 0.05	0.65 ± 0.03	0.87 ± 0.02	0.87 ± 0.04
medium	0.78 ± 0.06	0.64 ± 0.08	0.81 ± 0.04	0.80 ± 0.03
hard	0.75 ± 0.06	0.71 ± 0.07	0.71 ± 0.04	0.72 ± 0.06

	AUROC by compound difficulty
Compound difficulty	ExperimentalNet	Vina	KinCoNet-M1	KinCoNet-M2
easy	0.77 ± 0.03	0.64 ± 0.02	0.81 ± 0.04	0.82 ± 0.04
medium	0.74 ± 0.04	0.73 ± 0.04	0.78 ± 0.04	0.80 ± 0.02
hard	0.72 ± 0.08	0.65 ± 0.03	0.79 ± 0.02	0.79 ± 0.02

^aMedian of five CV splits ± half of the interquantile range.

Training on KinCo Structures Improves Binding Affinity Prediction

Next we assessed KinCoNet on the quantitative prediction of binding affinities by computing the Pearson correlation between predicted and experimental values. KinCoNet outperformed ExperimentalNet and Vina on the overall data set (Figure 4A-C). KinCoNet achieved a median Pearson correlation of 0.43, compared to 0.35 for ExperimentalNet. In the easy compound category, the improvement was more substantial, with a median Pearson correlation of 0.5 for KinCoNet-M₂ compared to 0.27 for ExperimentalNet. Furthermore, KinCoNet performed best on the easy kinase/easy compound combination, where it achieved a Pearson correlation of around 0.6 (Figure 4D, Figure S4). These results suggest that KinCo structures aid in both qualitative and quantitative prediction of binding affinity, with much of the improvement deriving from easy kinases and compounds. As the kinase or compound prediction task became more difficult (more distant from the training set), the performance of all models decreased, highlighting the challenge of out-of-domain generalization. At all difficulty levels, KinCoNet-M₁ and KinCoNet-M₂ achieved similar performance, showing that additional iterations of training do not generally lead to accuracy improvements beyond the first self-distillation phase.

Figure 4.

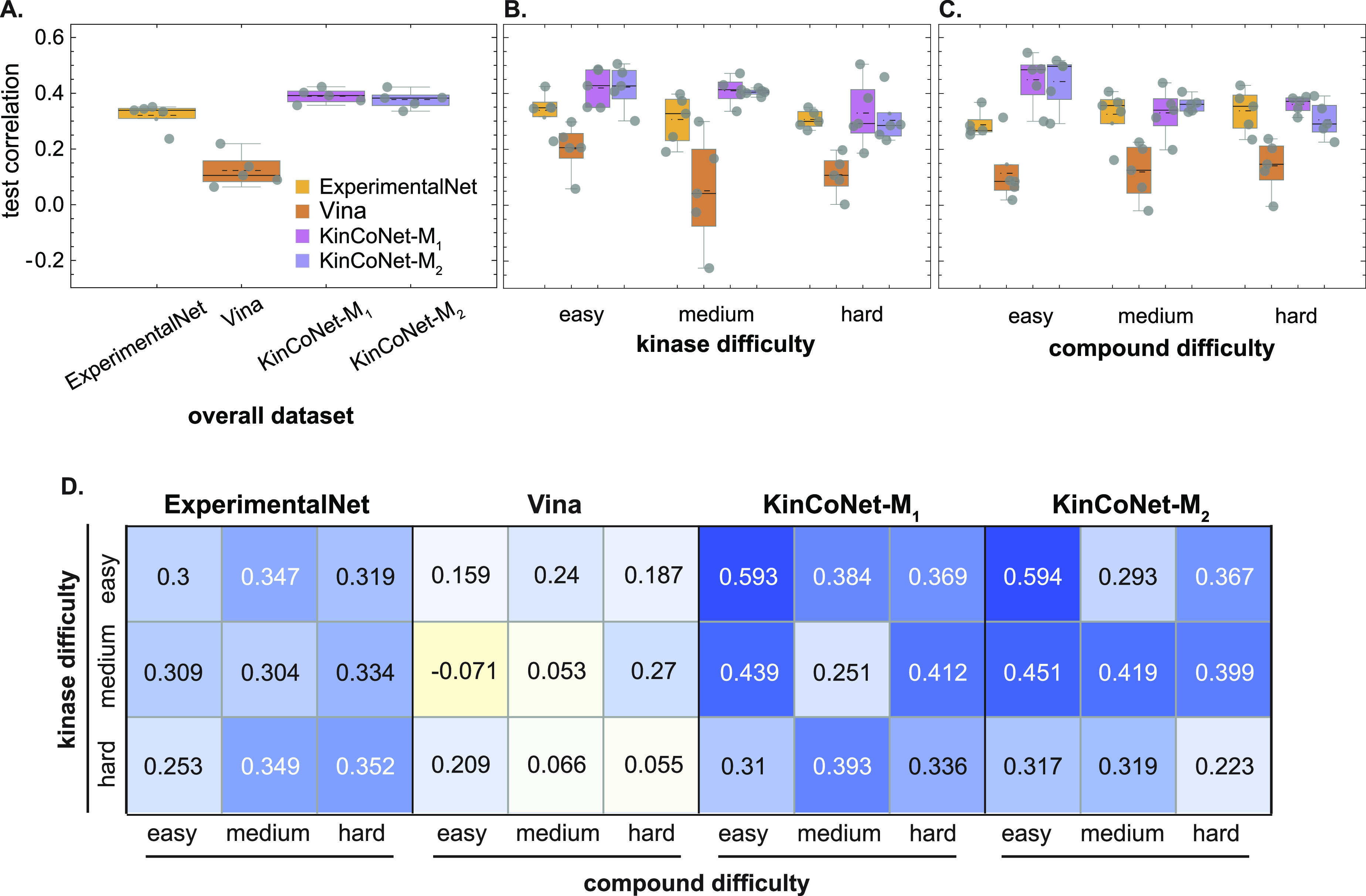
Predictions from models trained on correlations better with experimental affinities. Correlation between the experimental affinities and the predictions on (A) the overall test set across all kinase and compound difficulties, (B) the test sets with increasing kinase difficulties, and (C) the test sets with increasing compound difficulties. ExperimentalNet – models trained on pairs with crystal structures in PDBBind2018; Vina – scoring function from Autodock Vina; KinCoNet-M₁ – models trained on KinCo (docked structures were selected by Autodock Vina and combined with PDBBind-kinase); KinCoNet-M₂ – models trained on KinCo (docked structures were selected by KinCoNet-M₁ and combined with PDBBind-kinase). Each gray dot represents the correlation on a test set from one of the five independent partitions of the data set. Black dotted lines represent the mean. (D) Correlation between the experimental affinities and the affinities on test sets with various kinase-compound difficulty combinations. Median correlations from the performance on the 5 independent partitions are shown.

Kinome-Wide Affinity Data Help KinCoNet Recapitulate the Biophysics of Binding

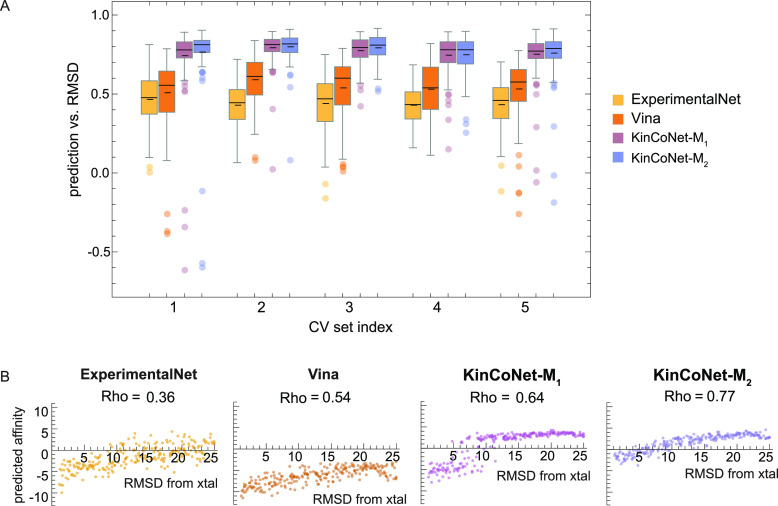
Experimental structures of kinase-compound complexes provide rich and accurate structural information for guiding the development of energy-based modeling methods.⁴⁷ While computationally docked structures of the type found in KinCo attempt to recapitulate the lowest energy state, this type of docking is subject to both systematic and random error. As a result, KinCo-derived models risk associating spurious structural features with the determinants of binding affinity. To assess the extent of this problem, we analyzed the lowest energy poses found in KinCo-derived models. For all kinase-compound pairs in the test set having a corresponding experimental structure, we computed the Pearson correlation coefficient between the predicted binding energy of the docked poses and the deviation (measured using the root-mean-square deviation in Å; RMSD) of the docked compound from its counterpart in the experimental structure. Using KinCoNet, ExperimentalNet, and Vina as energy models, we found that KinCoNet-derived energies correlated better with docked compound RMSD than energies derived from ExperimentalNet and Vina (Figure 5A). This was unexpected since ExperimentalNet was derived exclusively from experimental structures, while KinCoNet contained noisier, computationally docked poses. We propose that the greater quantity of structures utilized by KinCoNet, as well as the modeling “funnel” it created by forced concordance between computational poses and experimentally derived binding affinities, resulted in a model that appears to better capture the underlying biophysics of kinase-compound interaction than ExperimentalNet.

Figure 5.

Predictions from models trained on KinCo better recapitulate the biophysics of binding. (A) Distribution of Spearman’s rank correlation between model predictions and pose deviations from the crystal structure (RMSD) for all kinase-compound pairs with a crystal structure in the test set. Spearman’s rank correlation (Rho) was calculated between model predictions and poses within a 10-Å root-mean-squared-deviation (RMSD) from the crystal structure. (B) Model predictions on poses deviating from the crystal structure. Predictions on the docked poses of a representative kinase-compound complex with high affinity (PDBID: 5DIA).

To examine model behavior on specific compounds and kinases having a range of binding affinities, we analyzed a high affinity complex involving PIM1 and its diamine inhibitor (PDBID: 5DIA). Binding energy predictions made by ExperimentalNet, Vina, and KinCoNet all positively correlated with RMSD values (Figure 5B), confirming that, for a high-affinity interactions, lower predicted energies corresponded to poses that were structurally closer to the experimentally determined complex (which we assumed to represent the ground truth). On the other hand, for a small molecule fragment with low affinity for target binding (IC₅₀ ∼ 300 μM), we do not expect a further decrease in affinity for poses in which the fragment is found to sites outside of the active site (with an optimized competitive inhibitor interaction with the active site is expected to have a much higher affinity than to any peripheral site). Consistent with this expectation, KinCoNet-derived binding energies correlated poorly with the pose’s RMSD (Spearman’s rank correlation of −0.15 and 0.37 for KinCoNet-M₁ and -M₂, respectively; Figure S5). ExperimentalNet performed similarly to KinCoNet, exhibiting low correlation between deviation from the experimental pose and the predicted binding affinity. We conclude that KinCoNet captures key biophysical features of active site binding.

Structure-Based Models Generalize Better than Structure-Free Models

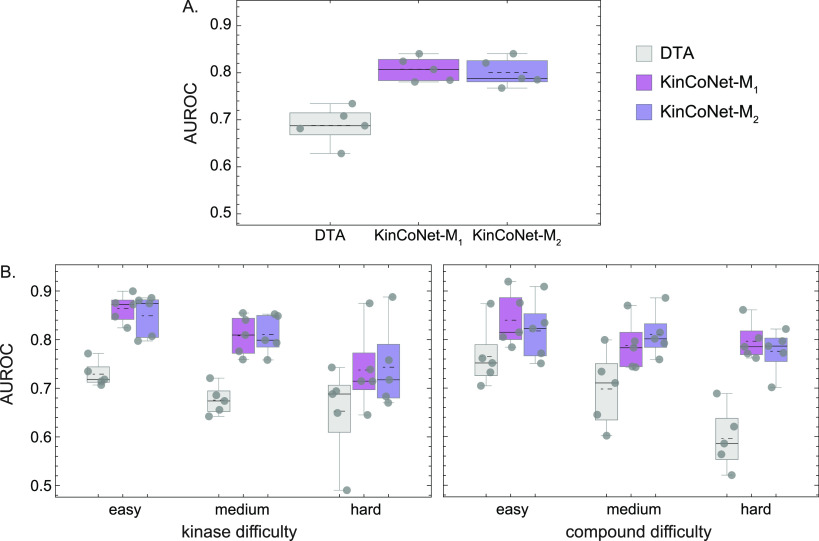
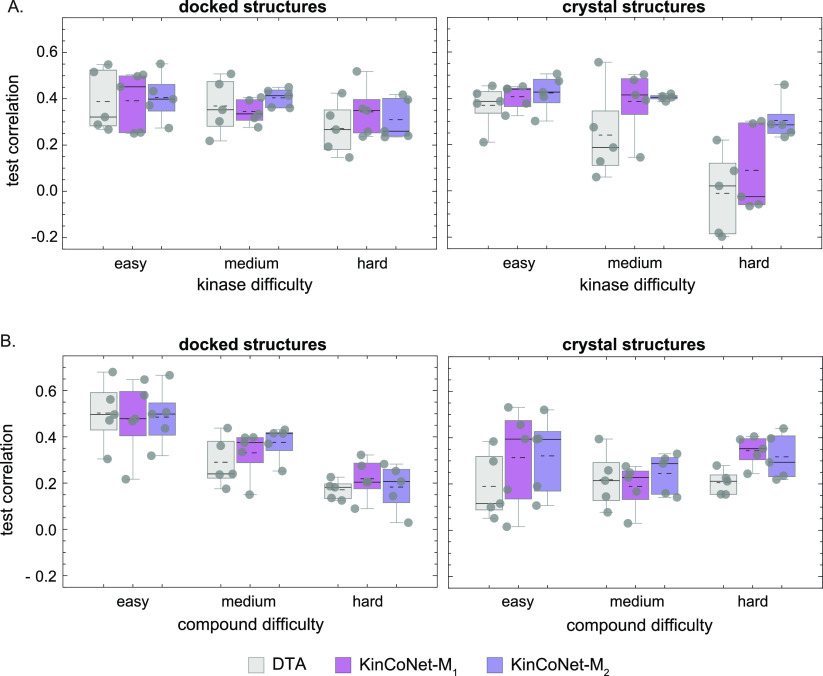
As an alternative to structure-based modeling, we explored a structure-free approach involving sequence-based representations of proteins and 2D textual notation for compounds (SMILES).⁴⁸ Structure-free methods can use a larger set of binding affinity data for training but cannot discriminate between different poses of the same kinase-compound pair. We compared our structure-based models to the structure-free Deep Drug Target Affinity (DTA) method, which has achieved leading performance on protein-compound affinity prediction tasks.²¹ To make the comparison relevant and kinase-specific, we retrained DTA on the binding affinity data in KinCo. We found that DTA achieved an overall AUC score of <0.7 as compared to ∼0.8 for KinCoNet (Figure 6A). KinCoNet outperformed DTA across all kinase and compound difficulty levels (Figure 6B), with an AUC of 0.88 vs 0.72 for easy kinase-compound pairs, 0.8 vs 0.68 for moderate difficulty pairs, and 0.78 vs 0.66 for high difficulty pairs. We also assessed model performance on kinase-compound pairs lacking experimental structures versus ones with available structures. For pairs without experimental structures, KinCoNet exhibited a slightly better performance on the hard kinase test set (Figure 7A). On pairs with experimental structures, KinCoNet exhibited substantial improvements over DTA for medium difficulty and hard kinases (Pearson correlation of 0.4 vs 0.18 for the former and 0.3 vs 0.1 for the latter) (Figure 7A). This distinction was less pronounced when the assessment was broken down by compound difficulty, where KinCoNet outperformed DTA on hard compounds in instances where experimental structures were available (Figure 7B). We conclude that KinCoNet outperforms a leading structure-free method for kinase-compound affinity prediction.

Figure 6.

Structure-based methods outperform structure-free methods for predicting whether a kinase-compound pair interacts. Comparison of the AUROC of DTC, KinCoNet-M₁, and KinCoNet-M₂ (A) on the overall test set across all kinase and compound difficulty levels, (B) on test sets with increasing kinase difficulty (left), and on test sets with increasing compound difficulty (right). Comparison of the correlation between experimental affinities and predictions from the three models. Each gray dot represents the AUC from a CV split. Black dotted lines represent the mean. DTA – structure-free models trained with the DTA architecture on DTC and PDBBind-kinase; KinCoNet-M₁ – models trained on KinCo with docked structures selected by Autodock Vina combined with PDBBind-kinase; KinCoNet-M₂ – models trained on KinCo with docked structures selected by M1 combined with PDBBind-kinase.

Figure 7.

Structure-based methods generalize better in binding affinity predictions compared with structure-free methods. (A) Correlation on test sets with increasing kinase difficulty on the subset of kinase-compound pairs without a crystal structure (left) and on the subset with crystal structures (right). (B) Correlation on test sets with increasing compound difficulty on the subset of kinase-compound pairs without a crystal structure (left) and on the subset with crystal structures (right). Each gray dot represents the AUC from a CV split. Black dotted lines represent the mean. DTA – structure-free models trained with the DTA architecture on DTC and PDBBind-kinase; KinCoNet-M₁ – models trained on KinCo with docked structures selected by Autodock Vina combined with PDBBind-kinase; KinCoNet-M₂ – models trained on KinCo with docked structures selected by M1 combined with PDBBind-kinase.

Discussion

In this work, we described the development and evaluation of a kinase-inhibitor complex data set (KinCo) and models (KinCoNet) that use this data to predict kinase small molecule binding. KinCo includes over 10,000 small molecules bound to 393 human kinases, resulting in a total of 139,637 kinase-compound pairs (including crystal structures). For each such pair, KinCo contains a library of computationally predicted structural complexes capturing the conformational diversity of kinases and the poses of their bound small molecule ligands. This structural information is coupled with qualitative and quantitative experimental binding affinity data, facilitating the development of structure-based models that leverage the full ensemble of bound conformations. As a demonstration of the utility of this new resource, we showed that the machine learning model KinCoNet can perform kinase-compound affinity prediction by using a novel loss function. The training regimen for KinCoNet exploits the combination of quantitative and qualitative binding data in KinCo as well as its conformational diversity in the set of docked structures. This was achieved using predictions from Ensembler,³⁹ but it is likely that even better performance could be achieved in the future by combining predictions from AlphaFold2⁴⁵ with molecular dynamics methods for generating conformational diversity. However, even in its current iteration, we found that KinCoNet outperformed similar models trained on experimental structures alone and that it behaves in a more biophysically consistent manner. Compared with structure-free methods, KinCoNet also exhibited greater gains in accuracy and generalizability.

The use of computationally docked structures to train machine learning models was explored previously. Francoeur et al.³⁴ generated computational complexes by docking small molecules observed in experimental cocomplex structures into proteins with similar binding pockets, a method known as “cross-docking”. KinCo builds on this approach while addressing some of its key limitations. First, as previously noted, experimentally solved protein-compounds pairs occupy a much smaller chemical space as compared to pairs lacking structural data.⁴⁹ Thus, the focus on cross-docking from experimental structures can lead to biases that limit the generalizability of downstream models. Second, Francoeur et al. treated the binding affinity of all cross-docked structures as equal to the original experimental cognate structure, an assumption unlikely to hold in many circumstances. KinCo does away with this assumption by using known binding affinities for experimentally characterized kinase-compound pairs and then computationally docks all known pairs using a large ensemble of kinase conformations, generating structural diversity in the process.

It should be noted that our model focuses on predicting the affinity between ATP competitive inhibitors and kinases. As such, during docking, the model assumes the compound will bind to the ATP binding site and, during model training, that the direct binding affinity correlates with the strength of inhibition. Therefore, our model should not be used to predict the binding affinity of allosteric inhibitors.

The ability of KinCo and KinCoNet to use a mixture of experimental and computationally docked structures to increase prediction accuracy is notable since most structure-based models to date have been trained exclusively on experimental structures from PDBBIND.³⁷ Chen et al.⁵⁰ have shown that models trained on PDBBIND perform at most comparably to docking algorithms in predicting computationally docked protein-compound pairs outside of the training set. This is a serious limitation since, in most drug discovery campaigns, proteins and compounds dissimilar to those in PDBBIND and lacking experimental structures often become an important part of the discovery effort. KinCoNet overcomes this limitation by directly training on computationally docked poses coupled to experimental binding affinities. By doing so, it surpasses the accuracy of a similar model (ExperimentalNet) trained exclusively on experimental structures while also expanding the diversity of kinases and compounds that can be modeled. It should also be noted that when predicting whether a kinase-compound pair interacts, KinCoNet loses its advantage to ExperimentalNet as the test kinase becomes more dissimilar to those in the training set. We surmised that this is because ExperimentalNet was trained on all 16,000 protein–ligand crystal structures in PDBBIND2018, and it might infer more general structural motifs that allowed it to extrapolate to foreign kinases. On the other hand, KinCoNet was fine-tuned on a mixture of high-quality structure and docked structures so it can focus on inferring kinase family specific binding interactions from both structural motifs as well as sequences (especially when structural input is noisy). When the kinases become more distant in sequence, the family specific rules might be harder to generalize, so KinCoNet might lose some of its predictive power, while ExperimentalNet can still extract general structural motifs that can be broadly applied.

KinCoNet also outperforms structure-free methods trained on identical binding affinity data but lacking structural information; to ensure a fair comparison of performance, we undertook an extensive hyperparameter search using the structure-free DTA method. Nonetheless, technical differences in the architecture of KinCoNet and DTA cannot be ruled out as contributors to differences in performance. KinCoNet exhibits the greatest improvements relative to structure-free methods when predicting hard kinases bound to hard compounds, and this is likely due to the use of 3D structural data. KinCoNet learns not only from docked poses predicted to best capture the binding geometry but also from nonbound poses far from the active site (corresponding to negative binding pairs), which may facilitate learning of physical interaction features inaccessible to structure-free models. KinCoNet’s performance edge applies both to binary classification as well as quantitative affinity prediction (Figure 7), suggesting it is capable, by virtue of accessing the underlying bound structural complex, of discerning geometric features that differentiate between degrees of binding and doing so in a more generalizable fashion.

Future Prospects

While KinCoNet can use structural data to its advantage, it is most performant when the input features are derived from high-quality experimental structures instead of computationally docked ones (Figure 7). In effect, KinCoNet leverages structural information when it is of high quality but degrades gracefully to behave more similarly to structure-free methods when it is not. With the advent of better structure prediction methods,^45,51,52 the accuracy of KinCoNet-like models will continue to improve. KinCoNet implements a specific neural network architecture (3D convolutions) to learn kinase-compound affinities, but rapid progress in deep learning has resulted in many new architectures potentially better suited to structure-based learning. For example, MONN is a graph neural network⁵³ that uses pairwise protein-compound interaction features to predict interaction affinity, while a method from Feinberg et al.²⁸ learns directly from protein-compound structures by incorporating spatial information into the graph representation. In general, graph neural networks have the advantage of representing molecular data in a rotationally and translationally invariant way, unlike 3D convolutional networks. These and future models can be trained and evaluated on KinCo, which provides ready training/validation/test splits that benchmark new models across a range of kinase and compound difficulty levels.

As currently constituted, KinCo contains data only for human proteins with a Protein Kinase Like (PKL) fold. However, kinases unrelated to protein kinases (uPKs) can interact with inhibitors of PKL kinases³ with potential off-target effects. One natural extension of KinCo is to include uPKs and to test the generalizability of KinCoNet on uPK kinases. Another possible extension is to include multidomain kinases; we currently exclude data from these 14 human kinases due to the difficulty of associating binding activity with a specific domain. Nonetheless, multidomain kinases such as JAK kinases are important drug targets, and domain-specific target information is sometimes available in the original source publications or could be acquired denovo. A third extension would include using binding affinity data other than biochemical equilibrium dissociation constants (K_d) such as cell-based half-maximal inhibitory concentration values (IC₅₀). For instance, DTC contains over 100,000 IC₅₀ measurements, the inclusion of which would effectively double the size of KinCo. One challenge in the use of these data is the dependence of IC₅₀ values on assay conditions such as kinase substrate concentration and K_m, which in many instances are not recorded in DTC making it difficult to convert IC₅₀ measurements to K_i constants. Nonetheless, more advanced machine learning techniques may be able to infer assay conditions using meta learning procedures.⁵⁴ A fourth extension involves the use of negative binding data (experimental evidence of no high affinity interaction), which we found to form the bulk of the proprietary affinity data available in a major pharmaceutical company. Although negative data remains underrepresented in the public domain, an untapped reservoir of nonbinding information resides in chemoproteomics assays, which profiles the binding of a compound to native proteins without relying on recombinant protein panel. Such assays can provide unbiased nonbinding data when correctly filtered for technical error and biases, such as protein detection.

On the structural side, KinCo relies on docking and homology modeling to create a conformationally diverse kinase-compound data set. Complementary methods can augment this approach and potentially reduce its systematic biases. These include molecular dynamics (MD) simulations and free energy perturbation (FEP) methods. MD simulations have been performed to reconstruct the dynamics of compound-kinase interactions⁵⁵⁻⁵⁷ and can yield ensembles of structures that additionally increase the conformational diversity in KinCo. FEP methods are particularly adept at capturing small changes in binding pockets induced by related compounds and computing the resulting changes in free energy. FEP can thus be potentially used to augment KinCo by using synthetically generated structural and binding affinity data, particularly for compounds near the chemical space already spanned by KinCo.

Kinases are targets of many drug discovery programs that explore unchartered chemical space for well-studied and understudied kinases. Although computer-aided drug discovery programs have enabled a number of new kinase targets, significant challenges remain in prioritizing hits in such unfamiliar chemical spaces and in providing actionable mechanistic insights to medicinal chemists.⁵⁸ We envision KinCoNet to be used in early drug discovery to help prioritize small molecules targeting kinases of interest for experimental follow-ups as well as to identify potential kinase targets for a small molecule. In addition to providing an immediately usable model, KinCoNet suggests a strategy for unlocking unexplored chemical spaces by combining targeted measurements of the binding affinities of compounds in high priority regions of chemical space with predicted structures of kinase-compound complexes. Combined with KinCo as a starting data set, future models could tackle more challenging chemical modalities. In addition, the approaches outlined here can potentially be applied to proteins other than kinases. Our docking strategy and model training regime could also help to improve model performance for other target classes such as nuclear receptors; currently, this target class has rich profiling data available, but structural data is limited. Finally, we expect that KinCo and KinCoNet will serve as building blocks for efforts focused on intentional drugging of multiple kinases with a single molecule, which remains an important goal of many programs in oncology and inflammatory diseases.

Methods

PDBBind2018 Preparation

The expansive “general” PDBBind2018 data set containing 11,663 crystal structures with matched binding affinities was used for training. From the PDBBind2018 general set, kinase-ligand pairs involving a kinase as enumerated in the “curated kinome” (kinase with a Protein Kinase Like fold plus STK19)³ were identified to create the PDBBind2018-kinase data set.

The cocrystal structures of these kinase-ligand pairs were processed as described in Pafnucy⁴⁶ with the following modifications. The protein chain interacting with the ligand was identified, and the full-length protein rather than the “pockets” as identified in PDBBind2018 was fed into the processing pipeline to generate a 20 Å 3D box around the ligand. To minimize the systemic difference from the docked structures, all hydrogens were removed from the protein crystal structures. The partial charge was calculated for the protein and the ligand separately by using the prepare_receptor_v4.py and prepare_ligand_v4.py scripts in the AutoDock software package. All binding affinities were converted into log scale using log(affinity [μM]).

Extracting Kinase-Compound Pairs with Binding Constant Measurements from DTC

All pairs with a binding constant measurement (K_i or K_d) involving a kinase in the curated kinome were extracted from DTC. Binding constants denoted as K_i were usually determined in an enzymatic assay,⁹ while those denoted as K_d were usually produced in assays measuring direct binding.^12,13,35 To account for systemic biases in these assays, kinase-compound pairs with a K_i or K_d were identified separately and converted into log scale via log(affinity [μM]). If a pair has multiple measurements for K_i or K_d, the highest affinity (lowest value) was used as the binding affinity. If both K_i and K_d measurements exist for a pair, then both were included in training. To reduce noise in the data set, kinases with multiple kinase domains were excluded from the data set due to lack of metadata denoting the interacting kinase domain.

Training/Validation/Test Partitioning

DTC and PDBBind2018 were combined to form the data set for partitioning. The training/validation/test set splits was performed following a similar procedure outlined in AlQuraishi et al.⁴² using the script cluster_v6-ordered_script.py. The kinases were first aligned using jackhmmer, and the sequence identity was calculated from the multiple sequence alignment profiles.⁵⁹ The similarity among nonkinases (from PDBBind2018) and between nonkinases and kinases was assigned to be 0%. The similarity between compounds was the Tanimoto similarity based on their 1024-bit Morgan fingerprints.⁶⁰

Proteins were first clustered using hierarchical clustering, and clusters were generated by applying a threshold cutoff at 90% similarity such that proteins from any two clusters shared at most 90% sequence identity (corresponding to the “hard kinase” category). Compounds were also clustered using hierarchical clustering, and clusters were generated by applying a threshold cutoff at 0.4 Tanimoto similarity such that compounds have a Tanimoto similarity of at most 0.4 (corresponding to the “hard compound” category).

To create the validation and test sets, we sampled 10% of the protein clusters and, from these clusters, sampled 50 compound clusters. Only one compound from each of the sampled clusters was kept in the test set.

The remaining protein-compound pairs were sequentially clustered at 95% sequence identity and random sampling for proteins and 0.6, 0.8 Tanimoto similarity for compounds.

After a validation set was created, a test set was partitioned from the data set with the remaining data points following the same procedure. Each validation or test set with a different kinase-compound difficulty combination (a “grid” in Figure 1) therefore contains 50 unique kinase-compound pairs representing diverse chemical scaffolds. Overall each validation or test set contains about 450 kinase-compound pairs. Validation and test sets involving nonkinase pairs and kinase pairs were created sequentially.

The partitioning scheme was repeated 5 times to obtain 5 independent training/validation/test set splits.

A workflow schematic is illustrated in Figure S1 and detailed in the Supporting Information.

Homology Modeling

Homology models were generated for all kinases in the data set using the Ensembler python module.³⁹ Specifically, the sequences of all human kinase domains were extracted from UniProt. The crystal structures of all mammalian kinase domains and their sequences (assessed in 2017) were curated as templates. For each human kinase of interest, comparative structural modeling was performed with Modeler⁶¹ using the crystal structures of all mammalian kinases as templates. The resulting homology models were clustered by their structural similarity. To ensure the quality of the homology models, homology models whose templates share more than 40% sequence identity with the target kinase were collected for docking. The script pipeline_nocutoff.py was used to run the Ensembler pipeline.

Ensembler performs homology modeling using all available structures of mammalian kinases as templates, including ones of the same kinases in different conformations (corresponding, in some instances, to substantial movements of the kinase domain). Ensembler predates structure prediction using AlphaFold2,⁴⁵ which is generally regarded as the best method for ab initio prediction of protein structure. However, homology modeling using Ensembler has the key advantage of sampling many different conformations for each structure. It is known that many kinases have multiple conformations, and this can influence inhibitor affinity.⁶

Generating in Silico Structures in KinCo

For each of the 137,000 kinase-compound pairs identified from DTC, the compound was docked into the qualified homology models as described above. The docking workflow for each pair was conducted using the scripts dockpipe_qvina_v4.py and run_dockpipe_qvina_v4.py. Using QVina, a fast variant of Autodock Vina,⁴⁰ docking was performed in 560 runs for each pair: for kinases with over 560 homology models, 560 unique models were randomly sampled, and docking was performed on each once. For kinases with fewer than 560 models, the compound was docked into the qualified homology models multiple times. The search space was defined as a box centered around the ATP binding site and enclosing the kinase. The box was intentionally kept large to generate nonbinding poses for training. About 20 docked poses were generated from each docking run, and all docked poses were kept.^{40,41,62−64} This resulted in over 11,000 docked poses in various conformations of the kinase for each kinase-compound pair. The docked poses and paired experimental binding constants were organized to form KinCo.

These in silico structures were processed into a 3D grid as described in Pafnucy,⁴⁶ with the exception that the partial charge on the protein and compound was calculated using the prepare_receptor_v4.py and prepare_ligand_v4.py scripts in the AutoDock software package.

To compare the performance of Vina and our models, we rescored the docked poses with Autodock Vina.⁴¹ As Autodock Vina outputs “Affinity” in kcal/mol, we converted the “Affinity” value into K_d in μM. The predicted affinities from Vina are then compared to those from KinCoNet (also in μM) via AUROC (experimental values binarized at 10 μM) and Pearson correlation.

Model Architecture and Customized Loss Function

The model architecture is as described in Pafnucy.⁴⁶ We applied 3 layers of 3D convolutions with increasingly more filters (64, 128, and 256 filters each with 5 Å * 5 Å * 5 Å dimension). Each convolution layer is followed by a max pooling layer with 2 Å * 2 Å * 2 Å patch. After the convolution operation, the filters are concatenated and passed through a series of fully connected neural networks (1000, 500, and 200 neurons) to predict the binding affinity. Hyperparameters used were listed in Table S2. We also customized the Pafnucy architecture with the following modifications: (i) The initial set of general models was trained on all crystal structures in PDBBind2018 with the mean-squared-error (MSE) as the loss function. These models were referred to as ExperimentalNet. (ii) Kinase-specific models were then trained on DTC and PDBBind2018-kinase pairs with weights in the convolutional layers initialized with the pretrained parameters from ExperimentalNet. Weights in the fully connected layers were randomly initialized. (iii) Instead of using the MSE as the loss function, these kinase-specific models adopted a customized MSE-based loss function

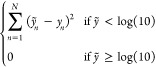1

where ỹ_n is the model prediction, and y_n is the experimental binding constant for the n^th pair. Specifically, for pairs with a binding constant < 10 μM, the MSE was used; for nonbinding pairs with a binding constant ≥ 10 μM, the model was penalized with the MSE if the prediction was < 10 μM, but no loss was accrued if the prediction was ≥ 10 μM.

Iterative Training

To begin iterative training, the docked pose predicted to have the highest binding affinity by Autodock Vina was selected for each kinase-compound pair. The selected docked poses were used as the structure inputs for the kinase-compound pairs without a corresponding crystal structure. For each pair in the DTC, a negative nonbinding pose (a pose with a centroid over 10 Å from the kinase active site) was randomly selected and given a nonbinding label (e.g., affinity = 15 μM). These nonbinding pairs were combined with the pairs with predicted docked poses as well as pairs with crystal structures to train the first iteration model KinCoNet-M₁. KinCoNet-M₁ was used to make predictions on docked poses for all kinase-compound pairs and select the docked pose with the highest binding affinity for each pair to represent the in silico structure. These docked poses selected by KinCoNet-M₂ as well as newly sampled nonbinding poses were combined with crystal structures to be the structure input to train the second iteration model KinCoNet-M₂.

To assess the performance of the models, KinCoNet-M₁ was applied to predict the affinities for poses selected by Autodock Vina, and KinCoNet-M₂ was used to predict the affinities for poses selected by KinCoNet-M₁. Models with the highest correlation between the predictions and the experimental affinities on the overall validation set were selected, and their performance on the test set is reported.

Biochemical Behavior Analysis

For about 130 kinase-compound pairs in the test sets with a crystal structure, the compound was docked into the homology models of the cognate kinase following the docking protocol outlined in “Generating in Silico Structures in KinCo”. Each in silico complex was aligned with the reference crystal structure using TMAlign.⁶⁵ The root-mean-square deviation (RMSD, in Å) between the homology model and the cognate protein was reported from the software, and the RMSD between the docked pose and the reference crystal structure ligand was calculated based on the Euclidean distance between the aligned pose and the crystal structure pose. The kinase RMSD and the compound RMSD were summed to give the final RMSD of the complex. The distance between the in silico structure and the crystal structure was divided into 1 Å bins (e.g., 2–3 Å, 3–4 Å, ..., 19–20 Å) and 20 in silico structures from each distance bin were sampled. Predictions were made for these in silico structures using ExperimentalNet, Autodock Vina, KinCoNet-M₁, and KinCoNet-M₂, and their Spearman’s rank correlation with the RMSD was calculated.

Retraining DTA

The DTA architecture was applied directly to KinCo and PDBBind-kinase. The models were trained and tested with the same cluster-based training, validation, and test partitioning scheme described above.

Data Availability Statement

The code required to generate the docked structures and to train the models is deposited in https://github.com/labsyspharm/KinCo [DOI: 10.5281/zenodo.7703409]. The kinase-compound affinities used for training are available under https://github.com/labsyspharm/KinCo/tree/main/resources. Selected docked poses of all kinase-compound pairs in KinCo are available for interactive viewing on the Rshiny app https://lsp.connect.hms.harvard.edu/ikinco/. Due to the size of the files (∼2TB), all docked structures and homology models in KinCo are available for download via Globus. Instructions for accessing the data can be found on https://lsp.connect.hms.harvard.edu/ikinco/ and at https://github.com/labsyspharm/KinCo [DOI: 10.5281/zenodo.7703409].

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.3c00347.

• Figure S1. Workflow to create the training, validation, and test sets. Similarity between each kinase-ATP competitive inhibitor pair was calculated based on both kinases (sequence similarity) and compounds (1024 Morgan Fingerprint-based Tanimoto Similarity). The validation set and test set were created by sampling sequentially the kinase and compound-based clusters and removing similar pairs from the training set. See Methods – “Training/validation/test partitioning” for more details. Gray color indicates the potential training set. The colored box indicates the sample selected to be in the validation or test set from that cluster, and transparent samples from that cluster indicate samples not selected and will be removed from both the training and validation/test set. The crossed gray box indicates clusters removed from the training set due to similarity to the compounds in the validation/test set. Orange, yellow, and green indicate “hard”, “medium”, and “easy” compound sets, respectively. Figure S2. In silico structures for training make it easier to predict more kinases. Training on KinCo allowed the models to include more kinases during training. This nearly tripled the number of kinases in the easy category (left) and substantially increased the number of kinase-compound pairs involving an easy kinase (right). Figure S3. (A) Example kinases and compounds in the training set and their nearest neighbors in the test set. (Top) Three kinases in the training set, their closest kinase neighbors in the test set, and the kinase difficulty of the test sets where the kinase neighbors belong. Numbers in the parentheses represent the sequence identity between the training-test set kinase neighbor pair. (Bottom) Three compounds in the training set, their closest compound neighbors in the test set, and the compound difficulty of the test sets where the compound neighbors belong. Numbers in the parentheses represent the Tanimoto similarity between the training-test set compound neighbor pair. Colored circles highlight the different chemical moieties between the training and test set compounds. (B) Left: Distribution of the kinase sequence similarity of all kinases in the data set. Yellow and red vertical lines indicate the cutoff at 95% and 90% sequence similarity for medium and hard kinase validation/test set, respectively. Right: Distribution of the similarity between training set kinase and test set kinases in CV1. (C) Left: Distribution of the Tanimoto similarity of all compounds in the data set. Green, yellow, and red lines indicate the cutoff at 0.8, 0.6, and 0.4 Tanimoto similarity for easy, medium, and hard compound validation/test set, respectively. Right: Distribution of the similarity between training set and test set compounds in CV1. Figure S4. Correlation between the experimental affinities and the affinities on test sets with various kinase-compound difficulty combinations. (A) Median correlations from the performance on the 5 independent partitions were shown. Half of the interquantile range is shown in parentheses. (B) The correlation between a model trained on different CV splits and experimental values was shown. Each dot represents a model trained on one of the 5 CV splits. Black line: mean; white line: median; lower and upper bounds of the box: 25% and 75% quantile. Figure S5. Model predictions on poses deviating from the crystal structure. Predictions on the docked poses of a representative kinase-compound complex with low affinity (PDBID: 3ZLY). Table S1. Composition of training, validation, and test sets. Table S2. Hyperparameter screened during hyperparameter optimization. GlossaryTable. Definition of key terms in the paper. Detailed methods for validation/test set generation (PDF)

Author Contributions

M.A. and P.K.S. contributed equally and are cocorresponding authors.

Author Contributions

CL trained the model and analyzed the data. PK generated proprietary data at Merck for model training. NN created the Rshiny app. MA and PKS conceived of the study. CL, MA, and PKS designed the experiments and wrote the paper.

The authors declare the following competing financial interest(s): PKS is a co-founder and member of the BOD of Glencoe Software, a member of the BOD for Applied Biomath, and a member of the SAB for RareCyte, NanoString, and Montai Health; he holds equity in Glencoe, Applied Biomath, and RareCyte. PKS is a consultant for Merck, and the Sorger lab has received research funding from Novartis and Merck in the past five years. MAQ is a member of the SAB and holds equity in Cyrus Biotechnology, Deep Forest Sciences, FL-2021-002, Nabla Biotechnology, and Oracle Therapeutics. He is also a member of the SAB of Interline Therapeutics. CL is currently an employee of Bristol Myers Squibb. PK is an employee of Novartis. NN is an employee of Peptilogics.