Nonlinear effects in optical trapping of titanium dioxide and diamond nanoparticles

Abstract

Optical trapping in biophysics typically uses micron-scale beads made of materials like polystyrene or glass to probe the target of interest. Using smaller beads made of higher-index materials could increase the time resolution of these measurements. We characterized the trapping of nanoscale beads made of diamond and titanium dioxide (TiO₂) in a single-beam gradient trap. Calculating theoretical expectations for the trapping stiffness of these beads, we found good agreement with measured values. Trap stiffness was significantly higher for TiO₂ beads, owing to notable enhancement from nonlinear optical effects, not previously observed for continuous-wave trapping. Trap stiffness was over 6-fold higher for TiO₂ beads than polystyrene beads of similar size at 70 mW laser power. These results suggest that diamond and TiO₂ nanobeads can be used to improve time resolution in optical tweezers measurements.

Significance

Reducing the size of the beads trapped in optical tweezers can increase the time resolution of tweezers measurements, but only if high trap stiffness can be maintained. This work shows a way to do so by using TiO₂ or diamond nanoparticles, which can achieve high stiffness. The stiffness of TiO₂ nanoparticles is enhanced significantly by strong nonlinear contributions to the refractive index, making them particularly effective for small beads at high laser intensity.

Introduction

The controlled manipulation of nanoparticles in a fluidic environment is useful for studying and understanding biophysical processes. Single-molecule approaches allow us to probe the dynamics of molecular processes in real time. Single-molecule force spectroscopy, including optical tweezers that employ a tightly focused laser beam (1,2) to trap an approximately micron-sized dielectric sphere to apply force on single biomolecules, have been used to study fundamental biological processes (3,4,5,6,7) with high spatial (8) and temporal resolution (9,10,11,12,13). Examples range from short-lived events associated with barrier crossing during folding transitions to very slow or long-lived events involving high energy barriers (14).

However, the current temporal resolution achieved in optical tweezers is insufficient to study the dynamics of the very fastest systems, such as proteins that fold near the speed limit (∼1 μs) (15,16,17). Atomic force microscopy (AFM) employing custom-designed cantilevers has achieved a time resolution as fast as 1 μs (18), but at the cost of reduced force stability (19), and the bulky AFM probe may influence the dynamics of the attached biomolecules and introduce kinetic artifacts (20,21). As the time response of a particle in an optical trap is proportional to the particle size and inversely proportional to the trap stiffness (τ_trap ∼ γ/κ, where γ = 6πηa is the hydrodynamic drag on the bead, η the buffer viscosity, a the bead radius, and κ the trap stiffness), it is desirable to look for small trapping particles that achieve higher trap stiffness to increase temporal resolution. Indeed, high refractive index metal particles have been explored (12,22,23,24), and small gold nanoparticles achieved ∼7 times higher stiffness compared to similar size polystyrene beads that are commonly used. However, the associated increased heating of metal particles limited their application as handles for biomolecular manipulations using optical tweezers (23,24).

In recent years, nanotechnology has been used to fabricate several nanostructures with unique features for biotechnological applications. Titanium dioxide (TiO₂) (25,26) and nanodiamond (ND) (27,28) are two biocompatible materials that have been used in biomedical fields (25,26,27,28). They are interesting as optical trapping probes due to their high refractive index. Additionally, the refractive index of TiO₂ particles further increases with increasing laser power due to a significant nonlinear dependence of refractive index on laser intensity. Similar to large gold particles (29), micron-sized TiO₂ particles cannot be trapped using a single-beam optical trap, but they have been trapped in the counter-propagating optical tweezer configuration (30). However, the optical trapping of small TiO₂ and ND nanoparticles is not well explored.

Here, we investigate theoretically and experimentally the dynamics of nanometer-sized TiO₂ and diamond particles in a single-beam optical trap. Numerical simulations showed that TiO₂ and ND particles of radius smaller than ∼200 nm can be trapped efficiently in continuous-wave single-beam tweezers. Interestingly, we found compelling evidence of a nonlinear dependence of the refractive index of TiO₂ nanoparticles on the intensity of the trapping laser beam, which results in increased trap stiffness. Theoretical results for the trap stiffness agreed with the experimentally measured values for both the ND and TiO₂ particles. Furthermore, we demonstrated that using these nanoparticles, the time resolution of optical tweezers-based force spectroscopic measurements can be increased to capture folding dynamics at the speed limit of protein folding.

Materials and methods

Numerical calculations of optical trapping potentials

We used the T-matrix approach (31) as described in detail previously (31,32,33) to estimate the electromagnetic momentum of incoming and outgoing fluxes giving rise to optical forces and thereby calculate the trapping efficiency, Q(r, z, n^p), where r is the radial coordinate perpendicular to the axis of laser beam propagation, z the axial coordinate along the direction of propagation, and n^p the refractive index of particle. The total force experienced in the trap is then F(r, z) = (n^mP/c)Q(r, z, n^p), where n^m is the refractive index (RI) of the medium, c the speed of light, and P the laser power at the objective focal plane. Nonlinear effects altering RI of the trapped particle or medium may arise because of the high laser intensity at the focal plane. Including nonlinear effects, RI can be expressed for the medium (m) and particle (p) as follows (34,35,36):

$$n^{\mathrm{m}/\mathrm{p}}=n_0^{\mathrm{m}/\mathrm{p}}+n_2^{\mathrm{m}/\mathrm{p}}\frac{2P}{\pi {\omega }_0^2}+\left(\frac{d{n}^{\mathrm{m}/\mathrm{p}}}{dT}\Delta T^{\mathrm{m}/\mathrm{p}}\right)\text{,}$$ (1)

where n₀^m/p is the linear RI of the medium/particle, n₂^m/p is the second-order nonlinear RI, ω₀ is the laser spot size (Gaussian beam radius at focus, given by 0.82 λ/NA for wavelength λ and numerical aperture NA), dn^m/p/dT is the thermo-optic coefficient for the medium/particle, and ΔT^m/p is the temperature change. For a trapped bead, ΔT^p = (Pα^p/2πκ^p)ln[(2πa/λ)² + 1]/2, where a is the particle radius, α^p the absorption coefficient of the particle, and κ^p the thermal conductivity of the particle; whereas for the medium, ΔT^m = (Pα^m/2πκ^m)[ln(2πh/λ) − 1], where h is the distance from the coverslip to the bead, α^m the absorption coefficient of the medium, and κ^m the thermal conductivity of the medium (37). The second term in Eq. 1 corresponds to the optical nonlinearity and the third to the thermal nonlinearity, both of which depend on the laser power. At 1064 nm, the nonlinearity of the medium (buffer) is negligible because the nonlinear terms in Eq. (1) are much smaller than the linear RI. All parameters used in the numerical simulations are listed in Table S1.

Sample preparation

Trap stiffness measurements were done on 150-nm radius TiO₂ particles (914177; Sigma-Aldrich) and 100-nm radius bare ND particles produced according to previously described methods (27). ND particles were not coated with dopamine, as dopamine coatings melted in the laser trap. Nanoparticles were diluted 1:10,000 (v:v) in water and sonicated in an ice bath (∼5 min for TiO₂ and ∼30 min for ND, in each case using a Branson 450 Sonifier operated at 400 W in pulsed mode with 80% duty cycle) to produce single-particle suspensions at ∼1 pM. Roughly 5–10 μL of particle suspension was placed in a channel on a microscope slide closed by a coverslip and sealed with vacuum grease to prevent evaporation. Each sample was used for approximately 4–5 h. Using field-emission scanning electron microscopy, TiO₂ particles were confirmed to be spherical, of mean radius 147 ± 2 nm, and the size distribution was measured (Fig. S1). ND particles were more variable in shape (27); particle asymmetry was minimized by selecting NDs with a Lorentzian power spectral density (38).

Trap stiffness measurements

We used a custom-built optical tweezer setup to make stiffness measurements (Fig. S2). A ∼1-W polarized laser beam in the Gaussian TEM₀₀ mode from a 1064-nm diode-pumped solid-state laser (Nd:YVO₄) was used to create the trap (39), and a 633-nm He-Ne laser was used as a detection beam. Bead positions were monitored from the light scattered from the beads onto a standard quadrant photodiode (QP50-6SD2-1M; First Sensor), calibrated as described (3). Data were sampled at 1 MHz and filtered at 500 kHz with an 8-pole Bessel filter (Krohn-Hite). Trap stiffness was estimated from the average of two methods: (1) the roll-off frequency of the noise power spectral density and (2) the position variance of the trapped particle (3). (1) The noise power spectral density calculated from 100 distinct 1-s trajectories was averaged and fit to a Lorentzian function Fig. S3 A) and the trap stiffness, κ, found from the roll-off frequency defined as f₀ = κ/2πγ, where γ = 6πηa and η is the medium viscosity (here, ∼1 × 10⁻³ Pa s). Measurements were taken at a height of ∼450 nm above the glass surface, applying Faxen’s correction to the viscosity as described previously (3). (2) Trap stiffness was estimated from the bead position variance using the equipartition theorem, ½κ〈x²〉 = ½k_BT, where k_B is the Boltzman constant and T the absolute temperature (Fig. S3 B). Averaging the two results reduced the effects of independent systematic errors in the different methods (3). The trap stiffness was not identical in the two radial axes (Fig. S4), because of the linearly polarized trapping beam, consistent with previous work using polystyrene beads (40); here, we report only the stiffness in the x axis. All data analysis was done in Igor Pro 8. A total of 70 TiO₂ beads and 10 ND beads were measured.

Time resolution measurements

Time resolution was estimated from the autocorrelation time of the bead position. Bead position autocorrelations were calculated directly from trajectories in Igor Pro 8 and fit to single-exponential decay, with the decay constant yielding the response time of the particle in the trap. An additional estimate was obtained by abruptly jumping the position of the trap ∼100 nm from its initial position using an electro-optic deflector (Conoptics), recording the trajectory of the bead after the trap position change, and measuring the time required for the bead to relax into the new trap position. The post-jump trajectories at each trap stiffness were averaged (590–936 jumps from four beads), and the last 50% of the relaxation distance was fit to a single-exponential decay function, using the decay constant to estimate the response time.

Results

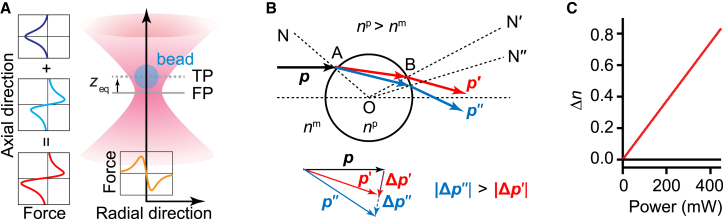
In an optical trap created by a highly focused laser beam, a particle experiences forces due to interactions with the electromagnetic field created by the incident beam. The particle experiences a gradient force along the radial direction (perpendicular to the beam propagation) but both a gradient and a scattering force along the axial direction, z (41) (Fig. 1 A). The gradient forces are responsible for trapping the particle at the beam center, but the scattering force pushes the particle along the beam propagation direction, such that the trapping plane in which the particle is held at equilibrium (trapping plane (TP); z = z_eq) is displaced forward from the focal plane (FP; z = 0).

Figure 1.

Nonlinear effects in trap optical trapping. (A) Schematic representation of optical tweezers (not to scale). A particle (bead) is trapped in a highly focused laser beam at the trapping plane (TP). The equilibrium position of the particle in TP (z_eq) is slightly displaced from the focal plane (FP) of the laser beam in the direction of laser propagation owing to the scattering force. Insets: forces experienced by the particle: the particle experiences only the gradient force along radial direction (bottom inset, yellow), but the sum (left inset, red) of the gradient (left inset, cyan) and the scattering (left inset, blue) forces along the axial direction. (B) Schematic representation of the beam directions and the resulting change in the momentum (inset) for particle with linear (red arrows) or nonlinear (blue arrows) interactions; a ray diagram is used for illustrative purposes only, as the beads are much smaller than the trap wavelength. (C) Change in refractive index for TiO₂ (red) and ND (black) particles with incident laser power, calculated from Eq. (1). To see this figure in color, go online.

The resultant force on the particle in the trap depends on parameters such as the RI of the particle and trapping medium/buffer, the change in RI due to laser power as a result of optical and thermal nonlinearities, and the temperature gradient. In the presence nonlinear effects, the RI is given by Eq. (1) (36). The effects of nonlinearities on the gradient force are illustrated in Fig. 1 B. A ray incident on the particle (point A) bends more toward the normal (gray dashed line from the point O to A) for higher RI. Since RI is higher for the bead in the nonlinear case compared to the linear case, owing to the contribution from the higher-order terms, the light bends more for nonlinear RI. At point B, the ray is bending away from the normal (gray dashed line N′ from point O to B) while traveling from the higher-RI bead to the lower-RI medium. As a result, the change in momentum (and hence force) experienced is higher for a nonlinear bead than that for a linear bead (Fig. 1 B, inset). The linear RI is similar for TiO₂ and ND particles (Table S1), but TiO₂ has a higher thermo-optic coefficient and second-order nonlinear RI. Significantly, the nonlinear RI coefficient is much larger for TiO₂ than ND particles, with a notable deviation in n^p from n₀ that increases linearly with the laser power; in contrast, no power-dependent deviation is evident for ND particles (Fig. 1 C).

Numerical simulations of trapped TiO₂ and ND particles

To explore the trapping of TiO₂ and ND particles, we first performed numerical simulations to estimate the forces exerted on the particles in the optical trap. The force was symmetrical in the radial direction for both TiO₂ (Fig. 2 A) and ND particles (Fig. 2 B). The direction of the force changed on either side of the radial center indicating a harmonic potential, trapping the particles in the radial plane. Moreover, the magnitude of the force increased as particle size increased from 100 nm to 150 nm (radius). Along the axial direction, however, the total force was asymmetric for both TiO₂ (Fig. 2 C) and ND particles (Fig. 2 D), due to the significant contribution of the scattering force: although the magnitude of the force increased with particle size along both directions at a given distance from the TP, the increase was in the negative direction, resulting in an anharmonic potential. Intriguingly, as a result of the increased nonlinearity for TiO₂, the magnitude of the force was higher for TiO₂ particles along both the radial and axial directions compared to that of ND particles (Fig. 2).

Figure 2.

Calculated forces experienced by a particle in the trapping plane in an optical trap at a laser power of 100 mW. (A and B) Forces along the radial direction for (A) TiO₂ and (B) ND particles. (C and D) Forces along the axial direction for (C) TiO₂ and (D) ND particles. Dashed lines represent force expected in the absence of nonlinearity (showing that nonlinearity increased the force on TiO₂ particles). Insets: expanded view near the focal and the trapping planes. Because of the scattering force, the equilibrium position of the particle is displaced by a distance z_eq, that depends on the material, particle size, and laser power. To see this figure in color, go online.

Next, we calculated the stiffnesses of optically trapped TiO₂ and ND particles. For both TiO₂ (Fig. 3, left column) and ND particles (Fig. 3, right column), the radial (solid lines) and axial (dotted lines) stiffness (Fig. 3, top row) at a given laser power increased nonlinearly with the particle size, reached a maximum, and then decreased. For ND particles, the shape of the stiffness versus particle size curve did not change with laser power, such that the particle size achieving maximum stiffness remained unchanged along both radial and axial directions (Fig. 3 B). For any laser power, ∼195-nm radius ND particles were predicted to produce maximum stiffness, in both directions. Turning to TiO₂ particles, the overall stiffness increased with laser power along both directions (Fig. 3 A), but surprisingly, the peak of the stiffness profile moved to smaller particle sizes as laser power increased (Fig. S5). Higher stiffness could thus be obtained from small-sized particles when compared to ND: the radius of TiO₂ particles yielding maximum stiffness decreased from ∼180 nm to ∼145 nm on increasing the laser power at the TP from ∼50 mW to ∼400 mW (Fig. 3 A). This effect is exactly what is desired to increase the time resolution of optical trapping—increasing the stiffness for smaller particles.

Figure 3.

Size-dependence of trapping. (A and B) Calculated trap stiffness as a function of particle size and average laser power. Solid lines: stiffness in radial direction; dashed lines: stiffness in axial direction. (C and D) Equilibrium displacement of trapping plane with respect to the focal plane along axial direction. To see this figure in color, go online.

Due to the asymmetric nature of the axial force (Fig. 2C and 2D), the equilibrium position of the particle (z = z_eq) changed with the particle size (Fig. 3C and 3D). Qualitatively, z_eq increased from zero nonlinearly with particle size for both particle types, reached a local maximum before decreasing to a local minimum, and finally increased to such an extent that the particle could no longer be trapped but escaped in the axial direction. The profile of z_eq did not change with laser power for ND particles, but for TiO₂ particles, the position of the local maxima and minima moved toward smaller particle sizes with increasing laser power. Notably, the position of the local minimum in z_eq coincided with the local maximum of the stiffness along both directions (Fig. 3) for a given laser power, thereby producing the most stable trap. Small-sized particles could be trapped, up to ∼200 nm radius for TiO₂ and ∼230 nm for ND, but bigger particles could not, as expected (30).

Measurements of trapped TiO₂ and ND particles

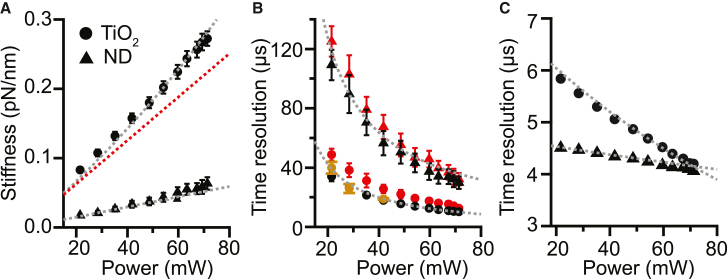
To compare theoretical estimates of stiffness with experiment, we measured the stiffness of optically trapped TiO₂ and ND particles. Particles were trapped using custom-built, single-beam optical tweezers (39) with a 1064-nm trapping laser, and the signal was monitored by measuring scattering of a 633-nm He-Ne laser from the beads onto a quadrant photodiode. We tested 150-nm radius TiO₂ particles and 100-nm radius ND particles. We verified that a single particle was trapped by confirming the presence of a single step in the scattered intensity measured on the diodes (Fig. S6) as well as by analyzing the power spectrum of the recorded intensity. Determining the trap stiffness from the average of the values returned from two different methods (power spectral density roll-off frequency and bead position variance), we found reasonable agreement with the theoretical expectations for both TiO₂ and ND nanoparticles (Fig. 4 A). For a given trap power in the objective FP, TiO₂ nanoparticles achieved significantly higher stiffness compared to the ND particles as a result of their stronger optical nonlinearity. Consistent with the theoretical estimates, the enhancement of the stiffness due to the nonlinear response increased as the average power increased for TiO₂ particles (Fig. 4 A).

Figure 4.

Stiffness and temporal resolution of trapped TiO₂ and ND particles. (A) Radial stiffness as a function of laser power. Dashed lines: theoretical estimates of stiffness with (gray) and without (red) nonlinear effects. (B) Time response of trapped particles estimated based on stiffness (black), decay time of the bead position autocorrelation (red), and response to abrupt jump in trap position (brown). (C) Estimated time resolution for single-molecule force spectroscopy measurements at 15 pN. Error bars represent standard error of the mean. To see this figure in color, go online.

Next, we explored the temporal resolution that could be achieved with these optically trapped nanoparticles, τ_trap. We first estimated τ_trap from the stiffness via the characteristic time τ_trap = γ/κ, which indicates resolution should be higher for smaller beads and stiffer traps. As laser power was increased from ∼20 mW to ∼70 mW, γ/κ decreased from ∼110 μs to ∼30 μs for the ND particles and from ∼35 μs to ∼10 μs for the TiO₂ particles (Fig. 4 B, black). We then obtained a second estimate for τ_trap from the decay time for the bead position autocorrelation function (Fig. 4 B, red), found from single-exponential fits to the autocorrelation (Fig. S3 C). These two estimates were similar and agreed well with the theoretical estimates based on predicted trap stiffness. A third estimate was also obtained for the TiO₂ particles (Fig. 4 B, brown) from the time required for a bead to move in response to an abrupt jump in the trap position (Fig. S7), which agreed within error with the other estimates.

Finally, we estimated the temporal resolution that could be achieved in single-molecule force spectroscopy measurements using these nanoparticles, for example in studies of folding reactions (42). Using the bead to apply force to a tethered molecule in single-molecule force spectroscopy measurements is expected to increase the time resolution further, by increasing the effective stiffness of the measurement construct (9). As a concrete example, we considered dual-trap measurements, wherein the molecule of interest is linked to two particles in traps of stiffnesses κ_T1 and κ_T2 via a DNA linker of stiffness κ_DNA (Fig. S8). The stiffness of the DNA linker increases with the application of force (Fig. S9). The effective trap stiffness of a trap (say trap 1) in such a configuration is given by κ_eff = κ_T1 + [κ_T2⁻¹ + κ_DNA⁻¹] ⁻¹ (43). For an optical tweezers experimental setup with a TiO₂ or ND particle in trap 1, an ∼600-nm diameter polystyrene bead in trap 2 with stiffness ∼1 pN/nm (comparable to stiffnesses used to measure fast dynamics previously (9)) and κ_DNA ∼0.8 pN/nm for a linker of ∼2000 bp length at 15 pN of applied force (Fig. S9 B), the temporal resolution was predicted to increase to ∼4–6 μs for 150-nm TiO₂ particles and ∼4–4.5 μs for 100-nm ND particles at trapping powers in the range ∼20–70 mW (Fig. 4 C).

Discussion

These results show that small (200- to 300-nm diameter) TiO₂ and ND particles can be trapped with high stiffness in a standard single-beam optical trap, with the stiffness enhanced significantly by nonlinear effects. The strong dependence of the stiffness on particle size should, in principle, allow a wide range of stiffnesses to be accessed using such nanoparticles, as appropriate for different types of measurements, but it will also result in significant variations in stiffness associated with the dispersion in particle sizes. Indeed, such variability in stiffness was observed here: for example, at 50 mW the stiffness of the TiO₂ beads varied from 0.13 to 0.37 pN/nm, matching the range of values expected from the observed size distribution of these beads (Fig. S10). Size variability can also lead to mis-estimation of stiffness using methods like the power spectral density that depend on bead size, suggesting that it is best to use methods that are size independent (44,45), especially for verifying the stiffness of individual beads. We note that the good agreement between theoretical estimates and experimentally measured values permits the particle size to be determined from the observed stiffness, if the laser power at the TP is known.

Such small beads provide three chief benefits to biophysical measurements using optical tweezers. We focused here on the possibility for increased time resolution: for a given trap stiffness, the time required for beads to move in response to changes in the system being probed will be reduced as the bead size becomes smaller, owing to the linear dependence of the bead diffusion coefficient on radius. For the bead sizes discussed above (150-nm radius TiO₂ and 100-nm radius ND particles), we can extrapolate from observed and predicted stiffnesses (Fig. 4 A) to higher laser power, leading to an expected maximum stiffness of ∼4 pN/nm for TiO₂ and ∼0.3 pN/nm for ND at ∼370 mW laser power (Fig. S11 A). Such stiffnesses would correspond to τ_trap ∼ 0.7 μs for TiO₂ and ∼7 μs for ND (Fig. S11 B), permitting time resolution in a force spectroscopy experiment at ∼15 pN of ∼0.6 μs for TiO₂ and ∼2.5 μs for ND particles (Fig. S11 C), comparable to the best performance reported in AFM measurements (46). We note that the stiffness (and hence time resolution) does not increase without limit along with the laser power, however: at high enough laser power, the scattering force displaces the trapped particle sufficiently far from the focal point that the stiffness begins to drop (Fig. S11 A).

We found that TiO₂ particles provided better time resolution compared to ND particles. Over the entire particle-size range that could be stably trapped (Fig. 3), TiO₂ particles produced higher stiffness, and hence higher temporal resolution, compared to ND particles, in both the radial and axial directions (Fig. S12). This advantage is more pronounced for higher laser power, specifically for the particle sizes that resulted in the stiffest trapping of TiO₂ particles, in the range of ∼140–160 nm (Fig. S12), for which the stiffness was a factor of as much as ∼4.4-fold greater than for ND particles of the same radius. The pronounced increase of stiffness for 140- to 150-nm TiO₂ particles with increasing laser power indicates that this range of particles sizes maximizes stiffness and time resolution. TiO₂ and ND particles produced significantly higher stiffness compared to polystyrene particles of similar sizes. For example, the stiffness of ∼0.013 pN/nm produced by 100-nm-radius polystyrene particles at 155 mW average power (47) is about an order of magnitude lower than our estimate at this power of ∼0.11 pN/nm and ∼0.15 pN/nm for ND and TiO₂ particles (respectively) of the same size; this advantage extends and is even magnified at higher trap power (Fig. S11 A). Similarly, TiO₂ and ND particles produced several-fold higher stiffness compared to germanium particles: at 71 mW, the trap stiffness for 100- and 150-nm-radius germanium particles is expected to be ∼0.014 pN/nm and 0.046 pN/nm (12,48), respectively, compared to ∼0.06 pN/nm and ∼0.27 pN/nm for 100-nm ND and 150-nm TiO₂ particles, respectively.

A second benefit of using smaller beads, even if higher time resolution is not achieved or desired, is that they can reduce the kinetic artifacts observed in force spectroscopy measurements (20,21,49). The mechanical coupling of a molecule to a bead used for applying force via an elastic linker can lead to underestimation of the true rate at which molecular processes (e.g., folding) occur, when the bead dynamics are slower than the molecular dynamics and the mechanical linker is stiff. Some kinetic properties, such as transition path times, are particularly sensitive to such artifacts. By reducing the size of the bead and hence increasing its diffusion constant, such kinetic artifacts can be reduced or minimized. A third benefit of smaller beads is that the fluctuation-dissipation theorem leads to increased spatial resolution (or equivalently, force precision) per unit time when bead size is reduced—the increase being proportional to the square root of the bead radius—owing to the reduction in drag coefficient (8).

These nanoparticles nevertheless pose some challenges for applications in optical trapping. Although TiO₂ particles are relatively uniform in their spherical shape, ND particles are less so. Such shape nonuniformities can lead to preferential alignment of the particle in the laser beam, changes in the radial and axial force profiles, and increased anisotropy in the radial stiffness, as well as mis-estimation of trap stiffness if the shape is assumed to be spherical. Another potential issue is heating owing to absorption of the trapping beam by the particles. Because the viscosity of water decreases significantly with increasing temperature, heating will result in a stiffness from the power spectral density that increases faster with laser power than the stiffness from the position variance. No such effect could be detected within error, suggesting any heating is small, as confirmed by the theoretical model, which estimated heating of under 1 K even at high laser (Fig. S13). For applications requiring attachment to the beads, bioconjugation can also be challenging: although protocols have been developed for conjugation of TiO₂ and ND particles (27,50,51), they are more involved than those used for polystyrene. The balance between these challenges and benefits will determine which material is most appropriate for a given application. Similar considerations apply to comparisons with Ge nanoparticles, which have a higher index of refraction than either TiO₂ or NDs but lower nonlinear optical susceptibility than TiO₂, absorb light more strongly than either (which may lead to larger heating effects), are somewhat cytotoxic (52), tend to aggregate without surface passivation, are not yet available commercially (unlike TiO₂ and ND beads), and like TiO₂ and NDs can be functionalized biochemically (53) but less easily than polystyrene.

Conclusions

We characterized theoretically and experimentally the stiffness and response time of optically trapped TiO₂ and diamond nanoparticles, showing that 150- and 100-nm TiO₂ and ND particles were trapped efficiently at stiffnesses that matched theoretical expectations. Because of a larger optical nonlinearity, TiO₂ particles produced higher trap stiffness compared to ND particles. Nanoparticles like these thus offer a promising avenue to improve the temporal resolution of single-molecule force spectroscopy experiments probing fast dynamics in biomolecular processes, with the potential to achieve sub-microsecond resolution, although such applications require the deployment of robust biocompatible surface functionalizations for linking the particles to the biomolecules of interest (27,50). These findings point the way to future work using optical tweezers to probe the dynamics of single molecules on faster timescales, close to the speed limit for protein folding (14).

Author contributions

A.D., K.N., and M.T.W. designed the research; A.D. performed experiments and theoretical simulations; A.D. and K.N. analyzed data; H.J. and K.C.N. provided nanodiamond particles; A.D., K.N., and M.T.W. wrote the manuscript; all authors edited the manuscript.

Editor: William Hancock.