Virtual Human Models for Electromagnetic Studies and Their Applications

Abstract

Numerical simulation of the electromagnetic, thermal and mechanical responses of the human body to different stimuli in MRI safety, antenna research, electromagnetic tomography, and electromagnetic stimulation is currently limited by the availability of anatomically adequate and numerically efficient cross-platform computational models or “virtual humans”. The objective of this study is to provide a comprehensive review of modern human models and body region models available in the field and their important features. The major emphasis is made on various model applications in Computational Electromagnetics (CEM) and antenna-related research.

I. Virtual Humans and their Major Applications

A. Virtual Humans

Computational modeling with virtual humans combines mathematics, physics, anatomy, physiology, and computer science to study the behaviors and reactions of complex biomedical problems in-silico. The National Institutes of Health states that “modeling can expedite research by allowing scientists to conduct thousands of simulated experiments by computer in order to identify the actual physical experiments that are most likely to help the researcher find the solution to the problem being solved” [1]. Among other computer simulation tools, realistic computational human models or “virtual humans” are becoming a significant component of modern biomedical research.

B. Use of Computational Human Models for Development of Medical Devices

In the past decade, general biomedical research has emerged as one of the industries showing great potential to stimulate the US economy. Table I lists the major medical device market sectors with the potential need for computational human phantoms. In the case of general medical device development, relevant study areas include fluid dynamics (e.g., shear stress and stagnation calculations in ventricular assist devices), solid mechanics (e.g., maximum stress locations in a hip implant), electromagnetics and optics (e.g., radiofrequency dosimetry in magnetic resonance imaging), ultrasound propagation (e.g., absorbed energy distribution for therapeutic ultrasound), and thermal propagation (e.g., radiofrequency and laser ablation devices) [2].

Table I.

Major Medical Device Market Sectors with the Potential Use of Computational Human Models

Market Sectors	Market Size (2015)	Annual Growth (%)	Market Size (out year)
General Medical Devices/Implants	$260 Ba	6.1b	$302 B (2017)b
Medical Imaging Safety (MRI, CT)a	$24.4 B	4.0	$35.4 B (2019)
Electric/Electromagnetic Therapeuticsa	$4.2 B	8.2	$6.0 B (2018)
Diagnostics – Traumatic Brain Injuryd	$1.54 B	3.8	$2.0 B (2017)
Diagnostics – Endoscopye	$23.3 B	6.6	$75.8 B (2022)

^aEspicom Business Intel

^bLucintel

^cTransparency Market Res.

^dGlobalData

^eVisiongain

C. Use of Computational Human Models in Automotive Safety Research

Along with the medical device field, computational human body models have been actively developed for biomechanical and automotive safety research over the past three decades [3]–[12]. Although vehicular crash safety performances are evaluated with crash test dummies regulated by respective federal governments, it is believed that examination of the impact biomechanics with computational human body models would provide better understandings of injury mechanisms relevant to automotive crashes. Body sizes of computational human models in automotive research are selected from a review of standardized anthropometries [13], the most common being an American adult male 50^th percentile (commonly called AM50). One popular example is the Total Human Model for Safety, which is an extremely detailed finite-element computational model of the human body used in various impact scenarios. It has been actively developed by Toyota Motor Corporation and Toyota Central R&D Labs since approximately 2000 [4]–[8]. Another example is given by the very detailed Global Human Body Models Consortium products [9]–[12] developed by General Motors, Honda, Nissan, etc., and sponsored by the U.S. National Highway Traffic Safety Administration. An example is given in Fig. 1. These human models are also widely used for university research; examples are given in [14],[15]. The automotive-safety models do not correspond to real subjects, but they usually have extremely high-quality surface quadrilateral CAD (Computer Aided Design) surface representations best suited for accurate FEM modeling, including mechanical applications [16].

Fig. 1.

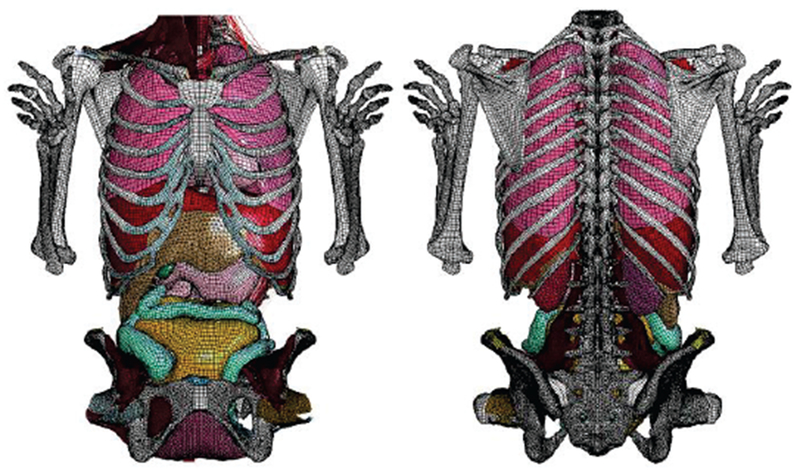
Fo5-O quadrilateral model resolution in the abdominal region [12].

In general, we understand the CAD format as a representation such as in ACIS, ProE, Catia, where smooth surfaces are defined (not volumetric “meshes”), and most important there is a consistent (watertight and manifold) topology of shapes, faces and edges. What matters for this article is just a practical and proven FEM-meshability, i.e. it is enough to have a consistent surface model coarse enough to be meshed into tetrahedra or other for FEM electromagnetic or structural simulations. The surface model may be based on triangles, quadrilaterals, or nonuniform rational basis splines (NURBS). Every CAD model and/or its parts could be 3D printed.

D. Use of Human Models in Electromagnetic Studies

For general electric and magnetic fields applications, computational human models are used to perform safety and performance evaluations on a variety of medical devices [2]. These include electrophysiology monitoring devices such as EEG (Electroencephalography), ECG (Electrocardiography), MEG (Magnetoencephalography), and MRI systems. MR conditional implanted devices like orthopedic devices, stents, pacemakers, and neurostimulators are other devices benefiting from these models along with devices for radiofrequency ablation, optical coherence tomography, fluorescence spectroscopy, laser surgery, and optical therapy. In application to antennas, computational human models are used in the modeling of body-centric wireless communications such as the safety and performance evaluations of cellphone radiation, implanted antennas, microwave ablation, and microwave imaging systems.

E. Use of Computational Human Models in Radiology

In radiology, human models are applied for ionizing radiation dosimetry studies. The design and application of human models (mostly voxel models) in radiation dosimetry pertinent to organ doses resulting from CT and Positron Emission Tomography or PET examinations, as well as nuclear exposure in power plants, have been documented in Refs. [17]–[20].

II. Overview of Human Models for CEM Research

A. Full-Body Human Models

Table II, which is an updated extension of the IEEE document [21], lists major full-body models currently available for computational electromagnetics (CEM) and radiological simulations along with major anatomical information and country of origin. It specifies the model type, resolution, availability of the original data etc., availability of a free version, and other model characteristics. Models based on the Visible Human Project^® [22]–[26] are marked blue.

Table II.

Major Anatomical Full-Body Human Models for CEM and Radiological Simulations (After 2004)

Entity/Country	Model Name	G/A/H/W	Da	TYPE	RES, mm2	FV	D	Ref.
IT’IS Found. Switzerland	Glenn	m/84/173/61.1	N	V	0.5×0.5×1.0h 0.9×0.9×2b	N	Y	[28],[29]
IT’IS Found. Switzerland	FATS	m/37/182/119	N	V	0.5×0.5×1.0h 0.9×0.9×2b	N	Y	[28],[29]
IT’IS Found. Switzerland	DUKE	m/34/177/70.3	N	V/S	0.5×0.5×1.0h 0.9×0.9×2b	Y	Y	[27]–[29]
IT’IS Found. Switzerland	ELLA	f/26/163/57.3	N	V/S	0.5×0.5×1.0h 0.9×0.9×2b	Y	Y	[[27]–[29]
IT’IS Found. Switzerland	LOUIS	m/14/168/49.7	N	V	0.5×0.5×1.0h 0.9×0.9×2b	N	Y	[[28],[29]
IT’IS Found. Switzerland	BILLIE	f/11/149/34.0	N	V/S	0.5×0.5×1.0h 0.9×0.9×2b	Y	Y	[27]–[29]
IT’IS Found. Switzerland	EARTHA	f/8/136/29.9	N	V	0.5×0.5×1.0h 0.9×0.9×2b	N	Y	[28],[29]
IT’IS Found. Switzerland	DIZZY	m/8/137/25.4	N	V	0.5×0.5×1.0h 0.9×0.9×2b	N	Y	[28],[29]
IT’IS Found. Switzerland	THELONIOUS	m/6/115/18.6	N	V/S	0.5×0.5×1.0h 0.9×0.9×2b	Y	Y	[27]–[29]
IT’IS Found. Switzerland	ROBERTA	f/5/109/17.8	N	V	0.5×0.5×1.0h 0.9×0.9×2b	N	Y	[[28],[29]
IT’IS Found. Switzerland	NINA	f/3/92/13.9	N	V	0.5×0.5×1.0h 0.9×0.9×2b	N	N	[28],[29]
IT’IS Found. Switzerland	CHARLIE	f/8w/na/4.3	N	V	0.5×0.5×1.0h 0.9×0.9×2b	N	N	[28],[29]
China Acad. of Tel. Res.	CHINESE MALE	m/35/172/64	Y1	V/S	1×1×1	N	N	[30],[33],[34]
China Acad. of Tel. Res.	CHINESE FEMALE	f/22/162/54	Y1	V/S	1×1×1	N	N	[30],[33],[34]
Huazhong Univ, China	CDH M2	m/166	Y2	V/S	0.1×0.1×0.2	N	N	[31],[33],[34]
Huazhong Univ, China	CHINESE REF. MAN	m/166	Y	S	2×2×2	N	Y	[32]–[34]
Natl. Inst. of Inform. and Comm. Technol., Japan	NAGAOKA MAN (TARO)	m/22/173/65	N	V	2×2×2	N	N	[35]
Natl. Inst. of Inform. and Comm. Technol., Japan	NAGAOKA WOMAN	f/22/160/53	N	V	2×2×2	N	N	[35]
ETRI, Korea Flanyang University	KOREAN MAN	m/21/176/67	N	V/S	1×1×1 (head) 3×3×3(body)	N	N	[36],[37]
ETRI, Korea Flanyang University	KOREAN CHILD	m/7/122.4/25.5	N	V	1×1×3	N	N	[38]
ETRI, Korea Flanyang University3	KOREAN WOMAN	f/26/161/54	N	V	2×2×2	N	N	[39]
Nat. Radiological Protection Board, UK	NAOMI	f/23/163/60	N	V	2×2×2	N	N	[40]
REMCOM, PennState	Male/Female	m/f	Y	V	5×5×5(both)	N	Y	[41]
Helmholtz Zentrum Munchen, Germany CST AG, Germany	BABY	f/8w/57/4.2	N	V	0.85×0.85×4	N	N	[42],[40]
	CHILD	f/7/115/21.7	N	V	1.54×1.54×8	N	N	[42]
	DONNA	f/40/176/79	N	V	1.88×1.88×10	N	N	[42]
	EMMA	f/26/170/81	N	V	0.98×0.98×10	N	N	[42]
	GUSTAV	m/38/176/69	N	V	2.1×2.1×8	N	N	[42]
	LAURA	f/43/163/51	N	V	1.88×1.88×5	N	N	[42]
	HUGO, posable	m/38/187/113	Y	V	1×1×1	N	Y	[43]
U Texas Austin, USA	AUSTIN MAN	m/38/187/113	Y	V	1×1×4	Y	Y	[44], [45]
U Texas Austin, USA	AUSTIN WOMAN	f/60/162/88	Y	V	1×1×4	Y	Y	[44], [45]
Duke University Medical Center, USA	XCAT FAMILY	Orig: f/60/162/88 m/38/187/113	Y	NURBS&S4	variable	Y	Y	[46]–[52]
NEVA EM LLC, WPI, USA	VHP-Female (NELLY)	f/60/162/88	Y	FEM	variable			[53]–[58]
NEVA EM LLC, WPI, USA	VHP-MALE	m/38/180/90.3	Y	FEM	variable			[59]

The most comprehensive model family in Table II is certainly the virtual population from IT’IS Foundation Switzerland [27]–[29]. Major members of the virtual population are shown in Fig. 2.

Fig. 2.

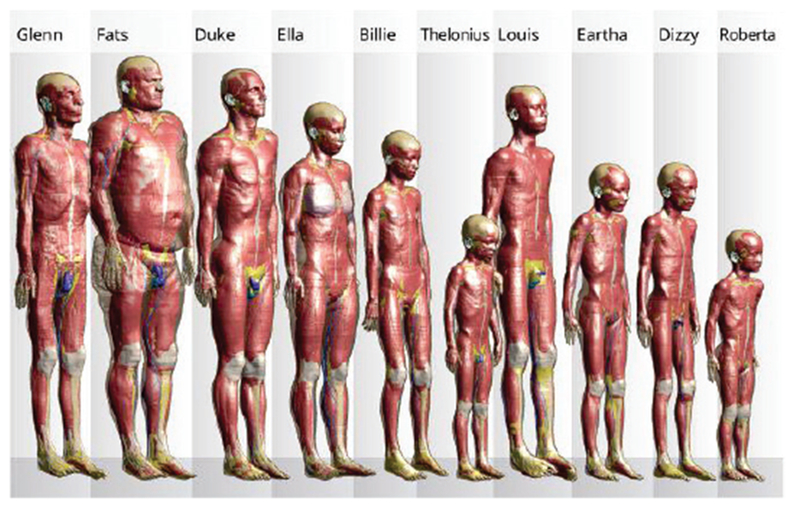
Members of the Virtual Population [27]–[29] – voxel models. Many of the models are posable.

Some models in Table II are based on the legendary Visible Human Project^®. In 1990, the U.S. National Library of Medicine started this project, building a digital image library of volumetric data representing a complete adult human male and female. This Visible Human Project^® (VHP) included digitized photographic images from cryosectioning, digital images derived from computerized tomography, and digital magnetic resonance images of two cadavers. Even today, the corresponding cryosection images (24 bits of color, pixel resolution of 0.33 mm) provide state-of-the-art resolution of muscle, other soft tissues as well as bone. The datasets have applied to a wide range of virtual reality uses by over 3500 licensees in 64 countries [22],[26].

Table II is primarily based on Refs. [21], [28]–[59] and does include all the models, indeed. The number of voxel-based full-body human models developed so far approaches 40 [19]. A detailed list of human phantoms developed as of 2010 is provided in Ref. [19] and a more recent (covering the period up to 2014) list is provided in Ref. [21]; voxel models have been separately reviewed in Ref. [60]. Fig. 3 shows a FEM-compatible VHP-Female model (also called NELLY) of NEVA Electromagnetics [53]–[58].

Fig. 3.

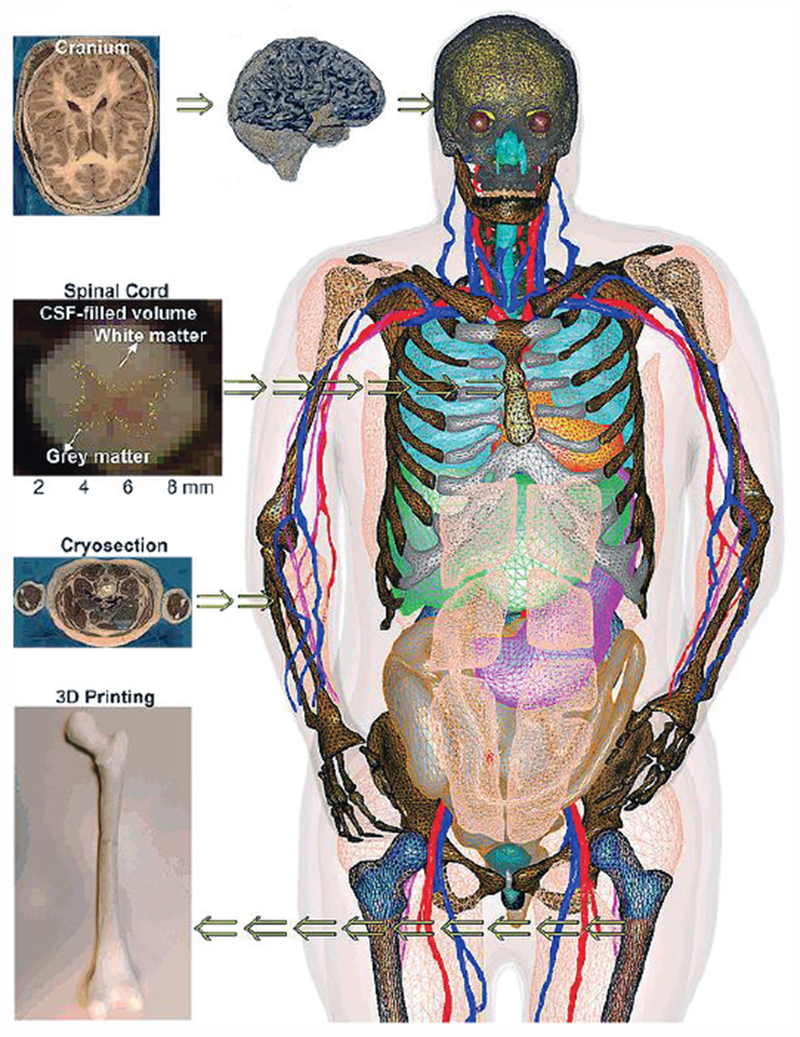
VHP-Female v. 3.0 CAD model [53]–[58] with about 250 individual parts; some tissues have been removed for visual clarity.

B. Detailed Models of Body Regions Including Anisotropic Models

Table III based on Refs. [60]–[81] lists some detailed models of individual body regions known to the authors and mostly used for accurate bioelectromagnetic modeling at low and high frequencies. Of special note is the detailed MIDA (Multimodal Imaging-Based Detailed Anatomical) human-head model [61] shown in Fig. 4, which includes 153 structures and anisotropic white matter information.

Table III.

Major Detailed Models of Body Regions (After 2004)

Entity/Country	Model Name	Region	Da	TYPE	RES, mm2	FV	D	Ref.
IT’IS Found. Switzerland FDA, USA	MIDA, anisotropy included	Head, neck (female, 29 years)	N	V/s	0.5×0.5×0.5	Y	N	[61]
University of Wisconsin-Madison, USA	HUMAN BREASTS	Human breast	N	V		Y	N	[62]–[65]
Universidade de Lisboa, Portugal	BRAIN/SPINAL CORD, anisotropy included	Head (female, 20 years), spinal cord (from DUKE)	N	FEM	T1/T2: 1×1×1 DTI: : 1.3×1.3×3.5	N	N	[66],[67]5
University of Minnesota, USA	PELVIS Biomechanical modeling	Pelvic region (female, 20 years)	N	FEM	NA	N	N	[68],[69]
Ministry of Education, Japan	Based on TARO [34]	All separate body regions for m/22/173/65	N	V	2×2×2	Y		[70]
Mass General Hospital, USA	Connectome Project, brain anisotropy and brain fiber	Cortical reg., patient-specific	Y	v/s	1.0×1.0×1.0	Y	N	[71]–[75]
Max Planck Inst, for Human Cognitive and Brain Sciences, Germany	MGDM	Cortical reg., patient-specific	N	S	1.0×1.0×1.2	Y	N	[76]–[81]
The Third Military Medical University and The Chinese University of Hong Kong	CMODEL	Voxel Human Head	Y	V	0.25×0.25×0.25	N	N	[60]

Abbreviations and comments:

G/A/H/W – Gender/Age/Height/Weight; Da – Original image dataset made available for independent evaluation (Y/N); TYPE (V – voxel; S – surface-based model, but without proven FEM meshability; FEM – surface-based FEM-meshable model); RES – Lowest image resolution (before or after post-processing) of the model declared by the provider (h=head, b=body); FV - Free version for available (Y/N); D – Deformable/posable (Y/N);

¹The original link cited in [33] http://www.chinesevisiblehuman.com is not responding (5/7/2016);

²The original link cited in [31] http://www.vch.org.cn/ is not responding (5/7/2016);

³More references including voxel, surface, and tetrahedral models are available from http://hurel.hanyang.ac.kr/;

⁴XCAT family is not directly FEM-meshable but Simpleware has created a FEM meshable model based on XCAT (http://www.humanbodymodels.com/. 2013);

⁵The spinal cord model from [66] was developed by manual adaption of the DUKE model. Only the brain model from [67] was developed from a dataset of a 20 year old female with the stated resolution.

Fig. 4.

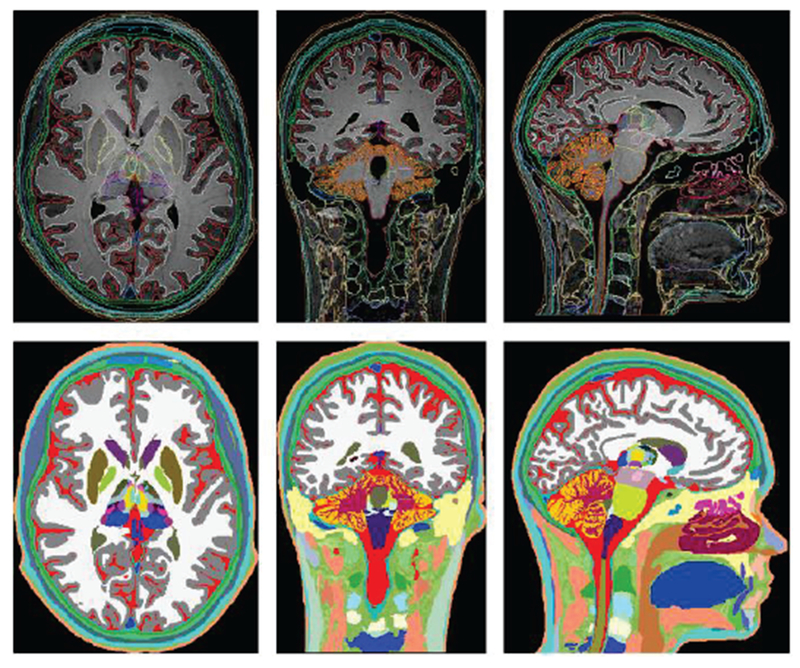
Axial, coronal, and sagittal views of the segmented head and neck (top row) of the MIDA head and color-coded label maps (bottom row) [61].

Another source of note is an open-source project called BodyParts3D [70]. This active project has been funded by the Ministry of Education of Japan. The goal of the project is to create “a dictionary-type database for anatomy in which anatomical concepts are represented by 3D structure data that specify corresponding segments of a 3D whole body model for an adult human male.” Geometries for the database were constructed from the voxel human model TARO [35]. The project is an online database providing native 3D models of rendered body parts for download. This database has been used by Wolfram Alpha Human Anatomy Tool [82].

We must separately mention a very comprehensive and detailed repository of human breast voxel models [62]–[65] intended for breast cancer and radio-frequency ablation studies.

Finally in this section, we point out automatic (or patient-specific) cranium model generation (brain segmentation and cortical surface modeling) packages from Massachusetts General Hospital (MGH) [71]–[75] and Max Planck Institute [76]–[81], one of which (FreeSurfer of MGH) is a freeware.

C. Detailed Models of Pregnant Women

Table IV based on Refs. [28],[29], [83]–[93] lists computational models of a pregnant woman and/or a fetus currently available for electromagnetic and radiological simulations. Almost all of them (except for Refs.[86],[90]) are based on insertion of a fetus or its modification into an existing non-pregnant female model(s). At the same time, the models presented in [86],[90] cover the abdominal region only.

Table IV.

Major Computational Pregnant-Woman Models (after ~2004).

Entity/Country	Model Name	A/H/W	Da	TYPE	RES, mm3	FV	D	Ref.
IT’IS Found., Switzerland	PREGNANT WOMAN1	26/163/57.3 3, 7, 9 months fetus	N	V	0.5×0.5×1.0 head 0.9×0.9×2 body	Y	N	[28],[29]
Natl. Inst. of Inform. and Comm. Technol., Japan	PREGNANT WOMAN (based on non-pregnant model [35])	22/160/53 12, 20, 23, 26, 29, 32 and 33 weeks fetus	N	V	2×2×2	Y	N	[83],[84],[85]
Imperial College, UK	PREGNANT WOMAN2	28 weeks fetus	N	V	1×1×5	N	N	[86]
Health Protection Agency, UK	PREGNANT WOMAN3	23/163/60 8, 13, 26, 38 weeks fetus	N	V	2×2×2	N	N	[87]
Graz University of Technology, Austria	SILVY	89 kg 30 weeks fetus	N	V	2×2×7	N	N	[88]
Helmholtz Zentrum Munchen, Germany CST AG, Germany	KATJA	43/163/62 24 weeks fetus	N	V	1.8×1.8×4.8	N	N	[89]
Rensselaer Poly. Institute, NY, USA	PREGNANT WOMAN4	30 weeks fetus	N	V	6×6×7	N	N	[90]
Rensselaer Poly. Institute, NY, USA	RPI P-3, P-6, P-95	first, second, third trimesters fetus	N	V/S/NURBS	6×6×7 for fetus	N	N	[91]
NEVA EM LLC, WPI	PREGNANT WOMAN6	f/60/162/88	Y	FEM	3×3×3	N	N	[92],[93]

Comments:

¹Based on ELLA [27],[28],[29]

²Abdominal region only

³Based on NAOMI [40]

⁴Abdominal region only (body from above liver to below pubic symphysis)

⁵Anatomical data for the pregnant female and the fetus are gathered from several origins

⁶Based on the voxel data from [83],[84], [85].

All models in Table IV are voxel models, except for Ref. [91] which used B-splines or NURBS while some parts of the body are adopted from the Visible Human Project [23]–[26] and Refs. [92],[93] which use the FEM meshable CAD format. One of the investigated concerns has been a significant electric current density, which may develop in the highly conductive amniotic fluid surrounding the fetus and subject to an external time-varying magnetic field [87],[88]. Fig. 6 shows a voxel model family from Ref. [83].

Fig. 6.

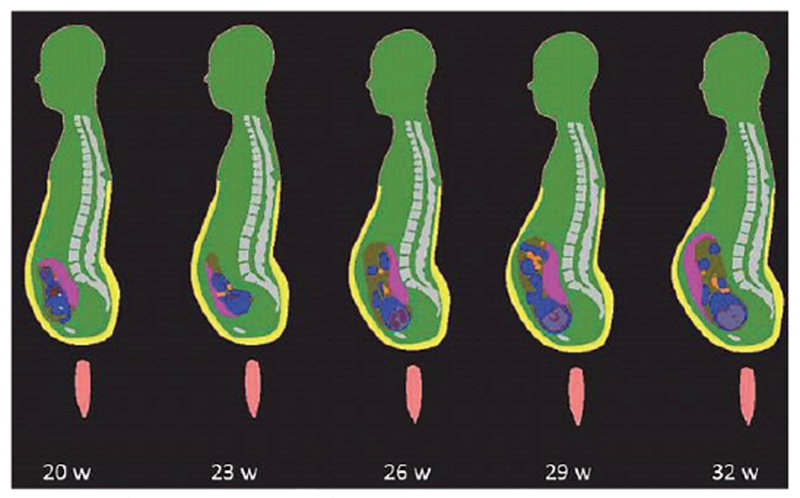
Anatomically-correct fetus positions at different stages of pregnancy [83].

D. Relevant 3D Anatomical Products

Fig. 7 shows a 3D full-body male model from Zygote Media Group, Inc. [94]. This and simlar models are primarily intended for medical illustrations and animations, broadcast television, films, computer games, and educational software. Given a sufficient anatomical accuracy, nothing in principle prevents us from using such models for electromagnetic and other simulations. However, since these types of models are in general not based on real subjects, their applications for regulatory purposes (submitted to the FDA or FCC) might be limited.

Fig. 7.

Full-body male model from Zygote Media Group, Inc. [94].

Fig. 8 illustrates the “world distribution” of major detailed virtual human models suitable for electromagnetic safety evaluation and for electromagnetic device design as of 2016-2017. This information is based on Refs. [20],[21] and other sources; it is summarized above in Tables II through IV. The projects performed by the IT’IS Foundation over 2010-2016 [27]–[29] have made them, and a number of the Foundation’s commercial spin-offs, the clear world leaders in the modern regulatory safety- and performance-assessment markets.

Fig. 8.

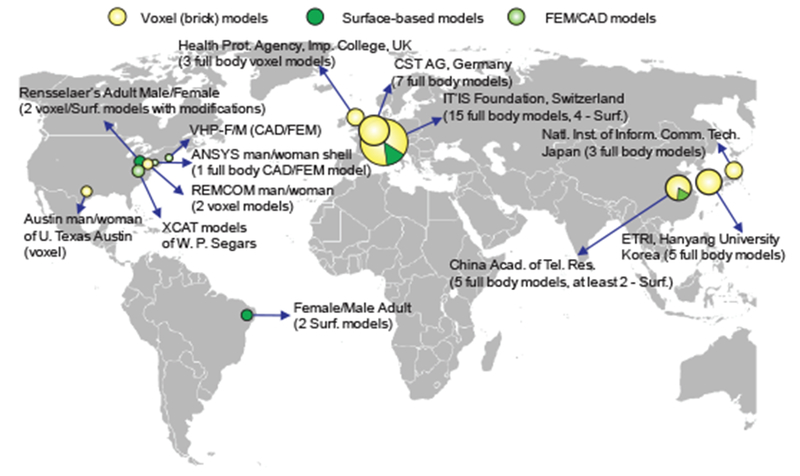
Distribution and origin of major full-body detailed virtual human models applicable for CEM.

III. Human Model Construction. Voxel and CAD Models

It follows from Tables II–IV that the vast majority of the virtual-human models currently available are voxel models and not CAD models. The difference between voxel and CAD models appears to be quite significant. It influences (i) the type of the CEM problems to be solved (resonant or not) and; (ii) the electromagnetic solver type. This difference can be explained best when we review the human model creation process.

A. Human Model Construction. Manual Segmentation

Computational phantoms or virtual humans are created via a set of 3D mathematical algorithms commonly called image segmentation. Segmentation is one of the most studied problems in the field of biomedical image analysis. Consider one body image (a slice in the xy-plane) in Fig. 9a which shows a cross-section of a human leg including the patella [25]. The complete stack of images continues in the z-direction. A skilled operator traces the patella boundary with a set of discrete points in the xy-plane (a polygon) shown by crosses in Fig 9a. A z-coordinate corresponding to the global coordinate system is added. Then, another cross-sectional image is traced, and all 3D points are collected, image by image. The end result is a complete patella boundary in three dimensions given in the form of a point cloud shown in Fig. 9b. This process is known as manual segmentation, still the “gold standard” of image segmentation. Other tissues are segmented similarly. The inner volume of the point cloud is either empty or can be filled with a set of (uniformly distributed) inner nodes. In the latter case, we arrive at a volumetric voxel model of a tissue, which is a typical final result of image segmentation. A large number of such volumes may exist, either interconnected or separate.

Fig. 9.

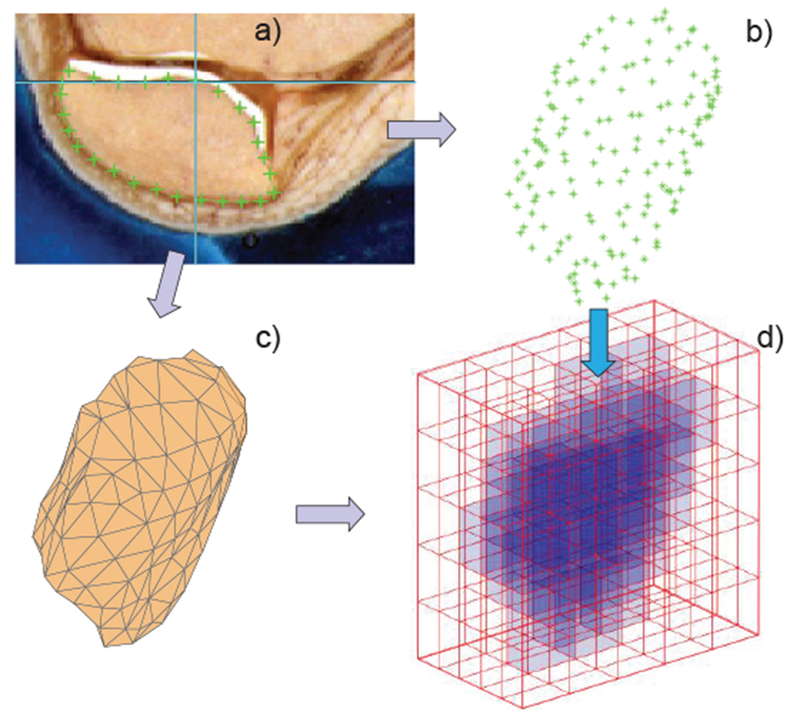
a) – Image of a patella with a traced boundary; b) – resulting point cloud; c) – patella CAD model; d) – patella voxel model.

B. Semi-Automatic Segmentation

Manual segmentation of datasets is extremely labor intensive and expensive. Depending on the images and segmentation quality, this effort is often measured by many man-months or years for a single model [95]. Therefore, most research has focused on semi-automatic or fully automatic approaches. The basic segmentation algorithm is a threshold or pixel contrast method [96], which is similar to manual tracing of the boundaries of 2D object slices outlined above. A more elaborate example is an active contour segmentation technique [97]. For medical image segmentation review, please see [98]–[100]. There is a plethora of image segmentation software packages [101].

A popular and powerful open-source semi-automatic image segmentation tool is ITK-SNAP [98] from University of Pennsylvania, which includes a multi-modality segmentation capability and machine learning to differentiate tissue classes based on texture, location, and intensity.

C. Automatic Cranium Segmentation

A few packages known to the authors that perform automatic segmentation of the cranium MRI data for brain compartments are the open-source FreeSurfer package from Massachusetts General Hospital (MGH) [71]–[75], [102], open-source Oxford’s FSL [103], and CRUISE from the Max Planck Institute for Human and Cognitive Brain Sciences [76]–[81]. Open-source Slicer package [104] is also quite useful. Segmentation of the skull itself may be less straightforward.

As an example, Fig. 10 shows an FEM model with 8 distinct tissues obtained from automatic cranium segmentation via FreeSurfer. The model was (optionally) post-processed in SpaceClaim of ANSYS, Inc. and specifically optimized for fast FEM simulations.

Fig.10.

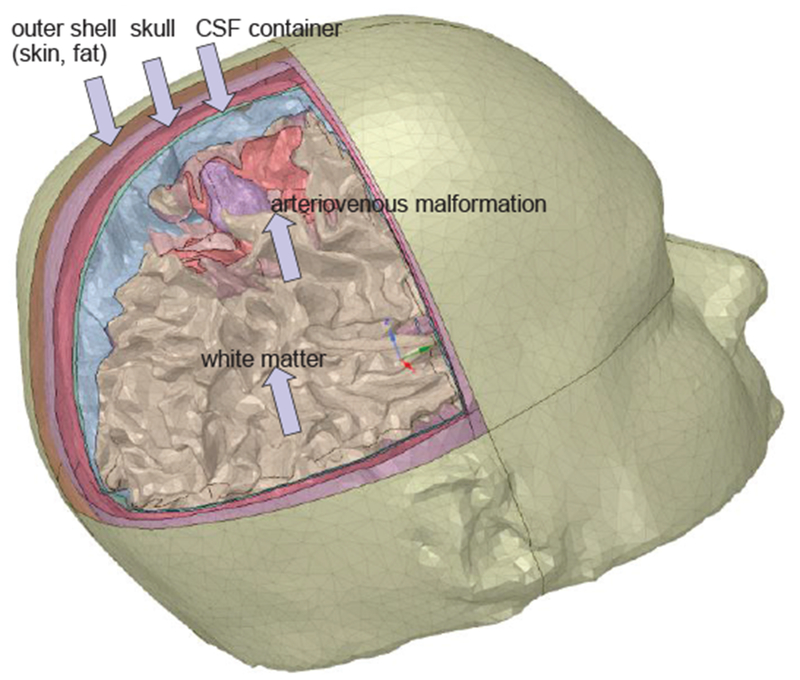
CAD FEM cranium model of a patient with brain pathology obtained via automatic segmentation with FreeSurfer and post-processed in ANSYS SpaceClaim.

D. Automatic Whole Body Segmentation

Efforts have been made to create subject-specific human models via automatic and semi-automatic segmentation. This task is generally very complicated. Fig. 11 shows a USARIEM model, a soldier CAD model (called an anatomy avatar) from the U.S. Army Research Institute of Environmental Medicine (March 2016, [105]). Such models could make an impact on the design of military gear, protective equipment and vehicles, and other applications across military medicine [105].

Fig. 11.

Soldier CAD model from U.S. Army Research Institute of Environmental Medicine (March 2016).

E. Triangular CAD Models

After image segmentation and creation of a point cloud, a surrounding surface may be extracted in the form of a triangular or quadrilateral mesh or a BREP CAD model described below. This operation is called surface extraction or 3D geometry (surface) reconstruction.

In CAD models, which are all suitable for 3D printing (an example is the STL or STereoLithography format), each individual tissue is characterized by its closed surface. In its most common form, the surface is fully described by a set of small adjacent triangles defined through an array of nodes P and an array of triangles t shown in Fig. 9c – a mesh. Every m-th row of array P gives Cartesian coordinates of a nodal point m on the surface, while every n-th row of array t gives three numbers of nodal points forming the n-th triangle. Any observation point inside the triangulated surface is assigned (the same) unique tissue properties. To find the point status (inside/outside), an arbitrary ray emanating from this point is considered. If the point is inside, the number of intersections with the surface is always odd, otherwise it is even. Further, the ray-triangle intersection algorithm is applied [106].

The task of generating a CAD model from the point cloud is illustrated through creating a patella mesh in Fig. 9c from the corresponding point cloud in Fig. 9b. The entire problem in general is quite complex; among the popular methods are the method of marching cubes (marching triangles) [107],[108] and the region-growing ball-pivoting method [109]. The human models shown above in Figs. 1, 3, 5, 10, 11 are all CAD models.

Fig. 5.

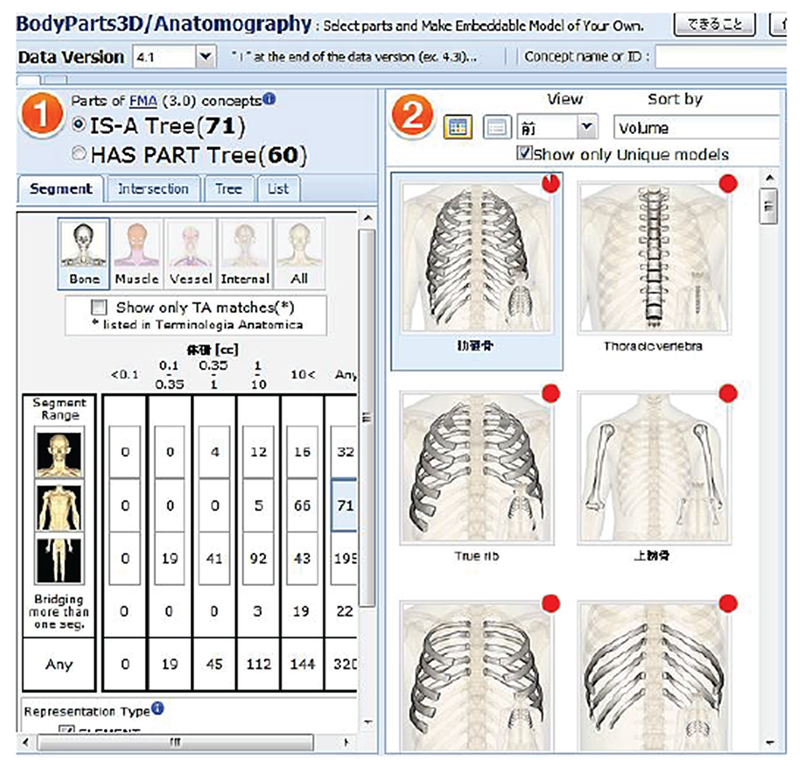
Open-access BodyParts3D online repository [70].

F. Voxel Models

The voxel model directly follows from the segmentation results: given that the point cloud in Fig. 9b is filled with the inner nodes, we can directly arrive on Fig. 9d. Alternatively, the voxel model is straightforwardly constructed from the CAD model. We subdivide the entire 3D space into many small equal brick cells (unit cells) with the size Δx,Δy,Δz shown in Fig. 9d. If the cell center lies within the CAD tissue object in Fig. 9c, the cell is assumed to be a part of the object. Other approaches are also possible. As a result, the entire tissue volume is approximated by a large number of cells seen in Fig. 9d. Every such cell has a unique value for the tissue property (or properties), which is a voxel. Frequently, the entire unit cell along with the assigned tissue properties is designated as a voxel. The voxel model does not have to be constructed from the CAD model. Usually, exactly the opposite is done. In principle, any segmentation result is already the voxel model.

In order to display the staircase surface of a voxel model as a visually smooth boundary, an isosurface or isosurface rendering (a very detailed but often excessive triangular surface mesh) is quickly created. The isosurface algorithm [110],[111] is implemented in many software packages including MATLAB®. The human models shown in Figs. 2, 4, 6 above are voxel models. These voxel models can be and have been converted to large-size surface-based models via isosurface rendering [28],[29],[61].

G. Comparison of CAD and Voxel Models

As of now, the human models with the highest resolution are all static voxel models. Why is it so? This is due to the fact that voxel-based models naturally represent highly-inhomogeneous inter-tissue regions and can replicate these tissues exactly as they appear in the source images. The 3D CAD model of a multi-tissue body (or even of a single tissue) is much more difficult to construct. Furthermore, detailed triangulated human models with a very large number of triangles in excess of 1-5×10⁶ [28], [61] may require extremely large FEM meshing times (creating a volumetric tetrahedral mesh) and quite large FEM (or BEM, MoM) simulation times, which could make their use prohibitive for a number of optimization tasks. In particular, in ANSYS Electronics Desktop, the meshing time can be 10–100 times greater than the simulation time for low-quality surface shell meshes. Therefore, the CAD models tend to be significantly less accurate in general despite their clear mathematical advantage which is a linear (in case of triangles or plane quadrilaterals) or polynomial (in case of a spline representation) surface approximation in contrast to the staircase approximation of the voxel grid. For voxel models, the segmentation accuracy, which is the deviation from the true surface along the normal direction, is equal to the size of the unit cell.

However, the CAD model is inherently deformable (cf. [46]–[52],[112]) including both free-form deformations and affine transformations, while the voxel model is essentially “cast in stone”. Although very realistic, modern voxelized phantoms, based upon direct image segmentation, have the disadvantage of being inflexible. The resolution is fixed, and it is difficult to model variations in anatomy, patient positioning, or motion. Last but not least, the CAD model is fully compatible with the standard FEM analysis on unstructured grids and 3D printing while the voxel model is not.

H. Specific Conditions for CAD Models

The following two conditions are required for a true CAD human body model: (1) a 3D triangular mesh representing a solid object must not have holes; (2) the surface of a well-behaved triangular mesh in 3D must satisfy one critical condition, which is the so-called manifold condition. A mesh is 2-manifold if every node of the mesh has a disk-shaped neighborhood of triangles. This neighborhood can be continuously deformed to an open disk. Every edge of a 2-manifold mesh is a manifold edge with only two attached triangles. All other meshes are non-manifold meshes and are not suitable for FEM analysis. Fig. 12 gives examples of a manifold edge, a non-manifold edge and, a non-manifold mesh with a non-manifold node.

Fig. 12.

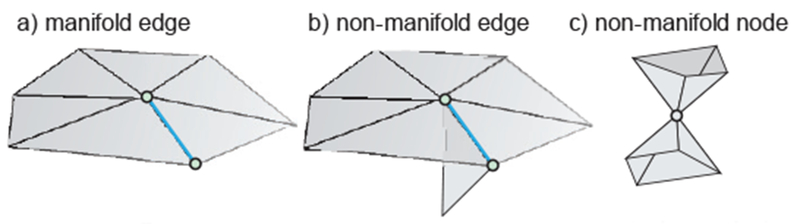
a) – Examples of a manifold edge; b) – non-manifold edge, and c) – non-manifold node.

I. Contact regions

Constructing a multi-tissue voxel model is straightforward. Different cells are simply assigned different tissue properties. Construction of a multi-tissue CAD model is more difficult. First, different tissue meshes must not intersect, though fully-enclosed meshes are still allowed. Another well-known problem with multi-object models is object matching in a contact region. Usually, the contact region is not explicitly defined in a CAD model, so that it has to be discovered separately by testing for face-to-face overlaps and matching CAD faces/edges in the contact region [113]. This circumstance may create problems for certain CAD kernels such as ACIS. In order to prevent CAD import errors, a thin gap can be introduced between different tissue objects filled with “average body properties” of an outer enclosing shell. In some sense, this gap has the physical meaning of a membrane separating different tissues. If the gap is reasonably small it provides a close approximation to reality for different physical processes. However, for a number of purposes, the gaps may not be acceptable.

J. Mesh Processing Tools and CAD Model Construction

Many free and commercial mesh processing tools exist. MeshLab of the Italian National Research Council and Univ.of Pisa [114]. ParaView of Sandia National Laboratories [115], GMV of Los Alamos National Laboratory [116], and CGAL [117] are all open–source mesh tools. An excellent commeercial mesh processing tool capable of mesh healing and separation of multiple surface objects is ANSYS SpaceClaim^®.

Generation of a CAD model may start with a point cloud as shown in Fig. 9b or with a voxel model. A very detailed triangular isosurface mesh described above is created first. Then, mesh decimation [118], smoothing [119]–[125], and intersection resolution [126]–[132] processes are applied, often interchangeably. When a thin gap between individual objects is allowed, the shallow intersections between the nearby objects may be resolved via deforming individual meshes in the contact area in the inner normal directions.

K. NURBS or BREP Representation

Another approach common in manufacturing and computer graphics is the subdivision of the original surface into a smaller number of relatively-large curved spline surfaces – NURBS (Non-uniform Rational Bézier Spline surfaces) or B-splines [132], which are common in manufacturing and computer graphics. As an example, Fig. 13 shows a conversion of the original triangulated skin shell surface with about 7,000 triangles to a set of NURB surfaces (~60 B-splines) done via SpaceClaim of ANSYS. NURB surfaces enable refined meshes without sharp edges in specific areas of interest, i.e. adaptive surface refinement.

Fig. 13.

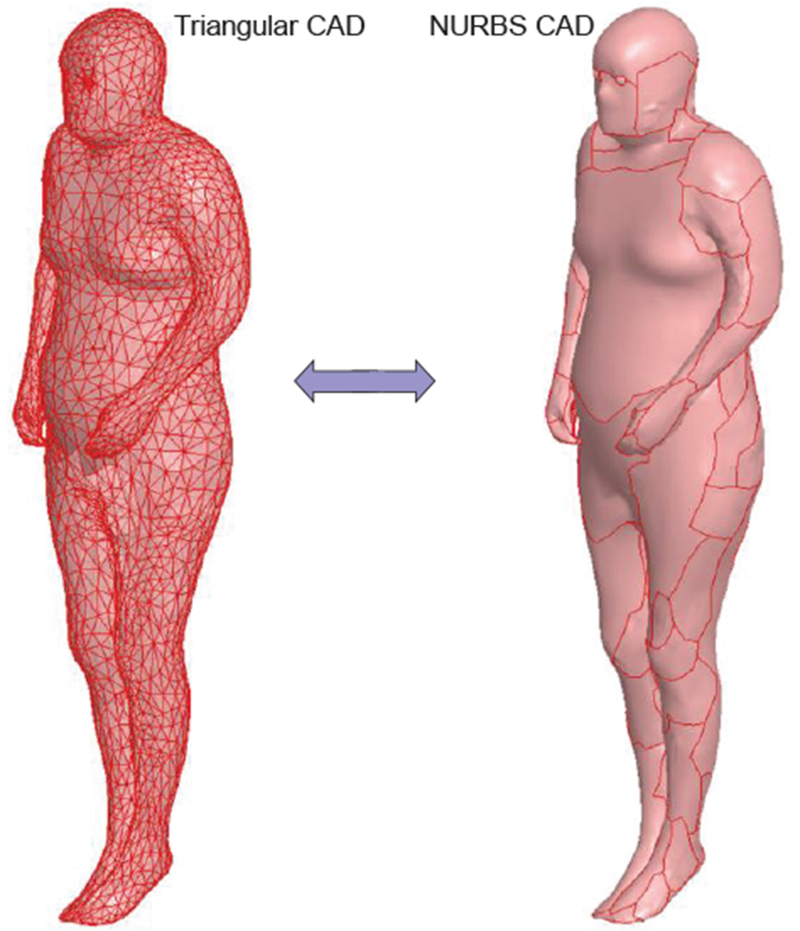
Left – initial triangular surface of a human model; Right – the same surface converted to NLTRBS (B-splines).

Furthermore, the NURBS are ideal for deformation purposes. Unfortunately at present, the NURB surfaces have a rather limited value for an FEM/MoM solver, which internally operates with geometry primitives, triangular/quadrilateral facets and tetrahedra. A double conversion, extracted triangular surfaces →NURBS →FEM triangular surfaces, may require potentially significant additional meshing times.

A pipeline for multi-modality deformable NURBS-based human models is being developed by Dr. W. Segars and his coworkers at Duke University, USA [48]–[52]. To change the anatomy, one has to apply transforms (rigid or non-rigid) to the surfaces. The 4D XCAT phantom was developed by this group as a computational model of the human anatomy and physiology primarily for use in medical imaging research. Starting with two detailed whole-body adult male and female anatomies, based upon the Visible Human Project anatomical datasets from the National Library of Medicine, the XCAT has been expanded into a population of models representing the human body of varying ages, heights, and weights from newborn to adult.

IV. Material Properties

A. Isotropic Electromagnetic Tissue Properties

Every human model must be augmented with electrical, mechanical and thermal tissue properties for further use. In the isotropic case, the electromagnetic material properties usually include scalar relative permittivity and scalar conductivity of a tissue, both as functions of frequency. The pioneering work of C. Gabriel and colleagues from UK [133]–[136], supported by the US Air Force Research Laboratory and their latest results [137], reported the corresponding data from 10 Hz to 100 GHz for the bulk of tissues. Most of the measurements performed were on animal tissues carried out in-vitro. Measurements were also made, in-vivo, on accessible parts of the human body such as palm, sole and forearm skin, tongue, etc. This data is considered standard and has been replicated in the IT’IS (Zurich, Switzerland) database for electromagnetic parameters [138]. Wagner et al [139] recently measured in-vivo impedances of human cranial tissues (skull, grey matter, white matter) from 10 Hz to 50 kHz.

B. Anisotropic Tissue Models. Tensorial Approach

Many tissues such as the brain and the spinal cord of the central nervous system, the peripheral nervous system, and muscles including the heart, are fibrous in nature. Isotropic human models that assume homogeneous volumes for every individual tissue cannot resolve this fine structure. Instead, conductivity and permittivity tensors may be considered, which characterize the fibrous structure in an average sense. In the local coordinate system, the permittivity and conductivity tensors are strictly diagonal. Yet, for a numerical simulation, a global coordinate system must be chosen.

The approach is thus to consider a CAD or voxel human tissue augmented with the anisotropic conductivity/permittivity tensors. Anisotropic muscle tissue models have been developed in [140]–[143] and in application to the voxel grid in [142],[143]. In particular, an anisotropic ratio of 10 for both conductivity and permittivity over the audio frequency range (20 Hz–20 kHz) has been observed [143]. For an anisotropic arm model in COMSOL, please refer to [144].

Effective-medium brain modeling based on the anisitropic conductivity tensor is under active investigation by a group of researchers from the Swiss Federal Institute of Technology (ETH) [145]–[147], [61]. The concept is to utilize a shell tissue model (e.g., the grey matter), but with an anisotropic material inside.

C. Fiber Models

Diffusion MRI allows for the determination of the anisotropy of water diffusion in the human tissue (e.g., the brain) non-invasively and has numerous applications including reconstruction of the major white matter pathways (for a review, see [148]). As an example, Fig. 14 shows a fiber connectivity map (or connectome) of white matter where different colors indicate different fiber directions. The number of fibers in the map may be on the order of 100,000. The fiber network may replace the entire white matter shell.

Fig. 14.

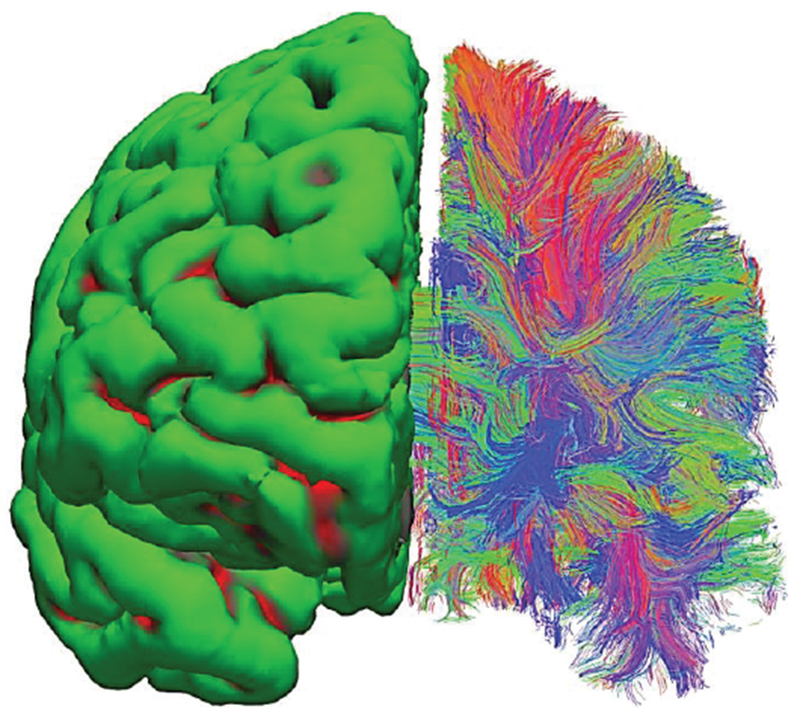
Surface-based vs. neural-fiber model of white matter. A set of in-vivo diffusion MRI images from Connectome Project [75] has been processed via FreeSurfer software [74], [102]. Left hemisphere – surface-based homogeneous model; right hemisphere – fiber model. Different colors indicate dominant fiber directions: red-vert.; green-horizontal; blue-into the page.

In the effective-medium approach discussed above, the electrical conductivity tensor of tissue is derived from the diffusion tensor measured by MRI [149]. Such a method is not without its limitations. The basic tensor model is not capable of accurately capturing the more complex fiber geometries such as intravoxel crossings (or fiber crossings) [150]. For this purpose, more general methods [151],[152] have been developed. Furthermore, numerical modeling of individual fibers [153],[154] is possible and might offer more insight into the realistic fibrous structures.

The fibers in Fig. 14-right are not individual axons but they are tractrographic reconstruction of white matter tracts or bundles of actual nerve fiber containing multiple axons, each of which has a cross-section on the order of micrometers, that are computationally generated based on local diffusion orientation information. An analog to such a fiber bundle is a thick electric cable consisting of multiple thin conductors. In any case, this is the most accurate representation of brain connectivity obtained non-invasively in vivo to date, with the best voxel resolution of about 1 mm. Ongoing progress in diffusion MRI [71]–[73], [75], [155],[156] continuously pushes this limit.

V. Computational Electromagnetics Software for Working with Virtual Humans

The type of electromagnetic, thermal or mechanical stress analysis software used depends on the human model availability; e.g. voxel or CAD.

A. Finite-Difference Method for Voxel Models

Voxel-based models are primarily suitable for finite-difference (FD) methods [157] on uniform rectangular grids at low frequencies and for the finite-difference time-domain (FDTD) method on uniform rectangular grids at high frequencies [157]–[159]. The latter option assumes that the entire solution is computed in the time domain. The finite integration technique (FIT) of T. Weiland [160],[161] used by the time-domain electromagnetic solver of CST AG is reduced to the standard FDTD on a uniform rectangular grid as shown in Fig. 15a. Simultaneously, it expands the FDTD method to tetrahedral grids as shown in Fig. 15b. At present, grids with a few billions unit cells can be processed. The FDTD method is currently the major tool for high-frequency electromagnetic simulations with computational human models.

Fig. 15.

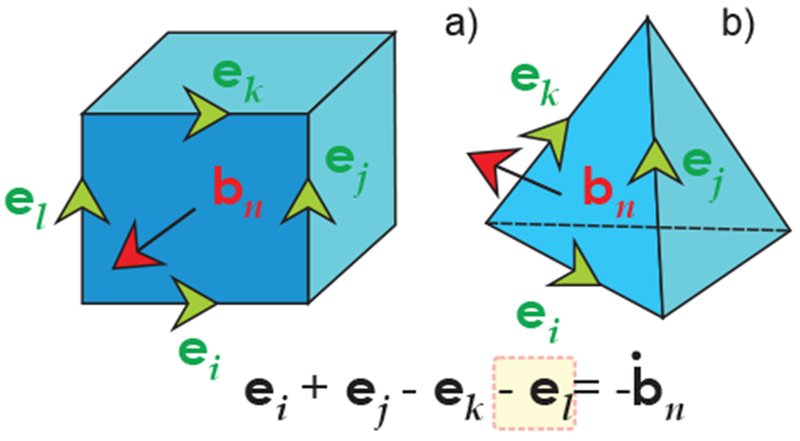
a) – Using FIT to discretize Faraday’s equation for a brick (similar to the FDTD Yee cell); b) – using FIT for a tetrahedral mesh.

B. Subgridding Techniques in Finite-Difference Methods

Subgridding techniques allow us to vary the FDTD mesh size in specific domains of interest [159],[162], which is a very significant advantage as compared to the standard uniform finite differences. Recall that one major “flaw” of the standard voxel models experienced by many users dealing with human models is the inability to selectively refine the grid. Indeed, the resolution of the voxel model should be equal to the finest grid resolution. For example, a time-domain version of the transmission-line matrix method (TLM) [163],[164] implemented in CST Studio Suite^® uses a multi-grid formulation. The uniform mesh is first refined or graded to capture detail in the geometry. Small mesh cells are subsequently automatically combined or “lumped”, with the level of lumping increasing with distance from geometric boundaries. This process removes any “bleeding” in the mesh, minimizing the cell count and reducing computational requirements to the absolute minimum. The end result is a multi-level octree mesh. In many cases, the total number of mesh cells is reduced by over 90%.

C. Finite Element Method (FEM) for CAD Models. Frequency-Domain Solution

A CAD-based human model is suitable for both the finite-difference method (after a trivial voxelization) and the finite element method. The FEM for electromagnetic simulations is used by ANSYS Electronics Desktop (both HFSS and Maxwell), CST Studio Suite, COMSOL, and Abaqus. The FEM method typically employs vector basis functions on tetrahedral [165]–[168], first described by Nédélec [168]. An advantage of the FEM is a powerful adaptive mesh refinement procedure implemented in ANSYS Electronics Desktop and CST Studio Suite. This enables tetrahedral mesh optimization such that the simulation may be handled accurately while significantly reducing computational runtime.

For radio wave propagation, the FEM method has been primarily used in the frequency domain (after converting all quantities to phasors). The frequency domain solution allows us to better resolve resonances. The frequency domain FEM method (and potentially any frequency domain method) may significantly outperform FDTD computations for MRI-related research [169]. The use of unstructured meshes, combined with automatic mesh adaptation in the frequency domain has been instrumental in delivering accurate results for complicated geometries.

D. Which Method to Choose?

Traditionally, it was difficult to implement finite element methods in time domain, i.e., for a broadband system response. Recent advances in finite element techniques have led to a new scheme based on the discontinuous Galerkin family of numerical methods [170]–[173]. This scheme retains the flexibility, accuracy and reliability of unstructured mesh finite element methods but avoids the solution of a large matrix equation at each time step. Instead, each mesh element advances in time using its own time step in a synchronous manner. This results in a significant speed-up on unstructured meshes, as the largest mesh elements typically utilize time steps that are two to five orders of magnitude larger than those of the smallest mesh elements. The corresponding scheme is now implemented in ANSYS Electronics Desktop.

On the other hand, the time-domain methods have been traditionally associated with uniform structured meshes (rectangular grids) without an ability to adaptively refine (or coarsen) the mesh. However, the FIT technique outlined in Fig. 15b may now handle general tetrahedral or hexahedral meshes, and may be regarded as a variation of the FEM. Also, the subgridding techniques are able to at least partially overcome the mesh refinement difficulty.

E. Boundary Element Method (BEM) or Method of Moments (MoM)

The boundary element method [157], [174]–[179] does not require special boundary conditions typical for FDTD and FEM; it is simple and versatile [179]. However, this method operates with dense matrices and requires matrix inversion. Therefore, it is less common in applications to human models. Specific applications have been developed for the cranium. In the field of electromagnetic brain mapping, the simple and robust BEM method has been widely adopted for MEG/EEG source localization applications (see Section IX). The BEM approach has been shown to improve the computational targeting of Transcranial Magnetic Stimulation (TMS) [180] in comparison with spherical models; it has also been employed in large-scale empirical studies to quantify the TMS electric field distribution “hot spots” across subjects [181]. The BEM approach has been employed to estimate the efficacy of TMS on stimulating the fiber bundles projecting from cortex [182] and to computationally determine the optimal coil location to stimulate a pre-determined fiber bundle. MoM volume integrals have recently been reviewed for accurate analysis of antennas near/on/in human models [183]. MoM (BEM) can be applied to fiber models using a one-dimensional model along the fiber.

Recent advantages in the fast and iterative MoM (BEM) solvers (see, for example [184]–[187]) may lead to a more widespread use of these methods.

F. Typical Computational Times and Expected Accuracy

One benchmark example in electromagnetics is the scattering problem with plane wave incidence at, say, 300 MHz shown in Fig. 16. The incident wave polarization is vertical. As an example, the full-body CAD VHP-Female BASE model with about 180 individual tissue parts was simulated simultaneously in ANSYS HFSS and CST Studio Suite frequency-domain solver [56]. Table V shows the corresponding simulation times in ANSYS for different server configurations [54].

Fig. 16.

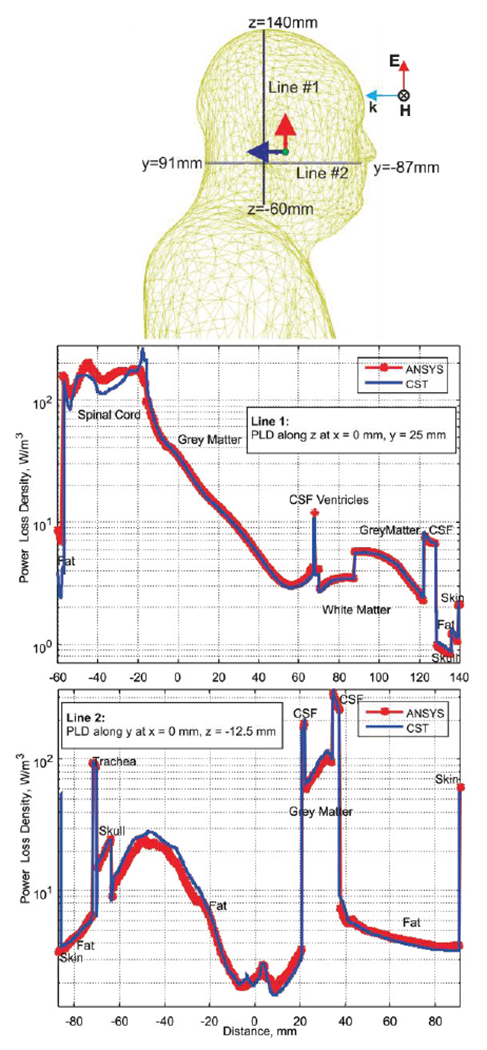
Paths within the body chosen for power loss density evaluation and power loss density along line segments.

Table V.

Simulation Benchmarks for Plane Wave Test (circa 2015-2016).

Execution parameters for four representative servers
System	Tetrahedral mesh size & total RAM (start/stop)	Execution time for 5 passes
System #1 (one task, one core)
Intel(R) Xeon(R) CPU E5-2697 V2, 256 GB. 64-bit OS Windows Server 2008 R2 Enterprise. ANSYS EM Suite® 16	450,000/1,000,000 2.6GB/87 GB	Meshing time: 50 min Sim. time: 10 hr 48 min
System #2 (one task, one core)
4 AMD OPTERON 6174 12 core processors, 192 GB, 64-bit OS, Windows Server 2008 R2 Enterprise, ANSYS EM Suite® 15	450,000/1,000,000 2.0GB/115 GB	Meshing time: 70 min Sim. time: 28 hr 55 min
System #3 (one task, one core)
Intel(R) Xeon(R) CPU E5-2690, 192 GB, 64-bit OS Red Hat Enterprise Linux 2.6.32, ANSYS EM Suite® 15	450,000/1,000,000 2.0 GB/87 GB	Meshing time: 63 min Sim. time: 10 hr 40 min
System #4 (one task, eight cores, HPC option) a
Intel(R) Xeon(R) CPU E5-2697 V2, 256 GB. 64-bit OS Windows Server 2008 R2 Enterprise, ANSYS EM Suite® 16	450,000/1,000,000 2.6GB/87 GB	Meshing time: 50 min Sim. time: 2 hr 43 min

^a.Systems 1 and 4 differ by the HPC option only.

CST Studio Suite simulation times are quite similar. For a quantitative comparison between different simulation methods, we have evaluated the volume power loss density in W/m³ along certain paths within the body. Those paths are two line segments shown in Fig. 16. The volume power loss density is given by $\frac{\sigma (r)}{2}{\mid \mathit{E}(\mathit{r})\mid }^2$ where σ(r) is the local tissue conductivity. It is computed for the total electric field in the phasor form, E(r), which is the scattered field plus the incident field.

Fig. 16 shows results of the CST Studio Suite and ANSYS HFSS simulations for this particular problem. Although a general agreement is excellent; certain deviations may be observed and partially explained by the use of different averaging methods for the power loss density.

VI. Human Model Validation

A. MRI RF Coil Test

There is no generally accepted routine to justify the numerical (as well anatomical) accuracy of a virtual human model for a broad application range. A logical and common test today, supported by the FDA, includes specific absorption rate (SAR) computations in an RF MRI transmit coil.

For example, when very sharp peaks of the specific absorption rate are observed, this is often an indication of a “flaw” in the human model in a certain anatomical region. The flaw may be due to isolated pieces of one tissue within another and/or by fragmented tissues (the voxel model). The flaw may be also given by low-quality or very large triangles, sharp bends and small gaps, as well as sharp contact angles (for the CAD model). Adaptive mesh refinement is a way to make sure that observed “flaws” (if any) are not due to coarse meshing (large triangles). However, it cannot generally validate the human model. As an example, consider Fig. 17 which shows the local SAR distribution for a full-body birdcage coil with all ports driven and loaded with the VHP-Female v. 3.0 model [55],[56] at 1 W input power in the coronal plane at 63.87 MHz (1.5 T field). There are some noticeable differences in the solution when using one versus eight adaptive mesh refinement passes. For example, hot spots at the top of the head disappear.

Fig. 17.

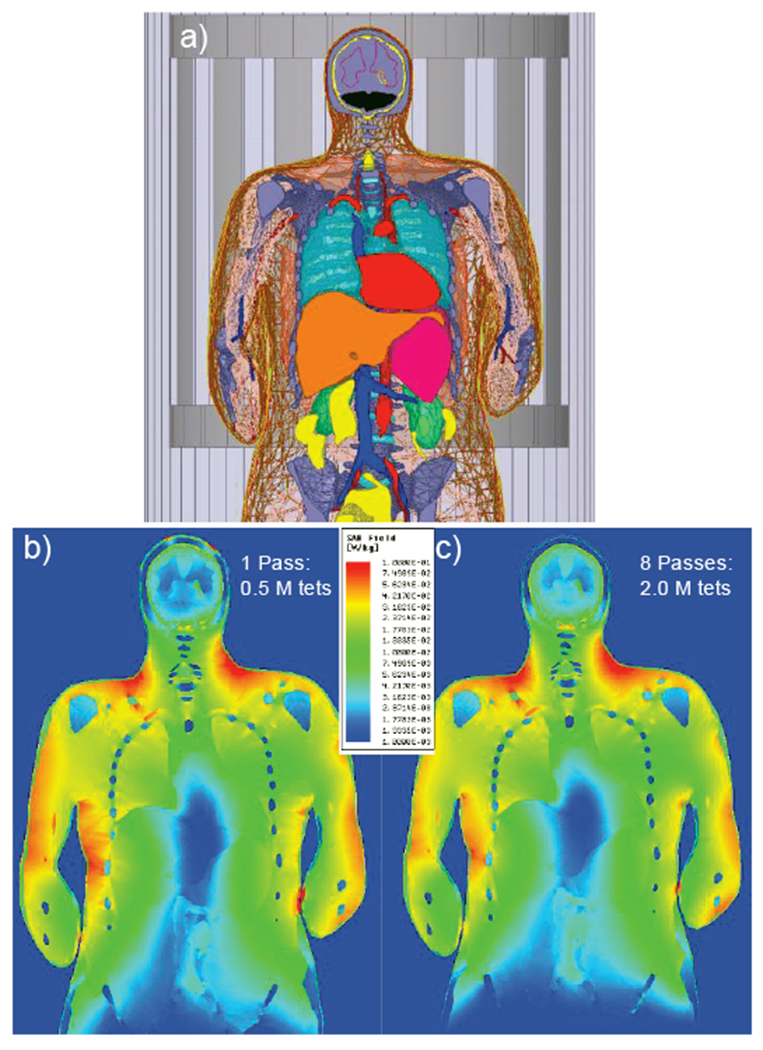
Local SAR distribution for a coil loaded with the VHP-Female v. 3.0 model [55],[56] at 1 W input power in the coronal plane at 63.87 MHz. a) – Landmark of model inside the birdcage; b) – solution with one adaptive pass; c) – solution with eight adaptive passes.

B. SAR Margins

The local SAR (W/kg) is defined by averaging the dissipated power per unit mass over a small (ideally infinitesimally small) volume V, that is

$$\mathit{SAR}(\mathit{r})=\frac{1}{V}{\int }_V\frac{\sigma (\mathit{r})}{2\rho (\mathit{r})}\mid \mathit{E}(\mathit{r}){\mid }^{2}dV$$ (1)

Here, σ(r) is the local tissue conductivity, ρ(r) is the local mass density, and |E(r)| is the electric field magnitude at an observation point. The body-averaged or the whole-body (global-body) SAR_body is given by averaging the local SAR over the entire body volume, as

$${\mathit{SAR}}_{\mathit{body}}=\frac{1}{V_{\mathit{body}}}{\int }_{V_{\mathit{body}}}\frac{\sigma (\mathit{r})}{2\rho (\mathit{r})}\mid \mathit{E}(\mathit{r}){\mid }^{2}dV$$ (2)

Similarly, SAR_1g is given by averaging over a contiguous volume with the weight of 1 g

$${\mathit{SAR}}_{1g}(\mathit{r})=\frac{1}{V_{1g}}{\int }_{V_{1g}}\frac{\sigma (\mathit{r})}{2\rho (\mathit{r})}\mid \mathit{E}(\mathit{r}){\mid }^{2}dV$$ (3)

SAR_10g(r) is found in the same fashion.

The SAR values vary with the applied RF source strength. We often normalize the fields solutions given the desired magnitude of ${\mathit{B}}_1^{+}$ field at the coil center of 1 μT. The normalization is done in the form

$$\mathit{SAR}=\frac{\mathit{SAR}}{{({\mathit{B}}_1^{+}∕1\mu T)}^2}$$ (4)

Some recent reference data on SAR comptutations for human models are given in Refs. [188]–[196], [16]. Table VI presents the bulk of this data. Although the SAR data vary widely, we may still observe the following margins (all data in W/kg) for

1. the heart, shoulder, abdominal, and pelvic landmarks;

2. different human models;

3. different RF coil types, and for 1.5 T and 3 T fields, respectively,

based on Table VI and other sources:

$$0.13<{\mathit{SAR}}_{\mathit{body}}<0.54\text{for}1\mu \mathrm{T}\text{field}$$ (5)

$$2.46<\mathit{max}\left({\mathit{SAR}}_{1g}(\mathit{r})\right)<14.8\text{for}1\mu \mathrm{T}\text{field}$$ (6)

$$1.23<\mathit{max}\left({\mathit{SAR}}_{10g}(\mathit{r})\right)<8.9\text{for}1\mu \mathrm{T}\text{field}$$ (7)

Table VI.

Computed SAR values from different sources (W/kg) given 1 μT ${\mathit{B}}_1^{+}$ field (at the coil isocenter).

Ref #	Method	Model	Coil landmark	Whole-body SAR Eq. (2)	Max. non-averaged local SAR Eq.(1)	Max. 1g local SAR Eq. (3)	Max. 10g local SAR Eq. (3)
Ref. [189]	FDTD 5 mm voxel	Voxel Vis. Human Male 122kg [189], 128 MHz	Abdominal	0.58	22.78	11.90	8.79
Ref. [189]	FDTD 3.5 mm voxel	Voxel Vis. Human Male 122 kg [189], 128 MHz	Abdominal	0.57	24.91	11.63	6.98
Ref. [189]	FDTD 2.5 mm voxel	Voxel Vis. Human Male 122 kg [189], 128 MHz	Abdominal	0.54	35.68	13.76	8.88
Ref. [193]	FDTD 3 mm voxel	Voxel Vis. Human Female 128 MHz	Heart	Normalized to 0.15 (present report)	NA	2.46-4.11 Varies with coil type	1.23-2.03 Varies with coil type
Ref. [193]	FDTD 3 mm voxel	Voxel Vis. Human Male 128 MHz	Pelvic	Normalized to 0.54 (Ref. [189])	NA	8.91-14.8 Varies with coil type	4.21-6.86 Varies with coil type
Ref. [194]	FDTD Voxel size unknown	Voxel Vis. Human Female, 64 MHz	Heart	Normalized to 0.15 (author’s study)	NA	NA	3.35
Ref. [195]	FDTD Voxel size 2mm	Voxel Nagaoka Female 64 MHz	Abdominal	0.13	NA	3.2	2.1
Ref. [195]	FDTD Voxel size 2mm	Voxel Vis. Human Male 122 kg 64 MHz	Abdominal	0.18	NA	3.6	2.4
Ref. [195]	FDTD Voxel size 2mm	Voxel Nagaoka Female 128 MHz	Abdominal	0.24	NA	5.3	3.9
Ref. [195]	FDTD Voxel size 2mm	Voxel Vis. Human Male 122 kg 128 MHz	Abdominal	0.31	NA	5.2	3.9
Authors’ study	FEM 8 adaptive passes (ANSYS)	CAD VHP-Female 3.0 [55],[56] 88 kg, 64 MHz	Shoulder/heart (top of vert. T7)	0.15	12.0	3.05	1.37

More differentiated estimates, which are specifically based on body mass and body mass index (BMI), could be obtained. Thus, for a human model under test, we could compute three parameters: SAR_body, $\mathit{max}\left({\mathit{SAR}}_{1g}(\mathit{r})\right)$ and $\mathit{max}\left({\mathit{SAR}}_{10g}(\mathit{r})\right)$ . Once these values are within the established margins, the model passes a very basic SAR test.

VII. Low and High Frequency Simulation Tasks

A. When can a Low-Frequency (Quasistatic) Approximation be Applied?

One critical parameter that sets a distinct operational region for an electromagnetic solver as applied to a human body is the skin layer depth,

$$\delta =\sqrt{\frac{2}{\omega \mu \sigma }}$$ (8)

where ω is the angular frequency, μ = 4π × 10⁻⁷H/m is the magnetic permeability of vacuum (body), and σ is the tissue conductivity in S/m. In contrast to metals, human tissues have a conductivity that is six to seven orders of magnitude smaller. Therefore the skin depth may be large as compared to the tissue or body size, even at relatively high frequencies, which is known as the thin limit condition. This literally means that the (secondary or internal) magnetic field of body currents is also small as compared to the known external large magnetic field in Faraday’s law of induction. Such an approximation leads to the Poisson equation for the electric potential of eddy currents, similar to the Poisson equations used in electrostatics [179]. As an example, the skin depth at 1 MHz and σ = 0.15 S/m is about 1.3 m (i.e., considerably larger than the size of the head), which makes it possible to consider a wireless link between two ears even at 1 MHz as an approximately quasistatic problem with a sufficient degree of accuracy. The quasistatic approach is widely used in particular for modeling cancer-treating RF fields [67],[197],[198].

B. Contribution of Displacement Currents

Another critical parameter is the charge relaxation time, τ = ε/σ, where ε is tissue’s electric permittivity. The well-known quasistatic condition,

$$\omega \tau <<1\mathit{or}\frac{\epsilon \omega }{\sigma }<<1$$ (9)

allows us to neglect displacement currents in Ampere’s law as compared to the conduction currents. Due to the very high dielectric tissue constants, especially at low frequencies [133]–[139], Eq. (9) is often barely satisfied. For example, in a muscle tissue at 1 MHz, εω/σ = 0.2. Therefore, the displacement currents may need to be taken into account both in high- and low-frequency limits.

For the quasistatic approximation in frequency domain, this task is trivially accomplished by using complex conductivity, σ → σ + jωϵ = σ + jωε₀ε_r. Fig. 18 shows relative contributions of displacement and conduction currents,

$$\mathit{J}=\underset{\mathrm{conduction}\mathrm{curent}}{\overset{\sigma \mathit{E}}{\underbrace{}}}+j\times \underset{\mathrm{displacement}\mathrm{current}}{\overset{\omega {\epsilon }_0{\epsilon }_r\mathit{E}}{\underbrace{}}}$$ (10)

to the total current density, J, in some common tissues including cortical and cancellous bone. Both of these tissue currents very significantly dominate the displacement current in vacuum, also shown in Fig. 18 by a blue line, in the frequency band up to 1 GHz.

Fig. 18.

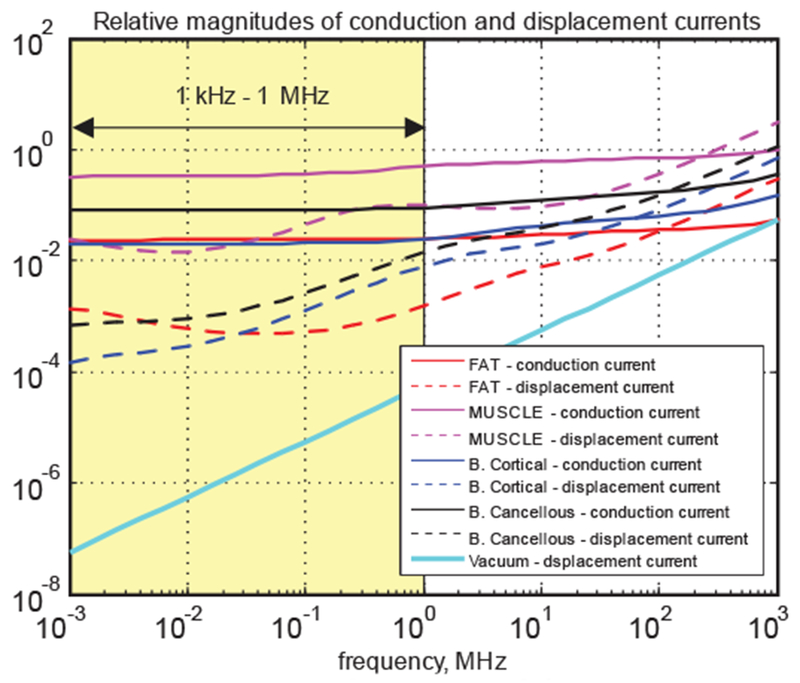
Relative magnitudes of conduction and displacement currents in common tissues.

VIII. Modern High Frequency Applications

A. Body Area Networks (BANs)

As wearable and implantable devices connected to the Internet or to each other multiply (as the Internet of Things becomes pervasive), individuals are quickly developing into complex body-area networks (BANs). Fig. 19 shows a sketch of a BAN communication for two different human models derived from the Visible Human Project^® of the U.S. National Library of Medicine [22]–[26].

Fig. 19.

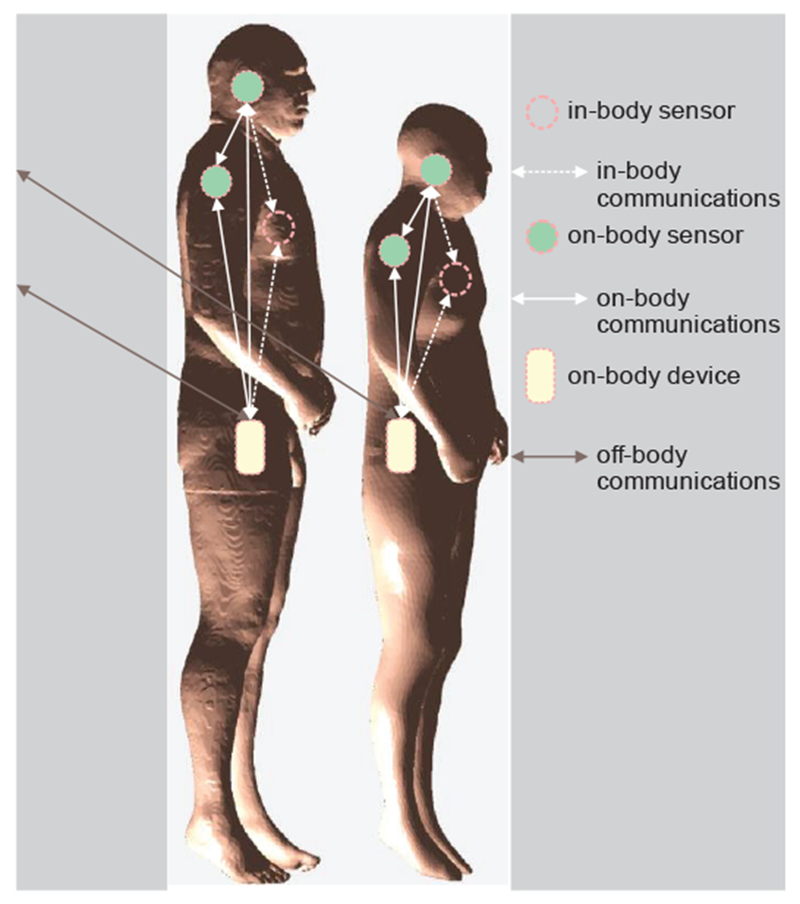
An overview of a BAN communication. Note change in the network topology depending on body composition.

It is extremely difficult to test all such possible configurations, and it is also challenging to obtain FDA or FCC approval for each new device. Therefore, market leaders use engineering simulation to model both the device and the human body, while also considering performance and safety metrics with different body types (male, female, child, slim, average, overweight, etc.) [199].

The IEEE 802.15.6 standard is the latest international standard for Wireless Body Area Networks (WBANs). WBANs supports a variety of real-time health monitoring and consumer electronics applications [200]–[203]. Various communication bands are dispersed between 400 MHz to 2.4 GHz and beyond, including Medical Body Area Network (MBAN) spectrum of 2360 to 2400 MHz. Table VII lists major scenarios [204].

Table VII.

List of Scenarios and Their Description for IEEE 802.15.6 Standard (after [204]).

Scenario	Description	Frequency band	Channel Model
S1	Implant to Implant	402–405 MHz	CM1
S2	Implant to body surface	402–405 MHz	CM2
S3	Implant to external	402–405 MHz	CM2
S4	Body surface to body surface (LOS)	13.5, 50, 400, 600, 900 MHz 2.4, 3.1–10.6 GHz	CM3
S5	Body surface to body surface (NLOS)	13.5, 50, 400, 600, 900 MHz 2.4, 3.1–10.6 GHz	CM3
S6	Body surface to external (LOS)	900 MHz 2.4, 3.1–10.6 GHz	CM4
S7	Body surface to external (NLOS)	900 MHz 2.4, 3.1–10.6 GHz	CM4

B. Value of Virtual Human Model for BAN

For off-body communications related to indoor geolocation, the detailed human model is often unnecessary, since both the transmitter and the receiver are typically located far away from the body. Simplified models in the form of a homogeneous shell [205] or geometry primitives (cylinders) have been used. For all other types of BAN, some sort of a detailed human model is necessary; this need has been recognized since approximately 2007 [206],[207]. It is believed that an otherwise homogeneous human model with several shells (skin, fat, average body) may be sufficient for a number of tasks. This simplification has been confirmed by MRI-related studies [189].

C. Challenge of on-Body and In-Body Antenna Design: Shorting out Antenna Near-Field

Design of a small and efficient on-body antenna for WBAN applications is difficult. One well-known problem is illustrated in Fig. 20. Here, we use a distributed-circuit approach (or the 3-D impedance method [208]–[213]) and replace a tissue by a distributed network of capacitances, resistances, and possibly inductances. Note that smaller distributed inductances may be ignored in the near field of the antenna and/or at lower frequencies. A dipole antenna is considered for three different configurations: on the body surface, within the body, and within the body but isolated inside a container.

Fig. 20.

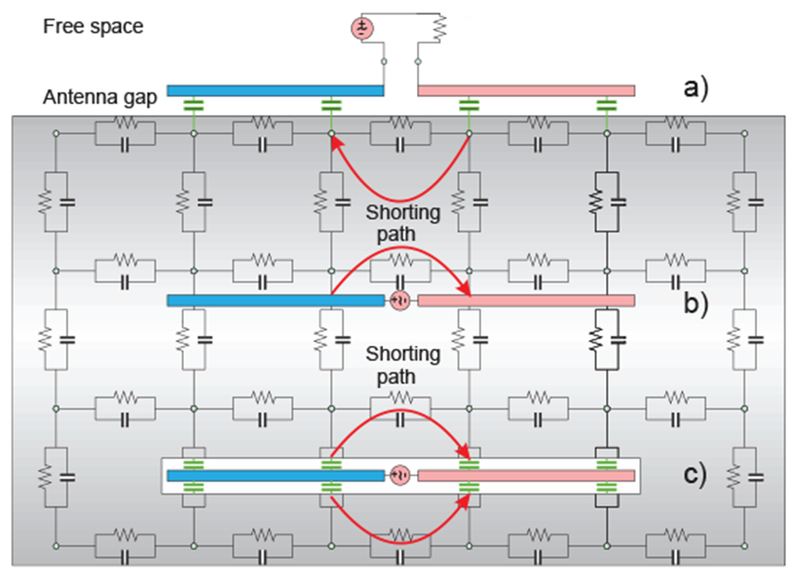
Antenna behavior in a lossy tissue with a high value of dielectric constant and high conductivity. Coupling capacitances are marked green.

For an on-body antenna located very close to the skin surface in Fig. 20a, the coupling capacitance to the body (marked green in Fig. 20a) may be significant. As a result, the antenna is partially shorted out directly at the antenna feed. Instead of flowing along the entire antenna length, a significant portion of the antenna current will flow directly through the lossy body. Thus, the antenna design will likely predict a wide impedance bandwidth (due to the losses), but a very low antenna efficiency. The antenna literally becomes a heater and not a radiator.

The effect of the body on the antenna is in fact twofold. The capacitive (non-lossy) displacement current flowing through the body leads to the strong antenna mismatch but does not generally decrease efficiency. Such a mismatch can be mitigated by a proper antenna design. The conduction current, on the other hand, directly contributes to the power loss but “improves” antenna matching. For the non-isolated in-body antenna in Fig. 20b, the situation potentially becomes even worse since a direct ohmic contact with a conducting tissue further facilitates shorting out the antenna feed. The impedance bandwidth is expected to be large but the efficiency is very low.

Even the isolated antenna in Fig. 20c may experience a strong capacitive coupling with the surrounding tissue when the enclosing container has a very small thickness. However, in many cases, the container size cannot be significantly increased as seen in Fig. 21 [214],[215].

Fig. 21.

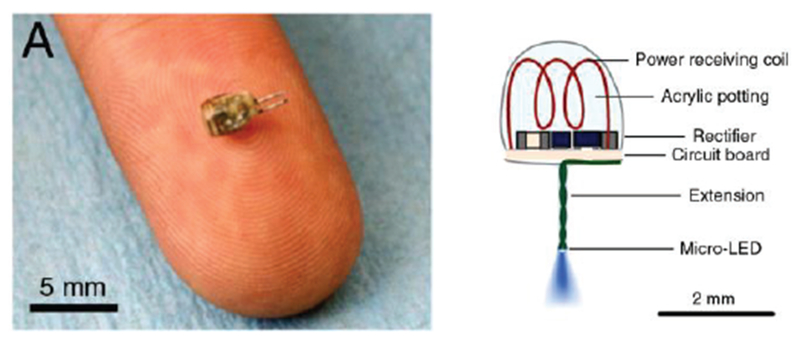
An energy-harvesting in-body coil antenna for a micro-implant in the low-gigahertz range (1.6 GHz) [214],[215].

D. Challenge of on-Body and In-Body Antenna Design: Creeping and Surface Waves

Creeping wave around the body is a part of the full-wave diffraction problem solution [216]–[219]. The creeping wave exists for a perfectly conducting object where the classic surface waves are impossible. Thus, the creeping wave may or may not include the true surface waves.

Trapped surface wave was originally discovered for a grounded dielectric slab [220],[221].

Zenneck surface wave exists at the boundary between conducting and non-conducting media [222]–[229]. It is very difficult to excite a Zenneck wave due to its large extend in the transversal direction. However, a combination of both surface waves [230],[231] may exist and be probably well localized at the air/fat/muscle interface.

Quite often, creeping/surface waves work to our advantage and enable NLOS (non-line-of-sight) communications between different body parts [217], [232]–[234].

E. On-Body Antenna Design

On-body antenna design has been a tremendous field of research. The bulk of the effort has been geared toward wireless communication antennas which must radiate from the body surface to air (cf. [235]–[241]). In a number of cases, on-body antennas are communicating with implants or smart pills [242]–[249], [214],[215]. Dedicated antennas for microwave tomography (for radiating into the body) have been broadband monopoles/dipoles [250]–[260] including their modern printed versions [261]–[263] as well as small-size arrays [248]–[261], [264],[265]. Recently, wideband and multiband (slotted) patch antennas have been suggested and investigated [265]–[270]. Emphasis is usually on the (ultra)wideband performance.

As an example, Fig. 22 shows cloth-mounted antenna design performed by CST AG [271] with the VHP-Female CAD model (the second last row in Table II). Differences in volume power loss density or PLD between homogeneous (a) and inhomogeneous (b) models are clearly seen.

Fig. 22.

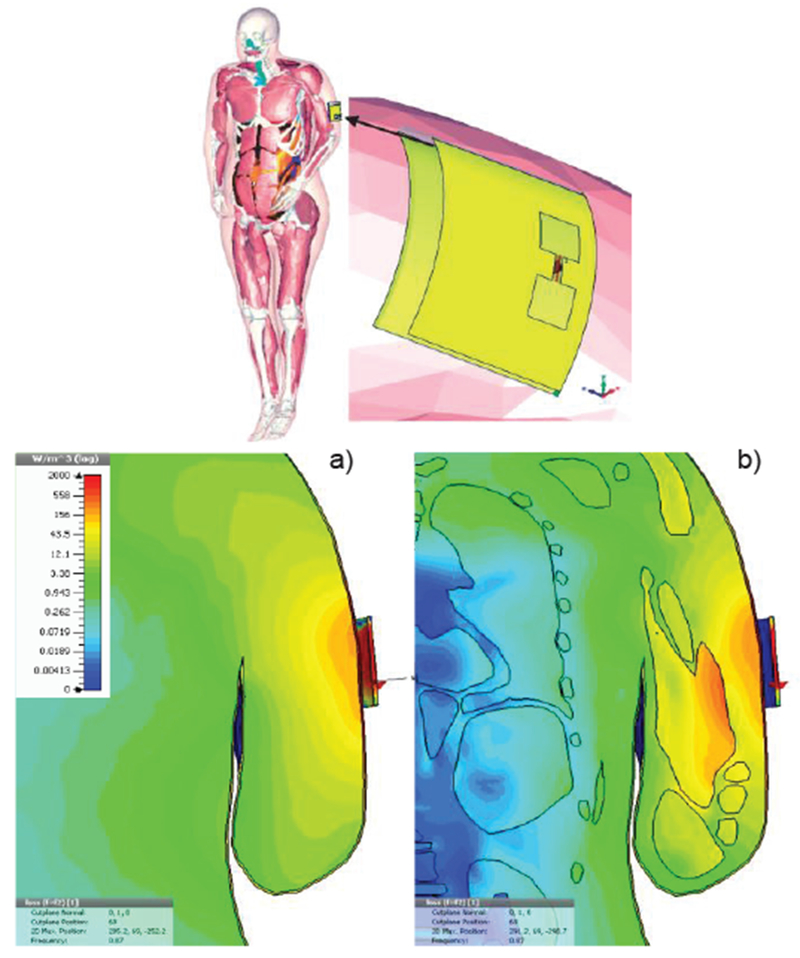
Volume power loss density in W/m³ for cloth-mounted antenna design at 870 MHz [271]. a)- Homogeneous body model; b) – inhomogeneous model.

As another example, Fig. 23 illustrates antenna performance in MICS (Medical Implant Communications Service) band in proximity to varying body types/sizes using the same VHP-Female CAD model in ANSYS HFSS [272]. MICS is an earlier version of the Medical Device Radiocommunications Service (MedRadio) covering 401–406, 413–419, 426–432, 438–444, and 451–457 MHz bands. Creeping waves around the body are clearly seen in Fig. 23.

Fig. 23.

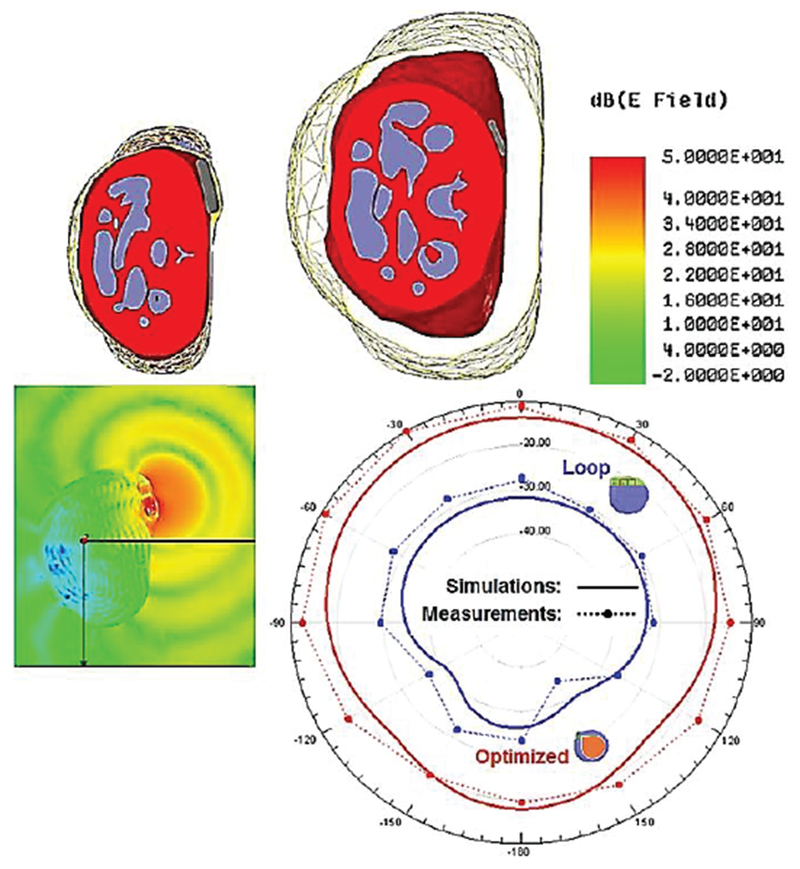
Near-body antenna performance for different body sizes [272].

In this paper, we do not specifically address safety issues of stand-alone BANs, which seem to be a relatively minor point of concern. MRI safety and MRI-conditional safety of implanted devices (including BAN) are discussed next.

F. MRI Safety

Regulatory and standardization organizations (e.g. FDA or IEC) require the determination of the specific absorption rate or SAR for MRI radiofrequency (RF) coil safety assessment. Different international safety standards have been developed to ensure that RF heating in MRI stays within safe limits. The major applicable standard is issued by the International Electrotechnical Commission (IEC) [273]. The IEC limits are now also accepted by the U.S. Food and Drug Administration. The IEC standard normal mode (mode of operation that causes no physiological stress to patients) limits global-body SAR to 2 W/kg, global-head SAR to 3.2 W/kg, local head and torso SAR to 10 W/kg, and local extremity SAR to 20 W/kg [189]. The global SAR limits are intended to ensure a body core temperature of 39°C or less [189],[273].

However, SAR measurements are not easily performed for human subjects in-vivo and, thus, SAR is typically derived from numerical electromagnetic simulations with virtual humans. A number of relevant references have already been provided in Table VI.

As an example, Fig. 24 [81] investigates how cerebrospinal fluid simulated as a single electrically connected object, and variation of the geometry of an anatomical human head model, influence the transmit and safety excitation efficiencies of a 7 T magnetic resonance imaging transmit array. There, an early ANSYS human body model without cerebrospinal fluid (CSF) is compared to the VHP-Female CAD model with a manifold CSF shell. The comparison results of Ref. [81] partially replicated in Fig. 24 indicate that the CSF shell simulated as a single electrically connected object partially shields the brain from the RF radiation and resulted in decreases of both transmit and safety excitation efficiencies on the order of 10-15%.

Fig. 24.

SAR10g as result of MRI exposure using VHP-Female v.3.0 mode 1 (top) with a continuous CSF shell versus a model with no CSF (bottom) [81].

G. MRI-Conditional Safety of Passive Implants

Multiphysics modeling of heating large passive metallic implants in an MRI coil is a problem of significant importance today [274],[275]. Numerical simulations with realistic human models are widely employed. As an example, Fig. 25 [274] shows the local SAR distribution (top) and the temperature rise (bottom) for a shoulder implant computed with COMSOL^® Multiphysics for a realistic CAD NURBS human model derived from Visible Korean Human [36] via ScanIP software (Simpleware, Exeter UK).

Fig. 25.

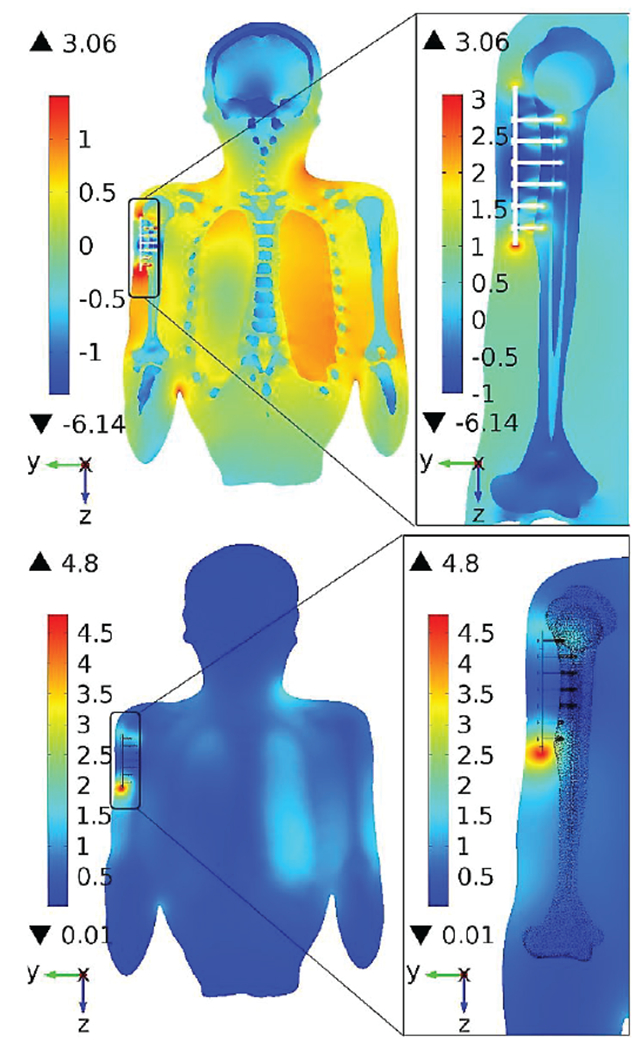
MRI-induced heating of a passive shoulder implant [274]. Top – SAR (log10); bottom - temperature rise after 900 s RF Application (C), slice parallel to humerus.

H. MRI-Conditional Safety of Active Implants

Patients with Active Implantable Medical Devices (AIMD) including BAN are generally denied access to MRI, despite that imaging modality’s preferred status for soft tissue imaging. However, it has been estimated that 17% of pacemaker patients need an MRI during the first 12 months of implantation [276]. During MRI, the RF fields will induce voltages at the various conductors external to the device enclosure. These voltages can cause device malfunction, or can be rectified by active elements within the AIMD and cause unintended stimulation of tissue. AIMD manufacturers evaluate conditional safety of devices in MRI by conservatively calculating these voltages using computational human models [276], [277].

The size of these devices compared to the wavelength provides some contrast to the corresponding analysis for passive implants. Recent example references in this area include [276]–[281].

IX. Major Low Frequency Applications

A. Neurostimulation

Transcranial Magnetic Stimulation (TMS).

Transcranial magnetic stimulation (TMS) with an external excitation coil is increasingly used as a diagnostic and therapeutic tool for neuropsychiatric disorders. Recent studies confirm the efficacy of Transcranial Magnetic Stimulation (TMS) as a non-invasive treatment of medication-resistant depression [282],[283] and in the US, at least four different devices, the Neuronetics Neurostar Stimulator, Brainsway H-Coil system, Magstim Magnetic Stimulator, and MagVenture Stimulator have been cleared by the Food and Drug Administration (FDA) for the treatment of medication-resistant depression [284],[285]. TMS has been proposed as a method to treat maternal depression while avoiding fetal exposure to drugs [286],[287] and the risk-benefit profile is argued to be better for TMS than for medications. Numerical modeling with virtual humans has been proven to be a very useful tool for TMS research. Early [288],[289] and recent [290]–[298] simulation results reveal both efficiency and safety of the TMS. As an example, Fig. 26 shows induced current distribution in a body of a pregnant patient (second trimester) due to CW (continuous wave) excitation with a figure-eight TMS coil used for safety estimates [93].

Fig. 26.

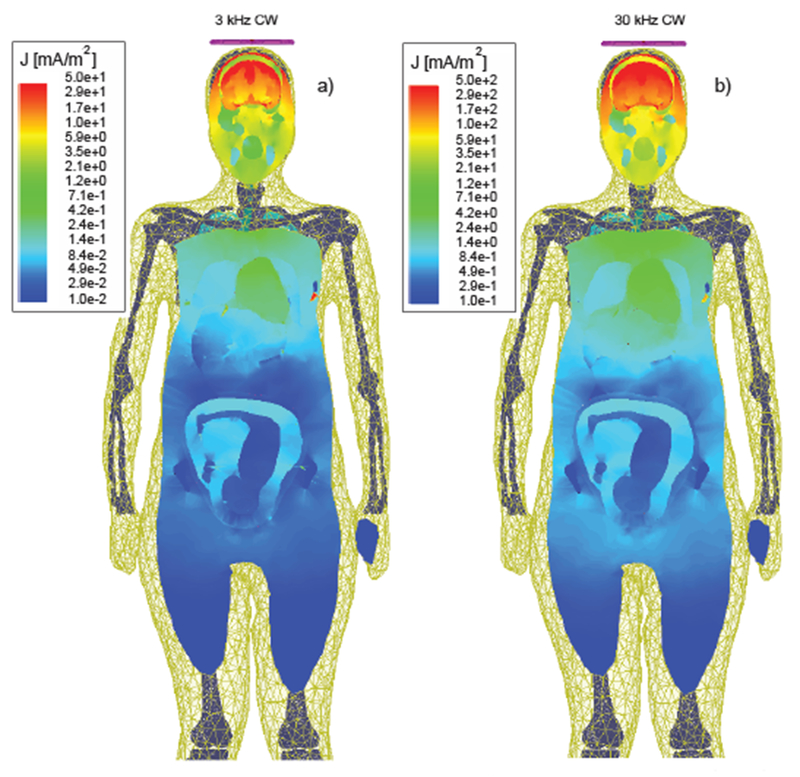
Induced current density distribution in a body of a pregnant patient due to CW excitation with a figure-eight TMS coil at two different test frequencies [93]

Transcranial Direct Current Stimulation (tDCS).

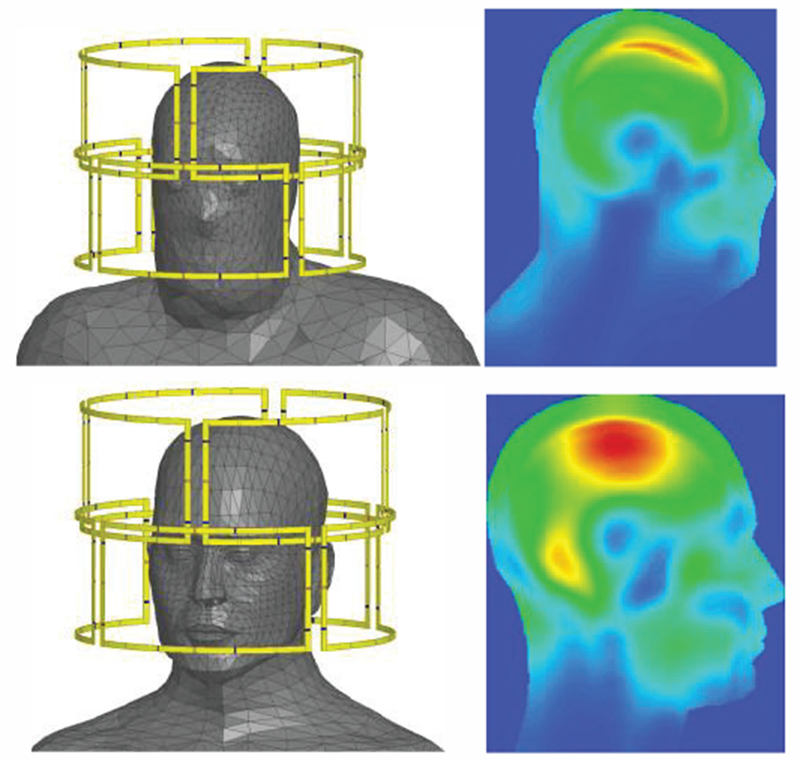
This neurostimulation method uses direct current delivered to the brain area of interest via electrodes on the scalp [299]–[301]. Dr. M. Bikson’s research group from the City University of New York is very active in this area including detailed simulations with human models and moving toward cellular mechanisms of tDCS (cf. [302]–[307]).

To illustrate differences and similarities between TMS and tDCS, Fig. 27 presents comparative simulations results for both methods using the same high-fidelity FEM head model [296] shown in Fig. 27a. Fig. 27b yields the TMS simulation results (the current in the coil is varied sinusoidally with a frequency of 5 kHz and a maximum rate of change of 67 A/μs) while Fig. 27c is the tDCS with total 1 mA injection current.

Fig. 27.

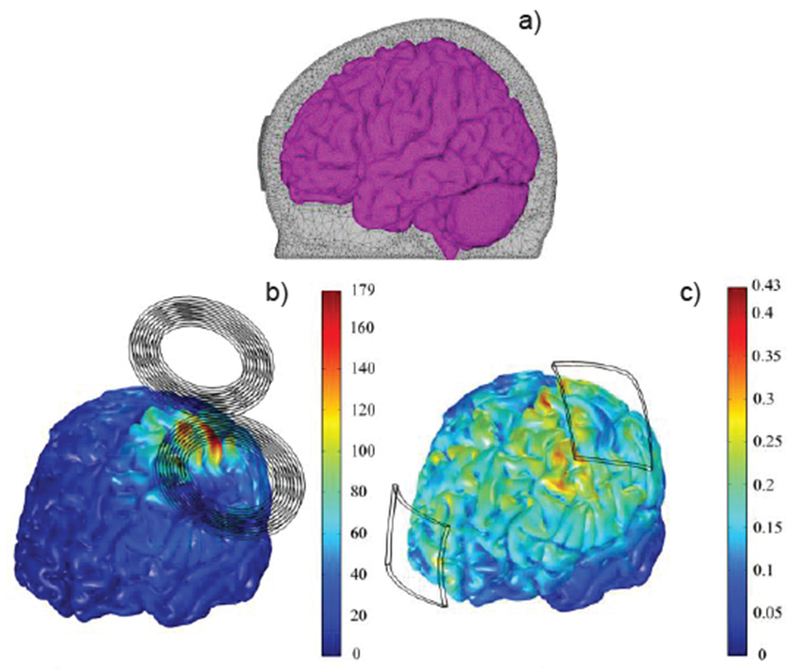
Magnitude of the E-field in the cortex (a) during TMS (b) and tDCS (c) [296]. The electric field scale is in V/m.

Evaluation of different numerical methods and their accuracy for a current injection problem (isotropic and anisotropic head models) has been performed in Ref. [308].

B. MEG/EEG Source Localization

EEG (Electroencephalography) and MEG (Magnetoencephalography) [309] source analyses have largely relied in the past upon (multi-layered) spherical conductor models of the head to simplify forward calculations of the brain’s magnetic field [310],[311]. However, it has been shown that the spherical models can contribute in the order of 1 cm to the localization bias in regions of the head that depart significantly from a sphere (inferior frontal and temporal). Given these limitations, realistic FEM/FDTD/BEM head models have been employed recently [180],[308],[311].

C. Tumor Treating Fields

One new development is represented by Tumor Treating Fields (TTFields), low-intensity electric fields in the frequency range of 100–500 kHz, which exhibit antimitotic activity in cancer cells. TTFields were approved by the U. S. Food and Drug Administration for the treatment of recurrent glioblastoma in 2011. Studies have shown that inhibition of cell division in glioma is achieved when the applied alternating electric field has a frequency in the range of 100–500 kHz and an amplitude of 1–3 V/cm [312]–[316]. Preclinical evidence and pilot studies suggest that TTFields could be also effective for treating certain types of lung cancer, and that treatment efficacy depends on the electric field intensity [317].

Extensive numerical simulations of the TTFields have recently been performed with detailed human models [197],[198],[317]–[319]. A unique feature of the most recent simulations pertinent to the human head is the full-scale anisotropic modeling [67],[198]. As an example, Fig. 28 [67] demonstrates electric field strength (V/cm) distribution in axial (top row), sagittal (middle row) and coronal (bottom row) slices through an artificial spherical tumor for the left panel electrode stimulations. Isotropic results are plotted on the left and corresponding anisotropic results for vN (volume normalized conductivity mapping [320]) and dM (direct conductivity mapping [149]) are illustrated in the middle and right columns respectively. The color range is the same for all figures and varies between 0 (dark blue) and 4 (dark red) V/cm.

Fig. 28.

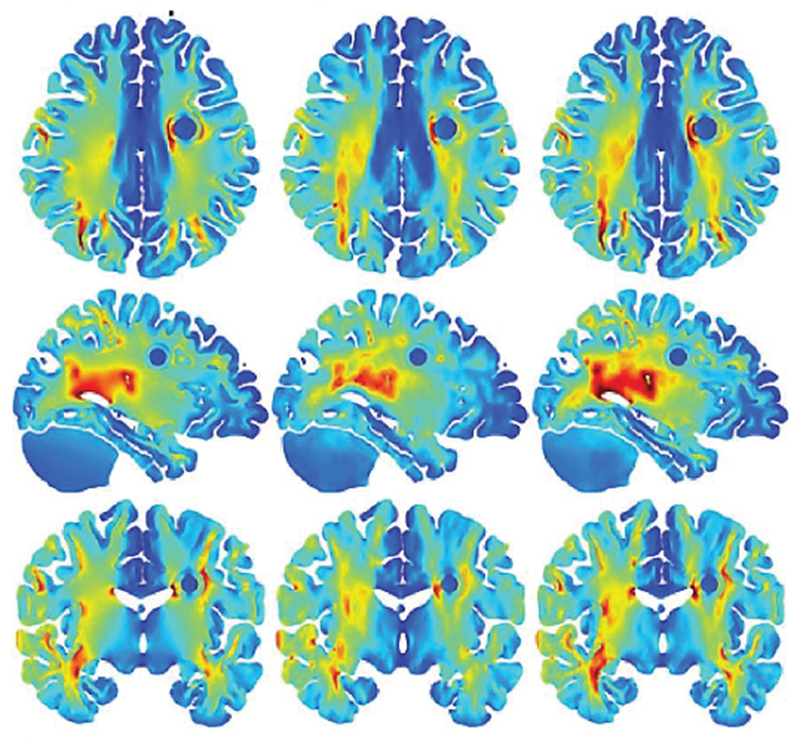
Electric field strength (V/cm) distribution in axial (top row), sagittal (middle row) and coronal (bottom row) slices through am artificial spherical tumor [67]. Anisotropic results for vN and dM are illustrated in the middle and right columns, respectively.

Ready-to-use open-access simulation packages [321] already exist for the low-frequency modeling tasks with human models.

X. Concluding Remarks

Anatomical human models (i.e. virtual humans) replicate local tissue responses of real humans and are being used today with exponentially increasing frequency for the safety assessment of various industrial and medical devices, and for diverse R&D purposes. Even today, detailed and accurate human models are difficult and very time-consuming to create. Two major challenges are related to the reconstruction of a unique subject-specific multi-tissue body structure with hundreds of individual parts and to a limited ability to justify the final model assembly and accuracy by direct measurements. Yet another challenge is related to the material properties, specifically to electrical permittivity and conductivity behavior at various frequencies and degrees of anisotropy.

The bulk of existing human models are assemblies of isotropic compartments that assume homogeneous volumes for every individual tissue. The modern tendency is to incorporate realistic anisotropic (fibrous) tissue structures into the computational models.