A stationary Weibull process and its applications

Abstract

In this paper we introduce a discrete-time and continuous state-space Markov stationary process $\{X_n;n=1,2,\dots \}$, where $X_n$ has a two-parameter Weibull distribution, $X_n$'s are dependent and there is a positive probability that $X_n=X_{n+1}$. The motivation came from the gold price data where there are several instances for which $X_n=X_{n+1}$. Hence, the existing methods cannot be used to analyze this data. We derive different properties of the proposed Weibull process. It is observed that the joint cumulative distribution function of $X_n$ and $X_{n+1}$ has a very convenient copula structure. Hence, different dependence properties and dependence measures can be obtained. The maximum likelihood estimators cannot be obtained in explicit forms, we have proposed a simple profile likelihood method to compute these estimators. We have used this model to analyze two synthetic data sets and one gold price data set of the Indian market, and it is observed that the proposed model fits quite well with the data set.

1. Introduction

The aim of this paper is to introduce a new discrete-time and continuous state-space Markov Weibull process $\{X_n;n=1,2,\dots \}$, which is flexible and it has certain distinct features so that it can be used in practice in different areas. In this case, the marginals are non-negative two-parameter Weibull distributions and $X_n$s are dependent. It is a lag-1 process based on a minimization approach and $X_n=X_{n+1}$ with a positive probability. Therefore, if there is a non-negative time series data which are positively skewed and there is a positive probability that the consecutive values might be equal then the proposed model can be used quite effectively to analyze this data set.

The motivation for this work came when we were trying to analyze gold price data in the Indian market during the month of December 2020 and January 2021. It is observed that the data are coming from a positive valued lag-1 stationary process, there are several instances for which $X_n=X_{n+1}$, and this cannot be ignored. It may be mentioned that there are several positive valued stationary processes available in the literature, for example, the exponential process by Tavares [14], Weibull and Gamma processes by Sim [13], the logistic process by Arnold [1], Pareto process by Arnold and Hallet [2], semi-Parero process by Pillai [12], generalized Weibull process by Jayakumar and Girish Babu [6], see also Yeh et al. [15], Arnold and Robertson [3], Jose et al. [7] and the reference cited therein. But none of these can be applied in this case, as in all these cases $P(X_n=X_{n+1})=0$.

We have provided different properties of the proposed process $\{X_n\}$. The Weibull process $\{X_n\}$ has one shape parameter and two scale parameters. If the shape parameter is one, it becomes a stationary exponential process. The generation from $\{X_n\}$ is quite straightforward, hence, different simulation experiments can be performed quite conveniently. The joint distribution of $X_n$ and $X_{n+1}$ has a very convenient copula structure. Therefore, several dependence properties and the dependence measures can be computed quite conveniently. We provide a characterization of the process. The marginals and the joint PDF can take a variety of shapes. The autocovariance and autocorrelation are not in convenient forms. However, we have provided the necessary expressions in Appendix for completeness purposes.

The maximum likelihood estimators (MLEs) cannot be obtained in explicit form. Moreover, it cannot be obtained in a routine manner. Based on some re-parameterization and using the profile likelihood method the MLEs can be obtained. The parametric bootstrap method can be used to compute the confidence intervals of the unknown parameters. We propose a goodness of fit test based on the parametric bootstrap approach. We have analyzed two synthetic data sets and one gold price data set for two months of the Indian market. It is observed that the proposed model fits the gold price data set quite well and it can be used quite effectively to analyze the gold price in the Indian market. It may be mentioned that the proposed process is a lag one process, but it can be extended to a lag-q process also, and it has been indicated how it can be done.

I think the major difference between the existing literature and the present manuscript is in its construction. The present manuscript allows to have ties, which are not available in the literature. Moreover, in the present manuscript we have provided the detailed inference procedure and showed with real data examples how it can be implemented in practice. This seems to be the main contribution of the present manuscript.

The rest of the paper is organized as follows. In Section 2 we have defined the Weibull process and provided its different properties. The maximum likelihood estimators have been discussed in Section 3. In Section 4 one goodness of fit test has been proposed based on the parametric bootstrap approach. The analyses of three data sets have been presented in Section 5. Finally, we conclude the paper in Section 6.

2. Weibull process and its properties

We will use the following notations in this paper. A Weibull random variable with the shape parameter $\alpha >0$ and the scale parameter $\lambda >0$ has the following probability density function (PDF);

$$f_{WE}(x;\alpha ,\lambda )=\{\begin{array}{ll}{\displaystyle \alpha \lambda x^{\alpha -1}{\mathrm{e}}^{-\lambda x^{\alpha }}}& \mathrm{if}x>0,\\ {\displaystyle 0}& \mathrm{if}x\le 0,\end{array}$$ (1)

and it will be denoted by WE $(\alpha ,\lambda )$. It has the following cumulative distribution function and hazard function, respectively, for x>0;

$$\begin{array}{rl}{F}_{WE}(x;\alpha ,\lambda )& =1-{\mathrm{e}}^{-\lambda x^{\alpha }},\\ h_{WE}(x;\alpha ,\lambda )& =\alpha \lambda x^{\alpha -1}.\end{array}$$

The mean and variance of WE $(\alpha ,\lambda )$ is

$$\frac{1}{{\lambda }^{1/\alpha }}\mathrm{\Gamma }(\frac{1}{\alpha }+1)\text{and}\frac{1}{{\lambda }^{2/\alpha }}[\mathrm{\Gamma }(\frac{2}{\alpha }+1)-{\left(\mathrm{\Gamma }(\frac{1}{\alpha }+1)\right)}^2],$$ (2)

respectively. A uniform random variable on (0,1) will be denoted by $U(0,1)$. Now, we are in a position to define the Weibull process.

Definition 2.1

Suppose $U_0,U_1,\dots$ are independent identically distributed (i.i.d.) $U(0,1)$ random variables, then for ${\lambda }_0>0$, ${\lambda }_1>0$ and $\alpha >0$, let us define a new sequence of random variables $\{X_n;n=1,2,\dots \}$, where

$$X_n=min\{{[-\frac{1}{{\lambda }_0}\ln U_n]}^{\frac{1}{\alpha }},{[-\frac{1}{{\lambda }_1}\ln U_{n-1}]}^{\frac{1}{\alpha }}\}.$$ (3)

Then the sequence of random variables $\{X_n\}$ is called a Weibull process.

A Weibull process as defined in (3) will be denoted by WEP $(\alpha ,{\lambda }_0,{\lambda }_1)$. Here α is the shape parameter and ${\lambda }_0$ and ${\lambda }_1$ are the scale parameters. It may be mentioned that a location parameter can easily be incorporated into the model, which has not been tried here. The name Weibull process comes from the following results.

Theorem 2.1

If $\{X_n\}$ is as defined in (3), then

1. $\{X_n\}$ is a stationary process.

2. $X_n$ follows WE $(\alpha ,{\lambda }_0+{\lambda }_1)$.

Proof.

Part (i) follows from the definition. To prove Part (ii), note that

$$\begin{array}{rl}P(X_n>x)& =P\{{[-\frac{1}{{\lambda }_0}\ln U_n]}^{\frac{1}{\alpha }}>x,{[-\frac{1}{{\lambda }_1}\ln U_{n-1}]}^{\frac{1}{\alpha }}>x\}\\ & =P\{U_n<{\mathrm{e}}^{-{\lambda }_0{x}^{\alpha }},U_{n-1}<{\mathrm{e}}^{-{\lambda }_1{x}^{\alpha }}\}\\ & =P\{U_n<{\mathrm{e}}^{-{\lambda }_0{x}^{\alpha }}\}P\{U_{n-1}<{\mathrm{e}}^{-{\lambda }_1{x}^{\alpha }}\}\\ & ={\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)x^{\alpha }}.\end{array}$$

The following result characterizes the Weibull process.

Theorem 2.2

Let $X_1\sim$ WE $(\alpha ,{\lambda }_0+{\lambda }_1)$, and $U_i$s are i.i.d. random variables with an absolute continuous distribution function $F(\cdot )$ on (0,1). Then the process as defined in (3) is a strictly stationary Markov process if and only if $U_0\sim U(0,1)$.

Proof.

‘If’ part is trivial. Now to prove the ‘only if’ part, we assume $S(x)=1-F(x)$, and $F^{\prime }(x)=-S^{\prime }(x)=f(x)$, for x>0. Therefore, for $x>0$,

$${\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)x^{\alpha }}=F({\mathrm{e}}^{-{\lambda }_0{x}^{\alpha }})F({\mathrm{e}}^{-{\lambda }_1{x}^{\alpha }}).$$

If we write $y={\mathrm{e}}^{-x^{\alpha }}$, then for 0<y<1,

$$y^{{\lambda }_0+{\lambda }_1}=F(y^{{\lambda }_0})F(y^{{\lambda }_1})\Rightarrow \frac{F(y^{{\lambda }_0})}{y^{{\lambda }_0}}\times \frac{F(y^{{\lambda }_1})}{y^{{\lambda }_1}}=1\Rightarrow \frac{F(y)}{y}=1\Rightarrow F(y)=y.\text{■}$$

Now we present the joint distribution of $X_n$ and $X_{n+m}$, for $m\ge 1$.

Theorem 2.3

If $\{X_n\}$ satisfies (3), then the joint survival function of $X_n$ and $X_{n+m}$, $S_{n,n+m}(x,y)=P(X_n>x,X_{n+m}>y)$ is

$$S_{n,n+m}(x,y)=\{\begin{array}{ll}{\displaystyle {\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)x^{\alpha }}{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)y^{\alpha }}}& \mathrm{if}m\ge 2\\ {\displaystyle {\mathrm{e}}^{-{\lambda }_1{x}^{\alpha }}{\mathrm{e}}^{-{\lambda }_0{y}^{\alpha }}g(x,y)}& \mathrm{if}m=1,\end{array}$$ (4)

where $g(x,y)=min\{{\mathrm{e}}^{-{\lambda }_0{x}^{\alpha }},{\mathrm{e}}^{-{\lambda }_1{y}^{\alpha }}\}$.

Proof.

The proof is quite simple and it is avoided.

The above theorem indicates that $X_n$ and $X_{n+m}$ are dependent for m = 1, and they are independently distributed if m>1. This makes the process as the lag-1 process. The joint distribution function of $X_n$ and $X_{n+1}$ will help to develop the dependence properties of the Weibull process and we would like to study it in more detail. The joint survival function of $X_n$ and $X_{n+1}$ can be written explicitly as

$$S_{n,n+1}(x,y)=\{\begin{array}{ll}{\displaystyle {\mathrm{e}}^{-{\lambda }_1{x}^{\alpha }}{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)y^{\alpha }}}& \mathrm{if}{\lambda }_0{x}^{\alpha }<{\lambda }_1{y}^{\alpha }\\ {\displaystyle {\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)x^{\alpha }}{\mathrm{e}}^{-{\lambda }_0{y}^{\alpha }}}& \mathrm{if}{\lambda }_0{x}^{\alpha }>{\lambda }_1{y}^{\alpha }\\ {\displaystyle {\mathrm{e}}^{-z\frac{{\lambda }_1^2+{\lambda }_0^2+{\lambda }_0{\lambda }_1}{{\lambda }_0{\lambda }_1}}}& \mathrm{if}{\lambda }_0{x}^{\alpha }={\lambda }_1{y}^{\alpha }=z.\end{array}$$ (5)

Therefore, if ${\lambda }_0={\lambda }_1=\lambda$, then

$$S_{n,n+1}(x,y)=\{\begin{array}{ll}{\displaystyle {\mathrm{e}}^{-\lambda x^{\alpha }}{\mathrm{e}}^{-2\lambda y^{\alpha }}}& \mathrm{if}x<y\\ {\displaystyle {\mathrm{e}}^{-2\lambda x^{\alpha }}{\mathrm{e}}^{-\lambda y^{\alpha }}}& \mathrm{if}x>y\\ {\displaystyle {\mathrm{e}}^{-3\lambda z^{\alpha }}}& \mathrm{if}x=y=z.\end{array}$$ (6)

It may be mentioned that (6) is the joint survival function of the Marshall–Olkin bivariate Weibull distribution, and its properties have been well studied in the literature. See for example Kundu and Dey [8] and Kundu and Gupta [10] and the references cited therein. It can be easily seen that the $S_{n,n+1}(x,y)$, for $0<\delta <1$, has the following survival copula

$$\tilde{C}(u,v)=\{\begin{array}{ll}{\displaystyle u^{\delta }v}& \mathrm{if}{u}^{\delta }>v^{1-\delta }\\ {\displaystyle u{v}^{1-\delta }}& \mathrm{if}{u}^{\delta }\le v^{1-\delta }.\end{array}$$ (7)

The corresponding copula density function becomes

$$c(u,v)=\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }u\mathrm{\partial }v}\tilde{C}(u,v)=\{\begin{array}{ll}{\displaystyle \delta u^{\delta -1}}& \mathrm{if}{u}^{\delta }>v^{1-\delta }\\ {\displaystyle (1-\delta )v^{-\delta }}& \mathrm{if}{u}^{\delta }\le v^{1-\delta }.\end{array}$$ (8)

Based on the copula density function, the Spearman's ρ and Kendall's τ can be obtained as

$$\begin{array}{rl}\rho & =\frac{3\delta (1-\delta )}{{\delta }^2-\delta +2}\\ \tau & =\frac{\delta (1-\delta )(1-\delta (1-\delta ))}{{\delta }^3+\delta (1-\delta )+{\delta }^2(1-{\delta }^2)+(1-\delta {)}^3},\end{array}$$

respectively.

We will introduce the following regions, which will be used later.

$$\begin{array}{rl}{S}_1& =\{(x,y);x>0,y>0,\beta x<y\}\\ S_2& =\{(x,y);x>0,y>0,\beta x>y\}\\ C& =\{(x,y);x>0,y>0,\beta x=y\}.\end{array}$$

Here, $\beta =({\lambda }_0/{\lambda }_1{)}^{1/\alpha }$, and it may be noted that the curve C has the parametric form $(t,\gamma (t))$, for $0<t<\mathrm{\infty }$, where $\gamma (t)=\beta t$. The following results are needed for further development.

Theorem 2.4

If $\{X_n\}$ satisfies (3), then the joint survival function of $X_n$ and $X_{n+1}$ can be written as

$$S_{n,n+1}(x,y)=p{S}_a(x,y)+(1-p)S_s(x,y),$$ (9)

here $p=\frac{{\lambda }_0^2+{\lambda }_1^2}{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}$,

$$S_s(x,y)={(g(x,y))}^{\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_0{\lambda }_1}},$$

and $S_a(x,y)$ can be obtained by subtraction, i.e.

$$S_a(x,y)=\{\begin{array}{ll}{\displaystyle \frac{1}{p}{\mathrm{e}}^{-{\lambda }_1{x}^{\alpha }}{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)y^{\alpha }}-\frac{1-p}{p}{\mathrm{e}}^{-\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_0}{y}^{\alpha }}}& \mathrm{if}\beta x<y\\ {\displaystyle \frac{1}{p}{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)x^{\alpha }}{\mathrm{e}}^{-{\lambda }_0{y}^{\alpha }}-\frac{1-p}{p}{\mathrm{e}}^{-\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_1}{x}^{\alpha }}}& \mathrm{if}\beta x>y.\end{array}$$ (10)

Proof.

See in Appendix.

Now we provide the joint probability density function (PDF) of $X_n$ and $X_{n+1}$, and because of the Markov property, it will be useful to compute the joint PDF of $X_1,\dots ,X_n$. It should be mentioned that since the joint distribution (survival) function is not an absolutely continuous distribution function the joint PDF does not exist in the terms of two-dimensional Lebesgue measure dominating. In this case, we need to consider the dominating measure in a different way similarly as in Bemis et al. [4]. Here, the dominating measure is the two-dimensional Lebesgue measure on $S_1\cup S_2$, and one-dimensional Lebesgue measure on the curve C. Based on the above dominating measure the joint PDF of $X_n$ and $X_{n+1}$, for $x>$ and $y>0$, can be written as follows.

Theorem 2.5

If $X_n$ satisfies (3), then the joint PDF of $X_n$ and $X_{n+1}$ is

$$f_{n,n+1}(x,y)=\{\begin{array}{ll}{\displaystyle f_1(x,y)}& \mathrm{if}\beta x<y,\\ {\displaystyle f_2(x,y)}& \mathrm{if}\beta x>y,\\ {\displaystyle f_0(x)}& \mathrm{if}\beta x=y,\end{array}$$ (11)

where

$$\begin{array}{rl}{f}_1(x,y)& =f_{WE}(x;\alpha ,{\lambda }_1)f_{WE}(y;\alpha ,{\lambda }_0+{\lambda }_1),\\ f_2(x,y)& =f_{WE}(x;\alpha ,{\lambda }_0+{\lambda }_1)f_{WE}(y;\alpha ,{\lambda }_0),\\ f_0(x)& =\frac{\alpha {\lambda }_0}{\beta }{x}^{\alpha -1}{\mathrm{e}}^{-\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_1}{x}^{\alpha }}.\end{array}$$

Proof.

See in Appendix.

The following conditional PDF will be useful for prediction purposes. The conditional PDF of $X_{n+1}$ given $X_n$ can be written as follows:

$$f_{X_{n+1}|X_n=x}(y)=\{\begin{array}{ll}{\displaystyle \frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}{\mathrm{e}}^{{\lambda }_0{x}^{\alpha }}{f}_{WE}(y;\alpha ,{\lambda }_0+{\lambda }_1)}& \mathrm{if}\beta x<y\\ {\displaystyle f_{WE}(y;\alpha ,{\lambda }_0)}& \mathrm{if}\beta x>y\\ {\displaystyle \frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1}{\mathrm{e}}^{-\frac{{\lambda }_0^2}{{\lambda }_1}{x}^{\alpha }}}& \mathrm{if}\beta x=y\end{array}$$ (12)

When α = 1, it becomes an exponential process. When ${\lambda }_0={\lambda }_1=\lambda$, then the joint PDF of $X_n$ and $X_{n+1}$ for a Weibull process is

$$f_{n,n+1}(x,y)=\{\begin{array}{ll}{\displaystyle 2{\alpha }^2{\lambda }^2{x}^{\alpha -1}{\mathrm{e}}^{-\lambda x^{\alpha }}{y}^{\alpha -1}{\mathrm{e}}^{-2\lambda y^{\alpha }}}& \mathrm{if}x<y,\\ {\displaystyle 2{\alpha }^2{\lambda }^2{x}^{\alpha -1}{\mathrm{e}}^{-2\lambda x^{\alpha }}{y}^{\alpha -1}{\mathrm{e}}^{-\lambda y^{\alpha }}}& \mathrm{if}x>y,\\ {\displaystyle \alpha \lambda x^{\alpha -1}{\mathrm{e}}^{-3\lambda x^{\alpha }}}& \mathrm{if}x=y.\end{array}$$

The conditional PDF of $X_{n+1}$ given $X_n$ can be written as

$$f_{X_{n+1}|X_n=x}(y)=\{\begin{array}{ll}\frac{1}{2}{\mathrm{e}}^{\lambda x^{\alpha }}{f}_{WE}(y;\alpha ,2\lambda )& \mathrm{if}x<y\\ {\displaystyle f_{WE}(y;\alpha ,\lambda )}& \mathrm{if}y>x\\ \frac{1}{2}{\mathrm{e}}^{-\lambda x^{\alpha }}& \mathrm{if}x=y\end{array}$$

It follows that both for the Weibull and exponential processes,

$$P(X_n=X_{n+1})=P(X_n<X_{n+1})=P(X_n>X_{n+1})=\frac{1}{3}.$$

The autocovariance and autocorrelation of a Weibull process cannot be obtained in convenient forms. In the case of exponential process, however, they can be obtained in explicit forms. We have provided all the necessary expressions in Appendix 2, for completeness purposes.

The joint PDF of $X_1,\dots ,X_n$ can be obtained as

$$\begin{array}{rl}{f}_{X_1,\dots ,X_n}(x_1,\dots ,x_n)& =f_{X_n|X_{n-1},\dots ,X_1}(x_n)\times \dots \times f_{X_2|X_1}(x_2)\times f_{X_1}(x_1)\end{array}$$ (13)

$$\begin{array}{rl}& =f_{X_n|X_{n-1}}(x_n)\times \dots \times f_{X_2|X_1}(x_2)\times f_{X_1}(x_1)\end{array}$$ (14)

$$\begin{array}{rl}& =\frac{f_{X_{n-1},X_n}(x_{n-1},x_n)}{f_{X_{n-1}}(x_{n-1})}\times \dots \times \frac{f_{X_1,X_2}(x_1,x_2)}{f_{X_1}(x_1)}\times f_{X_1}(x_1)\end{array}$$ (15)

$$\begin{array}{rl}& =\frac{\prod _{i=1}^{n-1}{f}_{X_i,X_{i+1}}(x_i,x_{i+1})}{\prod _{i=2}^{n-1}{f}_{X_i}(x_i)}.\end{array}$$ (16)

Note that (13) is obtained by the conditioning approach, (14) is obtained by using the Markov property, (15) is obtained by using the conditional density function, and the last step is obtained by simple algebraic calculation.

Now we will be discussing about the stopping time. It may be mentioned that the stopping time has been discussed quite extensively in the time series literature, see for example Christensen [5], Novikov and Shiryaev [11], and see the references cited therein. Let L>0 be a fixed real number, and let us define a new random variable N, such for $k\ge 1$,

$$\{N=k\}\iff \{X_1>L,\dots ,X_{k-1}>L,X_k\le L\}.$$

Then clearly, N is a stopping time. Now for $\lambda =max\{{\lambda }_0,{\lambda }_1\}$, first we obtain

$$\begin{array}{rl}P(X_1>L,\dots ,X_k>L)& =P(U_0<{\mathrm{e}}^{-{\lambda }_1{L}^{\alpha }},U_1<{\mathrm{e}}^{-{\lambda }_0{L}^{\alpha }},\dots U_{k-1}<{\mathrm{e}}^{-{\lambda }_1{L}^{\alpha }},U_k<{\mathrm{e}}^{-{\lambda }_0{L}^{\alpha }})\\ & ={\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)L^{\alpha }}-{\mathrm{e}}^{-(k-1)\lambda L^{\alpha }}\\ P(N=1)& =P(X_1\le L)=1-{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)L^{\alpha }}\\ P(N=2)& =P(X_1>L,X_2\le L)=P(X_1>L)-P(X_1>L,X_2>L)\\ & ={\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)L^{\alpha }}\\ & -P(U_1<{\mathrm{e}}^{-{\lambda }_0{L}^{\alpha }},U_0<{\mathrm{e}}^{-{\lambda }_1{L}^{\alpha }},U_2<{\mathrm{e}}^{-{\lambda }_0{L}^{\alpha }},U_1<{\mathrm{e}}^{-{\lambda }_1{L}^{\alpha }})\\ & ={\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)L^{\alpha }}(1-{\mathrm{e}}^{-\lambda L^{\alpha }})\\ P(N=3)& =P(X_1>L,X_2>L,X_3\le L)\\ & =P(X_1>L,X_2>L)-P(X_1>L,X_2>L,X_3>L)\\ & ={\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)L^{\alpha }}{\mathrm{e}}^{-\lambda L^{\alpha }}(1-{\mathrm{e}}^{-\lambda L^{\alpha }})\\ P(N=k)& ={\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)L^{\alpha }}{\mathrm{e}}^{-(k-2)\lambda L^{\alpha }}(1-{\mathrm{e}}^{-\lambda L^{\alpha }}).\end{array}$$

The probability generating function of N can be obtained as

$$\begin{array}{rl}G(z)& =E(z^N)=\sum _{k=1}^{\mathrm{\infty }}P(N=k)z^k\\ & =\frac{z(1-{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)L^{\alpha }})+z^2({\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)L^{\alpha }}-{\mathrm{e}}^{-\lambda L^{\alpha }})}{(1-z{\mathrm{e}}^{-\lambda L^{\alpha }})}.\end{array}$$

Using the probability generating function, different moments and other properties can be easily derived.

3. Maximum likelihood estimators

In this section we consider the maximum likelihood estimators of the unknown parameters of a Weibull process based on a sample of size n, namely $x_1,\dots ,x_n$. We consider two cases separately.

Case 1: ${\lambda }_0$ = ${\lambda }_1$

In this case it is assumed that ${\lambda }_0={\lambda }_1=\lambda$. Our problem is to estimate α and λ based on $\mathcal{D}=\{x_1,\dots ,x_n\}$. We use the following notations: $I=\{1,\dots ,n-1\}$

$$I_1=\{i:i\in I,x_i<x_{i+1}\},I_2=\{i:i\in I,x_i>x_{i+1}\},I_0=\{i:i\in I,x_i=x_{i+1}\}.$$

The number of elements in $I_0$, $I_1$ and $I_2$ are denoted by $n_0$, $n_1$ and $n_2$, respectively. Based on the joint PDF (16), the log-likelihood function can be written as

$$\begin{array}{rl}l(\alpha ,\lambda |\mathcal{D})& =\sum _{i\in I_0\cup I_1\cup I_2}\ln f_{X_i,X_{i+1}}(x_i,x_{i+1})-\sum _{i=2}^n\ln f_{X_i}(x_i)\\ & =(n_1+n_2+1)\ln \alpha +(n_1+n_2+1)\ln \lambda \\ & +(\alpha -1)(\ln x_1+\sum _{i\in I_1\cup I_2}\ln x_{i+1})-\lambda g_1(\alpha |\mathcal{D})\end{array}$$ (17)

where

$$g_1(\alpha |\mathcal{D})=\sum _{i\in I_1}(x_i^{\alpha }+2x_{i+1}^{\alpha })+\sum _{i\in I_2}(2x_i^{\alpha }+x_{i+1}^{\alpha })+3\sum _{i\in I_0}{x}_i^{\alpha }-2\sum _{i=2}^{n-1}{x}_i^{\alpha }.$$

It is immediate that for any α, $g_1(\alpha |\mathcal{D})>0$. Hence, for a given α, the MLE of λ, say $\hat{\lambda }(\alpha )$ can be obtained as

$$\hat{\lambda }(\alpha )=\frac{n_1+n_2+1}{g_1(\alpha |\mathcal{D})},$$ (18)

and the MLE of α, say $\hat{\alpha }$ can be obtained by maximizing

$$\begin{array}{rl}h(\alpha )& =(n_1+n_2+1)\ln \alpha +(n_1+n_2+1)(\ln (n_1+n_2+1)-\ln g(\alpha |\mathcal{D}))\\ & +\alpha (\ln x_1+\sum _{i\in I_1\cup I_2}\ln x_{i+1}).\end{array}$$ (19)

Once, $\hat{\alpha }$ is obtained, then the MLE of λ, say $\hat{\lambda }$ can be obtained as $\hat{\lambda }(\hat{\alpha })$. Due to the complicated nature of $h(\alpha )$ it is difficult to prove that it is a unimodal function. But in our data analysis, it is observed that $h(\alpha )$ is a unimodal function, and it will be explained later. In the case of exponential process, the MLE of λ can be obtained as

$$\hat{\lambda }=\frac{n_1+n_2+1}{g_1(1|\mathcal{D})}.$$ (20)

Case 2: ${\lambda }_0\ne {\lambda }_1$

In this section, we consider the case when ${\lambda }_0$ and ${\lambda }_1$ are arbitrary. We use the following notations

$$\begin{array}{rl}{I}_1(\beta )& =\{i:i\in I,\beta x_i<x_{i+1}\}\\ I_2(\beta )& =\{i:i\in I,\beta x_i>x_{i+1}\}\\ I_0(\beta )& =\{i:i\in I,\beta x_i=x_{i+1}\},\end{array}$$

and $n_0(\beta )=|I_0(\beta )|$, $n_1(\beta )=|I_1(\beta )|$ and $n_2(\beta )=|I_2(\beta )|$. Here, β is same as defined before. Based on the data vector $\mathcal{D}$, the log-likelihood function of ${\lambda }_0$, ${\lambda }_1$ and α becomes

$$\begin{array}{rl}l({\lambda }_0,{\lambda }_1,\alpha |\mathcal{D})& =(n_1(\beta )+n_2(\beta )+1)\ln \alpha +n_1(\beta )\ln {\lambda }_1+(n_2(\beta )+n_0(\beta ))\ln {\lambda }_0\\ & +(n_1(\beta )+n_2(\beta )+2-n)\ln ({\lambda }_0+{\lambda }_1)\\ & +(\alpha -1)\{\ln x_1+\sum _{i\in I_1(\beta )\cup I_2(\beta )}\ln x_{i+1}\}\\ & -{\lambda }_1\sum _{i\in I_1(\beta )}{x}_i^{\alpha }-({\lambda }_0+{\lambda }_1)\sum _{i\in I_2(\beta )}{x}_i^{\alpha }-\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_1}\sum _{i{\in }_0(\beta )}{x}_i^{\alpha }\\ & -({\lambda }_0+{\lambda }_1)\sum _{i\in I_1(\beta )}{x}_{i+1}^{\alpha }-{\lambda }_0\sum _{i\in I_2(\beta )}{x}_{i+1}^{\alpha }\\ & -n_0(\beta )\ln \beta +({\lambda }_0+{\lambda }_1)\sum _{i=2}^{n-1}{x}_i^{\alpha }.\end{array}$$ (21)

It is not trivial to maximize (21) directly. Hence, we use the following re-parameterization. We use the following transformed parameters, $(\gamma ,{\lambda }_1,\alpha )$, where $\gamma =\frac{{\lambda }_0}{{\lambda }_1}$ and based on the transformed parameters, the log-likelihood function can be written as

$$\begin{array}{rl}l(\gamma ,{\lambda }_1,\alpha )& =(n_1(\beta )+n_2(\beta )+1)(\ln {\lambda }_1+\ln \alpha )\\ & -{\lambda }_1{g}_2(\alpha ,\gamma |\mathcal{D})-(n_0(\beta )-1)\ln (1+\gamma )\\ & +((n_0(\beta )-\frac{1}{\alpha })+n_2(\beta ))\ln (\gamma )+(\alpha -1)h_2(\mathcal{D}),\end{array}$$ (22)

where

$$\begin{array}{rl}{g}_2(\alpha ,\gamma |\mathcal{D})& =\sum _{i\in I_1(\beta )}{x}_i^{\alpha }+(1+\gamma )(\sum _{i\in I_1(\beta )}{x}_{i+1}^{\alpha }+\sum _{i\in I_2(\beta )}{x}_i^{\alpha })+\gamma \sum _{i\in I_2(\beta )}{x}_{i+1}^{\alpha }\\ & +({\gamma }^2+\gamma +1)\sum _{i\in I_0(\beta )}{x}_i^{\alpha }-(1+\gamma )\sum _{i=2}^{n-1}{x}_i^{\alpha }\\ h_2(\mathcal{D})& =\ln x_1+\sum _{i\in I_1(\beta )\cup I_2(\beta )}\ln x_{i+1}.\end{array}$$

We propose to use the profile likelihood method to maximize (22). For fixed γ and α (β is also fixed in that case), first, we maximize (22) with respect to ${\lambda }_1$, say ${\hat{\lambda }}_1(\gamma ,\alpha )$, and it can be obtained in explicit form as

$${\hat{\lambda }}_1(\gamma ,\alpha )=\frac{n_1(\beta )+n_2(\beta )+1}{g_2(\alpha ,\gamma |\mathcal{D})}.$$

The MLEs of γ and α, say $\hat{\gamma }$ and $\hat{\alpha }$, respectively, can be obtained by maximizing $l(\gamma ,{\hat{\lambda }}_1(\gamma ,\alpha ),\alpha )$. Finally, the MLE of ${\lambda }_1$ can be obtained as ${\hat{\lambda }}_1(\hat{\gamma },\hat{\alpha })$. We will denote this as ${\hat{\lambda }}_1$. Due to complicated nature of the function $g_2(\alpha ,\gamma |\mathcal{D})$, it is difficult to prove that it has a unique maximum. But in our data analysis, it is observed from the contour plot that $g_2(\alpha ,\gamma |\mathcal{D})$ is a unimodal function. In both the cases we have suggested the parametric bootstrap method to construct confidence intervals of the unknown parameters. They can be very easily implemented in practice. In the case of exponential process, the MLE of ${\lambda }_1$ for a given γ can be obtained as

$${\hat{\lambda }}_1(\gamma )=\frac{n_1(\beta )+n_2(\beta )+1}{g_2(1,\gamma |\mathcal{D})},$$

and the MLE of γ can be obtained by maximizing $l(\gamma ,{\hat{\lambda }}_1(\gamma ),1)$. It is a one-dimensional optimization problem.

4. Goodness of fit

In this section, we provide a goodness of fit test so that whether a given data set comes from a Weibull process or not can be tested. Suppose $\{x_1,\dots ,x_n\}$ is a sample from a stationary sequence $\{X_1,\dots ,X_n\}$. We want to test the following null hypothesis

$$H_0:\{X_1,\dots ,X_n\}\sim \text{WEP}(\alpha ,{\lambda }_0,{\lambda }_1).$$

Let us use the following notations. We denote $X_{1:n}<\dots <X_{n:n}$ as the ordered $\{X_1,\dots ,X_n\}$, similarly, $x_{1:n}<\dots <x_{n:n}$ as the ordered $\{x_1,\dots ,x_n\}$, and $a_1=E_{H_0}(X_{1:n}),\dots ,a_n=E_{H_0}(X_{n:n})$ as their ordered expected values under $H_0$. Here, $a_1,\dots ,a_n$ depend on $\alpha ,{\lambda }_0,{\lambda }_1$, but we do not make it explicit. We use the following statistic for goodness of fit test.

$$W_n=\underset{1\le i\le n}{max}|X_{i:n}-a_i|.$$

It is expected that if $H_0$ is true, then $W_n$ should be small. Hence, we use the following test criterion for a given level of significance $0<\beta <1$

$$\text{Reject}{H}_0\mathrm{if}{W}_n>c_n(\beta ),$$

where $c(\beta )$ is such that

$$P_{H_0}(W_n>c_n(\beta )=\beta .$$

Note that $c_n(\beta )$ also depends on $\alpha ,{\lambda }_0,{\lambda }_1$, but we do not make it explicit for brevity. It is difficult to obtain $c_n(\beta )$ theoretically even for large n. Hence, we propose to use the parametric bootstrap technique to approximate $c_n(\beta )$ from a given observed sample $\{x_1,\dots ,x_n\}$

Hence, if $w_n=\underset{1\le i\le n}{max}|x_{i:n}-{\hat{a}}_i|>{\hat{c}}_n(\beta )$, then we reject the null hypothesis with β% level of significance, otherwise we accept the null hypothesis.

5. Data analysis

In this section we have analyzed three data sets; two synthetic data sets and one real gold price data set of the Indian market for two months. The main idea of these data analyses is to see how the proposed MLEs work in practice and also how the proposed model works in real life.

5.1. Synthetic data set 1:

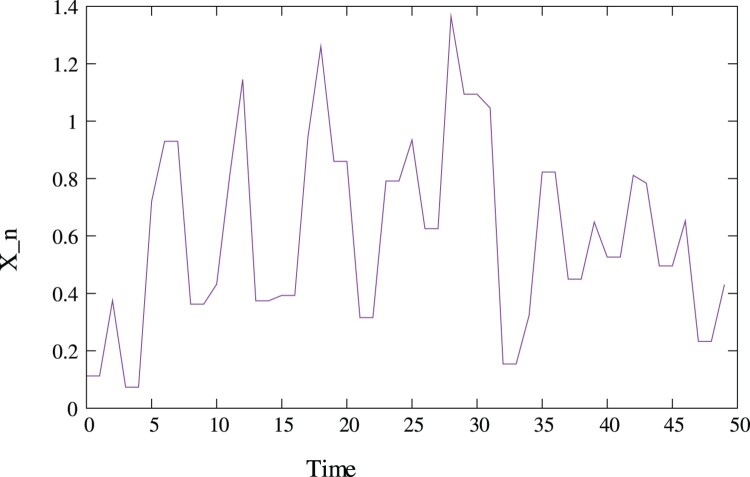
In this section, we analyze one synthetic data set, and it has been generated using the following model specification: α = 2.0, ${\lambda }_0={\lambda }_1=1.0$, n = 50. The data set (Data Set 1) has been presented in Figure 1.

Figure 1.

Synthetic data set with α = 2.0, ${\lambda }_0={\lambda }_1=1$.

In this case it is observed $n_0$ = 17, $n_1$ = 18 and $n_2$ = 14. We would like to compute the MLEs of the unknown parameters based on the assumption ${\lambda }_0={\lambda }_1=\lambda$. It involves solving a one-dimensional optimization problem. The profile log-likelihood function of α has been presented in Figure 2.

Figure 2.

The profile log-likelihood of the synthetic data set.

It is a unimodal function. Based on the profile maximization we obtain the MLEs of α and λ as $\hat{\alpha }$ = 1.912 and $\hat{\lambda }$ = 1.068. The associate 95% confidence intervals are (1.714, 2.106) and (0.878, 1.245), respectively.

5.2. Synthetic data set 2:

In this section, we analyze one synthetic data set, and it has been generated using the following model specification: α = 3.0, ${\lambda }_0$ = 0.15, ${\lambda }_1$ = 0.04 and n = 75. The data set (Data Set 2) has been presented in Figure 3.

Figure 3.

Synthetic data set with α = 3.0, ${\lambda }_0$ = 0.15 and ${\lambda }_1$ = 0.04.

Now we would like to compute the MLEs of the unknown parameters. We have adopted the two-dimensional grid search method to compute the MLEs of the unknown parameters. The MLEs of α, ${\lambda }_0$ and ${\lambda }_1$ become $\hat{\alpha }$ = 3.344, ${\hat{\lambda }}_0$ = 0.154 and ${\hat{\lambda }}_1$ = 0.029. The associated 95% bootstrap confidence intervals become (2.876, 3.954), (0.137, 0.173) and (0.019, 0.047), respectively.

5.3. Gold price data

In this section, we present the analyses of the gold price data in India for two months period from 1 December 2020 to 31 January 2021. The data represents the price of one gram of gold in Indian rupees. It is presented in Figure 4. In this case n = 62, the minimum, maximum and median values are 4280, 4580 and 4355, respectively. There are 29, 22 and 10 cases, so that $\{x_i<x_{i+1}\}$, $\{x_i>x_{i+1}\}$ and $\{x_i=x_{i+1}\}$, respectively. We have performed the run test on the entire data set $\{x_1,\dots ,x_{62}\}$, there are 28 runs, and the associated p value is less than 0.001. Hence, we reject the null hypothesis that they are independently distributed.

Figure 4.

Gold price data in India (rupees/gram) from 1 December 2020 to 31 January 2021.

We have plotted the autocorrelation function (ACF) and the partial autocorrelation (PACF) of the gold price data in Figures 5 and 6, respectively. It is clear from the ACF and PACF that although $x_i$ and $x_{i+k}$ are correlated, they are uncorrelated given $x_{i+1},\dots ,x_{i+k-1}$, for $k=1,2,\dots$.

Figure 5.

Autocorrelation function of the gold price data.

Figure 6.

Partial autocorrelation function of the gold price data.

We have performed run tests on two lag-1 series. The number of runs are 16 and 17, respectively. The associated p values are 0.07 and 0.18, respectively. We have performed run tests on three lag-2 series also. The number of runs are 12, 12 and 11, respectively. The associated p values are 0.56, 0.56, 0.25, respectively. Hence, based on the p values we cannot reject the null hypothesis that lag-2 observations are independently distributed. We have fitted Weibull distribution to all the three lag-2 series, the Kolmogorov–Smirnov distances and the associated p values reported in brackets are 0.1453 (0.7920), 0.2163 (0.3066) and 0.2227 (0.2743). Based on the p values we cannot reject the null hypothesis that lag-2 observations are from i.i.d. Weibull distribution.

Now we would like to compute the MLEs of the unknown parameters under the assumption ${\lambda }_1={\lambda }_2=\lambda$. It may be mentioned that in this case reasonable estimates of α and λ can be obtained in explicit forms without solving any optimization. In case of a Weibull distribution, the approximate MLEs of the unknown parameters can be obtained in explicit forms by expanding the log-likelihood function using the first-order Taylor series expansion, see for example Kundu and Gupta [9]. Based on this approach we can obtain estimates of α and λ from the odd sequence as well as from the even sequence of the data. By taking the averages of these two estimates, we obtain estimates of α and λ as 2.9878 and 0.1154, respectively.

Now we would like to obtain the MLEs of α and λ by maximizing the log-likelihood function. The profile log-likelihood function of α has been plotted in Figure 7. By maximizing the profile log-likelihood function, we obtain the MLE of α as 2.6640, the MLE of λ as 0.0729 and the associated log-likelihood value becomes −116.9681. Based on parametric bootstrapping the associated 95% confidence intervals of α and λ are (2.1375, 3.1231) and (0.0548, 0.0976), respectively.

Figure 7.

The profile log-likelihood function of α.

Further, we have calculated the MLEs of the unknown parameters when ${\lambda }_0\ne {\lambda }_1$. We have computed the MLEs of the unknown parameters by maximizing the profile log-likelihood of γ and α, i.e. $l(\gamma ,{\hat{\lambda }}_1(\gamma ,\alpha ),\alpha )$, with respect to γ and α. It is being performed by using the grid search method, and the MLEs are as follows: $\hat{\alpha }$ = 3.2238, ${\hat{\lambda }}_0$ = 0.0917, ${\hat{\lambda }}_1$ = 0.0192 and the corresponding log-likelihood value becomes −115.9317. The associated 95% confidence intervals of α, ${\lambda }_0$ and ${\lambda }_1$ become (2.6213, 3.8231), (0.0529, 0.1412), (0.0123, 0.0204), respectively.

It is clear that based on the BIC model selection criterion we prefer the model WIP( $\alpha ,\lambda ,\lambda$) than WIP $(\alpha ,{\lambda }_0,{\lambda }_1)$. Now we would like to see whether both the models fit the data or not. We have used the bootstrap method proposed in Section 4 with B = 1000. The histogram of the generated $\{w^b:1\le b\le 1000\}$ when ${\lambda }_0={\lambda }_1=\lambda$ and when ${\lambda }_0\ne {\lambda }_1$ are provided in Figures 8 and 9, respectively.

Figure 8.

Histogram of the generated test statistics when ${\lambda }_0={\lambda }_1$.

Figure 9.

Histogram of the generated test statistics when ${\lambda }_0\ne {\lambda }_1$.

The test statistic for the model WIP( $\alpha ,\lambda ,\lambda$) is 0.1685, and the associated p-value is greater than 0.90. It seems it provides a good fit for the data set. The test statistic for the model WIP( $\alpha ,{\lambda }_0,{\lambda }_1$) is 0.6291, and the associated p value is less than 0.05. Hence, it does not provide a good fit for the data set.

6. Conclusions

In this paper, we have proposed a new discrete-time and continuous state-space stochastic process based on the Weibull distributions. The distinct feature of the proposed process is that there is a positive probability that $X_n=X_{n+1}$, for some n. Hence, this model can be used quite effectively when there are ties in the two consecutive time points. We have studied different properties of the proposed process, and also provided the inference procedures of the unknown parameters.

Note that the proposed stochastic process is a lag-1 process, but it can be easily extended to lag-q process as follows: Suppose $U_0,U_1,U_2,\dots$ are independently and identically distributed (i.i.d.) uniform $U(0,1)$ random variables, and $\alpha >0,{\lambda }_0>0,{\lambda }_1,\dots ,{\lambda }_q>0$. Then

$$X_n=min\{{[-\frac{1}{{\lambda }_0}\ln U_n]}^{\frac{1}{\alpha }},\dots ,{[-\frac{1}{{\lambda }_q}\ln U_{n-q}]}^{\frac{1}{\alpha }}\}$$

is a lag-q stationary Weibull process. It can be easily checked that there is a positive probability that $X_n=X_{n+1}=\dots =X_{n+k}$, for some n, and for $k=1,\dots ,q$. It also has a convenient copula structure. It will be interesting to develop different properties and classical inferences of this process. More work is needed in this direction.

Appendices.

Appendix 1. Proofs

Proof Proof of Theorem 2.4 —

Note that p and $S_a(x,y)$ can be obtained from $S_{n,n+1}(x,y)$ as follows:

$$p={\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{\partial }}^2{S}_{n,n+1}(x,y)}{\mathrm{\partial }x\mathrm{\partial }y}\mathrm{d}x\mathrm{d}y,$$

and

$$p{S}_a(x,y)={\int }_y^{\mathrm{\infty }}{\int }_x^{\mathrm{\infty }}\frac{{\mathrm{\partial }}^2{S}_{n,n+1}(u,v)}{\mathrm{\partial }u\mathrm{\partial }v}\mathrm{d}u\mathrm{d}v.$$

Now, from

$$\frac{{\mathrm{\partial }}^2{S}_{n,n+1}(x,y)}{\mathrm{\partial }x\mathrm{\partial }y}=\{\begin{array}{ll}{\displaystyle f_1(x,y)}& \mathrm{if}(x,y)\in S_1\\ {\displaystyle f_2(x,y)}& \mathrm{if}(x,y)\in S_2,\end{array}$$

where

$$\begin{array}{rl}{f}_1(x,y)& =f_{WE}(x;\alpha ,{\lambda }_1)f_{WE}(y;\alpha ,{\lambda }_0+{\lambda }_1)\\ f_2(x,y)& =f_{WE}(x;\alpha ,{\lambda }_0+{\lambda }_1)f_{WE}(y;\alpha ,{\lambda }_0).\end{array}$$

Since

$$\begin{array}{rl}{\int }_0^{\mathrm{\infty }}{\int }_{\beta x}^{\mathrm{\infty }}{f}_1(x,y)\mathrm{d}y\mathrm{d}x& =\frac{{\lambda }_1^2}{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}\text{and}{\int }_0^{\mathrm{\infty }}{\int }_{y/\beta }^{\mathrm{\infty }}{f}_2(x,y)\mathrm{d}x\mathrm{d}y=\frac{{\lambda }_0^2}{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1},\\ p& =\frac{{\lambda }_0^2+{\lambda }_1^2}{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}.\end{array}$$

Using this p, $S_a(x,y)$ can be obtained by simple integration, and after that $S_s(x,y)$ can be obtained by subtraction.

Alternatively, a simple probabilistic argument also can be given as follows. Suppose A is the following event

$$A=\{[-\frac{1}{{\lambda }_0}\ln U_n]<[-\frac{1}{{\lambda }_1}\ln U_{n-1}]\}\cap \{[-\frac{1}{{\lambda }_1}\ln U_n]<[-\frac{1}{{\lambda }_0}\ln U_{n+1}]\},$$

then

$$P(A)=P(U_n>U_{n-1}^{\frac{{\lambda }_0}{{\lambda }_1}},U_n>U_{n+1}^{\frac{{\lambda }_1}{{\lambda }_0}})={\int }_0^1{u}^{\frac{{\lambda }_0}{{\lambda }_1}+\frac{{\lambda }_1}{{\lambda }_0}}\mathrm{d}u=\frac{{\lambda }_0{\lambda }_1}{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}=1-p.$$

Moreover,

$$P(X_n>x,X_{n+1}>y)=P(X_n>x,X_{n+1}>y|A)P(A)+P(X_n>x,X_{n+1}>y|A^{\prime })P(A^{\prime }),$$

and

$$P(X_n>x,X_{n+1}>y|A)=P(U_n<{\mathrm{e}}^{-{\lambda }_0{x}^{\alpha }},U_n<{\mathrm{e}}^{-{\lambda }_1{y}^{\alpha }})=g(x,y).$$

The rest can be obtained by subtraction.

Proof Proof of Theorem 2.5 —

We need to show that for all $0<x,y<\mathrm{\infty }$,

$$S_{n,n+1}(x,y)=\int {\int }_{B_1}{f}_1(u,v)\mathrm{d}u\mathrm{d}v+\int {\int }_{B_2}{f}_2(u,v)\mathrm{d}u\mathrm{d}v+{\int }_{h(x,y)}^{\mathrm{\infty }}{f}_0(t)|{\gamma }^{\prime }(t)|\mathrm{d}t,$$

here for $R(x,y)=\{(u,v);x\le u<\mathrm{\infty },y\le v<\mathrm{\infty }\}$, $B_1=R(x,y)\cap S_1$, $B_2=R(x,y)\cap S_2$, and $h(x,y)=max\{x,\frac{y}{\beta }\}$. It has already been shown in Theorem 2.4 that

$${\iint }_{B_1}{f}_1(u,v)\mathrm{d}u\mathrm{d}v+\int {\int }_{B_2}{f}_2(u,v)\mathrm{d}u\mathrm{d}v=p{S}_a(x,y),$$

hence, the result is proved if we can show

$${\int }_{h(x,y)}^{\mathrm{\infty }}{f}_0(t)|{\gamma }^{\prime }(t)|\mathrm{d}t=(1-p)S_s(x,y).$$

Since, $|{\gamma }^{\prime }(t)|=\beta$ and $(1-p)=\frac{{\lambda }_0{\lambda }_1}{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}$,

$$\begin{array}{rl}{\int }_{h(x,y)}^{\mathrm{\infty }}{f}_0(t)|{\gamma }^{\prime }(t)|\mathrm{d}t& ={\int }_{h(x,y)}\alpha {\lambda }_0{t}^{\alpha -1}{\mathrm{e}}^{-\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_1}{t}^{\alpha }}\mathrm{d}t=(1-p){\int }_{v(x,y)}{\mathrm{e}}^{-u}\mathrm{d}u,\end{array}$$

where $v(x,y)=max\{\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_1}{x}^{\alpha },\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_0}{y}^{\alpha }\}$. Let us remember,

$$S_s(x,y)=\{\begin{array}{ll}{\displaystyle {\mathrm{e}}^{-\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_0}{y}^{\alpha }}}& \mathrm{if}y>\beta x\\ {\displaystyle {\mathrm{e}}^{-\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_1}{x}^{\alpha }}}& \mathrm{if}y<\beta x.\end{array}$$

Hence, the result follows

Appendix 2. Autocovariance and autocorrelation functions

In this section, we provide all the expressions of the autocorrelation function of the GE process mainly for completeness purposes. First, we will calculate $E(X_{n+1}{X}_n)$. If $I_A$ denotes the indicator function on the set A, then

$$\begin{array}{rl}E(X_{n+1}{X}_n)& =E(X_{n+1}{X}_n\cdot I_{\{\beta X_n<X_{n+1}\}})+E(X_{n+1}{X}_n\cdot I_{\{\beta X_n>X_{n+1}\}})\\ & +E(X_{n+1}{X}_n\cdot I_{\{\beta X_n=X_{n+1}\}})\\ & =E_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n<X_{n+1}\}}|X_n)\\ & +E_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n>X_{n+1}\}}|X_n)\\ & +E_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n=X_{n+1}\}}|X_n).\end{array}$$

Now

$$\begin{array}{rl}{E}_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n=X_{n+1}\}}|X_n)& =\alpha \beta {\lambda }_0{\int }_0^{\mathrm{\infty }}{x}^{\alpha +1}{\mathrm{e}}^{-\frac{{\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1}{{\lambda }_1}{x}^{\alpha }}\mathrm{d}x\\ & =\mathrm{\Gamma }(\frac{2}{\alpha }+1)\frac{({\lambda }_0{\lambda }_1{)}^{1+\frac{1}{\alpha }}}{({\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1{)}^{\frac{2}{\alpha }+1}}\end{array}$$

If we denote $\mathrm{\Gamma }(x,a)={\int }_x^{\mathrm{\infty }}{t}^{a-1}{\mathrm{e}}^{-t}\mathrm{d}t$ and $\gamma (x,a)={\int }_0^x{t}^{a-1}{\mathrm{e}}^{-t}\mathrm{d}t$ as incomplete gamma functions, then

$$\begin{array}{rl}& E_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n<X_{n+1}\}}|X_n)\\ & ={\alpha }^2{\lambda }_1{\int }_0^{\mathrm{\infty }}{x}^{\alpha }{\mathrm{e}}^{-{\lambda }_1{x}^{\alpha }}\left\{{\int }_{\beta x}^{\mathrm{\infty }}{y}^{\alpha }{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)y^{\alpha }}\mathrm{d}y\right\}\mathrm{d}x\\ & =\frac{\alpha {\lambda }_1}{({\lambda }_0+{\lambda }_1{)}^{1/\alpha }}{\int }_0^{\mathrm{\infty }}{x}^{\alpha }{\mathrm{e}}^{-{\lambda }_1{x}^{\alpha }}\mathrm{\Gamma }(\frac{{\lambda }_0({\lambda }_0+{\lambda }_1)x^{\alpha }}{{\lambda }_1},\frac{1}{\alpha }+1)\mathrm{d}x.\\ & E_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n>X_{n+1}\}}|X_n)\\ & ={\alpha }^2{\lambda }_0({\lambda }_0+{\lambda }_1){\int }_0^{\mathrm{\infty }}{x}^{\alpha }{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)x^{\alpha }}\left\{{\int }_0^{\beta x}{y}^{\alpha }{\mathrm{e}}^{-{\lambda }_0{y}^{\alpha }}\mathrm{d}y\right\}\mathrm{d}x\\ & =\frac{\alpha ({\lambda }_0+{\lambda }_1)}{{\lambda }_0^{1/\alpha }}{\int }_0^{\mathrm{\infty }}{x}^{\alpha }{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)x^{\alpha }}\gamma (\frac{{\lambda }_0^2{x}^{\alpha }}{{\lambda }_1},\frac{1}{\alpha }+1)\mathrm{d}x.\end{array}$$

We have already indicated the mean and variance of a Weibull random variable in (2). Now based on the above expressions, the autocovariance and autocorrelation functions can be obtained. In the case of exponential process i.e. when α = 1, the above expressions can be obtained in explicit forms. For example

$$\begin{array}{rl}& E_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n=X_{n+1}\}}|X_n)=\frac{2({\lambda }_0{\lambda }_1{)}^2}{({\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1{)}^3}\\ & E_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n<X_{n+1}\}}|X_n)\\ & =\frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}{\int }_0^{\mathrm{\infty }}x{\mathrm{e}}^{-{\lambda }_{1}x}({\mathrm{e}}^{-\frac{{\lambda }_0({\lambda }_0+{\lambda }_1)}{{\lambda }_1}x}+\frac{{\lambda }_0({\lambda }_0+{\lambda }_1)}{{\lambda }_1}x{\mathrm{e}}^{-\frac{{\lambda }_0({\lambda }_0+{\lambda }_1)}{{\lambda }_1}x})\mathrm{d}x\\ & =\frac{{\lambda }_1^3}{({\lambda }_0+{\lambda }_1)({\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1{)}^2}+\frac{2{\lambda }_0{\lambda }_1^3}{({\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1{)}^3}\\ & E_{X_n}(X_n{E}_{\{X_{n+1}|X_n\}}(X_{n+1}\cdot I_{\{\beta X_n>X_{n+1}\}}|X_n)\\ & =\frac{{\lambda }_0+{\lambda }_1}{{\lambda }_0}{\int }_0^{\mathrm{\infty }}x{\mathrm{e}}^{-({\lambda }_0+{\lambda }_1)x}(1-{\mathrm{e}}^{-\frac{{\lambda }_0^2}{{\lambda }_1}x}-\frac{{\lambda }_0^2}{{\lambda }_1}x{\mathrm{e}}^{-\frac{{\lambda }_0^2}{{\lambda }_1}x})\mathrm{d}x\\ & =\frac{1}{{\lambda }_0({\lambda }_0+{\lambda }_1)}-\frac{{\lambda }_1^2({\lambda }_0+{\lambda }_1)}{{\lambda }_0({\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1{)}^2}-\frac{2{\lambda }_0{\lambda }_1^2({\lambda }_0+{\lambda }_1)}{({\lambda }_0^2+{\lambda }_1^2+{\lambda }_0{\lambda }_1{)}^3}.\end{array}$$

Since,

$$E(X_n)=E(X_{n+1})=\frac{1}{{\lambda }_0+\lambda }\text{and}V(X_n)=V(X_{n+1})=\frac{1}{({\lambda }_0+\lambda {)}^2},$$

the autocovariance and autocorrelation can be obtained in explicit forms.

Disclosure statement

No potential conflict of interest was reported by the author(s).