Diamond rotors

Abstract

The resolution of magic angle spinning (MAS) nuclear magnetic resonance (NMR) spectra remains bounded by the spinning frequency, which is limited by the material strength of MAS rotors. Since diamond is capable of withstanding 1.5–2.5x greater MAS frequencies, compared to state-of-the art zirconia, we fabricated rotors from single crystal diamond. When combined with bearings optimized for spinning with helium gas, diamond rotors could achieve the highest MAS frequencies to date. Furthermore, the excellent microwave transmission properties and thermal conductivity of diamond could improve sensitivity enhancements in dynamic nuclear polarization (DNP) experiments. The fabrication protocol we report involves novel laser micromachining and produced rotors that presently spin at ω_r/2π = 111.000 ± 0.004 kHz, with stable spinning up to 124 kHz, using N₂ gas as the driving fluid. We present the first proton-detected ¹³C/¹⁵N MAS spectra recorded using diamond rotors, a critical step towards studying currently inaccessible ex-vivo protein samples with MAS NMR. Previously, the high aspect ratio of MAS rotors (~10:1) precluded fabrication of MAS rotors from diamond.

1. Introduction

Magic angle spinning (MAS) nuclear magnetic resonance (NMR) is one of the few spectroscopic techniques that can determine molecular structures at atomic resolution while probing molecular dynamics in insoluble, non-crystalline biomolecules and materials [1,2]. Accordingly, over the past two decades, MAS, together with dipole recoupling experiments [3], has evolved into a critical tool for structural biology research in systems such as amyloid fibrils [4-8] membrane proteins [9-11], macromolecular viral assemblies [12,13] and in a variety of materials science problems [14-16]. Despite these successful studies, many of the most pressing and complex biomedical and materials science challenges remain inaccessible due to limited resolution, inherently poor sensitivity, and the requirements for copious isotopically enriched samples.

To address these limitations in solids, several decades of development have led to the advent of sophisticated MAS stators and rotors, and a progressively miniaturized series of yttria-stabilized zirconia (YSZ) cylindrical and more recently spherical rotors [17-21]. While MAS rotors have been fabricated using a variety of materials — silicon nitride, sapphire, Delrin^® and MACOR^® — only YSZ has been employed to date in the fabrication of commercially available rotors less than 3 mm in outer diameter. With commercially available 0.7 mm YSZ rotors and N₂ gas as the driving fluid, MAS frequencies up to 111 kHz are routinely achieved. More recently prototype 0.4 mm and 0.5 mm YSZ rotors were reported to spin at ω_r/2π = 150 to 200 kHz MAS [22,23], again using N₂. At present the spinning frequencies are limited by the speed of sound in N₂. However, the improved resolution and sensitivity from spinning frequencies >100 kHz have enabled important insights into the study of samples ranging from amyloid fibrils to membrane proteins [24-26]. Despite these significant advances, the achievable proton resolution under MAS restricts ubiquitous adoption of proton detection in the solid-state, as is performed in solution NMR. We note in some samples, the inhomogeneous linewidth due to sample specific parameters may dominate over the homogenous linewidth and will not be modulated by faster MAS frequencies. Despite this, in many fully protonated protein samples, it has been shown that the homogeneous linewidth due to the dense dipolar coupled proton network dominates the observed linewidth and would benefit from increased MAS frequencies. Recognizing this limitation, several groups have calculated the theoretical MAS frequency required to yield solution like linewidths and coherence lifetimes in solids to be ~ 300 kHz and in many cases up to 1 MHz (18–60 × 10⁶ RPM) [27-29].

In addition to proton-detected MAS methods, dynamic nuclear polarization (DNP) can be used to enhance the sensitivity of solid-state NMR. DNP uses microwave irradiation to transfer the high spin polarization of electrons to nuclear spins at cryogenic temperatures (typically ~ 100 K), offering a theoretical maximum enhancement of ~ 660 relative to conventional NMR [30,31]. This has stimulated significant developments with gyrotron microwave sources and low temperature MAS probes that have enabled DNP on biomolecules in frozen solution with enhancements routinely yielding ~ 50–100 [32-34]. However, at the high magnetic fields (>16.4 T) required for improved spectral resolution, typical CW DNP mechanisms become less efficient. Consequently, the continued development of high field DNP methods is focused on improving (a) polarizing agent efficiency, (b) microwave coupling efficiency into the rotor, (c) the achievable sample temperature, with lower temperatures yielding higher enhancements, (d) instrumentation for time domain DNP experiments and (e) the achievable MAS frequency at 100 K [35-44].

The continued expansion of MAS NMR to the most biomedically relevant systems likely requires realizing spinning frequencies >300 kHz coupled with improved efficiency during DNP experiments. Current MAS NMR rotor technology has relied solely on decreasing the rotor diameter to achieve higher spinning frequencies, with a resulting decrease in sample volume up to the cube of the rotor radius. However, rotor diameters and associated spinning components are approaching fabrication limitations while the MAS frequency remains insufficient. Thus, without introducing new rotor materials used to fabricate MAS rotors, the required higher MAS frequencies are increasingly difficult to achieve.

The study of currently inaccessible ex-vivo protein samples using MAS NMR motivated our development of novel laser micromachining methods. These applications require the combination of high spinning frequencies, ω_r/2π > 100 kHz, with large sensitivity enhancements from DNP at high magnetic fields. In particular, it is critical to employ a new rotor material and associated fabrication methodology that will enable MAS in the 150–300 kHz regime. The desirable properties of the material should include high strength, high thermal conductivity, and low THz absorption material, and, as illustrated in Fig. 1 the ideal material to simultaneously satisfy these three criteria is single crystal diamond. Additional data relevant to this point is available in the Supporting Information, Figure S1. Diamond’s cubic crystal structure provides exceptionally high atomic bond strengths, making it one of the strongest materials available. However, the high strength of diamond also prohibits application of traditional mechanical drilling or abrasive grinding methods. While laser machining is utilized to fabricate diamond micro-structures, the required ~ 10:1 aspect ratio (referring to the ratio between the length and inner diameter of the rotor), μm tolerances and near zero internal taper of MAS rotors were thought to be unattainable using available laser machining strategies. As such, there were no commercially available methods of fabricating diamond rotors.

Fig. 1.

Advantages of diamond rotors. (A). The diamond mechanical failure region is estimated to be a factor of 1.5–2.5 times higher than that of conventional YSZ rotors. Over the range of required temperatures for DNP NMR, using diamond will allow for MAS frequency increase by taking advantage of helium gas’s high speed of sound. Speed of sound data for both helium and nitrogen gases as a function of temperature were obtained from Ref [45]. (B). The improved thermal conductivity of single crystal diamond relative to sapphire or zirconia offers rapid sample temperature equilibration and efficient heat dissipation induced during at high spinning frequencies and microwave irradiation under DNP. Thermal conductivity data obtained from Ref [46-48]. (C). THz field transmission measurement for diamond, sapphire (‘C-cut’ orientation), and zirconia.

Herein we describe a novel laser micromachining strategy using dual-sided axial ablation to fabricate diamond rotors with less than 0.05° of internal taper while maintaining micron tolerances. We quantify spinning stability at ω_r/2π = 111 kHz with a standard deviation in spinning frequency of less than 4 Hz (0.004%), further demonstrating the success of the machining strategy. Finally, we present the initial ¹H detected MAS NMR spectra obtained using diamond rotors. These results highlight the feasibility and potential dramatic change that continued development of such technology can bring to the field of solid-state NMR.

2. Experimental

2.1. Rotor fabrication

Rotors were fabricated using an Oxford Lasers (Didcot, Oxfordshire, UK) A-series laser micromachining system equipped with a Q-switched 532 nm diode-pumped Nd:YAG laser with a spot size of 13–14 μm. The pulse duration was ~ 20 ns at a repetition rate of 5 kHz. Single crystal high pressure high temperature (HPHT) type Ib diamond was purchased from Element6 (Didcot, Oxfordshire, UK) for ~ $20/mm³. All machining operations were aligned to the 100 (4 point) crystal axis to avoid the (111) diamond cleavage plane. A lab-fabricated precision lathe apparatus was used for all machining operations and relied upon a Thorlabs (Newton, NJ, USA) DDR100 direct drive rotary stage to achieve rotational frequency of 2.76 Hz (166 RPM) during both inner and outer diameter machining steps. The diamond was secured using a flexural clamp fabricated from 17–4 stainless steel and was mechanically flipped for a second axial machining step to reduce inner diameter taper. Alignment was maintained in this process through use of a fabricated Kelvin-style magnetic kinematic coupling system (Figure S2). Typical laser fluences employed ranged from 300 J/cm² to 770 J/cm². A complete description of the fabrication process is given in Figure S3. Following fabrication, the rotors were subjected to 24 h of heat treatment at 600 °C in air using a tabletop oven to remove the graphite and amorphous carbon film formed and deposited on the diamond during machining.

2.2. Rotor characterization

Immediately following machining, graphite coated machined surfaces were characterized using a Hitachi scanning electron microscope FlexSEM1000 (Tokyo, Japan). Inner diameter tapers were measured using a Nikon Metrology XT H 160 (Micro Computed-Tomography) scanner (Tring, UK) at 3 μm voxel resolution. CT reconstruction was performed using CT Pro3D XT 5.4 software (Nikon Metrology, Tring, UK) and visualized using VGStudio by Volume Graphics Inc. (Charlotte, NC, USA). Rotor inner and outer diameters were characterized using a Keyence (Osaka, Japan) TM-X5006 telecentric measurement system with ± 0.2 μm measurement positional accuracy. A detailed description of rotor measurements is given in Section S3.

2.3. Raman analysis

Single crystal HPHT diamond was analyzed without modification, in addition to machined samples pre- and post-heat treatment. Highly ordered pyrolytic graphite (HOPG) ZYB quality was purchased and used without modification from Ted Pella (Redding, CA, USA) as a graphite standard. Raman analysis was performed using a Renishaw Invia Reflex spectrometer equipped with a confocal microscope. Raman excitation was performed using a 532 nm laser. Raman shifts were calibrated against a silicon standard and data was processed using Renishaw’s WiRE^™ software.

2.4. THz transmission measurements

Terahertz transmission spectra were collected using a standard terahertz time-domain spectroscopy (THz-TDS)[49]. Broadband THz radiation was generated by optical rectification in a 1 mm thick ZnTe crystal using the 1 mJ, 100 fs output of an Astrella Ti: Sapphire regenerative amplifier (Coherent Inc, Santa Clara, CA USA) operating at a repetition rate of 1 kHz and with a center wavelength of 800 nm. The THz beam was focused onto the sample (beam waist ~ 2 mm) at normal incidence, and then collected and refocused onto a 2 mm thick ZnTe crystal for electro-optical detection using three paraboloid mirrors after sample transmission. Sample thicknesses were 1.93 mm, 1.17 mm, and 6.37 mm for zirconia, diamond, and sapphire, respectively. 10% of the amplified laser output was split off prior to THz generation, time-delayed, and recombined with the THz beam at the detection crystal. Time-domain traces of the THz electric field were obtained by time delaying the THz and 800 nm probe pulses with respect to each other in a stepwise fashion. In this process, the instantaneous THz electric field at each time-step is encoded onto the polarization state of the probe pulse, which is then read out using a typical balanced detection scheme. THz transmission spectra were then obtained by computing the fast Fourier transform of the time-domain THz traces collected with and without the sample in place. The refractive index, surface reflections, and absorption coefficient were used to compute the absorption and reflection coefficients, A and R (Figure S1). These were then used to compute the percent transmission for a 1 mm sample thickness of each material using the equation T = 1-A-R.

2.5. MAS stability testing

Diamond rotors were machined to accommodate Bruker BioSpin (Billerica, MA, USA) Vespel drive tips and end caps. For MAS stability tests, rotors were packed with potassium bromide powder (KBr) purchased from Millipore-Sigma (Burlington, MA). Spinning frequency control was achieved using dry N₂ spinning gas, a MAS 3 Controller (Bruker BioSpin, Billerica MA, USA), and a 0.7 mm test stand system (Bruker BioSpin, Billerica, MA USA) (Figure S9). The MAS frequency was recorded at 1 s intervals using a Rigol oscilloscope (Suzhou, China) DS1104Z oscilloscope and logged using a Python script. The spinning frequency data was analyzed using Matlab (Mathworks, Natick MA). A 0.7 mm YSZ rotor was used as a standard in MAS stability measurement and was purchased from Bruker BioSpin. 1.3 mm YSZ rotors used in failure testing were purchased from Bruker and O’Keefe Ceramics (Woodland Park, CO USA), packed with KBr, and fitted with end caps and drive tips which were purchased from Bruker BioSpin.

2.6. NMR spectroscopy

A diamond rotor was packed with a 1:1 mixture of (U-¹³C,¹⁵N)-N-Formyl-methionyl-leucyl-phenylalanine-OH ((U-¹³C,¹⁵N)-N-f-MLF-OH) previously packed into a larger MAS rotor and zirconia powder (Sigma Aldrich, St. Louis MO). All spectra were acquired at a static field of 18.8 T (800 MHz ¹H) with a three channel (HCN) 0.7 mm Bruker MAS probe. The sample was spun at ω_r/2π = 111 kHz using a MAS 3 controller. The 90° pulse durations were 1.875 μs, 3 μs, and 3 μs for ¹H, ¹³C, and ¹⁵N, respectively. Dipolar based CP-HSQC spectra were recorded using the pulse sequence previously described [50]. ¹H→¹³C forward cross polarization (CP) was achieved with a contact time of 2 ms while the ¹H RF-field amplitude was ramped from 142 kHz to 158 kHz and the carbon RF field was constant at 36 kHz. ¹³C→¹H reverse CP was achieved using a contact time of 1.2 ms while the proton RF field amplitude was ramped from 158 kHz to 142 kHz while the ¹³C RF amplitude was constant at 45 kHz. ¹H→¹⁵N forward CP was achieved with a contact time of 1.5 ms while the proton RF amplitude was ramped from 140 kHz to 156 kHz and the ¹⁵N RF amplitude was constant at 28 kHz. The ¹⁵N→¹H reverse CP was achieved with a 1.2 ms contact time during which the ¹H RF field was ramped from 156 kHz to 140 kHz while the ¹⁵N RF amplitude was constant at 40 kHz. During both CP-HSQC experiments, swept-low power TPPM at an RF field amplitude of 22.6 kHz was used for proton decoupling during t₁ and WALTZ-16 was applied to ¹³C or ¹⁵N at RF field strengths of 10 kHz [51,52]. Water suppression was achieved through the MIS-SISSIPPI pulse sequence without homospoil gradients [53], using a 23 kHz RF field and 200 ms pulse duration. Spectra were apodised using 60° shifted squared sine bells and zero filled to at least twice the number of points in the indirect dimension. Additional acquisition parameters are given in Table S2.

3. Results and discussion

To address current limits in MAS instrumentation, and thus applications of MAS NMR, we developed laser micromachining methods to fabricate diamond rotors. Prior to this work, it was predicted that the combined high aspect ratio, micron tolerances and near zero required internal taper angle could not be achieved in diamond. However, we demonstrated a dual-sided axial machining strategy that enabled fabrication of diamond rotors. During nanosecond laser machining of diamond, thermal energy is absorbed by imperfections in the diamond crystal lattice, resulting in a phase transformation from diamond to graphite. At radiation levels beyond the threshold fluence of diamond, graphite is largely vaporized and expelled from the inner diameter of the hole. However, during this process, the laser beam becomes partially attenuated by the formation of a plasma, effectively reducing the depth of hole that can be obtained in diamond. Fluences at least twenty-five times the ablation threshold for diamond combined with dual-sided axial machining allowed sufficient radiation incident to the diamond, enabling the fabrication of ~ 5 mm deep holes in diamond with ~ 0.5 mm diameters as illustrated in Fig. 2.

Fig. 2. Diamond rotors.

(A). CAD model of 0.7 mm rotor and associated dimensions. (B). Photograph of assembled diamond rotor including drive tip and end cap. (C). Isometric view of diamond rotor from a microCT scan. (D). Cross section view of a microCT scan of a diamond rotor.

To quantify the geometric dimensions and tolerances achieved during laser micromachining, we employed a variety of methods including SEM, microCT and optical telecentric measurement. The dimensions for several commercial zirconia rotors and diamond NMR rotors fabricated in-house are tabulated in the supporting information, (Table S1). Typical measured outer diameters and rotor-to-rotor tolerances are 695 ± 5 μm, as determined using a non-contact optical telecentric measurement system with a published accuracy of ± 0.2 μm. With this method, we were able to achieve typical internal tapers of less than ~ 0.05° over 4.6 mm, as determined by analysis of SEM data (Fig. 3) and verified by microCT (Fig. 2D). The resulting rotors produced using mechanical re-orientation (Figure S2) demonstrated an inner and outer diameter concentricity error of less than 13 μm for all rotors, as shown in the SEM measurements (Fig. 3).

Fig. 3. Scanning electron microscopy of diamond rotor.

(A). Diamond rotor side 1 with annotated wall thickness. (B). Diamond rotor side 2.

The total fabrication time per rotor, which is mostly automated, is currently ~ 6–10 h, with the potential for optimization to further reduce the fabrication time. The reproducibility of the fabrication scheme used to date is highly dependent on the structural integrity of the flexural clamping mechanism used to hold the rotor during fabrication, illustrated in the supplemental information, along with operator technique and careful alignment of the machining apparatus. These shortcomings can be further improved by changing the machining methodology to reduce the need for manual manipulation of partially machined rotors. Despite this, our current strategy for fabricating diamond rotors is uniquely suited to continued miniaturization of MAS components, whereas conventional ceramic drilling technologies are already approaching feasibility limitations. For further details on the machining process, we refer the reader to the supplementary information.

Raman spectra shown in Fig. 4 was used to confirm the laser ablation mechanism previously presented in the literature [54-57]. We confirmed the presence of the single, narrow resonance associated with single crystal diamond (Fig. 4A) in the starting, un-machined material at ~ 1332 cm⁻¹ (Fig. 4D), in accordance with literature values [58]. Following laser ablation (Fig. 4B), a resonance at ~ 1585 cm⁻¹ was observed, characteristic of the G band of graphite [59]. In the machined sample, we observed this band had broadened relative to a highly orientated pyrolytic graphite (HOPG) standard sample (Fig. 4E). Therefore, we conclude amorphous carbon species are formed as indicated by the broadening of both resonances in addition to graphite formation. Finally, we note the reduced intensity of the graphite signal relative to the diamond signal in the machined sample. This supports optical telecentric measurements taken before and after heat treatment indicating the layer of graphite formed is on the order of 1–2 μm thick.

Fig. 4. Raman analysis of diamond rotor fabrication.

(A, D). In the starting material only diamond is detected. (B). Photograph of machined diamond material without heat treatment; graphite layer is visually contrasted with unmachined yellow diamond. (C). After heat treatment the graphite is observed to be removed. (E). Raman spectroscopy of HOPG graphite Raman spectra (red) used as a standard sample used to confirm presence of graphite on machined sample (black). (F). Following 24-hour heat treatment, graphite is removed from the machined sample.

For use in DNP and conventional NMR applications, the electrically conductive graphite species must be entirely removed from the rotor prior to use in experiments. The surface graphite could prohibit efficient transmission of microwaves into the rotor for DNP and serve as a potential source of electrical arcing to the transmit and receive coil. To remove the accumulated graphite, a high temperature oxidative step was employed at 600 °C for 24 h [60,61]. Following heat treatment, the Raman analysis was repeated, and a signal from graphite or other sp² carbon species was absent (Fig. 4C and 4F). Overall, Raman spectroscopy confirmed the ablation mechanism and importantly verified the absence of graphite at the end of rotor processing.

All 0.7 mm rotors were packed with potassium bromide (ρ_KBr = 2.75g/cm³) and spun to 111 kHz manually using a test stand with MAS 3 controller supplied by Bruker. As illustrated in Fig. 5, the standard deviation in spinning stability over the course of one hour at 111 kHz was determined to be 3.13 Hz and 4.04 Hz for each of the two diamond rotors we tested (Fig. 5B, C, E, F). The standard deviation in spinning stability over one hour was also measured for a zirconia rotor at 111 kHz and was determined to be 4.43 Hz (Fig. 5A, D). We note here the spinning stability is impacted by both the rotor-bearing interaction, which is modulated by rotor mass imbalance, and the stability of the drive and bearing gas regulation. The measured stability of the MAS 3 controller used for these experiments was 2696 ± 2.14 mBar and 4112 ± 5.35 mBar, for bearing and drive gas, respectively. Importantly, using diamond rotors results in a decrease in the force exerted on the rotor by ~ 40%, afforded by the reduction in rotor density when using diamond (3.5 g/cm³) relative to YSZ (~6.0 g/cm³).

Fig. 5. MAS stability measurements.

Top Row shows time dependent traces of (A) YSZ rotor. (B). Diamond rotor 1. (C). Diamond rotor 2. Bottom row shows histogram plot at a mean spinning frequency of 111.001 kHz (D) YSZ rotor, standard deviation of 4.43 Hz (E). Diamond rotor 1, standard deviation of 3.13 Hz. (F). Diamond rotor 2, standard deviation of 4.04 Hz.

In Fig. 6 we show ¹H-detected ¹³C and ¹⁵N MAS NMR spectra of N-formyl-methionyl-leucyl-phenylalaninol (N-f-MLF-OH) recorded using a diamond rotor for a proof of concept set of experiments at ω_r/2π = 111 kHz. Likely due to the minor remaining concentricity errors discussed previously, the spin-up profile of the diamond rotors is non-linear (Figure S11); we attribute this behavior to excitation of translational and whirl resonance conditions between 2 and 20 kHz [62]. To reduce risk to the NMR probe while increasing ω_r/2π, the N-f-MLF-OH powder was mixed in a 1:1 ratio with YSZ powder, which reduced the effective concentricity error, lowering the translational and whirl resonance conditions. This improved the linearity of response to drive gas and ensured the NMR probe was not damaged during these initial experiments. However, the rotors are sufficiently concentric and balanced to achieve highly stable rotation at ω_r/2π > 111 kHz (6.6 × 10⁶ RPM) with lower density samples. The dipolar based (H)NH and (H)CH heteronuclear correlation experiments were recorded without electric arcing, confirming the absence of electrically conductive graphite. Additionally, the spectra obtained were free of any ¹³C background signal from the diamond rotor itself. Recall, the ¹³C occurs at natural abundance, and the ¹³C T_1n diamond is long. Of course, the use of cross polarization transfer steps insured excitation of only ¹⁵N or ¹³C adjacent to ¹H, preventing detection of ¹³C from the diamond rotor itself. The acquisition of proton-detected heteronuclear correlation spectra in Fig. 6 demonstrates the utility of diamond rotors for use in NMR and their compatibility with standard, commercially available instrumentation.

Fig. 6. ¹H detected spectra of U-¹⁵N,¹³C-N-f-MLF-OH recorded using a diamond rotor.

(A). (H)CH correlation spectrum. (B). (H)NH correlation spectrum.

Resolution in MAS NMR experiments remains limited by the accessible spinning frequency. To date, rotor outer diameters have been continuously decreased to access higher MAS frequencies using YSZ. Despite these efforts, the current maximum MAS frequency achievable is 200 kHz, only 20% of the upper bound of the MAS frequency theoretically thought to be necessary to achieve solution-like resolution in complex, solid state biomolecules. At present, the highest MAS frequencies can be achieved using 0.4 mm rotors, which approach the practical limit of conventional ceramic machining practices.

The maximum achievable MAS frequency is ultimately determined by three factors: (1) the speed of sound of the gas used in the air bearings and gas turbine, (2) the structural integrity of the rotor material used, and (3) the efficiency of the turbine and air bearings. Significant rotor turbulence and reduced drive efficiency is expected as the circumferential frequency of the rotor approaches the speed of sound for a given spinning gas [63]. The maximum MAS frequency of a rotating cylinder is given by the rotor’s circumferential frequency of ν/2πr, where v is speed of sound of the gas used and 2πr is the rotor outer diameter. For a 0.7 mm diameter rotor and nitrogen gas, the maximum circumferential frequency is 161 kHz or a surface velocity of 354 m/s. In practice, MAS rotors typically operate at a maximum ~ 80% of the speed of sound in N₂ or air (~125 kHz) due to frictional losses in the air bearings [63]. Using nitrogen gas, we achieved maximum MAS frequencies of 123 kHz, which has a corresponding surface speed of 264 m/s, or roughly 75% the speed of sound. 0.7 mm YSZ rotors are rated to 111 kHz, or 68% the speed of sound.

To exceed these frequencies, helium gas can in principle be used to access a ~ 3 times improvement in spinning frequency afforded by a ~ 3 times increase in the speed of sound of helium gas relative to nitrogen, (Fig. 1A) [45]. To date, helium has mainly been used in solid-state NMR to realize low temperature experiments for improved sensitivity under DNP, notably without observation of electrical arcing [17,64-69]. However, the use of helium to achieve higher spinning frequencies at room temperature has been restricted to use with large rotors due to challenges with the stability of current air bearing designs which are not sized for use with helium lubricant [20,70]. Recently, significant efforts in the optimization of air bearings for use with helium gas and 0.4 mm zirconia rotors resulted in a maximum spinning frequency of only 18 kHz, compared to 110 kHz in air [70]. The maximum MAS frequency we achieved with a 0.7 mm rotor and 100% helium gas was 80 kHz. When tested, the rotor stability was extremely poor and changes in drive or bearing pressures by less than 10–20 mbar resulted in fluctuations in the MAS frequency of several kHz or could lead to rotor crash. With a 70:30 volumetric mixture of helium: nitrogen gas, diamond rotors were spun to 124 kHz but could not be increased past this point (Figure S10). At 124 kHz the significant rotor instability led to a diamond rotor crash, however, the rotor was recovered intact and without damage. The same rotor was spun to ~ 123 kHz with nitrogen gas and did not display this instability, in agreement with past observations using helium gas. As shown in Figure S12, using He gas as the driving fluid, we found the initiation of MAS is nontrivial and generally unreproducible with 0.7 mm rotors. 1.3 mm YSZ rotors achieved 88–89 kHz using 100% helium gas when packed with KBr, however, this required considerable optimization of the bearing and drive pressures.

The non-trivial application of helium gas to rotors less than 1.3 mm in diameter is likely due to insufficient bearing stiffness when helium gas is used in bearings design for air or nitrogen. Thus, access to higher MAS frequencies using helium requires fabricating bearings designed for helium gas by varying both the radial air gap and nozzle diameter to increase radial bearing stiffness. Overall, our result of ω_r/2π = 124 kHz using a mixture of He and N₂ represents to our knowledge the highest MAS frequency achieved with helium. Prior to the fabrication of diamond rotors, the insufficient material strength of YSZ did not make the considerable investment into helium optimized bearings worthwhile. However, with the demonstration of diamond rotor technology and in-house diamond machining capabilities, helium optimized bearings have become a necessary and realistic research objective.

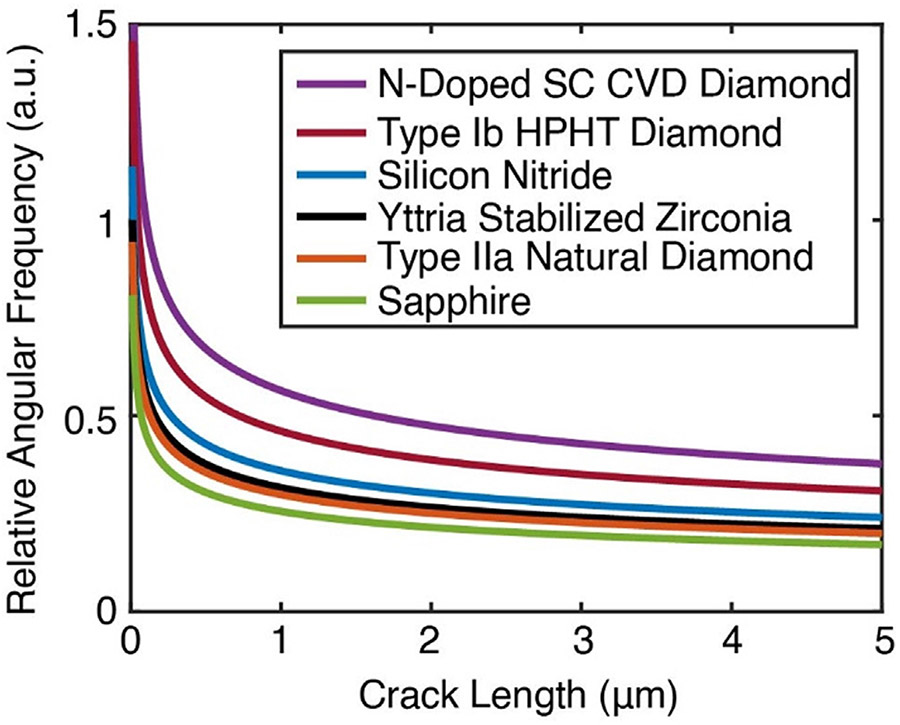
As the failure point of diamond rotors could not be obtained experimentally, we evaluated three models associated with rotor failure. Previous literature describing rotor failure is based on the tensile strength or the elastic modulus in determining hoop stress and bending mode limited frequencies, respectively [20,71,72]. In practice, failure of MAS rotors fabricated from brittle materials is more likely due to surface defects (flaws and cracks) serving as a stress concentration point from which failure is initiated [73-75]. These defects reduce the effective toughness of the material below its theoretical maximum with corresponding underperformance in MAS. In general, given comparable surface defect concentrations, a material with a higher fracture toughness resists crack propagation and performs more closely to its theoretical strength and toughness than a material with a low fracture toughness. The relative performance of MAS rotor materials is properly predicted using basic fracture mechanics, given in terms of relative angular frequency to that of YSZ in Fig. 7 and considers the fracture toughness, density, and Poisson’s ratio for each material [76]. For further details on this calculation, we refer the reader to the supporting information. The fracture toughness of YSZ can vary as a function of mol % yttria stabilization with typical values between 3 and 8 MPa•m^1/2[77-79]. For the 1.3 mm YSZ rotors tested in this paper and stabilized with 5 mol % yttria the fracture toughness is 7 MPa•m^1/2. We note that specially engineered zirconia has reached fracture toughness up to 15 MPa•m^1/2[80]. For further comparison, we included silicon nitride which has been used in larger MAS rotors and typically achieve higher MAS frequencies than YSZ rotors. The fracture toughness is comparable to YSZ, but the reduced density accounts for improved performance over YSZ. Finally, fracture mechanics properly predicts that sapphire has the lowest anticipated MAS performance due to its low fracture toughness.

Fig. 7.

Fracture mechanics derived relative angular frequencies. All angular frequencies are relative to YSZ.

Basic fracture mechanics were applied to determine the theoretical performance of nitrogen doped single crystal chemical vapor deposition (CVD) diamond, type Ib HPHT diamond (used in this work), silicon nitride, type IIa natural diamond, and sapphire all relative to yttria stabilized zirconia.

Diamond offers the advantage of improved fracture toughness and reduced density relative to YSZ. HPHT type Ib diamond has a fracture toughness in the range of 10 ± 2 MPa•m^1/2, while nitrogen and/or boron doping of CVD diamond can increase the fracture toughness beyond 34 MPa•m^1/2[81]. Type IIa natural diamond has a lower fracture toughness between 4 and 5 MPa•m,^1/2 but the reduced density results in comparable predicted performance, relative to YSZ, using fracture mechanics. A forthcoming publication demonstrates that nanosecond laser machining of diamond does not significantly alter the crystal lattice or introduce strain that would result high concentrations of surface defects leading to reduced performance in MAS. Finally, on the basis of hoop stress and bending mode failure regimes, the high tensile strength of diamond and high elastic modulus offer superior performance over other MAS rotor materials, as described in the supplemental information. Across the three analyses, we estimate an increase in achievable MAS frequency by ~ 1.5–2.5 times with diamond rotors.

We emphasize the approximate nature of these calculations, rotor failure can occur below the estimated frequencies due to the role of surface defects, sample packing, turbine imperfections, gas delivery failures and user error. For a precise model of rotor failure, complex fracture mechanics based finite element analysis or machine learning may be employed considering surface defects, fracture toughness, and yield strength[75,82]. Finally, efforts into measuring these parameters of MAS rotors could be worthwhile, though previously non-trivial given the small sample sizes[83]. Ultimately, the only way to determine the failure regime of diamond rotors is through extensive failure testing with helium gas.

Beyond the improvement in accessible MAS frequency, diamond rotors offer significant advantages for both ambient MAS NMR and DNP NMR. The higher thermal conductivity and improved microwave transmission properties are expected to result in improved sample cooling and stability larger DNP enhancements compared to traditional zirconia rotors. The improved thermal conductivity of diamond is expected to dissipate heat resulting more efficiently from microwave irradiation or frictional heating at fast MAS. More rapid and effective dissipation of heat reduces cooling demands for MAS NMR of biological samples at room temperature, in addition to DNP conditions. A potentially lower sample temperature afforded by diamond rotors with more effective sample cooling under DNP is expected to result in increased enhancements for the same microwave irradiation power in a zirconia rotor. As shown in Fig. 1C, the THz transmission spectra of diamond and sapphire are relatively comparable, with diamond having a slight advantage. However, as shown in the supplementary material, diamond has lower surface reflection afforded by the low refractive index. In contrast, sapphire has a relatively high transmission across the THz regime, but the increased refractive index results in higher surface reflections. Overall, zirconia offers poor THz transmission in addition to high surface reflections. The high transparency of diamond coupled with low surface reflections makes diamond an optimal material for MAS DNP rotors at high fields. The experimental validation of diamond rotors under DNP is the subject of future work.

4. Conclusion

Diamond rotors offer the most promising technology to achieve solution-like resolution and coherence lifetimes in the solid-state. We have presented a new and novel laser machining method using dual-sided axial ablation to fabricate 0.7 mm diamond rotors, spun the rotors to ω_r/2π = 123 kHz using N₂ gas, and used the rotors to record ¹H detected MAS spectra at 18.8 T. Importantly, future developments and applications of this work can enable improved resolution and sensitivity in NMR and DNP enhanced NMR. In particular, diamond rotors, in addition to drive tips and end caps fabricated from diamond and helium bearings optimized for diamond rotors, should offer the ability to reach higher MAS frequencies. Along with improved microwave transmission and thermal conductivity diamond rotors offer a route toward performing high resolution ¹H detected DNP for unprecedented sensitivity and resolution of currently inaccessible biomolecules.

Data availability

No data was used for the research described in the article.