Different sensory information is used for state estimation when stationary or moving

Abstract

Accurate estimation of limb state is necessary for movement planning and execution. State estimation requires both feedforward and feedback information; here we focus on the latter. Prior literature has shown that integrating visual and proprioceptive feedback improve estimates of static limb position. However, differences in visual and proprioceptive feedback delays suggest that multisensory integration could be disadvantageous when the limb is moving. To investigate multisensory integration in different passive movement contexts, we compared the degree of interference created by discrepant visual or proprioceptive feedback when estimating the position of the limb either statically at the end of the movement or dynamically at movement midpoint. In the static context, we observed idiosyncratic interference: discrepant proprioceptive feedback significantly interfered with reports of the visual target location, leading to a bias of the reported position toward the proprioceptive cue. In the dynamic context, no interference was seen: participants could ignore sensory feedback from one modality and accurately reproduce the motion indicated by the other modality. We modeled feedback-based state estimation by updating the longstanding maximum likelihood estimation model of multisensory integration to account for sensory delays. Consistent with our behavioral results, the model showed that the benefit of multisensory integration was largely lost when the limb was passively moving. Together, these findings suggest that the sensory feedback used to compute a state estimate differs depending on whether the limb is stationary or moving. While the former may tend toward multimodal integration, the latter is more likely to be based on feedback from a single sensory modality.

INTRODUCTION

Knowing the current state of the limb (i.e., its position and motion) is critical for the planning and online control of movement. Limb state estimation is thought to involve both feedforward and feedback processes (Stengel, 1994; Wolpert et al., 1995). Here we focus on the latter case. Previous work studying feedback integration in state estimation has shown that it is advantageous to integrate information from multiple sensory inputs (e.g., vision and proprioception) to reduce overall noise and produce a more reliable position estimate (Berniker and Kording, 2011; Ernst and Banks, 2002; van Beers et al., 1999, 1996). When the limb states sensed by vision and proprioception are in significant disagreement, this discrepancy is reduced by changing the degree to which the system relies on vision versus proprioception (i.e., reweighting; Smeets et al., 2006) or by recalibrating one sense to align with the other (i.e., realignment; Block and Bastian, 2010^; Rossi et al., 2021). An extreme example of sensory discrepancy reduction is the rubber hand illusion (Botvinick and Cohen, 1998), in which people experience the transient illusion that their proprioceptively sensed arm position is aligned with the visually observed location of a fake stationary arm. This illusion is induced by integrating synchronous visual and somatosensory feedback (i.e., simultaneous stroking of the fake and real arm).

Prior work studying multisensory integration has focused on state estimation when the limb is stationary. However, multisensory integration becomes problematic when the limb is moving, especially when one considers differences in the timing of feedback delays across modalities (Crevecoeur et al., 2016; Kasuga et al., 2022). For example, in the macaque, there is a delay of approximately ~70 ms for visual information to reach V1, whereas the delay of proprioceptive information to S1 is only ~20 ms (Bair et al., 2002; Nowak et al., 1995; Raiguel et al., 1989; Song and Francis, 2013). In this context, multisensory integration requires the system to wait for feedback information to become available from the slowest modality or to integrate feedback from different modalities that are delayed to different extents. The former would lead to a state estimate that is chronically out-of-date, while the latter would increase estimation noise since each sensory system would be reporting the position of the limb when it is in a different physical location. Either way, a feedback-based estimate of the moving limb that relies on multisensory integration is likely to be unreliable relative to an estimate made with the same sensory input when the limb is stationary. During active limb movements, this problem may be partially resolved by the availability of sensory prediction signals, which provide a real-time prediction of the current limb position and thus can be used to resolve erroneous motor commands (Crevecoeur et al., 2016; Kasuga et al., 2022). However, the availability of sensory prediction signals does not fully resolve the problem because real albeit delayed sensory feedback is still required to respond to unexpected environmental perturbations. While it is possible that the benefits of multisensory integration outweigh the potential noise introduced by moving for both active and passive movements, in some circumstances, it might be better to rely on a single source of sensory feedback.

This study compared feedback integration in state estimation when the limb was stationary to when it was being passively moved, and examined the conditions and extent to which estimates were dependent upon multisensory integration. We opted to focus on passive movements to specifically study the sensory feedback integration process in the absence of any sensory prediction signals. We asked individuals to report a position or motion cued by one sensory modality (i.e., vision or proprioception) while ignoring discrepant feedback from a second modality. We found that when the limb was stationary, individuals exhibited a bias toward the discrepant sensory modality, suggesting that they relied on multisensory integration to compute state estimates. This finding is in line with the prior literature. However, individuals exhibited no bias when the limb was moving, suggesting that they were computing state estimates based largely on a single sensory modality. We present a computational model in which we update the classic maximum likelihood estimation model of multisensory integration (Ernst and Banks, 2002; van Beers et al., 1996) to account for differences in sensory delays. Using this model, we show that multisensory integration is advantageous when the limb is stationary or moving at very low movement speeds. Yet, this advantage is lost when limb speed increases. Taken together with our behavioral results, it seems that feedback integration in state estimation differs when moving versus when stationary.

MATERIALS AND METHODS

Twenty-five right-handed adult neurotypical individuals were recruited for this study. Of those individuals, 22 participated in both the static and dynamic estimation tasks (age 19–36 years, average 26.0 years, standard deviation 4.9 years; 17 identified as female, 4 identified as male, 1 preferred not to respond), one individual participated only in the static estimation task (25 year old who identified as female), and one individual participated only in the dynamic estimation task (29 year old who identified as male). One individual was excluded from the study for failing to comply with task instructions. Sessions were spaced at least 1 week apart (average, 17 days). Sample sizes were chosen to be comparable to previous studies utilizing a similar task (e.g., Block and Bastian, 2010^; Block and Liu, 2023^; Reuschel et al., 2010). All participants were naïve to the purposes of this study and provided written informed consent. Experimental methods were approved by the Albert Einstein Healthcare Network Institutional Review Board, and participants were compensated for their participation as a fixed hourly payment ($20/hr).

Participants were seated in a Kinarm Exoskeleton Lab (Kinarm, Kingston, ON, Canada), which the restricted motion of the arms to the horizontal plane. Hands, forearms, and upper arms were supported in troughs appropriately sized to each participant’s arms, and the linkage lengths of the robot were adjusted to match the limb segment lengths for each participant to allow smooth motion at the elbow and shoulder. Vision of the arm was obstructed by a horizontal mirror, through which participants could be shown targets and cursors in a veridical horizontal plane via an LCD monitor (60 Hz). Movement of the arm was recorded at 1000 Hz.

Experimental Tasks

Participants were asked to complete, in separate sessions with order counterbalanced, a static and a dynamic estimation task (Fig 1). Simulink code to run the tasks on the Kinarm are available on the lab GitHub page (https://github.com/CML-lab/KINARM_Static_Sensory_Integration and https://github.com/CML-lab/KINARM_Dynamic_Sensory_Integration respectively). Participants began each trial with the robot bringing their hand into one of five possible starting positions randomly selected on each trial.

Figure 1.

Methods. (A) The static estimation task involved a block of baseline unimodal (V and P) trials, followed by a block of unimodal and bimodal (VP) trials. Report accuracy feedback was provided on V and P trials only. On VP trials, participants were informed prior to each trial if they should report the location of the visually or proprioceptively cued endpoint. (B) The dynamic estimation task included a baseline block of unimodal V and P trials, and a test block that included unimodal and bimodal (VP) trials. Participants reported the experienced movement. Midpoint accuracy feedback was provided on unimodal trials.

Static Estimation Task

Figure 1a shows a schematic of the static estimation task. Here, participants experienced 4 types of trials modeled after tasks by Block and colleagues (Block and Bastian, 2011, 2010). The first 2 trial types tested unimodal sensory estimation. In Visual (V) trials, participants were shown a stationary visual target 18 cm in front of the starting position and heard an auditory tone cueing them to focus on the target location. After 1000 ms, the target vanished, and participants were asked to move their dominant hand to align the index finger to the remembered target location. In Proprioceptive (P) trials, participants’ dominant hands were passively moved to align the index finger with a stationary endpoint 12 cm in front of the starting position (6 cm away from the V target) via a randomly selected Bezier curved path constructed from 4 control points. They were then presented with an auditory tone cueing them to focus on the target position. After 1000 ms had elapsed, the hand was returned to the starting position along another Bezier curve. Once the hand was passively returned to the start position, participants were allowed to move their hand to re-align their index finger to the previously perceived endpoint. In the unimodal V trials and P trials, participants received visual feedback about the accuracy of their endpoint localization relative to the actual target position. No visual feedback was provided during hand movements. The remaining 2 trial types tested bimodal sensory estimation. At the start of these trials, participants were instructed to attend to one sensory modality and ignore the other. In these trials, the unseen dominant hand was passively moved along a Bezier curve to align the index fingertip with a stationary endpoint. Once at the endpoint, the visual target was also displayed, and an auditory tone cued participants to focus. After 1000 ms, the visual target was extinguished, and the hand was returned to the starting position. Participants were then instructed to move their unseen hand to align the index finger with the visual target (VP_V trials) or the proprioceptive endpoint (VP_P trials), depending on which sensory modality had been cued at the trial’s start. In all trials, the visual target and proprioceptive endpoint were consistently misaligned such that the visual target was 6 cm further from the subject than the proprioceptive endpoint. No feedback of reporting accuracy was provided. Because participants were explicitly instructed on which sensory modality they should attend to and report, systematic errors in the direction of the “ignored” target could be attributed to unintentional biases due to experiencing the other modality.

The static estimation task consisted of two blocks of trials. In the first block (baseline; 120 trials), participants experienced an equal number of unimodal V trials and P trials in random order. This block served as a baseline and allowed us to estimate perceptual reports for the unimodal trials alone. The second block comprised a mix of unimodal (24 V and 24 P trials) and bimodal trials (60 VP_V and 60 VP_P trials), randomly intermixed.

Dynamic Estimation Task

Figure 1b shows a schematic of the dynamic estimation task. Here, all outward movements of the visual stimulus and the hand occurred along symmetric arc-shaped Bezier curves with 3 control points, with all leftward-curved arcs associated with cues in one sensory modality and all rightward-curved arcs associated with cues in the other sensory modality. The pairing of arc direction and sensory modality was counterbalanced across participants. Half of the participants experienced visual cues on the left and proprioceptive cues on the right, and the other half experienced the opposite. The midpoint of the arc was displaced 3 cm from the midline. As in the static task, the dynamic estimation task comprised four trial types. The first two trial types tested unimodal estimation. In V trials, participants watched a visual cursor move along an arcing trajectory. At the end of the arc, the cursor paused for 500 ms before being extinguished. Participants were then presented with an auditory tone, which cued them to move their dominant hand to trace the observed motion with their index fingertip. In P-trials, the dominant hand was passively moved such that the index fingertip traced an unseen arcing trajectory and was held at the endpoint for 500 ms. The hand was then passively returned to the starting position in a straight-line path. Participants were instructed to move the unseen hand to reproduce the perceived trajectory of the index fingertip. Feedback was provided at the end of unimodal trials by displaying a short line segment indicating the position of the target arc midpoint, along with a cursor showing the reproduced midpoint. The timing of events during each trial, as well as passive and active movement speed ranges, were matched to those of the static estimation task; hence any observed differences between the static and dynamic estimation tasks are unlikely to be due to differences in working memory requirements or speed of movement.

The dynamic estimation task also tested 2 bimodal trial types. At the beginning of each bimodal trial, participants were instructed to attend to either the visual (VP_V-trials) or the proprioceptive (VP_P-trials) trajectory and ignore information from the other modality. At the midpoint, the visual and proprioceptive arcs were separated by a total of 6 cm (3 cm on either side of the midline). The side of the workspace where the visual and proprioceptive arcs were located (i.e., the direction of the arc curvature associated with the visual or the proprioceptive cues) was counterbalanced across participants.

The dynamic estimation task consisted of two blocks. In the first baseline block (60 trials), participants experienced only unimodal V and P trials in random order. The second block consisted of a mix of unimodal and bimodal trials (20 V, 20 P, 60 VP_V and 60 VP_P trials) presented in random order.

Prior to the start of block 1, participants were exposed to a series of familiarization blocks to ensure that they could reasonably reproduce the arc trajectory and stop near the desired endpoint without online visual feedback of their hand position. Participants first practiced making point-to-point reaches to a desired endpoint, starting with online cursor feedback of the hand and then practicing without that feedback (but with endpoint feedback to see their movement errors). They then learned to produce arcing motions that passed through an indicated midpoint target and stopped at an endpoint target; as before, they did this with and without online cursor feedback. Participants only began the main task once they were reasonably comfortable and accurate at producing the desired movement.

Data Analysis

Reaches were analyzed offline using programs written in MATLAB (The MathWorks, Natick, MA, USA). Data, analysis code, and model code are available at https://osf.io/wt6hz (DOI: 10.17605/OSF.IO/WT6HZ). For trials in the static estimation task, the movement endpoint was determined as the hand position along the y-axis after the hand velocity in the y-axis remained below 0.06 m/s for 500 ms (selected to identify the first time the hand came to a stop and exclude any subsequent motor corrections). For trials in the dynamic estimation task, the movement midpoint was defined as the horizontal position of the hand when the hand had moved halfway (i.e., 7.5 cm along the y-axis) from the starting position to the ideal endpoint. The movement endpoint was determined as the position after the x- and y-hand velocity remained below 0.05 m/s for 2000ms, to allow time for the hand to come to a complete stop along both axes (note, the movement midpoint is the position of interest in this task). For both the static and dynamic estimation tasks, the movement endpoint (y-axis position when the hand was stationary) and midpoint (x-axis position when the y-axis position of the hand was 7.5 cm), respectively, was used to calculate a report error, defined as the difference between the actual reported position and the ideal position. For unimodal trials, the report error was calculated separately for the baseline (block 1) and mixed trial (block 2) blocks. In bimodal trials, report error was calculated using the target/trajectory modality participants were instructed to reproduce. Positive report errors in bimodal trials reflected a reported position that was shifted toward the cued position of the other modality. Biases on bimodal trials (i.e., the extent to which the hand position was shifted by the presence of discrepant feedback from another sensory modality) were calculated as the difference between the reported position and the average reported position in corresponding baseline unimodal trials (e.g., VP_V – V_{average, baseline}). Positive biases reflect a shift toward the ideal location of the other modality. For all tasks, movement peak velocity was identified as the greatest hand-speed vector magnitude achieved during the movement.

Differences in hand position (endpoint, midpoint) or biases (VP_V – V and VP_P – P) across trial types, both within individual tasks as well as across tasks, were analyzed with mixed-effects regression models using the lme4 package in R (Bates et al., 2015). Models included a random intercept of subject and a random slope of trial type by subject. Factors were tested for significance using likelihood ratio tests comparing models with and without the factor of interest. Posthoc comparisons were examined using the emmeans package in R with Kenwood-Roger estimates of degrees of freedom and corrected for multiple comparisons using the Tukey method (Lenth et al., 2021). Models that included the dynamic estimation task initially included a nuisance factor of Side (V-left or V-right), which was removed from the final analysis as it showed no significant effects (p > 0.59). Models that included both static and dynamic estimation tasks initially also included a nuisance factor of task order. This factor was removed from the final analysis because it showed no significant effects (p > 0.28). Although individuals were asked to move within a desired speed range, models included a nuisance factor of peak velocity to control for differences in movement speed; this factor was found to be significant (p < 0.001) and was included in all models. In some cases, simple regressions were performed to examine correlations among variables of interest and/or for data visualization purposes.

Model

Multisensory integration for state estimation has previously been modeled using a maximum likelihood estimation (MLE) approach (Ernst and Banks, 2002). We propose an update to this approach that accounts for the effect of sensory delays during movement (see Fig. 5A). In particular, we start with the assumption that the hand is moving at speed $v$ and the temporal delay for feedback from sensory system $i$ (either Vision, $\text{V}$, or Proprioception, $\text{P}$) is ${\tau }_i$. If we assume that sensory feedback is distributed as a Gaussian with mean ${\mu }_i$ and variance ${\sigma }_i{ }^2$, then the sensed position available at time $t$ can be described as the position sensed ${\tau }_i$ seconds ago that is spatially displaced by an amount equal to the sensory time delay times the movement speed:

$$\begin{gathered} \widehat{{\mu }_V}={\mu }_{{\tau }_V}+\nu \left(t-{\tau }_{\nu }\right) \\ \widehat{{\mu }_P}={\mu }_{{\tau }_P}+\nu \left(t-{\tau }_P\right) \end{gathered}$$ (1)

Figure 5.

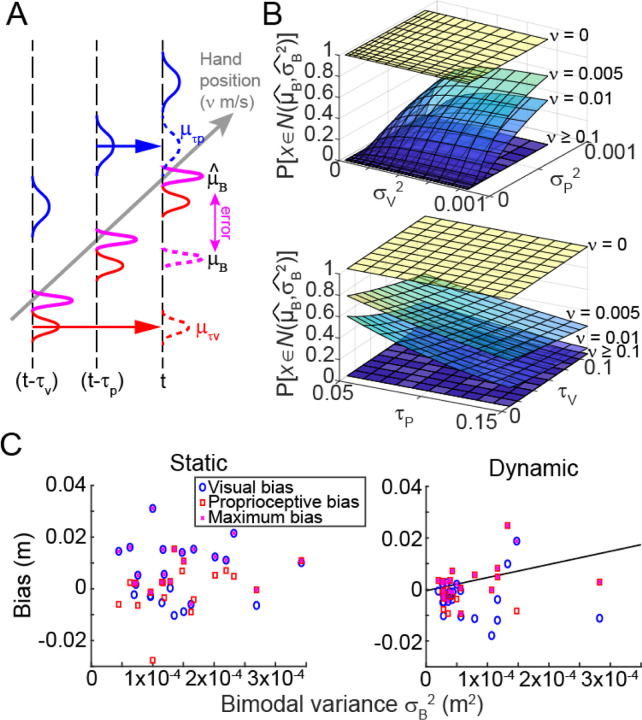
Model results. (A) Updated MLE model accounting for limb movement and sensory delays. If the limb moves with speed ν, at time t we have delayed sensory feedback of the limb sometime in the past (μ_τv, μ_τp) instead of its current position. This leads to an erroneous bimodal state estimate (μ_B) that is offset from the ideal bimodal estimate by some error (purple arrow). (B) Simulation results suggest that as movement speed increased, the probability of obtaining an accurate bimodal sensory estimate decreased; in such cases it may be better to use a unimodal state estimate. (C) Observed data was used to estimate the bimodal variance via the MLE combination of the observed unimodal sensory variances. For the static estimation task (left), no relationship was observed between the bimodal variance and the observed bias. In contrast, in the dynamic estimation task (right) there was a clear correlation across individuals. Consistent with the model, this suggests that individuals with greater bimodal variance likely relied on an integrated state estimate, and hence were more susceptible to discrepant information from the other sensory modality.

According to the MLE estimate, combining sensory feedback from the two modalities (e.g., akin to the bimodal condition in our task) should result in a Gaussian defined by:

$$\widehat{{\mu }_B}=\frac{{\sigma }_P{ }^2}{\left({\sigma }_V{ }^2+{\sigma }_P{ }^2\right)}\widehat{{\mu }_V}+\frac{{\sigma }_V{ }^2}{\left({\sigma }_V{ }^2+{\sigma }_P{ }^2\right)}\widehat{{\mu }_P}$$ (2)

$$\widehat{{\sigma }_B{ }^2}=\frac{{\sigma }_P{ }^2\ast {\sigma }_V{ }^2}{\left({\sigma }_V{ }^2+{\sigma }_P{ }^2\right)}$$ (3)

However, the unimodal sensory feedback that is actually available is the delayed sensory feedback given in the pair of equations (1) above. Hence, the actual integrated sensory feedback at time $t$ is:

$${\mu }_{B_t}=\frac{{\sigma }_P{ }^2}{\left({\sigma }_V{ }^2+{\sigma }_P{ }^2\right)}{\mu }_{{\tau }_V}+\frac{{\sigma }_V{ }^2}{\left({\sigma }_V{ }^2+{\sigma }_P{ }^2\right)}{\mu }_{{\tau }_P}+\frac{{\sigma }_P{ }^2\nu \left(t-{\tau }_{\nu }\right)+{\sigma }_V{ }^2\nu \left(t-{\tau }_P\right)}{\left({\sigma }_V{ }^2+{\sigma }_P{ }^2\right)}$$ (4)

where the third term reflects the offset of the state estimate due to sensory delays. With this information, we can calculate the degree of overlap between the actual (equation 4) and ideal (equation 2) bimodal Gaussians (where the ideal bimodal estimate is calculated assuming that sensory feedback is available instantaneously, or is equal to equation (4) without the offset term). The overlap enables us to estimate the probability with which the two sensory estimates (actual and ideal) will correspond. That is, the overlap between $\mathcal{N}\left({\mu }_{B_t},{\sigma }_{B_t}{ }^2\right)$ and $\mathcal{N}\left(\widehat{{\mu }_B},\widehat{{\sigma }_B{ }^2}\right)$ reflects the probability that the bimodal state estimate accounting for sensory delays and movement speed will fall within the ideal bimodal distribution had the limb been stationary. This probability tells us the degree to which an individual could expect to calculate a reasonable bimodal state estimate given their current (instantaneous) movement speed and the uncertainty associated with each sensory modality. Using this model, we calculated this probability over a range of physiologically reasonable movement speeds, sensory delays, and sensory variances, to examine how these parameters change the degree to which an individual should rely on unimodal versus bimodal state estimates.

To confirm the validity of the model, we calculated an estimate of each individual’s ideal bimodal variance based on the variances of vision and proprioception observed during baseline unimodal trials according to equation (3). We then tested the correlation between the estimated bimodal variance and the largest mean bias exhibited in bimodal trials of the static and dynamic estimation tasks (regardless of sensory modality), under the hypothesis that larger biases should reflect a greater tendency for that individual to rely on multisensory integration.

RESULTS

This study examined the degree to which individuals could report limb state using sensory information from one modality while ignoring discrepant information from another. Performance was measured by examining the accuracy with which the perceived movement endpoint (static task) or midpoint (dynamic task) was reported. Positive report errors reflected a shift toward the location of the opposing sensory modality (i.e., an inability to ignore information from the other sensory modality), and report biases were computed as the difference between the report error on each bimodal trial relative to the average report error on corresponding unimodal trials.

In the static estimation task (Fig 1A), static visual cues were displaced 6 cm farther along the y-axis compared to proprioceptive movement endpoints (Block and Bastian, 2011, 2010). Individuals were asked to report the perceived locations of these cues. Report error was significantly different across the four types of trials (Fig. 2A,B): V, P, VP_V, and VP_P (unimodal trials at baseline and bimodal trials in block 2: χ²(3) = 10.51, p = 0.015). This effect was driven by a difference between VP_V and V trials (p = 0.010), in which VP_V trials exhibited a larger positive report error (i.e., they were shifted toward the location of the P cue). There was also a difference between VP_V and VP_P trials (p = 0.012), with VP_V trials exhibiting more positive report errors than VP_P trials. The difference between VP_P and P trials (p = 0.54) and the difference between V and P trials (p = 0.058) did not reach significance. At the individual subject level (Fig 3A), there was no relationship observed between the bias in the Visual modality and the bias in the Proprioceptive modality (r² = 0.10, p = 0.13). Within sensory modality, there was no relationship observed between the report error variance exhibited in unimodal trials versus the bias in bimodal trials (Vision: r² = 0.04, p = 0.37; Proprioception: r² = 0.05, p = 0.30). Peak velocity was consistent across all trial types (χ²(1) = 0.02, p = 0.88). Together, these results suggest that when reporting the location of visually cued targets, individuals have difficulty ignoring discrepant proprioceptive feedback when the limb is stationary.

Figure 2.

Static and dynamic estimation tasks. (A) Data from a single participant in the static estimation task performing baseline unimodal trials (left panel) and bimodal trials (right panel). The cued endpoint location is indicated by a black x. (B) The average reported endpoint position for each participant is shown along with the group mean, for visual (V and VP_V, red) and proprioceptive (P and VP_P, blue) trials. (C) Data from the same participant in the dynamic estimation task performing baseline unimodal (left) and bimodal (right) trials. (D) Group data for the Dynamic task akin to panel B.

Figure 3.

Report biases. (A) Across individuals within task, there was no relationship between the biases observed when reporting visual and proprioceptive cues. (B) Across the static and dynamic estimation tasks, there were no relationships between the biases observed on bimodal trials in response to the visual cue or in response to the proprioceptive cue.

For the dynamic estimation task (Fig 1B), individuals experienced arcing motion patterns that curved either to the right or left, with visual cues consistently arcing in one direction (e.g., rightward) and proprioceptive cues arcing in the other direction (e.g., leftward). Arc midpoints were separated by 6 cm. Individuals were asked to report the perceived motion on each trial, with a focus on reproducing the position at the midpoint of the movement.

Across all participants there was no significant effect of the pairing of arc direction and sensory modality on report error (χ²(1) = 0.26, p = 0.61), so data were analyzed together (data were collapsed across participants who experienced V trials that curved rightward and those who experienced the V trials that curved leftward). Report error (Fig 2C,D) showed no significant differences across the four trial types (χ²(3) = 4.49, p = 0.21). At the individual subject level (Fig 3A), there was no relationship between the bias observed in the Visual modality and the bias observed in the Proprioceptive modality (r² = 0.01, p = 0.69). Within sensory modality, there was also no relationship between the variance in report error exhibited in unimodal trials versus the bias observed in bimodal trials (Vision: r² = 0.02, p = 0.48; Proprioception: r² = 0.08, p = 0.18). There was a significant negative effect of peak velocity on report error, in which the report error became more positive (i.e., the movement curvature decreased) as peak velocity decreased (χ²(1) = 172.46, p < 0.001). However, there were no systematic differences in peak velocity across the different trial types (interaction: χ²(3) = 0.35, p = 0.94). Together, these results suggested that individuals were not susceptible to the influence of discrepant sensory feedback when reporting limb movement.

Comparing report error in the static and dynamic estimation tasks, we first ruled out an effect of task order (χ²(1) = 1.16, p = 0.28). There was a significant negative effect of peak velocity (χ²(1) = 153.01, p < 0.001) on report error, so this variable was included as a nuisance parameter in our regression model. The analysis showed a significant main effect of task (χ²(5) = 3235.8, p < 0.001) wherein participants showed more positive report errors (i.e., greater bias) in the static compared to the dynamic estimation task. There was also a significant main effect of trial type (χ²(7) = 424.08, p < 0.001), in which the report error was different for each trial type (post hoc comparisons all showed p < 0.001). Finally, there was a significant interaction between task and trial type (χ²(3) = 414.68, p < 0.001). The interaction arose from differences in report error across trial types in the static estimation task that were not present in the dynamic estimation task. That is, for the static task, report error in V trials was more positive compared to P trials (p = 0.02), in VP_V trials compared to V trials (p = 0.0001), and in VP_V trials compared to VP_P trials (p = 0.0004). In contrast, for the dynamic task, report error was significantly less positive in VP_V trials compared to VP_P trials (p = 0.03), with no observed differences between the other trial types (p > 0.12).

Biases across the static and dynamic estimation tasks were not significantly correlated for either the Visual or the Proprioceptive modality (Visual bias: r² = 0.00, p = 0.83; Proprioceptive bias: r² = 0.02, p = 0.49, Fig. 3B). Additionally, the variance that participants exhibited on unimodal trials at baseline was not correlated across tasks (i.e., individuals were not consistently variable across tasks), for either Vision or Proprioception (Visual variance: r² = 0.15, p = 0.07; Proprioceptive variance: r² = 0.06, p = 0.25). Thus, individual performance in the static and dynamic estimation tasks was uncorrelated, consistent with the analysis of report error above.

Since participants received no performance feedback on bimodal trials, unimodal trials with feedback were presented in block 2 to keep participants’ movements relatively stable. The presence of these unimodal trials afforded an opportunity to examine whether the sensory conflicts in bimodal trials would also modulate the performance of unimodal trials (e.g., through recalibration; Fig 4). Within the static estimation task, we observed a significant main effect of block (χ²(2) = 12.90, p = 0.002) with unimodal trials in block 2 being more positively biased compared to block 1. There was no effect of trial type (V versus P trials; χ²(2) = 3.40, p = 0.18) and no block-by-trial-type interaction (χ²(1) = 0.12, p = 0.73). In contrast, for the dynamic estimation task, we observed no effect of block (χ²(2) = 0.94, p = 0.62) or trial type (χ²(2) = 1.70, p = 0.43), nor was there an interaction (χ²(1) = 0.003, p = 0.95). These findings suggest that exposure to conflicting sensory cues induced biases toward the opposing sensory modality for both unimodal and bimodal trials in the static task but not in the dynamic estimation task. Notably, these biases were observed even though conflicting sensory cues were not present during unimodal trials. This may be an indication that sensory recalibration occurred in the static but not the dynamic estimation task.

Figure 4.

Shift in report error for unimodal trials. In the static estimation task (left panel), participants exhibited a shift in report error on unimodal trials in the context of conflicting bimodal sensory cues relative to baseline. In contrast, unimodal trials in the dynamic estimation task exhibited no such shift when bimodal trials were introduced.

Modeling

Our experimental findings suggested that when computing a state estimate based on sensory feedback, individuals should rely on multisensory integration only when it is advantageous to do so, such as when the limb is stationary. When the limb is passively moved, it may be more beneficial to rely on unimodal feedback, to potentially avoid uncertainty arising from sensory delays. However, the most widely accepted model of multisensory integration, the maximum likelihood estimation model (Ernst and Banks, 2002; van Beers et al., 1996), makes no such prediction. To examine the effect of sensory delays on the reliability of multisensory integration, we present an update to the maximum likelihood model (see Methods and Fig. 5). Rather than assuming one knows the current limb position at each instant in time, we instead assume that one only knows the limb position sometime in the past, with each sensory modality potentially reporting a different limb position based on differences in sensory delays. To simulate this, we included terms in the model that reflected the perceived limb position sometime in the past, where the difference in limb position was calculated according to the sensory delay and the current limb speed (see Methods, Equation 1). Note that we did not make any changes to the sensory uncertainty terms of the original model: we assumed that the perceived limb position did not degrade over time, and that sensory uncertainty did not scale with movement speed. We also made no assumptions regarding the magnitude of any intrinsic visual or proprioceptive biases in limb position.

Simulations using this model showed that when estimating the position of a stationary limb, bimodal integration offered the greatest reliability, replicating previous work (Berniker and Kording, 2011; Ernst and Banks, 2002; van Beers et al., 1999, 1996). The advantage afforded by bimodal state estimation persisted at very slow movement speeds (< 0.01 m/s), particularly when the uncertainty of the individual sensory modalities was high or when sensory delays were short. As movement speed increased, however, the bimodal sensory estimate became quite poor (i.e., there was no overlap between the Gaussian representing the estimate given sensory delays and that of the ideal estimate assuming the system had access to the current limb position). The error arose because the state estimate was reliant on temporally delayed sensory feedback informing the system of where the limb was located some time ago rather than its current location. Under these circumstances, the model predicted that it may be better to use unimodal sensory feedback rather than integrated multisensory feedback to derive a state estimate (Fig. 5B).

One of the implications of this model is that individuals should be more likely to rely on a bimodal estimate of limb movement if they have greater sensory uncertainty overall. Since the Gaussian representing the bimodal estimate will be wider (i.e., the calculated variance of the bimodal estimate will be larger), it is more likely that any bimodal estimate will fall within the bounds of the ideal estimate had current (non-delayed) sensory information been available. Therefore, the degree of bias toward the discrepant sensory modality in bimodal trials of the dynamic estimation task should be correlated with the magnitude of bimodal variance according to the maximum likelihood estimation model (Methods, Equation 3).

To check this prediction, we examined the biases exhibited by individual participants in both the static and dynamic estimation tasks. Although people were only significantly biased in the static estimation task, there was variability across individuals, with some showing a bias in the dynamic task as well. We compared the largest bias individuals exhibited, regardless of sensory modality, against the estimated bimodal variance calculated using the variances exhibited in baseline V and P trials. Consistent with the model prediction, we found a positive correlation between the theoretical bimodal variance and the extent to which individuals exhibited a bias in the dynamic estimation task (Fig. 5C; r² = 0.18, p = 0.047; after removing the one outlier participant: r² = 0.47, p = 0.001). When an individual’s ideal bimodal variance was quite large (which according to the model was a condition under which a bimodal state estimate remained reasonable to use), their reports of limb movement were more strongly biased by the discrepant sensory modality they were asked to ignore. On the other hand, individuals with low bimodal variance tended to exhibit less bias in the dynamic estimation task, consistent with relying more on unimodal sensory information to report their sensed limb movement. In contrast, during the static estimation task, individuals all exhibited a bias regardless of their sensory uncertainty (r² = 0.004, p = 0.78); this suggests that all participants in the static estimation task favored a bimodal state estimate regardless of their bimodal variance because their movement speed was zero. This finding was also predicted by our model.

DISCUSSION

Estimating the current limb state is critical for proper motor control and uses both feedforward and feedback information. Multisensory integration is thought to be a key process supporting feedback-based state estimation, but studies of the phenomenon have largely focused on estimating static limb position. Due to differing temporal delays across sensory modalities, multisensory integration may be less useful when estimating limb movement (i.e., a dynamic context in which the limb position is constantly changing). Here, we examined whether multisensory integration for state estimation is obligatory by asking to what extent feedback from one modality interfered with the attempt to estimate the state of the limb according to a different sensory modality. Our results showed that when estimating static limb position, it was not possible to entirely ignore incoming sensory information from another modality, even when individuals knew that such feedback was task-irrelevant. In particular, when instructed to ignore proprioceptive information on bimodal trials, position reports based on visual information were more biased toward the proprioceptively cued limb position compared to unimodal baseline trials involving visual information alone. The degree of bias an individual exhibited was unrelated to the amount of variance they exhibited in baseline visual-only trials. Similarly, this bias when reporting visually cued position was unrelated to any bias exhibited when instructed to ignore vision and report only the proprioceptively cued position. Multisensory integration is known to be useful as it improves the position estimate while reducing uncertainty compared to an estimate based on a single modality alone (Berniker and Kording, 2011; Ernst and Banks, 2002; van Beers et al., 1996). However, our findings suggest that when estimating static limb position, the integration of proprioceptive information may be unavoidable.

In contrast to the static estimation task, individuals exhibited no biases when reporting perceived passive limb movement in bimodal trials of the dynamic estimation task. That is, participants were able to accurately report either the visually or proprioceptively cued motion while successfully ignoring conflicting information from the other sensory modality. Any small bias that individuals did exhibit when reporting dynamic motion was unrelated to the bias they exhibited when reporting static position, for either the visually cued or the proprioceptively cued limb state. These results suggest that estimation of the perceived limb state may be more reliant on a single sensory modality when the limb is moving. This is reasonable, given the differences in the timing of when sensory information from vision and proprioception become available for use. Since proprioception becomes available much more quickly than vision (delay of ~20 ms to S1 vs ~70 ms to V1 in macaques; Bair et al., 2002^; Nowak et al., 1995^; Raiguel et al., 1989^; Song and Francis, 2013), an instantaneous bimodal state estimate of the moving limb may be less accurate than a state estimate based only on a single sensory modality, particularly when the limb is moving quickly. Hence, it is reasonable that state estimation during movement may use sensory information in a different manner compared to when the limb state is not significantly changing over time.

The bias observed on bimodal trials when reporting static position and the lack of bias when reporting limb movement were echoed in the report errors observed for unimodal trials. Unimodal trials were presented by themselves in block 1 (baseline) and were interleaved with bimodal trials in block 2 when individuals experienced discrepant sensory feedback. In the static estimation task, participants shifted the reported position of unimodal targets in block 2 relative to baseline, mimicking the bias observed in bimodal trials. In contrast, report errors for unimodal trials in block 2 of the dynamic estimation task show no such shift. These findings suggest that the nature of the feedback information used to compute a state estimate – and perhaps also the degree to which individual sensory modalities are recalibrated in the presence of a sensory mismatch – depends on whether this estimate is made while the limb is moving or stationary.

Our findings are at odds with a prior study that showed individuals optimally integrate multisensory information when reporting the geometry of a perceived passive movement trajectory as following either an acute or obtuse angle (Reuschel et al., 2010). Specifically, the prior work demonstrated improved accuracy when reporting the angle under bimodal conditions as compared to only having vision or proprioception alone. This may seem to contradict our current findings. However, it is not clear whether individuals in the prior study relied on sensory integration throughout the entire movement. It is possible that in the prior task, individuals sensed the angle according to the positions of the movement endpoints or when the hand slowed down at the via point of the trajectory (i.e., when the hand changed direction to define the angle). In contrast, in our task, individuals were asked to reproduce the position at the midpoint of the passive movement, which occurred at the peak velocity when sensory delays were likely to have a large effect on the accuracy of feedback-based state estimates.

Our model simulations were consistent with our behavioral findings. By modifying the conventional maximum likelihood estimation model (Ernst and Banks, 2002; van Beers et al., 1996) to account for limb movement and sensory delays, we were able to examine the conditions under which individuals should favor a bimodal state estimate. Our model revealed that state estimates were likely to be bimodal when individuals moved very slowly or were stationary, as feedback delays did not cause wildly out-of-date estimates under these conditions. Our model also predicted increasing reliance on multisensory integration as sensory uncertainty increases, even when moving. These predictions were supported by an analysis of the data from our study showing that individuals with greater bimodal variance in the dynamic estimation task were more likely to exhibit a positive bias in report error, suggesting that they continued to rely on multisensory integration to a small extent even when moving. This correlation was not observed in the static estimation task, when all individuals were expected to rely on bimodal state estimates regardless of their estimate variance. Future studies are needed to test the predicted dependence of multisensory integration on movement speed more rigorously by asking individuals to report limb movement at different movement speeds.

In our behavioral task and model, we consider state estimation only in the case when the limb is passively moving. That is, we are specifically focusing on times when state estimation is reliant on sensory feedback alone. This stands in contrast to other studies in which individuals were asked to report their perception following actively generated movements (Block and Bastian, 2011, 2010; Block and Liu, 2023), in which state estimates could potentially additionally benefit from sensory predictions based on an efference copy of the ongoing motor command. Since sensory predictions provide an estimate of where the limb is expected to be at the current time, they can help overcome delays that would otherwise lead to out-of-date position estimates based on sensory feedback alone (Shadmehr et al., 2010). A previous study offered a more complex dynamic Bayesian model with Kalman filtering that attempted to account for sensory delays in an active arm movement task (Crevecoeur et al., 2016; Kasuga et al., 2022). Notably, these authors also concluded that individuals are likely to base state estimates on unimodal (in their case, reliant on proprioceptive feedback) in the face of sensory delays. Nevertheless, the contribution of sensory predictions to state estimation when the limb is actively moving and how that affects the integration of feedback from multiple sensory modalities needs further study.

Our study design also included another key distinction from prior work. In bimodal trials of prior studies, individuals were encouraged to integrate visual and proprioceptive information and report a single unified percept (e.g., Block and Bastian, 2011^{, 2010;} Block and Liu, 2023^; Reuschel et al., 2010^; van Beers et al., 1999^{, 1996}). These prior studies often presented surreptitious sensory mismatches with the intent that people should combine the two senses in some weighted manner to come up with an integrated position percept (Block and Bastian, 2010; Reuschel et al., 2010). Their approach enabled an assessment of the weights applied to vision and proprioception during sensory integration, but it led to the assumption that multisensory integration automatically occurs when deriving a state estimate. In our study, participants were made aware of the discrepancy between visual and proprioceptive cues, and they were asked to ignore one sensory modality (i.e., deliberately shift the degree to which they relied on one modality versus the other). Thus, our design permitted the assessment of whether multisensory integration is obligatory, but it did not allow us to assess the weights assigned to each modality.

Indeed, our findings suggested that multisensory integration may not be obligatory when estimating limb state, even for static positions. While it was difficult for individuals to ignore proprioception and report only the location of a visual target, it was possible to ignore vision and report only the perceived proprioceptive position estimate. This idiosyncrasy may have arisen because proprioceptive information is available before vision (Crevecoeur et al., 2016). The central nervous system may be unable to disregard incoming sensory information while waiting for future information (as was required in VP_V trials) but is able to ignore sensory information that comes later in time (as was the case in VP_P trials). Alternatively, people in our study knew that the visual target was misaligned with their finger, and thus, may have had an easier time ignoring it simply because they assumed the visual cue bore no relation to their limb state. Regardless, even if sensory integration is automatic for static position estimates, our findings suggest that this is not the case for feedback-based state estimation while moving, as people can easily ignore the information coming from a second, discrepant modality.

When individuals appear to rely on a unimodal state estimate, our model does not make any strong predictions regarding which modality they should use. We suspect that the choice of modality may be determined by the relative sensory delays between vision and proprioception (and their effects on estimated limb position at different movement speeds), as well as their respective reliabilities. An interesting prediction of our model is that the choice of sensory modality may additionally depend on the direction of the sensory bias and the degree to which that bias aligns with the direction of the movement. That is, moving toward the direction of the sensory bias for a particular modality should improve the delayed feedback estimate coming from that modality, while moving away from the direction of the sensory bias should exaggerate the error. This prediction would need to be tested in future studies.

In summary, we have observed differences in the ability to ignore conflicting sensory information when reporting perceived position versus movement. Our computational model suggests that these differences arise because sensory delays cause bimodal state estimates to be more unreliable at higher movement speeds. Such a pattern of results is consistent with the idea that feedback-based estimates of current limb state are computed differently when stationary and when moving.

SIGNIFICANCE STATEMENT.

The estimation of limb state involves feedforward and feedback information. While estimation based on feedback has been well studied when the limb is stationary, it is unknown if similar sensory processing supports limb position estimates when moving. Using a behavioral experiment and computational model, we show that feedback-based state estimation may involve multisensory integration in the static case, but it is likely based on a single modality when the limb is moving. This difference may stem from visual and proprioceptive feedback delays.