Steady Flow in a Patient-Averaged Inferior Vena Cava—Part I: Particle Image Velocimetry Measurements at Rest and Exercise Conditions

Abstract

Although many previous computational fluid dynamics (CFD) studies have investigated the hemodynamics in the inferior vena cava (IVC), few studies have compared computational predictions to experimental data, and only qualitative comparisons have been made. Herein, we provide particle image velocimetry (PIV) measurements of flow in a patient-averaged IVC geometry under idealized conditions typical of those used in the preclinical evaluation of IVC filters. Measurements are acquired under rest and exercise flow rate conditions in an optically transparent model fabricated using 3D printing. To ensure that boundary conditions are well-defined and to make follow-on CFD validation studies more convenient, fully-developed flow is provided at the inlets (i.e., the iliac veins) by extending them with straight rigid tubing longer than the estimated entrance lengths. Velocity measurements are then obtained at the downstream end of the tubing to confirm Poiseuille inflow boundary conditions. Measurements in the infrarenal IVC reveal that flow profiles are blunter in the sagittal plane (minor axis) than in the coronal plane (major axis). Peak in-plane velocity magnitudes are 4.9 cm/s and 27 cm/s under the rest and exercise conditions, respectively. Flow profiles are less parabolic and exhibit more inflection points at the higher flow rate. Bimodal velocity peaks are also observed in the sagittal plane at the elevated flow condition. The IVC geometry, boundary conditions, and infrarenal velocity measurements are provided for download on a free and publicly accessible repository. These data will facilitate future CFD validation studies of idealized, in vitro IVC hemodynamics and of similar laminar flows in vascular geometries.

1. Introduction

Computational fluid dynamics (CFD) is a tool used to predict fluid flow by numerically solving the governing equations for conservation of mass and momentum. Such modeling has been used in previous work to study healthy and pathological cardiovascular physiology (e.g., [1, 2]), hemodynamics in patient-specific vessel geometries (e.g., [3–5]), congenital deformities (e.g., [6–8]), and even to predict the outcome of surgical modifications to vascular anatomy (e.g., [8–10]). Additionally, applications of CFD to medical devices span the entire device development lifecycle and include: simulating device hemodynamics to guide early design decisions, optimizing device design, investigating the influence of manufacturing processes and tolerances, determining worst-case physiological conditions to minimize the burden of pre-clinical experimental studies, and performing post-market failure analyses to investigate the cause of adverse events.

An emerging use of CFD is to generate evidence of medical device safety and effectiveness or substantial equivalence for regulatory submissions to the US Food and Drug Administration (FDA). For these and other uses of computational modeling and simulation, simulation predictions should be verified and validated to a level commensurate with the risk associated with use of computational evidence in decision making [11]. Previous studies have been performed by FDA and collaborators to generate experimental data for benchmark problems with flow features typical of medical devices. These include the FDA nozzle [12–14] and FDA blood pump [15], which have been investigated both experimentally and computationally and have generated a body of data for laminar, transitional, and turbulent flow fields. The studies have provided an opportunity to investigate best practices in CFD simulation and validation and have contributed to the development of standards (e.g., [11]) and FDA guidance documents (e.g., [16]) on reporting and establishing credibility of modeling and simulation evidence in regulatory submissions. However, neither of the aforementioned benchmarks consider flow in an anatomical model and its influence on the performance of a medical device.

Here, experimental particle image velocimetry (PIV) measurements are presented in a patient-averaged inferior vena cava (IVC) model under idealized conditions that are typically used to evaluate the preclinical performance of IVC filters. The anatomical model includes elliptical vessel cross sections, iliac vein bifurcation, and anteroposterior curvature of the infrarenal IVC.

IVC filters have been used for decades to trap blood emboli and prevent pulmonary embolism (PE); however, adverse events continue to occur [17], including some breakthrough PE [18–21]. Hemodynamics in the IVC are relatively low in Reynolds number ($\mathrm{R}\mathrm{e}\approx 200$ under rest conditions and up to $\mathrm{R}\mathrm{e}\approx 1500$ during exercise [22, 23]) compared to the aorta ($\mathrm{R}\mathrm{e}\approx 4400$ during peak systole under resting conditions [24]). Even so, flow in the IVC is complicated by the secondary flow arising from vessel curvature and vessel confluence (e.g., [25]). Because this secondary flow is thought to influence embolus transport and capture [26, 27], CFD models used to predict IVC filter embolus trapping performance should first be validated to predict baseline IVC hemodynamics accurately.

Although many previous CFD studies investigate IVC hemodynamics [5, 23, 25–34], only a few studies [34–39] compare computational predictions with experimental measurements in a bench-top IVC model, and the comparisons are largely qualitative. Furthermore, the IVC geometries in previous experimental studies are idealized either as a single, straight circular tube [34, 35, 37–39] or as a collection of straight circular branches [36], and no model has considered anteroposterior curvature or the secondary flow it generates. The validation dataset presented here uses a more anatomically realistic geometry with well-defined boundary conditions to facilitate the validation of future CFD simulations of IVC hemodynamics under the idealized conditions typically used in the preclinical evaluation of IVC filter embolus-trapping performance (e.g., ISO 25539–3:2011).

2. Materials and methods

2.1. Inferior vena cava (IVC) model

Experiments were performed in an optically transparent patient-averaged model of the human IVC from the literature [33]. This model was generated based on average computed tomography (CT) measurements from ten patients with normal caval anatomy (i.e., no anatomical anomaly). The model includes elliptical vessel cross-sections (Fig.1a) and anteroposterior curvature of the infrarenal IVC (Fig.1b).

Figure 1:

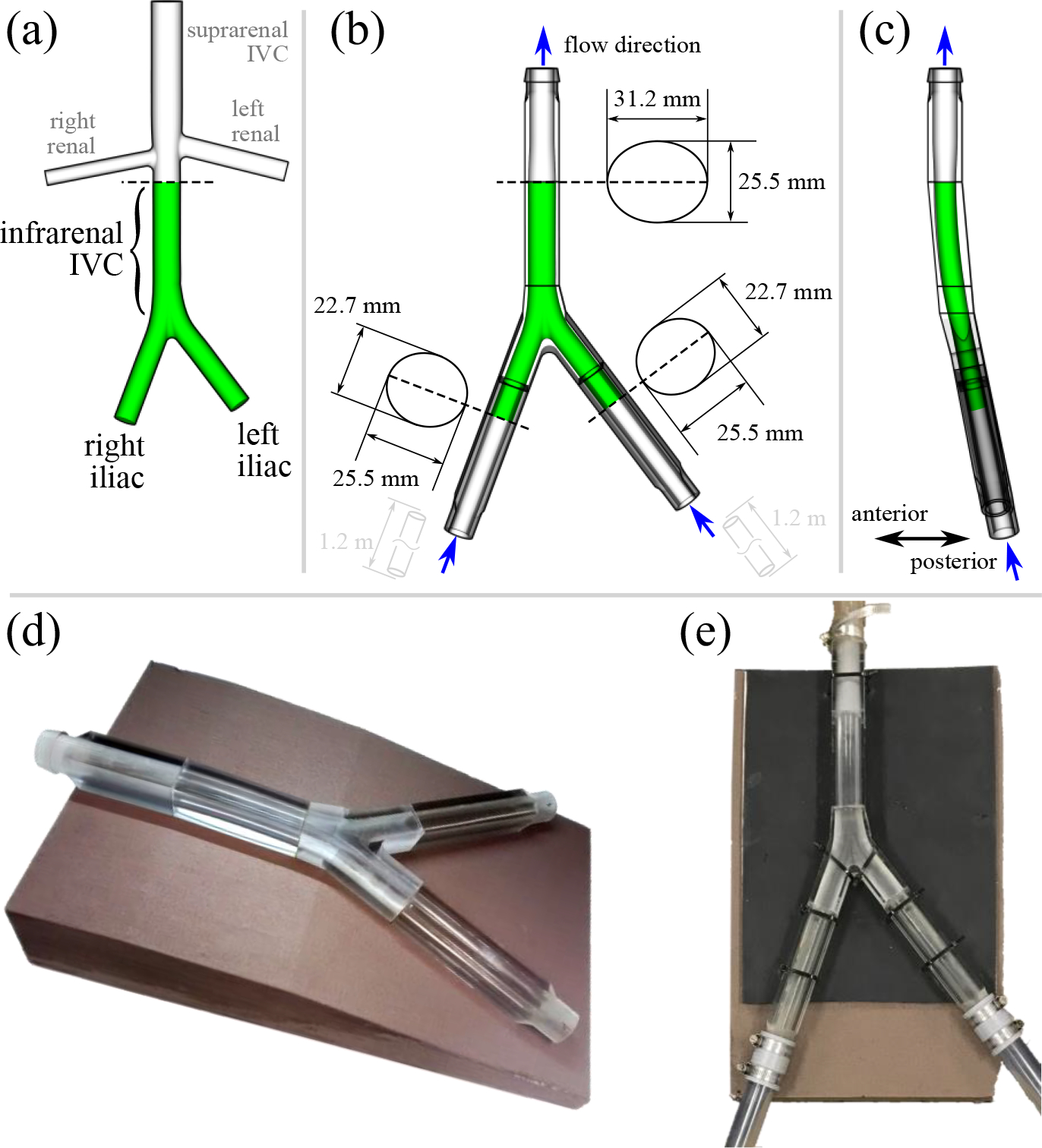
(a) Original IVC model from [33] based on computed tomography measurements from ten patients. Only the iliac veins and infrarenal IVC (green) were included in the experimental model used herein. (b) Anterior view of the IVC model used in the particle image velocimetry (PIV) experiments. The IVC was scaled up to obtain an average hydraulic diameter of 28 mm in the infrarenal IVC. Upstream and downstream attachments were designed to transition from circular tubing to the elliptical cross-sectional shape of the vessels. (c) Sagittal view of the scaled IVC model. (d) Printed and polished physical model with foam support platform. (e) Assembled model connected to the mock flow loop.

A number of modifications were made to the original model from [33] in preparation for this study and follow-on computational fluid dynamics (CFD) validation studies of IVC hemodynamics [40] and embolus trapping by an IVC filter. First, the model was scaled up by a constant factor of 1.4192 in all directions to obtain an average hydraulic diameter in the infrarenal IVC of 28 mm (Fig. 1). This is the largest indicated IVC diameter for most IVC filters and represents a worst-case scenario for embolus trapping efficiency, which will be investigated in future studies. After scaling, the radius of curvature in the anteroposterior direction was approximately 1 m.

Second, since the flow in the infrarenal IVC is of greatest interest here, the downstream renal veins and suprarenal IVC were removed (Fig. 1a) in consistency with previous in vitro evaluations of IVC filters (e.g., [41, 42]). Because of: i) the unidirectional nature of the flow in the IVC [22], ii) the greater volumetric flow coming from the iliacs with respect to the renal veins [22], and iii) the renal vein entry angles favoring downstream flow (e.g., [32, 33]), the presence of the renal veins is unlikely to appreciably influence the upstream flow in the infrarenal IVC. Indeed, previous computational studies performed with [32] and without [29] renal veins have also confirmed the negligible influence of the renal veins on infrarenal IVC hemodynamics.

Third, inlet attachments were fabricated for the region upstream of the iliac veins to provide a smooth transition from the original elliptical cross-sectional vessel shape to a circular shape (Fig. 2). The exterior cross sections of the attachments are rectangular to facilitate PIV measurements of the inlet flow profiles.

Figure 2:

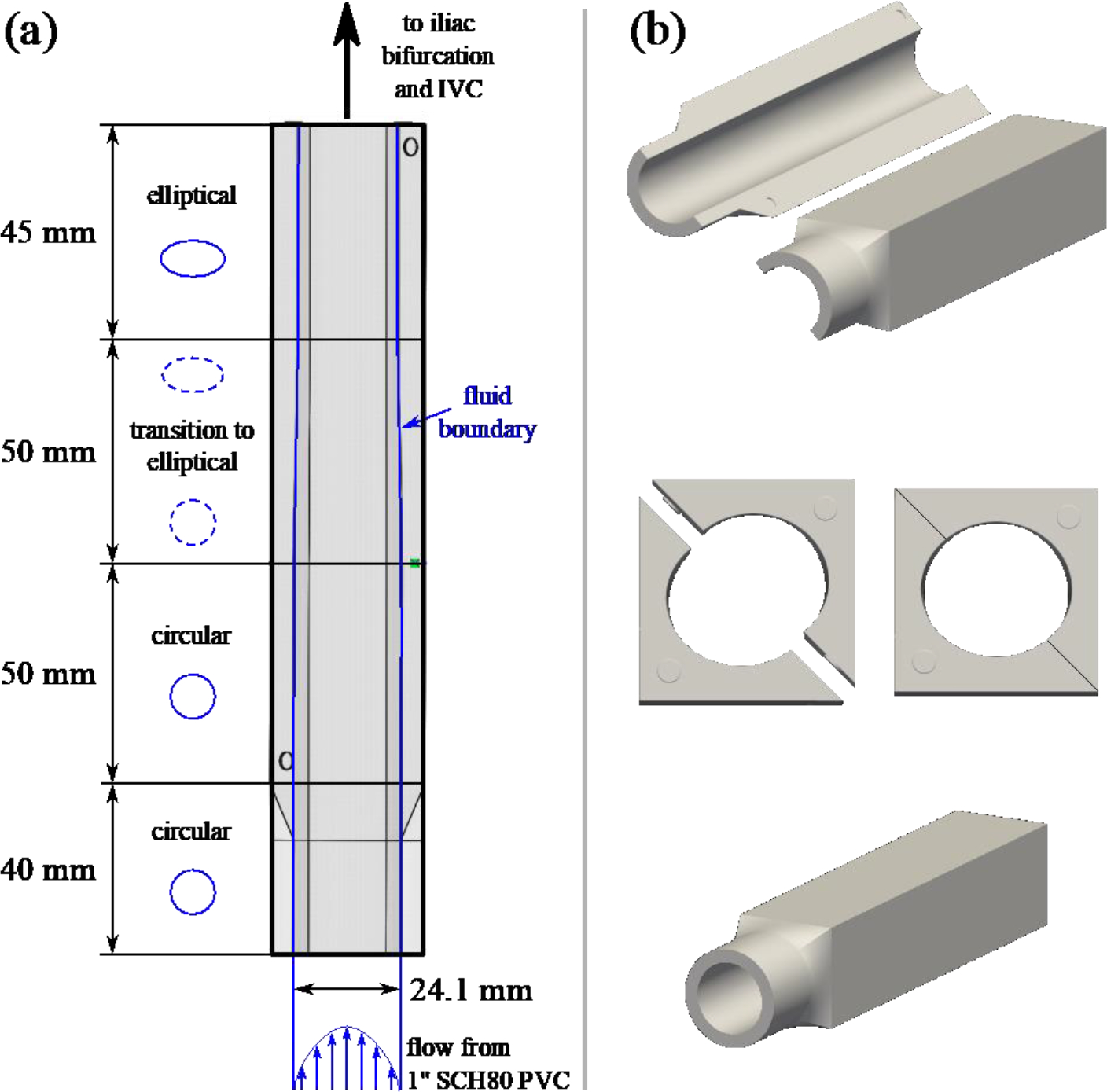
(a) Schematic showing the iliac attachments used to transition from circular to elliptical interior vessel cross-sections. The upstream portion attaches to one-inch SCH80 clear PVC pipe, and the downstream portion attaches to the iliac bifurcation. Both connections are smooth internally, without any step changes in cross-sectional geometry. (b) Assembled and exploded views of the iliac attachments fabricated in VeroClear material using inkjet 3D printing.

2.2. IVC model fabrication

The scaled patient-averaged IVC geometry was fabricated [43] in a rigid, optically transparent material using PolyJet (inkjet) 3D printing. Although the IVC deforms in vivo in response to diaphragmatic motion that occurs during breathing and Valsalva (e.g., [44, 45]), IVC motion was neglected from the present study for consistency with typical in vitro testing [41, 42].) In brief, the iliac veins, iliac bifurcation, infrarenal IVC, and IVC outlet (Fig.1b) were printed as individual parts using an Objet260 Connex 3D printer (Stratasys, Ltd., Eden Prairie, MN) and stock resin (VeroClear RGD810). Short raised or embossed pins were included on the mating surfaces of the individual printed parts to facilitate alignment (e.g., Fig.2b).

For the iliac and infrarenal IVC sections, printing layers were oriented 45° to the flat exterior surfaces to maximize optical transparency [43, 46]. The infrarenal IVC was printed as a single piece and, after printing, the inner and outer surfaces of the model were sanded and polished to further improve optical transparency [43]. The iliac veins were instead split lengthwise along a plane passing through the vessel centerlines and printed as two separate pieces (Fig.1b) with the interior side of the vessels oriented vertically in the printer to obtain a glossy surface finish. Only the outside surfaces of the iliac pieces were sanded and polished.

The iliac bifurcation and the outlet parts were not polished since no PIV data were collected in these regions.

Each pair of iliac pieces was fused together using a cyanoacrylate adhesive (Fig.1b) and then similarly fused to the iliac bifurcation. The iliac bifurcation, infrarenal IVC, and the outlet were also fused together (Fig.1d).

2.3. Flow loop

The physical IVC model was integrated into a flow loop consisting of a reservoir, a continuous flow centrifugal pump (Cole-Parmer Instrument Company, Barrington, IL), and two 1.2 m long circular inlet tubes used to generate fully-developed flow at the iliac veins. A Fluke 116 True RMS Multimeter (Fluke Corporation, Everett WA) with a type-K thermocouple was used to measure the fluid temperature just upstream of the iliac veins and downstream of the IVC outlet (Table 1).

Table 1:

Equipment and reported measurement accuracies.

Equipment	Measurement	Company/Product	Accuracy
flow probes	inlet flow rates	Transonic Systems / TS410, 8XL	± 10%
multimeter	fluid temperature	Fluke / 116 True RMS	± 1%
thermocouple	fluid temperature	Fluke / 80BK Type-K	± 2.2%

Because non-Newtonian effects are believed to be of greater importance in the IVC than elsewhere in the circulation [25] due to the presence of relatively low shear rates (i.e., less than 100 s⁻¹), attempts were first made at developing a non-Newtonian working fluid a solution of water, glycerin, sodium iodide (NaI), and xanthan gum (XG). Unfortunately, after numerous attempts, we were unsuccessful and could not obtain both blood-mimicking non-Newtonian rheology and the high index of refraction required to match that of VeroClear resin (approximately 1.514; [47]). This is likely due to an interaction between NaI and XG that reduces the shear-thinning properties normally imparted by the addition of XG [48]. Thus, it appears that matching both index of refraction and non-Newtonian hemorheology is not possible with XG and NaI at such a high refractive index. Furthermore, although the use of a fluid with a scaled non-Newtonian behavior may at first seem like an attractive alternative, achieving appropriate scaling of both the Reynolds number and the shear-thinning non-Newtonian behavior simultaneously at all locations in the flow is exceedingly difficult and may not be possible [49].

Therefore, consistent with previous laboratory tests of IVC filters (e.g., [41, 42]), a simplified Newtonian blood analog composed of 60.2 wt% NaI, 32.4 wt% water, and 7.36 wt% glycerin was used instead to obtain a refractive index of 1.515 (Abbe Mark III Refractometer, Reichert Technologies, Buffalo, NY), closely matching that of the 3D printed model material, and a kinematic viscosity of $\nu =3.18$ cSt (at 25 °C; Vilastic-3 Viscometer, Vilastic Scientific, Inc., Austin, TX), closely matching the asymptotic viscosity of blood. The fluid density was also measured at 25 °C and found to be 1.817 g/ml.

Because the working temperature of the fluid varied slightly between resting and exercise conditions, additional viscosity and density measurements were obtained at temperatures of 20 °C ($\nu =3.82\mathrm{c}\mathrm{S}\mathrm{t}$) and 30° C ($\nu =2.75\mathrm{c}\mathrm{S}\mathrm{t}$). A 2nd-order polynomial fit of the viscosity—temperature data was then used to determine the viscosity at operating conditions:

$$\nu =0.004279T^2-0.3203T+8.511.$$ (1)

Steady, clinically relevant rest and exercise iliac flow rates of 0.5 l/min and 3.0 l/min [22] were studied (i.e., infrarenal IVC flow rates of 1 l/min and 6 l/min), measured by ultrasonic flow probes (Transonic Systems, Ithaca, NY) calibrated for similar NaI-rich blood-mimicking fluids (Table 1). Although the patient-averaged IVC model was scaled up from a normal hydraulic diameter of 20 mm to 28 mm, the literature shows that IVC diameter is not correlated with body size or cardiac output [50–52]. Thus, despite the enlarged IVC diameter, the flow rates prescribed herein are still representative of physiological conditions. Indeed, similar flow rates have been used in previous investigations of the worst-case clot trapping performance of IVC filters in large, 28 mm diameter IVCs (e.g., [41, 42]).

2.4. Particle image velocimetry (PIV) measurements

Two-dimensional PIV measurements of velocity were acquired over six planes for each flow rate: coronal and sagittal bisections of the left and right iliac veins and the infrarenal IVC (Fig. 3). Temperature and flow rate measurements were recorded for each flow rate and PIV plane. An EverGreen double-pulsed Nd:YAG laser (Quantel, Les Ulis, France) was focused into a 750 micron-thick light sheet to illuminate 10-micron fluorescent polymer microspheres (Fluoro-Max 36–3B, Thermo Scientific Inc., Fremont CA) in the blood analog fluid, and a four-megapixel, digital CCD PowerView Plus Camera (TSI, Inc., Shoreview, MN) was used to capture images.

Figure 3:

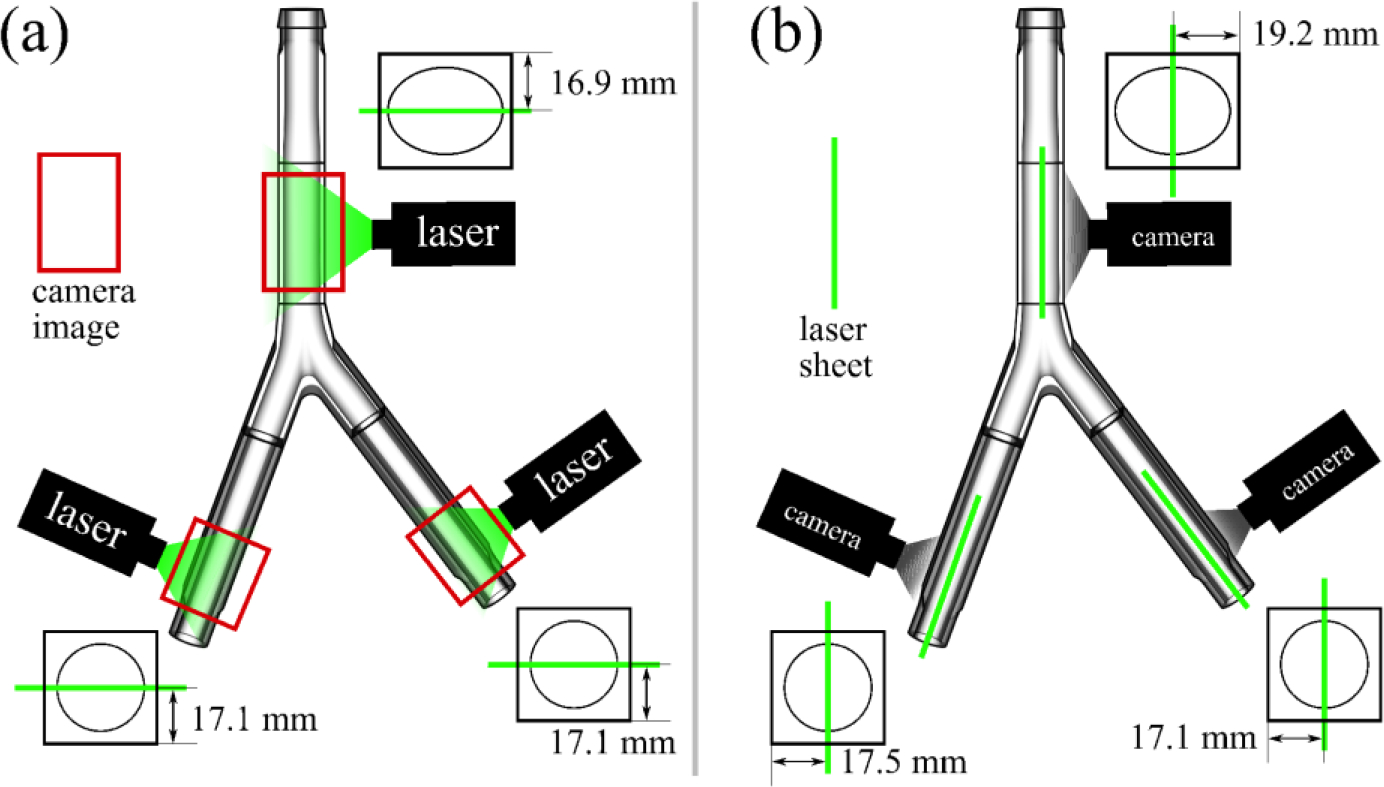
(a) Coronal and (b) sagittal measurement planes for the particle image velocimetry (PIV) experiments. Six PIV planes are studied at resting and exercise flow conditions.

A frame-to-frame time delay ($\mathrm{\Delta }\mathrm{t}$) was chosen for each flow rate so that particle displacements were less than or equal to one quarter of the interrogation window size. The resulting values were $\mathrm{\Delta }\mathrm{t}=2.4\mathrm{m}\mathrm{s}$ for the resting flow rate $\mathrm{\Delta }\mathrm{t}=0.6\mathrm{m}\mathrm{s}$ for the exercise flow rate.

Image pairs were processed with Insight 4G software (TSI, Inc., Shoreview, MN). For each plane at an IVC flow rate of 1 l/min, 250 image pairs were captured, and for each plane at 6 l/min, 1000 image pairs were captured. The adequacy of the number of image pairs collected was evaluated by calculating the mean absolute percent change in local standard deviation associated with using half versus all of the image pairs

$$\frac{1}{n}{\sum }_{i=1}^n\frac{|{\sigma }_{\frac{N}{2},i}-{\sigma }_{N,i}|}{{\sigma }_{N,i}}\times 100\mathrm{\%}$$ (2)

where $\sigma$ is the standard deviation in the velocity magnitude, $n$ is the number of velocity vectors extracted over the PIV plane, and $N$ is the number of image pairs used to calculate $\sigma$. Following spatial calibration and image masking, cross-correlation was performed and velocity data were extracted using a recursive Nyquist grid, a Hart correlator, and a Gaussian bilinear peak algorithm. Mean and standard deviations of the velocity fields were then calculated using custom MATLAB scripts (MathWorks Inc., Natick, MA).

As a secondary check, image pairs for one plane and flow rate were also processed in DaVis (LaVision GmbH, Goettingen, Germany) for comparison to the velocity data extracted in Insight.

Finally, inlet and infrarenal flow profiles were extracted from the velocity fields using custom Python scripts and the NumPy, SciPy, and Matplotlib libraries [53–55]. Profiles for the four inlets planes at both flow rates were compared to theoretical Poiseuille flow profiles to confirm fully-developed inflow boundary conditions.

3. Results

Variability in flow rate and temperature is relatively low from image plane to image plane at a given flow condition, with percent coefficient of variation values (i.e., the standard deviation divided by mean × 100%) all less than 5% (Table 2). Based on the temperature measurements and the temperature–viscosity relationship determined previously (Eqn. 1), the Reynolds numbers were approximately 236 and 1504 for the resting and exercise flow rates, respectively (Table 3). The mean absolute percent change in the local standard deviation of the velocity field magnitude between $N$ and $\frac{N}{2}$ image pairs (Eqn. 2) was found to be approximately 3% for both rest and exercise measurements, thereby justifying the number of image pairs collected for each case.

Table 2:

Experimental variability expressed as percent coefficient of variation.

Measurement	Resting flow rate	Exercise flow rate
flow rate (1/min) - left iliac	1.79%	0.27%
flow rate (1/min) - right iliac	1.79%	0.25%
fluid temperature (°C)	1.54%	3.88%

Table 3:

Mean fluid temperature and calculated nominal fluid viscosity, Reynolds number (Re no.), and Dean number (De no.) for the studied flow conditions.

IVC flow rate	fluid temperature	viscosity	Re no.	De no.
1.0 1/min	24.7 °C	3.21 cSt	236	28
6.0 1/min	26.6 °C	3.02 cSt	1504	175

3.1. Inlet boundary conditions

Velocity measurements in the iliac veins show little to no variation in the streamwise direction (Fig. 4). Extracted velocity profiles confirm that the flow is indeed fully-developed and parabolic (Fig. 4) in both iliac veins at both flow rates. The greatest deviations from the expected parabolic flow profile shapes occur in the sagittal plane for the left iliac vein (Fig. 4b–*), where the peak velocity is lower than the theoretical value and flow near the wall is not captured. The coronal plane in the left iliac, however, shows good agreement with theoretical Poiseuille flow (Fig. 4a). Thus, error in the sagittal plane is likely due to lower optical transparency in this printed component caused by the seam (e.g., Fig. 2b) or imperfections in printing and polishing, or possibly due to a slight lateral shift of the laser sheet away from the intended bisection plane.

Figure 4:

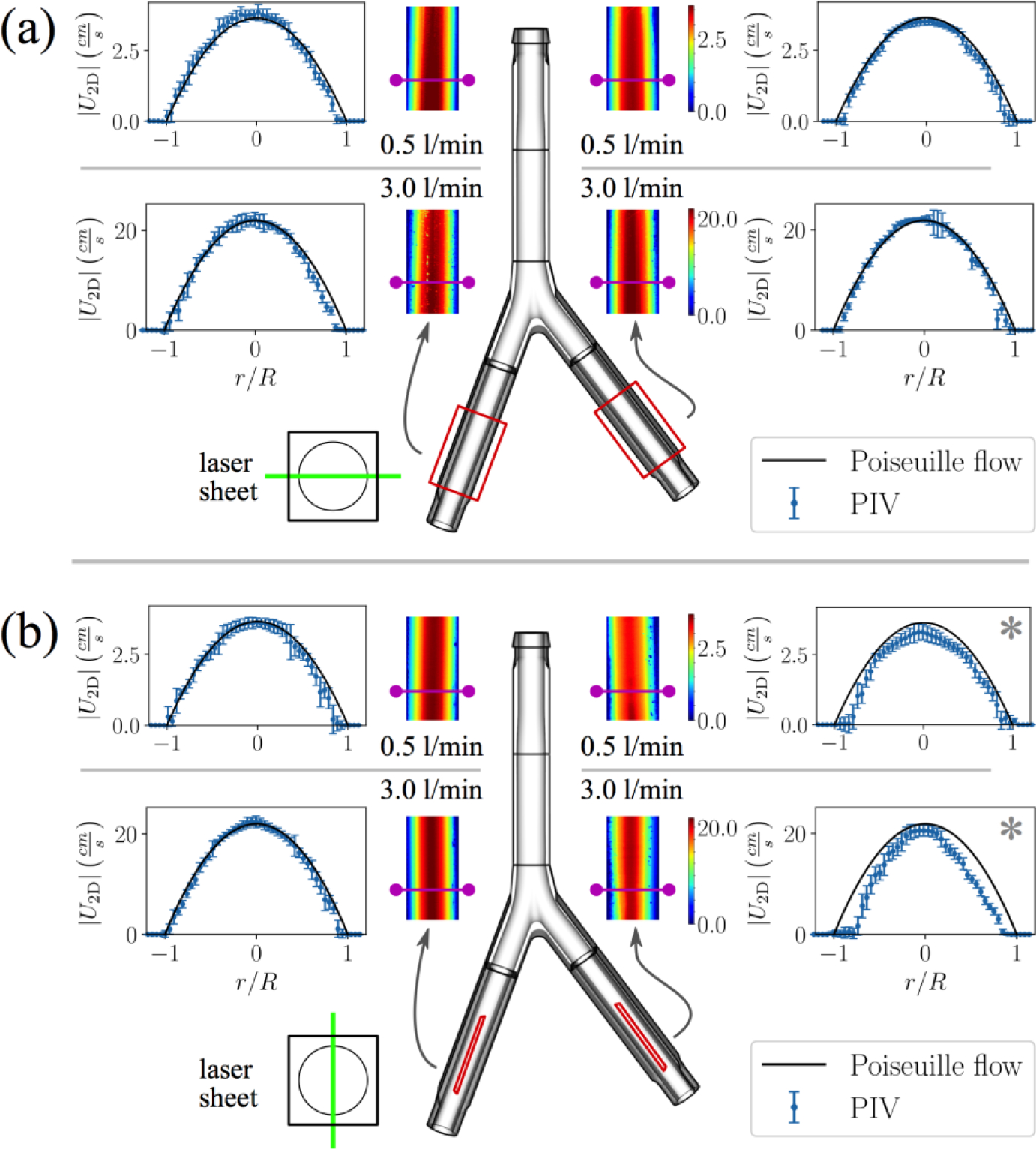
Two-dimensional velocity magnitude contours for (a) coronal and (b) sagittal planes in the iliac veins at resting and exercise flow rates. Flow profiles are extracted from the upstream portion of the planes (magenta lines), where the cross-sections are circular. Error bars represent local variability in the PIV velocity measurements (one standard deviation). Analytical fully-developed flow profiles at the nominal flow rates are plotted for comparison with the PIV velocity data. (*) Lower optical transparency in left iliac vein under the sagittal view results in loss of near-wall velocity vectors. This is possibly caused by incomplete wetting of the adhesive while assembling the inlet section (see Fig. 2b) or by imperfections in printing and polishing. A slight lateral shift of the laser sheet away from the intended bisection plane may have also occurred

3.2. Infrarenal IVC

Resting conditions in the infrarenal IVC generate relatively uniform and developed flow, with only subtle changes moving downstream (Fig. 5a). Flow is approximately parabolic in the coronal plane, although there is a slight bias in peak velocity to the anatomical right side (Fig. 5a). The flow is also approximately parabolic in the sagittal plane near the walls but is quite blunt in the core region from $-\frac{1}{2}<\frac{r}{R}<\frac{1}{2}$ (Fig. 5b).

Figure 5:

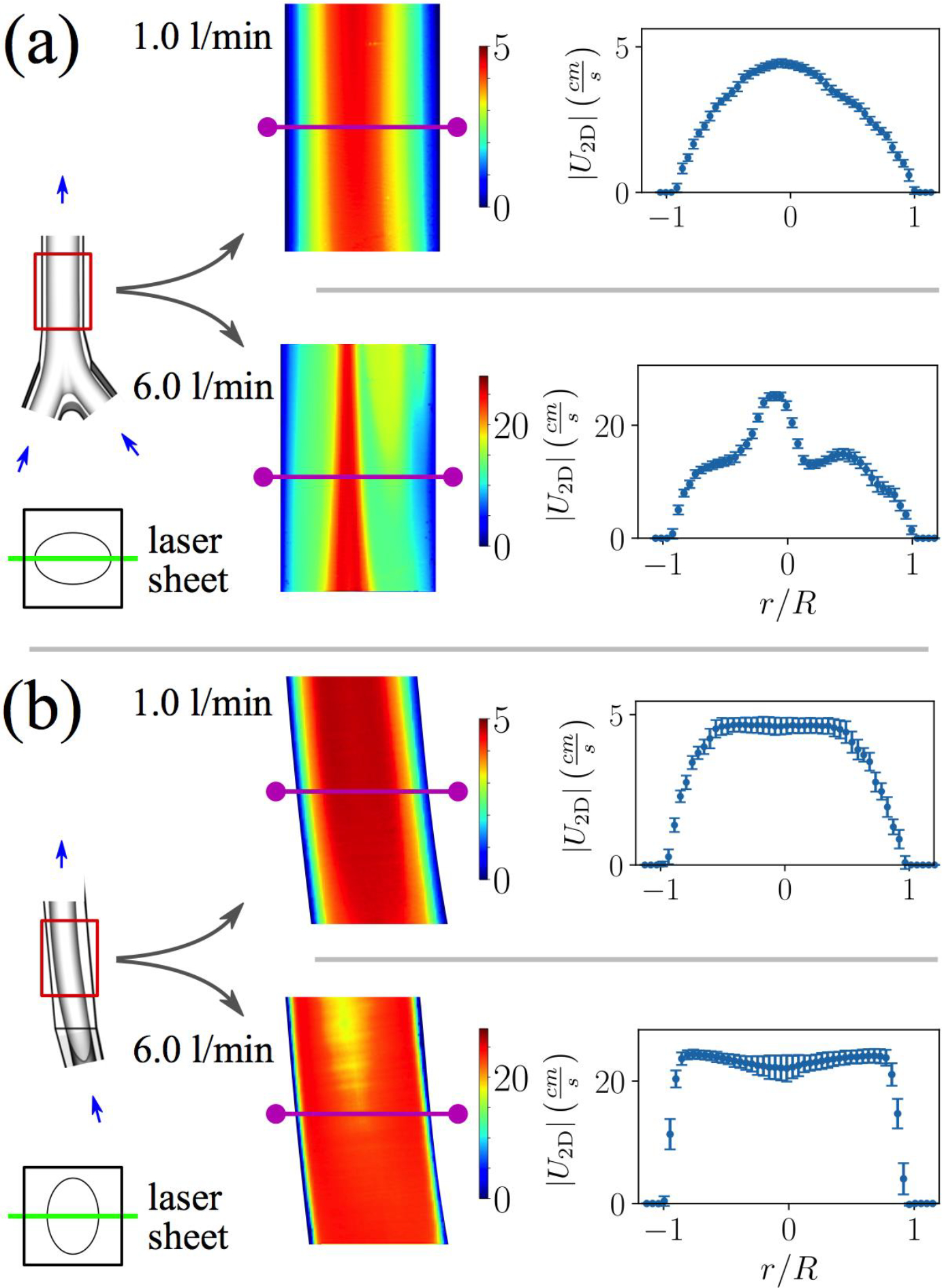
Two-dimensional velocity magnitude contours for (a) coronal and (b) sagittal planes in the infrarenal IVC at resting and exercise flow rates. Flow profiles are extracted midway down the PIV planes (magenta lines) and plotted with error bars representing the experimental variability (one standard deviation). The flow becomes more complex at the higher flow rate, with more inflections points in the flow profiles.

Flow at exercise conditions is more complex: the flow changes moving downstream, cross-stream velocity gradients are greater, and multiple inflection points are present in the flow profiles (Fig. 5). In the coronal plane, a jet-like flow structure (in 2D) appears just to the right of the centerline that contracts moving downstream (Fig. 5a). Some flow stagnation is also present along the IVC wall on the anatomical left side (Fig. 5a). In the sagittal plane, plug-like flow occurs, with large velocity gradients at the walls (Fig. 5b). Flow profiles are also bimodal, exhibiting peaks near $\frac{r}{R}\approx 0.8$ and a decrease in velocity near the vessel centerline (Fig. 5b).

4. Discussion

Computational fluid dynamics simulations are useful for predicting real-world fluid physics outside of the laboratory. However, experimental data are necessary to validate these models and to build evidence of simulation credibility. Here, we have used two-dimensional PIV to measure velocity fields in a patient-averaged model of the human IVC. This data set will be a valuable tool for validating CFD models created to study IVC hemodynamics under simplified conditions typical of those used in the preclinical evaluation of IVC filters or flows in similar vascular geometries under comparable flow conditions (i.e., similar Reynolds numbers and simplifications).

Inlet flow profiles were parabolic and symmetric across both coronal and sagittal planes in the iliac veins, demonstrating fully-developed flow at both resting and exercise flow rates (Fig. 4). Use of fully-developed boundary conditions provides two primary advantages: 1) greater confidence in experimental boundary conditions, and 2) convenience of applying the boundary conditions computationally. This approach overcomes the difficulty encountered in [36], where non-parabolic asymmetric inflow occurred and the true three-dimensional shape of the boundary conditions was unknown. In this case, it was necessary to extrapolate three-dimensional boundary conditions from a single asymmetric two-dimensional flow profile, limiting the ability of the model to accurately match the actual experimental conditions. Thus, use of fully-developed flow here increases the likelihood of consistent application of boundary conditions between experiments and simulations in future validation exercises.

Although the flow is relatively simple and parabolic in the infrarenal IVC at the lower flow rate, unique flow patterns are generated at the higher exercise flow rate conditions (Fig. 5). Specifically, coronal planes reveal a jet-like structure (in 2D) with a subtle bias to the anatomical right side of the IVC, and flow profiles in the sagittal plane exhibit a blunt shape with bimodal velocity peaks (Fig. 5). Similar flow profile shapes are reported in previous computational work (e.g., Fig. 4b in [25]) for the same IVC model, although the jet and bimodal peaks are less exaggerated, likely due to the lower Reynolds number in the previous study ($\mathrm{R}\mathrm{e}=522$ in [25] versus $\mathrm{R}\mathrm{e}=1504$ here). A thin region of increased flow velocity along the centerline of the infrarenal IVC in the coronal plane is also predicted in the computational study by Ren et al. [23] (Fig. 2b,c in [23]) at the “exercise” and “high exercise” flow rates investigated therein (corresponding to $\mathrm{R}\mathrm{e}=1400$ and 1640).

Readers may question whether the exercise conditions reported herein are truly “laminar” given the proximity of the reported $\mathrm{R}\mathrm{e}$ under exercise conditions to the critical Reynolds number for standard pipe flow $\left({\mathrm{R}\mathrm{e}}_{cr}\approx 2000\right)$ and the mixing generated at the confluence of the iliac veins. Indeed, researchers have speculated for decades that some turbulence may be generated at the iliac bifurcation (e.g., see Discussion in [56]). Roach et al. [57] measured the critical Reynolds number for reversed flow in a bifurcation, representative of the flow at the confluence of two veins, at various bifurcation angles. Based on their findings, the critical $\mathrm{R}\mathrm{e}$ for the bifurcation angle herein of 57° under steady flow conditions is ${\mathrm{R}\mathrm{e}}_{cr}\approx 1800$, indicating that our exercise flow conditions ($\mathrm{R}\mathrm{e}=1504$) remain within the laminar regime. Additionally, variability in the local velocity measurements (e.g., Fig. 5) is similar in magnitude relative to the respective mean velocities, providing further evidence that the observed flows are laminar. Finally, Ren et al. [23] predicted negligible turbulence intensities in their investigations of exercise conditions in the same unoccluded patient-averaged geometry up to $\mathrm{R}\mathrm{e}=1640$. Thus, at least under the simplified conditions considered herein (i.e., steady flow in a rigid vessel), we believe that the flow remains laminar even at elevated “exercise” flow rates.

Interestingly, Roach et al. [57] report a lower ${\mathrm{R}\mathrm{e}}_{cr}\approx 1100$ under pulsatile conditions for the same bifurcation angle. Accordingly, some transitional flow may occur in vivo due to respiratory or Valsalva-generated pulsatility, and flow transition and turbulence should be considered in future work if higher Reynolds number or pulsatile conditions are studied. Importantly, however, quantification of in vivo transitional and turbulent flow in the human vasculature remains an open research topic that is perhaps best addressed using in vivo measurements with high spatial and temporal resolution (e.g., [24]).

4.1. Study limitations

Because data were only measured on coronal and sagittal planes herein, it was not possible to directly measure or characterize the secondary flow in the IVC predicted by previous computational studies (e.g., [25, 27]). Recording of secondary flow using two-dimensional PIV is usually difficult or impossible since the bulk flow normally dominates the cross-flow and, thus, particles exit the illumination plane between images in an image pair at the required time delay size. However, given the relatively high Dean number ($\mathrm{D}\mathrm{e}=175$) associated with the exercise flow rate case considered herein, secondary and axial flow velocities are likely on the same order of magnitude, and thus measurement of the secondary flow may be tractable for this case. Velocity measurements on axial planes perpendicular to the bulk flow would add to the three-dimensional understanding of the flow patterns in the IVC and would be useful for directly validating computational predictions of secondary flow. Attempts at measuring these secondary flow data are a topic of future work.

Despite the laminar nature of the flow studied herein, local variability in velocity was relatively large at some locations, possibly due to laser sheet thickness and large out-of-plane velocity gradients (e.g., Fig. 5b near centerline), or due to a low signal-to-noise ratio in some locations caused by bubbles or local imperfections in the printing or polishing of the 3D–printed model (e.g., Fig. 4). The seam in the iliac extensions (Fig. 2b) may have also contributed to the larger variability in the iliac PIV data (Fig. 4) and the loss of near-wall velocity vectors in the sagittal plane data for the left iliac vein (Fig. 4b). Importantly, however, the large variability in the iliacs does not impact the final validation dataset, as the iliac data were obtained only to confirm fully-developed inflow. Nonetheless, care should be taken in future work to mitigate this spurious variability in velocity measurements as much as possible, especially in turbulent flow experiments where this false variability could adversely affect the quality of computed turbulence statistics.

Additionally, although multiple image pairs were acquired for each condition, the averaged velocity data for each PIV plane effectively represent $\mathrm{n}=1$ experiments since data was only collected in a single laboratory and a single physical model. Round robin studies such as those performed for the FDA nozzle and FDA blood pump can be used to more rigorously quantify experimental variability, which can then be leveraged for validation by comparing observed experimental variability to that predicted by stochastic simulations (e.g., as described in [58]). Such approaches should be considered for modeling applications where the risk associated with making decisions based on model predictions is especially high and greater model credibility is required [11].

A number of simplifications were also made to IVC mechanics and hemodynamics. Although these same simplifications are typically used in current preclinical testing of IVC filters (e.g., ISO 25539–3:2011), the difference between the in vitro and in vivo conditions should still be acknowledged and their influence on testing conclusions investigated in future work.

First, blood was approximated as Newtonian when in reality it behaves as a complex viscoelastic and shear-thinning fluid, and these properties can become important at low shear rates such as those encountered in the IVC at rest conditions (e.g., [25]). As shown in our previous work [25], we expect that the hemodynamics would be approximately the same using a non-Newtonian fluid at Reynolds number-matched conditions (i.e., with the non-Newtonian Reynolds number calculated using a representative viscosity based on the characteristic shear rate). For example, maximum differences in peak velocity were only approximately 10% when using Reynolds number-matched conditions in our previous study (Fig. 4b in [25]). Differences in wall shear stress were much larger (up 50% [25]), but whether such differences influence in vivo clot transport has yet to be determined. Second, inflow from the renal veins was neglected since the vessels are located downstream of the hemodynamic region of interest and do not influence the bulk hemodynamics upstream (e.g., [29, 32]). Even so, renal inflow could have a minor influence on upstream secondary flow, especially during the increased renal flow that occurs following a meal (e.g., [59, 60]). Third, the flow was approximated as steady and the IVC wall was approximated as rigid, although in vivo the vessel deforms subtly in response to breathing (e.g., [61]) and more so during Valsalva maneuver (e.g., [44]). Pulsatility and IVC wall motion are intimately coupled but are challenging to investigate without detailed respiratory-resolved measurements of in vivo boundary conditions, and these are currently not available in the literature. The influence of renal inflow could also be greater under pulsatile conditions. Fourth, an idealized patient-averaged geometry was studied as opposed to a more realistic patient-specific IVC (e.g., [5, 27]), and this idealized model may underestimate the degree of mixing and secondary flow present under true physiological conditions.

Unfortunately, a well-controlled in vitro experiment considering all complexities of IVC mechanics and hemodynamics, including patient anatomical variability, is currently intractable. In future work, phase contrast MRI measurements that resolve the IVC wall motion and hemodynamics in a real patient during normal and deep breathing, Valsalva maneuver, coughing episodes, and exercise could be used to improve the boundary conditions used for preclinical evaluation of IVC filter safety (e.g., migration, perforation, and fatigue fracture resistance) and effectiveness (e.g., clot trapping). Nonetheless, the present study represents an advance over previous preclinical experimental investigations of flow in the human IVC.

5. Summary

This study has produced a set of two-dimensional PIV velocity measurements with clearly-defined boundary conditions that can be used to validate CFD models of the idealized IVC hemodynamic conditions typically used in the preclinical evaluation of IVC filters. The anatomical geometry and the velocity data acquired herein are made publicly available for use in validating computational modeling of in vitro IVC hemodynamics (see Supplemental Material). Future work will extend the validation dataset to embolus-trapping for validation of computational models of embolus transport and capture.

Figure 6:

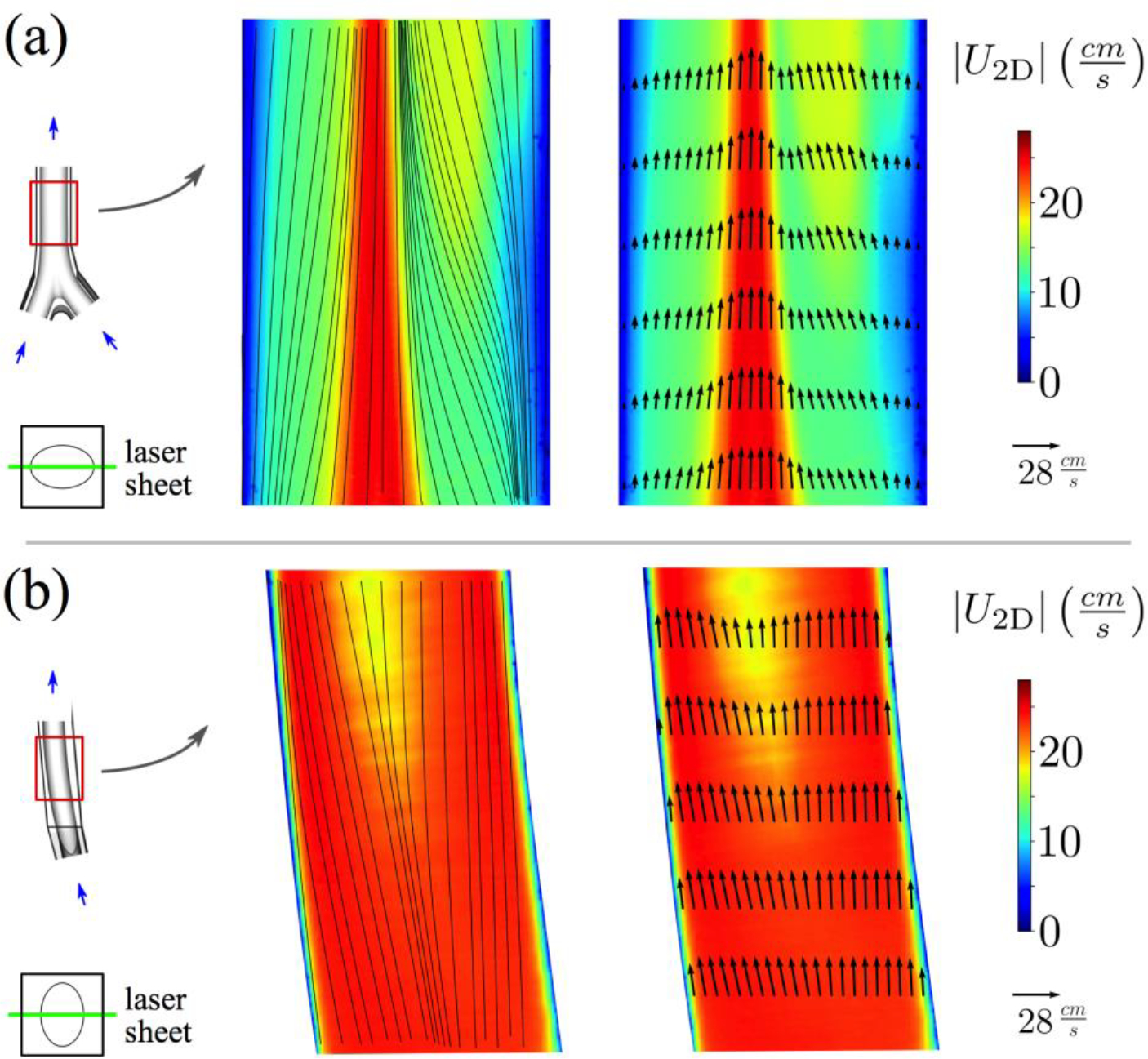
Two-dimensional velocity magnitude contours for (a) coronal and (b) sagittal planes in the infrarenal IVC at the exercise flow rate. In-plane streamlines and velocity vectors are shown on the left and right, respectively.