Kinetic and Thermodynamic Considerations in the Rh-Catalyzed Enantioselective Hydrogenation of 2-Pyridyl-Substituted Alkenes

Abstract

The mechanism of asymmetric hydrogenation of 2-pyridyl alkenes catalyzed by chiral Rh-phosphine complexes at ambient temperature is examined using kinetic, spectroscopic, and computational tools. The reaction proceeds with reversible substrate binding followed by rate-determining addition of hydrogen. Substrate binding occurs only through the pyridine nitrogen in contrast to other substrate classes exhibiting stronger substrate direction. The lack of influence of hydrogen pressure on the product enantiomeric excess suggests that a pre-equilibrium in substrate binding is maintained across the pressure range investigated. An off-cycle Rh-hydride species is implicated in the mild catalyst deactivation observed. In contrast to Ru-phosphine-catalyzed reactions of the same substrate class, the stereochemical outcome in this system correlates generally with the relative stability of the E and Z rotamers of the substrate.

Graphical Abstract

INTRODUCTION

Asymmetric hydrogenation has grown to be an important pharmaceutical reaction class in the past several decades since the earliest successful application of the protocol in the 1980s, including the Rh-catalyzed enamide hydrogenation to produce l-Dopa by Monsanto,¹ Takasago’s Ru-catalyzed menthol synthesis,² and Ir-catalyzed imine hydrogenation for the agrochemical metolachlor for Ciba-Geigy.³ The classic study of Landis and Halpern,⁴ focusing primarily on enamide substrates, remains one of the most comprehensive experimental mechanistic probes of the origin of enantioselectivity in asymmetric hydrogenation. More recently, extensive mechanistic studies have been carried out in Merck’s synthesis of sitagliptin involving a Rh/Josiphos-catalyzed enantioselective enamine reduction.⁵ Other classes of prochiral molecules, including trisubstituted olefins, have also received attention primarily for Ir-catalyzed systems.⁶ Asymmetric hydrogenation of minimally functionalized olefins was developed by the groups of Pfaltz^8a–c and Burgess,^8d who extended Crabtree’s Ir complexes⁷ to include chiral P–N ligands, and a very recent work has extended these systems to the hydrogenation of tetrasubstituted acyclic olefins.^8c Ti, Co, and Ru complexes followed.^9,10 The use of Rh complexes in asymmetric hydrogenation of minimally substituted olefins, where substrate direction is less prominent a feature than with enamides, has been less extensive, and no detailed mechanistic work has been reported. Herein, we report the enantioselective hydrogenation of 2-pyridyl-substituted alkenes 1 using Rh-phosphine catalysts (Scheme 1). We recently reported an enantioselective Ru-phosphine-catalyzed reaction of the same class of substrates, and here we compare the mechanistic details of the two systems.

Scheme 1.

Asymmetric Hydrogenation of 2-Pyridyl-Substituted Olefins

BACKGROUND

The early development of ferrocenyl-based phosphine ligands in asymmetric hydrogenation has been extensively reviewed.¹¹ Successful attempts at hydrogenation of alkenes has largely been limited to substrates bearing polar functional groups or heteroatoms adjacent to the olefin. Recently, researchers from Amgen reported highly efficient and enantioselective hydrogenation of a styrene-type substrate containing a directing hydroxyl substituent catalyzed by Rh using a number of different phosphines including Josiphos-type ligands.¹² The substrate hydroxyl group was found to be essential to achieving enantioselectivity, and the catalyst system offers improvements over Ir(P–N) catalysts in its ability to employ E/Z substrate mixtures.

Asymmetric hydrogenation of substrates of type 1 provides nitrogen heterocycles that are important pharmaceutical building blocks. As part of a recent early-stage program at BMS, an enantiopure pyridyl-pyrrolidine was required, and we explored asymmetric hydrogenation of 1a as a potential route. As part of this work, we reported a mechanistic study of the highly enantioselective hydrogenation of these substrates catalyzed by Ru-segphos, in which we also observed an unusual H/D exchange process between the methanol solvent and the substrate.¹³ In the current work, we reveal that the H/D exchange does not occur in the Rh-catalyzed hydrogenation reaction and that enantioselectivity is much more sensitive to substitution in the pyridyl substrate compared to Ru. Detailed kinetic, spectroscopic, and computational studies give a comprehensive mechanistic picture of the role of substrate 1 functional groups in this reaction system in achieving both rapid reaction rates and high enantioselectivities at ambient temperature and low pressure.

RESULTS AND DISCUSSION

High-throughput screening tools have greatly accelerated the uptake of asymmetric hydrogenation methodology in complex molecule synthesis, especially for practical pharmaceutical applications. A selection of chiral ligands was used in the reaction of Scheme 1 with substrate 1a with the results as shown in Scheme 2. Enantioselectivity is enhanced with electron-withdrawing R-groups para to phosphine in the aryl groups, although the reaction rate is suppressed.¹⁴ The tert-butyl R′-groups appear to be crucial for enantioselectivity. Ligand L1 was chosen for further mechanistic studies.

Scheme 2.

Ligand Screening for the Reaction of Scheme 1

These small-scale screening studies were carried out at a hydrogen pressure of 500 psi and 7.5 mol % Rh with Rh/ligand = 1:1. We next explored the effect of lowering both [H₂] and [Rh]. As shown in Figure 1, in situ reaction monitoring of hydrogen uptake revealed that the reaction of 1a using Rh(cod)₂BF₄/L1 could be carried to quantitative yield in less than 2 h at pressures as low as 10 psi and catalyst loadings as low as 0.25 mol %. The reactions carried out at higher pressures of 250–50 psi were completed within minutes, suggesting that the system may have been under gas–liquid mass-transfer limitations under these screening conditions. Strikingly, and similar to the Ru-catalyzed reactions of this substrate class, enantiomeric excess remained at 79% ee at all pressures.

Figure 1.

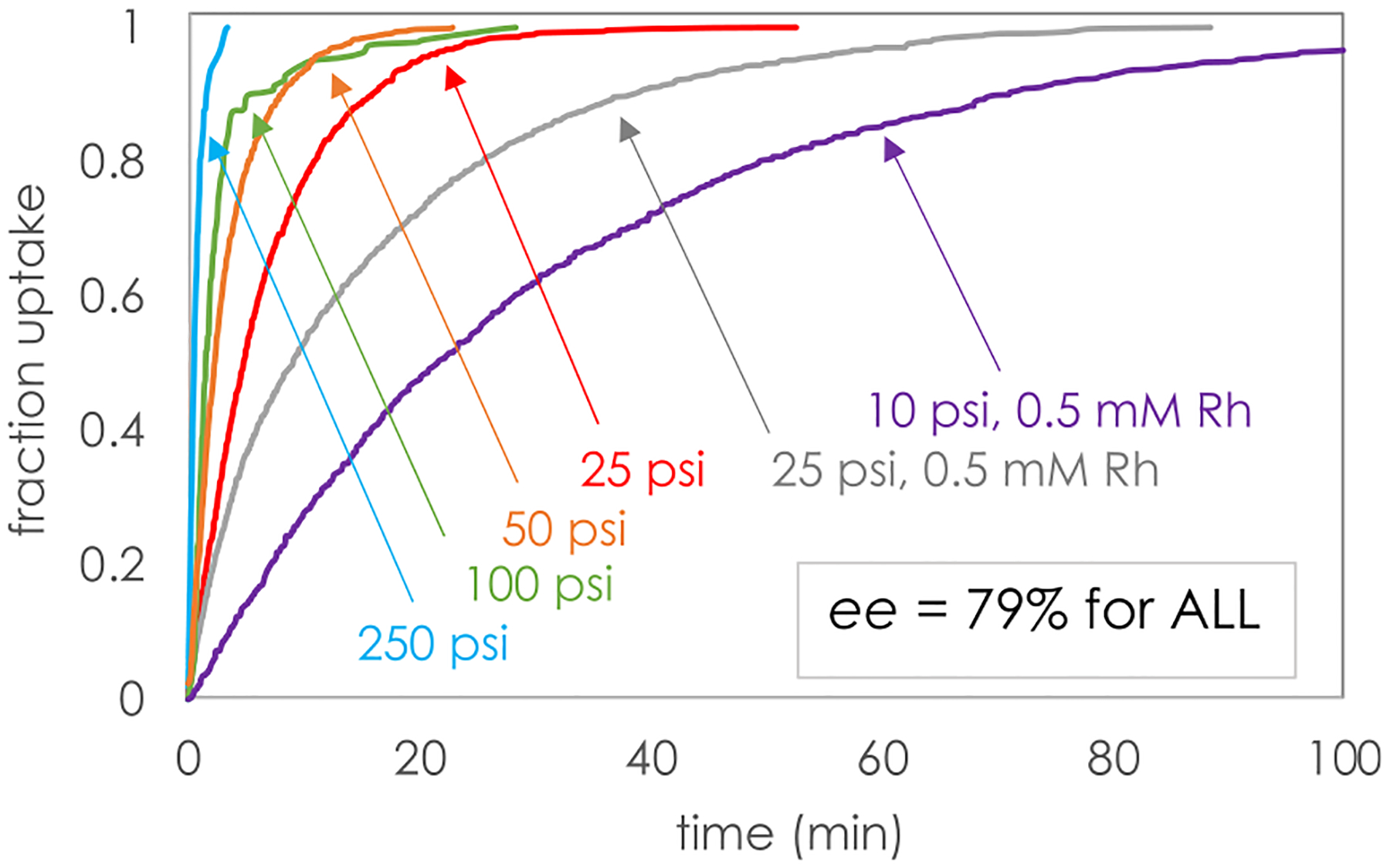
Effect of hydrogen pressure and catalyst loading on the reaction rate, final yield, and enantiomeric excess in the reaction of substrate 1a using Rh(cod)₂BF₄/L1 at 25 °C. All reactions employed 0.2 M 1a except the run at 250 psi, which used 0.1 mM. [Rh] = 1 mM except where noted.

Scheme 3 shows substrate conversion and product ee values for a range of substituted pyridine-pyrroline substrates in the reaction of Scheme 1 using Rh(cod)₂BF₄/L1 under conditions shown in Scheme 3. Several key contrasts with this series of substrates are observed compared to the same reactions catalyzed by Ru-segphos we recently reported. While Ru-segphos-catalyzed reactions gave high ee values across the range of substrates in Scheme 3, in the case of Rh-L1 catalysis, substituents are revealed to have a significant influence on enantioselectivity, with ee values ranging from 89% ee (1g, 1c) to less than 30% ee (1b, 1k). These low ee cases show that substitution on the pyridine ring ortho to the 3-pyrroline group is critical for attaining high enantiomeric excess with Rh/L1.

Scheme 3.

Substrate Variation Effects of Scheme 1 Run at 25 psi, 0.2 M Substrate, 0.5 mol % Rh-L1 for 1 h

A number of features of the substrate scope are similar to what was found with the Ru phosphine system.¹⁴ When the pyridine nitrogen is not ortho to the pyrroline ring, reactivity is lost (substrates 1n, 1o, and 1p). Simple aryl rings lacking nitrogen are inactive under our standard conditions (1q and 1r), again as was found for the Ru system. The hydroxylated substrate 1r, which resembles 2-hydroxyl substituted styrene recently reported to give high ee using Rh phosphine complexes,¹² was inert in our protocol. Addition of NEt₃ as in ref 12 resulted in high yield, albeit with low enantioselectivity. Thiophene instead of pyridine was unreactive (1s). Nitrile substitution resulted in no reaction (1l), presumably due to off-cycle binding of the substrate to Rh, as suggested by NMR studies.

In contrast to the Ru system,¹³ dihydrofuran instead of pyrroline was active but less selective (1t). Substrates with a 2-pyrroline group, where the olefin double bond is conjugated with the protected amine, gave low ee (1x) and, in one case, a sluggish reaction and a reversal of enantioselectivity to −40% ee (1w).

Kinetic experiments using variable time normalization analysis (VTNA)¹⁵ revealed that the reaction exhibits positive-order kinetics in [1a] (Figure 2, top, n ≈ 0.75), first-order kinetics in hydrogen pressure (Figure 2, middle), and close to first-order kinetics in [Rh] (n ≈ 1.2) (Figure 2, bottom).

Figure 2.

Reaction progress kinetics with VTNA for the reaction in Scheme 1 using 1a at ambient temperature. Top: H₂ as noted in legend, [Rh] = 0.001 M, [1a]₀ = 0.2 M; middle: [1a]₀ as noted in legend, [Rh] = 0.001 M, H₂ = 25 psi; bottom: [Rh] as noted in legend, [1a]₀ = 0.2 M, H₂ = 25 psi.

The observed reaction order of 0.75 in the substrate concentration for substrate 1a can be shown to correlate with a binding constant of ca. 3.3 M⁻¹ in a standard Michaelis–Menten model (eq 1, Figure 3). This was corroborated with ¹⁹F NMR titrations¹⁴ for substrate 1d, which exhibits similar kinetics, yielding a binding constant of ca. 3 M⁻¹. This relatively weak binding (compared to Rh phosphine systems with enamide substrates⁴ where K_eq = ca. 10⁴ M⁻¹) corresponds to approximately one-third of the catalyst present with bound substrate at the outset of the reaction while two-thirds remains free.

Figure 3.

General comparison of power law kinetics to the Michaelis–Menten rate expression giving a correlation between order, x = 0.75, and substrate binding constant, K_eq = 3.3 M⁻¹, over the concentration range of the experiments in Figure 2.

$$\text{rate}=a\cdot {\left[\text{sub}\right]}^x\approx \frac{a^{\prime }\cdot \left[\text{sub}\right]}{1+K_{\text{eq}}\cdot \left[\text{sub}\right]}$$ (1)

Substrate binding was also measured for substrate 1k, which, lacking substitution in the 3-position, gives significantly reduced ee. Interestingly, stronger binding was observed for 1k.¹⁴ This difference in binding strength for 1d versus 1k is supported by VTNA analysis giving x = 0.45 for 1k; modeling of the kinetic profile in Figure 4 gives K_eq = 24 M⁻¹, corresponding to eight-fold stronger binding and ca. 80% of the catalyst being substrate bound under initial reaction conditions for 1k. Although the time to reaction completion is similar for substrates 1k and 1d in separate experiments, a competitive reaction using equimolar amounts of 1d and 1k paused after 10 min showing that the stronger binding substrate accounted for more than 90% of the substrate conversion at the time the reaction was interrupted. This implies that competitive binding diverts most of the catalyst toward the reaction of 1k when both substrates 1d and 1k are available to the Rh catalyst.

Figure 4.

Separate and competitive reaction of 0.2 M substrates 1d and 1k in the reaction of Scheme 1 using 0.001 M Rh with ligand L1 and 10 psi H₂. Competitive reaction data taken after 10 min reaction time.

A reaction exhibiting an apparent order in [catalyst] slightly greater than first order by VTNA can be a sign of catalyst deactivation as the rate is observed to decrease over time more rapidly than might be rationalized with a reaction exhibiting first-order kinetics with a constant catalyst concentration. Applying reaction progress kinetic analysis¹⁶ in reactions with 1a, the observed lack of overlay in time-adjusted “same excess” experiments, along with overlay in experiments carried out in the presence of the product, confirms that mild catalyst deactivation occurs but is not caused by product inhibition (Figure 5).

Figure 5.

Time-adjusted reaction progress kinetics for the reaction in Scheme 1 using 1a and Rh-L1 at ambient temperature with [1a]₀ and [2a]₀ as noted in the legend. [Rh] = 0.001 M, H₂ = 25 psi. Lack of overlay in the time-shifted curve blue, along with the overlay between the blue curve and the open circle points, implicates catalyst deactivation rather than product inhibition.

Clues about possible catalyst deactivation arise from detailed NMR studies of the interaction of Rh-L1 with hydrogen which revealed the presence of a Rh-hydride species with a peak at ca. −22.7 ppm in ¹H NMR.¹⁴ Full characterization allowed identification of the Rh-L1-H complex (Scheme 4) and was completed using a variety of NMR techniques. ³¹P NMR showed that the signal for P bound to aromatic groups is a singlet. NOESY spectra revealed correlation of the hydride only with the ^tBu groups and not with the aromatic groups. Similarly, ¹H–³¹P HMBC revealed correlation of the hydride with phosphorus bound to alkyl but not with aromatic groups. Decoupling the aromatic P signal resulted in no change to the ¹H hydride signal, while decoupling the alkyl ³¹P signal resulted in the ¹H hydride signal changing from a triplet to a doublet. This indicates coupling of the hydride to Rh and the alkyl P only and not to the aromatic P.¹⁴ The aromatic P appearing as a singlet indicated no coupling to Rh or the alkyl P, which is observed in chelated species. P–P coupling, not observed here but often seen in chelating species, may arise from “through-space” coupling as detailed by Hierso et al.¹⁷ These findings reveal that the Rh–H species is formed with Rh bound only to the phosphine atom containing the ^tBu groups rather than chelating to both phosphines.

Scheme 4.

Rh-L1-H Hydride Complex Characterized by ¹H, ¹³C, and ³¹P NMR Spectroscopy

The presence of an Rh hydride species raises the question of whether this is an active catalytic species or an off-cycle spectator. While the classic asymmetric hydrogenation mechanism for reactions of enamides catalyzed by cationic Rh species invokes pre-equilibrium substrate binding followed by oxidative addition of hydrogen, proposals for the opposite order of addition have been made.¹⁸ Evidence that the Rh-L1-H hydride species shown in Scheme 4 is most likely an inactive spectator species comes from ³¹P NMR studies as shown in Figure 6. The Rh hydride species Rh-L1-H exhibits a doublet-of-doublets near 124 ppm that does not change when substrate 1d is added, while the signal for Rh-L1 is suppressed, suggesting that the hydride species does not appear to interact with the substrate and that it may be responsible for the catalyst deactivation detected from the data in Figure 5. This likely renders the Rh–H species inert toward substrate binding and reaction, decreasing the concentration of active Rh in the catalytic cycle.

Figure 6.

³¹P NMR studies of Rh-L1 under hydrogen in the absence (bottom spectrum) and presence (top spectrum) of 1d.

Taken together, these kinetic and spectroscopic results point toward a mechanism where substrate binding precedes rate-determining oxidative addition of hydrogen, as was found for Ru catalysts with this substrate class. We turned to calculations to probe the origin of enantioselectivity. Computational studies of Rh-catalyzed asymmetric hydrogenation have largely been directed at enamide substrates, where much stronger binding occurs. Substrate-first proposals, supporting the classic experimental studies of Landis and Halpern,⁴ and H₂-first¹⁸ mechanisms have both been investigated.

DFT calculations of the relative stability of the rotamers of the substrates formed from rotation around the pyridine-pyrroline bond show that the E conformation is more stable than the Z one (eq 2). Strikingly, in most cases, the magnitude of the difference in stability bears a reasonable correlation with the hydrogenation product enantiomeric excess (Figure 7).

Figure 7.

Computational equilibrium constant for relative stability of the E and Z conformers of substrates 1 vs the experimental ratios for products 2 [S]/[R]. Structures are shown for E-1e and E-1k, which follow the trend, and for E-1g and E-1h, which give identical experimental ee values but very different computed stabilities outside the trend. Calculations by three different functionals as noted in the legend. Shaded area shows ca. ±0.5 kcal/mol from the trend.¹⁴

(2)

Such a correlation between rotamer stability and product enantiomeric excess was not observed for this substrate class in recent studies of Ru-phosphine catalyzed asymmetric hydrogenation, highlighting the difference in the reaction mechanism for the two catalytic systems. Indeed, such a correlation is surprising because it suggests that factors related to the strength of binding to the asymmetric catalyst or reactivity of the bound species are less important than the fundamental thermodynamic stability of the substrate conformers themselves.

Calculations show that there are four possible diastereomeric species of E-1 and Z-1 bound to the catalyst, with the pyridine ring “up” and “down” for each.¹⁴ The calculations also show the positioning of the pyrroline double bond for optimal proximity to Rh to undergo subsequent hydrogenation (Scheme 5, top).¹⁴ The more stable E rotamer approaches Rh with the pyridine ring “down,” while for the Z rotamer, the approach is inverted and the pyridine ring is “up.” In agreement with the DFT calculations, a combination of 2D NMR methods confirmed the structures of the diastereomeric species of substrate 1d bound to catalyst Rh-L1.¹⁴

Scheme 5.

Calculated Structures of Substrate Rotamers Bound to Rh-L1 with Pyrroline Double Bond Positioned in Optimal Proximity to Rh for Hydrogenation

Calculations also show that Rh interacts with the pyridine nitrogen and that there is no direct interaction between Rh and the pyrroline double bond (Scheme 5, bottom). This supports the designation of these substrates as minimally functionalized olefins and is in contrast to Rh-catalyzed hydrogenation of enamides, where multiple interactions between Rh and the substrate play a significant role in achieving high enantioselectivity.^4,18

The combined processes of the rapid equilibration of the conformers of substrate 1 shown in eq 1, their reversible addition to catalyst Rh-L1, and the subsequent rate-determining addition of hydrogen describe a case of the Curtin–Hammett principle (Scheme 6),¹⁹ where the relative rates of formation of the S and R hydrogenation products will be formally dictated by the relative magnitudes of the binding equilibrium constants K_eq^Z and K_eq^E, the relative magnitudes of the kinetic constants k_rds^S and k_rds^R, as well as the relative stability of the rotamers as given by K_eq. This means that for substrates that follow the correlation shown in Figure 7, such as E-1-I, where rotamer relative stability dominates the outcome, the product of the kinetic term (k_rds^E/k_rds^Z or ΔG^‡E/ΔG^‡Z) and the thermodynamic term (K_eq^E/K_eq^Z or ΔG_eq^E/ΔG_eq^Z) is close to 1. In these cases, it may be suggested that enantioselectivity is guided primarily by the approach of the E-1 and Z-1 rotamers of the substrate to the catalyst to form intermediate species E-1-I and Z-1-I, and differential binding or reactivity is less influential. In cases of substrates where the correlation of product ee with rotamer stability fails, such as 1g and 1h, the kinetic and thermodynamic terms may play a more significant role.

Scheme 6.

Curtin–Hammett Description of the Role of Equilibrium and Kinetic Constants in Product Enantioselectivity

Table 1 shows the results of DFT calculations that were carried out to determine the free energies of the bound substrates E-1-I and Z-1-I and their transition state free energies for the rate-determining oxidative addition of hydrogen for a selection of substrates that follow and do not follow the correlation with ΔG_eq in Figure 7. The final row in the table shows the product of the kinetic and equilibrium contributions as given in Scheme 4. The closer to unity this value is, the closer the reaction will follow the correlation in Figure 7.

Table 1.

Computed Kinetic and Thermodynamic Contributions to Product Enantiomeric Excess in the Hydrogenation Reactions of Scheme 1^a

substrate	1e	1k	1g	1h
ΔG‡E	8.14	9.02	7.60	9.50
ΔG‡Z	7.58	8.06	7.54	7.35
ΔG‡E/ΔG‡Z	1.07	1.12	1.01	1.29
ΔGeqE	−8.68	−10.12	−12.39	−10.59
ΔGeqZ	−9.84	−10.29	−13.86	−10.62
ΔGeqE/ΔGeqZ	0.88	0.98	0.89	1.00
product b	0.95	1.10	0.90	1.29

^aFree energy values in kcal/mol.

^bProduct = (ΔG^‡E/ΔG^‡Z) * (ΔG_eq^E/ΔG_eq^Z).

Substrates 1e and 1k, which exhibit high and low enantioselectivity, respectively, follow the rotamer stability correlation shown in Figure 7. Table 1 shows that in the case of 1e, E-1-I is slightly more stable and Z-1-I slightly more reactive, while for 1k, the opposite holds. The correlation with rotamer stability arises because the two terms nearly compensate one another.

Table 1 shows that the cases of substrates 1g and 1h, both of which give experimental values that deviate significantly from the correlation in Figure 7, deserve further discussion. For 1g, the ratio of transition state energies ΔG^‡E/ΔG^‡Z lies very close to 1, and therefore, we expect that the discrepancy between the experimental ee and the rotamer stability should arise from the kinetic term. For 1h, the opposite holds. Table 1 does show deviations from unity in each case, however, in the opposite direction from that predicted by the Curtin–Hammett relationship. This indicates that product 2g should exhibit lower ee than dictated by the rotamer stability and that product 2h should exhibit higher ee than predicted by rotamer reactivity. This conundrum may be addressed by considering that the calculated transition states for rotamer interconversion in the cases of both 1g and 1h are less than the 3.7 kcal/mol barrier calculated for the diffusion-controlled substrate–catalyst interaction,²⁰ while the calculated transition state barriers for substrates 1e and 1k that follow the trend in Figure 7 are lower than this value. The interconversion between the minor Z-1 and major E-1 rotamers for 1g and 1h may occur more rapidly than their interaction with the catalyst, thus altering the relative concentration of E-1 and Z-1 from that expected from the relative rotamer thermodynamic stability. In general, however, the correlation between the relative stability of E-1 and Z-1 and the product enantiomeric excess holds within reasonable errors of the DFT calculations.

CONCLUSIONS

Mechanistic studies of the asymmetric hydrogenation of trisubstituted heterocyclic alkenes catalyzed by Rh phosphine catalysts were carried out using kinetic, spectroscopic, and computational tools. The reaction proceeds under mild temperature and pressure. Product enantioselectivity appears to be governed largely by the relative stability of the E and Z isomers of the substrate, in contrast with results from hydrogenation reactions employing Ru-phosphine catalysts for the same substrate class. The observation of a persistent Rh-hydride species indicates that it exists off the main catalytic cycle. The kinetic data implicate a mechanism involving reversible substrate binding followed by rate-determining oxidative addition of hydrogen. This work expands our understanding of asymmetric hydrogenation into a little-studied but pharmaceutically important substrate class.