Deep Learning-based Fast Volumetric Imaging using kV and MV Projection Images for Lung Cancer Radiotherapy: A Feasibility Study

Abstract

Purpose:

The long acquisition time of CBCT discourages repeat verification imaging, therefore increasing treatment uncertainty. In this study, we present a fast volumetric imaging method for lung cancer radiation therapy using an orthogonal 2D kV/MV image pair.

Methods:

The proposed model is a combination of 2D and 3D networks. The proposed model consists of five major parts: 1) kV and MV feature extractors are used to extract deep features from the perpendicular kV and MV projections. 2) The feature-matching step is used to re-align the feature maps to their projection angle in a Cartesian coordinate system. By using a residual module, the feature map can focus more on the difference between the estimated and ground truth images. 3) In addition, the feature map is downsized to include more global semantic information for the 3D estimation, which is useful to reduce inhomogeneity. By using convolution-based reweighting, the model is able to further increase the uniformity of image. 4) To reduce the blurry noise of generated 3D volume, the Laplacian latent space loss calculated via the feature map that is extracted via specifically-learned Gaussian kernel is used to supervise the network. 5) Finally, the 3D volume is derived from the trained model. We conducted a proof-of-concept study using 50 patients with lung cancer. An orthogonal kV/MV pair was generated by ray tracing through CT of each phase in a 4D CT scan. Orthogonal kV/MV pairs from 9 respiratory phases were used to train this patient-specific model while the kV/MV pair of the remaining phase was held for model testing.

Results:

The results are based on simulation data and phantom results from a real Linac system. The mean absolute error (MAE) values achieved by our method were 57.5 HU and 77.4 HU within body and tumor region-of-interest (ROI), respectively. The mean achieved peak-signal-to-noise ratios (PSNR) were 27.6 dB and 19.2 dB within the body and tumor ROI, respectively. The achieved mean normalized cross correlation (NCC) values were 0.97 and 0.94 within the body and tumor ROI, respectively. A phantom study demonstrated that the proposed method can accurately re-position the phantom after shift. It is also shown that the proposed method using both kV and MV is superior to current method using kV or MV only in image quality.

Conclusion:

These results demonstrate the feasibility and accuracy of our proposed fast volumetric imaging method from an orthogonal kV/MV pair, which provides a potential solution for daily treatment setup and verification of patients receiving radiation therapy for lung cancer.

1. Introduction

In clinical radiation oncology practice, a 4D computed tomography (4DCT) scan is commonly performed during simulation for lung cancer patients to evaluate respiratory motion. Images derived from this 4DCT study, such as the average composite image and the maximum intensity projection (MIP) are then used for treatment planning. At the time of treatment, a cone-beam computed tomography (CBCT) scan is often acquired; the subsequent volumetric image is then registered with the planning CT to accurately position the patient. Compared with conventional 2D kilovoltage (kV) radiography and megavoltage (MV) portal imaging, the volumetric image provided by a CBCT scan shows finer anatomical details in 3D space as well as better soft tissue contrast by removing the underlying and overlying anatomy. CBCT also enables fine-scale patient positioning in combination with six degrees of freedom (6 DoF) of couch motion.

A linear accelerator (linac)-mounted CBCT imaging system is limited by the rotation speed of the gantry. A CBCT acquisition takes approximately one minute; if a 4D or phase-gated CBCT protocol is used, it may take up to several minutes, which is often comparable to treatment beam-on time. A long image acquisition time may increase patient discomfort, which in turn can increase intra-fraction setup errors. Another issue is that if each patient spends more time in the vault, clinic throughput decreases. More importantly, a long acquisition time discourages a second CBCT scan for the verification of patient positioning to ensure accurate dose delivery. Specifically, in current clinical practice a patient is often treated immediately after the treatment couch is repositioned based on the CBCT-planning CT registration without taking another verification CBCT to validate the patient position. If the couch fails to move correctly due to a mechanical or communication fault with the treatment console, these errors may not be detected. Such errors, though rare, can be catastrophic since an erroneous shift can move a target out of the treatment field or a critical organ into it. For stereotactic body radiation therapy (SBRT) and stereotactic radiosurgery (SRS), it is common to have a time gap of several minutes between CBCT acquisition and confirmation from the supervising physician. This delay can mean that post- CBCT patient movement may go undetected. While repeat volumetric imaging is a potential solution, technological innovations are needed to reduce imaging time. Fast on-board volumetric imaging could allow for repeat verification volumetric imaging, which would improve treatment accuracy clinical efficiency.

Recently, several deep learning-based methods have been introduced to reconstruct volumetric images from two orthogonal 2D kV x-ray images.^1–6 However, as current linac imaging systems cannot simultaneously acquire two orthogonal x-ray images, gantry rotation is still required to take the second image. There are two potential ways to eliminate this gantry rotation to further reduce the acquisition time. One approach is to estimate a volumetric image from a single 2D kV projection, but this is challenging because the problem is much more difficult than using 2 orthogonal projections. Li et al. proposed machine learning-based 2D–3D registration methods to estimate a 3D volumetric image from a 2D projection.^7,8 However, the performance of this method is affected by the image similarity between the test image and those in the atlas database. Shen et al. proposed to use a deep neural network to generate synthetic CT images using only a single anterior-posterior projection view.⁹ Shen et al. showed that their method outperformed Li’s registration-based method when the patient position deviates slightly from that of the reference scan, which is common in radiation therapy as patient position varies on the treatment couch.⁹ The contribution of Shen et al. work is to develop a deep neural network to learn the feature-space transformation between a 2D projection and a 3D volumetric CT image, and used this trained model to derive volumetric CT image from an anterior-posterior single projection view. We previously proposed to develop an advanced perceptually supervised generative adversarial network to learn a patient-specific 2D to 3D transformation in order to provide an image volume from a single 2D projection at an arbitrary projection angle.¹⁰ We have found that the limited information contained in a single projection results in image quality that varies with the view angle of the projection.

We investigated another potential solution to eliminate gantry rotation for fast on-board volumetric imaging by using deep learning to generate 3D images from a pair of 2D orthogonal kV and MV images.¹¹ The two orthogonal projections provided more spatial information than the single image we used in our previous work. Because the kV and MV imaging systems are mounted orthogonally on a conventional linac, the 2D kV/MV image pair can be acquired rapidly without the need for gantry rotation. The contribution of this work is that adding an orthogonal MV projection to original kV can include additional tissue information as compared with single original kV due to the collection of the attenuation coefficients to the MV planar which is perpendicular to kV planar. Juan et al. proposed a 3D tomographic patient models that can be generated from two-view scout images using deep learning strategies, and the reconstructed 3D patient models indeed enable accurate prescriptions of fluence-field modulated or organ-specific dose delivery in the subsequent CT scans.¹² The contribution of their work is that 3D tomographic attenuation models generated by deep learning-based model from two-view scout images can be used to prescribe fluence-field-modulated or organ-specific CT scans with high accuracy for the overall objective of radiation dose reduction or image quality improvement for a given imaging task.

We hypothesize that the proposed method could be an alternative to CBCT to position lung cancer patients for radiation therapy with a much shorter acquisition time, and this method could also serve as a rapid post-CBCT check to ensure the correct alignment of critical internal anatomy right before treatment. However, the inferior estimated image quality, such as blurry and inhomogeneity, exists due to the input projection is still few. A potential challenge is the replacement of one of the kV views with an MV view. The MV projection image may be degraded as compared to kV and thus reduce more information as compared to kV. In this current study, we improve our previous method¹¹ via two additional strategies. First, a convolution-based reweighting is aimed to increase the uniformity of the derived the volumetric image. Then, a Gaussian kernel-based Laplacian loss is utilized for the deblurring. The main goal of this work is to perform patient positioning verification and repositioning via the generated volumetric image. The other contribution of this work includes more focus on radiotherapy and the validation of patient setup using anthropomorphic phantom. As compared to existing two-view work, the proposed method is patient-specific and re-training is needed for a different patient.

2. Methods and materials

2.A. Overview

Conventional linacs have orthogonally-mounted kV imaging and MV portal imaging systems. The goal of this work is to use a kV/MV image pair to provide more spatial information without the need for gantry rotation during image acquisition to derive a 3D image that accurately represents the true 3D anatomy. However, there are challenges. Notably, the MV projection images have much lower soft tissue contrast compared to the kV projection images. In addition, this approach is faced with an ill-posed image reconstruction problem caused by insufficient angular sampling due to only using two projections. To address these issues, first, a residual module with convolution-based re-weighting scheme was used to include more global semantic information for the 3D image estimation. The aim was to reduce image inhomogeneity. The resulting images have textured, blurry noise. To reduce this noise at a certain spatial frequency that has patchy or blurring appearance, an auto-learned Gaussian kernel that represents the blurry noise was used with Laplacian loss to suppress the noise.

Figure 1 outlines the process for generating a 3D image. The training and the inference steps followed the same feed-forward path of the feature matching network. The training dataset consisted of two perpendicular 2D projections (n°±90° for kV P_kV ∈ R^h×d and n° for MV P_MV ∈ R^h×w) and the 3D CBCT/CT volume I ∈ R^H×W×D, which was derived by image reconstruction from a sufficiently-sampled set of kV projection images. The proposed network Using the 2D projections {P_kV, P_MV} as input, the proposed network generated the volumetric image $\overline{I}\in R^{H\times W\times D}$. The corresponding 3D CBCT/CT I was used as the ground truth to supervise the network-based estimation model. In this work, the h, w, d of projection images were set to 384, 512, 512 pixels, and the H, W, D of output image were set to 192, 512, 512 pixels.

Figure 1.

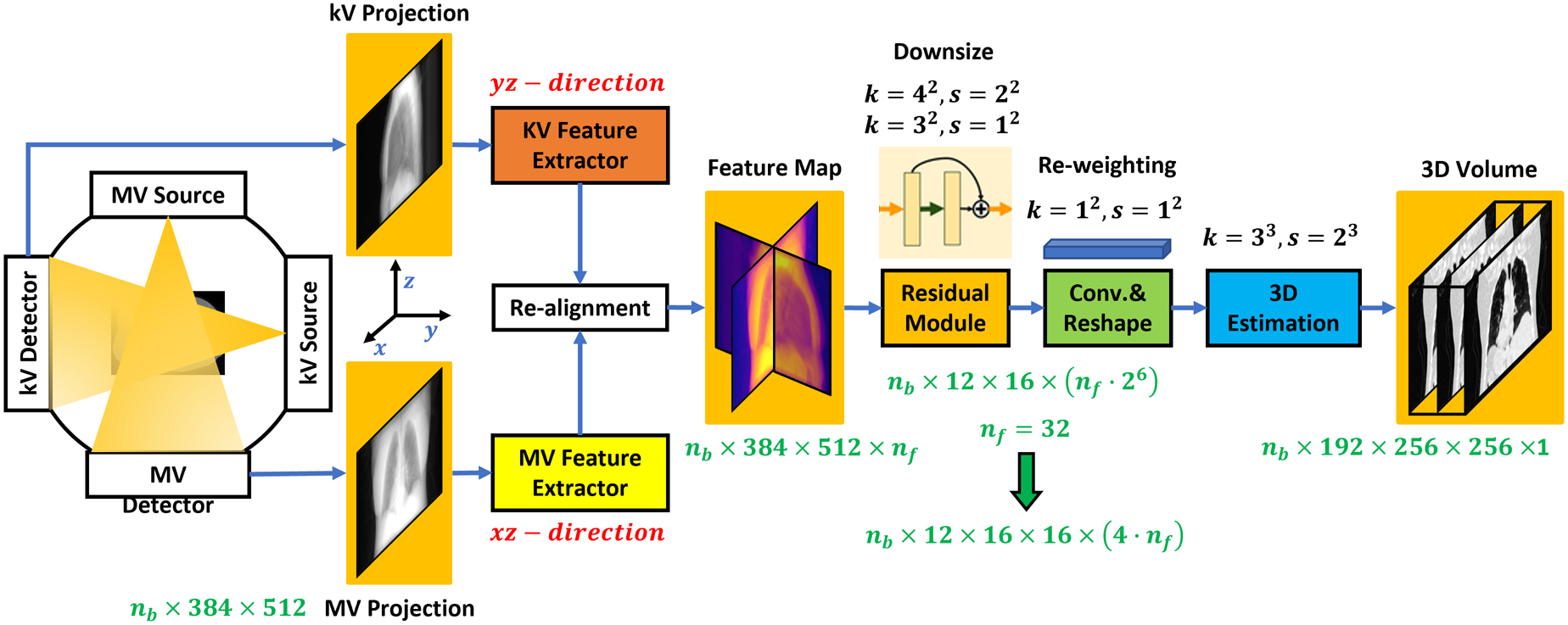
The workflow of the proposed deep learning-based 3D image estimation method is represented by a flow chart. Arrows point in the direction of the feed-forward path.

2.B. Generative network architecture

As can be seen from Figure 1, the proposed network consists of six basic modules: a kV feature extractor, MV feature extractor, feature re-alignment module, residual module, convolutional re-weighting and reshaping module, and 3D estimation module. The kV feature extractor and MV feature extractor are used to explore 2D features in the respective kV and MV projection images. These feature extractors are implemented via 2D convolutional neural networks (CNNs) and share similar network structures but are optimized with different learnable parameters. After optimization, the two feature extractors output feature maps with resolution of h × d × n_f and h × w × n_f from kV and MV projections, respectively.

Note that the integral of the 3D CT accumulated along the projection angles (n°±90° of kV and n° of MV) should be directly correlated to these two feature maps. To register these two feature maps, we first used 3D re-alignment based on the angles of the two projections. This step re-directs and warps the feature map so that it can be transformed back to the 3D Cartesian coordinate system. Additionally, d was set equal to w to streamline the network Thus, after re-alignment, a feature map has dimensions of h × d × (2 · n_f) where n_f = 32. As a result, the feature map dimensions are 384×512×64, which is a multi-channel 2D feature map. The re-alignment denotes the rotate the 2D feature maps in 3D space. For kV or MV projection image, we first used several 2D convolutional layers to generate its feature maps, this feature map is then a 3D tensor manner since we have several convolutional kernels and each kernel generate one channel feature map. Then, we regarded this multi-channel 2D feature map as 3D manner image and rotate it to align with the direction that is perpendicular to the kV or MV. The rotating is performed via tensorflow’s operator “tfa.image.rotate”.

Then a residual module is used to explore more features and downsize the resolution of feature map. The residual module includes five 2D convolutional residual blocks, each with one layer of kernel size of 4×4 and step size of 2×2, and the other one layer of kernel size of 3×3 and step size of 1×1. Thus, after the residual module, the feature map dimensions are $\frac{h}{2^5}\times \frac{d}{2^5}\times \left(2^6·n_{\text{f}}\right)$.

Then, a convolutional layer with kernel size of 1×1 and step size of 1×1 is used to re-weight the feature map. Via deep learning, the re-weighting can assign different weights for different feature map channels. A tensor reshaping operator is used to reshape the feature map to the size of $\frac{h}{2^5}\times \frac{d}{2^5}\times 16\times \left(4·n_{\text{f}}\right)$. Since w = h = 512, the derived feature map dimensions can be re-written as $\frac{h}{2^5}\times \frac{w}{2^5}\times \frac{d}{2^5}\times \left(4·n_{\text{f}}\right)$, which is a 3D feature map with 4 · n_f channels. Finally, a 3D estimation module, which consists of four deconvolutional layers, is used to derive the estimated 3D volume $\overline{I}\in R^{H\times W\times D}$.

The network-based model is supervised to generate a volumetric image that closely approximates the true 3D anatomy by using image difference loss calculated between the ground truth volume I and the estimated image $\overline{I}$ during training. During inference, the trained network accepts kV and MV projections as inputs and selects the same projections angles as compared to the training kV and MV projections angles to derive the volumetric image. More details of the network can be found in Supplement 2.B.1–2.B.4.

2.C. Numerical training

In our current clinical practice, kV/MV paired images are not routinely used for patient positioning. In order to evaluate the feasibility of the proposed method, we generated kV/MV image pairs by ray tracing through each CT phase from the ten phases in a 4DCT study in order to simulate the combination of kV/MV pairs that could be acquired when a patient is on the treatment couch. Specifically, the 4DCT images of 50 patients with lung cancer were collected at random from an institutional database and anonymized. All of these 4DCT images were acquired by a Siemens SOMATOM Definition AS CT scanner with a resolution of 0.977×0.977×2mm³. Each 4DCT study consists of CT images across 10 respiratory phases.

Synthetic kV and MV images were generated at respective gantry angles of 0° and 270° by accounting for the geometry of the imaging systems on a Varian (Palo Alto, CA) Truebeam linac in a forward projection through each of the phase-binned CT images. To generate the MV portal image, the HU number on CT image was first converted to a linear attenuation coefficient. The converted linear attenuation coefficient was assumed to be at 40 keV given that the CT was acquired at 120 kVp. The density and linear attenuation coefficient of lung, adipose, soft tissue, and cortical bone at 40keV and 2MV are looked up from (National Institute of Standards and Technology) NIST. The converted 40 keV linear attenuation coefficients on the CT images were then interpolated by the looked-up values to generate the linear attenuation coefficients at 2MV, given that the portal imaging field is usually 6MV. The generated 40 keV and 2MV linear attenuation coefficient maps were then forward projected to simulate kV and MV images respectively, based on the geometry of the imaging systems. Focal spot size and scatter were not simulated during the forward projecting process.

This study design differs from many deep learning strategies, where models are trained using data from a large patient cohort. In this work, the model is patient-specific. Training was based on 9 of 10 phase-binned CT images from an individual patient while the remaining phase was withheld for model testing.

More specifically, for each patient, our networks were trained using the kV/MV pairs and CTs from 9 phases and tested using the kV/MV pair of the remaining phase. We repeated this procedure 10 times for each patient in order to test each phase with its inference model trained on the data from the other 9 phases. This approach ensured that the extremes of inspiration and expiration were tested. We repeated these patient-specific training and testing procedures for 50 patients.

The investigated deep learning networks were designed using Python 3.6 and TensorFlow and implemented on an NVIDIA Tesla V100 GPU that had 32GB of memory. Optimization was performed using the Adam gradient optimizer. The learning rate was 2e-4.

2.D. Anthropomorphic phantom validation

To demonstrate the patient positioning accuracy of the proposed method, antropomorphic phantom studies were performed. For head and neck site, we scanned the phantom on an EDGE Linac (Varian Medical Systems, Inc., Palo Alto, CA) using on-board CBCT (100 kVp, 270 mAs, 1000 projections per scan, full fan), as well as 90° kV (85 kVp, 5 mAs, imager distance of 50 cm) and 0° MV (6 MV, high quality protocol, 3MU, imager distance of 50 cm) projection images with known translations (couch shift from treatment iso by either 1 cm, 2 cm or 3cm laterally or vertically) on the phantom to collect training data. For chest site, we scanned the phantom using on-board CBCT (125 kVp, 270 mAs, 1000 projections per scan, half fan), as well as 90° kV (100 kVp, 5 mAs, imager distance of 50 cm) and 0° MV (6 MV, high quality protocol, 3MU, imager distance of 50 cm) projection images with known translations. These translations used for training includes the couch shift from treatment iso by 1 cm, 2 cm and 3cm, respectively laterally and vertically, respectively on the phantom to collect training data (kV, MV and CBCT).

The testing data was collected by the couch shift of both 1.5 cm laterally and vertically, which is different from the training data. The kV and MV of testing data is used as input projections. The volumetric image generated from the testing input projections by the proposed method (the model trained on collected training data) was then fused with the CBCT image, which was taken without any shifts. 6 degree-of-freedom (6DoF) couch translational and rotational movement were used for repositioning. The fusion is performed via rigid registration in Velocity. Fig. 2 shows the image of the phantom. We then compared the shift with known shift (which was taken as ground truth).

Figure 2.

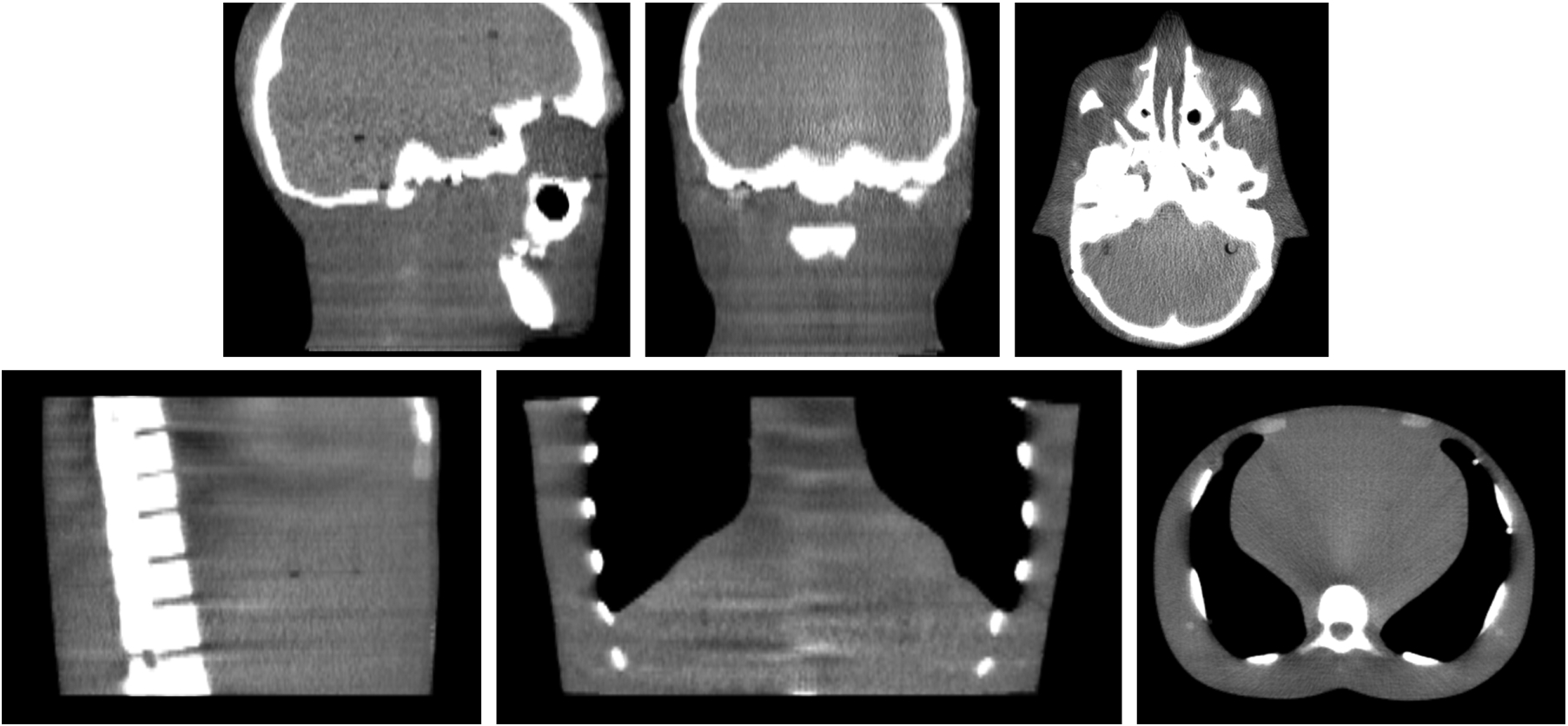
The first row shows the CBCT scan of the head and neck site. The second row shows the CBCT scan of the chest site.

For patient study, the generated images were evaluated in a region of interest (ROI) surrounding the gross lung tumor using three quantitative metrics: mean absolute error (MAE), peak signal to noise ratio (PSNR) and normalized cross correlation (NCC). The MAE quantifies the absolute difference between the predicated image and ground truth CT while PSNR compares the noise level between these images. NCC is a similarity metric used for same-modality image registration, pattern matching and other image analysis tasks. Furthermore, these same metrics were used to evaluate the entire image volume for a global assessment of image quality. P-values calculated via Student’s t-test are reported between the proposed and comparing methods’ results. P-values that are less than 0.005 was taken as criteria to indicate the significance of the comparison.

3. Results

3.A. Parameter setting and ablation study

The performance of the proposed model depends on the hyperparameters setting of Eq. (1). We selected the optimal hyperparameters based on the experimental results shown in Table 1* of Supplement. Different kV/MV angle setup was tested and shown in Table 2* of Supplement. The performance of the trained model via different number of phases were also evaluated and shown in Figure S-1 of Supplement. To evaluate the efficacy of the used residual module and convolution-based reweighting, ablation study was performed and summarized in Table 3* of Supplement.

3.B. Comparison with state-of-the-art on patient simulation

To demonstrate the superiority of the proposed method, we compare our proposed method with our previous method, which is a single onboard kV setting only method, called as TransNet.¹⁰ We also compared the proposed method with using two orthogonal projections only. In this case, rather than using perpendicular kV and MV, we used two orthogonal MV projections as input. Fig. 3 shows the result of using 0° MV and 90° kV as model input for proposed method, (i) the two orthogonal MV method (proposed method taken 0° MV and 90° MV as input), (ii) the single onboard kV setting only method (TransNet using 90° kV taken as input) and (iii) the two orthogonal kV method (directly used 2 kV projections for rigid registration). The estimated CT via (i) is blurrier and has greater differences in HU values as shown in (d1) of Fig. 3. As compared to (i), the proposed method improves image quality and shows more small structural details on lung windows ((c2) of Fig. 1. The estimated CT via (ii) is a degradation of the proposed method. This is because the lower image quality of MV provides worse information as compared to kV/MV setup. The profile of the red dashed line (e1) in Fig. 3 shows that that the proposed method is in better agreement with the ground truth. As evident in the semi-log histogram (e2) in Fig. 3, the TransNet method’s results (blue and orange lines) are less well aligned with the ground truth (red line) than proposed. The result of (iii) does not have the image quality degradation issue since it is derived by directly shifting the CT image via the shifts obtained by rigidly matching the two orthogonal kV projections to the DRR of the CT image. However, the kV/MV setting of the proposed method is gantry rotation free while the other two-view methods, including (i) and (iii), are not.

Figure 3.

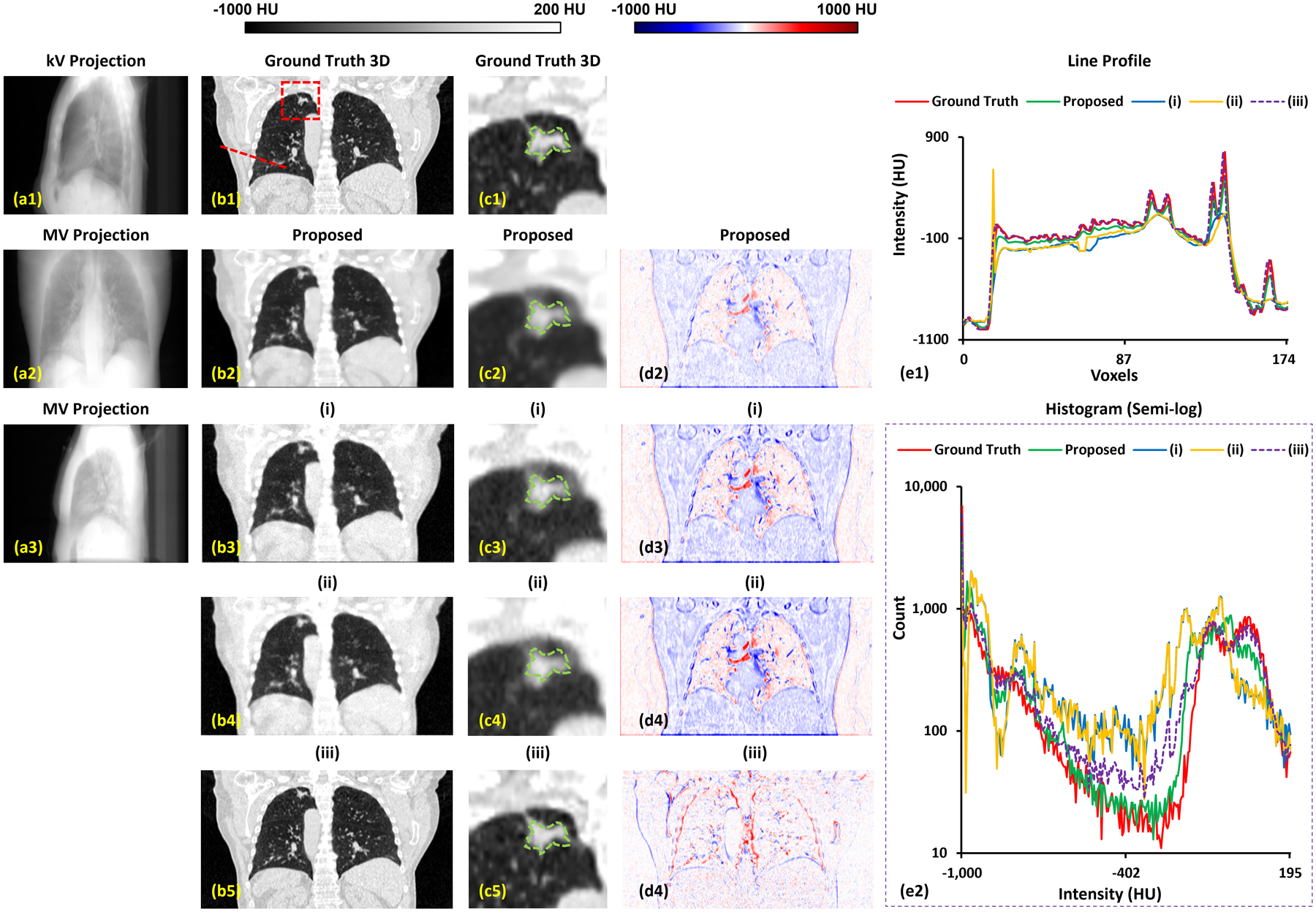
A representative case of proposed method and comparing methods (i), (ii) and (iii). The 1^st column shows input kV and MV forward projection images. The MV image of (a3) is used in method (i). The 2^nd column shows coronal slices of the ground truth CT and the corresponding estimated slice derived by the proposed method and comparing methods (i) and (ii). The 3^rd column shows the region surrounding the tumor on the same slice, as indicate by the red rectangle in the 2^nd column. Dashed green circle denotes the manual contour of tumor. The 4^th column shows the difference images of the predicted image as compared to ground truth image. The 5^th column shows profiles across the CTs corresponding to the red dashed line in (b1) and a histogram of HU values.

Table 1 lists the quantitative results from 50 cases with 3D images generated via proposed method of using 0° MV and 90° kV as input and TransNet using either 0° MV or 90° kV as input. The MAE value achieved by our method for the 50 cases reached a mean value of 57.5 HU and 77.4 HU within the body and the tumor ROI, respectively. The PSNR reached at a mean value of 27.6 dB and 19.2 dB within body and tumor ROI, respectively. The NCC mean value was 0.97 and 0.94 within body and tumor ROI, respectively. In Table 4* of Supplement, p-values calculated via Student’s t-test are reported between the proposed and TransNet results, all of which were less than 0.005.

Table 1.

Numerical comparison result of proposed method and comparing methods.

Body	MAE (HU)	PSNR (dB)	NCC
Proposed	57.5±21.9	27.6±3.3	0.97±0.02
(i)	87.2±21.4	25.7±2.6	0.95±0.05
(ii)	89.5±21.7	25.6±2.9	0.94±0.04
Tumor ROI	MAE (HU)	PSNR (dB)	NCC
Proposed	77.4±14.6	19.2±2.7	0.94±0.04
(i)	108.7±13.7	17.3±2.7	0.88±0.06
(ii)	110.3±14.5	17.5±2.6	0.87±0.08

3.C. Comparison with state-of-the-art on anthropomorphic phantom

To demonstrate the accuracy of patient positioning of the proposed method as compared to method (i) and (ii). In addition, method (iii), which is derived by directly shifting the CT image via the shifts obtained by rigidly matching the two orthogonal kV projections to the DRR of the CT image, is also evaluated. Anthropomorphic phantom studies was used to test the positioning accuracy on chest and head and neck sites, as explained in subsection 2.D. Table 2 and 3 summarizes the shift error as compared to the ground truth movement using rigid registration. From Table 5* and 6* of Supplement, the proposed method has minimal shift error, and significantly outperforms the comparing methods (i) and (ii) for translational positioning accuracy. The method (iii) shows zero rotational error, since orthogonal kVs matching only include three degrees of freedom (3 DoF) of couch motion.

Table 2.

Positioning error of proposed method and comparing methods of head and neck scan of antropomorphic phantom studies.

Translational	X (mm)	Y (mm)	Z (mm)
Proposed	−0.02±0.01	−0.01±0.01	0.02±0.02
(i)	0.09±0.05	−0.12±0.09	0.07±0.05
(ii)	−0.11±0.04	−0.15±0.07	0.05±0.04
(iii)	0.03±0.01	0.03±0.01	−0.02±0.01
Rotational	X (degree)	Y (degree)	Z (degree)
Proposed	−0.03±0.01	0.03±0.02	0.01±0.01
(i)	−0.04±0.02	0.05±0.02	0.02±0.01
(ii)	−0.03±0.02	0.04±0.01	0.01±0.03
(iii)	0.00±0.00	0.00±0.00	0.00±0.00

Table 3.

Positioning error of proposed method and comparing methods of chest scan of antropomorphic phantom studies.

Translational	X (mm)	Y (mm)	Z (mm)
Proposed	−0.17±0.05	0.03±0.01	0.07±0.03
(i)	0.31±0.12	0.08±0.03	0.09±0.04
(ii)	−0.11±0.04	−0.15±0.07	0.05±0.04
(iii)	0.08±0.04	−0.09±0.03	0.05±0.04
Rotational	X (degree)	Y (degree)	Z (degree)
Proposed	−0.01±0.01	−0.03±0.01	−0.02±0.01
(i)	0.02±0.01	−0.03±0.02	−0.02±0.01
(ii)	−0.02±0.01	−0.03±0.02	−0.02±0.02
(iii)	0.00±0.00	0.00±0.00	0.00±0.00

4. Discussion

4.A. Summary

Our approach for estimating a 3D image from orthogonal 2D projections has three distinctive strengths: 1) The feature matching strategy enables the spatial correlations between the features extracted from the perpendicular kV and MV 2D projections to be obtained more directly by transforming their positions to the Cartesian coordinate system of the 3D image. 2) The residual module allows the feature map to focus more on the differences between estimated and ground truth images. In addition, the feature map is downsized to include more global semantic information for the 3D image estimation, which improves the accuracy of soft tissue CT values. By adding a convolution-based reweighting step, the model was able to further improve image uniformity. 3) An auto-learned Gaussian kernel is implemented that models the textured noise, which is then suppressed in the final image via Laplacian loss.

In this proof-of-concept study, we demonstrate that our proposed method is able to generate volumetric images from the spatial information in an orthogonal kV/MV pair. Note that the kV/MV pair is simulated because this imaging protocol is not used in our clinic; for this analysis, we generated a kV/MV pair from one of the ten phases from a 4DCT obtained at simulation. The kV/MV pair is a good surrogate for a real kV/MV pair since the generated image resolution, size, and pixel value are based on mean-energy attenuation coefficients and realistic machine geometry. There remains some discrepancy from real kV/MV images, however. For example, the generated kV/MV images do not include the photon scatter from a cone of rays acquired by a flat panel detector. The scatter can degrade the image quality of the input kV/MV, thus may affect the final result of volumetric images. In our future work, we plan include a more physically-realistic processes for generating kV/MV pairs using Monte Carlo simulation.

After the kV/MV pair is acquired, which can usually be done in a few seconds, it takes about 20–30 seconds for our proposed method to generate volumetric images from the kV/MV pair. The time of volumetric image generation could be further reduced to 1–2 seconds if a powerful computer with an advanced GPU is used. Compared to CBCT, the proposed workflow shortens significantly the on-couch imaging time for patients. Decreasing imaging time is likely to improve patient comfort while also reducing intrafraction positioning errors. The proposed method can also serve as a faster technique for verification imaging, including after CBCT-based 6 DoF corrections prior to or as needed during treatment.

4.B. Literature review

A single 2D projection may not provide enough information to create a high-quality 3D volumetric image. Recently patient-specific 2D–3D models were built to estimate a 3D volumetric image via a single projection taken as input.^9,10 In our previous work, we tested the performance of these two 2D–3D models, which are introduced in the work of^9,10 on our dataset. Results shows that for a 0° kV projection input, the model introduced in¹⁰ and the model introduced in¹¹ achieve MAE of 115.7 ± 23.2 HU and 90.3 ± 15.8 HU, respectively, PSNR of 14.5 ± 2.2 dB and 15.6 ± 2.2 dB, respectively, for the inhalation phase. With a 90° kV projection input, the two models achieve MAE of 123.5 ± 15.3 HU and 103.9 ± 12.1 HU, respectively, and PSNR of 14.2 ± 2.8 dB and 15.2 ± 2.8 dB, respectively, for the inhalation phase. For the exhalation phase, the performance of the two single projection input-based models has similar performance. In this work, with the input of 0° kV and 90° MV, our proposed model can achieve average MAE along all phases of 57.9±22.9 HU and PSNR of 27.9±3.4 dB within body. With the input of 90° kV and 0° MV, our proposed model can achieve MAE of 57.5±21.9 HU and PSNR of 27.6±3.3 dB within body. These findings demonstrate that our model can use perpendicular projection inputs to successfully generate a 3D volumetric image. Additional research is needed to determine how target delineation or localization accuracy is affected by the projection angle selection.

4.C. Limitation and future work

One of the challenges in the proposed method is the high computational burden during model training. Training one patient’s angle-specific model takes about 6.5 hours on a NVIDIA Tesla V100 GPU card. In clinical implementation, the training process can be performed in the background and in parallel with treatment planning, so the information is available at the time of treatment. Recognizing that reduced training time is advantageous, an alternative approach would to pre-train a model using a patient database, and then apply the model to each individual patient via transfer learning, which may reduce the computational cost. This is a future research direction.

There are inherent drawbacks to mapping two 2D projections, which are highly under-sampled data, to a 3D volume, which would typically include much more information. Even with network designs and loss terms, this under-sampling,¹³ means that the estimated 3D volume is hard to reach at a level of image quality comparable to directly-acquired 3D images. Another limitation of this work is therefore the requirement for the model to be trained specifically for each patient, since the under-sampling requires maximum likeness between training and testing input to generate more accurate results. If there is a dramatic geometry change between a patient’s training data, namely the 4DCT, and testing data during treatment (such as substantial weight loss, or lung collapse, or extensive patient motion, on the couch), our method may not perform well. In our study, we used the 10 phase-binned CT images of training 4DCT scans, which share similar anatomical structure but are captured under different respiratory phases. The variation of training data is always fulfilled for each patient. Hence, as long as no significant anatomic differences exist between training and testing data, the output image quality should be robust across different patients, including those with atypical lung shapes or volumes. Another potential challenge is that abnormal lung function and inconsistent breathing patterns may cause unpredicted conditions for the patient-specific model. Our future plans include evaluation of the robustness of our proposed method across a larger patient cohort, including unusual cases. In addition, our model is a combination of 2D and 3D network, it cannot take one patient’s 4D CT with its each phase’s corresponding projections as input to train the model. Thus, our model may lack the spatial correlation information between phases during training. Using 4D CT as additional network input to only estimate the deviations from the input CT volume might be an alternative for us to try in our future work. When the final method is ready for clinical use, for every new patient, after the 4D CT images are acquired for treatment planning purpose, we will retrieve those patient-specific 4D CT images and use all the ten phases of 3D CT images to simulate the orthogonal kV-MV projection pairs as the training data. Data augmentation such as translation, rotation, and deformation will be used to increase the diversity of the training data. The network training will be conducted offline during the time gap between 4D CT scanning and the first treatment fraction, which is for contouring and treatment planning and is usually at least one week long. At each treatment fraction, after patient setup we will acquire a pair of orthogonal kV-MV projections, and feed into our well-trained network to derive the 3D image. The obtained 3D image will then be aligned with the original planning CT image via rigid registration to obtain the couch movement required for patient positioning. Following our current institutional protocol, if the couch movement is larger than our institution-specified threshold (e.g., 1 cm for SBRT treatment), we will verify the final position after moving the treatment couch by acquiring another pair of projections. For the sake of patient safety in routine clinical use, we will also conduct a quality assurance (QA) procedure at the first treatment fraction (or every five fractions), as a step of clinical workflow, for every individual patient. In the QA procedure, we will acquire a CBCT scan to see whether obvious anatomical changes have occurred as well as to verify the accuracy of our generated 3D image with the presence of anatomical changes.

As mentioned before, compared to deep learning applications in computer vision and other fields, data availability is often a limiting factor in a medical setting, making it a fundamental challenge to achieve generalizability of deep learning models for a large patient population of big variations in patient body size, tumor size, location and motion. On the other hand, despite the patient’s anatomy and treatment setup changes, a same patient still holds a relatively high anatomical similarity throughout the treatment course, which however has been entirely under-utilized. Inspired by a recent study on a patient-specific deep learning model for auto-contouring¹⁴, we propose to leverage patient’s own similarity among treatment simulation and each treatment fraction to build a patient-specific deep learning model, with the aid of data augmentation techniques, to overcome the aforementioned fundamental challenge and improve the accuracy of fast volumetric imaging for every individual patient. Hence, the final method will still be patient specific. We will use patient-specific 4D CT images to generate kV/MV projections for network training, and acquire the actual projections at every treatment fraction for patient positioning.

The experiments based on the phantoms are simplified cases, compared to real patient cases, due to the relatively simple geometry and well-defined edges between the inserts. Variation in the performances of the proposed method should be expected. Currently, the evaluations based on patient image data are limited with retrospective simulations. Although this simulation study is anticipated to be representative for clinical cases to a certain extent, prospective investigations are necessary for the proposed method towards practical clinic utilization and will be conducted in the future under proper regulation permission. During these future studies, the questions regarding image registration method can also be explored, such as whole image vs ROI based registration approaches.

5. Conclusion

In summary, we investigated a novel feature-matching method to achieve fast on-board volumetric imaging from a pair of orthogonal kV/MV projection images. The performance and robustness of our method have been tested patient-specifically in this study. In this proof-of-concept study, we have validated the feasibility of deriving more informative 3D images from perpendicular kV and MV images. Adding an orthogonal MV projection to original kV can include additional tissue spatial information as compared with single original kV due to the collection of the attenuation coefficients to the MV planar which is perpendicular to kV planar. Fast on-board volumetric imaging can facilitate daily treatment setup and positional verification, thereby improving the quality of radiation therapy delivery to patients with lung cancer.