Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Aug 29;23(17):7852–7858. doi: 10.1021/acs.nanolett.3c01511

Selective and Scalable Control of Spin Quantum Memories in a Photonic Circuit

D Andrew Golter †,*, Genevieve Clark †,‡,*, Tareq El Dandachi ‡, Stefan Krastanov ‡, Andrew J Leenheer §, Noel H Wan ‡, Hamza Raniwala ‡, Matthew Zimmermann †, Mark Dong †,‡, Kevin C Chen ‡, Linsen Li ‡, Matt Eichenfield §,∥,*, Gerald Gilbert ⊥,*, Dirk Englund ‡,*
PMCID: PMC10510697  PMID: 37643457

Abstract

graphic file with name nl3c01511_0005.jpg

A central goal in many quantum information processing applications is a network of quantum memories that can be entangled with each other while being individually controlled and measured with high fidelity. This goal has motivated the development of programmable photonic integrated circuits (PICs) with integrated spin quantum memories using diamond color center spin-photon interfaces. However, this approach introduces a challenge into the microwave control of individual spins within closely packed registers. Here, we present a quantum memory-integrated photonics platform capable of (i) the integration of multiple diamond color center spins into a cryogenically compatible, high-speed programmable PIC platform, (ii) selective manipulation of individual spin qubits addressed via tunable magnetic field gradients, and (iii) simultaneous control of qubits using numerically optimized microwave pulse shaping. The combination of localized optical control, enabled by the PIC platform, together with selective spin manipulation opens the path to scalable quantum networks on intrachip and interchip platforms.

Keywords: diamond color center, integrated photonics, spin control, optimal control, quantum information

A network of entangled quantum memories is an essential component of many emerging quantum technologies. These memories must be individually controllable with high fidelity, have long coherence times, and be implemented in a scalable way. Recently proposed blueprints for general-purpose quantum information processing call for solid-state spin-based quantum memories connected by switchable photonic links.1−3 These blueprints have motivated the development of cryogenic photonic integrated circuit (PIC) platforms4,5 and hybrid integration with diamond color centers.6,7

As a first step toward integrating spin memories8−12 into such scalable PIC-based architectures, high-performance single-channel devices were demonstrated with single color centers coupled to photonic waveguides.13−18 Recently multichannel diamond waveguide arrays supporting multiple stable color centers were successfully incorporated into a photonic integrated circuit using a high-yield, scalable process.6,17 To realize the potential of these color-center-based devices for large-scale quantum information processing, this scalable photonic integration needs to be accompanied by scalable electron spin control. Microwave control of color center spins enables state manipulation,19,20 entanglement generation,21−24 and state transfer with long-lived nuclear memories.25−29

Here we demonstrate microwave control over many spins integrated into a scalable piezo-optomechanical photonics platform and explore methods of scaling this control.

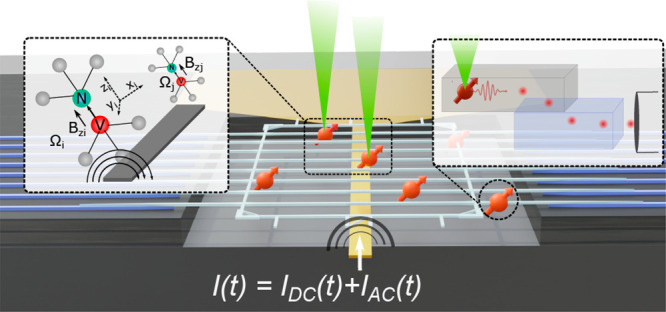
First we describe on-chip spin control of diamond nitrogen-vacancy (NV) centers integrated into our PICs, fabricated in a wafer-scale, 200 mm CMOS-foundry process.4,5,30,31 Our device structure, shown in Figure 1a, couples NV fluorescence to on-chip silicon nitride (SiN) waveguides and an edge-coupled optical fiber, enabling scalable and efficient optically networked state readout. A microwave transmission line beneath the color centers delivers a time-varying current, with a corresponding magnetic field, that allows for spin-state control.

Figure 1.

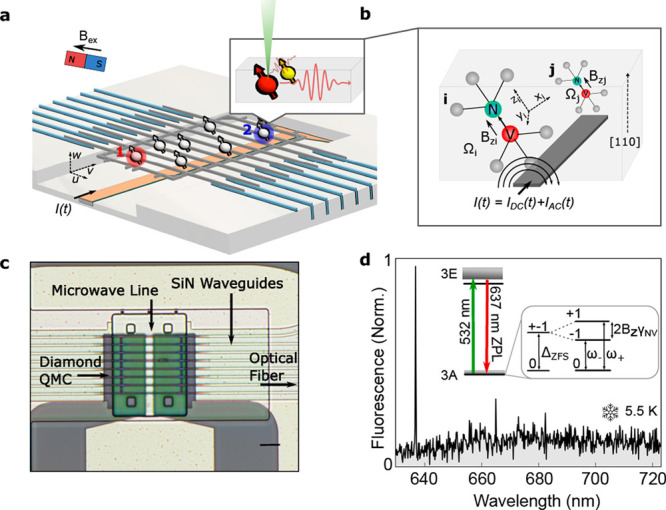
Figure 1

Open in a new tab

(a) Device structure showing spins in a QMC heterogeneously integrated into a PIC. A free-space laser excites NV centers at a particular location in the diamond waveguide, while NV fluorescence couples to the diamond waveguide mode. In the diamond sample used here, multiple NVs were present at each excitation spot. (b) A current I(t) supplied through the microwave line is used to manipulate NV spin qubits in the QMC. (c) Optical microscope image of the PIC showing an integrated wire for the delivery of microwaves below the diamond QMC. The scale bar is 6 μm. (d) Low-temperature photoluminescence (PL) spectrum of NV centers in the QMC. The inset shows the energy level diagram for NV centers subject to magnetic field Bz.

Scalability requires that individual, high-fidelity state control must be applied simultaneously to many optically networked spin qubits. However, maintaining separate microwave control channels for each qubit would dramatically increase the hardware requirements. Time-frequency multiplexed microwave control offers an alternative in which many spin qubits can be controlled through a single microwave channel. In a multiplexed scheme, scalability requires selectivity in control;32−35 i.e., it should be possible to apply a single-qubit gate on one spin while keeping the level of cross-talk with other spins low. Upon application of a single-qubit rotation by operator Ui on a selected spin i, the error on another spin j is given by

graphic file with name nl3c01511_m001.jpg 1

where Uj is the corresponding time propagator for spin j and the notation indicates that the expectation value is calculated in the ground or excited state.

In the rotating frame of a microwave control field with angular frequency ωmw, Rabi frequency Ω(t), and phase φ(t), the Hamiltonian describing the interaction with spin i (which we model as a two-level system) is

graphic file with name nl3c01511_m002.jpg 2

where Ωi and Δi must be real and σx and σy are Pauli matrices. Δi = ω+,i – ωmw is the detuning from spin transition frequency ω+,i, which in a static magnetic field B⃗(r⃗i), with small off-axis components, is approximately

graphic file with name nl3c01511_m003.jpg 3

where Dzfs is the zero-field splitting, Bz,i = ẑ•B⃗(r⃗i) is the magnetic field component along the dipole axis (see Figure 1b), and γNV is the NV gyromagnetic ratio.

Applying a σx rotation on spin i involves setting Δi = 0, Ωi(t) = Ωi, and φi(t) = 0 for a time T ≪ T2, where TΩi = π and T2 is the spin coherence time. During this process, spin j undergoes evolution from state |j0⟩ → ||jT⟩ = Uj|j0⟩. If Ωj/Δj ≪ 1, the state error is bounded from above by εj = (Ωj/Δj)2 (see Supporting Information 1). This means that a low level of cross-talk is possible if the spin transitions are well separated compared to Rabi frequency Ωj. To achieve the Ωj/Δj ≪ 1 requirement for “selective frequency addressing”, we use a magnetic field gradient, generated on chip and localized to the quantum memory register, to produce a position-dependent shift in ω+,i. Using this method, we demonstrate frequency-resolved control over spins at several different locations within a single waveguide.

However, if spectral spacing Δj is too small or we want to drive the dynamics quickly, yielding a large Ωj, selective spin control is also possible by temporal modulation of Ω(t) and φ(t). Under this scheme, all spins will exhibit non-negligible evolution under the application of the control field, but they will follow different trajectories. This opens up the possibility that, through the careful shaping of Ω(t) and φ(t) via the tools of optimal control theory, the spins can be guided to a desired end state, effectively executing selective control even when the conditions for full frequency resolution are not met. We conclude by considering, theoretically and experimentally, this simultaneous control using optimally shaped microwave pulses.

We performed experiments on naturally occurring NV– centers in an eight-waveguide single-crystal diamond “quantum micro-chiplet” (QMC) integrated over a microwave transmission line on a silicon nitride (SiN) PIC, as shown in panels a and c of Figure 1. The diamond QMC waveguides (see ref (12) for fabrication) and SiN waveguides on the PIC (see ref (17)) couple optically via inverse tapering, as detailed previously.17 Details of the waveguide dimensions and coupling efficiency are described in Supporting Information 2. Optical excitation of the color centers occurs through free space perpendicular to the chip, while fluorescence is collected from the SiN waveguides into an edge-coupled optical fiber. With the excitation laser positioned at location 1 in Figure 1a, we observe a clear NV zero-phonon line when collecting fluorescence through the PIC at 5 K, as shown in Figure 1d. All of the other measurements were performed at room temperature.

Figure 1b illustrates our approach to spin control of NV centers in a QMC using the microwave line. A current with both an ac component and a dc component, I(t) = Idc + Iac(t) sin(ωmwt + ϕmw), where Iac(t) varies slowly compared with ωmw, is applied through the microwave line creating a spatially dependent dc magnetic field, B⃗dc(r⃗), and a time and spatially dependent ac magnetic field, B⃗ac(t, r⃗) sin (ωmwt + ϕmw), with |B⃗dc| ∝ Idc and |B⃗ac| ∝ Iac. In addition, an external magnet provides a constant magnetic field, B⃗ext, that is spatially invariant at the length scale of the QMC. The spin |±1⟩ sublevels for NV i at position r⃗i undergo a Zeeman shift (see eq 3) yielding spin transitions at

graphic file with name nl3c01511_m004.jpg 4

as shown in the inset of Figure 1. When ωmw = ω±,i, the spin transition is driven at the Rabi frequency, 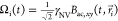Inline graphic, where Bac,xy is the component of the ac magnetic field perpendicular to the dipole axis.

We begin by setting Idc to 0. Figure 2a shows optically detected magnetic resonance (ODMR) when optically pumping location 2 is indicated in Figure 1a. We observe three resonance pairs, indicating at least three NV centers at this location in the QMC, with different orientations relative to B⃗ext. The inset shows the spin-triplet hyperfine structure of the prevalent 14NV isotope. With the microwave field tuned to one of the resonances, ωmw/2π = 3.00 GHz, measurements following the pulse sequence shown in the inset of Figure 2b produce Rabi oscillations at Ωi/2π = 7.5 MHz. We next apply this spin control to Ramsey fringe (Figure 2c) and Hahn echo (Figure 2d) measurements, yielding coherence times for this spin memory of T2* = 1.7 μs and T2 = 150 ± 5 μs, typical for NV spins in diamond nanostructures.34−38 For the remainder of the measurements in this paper, we consider only the NV subpopulation corresponding to the feature at 3.00 GHz in Figure 2a and set ẑ along the corresponding dipole axis.

Figure 2.

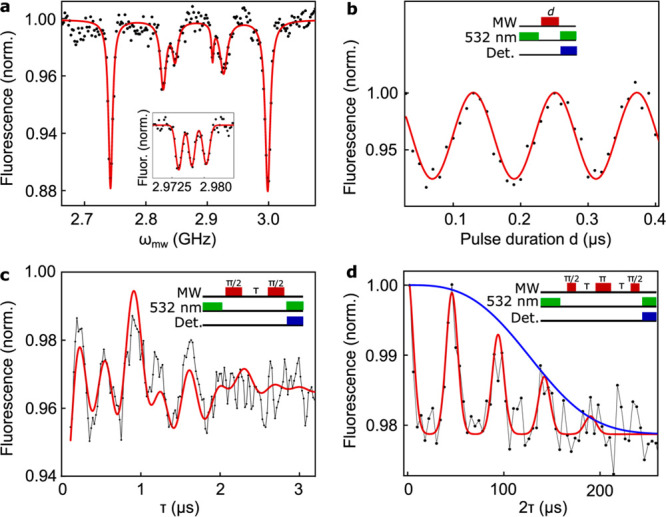
Figure 2

Open in a new tab

(a) ODMR spectrum measured in a static uniform dc magnetic field under continuous microwave excitation. The inset that shows the ODMR spectrum measured under low excitation power reveals triplet hyperfine structure due to coupling to the nitrogen nuclear spin. (b) Spin-dependent fluorescence as a function of the microwave pulse duration shows Rabi oscillations when the microwave field is resonant with a particular spin transition. (c) Ramsey fringes reveal a T2* of 1.7 μs. The red line is a fit using three exponentially decaying sine waves with frequencies given by the detuning for each of the hyperfine states. (d) A Hahn echo sequence reveals a T2 of 150 μs. The echo signal collapses and is revived at the frequency of the Larmor precession of nearby 13C nuclear spins.

To demonstrate selective frequency addressing, we now set Idc ≠ 0, giving ω±,i a spatial dependence (eq 4). Assuming all spins are initialized to |0⟩, the cross-talk error on spin j under a π-pulse on spin i is εj = 1 – ⟨0|Uj|0⟩2. Figure 3a plots the simulated εj for a spin at different spatial locations relative to the microwave line at u = 0, when a π-pulse, with Ωi/2π = 10 MHz chosen to match the experiment, is applied to a target spin i located at u = 1.5 μm. The cases in which Idc = 0 and 150 mA are compared. We determine the spatial dependence of B⃗dc and B⃗ac from finite-element simulations based on the current in the microwave line. We then calculate Bdc,z and Bac,xy for an NV dipole axis with θw = 54.7° for NVs in a [100]-oriented diamond and with θu = 41.0° set to be consistent with our experimental data for the subpopulation of NV centers considered in this work. When Idc = 150 mA, εj is expected to decrease significantly within a few micrometers of the target spin, while when Idc = 0 mA, εj remains large at locations many micrometers from the target qubit [Figure 3b(i)]. The spatially varying Zeeman shift [Figure 3b(ii)] has led to a position-dependent ωj, yielding a Δj sufficiently large to satisfy the condition Ωj/Δj ≪ 1 even for closely spaced spins.

Figure 3.

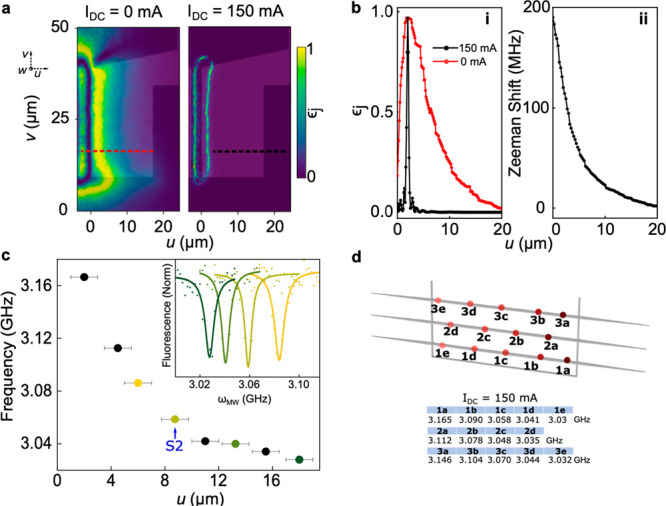
Figure 3

Open in a new tab

(a) Simulated-state error εj with Idc values of 0 and 150 mA. (b) (i) Line cuts taken from panel a, showing the simulated εj as a function of u. (ii) Calculated Zeeman shift as a function of u for Idc = 150 mA. (c) Measured transition frequency, with Idc = 150 mA, for spins at different locations along a single diamond waveguide, as set by the optical excitation spot, exhibiting a position-dependent Zeeman shift. Error bars correspond to uncertainty in the location along the QMC. In the inset, a sample of ODMR measurements was used to determine the transition frequencies in the main plot. The spatially varying Zeeman shift allows for selective excitation of multiple spins. (d) Spins at different locations in the QMC are mapped to specific microwave frequency “addresses” for a given dc current. Experimentally measured frequency addresses are shown for multiple locations along three different diamond waveguides in our device (located between u = 0 and 14 μm). Waveguide 1 corresponds to the data shown in panel c.

To demonstrate this experimentally, we apply a dc current (Idc = 150 mA) to the microwave line. In ODMR measurements, the NV orientation corresponding to the 3 GHz feature at spot 2 (measured in Figure 2) shifts to 3.06 GHz, as one can see in the labeled measurement in Figure 3c. Mapping the transition frequency for this orientation subpopulation along the length of a single diamond waveguide (along coordinate u as shown in Figures 1a and 3a), the Zeeman shift increases to >160 MHz at u = 2 μm. This allows multiple spins in the same waveguide to be resolved, as shown in the inset. Here, the center of each ODMR dip represents a π-rotation performed on spins at that particular location, thus demonstrating position-dependent selective control at multiple locations. Figure 3d summarizes the potential of this technique to enable the selective addressing of single spins within a dense register. The spatial variation of B⃗dc allows each spin in the QMC to be mapped to a specific address, in either ωmw or Idc. Figure 3d shows the measured ωmw address for spins at various locations within three waveguides of the QMC at an Idc of 150 mA.

The NV electron spin is coupled to the nitrogen nuclear spin. For these simulations and measurements, we have considered the case in which manipulation of the electron spin is independent of the nuclear spin state. This leads to a trade-off between the control fidelity (improved by a larger Ωi) and the reduction in εj (improved by a smaller Ωj). For a discussion of the case in which there is no hyperfine coupling or the control is dependent on the nuclear spin, see Supporting Information 6.

The scalability of this selective control scheme is limited by the steepness of the field gradient due to the requirement that Δj ≫ Ωj. Scaling to hundreds of spins and beyond calls for a technique for selectively controlling spins with more closely spaced transition frequencies. Using optimal control techniques, we can relax the requirement that Δj ≫ Ωj, pushing the limits of selective control even further.

Consider the special case of a spin flip operation performed on a single target spin i, and a single neighbor spin j that we wish to remain unchanged, with ωi – ωj ≠ 0 and with both spins initialized into their respective ground states, |0i⟩ and |0j⟩. (See Supporting Information 7 for examples of other control scenarios, including more than two spins and arbitrary rotations.)

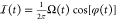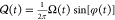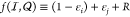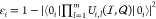Our optimal control technique works by shaping the time-dependent in-phase, Inline graphic, and out-of-phase, Inline graphic, components of a microwave control pulse. This pulse is composed of m discrete time steps, with Ω and φ constants during each step. 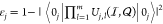We then apply gradient descent36−40 to minimize a cost function, Inline graphic, which includes the state error for each qubit, Inline graphic and Inline graphic, where Ui,l and Uj,l are the evolution operators for a given time step l. 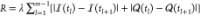Also included in the cost function is a regularization term, Inline graphic, weighted by λ (real, typically set to <1 MHz–1), that is included to ensure that the pulse is smooth enough to be generated by the microwave source.

As mentioned above, the coupling between the NV electron spin and the nitrogen nuclear spin produces a hyperfine triplet with splitting at 2.2 MHz. The nuclear spin is in a mixed state, so to include this hyperfine interaction we model and average over three two-level systems for both spin i and spin j. Optimally shaped pulses can be designed to flip one spin selectively on the corresponding nuclear spin state. However, experimentally, we consider the case in which manipulation of the electron spin is independent of the nuclear spin state. While this placed a limit on the effectiveness of frequency addressing, we show that our use of optimal control pulses can mitigate this limitation, as well.

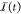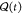We experimentally demonstrate an optimized control for the case in which Δj/2π = 1.1 MHz. This represents an order of magnitude improvement in the minimum frequency separation needed for selective control compared to the Δj/2π > 20–30 MHz needed for the frequency resolution demonstrated in Figure 3. Figure 4a shows the Inline graphic and Inline graphic components of a control pulse designed using the optimization method described above. The calculated spin evolution during the application of this pulse is plotted in Figure 4b for each of the hyperfine states of i and j, with both spins starting at |0⟩ and with an arrow indicating the end state.

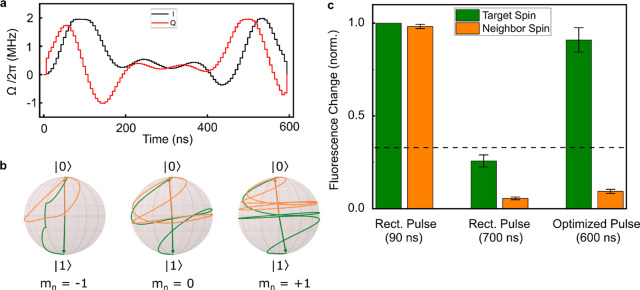
Figure 4.

Figure 4

Open in a new tab

(a) Optimized pulse shape for selectively applying a π-rotation on spin i while leaving spin j unchanged, where ωi – ωj = 1.1 MHz. The amplitudes of the in-phase, 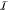Inline graphic (black), and out-of-phase, 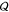Inline graphic (red), components of the microwave signal are shown as a function of time. (b) Calculated paths traced out on the Bloch sphere by spin i (green) and spin j (orange) during application of the optimized pulse. The hyperfine coupling to the nuclear spin has been included, and the spin evolution is shown for each of the three nuclear spin states, mn. (c) Comparison of the cross-talk caused by rectangular control pulses and the optimized control pulse. The change in the spin-dependent fluorescence resulting from the application of the respective pulses is shown for each spin, normalized to the case of a rectangular pulse on resonance with that spin. The dashed line indicates the maximum expected fluorescence change (1/3) if the spin is flipped for only one hyperfine case. Error bars indicate the standard error of repeated measurements.

We choose two spatially separated sites in the QMC and adjust Idc to achieve Δj/2π = 1.1 MHz for the two sites. For the purpose of demonstration, we selected two sites approximately 3 μm apart; however, as shown in Figure 3c, this detuning can be realized for much more closely spaced spins. Spins at both sites are optically initialized into the |0⟩ state. In Figure 4c, we show, for each spin, the population found to be in the |1⟩ state after the application of a microwave pulse, as measured by the change in fluorescence. This is normalized to the case of a rectangular π-pulse on resonance with that spin. A short, rectangular pulse can flip spin i with high fidelity; however, the cross-talk with spin j is significant (εj > 0.9). A longer rectangular pulse can achieve better resolution, but it becomes hyperfine-state selective, flipping at most a third of the population. In comparison, the optimized pulse successfully flips i while significantly reducing the level of cross-talk with j.

In our calculations, this pulse shape achieves an εj of 0.006 and an εi of 0.995; however, this is extremely sensitive to Δj (Supporting Information 8) as well as to pulse amplitude. The higher level of cross-talk in our measurement is likely due to a limit in the precision with which these parameters were set, as well as to limitations in our spin-state measurements (see below).

We have demonstrated scalable methods for controlling spins in dense registers with a low level of cross-talk in a CMOS compatible PIC platform. Using an on-chip microwave signal line, we controlled the state of NV center spins hosted in optically integrated diamond waveguides. We also use this line to generate a local magnetic field gradient, enabling frequency addressing of multiple spins within a single waveguide for individual control. Finally, we use tailored microwave pulses optimized through a gradient-based search to selectively control spins where the requirement for frequency resolution is not met, demonstrating control with minimal cross-talk for frequency separations as small as 1.1 MHz.

These control methods can be applied to large numbers of spins (see Supporting Information 6), are fully coherent, and are compatible with state transfer to nuclear memories. While the measurements shown here are limited to π-rotations and state population readout, selective spin control is effective for arbitrary rotations. In this case, the criterion for frequency addressing (Ωj/Δj ≪ 1) remains the same (see Supporting Information 1), and the optimal control pulses can be designed to generate any desired end states (see Supporting Information 7).

To aid in optical integration and to explore the spatial dependence of the Zeeman shift, we used a diamond QMC with a moderately high density of color centers throughout (<1 ppm nitrogen concentration leading to >1 NV per excitation spot). This made spin-state measurements challenging due to a large position-dependent background from color centers of the wrong orientation and to the existence of multiple color centers of the correct orientation at different locations within the optical excitation spot. These limitations will be mitigated by using lower-density samples (<1 NV per excitation spot) and resonant optical addressing.6,32

Our device used a single, straight line to generate the magnetic field gradient. In the future, more sophisticated line designs could allow for tailored gradient shapes and steepness, and multiple lines would enable tuning of the field direction for alignment with color centers.

The results shown here represent an important step toward the development of scalable quantum networks with nodes containing large numbers of spin qubits that can be selectively manipulated with high fidelity while being interfaced with on- and off-chip optics.

Acknowledgments

Major funding for this work is provided by The MITRE Corp. for the Quantum Moonshot Program. N.H.W. acknowledges support from the Army Research Laboratory (ARL) Center for Distributed Quantum Information (CDQI) (Program W911NF-15-2-0067). H.R. acknowledges support from the NDSEG Fellowship and the NSF Center for Ultracold Atoms (CUA). K.C.C. acknowledges additional funding support by the National Science Foundation RAISE-TAQS (Grant 1839155). L.L. acknowledges funding from NSF QISE-NET Grant DMR-1747426 and the ARO MURI W911NF2110325. M.E. performed this work, in part, with funding from the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy Office of Science. D.E. acknowledges the National Science Foundation (NSF) Engineering Research Center for Quantum Networks (CQN), awarded under Cooperative Agreement 1941583.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.3c01511.

  • Derivation of the exact expression for the error function; layer stack and dimensions for the QMC and photonic chip; methods for microwave signal generation; additional ODMR, Rabi oscillation, and Zeeman shift measurements; simulations demonstrating the scalability of the selective control schemes; simulations demonstrating additional optimal control examples; and ODMR with the optimized pulse (PDF)

Author Contributions

D.A.G. and G.C. contributed equally to this work. D.A.G. and G.C., with assistance from H.R., built the experimental setups and performed the experiments. T.E.D. and S.K. performed the gradient descent numerical analysis to design the microwave pulse shapes for optimal control, and M.Z. assisted in experimental microwave pulse generation. G.G. provided additional theory support. N.H.W., K.C.C., and L.L. designed and fabricated the diamond microchiplets. G.C. and N.H.W., with assistance from M.D., A.J.L., and M.E., designed the PIC for diamond integration. M.E. developed the PIC platform and concept of operation. M.E. and A.J.L. developed the fabrication methodology of the PIC platform. D.E., D.A.G., and G.C. conceived the experiments. G.G., M.E., and D.E. supervised the project. D.A.G. and G.C. wrote the manuscript with input from all authors.

The authors declare no competing financial interest.

Supplementary Material

nl3c01511_si_001.pdf (918.4KB, pdf)

References

  1. Choi H.; Pant M.; Guha S.; Englund D. Percolation-Based Architecture for Cluster State Creation Using Photon-Mediated Entanglement between Atomic Memories. npj Quantum Information 2019, 5, 104. 10.1038/s41534-019-0215-2. [DOI] [Google Scholar]
  2. Nickerson N. H.; Fitzsimons J. F.; Benjamin S. C. Freely Scalable Quantum Technologies Using Cells of 5-to-50 Qubits with Very Lossy and Noisy Photonic Links. Phys. Rev. X 2014, 4, 041041 10.1103/PhysRevX.4.041041. [DOI] [Google Scholar]
  3. Nemoto K.; Trupke M.; Devitt S. J.; Stephens A. M.; Scharfenberger B.; Buczak K.; Nöbauer T.; Everitt M. S.; Schmiedmayer J.; Munro W. J. Photonic Architecture for Scalable Quantum Information Processing in Diamond. Phys. Rev. X 2014, 4, 031022 10.1103/PhysRevX.4.031022. [DOI] [Google Scholar]
  4. Dong M.; Clark G.; Leenheer A. J.; Zimmermann M.; Dominguez D.; Menssen A. J.; Heim D.; Gilbert G.; Englund D.; Eichenfield M. High-Speed Programmable Photonic Circuits in a Cryogenically Compatible, Visible–near-Infrared 200 Mm CMOS Architecture. Nat. Photonics 2022, 16, 59. 10.1038/s41566-021-00903-x. [DOI] [Google Scholar]
  5. Stanfield P. R.; Leenheer A. J.; Michael C. P.; Sims R.; Eichenfield M. CMOS-Compatible, Piezo-Optomechanically Tunable Photonics for Visible Wavelengths and Cryogenic Temperatures. Opt. Express 2019, 27, 28588. 10.1364/OE.27.028588. [DOI] [PubMed] [Google Scholar]
  6. Wan N. H.; et al. Large-Scale Integration of Artificial Atoms in Hybrid Photonic Circuits. Nature 2020, 583, 226. 10.1038/s41586-020-2441-3. [DOI] [PubMed] [Google Scholar]
  7. Awschalom D. D.; Hanson R.; Wrachtrup J.; Zhou B. B. Quantum Technologies with Optically Interfaced Solid-State Spins. Nat. Photonics 2018, 12, 516. 10.1038/s41566-018-0232-2. [DOI] [Google Scholar]
  8. Sukachev D. D.; Sipahigil A.; Nguyen C. T.; Bhaskar M. K.; Evans R. E.; Jelezko F.; Lukin M. D. Silicon-Vacancy Spin Qubit in Diamond: A Quantum Memory Exceeding 10 Ms with Single-Shot State Readout. Phys. Rev. Lett. 2017, 119, 223602 10.1103/PhysRevLett.119.223602. [DOI] [PubMed] [Google Scholar]
  9. Maurer P. C.; et al. Room-Temperature Quantum Bit Memory Exceeding One Second. Science 2012, 336, 1283. 10.1126/science.1220513. [DOI] [PubMed] [Google Scholar]
  10. Atatüre M.; Englund D.; Vamivakas N.; Lee S.-Y.; Wrachtrup J. Material Platforms for Spin-Based Photonic Quantum Technologies. Nature Reviews Materials 2018, 3, 38. 10.1038/s41578-018-0008-9. [DOI] [Google Scholar]
  11. Zhu T.-X.; Liu C.; Jin M.; Su M.-X.; Liu Y.-P.; Li W.-J.; Ye Y.; Zhou Z.-Q.; Li C.-F.; Guo G.-C. On-Demand Integrated Quantum Memory for Polarization Qubits. Phys. Rev. Lett. 2022, 128, 180501 10.1103/PhysRevLett.128.180501. [DOI] [PubMed] [Google Scholar]
  12. Chen S.; Raha M.; Phenicie C. M.; Ourari S.; Thompson J. D. Parallel Single-Shot Measurement and Coherent Control of Solid-State Spins below the Diffraction Limit. Science 2020, 370, 592. 10.1126/science.abc7821. [DOI] [PubMed] [Google Scholar]
  13. Sipahigil A.; et al. An Integrated Diamond Nanophotonics Platform for Quantum-Optical Networks. Science 2016, 354, 847. 10.1126/science.aah6875. [DOI] [PubMed] [Google Scholar]
  14. Bhaskar M. K.; et al. Experimental Demonstration of Memory-Enhanced Quantum Communication. Nature 2020, 580, 60. 10.1038/s41586-020-2103-5. [DOI] [PubMed] [Google Scholar]
  15. Schrinner P. P. J.; Olthaus J.; Reiter D. E.; Schuck C. Integration of Diamond-Based Quantum Emitters with Nanophotonic Circuits. Nano Lett. 2020, 20, 8170. 10.1021/acs.nanolett.0c03262. [DOI] [PubMed] [Google Scholar]
  16. Patel R. N.; Schröder T.; Wan N.; Li L.; Mouradian S. L.; Chen E. H.; Englund D. R. Efficient Photon Coupling from a Diamond Nitrogen Vacancy Center by Integration with Silica Fiber. Light Sci. Appl. 2016, 5, e16032 10.1038/lsa.2016.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mouradian S. L.; et al. Scalable Integration of Long-Lived Quantum Memories into a Photonic Circuit. Phys. Rev. X 2015, 5, 031009 10.1103/PhysRevX.5.031009. [DOI] [Google Scholar]
  18. Nguyen C. T.; et al. Quantum Network Nodes Based on Diamond Qubits with an Efficient Nanophotonic Interface. Phys. Rev. Lett. 2019, 123, 183602 10.1103/PhysRevLett.123.183602. [DOI] [PubMed] [Google Scholar]
  19. Awschalom D. D.; Bassett L. C.; Dzurak A. S.; Hu E. L.; Petta J. R. Quantum Spintronics: Engineering and Manipulating Atom-like Spins in Semiconductors. Science 2013, 339, 1174. 10.1126/science.1231364. [DOI] [PubMed] [Google Scholar]
  20. Pingault B.; Jarausch D.-D.; Hepp C.; Klintberg L.; Becker J. N.; Markham M.; Becher C.; Atatüre M. Coherent Control of the Silicon-Vacancy Spin in Diamond. Nat. Commun. 2017, 8, 15579. 10.1038/ncomms15579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hensen B.; et al. Loophole-Free Bell Inequality Violation Using Electron Spins Separated by 1.3 Kilometres. Nature 2015, 526, 682. 10.1038/nature15759. [DOI] [PubMed] [Google Scholar]
  22. Humphreys P. C.; Kalb N.; Morits J. P. J.; Schouten R. N.; Vermeulen R. F. L.; Twitchen D. J.; Markham M.; Hanson R. Deterministic Delivery of Remote Entanglement on a Quantum Network. Nature 2018, 558, 268. 10.1038/s41586-018-0200-5. [DOI] [PubMed] [Google Scholar]
  23. Pompili M.; et al. Realization of a Multinode Quantum Network of Remote Solid-State Qubits. Science 2021, 372, 259. 10.1126/science.abg1919. [DOI] [PubMed] [Google Scholar]
  24. Bernien H.; et al. Heralded Entanglement between Solid-State Qubits Separated by Three Metres. Nature 2013, 497, 86. 10.1038/nature12016. [DOI] [PubMed] [Google Scholar]
  25. Metsch M. H.; Senkalla K.; Tratzmiller B.; Scheuer J.; Kern M.; Achard J.; Tallaire A.; Plenio M. B.; Siyushev P.; Jelezko F. Initialization and Readout of Nuclear Spins via a Negatively Charged Silicon-Vacancy Center in Diamond. Phys. Rev. Lett. 2019, 122, 190503 10.1103/PhysRevLett.122.190503. [DOI] [PubMed] [Google Scholar]
  26. Bartling H. P.; Abobeih M. H.; Pingault B.; Degen M. J.; Loenen S. J. H.; Bradley C. E.; Randall J.; Markham M.; Twitchen D. J.; Taminiau T. H. Entanglement of Spin-Pair Qubits with Intrinsic Dephasing Times Exceeding a Minute. Phys. Rev. X 2022, 12, 011048 10.1103/PhysRevX.12.011048. [DOI] [Google Scholar]
  27. Bradley C. E.; Randall J.; Abobeih M. H.; Berrevoets R. C.; Degen M. J.; Bakker M. A.; Markham M.; Twitchen D. J.; Taminiau T. H. A Ten-Qubit Solid-State Spin Register with Quantum Memory up to One Minute. Phys. Rev. X 2019, 9, 031045 10.1103/PhysRevX.9.031045. [DOI] [Google Scholar]
  28. Dutt M. V. G.; Childress L.; Jiang L.; Togan E.; Maze J.; Jelezko F.; Zibrov A. S.; Hemmer P. R.; Lukin M. D. Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond. Science 2007, 316, 1312. 10.1126/science.1139831. [DOI] [PubMed] [Google Scholar]
  29. Neumann P.; Beck J.; Steiner M.; Rempp F.; Fedder H.; Hemmer P. R.; Wrachtrup J.; Jelezko F. Single-Shot Readout of a Single Nuclear Spin. Science 2010, 329, 542. 10.1126/science.1189075. [DOI] [PubMed] [Google Scholar]
  30. Dong M.; et al. Piezo-Optomechanical Cantilever Modulators for VLSI Visible Photonics. APL Photonics 2022, 7, 051304 10.1063/5.0088424. [DOI] [Google Scholar]
  31. Dong M.; et al. Programmable Photonic Integrated Meshes for Modular Generation of Optical Entanglement Links. npj Quantum Information 2023, 9, 42. 10.1038/s41534-023-00708-6. [DOI] [Google Scholar]
  32. Bersin E.; Walsh M.; Mouradian S. L.; Trusheim M. E.; Schröder T.; Englund D. Individual Control and Readout of Qubits in a Sub-Diffraction Volume. npj Quantum Information 2019, 5, 38. 10.1038/s41534-019-0154-y. [DOI] [Google Scholar]
  33. Grinolds M. S.; Maletinsky P.; Hong S.; Lukin M. D.; Walsworth R. L.; Yacoby A. Quantum Control of Proximal Spins Using Nanoscale Magnetic Resonance Imaging, Nat. Phys. 2011, 7, 687. 10.1038/nphys1999. [DOI] [Google Scholar]
  34. Zhang H.; Arai K.; Belthangady C.; Jaskula J.-C.; Walsworth R. L. Selective Addressing of Solid-State Spins at the Nanoscale via Magnetic Resonance Frequency Encoding. npj Quantum Information 2017, 3, 31. 10.1038/s41534-017-0033-3. [DOI] [Google Scholar]
  35. Sekiguchi Y.; Matsushita K.; Kawasaki Y.; Kosaka H. Optically Addressable Universal Holonomic Quantum Gates on Diamond Spins. Nat. Photonics 2022, 16, 662. 10.1038/s41566-022-01038-3. [DOI] [Google Scholar]
  36. Khaneja N.; Reiss T.; Kehlet C.; Schulte-Herbrüggen T.; Glaser S. J. Optimal Control of Coupled Spin Dynamics: Design of NMR Pulse Sequences by Gradient Ascent Algorithms. J. Magn. Reson. 2005, 172, 296. 10.1016/j.jmr.2004.11.004. [DOI] [PubMed] [Google Scholar]
  37. Heeres R. W.; Reinhold P.; Ofek N.; Frunzio L.; Jiang L.; Devoret M. H.; Schoelkopf R. J. Implementing a Universal Gate Set on a Logical Qubit Encoded in an Oscillator. Nat. Commun. 2017, 8, 94. 10.1038/s41467-017-00045-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Rembold P.; Oshnik N.; Müller M. M.; Montangero S.; Calarco T.; Neu E. Introduction to Quantum Optimal Control for Quantum Sensing with Nitrogen-Vacancy Centers in Diamond. AVS Quantum Sci. 2020, 2, 024701. 10.1116/5.0006785. [DOI] [Google Scholar]
  39. Nöbauer T.; Angerer A.; Bartels B.; Trupke M.; Rotter S.; Schmiedmayer J.; Mintert F.; Majer J. Smooth Optimal Quantum Control for Robust Solid-State Spin Magnetometry. Phys. Rev. Lett. 2015, 115, 190801 10.1103/PhysRevLett.115.190801. [DOI] [PubMed] [Google Scholar]
  40. Krastanov S.; Zhou S.; Flammia S. T.; Jiang L. Stochastic Estimation of Dynamical Variables. Quantum Sci. Technol. 2019, 4, 035003 10.1088/2058-9565/ab18d5. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl3c01511_si_001.pdf (918.4KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES