Global Odds Model with Proportional Odds and Trend Odds Applied to Gross and Microscopic Brain Infarcts

Abstract

Medical and epidemiological researchers commonly study ordinal measures of symptoms or pathology. Some of these studies involve two correlated ordinal measures. There is often an interest in including both measures in the modeling. It is common to see analyses that consider one of the measures as a predictor in the model for the other measure as outcome. There are, however, issues with these analyses including biased estimate of the probabilities and a decreased power due to multicollinearity (since they share some predictors). These issues create a necessity to examine both variables as simultaneous outcomes, by assessing the marginal probabilities for each outcome (i.e. using a proportional odds model) and the association between the two outcomes (i.e. using a constant global odds model). In this work we extend this model using a parsimonious option when the constraints imposed by assumptions of proportional marginal odds and constant global odds do not hold. We compare approaches by using simulations and by analyzing data on brain infarcts in older adults. Age at death is a marginal predictor of gross infarcts and also a marginal predictor of microscopic infarcts, but does not modify the association between gross and microscopic infarcts.

1. Introduction

Medical and epidemiological researches commonly study ordinal measures of symptoms or pathology. Such is the case in studies of stroke, a common and deleterious neurological condition associated with aging. On postmortem neuropathologic examination of older people, brain infarcts are much more common than clinically recognized strokes, with about half of older people showing infarcts [1–4]. Some infarcts are large enough to be seen and counted by visual examination of the brain. These are termed “gross” infarcts. Smaller infarcts, however, can only be seen with a microscope and are termed “microscopic” infarcts. Because microscopic infarcts are too small to be seen by conventional neuroimaging, much less is known about microscopic infarcts than about gross infarcts. Moreover, though infarct size is associated with morbidity and mortality, microscopic infarcts are associated with multiple morbidities including dementia [5]. One measure of the burden of gross and microscopic infarcts is the number of gross and microscopic infarcts counted at autopsy. A robust measure of the infarct burden for an individual consists of summarizing the numbers of infarcts as None/Single/Multiple. A natural analysis for this type of outcome is a cumulative constrained ordinal model, or “ordinal logistic regression.”

Gross and microscopic infarcts are correlated. However, the correlation is not perfect and it is quite possible that gross and microscopic infarcts have some separate predictors. For this reason, infarct types are often studied in separate models [5], and the alternate type of infarct is sometimes used as a covariate in these models. For example, a term for gross infarct may be included in a model of microscopic infarct as the outcome [6]. Problems arise with such strategies. Bias may be introduced when attempting to estimate the patient probability of having a combination of the two outcomes. In addition, power to detect associations may be decreased.

An alternative approach is to use a type of shared-parameter model, termed global odds model [7] to model both outcomes simultaneously. This model assesses the marginal probabilities for each outcome and the association between the two outcomes simultaneously. The marginal probabilities are assessed using a proportional odds model [8], and the association between the two outcomes is assessed using a constant global odds model (i.e. the Dale model) [9]. The model has some important constraints. These constraints lead the log odds for each marginal outcome, as well as the global odds, to be independent of the ordinal level.

In this paper, we first review the proportional odds and global odds concept and constraints. We introduce a parsimonious alternative for situations where the models assumptions do not hold. We compare the simultaneous and separate modeling approaches using computer simulations, as well as data on gross and microscopic infarcts based on 1,135 deceased participants from the Religious Orders Study and the Rush Memory and Aging Project [10, 11]. We present models showing the association of these infarcts with age at death and other demographic factors. Finally, we present simulation results of the global odds model and approaches using marginal and conditional marginal modeling and provide sample code to fit global odds with SAS PROC NLMIXED (Appendix A; Supplementary Material).

2. Constrained ordinal models for marginal modeling of each ordinal outcome

Suppose there is an ordinal outcomes Y with I+1 categories (Y= 0, 1, …, I). At a given cut-point i that can be assigned the values {1, …, I}, we can calculate the probability of being above or below the cut-point. Consider a single covariate X that modifies this probability. The log cumulative odds (${\psi }_{iX}$) is therefore:

$${\psi }_{iX}=log\left(\frac{P(Y\ge i|X=x)}{P(Y<i|X=x)}\right),\mathrm{i}=1,\dots \mathrm{I}.$$

An unconstrained cumulative odds model posits that all i of these logits are linear functions of X, with different coefficients for each cumulative logit. Following Agresti’s [12] taxonomy, the marginal cumulative logit for a single predictor X is:

$${\psi }_{iX}^Y={\alpha }_i^Y+{\beta }_i^{Y}X$$ (1).

These models reduce to a binary logistic model when the outcome has only two levels (I=1). For outcomes with more than two levels (I≥2), it is possible to use a more parsimonious model than the model represented by equation 1. For example, it is common to use the proportional odds model [8] in which the cumulative odds for cut-point i is proportional to the cumulative odds for cut-point i+1. This implies that β_i= β for all i, and

$${\psi }_{iX}^Y={\alpha }_i^Y+{\beta }^{Y}X$$ (2).

The proportional odds assumption may not hold in certain cases. The trend odds model was introduced as an alternative model when the cumulative logits differ but demonstrate increasing or decreasing trends. For example, assume that the proportional odds assumption is violated but the trend odds assumption holds for Y. In this case a trend parameter γ^Y can be introduced, such that

$${\psi }_{iX}^Y={\alpha }_i^Y+({\beta }^Y+{\gamma }^Y{t}_i)X,t_i<t_{i+1},$$

where t_i is a multiplicative scalar that varies with the cut-point (i.e. t₁=0 and t_i+1= t_i+1). For models including multiple covariates, it may not be necessary to include the trend parameters for all the covariates.

3. Constrained ordinal approaches for analyzing associated ordinal outcomes

Models of bivariate ordinal outcomes involve simultaneous marginal models of each individual outcome, while including a parameter that characterizes the associations of the outcomes. To understand the association portion of the model, suppose the ordinal outcome Y has I+1 categories (Y= 0, 1, …, I) and Z has J+1 categories (Z= 0, 1, …, J). The log global odds ratio is the logarithm of the odds ratio defined by requiring that both Y and Z are at least equal to, respectively, cut-points i and j. Consider that a single covariate X modifies the probabilities that compose the global odds ratio. The log cumulative global odds ratio (${\psi }_{ijX}$) is therefore:

$${\psi }_{ijx}=log\left(\frac{P(Y\ge i,Z\ge j|X=x)P(Y<i,Z<j|X=x)}{P\left(Y<i,Z\ge j|X=x\right)P\left(Y\ge i,Z<j|X=x\right)}\right)$$ (3).

The general form of the association model described by Dale is

$${\psi }_{ijX}={\alpha }_{ij}^G+{\beta }^{G}X.$$

Further, Dale describes the constrained form of the equation above based on constant odds assumption, such that

$${\psi }_{ijX}={\alpha }^G+{\beta }^{G}X$$ (4).

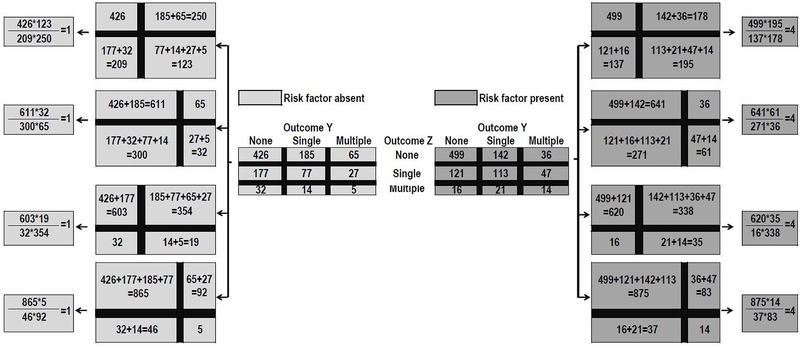
Figure 1 shows a constructed numerical example of the global odds calculation for which the constant odds assumption holds. Note that the general and constrained forms described assume a uniform predictor effect in which ${\beta }_{ij}^G={\beta }^G$, for all (i, j). It is possible, however, to have a completely unconstrained model. Such unconstrained model posits that each of these log global odds is a linear function of X but with different coefficients for each cumulative log global odds. The unconstrained global odds model [9, 12, 13] for a single predictor X is therefore:

$${\psi }_{ijX}={\alpha }_{ij}^G+{\beta }_{ij}^{G}X$$ (5).

Figure 1.

Constructed numerical example: uniform global odds assumption

Parameterizations with parsimony between equation 4 and 5 can be used in modeling. For example one may consider a model that includes a monotonic increase in global odds with i and j, such as ${\psi }_{ijX}={\alpha }^G+\beta X+\gamma v_i{v}_j$ where γ represents a type of trend and v_i and v_j a monotonic scalar associated with the level i and j.

The assumptions of proportional odds, trend odds and the constant odds can be verified using the likelihood ratio tests, as the models with fewer parameters are nested in the models with more parameters. Other strategies include score tests and graphical visualization [14].

4. Latent underlying distributions

Although this section is theoretical in the sense that we don’t model or try to characterize the underlying distribution, it is important for a deeper understanding of models. The models used to assess the marginal probabilities of each outcome (proportional odds and the trend odds model) were developed from the idea of an underlying distribution that is unobserved or latent. That is, while Y is the observed ordinal realization, Y* is a continuous distribution that is not observed.

The proportional odds and the trend odds models were developed considering an underlying logistic distribution. The concept was introduced by Snell in 1964 and was popularized by McCullagh [8, 15] under the assumption of proportional odds and extended by Capuano and Dawson [16] under the assumption of trend odds. Consider again that underlying the observed ordinal variables Y and Z, there are unobserved continuous distributions, respectively Y* and Z*. Suppose that each ordinal variable, Y and Z, takes on values 0, 1, 2, …, I, respectively based on the latent variables, Y* and Z*, according to c_i and d_j values. Specifically, let

$$\mathrm{Y}=\mathrm{i}\leftrightarrow \mathrm{Y}*\in \left({\mathrm{c}}_{\mathrm{i}},{\mathrm{c}}_{\mathrm{i}+1}\right],$$

$$\mathrm{Y}>=\mathrm{i}\leftrightarrow \mathrm{Y}*\ge {\mathrm{c}}_{\mathrm{i}},$$

$$\mathrm{Z}=\mathrm{j}\leftrightarrow \mathrm{Z}*\in \left({\mathrm{d}}_{\mathrm{j}},{\mathrm{d}}_{\mathrm{j}+1}\right],\mathrm{a}\mathrm{n}\mathrm{d}$$

$$\mathrm{Z}>=\mathrm{j}\leftrightarrow \mathrm{Z}*\ge {\mathrm{d}}_{\mathrm{j}},$$

where c₀=−∞, c_I+1=∞, and d_J+1=∞. The proportional odds model and the trend odds model can be derived from the assumption that the latent Y* and Z* follow separate logistic distributions with the location parameter m and scale parameter s being function of a predictor variable X. For example, in the next section, we will discuss a dataset containing two variables (gross and microscopic infarcts), with each variable having three ordinal levels: None/Single/Multiple. These measures represent categories of increasing cerebrovascular disease, where the ordinal levels of gross and microscopic infarcts (say Y and Z) come from unobserved continuous distributions burdens of two types of cerebrovascular disease (say Y* and Z*). These marginal distributions can be represented by

$${\text{Y}}^{\text{*}}|\text{X}=\text{x}\sim \text{Logistic}\left({\text{m}}_{\text{x}}^{{\text{Y}}^{\text{*}}},{\text{s}}_{\text{x}}^{{\text{Y}}^{\text{*}}}\right)$$

and

$${\text{Z}}^{\text{*}}|\text{X}=\text{x}\sim \text{Logistic}\left({\text{m}}_{\text{x}}^{{\text{Z}}^{\text{*}}},{\text{s}}_{\text{x}}^{{\text{Z}}^{\text{*}}}\right).$$

The proportional odds model results from a shift in the location of the underlying variable with the predictor (e.g. ${\text{m}}_{\text{x}=1}^{{\text{Y}}^{\text{*}}}>{\text{m}}_{\text{x}=0}^{{\text{Y}}^{\text{*}}}$$)$. In contrast, the trend odds model results from a shift in the location and scale of the predictor (e.g. ${\text{m}}_{\text{x}=1}^{{\text{Y}}^{\text{*}}}>{\text{m}}_{\text{x}=0}^{{\text{Y}}^{\text{*}}}$ and ${\text{s}}_{\text{x}=1}^{{\text{Y}}^{\text{*}}}>{\text{s}}_{\text{x}=0}^{{\text{Y}}^{\text{*}}}$). Note that if the cut-points c_i and d_j are known, then they can be used as the multiplicative scalar. Further details on the latent underlying distribution concept are provided elsewhere [8, 16].

The global odds ratio, also termed the cross ratio in the literature, is based on the idea of an underlying bivariate distribution. In 1965, Plackett proposed a family of bivariate distributions defined by the marginal distributions and a single association parameter [17]. Plackett’s approach was to divide the plane into quadrants at any given point (Y*= c_i, Z*= d_j), which then results in four probabilities: a=P(Y*≥ c_i, Z*≥ d_j), b=P(Y*≥ c_i, Z*< d_j), c=P(Y*< c_i, Z*≥ d_j) and d=P(Y*< c_i, Z*< d_j). Plackett proved that for any two marginal distributions, there is a unique bivariate distribution with these margins having the property that the odds ratio determined by these probabilities is the same for every pair (c_i, d_j), which implies that this odds ratio is then a natural measure of association between Y* and Z*:

$$\psi =log\left(\frac{ad}{bc}\right)$$ (6).

Given any underlying marginal distributions, the bivariate distribution is derived from types of multinomial allocation of the marginal probabilities and measures of association[17, 18], the true global odds ratio, or ${\text{e}}^{{\text{ψ}}^{+}}$, is asymptotically normal with mean ${\mathrm{e}}^{\mathrm{\psi }}$ and variance ${\text{e}}^{{\text{2ψ}}^{+}}({\mathrm{a}}^{-1}+{\mathrm{b}}^{-1}+{\mathrm{c}}^{-1}+{\mathrm{d}}^{-1})$ [17]. Building upon Plackett’s work, in 1986, Dale gave an explicit solution to Plackett’s equation expressing the probability of the ordinal bivariate outcomes in terms of cumulative marginal and a constant global odds ratio, as a function of the fixed set of predictors [9].

Let the marginal cumulative distribution function be

$$F_{ix}=\text{P}({\text{Y}}^{\text{*}}\ge \text{i|X}=\text{x})$$

and

$$F_{jx}=\text{P}({\text{Z}}^{\text{*}}\ge \text{j|X}=\text{x}),$$

and let the joint cumulative distribution function be

$$F_{ijx}=\mathrm{P}({\mathrm{Y}}^{*}\ge \mathrm{i},{\mathrm{Z}}^{*}\ge \mathrm{j}|\mathrm{X}=\mathrm{x}).$$

When there is no association between Y and Z, the cell cumulative probabilities can be calculated as the simple product of the marginal probabilities, F_ijx=F_ix●F_jx. Otherwise, for $e^{{\Psi }_{ijx}}>0$ or $e^{{\Psi }_{ijx}}<0$ the probability will be

$$F_{ijx}=\frac{1+\left(F_{ix}+F_{jx}\right)\left(e^{{\Psi }_{ijx}}-1\right)-{\left\{{\left[1+\left(F_{ix}+F_{jx}\right)\left(e^{{\Psi }_{ijx}}-1\right)\right]}^2+4e^{{\Psi }_{ijx}}\left(1-e^{{\Psi }_{ijx}}\right)F_{ix}{F}_{jx}\right\}}^{1/2}}{2\left(e^{{\Psi }_{ijx}}-1\right)}$$ (7).

The bivariate probability F_ijX depends on the global odds ${\Psi }_{ijx}$ and on the marginal probabilities F_ix and F_jx. So, although the global odds ratio was not theoretically justified by the underlying marginal that specifically follows the logistic distribution, this is the underlying theory of the joint modeling.

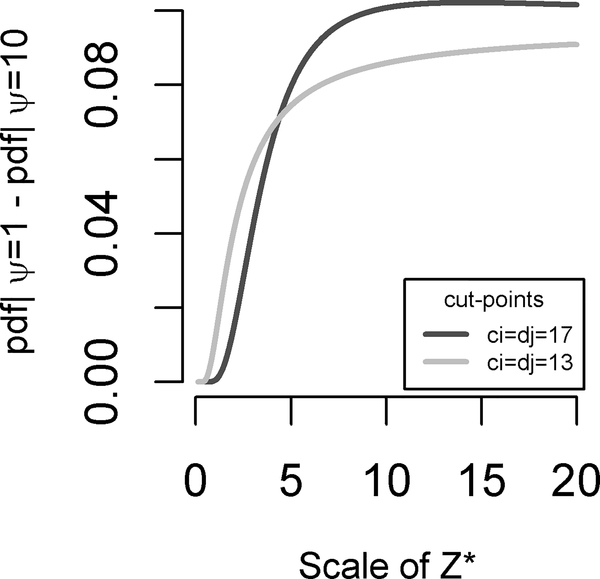
It is important to note that the bias generated by ignoring the association between observed Y and Z can be seen as a function not only of the levels of association between the latent Y* and Z*. It is also a function of the variation in location and shape of the underlying distribution. Figure 2 illustrates differences in the bivariate probability obtained when a global odds of 10 is compared to a global odds of 1. In the figure, Y* and Z* have the same scale but different location, and Y* and W* differ in both location and scale, showing that the change in the bivariate distribution as a function of the location and shape of the underlying distribution. Heatmaps of these differences in the bivariate probability are available in appendix B of the supplementary material. In addition, figure 3 illustrates changes in probability differences with changes in the scale of W*.

Figure 2.

Bivariate probability distribution with global odds of 10 and global odds of 1, where Y*~Logistic(15,2), Z*~Logistic(10,2) and W*~Logistic(10,1).

Figure 3.

Bias for Y*~Logistic(15,2) and Z*~Logistic(10,scale from 0.1 to 20) and a choice of two cut-points.

5. Gross and microscopic infarcts

The data that motivated this work were collected in two clinical neuropathologic cohort studies of cognitive decline in aging: the Religious Orders Study and the Rush Memory and Aging Project [10, 11]. These studies enroll older people without known dementia who agree to brain donation at death and have high follow-up and autopsy rates. Both studies are designed to examine associations among clinical predictors, brain findings at autopsy, and clinical phenotypes measured prior to death. The essential details of clinical and pathologic data collection are identical in the two studies [5, 19]. The numbers of gross and microscopic infarcts was examined at autopsy following established protocols [10, 11]. About half of the 1,135 autopsied participants had at least one infarct of any kind, and less than one fifth had both gross and microscopic infarcts (Table 1).

Table 1.

Observed cell frequencies for gross and microscopic infarcts of the Religious Order Study and the Memory and Aging Project

Microscopic infarcts	Gross infarcts
	None	Single	Multiple	Subtotal
None	585	122	104	811
Single	110	48	46	204
Multiple	41	27	52	120
Subtotal	736	197	202	1135

The question we examine here arose in assessing clinical predictors for brain infarcts. It is well established that brain infarcts are an underlying pathology associated with clinical strokes, clinical events characterized by the acute onset of focal neurologic deficit [20, 21]. In addition, it is also well-established that brain infarcts detected at autopsy can be found in people without a clinical history of stroke. These infarcts are often referred to as evidence of “silent strokes”. About one third of older brains harbor gross infarcts and about one third harbor microscopic infarcts. Gross infarcts are detected by visual examination of brain at autopsy, and microscopic infarcts are detected by examination of specific brain region under the microscope [5]. Gross and microscopic infarcts are separately classified as None/Single/Multiple.

To apply the general notation to this example, we take Y to represent gross infarcts and Z to represent microscopic infarcts. Since Y and Z each have three levels, there are four marginal cumulative odds:

$$\mathrm{o}\mathrm{d}\mathrm{d}{\mathrm{s}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}}={\mathrm{e}}^{{\mathrm{\psi }}_1^{\text{Y}}}=\frac{\mathrm{P}\mathrm{r}(\text{Y}=1\text{or}2)}{\mathrm{P}\mathrm{r}(\text{Y}=0)},$$

$$\mathrm{o}\mathrm{d}\mathrm{d}{\mathrm{s}}_{\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}}={\mathrm{e}}^{{\mathrm{\psi }}_2^{\text{Y}}}=\frac{\mathrm{P}\mathrm{r}(\text{Y}=2)}{\mathrm{P}\mathrm{r}(\text{Y}=0\mathrm{o}\mathrm{r}1)},$$

$$\mathrm{o}\mathrm{d}\mathrm{d}{\mathrm{s}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{m}\mathrm{i}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{p}\mathrm{i}\mathrm{c}}={\mathrm{e}}^{{\mathrm{\psi }}_1^{\text{Z}}}=\frac{\mathrm{P}\mathrm{r}(\text{Z}=1\text{or}2)}{\mathrm{P}\mathrm{r}(\text{Z}=0)},\mathrm{a}\mathrm{n}\mathrm{d}$$

$$\mathrm{o}\mathrm{d}\mathrm{d}{\mathrm{s}}_{\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{i}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{p}\mathrm{i}\mathrm{c}}={\mathrm{e}}^{{\mathrm{\psi }}_2^{\mathrm{Z}}}=\frac{\mathrm{P}\mathrm{r}(\text{Z}=2)}{\mathrm{P}\mathrm{r}(\text{Z}=0\mathrm{o}\mathrm{r}1)}.$$

There are also four possible global odds denoted with a double subscript corresponding to the four possible choices of points to determine quadrants:

$${\text{global}\text{odds}}_{\text{both}\text{present}}={\text{e}}^{{\text{ψ}}_{11}}=\frac{\text{P}\left(\text{Y}\ge 1,\text{Z}\ge 1\right)\text{P}\left(\text{Y}<1,Z<1\right)}{\text{P}\left(\text{Y}<1,Z\ge 1\right)\text{P}\left(\text{Y}\ge 1,\text{Z}<1\right)},$$

$${\text{global}\text{odds}}_{\text{both}\text{multiple}}={\text{e}}^{{\text{ψ}}_{22}}=\frac{\text{P}\left(\text{Y}\ge 2,\text{Z}\ge 2\right)\text{P}\left(\text{Y}<2,Z<2\right)}{\text{P}\left(\text{Y}<2,Z\ge 2\right)\text{P}\left(\text{Y}\ge 2,\text{Z}<2\right)},$$

$${\text{global}\text{odds}}_{\begin{array}{c}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}\\ \mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{i}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{p}\mathrm{i}\mathrm{c}\end{array}}={\text{e}}^{{\text{ψ}}_{12}}=\frac{\text{P}\left(\text{Y}\ge 1,\text{Z}\ge 2\right)\text{P}\left(\text{Y}<1,Z<2\right)}{\text{P}\left(\text{Y}<1,Z\ge 2\right)\text{P}\left(\text{Y}\ge 1,\text{Z}<2\right)},\mathrm{a}\mathrm{n}\mathrm{d}$$

$${\text{global}\text{odds}}_{\begin{array}{c}\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}\\ \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{m}\mathrm{i}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{p}\mathrm{i}\mathrm{c}\end{array}}={\text{e}}^{{\text{ψ}}_{21}}=\frac{\text{P}\left(\text{Y}\ge 2,\text{Z}\ge 1\right)\text{P}\left(\text{Y}<2,Z<1\right)}{\text{P}\left(\text{Y}<2,Z\ge 1\right)\text{P}\left(\text{Y}\ge 2,\text{Z}<1\right)}.,$$

Our complete analyses of two associated ordinal outcomes follow four steps; we provide an overview before we discuss all of the steps for our example. Preliminary analyses included an examination of the frequency distributions of each outcome [22]. As shown in table 1, the data are not too sparse, because each level has more than 50 observations. Our second step was to compute the association between gross and microscopic infarcts by calculating the global odds values. The third step is represented as models I and III in Table 2, where we fit separate marginal models for each outcome employing the covariates of interest. These models can be programmed in SAS using PROC LOGISTIC. Violations of the proportional odds assumption can be detected with the score test for proportional odds or with the likelihood ratio test. If the proportional odds assumption does not hold, a trend odds model can be fit in SAS with the PROC NLMIXED, as described in a detailed tutorial [22]. The parameter estimates from the marginal models (proportional odds or trend odds model) are stored to be used as initial values in the fourth step. In our analyses, all models include three demographic covariates: age at death, years of education and sex (coded as an indicator variable of male sex). As entered into the models, age and education were centered at round numbers near their means so that intercept terms correspond to a typical participant: a female 88 years old at death and with 16 years of formal education. The fourth and final step is to fit the global odds model. This can be accomplished in PROC NLMIXED and shown in the sample SAS code supplied in Appendix A; Supplementary Material. The results of the global odds models include simultaneous estimates of the odds of each infarct type marginally and of the association of these outcomes quantified via the global odds parameter.

Table 2.

Marginal Models of ordinal levels of infarcts assuming proportional odds

Parameter	Gross Infarcts						Microscopic Infarcts
	Model I			Model II			Model III			Model IV
	Estimate	SE	p-value	Estimate	SE	p-value	Estimate	SE	p-value	Estimate	SE	p-value
Intercept (multiple)	−1.685	0.094	<.001	−1.29	0.104	<.001	−2.192	0.11	<.001	−1.929	0.114	<.001
Intercept (present)	−0.746	0.08	<.001	−0.288	0.095	0.003	−0.966	0.083	<.001	−0.638	0.092	<.001
Age at death (y)	0.052	0.01	<.001	0.046	0.01	<.001	0.028	0.01	0.006	0.016	0.011	0.125
Male	0.307	0.132	0.02	0.289	0.135	0.033	0.11	0.14	0.432	0.032	0.144	0.824
Education (y)	−0.026	0.017	0.132	−0.024	0.018	0.178	−0.019	0.018	0.3	−0.008	0.019	0.647
Microscopic infarct
Single vs. absent	---	---	---	−0.063	0.11	0.566	---	---	---	---	---	---
Multiple vs. absent	---	---	---	0.831	0.126	<.001	---	---	---	---	---	---
Gross infarct
Single vs. absent	---	---	---	---	---	---	---	---	---	0.1	0.11	0.362
Multiple vs. absent	---	---	---	---	---	---	---	---	---	0.632	0.106	<.001

Age and education covariates in the models were centered so that intercept terms correspond to female participants 88 years old at death with 16 years of formal education.

Preliminary analyses indicate that there is a substantially greater burden of gross infarcts in people with microscopic infarcts. Specifically, Table 1 shows the frequency distribution from which we can determine the marginal odds and the global odds, ignoring covariates. The odds of having at least one gross infarct was 0.5 $({\text{e}}^{{\widehat{\mathrm{\psi }}}_1^{\text{Y}}}=399/736)$ and of multiple gross infarcts was 0.2 $({\text{e}}^{{\widehat{\mathrm{\psi }}}_2^{\text{Y}}}=202/933)$. The odds of having at least one microscopic infarct was 0.4 $({\text{e}}^{{\widehat{\mathrm{\psi }}}_1^{\mathrm{Z}}}=324/811)$ and multiple microscopic infarcts was 0.1 $({\text{e}}^{{\widehat{\mathrm{\psi }}}_2^{\mathrm{Z}}}=120/1015)$. Thus for each level of severity, the odds of gross infarcts is higher than the odds of microscopic infarcts. Similarly it is possible to estimate the four global odds: ${\text{e}}^{{\text{ψ}}_{11}}=4.4,{\text{e}}^{{\text{ψ}}_{12}}=2.9,{\text{e}}^{{\text{ψ}}_{21}}=4.2$ and ${\text{e}}^{{\text{ψ}}_{22}}=3.0$. All of these global odds are around 3 to 4, suggesting a strong association between gross and microscopic infarcts. The association is especially strong when microscopic infarcts are classified as present/absent, but these global odds parameters are similar enough that it will be appropriate to examine models in which the global odds is constrained to be the same over all i and j $({\Psi }_{ij}=\Psi )$.

In the third step, we fit marginal models considering each infarct type as a single outcome. In additional to the models needed in the global odds process described above (Table 2, models I and III), we also illustrate models with the other type of infarct outcome as a covariate (Table 2, models II and IV). Finally, we fit a series of global odds models. We saw no major violation of the proportional odds assumption (non-significant trend odds parameter), therefore proportional odds are assumed for marginal probability estimation. The first marginal model for gross infarcts (Table 2, model I) shows that two demographic covariates are associated with higher odds of gross infarcts: the log-odds for men is 0.307 higher than for women (p=0.020) and an increment of ten years in age at death is associated with 0.52 higher log-odds (estimate per year of age: 0.052, p <0.001). In the corresponding marginal model of microscopic infarcts (Table 2, model III), we only found higher odds for age at death (estimate of 0.28 per decade, p=0.010). In the models with the other type of infarct as a covariate (Models II and IV in Table 2), the demographic coefficients were closer to 0, and p-values less significant. Indeed, age is not significant when the marginal model of microscopic infarcts includes gross infarcts as a covariate (Table 2, model IV).

Table 3 shows estimates from two constant global odds models that include the three demographic covariates. Model I of Table 3 shows that neither of the covariates entered have significant effect on the association between gross and microscopic infarct. The model also provides information on the covariates that increase odds of more gross and microscopic infarcts marginally. Similar effects are found when comparing these results to the results of separate models of gross infarcts as an outcome and of microscopic infarcts as an outcome (Table 2, models I and III). We reran the model removing covariates that are non-significant (Table 3, model II). With the estimates obtained it is possible to predict the set of two-way probabilities of gross and microscopic infarcts for different combinations of age, sex and education.

Table 3.

Global Odds Model of bivariate ordinal levels of infarcts assuming constant global odds

Parameter	Model I			Model II
	Estimate	SE	p-value	Estimate	SE	p-value
Global odds parameters
Intercept - Log global odds ratio	1.148	0.167	<.001	1.145	0.13	<.001
Age at death (y)	−0.027	0.02	0.17	−0.028	0.019	0.155
Male vs. female	−0.034	0.275	0.9	---	---	---
Education (y)	0.028	0.037	0.457	---	---	---
Marginal parameters for gross infarcts
Intercept gross (multiple)	−1.683	0.094	<.001	−1.669	0.093	<.001
Intercept gross (single )	−0.742	0.08	<.001	−0.73	0.079	<.001
Age at death years	0.052	0.01	<.001	0.053	0.01	<.001
Male vs. female	0.304	0.132	0.022	0.248	0.126	0.05
Education (y)	−0.026	0.017	0.122	---	---	---
Marginal parameters for microscopic infarcts
Intercept microscopic (multiple)	−2.182	0.11	<.001	−2.146	0.097	<.001
Intercept microscopic (single)	−0.957	0.083	<.001	−0.923	0.066	<.001
Age at death years	0.029	0.01	0.005	0.029	0.01	0.004
Male vs. female	0.112	0.14	0.421	---	---	---
Education (y)	−0.015	0.018	0.418	---	---	---

Age and education covariates in the models were centered so that intercept terms correspond to female participants 88 years old at death with 16 years of formal education.

6. Simulations

Simulation was performed in SAS software, Version 9.3, of the SAS(R) system for Linux. Three procedures were compared. First, the constant global odds model and marginal proportional odds models were coded together using the PROC NLMIXED. Second, separate marginal proportional odds model were fit for each outcome using the PROC LOGISTIC. Finally, separate marginal odds controlling for the other type of infarct was fit using the PROC LOGISTIC. The simulation followed suggestions by Burton et al [23].

Simulated scenarios included different combinations of α^G, β^G, β^Y and β^Z (Table 4). A total of 500 datasets with 300 observations per binary predictor group was randomly generated from a multinomial distribution using different seeds. Bias, coverage, and accuracy performance were evaluated in the statistical methods for different scenarios. In addition, cell probability estimates were computed using the conditional probabilities based on the proportional odds model with and without the other type of predictor.

Table 4.

Simulation results for the global odds model and proportional odds model

	Simulation number
	1	2	3	4	5	6	7	8
True parameters
αG	0	1	2	0	1	2	0	1
βG	0	0	0	1	1	1	2	2
βY	2	2	2	2	2	2	2	2
βZ	2	2	2	2	2	2	2	2
Bias
GOM - βY	0.012	0.012	0.012	0.011	0.012	0.012	0.011	0.012
GOM - βZ	0.009	0.005	0.003	0.01	0.003	0.004	0.008	0.005
POM - βY	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012
POM - βZ	0.009	0.005	0.002	0.009	0.003	0.004	0.008	0.005
POMc - βY	0.012	−0.396	−0.702	−0.325	−0.62	−0.857	−0.559	−0.775
POMc - βZ	0.01	−0.35	−0.603	−0.284	−0.534	−0.709	−0.479	−0.646
MSE
GOM - βY	0.041	0.040	0.040	0.040	0.040	0.040	0.040	0.040
GOM - βZ	0.036	0.036	0.037	0.035	0.036	0.036	0.035	0.035
POM - βY	0.041	0.041	0.041	0.041	0.041	0.041	0.041	0.041
POM - βZ	0.036	0.036	0.038	0.035	0.036	0.037	0.036	0.036
POMc - βY	0.048	0.202	0.542	0.149	0.433	0.797	0.360	0.662
POMc - βZ	0.041	0.164	0.410	0.120	0.331	0.556	0.273	0.471
Coverage (%)
GOM - βY	95.4	94.6	94.4	95.8	95.0	95.6	95.4	95.6
GOM - βZ	95.2	95.2	94.4	95.6	95.6	94.4	95.4	95.4
POM - βY	95.2	95.2	95.2	95.2	95.2	95.2	95.2	95.2
POM - βZ	94.8	93.6	94.6	95.4	93.8	93.2	95.4	94.8
POMc - βY	95.0	53.0	13.2	64.8	22.2	6.2	28.0	10.4
POMc - βZ	94.6	57.6	17.2	69.2	26.0	10.4	34.6	14.6

GOM = global odds model, POM = proportional odds model, POMc= Proportional odds model of Y controlling for Z or Z controlling for Y

$$\text{Pr}(\text{Y},\text{Z}|\text{X})=\text{Pr}(\text{Y}|\text{Z},\text{X})•\text{Pr}(\text{Z}|\text{X})$$

For example, the probability that Y=1 and Z=1 given X=0, would correspond to the probability of exactly one gross and exactly one microscopic infarct given that the person did not have the predictor under study. We examine whether the additional complexity in coding global odds model using PROC NLMIXED (versus two separate proportional odds models using PROC LOGISTIC) would result in decreased bias in the estimation of cell probabilities.

Table 4 shows the simulation results for the global odds model and the proportional odds model. The marginal proportional odds with or without the parallel modeling of global odds gave essentially identical results for intercept and effect when the global odds was 2 or less. Controlling for the other type of infarct increased absolute bias, especially when both outcomes were highly associated. Not surprisingly, the power to detect significant predictors was also decreased, with inflated mean square errors. Table 5 provides comparison of the true cell probability under the eight scenarios of Table 4. Bias is reduced when probabilities are estimated using the global odds model versus two separate proportional odds models given that X=1 (i.e. having the predictor).

Table 5.

Cell probability based on simulation results for the global odds model and proportional odds

	Simulation number
	1	2	3	4	5	6	7	8
True probabilities, %
Pr(Y=1,Z=1|X=1)	10.56	15.51	20.20	15.51	20.20	24.06	20.20	24.06
Pr(Y=1,Z=2|X=1)	9.37	9.11	7.90	9.11	7.90	6.09	7.90	6.09
Pr(Y=2,Z=1|X=1)	7.60	7.90	7.48	7.90	7.48	6.46	7.48	6.46
Pr(Y=1,Z=3|X=1)	11.87	7.18	3.70	7.18	3.70	1.65	3.70	1.65
Pr(Y=3,Z=1|X=1)	15.05	9.79	5.52	9.79	5.52	2.68	5.52	2.68
Pr(Y=2,Z=2|X=1)	6.74	7.47	9.49	7.47	9.49	12.41	9.49	12.41
Pr(Y=2,Z=3|X=1)	8.54	7.51	5.91	7.51	5.91	4.02	5.91	4.02
Pr(Y=3,Z=2|X=1)	13.35	12.89	12.07	12.89	12.07	10.97	12.07	10.97
Pr(Y=3,Z=3|X=1)	16.92	22.64	27.72	22.64	27.72	31.67	27.72	31.67
Bias, E-2
GOM
Pr(Y=1,Z=1|X=1)	0.00	0.00	−0.04	0.00	−0.02	−0.02	−0.02	−0.01
Pr(Y=1,Z=2|X=1)	−0.03	−0.04	−0.03	−0.05	−0.04	−0.04	−0.04	−0.05
Pr(Y=2,Z=1|X=1)	0.02	0.03	0.02	0.03	0.03	0.05	0.03	0.06
Pr(Y=1,Z=3|X=1)	0.00	−0.02	−0.01	−0.02	0.00	0.00	0.00	0.00
Pr(Y=3,Z=1|X=1)	−0.02	−0.01	−0.01	−0.01	−0.01	0.00	−0.01	0.00
Pr(Y=2,Z=2|X=1)	0.06	0.06	0.06	0.06	0.04	0.03	0.04	0.02
Pr(Y=2,Z=3|X=1)	0.02	0.01	0.02	0.01	0.02	0.01	0.02	0.02
Pr(Y=3,Z=2|X=1)	−0.03	−0.02	−0.03	−0.03	−0.04	−0.02	−0.05	−0.04
Pr(Y=3,Z=3|X=1)	−0.01	0.00	0.01	0.00	0.02	−0.02	0.03	0.00
POM times POMc
Pr(Y=1,Z=1|X=1)	0.01	0.03	−0.04	−0.95	−1.28	−1.28	−2.25	−2.53
Pr(Y=1,Z=2|X=1)	−0.02	0.10	0.55	0.16	0.79	1.46	0.94	1.87
Pr(Y=2,Z=1|X=1)	0.03	0.05	0.14	0.08	0.36	0.70	0.49	1.05
Pr(Y=1,Z=3|X=1)	−0.02	−0.04	−0.14	0.79	0.69	0.30	1.39	0.98
Pr(Y=3,Z=1|X=1)	−0.04	−0.08	−0.12	0.89	0.93	0.63	1.78	1.55
Pr(Y=2,Z=2|X=1)	0.04	−0.28	−1.05	−0.40	−1.45	−2.57	−1.69	−3.23
Pr(Y=2,Z=3|X=1)	0.02	0.05	0.21	0.32	0.70	0.98	1.05	1.60
Pr(Y=3,Z=2|X=1)	−0.03	0.17	0.49	0.22	0.62	1.08	0.70	1.29
Pr(Y=3,Z=3|X=1)	0.01	−0.01	−0.04	−1.10	−1.35	−1.31	−2.39	−2.58

GOM = global odds model, POM = proportional odds model, POMc= Proportional odds model of Y controlling for Z or Z controlling for Y

7. Discussion

Understanding how different predictors can alter the association between gross and microscopic infarcts may help advance knowledge about the etiology and consequences of these common vascular disorders. The predicted probabilities of the combination of gross and microscopic infarcts may be important information for medical decisions. These probabilities depend on the marginal probabilities and on the association of the outcomes, represented by the global odds. We examined how shifts in location versus shifts in scale of the theoretical marginal underlying logistic distributions would influence the departure from the bivariate probability under independence given a constant global odds value. As illustrated, the gain in information will depend on the location and scale of the underlying latent variables.

Simulation results indicated that the global odds models yield decreased bias when compared to approaches using marginal and conditional marginal modeling. Although modeling the global odds requires more advanced statistical methods, models with global odds parameters provide better summaries of the data and better information. For example, it can be difficult to reconcile separate models.

The use of the proportional odds assumption to ascertain the marginal probabilities relies on the theory that there is an underlying unobserved variable that follows a logistic distribution and that is observed as an ordinal manifestation. The marginal probabilities, along with the association level, are important determinants of the distribution of the bivariate ordinal distribution. If there is a shift in location and scale of such marginal logistic distribution, the trend odds assumption will hold. The global odds with trend odds margins can be considered as an extension of the global odds with proportional odds margins. Similarly, the constant global odds assumptions may not hold in some cases. In this case, exploring trend of global odds can be a parsimonious alternative.

The appropriate modeling choice will depend on the research question. Regardless, if two correlated outcomes are to be studied and separate models are used, these models should not include the other outcome as a covariate. A global odds model should be considered if different predictors can alter the association between two outcomes. The global odds model should also be considered when estimating the probability that an individual has a specific combination of the two outcomes.

In this paper, we applied the global odds model to data on gross and microscopic infarcts. This approach can be used to answer other research questions involving associated ordinal outcomes, such as Likert scales or levels antibodies for virus that cross-react. Although the examples include just three ordinal levels, for reason of parsimony, the approach becomes even more appealing for more than three levels, as long as trend odds or proportional odds holds for the margins and constant global odds holds for the association.