Abstract
The spatiotemporal organization of networks of dynamical units can break down resulting in diseases (e.g., in the brain) or large-scale malfunctions (e.g., power grid blackouts). Re-establishment of function then requires identification of the optimal intervention site from which the network behavior is most efficiently re-stabilized. Here, we consider one such scenario with a network of units with oscillatory dynamics, which can be suppressed by sufficiently strong coupling and stabilizing a single unit, i.e., pinning control. We analyze the stability of the network with hyperbolas in the control gain vs coupling strength state space and identify the most influential node (MIN) as the node that requires the weakest coupling to stabilize the network in the limit of very strong control gain. A computationally efficient method, based on the Moore–Penrose pseudoinverse of the network Laplacian matrix, was found to be efficient in identifying the MIN. In addition, we have found that in some networks, the MIN relocates when the control gain is changed, and thus, different nodes are the most influential ones for weakly and strongly coupled networks. A control theoretic measure is proposed to identify networks with unique or relocating MINs. We have identified real-world networks with relocating MINs, such as social and power grid networks. The results were confirmed in experiments with networks of chemical reactions, where oscillations in the networks were effectively suppressed through the pinning of a single reaction site determined by the computational method.
In a network, the units influence each other by coupling—the most influential node in the network can enforce the entire network to follow its dynamics as long as the coupling is sufficiently strong. However, even in a relatively small network (e.g., ten nodes), finding the most influential node (MIN) is a challenging task without extensive modeling. Here, we carefully tested mathematical measures that can predict the location of the MIN by performing experiments with coupled chemical oscillators, where the most influential unit was selected to suppress wild fluctuations in the network. In particular, we found that in some networks, the MIN can relocate for weakly or strongly coupled networks without any rewiring; for example, in such a social network, the leader could change without making new connections but instead by strengthening the existing connections throughout the network.
I. INTRODUCTION
Complex systems constituted by a network of coupled nonlinear dynamical units are prevalent in nature and human society. Such networks have their properties tuned for normal functioning that generates specific spatiotemporal patterns. A disruption of the network properties can lead to malfunction, which in biological systems can result in diseases, e.g., Parkinson’s disease and epilepsy, which are linked to excessive synchronization of neural activities.1,2 Under these circumstances, a control policy—intervention on dynamic properties using exogenous inputs—can be applied to re-establish the normal functioning of the system.2 For large networks, the application of exogenous inputs is often limited to a single or a small number of sites due to physical or cost constraints, e.g., for secondary frequency control of microgrids,3 and an important intervention task is to stabilize the network behavior at a certain state.4
The feedback strategy, referred to as pinning control, can achieve network stabilization by propagating the stabilizing effect of the feedback site through couplings between nodes to the entire network. One compelling application of such an approach is the suppression of wild fluctuations in a network in order to retrieve normal stationary behavior. Prominent examples include the use of neurostimulation to mediate epileptic seizures5–7 and the application of medications to the infected nodes in a high-risk contact network to preclude the spread of disease, such as HIV.8 Notions of pinning control have also been extensively introduced to analyze dynamic structures in a complex network, such as synchronization,9,10 stabilization,11–13 and consensus.14,15
The question of interest is to determine the site (node) in the network that has the most influence on the network dynamics. While many definitions for measuring influence are possible and can depend on the underlying node dynamics, here, we consider a particular example where the nodes exhibit (stable) oscillatory dynamics and an unstable fixed point. It is assumed that this fixed point can be stabilized with external local feedback at a sufficiently large feedback gain ( ). It is also assumed that there is a bidirectional coupling in the network such that with strong coupling ( ), a nearly uniform state can be achieved. Within this framework, the most influential node (MIN) can be defined as the node that can stabilize the network to the global steady state with minimum coupling strength. The choice of this definition was motivated by our experiments with electrochemical oscillator networks where coupling strength can be changed and individual nodes can be stabilized with external feedbacks.16,17 We note, however, that similar experiments with synchronization and control can be achieved in a wide range of systems, e.g., with mechano-chemical oscillators18 or BZ systems.19 The location of MIN depends upon the network topology, which has been the primary method of investigation for the existing methods; several methods leveraging measures defined on the network topology, such as eigenratio, degree, and distance, have been proposed.20,21
A fundamental challenge is to accurately and efficiently identify the most influential site for establishing stable behavior in the network and to reveal the impact of network properties on the site location and its uniqueness. When the strength of the coupled elements is uniform throughout, one can represent the network with an adjacency matrix, whose elements are 1 when coupled or zero otherwise. From linear algebra and graph theory, we know that the coupling strength will simply rescale (e.g., multiply) network properties, in particular, its eigenvalues. Therefore, if are the smallest eigenvalues of the network when the feedback is applied at nodes a and b, respectively, one would expect this relationship to remain unchanged with uniformly increasing the coupling. Extensive works have been developed for identifying influential nodes in pinning control20,21 based on the adjacency matrix alone. In these previous studies, particular measures, e.g., eigenratio, degree, and distance, were employed, and hence, the interaction between the feedback and the coupling was not considered, and thus, a unique MIN was assumed, which is independent of the feedback gain ( ) and other system parameters.
In this report, we explore the properties of network stabilization through the non-trivial interactions between the coupling (i.e., overall strength and topology) and the local feedback. The central concept of our approach is developing phase diagrams in the vs. parameter space using “stability hyperbolas,” identifying the MIN for a given network, and determining whether the MIN can relocate in the given network by changing or values.
This paper is structured as follows. In Sec. II, we introduce the mathematical model and the assumptions. In Sec. III, phase diagrams are constructed in which the stability boundary is described by a shifted hyperbola. The limiting values of the hyperbola are determined by network measures related to the number of nodes and the smallest eigenvalue of the Laplacian matrix of the system under infinitely strong feedback. As the latter is difficult to determine (especially, for large networks), in Sec. IV, we show the use of the diagonal values of the Moore–Penrose pseudoinverse of the coupling Laplacian matrix (without feedback) for selection of the most influential nodes. In Sec. V, by analyzing a wide variety of networks (random, small-world, scale-free, tree), the fundamental hyperbola properties (shifts and steepness) are applied for the classification of the networks into those with unique optimal pinning locations (most influential nodes) and those whose locations can relocate. These results then enable the identification of real-world networks whose structure could support the relocation of the most influential site as shown in Sec. VI; the numerical and theoretical findings are demonstrated with the network stabilization experiments with chemical oscillators. Finally, the main findings of this paper are discussed in Sec. VII.
II. ASSUMPTIONS AND DESCRIPTIONS OF NETWORK DYNAMICS
We aim to identify the node that, by propagating its influence throughout the network, can most effectively stabilize the network to an otherwise unstable steady state. We assume that a single isolated node can be stabilized using state feedback, and there is a coupling mechanism between nodes such that strong coupling leads to uniform behavior. With these assumptions, we focus on the more complex task of stabilizing the entire network by pinning a single site.
Here, we consider an undirected network consisting of identical dynamic units, diffusively coupled (i.e., the interaction strength between two nodes is proportional to the difference of their states), in which each unit has an unstable fixed point. The network of coupled oscillators can be written in the general form as
| (1) |
where and are the state and the dynamics of the th oscillator, respectively, with . The term represents the diffusive coupling function with uniform coupling strength , while the ’s are the entries of the adjacency matrix associated with the graph (network) , with (for ), if the elements and are coupled; otherwise, . Last, the control is the form , where if the th node is pinned; otherwise, . It is important to note that the topology of the networks is considered fixed and that is reinforced by restricting the coupling strength in a finite set ). Therefore, at no time, the topology changes due to the value of the coupling strength.
As a prototype model, Stuart–Landau (SL) oscillators are considered. A network of elements with coupling in both and state variables stimulated by external inputs is modeled by
| (2) |
where , (with and real parameters), and and are the pinning inputs applied to the oscillator . A difference-based control is applied to stabilize the desired behavior, ,
| (3) |
In the given examples, unstable stationary states satisfying are considered.
III. STABILITY HYPERBOLA-BASED NETWORK ANALYSIS
A. Stability boundary
To evaluate the node influence, the stability of the node is established with a given feedback gain in Eq. (3), while the coupling strength ( ) is increased until the entire network gains stability. With the Stuart–Landau system, the stable limit cycle is converted into a stable equilibrium point (the origin) that was originally unstable through amplitude death.22–24 The most influential node can achieve this task at the weakest coupling strength.
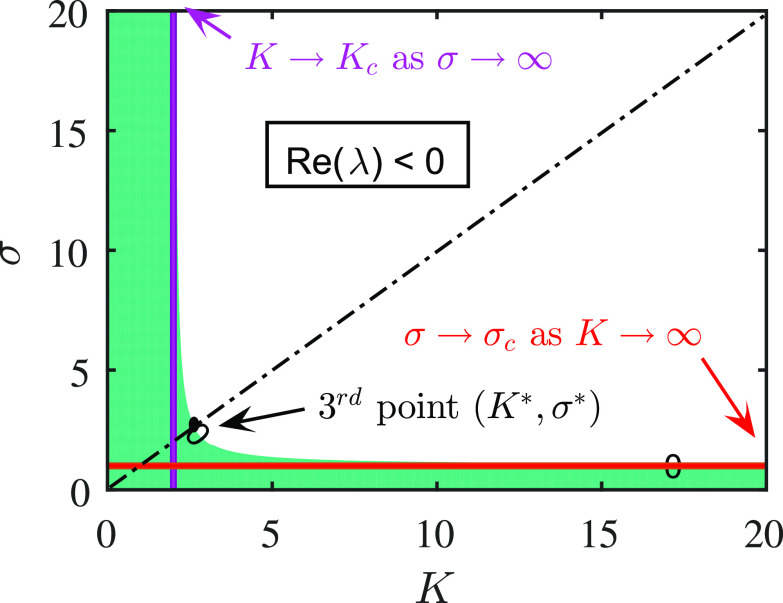
The stability boundary of the network at different coupling strengths and feedback gains can be represented in a phase diagram as shown in Fig. 1 for the simplest network with two oscillators. The figure shows that the stability boundary is a hyperbola with horizontal and vertical shifts. At strong feedback ( ), there is a critical coupling strength, , above which the entire network has a stable stationary point; this (see Sec. 1.3 in the supplementary material) results in a vertical shift of the hyperbola. Similarly, for strong coupling strength ( ), there is a minimal feedback gain, required for the stability, resulting in a horizontal shift of the hyperbola.
FIG. 1.
Stability hyperbola of a two-node network. The stable (white) and unstable (green) operating regions are separated by a hyperbola with asymptotes given by the critical feedback and critical coupling , where . The dotted black line, given by , defines the steepness of the hyperbola.
In Sec. 1 of the supplementary material, a linear stability analysis was performed for a complex network; in general, we found that a complex network with a given pinning node will exhibit a similar stability hyperbola to that with two oscillators. In Sec. 2 of the supplementary material, an analytical formula is obtained for the stability hyperbola as
| (4) |
Equation (4) is characterized by three main quantities: the critical gain ( ), the coupling strength ( ), and the steepness of the hyperbola [determined at a point ( ) on the hyperbola]. The analysis of the properties of the derived stability hyperbola provides a convenient and unified framework to evaluate the node influence and ultimately to select the most influential site.
B. Strong coupling limit
At sufficiently strong coupling, the entire system synchronizes, hence, behaves like a large unit, and the network properties play a negligible role in the dynamics. Therefore, independent of the network topology, the critical feedback gain (the horizontal shift in the phase diagram) is a constant that is proportional to the network size but inversely proportional to the number of control sites (see Sec. 1.3 in the supplementary material), i.e.,
| (5) |
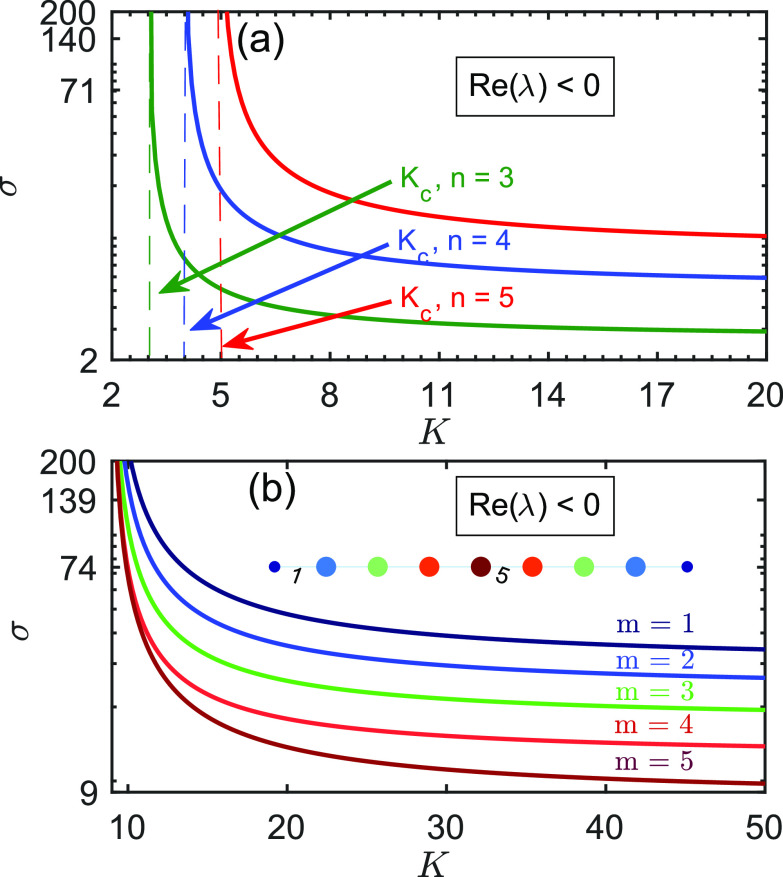
where and are the network size and number of pinned nodes, respectively. Figure 2(a) illustrates how the stability hyperbolas shift upward toward the right as the network size increases with a chain network. As the hyperbola shifts horizontally to the right, the critical gain increases, which means that larger networks are increasingly difficult to control and require higher feedback gain and coupling values to achieve network stability. The illustration in Fig. 2(a) was generated using chain networks; however, complex networks also follow a similar trend.
FIG. 2.
Dependence of the stability hyperbola on the network size (top) and the location of the pinning node (bottom) and for a chain network. (a) Dependence on the size of the network. The critical gain increases with the size of the network, and , for and , respectively. (b) Dependence on the control site. For the nine-node network shown in the inset, with color-coded node influences (where dark red represents the most influential node), the critical coupling increases as follows: , , , , and , where denotes the node number.
C. Weak coupling limit
In the more realistic weak coupling limit, the critical coupling (the vertical shift in the phase diagram) is determined by the network topology and the position of the control site. This is illustrated in Fig. 2(b), where for a fixed-size chain network, the stability hyperbola progressively shifts upward as the control site moves away from the center node.
In general, for many complex networks, we observe a similar upward shift where the central node is the most influential site. For each control site in a given network, can be calculated, and it is inversely proportional to the smallest positive eigenvalue ( ) of the Laplacian matrix in the limit of infinity feedback gain (see Sec. 1.3 in the supplementary material), i.e.,
| (6) |
where is the control matrix. The derivation of the expression of the critical coupling shows the dependence of on the network structure through the eigenvalue of the matrix of the pinned network.
Figure 2(b) shows that in a chain network, the central node corresponds to the smallest vertical shift ( ) and, thus, the largest stable area in the phase diagram. Therefore, in our definition, this is the most influential site for any feedback gain. However, the properties of the stability hyperbolas make the selection of the most influential node a relatively simple procedure. For each node, one can calculate the quantity and select the node with the smallest value, as this corresponds to the smallest according to Eq. (6). The inset of Fig. 2(b) shows that indeed the central node has the smallest value.
D. σc and the eigenvalue ratio
Note that estimation of to identify the most influential node using Eq. (6) is a computationally extensive process. To address the challenges of applying network centrality measures to find MIN, we demonstrate the effectiveness of one such measure, the eigenvalue ratio ( ).
The eigenratio ( ) has been shown to be an effective measure for determining the optimal site for network synchronization.20,21,25 However, it does not always yield the MIN for network stabilization due to its sensitivity to feedback gain. We illustrate this through a numerical simulation on three different network topologies (100 different network realizations for each topology) where we employ to identify the control site for three different feedback gains. The sensitivity of to the feedback is evaluated by the ratio , where is the critical coupling at the MIN that was selected by computing and is the smallest critical coupling of the network. Note that the selected node is the MIN only if . Figure 3 shows that when the feedback gain is small ( ), utilizing to evaluate MIN results in a high ratio, and the performance improves as the value of increases for three distinct network topologies, emphasizing the sensitivity of to the feedback . We have explored using different centrality measures in order to reliably identify MIN at a relatively small computational expense.
FIG. 3.
A comparison of the performance of eigenratio centrality and the proposed technique (M1) for identification of MIN with different feedback gains. (a) BA scale-free networks. (b) ER random networks. (c) WS small-world networks. Networks of 100 nodes were used to produce these plots, and the eigenratio method was evaluated for different feedback gain values to show its sensitivity to the gain. M1 is our proposed method, which is independent of .
IV. IDENTIFICATION OF THE MOST INFLUENTIAL NODE
Here, we present a computationally efficient technique for selecting MIN and a theoretical analysis on the uniqueness of MIN with different coupling strengths.
A. Moore–Penrose pseudoinverse centrality for identifying the MIN
The identification of the MIN, i.e., the node at which the feedback gain will have the most stabilizing impact, can be tackled using the notion of a geometric measure of modal controllability.26 In linear dynamical systems, this technique allows one to quantify the influence of each input (i.e., each pinning site, in the context of this paper) on a particular eigenvalue of the system. However, extra care must be taken when this method is applied to systems with repeated eigenvalues.27 In addition, this method also requires the computation of eigenvalues for each possible control site in the network, which is impractical for very large networks or time-varying networks.
Here, we propose a notion of pseudoinverse centrality together with a Lyapunov-based approach to resolve this bottleneck. Consider a control system described by the Laplacian dynamics (see Sec. 1.2 in the supplementary material) associated with a network of nodes, given by
| (7) |
where and is the graph Laplacian of the given network, is an input matrix, and is a feedback control law with . In particular, we consider (an identity matrix), which implies that every node in the network is receiving feedback. It is known that modes (eigenvalues of the matrix) that are difficult to control from a given input (pinning site in this context) require higher control gains.28 Therefore, by computing the feedback gain for each possible pinning site and using them as a measure of node centrality, one can determine the node that requires the least amount of gain, which can be considered the most influential one.
To establish pseudoinverse centrality, we exploit Lyapunov’s method in feedback design. Indeed, it has been shown that the control of the form , where is the steady-state solution to the Lyapunov equation,
| (8) |
can result in a minimum time response.29 The solution to Eq. (8) is of the form
| (9) |
where is symmetric and positive definite (PD), which is chosen here as . The integral in Eq. (9) exists for only when is Hurwitz; i.e., Re for .30 However, in the case of the Laplacian dynamics, is not Hurwitz; therefore, we can only approximate the steady-state solution by taking a sufficiently large time horizon . We can then obtain an approximation to the steady-state solution, given by
| (10) |
derived by setting the left-hand side of Eq. (8) to zero and then solving for under the assumption that and commute. The term (with in the order of ) was introduced to shift the zero eigenvalue so that one can invert the matrix. This technique is often used in nonlinear systems analysis30 and signal processing applications31 when is singular or ill-conditioned.
Since only the relative values of the entries in play a role in identifying the most influential node, we propose to use the Moore–Penrose inverse (MPi) in place of Eq. (10) as follows:
| (11) |
where is the MPi of . Note that the solution given in Eq. (11) is preferred to Eq. (10) as it is less likely to introduce numerical errors even for large matrices. We will then use Eq. (11) to compute the node centrality measure, which we refer to as the MPi centrality.
1. MPi centrality measure
Let be the vector of centrality measures with , where is the th diagonal element of for . Then, the most influential node is the th node that corresponds to the largest centrality measure in .
Figure 3(a) shows that the method correctly identifies the MIN in all the considered BA scale-free, ER random, and WS small-world networks even at weak feedback gains where the eigenvalue ratio method is not reliable. Note that the control centrality is computed by simultaneous application of feedback controls with the input matrix and the gain matrix . Under this scenario, the MPi centrality expresses to what extent each node contributes to the stability of the state with strong feedback gain ( ) when all the nodes are simultaneously controlled.
By avoiding the estimation of eigenvalues for each control site and computing all centrality measures simultaneously, we are able to identify the MIN in a computationally efficient manner.
V. NETWORKS WITH INTERSECTING HYPERBOLAS
A. Networks with relocating MINs
As it was pointed out, in a given network, the stability hyperbolas for the different nodes exhibit the same horizontal shift ( ) but can have different steepness and vertical shift ( ). So far, we focused on identifying the MIN based on a single measure ( or MPi centrality). If the MIN has the steepest hyperbola and the smallest , then this node is unique in the sense that it is independent of the coupling strength, and the stabilization of the network will be achieved with the weakest feedback gain. However, if some nodes have steep hyperbolas and other nodes’ smaller values, then the hyperbolas can intersect, and the MIN will relocate by uniformly changing the coupling strength across the network.
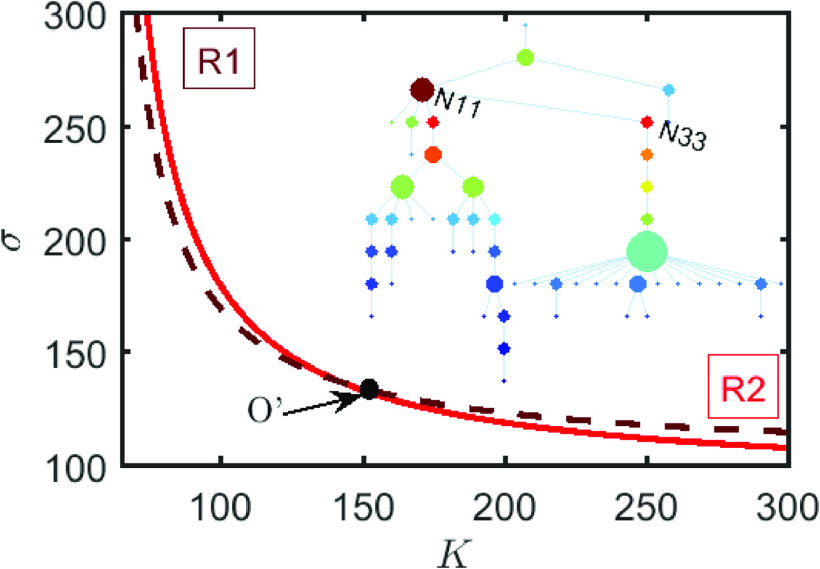
We illustrate this relocation phenomenon of the MIN in Fig. 4 using a 55-node tree network that has intersecting hyperbolas. Indeed, the hyperbolas of nodes N11 and N33 intersect at O and observe that the steepest hyperbola (red dashed line corresponding to N11) will require a weaker feedback gain in the strong coupling operating regime; hence, N11 is the MIN. However, after the intersection, we see that the situation has been reversed, i.e., now for a fixed coupling strength , it is N33 (red solid line) that requires the smallest feedback gain, and therefore, it is the MIN in the weak coupling regime.
FIG. 4.
Illustration of relocating MIN due to intersecting hyperbolas in a 55-node tree network. R1 (node N11): strong and weak operating regime. R2 (node N33): weak and strong operating regime.
Being able to quickly identify networks with relocating MINs is of practical importance in the sense that it will allow one to correctly access the node’s influence at different operating regimes, i.e., various values of the coupling strength and the control feedback gain. Hence, in the following, we devise a numerical procedure for detecting such networks.
B. Identification of networks with relocating MINs
An indication that the stability hyperbolas may intersect is when the MIN for a given network is predicted by MPi centrality does not have the smallest calculated value. A natural approach to determine intersecting points among hyperbolas is to check the existence of the solution satisfying the equation defining the stability hyperbola. However, this approach, though accurate, is computationally costly and time-consuming for large networks. To give an idea, the computation of at each node in the power grid shown in Fig. 6(a) took approximately 8 h on a standard desktop computer, and furthermore, the computation for finding the point , where on the hyperbola (see Fig. 1), requires an iterative scheme.
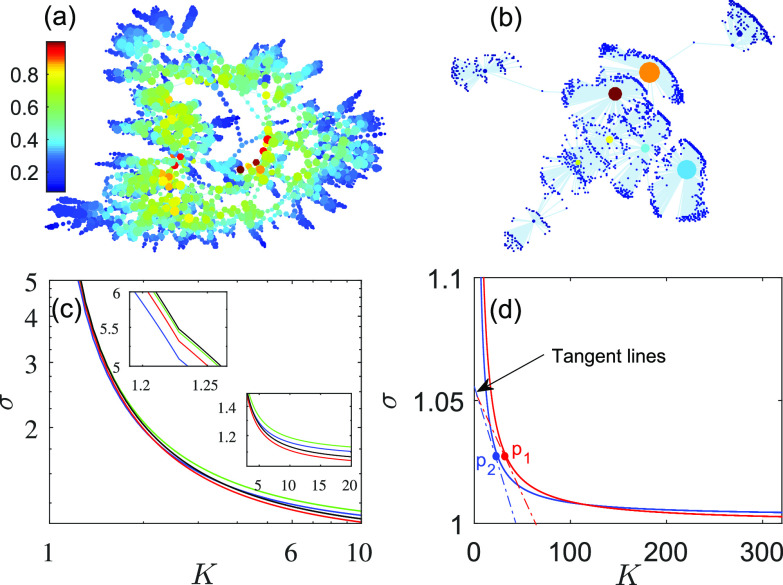
FIG. 6.
Real-world networks exhibiting relocating MINs. (a) Western States’ power grid of the United States. (b) Ego-Facebook networks. The colormap represents the normalized control centrality of each node from zero to one. (c) and (d) Intersecting hyperbolas for the power grid and ego-Facebook networks, respectively. (c) Hyperbolas normalized by (N427, red hyperbola) and . The other hyperbolas have (N394, black), (N1244, blue), and (N1309, green). (d) Hyperbolas normalized by the network and . The tangent lines show the steepness of the hyperbolas.
The procedure proposed here is a result of analyzing the contribution of each node to the feedback control in the general form , where the gain matrix is . Assuming that the feedback is applied only to node 1, and then the input matrix reduces to vector . Therefore, the feedback gain becomes a row vector, , that is the first row of the matrix . For the general feedback configuration that utilizes every node states, each entry in the gain vector will contribute to the control signal.
In networks with unique MIN, the MPi centrality-based method is used to identify the pinning site that requires the least feedback gain for network stabilization. By reviewing a large number of networks with relocating MINs, we observed that the diagonal elements of the Moore–Penrose pseudoinverse may not follow the same trend as the norm of the gains , related to the off-diagonal elements.
Based on this observation, the following procedure was found to be effective for identifying networks with relocating MINs:
-
Step 1. Use the diagonal entries, , of the matrix to form the vector .
-
Step 2. Compute the weights for , where is the th row of and then rescale to get .
-
Step 3. Compute the difference of the two vectors .
-
Step 4. Assume that is the index of the most influential node selected using the MPi centrality with denoting the corresponding critical coupling, then for any , , compute . If , then the stability hyperbolas of nodes and can intersect. Hence, the network has relocating MINs.
Note that the number of nodes satisfying is much less than the size of the network , which makes this procedure computationally more tractable than computing the critical coupling for all nodes in the network. The effectiveness of the proposed algorithm is validated in Sec. VI.
VI. APPLICATIONS AND EXPERIMENTS
A. Identification of most influential nodes with synthetic networks
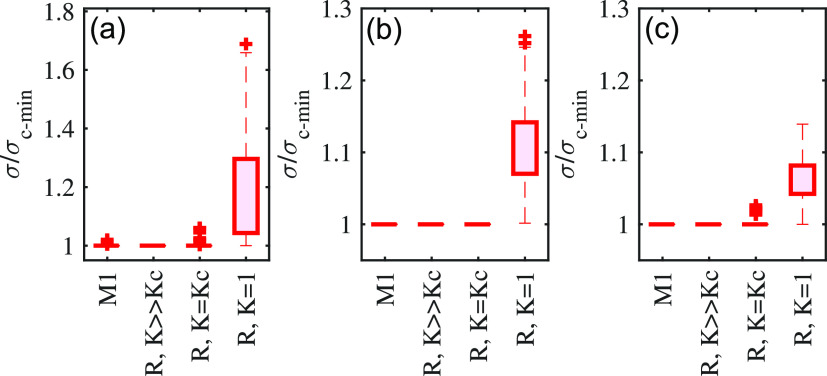
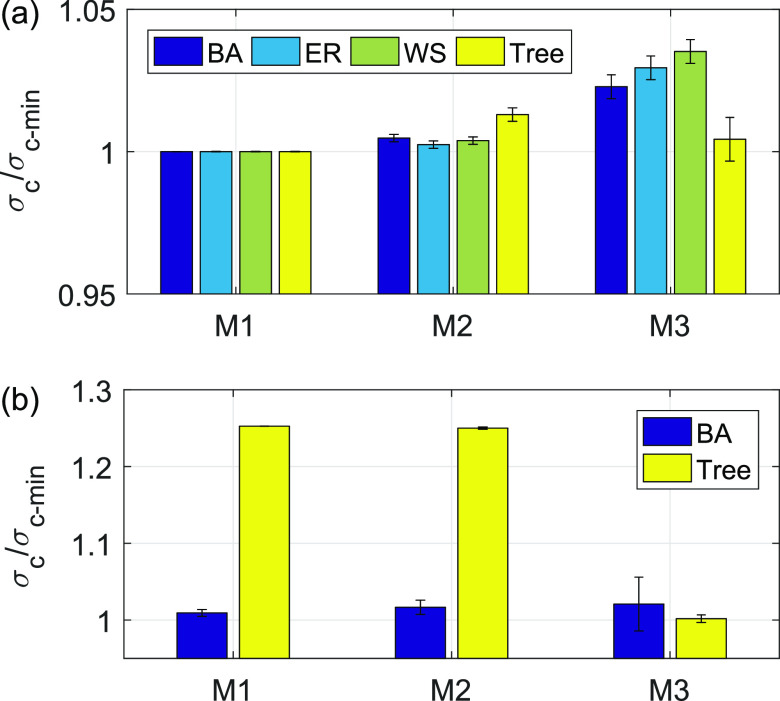
To evaluate the performance of the MPi centrality measures, we illustrate the results in terms of the ratio . The MPi centrality was evaluated against some of the commonly used centralities, including the degree, closeness, and eigenvector centralities. In Fig. 5(a), the results for networks with unique MIN are presented where means that the method successfully identifies the most influential node, while means that the MIN was not identified. Figure 5(a) shows that for these networks of 100 nodes, including Barabási–Albert (BA) scale-free,32 Erdős–Rényi (ER) random,33 Watt–Strogatz (WS) small-world,34 and tree35 networks, our approach (M1) uniquely identifies the most influential sites and outperformed the other approaches. (We note that while is somewhat small to completely reflect the properties of scale-free networks, we used 1000 realizations to capture the salient features, such as presence of hubs and short path lengths.)
FIG. 5.
Performance measure ( ) of identifying MIN with the proposed MPi centrality-based method (M1) and with other commonly used techniques (M2 and M3) in different networks. (a) and (b) Ratios of the critical coupling for the pinning sites (selected with the methods M1–M3) to the smallest in each network (plot of average values and their confidence intervals). (a) Networks with unique MIN. (b) Networks with relocating MINS in BA and tree networks for 1000 sample networks. M1: our proposed method; M2: node degree-based method for BA, ER, and WS networks; and average distance-based method for trees. M3: based on the ratio of a node degree over an average distance for BA, ER, and WS networks and based on the eigenvector centrality (Fiedler vector) for tree networks. Tree networks used in the numerical experiment were generated with 7 generations but a different number of nodes at each run, while the spanning trees were obtained from ER random networks of 100 nodes. The other networks had 100 nodes. Error bars represent standard deviations of the performance measures for the sample networks.
The results shown in Fig. 5(b) illustrate the performance of the proposed method when the networks have relocating MINs as predicted by the technique in Sec. V. The ratio was greater than one, which implies that the proposed method did not uniquely identify the MIN because the stability hyperbolas intersect. In this case, the MIN selected using the MPi centrality, which is the most influential control node in strong coupling (weak feedback), could require up to 25% more coupling strength when the network is operating in the weak coupling regime.
We, thus, see that it is essential to identify networks with relocating MINs. We also validated the relocating MIN identification algorithm in a sample of 1000 networks (with 100 nodes) for various network topologies (Table I). For each of the networks, the stability hyperbolas were determined, and the percentage of networks with intersecting hyperbolas was calculated. For BA scale-free, ER random, and WS small-world networks, a large majority ( ) of the networks had unique MIN. However, 37% of the tree networks had relocating MINs. Our algorithm to identify the networks with relocating MINs worked quite well with the false positive rate (FPR) for all the networks and a true positive rate (TPR) of for ER random, WS small-world, and BA scale-free networks (TPR = 0.77 for the tree networks). Apparently, tree networks have a tendency to exhibit relocating MINs, and it is more challenging to identify them.
TABLE I.
Quantification of MIN relocation phenomena in a sample of 1000 networks of 100 nodes. The estimated percentage of relocating MIN networks is obtained by applying the proposed technique in Sec. V.
| Percentage of networks with relocating MIN | Accuracy | |||
|---|---|---|---|---|
| Network type | True | Estimated | TPR | FPR |
| BA scale-free | 1.60 | 1.70 | 1 | 0.001 |
| ER random network | 0.40 | 0.40 | 1 | 0 |
| WS small-world | 0.10 | 0.10 | 1 | 0 |
| Tree networks | 37.0 | 28.4 | 0.77 | 0 |
B. Real-world networks with relocating most influential nodes
We have also found networks with relocating MINs in some real-world networks, e.g., in power and social networks. Specifically, here, we consider the Western States power grid of the United States and the ego-Facebook networks. The former is represented by an undirected network where a node represents either a generator, a transformer, or a substation and the edges represent the transmission lines,34 while the latter represents users’ friendship with users as nodes and the friendship as edges.36
Figures 6(a) and 6(b) show the Western States power grid of the United States (4941 nodes and 6594 edges) and the ego-Facebook network (2888 nodes and 2981 edges), respectively, in which the color bar denotes the calculated control centrality (normalized to 1) for each node. Note that we analyze the structure of these two networks without considering their true node dynamics, but instead treat them as if they were oscillator networks. In addition, we consider the coupling strength to be uniform. For the power network, the MPi centrality-based method identified the optimal site N1244 in the weak gain region, and the steepness analysis revealed that this network has three possible MINS (N1244, N427, and N394) that created two hyperbola intersections (N1244 with N427 and N1244 with N394), shown in Fig. 6(c). As a result, either node N427 or N1244 can be the most influential site in the high gain region, depending on the coupling strength. This case also indicates that when the degree centrality fails to select the most influential site, the resulting control node can be far from optimal. Indeed, in this network, node N2554 has the highest node degree with the critical coupling , while the two best control sites N427 and N1244 have a lower node degree, , with the corresponding critical couplings, and , that are and lower than that of N2554.
As for the social network, we found two potential MINs, N288 (node degree ) and N603 ( ), with and , respectively. The most influential site is switched from node N288 in the weak feedback region to N603 in the high feedback region [see Fig. 6(d)]. This example illustrates that the most influential node can relocate without a change in the network structure by simply increasing the overall coupling strength in the network. In a social network, this would be equivalent to a relocation of leadership when the people get to know each other better, but without making any new acquaintances.
C. Experiments with networks of chemical oscillators
To corroborate the theoretical findings, experiments were performed with networks of coupled oscillatory chemical reactions. The nodes of the network are corroding nickel wires in sulfuric acid, and without external control, the corrosion rate (current) is oscillatory. The perturbation of the circuit potential through feedback can stabilize the chemical reaction, hence suppressing oscillations. The coupling between nodes is established by cross-resistances whose currents affect the reaction rate37 (see Sec. 4 in the supplementary material).
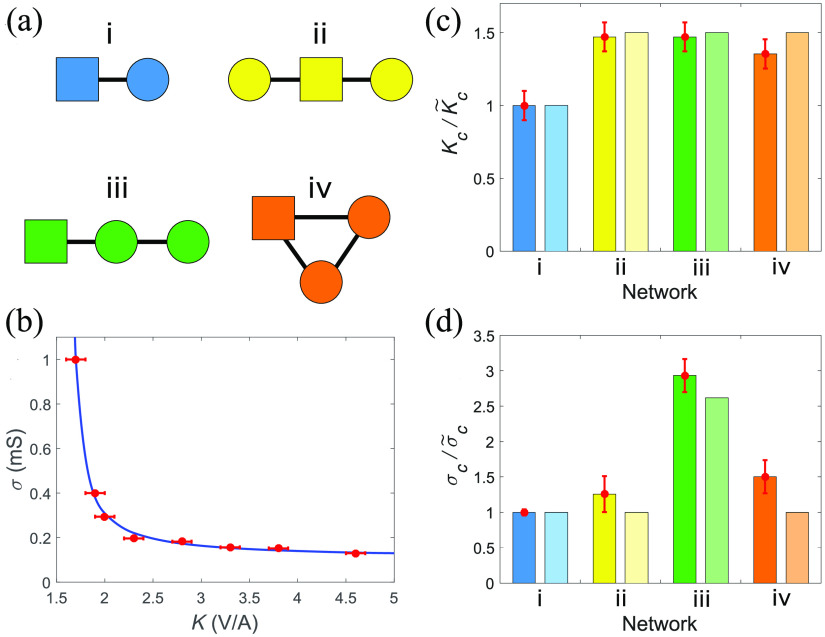
In the two-node network [Fig. 7(a)], the experimentally determined stable behavior follows very well the theoretically predicted stability hyperbola [Fig. 7(b)] with the critical values V/A and mS, respectively. We further compare the critical gain of the three-node networks to the critical gain of the two-node network in Fig. 7(a) in terms of the ratio , which agrees with the theory that predicted a 3/2 ratio regardless of the topology and control site [Fig. 7(c)]. Similarly, the critical couplings are compared using the ratio [Fig. 7(d)]. The experiments follow the trends of the theoretical predictions: for networks (ii) and (iv) in Fig. 7(a), the critical coupling strength ratios are nearly the same, and networks (iii) and (i) have a ratio of approximately 2.9, which is close to the theoretical prediction of 2.62.
FIG. 7.
Experiments: Pinning control of small networks. (a) Network topologies studied, where the square indicates controlled nodes. (b) Phase diagram of coupling and feedback gain for a pair of coupled oscillators (network i). The errorbars (red) represent the experimental data. Line (blue): theoretical prediction using Eq. (4). (c) Comparison of critical feedback gains at a strong coupling limit ( mS) for the four networks in panel (a), from experiments (bars) to the theoretical predictions (errorbars) via , where of network i. (d) Comparison of critical coupling at strong feedback gain ( V/A) from experiments to theoretical predictions via where of network i. The errorbars in panels (b)–(d) indicate where the oscillatory state (lower bound) and the stationary state (upper bound) are observed. Operating conditions: mV, k .
We note that there are certainly small differences between the theoretical predictions and the experiments, which can be attributed to the theoretical assumptions not completely satisfied in the experiments. In particular, the nodes have small heterogeneities (e.g., different oscillation frequencies ), and these deviations can be important, especially at weak coupling. Indeed, measurements at the strong feedback regime (expressed as ) deviate from theory more than at strong coupling (expressed as ).
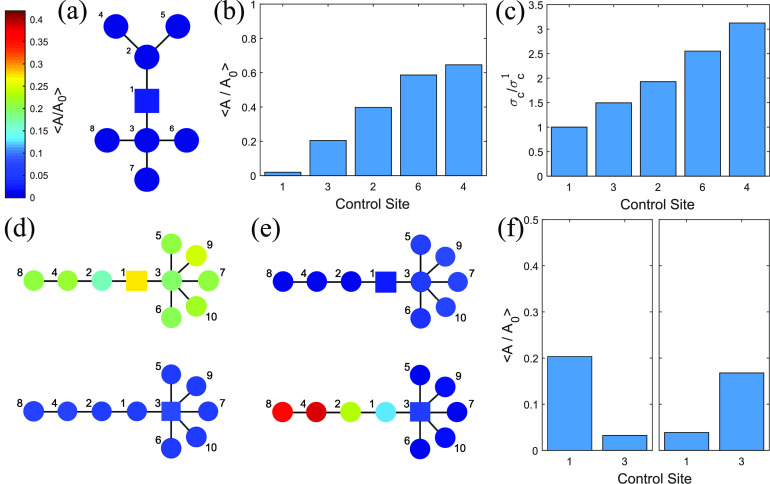
The validation of the developed MPi centrality-based method for selecting the most influential site is carried out using an eight-node irregular tree network shown in Fig. 8(a). The theory predicted a unique MIN at node 1. We first determined a stabilizing feedback gain in a weak coupling regime by pinning node 1 and then measured the mean oscillation amplitudes of the oscillations for different control sites [with the same , see Fig. 8(b)]. The results show that as the control site moves away from node 1, the control becomes less effective resulting in a higher mean amplitude of oscillations. In Fig. 8(c), we show the trend of the critical couplings as the ratio ( is the critical coupling for node 1), which agrees with experimental variations of the amplitudes.
FIG. 8.
Experiments: pinning control of large networks. (a) Eight-electrode tree network, with node one as the optimal site. The color represents the mean percent of the natural amplitude; V = 1110 mV, mS, A/V. (b) Mean amplitude remaining for various control nodes at sufficient to control the network by the optimal control node. (c) The quotient at each control site, where . (d) Ten-electrode tree network (with relocating MINs) in the limit of (strong ); mV, mS, V/A. The square indicates the pinned node. (e) Ten-electrode tree network (with relocating MIN) in the limit of (strong ); mV, mS, V/A. (f) The mean percent amplitudes in the strong coupling (left) and weak coupling (right). Individual resistance k .
MIN relocation was theoretically predicted and experimentally observed in the ten-node network [Figs. 8(d) and 8(e)] obtained by adding a star motif to the end of a chain network. Using the MPi centrality-based method, node 3 was predicted as the MIN in the strong coupling (weak gain) regime and node 1 as the MIN in the weak coupling (strong gain) regime. This is experimentally confirmed by measuring the mean oscillation amplitudes of the network for both control sites, in the weak and strong coupling regimes, respectively [see Fig. 8(f)]. The results, thus, show that the distance of a node to the peripheries of the network becomes more important as the coupling strength is weakened, while at strong coupling, more weight is placed on the degree of nodes causing the shift in the optimal control site. These experimental observations support the stability hyperbola-based selection of the most influential site.
VII. CONCLUSIONS
The results, thus, show that the analysis of stability hyperbolas in the coupling strength vs. feedback gain plane provides valuable information about the location of the most influential node in the network. For a given network, the critical coupling strength in the limit of infinity gain is an excellent indicator about the performance of the node, and this quantity can be obtained from the smallest eigenvalue of the system’s Laplacian matrix (under control). However, determining can be difficult for large networks. Therefore, we showed that the inverse of the diagonal elements of the Moore–Penrose pseudoinverse of the coupling Laplacian (without feedback) has an important physical meaning: These values express to what extent a given node contributes to the stability of the network when all nodes have feedback. Then, one can use this quantity to approximate the relative influence of the node when only one node has feedback. Calculating the Moore–Penrose pseudoinverse of the coupling Laplacian provides a quick and convenient technique to evaluate the node influences. Once the most influential node is identified, one should apply feedback at that node to achieve the best performance.
By careful examination of the stability hyperbolas, we have found that in addition to the limiting values of the hyperbolas, the steepness is also an important quantity, especially with strong coupling. For many networks, the stability hyperbolas that have the smallest (small vertical shift) are also steep, and thus, there is a unique most influential node. However, in some examples, certain nodes can perform better with strong coupling (due to steep hyperbolas) and other nodes at weak coupling (because they have small values). The most influential node, thus, can relocate even without changing the network structure (i.e., connectivity) but simply by changing the uniform overall coupling strength throughout the network. We found that such relocation is an essential property of tree networks but can also occur in network models (Erdős–Rényi random, small-world, scale-free) and real-world networks. In addition, this relocation phenomenon has also been observed in undirected networks with two pinning sites (i.e., where two influential sites are controlled simultaneously) as well as in directed networks with uniform coupling (see Fig. 3 in the supplementary material where the sensitivity of the influential node on the value of is very clear). We provided a simple numerical algorithm, with which a network with a unique or relocating most influential site can be determined.
In the theoretical aspect of the study, we used Stuart–Landau oscillators to confirm the findings. We should note that the theory is based on linear stability analysis, where the stabilization was achieved by controlling an unstable focus type of stationary state at the pinning site. Therefore, it would be expected that other systems with an unstable focus type of instabilities can be controlled with the proposed scheme; for example, in the experiments with oscillatory electrochemical reactions, the oscillations occurred through a supercritical Hopf bifurcation,38 and thus, it was expected that the stabilized state was an unstable focus. Extending the technique to stabilization of other types of unstable steady states will be considered a future direction.
Identifying influential nodes in a network is a key to efficiently manipulating its dynamic behavior and functioning, such as efficient control of rumors, suppression of disease spreading, and establishment of new marketing tools;39 for example, by careful network design (e.g., adding and removing links), one can guarantee unique leadership and optimize resources accordingly. Similarly, a network can be designed with separate leadership optimized for weak and strong coupling scenarios (e.g., when social distancing or communication outages are expected). The developed methods are directly applicable to facilitate and advance applications in network science, for instance, identifying the so-called influential spreader40 to determine the foci and dosage required for immunization in an epidemic network,41 efficient distribution of resources in tree-like networks (e.g., in the nephrons of kidney42), and locate optimal pacemaker position for synchronization.43,44 In addition, an analogy could be made between pinning amplitudes (as shown in our work) and pinning phases (as studied with charge density waves and swarmalators45,46), which could further widen the applications of finding MINs with pinning control.
SUPPLEMENTARY MATERIAL
The supplementary material includes the linear stability analysis of the studied system, the description of the properties of the stability hyperbola, additional examples of networks with relocating MINs, and the experimental procedure.
ACKNOWLEDGMENTS
I.Z.K. would like to express gratitude for Juergen Kurths for his remarkable contributions to nonlinear dynamics, which greatly helped understanding the functioning of complex chemical systems. In addition, Juergen’s unwavering support of young scientists created a community with free exchange of ideas in and around the Berlin–Potsdam area, which served as a scientific hub for synchronization and network dynamics. This collaboration was supported in part by the NSF Award Nos. ECCS-181020 (J.-S.L.) and CHE-1900011 (I.Z.K.), the NIH grant 1R01GM131403-01 (J.-S.L.), and the grants FAPESP (Nos. 2016/01817-9 and 2018/21619-2) (R.N.).
Note: This paper is part of the Focus Issue on Nonlinear dynamics, synchronization and networks: Dedicated to Juergen Kurths' 70th birthday.
Contributor Information
István Z. Kiss, Email: mailto:istvan.kiss@slu.edu.
Jr-Shin Li, Email: mailto:jsli@wustl.edu.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Author Contributions
Walter Bomela: Conceptualization (equal); Formal analysis (equal); Investigation (equal); Writing – original draft (equal); Writing – review & editing (equal). Michael Sebek: Investigation (equal); Writing – review & editing (equal). Raphael Nagao: Investigation (equal); Writing – review & editing (equal). Bharat Singhal: Investigation (equal); Writing – review & editing (equal). István Z. Kiss: Conceptualization (equal); Investigation (equal); Writing – review & editing (equal). Jr-Shin Li: Conceptualization (equal); Investigation (equal); Writing – review & editing (equal).
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.D.-B. S. for Parkinson’s Disease Study Group, “Deep-brain stimulation of the subthalamic nucleus or the pars interna of the globus pallidus in Parkinson’s disease,” N. Engl. J. Med. 345, 956–963 (2001). 10.1056/NEJMoa000827 [DOI] [PubMed] [Google Scholar]
- 2.Schaus M. J. and Moehlis J., “On the response of neurons to sinusoidal current stimuli: Phase response curves and phase-locking,” in Proceedings of the 45th IEEE Conference on Decision and Control (IEEE, 2006), pp. 2376–2381.
- 3.Amani A. M., Gaeini N., Jalili M., and Yu X., “Which generation unit should be selected as control leader in secondary frequency control of microgrids?,” IEEE J. Emerg. Sel. Top. Circuits Syst. 7, 393–402 (2017). 10.1109/JETCAS.2017.2655020 [DOI] [Google Scholar]
- 4.Porfiri M. and Di Bernardo M., “Criteria for global pinning-controllability of complex networks,” Automatica 44, 3100–3106 (2008). 10.1016/j.automatica.2008.05.006 [DOI] [Google Scholar]
- 5.Ching S., Brown E. N., and Kramer M. A., “Distributed control in a mean-field cortical network model: Implications for seizure suppression,” Phys. Rev. E 86, 021920 (2012). 10.1103/PhysRevE.86.021920 [DOI] [PubMed] [Google Scholar]
- 6.Gluckman B. J., Nguyen H., Weinstein S. L., and Schiff S. J., “Adaptive electric field control of epileptic seizures,” J. Neurosci. 21, 590–600 (2001). 10.1523/JNEUROSCI.21-02-00590.2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mikkelsen R., Andreasen M., and Nedergaard S., “Suppression of epileptiform activity by a single short-duration electric field in rat hippocampus in vitro,” J. Neurophysiol. 109, 2720–2731 (2013). 10.1152/jn.00887.2012 [DOI] [PubMed] [Google Scholar]
- 8.Du Toit E. F. and Craig I. K., “Selective pinning control of the average disease transmissibility in an HIV contact network,” Phys. Rev. E 92, 012810 (2015). 10.1103/PhysRevE.92.012810 [DOI] [PubMed] [Google Scholar]
- 9.Li X., Wang X., and Chen G., “Pinning a complex dynamical network to its equilibrium,” IEEE Trans. Circuits Syst. I: Regul. Pap. 51, 2074–2087 (2004). 10.1109/TCSI.2004.835655 [DOI] [Google Scholar]
- 10.Yu W., Chen G., Lu J., and Kurths J., “Synchronization via pinning control on general complex networks,” SIAM J. Control Optim. 51, 1395–1416 (2013). 10.1137/100781699 [DOI] [Google Scholar]
- 11.Wang X. and Su H., “Pinning control of complex networked systems: A decade after and beyond,” Annu. Rev. Control 38, 103–111 (2014). 10.1016/j.arcontrol.2014.03.008 [DOI] [Google Scholar]
- 12.Tang Y., Gao H., Kurths J., and Fang J.-A., “Evolutionary pinning control and its application in UAV coordination,” IEEE Trans. Ind. Inform. 8, 828–838 (2012). 10.1109/TII.2012.2187911 [DOI] [Google Scholar]
- 13.Tang Y., Gao H., Zou W., and Kurths J., “Identifying controlling nodes in neuronal networks in different scales,” PLoS One 7, e41375 (2012). 10.1371/journal.pone.0041375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen F., Chen Z., Xiang L., Liu Z., and Yuan Z., “Reaching a consensus via pinning control,” Automatica 45, 1215–1220 (2009). 10.1016/j.automatica.2008.12.027 [DOI] [Google Scholar]
- 15.DeLellis P., di Bernardo M., and Russo G., “On quad, Lipschitz, and contracting vector fields for consensus and synchronization of networks,” IEEE Trans. Circuits Syst. I: Regul. Pap. 58, 576–583 (2010). 10.1109/TCSI.2010.2072270 [DOI] [Google Scholar]
- 16.Zou W., Senthilkumar D. V., Nagao R., Kiss I. Z., Tang Y., Koseska A., Duan J., and Kurths J., “Restoration of rhythmicity in diffusively coupled dynamical networks,” Nat. Commun. 6, 7709 (2015). 10.1038/ncomms8709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nagao R., Zou W., Kurths J., and Kiss I. Z., “Restoring oscillatory behavior from amplitude death with anti-phase synchronization patterns in networks of electrochemical oscillations,” Chaos 26, 094808 (2016). 10.1063/1.4954040 [DOI] [PubMed] [Google Scholar]
- 18.Phogat R., Tiwari I., Kumar P., Rivera M., and Parmananda P., “Cessation of oscillations in a chemo-mechanical oscillator,” Eur. Phys. J. B 91, 111 (2018). 10.1140/epjb/e2018-80625-8 [DOI] [Google Scholar]
- 19.Totz J. F., Rode J., Tinsley M. R., Showalter K., and Engel H., “Spiral wave chimera states in large populations of coupled chemical oscillators,” Nat. Phys. 14, 282–285 (2018). 10.1038/s41567-017-0005-8 [DOI] [Google Scholar]
- 20.Jalili M., Sichani O. A., and Yu X., “Optimal pinning controllability of complex networks: Dependence on network structure,” Phys. Rev. E 91, 012803 (2015). 10.1103/PhysRevE.91.012803 [DOI] [PubMed] [Google Scholar]
- 21.Amani A. M., Jalili M., Yu X., and Stone L., “Controllability of complex networks: Choosing the best driver set,” Phys. Rev. E 98, 030302 (2018). 10.1103/PhysRevE.98.030302 [DOI] [Google Scholar]
- 22.Mirollo R. E. and Strogatz S. H., “Amplitude death in an array of limit-cycle oscillators,” J. Stat. Phys. 60, 245–262 (1990). 10.1007/BF01013676 [DOI] [Google Scholar]
- 23.Prasad A., Dhamala M., Adhikari B. M., and Ramaswamy R., “Amplitude death in nonlinear oscillators with nonlinear coupling,” Phys. Rev. E 81, 027201 (2010). 10.1103/PhysRevE.81.027201 [DOI] [PubMed] [Google Scholar]
- 24.Hai-Ling C. and Jun-Zhong Y., “Transition to amplitude death in coupled system with small number of nonlinear oscillators,” Commun. Theor. Phys. 51, 460 (2009). 10.1088/0253-6102/51/3/16 [DOI] [Google Scholar]
- 25.Tang Y., Gao H., and Kurths J., “Distributed robust synchronization of dynamical networks with stochastic coupling,” IEEE Trans. Circuits Syst. I: Regul. Pap. 61, 1508–1519 (2013). 10.1109/TCSI.2013.2285699 [DOI] [Google Scholar]
- 26.Hamdan A. and Elabdalla A., “Geometric measures of modal controllability and observability of power system models,” Electr. Power Syst. Res. 15, 147–155 (1988). 10.1016/0378-7796(88)90018-1 [DOI] [Google Scholar]
- 27.Porter B. and Crosslet R., Modal control theory and applications (Taylor & Francis, London, 1972). [Google Scholar]
- 28.Tarokh M., “Measures for controllability, observability and fixed modes,” IEEE Trans. Autom. Control 37, 1268–1273 (1992). 10.1109/9.151124 [DOI] [Google Scholar]
- 29.Brogan W. L., Modern Control Theory (Pearson Education India, 1991). [Google Scholar]
- 30.Khalil H. K., Nonlinear Systems (Prentice Hall, Upper Saddle River, NJ, 2002), Vol. 3. [Google Scholar]
- 31.Hayes M. H., Statistical Digital Signal Processing and Modeling (John Wiley & Sons, 2009). [Google Scholar]
- 32.Albert R. and Barabási A.-L., “Statistical mechanics of complex networks,” Rev. Mod. Phys. 74, 47 (2002). 10.1103/RevModPhys.74.47 [DOI] [Google Scholar]
- 33.Erdős P. and Rényi A., “On the evolution of random graphs,” Publ. Math. Inst. Hung. Acad. Sci. A 5, 17–61 (1960). [Google Scholar]
- 34.Watts D. J. and Strogatz S. H., “Collective dynamics of a small-world networks,” Nature 393, 440 (1998). 10.1038/30918 [DOI] [PubMed] [Google Scholar]
- 35.Molitierno J. J., Applications of Combinatorial Matrix Theory to Laplacian Matrices of Graphs (Chapman & Hall/CRC, 2016). [Google Scholar]
- 36.Kunegis J., “KONECT: The Koblenz network collection,” in Proceedings of the 22nd International Conference on World Wide Web (ACM, 2013), pp. 1343–1350.
- 37.Wickramasinghe M. and Kiss I. Z., “Spatially organized dynamical states in chemical oscillator networks: Synchronization, dynamical differentiation, and chimera patterns,” PLoS One 8, e80586 (2013). 10.1371/journal.pone.0080586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kiss I. Z., Kazsu Z., and Gáspár V., “Tracking unstable steady states and periodic orbits of oscillatory and chaotic electrochemical systems using delayed feedback control,” Chaos 16, 033109 (2006). 10.1063/1.2219702 [DOI] [PubMed] [Google Scholar]
- 39.Chen D., Lü L., Shang M.-S., Zhang Y.-C., and Zhou T., “Identifying influential nodes in complex networks,” Physica A 391, 1777–1787 (2012). 10.1016/j.physa.2011.09.017 [DOI] [Google Scholar]
- 40.Kitsak M., Gallos L. K., Havlin S., Liljeros F., Muchnik L., Stanley H. E., and Makse H. A., “Identification of influential spreaders in complex networks,” Nat. Phys. 6, 888 (2010). 10.1038/nphys1746 [DOI] [Google Scholar]
- 41.Hébert-Dufresne L., Allard A., Young J.-G., and Dubé L. J., “Global efficiency of local immunization on complex networks,” Sci. Rep. 3, 2171 (2013). 10.1038/srep02171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Postnov D., Postnov D., Marsh D., Holstein-Rathlou N.-H., and Sosnovtseva O., “Dynamics of nephron-vascular network,” Bull. Math. Biol. 74, 2820–2841 (2012). 10.1007/s11538-012-9781-6 [DOI] [PubMed] [Google Scholar]
- 43.Dekker A., Phelps B., Dijkman B., van Der Nagel T., van Der Veen F., Geskes G., and Maessen J., “Epicardial left ventricular lead placement for cardiac resynchronization therapy: Optimal pace site selection with pressure-volume loops,” J. Thorac. Cardiovasc. Surg. 127, 1641–1647 (2004). 10.1016/j.jtcvs.2003.10.052 [DOI] [PubMed] [Google Scholar]
- 44.Sun J. P., Chinchoy E., Donal E., Popović Z. B., Perlic G., Asher C. R., Greenberg N. L., Grimm R. A., Wilkoff B. L., and Thomas J. D., “Evaluation of ventricular synchrony using novel Doppler echocardiographic indices in patients with heart failure receiving cardiac resynchronization therapy,” J. Am. Soc. Echocardiogr. 17, 845–850 (2004). 10.1016/j.echo.2004.04.012 [DOI] [PubMed] [Google Scholar]
- 45.Strogatz S. H., Marcus C. M., Westervelt R. M., and Mirollo R. E., “Collective dynamics of coupled oscillators with random pinning,” Physica D 36, 23–50 (1989). 10.1016/0167-2789(89)90246-7 [DOI] [Google Scholar]
- 46.Sar G. K., Ghosh D., and O’Keeffe K., “Pinning in a system of swarmalators,” Phys. Rev. E 107, 024215 (2023). 10.1103/PhysRevE.107.024215 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The supplementary material includes the linear stability analysis of the studied system, the description of the properties of the stability hyperbola, additional examples of networks with relocating MINs, and the experimental procedure.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.