Imputation and missing indicators for handling missing data in the development and deployment of clinical prediction models: A simulation study

Abstract

Background: In clinical prediction modelling, missing data can occur at any stage of the model pipeline; development, validation or deployment. Multiple imputation is often recommended yet challenging to apply at deployment; for example, the outcome cannot be in the imputation model, as recommended under multiple imputation. Regression imputation uses a fitted model to impute the predicted value of missing predictors from observed data, and could offer a pragmatic alternative at deployment. Moreover, the use of missing indicators has been proposed to handle informative missingness, but it is currently unknown how well this method performs in the context of clinical prediction models. Methods: We simulated data under various missing data mechanisms to compare the predictive performance of clinical prediction models developed using both imputation methods. We consider deployment scenarios where missing data is permitted or prohibited, imputation models that use or omit the outcome, and clinical prediction models that include or omit missing indicators. We assume that the missingness mechanism remains constant across the model pipeline. We also apply the proposed strategies to critical care data. Results: With complete data available at deployment, our findings were in line with existing recommendations; that the outcome should be used to impute development data when using multiple imputation and omitted under regression imputation. When missingness is allowed at deployment, omitting the outcome from the imputation model at the development was preferred. Missing indicators improved model performance in many cases but can be harmful under outcome-dependent missingness. Conclusion: We provide evidence that commonly taught principles of handling missing data via multiple imputation may not apply to clinical prediction models, particularly when data can be missing at deployment. We observed comparable predictive performance under multiple imputation and regression imputation. The performance of the missing data handling method must be evaluated on a study-by-study basis, and the most appropriate strategy for handling missing data at development should consider whether missing data are allowed at deployment. Some guidance is provided.

1. Background

Clinical prediction models (CPMs) can be used to guide clinical decision making and facilitate conversations about risk between care providers and patients. ¹ A CPM is a mathematical tool that takes patient and clinical information (predictors) as inputs and, most often, produces an estimated risk that a patient currently has (diagnostic model) or will develop (prognostic model) a condition of interest. ² A common challenge in the development, validation and deployment of CPMs is the handling of missing data on predictors and outcome data. The most commonly used methods to handle missing data in CPM development and validation are complete case analysis or multiple imputation (MI) approaches,^1,3 the latter of which is often heralded as the gold standard in handling missing data. Much of the past research around this topic has focused on the performance of different imputation methods to recover unbiased parameter estimates, for example, in causal inference or hypothesis testing.^4–8 However, this topic has recently received renewed interest in the context of producing CPMs, with authors arguing the basis on which MI is commonly used relies too heavily on principles relevant to causal inference and descriptive research, which are less relevant when the goal is to provide accurate predictions. ⁹

Indeed, the objectives of prediction research differ from those of descriptive or causal inference studies. For the latter, missing data should be handled in such a way that minimises bias in the estimation of key parameters, and generally this is achieved through MI of missing data. In the development of prediction models, however, unbiased parameter estimates are not necessarily the ones that optimise predictive performance. ⁹ Moreover, in prediction research we must distinguish between handling missing data across the entire model pipeline; model development, model validation, and model deployment (or prediction time), and anticipate whether missing data shall be expected at deployment. Ideally, all predictors considered for inclusion in a CPM should be either readily available, or easily measured, at the point of prediction. There exist, however, notable examples that allow missingness at the point of prediction ³ ; the QRisk3 ¹⁰ and QKidney ¹¹ algorithms are examples of such models that allow users to make a prediction in the absence of clinical predictors (such as cholesterol) that may not be available, or easily measured, at the time of prediction.

Best practice states that the outcome should be used in the imputation model when applying MI, ¹² creating a congenial imputation model. Clearly, the outcome is unknown at the prediction time, and applying imputation without the outcome would violate the assumption of congeniality. Since model validation should evaluate predictive performance under the same missing data handling strategy to be used in practice, the outcome should be omitted from any imputation model at validation, potentially resulting in less accurate imputations since predictors are normally predictive of the outcome. We, therefore, define ‘performance under no missingness’, where we assume all predictors are always available (or easily obtained) at deployment, and ‘performance under missingness’, assuming missing data is allowed and will be imputed at deployment.

Single imputation methods such as (single) regression imputation (RI) could provide a more pragmatic alternative to MI in the context of prediction. Here we use the term ‘regression imputation’ to refer to the form of single imputation that fits a regression model to impute missing values of missing predictors using observed data. The key difference between RI and MI is that RI is a deterministic process, that imputes the predicted value under the fitted imputation model (without error), whereas MI is a stochastic sampling process that can repeatedly sample from a distribution, incorporating the error associated with the fitted imputation model. It is important to note, however, that MI methods can also be underpinned by a regression model, but for illustrative purposes in this study we use the term ‘multiple imputation’ to refer to a method that produces multiple imputed datasets, and ‘regression imputation’ to one that imputes a single value for any missing predictors.

For RI to be applied in practice, only the imputation model(s) needs to be available alongside the full prediction model, as opposed to MI which generally also requires access to the development dataset. ¹³ Existing literature has, however, demonstrated several pitfalls of RI in the context of causal estimation – it is highly sensitive to model misspecification, can increase the correlation between predictors and underestimate variability in parameter estimates. ¹⁴ Although these issues may therefore persist within the prediction context, they may not apply since – as discussed above – the recovery of unbiased parameter estimates is no longer of direct concern. RI may also overcome some of the previously mentioned issues related to predictive modelling with MI since the inclusion of the outcome in the imputation model is not recommended. ¹ To our knowledge these issues and challenges have not been studied to date.

Both MI and RI are techniques devised under the assumption that data are missing at random, that is, missingness does not depend on unobserved values. The validity of the MAR assumption within health data is often dubious, especially when using routinely collected data,^15,16 however these definitions were created with the goal of recovering unbiased parameter estimates in mind and therefore may be less relevant to the prediction modelling context. ⁹ Within routinely collected data, the recording of key clinical markers is often driven by the needs of the patient and the clinical judgments of the care provider. ¹⁶ Missingness is therefore potentially informative with respect to a patient's current or future condition, and including information about the way an individual has been observed in a prediction model has the potential to improve its predictive performance. ¹⁷ A commonly used, effective approach to achieve this is through the inclusion of missing indicators as predictors in a CPM.

This study, therefore, aims to explore the use of missing indicators as model predictors alongside both RI and MI. We explore the effect of omitting/including the outcome from each imputation model at development and imputing data without the outcome at validation (and therefore deployment). We compare the two imputation strategies when missingness is both allowed and prohibited at the point of prediction. Our results will inform recommendations on the handling of missing data during model development and deployment that will be especially relevant to applied researchers developing clinical prediction models.

2. Methods

We performed an extensive simulation study in which we evaluated a range of different missingness mechanisms. Our study has been designed according to best practice and reported according to the ADEMP structure (modified as appropriate for a prediction-focused study), proposed by Morris et al. ¹⁸ We also applied the methods to a real-world critical care dataset. In this section, we first describe the methods of the simulation study before describing the empirical study methods in Section 2.8.

2.1. Aims

The primary aim of this study is to compare MI and RI approaches in imputing missing data when the primary goal is in developing and deploying a prediction model, under a range of missing data mechanisms (Missing Completely at Random (MCAR), Missing at Random (MAR) Missing Not at Random (MNAR)), with/without a missing indicator and with/without the outcome included in the imputation model. Each of these will be examined both allowing for and prohibiting missing data at deployment, and performance will be estimated separately for each of these two scenarios.

Throughout this study, we assume that both the missingness mechanism and handling strategy will remain the same across validation and deployment, and therefore validation is a valid replication of model deployment and our performance estimates are reliable estimates of model performance at deployment. The only case where this is not true is when we impute data using the outcome at validation, which will be discussed in more detail in the following sections.

2.2. Data-generating mechanisms

We focus on a logistic regression-based CPM to predict a binary outcome, Y, that is assumed to be observed for all individuals (i.e. no missingness in the outcome) during the development and validation of the model. Without loss of generality, we assume that the data-generating model contains up to three predictors, $X_1$ , $X_2$ and U, where $X_1$ is partially observed and potentially informatively missing (depending on the simulation scenario, as outlined below), $X_2$ is fully observed and U is unobserved. We denote missingness in $X_1$ with a binary indicator $M_1$ , where $M_1=1$ , if $X_1$ is missing, and $M_1=0$ if it is observed.

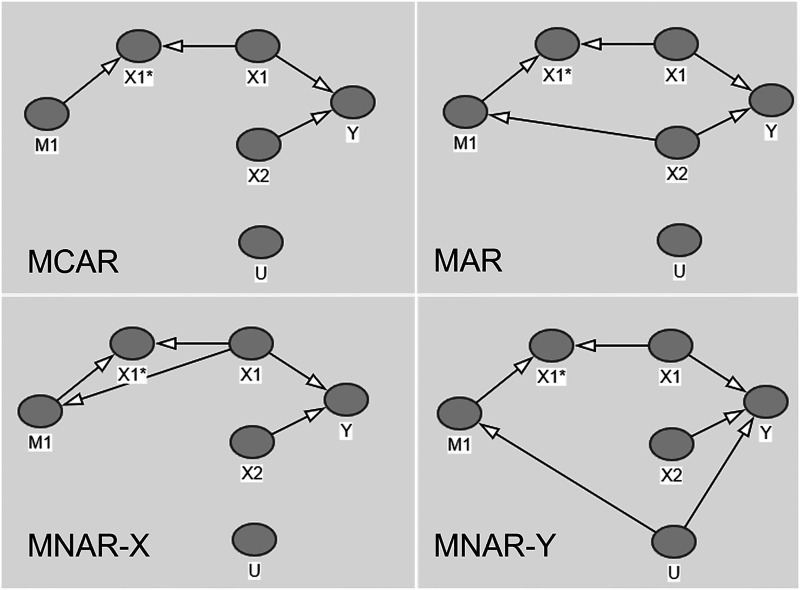
We construct four separate DAGs depicted in Figure 1, each representing different missingness structures covering: MCAR, MAR, MNAR dependent on $X_1$ (MNAR-X) and MNAR dependent on Y (MNAR-Y).

Figure 1.

Directed acyclic graphs for four missingness structures.

The DAGs further illustrate how missingness in $X_1$ is related to $X_1$ or $X_2$ . In each of the DAGs, $X_1^{*}$ represents the observed part of $X_1$ and $M_1$ is the missing indicator.

In order to reconstruct these DAGs in simulated data, we stipulate the following parameter configurations:

• $X_1$ and $X_2$ are drawn from a bivariate normal distribution to allow a moderate correlation between the two predictors, such that

  $$\mathit{X}\sim MVN(\mathit{\mu },\mathrm{\Sigma })$$

where $\mathit{\mu }=\left[\begin{array}{r}0\\ 0\end{array}\right]$

and $\mathbf{\Sigma }=\left[\begin{array}{rr}1& 0.4\\ 0.4& 1\end{array}\right]$

• $M_1\in \{0,1\}$ , and $P[M_{1i}=1]=expit({\beta }_0+{\beta }_{X_1}{X}_{1i}+{\beta }_{X_2}{X}_{2i}+{\beta }_Y{Y}_i)$ , that is, missingness in $X_1$ can depend on $X_1$ , and/or $X_2$ , and/or Y.

• ${\beta }_{X_1}$ , ${\beta }_{X_2}$ and ${\beta }_Y$ were varied across $\{0,0.5,1\}$

• $Y$ is binary, with $P[Y_i=1]=expit({\gamma }_0+{\gamma }_{X_1}{X}_{1i}+{\gamma }_{X_2}{X}_{2i}+{\gamma }_{X_1{X}_2}{X}_{1i}{X}_{2i})$

• ${\gamma }_{X_1}$ and ${\gamma }_{X_2}$ were varied across $\{0.5,0.7\}$

• $P[Y=1]={\pi }_Y$ was fixed to be 0.1.

• $P[M_1=1]={\pi }_{M1}\in \{0.1,0.25,0.5,0.75\}$

• ${\gamma }_{X_1{X}_2}$ can take values $\{0,0.1\}$ .

• ${\beta }_0$ and ${\gamma }_0$ are calculated empirically as required to set the desired level of ${\pi }_{M1}$ and ${\pi }_Y$ .

• $U$ was not directly simulated, but the MNAR-Y scenario generated via the inclusion of ${\beta }_Y\ne 0$ .

The parameter values above were selected to represent what might be observed in real-world data, assuming that $X_1$ and $X_2$ can represent some summary of a set of model predictors.

Datasets were generated with $n=10,000$ records from the DGMs described above and split 50/50 into development and validation sets. The development and validation sets, therefore, contained $5000$ records each. This is chosen as a suitably large size that should be sufficient to estimate underlying parameters, and avoid overfitting: assuming a desired shrinkage of 0.95, 5 predictors, an outcome prevalence of 0.1 and a C-statistic of 0.7, we obtain a minimum required sample size of 1989 using Riley et al.'s criteria, ¹⁹ which our selected sample size comfortably surpasses. Although we recognise that the split-sample approach to model development is statistically inefficient, our simulated sample size is sufficiently large that this should not pose an issue. ²⁰

We further vary the available sample size $(N\in \{500,1000,5000,10,000\})$ for a subset of the parameter configurations, one for each of the DAGs presented in Figure 1.

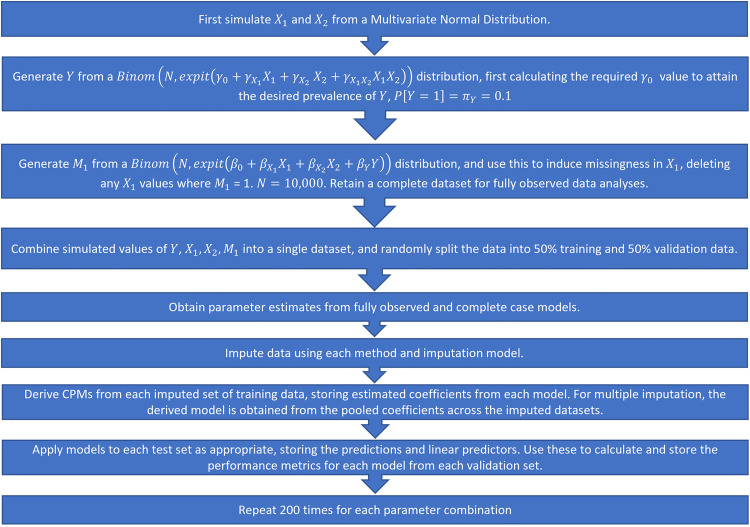
We fit the models on the development data and calculate performance measures on the derived models applied to the validation set. The full simulation procedure is illustrated in Figure 2. Note that in this instance, we fit the imputation models separately in the development and validation sets. Since the DGMs and missingness mechanisms remain constant between the two datasets, we assume that the fitted imputation model would not change and this is therefore a valid approach to take. In a real-world setting, however, this would not be feasible as only a single patient's data would be available at the point of prediction, and we would want to use the same imputation model as was used/developed in the development data. We explore this further by adopting a different strategy in the real data example (Section 3.8).

Figure 2.

Simulation procedure, step-by-step.

Each simulated DGM was repeated for 200 iterations. The parameter values listed above result in a total of 864 parameter configurations. A total of 200 iterations was selected as optimal to balance the requirement to obtain reliable estimates of key performance metrics (by using a sufficient number of repetitions) with the size of the study and computational requirements of repeatedly running MI over a large number of simulated scenarios.

2.3. Missing data handling strategies

We consider two main methods for handling missing data at the development and deployment stages of the CPM pipeline: MI and RI. MI can be applied with relative ease at the model development stage, specifying an imputation model and method for every predictor with missing data (in this case just $X_1$ ), conditional on other data available at model development. Multiple draws are then made from the imputation model, accounting for the associated error, and resulting in multiple completed datasets. The relevant CPMs are then fit separately to each resulting imputed dataset, and the model coefficients are pooled according to Rubin's rules to obtain a single set of model coefficients. ²¹ For RI, we follow a similar process in fitting a model to the missing predictor(s) based on observed data. The key difference between MI and RI here is that RI imputes the (single) predicted value of the missing predictor without any error. We can then fit the analysis model to this new complete data to obtain the CPM's parameter estimates. Both methods can be implemented using the mice package in R (amongst others), but more flexible user-defined imputation models for RI could be fit manually with relative ease using alternative modelling packages.

Applying MI to incomplete data for new individuals at deployment is more challenging as it is not generally possible to extract the final imputation model from the output provided by standard statistical software. In order to ‘fix’ the imputation model for new individuals, it has therefore instead been proposed that the new individual's data should first be appended to the original (imputed) development data, and the imputation re-run on the new stacked dataset.^13,22,23 RI, on the other hand, is easier to implement at the point of prediction, since models can be defined for each (potentially) missing predictor, and these models can be stored (alongside the actual CPM) and used to impute at deployment for new individuals. Ideally, model validation should follow the same steps as model deployment in order to properly quantify how the model will perform in practice. ³ However, since validation is usually completed for a large cohort of individuals at once (as opposed to a single individual), it is likely that missing data imputation would take place as a completely separate exercise, with the imputation model depending solely on the validation data.

2.4. Fitted CPMs

We fit three possible CPMs to the development data (under each different imputation method), firstly with a simple model including both derived predictors and their interaction. We then fit models incorporating missing indicators, as well as considering a model with an interaction between the missing covariate $X_1$ and its missing indicator $M_1$ ²⁴ :

• Predictors and their interaction only: $P[Y_i=1]=expit({\gamma }_0+{\gamma }_{X_1}{X}_{1i}+{\gamma }_{X_2}{X}_{2i}+{\gamma }_{X_1{X}_2}{X}_{1i}{X}_{2i})$

• Inclusion of an additional missing indicator: $P[Y_i=1]=expit({\gamma }_0+{\gamma }_{X_1}{X}_{1i}+{\gamma }_{X_2}{X}_{2i}+{\gamma }_{X_1{X}_2}{X}_{1i}{X}_{2i}+{\gamma }_{M_1}{M}_{1i})$

• Inclusion of an interaction between the $X_1$ and $M_1$ terms in the outcome model: $P[Y_i=1]=expit({\gamma }_0+{\gamma }_{X_1}{X}_{1i}+{\gamma }_{X_2}{X}_{2i}+{\gamma }_{X_1{X}_2}{X}_{1i}{X}_{2i}+{\gamma }_{M_1}{M}_{1i}+{\gamma }_{M_1{X}_1}{X}_{1i}{M}_{1i})$

Each model was developed using completed datasets derived under MI and RI, with and without the outcome in the imputation model. The derived models were then applied to the validation set according to the strategies listed in Table 1.

Table 1.

Imputation and validation strategies.

		Missingness allowed at
Strategy	Description	deployment
$DA+VA$	All data, before inducing missingness, at development and validation	No
$DY+VY$	With Y in the imputation model at development and validation	No
$D\overline{Y}$  +  $V\overline{Y}$	Without Y in the imputation model at development and validation	Yes
$DY+V\overline{Y}$	With Y in the imputation model at development, but not at validation	Yes
$DY+VA$	With Y in the imputation model at development, all (completed) data required at validation	No
$D\overline{Y}+VA$	Without Y in the imputation model at development, all (completed) data required at validation	No

2.5. Development/validation scenarios

We apply each of the imputation and validation strategies described in Table 1, $DA+VA$ to $D\overline{Y}+VA$ . MI was performed using Bayesian linear regression as the underlying form of the imputation model (as implemented by mice.impute.norm in the mice package in R) and 20 imputed datasets. Bayesian linear regression was chosen as the underlying imputation model for MI since the resulting imputation models should be comparable between RI and MI. This allows assessment and quantification of any added benefit of the stochastic sampling process inherent to MI since the main challenges associated with applying MI at deployment are related to this process.

Parameter estimates were pooled across the imputed datasets according to Rubin's rules, and, similarly, we took the ‘pooled performance’ approach to validation whereby imputation-specific predictions are obtained in the multiply imputed validation datasets, the predictive performance of each imputed dataset is calculated, and then these estimates of model performance are pooled across the imputed datasets. ²⁵

$DY+VA$ and $D\overline{Y}+VA$ can be considered estimates of ‘performance under no missingness’, and to estimate this we retain the fully observed (simulated) validation data before missing data are induced. $DY+VY$ will be classed as ‘approximated performance under no missingness’, since it attempts to estimate performance assuming no missingness at deployment, but with missing data in the validation set. Note, however, that this strategy could not realistically be applied in a real-world setting (at prediction/deployment time) due to the inclusion of Y during imputation of the validation data.

$D\overline{Y}+V\overline{Y}$ and $DY+V\overline{Y}$ are both strategies that could be applied in practice when missingness is allowed, with the key difference between the two being that Y is omitted from the imputation model at validation and deployment. They, therefore, correspond to measures of ‘performance under missingness’, assuming this imputation strategy could reasonably be applied at the point of prediction. For this approach, we do not have a true estimand that we are targeting, so the methods were compared against each other to establish the optimal missing data handling strategy.

The fully observed data strategy in $DA+VA$ was considered to be the reference approach, since this is equivalent to the data-generating model prior to applying any missing data strategy, and was used as a comparator for other methods. Strategies that do not allow missingness at deployment were directly compared against this approach, as was $DY+VY$ since it aims to approximate performance under no missingness.

In strategies $DA+VA$ , $DY+VY$ and $D\overline{Y}+V\overline{Y}$ , we assume that the missingness mechanism, the missing data strategy, and the proportion of missing data remain constant between model development and validation, which is perhaps a strong assumption in practice. For strategies that allow missingness at deployment, we assume that the missingness mechanism and the proportion of missingness remain constant across the pipeline.

2.6. Target and performance measures

Our key target is an individual's predicted risk, and we compare each method's ability to estimate this using the following metrics of predictive performance, covering both calibration and discrimination^1,26:

• Calibration-in-the-large (CITL) – the intercept from a logistic regression model fitted to the observed outcome with the linear predictor as an offset.

• Calibration slope – the model coefficient of the linear predictor from a model fitted to the observed outcome with the linear predictor as the only explanatory variable.

• Discrimination (Concordance/C-statistic) – a measure of the discriminative ability of the fitted model. Defined as the probability that a randomly selected individual who experienced the outcome has a higher predicted probability than a patient that did not experience the outcome.

• Brier score – a measure of overall predictive accuracy, equivalent to the mean squared error of predicted probabilities.

We assume that the estimates of the above measures are valid representations of performance at model deployment, based on the following assumptions: (1) when missingness is allowed at deployment, it will be imputed in the same way as performed in our validation set, (2) the missingness mechanism will not change between validation and deployment, and (3) when missingness is not allowed at deployment, we assume that the data-generating mechanism remains constant across validation and deployment.

We also extract the obtained parameter estimates and any associated bias from each fitted CPM.

2.7. Software

All analyses were performed using R version 3.6.0 or greater. ²⁷ The pROC library ²⁸ was used to calculate C-statistics and the mice package ²⁹ was used for all imputations. Code to replicate the simulation can be found in the following GitHub repository: https://github.com/rosesisk/regrImpSim.

2.8. Application to MIMIC-III data

2.8.1. Data

To illustrate the proposed missing data handling strategies, we applied the methods studied through the simulation to the Medical Information Mart for Intensive Care III (MIMIC-III) dataset. ³⁰ MIMIC-III contains information on over 60,000 critical care admissions to the Beth Israel Deaconess Medical Center in Boston, Massachusetts from 2001 to 2012.

2.8.2. Prediction model: predictors, outcome and cohort

We develop, apply and validate a CPM in the MIMIC-III data based on the set of predictors used in the qSOFA score, ³¹ a CPM used to predict in-hospital mortality in patients with suspected sepsis. Bilirubin is included as an additional model predictor since the qSOFA predictors are likely to be completely observed for the majority of patients and would therefore not allow a proper illustration of our proposed methods. Bilirubin is included in other commonly-used critical care mortality scores such as SAPS III ³² and MODS. ³³ Additionally, we include age and gender in the model as these are always observed in the example dataset and often provide prognostic information.

Data for the clinical predictors was taken from the first 24 h of each patient's critical care stay, and therefore the cohort is restricted to only patients with a stay of at least one full day, and only a single stay was used for each patient. Where repeated predictor measurements are made over the first 24 h, the maximum is taken for respiratory rate and the minimum for systolic blood pressure and Glasgow Coma Scale. All numeric predictors (age, respiration rate, systolic blood pressure, Glasgow Coma Scale and serum bilirubin) are entered into the model in their original forms. For each missingness strategy, the same three CPMs were fit and evaluated as in the simulation: main effects only ( $X$ ), main effects and missing indicators ( $X+M$ ), and main effects, missing indicators and their interactions ( $X+M+X:M$ ).

2.8.3. Imputation strategies

In the simulation part of this paper, RI is applied using the mice package in R under the ‘norm.predict’ method. This method, however, can only be used in the case of a single missing predictor. For the real data application, therefore, we will manually derive the underlying imputation models (in the development data) and use these to impute the missing predictors in both the development and test sets.

RI models were derived within the subset of patients that the model will be used within. For example, the imputation model used to impute GCS using age, gender and systolic blood pressure will only be derived in patients that have missing bilirubin and respiratory rate, as it will only be applied to patients with this observed missingness pattern. Where the sample size is insufficient in the target missingness-pattern cohort, data from complete cases were instead used to develop the imputation model. ¹³ The minimum required sample size required for the development of each imputation model is $2^{*}(p+1)$ , where p is the number of model predictors, as suggested by Fletcher Mercaldo and Blume. ¹³

In the simulation part of this study, MI is run independently in the development and test sets. Clearly, this is not feasible at the point of prediction with real data as only a single new observation is available at a time. Incomplete data from the MIMIC-III dataset was therefore stacked on top of (multiply) imputed development datasets on a patient-by-patient basis, therefore fixing the imputation model used during development. This process is illustrated in Appendix 5 of the Supplemental Materials. To mimic a real-world deployment, the outcome was set to missing in the appended test patient data and (where necessary) this was imputed and used to inform imputations for the remaining missing predictors (under a new strategy, $DY+V{Y}^I$ ). The ‘true’ observed outcome was then reattached to the imputed data for use in model validation.

Due to the described differences in the way MI was run between the simulated data and the real-data example, results are presented in the Supplemental Materials for an equivalent ‘independent MI’ run in the MIMIC-III data for comparison.

2.8.4. Model validation

A split-sample approach to validation in the MIMIC-III data was taken, using a random 70%/30% development/validation split. The same four performance metrics were evaluated in the empirical test data as in the simulation study.

3. Results: simulation

In this section, we report the results of the simulation study. Select parameter combinations have been chosen to highlight important results here, but full results for all combinations are made available in a rShiny dashboard at https://rosesisk.shinyapps.io/regrimpsim.

3.1. Predictive performance

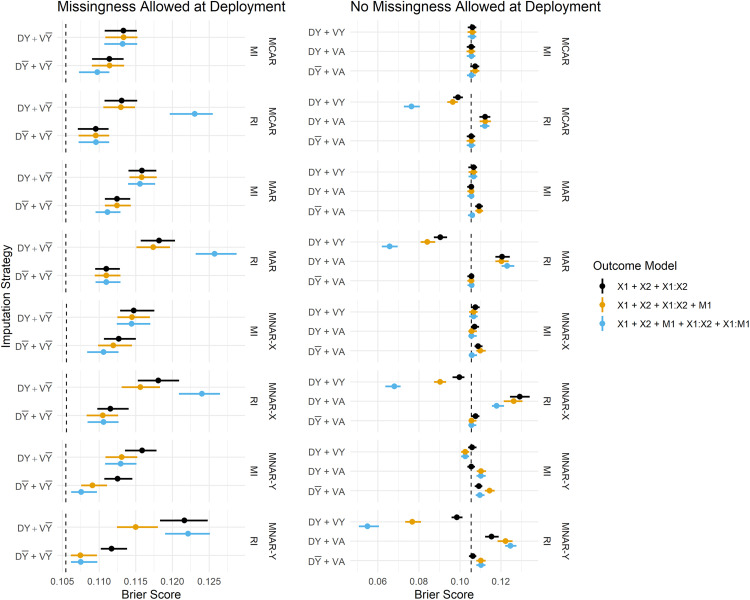
Figure 3 summarises the estimated Brier Scores for each strategy defined in Table 1 for both imputation methods and all fitted outcome models, and calibration slopes are presented in Figure 4. The imputation strategies have been split according to whether or not they allow missingness at model deployment.

Figure 3.

Brier Score estimates across development/validation scenarios, imputation methods and missingness mechanisms. The vertical dashed lines represent estimates from the complete data scenario (DA + VA). DY = Y included in the imputation model at development, D $\overline{Y}$ = Y omitted from the imputation model at development, VY = Y included in the imputation model at validation, V $\overline{Y}$ = Y omitted from the imputation model at validation, DA = complete data available at model development, VA = complete data available at validation.

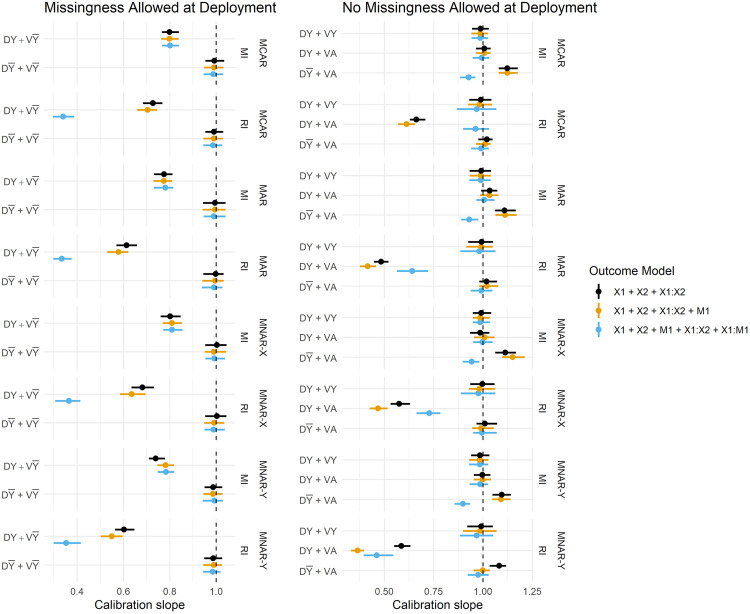
Figure 4.

Calibration slope estimates across imputation strategies, imputation methods and missingness mechanisms. Vertical dashed lines are placed at 1. DY = Y included in the imputation model at development, D $\overline{Y}$ = Y omitted from the imputation model at development, VY = Y included in the imputation model at validation, V $\overline{Y}$ = Y omitted from the imputation model at validation, DA = complete data available at model development, VA = complete data available at validation.

For simplicity, we restrict our results to a single parameter configuration for each missingness mechanism. The following parameters remain fixed throughout this section: ${\gamma }_{X1}={\gamma }_{X2}=0.7$ , ${\gamma }_{X1X2}=0.1$ , ${\pi }_{M1}=0.5$ .

3.1.1. Inclusion of the outcome in the imputation model

When missingness is allowed at deployment (i.e. imputation will be applied at the point of prediction), we primarily want to know whether imputation should be performed with or without the outcome at development, since at deployment it must be omitted from the imputation model (by definition). We observe that predictions in the validation set are far better calibrated under $D\overline{Y}+V\overline{Y}$ than $DY+V\overline{Y}$ , that is, when the imputation model remains consistent between development and validation/deployment (Figure 4). The estimates of calibration slope in Figure 4 illustrate that when models are developed using the outcome to impute missing predictors, but are applied to test data imputed without the outcome ( $DY+V\overline{Y}$ ), the resulting predictions are too extreme (calibration slope < 1). Marginal improvements in the Brier Score (Figure 3) from $D\overline{Y}+V\overline{Y}$ over $DY+V\overline{Y}$ can also be observed, and these are consistent across all missingness mechanisms.

When complete data is required at deployment, RI still performs better under $D\overline{Y}+VA$ than $DY+VA$ in terms of calibration (Figure 4), and this result becomes more pronounced when data are MAR or MNAR. MI, on the other hand, favours retention of Y in the imputation model at development in terms of both Brier Score and model calibration (under no missingness at deployment). Figure 5 summarises the parameter estimates from the fitted models, and we can see that effect estimates are less biased for RI: $D\overline{Y}$ and MI: $DY$ , which is in line with the predictive performance estimates.

Figure 5.

Parameter estimates across all missingness mechanisms. Missingness is fixed at 50%. DY = Y included in the imputation model at development, D $\overline{Y}$ = Y omitted from the imputation model at development, VY = Y included in the imputation model at validation, V $\overline{Y}$ = Y omitted from the imputation model at validation, DA = complete data available at the development, VA = complete data available at validation.

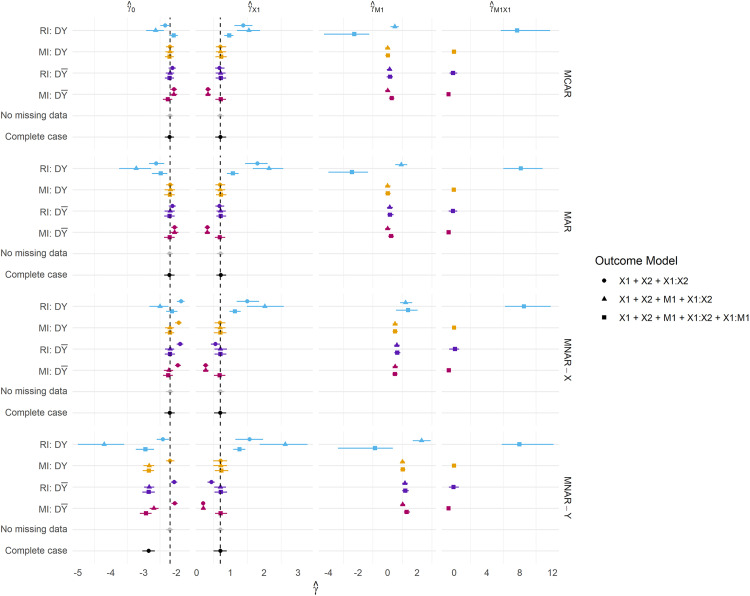
A notable result is that the $DY+VY$ strategy fails to recover the performance under no missingness ( $DY+VA$ ) for both imputation methods, that is, when Y is used to impute at both development and validation. Under MI, this strategy should be a valid means of estimating the performance under complete data at deployment, but there are marginal differences in the calibration slope between MI: $DY+VY$ and MI: $DY+VA$ . Moreover, the performance of RI considerably breaks down with the inclusion of Y in the imputation model under all missingness mechanisms and regardless of whether missingness is allowed at deployment. This same result is evident in Figure 5: parameter estimation, where RI: $DY$ consistently fails to recover unbiased parameter estimates.

3.1.2. Comparison of imputation methods

Overall, the performance estimates from MI are more stable than those from RI; the differences in Brier Score between the various imputation strategies (e.g. $D\overline{Y}+VA$ vs. $DY+VA$ ) are smaller for MI as can be seen in Figure 3. When RI performs poorly, the poorer model tends to be even worse than the worst MI model, in terms of both Brier Score and calibration. RI does, however, often perform at least as well as, or better than, MI when the preferred imputation model is applied (i.e. omitting the outcome when applying RI). For example, both methods perform comparably under $D\overline{Y}+V\overline{Y}$ . With missingness permitted at deployment, performance is comparable between MI: $DY+VA$ and RI: $D\overline{Y}+VA$ .

3.1.3. Inclusion of a missing indicator

The inclusion of a missing indicator appears to have minimal impact on the Brier Score and calibration under most methods and imputation strategies, with a few notable exceptions.

3.1.3.1. Missingness allowed at deployment

Under MNAR mechanisms and missingness allowed at deployment, the inclusion of a missing indicator in the outcome model provides reductions in the Brier Score, and considerable improvements in the C-statistic (under MNAR-Y for both imputation methods, C-statistics presented in Appendix 2 of the Supplemental Materials).

The inclusion of a missing indicator and its interaction with $X_1$ produces severely overfit models for RI (Calibration slope < 1, Figure 4) when the outcome is also used to impute missing data at development. This result is explored further in the Supplemental Materials, where we present plots of the predicted risk distributions – we see that this method produces predictions that are very close to 0 and 1. Including the outcome in the imputation model under RI is, however, never recommended.

3.1.3.2. No missingness allowed at deployment

Inclusion of the indicator corrects the CITL for both MI: $DY+VA$ and RI: $D\overline{Y}+VA$ under MAR and MNAR-X structures when missingness is not allowed at deployment (in Appendix 1 of the Supplemental Material). Further (marginal) improvements in the calibration slope can be achieved through the inclusion of the additional $X_1:M_1$ term under the preferred imputation model for both methods, with the exception of missingness dependent on Y (MNAR-Y), where models developed using RI are better calibrated when they include the missing indicator alone – there is some evidence of marginal overfitting with the inclusion of this term for both imputation methods under MNAR-Y. Models developed using either imputation method under MNAR-Y, are, however generally still well calibrated (slope close to 1) whether or not missing data are allowed at deployment.

Interestingly, the inclusion of the $X_1:M_1$ interaction term where only complete data will be used at deployment appears to (marginally) improve the calibration slope for MI under both MAR and MNAR-X. Clearly, this term would be 0 for all new individuals however its inclusion at development seems to aid model performance at deployment.

3.1.4. Sample size

For the scenarios presented in this section, simulations were repeated, varying the sample size across 500, 1000, 5000 and 10,000. Visualisations of these results are presented in Appendix 4 of the Supplemental Materials. As expected, estimates of model performance were far more unstable at smaller sample sizes (< 5000), and model calibration improved as the sample size increased. There is some evidence of overfitting at smaller sample sizes, which is more pronounced in the models including missing indicators and their interactions than main effects alone.

3.2. Parameter estimation

We further present results for the CPM parameter estimates for selected scenarios presented in Figure 5. The same parameter configurations as specified in previous sections are used here.

Presented are the coefficients obtained from fitting each model within the development data. For MI, we present coefficients pooled according to Rubin's rules.

RI using the outcome in the imputation model consistently produces parameter estimates that are both biased and much larger in magnitude than any other method, and this is reflected in the predictive performance estimates. We frequently observe Brier Scores (Figure 3) that are too extreme under $DY+VY$ , and calibration slopes that suggest the predicted risks are too extreme under any $RI:DY$ strategy. Both of these are indicative of overfitting and are likely due to the relative size of the parameter estimates compared to other methods. RI: $D\overline{Y}$ generally estimates parameters with minimal bias, and the inclusion of a missing indicator appears to correct bias in the estimation of the coefficient for the missing predictor ( ${\gamma }_{X1}$ ) under MNAR mechanisms.

Perhaps as expected, MI: $D\overline{Y}$ using main effects only fails to recover unbiased parameter estimates under all missingness mechanisms, however under MAR and MNAR mechanisms, bias in estimates of ${\gamma }_{X1}$ are attenuated by the inclusion of the $X_1:M_1$ term in the outcome model. MI: $DY$ generally recovers the true parameter values well, even under MNAR mechanisms. It can however be observed that biased parameters do not necessarily result in worse predictive performance, as models developed under MI: $D\overline{Y}$ , and missing data imputed in this same way at validation/deployment were favoured over models developed using the outcome at development.

4. Results: MIMIC-III data example

A total of 33,306 patients were included in the analysis of the MIMIC-III data. A total of 23,314 were randomly assigned to the development set, and the outcome prevalence in the development cohort was 2610/23,314 = 11.2%. The remaining 9992 patients formed the validation set, and had an outcome prevalence of 1084/8908 = 10.8%. A total of 14,474 patients had complete data in all predictors. 18,713 patients were missing bilirubin, 424 were missing Glasgow Coma Scale, 447 missing respiratory rate and 439 missing systolic blood pressure. A total of 10 different missingness patterns were observed (where complete cases are classed as a missingness pattern) resulting in 17 derived (regression) imputation models. Given the six model predictors, the minimum required sample size for the development of the imputation models was $(6+1{)}^{*}2=14$ , where this was not met, imputation models were derived in the complete case cohort. The patient cohort is summarised in Appendix 6 of the Supplemental Materials.

Since the MIMIC-III data contains missing data in the predictors, the two imputation/validation strategies dependent on complete predictor information at deployment ( $DY+VA$ , $D\overline{Y}+VA$ ) have not been evaluated in this empirical example, and we instead assume that missing data would be imputed at the point of prediction, and focus on illustrating the strategies that accommodate this. Since the MI process can impute the outcome, results are presented for MI under a new scenario $DY+V{Y}^I$ , whereby Y is first imputed, then used to impute any remaining missing predictors. The imputed value of the outcome is replaced with the true (observed) outcome for model validation.

Estimates of the predictive performance of the fitted CPMs applied to the MIMIC-III data under each imputation strategy and development/validation scenario are presented in Figure 6. The magnitude of difference in the performance metrics between methods and scenarios was generally smaller than in the simulation study, but some key findings remain. Summaries of all predictive performance measures, and differences between MI and RI, and omitting/including the outcome in the imputation model are presented in the Supplemental Materials in Appendices 7 to 9, respectively.

Figure 6.

Predictive performance of imputation methods, model forms and imputation/validation strategies. DY = Y included in the imputation model at development, D $\overline{Y}$ = Y omitted from the imputation model at development, VY = Y included in the imputation model at validation, V $\overline{Y}$ = Y omitted from the imputation model at validation, DA = complete data available at model development, VA = complete data available at validation, V $Y^I$ = Y imputed at validation.

4.1. Predictive performance

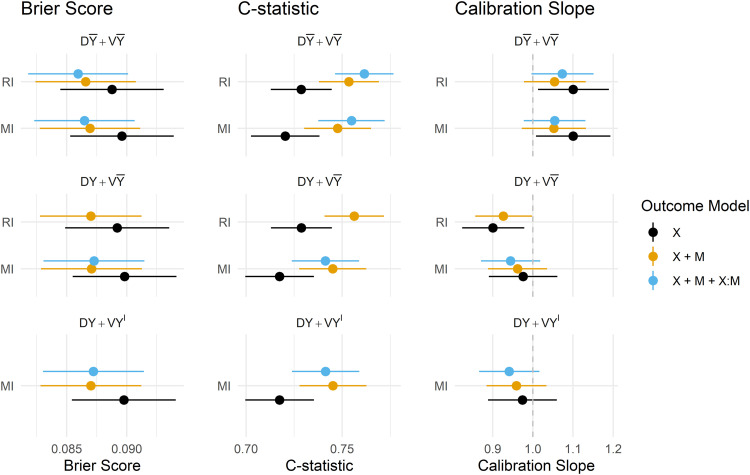
Under RI, omitting the outcome from the imputation model was again preferred in terms of model calibration, though in the MIMIC-III data, there was practically no difference in overall accuracy or model discrimination from including the outcome. Attempting to fit a CPM on data that uses the outcome to impute missing predictors, and also contains interactions between predictors and their missing indicators failed: models did not converge and resulted in extreme estimates of the model coefficients, and results for this outcome model under $DY+V\overline{Y}$ have, therefore, been omitted from Figure 6.

MI performed similarly under $DY+V{Y}^I$ , $D\overline{Y}+V\overline{Y}$ and $DY+V\overline{Y}$ in all performance metrics, apart from in the calibration slope, where models derived and applied under $DY+V{Y}^I$ and $DY+V\overline{Y}$ were slightly overfit, however, $D\overline{Y}+V\overline{Y}$ resulted in slight underfitting which is arguably preferable if the model is likely to be used in new out-of-sample populations.

The inclusion of missing indicators (and their interaction) mitigated the under/overfitting slightly for both RI and MI, and offered minor improvements in discrimination, Brier Score and calibration for both methods under $D\overline{Y}+V\overline{Y}$ . The estimates of model performance were practically indistinguishable between RI and MI under $D\overline{Y}+V\overline{Y}$ , which was found to be the preferred strategy (when missingness is imputed at the point of prediction) for both imputation methods in both the simulation and empirical analyses.

Predictions obtained via both the $DY+V{Y}^I$ and $DY+V\overline{Y}$ strategies were seemingly too extreme, as evidenced by the estimated calibration slopes < 1. Interestingly, estimates of all performance metrics were almost identical for these two strategies, suggesting that the imputed version of the outcome had little to no influence on the imputed predictor values.

5. Discussion

In this study, we have assessed model performance for MI and RI, with and without the use of missing indicators across a range of missingness mechanisms across simulated and real data. We considered how/when the outcome should be used in the imputation model for missing covariates, whether RI could offer a more practical and easier-to-implement solution than MI, and how the inclusion of missing indicators affects model predictive performance. All of these questions were considered in relation to whether or not missing data will be allowed once the model is deployed in practice. We have provided a concise list of recommendations in Table 2.

Table 2.

Table of recommendations for the use of multiple imputation, regression imputation and missing indicators in the development and deployment of clinical prediction models.

Recommendations
Assuming no missing data will be present at deployment, multiple imputation (including the outcome) or regression imputation (omitting the outcome) are recommended as the best strategies and estimates of predictive performance was comparable between the two.
Where missingness is allowed at deployment, and multiple imputation is impossible at deployment (e.g. where the original development data, or sufficient computational power is not available), regression imputation can be used as an alternative.
Always omit the outcome from the imputation model under regression imputation.
Where data are assumed to be MNAR-X or MNAR-Y and missingness is allowed at deployment, the inclusion of a missing indicator can offer marginal improvements in model performance, and does not harm performance under MCAR or MAR mechanisms
The use of missing indicators under MNAR-Y can harm model performance when missingness is not allowed at deployment, and is not recommended

In the context of recovering unbiased parameter estimates, the literature advocates the use of the observed outcome in the imputation model for MI. ¹² In the context of predictive performance, we found that RI consistently performed better when Y is instead omitted from the imputation. This strategy is recommended by Steyerberg ³⁴ for RI, where the author notes that including the outcome in the imputation model artificially strengthens the relationship between the predictors and outcome. MI overcomes this issue by introducing an element of randomness to the imputation procedure.

We further observed that the performance of a model with inconsistent imputation models between the development and validation stages ( $DY+V\overline{Y}$ ) performed worse than one where the imputation model remained consistent across the two stages. For instance, omitting the observed outcome at both stages resulted in better predictive performance, even when using MI. Although we have also observed that the inclusion of Y in the imputation model helps in recovering unbiased effect estimates, others have recommended a more considered approach when targeting a model that allows for missing data at deployment. Fletcher Mercaldo and Blume ¹³ observed that MI including the outcome produces a larger overall prediction error than omitting the outcome entirely, as the out-of-sample imputations were biased by attempting to use the imputation model derived during development (with $Y$ ) to impute in the test set (where Y is unobserved). This imputation bias carries through to the overall performance of the model. This is in line with our findings, whereby a consistent imputation model between development and deployment resulted in stronger performance overall, at the cost of slightly biased parameter estimates. An interesting result to note here is that a model with unbiased model parameters is not necessarily the one that predicts best, especially when missing data will be imputed at deployment.

A related issue lies in the inclusion of additional variables in the imputation model that are not model predictors. This could arise in external validation studies where missingness occurs in the predictors, and additional information is available and used to impute them. Although this was not directly covered by the study, we anticipate that the resulting inconsistency in imputation models between model development and validation could negatively impact the model performance since we observed that performance was strongest when imputation models remained consistent across development, validation and deployment. It is therefore worth considering (at the time of model development) which variables should be used in imputation models, and whether these are likely to be available in future validation and deployment scenarios.

We have demonstrated that RI could offer a practical alternative to MI within the context of prediction. Estimates of predictive performance were practically indistinguishable between RI and MI when the preferred imputation model was applied in both simulated and real data settings. As discussed above, there are several challenges associated with applying MI during the deployment of a CPM, including but not limited to requiring access to the development data and the availability of computational power and time. Recent developments have, however, proposed methods that potentially mitigate these requirements. ²³ RI also overcomes both of these major issues, in that only the deterministic imputation models would be required to produce imputations during model deployment. We emphasize, however, that RI consistently showed extremely poor performance when the observed outcome was included in the imputation model, and this method should therefore only be used when missing model covariates are imputed using observed covariates. MI, on the other hand, proved to be more stable across a range of scenarios and imputation models.

The careful use of missing indicators has also proven to be beneficial in specific cases. For example, under MNAR-X, MI has marginally stronger performance in both imputed and complete deployment data when a missing indicator is included in the outcome model. Under incomplete data at deployment, the inclusion of an indicator further provided small improvements in overall predictive accuracy to both methods under MNAR-Y. Since MI is only assumed to recover unbiased effects under MAR, the indicator appears to correct this bias under informative missingness patterns. However, we noted some surprising results in the use of indicators when data are MNAR-Y; specifically, when missing data are not allowed at deployment the inclusion of the indicator is harmful and resulted in small increases in the Brier Score, and poor Calibration-in-the-large. In our real data example, the inclusion of a missing indicator offered improvements in model discrimination, calibration and overall accuracy under the preferred strategy, omitting the outcome from the imputation at all stages of the model pipeline.

Related literature under a causal inference framework by Sperrin et al. ⁹ and Groenwold et al. ³⁵ has found that the inclusion of missing indicators is not recommended under MCAR, and can lead to biased parameter estimates under this missingness structure. van Smeden et al. ³⁶ discuss at length how missing indicators should be approached with caution in predictive modelling – inclusion of a missing indicator introduces an additional assumption that the missingness mechanism remains stable across the CPM pipeline; an assumption that is generally dubious, but especially within routinely collected health data. The propensity to measure certain predictors is likely to vary across care providers, settings and over time as clinical guidelines and practices change. This in turn potentially changes the relationship between the missing indicator and the outcome and could have implications for model performance. As others have highlighted, the strategy to handle missing data should be devised on an individual study basis, taking into consideration the potential drivers of missingness, how stable these are likely to be, and how/whether missing data will be handled once the model has been deployed.

We recommend that the strategy for handling missing data during model validation should mimic that to be used once the model is deployed, and that measures of predictive performance be computed in either complete or imputed data depending on whether missingness will be allowed in the anticipated deployment setting or not. For example, complex model applications integrated into electronic health record systems are better suited to applying imputation strategies at the point of prediction, whereas simple models that require manual data entry at the point-of-care are more likely to require a complete set of predictors. The difference between performance allowing for and prohibiting missing data at deployment may also be of interest in assessing any drop in performance related to the handling of missing data. Interestingly, we have observed somewhat different results depending on whether missingness is allowed at deployment or not. It may therefore be preferable to optimize a model for either one of these use cases, resulting in a different model (and hence different coefficients) dependent on whether we envisage complete data at deployment. Ideally, any model predictor considered for inclusion in a CPM should be either routinely available or easily measured at deployment. There are, however, several existing use cases where important predictors can be missing both at model development and deployment (e.g. QRisk3 ¹⁰ ) and we envisage that models integrated directly into existing clinical systems would be required to make predictions in the absence of some predictor information. We expect that the findings of this work are especially relevant to such use cases.

Although we have considered a wide range of simulated scenarios, a key limitation to this study is that we only considered a relatively simple CPM with two covariates, where only one was allowed to be missing. This was to restrict the complexity and size of the work, as only a limited set of scenarios can realistically be presented. We do, however, expect that the fundamental findings would generalise to more complex models (as was found in the MIMIC-III example) since we could consider each of the two model predictors to represent some summary of multiple missing and observed predictors. With more predictors in the model, there would not be any additional missingness mechanisms and we, therefore, anticipate that such complex models would not provide any additional insight. A further possible limitation is that this work has been restricted to the study of a single binary outcome, although we would not expect the results to change in the context of e.g., continuous or time-to-event outcomes. We accompany this work with a rShiny dashboard allowing readers to explore our results in more detail across the entire range of parameter configurations. Finally, we did not consider uncertainty in individual-level predictions as a measure of predictive performance. Typically, only point estimates of individual-level risk are provided during the deployment of a clinical prediction model so we focused on measures of predictive performance that validate these point estimates (i.e. calibration and discrimination). However, it is posssible that differences would be observed in the precision and coverage of prediction intervals, ³⁷ or the stability of the individual-level predictions derived under RI and MI.^38,39

Avenues for further work would include exploring the impact of more complex patterns of missingness in multiple predictor variables. As the number of incomplete predictors increases, so does the number of potential missing indicators eligible for inclusion in the outcome model, which could introduce issues of overfitting,^40,41 and variable selection becomes challenging. Here we have also limited our studies to scenarios where the missingness mechanism remains constant between development and deployment, however, it would be interesting to explore whether these same results hold if the mechanism were to change between the two stages, or indeed if different missing data handling strategies were to be used across different stages of the model pipeline.

6. Conclusion

We have conducted an extensive simulation study and real data example, and found that when no missingness is allowed at deployment, existing guidelines on how to impute missing data at the development are generally appropriate. However, if missingness is to be allowed when the model is deployed into practice, the missing data handling strategy at each stage should be more carefully considered, and we found that omitting the outcome from the imputation model at all stages was optimal in terms of predictive performance.

We have found that RI performs at least as well as MI when the outcome is omitted from the imputation model, but tends to result in more unstable estimates of predictive performance. Missing indicators can offer marginal improvements in predictive performance under MAR and MNAR-X structures, but can harm model performance under MNAR-Y. We emphasise that this work assumes that both the missingness mechanism and missing data handling strategies remain constant across model development and deployment, and the performance of the proposed approaches could vary when this assumption is violated.

We recommend that if missing data is likely to occur both during the development and deployment of a CPM, that RI be considered as a more practical alternative to MI, and that if either imputation method is to be applied at deployment, the outcome be omitted from the imputation model at both stages. Model performance should be assessed in such a way that reflects how missing data will occur and be handled at deployment, as the most appropriate strategy may depend on whether missingness will be allowed once the model is applied in practice. We also advocate for the careful use of missing indicators in the outcome model if MNAR-X can safely be assumed, but this should be assessed on a study-by-study basis since the inclusion of missing indicators also has the potential to reduce predictive performance, especially when missingness is not permitted at deployment.