Abstract
Knee cartilage and bone segmentation is critical for physicians to analyze and diagnose articular damage and knee osteoarthritis (OA). Deep learning (DL) methods for medical image segmentation have largely outperformed traditional methods, but they often need large amounts of annotated data for model training, which is very costly and time-consuming for medical experts, especially on 3D images. In this paper, we report a new knee cartilage and bone segmentation framework, KCB-Net, for 3D MR images based on sparse annotation. KCB-Net selects a small subset of slices from 3D images for annotation, and seeks to bridge the performance gap between sparse annotation and full annotation. Specifically, it first identifies a subset of the most effective and representative slices with an unsupervised scheme; it then trains an ensemble model using the annotated slices; next, it self-trains the model using 3D images containing pseudo-labels generated by the ensemble method and improved by a bi-directional hierarchical earth mover’s distance (bi-HEMD) algorithm; finally, it fine-tunes the segmentation results using the primal-dual Internal Point Method (IPM). Experiments on four 3D MR knee joint datasets (the SKI10 dataset, OAI ZIB dataset, Iowa dataset, and iMorphics dataset) show that our new framework outperforms state-of-the-art methods on full annotation, and yields high quality results for small annotation ratios even as low as 10%.
Keywords: Knee cartilage and bone segmentation, Sparse annotation, Ensemble learning, 3D MR images
1. Introduction
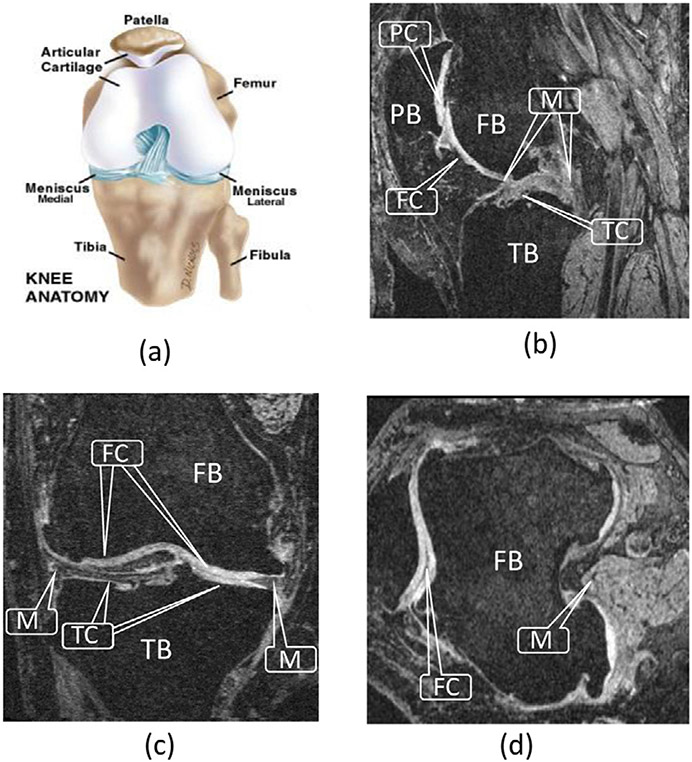
Osteoarthritis (OA) is a prevalent chronic disease caused by the damage and degeneration of cartilages. It is estimated that 20% of Americans may suffer from various levels of OA by 2030. Magnetic resonance imaging (MRI) has become a common technique for studying and assessing changes within the knee joint, including cartilages and bones. Fig. 1 illustrates the anatomical structure of the knee joint.
Fig. 1.
Knee joint. (a) Anatomy of the knee joint (adopted from Paley Orthopedic & Spine Institute (2018)). (b)–(d) Sagittal, coronal, and transverse MR image planes, showing the femur bone (FB), femoral cartilage (FC), tibia bone (TB), tibial cartilage (TC), patella bone (PB), patellar cartilage (PC), and meniscus (M).
Considering the knee joint anatomy, the femoral cartilage (FC), tibial cartilage (TC), patellar cartilage (PC), and menisci (M) are the main tissues affecting the knee joint health. To quantitatively measure the thickness of the knee cartilages and identify the bone–cartilage interface, accurate cartilage and bone segmentation is needed.
To capture the detailed structure of the knee anatomy, 3D MR images are commonly scanned at high in-plane resolution. However, labeling 3D MR images is very time-consuming.
In this paper, we propose a new framework, KCB-Net, for segmenting knee cartilages and bones in 3D MR images with sparse annotation. We first encode each 2D slice in an unlabeled training set of 3D images into a feature vector in an unsupervised manner. Second, a subset of the most representative slices (based on a given annotation ratio) for the training set is selected for experts to label. Third, we train three 2D modules using the selected labeled slices. Fourth, preliminary pseudo-labels of the training set are generated by the trained 2D modules, which are further used to train a 3D module. Fifth, we ensemble the three 2D modules and one 3D module, and generate pseud-labels of the entire training set, which are used to re-train the four modules and the 3D ensemble model for a few iterations. The feature maps generated by the ensemble model are post-processed to produce the final segmentation results.
We conduct experiments on four 3D MR knee joint datasets (the SKI10 dataset, OAI ZIB dataset, Iowa dataset, and iMorphics dataset; see Section 4). Our experiments show that with full annotation, our new KCB-Net framework outperforms state-of-the-art full annotation methods, and with sparse annotations, KCB-Net yields high quality results even with very sparse annotation ratios (e.g., 10%).
2. Related work
Automated and semi-automated methods for knee joint segmentation have been investigated for several decades. Shape models, graph optimization approaches, and deep learning (DL) methods exhibited high performance in recent years. 3D graph based methods are well suited for knee cartilage segmentation. Yin et al. (2010) proposed a layered optimal graph image segmentation for multiple objects and surfaces (LOGISMOS) framework to simultaneously segment multiple interacting surfaces of objects by incorporating multiple spatial interrelationships of surfaces in a D-dimensional graph. Kashyap et al. (2017) extended the LOGISMOS framework to simultaneously segment 3D knee objects for multiple follow-up visits of the same patient — effectively performing optimal 4D (3D + time) segmentation. Xie et al. (2022) proposed a primal–dual Internal Point Method (IPM) to first learn the parameters of the surface cost functions for the LOGISMOS algorithm and then solve an optimization problem for the final segmentation.
Several deep convolutional neural network (CNN) approaches showed close-to-human level performance. Liu et al. (2018) proposed a fully automatic musculoskeletal tissue segmentation method that integrates CNN and 3D simplex deformable approaches to improve the accuracy and efficiency. Ambellan et al. (2019) combined the strengths of statistical shape models and CNN to successfully segment knee bones/cartilages. Tan et al. (2019) proposed a method to first extract the regions of interest (ROIs) for three cartilage areas and then fuse the three ROIs to generate fine-grained segmentation results. Couteaux et al. (2019) presented an approach to localize and segment knee menisci and classify MRI slices based on tears in anterior and posterior menisci and their orientations using Mask R-CNN (He et al., 2017).
Zheng et al. (2019) proposed a 3D segmentation method that ensembles three 2D models and one 3D model (called base-learners). It first trains the base-learners using labeled data, and ensembles the base-learners by training a meta-learner (Yu et al., 2017). It then re-trains the base-learners and meta-learner with pseudo-labels to obtain a 3D segmentation model. However, such base-learners still rely on fully annotated 3D data. Zheng et al. (2020b) further proposed a sparse annotation strategy to select the most representative 2D slices for annotation. It first encodes each slice into a low-dimensional vector, and prioritizes the slices based on their representativeness in a set of 3D images. Next, three 2D modules and one 3D module (a 3D FCN (Çiçek et al., 2016) are trained, and pseudo-labels of the unlabeled data are generated using the base-learners. A Y-shape DenseVoxNet (Yu et al., 2017) is used to train a meta-learner, which ensembles the 2D and 3D modules. Zheng et al. (2020a) then extended this sparse annotation strategy, and designed a K-head FCN to compute the pseudo-label uncertainty of each slice and rule out highly uncertain pixels in the subsequent training process.
3. Method
3.1. Overview
Our KCB-Net combines and extends previously reported ensemble learning (Zheng et al., 2019) and sparse annotation (Zheng et al., 2020b) methods for 3D segmentation. Fig. 2 shows its main steps.
Fig. 2.
The pipeline of our proposed KCB-Net framework.
(1). Representative slice selection:
As in Zheng et al. (2020b), each 2D slice in every major orientation red(i.e., axial, coronal, or sagittal) in the entire set of 3D training images is encoded as a low-dimensional latent vector, and all slices are prioritized by their representativeness. The top-ranked slices are selected as the ones, in which to perform expert annotations.
(2). Base-learner training and pseudo-label generation:
As in Zheng et al. (2019), three 2D modules, one for each axial, sagittal, or coronal orientations, are trained on the selected and annotated slices. Once 2D modules are trained, pseudo-labels are assigned to all remaining un-annotated slices in and a 3D module is trained. -UNet mechanism (Chen et al., 2016) is newly used to extract multi-scale features. Each module extracts information across different scales to support fine-scale feature extraction. Instead of using sparse 3D FCN (Çiçek et al., 2016) as in Zheng et al. (2020b), we utilize 3D Attention UNet (Oktay et al., 2018), which uses labels of the expert-annotated slices and pseudo-labels of all the un-annotated slices.
As in Guo et al. (2021), an edge-aware branch is added to the 3D module to increase the weights of cartilage and bone surface locations. To explore the appearance consistency among consecutive slices and further improve the quality of the pseudo-labels generated, the H-EMD method (Liang et al., 2022) is newly enhanced by incorporating a bi-directional hierarchical earth mover’s distance (bi-HEMD) when generating pseudo-labels of the un-annotated slices. Our bi-HEMD method first produces object candidates by applying multiple threshold values on the probability maps, and then selects object instances by minimizing the earth mover’s distance based on a reference set of the object instances.
(3). Ensembling and self-training :
Following the pseudo-label generation, 2D and 3D modules are ensembled by training a 3D Y-shape DenseVoxNet (Zheng et al., 2019) as a meta-learner using the original input images and pseudo-labels, which learns the target object segmentation from the labels/pseudo-labels. The output of the ensemble model is utilized to iteratively re-train the modules in Step (2) and the ensemble model in Step (3), repeated until convergence.
(4). Post-processing :
We newly add a post-processing step exploiting the task-specific characteristics that knee bones and cartilages are anatomically adjacent with one other. A fine-tuning network (Xie et al., 2022) that incorporates the surface interrelationships between adjacent bones and cartilages is trained by taking the probability maps generated in Step (3) as input and the pseudo-labels as the learning targets. The fine-tuning network is optimized using the IPM algorithm (Xie et al., 2022).
3.2. Representative slice selection
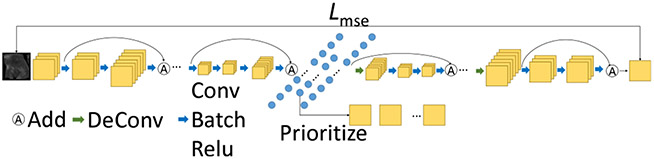
Identifying a small-enough set of the most representative 2D slices for annotation that subsequently facilitates the segmentation method training is critical for the success of our proposed approach. This section presents our slice selection scheme, called representative annotation (RA).
Medical experts often annotate a 3D image by choosing one orthogonal plane (axial, coronal, or sagittal) and labeling the corresponding slices one by one. It may, however, be beneficial to annotate 2D slices along each of the three orthogonal planes. Fig. 3 illustrates the slice selection method.
Fig. 3.
Illustrating the representative slice selection method. , denotes the mean square error.
3.2.1. Slice representation
For a specified annotation ratio (e.g., 10% of all slices), to select the most representative slices to label, we first need to efficiently represent the slices. Medical image slices can commonly be represented as latent feature vectors of a much smaller size compared to the original 2D image matrix. By comparing slices using their latent vectors, not only can we reduce the computation cost but also extract their most useful information.
We utilize an auto-encoder as the representation extractor for the slices in our 3D training image set , which learns efficient features in an unsupervised manner and conducts a lossy compression in the encoding process. It learns to store relevant information and disregard noise. This auto-encoder consists of two parts: An encoder produces a compressed knowledge representation for an input image (or slice) ; a decoder takes the representation as input and outputs as a reconstruction of the original image. The entire auto-encoder model is optimized by minimizing the sum of the reconstruction error , which measures the differences between the original image and the reconstruction produced, and a regularization term for alleviating overfitting. This can be formulated as:
| (1) |
where is the reconstruction loss between and , is a scaling parameter for the regularization term to adjust the trade-off between the sensitivity to the input and overfitting, is the parameter of the auto-encoder, and and are the parameters of the encoder and decoder, respectively.
To facilitate a fast training and convergence of the auto-encoder, we use a ResNet-101 (He et al., 2016) pre-trained on ImageNet (Deng et al., 2009) as the encoder backbone. A light-weight decoder (ResNet-50 He et al., 2016) is added to map the latent vectors to the original input space. Since slices along each orthogonal plane will be selected, we train the auto-encoder using all the slices of the 3D training set along the three orthogonal planes.
3.2.2. Prioritizing the slices
After training the auto-encoder, we measure the representativeness of each slice in the 3D training image set as in Zheng et al. (2020b). First, we feed a 2D slice to the encoder, and take the generated latent vector as the representation of the slice . Second, we define and compute the similarity between two slices and as , where and are the latent vectors of and respectively, and denotes cosine similarity.
Next, a subset of slices is selected from all the slices of the set (for an annotation ratio or a given size of ). The representativeness of with respect to is defined as:
| (2) |
Finding an optimal slice subset was formulated as a maximum cover problem in Zheng et al. (2020b), which is NP-hard, and a polynomial time approximation solution was obtained using a greedy method. Suppose a subset is the most representative for the images in . The next choice (if needed) is a slice in the remaining slice set that maximally increases the representativeness of the new subset , i.e.,
| (3) |
This selection process puts all the slices in in decreasing order based on their representativeness. The slices with better representativeness have higher priorities for annotation.
3.3. Base-learner training and pseudo-label generation
After the representative slice selection, the selected slices are labeled by experts, which we denote as , where is the number of slices selected.
Our 2D module follows the structure of CBAC-Net (Gu et al., 2021), since it outperforms other state-of-the-art 2D segmentation networks (e.g., UNet++ Zhou et al., 2018, TransUNet Chen et al., 2021, etc.) on our datasets in the experiments. This 2D module is a sequence of complete bipartite networks with asymmetric convolutions, which exploits multi-scale features and enhances the capability of standard convolution on extracting discriminative features. A bipartite network structure (Chen et al., 2017), -UNet scheme (Chen et al., 2016), asymmetric convolutions (Ding et al., 2019), and deep supervision (Lee et al., 2015) are integrated into this module.
A 2D segmentation model can have a relatively large receptive field, but it does not utilize the interactions between consecutive slices well, which may result in spatial slice-to-slice inconsistency. Hence, we follow the ensemble method in Zheng et al. (2019) and train a 3D module, which produces smoother 3D results.
We choose 3D Attention UNet (Oktay et al., 2018) as the backbone for our 3D module, since it outperforms other well-known 3D segmentation networks (e.g., 3D U-Net (Çiçek et al., 2016, DenseVoxNet Yu et al., 2017, TransUNet 3D Chen et al., 2021, UNet++ 3D Zhou et al., 2018, etc.) on our datasets in the experiments.
Similar to our 2D modules, we apply the -UNet design (Chen et al., 2016) and build a 3D -AttentionUNet as our 3D module to exploit 3D multi-scale features. In our 3D module of 3D -AttentionUNet, the coarse features extracted by one AttentionUNet submodule are fed to the next AttentionUNet submodule to obtain fine-grained features.
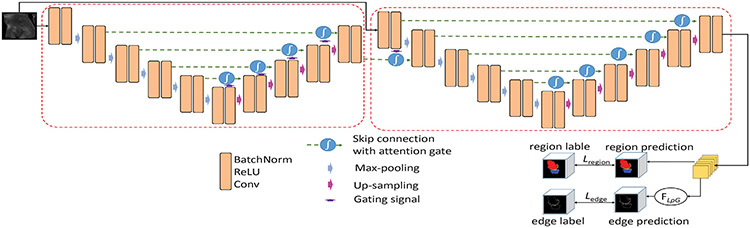
For knee joint segmentation, the bone and cartilage boundaries are often more important than other areas, since they usually serve as the main criteria to measure whether and/or how much a cartilage is damaged. Hence, we add an edge-aware regulation to our 3D -AttentionUNet to force the network to focus more on the object boundary areas. Fig. 4 shows the structure of our edge-aware 3D -AttentionUNet. The edge gate is defined as:
| (4) |
where and represent the Gaussian smoothing kernel and Laplacian kernel respectively, * denotes convolution, and is an activation function.
Fig. 4.
The structure of our 3D -AttentionUNet with edge-aware branches (). A dashed red box denotes a 3D AttentionUNet block.
The loss function of our 3D module is defined as:
| (5) |
where and are the cross entropy losses of the region branch and edge branch respectively, and is a scaling parameter to regularize the edge branch.
We first train our three 2D segmentation modules using the selected labeled slices for each of the three orthogonal planes, and generate the probability maps of the unlabeled slices using the three trained 2D modules. We then train our 3D edge-aware -AttentionUNet using the 3D images in that contain both the labeled slices and unlabeled slices that are now “labeled”. Specifically, the pseudo-labels produced by the three 2D modules are first improved by the bi-HEMD algorithm in Section 3.4. Then, the probability maps attained by the three 2D modules are averaged to generate the pseudo-labels used for training our 3D module. These four trained segmentation modules generate their pseudo-labels respectively for all the unlabeled slices. For simplicity, we average the results of these four modules as the probability map for each 3D image in .
3.4. Bi-directional hierarchical earth mover’s distance
After training our three 2D modules, probability maps of all the unlabeled slices in are obtained. One observation on the 3D knee images is that the appearances of bones and cartilages between consecutive slices are often similar in size and shape. Exploring such appearance similarity can help improve the pseudo-label quality. Hence, we apply the hierarchical earth mover’s distance (H-EMD) method (Liang et al., 2022) that uses many threshold values of the probability map for each unannotated slice and exploits the appearance consistency between consecutive slices to optimize the pseudo-labels.
The H-EMD method (Liang et al., 2022) takes two key steps. (i) Candidate instance generation: For a set of threshold values, , from the probability map of a slice in a 3D image, produce a set of possible object instance candidates. These object candidates can be organized into a forest structure . Also, a reference set of object instances is built on the slice (obtained iteratively). (ii) Candidate instance selection: For each pair of an instance candidate in and a reference instance in , compute their matching score as the cosine distance between their instance feature vectors. The goal is to maximize the sum of the weighted matching scores between the candidate set and reference set to select the “best” object instances for the slice . This can be solved by integer linear programming. For a dataset with different classes, a feature vector for each instance candidate is defined as (), whose first three items are the coordinates of its center pixel and the last items are for an -D one-hot vector denoting the category of the instance.
Rather than using the Euclidean distance as in Liang et al. (2022), our method applies cosine distance, since our vectors contain two different types of information, which make the distance unsuitable to measure the differences between these vectors.
Similar to the bi-directional RNN in Chen et al. (2016), we perform the H-EMD process in two opposite directions (bi-HEMD). That is, for any two labeled slices and in a 3D image, , we apply H-EMD along the direction of , and along . With the bi-HEMD process, the pseudo-labels generated by the 2D modules are improved, which are then used to train the 3D module in Section 3.3.
3.5. Tuning the final 3D model using pseudo-labels
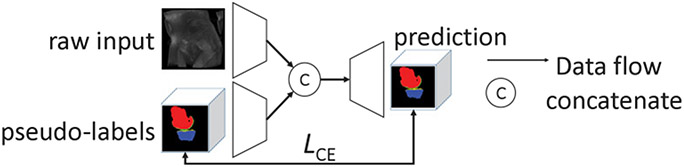
We now have three 2D -FCNs and one 3D -FCN trained with labeled or pseudo-labeled slices along the , , and planes. Next, we produce the probability maps of each 3D image in using these four FCN modules, denoted as , , , and , respectively. These probability maps are averaged, and the results are used to train our 3D meta-learner. This meta-learner is a Y-shaped -DenseVoxNet (Yu et al., 2017) that is aware of the raw images and their pseudo-labels so as to ease overfitting. Fig. 5 shows our meta-learner.
Fig. 5.
The structure of our meta-learner.
After training our 3D meta-learner, we apply the self-training strategy in Zheng et al. (2019) to further improve the model performance. In this self-training process, the segmentation results of the meta-learner are regarded as pseudo “ground truth” of the unlabeled slices, which are used to re-train the 2D/3D base-learners (the three 2D base-learners are re-trained with the “labeled” slices along the three orthogonal planes). Note that the base-learners are first trained in the step of Section 3.3. Here, we apply the SGD optimizer and a smaller learning rate to ensure the robustness and convergence of the entire training process. The loss function of the 3D meta-learner (see Fig. 5) is defined as the cross-entropy between the predictions and input pseudo-labels. The base-learners are re-trained, and generate four versions of pseudo-labels for each 3D image in , which are averaged and used to train the meta-learner again. We repeat this self-training process for a few iterations, until the meta-learner performance no longer improves, giving rise to our final 3D model.
3.6. Post-processing using IPM
Instead of applying the softmax function to the final probability maps, we further perform some post-processing to fine-tune the probability maps. One observation is that the surfaces of bones and cartilages are mutually “coupled” in some areas, within which the topology and relative positions of the bones and cartilages are known and the distances between them are within specific ranges. Furthermore, physicians care more about the “coupled” areas since osteoarthritis is usually caused by damages of the knee cartilages in such areas. Thus, we apply the IPM method (Xie et al., 2022) by incorporating the surface interrelationships between the bones and cartilages into the segmentation process to further improve the segmentation performance. An advantage of the IPM method over traditional graph based methods is that it parameterizes the surface cost functions in the graph model and leverages DL to learn the parameters rather than relying on hand-crafted features.
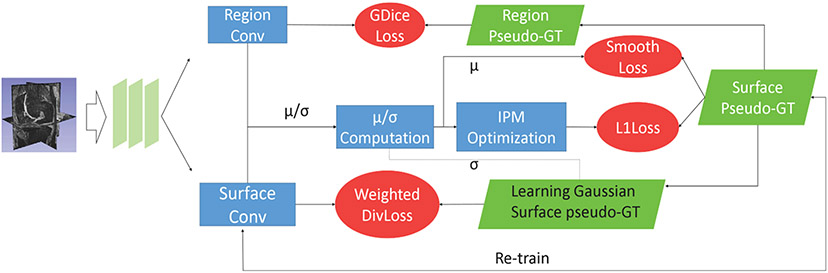
Instead of using ground truth to train the surface segmentation network of IPM (Xie et al., 2022), we use the pseudo-labels generated by our meta-learner to optimize this network in the first iteration. Afterwards, the pseudo-labels are updated by IPM and used to re-train the network. Such operations are repeated several times until convergence. The details of the above training process are shown in Fig. 7 (Xie et al., 2022).
Fig. 7.
The process of the post-processing step (Xie et al., 2022).
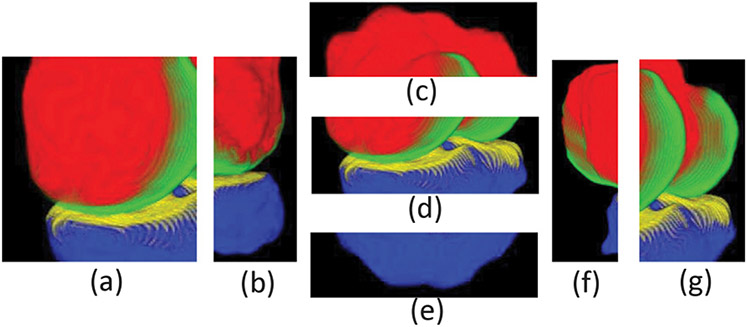
Since the bone and cartilage surfaces are not terrain-like, we need to first unfold the knee joint into seven parts following the practice in Zhou et al. (2019), i.e., the front, back, top, center, bottom, left and right parts, respectively, as shown in Fig. 6.
Fig. 6.
Illustrating the seven unfolded parts of the knee joint. The corresponding parts in the sagittal view are: (a) front; (b) back; (c) top; (d) center; (e) bottom; (f) left; (g) right.
Specifically, for the center part (see Fig. 6(d)), we replace U-Net used in the original IPM method (Xie et al., 2022) with the probability maps generated by our final fine-tuned ensemble model. Finally, we patch its 6 junction areas (i.e., the junction areas between center and front, center and back, center and top, center and bottom, center and left, and center and right), and average the center area and its corresponding junction areas processed by IPM to smooth the final results.
4. Experiments and analysis
To demonstrate the capabilities of our KCB-Net approach, its performance was compared with state-of-the-art knee segmentation methods using full annotations as well as compared with two state-of-the-art slice selection strategies: equal-interval annotation (EIA) and random slice selection (RSS). Furthermore, the effect of each component in our KCB-Net framework was assessed and the robustness of the method was quantified for different sparse annotation ratios.
4.1. Datasets and implementation details
Our experiments use four 3D MR knee joint datasets, the SKI10 dataset, OAI ZIB dataset, Iowa dataset, and iMorphics dataset, which we describe below.
The SKI10 Dataset
This dataset contains 60 3D MR images for training, 40 for validation, and 50 for testing, from the MICCAI SKI10 challenge. The images were from the surgical planning program of Biomet, Inc., and were annotated by experts. It only covers the time-point of baseline. Four compartments were annotated: femural bone (FB), femural cartilage (FC), tibia bone (TB), and tibia cartilage (TC). More details of this dataset can be found in Heimann et al. (2010).
The OAI dataset
Three sub-datasets, the OAI ZIB dataset, iMorphics dataset, and Iowa dataset, from the OAI dataset are used to evaluate the performance of our KCB-Net. The images of these three sub-datasets were from the Osteoarthritis Initiative database (OAI, http://www.oai.ucsf.edu/). (1) The OAI ZIB dataset consists of 507 3D MR images annotated by experts of the Zuse Institute Berlin. It only covers the time-point of baseline. The details of this dataset are depicted in Ambellan et al. (2019). (2) The iMorphics dataset (Bowes et al., 2015), available directly from the OAI database, includes 176 3D MR knee images acquired with 3T Siemens MAGNETOM Trio scanners and quadrature transmit–receive knee coils (USA Instruments, Aurora, OH, USA). The annotated compartments are femoral cartilage (FC), tibia cartilage (TC), patellar cartilage (PC), and menisci (M). It covers the time-point of baseline and 12 month follow-up. (3) The Iowa dataset, a University of Iowa annotated portion of the OAI dataset that was first segmented by the LOGISMOS method (Kashyap et al., 2017) and the automatic segmentations were then corrected by the just-enough-interaction (JEI) approach in 4D (3D + time) (Zhang et al., 2020). The Iowa dataset consists of 1462 double echo steady state (DESS) 3D MR images from 248 subjects. Four compartments were annotated: femur bone (FB), femoral cartilage (FC), tibia bone (TB), and tibial cartilage (TC). Different time-points were covered by this dataset: some subjects were covered with baseline and 12 month follow-up, and some were covered with baseline, 12, 24, 30, 36, 48, 72, and 96 month follow-ups.
We implemented all the tested networks using PyTorch (Paszke et al., 2019). For our auto-encoder, ResNet-101 (He et al., 2016) is used as the backbone of its encoder and ResNet-50 (He et al., 2016) as the backbone of its decoder. The encoder is initialized with a model pre-trained on ImageNet (Deng et al., 2009). All the other parameters are initialized as in He et al. (2016), and in Eq. (1) is set to . The network was optimized using the Adam optimizer (, , ). The 3D images were first cropped so as to remove the background clearly outside of the knee area. Each slice or 3D image was normalized to zero mean and unit standard variance. In the data augmentation for 3D model training, starting points are randomly selected in a 3D image, and a patch of size 80 × 192 × 160 is cropped at each starting point, making sure that the cropped patch locates completely inside the 3D image. Afterwards, common spatial transforms (e.g., rotation, scaling, and mirroring) are applied. In 2D model training, each slice is augmented with common spatial transforms.
We set for the CBAC-Net and 3D -AttentionUNet with edge-aware branches (for larger , the model costs increase largely but the accuracy improves little Chen et al., 2016). We use mean square error as the auto-encoder’s loss. We set the parameter of the edge regularizer in the edge-aware 3D -AttentionUNet as (see Eq. (5)).
4.2. Evaluation metrics
The following evaluation metrics are used in our experiments and comparisons.
4.2.1. Dice similarity coefficient
Dice similarity coefficient (DSC) is calculated as:
| (6) |
where is the ground truth, is the prediction, and denotes the volume of a 3D object .
4.2.2. Average symmetric surface distance
Average symmetric surface distance (ASSD) focuses on the absolute distances between surfaces of the segmented objects and their ground truths, calculated as:
| (7) |
where and denote the surfaces of objects and respectively, and denote the numbers of voxels on and respectively, and denotes the nearest Euclidean distance of a point to a surface .
4.2.3. Root Mean Square symmetric surface distance
Root Mean Square symmetric surface Distance (RMSD) is a variation of ASSD, except that all the distances are squared first and the root is conducted for the average value. RMSD is computed as:
| (8) |
in which all the terms are defined as in Eq. (7). In RMSD, a larger deviation is penalized stronger. This metric is used for comparison with previous methods on the SKI10 dataset.
4.2.4. Volume overlap error
The volume overlap error (VOE) between the GT and Pred is calculated as:
| (9) |
A smaller value of VOE means a better segmentation, with 0 for perfect segmentation and 1 for no overlap of GT and Pred at all. This metric is used for comparison with previous methods on the SKI10 dataset.
4.2.5. Volume difference
The volume difference (VD) between the GT and Pred is calculated as:
| (10) |
VD is used in the scoring of cartilages on the SKI10 dataset. It approximately indicates the deviation from the average cartilage thickness when the evaluation is limited on the respective ROIs.
4.3. Experimental results with full annotation
To evaluate the effectiveness of our approach, we compare the performance of KCB-Net with the following recent methods on the SKI10 dataset and ZIB dataset with full annotation. (i) CNN-SSM: integrating CNN with a statistical shape model (Ambellan et al., 2019). (ii) The ensemble method (Zheng et al., 2020b). (iii) UNet++ 3D (Zhou et al., 2018). (iv) Attention UNet 3D (Oktay et al., 2018). (v) TransUNet 3D (Chen et al., 2021). For fair comparison, we follow the dataset split strategy in Ambellan et al. (2019) and use the evaluation metrics in Heimann et al. (2010).
Tables 1 and 2 present the performance comparisons of our KCB-Net with the other methods trained on the SKI10 dataset and OAI ZIB dataset with full annotation, respectively. From Table 1, one can see that our KCB-Net outperforms the best-known method, CNN-SSM, in all the metrics except the ASSD on femoral bone and tibial bone. Our overall score on the SKI10 dataset is higher by 1.94 than that of CNN-SSM.
Table 1.
Comparison with state-of-the-art methods using full annotation on the SKI10 dataset following the data split in Ambellan et al. (2019) and evaluation metrics used in Heimann et al. (2010). Paired t-test values indicate the significance status of the improved performance of our method vs. the ensemble method (Zheng et al., 2020b).
| Femoral bone | Femoral cartilage | Tibial bone | Tibial cartilage | Overall score | |||||
|---|---|---|---|---|---|---|---|---|---|
| ASSD (mm) | RSSD (mm) | VOE (%) | VD (%) | ASSD (mm) | RSSD (mm) | VOE (%) | VD (%) | ||
| CNN-SSM (Ambellan et al., 2019)a | 0.430 ± 0.130 | 0.740 ± 0.270 | 20.99 ± 5.08 | 7.18 ± 10.51 | 0.350 ± 0.070 | 0.590 ± 0.190 | 19.06 ± 5.18 | 4.29 ± 12.34 | 74.00 ± 7.70 |
| UNet++ 3D (Zhou et al., 2018) | 0.541 ± 0.096 | 0.694 ± 0.252 | 20.86 ± 5.01 | 3.90 ± 11.79 | 0.521 ± 0.164 | 0.672 ± 0.448 | 20.07 ± 5.62 | 5.35 ± 12.35 | 72.03 ± 8.29 |
| TransUNet 3D (Chen et al., 2021) | 0.538 ± 0.072 | 0.680 ± 0.196 | 21.36 ± 5.02 | 5.42 ± 10.31 | 0.517 ± 0.152 | 0.654 ± 0.418 | 20.01 ± 5.44 | 6.04 ± 12.68 | 72.20 ± 8.60 |
| Attention UNet 3D (Oktay et al., 2018) | 0.519 ± 0.083 | 0.690 ± 0.454 | 18.77 ± 4.74 | 1.36 ± 9.69 | 0.519 ± 0.259 | 0.664 ± 0.648 | 18.14 ± 4.87 | 6.19 ± 11.21 | 74.54 ± 6.50 |
| Ensemble method (Zheng et al., 2020b) | 0.689 ± 0.858 | 0.732 ± 0.871 | 18.47 ± 4.75 | 4.71 ± 9.73 | 0.508 ± 0.200 | 0.640 ± 0.533 | 18.19 ± 5.11 | 3.00 ± 11.15 | 73.82 ± 9.51 |
| Our KCB-Net method | 0.498 ± 0.053 | 0.579 ± 0.104 | 18.66 ± 4.54 | −1.06 ± 9.20 | 0.504 ± 0.240 | 0.516 ± 0.602 | 17.60 ± 4.65 | 0.92 ± 10.73 | 75.94 ± 6.08 |
| p-value | 0.016 | 0.011 | 0.621 | 0.033 | 0.547 | ≪0.001 | 0.041 | ≪0.001 | 0.001 |
Marks the row in which the results are from the original paper.
Table 2.
Comparison with state-of-the-art methods using full annotation on the OAI ZIB dataset following the data split in Ambellan et al. (2019). Paired t-test values indicate the significance status of the improved performance of our method vs. the ensemble method (Zheng et al., 2020b).
| Femoral bone | Femoral cartilage | Tibial bone | Tibial cartilage | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| CNN-SSM (Ambellan et al., 2019)a | 98.60 ± 0.30 | 0.170 ± 0.050 | 89.90 ± 3.60 | 0.160 ± 0.070 | 98.50 ± 0.33 | 0.180 ± 0.060 | 85.60 ± 4.54 | 0.230 ± 0.120 |
| Ensemble method (Zheng et al., 2020b) | 98.40 ± 0.32 | 0.197 ± 0.054 | 88.13 ± 2.57 | 0.193 ± 0.054 | 98.53 ± 0.34 | 0.183 ± 0.067 | 84.64 ± 4.24 | 0.215 ± 0.085 |
| TransUNet 3D (Chen et al., 2021) | 98.33 ± 0.32 | 0.212 ± 0.068 | 88.66 ± 2.70 | 0.183 ± 0.055 | 98.53 ± 0.36 | 0.206 ± 0.205 | 83.86 ± 4.97 | 0.235 ± 0.101 |
| Attention UNet 3D (Oktay et al., 2018) | 98.41 ± 0.34 | 0.201 ± 0.068 | 88.90 ± 2.75 | 0.178 ± 0.056 | 98.56 ± 0.36 | 0.181 ± 0.084 | 84.99 ± 4.67 | 0.224 ± 0.096 |
| UNet++ 3D (Zhou et al., 2018) | 98.24 ± 0.42 | 0.266 ± 0.134 | 88.22 ± 2.77 | 0.192 ± 0.059 | 98.31 ± 0.53 | 0.856 ± 1.251 | 84.31 ± 5.04 | 0.242 ± 0.118 |
| Our KCB-Net method | 98.79 ± 0.30 | 0.181 ± 0.054 | 90.33 ± 2.84 | 0.152 ± 0.051 | 98.84 ± 0.34 | 0.164 ± 0.058 | 86.10 ± 4.50 | 0.212 ± 0.090 |
| p-value | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 |
Marks the row in which the results are from the original paper.
To further examine the robustness of our KCB-Net, five-fold cross validation is conducted on the four datasets. Note that for the SKI10 dataset, some of the utilized evaluation metrics require the ROIs of the femur and tibial areas, which are not available in some cases; thus, we compare KCB-Net in the commonly used DSC and ASSD metrics with the other methods. We split a whole dataset in the ratio of 7:1:2, corresponding to training, validation, and testing, for each fold on the four datasets using stratification by subject IDs. The final results are the averages of the five folds, which are given in Tables 3, 4, 5, and 6, respectively. As Tables 3 and 4 show, our approach achieves the best results on the SKI10 and OAI ZIB datasets.
Table 3.
Comparison with state-of-the-art methods using full annotation on the SKI10 dataset with five-fold cross validation. Paired t-test values indicate the significance status of the improved performance of our method vs. the ensemble method (Zheng et al., 2020b).
| Femoral bone | Femoral cartilage | Tibial bone | Tibial cartilage | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| TransUNet 3D (Chen et al., 2021) | 98.06 ± 0.76 | 0.236 ± 0.099 | 77.89 ± 5.24 | 0.343 ± 0.103 | 97.31 ± 1.91 | 0.322 ± 0.278 | 74.29 ± 7.05 | 0.345 ± 0.128 |
| UNet++ 3D (Zhou et al., 2018) | 98.10 ± 0.82 | 0.225 ± 0.093 | 77.20 ± 6.07 | 0.392 ± 0.201 | 97.64 ± 1.96 | 0.337 ± 0.548 | 71.40 ± 6.55 | 0.409 ± 0.149 |
| Ensemble method (Zheng et al., 2020b) | 98.15 ± 0.71 | 0.226 ± 0.091 | 78.89 ± 5.89 | 0.333 ± 0.150 | 97.68 ± 1.93 | 0.280 ± 0.311 | 75.67 ± 6.76 | 0.315 ± 0.124 |
| Attention UNet 3D (Oktay et al., 2018) | 98.29 ± 0.90 | 0.363 ± 0.789 | 79.93 ± 5.87 | 0.316 ± 0.144 | 97.84 ± 1.90 | 0.268 ± 0.292 | 76.01 ± 6.48 | 0.295 ± 0.104 |
| Our KCB-Net method | 98.41 ± 0.65 | 0.184 ± 0.077 | 81.67 ± 5.34 | 0.308 ± 0.166 | 97.97 ± 1.50 | 0.226 ± 0.194 | 78.19 ± 6.63 | 0.299 ± 0.124 |
| p-value | ≪0.001 | ≪0.001 | ≪0.001 | 0.030 | 0.017 | 0.035 | ≪0.001 | 0.302 |
Table 4.
Comparison with state-of-the-art methods using full annotation on the OAI ZIB dataset with five-fold cross validation. Paired t-test values indicate the significance status of the improved performance of our method vs. the ensemble method (Zheng et al., 2020b).
| Femoral bone | Femoral cartilage | Tibial bone | Tibial cartilage | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| Ensemble method (Zheng et al., 2020b) | 98.49 ± 0.30 | 0.182 ± 0.046 | 89.26 ± 3.08 | 0.176 ± 0.067 | 98.60 ± 0.30 | 0.172 ± 0.049 | 86.36 ± 3.88 | 0.196 ± 0.081 |
| UNet++ 3D (Zhou et al., 2018) | 98.44 ± 0.31 | 0.190 ± 0.047 | 89.19 ± 2.74 | 0.174 ± 0.052 | 98.57 ± 0.31 | 0.222 ± 0.340 | 84.96 ± 4.55 | 0.226 ± 0.102 |
| TransUNet 3D (Chen et al., 2021) | 98.47 ± 0.29 | 0.188 ± 0.048 | 89.25 ± 2.94 | 0.173 ± 0.060 | 98.61 ± 0.30 | 0.171 ± 0.050 | 85.34 ± 4.24 | 0.240 ± 0.114 |
| Attention UNet 3D (Oktay et al., 2018) | 98.55 ± 0.30 | 0.174 ± 0.048 | 89.56 ± 2.64 | 0.169 ± 0.059 | 98.70 ± 0.31 | 0.162 ± 0.067 | 86.74 ± 4.01 | 0.196 ± 0.089 |
| Our KCB-Net method | 98.62 ± 0.26 | 0.164 ± 0.039 | 90.24 ± 2.76 | 0.153 ± 0.049 | 98.76 ± 0.30 | 0.149 ± 0.048 | 87.19 ± 3.96 | 0.185 ± 0.085 |
| p-value | ≪ 0.001 | ≪ 0.001 | ≪ 0.001 | ≪ 0.001 | ≪ 0.001 | ≪ 0.001 | ≪ 0.001 | 0.006 |
Table 5.
Comparison with state-of-the-art methods using full annotation on the Iowa dataset. Paired t-test values indicate the significance status of the improved performance of our method vs. the ensemble method (Zheng et al., 2020b). “–” denotes that the corresponding results were not reported in the original paper.
| Femural bone | Femoral cartilage | Tibial bone | Tibial cartilage | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| LOGISMOS-4D (Kashyap et al., 2017)a | – | – | − | 0.550 ± 0.110 | – | – | – | 0.600 ± 0.140 |
| Ensemble method (Zheng et al., 2020b) | 94.86 ± 1.02 | 0.649 ± 0.269 | 84.38 ± 2.40 | 0.467 ± 0.170 | 94.40 ± 1.23 | 0.676 ± 0.234 | 81.96 ± 4.59 | 0.577 ± 0.170 |
| CML (Tan et al., 2019) | 94.95 ± 1.23 | 0.651 ± 0.173 | 83.63 ± 2.33 | 0.611 ± 0.152 | 94.44 ± 1.24 | 0.612 ± 0.204 | 81.51 ± 4.91 | 0.583 ± 0.152 |
| UNet++ 3D (Zhou et al., 2018) | 95.68 ± 0.91 | 0.691 ± 0.182 | 83.29 ± 2.75 | 0.487 ± 0.123 | 94.92 ± 1.71 | 0.658 ± 0.236 | 81.30 ± 4.30 | 0.421 ± 0.116 |
| Attention UNet 3D (Oktay et al., 2018) | 95.80 ± 1.14 | 0.645 ± 0.244 | 84.42 ± 2.71 | 0.480 ± 0.124 | 95.09 ± 1.65 | 0.635 ± 0.221 | 82.27 ± 4.31 | 0.413 ± 0.120 |
| TransUNet 3D (Chen et al., 2021) | 95.78 ± 0.79 | 0.663 ± 0.178 | 83.78 ± 2.85 | 0.441 ± 0.147 | 95.23 ± 1.51 | 0.705 ± 0.209 | 80.41 ± 4.51 | 0.480 ± 0.146 |
| Our KCB-Net method | 96.47 ± 0.88 | 0.542 ± 0.178 | 86.73 ± 2.76 | 0.349 ± 0.138 | 96.49 ± 1.59 | 0.524 ± 0.214 | 84.34 ± 4.27 | 0.416 ± 0.131 |
| p-value | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 |
Marks the row in which the results are from the original paper.
Table 6.
Comparison with state-of-the-art methods using full annotation on the iMorphics dataset. Paired t-test values indicate the significance status of the improved performance of our method vs. the ensemble method (Zheng et al., 2020b). “–” denotes that the corresponding results were not reported in the original paper.
| Femoral cartilage | Tibial cartilage | Patellar cartilage | Menisci | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| UDA (Panfilov et al., 2019)a | 90.70 ± 1.90 | – | 89.70 ± 2.80 | – | 87.10 ± 4.60 | – | 86.30 ± 3.40 | – |
| CML (Tan et al., 2019)a | 90.00 ± 3.70 | – | 88.90 ± 3.80 | – | 88.00 ± 4.30 | – | – | – |
| Ensemble method (Zheng et al., 2020b) | 90.68 ± 2.03 | 0.229 ± 0.075 | 90.18 ± 2.59 | 0.185 ± 0.117 | 88.25 ± 5.79 | 0.369 ± 0.204 | 87.65 ± 3.21 | 0.322 ± 0.192 |
| UNet++ 3D (Zhou et al., 2018) | 90.81 ± 2.06 | 0.221 ± 0.065 | 89.00 ± 2.59 | 0.271 ± 0.121 | 86.22 ± 5.90 | 0.349 ± 0.173 | 85.53 ± 3.21 | 0.428 ± 0.196 |
| Attention UNet 3D (Oktay et al., 2018) | 91.03 ± 2.02 | 0.213 ± 0.080 | 90.48 ± 2.88 | 0.196 ± 0.151 | 88.89 ± 6.00 | 0.307 ± 0.297 | 88.45 ± 3.01 | 0.314 ± 0.128 |
| TransUNet 3D (Chen et al., 2021) | 90.97 ± 1.84 | 0.205 ± 0.058 | 90.19 ± 2.37 | 0.247 ± 0.127 | 87.41 ± 4.68 | 0.273 ± 0.094 | 87.66 ± 3.03 | 0.322 ± 0.140 |
| Our KCB-Net method | 92.35 ± 1.81 | 0.188 ± 0.061 | 91.27 ± 2.40 | 0.184 ± 0.123 | 90.58 ± 4.76 | 0.254 ± 0.143 | 89.31 ± 3.11 | 0.255 ± 0.137 |
| p-value | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 | ≪0.001 |
Marks the rows in which the results are from the original papers.
Table 5 shows the performance comparison of our KCB-Net and the other methods trained on the fully annotated Iowa dataset. The Iowa dataset was used for comparison with the following known methods. (i) 4D LOGISMOS (Kashyap et al., 2017): utilizing a hierarchical set of random forest classifiers to learn the cartilage appearance and simultaneously segment multiple interacting surfaces of objects based on an algorithmic incorporation of multiple spatial interrelationships in an -dimensional graph. (ii) CML (Tan et al., 2019): detecting the regions of interest and fusing the cartilages by a fusion layer. Since we could not access the source code of the original method, we implemented the approach and applied it to the Iowa dataset. The hyper-parameters (e.g., the number of filters, down-samplings, and up-samplings) used in our implementation are the same as presented in the original paper. We experimented with both the 2D and 3D versions of CML, which showed that the 2D version yielded better results on the Iowa dataset. (iii) The ensemble learning method (Zheng et al., 2020b): Ensembling four 2D/3D FCNs and self-training with fully labeled 3D data. (iv) UNet++ 3D (Zhou et al., 2018). (v) Attention UNet 3D (Oktay et al., 2018). (vi) TransUNet 3D (Chen et al., 2021).
From Table 5, one can see that our KCB-Net outperforms LOGISMOS-4D on both the femoral and tibial cartilage segmentations. KCB-Net also outperforms the ensemble method (Zheng et al., 2020b), which demonstrates that the CBAC-Net based 2D modules, -UNet design, edge-aware 3D AttentionUNet, bi-HEMD method, and IPM post-processing method that we use in KCB-Net help improve the segmentation performance.
Table 6 presents the results achieved on the fully annotated iMorphics dataset. We compare with the following recent methods. (i) UDA (Panfilov et al., 2019): utilizing mixup and adversarial unsupervised domain adaptation to improve the robustness of DL-based knee cartilage segmentation in new MRI acquisition settings. (ii) CML (Tan et al., 2019). (iii) The ensemble method (Zheng et al., 2020b). (iv) UNet++ 3D (Zhou et al., 2018). (v) Attention UNet 3D (Oktay et al., 2018). (vi) TransUNet 3D (Chen et al., 2021). Our method attains better DSC scores on FC, TC, PC, and M compared to the UDA method. We also outperform the CML and ensemble methods in both DSC and surface errors of FC, TC, PC, and M, suggesting that our method can obtain more quantitatively accurate knee cartilage and bone segmentations.
Performance improvement of our KCB-Net over the original ensemble method (Zheng et al., 2020b) was evaluated on the four datasets, using paired t-tests. Tables 1, 2, 3, 4, 5, and 6 show that in most of the compared cases, our new approach significantly outperforms the ensemble approach (Zheng et al., 2020b) (with -values < 0.05).
4.4. Experimental results with sparse annotation
To evaluate the effectiveness of our approach on sparsely annotated data, we compare its performances on the four datasets with changing sparse annotation ratios vs. those achieved using different slice selection schemes. Specifically, we compare the representative annotation (RA) scheme used in our KCB-Net pipeline with two common slice selection schemes: equal-interval annotation (EIA) and random slice selection (RSS).
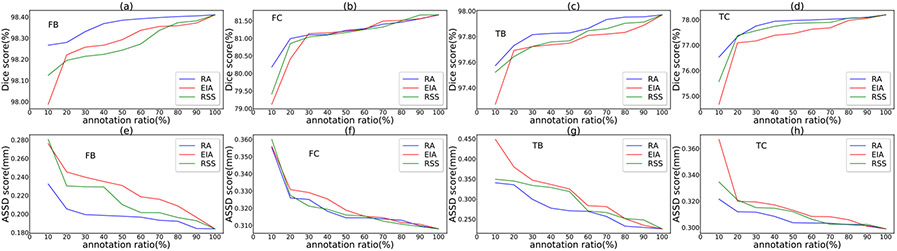
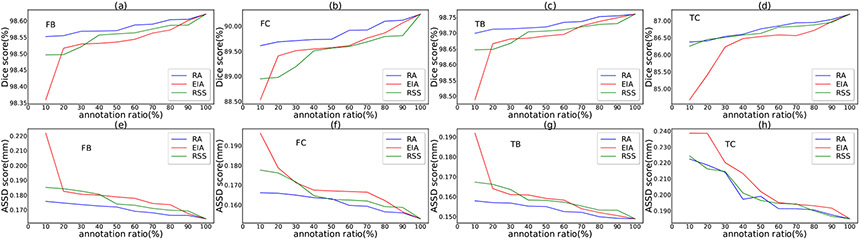
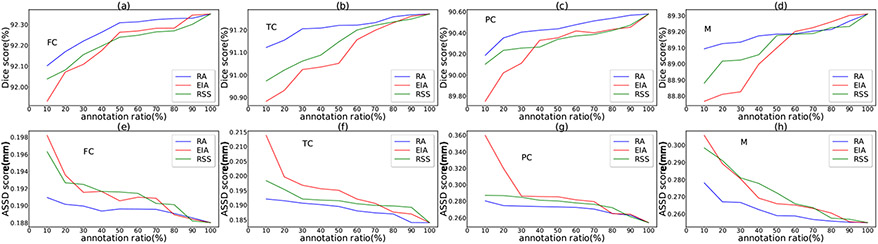
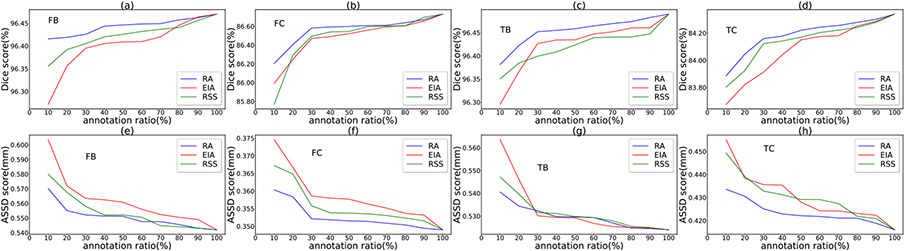
Suppose for a specified annotation ratio, slices are to be selected. The EIA scheme selects slices at equal distance along each axis, and the RSS scheme randomly selects slices along each axis. We repeat the RSS process 10 times, and take the average of the results as the RSS-based performance. 8, Figs. 9, 10, and 11 show the performance comparisons with various annotation ratios on the SKI10, OAI ZIB, iMorphics, and Iowa datasets, respectively.
Fig. 8.
Comparison of the three slice selection schemes (RA, EIA, and RSS) on the SKI10 dataset.
Fig. 9.
Comparison of the three slice selection schemes (RA, EIA, and RSS) on the OAI ZIB dataset.
Fig. 10.
Comparison of the three slice selection schemes (RA, EIA, and RSS) on the iMorphics dataset.
Fig. 11.
Comparison of the three slice selection schemes (RA, EIA, and RSS) on the Iowa dataset.
Figs. 8, 9, 10, and 11, one can see that our RA outperforms the EIA and RSS schemes on both the cartilage and bone segmentations in most the cases. Our method can notably alleviate performance degradation, especially for annotation ratios ≤30%. This is because EIA selects the locationally same slice indices in each 3D image, which might make the trained model overfit on the selected slices of the same indices and cause segmentation errors on the remaining slices. RSS performs better than EIA in very sparse annotation ratios (10%–30%) for most of the segmentation targets but sometimes performs worse than EIA in less sparse annotation ratios (e.g., >50%), since RSS can select different slices in different 3D images, likely incurring less overfitting. The performances of these three selection schemes are similar for annotation ratios >80% since many slices they select tend to be the same or similar at such dense annotation ratios.
Another observation from these four figures is that the performance drops quickly when the annotation ratios are <30% for most of the segmentation targets, suggesting that the annotation ratio of 30% might be a “lower limit” for a satisfactory performance for knee segmentation.
4.5. Ablation study
To examine the contribution of each key component in our KCB-Net, we conducted an ablation study to evaluate the performances of its components, denoted as follows. (1) SI: 2D module; (2) S2: 2D module; (3) S3: 2D module; (4) S4: 3D module; (5) S5: ensembling of the three 2D modules and the 3D module; (6) S6: bi-HEMD; (7) S7: self-training; (8) S8: IPM post-processing.
The performance of each individual component in S1, S2, S3, and S4 is given first, followed by the ensemble performance (S5) that combines all these four components. For S6–S8, components are sequentially added to the framework each time; the more the performance increases, the more contribution the corresponding component (in S6–S8) makes. Thus, note that S8 actually reflects the performance of the entire framework including all its components.
7, 8, 9, and 10 present the ablation study results on the SKI10, OAI ZIB, iMorphics, and Iowa datasets, respectively. We observe that the ensemble of the 2D and 3D modules can substantially improve the performance over the individual modules. The 3D module often attains better performance than the 2D modules since it exploits the interrelations among consecutive slices. The ensemble strategy can benefit from both the 2D modules (with a large receptive field) and the 3D module (exploiting the interactions among consecutive slices). Since some cartilages are very thin along the sagittal plane, it is quite difficult for DL models to detect them along one such plane, especially with very sparse annotation. Utilizing other 2D modules can help address this issue. Tables 7, 8, 9, and 10 show that the ensemble strategy and the self-training mechanism play more important roles than the other components. Figs. 12 and 13 qualitatively compare results in the sagittal view on the Iowa and iMorphics datasets.
Table 7.
Ablation study of our method on the SKI10 dataset.
| Femoral bone | Femoral cartilage | Tibial bone | Tibial cartilage | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| S1 (axial) | 98.08 ± 0.74 | 0.228 ± 0.095 | 77.92 ± 5.44 | 0.353 ± 0.131 | 97.50 ± 1.97 | 0.297 ± 0.283 | 74.52 ± 6.50 | 0.357 ± 0.133 |
| S2 (coronal) | 98.12 ± 0.76 | 0.221 ± 0.088 | 77.55 ± 6.26 | 0.373 ± 0.189 | 97.95 ± 0.78 | 0.230 ± 0.094 | 71.48 ± 6.87 | 0.402 ± 0.138 |
| S3 (sagittal) | 98.21 ± 0.78 | 0.216 ± 0.092 | 80.55 ± 5.50 | 0.321 ± 0.156 | 97.76 ± 1.80 | 0.275 ± 0.301 | 76.68 ± 6.59 | 0.320 ± 0.122 |
| S4 (3D) | 98.24 ± 0.69 | 0.210 ± 0.093 | 81.06 ± 5.76 | 0.321 ± 0.172 | 97.59 ± 2.86 | 0.281 ± 0.362 | 77.29 ± 6.70 | 0.321 ± 0.134 |
| S5 (ensemble) | 98.31 ± 0.64 | 0.199 ± 0.078 | 81.12 ± 5.56 | 0.316 ± 0.150 | 97.67 ± 2.79 | 0.263 ± 0.384 | 77.66 ± 6.51 | 0.305 ± 0.118 |
| S6 (bi-HEMD) | 98.29 ± 0.66 | 0.195 ± 0.080 | 81.22 ± 5.53 | 0.314 ± 0.150 | 97.56 ± 2.93 | 0.252 ± 0.405 | 77.80 ± 6.64 | 0.303 ± 0.124 |
| S7 (self-training) | 98.35 ± 0.67 | 0.189 ± 0.079 | 81.26 ± 5.46 | 0.310 ± 0.154 | 97.60 ± 2.84 | 0.236 ± 0.394 | 78.01 ± 6.59 | 0.305 ± 0.128 |
| S8 (IPM) | 98.41 ± 0.65 | 0.184 ± 0.077 | 81.67 ± 5.34 | 0.308 ± 0.166 | 97.97 ± 1.50 | 0.226 ± 0.194 | 78.19 ± 6.63 | 0.299 ± 0.124 |
Table 8.
Ablation study of our method on the OAI ZIB dataset.
| Femoral bone | Femoral cartilage | Tibial bone | Tibial cartilage | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| S1 (axial) | 98.51 ± 0.30 | 0.178 ± 0.042 | 89.46 ± 2.94 | 0.171 ± 0.061 | 98.64 ± 0.29 | 0.165 ± 0.047 | 86.40 ± 4.25 | 0.198 ± 0.108 |
| S2 (coronal) | 98.41 ± 0.34 | 0.196 ± 0.054 | 89.02 ± 2.58 | 0.176 ± 0.050 | 98.57 ± 0.31 | 0.190 ± 0.155 | 84.87 ± 4.52 | 0.225 ± 0.099 |
| S3 (sagittal) | 98.50 ± 0.28 | 0.182 ± 0.044 | 89.53 ± 2.95 | 0.167 ± 0.060 | 98.63 ± 0.29 | 0.168 ± 0.047 | 86.31 ± 3.99 | 0.202 ± 0.099 |
| S4 (3D) | 98.58 ± 0.27 | 0.170 ± 0.040 | 89.83 ± 2.70 | 0.163 ± 0.054 | 98.74 ± 0.30 | 0.153 ± 0.048 | 86.91 ± 4.01 | 0.199 ± 0.090 |
| S5 (ensemble) | 98.60 ± 0.27 | 0.168 ± 0.040 | 89.94 ± 2.66 | 0.160 ± 0.050 | 98.74 ± 0.30 | 0.152 ± 0.049 | 87.02 ± 4.04 | 0.193 ± 0.095 |
| S6 (bi-HEMD) | 98.61 ± 0.27 | 0.166 ± 0.041 | 90.00 ± 2.74 | 0.157 ± 0.051 | 98.74 ± 0.30 | 0.152 ± 0.049 | 87.04 ± 3.99 | 0.193 ± 0.092 |
| S7 (self-training) | 98.61 ± 0.26 | 0.165 ± 0.039 | 90.13 ± 2.80 | 0.156 ± 0.052 | 98.75 ± 0.30 | 0.151 ± 0.048 | 87.14 ± 3.94 | 0.188 ± 0.085 |
| S8 (IPM) | 98.62 ± 0.26 | 0.164 ± 0.039 | 90.24 ± 2.76 | 0.153 ± 0.049 | 98.76 ± 0.30 | 0.149 ± 0.048 | 87.19 ± 3.96 | 0.185 ± 0.085 |
Table 9.
Ablation study of our method on the iMorphics dataset.
| Femoral cartilage | Tibial cartilage | Patellar cartilage | Menisci | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| S1 (axial) | 89.03 ± 2.24 | 0.261 ± 0.061 | 88.91 ± 2.01 | 0.244 ± 0.150 | 86.98 ± 4.64 | 0.369 ± 0.142 | 85.87 ± 2.96 | 0.380 ± 0.096 |
| S2 (coronal) | 88.71 ± 2.25 | 0.284 ± 0.074 | 88.39 ± 3.08 | 0.332 ± 0.139 | 85.48 ± 5.06 | 0.326 ± 0.137 | 85.69 ± 3.31 | 0.345 ± 0.121 |
| S3 (sagittal) | 90.76 ± 1.97 | 0.234 ± 0.065 | 90.09 ± 2.55 | 0.251 ± 0.114 | 87.80 ± 5.15 | 0.297 ± 0.119 | 86.66 ± 3.35 | 0.389 ± 0.155 |
| S4 (3D) | 90.81 ± 1.96 | 0.235 ± 0.068 | 90.17 ± 2.74 | 0.228 ± 0.138 | 88.31 ± 5.19 | 0.287 ± 0.194 | 87.84 ± 3.15 | 0.357 ± 0.139 |
| S5 (ensemble) | 91.23 ± 1.76 | 0.210 ± 0.054 | 90.40 ± 2.51 | 0.223 ± 0.129 | 88.84 ± 5.23 | 0.264 ± 0.141 | 88.12 ± 3.18 | 0.323 ± 0.155 |
| S6 (bi-HEMD) | 91.86 ± 1.80 | 0.224 ± 0.101 | 90.50 ± 2.46 | 0.237 ± 0.126 | 89.47 ± 5.09 | 0.270 ± 0.148 | 88.60 ± 3.21 | 0.284 ± 0.181 |
| S7 (self-training) | 92.08 ± 1.75 | 0.206 ± 0.053 | 90.81 ± 2.41 | 0.185 ± 0.123 | 89.68 ± 5.01 | 0.273 ± 0.141 | 89.05 ± 3.14 | 0.280 ± 0.180 |
| S8 (IPM) | 92.35 ± 1.81 | 0.188 ± 0.061 | 91.27 ± 2.40 | 0.184 ± 0.123 | 90.58 ± 4.76 | 0.254 ± 0.143 | 89.31 ± 3.11 | 0.255 ± 0.137 |
Table 10.
Ablation study of our method on the Iowa dataset.
| Femural bone | Femoral cartilage | Tibial bone | Tibial cartilage | |||||
|---|---|---|---|---|---|---|---|---|
| DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | DSC (%) | ASSD (mm) | |
| S1 (axial) | 95.84 ± 0.90 | 0.690 ± 0.181 | 85.11 ± 2.86 | 0.417 ± 0.148 | 95.17 ± 1.48 | 0.690 ± 0.219 | 82.32 ± 4.40 | 0.460 ± 0.150 |
| S2 (coronal) | 95.71 ± 1.04 | 0.618 ± 0.238 | 85.43 ± 3.24 | 0.383 ± 0.123 | 94.97 ± 1.77 | 0.705 ± 0.243 | 80.88 ± 4.56 | 0.452 ± 0.114 |
| S3 (sagittal) | 95.77 ± 0.84 | 0.642 ± 0.194 | 85.13 ± 2.80 | 0.393 ± 0.126 | 95.23 ± 1.70 | 0.692 ± 0.241 | 80.64 ± 4.59 | 0.478 ± 0.125 |
| S4 (3D) | 95.87 ± 1.06 | 0.616 ± 0.166 | 85.45 ± 2.65 | 0.404 ± 0.170 | 95.41 ± 1.66 | 0.635 ± 0.396 | 82.93 ± 5.04 | 0.446 ± 0.111 |
| S5 (ensemble) | 96.09 ± 0.83 | 0.602 ± 0.160 | 85.79 ± 2.77 | 0.384 ± 0.150 | 95.71 ± 1.55 | 0.587 ± 0.210 | 83.13 ± 4.23 | 0.451 ± 0.151 |
| S6 (bi-HEMD) | 96.17 ± 0.88 | 0.590 ± 0.186 | 86.08 ± 2.69 | 0.371 ± 0.136 | 95.64 ± 1.64 | 0.561 ± 0.219 | 83.50 ± 4.27 | 0.442 ± 0.129 |
| S7 (self-training) | 96.35 ± 0.92 | 0.561 ± 0.185 | 86.42 ± 2.79 | 0.355 ± 0.132 | 96.05 ± 1.49 | 0.548 ± 0.210 | 83.91 ± 4.26 | 0.436 ± 0.124 |
| S8 (IPM) | 96.47 ± 0.88 | 0.542 ± 0.178 | 86.73 ± 2.76 | 0.349 ± 0.138 | 96.49 ± 1.59 | 0.524 ± 0.214 | 84.34 ± 4.27 | 0.416 ± 0.131 |
Fig. 12.
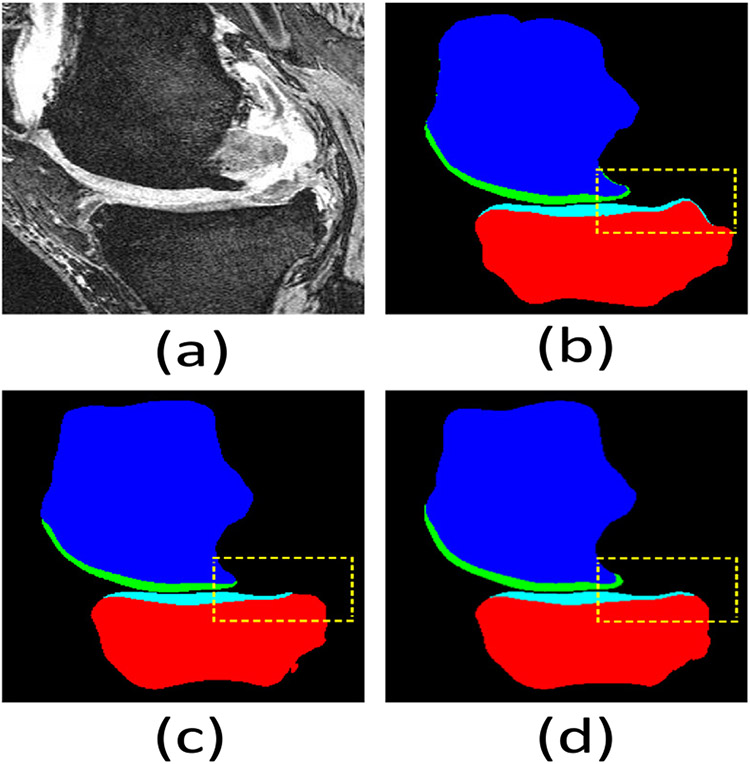
Visual comparison of knee bone and cartilage segmentation by our KCB-Net and Attention UNet 3D (a best-known 3D segmentation method) in the sagittal view on the Iowa dataset. (a) An input 2D slice from a 3D image; (b) segmentation ground truth; (c) segmentation by Attention UNet 3D; (d) segmentation by our KCB-Net. Our KCB-Net is able to correctly segment some thin boundary areas (e.g., see the dashed yellow boxes).
Fig. 13.
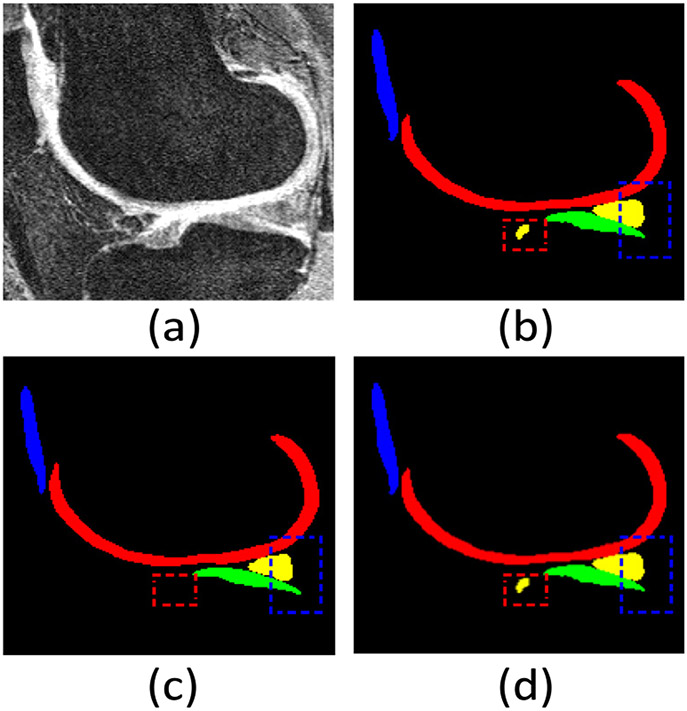
Visual comparison of knee bone and cartilage segmentation by our KCB-Net and Attention UNet 3D (a best-known 3D segmentation method) in the sagittal view on the iMorphics dataset. (a) An input 2D slice from a 3D image; (b) segmentation ground truth; (c) segmentation by Attention UNet 3D; (d) segmentation by our KCB-Net. Our KCB-Net is able to correctly segment some small cartilage areas (e.g., see the dashed red and blue boxes).
4.6. Discussion
From Figs. 8, 9, 10, and 11, one can see that our representative annotation (RA) scheme substantially reduces the performance gap between different sparse annotation ratios and full annotation, suggesting that our framework can achieve comparatively good results while using much less annotated data than required for full annotation. Our ensemble method and the self-training scheme using pseudo-labels improved by the bi-HEMD method largely improve the segmentation performance, because the training data we use contribute more information in an efficient way. Figs. 12 and 13 show that our ensemble and self-training strategies allow detection of small objects and thin boundary areas, despite the annotation sparsity. Our IPM post-processing helps further fine-tune the object boundary areas, making the overall segmentation results more accurate and reliable.
5. Conclusions
We reported a new framework, KCB-Net, for segmenting cartilages and bones in 3D knee joint MR images. Our method efficiently selects subsets of diverse image slices for expert annotations in a way that the most information-contributing slices are ranked most highly, allowing to train image segmentation models using high-sparsity ratio annotations. In the KCB-Net, three 2D segmentation modules and one 3D module integrating features across multiple scales with edge-aware branches are ensembled to generate pseudo-labels of the un-annotated slices, which are then used to re-train the 3D model. An IPM process is employed to post-process the probability maps generated by the 3D model. Experiments on four large knee datasets show that our new approach outperforms state-of-the-art methods on fully annotated datasets, and can notably improve segmentation performances when annotating only small data subsets.
Acknowledgments
This research was supported in part by NIH NIBIB Grant R01-EB004640 and National Science Foundation Grant CCF-1617735.
Footnotes
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Ambellan F, Tack A, Ehlke M, Zachow S, 2019. Automated segmentation of knee bone and cartilage combining statistical shape knowledge and convolutional neural networks: Data from the osteoarthritis initiative. Med. Image Anal 52, 109–118. [DOI] [PubMed] [Google Scholar]
- Bowes MA, Wolstenholme C, Vincent GR, Conaghan PG, 2015. A 3D MRI study of changes in the menisci of the OA knee: Data from the osteoarthritis initiative. Osteoarthr. Cartil 23, A254–A255. [Google Scholar]
- Chen J, Banerjee S, Grama A, Scheirer WJ, Chen DZ, 2017. Neuron segmentation using deep complete bipartite networks. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 21–29. [Google Scholar]
- Chen J, Lu Y, Yu Q, Luo X, Adeli E, Wang Y, Lu L, Yuille AL, Zhou Y, 2021. TransUNet: Transformers make strong encoders for medical image segmentation. arXiv preprint arXiv:2102.04306. [Google Scholar]
- Chen J, Yang L, Zhang Y, Alber M, Chen DZ, 2016. Combining fully convolutional and recurrent neural networks for 3D biomedical image segmentation. In: Conference on Neural Information Processing Systems, pp. 3036–3044. [Google Scholar]
- Çiçek O, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O, 2016. 3D U-net: Learning dense volumetric segmentation from sparse annotation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 424–432. [Google Scholar]
- Couteaux V, Si-Mohamed S, Nempont O, Lefevre T, Popoff A, Pizaine G, Villain N, Bloch I, Cotten A, Boussel L, 2019. Automatic knee meniscus tear detection and orientation classification with mask-RCNN. Diagn. Interv. Imaging 100 (4), 235–242. [DOI] [PubMed] [Google Scholar]
- Deng J, Dong W, Socher R, Li L-J, Li K, Li F-F, 2009. ImageNet: A large-scale hierarchical image database. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 248–255. [Google Scholar]
- Ding X, Guo Y, Ding G, Han J, 2019. ACNet: Strengthening the kernel skeletons for powerful CNN via asymmetric convolution blocks. In: Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 1911–1920. [Google Scholar]
- Gu P, Zheng H, Zhang Y, Wang C, Chen DZ, 2021. kCBAC-Net: Deeply supervised complete bipartite networks with asymmetric convolutions for medical image segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 337–347. [Google Scholar]
- Guo Z, Zhang H, Chen Z, van der Plas E, Gutmann L, Thedens D, Nopoulos P, Sonka M, 2021. Fully automated 3D segmentation of MR-imaged calf muscle compartments: Neighborhood relationship enhanced fully convolutional network. Comput. Med. Imaging Graph 87, 101835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He K, Gkioxari G, Dollar P, Girshick R, 2017. Mask R-CNN. In: Proceedings of the IEEE International Conference on Computer Vision (ICCV). [Google Scholar]
- He K, Zhang X, Ren S, Sun J, 2016. Deep residual learning for image recognition. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778. [Google Scholar]
- Heimann T, Morrison BJ, Styner MA, Niethammer M, Warfield S, 2010. Segmentation of knee images: A grand challenge. In: Proc. MICCAI Workshop on Medical Image Analysis for the Clinic, pp. 207–214. [Google Scholar]
- Kashyap S, Zhang H, Rao K, Sonka M, 2017. Learning-based cost functions for 3-d and 4-D multi-surface multi-object segmentation of knee MRI: Data from the osteoarthritis initiative. IEEE Trans. Med. Imaging 37 (5), 1103–1113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C-Y, Xie S, Gallagher P, Zhang Z, Tu Z, 2015. Deeply-supervised nets. In: Artificial Intelligence and Statistics. PMLR, pp. 562–570. [Google Scholar]
- Liang P, Zhang Y, Ding Y, Chen J, Madukoma CS, Weninger T, Shrout JD, Chen DZ, 2022. H-EMD: A hierarchical earth mover’s distance method for instance segmentation. IEEE Trans. Med. Imaging 10.1109/TMI.2022.3169449. [DOI] [PubMed] [Google Scholar]
- Liu F, Zhou Z, Jang H, Samsonov A, Zhao G, Kijowski R, 2018. Deep convolutional neural network and 3D deformable approach for tissue segmentation in musculoskeletal magnetic resonance imaging. Magn. Reson. Med 79 (4), 2379–2391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oktay O, Schlemper J, Folgoc LL, Lee M, Heinrich M, Misawa K, Mori K, McDonagh S, Hammerla NY, Kainz B, et al. , 2018. Attention u-net: Learning where to look for the pancreas. In: 1st Conference on Medical Imaging with Deep Learning (MIDL). [Google Scholar]
- Paley Orthopedic & Spine Institute, 2018. Anatomy of the knee joint. https://Paleyinstitute.org/Centers-of-Excellence/Cartilage-Repair/Anatomy-of-the-Knee-Joint/.
- Panfilov E, Tiulpin A, Klein S, Nieminen MT, Saarakkala S, 2019. Improving robustness of deep learning based knee MRI segmentation: Mixup and adversarial domain adaptation. In: IEEE/CVF International Conference on Computer Vision Workshops, pp. 450–459. [Google Scholar]
- Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L, et al. , 2019. PyTorch: An imperative style, high-performance deep learning library. arXiv preprint arXiv:1912.01703. [Google Scholar]
- Tan C, Yan Z, Zhang S, Li K, Metaxas DN, 2019. Collaborative multi-agent learning for MR knee articular cartilage segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 282–290. [Google Scholar]
- Xie H, Pan Z, Zhou L, Zaman FA, Chen DZ, Jonas JB, Wang Y, Wu X, 2022. Globally optimal OCT surface segmentation using a constrained IPM optimization. Opt. Express 30 (2), 2453–2471. [DOI] [PubMed] [Google Scholar]
- Yin Y, Zhang X, Williams R, Wu X, Anderson DD, Sonka M, 2010. LOGISMOS—Layered optimal graph image segmentation of multiple objects and surfaces: Cartilage segmentation in the knee joint. IEEE Trans. Med. Imaging 29 (12), 2023–2037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu L, Cheng J-Z, Dou Q, Yang X, Chen H, Qin J, Heng P-A, 2017. Automatic 3D cardiovascular MR segmentation with densely-connected volumetric ConvNets. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 287–295. [Google Scholar]
- Zhang H, Lee K, Chen Z, Kashyap S, Sonka M, 2020. LOGISMOS-JEI: Segmentation using optimal graph search and just-enough interaction. In: Zhou K (Ed.), Handbook of Medical Image Computing and Computer Assisted Intervention. Academic Press, pp. 249–272. [Google Scholar]
- Zheng H, Perrine SMM, Pitirri MK, Kawasaki K, Wang C, Richtsmeier JT, Chen DZ, 2020a. Cartilage segmentation in high-resolution 3D micro-CT images via uncertainty-guided self-training with very sparse annotation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 802–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng H, Zhang Y, Yang L, Liang P, Zhao Z, Wang C, Chen DZ, 2019. A new ensemble learning framework for 3D biomedical image segmentation. In: AAAI Conference on Artificial Intelligence, Vol. 33. pp. 5909–5916. [Google Scholar]
- Zheng H, Zhang Y, Yang L, Wang C, Chen DZ, 2020b. An annotation sparsification strategy for 3D medical image segmentation via representative selection and self-training. In: AAAI Conference on Artificial Intelligence, Vol. 34. pp. 6925–6932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Z, Siddiquee MMR, Tajbakhsh N, Liang J, 2018. UNet++: A nested u-net architecture for medical image segmentation. In: Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. Springer, pp. 3–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou L, Zhong Z, Shah A, Qiu B, Buatti J, Wu X, 2019. Deep neural networks for surface segmentation meet conditional random fields. pp. arXiv-1906, ArXiv E-Prints. [Google Scholar]