SUMMARY
Much of systems neuroscience posits the functional importance of brain activity patterns that lack natural scales of sizes, durations, or frequencies. The field has developed prominent, and sometimes competing, explanations for the nature of this scale-free activity. Here, we reconcile these explanations across species and modalities. First, we link estimates of excitation-inhibition (E-I) balance with time-resolved correlation of distributed brain activity. Second, we develop an unbiased method for sampling time series constrained by this time-resolved correlation. Third, we use this method to show that estimates of E-I balance account for diverse scale-free phenomena without need to attribute additional function or importance to these phenomena. Collectively, our results simplify existing explanations of scale-free brain activity and provide stringent tests on future theories that seek to transcend these explanations.
In brief
Nanda et al. developed and deployed controlled computational experiments to show that aspects of excitation-inhibition balance, a core homeostatic property of brain excitability, account, without need for additional assumptions, for diverse scale-free patterns of distributed brain activity.
Graphical Abstract:
INTRODUCTION
Coordinated neuronal interactions give rise to intricate patterns of distributed brain activity. Much of systems neuroscience seeks to understand the organization and function of these patterns. Studies in the field often do so by situating these patterns within long-standing experimental or theoretical frameworks.
One such framework centers on the study of phenomena that lack typical scales of size, duration, or frequency.1–3 These scale-free phenomena show up as functions or distributions that resemble straight lines on log-log plots. Scale-free phenomena in systems neuroscience include arrhythmic power spectra,4,5 long-range temporal correlations,6 and heavy-tailed avalanche distributions7–9 of brain activity. Systems neuroscience has developed distinct explanations for the nature and origin of these phenomena.
One prominent explanation has proposed that slopes of scale-free power spectra reflect the balance of neuronal excitation and inhibition, or excitation-inhibition (E-I) balance.10 E-I balance is essential to neural function because it allows neuronal responsiveness but prevents runaway excitation.11 On a molecular level, this balance largely reflects the interaction of glutamatergic excitation, mediated by fast AMPA-receptor kinetics, and GABAergic inhibition, mediated by slow GABAA-receptor kinetics.12–14 Gao et al.15 presciently noted that these distinct excitatory and inhibitory kinetics make it possible to infer E-I balance from slopes of power spectra. Specifically, increased excitation implies preponderance of faster signaling, greater high-frequency power, and correspondingly more positive slopes, or flatter lines. Correspondingly, increased inhibition implies preponderance of slower signaling, greater low-frequency power, and correspondingly more negative slopes, or steeper lines. The link between E-I balance and slopes of spectra has been robustly observed in intracranial15,16 and extracranial17,18 electroencephalography (EEG) recordings, and with causal evidence based on optogenetic,19 chemogenetic,20 and transcranial21 stimulation. Collectively, this literature anchors one scale-free phenomenon to a neurobiological mechanism, even as it does not seek to explain the nature and origin of scale-free phenomena more generally.
Separately, another prominent explanation has proposed that diverse scale-free phenomena reflect critical dynamics.22,23 This explanation posits that brain activity self-organizes24 or homeostatically tunes25 to a critical point on the border of stable and unstable states.26,27 Theoretical considerations suggest that critical dynamics show highly varying responses to perturbations,22 and give rise to power spectra,28 scale-free avalanche distributions,7 long-range temporal correlations,6 and weak dynamical stability.29 Critical dynamics have many theoretically appealing properties, including optimized detection30,31 and transformation7,32 of sensory input. A range of studies have correspondingly linked these dynamics with optimal brain function33 and deviations from these dynamics with pathological changes, including disrupted neuronal excitability,25,34 loss of consciousness,29 and seizures.35 Collectively, this literature explains the nature and origin of diverse scale-free activity, even as the theoretical nature of such explanations makes them contested and controversial.36–40
These two major interpretations of scale-free phenomena remain unreconciled. On the one hand, studies that emphasize links between E-I balance and slopes of spectra consider other scale-free phenomena to have distinct nature or origin.2 For example, Lendner et al.41 observed that “[scale-free] long-range temporal correlations of neuronal oscillations or the size and duration of neuronal avalanches [...] likely have a different neurophysiological basis than the drop-off of the power spectrum.” On the other hand, studies that emphasize links between critical dynamics and diverse scale-free phenomena23 do not necessarily consider that critical dynamics reflect E-I balance.42 For example, Tagliazucchi et al.43 observed that “long-range temporal correlations and spectra are generic features predicted by self-organizing criticality, a theory of collective interactions that naturally accounts for many empirical observations about brain activity at different scales [including] the presence of long-range spatial correlations, [and] power-law-distributed avalanches of activity.” Finally, other studies propose that E-I balance facilitates critical dynamics44 to optimize brain function24 and in this way implicitly support both interpretations. For example, Ma et al.25 observed that “criticality [is] a computationally attractive network regime poised at a phase transition between excitation and inhibition.” Some of these studies have shown that disruptions of E-I balance—with drugs7,29,31,34 or surgery25—robustly disrupt signatures of critical dynamics. However, the resulting attribution of independent function to E-I balance and criticality risks explaining the same aspect of the data twice.45 Collectively, this lack of consensus has resulted in an extensive literature of intriguing but inconclusive findings.
Here, we reconciled this literature in three steps. First, we defined a measure of time-resolved correlation between patterns of distributed brain activity at adjacent points. We showed that this simple measure accurately reflects -based estimates of E-I balance. Second, we developed methods to sample model time series constrained by time-resolved correlation. These methods allowed us to go beyond statistical associations and test the redundancy of scale-free phenomena with estimates of E-I balance. Third, we showed that these estimates can account for diverse scale-free phenomena across species and modalities without the need to make additional assumptions about the function or importance of these phenomena. Collectively, our results simplify and unify existing explanations of scale-free phenomena in systems neuroscience.
RESULTS
We focused our analyses on recordings with intracranial EEG modalities, namely stereotactic EEG and electrocorticography (Table 1). These recordings are optimally suited to the study of scale-free phenomena by their combination of millimeter-scale spatial resolution, millisecond-scale temporal resolution, and distributed cortical coverage.46 In practice, we analyzed and modeled highly sampled datasets that each comprised approximately 1 million time points recorded from around 100 depth (stereotactic EEG) or grid (electrocorticography) cortical electrode channels. In addition to these recordings, we also followed the recent literature to test scale-free phenomena in light-sheet calcium imaging of fictively swimming zebrafish.34 The spatiotemporal resolution of light-sheet calcium imaging data provides a unique opportunity to model brain-wide activity with cellular resolution.47 Nonetheless, the large number of neurons, the small number of time points, and the low temporal resolution of these data presented unique modeling challenges, as we discuss below.
Table 1.
Properties of analyzed and modeled datasets
| Species, experiment, modality | Nodes | Tested phenomena, sampling rate | Datasets (nodes × time points) |
|---|---|---|---|
|
| |||
| Macaque monkey, anesthesia, electrocorticography48 | grid electrode channels distributed over a cortical hemisphere | critical dynamics, 1,000 Hz. We followed previous work29 that established this sampling rate as a lower bound for detection of critical dynamics in empirical data | 128× (1.5 million) 128× (1.5 million) 128× (1.5 million) 128× (1.5 million) |
| Macaque monkey, resting state, electrocorticography48 | scale-free phenomena, 1,000 Hz. | 128× (1 million) 128× (1 million) 128× (1 million) 128× (1 million) |
|
| Humans, working memory task, intracranial EEG (electrocorticography and/or stereotactic EEG)49 | grid and/or depth electrode channels distributed over parts of frontal and temporal cortex | We adopted this sampling rate for consistency with tests of dynamical phenomena. Our results were robust to tests at a lower sampling rate of 250 Hz | 84 × (1 million) 110× (764,000) 106× (840,000) 126× (812,000) |
| Humans, resting state, stereotactic EEG50 | depth electrode channels distributed over diverse cortical regions | 148× (1 million) 157× (1 million) 166× (1 million) 186× (1 million) |
|
| Zebrafish, fictive swimming, light-sheet calcium imaging51 | neurons distributed over the whole brain | some scale-free phenomena, ~3 Hz. We followed previous work34 to adopt a modified avalanche-detection procedure most suitable for analysis of brain-wide light-sheet calcium imaging data | (110,000)× 7,100 (117,000)× 5,200 |
Time-resolved correlation reflects estimates of E-I balance
We defined a measure of time-resolved correlation as , where corr is the Pearson correlation coefficient, is a vector of distributed brain activity at time point , and is an integer lag. In this section, we motivate this simple measure as a brain-wide and time-resolved analog of -based estimates of E-I balance (Figure 1A). In subsequent sections, we leverage this relationship to sample time series constrained by time-resolved correlation and in this way test the redundancy of scale-free phenomena with estimates of E-I balance.
Figure 1. Motivation for, and properties of, time-resolved correlation.
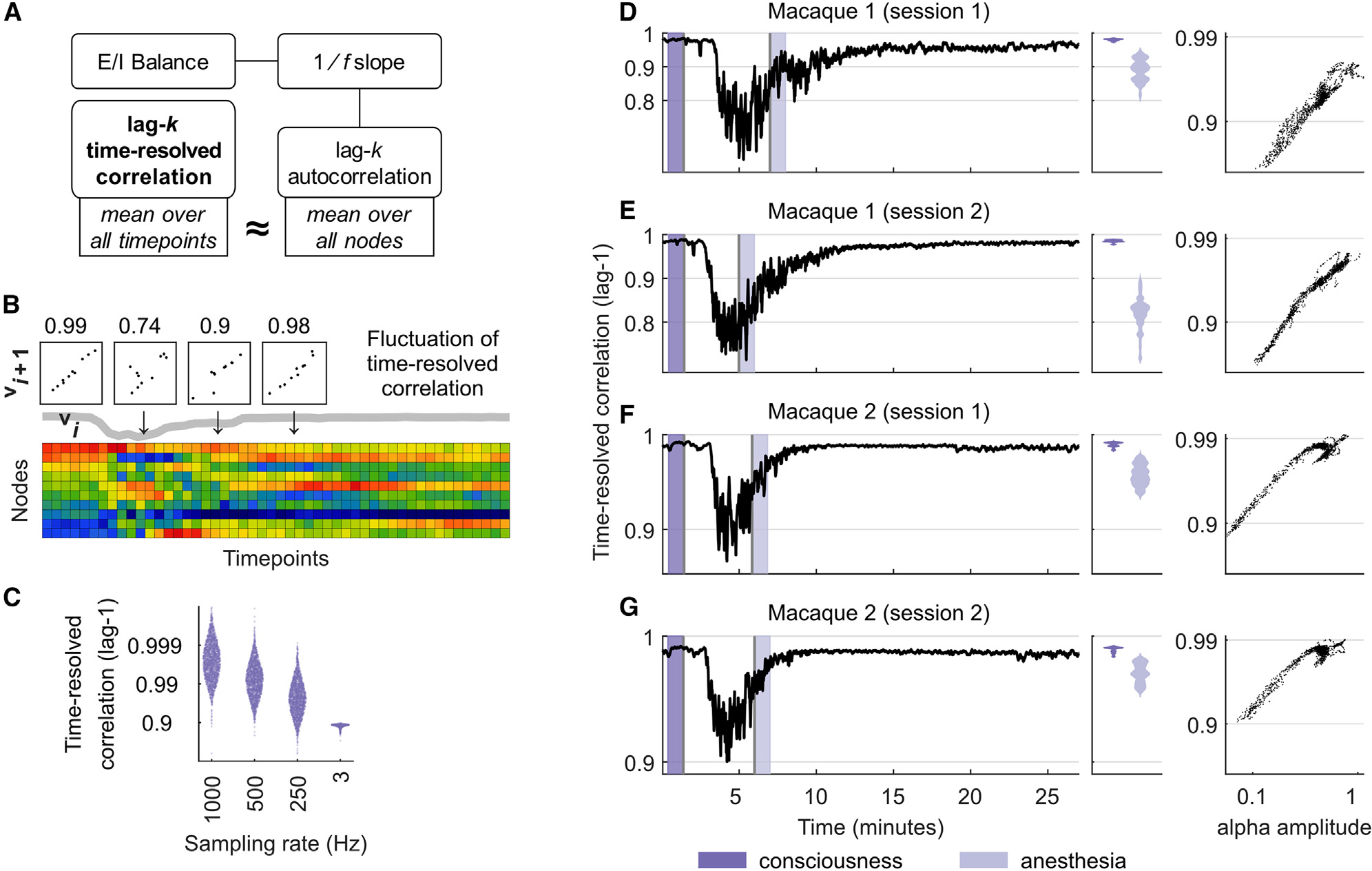
(A) Analytical links between time-resolved correlation and -based estimates of E-I balance. See the main text for details.
(B) Fluctuations of time-resolved correlation in a spatiotemporally subsampled macaque electrocorticography recording. Scatterplots show temporally adjacent patterns of distributed brain activity. Numbers denote corresponding values of time-resolved correlation, and the thick gray line shows the dynamics of time-resolved correlation over time.
(C) Distributions of lag-1 time-resolved correlation pooled across all intracranial EEG recordings (sampled at 1,000, 500, and 250 Hz), and separately for brain-wide calcium imaging data (sampled at ~3 Hz).
(D–G) Lag-1 time-resolved correlation tracks changes between consciousness and propofol anesthesia across two electrocorticography recordings of two macaque monkeys. (Left) Dark-purple intervals denote 1-min intervals immediately prior to injection of propofol. Light-purple intervals denote 1-min periods immediately following onset of anesthesia based on video observation. (Center) Violin plots of time-resolved correlation densities within shaded light-blue and dark-blue periods. (Right) Corresponding scatterplots of alpha amplitude and time-resolved correlation, averaged over 8-s windows.
We first noted that the full autocorrelation function of individual time series is directly related to the slope of power spectra of these time series, as described by the celebrated Wiener-Khinchin theorem.52 Moreover, analytical approximations of this relationship show that lag- autocorrelation for individual integers are likewise directly related to the slope of .53 At the same time, the temporally agnostic definition of autocorrelation cannot capture time-resolved changes in E-I balance, while its spatially specific definition contrasts with the brain-wide nature of some scale-free phenomena.
To overcome these shortcomings, we noted that lag- autocorrelation averaged over all nodes approximately equals lag- time-resolved correlation averaged over all time points (STAR Methods). This approximation only holds for averaged quantities—the non-averaged versions of these quantities are incommensurate because time-resolved correlation is defined on time points, while autocorrelation is defined on nodes. Figure 1A summarizes the links between time-resolved correlation and -based estimates of E-I balance, while Figure 1B illustrates the dynamics of this measure in a subsampled macaque electrocorticography recording. Figure 1C shows that lag-1 time-resolved correlation is unimodally distributed close to its maximal value of 1, reflecting gradual changes in distributed brain activity over time. The measure gradually drops with lower sampling rates and is considerably lower for calcium imaging data. Figures S1–S4 show the relationship of time-resolved correlation and other basic properties of the neurophysiological signal.
We next directly tested the link between time-resolved correlation and changes in E-I balance in four electrocorticography recordings of macaque monkeys across consciousness and propofol anesthesia. Propofol anesthesia alters E-I balance in large part by potentiating inhibitory GABAA receptors.54 Previous analyses of this macaque dataset used it as a benchmark to test the effects of -based estimates of E-I balance.15 Other analyses of these data have linked these changes to cortex-wide reductions to other electrophysiological properties, including the amplitude of alpha oscillations.55
Figures 1D–1G shows that lag-1 time-resolved correlation robustly tracked these estimates across all recordings. The median [95% uncertainty interval] correlation pooled over the four recordings was 0.987 [0.977, 0.992] in the 1-min interval preceding injection of propofol and 0.938 [0.767, 0.978] in the 1-min interval immediately following the onset of anesthesia, based on video observation29 (, Wilcoxon rank-sum test). Indeed, this metric dropped to even lower values at the peak effect time of propofol, roughly 2 min after injection.56 These changes strongly correlated with previously reported reductions in alpha amplitude in this dataset.55 Moreover, the smaller relative drop of this correlation in monkey 2 (Figures 1F and 1G) matched previous observations that this monkey was not fully anesthetized.57 These findings provide additional evidence for the link between time-resolved correlation and -based estimates of E-I balance.
Sampling time series constrained by time-resolved correlation
We next tested the redundancy of scale-free phenomena with time-resolved correlation, and by extension with estimates of E-I balance. Studies to date have not performed this important test. Instead, studies have typically tested the presence of scale-free phenomena in model time series constrained by trivial properties of brain activity, generated through simple randomization (shuffling) of empirical time series. Such tests, however, do not constitute rigorous statistical evidence for the significance of scale-free phenomena.37,58
Here, we designed more rigorous tests by developing a method for sampling time series constrained by time-resolved correlation, variance, and mean. Our method is unbiased and efficient: it samples data with no extraneous assumptions, and scales to long neurophysiological recordings. We informally describe the method here and provide extensive mathematical detail in the STAR Methods.
We formulated the sampling problem as a set of underdetermined sets of equations. We solved these equations sequentially, by using the solution of equation at time to define the equation at time (Figure 2A). Our problem then reduced to the sampling of brain activity patterns at time constrained by empirical correlation of these patterns to brain activity patterns at time . We solved this problem by expressing it as a system of linear equations. We computed the nullspace of the coefficient matrix, , and used this nullspace to parameterize the solution space to our problem. The schematic in Figure 2A shows the geometry of this space in three dimensions. The colored plane in this schematic represents the solution space, such that each point in this plane represents a solution to our problem. We uniformly sampled vectors from this solution space by expressing these vectors as the sum of two vectors: , a unique minimum-norm solution, and , where is a uniformly sampled weighting vector and is a scaling parameter. The sequential nature of this sampling made our method efficient relative to randomization methods that require the simultaneous solution of all constraints. Specifically, our method scaled linearly with the number of time points and quadratically with the number of nodes (STAR Methods) and was therefore especially well suited to long neurophysiological recordings we considered in this work.
Figure 2. Method to sample time series constrained by time-resolved correlation.
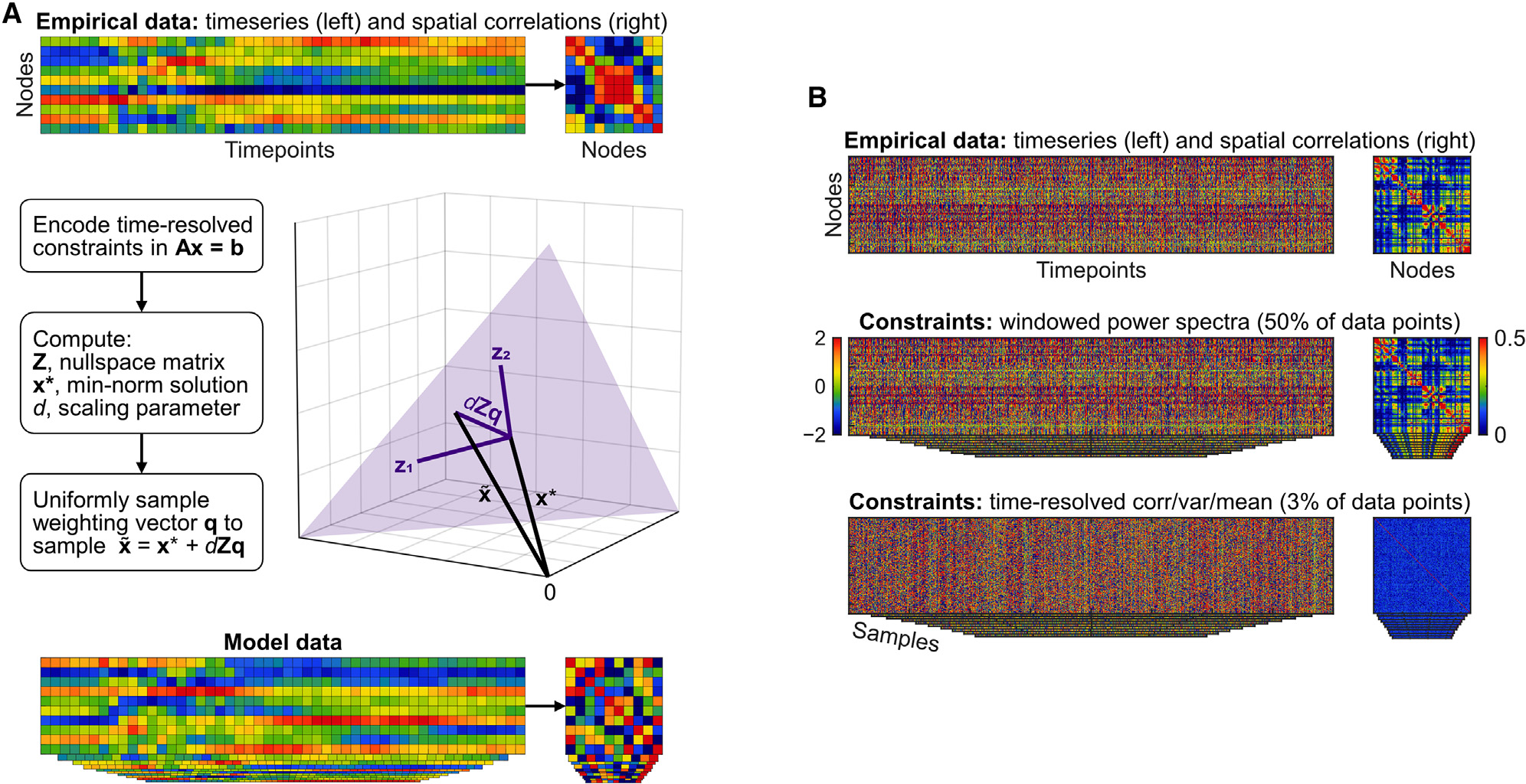
(A) Flowchart and visualization of nullspace sampling. See the text for an informal description, and STAR Methods for mathematical detail.
(B) Properties of the windowed phase-randomization model, and the time-resolved correlation, variance, and mean model. Both models performed similarly well, but time-resolved correlation, variance, and mean constraints were fewer in number and easier to interpret. These constraints also generated data that were devoid of spatial correlations and in this way were considerably different from empirical recordings.
Summary of models
Our primary model was constrained by time-resolved correlation, variance, and mean. We tested this model against four competing models defined with nullspace sampling, phase randomization, and frame-randomization methods. We now summarize the properties of these models in turn.
Nullspace-sampling models
Our primary model was constrained by lag- time-resolved correlation, variance, and mean. While our study primarily focuses on the importance of time-resolved correlation, nullspace sampling cannot constrain this property without also constraining the time-resolved variance and mean. Therefore, and in order to test the effects of time-resolved correlation relative to these more basic properties, we also considered a control model constrained by time-resolved variance and mean but not by time-resolved correlation. We set for all analyses except for analyses of calcium imaging data, as discussed below.
Phase-randomization models
We considered a popular6,29,57,59–61 phase-randomization method that constrains a large, and somewhat indiscriminate, number of empirical features, including power spectra of each node and lagged correlations between all pairs of nodes across all possible integer time lags.62 Despite the many constraints, a default version of this method is not time resolved. To circumvent this problem, we also considered a windowed extension of this method in which we segmented individual recordings into hundreds of windows and used phase randomization to sample data independently within each window.
Frame-randomization models
For completeness, we also considered a simple frame-randomization method that constrains exact brain activity patterns within each individual time frame but randomizes the order of the time frames.
In what follows, we found that time-resolved correlation and windowed phase-randomization models, but not the other evaluated models, accounted for diverse scale-free phenomena. Figure 2B illustrates these models relative to empirical data. Note that windowed phase-randomization constraints amounted to 50% of data points (STAR Methods), were difficult to interpret, and generated data that were quite similar to empirical recordings. By contrast, time-resolved correlation, variance, and mean constraints amounted to 3% of data points (STAR Methods), were linked with estimates of E-I balance, and generated data that were considerably different from empirical recordings. For these reasons, much of our subsequent discussion focuses on time-resolved correlation, variance, and mean, as well as its control comparisons with time-resolved variance and mean.
Time-resolved correlation accounts for critical dynamics
We first evaluated the extent to which time-resolved correlation, variance, and mean constraints induced weak dynamical stability, a signature of critical dynamics.63 We followed previous work to estimate dynamical stability using the eigenvalue spectrum of a time-resolved vector autoregressive model,26,29,64 a locally linear approximation of distributed brain activity. Theory predicts that weakly stable dynamics balance on the edge of order and disorder and have largest eigenvalues with magnitudes that approach 1. Conversely, strongly stable dynamics decay quickly and have largest eigenvalues with smaller magnitudes. Correspondingly, previous stability analyses of macaque electrocorticography recordings from Figures 1D–1G linked consciousness with weakly stable dynamics and propofol anesthesia with strongly stable dynamics.29,57,65
Figure 3 (see also Figures S5–S8) shows that time-resolved correlation, variance, and mean constraints accounted for these dynamical changes. We quantified dynamical stability by the median magnitude of the 5% largest eigenvalues. Stability estimates pooled across four empirical recordings showed that this index had a median [95% uncertainty interval] of 0.996 [0.989, 0.998] during an interval of consciousness and 0.985 [0.969, 0.993] during an interval of anesthesia. Similarly, time-resolved correlation, variance, and mean constraints accounted for weakly stable dynamics of 0.994 [0.992, 0.996] during consciousness and more strongly stable dynamics of 0.985 [0.936, 0.993] during anesthesia. This difference in stability fell within the empirical range (p = 0:492 that the difference in stability of model data was at least equal to the difference in stability of empirical data). By contrast, time-resolved variance and mean constraints alone resulted in strongly stable dynamics across both consciousness (0.560 [0.541, 0.586]) and anesthesia (0.612 [0.583, 0.647]), implying the importance of time-resolved correlation for critical dynamics.
Figure 3. Time-resolved correlation accounts for changes in dynamical stability across consciousness and propofol anesthesia.
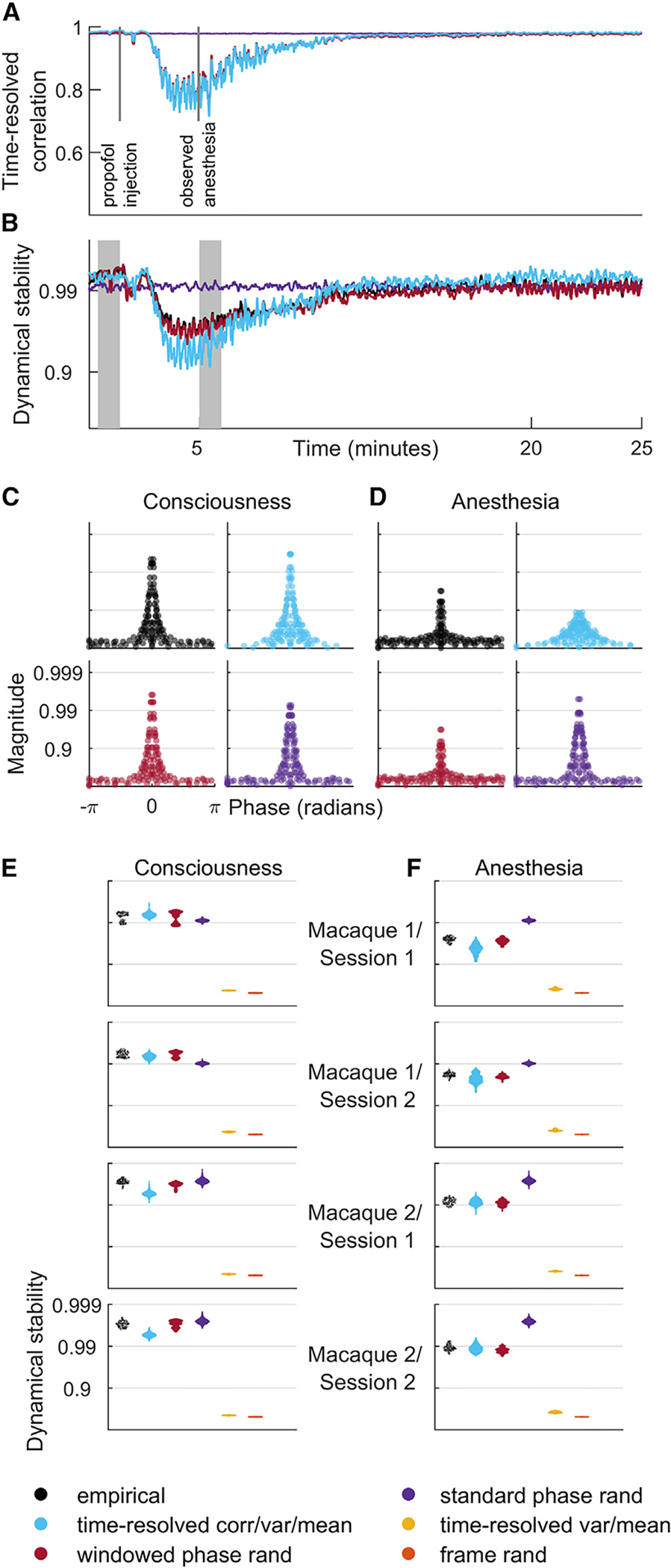
(A) Fluctuations of time-resolved correlation for model data of a representative electrocorticography recording.
(B) Dynamical stability index, the median value of the 5% largest eigenvalues, for the same recording. Note the strong correlation of time-resolved correlation with dynamical stability.
(C and D) Phase and magnitude of eigenvalues of a vector autoregressive model fit to a single window from periods of consciousness and anesthesia (shaded intervals in B, equivalent to intervals in Figures 1D–1G). Note the anesthesia-associated drop of dynamical stability in model data constrained by time-resolved correlation.
(E and F) Dynamical stability index across all empirical and model data, pooled over all recordings and averaged over all windows denoting periods of consciousness (E) and anesthesia (F).
Results for model data were derived using 50 samples for each model of each dataset. For completeness, Figures S5–S8 show individual results for all model datasets.
Separately, windowed phase-randomization constraints accounted for weakly stable dynamics. Note, however, that this result is somewhat trivial because these constraints are expected to preserve the autoregressive coefficients, and therefore the eigenvalues, by definition. By contrast, standard (non-windowed) phase-randomization constraints accounted for weakly stable dynamics (0.994 [0.989, 0.998]) during consciousness but showed negligible change in stability (0.994 [0.989, 0.998]) during anesthesia (p < 0:001).
Time-resolved correlation accounts for scale-free phenomena
We next evaluated the extent to which time-resolved correlation accounted for power-frequency relationships and long-range temporal correlations, two commonly studied scale-free phenomena. denotes the decay of spectral power as a function of frequency. This scale-free, or arrhythmic, power-frequency relationship is distinct from neuronal oscillations, which represent narrow peaks in frequency spectra.
Figures 4A–4C show that, in line with previous observations,4,66,67 we found robust scaling of spectral power in a broad 1- to 80-Hz frequency range. Specifically, we found that empirical data across all intracranial EEG recordings showed a median [95% uncertainty interval] exponent values of 2.788 [1.592, 4.156]. In line with our theoretical considerations (Figure 1A), time-resolved correlation, variance, and mean constraints accounted for this scaling, with corresponding exponents of 2.247 [1.885, 2.900] across all intracranial EEG recordings. The values of these exponents were considerably more uniform because time-resolved constraints are spatially agnostic. Nevertheless, these values were in line with empirical values (p = 0:228 that model exponents were at least equal to corresponding empirical exponents). By contrast, time-resolved variance and mean constraints alone did not result in scaling (Figures 4A–4C and S9–S20), implying the importance of time-resolved correlation for this scaling.
Figure 4. Time-resolved correlation accounts for empirical scaling and long-range temporal correlations.
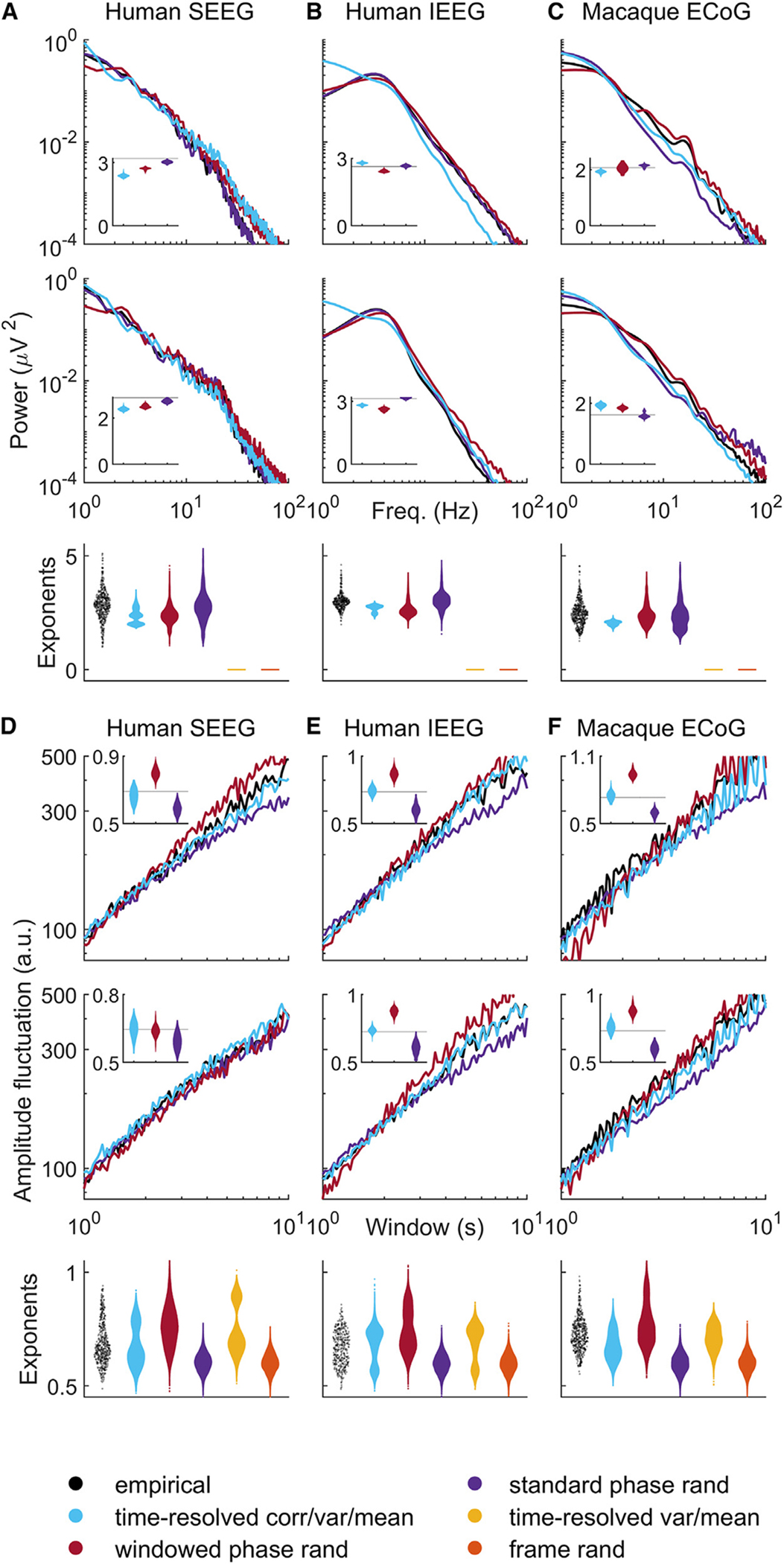
(A–C) Top two panels show scaling of spectral power as a function of frequency for two channels of representative intracranial EEG recordings. Insets show violin plots of slope exponents benchmarked against empirical exponents (solid black lines). Bottom panels show violin plots of exponents pooled across all channels and all empirical and model datasets.
(D–F) Top panels show scaling of time-resolved amplitude as a function of window for two representative channels. Insets show violin plots of scaling exponents, benchmarked against empirical exponents (solid black lines). Bottom panels show violin plots of all exponents pooled across all channels and all empirical and model datasets. Results on model time series were derived using 50 samples for each model of each dataset. For completeness, Figures S9–S20 show individual results for all empirical and model datasets. SEEG, stereotactic EEG; IEEG, intracranial EEG; ECoG, electrocorticography.
We next considered long-range temporal correlations, scale-free phenomena that track the statistical self-similarity of long time series. Typically, these correlations are defined by the scaling exponent of mean fluctuations in the amplitude envelope in alpha or beta frequency bands, using detrended fluctuation analysis, a method especially suitable to analysis of non-stationary time series.68 The scaling exponent between window sizes and mean fluctuations indexes the presence of statistical self-similarity. Values of this exponent considerably larger than 0.5 denote scale-free (fractal-like) structure. By contrast, values close to 0.5 denote random (white-noise-like) structure.6
Figures 4D–4F and S9–S19 show robust power-law scaling for mean fluctuations in amplitude for all empirical datasets in the alpha frequency band (results were similar for the beta frequency band, Figure S20). The scaling exponents for empirical datasets were within the range previously reported in the literature. Specifically, we found that empirical recordings across all intracranial EEG modalities showed a median [95% uncertainty interval] exponent value of 0.691 [0.549, 0.884].
Time-resolved correlation, variance, and mean constraints accounted for similar exponents across all intracranial EEG recordings (0.671 [0.544, 0.825], p = 0:430 that model exponents were at least equal to corresponding empirical exponents). In this case, however, time-resolved variance and mean constraints alone also resulted in similar exponents (0.711 [0.559, 0.914], p = 0:632), implying that time-resolved correlation was not important for this result.
Time-resolved correlation accounts for avalanche statistics
Neural avalanches are transient periods of coordinated activity between groups of neurons or brain regions. The study of avalanche dynamics plays a prominent role in the theory of neural criticality. One commonly studied phenomenon in this literature is the power-law scaling of avalanche size and duration distributions. Recent work has also emphasized more specific signatures of criticality, including power-law relationships between size and duration exponents,69 as well as shape collapse, a universal scaling relationship of avalanche phase with activity.34,69,70 Shape collapse, in particular, is a strict criterion of neural criticality, obtained through averaging hundreds or thousands of individual avalanches. Theory predicts that, at criticality, collapsed temporal profiles of avalanches will converge to a universal shape independent of avalanche duration.38,69,70
We first evaluated the presence of avalanche phenomena in all intracranial EEG datasets. Figure 5 shows robust signatures of power-law scaling for avalanche sizes, durations, and size-duration relationships. Specifically, across all intracranial EEG datasets, avalanche sizes decayed with a median [95% uncertainty interval] power-law exponent of 1.310 [1.100, 1.390]. Correspondingly, avalanche durations decayed with an exponent of 1.280 [1.000, 1.390]. Finally, avalanche sizes scaled as a function of avalanche durations with an exponent of 1.487 [1.144, 1.863].
Figure 5. Time-resolved correlation accounts for avalanche statistics.
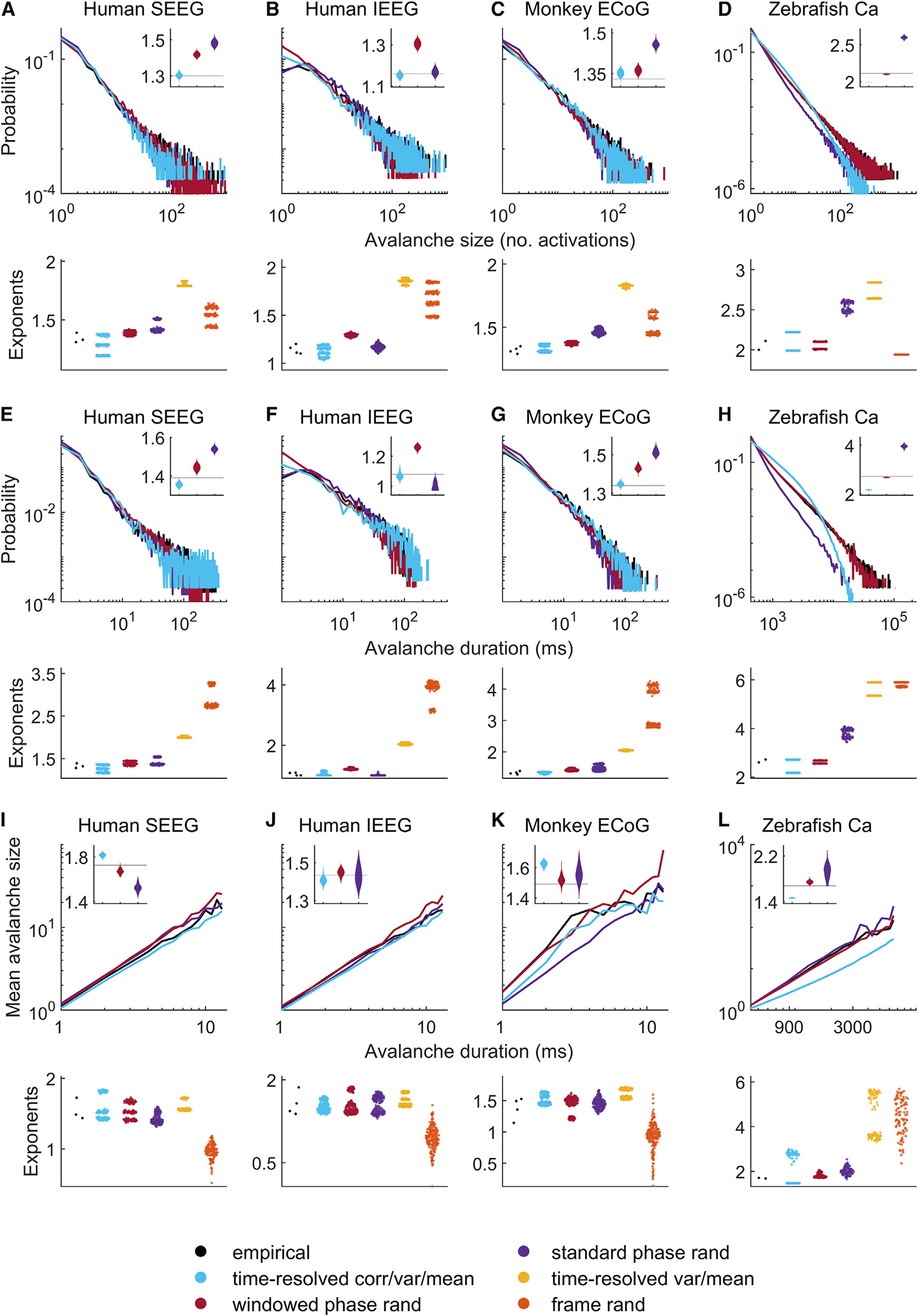
(A–D) Avalanche size probability distributions.
(E–H) Avalanche duration probability distributions.
(I–L) Scaling of avalanche size and duration exponents.
Inset violin plots show normalized distributions of model exponents, benchmarked against empirical exponents (solid black lines). Bottom panels show violin plots of all empirical and model exponents pooled across all empirical and model datasets. Results on model data were derived using 50 samples for each model of each dataset. For completeness, Figures S21–S33 show individual results for all empirical and model datasets. SEEG, stereotactic EEG; IEEG, intracranial EEG; ECoG, electrocorticography; Ca, calcium imaging.
Time-resolved correlation, variance, and mean constraints accounted for similar avalanches with exponents of 1.290 [1.050, 1.377] (p = 0:465 that model exponents were at least equal to corresponding empirical exponents) for avalanche sizes, 1.260 [1.000, 1.360] (p = 0:515) for avalanche durations, and 1.519 [1.397, 1.823] (p = 0:620) for scaling of size as a function of duration. By contrast, time-resolved variance and mean constraints resulted in exponents that were considerably different from observed empirical values of avalanche sizes (1.830 [1.790, 1.890], p > 0:999) and durations (2.030 [1.990, 2.090], p > 0:999), but not for scaling of size as a function of duration (1.569 [1.512, 1.787], p = 0:758). This implies the importance of time-resolved correlation for a substantial part of this result.
Figure 6 shows that empirical data exhibited avalanche shape collapses indicative of universal scaling. Time-resolved correlation, variance, and mean constraints accounted for similar shape collapses. The mean avalanche temporal profiles in these model data all peaked at similar times. Indeed, the variance between rescaled avalanche shapes had a median [95% uncertainty interval] of 0.447 [0.187, 0.747] for empirical data and 0.516 [0.228, 0.777] (p = 0:631 that model variance was at least equal to corresponding empirical variance) for model data constrained by time-resolved correlation. Time-resolved variance and mean constraints produced a similar result (1.569 [1.512, 1.787] p = 0:758) although, as Figure 6 shows, shape collapses were more variable in human EEG recordings.
Figure 6. Time-resolved constraints account for universal shape collapse.
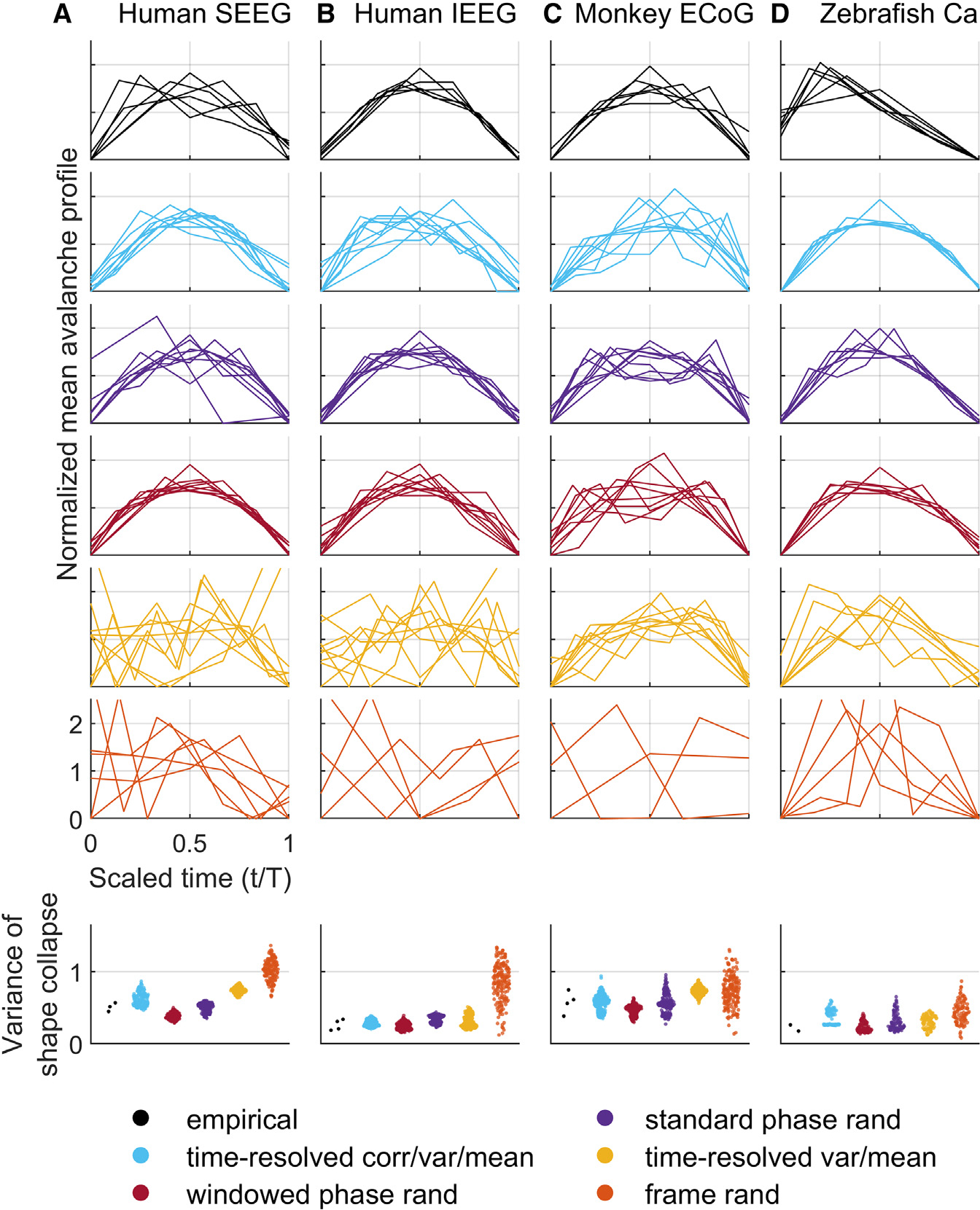
(A–D) Shape collapses: scaling of mean temporal profiles with avalanche activity. Bottom panels show violin plots of all empirical and model variance between avalanche scaling profiles (lower is better). Results on model data were derived using 50 samples for each model of each dataset. For completeness, Figures S21–S33 show individual results for all empirical and model datasets. SEEG, stereotactic EEG; IEEG, intracranial EEG; ECoG, electrocorticography; Ca, calcium imaging.
Time-resolved correlation of brain-wide calcium imaging data
Finally, we sought to evaluate scale-free phenomena in calcium imaging recordings of fictively swimming zebrafish. These data provide an unmatched spatiotemporal resolution of brain-wide cellular activity.47 At the same time, the distinct nature of these data (Table 1) present several methodological challenges. Specifically, in contrast to intracranial EEG recordings, brain-wide calcium imaging recordings had many more nodes (approximately 100,000), many fewer time points (approximately 6,000), and were imaged at a relatively low frequency (approximately 3 Hz). The large number of nodes imposed memory requirements which precluded the use of nullspace sampling and required the adoption of memory efficient but slower constrained randomization methods.71,72 The small number of time points limited our evaluation to avalanche phenomena, in line with recent work.34 The low-frequency imaging resulted in considerably lower values of time-resolved correlation (Figure 1C). We compensated for this drop in correlation by constraining time-resolved correlation between a single frame and its four adjacent neighbors. Finally, standard avalanche-detection methods in these data resulted in a trivial detection of a single never-ending brain-wide avalanche. We compensated for this problem by adopting a spatially contiguous definition of avalanches,34 which penalizes spatially non-specific constraints, such as time-resolved correlation.
These caveats aside, our modeling results on these datasets were generally in line with results on intracranial EEG data. Figures 5, S32, and S33 show that empirical calcium imaging avalanche sizes decayed as power laws with exponents 2.110 and 2.000, avalanche durations decayed as power laws with exponents 2.720 and 2.600, and avalanche sizes scaled as a function of durations with power-law exponents of 1.706 and 1.678. Time-resolved correlation, variance, and mean constraints accounted for similar median [95% uncertainty interval] values of these exponents. Specifically, they resulted in an avalanche size exponent of 2.105 [1.990, 2.220], a duration exponent of 2.445 [2.160, 2.720], and a size-duration scaling exponent of 1.893 [1.460, 2.947] (we do not report p values here because we only have two values of empirical exponents). Likewise, shape-collapse results were largely in line with those observed on intracranial EEG datasets (Figures 6, S32, and S33).
DISCUSSION
An extensive literature in systems neuroscience has probed the origin, nature, and function of scale-free phenomena. One part of this literature has narrowly interpreted one scale-free phenomenon, the slope of spectrum, in terms of E-I balance. Another part has broadly interpreted diverse scale-free phenomena in terms of critical dynamics. Other parts of the literature have attributed distinct or complementary functions to E-I balance and critical dynamics.
Here we reconciled these distinct interpretations in three ways. First, we analytically and numerically linked -based estimates of E-I balance with time-resolved correlation. Second, we developed methods to sample time series constrained by time-resolved correlation and in this way tested the redundancy of scale-free phenomena with estimates of E-I balance. Third, we showed that these estimates accounted for diverse scale-free phenomena across modalities and species.
Our results imply that diverse scale-free phenomena can arise as a byproduct of aspects of E-I balance. E-I balance plays an essential role in survival, much like core body temperature and many other homeostatic mechanisms. By contrast, scale-free phenomena have an uncertain function that is difficult to resolve through experimental manipulation, in large part because such manipulation primarily perturbs changes in E-I balance.7,25,29,31,34 These considerations suggest that the attribution of function to scale-free phenomena, without additional evidence for this function, is premature because it violates the principle of scientific parsimony.73 At the same time, our methods offer a natural future way to probe this question in more detail. Specifically, future high-resolution recordings in behaving animals can falsify our interpretation by discovering E-I regimes compatible with healthy function but not with scale-free phenomena. The discovery of such a regime would imply that scale-free phenomena occur independently of E-I balance and in this way support an independent function for these phenomena.
Similarly, our results offer to simplify existing theoretical frameworks in systems neuroscience. First, these results provide a roadmap for future neurobiological explanations of scale-free phenomena. Specifically, we propose that ongoing discovery of molecular, cellular, or circuit mechanisms of E-I balance will automatically shed light on similar mechanisms of scale-free phenomena.11,13,74 Second, our results provide an additional perspective on regional variation of scale-free activity.4,15,41 This variation is related, although not equivalent, to the notion of hierarchy of cortical time scales.75–79 Our results help explain this regional variation by noting that global, and spatially agnostic, changes in time-resolved correlation automatically give rise to scale-free regional activity. These findings suggest that the focus on the regional contribution to these changes may be equally judicious, and more parsimonious, in the investigation of this activity. Third, our results have considerable implications for translational literature that centers on the study of scale-free phenomena.80,81 Much of this literature seeks to find alterations in scale-free phenomena across healthy and diseased brain states.29,34,35 Our findings show that time-resolved correlation can offer a unified interpretation of these outwardly distinct biomarkers.
Finally, our results were made possible by the development of an efficient method to sample model data with time-resolved constraints. As systems neuroscientists come up against bigger and more highly resolved neurophysiological datasets, the development of similar methods will become increasingly important for rigorous analysis and modeling of these data. Ultimately, we consider that widespread adoption of such methods will be necessary to enable unified and cohesive explanations of distributed brain activity.
Limitations of the study
Our study has three main limitations. First, our sampling method constrains time-resolved correlation, variance, and mean. Therefore, by definition, the method also constrains time-resolved covariance, cosine similarity, and dot product. Future studies should evaluate the relationship of these related, yet distinct, measures of similarity with estimates of E-I balance and scale-free phenomena. Second, time-resolved correlation varies with the temporal and spatial resolution of individual recordings. Future studies should test our results across a range of spatial and temporal resolutions. Third, the slope of spectrum is an indirect estimate of E-I balance. Future studies should test the relationship between time-resolved correlation and more direct estimates of E-I balance, ideally excitatory and inhibitory currents in circuit recordings from model organisms.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources should be directed to Mika Rubinov (mika.rubinov@vanderbilt.edu).
Materials availability
No new materials were generated as part of this project.
Data and code availability
Data from this study are available upon request.
The main analysis code is publicly available (key resources table).
Any additional information is available from the lead contact upon request.
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Software and algorithms | ||
|
| ||
| MATLAB | The Mathworks | www.mathworks.com |
| Python | Python Software | www.python.org |
| Custom software | This study |
github.com/AdityaNanda/time_resolved_correlation
https://doi.org/10.5281/zenodo.7604194 |
| FieldTrip Toolbox | Oostenveld et al., 201182 | github.com/fieldtrip/fieldtrip |
| FOOOF | Donoghue et al., 20205 | github.com/fooof-tools/fooof |
| ARfit | Schneider et al., 200183 | github.com/tapios/arfit |
| Voluseg | Mu et al.51 | github.com/mikarubi/voluseg |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Macaque electrocorticography (neurotycho)
Data were collected at the Laboratory for Adaptive Intelligence, Brain Science Institute, RIKEN.48,84 Electrocorticography recordings were made from two male macaque monkeys before, during, and after administration of propofol anesthesia. Grid electrodes were implanted on the frontal, parietal, temporal, and occipital lobes. These data are publicly available from http://www.neurotycho.org.
Human intracranial EEG
Data were acquired at the University of California Irvine Hospital.49 Intracranial EEG recordings were made from adult patients with epilepsy performing a visuospatial working memory task. Grid and/or depth electrodes were implanted in frontal and medial temporal lobes. These data are publicly available from http://www.crcns.org.85
Human stereotactic EEG
Data were acquired at Vanderbilt University Medical Center.50 Stereotactic EEG recordings were made from adult patients with epilepsy, one day after electrode implantation and before medication wean. The patients were instructed to keep their eyes closed and remain awake for 20 min. Depth electrodes were implanted in cortical regions, depending on suspected seizure origin.
Zebrafish calcium imaging
Data were acquired at Janelia Research Campus, Howard Hughes Medical Institute.51 Light-sheet calcium imaging recordings were made from fictively swimming larval zebrafish embedded in agarose. The fish swam against a fixed-velocity one-dimensional moving stripe pattern, which represented virtual water flow. The imaging spanned almost all brain neurons expressing a genetically encoded calcium indicator (GCaMP6f).
Data preprocessing
Electrophysiology
We analyzed all recordings at their original sampling frequency of 1000Hz. Dynamical stability analyses necessitated this high sampling rate.29,57 All recordings were highpass filtered with a cutoff of 0.5Hz using the bandpassfilter function from Fieldtrip toolbox.82 In addition, macaque electrocorticography data were notch-filtered at 50Hz and 100Hz to remove line noise. Likewise, human stereotactic EEG and intracranial EEG data were notch-filtered at 60Hz and 120Hz to remove line noise.
Calcium imaging
All images were motion corrected, and cells were segmented in contiguous and overlapping three-dimensional blocks, using non-negative matrix factorization with sparseness constraints.51 The resulting demixed and denoised cell segmentations showed higher signal-to-noise ratio relative to raw pixel time series. Our segmentation software is publicly available (key resources table).
METHOD DETAILS
Definition of time-resolved correlation
All our analyses used mean-centered (demeaned) node time series. We defined lag- time-resolved correlation at timepoint as
where denotes the -dimensional activity of all nodes at timepoint and denote the mean and norm of this activity, and is an integer lag. Note that lag- time-resolved correlation averaged over all timepoints relates to lag- autocorrelation averaged over all nodes, as follows,
| (Equation 1) |
where is lag- autocorrelation of node . This approximation holds because both quantities in Equation 1 represent averaged dot products, normalized either over the activity of all nodes at a single timepoint (time-resolved correlation), or over the activity of a single node at all timepoints (node autocorrelation). However, this relationship holds only for the averaged quantities – the non-averaged versions of these quantities are incommensurate because time-resolved correlation is defined on timepoints, while autocorrelation is defined on nodes.
Nullspace sampling: General formulation
Our method uses insights from linear algebra to uniformly sample the solution space of an underdetermined linear system. This method allows us to constrain time-resolved correlation, variance, and mean by encoding these constraints in systems of linear equations. We first describe the general formulation of nullspace sampling and then describe specific algorithms for generating time-resolved constraints for the models in this study.
Consider a linear system
| (Equation 2) |
where is an empirical data vector, is a matrix that encodes features of interest, and denotes empirical values of these features. Let us assume, without loss of generality, that the features of interest are linearly independent or, equivalently, that the matrix has rank .
Our method samples vectors that match empirical features of interest, such that
where the operator denotes model (rather than empirical) vectors.
Note that the number of features will in general be much smaller than the number of elements . This implies that the system in Equation 2 has infinitely many solutions. The space of these solutions is affinely spanned by orthonormal unit vectors that form the basis of the nullspace of the matrix , such that and , where is the identity matrix and is a matrix of zeros.86 Let us now define as points on this solution space,
| (Equation 3) |
where is the unique minimum-norm solution, is a scaling constant, and is a unit-norm weighting vector.
Here, we sampled in two steps. First, we computed the nullspace matrix , and the minimum-norm solution where † denotes the Moore-Penrose pseudoinverse.86 We also computed the scaling parameter to restrict our sampling to all with empirical norm,. Note that, by the fundamental theorem of linear algebra, the minimum norm solution is orthogonal to all column vectors in . Because the additive components in Equation 3 are orthogonal, and because , we used Pythagoras theorem to set and thereby ensure that .
Second, we uniformly sampled weighting vectors from the dimensional standard normal distribution, and rescaled these vectors to have unit norm. This sampling guarantees to produce uniformly distributed random samples of .87
Nullspace sampling: Time-resolved correlation
We used a sequential variant of nullspace sampling to efficiently sample data constrained by lag- time-resolved correlation, variance, and mean. For , we first sampled to have empirical mean and norm. We then sampled , to have empirical mean, norm, and dot product with . We encoded these constraints as,
| (Equation 4) |
where 1 denotes a vector of ones.
In practice, this sequential generation of model time series required nullspace matrices with approximately elements, and scaled linearly with the number of timepoints . We computed these nullspaces using the singular value decomposition, with computational complexity of . Since we iteratively solved equations, the computational complexity for our algorithm is . In practice, this approach was feasible for intracranial EEG data , where it outperformed constrained randomization methods. On the other hand, the approach was not feasible for brain-wide cellular calcium imaging datasets , which required the use of constrained randomization methods. 71,72,88
Nullspace sampling: Time-resolved variance and mean
To constrain variance and mean alone, we sampled such that
| (Equation 5) |
In this special case, we derived an analytical expression for the nullspace ,
where and denote solutions to the following set of equations:
One can directly verify that this linear system has a unique solution which ensures that is an orthonormal nullspace of . Specifically, the first equation above ensures that , while the second and third equations ensure that .
Phase randomization
We generated phase-randomized model data using a well-known algorithm from the physics and neuroscience literature. 60,62 Briefly, we first used the Fourier transform to compute the phase and amplitude of each time series. We then rotated the phase of all nodes at each frequency by a random complex variable with uniformly distributed in . Finally, we obtained model time series by computing the inverse Fourier transform of these phase-randomized data. This method is guaranteed to generate maximally random data that preserve nodal power spectra and full cross-correlation structure.
For the windowed phase-randomized model, we first partitioned each time series into non-overlapping windows of length 500 timepoints . We chose this window length for consistency with dynamical stability analyses (below). We then applied the phase randomization algorithm to each windowed section of the time series. For zebrafish calcium imaging data, the low frequency of calcium imaging required us to adopt a different window length of 50 timepoints .
Number of model constraints
We estimated the number of constraints in nullspace-based and phase-randomization based models. For this estimation, we assumed that each dataset has nodes and timepoints. Nullspace-based models constrain the mean, variance, and optionally the covariance, at each timepoint. This results in or , or at most 2 – 3% of all data points. By contrast, phase-randomization based models constrained amplitudes for each node, and therefore 50% of all data points.
QUANTIFICATION AND STATISTICAL ANALYSIS
Dynamical stability analysis
We performed linearized dynamical stability analysis within temporally local time windows. We first divided the time series , into non-overlapping windows of length .29 We then fitted a time-invariant vector autoregressive model, representing a linear dynamical system, separately for time series at each window . The vector autoregressive model is defined as,
For each window, we first estimated the system matrix using least squares, 89 and then computed the eigervalues of this matrix, . These eigenvalues tracked the dynamical stability of this system. Specifically, the presence of all eigenvalues strictly inside the complex unit circle , for implies that the system is asymptotically stable, such that external perturbations will decay exponentially. In contrast, the presence of some eigenvalues outside the complex unit circle implies that the system is unstable and that external perturbations will grow exponentially. Finally, the presence of eigervalues on the complex unit circle , implies that the system is weakly stable and external perturbations will produce diverse responses29
Amplitude of alpha oscillations
We estimated the amplitude of alpha oscillations in each region of the macaque dataset as follows. First, we normalized the regional time series to have zero mean and unit standard deviation. Second, we divided this time series into 8 s non-overlapping windows. Third, we filtered the signal used 1 s Hanning windows and a bandpass finite-impulse-response filter with frequencies 8 and 12Hz (implemented in Fieldtrip toolbox). Finally, we computed the Hilbert transform of the filtered signal and derived the mean amplitude over all regions within each window.
Power spectral analysis
We used Welch’s method to characterize the power spectral density over a relatively large frequency range between 1 and 80Hz. In brief, power spectra were computed for each channel separately, using windowed time series convolved with Hanning windows of length 6 s and then averaged over all windows.
There has been significant recent progress in the development of methods for estimating slopes of neural power spectra. Unlike earlier methods, such as coarse grained spectral analysis, 4 which were strictly applicable only to completely aperiodic signals, 90 more recent methods, such as IRASA 90 and Fitting Oscillations and One Over f (FOOOF), 5 are able to estimate both periodic and aperiodic signal components.
Here, we adopted FOOOF to estimate the spectral exponent of empirical and model time series. Formally, the algorithm estimates
where is the power spectrum, is the frequency of interest, is the scaling exponent, is the offset frequency, and is the knee frequency. 5 More details about the application of this method to the study of neural spectra is provided in a recent study. 18 In this study, we set the maximum number of peaks to 6 , and the minimum peak height to 0.15.
Long-range temporal correlation analysis
Following initial preprocessing, we used the Fieldtrip toolbox to bandpass filter the data in the alpha (8–12Hz) frequency band, and applied the Hilbert transform to extract time-resolved amplitude at each electrode. We then used detrended fluctuation analysis to estimate amplitude scaling coefficients from these time-resolved amplitude time series. 68 Detrended fluctuation analysis is especially suitable for analysis of neurophysiological time series because it is unaffected by nonstationary structure. In practice, given a time series , we first defined the cumulative sum as follows,
where denotes the mean activity of node . We then segmented the time series into non-overlapping segments of varying lengths . We considered a broad range of temporal windows, from to , in order to robustly capture scaling behavior across multiple timescales.
For each timescale , we computed , the root-mean-square of the detrended cumulative signal within each segment, averaged over segments.
Finally, we fitted a power law of the form . The value of the exponent denotes the presence or absence of long-range temporal correlations. A value between 0.5 and 1.0 is indicative of long range temporal correlations, while values close to 0.5 denote an uncorrelated process.
For very long recordings, the DFA algorithm can be extremely slow. To overcome this problem, we implemented the DFA on randomly chosen 120 s segments of model and empirical datasets.
Avalanche analysis
Avalanche detection in electrophysiological datasets
In line with previous studies, we binarized electrophysiological imaging datasets by setting to 1 deflections in local field potentials that exceeded three standard deviations below the mean.64,91,92We then detected, at each timepoint, bursts of temporally contiguous coordinated activity in these binarized time series. Specifically, a new avalanche is instantiated if at least one of the constituent elements becomes active. The avalanche propagates until none of the constituent elements are active. The size of an avalanche is defined by the number of active constituent elements, and the duration of an avalanche is defined by the period of its activity.
Avalanche detection in calcium imaging datasets
In line with previous studies, we binarized calcium imaging datasets by setting to 1 deflections in calcium concentration that exceeded three standard deviations above the mean. 34 The standard method for avalanche detection fails for brain-wide cellular resolution data because the large number of cells produce a single never-ending avalanche. In line with recent work, we used a method to detect spatially contiguous avalanches from binarized zebrafish calcium imaging time series. 34 More specifically, we detected clusters of simultaneously active and spatially contiguous neurons. We used the MATLAB function bwconncomp to find these clusters. We then formed neuronal avalanches by detecting clusters that shared cells at adjacent timepoints. In this way, we followed the spatiotemporal structure of each avalanche as it started, propagated, and ended.
Power law fitting to avalanche distributions
We assessed the presence of power-law scaling in avalanche distributions, by adopting the methods of Clauset et al., 58implemented by Rubinov et al. 93 Specifically, we denoted the probability density function of avalanche size as .
with a cumulative distribution function
where is avalanche size, is the scaling exponent, and are the lower and upper cut-off sizes and is the generalized Hurwitz zeta function. The functions incorporate an upper cut-off because all empirical distributions are necessarily bounded by system size. 7 We defined the probability distributions for avalanche durations in exactly the same way. We then estimated the exponents of avalanche sizes and durations using the method of maximum likelihood.58,93
Exponent scaling and shape collapses
We quantified power-law exponents between mean avalanche size for a given avalanche duration. We estimated the slope of this power law using linear regression in log-log coordinates. 69 Finally, we quantified avalanche shape collapses by averaging all avalanches of a given duration in a single recording. We rescaled collapsed avalanche shapes to have unit area and avalanche durations to have unit length.
Supplementary Material
Highlights.
Time-resolved correlation reflects a validated estimate of E-I balance
Nullspace-based method samples time series constrained by time-resolved correlation
Time series constrained by time-resolved correlation manifest scale-free phenomena
Aspects of E-I balance induce scale-free phenomena without additional assumptions
ACKNOWLEDGMENTS
We thank Joe Lizier, Jeff Alstott, and James Fitzgerald for discussions that helped motivate this work; Neurotycho and Elizabeth Johnson for sharing data; Leandro Alonso and Adrián Ponce-Alvarez for sharing annotations or code; two anonymous reviewers for helpful suggestions; the NIH (1RF1MH 125933, K22ES028048, F31NS120401), the NSF (2207891), the NHMRC (GNT1095227), the NSFC (32171026), and STI2030-Major Projects (2021ZD 0203700, 2021ZD0204500) for financial support; and AI (DALL E 2) for two images in the graphical abstract.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2023.112254.
REFERENCES
- 1.Buzsáki G, and Mizuseki K (2014). The log-dynamic brain: how skewed distributions affect network operations. Nat. Rev. Neurosci. 15, 264–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.He BJ (2014). Scale-free brain activity: past, present, and future. Trends Cogn. Sci. 18, 480–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Roberts JA, Boonstra TW, and Breakspear M (2015). The heavy tail of the human brain. Curr. Opin. Neurobiol. 31, 164–172. [DOI] [PubMed] [Google Scholar]
- 4.He BJ, Zempel JM, Snyder AZ, and Raichle ME (2010). The temporal structures and functional significance of scale-free brain activity. Neuron 66, 353–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Donoghue T, Haller M, Peterson EJ, Varma P, Sebastian P, Gao R, Noto T, Lara AH, Wallis JD, Knight RT, et al. (2020). Parameterizing neural power spectra into periodic and aperiodic components. Nat. Neurosci. 23, 1655–1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Linkenkaer-Hansen K, Nikouline VV, Palva JM, and Ilmoniemi RJ (2001). Long-range temporal correlations and scaling behavior in human brain oscillations. J. Neurosci. 21, 1370–1377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Beggs JM, and Plenz D (2003). Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Petermann T, Thiagarajan TC, Lebedev MA, Nicolelis MAL, Chialvo DR, and Plenz D (2009). Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl. Acad. Sci. USA 106, 15921–15926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shriki O, Alstott J, Carver F, Holroyd T, Henson RNA, Smith ML, Coppola R, Bullmore E, and Plenz D (2013). Neuronal avalanches in the resting MEG of the human brain. J. Neurosci. 33, 7079–7090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Helfrich RF, Lendner JD, and Knight RT (2021). Aperiodic sleep networks promote memory consolidation. Trends Cogn. Sci. 25, 648–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Isaacson JS, and Scanziani M (2011). How inhibition shapes cortical activity. Neuron 72, 231–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Foster AC, and Kemp JA (2006). Glutamate-and GABA-based CNS therapeutics. Curr. Opin. Pharmacol. 6, 7–17. [DOI] [PubMed] [Google Scholar]
- 13.Chiu CQ, Barberis A, and Higley MJ (2019). Preserving the balance: diverse forms of long-term GABAergic synaptic plasticity. Nat. Rev. Neurosci. 20, 272–281. [DOI] [PubMed] [Google Scholar]
- 14.Sears SM, and Hewett SJ (2021). Influence of glutamate and GABA transport on brain excitatory/inhibitory balance. Exp. Biol. Med. 246, 1069–1083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gao R, Peterson EJ, and Voytek B (2017). Inferring synaptic excitation/inhibition balance from field potentials. Neuroimage 158, 70–78. [DOI] [PubMed] [Google Scholar]
- 16.Podvalny E, Noy N, Harel M, Bickel S, Chechik G, Schroeder CE, Mehta AD, Tsodyks M, and Malach R (2015). A unifying principle underlying the extracellular field potential spectral responses in the human cortex. J. Neurophysiol. 114, 505–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Colombo MA, Napolitani M, Boly M, Gosseries O, Casarotto S, Rosanova M, Brichant JF, Boveroux P, Rex S, Laureys S, et al. (2019). The spectral exponent of the resting EEG indexes the presence of consciousness during unresponsiveness induced by propofol, xenon, and ketamine. Neuroimage 189, 631–644. [DOI] [PubMed] [Google Scholar]
- 18.Waschke L, Donoghue T, Fiedler L, Smith S, Garrett DD, Voytek B, and Obleser J (2021). Modality-specific tracking of attention and sensory statistics in the human electrophysiological spectral exponent. Elife 10, e70068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chini M, Pfeffer T, and Hanganu-Opatz I (2022). An increase of inhibition drives the developmental decorrelation of neural activity. Elife 11, e78811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Trakoshis S, Martínez-Canñada P, Rocchi F, Canella C, You W, Chakrabarti B, Ruigrok AN, Bullmore ET, Suckling J, Markicevic M, et al. (2020). Intrinsic excitation-inhibition imbalance affects medial prefrontal cortex differently in autistic men versus women. Elife 9, e55684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Van Bueren NE, van der Ven SH, Sella F, and Kadosh RC (2022). Explaining and predicting the effects of neurostimulation via neuronal excitation/inhibition. bioRxiv. 10.1101/2022.04.29.489988. [DOI] [Google Scholar]
- 22.Cocchi L, Gollo LL, Zalesky A, and Breakspear M (2017). Criticality in the brain: a synthesis of neurobiology, models and cognition. Prog. Neurobiol. 158, 132–152. [DOI] [PubMed] [Google Scholar]
- 23.OByrne J, and Jerbi K (2022). How critical is brain criticality? Trends Neurosci. 45, 820–837. [DOI] [PubMed] [Google Scholar]
- 24.Shew WL, and Plenz D (2013). The functional benefits of criticality in the cortex. Neuroscientist 19, 88–100. [DOI] [PubMed] [Google Scholar]
- 25.Ma Z, Turrigiano GG, Wessel R, and Hengen KB (2019). Cortical circuit dynamics are homeostatically tuned to criticality in vivo. Neuron 104, 655–664.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Magnasco MO, Piro O, and Cecchi GA (2009). Self-tuned critical anti-Hebbian networks. Phys. Rev. Lett. 102, 258102. [DOI] [PubMed] [Google Scholar]
- 27.Bialek W (2018). Perspectives on theory at the interface of physics and biology. Rep. Prog. Phys. 81, 012601. [DOI] [PubMed] [Google Scholar]
- 28.Fontenele AJ, de Vasconcelos NAP, Feliciano T, Aguiar LAA, Soares-Cunha C, Coimbra B, Dalla Porta L, Ribeiro S, Rodrigues AJ, Sousa N, et al. (2019). Criticality between cortical states. Phys. Rev. Lett. 122, 208101. [DOI] [PubMed] [Google Scholar]
- 29.Solovey G, Alonso LM, Yanagawa T, Fujii N, Magnasco MO, Cecchi GA, and Proekt A (2015). Loss of consciousness is associated with stabilization of cortical activity. J. Neurosci. 35, 10866–10877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kinouchi O, and Copelli M (2006). Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2, 348–351. [Google Scholar]
- 31.Shew WL, Yang H, Petermann T, Roy R, and Plenz D (2009). Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J. Neurosci. 29, 15595–15600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Beggs JM, and Plenz D (2004). Neuronal avalanches are diverse and precise activity patterns that are stable for many hours in cortical slice cultures. J. Neurosci. 24, 5216–5229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ezaki T, Fonseca Dos Reis E, Watanabe T, Sakaki M, and Masuda N (2020). Closer to critical resting-state neural dynamics in individuals with higher fluid intelligence. Commun. Biol. 3, 52–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ponce-Alvarez A, Jouary A, Privat M, Deco G, and Sumbre G (2018). Whole-brain neuronal activity displays crackling noise dynamics. Neuron 100, 1446–1459.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Maturana MI, Meisel C, Dell K, Karoly PJ, D’Souza W, Grayden DB, Burkitt AN, Jiruska P, Kudlacek J, Hlinka J, et al. (2020). Critical slowing down as a biomarker for seizure susceptibility. Nat. Commun. 11, 2172–2212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bédard C, Kröger H, and Destexhe A (2006). Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 97, 118102. [DOI] [PubMed] [Google Scholar]
- 37.Stumpf MPH, and Porter MA (2012). Critical truths about power laws. Science 335, 665–666. [DOI] [PubMed] [Google Scholar]
- 38.Beggs JM, and Timme N (2012). Being critical of criticality in the brain. Front. Physiol. 3, 163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Touboul J, and Destexhe A (2017). Power-law statistics and universal scaling in the absence of criticality. Phys. Rev. E 95, 012413. [DOI] [PubMed] [Google Scholar]
- 40.Destexhe A, and Touboul JD (2021). Is there sufficient evidence for criticality in cortical systems? eNeuro 8. ENEURO.0551–20.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lendner JD, Helfrich RF, Mander BA, Romundstad L, Lin JJ, Walker MP, Larsson PG, and Knight RT (2020). An electrophysiological marker of arousal level in humans. Elife 9, e55092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Diaz MMS, Trejo EJA, Martin DA, Cannas SA, Grigera TS, and Chialvo DR (2021). Similar local neuronal dynamics may lead to different collective behavior. Phys. Rev. E 104, 064309. [DOI] [PubMed] [Google Scholar]
- 43.Tagliazucchi E, von Wegner F, Morzelewski A, Brodbeck V, Jahnke K, and Laufs H (2013). Breakdown of long-range temporal dependence in default mode and attention networks during deep sleep. Proc. Natl. Acad. Sci. USA 110, 15419–15424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lombardi F, Herrmann HJ, and de Arcangelis L (2017). Balance of excitation and inhibition determines 1/f power spectrum in neuronal networks. Chaos 27, 047402. [DOI] [PubMed] [Google Scholar]
- 45.Rubinov M (2022). Circular and unified analysis in network neuroscience. OSF Preprints. 10.31219/osf.io/mdqak. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Parvizi J, and Kastner S (2018). Promises and limitations of human intracranial electroencephalography. Nat. Neurosci. 21, 474–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ahrens MB, Orger MB, Robson DN, Li JM, and Keller PJ (2013). Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nat. Methods 10, 413–420. [DOI] [PubMed] [Google Scholar]
- 48.Yanagawa T, Chao ZC, Hasegawa N, and Fujii N (2013). Large-scale information flow in conscious and unconscious states: an ECoG study in monkeys. PLoS One 8, e80845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Johnson EL, Adams JN, Solbakk AK, Endestad T, Larsson PG, Ivanovic J, Meling TR, Lin JJ, and Knight RT (2018). Dynamic frontotemporal systems process space and time in working memory. PLoS Biol. 16, e2004274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Goodale SE, González HFJ, Johnson GW, Gupta K, Rodriguez WJ, Shults R, Rogers BP, Rolston JD, Dawant BM, Morgan VL, and Englot DJ (2020). Resting-state SEEG may help localize epileptogenic brain regions. Neurosurgery 86, 792–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mu Y, Bennett DV, Rubinov M, Narayan S, Yang CT, Tanimoto M, Mensh BD, Looger LL, and Ahrens MB (2019). Glia accumulate evidence that actions are futile and suppress unsuccessful behavior. Cell 178, 27–43.e19. [DOI] [PubMed] [Google Scholar]
- 52.Cohen L (1998). The generalization of the Wiener-Khinchin theorem. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98, 3, pp. 1577–1580. [Google Scholar]
- 53.Carpena P, and Coronado AV (2022). On the autocorrelation function of 1/f noises. Mathematics 10, 1416. [Google Scholar]
- 54.Hagihira S (2015). Changes in the electroencephalogram during anaesthesia and their physiological basis. Br. J. Anaesth. 115, i27–i31. [DOI] [PubMed] [Google Scholar]
- 55.Liu X, Yanagawa T, Leopold DA, Chang C, Ishida H, Fujii N, and Duyn JH (2015). Arousal transitions in sleep, wakefulness, and anesthesia are characterized by an orderly sequence of cortical events. Neuroimage 116, 222–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Schnider TW, Minto CF, Shafer SL, Gambus PL, Andresen C, Goodale DB, and Youngs EJ (1999). The influence of age on propofol pharmacodynamics. Anesthesiology 90, 1502–1516. [DOI] [PubMed] [Google Scholar]
- 57.Alonso LM, Solovey G, Yanagawa T, Proekt A, Cecchi GA, and Magnasco MO (2019). Single-trial classification of awareness state during anesthesia by measuring critical dynamics of global brain activity. Sci. Rep. 9, 4927–5011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Clauset A, Shalizi CR, and Newman MEJ (2009). Power-law distributions in empirical data. SIAM Rev. 51, 661–703. [Google Scholar]
- 59.Linkenkaer-Hansen K, Nikulin VV, Palva JM, Kaila K, and Ilmoniemi RJ (2004). Stimulus-induced change in long-range temporal correlations and scaling behaviour of sensorimotor oscillations. Eur. J. Neurosci. 19, 203–211. [DOI] [PubMed] [Google Scholar]
- 60.Liégeois R, Laumann TO, Snyder AZ, Zhou J, and Yeo BTT (2017). Interpreting temporal fluctuations in resting-state functional connectivity MRI. Neuroimage 163, 437–455. [DOI] [PubMed] [Google Scholar]
- 61.Ligeois R, Yeo BT, and Van De Ville D (2021). Interpreting null models of resting-state functional MRI dynamics: not throwing the model out with the hypothesis. Neuroimage 243, 118518. [DOI] [PubMed] [Google Scholar]
- 62.Prichard D, and Theiler J (1994). Generating surrogate data for time series with several simultaneously measured variables. Phys. Rev. Lett. 73, 951–954. [DOI] [PubMed] [Google Scholar]
- 63.Deco G, Jirsa VK, and McIntosh AR (2011). Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat. Rev. Neurosci. 12, 43–56. [DOI] [PubMed] [Google Scholar]
- 64.Solovey G, Miller KJ, Ojemann JG, Magnasco MO, and Cecchi GA (2012). Self-regulated dynamical criticality in human ECoG. Front. Integr. Neurosci. 6, 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Alonso LM, Proekt A, Schwartz TH, Pryor KO, Cecchi GA, and Magnasco MO (2014). Dynamical criticality during induction of anesthesia in human ECoG recordings. Front. Neural Circuits 8, 20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Peterson EJ, Rosen BQ, Campbell AM, Belger A, and Voytek B(2017). 1/f neural noise is a better predictor of schizophrenia than neural oscillations. bioRxiv. 10.1101/113449. [DOI] [PubMed] [Google Scholar]
- 67.Voytek B, Kramer MA, Case J, Lepage KQ, Tempesta ZR, Knight RT, and Gazzaley A (2015). Age-related changes in 1/f neural electrophysiological noise. J. Neurosci. 35, 13257–13265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Peng C-K, Havlin S, Stanley HE, and Goldberger AL (1995). Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 5, 82–87. [DOI] [PubMed] [Google Scholar]
- 69.Friedman N, Ito S, Brinkman BAW, Shimono M, DeVille REL, Dahmen KA, Beggs JM, and Butler TC (2012). Universal critical dynamics in high resolution neuronal avalanche data. Phys. Rev. Lett. 108, 208102. [DOI] [PubMed] [Google Scholar]
- 70.Sethna JP, Dahmen KA, and Myers CR (2001). Crackling noise. Nature 410, 242–250. [DOI] [PubMed] [Google Scholar]
- 71.Rubinov M (2016). Constraints and spandrels of interareal connectomes. Nat. Commun. 7, 13812–13911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Elsayed GF, and Cunningham JP (2017). Structure in neural population recordings: an expected byproduct of simpler phenomena? Nat. Neurosci. 20, 1310–1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Gros C (2021). A devil’s advocate view on self-organized brain criticality. J. Phys. Complex. 2, 031001. [Google Scholar]
- 74.Davis GW (2006). Homeostatic control of neural activity: from phenomenology to molecular design. Annu. Rev. Neurosci. 29, 307–323. [DOI] [PubMed] [Google Scholar]
- 75.Honey CJ, Thesen T, Donner TH, Silbert LJ, Carlson CE, Devinsky O, Doyle WK, Rubin N, Heeger DJ, and Hasson U (2012). Slow cortical dynamics and the accumulation of information over long timescales. Neuron 76, 423–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Murray JD, Bernacchia A, Freedman DJ, Romo R, Wallis JD, Cai X, Padoa-Schioppa C, Pasternak T, Seo H, Lee D, and Wang XJ (2014). A hierarchy of intrinsic timescales across primate cortex. Nat. Neurosci. 17, 1661–1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Chaudhuri R, Knoblauch K, Gariel M-A, Kennedy H, and Wang X-J (2015). A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex. Neuron 88, 419–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Gao R, van den Brink RL, Pfeffer T, and Voytek B (2020). Neuronal timescales are functionally dynamic and shaped by cortical microarchitecture. Elife 9, e61277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Raut RV, Snyder AZ, Mitra A, Yellin D, Fujii N, Malach R, and Raichle ME (2021). Global waves synchronize the brains functional systems with fluctuating arousal. Sci. Adv. 7, eabf2709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Zimmern V (2020). Why brain criticality is clinically relevant: a scoping review. Front. Neural Circuits 14, 54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Voytek B, and Knight RT (2015). Dynamic network communication as a unifying neural basis for cognition, development, aging, and disease. Biol. Psychiatry 77, 1089–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Oostenveld R, Fries P, Maris E, and Schoffelen J-M (2011). FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Schneider T, and Neumaier A (2001). Algorithm 808: ARfitA Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Trans. Math. Softw. 27, 58–65. [Google Scholar]
- 84.Nagasaka Y, Shimoda K, and Fujii N (2011). Multidimensional recording (MDR) and data sharing: an ecological open research and educational platform for neuroscience. PLoS One 6, e22561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Johnson E (2018). Intracranial EEG Recordings of Medial Temporal, Lateral Frontal, and Orbitofrontal Regions in 10 Human Adults Performing a Visuospatial Working Memory Task. http://crcns.org/data-sets/fcx/fcx-2.
- 86.Laub AJ (2005). Matrix Analysis for Scientists and Engineers (SIAM).
- 87.Smith RL (1984). Efficient Monte Carlo procedures for generating points uniformly distributed over bounded regions. Oper. Res. 32, 1296–1308. [Google Scholar]
- 88.Schreiber T (1998). Constrained randomization of time series data. Phys. Rev. Lett. 80, 2105–2108. [Google Scholar]
- 89.Neumaier A, and Schneider T (2001). Estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Trans. Math. Softw. 27, 27–57. [Google Scholar]
- 90.Wen H, and Liu Z (2016). Separating fractal and oscillatory components in the power spectrum of neurophysiological signal. Brain Topogr. 29, 13–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Palva JM, Zhigalov A, Hirvonen J, Korhonen O, Linkenkaer-Hansen K, and Palva S (2013). Neuronal long-range temporal correlations and avalanche dynamics are correlated with behavioral scaling laws. Proc. Natl. Acad. Sci. USA 110, 3585–3590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Varley TF, Sporns O, Puce A, and Beggs J (2020). Differential effects of propofol and ketamine on critical brain dynamics. PLoS Comput. Biol. 16, e1008418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Rubinov M, Sporns O, Thivierge J-P, and Breakspear M (2011). Neurobiologically realistic determinants of self-organized criticality in networks of spiking neurons. PLoS Comput. Biol. 7, e1002038. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data from this study are available upon request.
The main analysis code is publicly available (key resources table).
Any additional information is available from the lead contact upon request.
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Software and algorithms | ||
|
| ||
| MATLAB | The Mathworks | www.mathworks.com |
| Python | Python Software | www.python.org |
| Custom software | This study |
github.com/AdityaNanda/time_resolved_correlation
https://doi.org/10.5281/zenodo.7604194 |
| FieldTrip Toolbox | Oostenveld et al., 201182 | github.com/fieldtrip/fieldtrip |
| FOOOF | Donoghue et al., 20205 | github.com/fooof-tools/fooof |
| ARfit | Schneider et al., 200183 | github.com/tapios/arfit |
| Voluseg | Mu et al.51 | github.com/mikarubi/voluseg |


